Flow Separation Control and Aeroacoustic Effects of a Leading-Edge Slat over a Wind Turbine Blade
Abstract
1. Introduction
- (a)
- Turbulent boundary layer interaction with trailing edge, commonly known as trailing edge noise.
- (b)
- The flow separation at stalls induces detached eddies that impact the loading distribution over the blade surface, known as stall separation noise.
- (c)
- The high- and low-pressure difference in the blade’s pressure and suction side drives the flow field at the blade’s tip, creating a trailing tip vortex [17].
2. Methodology
2.1. Problem Definition
2.2. Turbulence Model
2.2.1. Steady-State Study Model
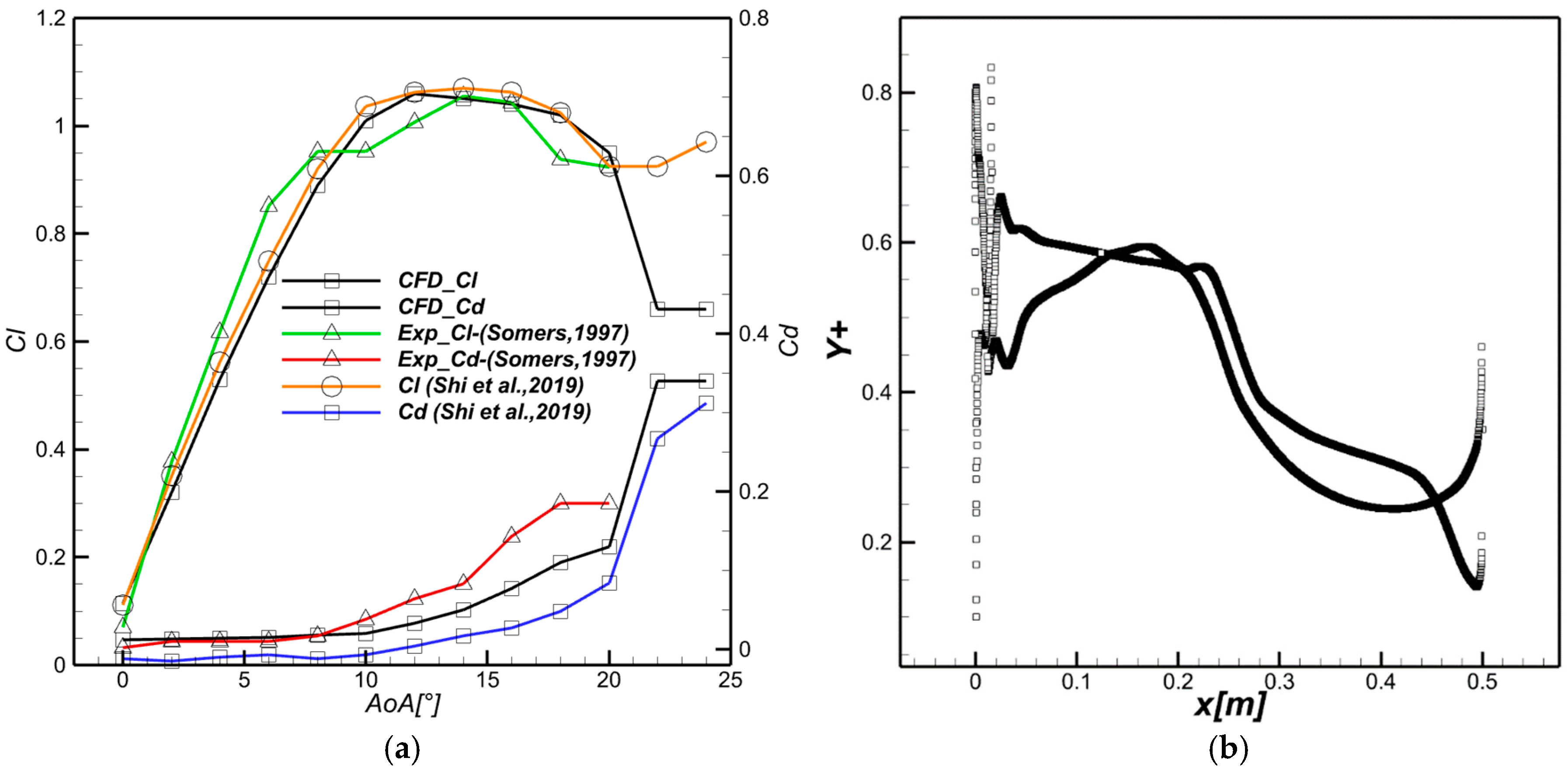
2.2.2. Model Validation
2.2.3. IDDES for Aeroacoustics
2.3. Ffowcs Williams and Hawkings Equation
2.4. Computational Grid and Boundary Conditions
2.4.1. Steady Two-Dimensional Study
2.4.2. Unsteady Three-Dimensional Study
Computational Gid
Computational Approach
3. Results and Discussion
3.1. Two-Dimensional Aerodynamic Study
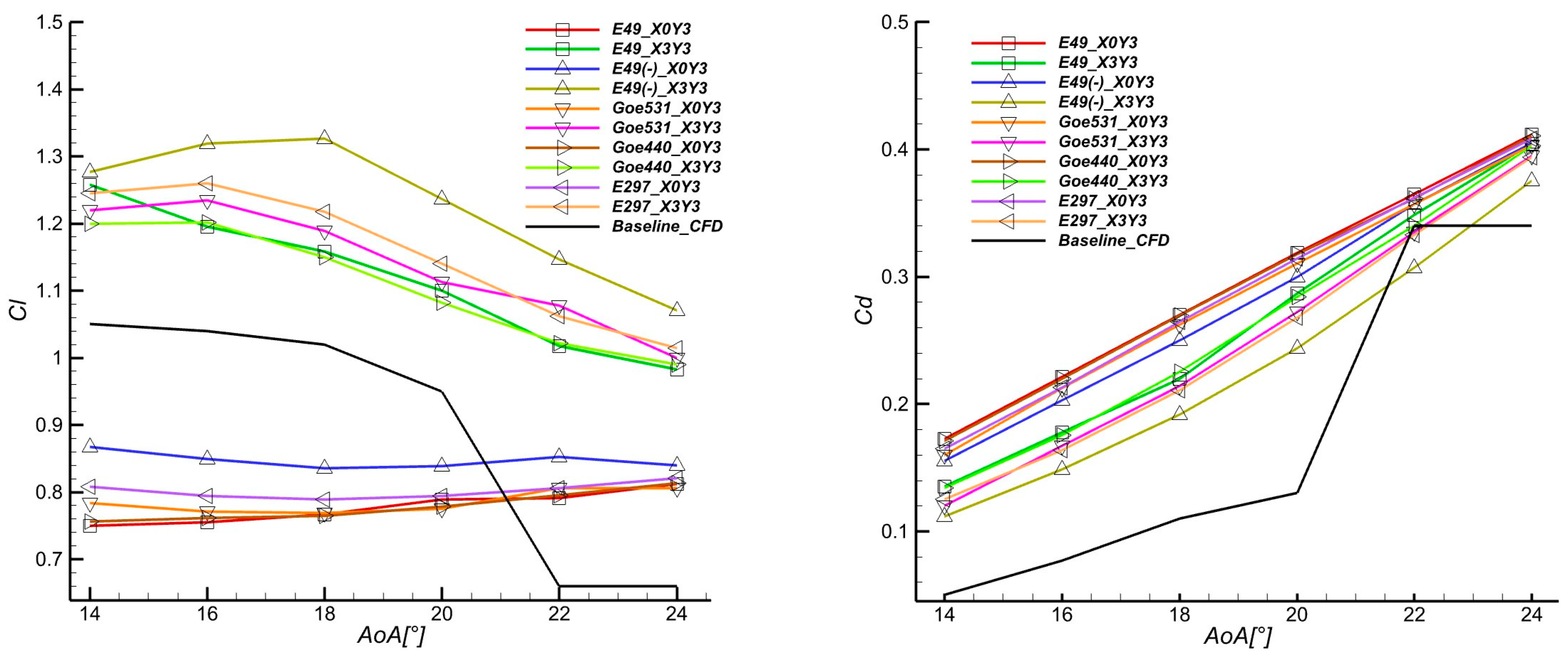
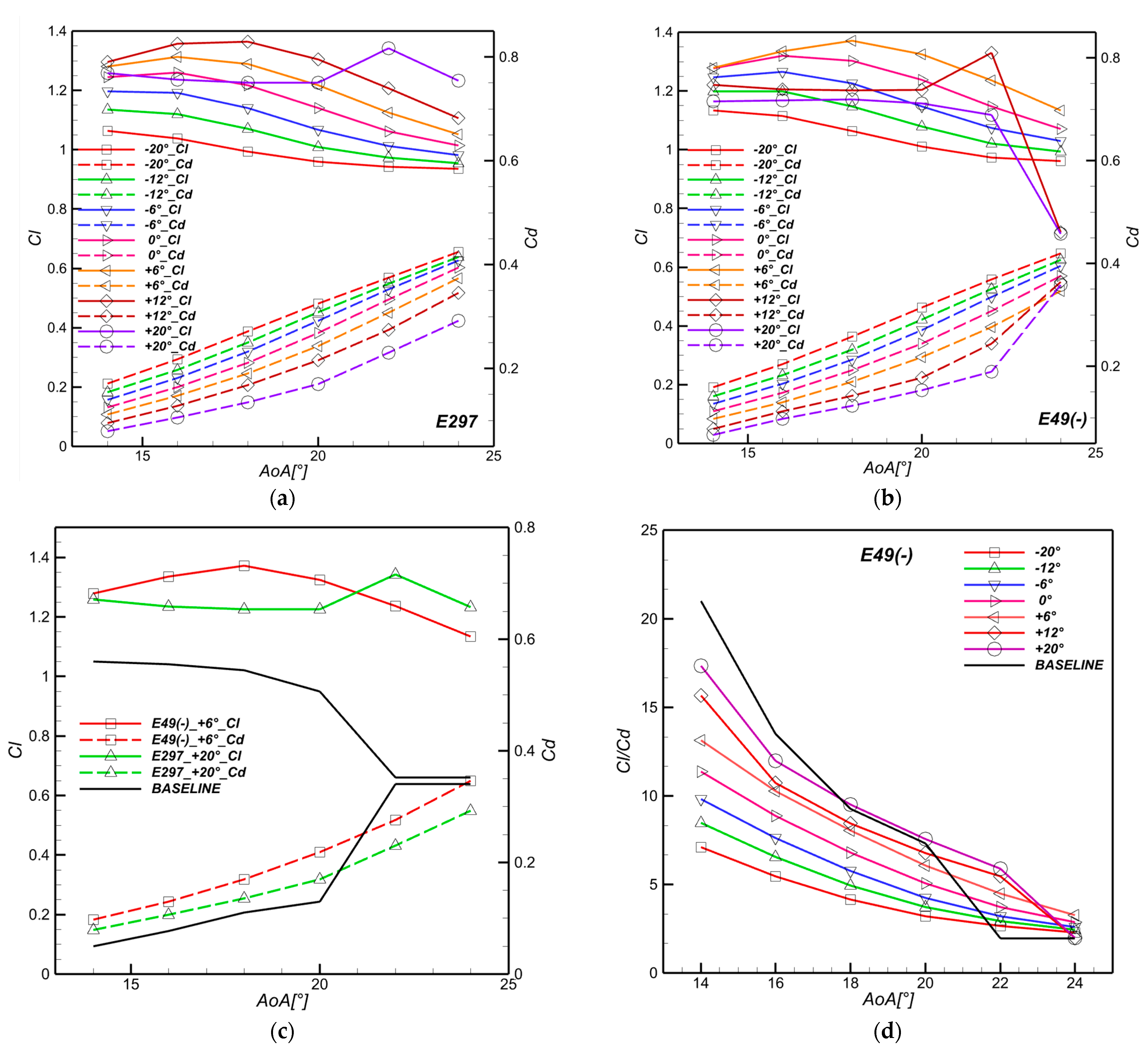
3.1.1. Aerodynamic Coefficients
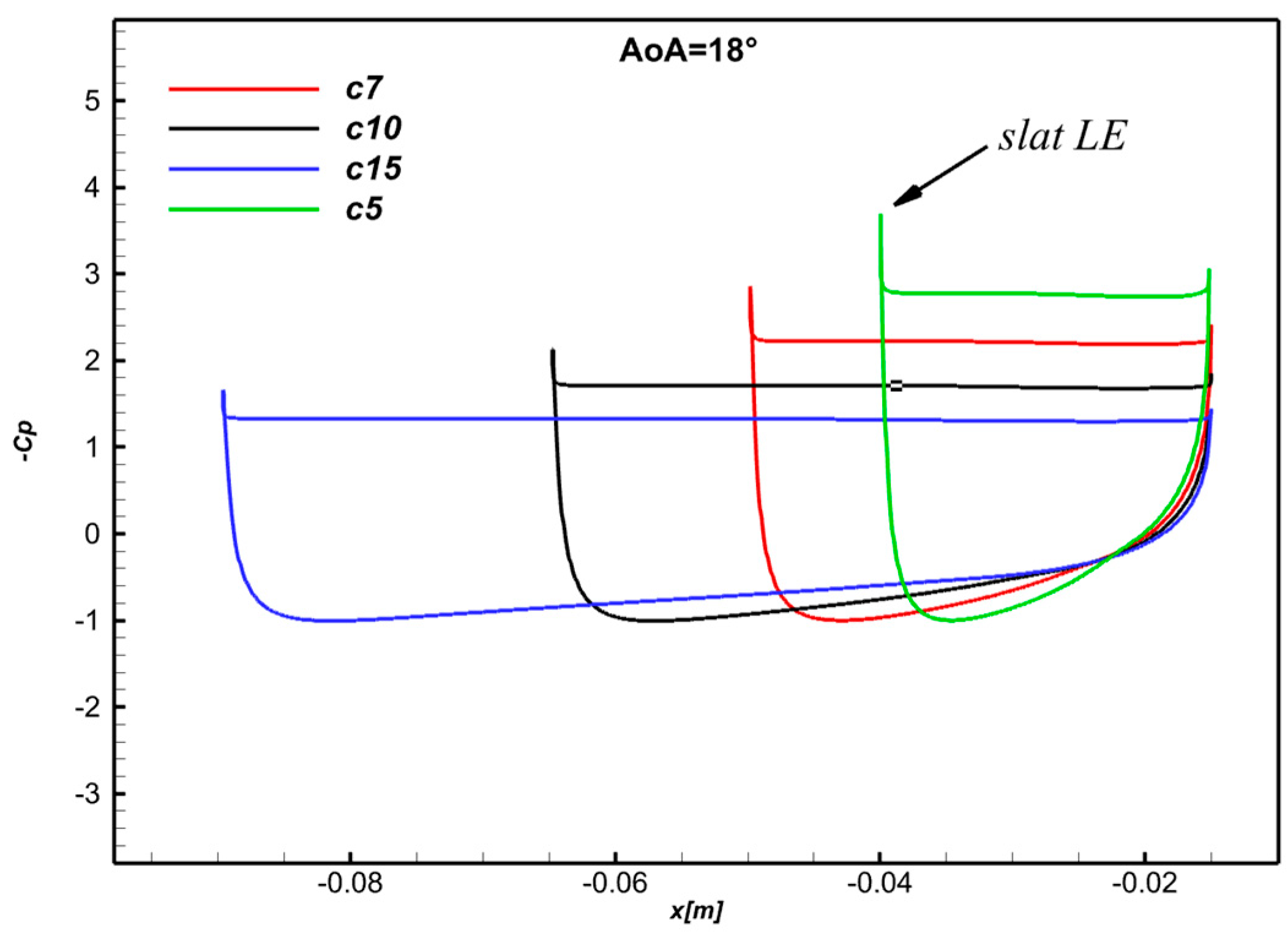
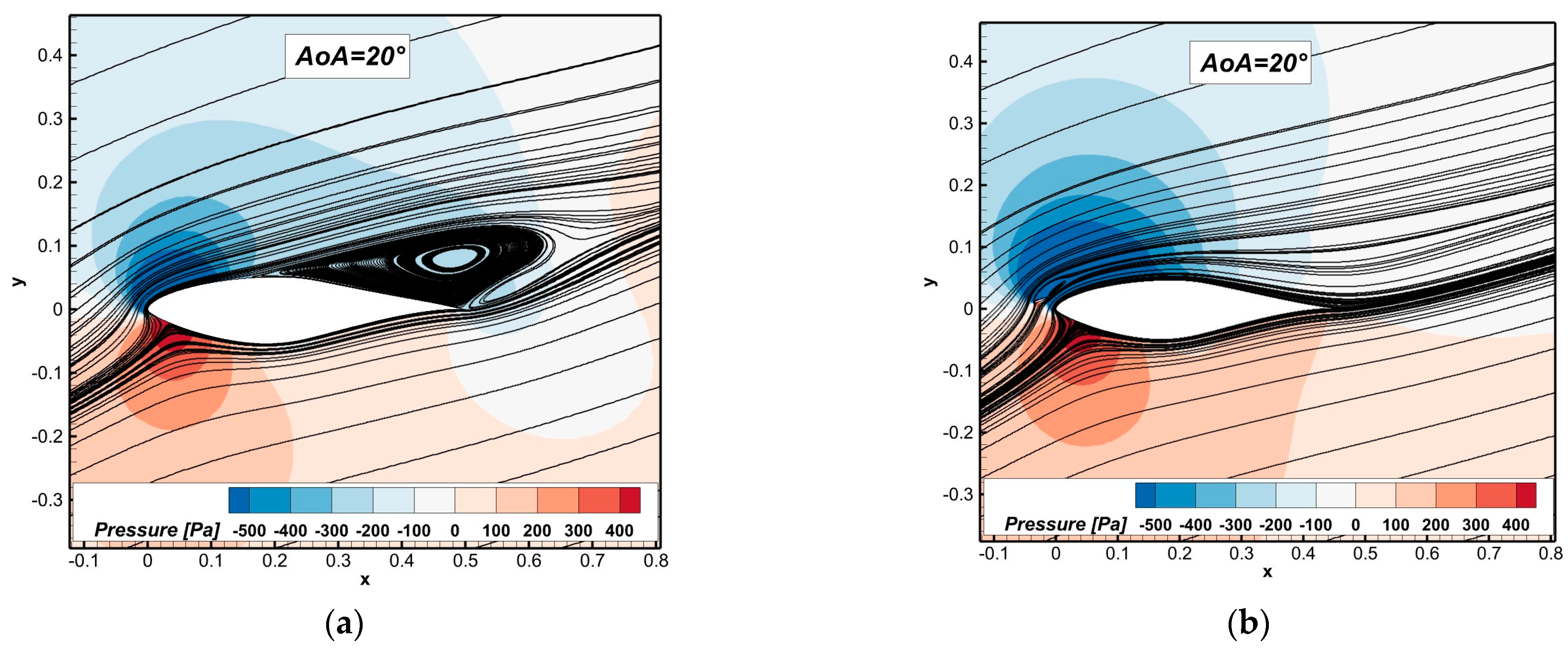
3.1.2. Pressure Contours and Velocity Streamlines
3.2. Three-Dimensional Aerodynamic and Aeroacoustic Study
3.2.1. Grid Requirements for LES
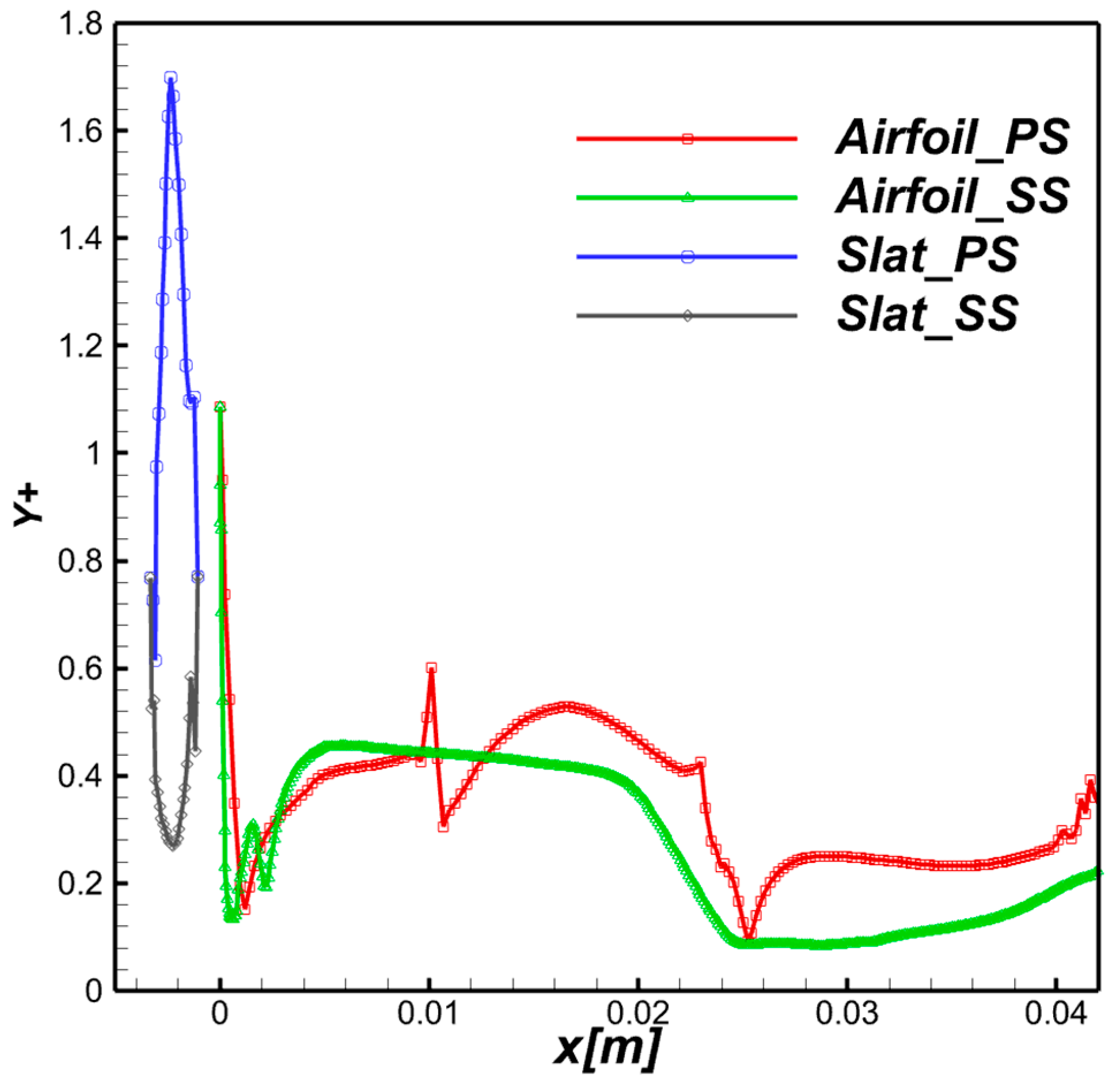
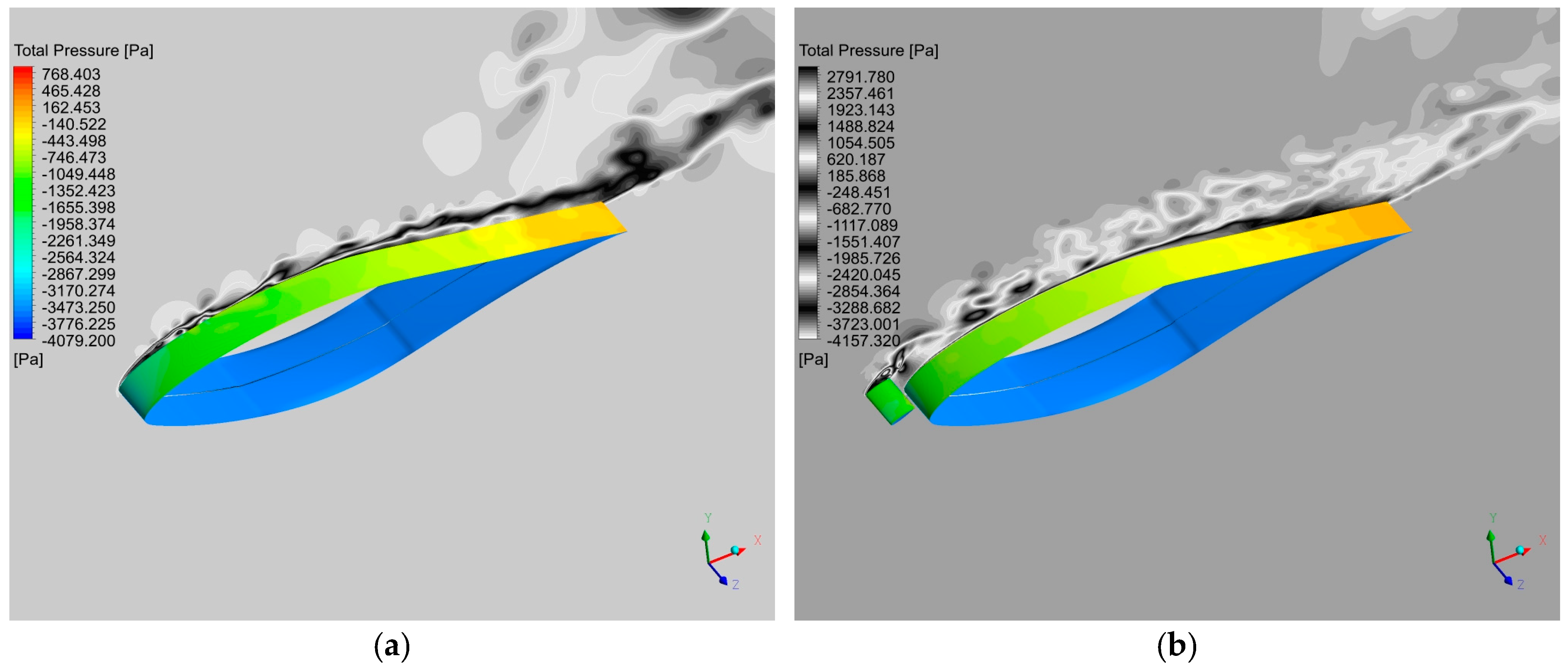
3.2.2. Aerodynamic Analysis and Surface Flow Topology
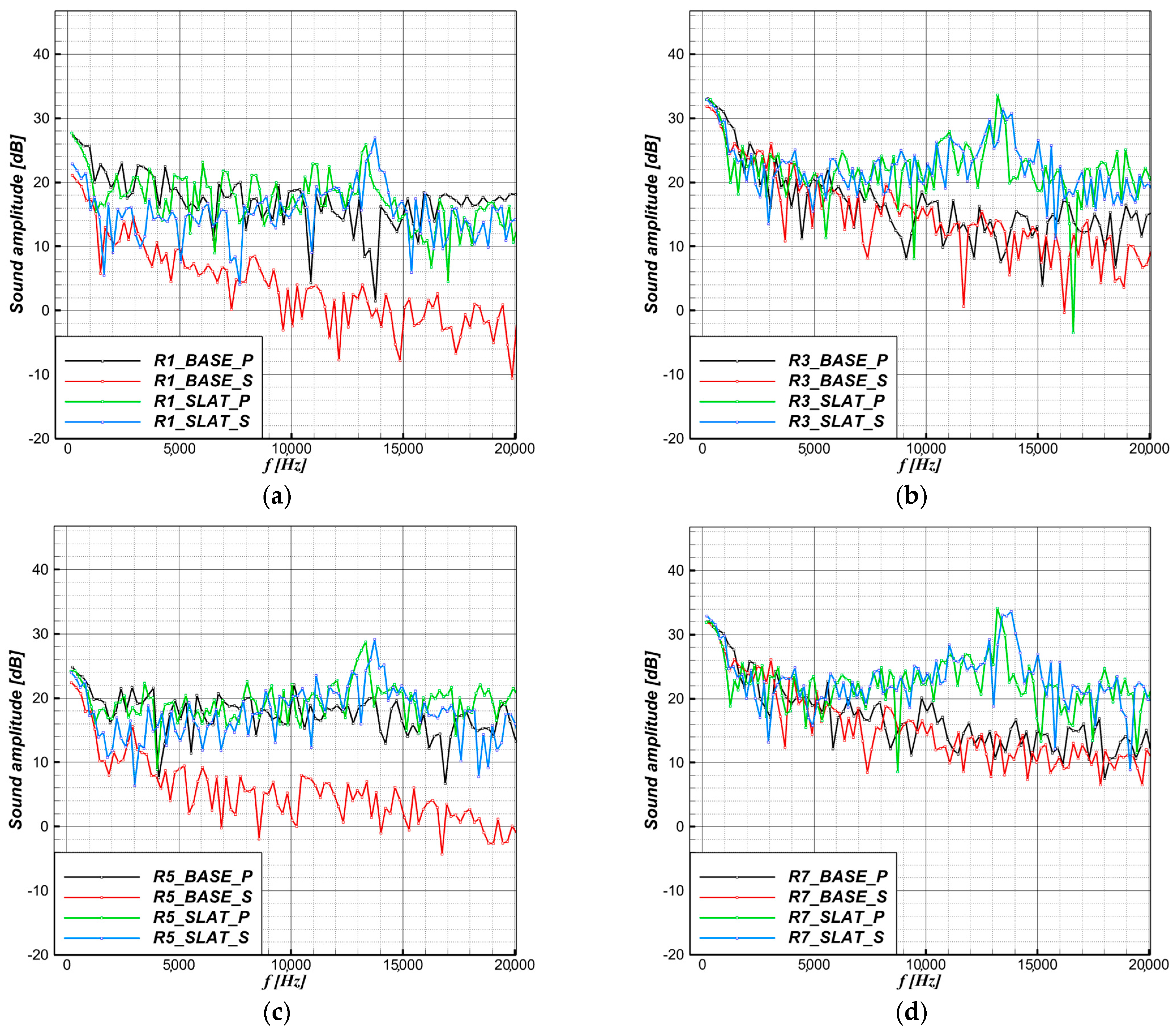
3.2.3. Aeroacoustic Analysis
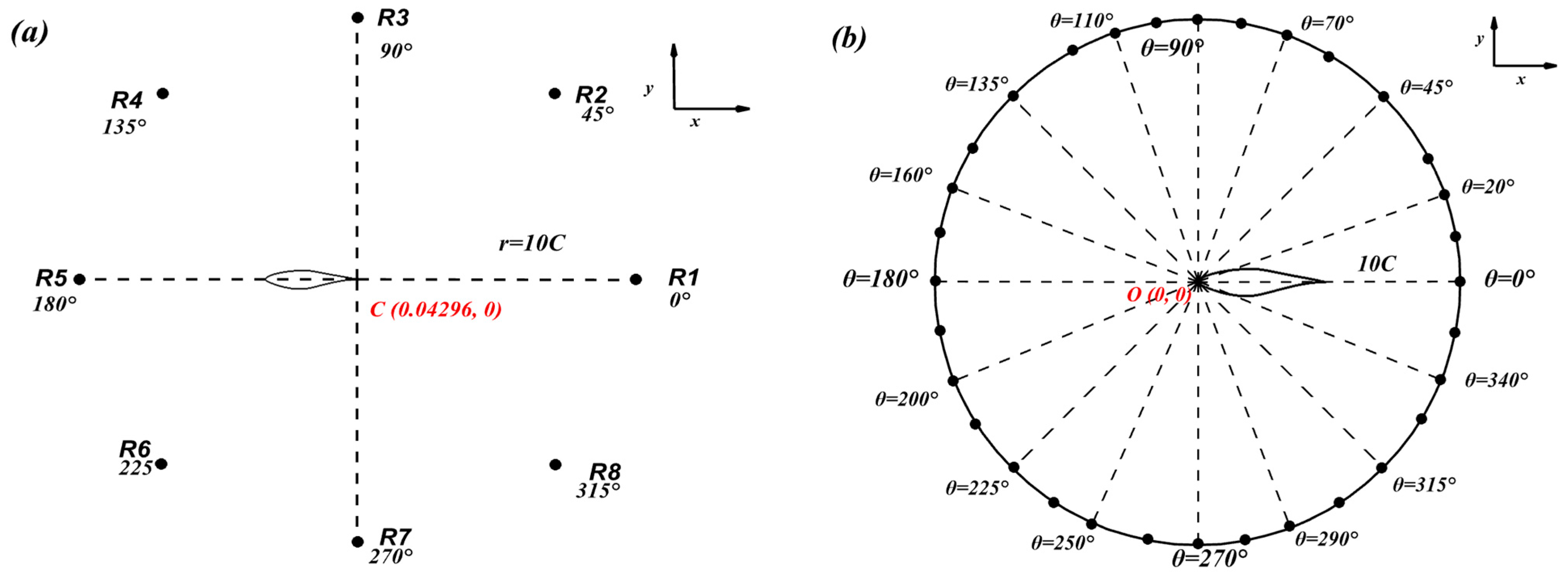
Validation of Acoustic Results
Slat Acoustics Influence
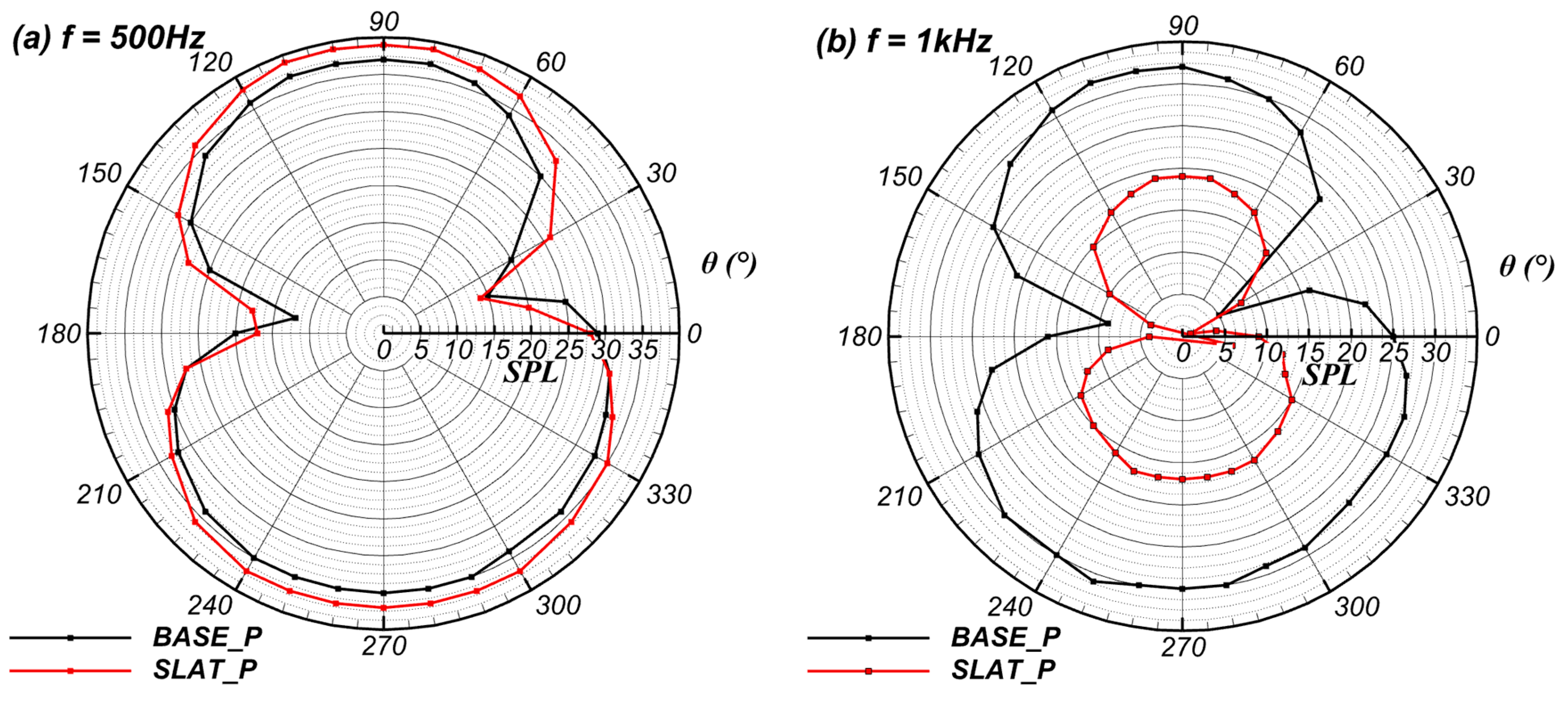
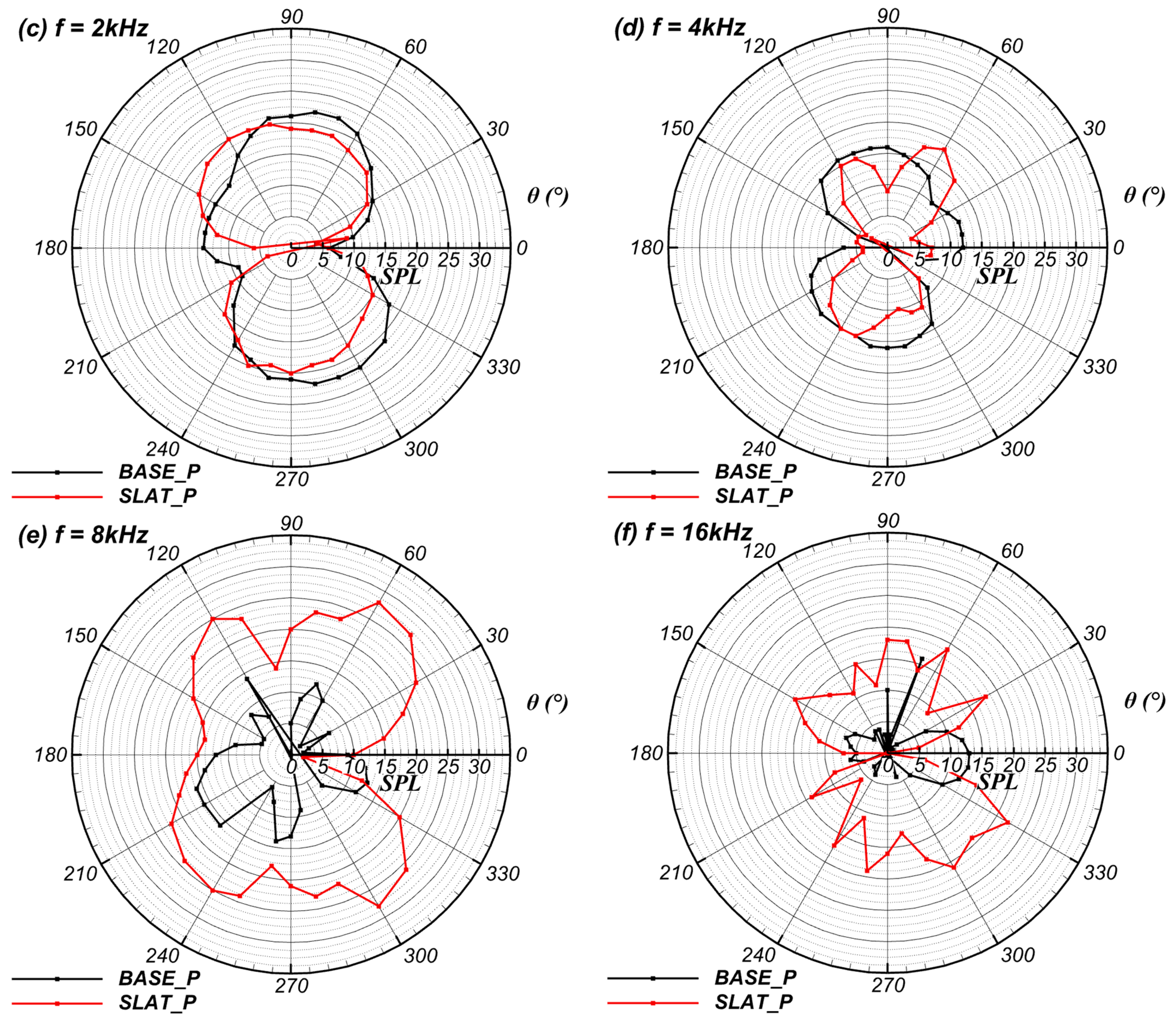
Directivity
4. Conclusions
- (a)
- Negative and symmetric cambers are revealed to be the most influential slat profiles, with the superiority of symmetric slats at high AoAs up to 111% lift increment.
- (b)
- There is inverse proportionality between slat chord length and aerodynamic betterment.
- (c)
- The slat positive inclination angles (nose down position) are superior to negative angles.
- (d)
- Finally, the position of the slat is important as it influences the gap between the slat trailing edge and the main element leading edge; thus, the wake distributes and has an influence on separation over the main element. Pressure and flow streamlines allow us to understand the pressure distribution altered by the slat that leads to flow attachment to the blade suction surface.
- (a)
- The leading-edge slat modifies the eddies topology over the airfoil suction surface, and the fluid accelerates near the wall.
- (b)
- The slat convergent–divergent-shaped gap with the airfoil leading edge induces flow acceleration, adding flow resistance to the adverse pressure gradient. Eddies are shed from the slat trailing edge, suction surface, and tip.
- (c)
- The slat contributes to low- and high-frequency noise, understandably due to pressure fluctuations calculated over additional slat surfaces against the baseline case.
- (d)
- The FWH permeable approach successfully captured additional noise components compared to the solid-surface approach. However, the expected drawbacks related to turbulence crossing and surface extent influence the permeable surface approach. Turbulent boundary layer eddies interaction with the slat and main element trailing edge substantially contributes to the overall noise spectra.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| pressure perturbation | |
| loading noise | |
| thickness noise | |
| eddy viscosity | |
| AoA | angle of attack |
| c | slat chord |
| C | airfoil chord |
| c0 | sound velocity |
| CAA | computational aeroacoustics |
| Cd | drag coefficient |
| CDES,k-ε | DES model constant |
| CDES,k-ω | DES model constant |
| CFL | Courant–Friedrichs–Lewy |
| Cl | lift coefficient |
| DES | detached eddy simulation |
| dw | distance to the wall |
| fd | hyperbolic blending function |
| FFT | fast Fourier transform |
| FWH | Ffowcs Williams–Hawkings |
| FWHp | permeable FWH |
| G(x,t; y,τ) | Green’s function |
| H(f) | Heaviside function |
| hx, hy, hz | cell sizes |
| IDDES | improved detached delayed eddy simulation |
| KARI | Korean Aerospace Research Institute |
| LES | large eddy simulation |
| LES_IQ | Index Of Resolution Quality |
| LK-ω SST | K-ω SST turbulent length scale |
| LLES | characteristic turbulent length LES |
| LLM | log layer mismatch |
| LRANS | characteristic turbulent length RANS |
| M | Mach number |
| Pij | viscous stress tensor |
| RANS | Reynolds Averaged Navier–Stokes |
| Re | Reynolds number |
| S-A | Spalart–Allmaras |
| SPL | sound pressure level |
| ß | slat inclination angle |
| Tij | stress tensor |
| U | free stream velocity |
| URANS | unsteady RANS |
| Vcell | grid cell volume |
| X | slat horizontal position |
| Y | slat vertical position |
| y+ | dimensionless distance |
| Δ | filter length |
| δ | Dirac’s delta function |
| δBL | boundary layer thickness |
| δij | Kronecker Delta |
| Δt | time step size |
| Δx | chordwise cell size |
| Δy | wall normal cell size |
| Von Karman constant | |
| Λ | turbulent length scale |
| ρ | fluid density |
| molecular viscosity |
References
- Akhter, M.Z.; Omar, F.K. Review of Flow-Control Devices for Wind-Turbine Performance Enhancement. Energies 2021, 14, 1268. [Google Scholar] [CrossRef]
- Jenkins, N.; Burton, T.; Bossanyi, E.; Sharpe, D.; Graham, M. Introduction. In Wind Energy Handbook 3e; Jenkins, N., Burton, T., Bossanyi, E., Sharpe, D., Graham, M., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2021; pp. 1–10. [Google Scholar]
- Chang, P.K. CHAPTER I—Introduction to the Problems of Flow Separation. In Separation of Flow; Chang, P.K., Ed.; Elsevier Science & Technology: Pergamon, Turkey, 1970; pp. 1–54. [Google Scholar]
- Corten, G.P. Flow Separation on Wind Turbine Blades. Ph.D. Thesis, University of Utrecht, Utrecht, The Netherlands, 2001. [Google Scholar]
- Aramendia, I.; Fernandez-Gamiz, U.; Ramos-Hernanz, J.A.; Sancho, J.; Lopez-Guede, J.M.; Zulueta, E. Flow Control Devices for Wind Turbines. In Energy Harvesting and Energy Efficiency: Technology, Methods, and Applications; Bizon, N., Mahdavi Tabatabaei, N., Blaabjerg, F., Kurt, E., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 629–655. [Google Scholar]
- Kundu, P. Numerical simulation of the effects of passive flow control techniques on hydrodynamic performance improvement of the hydrofoil. Ocean Eng. 2020, 202, 107108. [Google Scholar] [CrossRef]
- Belamadi, R.; Settar, A.; Chetehouna, K.; Ilinca, A. Numerical Modeling of Horizontal Axis Wind Turbine: Aerodynamic Performances Improvement Using an Efficient Passive Flow Control System. Energies 2022, 15, 4872. [Google Scholar] [CrossRef]
- Mustafa Serdar, G.; Kemal, K.; Hacımurat, D.; Halil Hakan, A. Traditional and New Types of Passive Flow Control Techniques to Pave the Way for High Maneuverability and Low Structural Weight for UAVs and MAVs. In Autonomous Vehicles; George, D., Ed.; IntechOpen: Rijeka, Croatia, 2020; Chapter 7. [Google Scholar]
- Bourgois, S.A. Experimental Study of Separation over Airfoils: Analysis and Control. Etude Expérimentale du Décollement Sur profils D’aile: Analyse et Contrôle. Ph.D. Thesis, Université de Poitiers, Poitiers, France, 2006. [Google Scholar]
- Manso Jaume, A.; Wild, J. Aerodynamic Design and Optimization of a High-Lift Device for a Wind Turbine Airfoil. In Proceedings of the New Results in Numerical and Experimental Fluid Mechanics X, Braunschweig, Germany, 8–9 November 2016; pp. 859–869. [Google Scholar]
- Wang, H.; Jiang, X.; Chao, Y.; Li, Q.; Li, M.; Zheng, W.; Chen, T. Effects of leading edge slat on flow separation and aerodynamic performance of wind turbine. Energy 2019, 182, 988–998. [Google Scholar] [CrossRef]
- Genç, M.S.; Kaynak, Ü.; Lock, G.D. Flow over an aerofoil without and with a leading-edge slat at a transitional Reynolds number. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2009, 223, 217–231. [Google Scholar] [CrossRef]
- Ullah, T.; Javed, A.; Abdullah, A.N.; Ali, M.; Uddin, E. Computational evaluation of an optimum leading-edge slat deflection angle for dynamic stall control in a novel urban-scale vertical axis wind turbine for low wind speed operation. Sustain. Energy Technol. Assess. 2020, 40, 100748. [Google Scholar] [CrossRef]
- Smith, A.M.O. High-Lift Aerodynamics. J. Aircr. 1975, 12, 501–530. [Google Scholar] [CrossRef]
- Hoerner, S.F.; Borst, H.V. Fluid-Dynamic Lift: Practical Information on Aerodynamic and Hydrodynamic Lift; L.A. Hoerner: Bakersfield, CA, USA, 1985. [Google Scholar]
- Maizi, M.; Mohamed, M.H.; Dizene, R.; Mihoubi, M.C. Noise reduction of a horizontal wind turbine using different blade shapes. Renew. Energy 2018, 117, 242–256. [Google Scholar] [CrossRef]
- Hansen, C.H.; Doolan, C.J.; Hansen, K.L. Noise Generation. In Wind Farm Noise: Measurement, Assessment; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2017; pp. 119–156. [Google Scholar]
- Singer, B.A.; Lockard, D.P.; Brentner, K.S. Computational Aeroacoustic Analysis of Slat Trailing-Edge Flow. AIAA J. 2000, 38, 1558–1564. [Google Scholar] [CrossRef]
- Housman, J.; Stich, G.-D.; Kocheemoolayil, J.; Kiris, C. Predictions of Slat Noise from the 30P30N at High Angles of Attack Using Zonal Hybrid RANS-LES. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019. [Google Scholar]
- Ashton, N.; West, A.; Mendonca, F. Slat Noise Prediction using Hybrid RANS-LES methods on Structured and Unstructured Grids. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Takeda, K.; Zhang, X.; Nelson, P.A. Computational aeroacoustic simulations of leading-edge slat flow. J. Sound Vib. 2004, 270, 559–572. [Google Scholar] [CrossRef]
- Akhter, M.Z.; Jawahar, H.K.; Omar, F.K.; Elnajjar, E. Performance characterization of a slotted wind turbine airfoil featuring passive blowing. Energy Rep. 2024, 11, 720–735. [Google Scholar] [CrossRef]
- Ye, X.; Hu, J.; Zheng, N.; Li, C. Numerical study on aerodynamic performance and noise of wind turbine airfoils with serrated gurney flap. Energy 2023, 262, 125574. [Google Scholar] [CrossRef]
- Lighthill, M.J. On Sound Generated Aerodynamically. I. General Theory. Proc. R. Soc. Lond. Ser. A 1952, 211, 564–587. [Google Scholar] [CrossRef]
- Azevedo, J.L.F.; Lele, S.K.; Wolf, W.R. Convective effects and the role of quadrupole sources for aerofoil aeroacoustics. J. Fluid Mech. 2012, 708, 502–538. [Google Scholar] [CrossRef]
- Kim, J.W.; Turner, J.M. Quadrupole noise generated from a low-speed aerofoil in near- and full-stall conditions. J. Fluid Mech. 2022, 936, A34. [Google Scholar] [CrossRef]
- Yu, C.; Wolf, W.; Lele, S. Quadrupole Noise in Turbulent Wake Interaction Problems. In Proceedings of the 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), Colorado Springs, CO, USA, 4–6 June 2012. [Google Scholar]
- Cho, T.; Kim, C.; Lee, D. Acoustic measurement for 12% scaled model of NREL Phase VI wind turbine by using beamforming. Curr. Appl. Phys. 2010, 10, S320–S325. [Google Scholar] [CrossRef]
- Turner, J.M.; Kim, J.W. Aerofoil dipole noise due to flow separation and stall at a low Reynolds number. Int. J. Heat Fluid Flow 2020, 86, 108715. [Google Scholar] [CrossRef]
- Wagner, C.; Hüttl, T.; Sagaut, P. Large-Eddy Simulation for Acoustics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Williams, J.E.F.; Hawkings, D.L. Sound Generation by Turbulence and Surfaces in Arbitrary Motion. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar]
- Wasala, S.H.; Storey, R.C.; Norris, S.E.; Cater, J.E. Aeroacoustic noise prediction for wind turbines using Large Eddy Simulation. J. Wind Eng. Ind. Aerodyn. 2015, 145, 17–29. [Google Scholar] [CrossRef]
- Francescantonio, P.d. A new boundary integral formulation for the prediction of sound radiation. J. Sound Vib. 1997, 202, 491–509. [Google Scholar] [CrossRef]
- Hajczak, A.; Sanders, L.; Vuillot, F.; Druault, P. Investigation of the Ffowcs-Williams and Hawkings Analogy on an Isolated Landing Gear Wheel. In Proceedings of the 2018 AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Yu, C.; Lele, S. Volume Noise Sources in Turbulent Wake Interaction Problems: True Quadrupole Noise? In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 16–20 June 2014.
- Testa, C.; Porcacchia, F.; Zaghi, S.; Gennaretti, M. Study of a FWH-based permeable-surface formulation for propeller hydroacoustics. Ocean Eng. 2021, 240, 109828. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. In Proceedings of the 4th: Internal Symposium, Turbulence, Heat and Mass Transfer, Antalya, Turkey, 12–17 October 2003; pp. 625–632. [Google Scholar]
- Michel, U.; Eschricht, D.; Greschner, B.; Knacke, T.; Mockett, C.; Thiele, F. Advanced DES Methods and Their Application to Aeroacoustics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 59–76. [Google Scholar]
- Shur, M.; Spalart, P.; Strelets, M.; Travin, A. Detached Eddy Simulation of an Airfoil at High Angle of Attack. In Engineering Turbulence Modelling and Experiments 4; Elsevier Science Ltd.: Oxford, UK, 1999; Volume 4. [Google Scholar]
- Strelets, M. Detached eddy simulation of massively separated flows. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. [Google Scholar]
- Travin, A.; Shur, M.; Spalart, P.; Kh, M.; Strelets, M. Improvement of delayed detached-eddy simulation for LES with wall modelling. Comput. Fluids 2006, 265, 106014. [Google Scholar]
- Shur, M.; Spalart, P.; Strelets, M.; Travin, A. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Davidson, L. Large Eddy Simulations: How to evaluate resolution. Int. J. Heat Fluid Flow 2009, 30, 1016–1025. [Google Scholar] [CrossRef]
- Addad, Y.; Benhamadouche, S.; Laurence, D. The negatively buoyant wall-jet: LES results. Int. J. Heat Fluid Flow 2004, 25, 795–808. [Google Scholar] [CrossRef]
- Celik, I.B.; Cehreli, Z.N.; Yavuz, I. Index of Resolution Quality for Large Eddy Simulations. J. Fluids Eng. 2005, 127, 949–958. [Google Scholar] [CrossRef]
- Hand, M.; Simms, D.; Fingersh, L.; Jager, D.; Cotrell, J.; Schreck, S.; Larwood, S. Unsteady Aerodynamics Experiment Phase VI: Wind Tunnel Test Configurations and Available Data Campaigns; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2001. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Wang, Y.; Li, G.; Shen, S.; Huang, D.; Zheng, Z. Investigation on aerodynamic performance of horizontal axis wind turbine by setting micro-cylinder in front of the blade leading edge. Energy 2018, 143, 1107–1124. [Google Scholar] [CrossRef]
- Shi, X.; Xu, S.; Ding, L.; Huang, D. Passive flow control of a stalled airfoil using an oscillating micro-cylinder. Comput. Fluids 2019, 178, 152–165. [Google Scholar] [CrossRef]
- Riyadh, B.; Djemili, A.; Ilinca, A.; Ramzi, M. Aerodynamic performance analysis of slotted airfoils for application to wind turbine blades. J. Wind Eng. Ind. Aerodyn. 2016, 151, 79–99. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Wu, Z. Aerodynamic characteristic of wind turbine with the leading edge slat and Microtab. Sustain. Energy Technol. Assess. 2022, 52, 101957. [Google Scholar] [CrossRef]
- Somers, D.M. Design and Experimental Results for the S809 Airfoil; National Renewable Energy Lab.: Golden, CO, USA, 1997. [Google Scholar]
- Spalart, P.; Jou, W.H.; Strelets, M.; Allmaras, S. Comments on the Feasibility of LES for Wings, and on a Hybrid RANS/LES Approach. In Advances in DNS/LES: Direct Numerical Simulation and Large Eddy Simulation; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Gritskevich, M.S.; Garbaruk, A.V.; Schütze, J.; Menter, F.R. Development of DDES and IDDES Formulations for the k-ω Shear Stress Transport Model. Flow Turbul. Combust. 2012, 88, 431–449. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M. Adaptation of Eddy-Viscosity Turbulence Models to Unsteady Separated Flow Behind Vehicles. In The Aerodynamics of Heavy Vehicles: Trucks, Buses, and Trains; Springer: Berlin/Heidelberg, Germany, 2004; pp. 339–352. [Google Scholar]
- Huck, V.; Morency, F.; Beaugendre, H. Grid study for Delayed Detached Eddy-Simulation’s grid of a pre-stalled wing. In Proceedings of the CASI Aero 2019-Canadian Aeronautics and Space Institute’s AERO 2019 Conference, Laval, QC, Canada, 14 May 2019. [Google Scholar]
- Xiao, M.; Zhang, Y. Assessment of the SST-IDDES with a shear-layer-adapted subgrid length scale for attached and separated flows. Int. J. Heat Fluid Flow 2020, 85, 108653. [Google Scholar] [CrossRef]
- Gritskevich, M.; Garbaruk, A.; Menter, F. Fine-tuning of DDES and IDDES formulations to the k-ω shear stress transport model. Prog. Flight Phys. 2013, 5, 23–42. [Google Scholar]
- Mockett, C. A Comprehensive Study of Detached-Eddy Simulation. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2009. [Google Scholar]
- Farassat, F. Linear Acoustic Formulas for Calculation of Rotating Blade Noise. AIAA J. 1981, 19, 1122–1130. [Google Scholar] [CrossRef]
- Wagner, S.; Bareiß, R.; Guidati, G. Introduction to Aeroacoustics. In Wind Turbine Noise; Springer: Berlin/Heidelberg, Germany, 1996; pp. 27–65. [Google Scholar]
- Greschner, B.; Thiele, F.; Jacob, M.C.; Casalino, D. Prediction of sound generated by a rod–airfoil configuration using EASM DES and the generalised Lighthill/FW-H analogy. Comput. Fluids 2008, 37, 402–413. [Google Scholar] [CrossRef]
- Spalart, P.; Streett, C. Young-Person’s Guide to Detached-Eddy Simulation Grids. 2001. Available online: https://ntrs.nasa.gov/api/citations/20010080473/downloads/20010080473.pdf (accessed on 3 November 2024).
- Schmidt, S.; Thiele, F. Detached Eddy Simulation of Flow around A-Airfoil. Flow Turbul. Combust. 2003, 71, 261–278. [Google Scholar] [CrossRef]
- Luo, D.; Huang, D.; Sun, X. Passive flow control of a stalled airfoil using a microcylinder. J. Wind Eng. Ind. Aerodyn. 2017, 170, 256–273. [Google Scholar] [CrossRef]
- Mellen, C.; Fröhlich, J.; Rodi, W. Lessons from LESFOIL Project on Large-Eddy Simulation of Flow Around an Airfoil. AIAA J. 2003, 41, 573–581. [Google Scholar] [CrossRef]
- Kaviani, H.R.; Nejat, A. Aerodynamic noise prediction of a MW-class HAWT using shear wind profile. J. Wind Eng. Ind. Aerodyn. 2017, 168, 164–176. [Google Scholar] [CrossRef]
- Aihara, A.; Goude, A.; Bernhoff, H. Numerical prediction of noise generated from airfoil in stall using LES and acoustic analogy. Noise Vib. Worldw. 2021, 52, 295–305. [Google Scholar] [CrossRef]
- Spalart, P.R.; Belyaev, K.V.; Shur, M.L.; Kh Strelets, M.; Travin, A.K. On the differences in noise predictions based on solid and permeable surface Ffowcs Williams–Hawkings integral solutions. Int. J. Aeroacoustics 2019, 18, 621–646. [Google Scholar] [CrossRef]
- Yavuz, T.; Koç, E.; Kılkış, B.; Erol, Ö.; Balas, C.; Aydemir, T. Performance analysis of the airfoil-slat arrangements for hydro and wind turbine applications. Renew. Energy 2015, 74, 414–421. [Google Scholar] [CrossRef]
- Mostafa, W.; Abdelsamie, A.; Sedrak, M.; Thévenin, D.; Mohamed, M. Quantitative impact of a micro-cylinder as a passive flow control on a horizontal axis wind turbine performance. Energy 2021, 244, 122654. [Google Scholar] [CrossRef]
- Bies, D.; Hansen, C.; Kelsall, T. Engineering Noise Control, Fourth Edition. Noise Control Eng. J. 2010, 58, 465. [Google Scholar] [CrossRef]
- Kato, C.; Iida, A.; Takano, Y.; Fujita, H.; Ikegawa, M. Numerical prediction of aerodynamic noise radiated from low Mach number turbulent wake. In Proceedings of the 31st Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1993. [Google Scholar]
- Abdessemed, C.; Bouferrouk, A.; Yao, Y. Aerodynamic and Aeroacoustic Analysis of a Harmonically Morphing Airfoil Using Dynamic Meshing. Acoustics 2021, 3, 177–199. [Google Scholar] [CrossRef]
- De Gennaro, M.; Kuehnelt, H.; Zanon, A. Numerical Prediction of the Tonal Airborne Noise for a NACA 0012 Aerofoil at Moderate Reynolds Number Using a Transitional URANS Approach. Arch. Acoust. 2017, 42, 653–675. [Google Scholar] [CrossRef][Green Version]
- Wagner, S.; Bareiß, R.; Guidati, G. Noise and its Effects. In Wind Turbine Noise; Springer: Berlin/Heidelberg, Germany, 1996; pp. 13–25. [Google Scholar]
- Chen, G.; Yang, X.; Tang, X.; Ding, J.; Weng, P. Effects of slat track on the flow and acoustic field of high-lift devices. Aerosp. Sci. Technol. 2022, 126, 107626. [Google Scholar] [CrossRef]
- Wagner, S.; Bareiß, R.; Guidati, G. Noise Mechanisms of Wind Turbines. In Wind Turbine Noise; Wagner, S., Bareiß, R., Guidati, G., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 67–92. [Google Scholar]
- Glegg, S.; Devenport, W. Chapter 15-Trailing edge and roughness noise. In Aeroacoustics of Low Mach Number Flows; Glegg, S., Devenport, W., Eds.; Academic Press: New York, NY, USA, 2017; pp. 365–395. [Google Scholar]
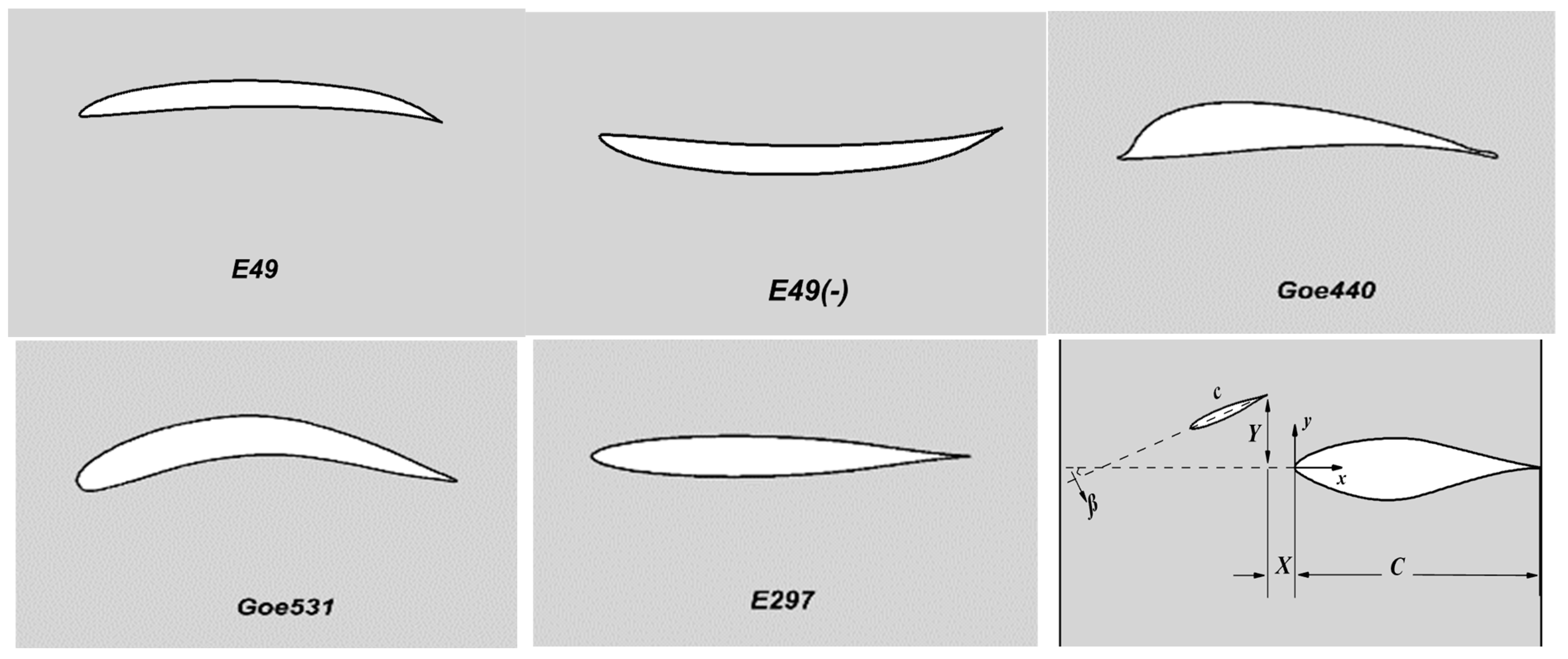

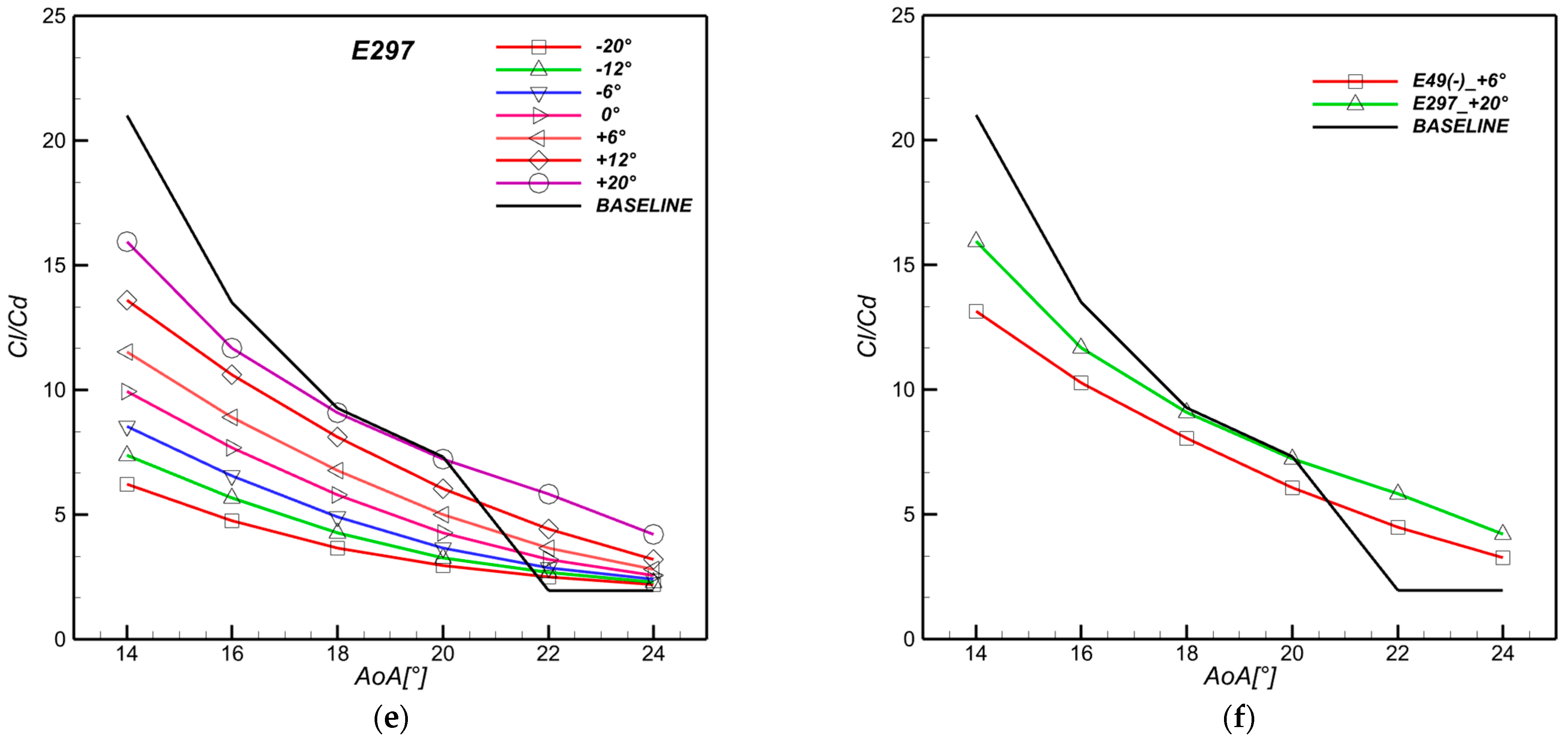
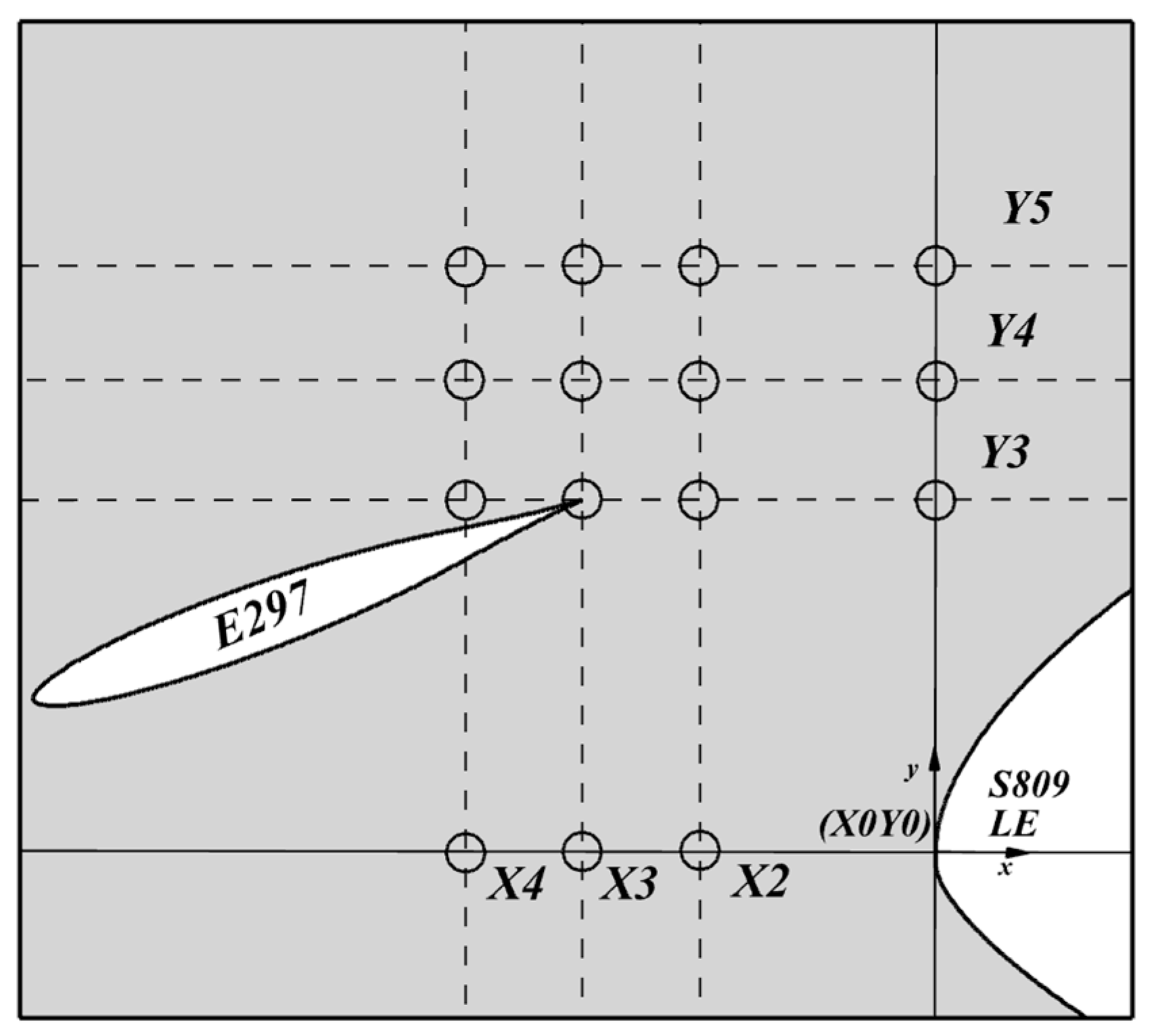
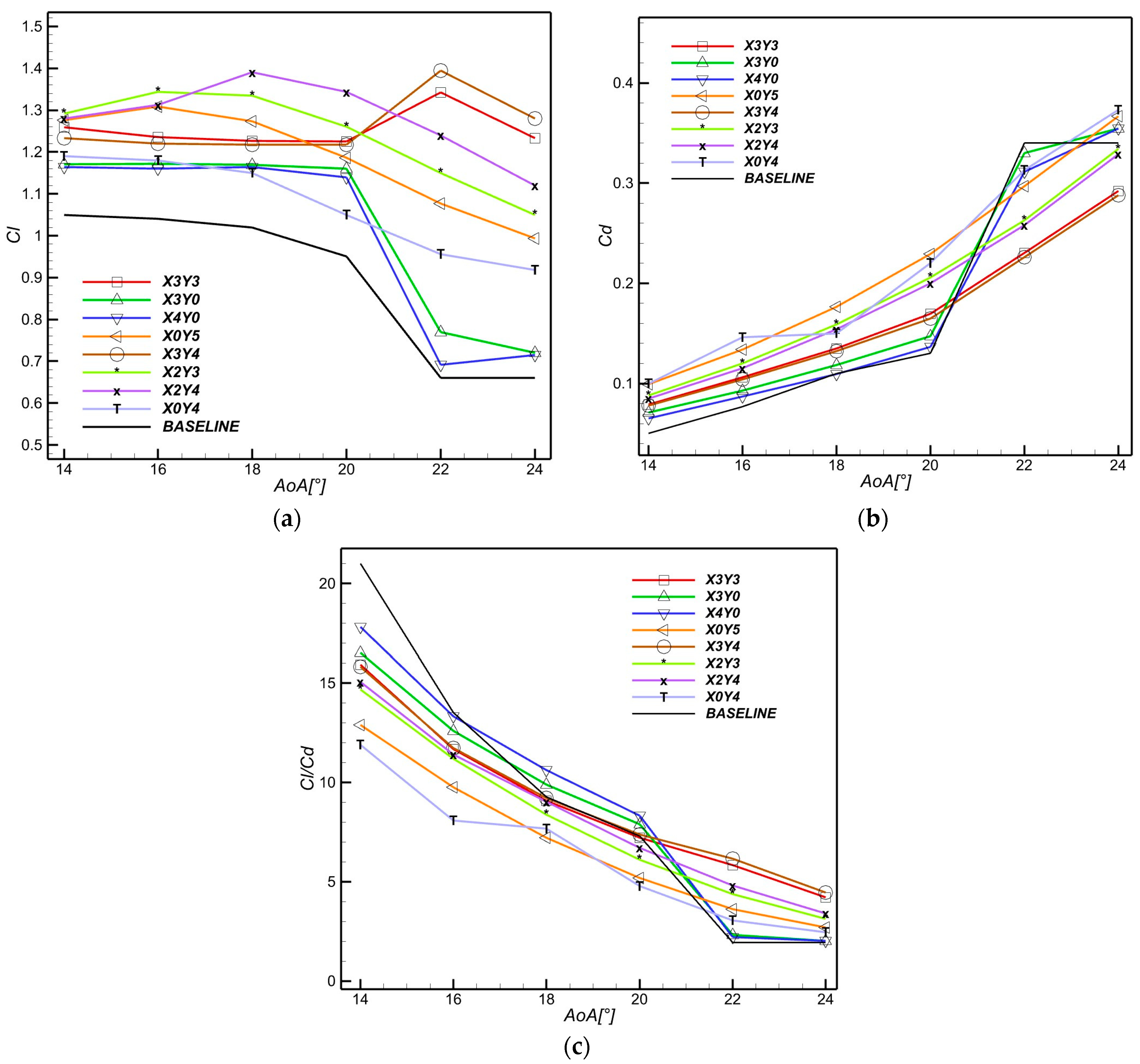
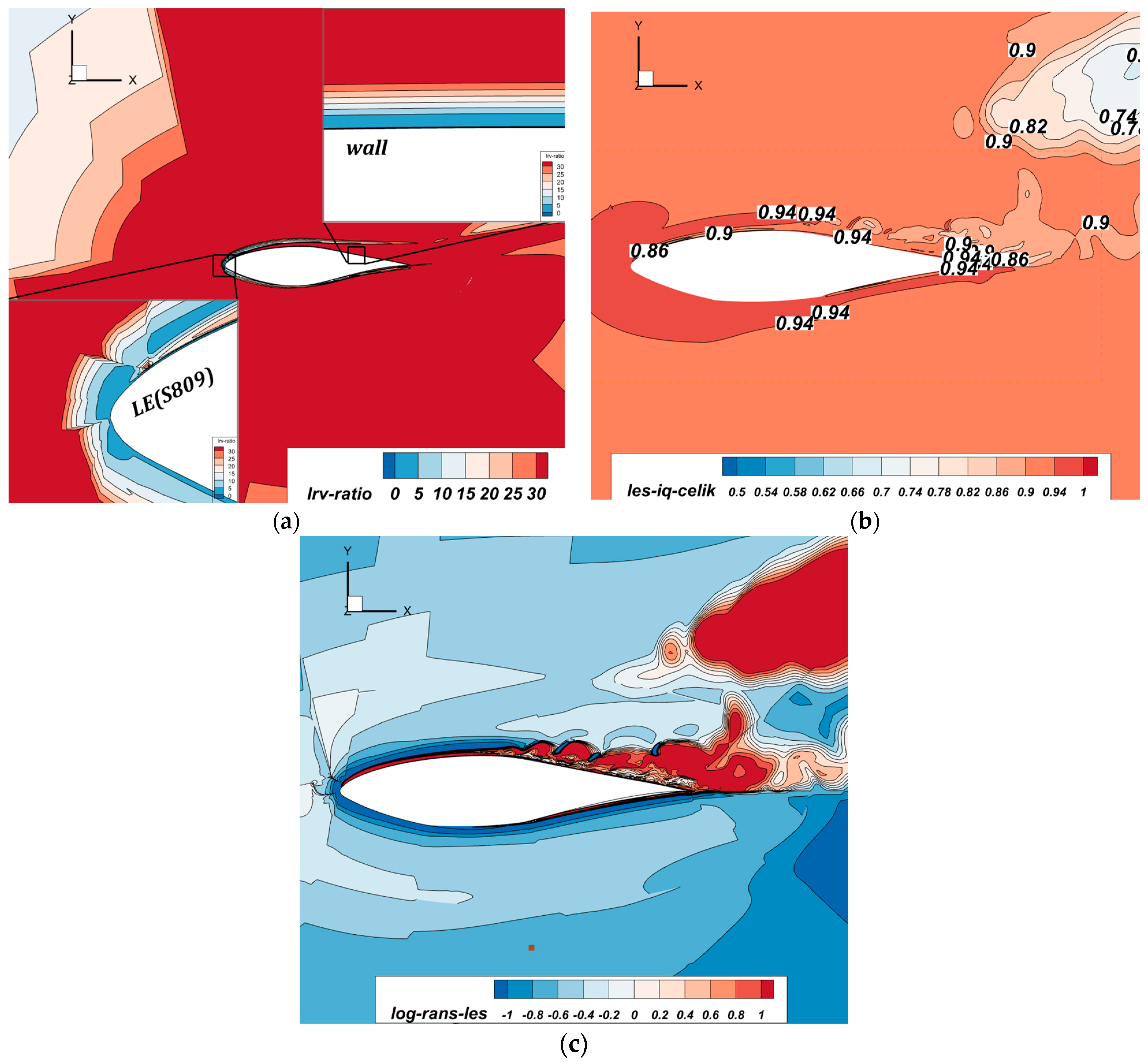

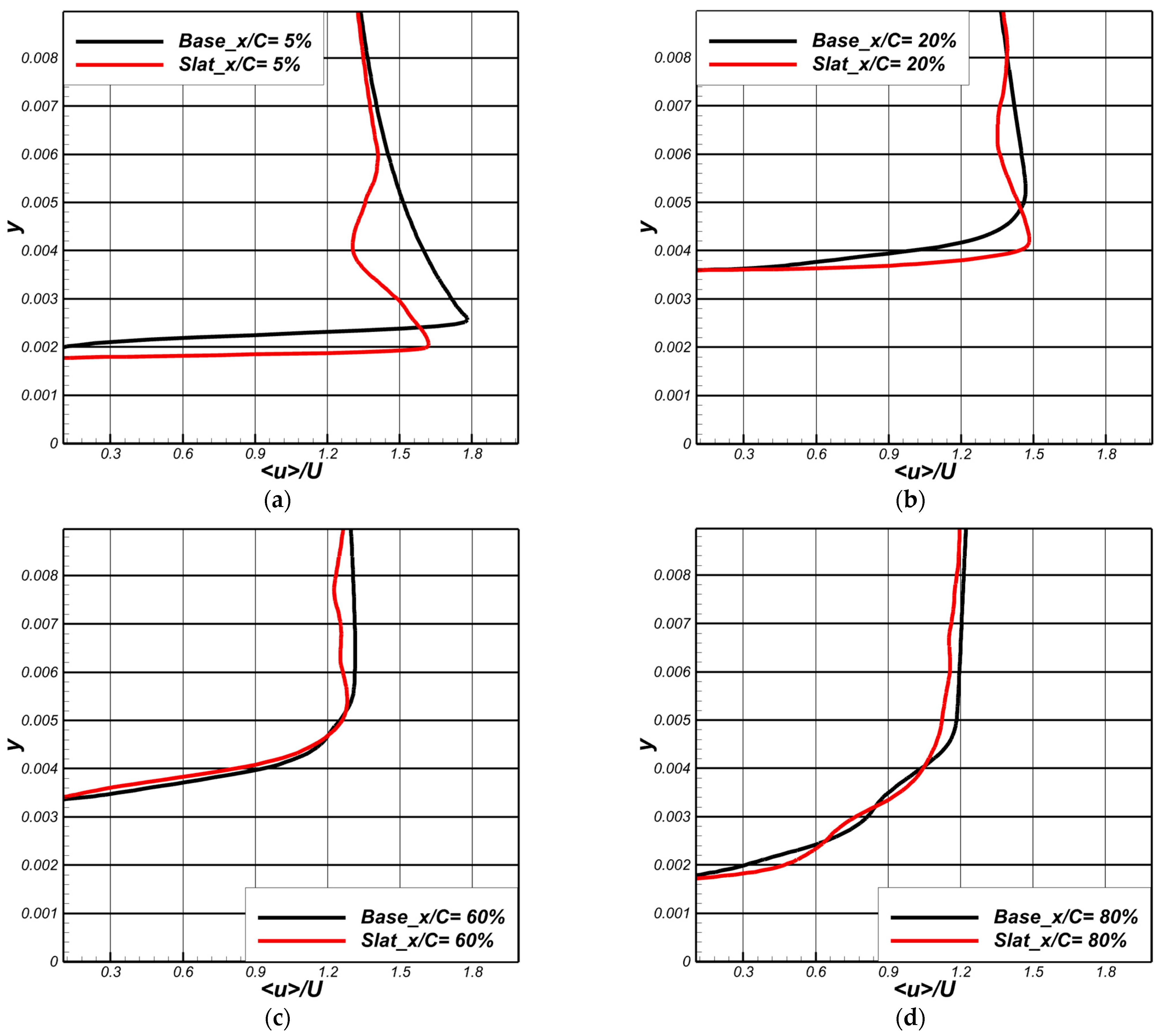
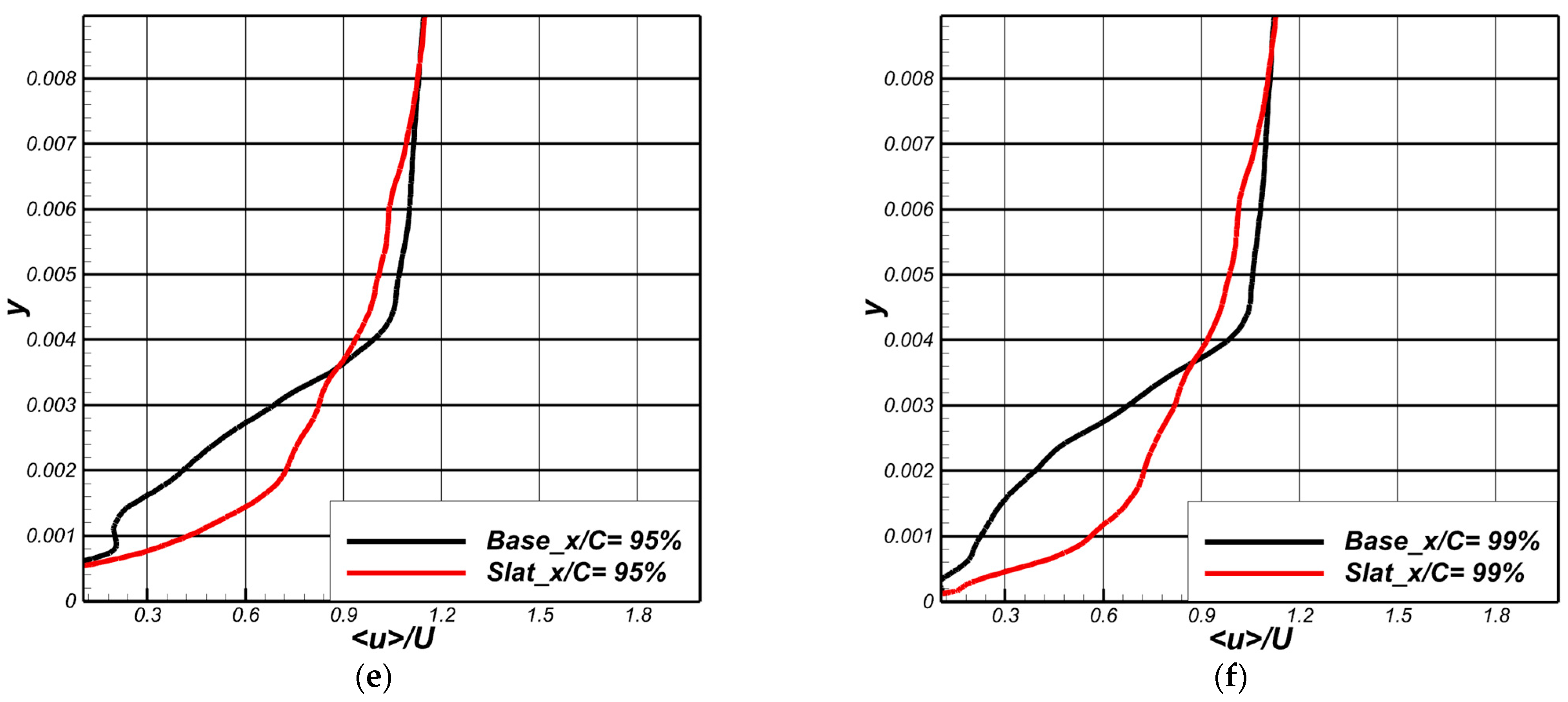



| Slat Profile | Max Thickness (%c) | Max Camber (%c) |
|---|---|---|
| E49 | 7.2 at 38.4%c | 6.5 at 62.2%c |
| Goe440 | 15.3 at 30%c | 9.7 at 40%c |
| Goe531 | 13.8 at19.5%c | 14.7 at 49.3%c |
| E297 | 11.4 at 37.7%c | 0 at 0%c |
| Grid | Number of Cells | Cl | Cd | Size of Wall Adjacent Cell (m) | Growth Factor | Cell Max Size (m) |
|---|---|---|---|---|---|---|
| G1 | 195,287 | 1.06 | 0.116 | 0.00015 | 1.3 | 0.5 |
| G2 | 218,851 | 1.1018 | 0.1154 | 0.00015 | 1.2 | 0.5 |
| G3 | 240,515 | 1.18 | 0.116 | 0.00016 | 1.2 | 0.5 |
| G4 | 244,217 | 1.2193 | 0.1174 | 0.00015 | 1.15 | 0.5 |
| G5 | 283,889 | 1.1395 | 0.1102 | 0.00017 | 1.1 | 0.5 |
| G6 | 291,187 | 1.227 | 0.118 | 0.00016 | 1.1 | 0.5 |
| G7 | 298,783 | 1.2231 | 0.1174 | 0.00015 | 1.1 | 0.5 |
| G8 | 316,611 | 1.2256 | 0.1179 | 0.00013 | 1.1 | 0.5 |
| G9 | 407,087 | 1.2236 | 0.1177 | 0.0002 | 1.05 | 0.6 |
| G10 | 482,477 | 1.2224 | 0.1174 | 0.00015 | 1.05 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouterra, S.; Belamadi, R.; Djemili, A.; Ilinca, A. Flow Separation Control and Aeroacoustic Effects of a Leading-Edge Slat over a Wind Turbine Blade. Energies 2024, 17, 5597. https://doi.org/10.3390/en17225597
Bouterra S, Belamadi R, Djemili A, Ilinca A. Flow Separation Control and Aeroacoustic Effects of a Leading-Edge Slat over a Wind Turbine Blade. Energies. 2024; 17(22):5597. https://doi.org/10.3390/en17225597
Chicago/Turabian StyleBouterra, Sami, Riyadh Belamadi, Abdelouaheb Djemili, and Adrian Ilinca. 2024. "Flow Separation Control and Aeroacoustic Effects of a Leading-Edge Slat over a Wind Turbine Blade" Energies 17, no. 22: 5597. https://doi.org/10.3390/en17225597
APA StyleBouterra, S., Belamadi, R., Djemili, A., & Ilinca, A. (2024). Flow Separation Control and Aeroacoustic Effects of a Leading-Edge Slat over a Wind Turbine Blade. Energies, 17(22), 5597. https://doi.org/10.3390/en17225597









