Synergistic Effects of Energy Storage Systems and Demand-Side Management in Optimizing Zero-Carbon Smart Grid Systems
Abstract
:1. Introduction
1.1. Literature Survey
| Study | RESs | ESS | DSM | Battery-Aging Model | LWF | Entire Green |
|---|---|---|---|---|---|---|
| [29] 2021 | PV and Wind | SLA | RTP | No | No | Diesel |
| [30] 2016 | PV and Wind | SLA | ToU | No | No | Diesel |
| [28] 2022 | PV and Wind | LIB and PHES | RTP | No | Yes | Diesel |
| [2] 2021 | PV and Wind | LIB and PHES | RTP | No | No | Yes |
| [13] 2019 | PV | LIB and SLA and VRFB flywheel | No | No | No | Yes |
| [1] 2023 | PV and Wind | LIB and PHES | RTP | Yes | No | Yes |
| Proposed | PV and Wind | LIB and PHES | RTP | Yes | Yes | Yes |
1.2. Motivation and Objectives
1.3. Innovation and Contribution
- Building an accurate model for different components of the ZCSG.
- Novel hourly models that predict degradation, efficiency, state of charge (SoC), and state of health (SoH) for both LIBs and VRFBs are introduced. These models are based on real-world operating data, providing a more accurate representation of battery performance.
- An optimal tariff-estimation model to enhance the stability and reliability of the ZCSG with the highest benefits for the customers is introduced.
- An accurate load and weather forecast methodology is introduced to estimate the current and future situation of the ESS to make the ZCSG system ready for any abnormal operating conditions.
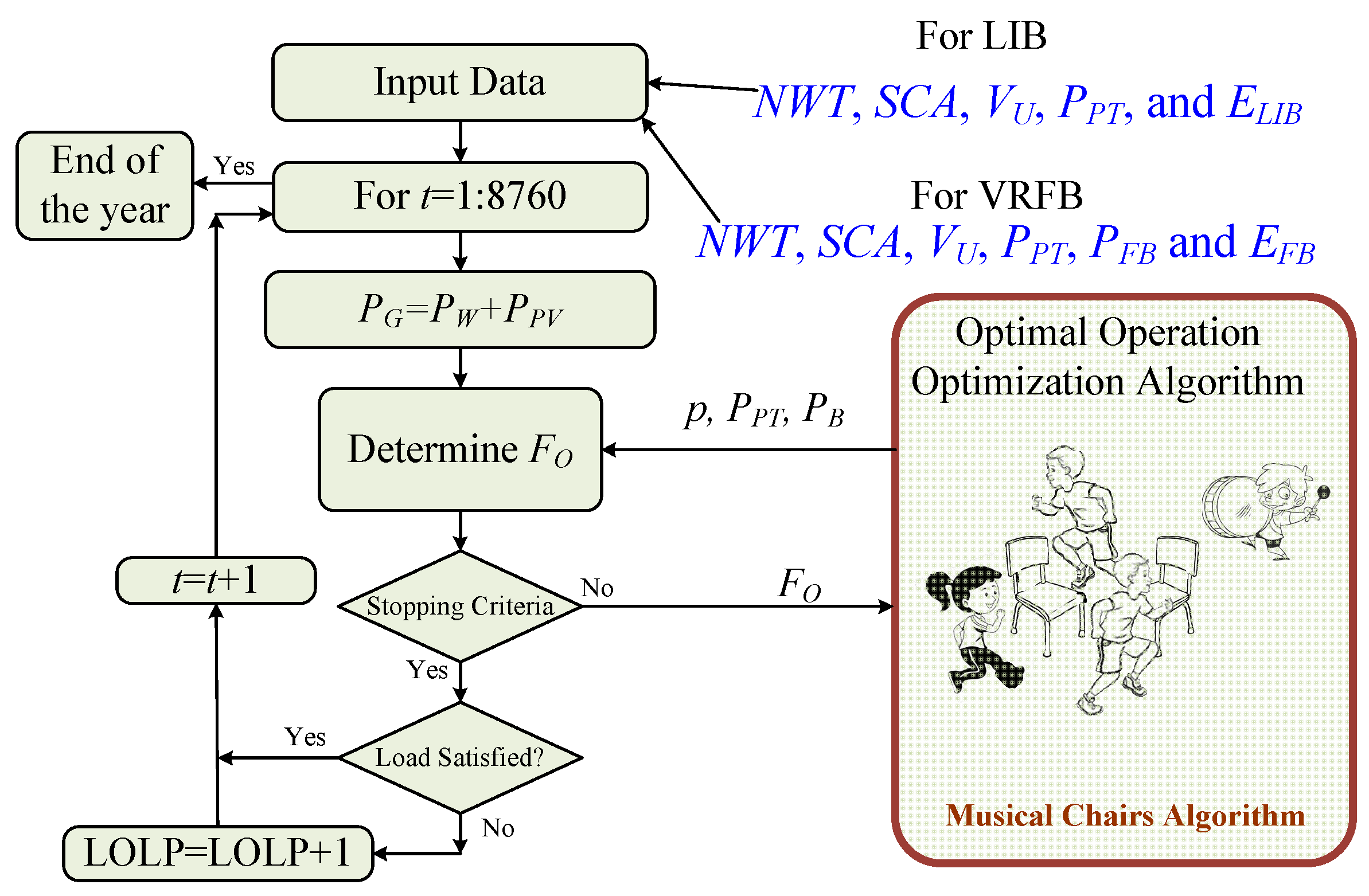
- A recent Musical Chair Algorithm (MCA) strategy is used for hourly optimal power dispatch for fast and accurate convergence compared to several metaheuristic algorithms.
1.4. Study Outlines
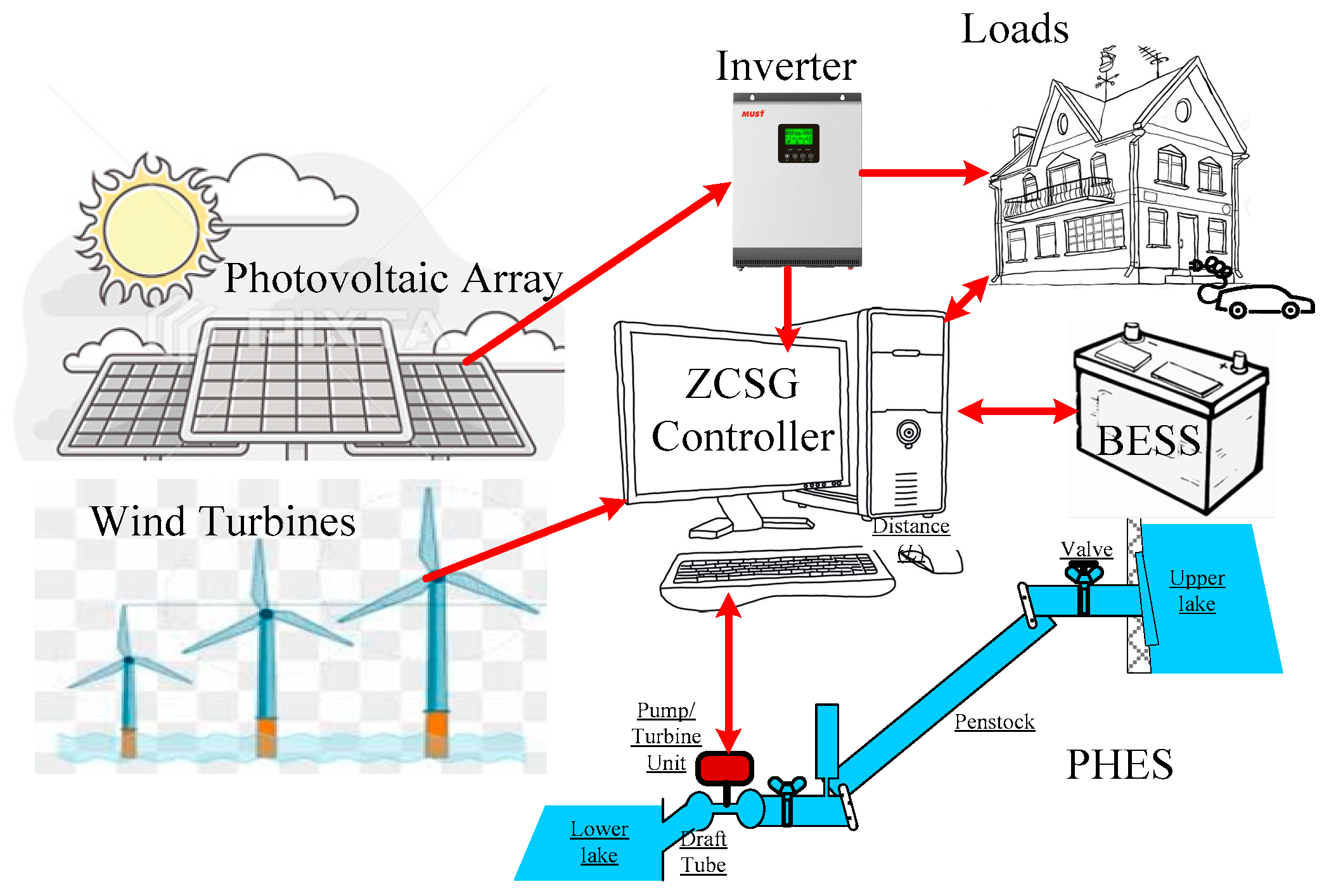
2. Zero-Carbon Smart Grid Configuration
2.1. Energy Storage Systems
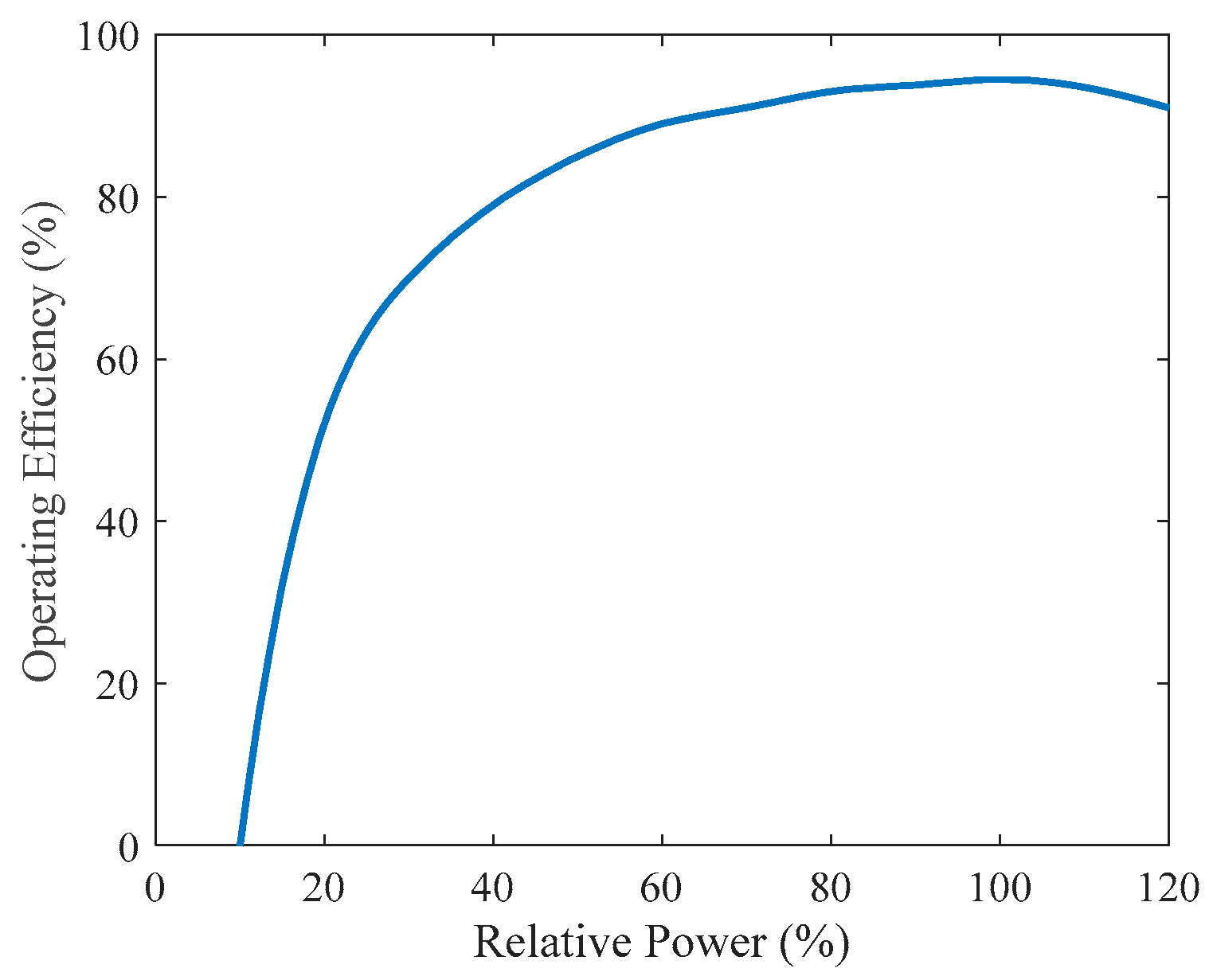
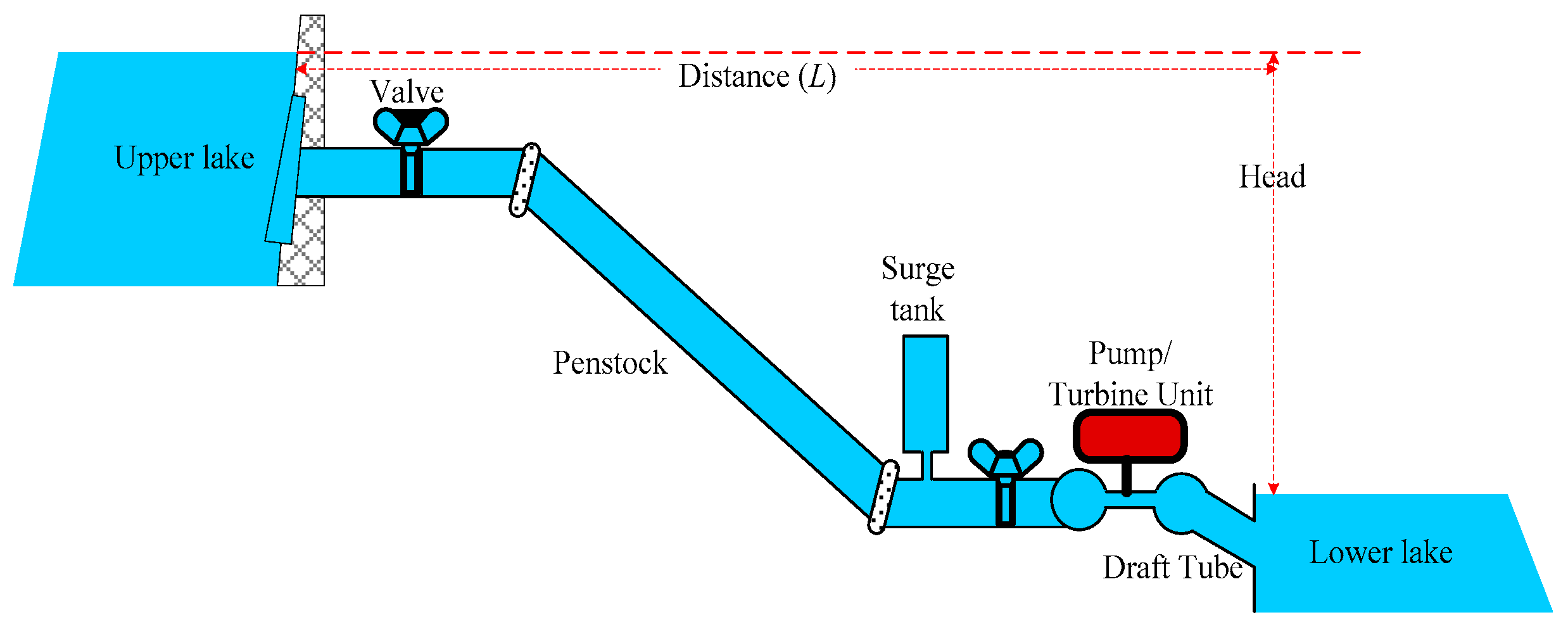
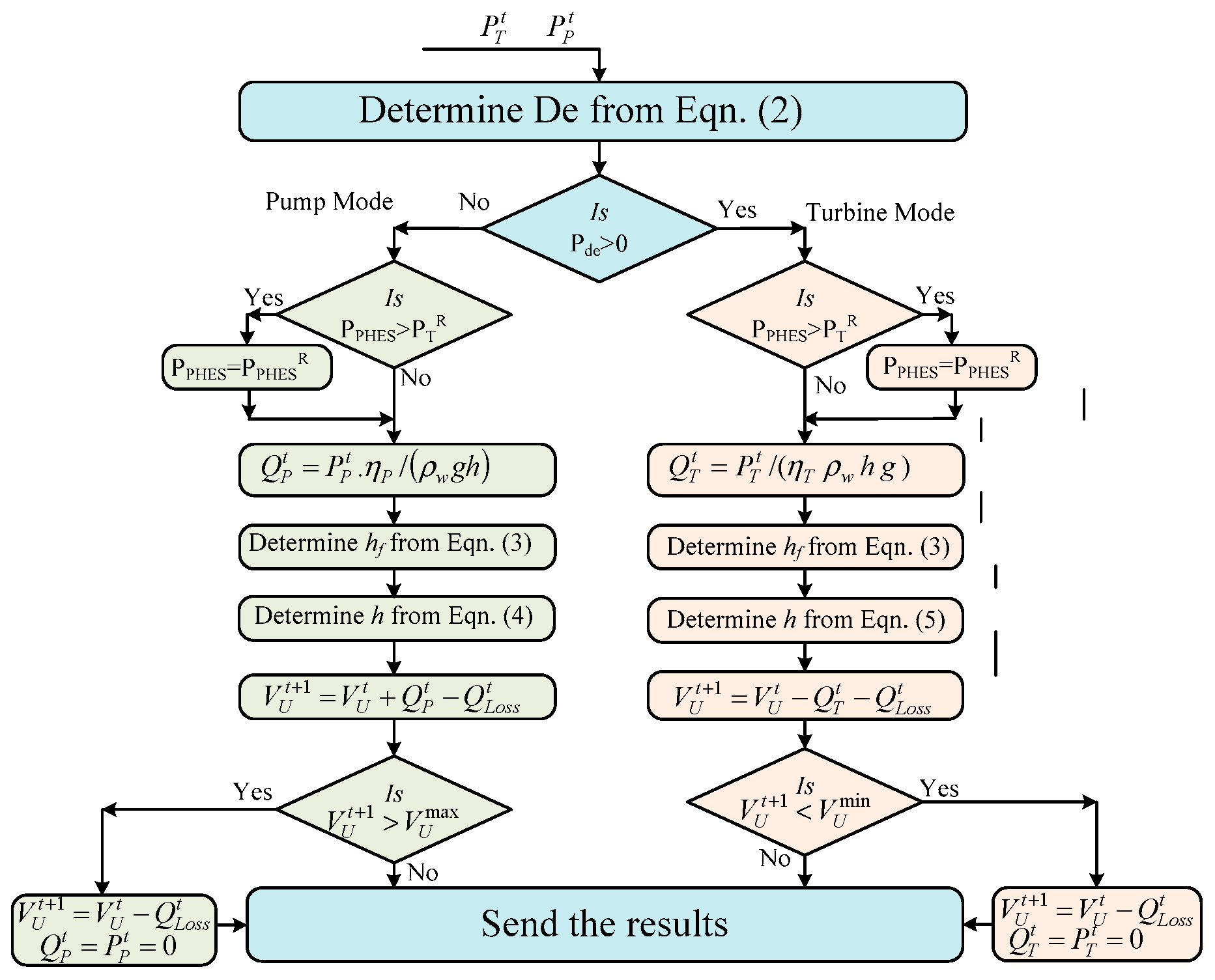
2.1.1. PHES Model
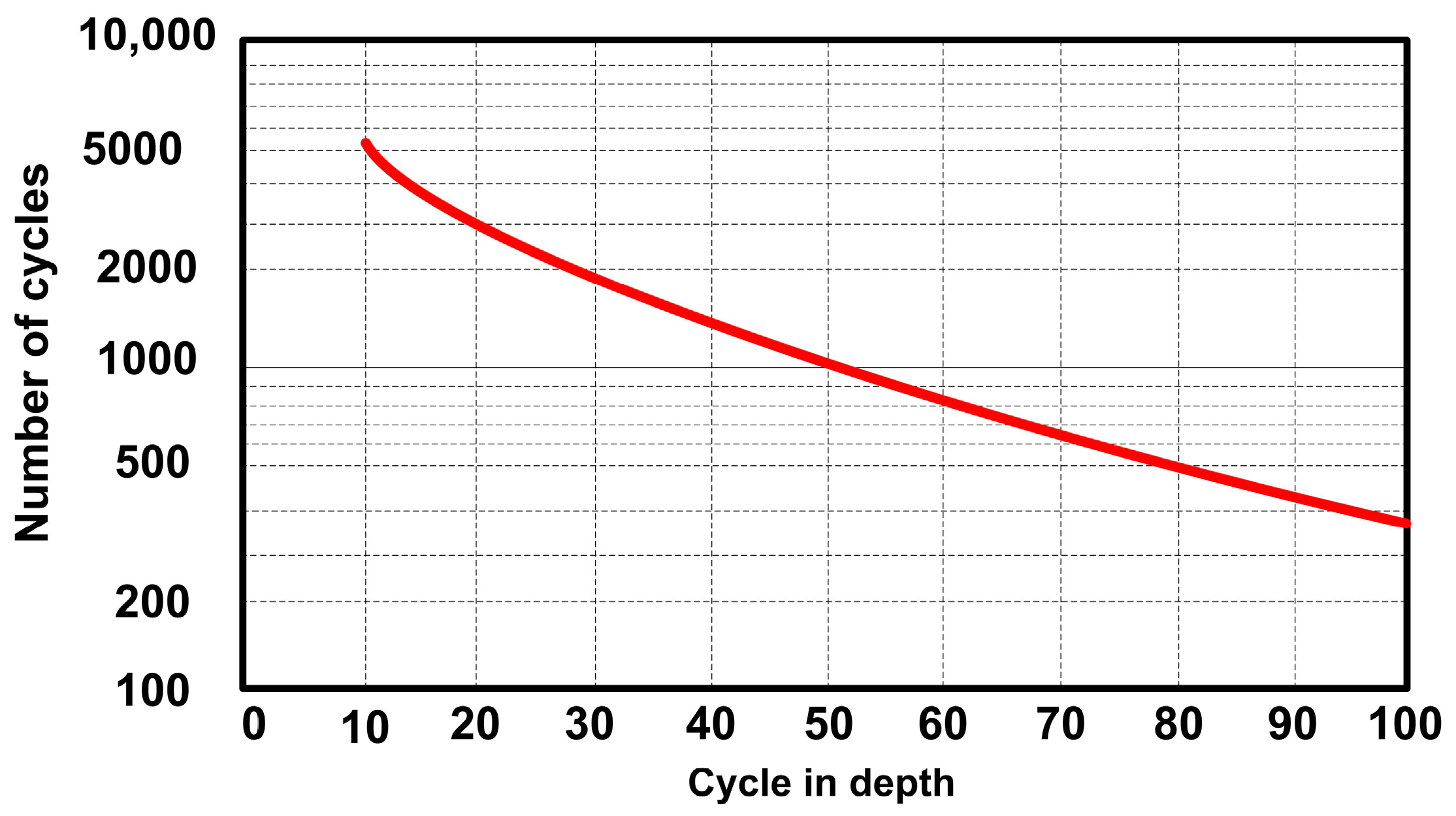
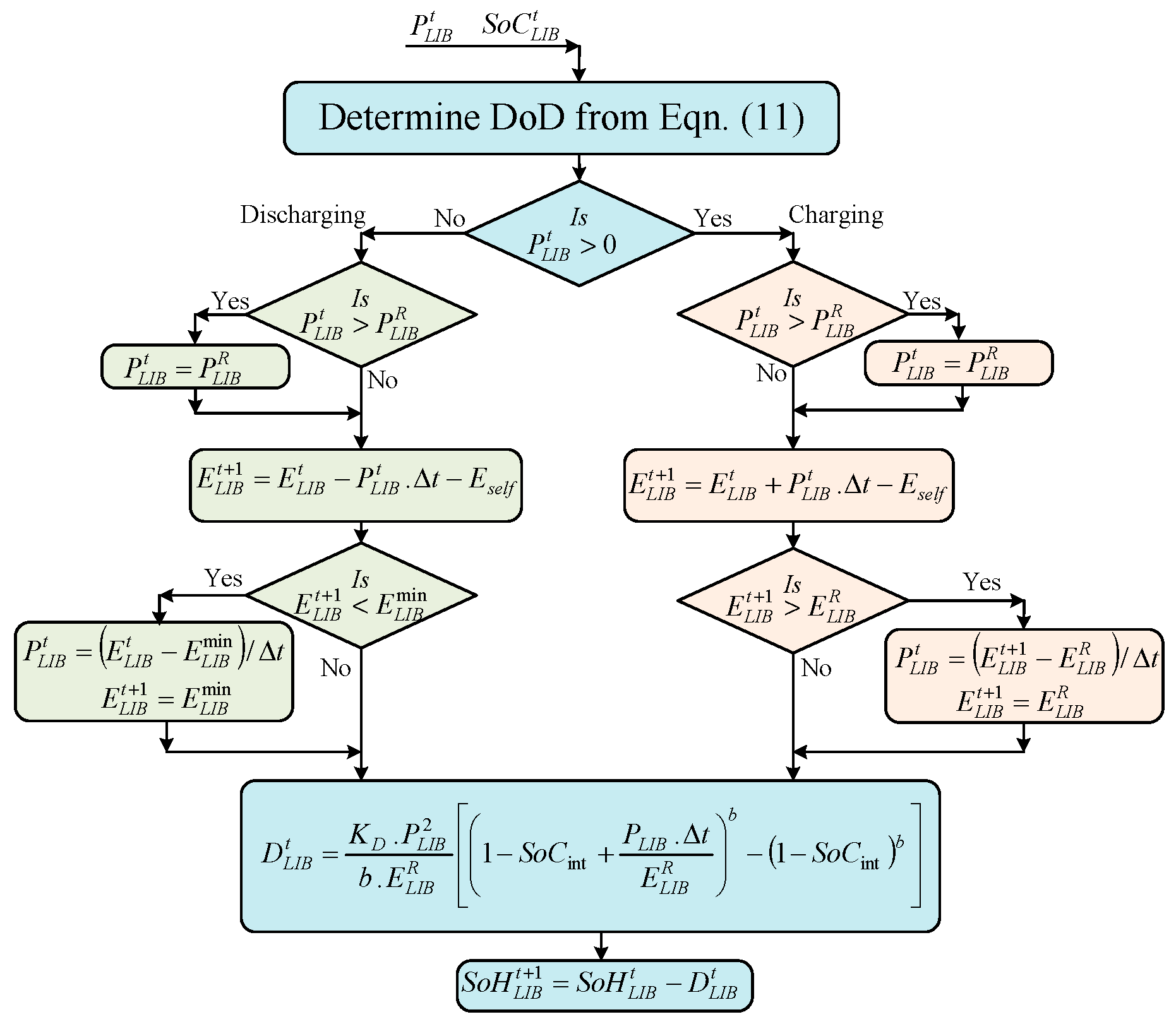
2.1.2. LIB Degradation Model
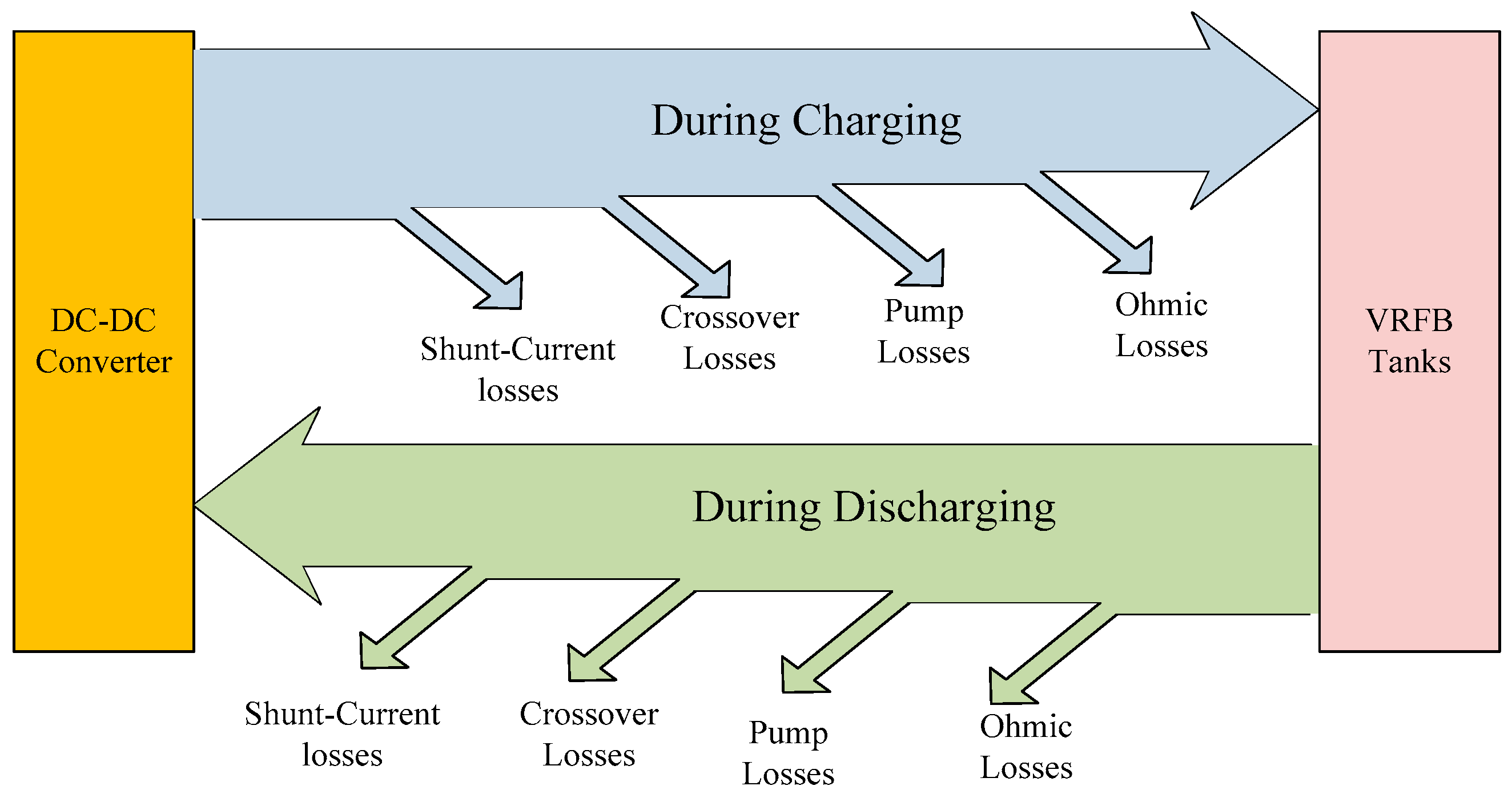
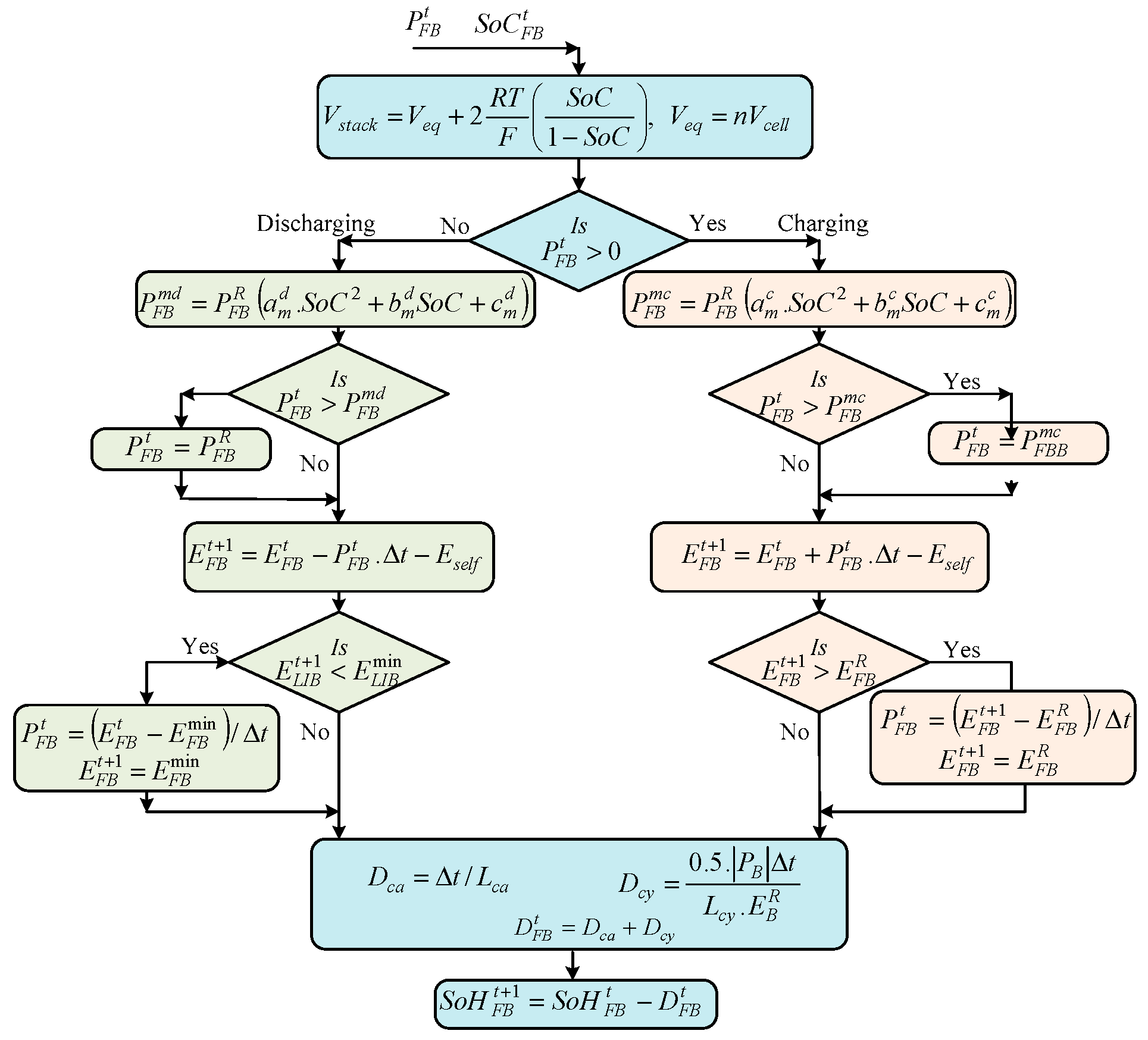
2.1.3. VRFB Model
2.2. Demand-Side Management
2.3. Zero-Carbon Smart Grid Reliability
2.4. The Revenue of the ZCSG
2.5. The Customer Satisfaction Factor
2.6. Multi-Objective Function
2.7. Energy-Balance Modeling
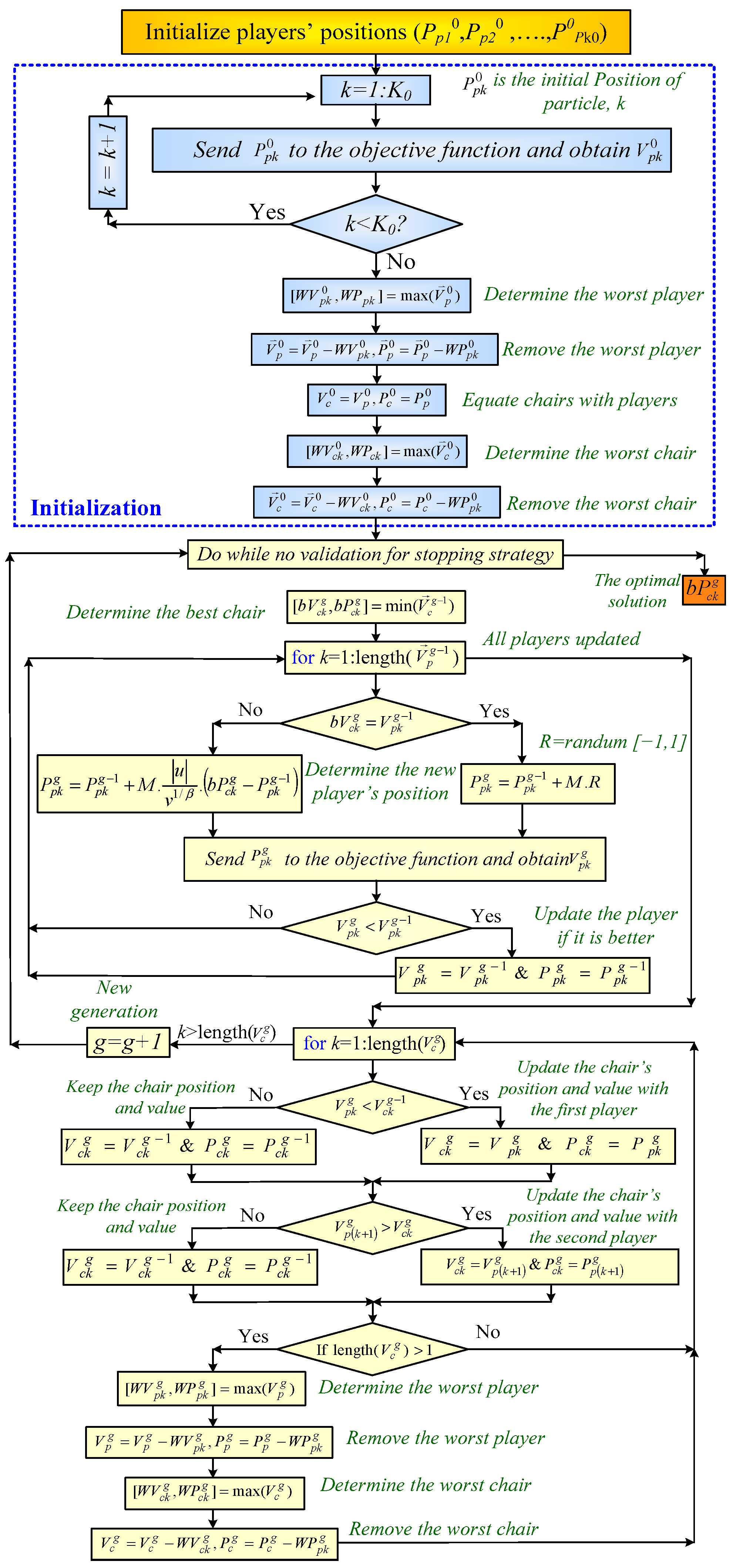
3. Musical Chairs Algorithm
3.1. Validating Player Positions and Evaluating Fitness
3.2. Competition Between Players and Chairs
3.3. Optimization and Stopping Criteria
4. The Simulation Program
5. Simulation Work
5.1. Input Data
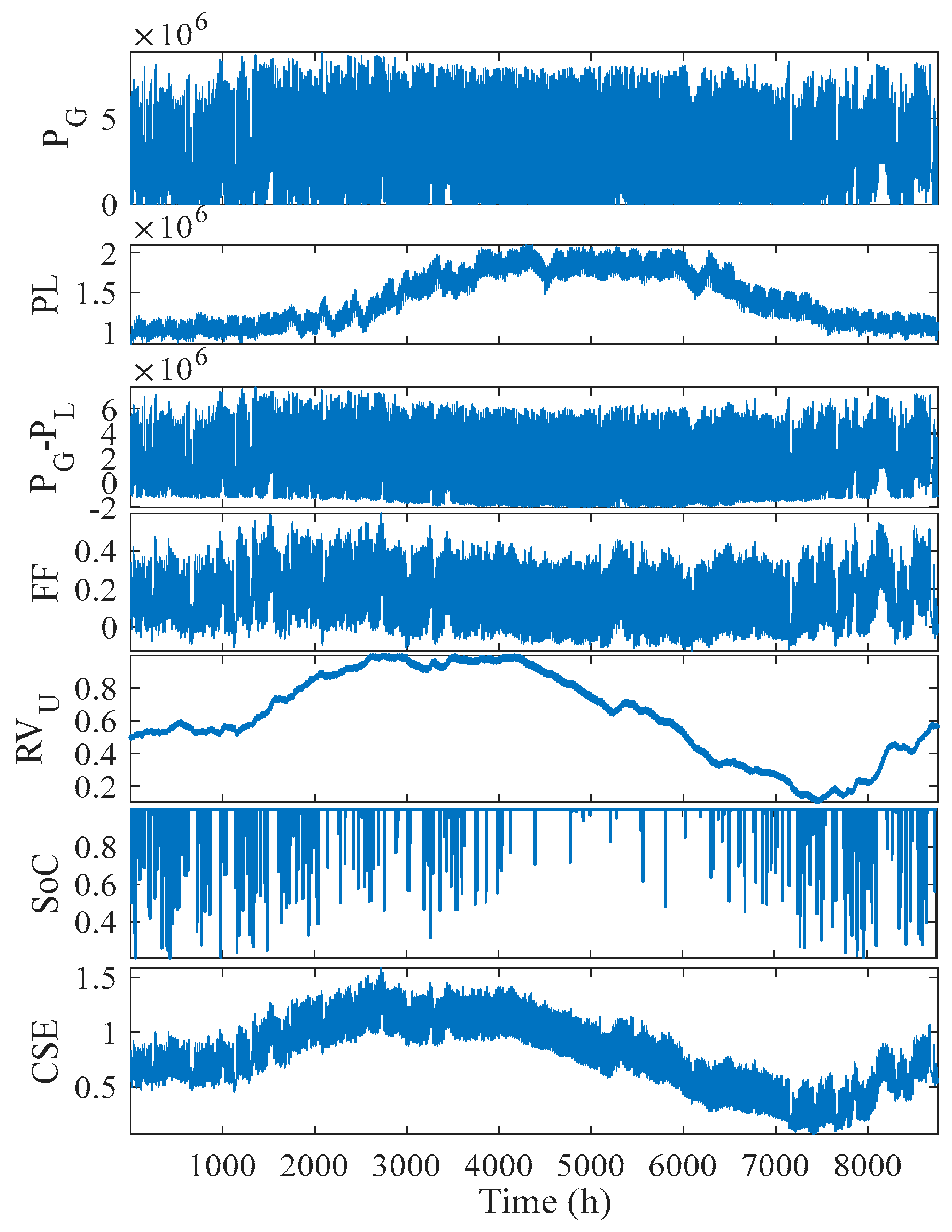
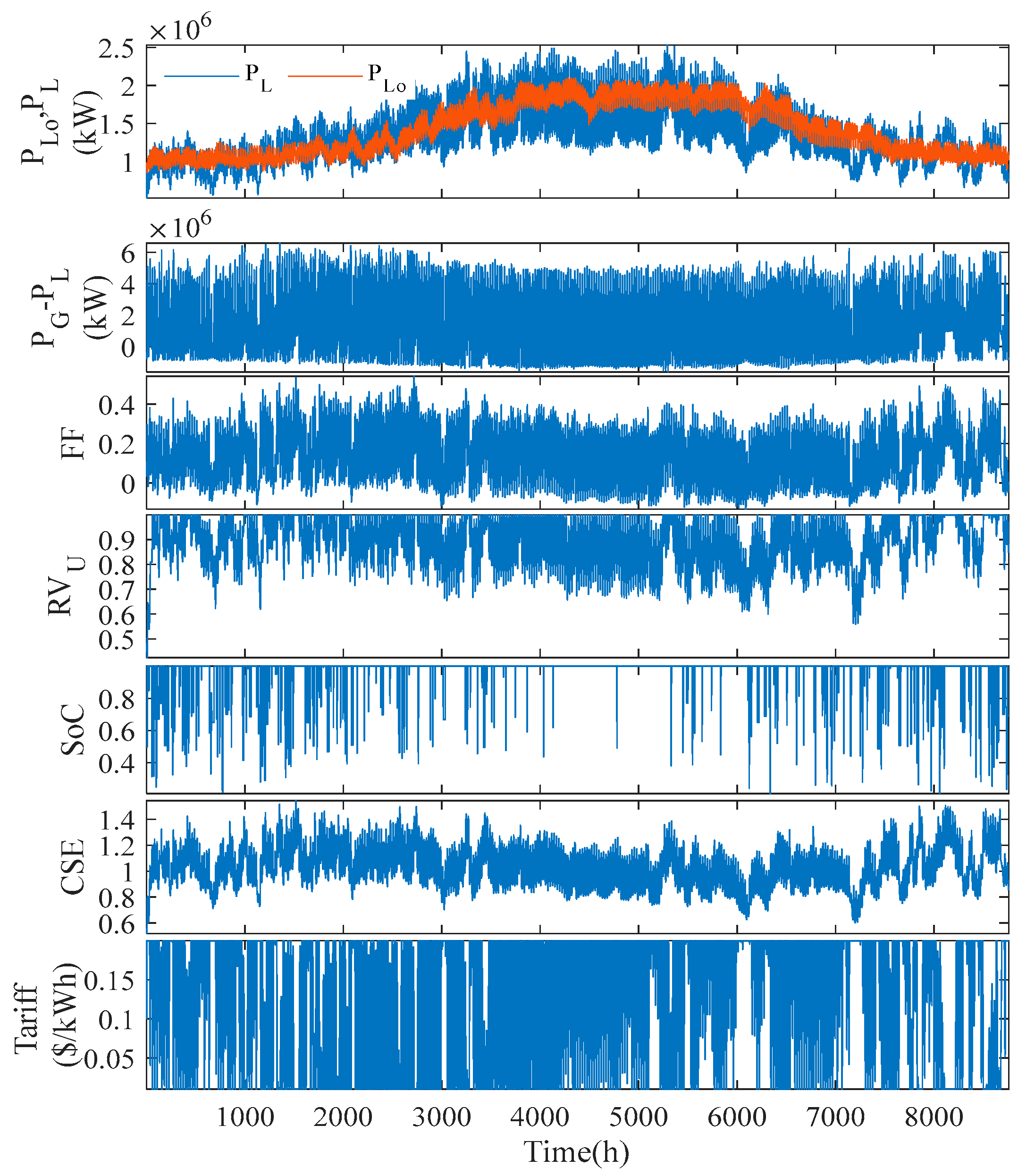
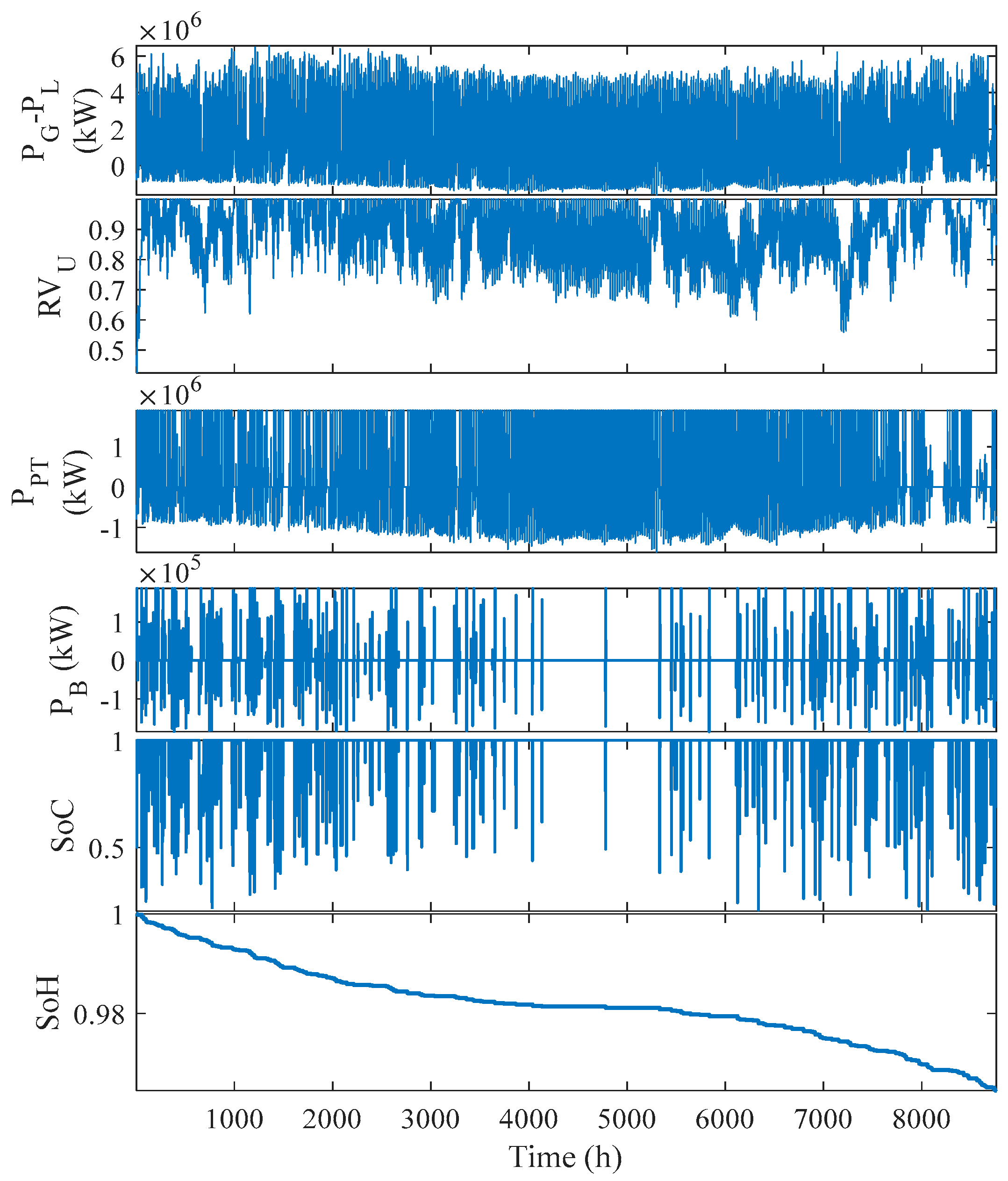
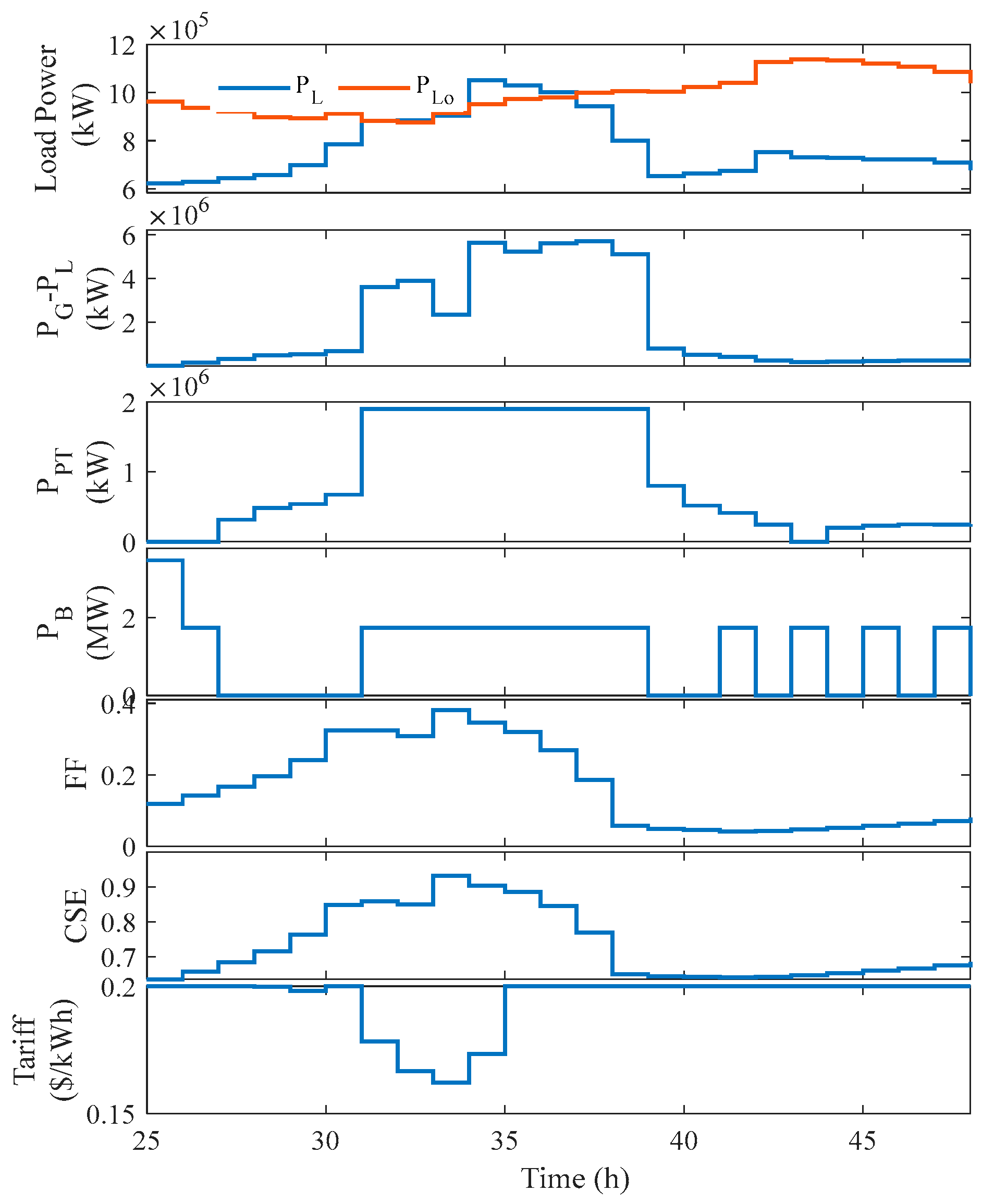
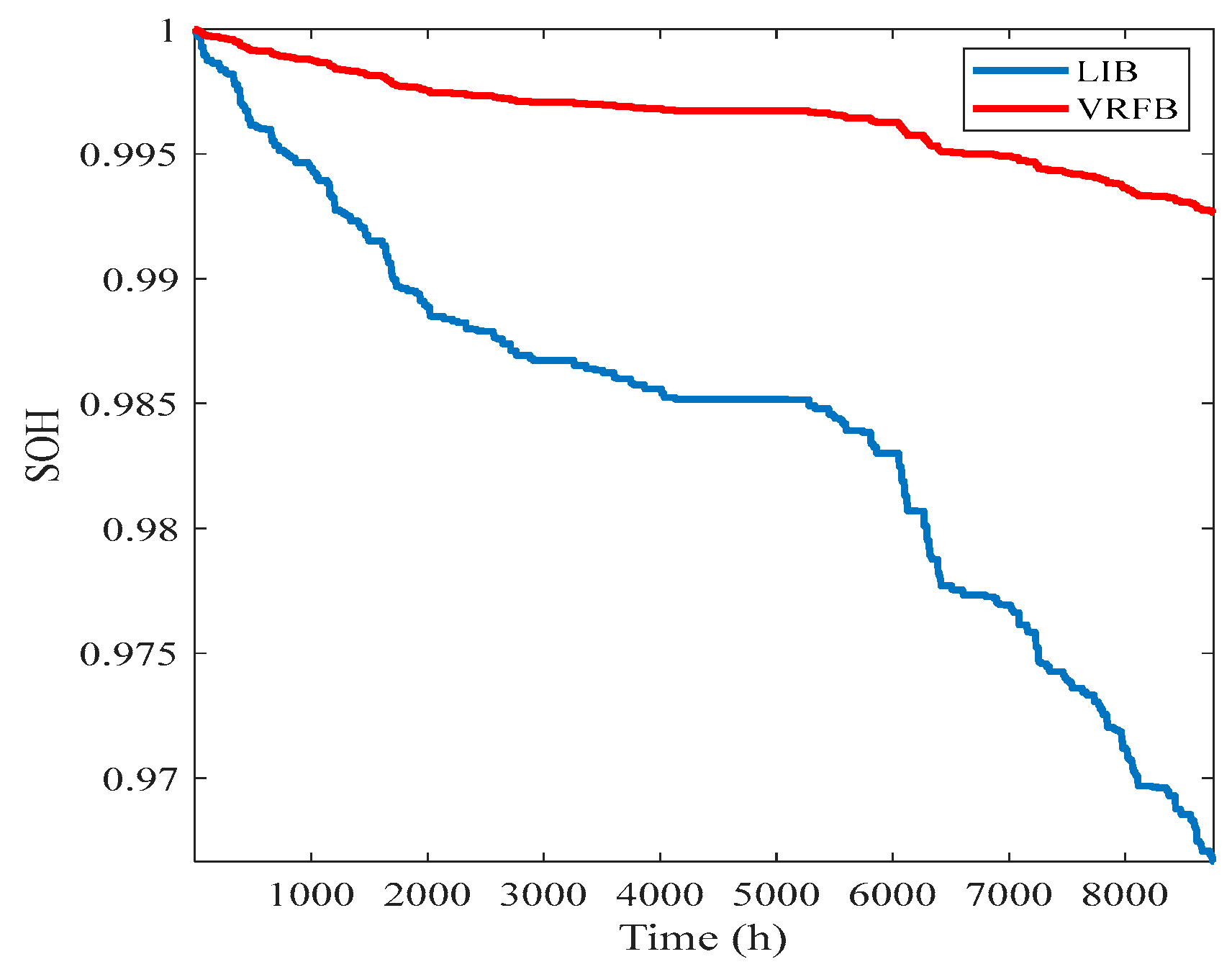
5.2. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eltamaly, A.M. A novel energy storage and demand side management for entire green smart grid system for NEOM city in Saudi Arabia. Energy Storage 2023, 6, e515. [Google Scholar] [CrossRef]
- Lu, B.; Blakers, A.; Stocks, M.; Cheng, C.; Nadolny, A. A zero-carbon, reliable and affordable energy future in Australia. Energy 2021, 220, 119678. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Addoweesh, K.E.; Bawa, U.; Mohamed, M.A. Economic modeling of hybrid renewable energy system: A case study in Saudi Arabia. Arab. J. Sci. Eng. 2014, 39, 3827–3839. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Al-Shammaa, A.A. Optimal configuration for isolated hybrid renewable energy systems. J. Renew. Sustain. Energy 2016, 8, 045502. [Google Scholar] [CrossRef]
- da Silva Lima, L.; Quartier, M.; Buchmayr, A.; Sanjuan-Delmás, D.; Laget, H.; Corbisier, D.; Mertens, J.; Dewulf, J. Life cycle assessment of lithium-ion batteries and vanadium redox flow batteries-based renewable energy storage systems. Sustain. Energy Technol. Assess. 2021, 46, 101286. [Google Scholar] [CrossRef]
- Vudata, S.P. Dynamic Modelling and Control of Grid-Level Energy Storage Systems. Ph.D. Thesis, Statler College of Engineering and Mineral Resources, Morgantown, WV, USA, 2021. [Google Scholar]
- Lei, J.Z.; Gong, Q.; Liu, J.; Qiao, H.; Wang, B. Optimal allocation of a VRB energy storage system for wind power applications considering the dynamic efficiency and life of VRB in active distribution networks. IET Renew. Power Gener. 2019, 13, 563–571. [Google Scholar] [CrossRef]
- Fathima, A.H.; Palanisamy, K. Integration and energy management of a hybrid Li-VRB battery for renewable applications. Renew. Energy Focus 2019, 30, 13–20. [Google Scholar] [CrossRef]
- Berrueta, A.; Heck, M.; Jantsch, M.; Ursúa, A.; Sanchis, P. Combined dynamic programming and region-elimination technique algorithm for optimal sizing and management of lithium-ion batteries for photovoltaic plants. Appl. Energy 2018, 228, 1–11. [Google Scholar] [CrossRef]
- Martins, R.; Hesse, H.C.; Jungbauer, J.; Vorbuchner, T.; Musilek, P. Optimal Component Sizing for Peak Shaving in Battery Energy Storage System for Industrial Applications. Energies 2018, 11, 2048. [Google Scholar] [CrossRef]
- Fathima, A.H.; Palanismay, K. Modeling and operation of a vanadium redox flow battery for PV applications. Energy Procedia 2017, 117, 607–614, 1876–6102. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Saha, H. Design and experimental validation of a generalised electrical equivalent model of Vanadium Redox Flow Battery for interfacing with renewable energy sources. J. Energy Storage 2017, 13, 220–232. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Cherubini, P.; Micangeli, A.; Pelosi, D.; Tacconelli, C. How Hybridization of Energy Storage Technologies Can Provide Additional Flexibility and Competitiveness to Microgrids in the Context of Developing Countries. Energies 2019, 12, 3138. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Skyllas-Kazacos, M.; Bao, J. Optimal Sizing of Vanadium Redox Flow Battery Systems for Residential Applications Based on Battery Electrochemical Characteristics. Energies 2016, 9, 857. [Google Scholar] [CrossRef]
- Tazvinga, H.; Zhu, B.; Xia, X.H. Optimal power flow management for distributed energy resources with batteries. Energy Convers. Manag. 2015, 102, 104–110. [Google Scholar] [CrossRef]
- Noack, J.; Wietschel, L.; Roznyatovskaya, N.; Pinkwart, K.; Tübke, J. Techno-Economic Modeling and Analysis of Redox Flow Battery Systems. Energies 2016, 9, 627. [Google Scholar] [CrossRef]
- Minke, C.; Kunz, U.; Turek, T. Techno-economic assessment of novel vanadium redox flow batteries with large-area cells. J. Power Sources 2017, 361, 105–114. [Google Scholar] [CrossRef]
- Boonluk, P.; Siritaratiwat, A.; Fuangfoo, P.; Khunkitti, S. Optimal Siting and Sizing of Battery Energy Storage Systems for Distribution Network of Distribution System Operators. Batteries 2020, 6, 56. [Google Scholar] [CrossRef]
- Bingying, W.; Buhan, Z.; Biao, M.; Jiajun, Z. Optimal capacity of flow battery and economic dispatch used in peak load shifting. In Proceedings of the 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, China, 6–9 July 2011; IEEE: Piscateville, NJ, USA, 2011; pp. 1395–1400. [Google Scholar]
- Barelli, L.; Bidini, G.; Ottaviano, P.; Pelosi, D. Vanadium redox flow batteries application to electric buses propulsion: Performance analysis of hybrid energy storage system. J. Energy Storage 2019, 24, 100770. [Google Scholar] [CrossRef]
- Skyllas-Kazacos, M. The History of the UNSW All-Vanadium Flow Battery Development. Flow Batter. Fundam. Appl. 2023, 2, 507–538. [Google Scholar]
- Uhrig, M.; Koenig, S.; Suriyah, M.R.; Leibfried, T. Lithium-based vs. Vanadium Redox Flow Batteries—A Comparison for Home Storage Systems. Energy Procedia 2016, 99, 35–43. [Google Scholar] [CrossRef]
- Sun, C.; Negro, E.; Nale, A.; Pagot, G.; Vezzù, K.; Zawodzinski, T.A.; Meda, L.; Gambaro, C.; Di Noto, V. An efficient barrier toward vanadium crossover in redox flow batteries: The bilayer [Nafion/(WO3)x] hybrid inorganic-organic membrane. Electrochim. Acta 2021, 378, 138133. [Google Scholar] [CrossRef]
- Alotaibi, M.A.; Eltamaly, A.M. A Smart Strategy for Sizing of Hybrid Renewable Energy System to Supply Remote Loads in Saudi Arabia. Energies 2021, 14, 7069. [Google Scholar] [CrossRef]
- Hayes, S.J.; Donalek, P.; Hartel, P.; Trouille, B.; King, K.; Bhattarai, M.; Krohn, R.; Gilbert, K.; Lee, H.; Haapala, J. Technical Analysis of Pumped Storage and Integration with Wind Power in the Pacific Northwest; MWH Americas, Inc.: Blomfield, CO, USA, 2009. [Google Scholar]
- Yu, M.G.; Ma, X.; Wu, D. A hierarchical framework for aggregating grid-interactive buildings with thermal and battery energy storage. J. Energy Storage 2024, 101, 113984. [Google Scholar] [CrossRef]
- Toffoletti, G.; Cortella, G.; D’Agaro, P. Thermodynamic and economic seasonal analysis of a transcritical CO2 supermarket with HVAC supply through ice thermal energy storage (ITES). J. Clean. Prod. 2024, 434, 139832. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Alotaibi, M.A.; Elsheikh, W.A.; Alolah, A.I.; Ahmed, M.A. Novel Demand Side-Management Strategy for Smart Grid Concepts Applications in Hybrid Renewable Energy Systems. In Proceedings of the 2022 4th International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 17–19 March 2022; IEEE: Piscateville, NJ, USA, 2022; pp. 1–7. [Google Scholar]
- Eltamaly, A.M.; Alotaibi, M.A.; Alolah, A.I.; Ahmed, M.A. A Novel Demand Response Strategy for Sizing of Hybrid Energy System with Smart Grid Concepts. IEEE Access 2021, 9, 20277–20294. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Mohamed, M.A.; Alolah, A.I. A novel smart grid theory for optimal sizing of hybrid renewable energy systems. Sol. Energy 2016, 124, 26–38. [Google Scholar] [CrossRef]
- Javed, M.S.; Zhong, D.; Ma, T.; Song, A.; Ahmed, S. Hybrid pumped hydro and battery storage for renewable energy based power supply system. Appl. Energy 2020, 257, 114026. [Google Scholar] [CrossRef]
- Kaunda, C.S.; Kimambo, C.Z.; Nielsen, T.K. Potential of small-scale hydropower for electricity generation in Sub-Saharan Africa. ISRN Renew. Energy 2012, 2012, 132606. [Google Scholar] [CrossRef]
- Botterud, A.; Levin, T.; Koritarov, V. Pumped Storage Hydropower: Benefits for Grid Reliability and Integration of Variable Renewable Energy; Argonne National Lab (ANL): Argonne, IL, USA, 2014. [Google Scholar]
- Warnick, C.C.; Mayo, H.A., Jr. Hydropower Engineering; Prentice-Hall: Upper Saddle River, NJ, USA, 1984; Available online: https://openlibrary.org/works/OL5603227W/Hydropower_engineering?edition=key%3A/books/OL3178549M (accessed on 9 August 2024)ISBN 978-0134484983.
- Singhal, M.K.; Kumar, A. Optimum design of penstock for hydro projects. Int. J. Energy Power Eng. 2015, 4, 216. [Google Scholar]
- Emmanouil, S.; Nikolopoulos, E.I.; François, B.; Brown, C.; Anagnostou, E.N. Evaluating existing water supply reservoirs as small-scale pumped hydroelectric storage options–A case study in Connecticut. Energy 2021, 226, 120354. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Nayak, P.K. PV-pumped energy storage option for convalescing performance of hydroelectric station under declining precipitation trend. Renew. Energy 2019, 135, 288–302. [Google Scholar] [CrossRef]
- Kusakana, K. Feasibility analysis of river off-grid hydrokinetic systems with pumped hydro storage in rural applications. Energy Convers. Manag. 2015, 96, 352–362. [Google Scholar] [CrossRef]
- Almutairi, Z.A.; Eltamaly, A.M.; El Khereiji, A.; Al Nassar, A.; Al Rished, A.; Al Saheel, N.; Al Marqabi, A.; Al Hamad, S.; Al Harbi, M.; Sherif, R.; et al. Modeling and experimental determination of lithium-ion battery degradation in hot environment. In Proceedings of the 2022 23rd International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 13–15 December 2022; IEEE: Piscateville, NJ, USA, 2022; pp. 1–8. [Google Scholar]
- Yao, L.W.; Aziz, J.A.; Kong, P.Y.; Idris, N.R.N. Modeling of lithium-ion battery using MATLAB/simulink. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; IEEE: Piscateville, NJ, USA, 2013; pp. 1729–1734. [Google Scholar]
- Mongird, K.; Viswanathan, V.; Balducci, P.; Alam, J.; Fotedar, V.; Koritarov, V.; Hadjerioua, B. An Evaluation of Energy Storage Cost and Performance Characteristics. Energies 2020, 13, 3307. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Smart Decentralized Electric Vehicle Aggregators for Optimal Dispatch Technologies. Energies 2023, 16, 8112. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Optimal Dispatch Strategy for Electric Vehicles in V2G Applications. Smart Cities 2023, 6, 3161–3191. [Google Scholar] [CrossRef]
- Eltamaly, A.M. An Accurate Piecewise Aging Model for Li-ion Batteries in Hybrid Renewable Energy System Applications. Arab. J. Sci. Eng. 2023, 49, 6551–6575. [Google Scholar] [CrossRef]
- Farzin, H.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M. A practical scheme to involve degradation cost of lithium-ion batteries in vehicle-to-grid applications. IEEE Trans. Sustain. Energy 2016, 7, 1730–1738. [Google Scholar] [CrossRef]
- Viswanathan, V.V.; Crawford, A.J.; Thomsen, E.C.; Shamim, N.; Li, G.; Huang, Q.; Reed, D.M. An Overview of the Design and Optimized Operation of Vanadium Redox Flow Batteries for Durations in the Range of 4–24 Hours. Batteries 2023, 9, 221. [Google Scholar] [CrossRef]
- Chen, S.; Sun, C.; Zhang, H.; Yu, H.; Wang, W. Electrochemical Deposition of Bismuth on Graphite Felt Electrodes: Influence on Negative Half-Cell Reactions in Vanadium Redox Flow Batteries. Appl. Sci. 2024, 14, 3316. [Google Scholar] [CrossRef]
- Woodfield, R.; Sun, C.; Zhang, H.; Yu, H.; Wang, W. Electro-thermal modelling of redox flow-batteries with electrolyte swapping for an electric ferry. J. Energy Storage 2022, 54, 105306. [Google Scholar] [CrossRef]
- Tang, A.; Bao, J.; Skyllas-Kazacos, M. Studies on pressure losses and flow rate optimization in vanadium redox flow battery. J. Power Sources 2014, 248, 154–162. [Google Scholar] [CrossRef]
- Hesse, H.C.; Martins, R.; Musilek, P.; Naumann, M.; Truong, C.N.; Jossen, A. Economic Optimization of Component Sizing for Residential Battery Storage Systems. Energies 2017, 10, 835. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Crow, M.L.; Elmore, A.C. Optimal Sizing of a Vanadium Redox Battery System for Microgrid Systems. IEEE Trans. Sustain. Energy 2015, 6, 729–737. [Google Scholar] [CrossRef]
- Turker, B.; Klein, S.A.; Hammer, E.-M.; Lenz, B.; Komsiyska, L. Modeling a vanadium redox flow battery system for large scale applications. Energy Convers. Manag. 2013, 66, 26–32. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A novel musical chairs algorithm applied for MPPT of PV systems. Renew. Sustain. Energy Rev. 2021, 146, 111135. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo search via lévy flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Hannan, M.A.; Wali, S.; Ker, P.; Rahman, M.A.; Mansor, M.; Ramachandaramurthy, V.; Muttaqi, K.; Mahlia, T.; Dong, Z. Battery energy-storage system: A review of technologies, optimization objectives, constraints, approaches, and outstanding issues. J. Energy Storage 2021, 42, 103023. [Google Scholar] [CrossRef]
- Rabie, A.H.; Eltamaly, A.M. A new NEST-IGWO strategy for determining optimal IGWO control parameters. Neural Comput. Appl. 2023, 35, 15143–15165. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Eltamaly, A.M.; Alolah, A.I. Swarm intelligence-based optimization of grid-dependent hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2017, 77, 515–524. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Optimal control parameters for bat algorithm in maximum power point tracker of photovoltaic energy systems. Int. Trans. Electr. Energy Syst. 2021, 31, e12839. [Google Scholar] [CrossRef]
- Eltamaly, A.M. An Improved Cuckoo Search Algorithm for Maximum Power Point Tracking of Photovoltaic Systems under Partial Shading Conditions. Energies 2021, 14, 953. [Google Scholar] [CrossRef]
- Farh, H.M.H.; Eltamaly, A.M.; Al-Shaalan, A.M.; Al-Shamma’A, A.A. A novel sizing inherits allocation strategy of renewable distributed generations using crow search combined with particle swarm optimization algorithm. IET Renew. Power Gener. 2021, 15, 1436–1450. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Rabie, A.H. A Novel Musical Chairs Optimization Algorithm. Arab. J. Sci. Eng. 2023, 48, 10371–10403. [Google Scholar] [CrossRef]




| (i, k) | ||||
|---|---|---|---|---|
| (o, v) | 0.079170 | −0.002440 | 1.276400 | - |
| (d, v) | −0.283330 | 0.13251 | 0.986140 | - |
| (d, p) | 1.033400 | 0.345400 | 0.119200 | - |
| (c, v) | 0.197390 | 0.161670 | 0.142080 | 0.974790 |
| (c, p) | −0.128000 | 1.050000 | 0.038000 | 0.118000 |
| (a, b) | −8.390400 | 8.663400 | 7.363200 | −7.504000 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Pump/Turbine Cost | USD 225/kW [24] | Rated Head | 1162 m [24] |
| Civil Work | USD 7.884 [24] | Friction factor, f | 0.34 [35] |
| ηP and ηT | 92% [24] | Pipe Diameter | [35] |
| Lifetime | 40 [24] | Pipe Length | 1200 m [35] |
| OMC | 1% of initial cost [24] |
| Items | LIB | VRFB |
|---|---|---|
| Battery cost | USD 156/kWh [55] | USD 426/kW and USD 100/kWh |
| BA_OMC | USD 0.02/kWh/year | USD 0.1/kWh/year |
| BA_SL | 20% BA_cost | 30% BA_cost |
| EOL Capacity | 40% | 40% |
| Efficiency | 0.95 | Equations (27) and (28) |
| σ | 0.02% | 0.035% |
| DOD | 70% | 100% |
| Algorithm | Convergence Time (s) | % Convergence Time Compared to MCA | Objective Function |
|---|---|---|---|
| MCA [61] | 3.4 | 100 | 2.180107 |
| GWO [56] | 6.6 | 194.1176 | 2.178874 |
| PSO [57] | 9.2 | 270.5882 | 2.178537 |
| BA [58] | 9.4 | 276.4706 | 2.178875 |
| CS [59] | 7.6 | 223.5294 | 2.179815 |
| CSA [60] | 11.6 | 341.1765 | 2.179496 |
| Cases | LIB | VRFB | |||||
|---|---|---|---|---|---|---|---|
| ITEMS | Without DSM (PED = 0) | With DSM (PED = −0.5) | % Change | Without DSM (PED = 0) | With DSM (PED = −0.5) | % Change | |
| LCOE | 0.0931 | 0.0625 | −32.87 | 0.0872 | 0.0594 | −31.88 | |
| NPC (109$) | 19.258 | 12.845 | −33.30 | 18.356 | 12.019 | −34.52 | |
| NPP (109$) | 25.615 | 25.623 | 0.03 | 25.627 | 25.621 | −0.02 | |
| NPV (109$) | 6.357 | 12.778 | 101.01 | 7.271 | 13.602 | 87.07 | |
| NWT | 41,000 | 32,800 | −20.00 | 39,523 | 31,815 | −19.50 | |
| SCA | 35,000,000 | 27,200,000 | −22.29 | 35,815,176 | 28,754,381 | −19.71 | |
| 450,000,000 | 32,000,000 | −92.89 | 360,000,000 | 24,000,000 | −93.33 | ||
| PPT | 2,000,000 | 1,888,000 | −5.60 | 1,953,000 | 1,574,000 | −19.41 | |
| PB | 250,000 | 186,500 | −25.40 | 438,500 | 253,400 | −42.21 | |
| EB | 500,000 | 373,000 | −25.40 | 743,000 | 419,000 | −43.61 | |
| BLT (years) | 5.5 | 5.5 | 0 | 14 | 14 | 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almutairi, Z.A.; Eltamaly, A.M. Synergistic Effects of Energy Storage Systems and Demand-Side Management in Optimizing Zero-Carbon Smart Grid Systems. Energies 2024, 17, 5637. https://doi.org/10.3390/en17225637
Almutairi ZA, Eltamaly AM. Synergistic Effects of Energy Storage Systems and Demand-Side Management in Optimizing Zero-Carbon Smart Grid Systems. Energies. 2024; 17(22):5637. https://doi.org/10.3390/en17225637
Chicago/Turabian StyleAlmutairi, Zeyad A., and Ali M. Eltamaly. 2024. "Synergistic Effects of Energy Storage Systems and Demand-Side Management in Optimizing Zero-Carbon Smart Grid Systems" Energies 17, no. 22: 5637. https://doi.org/10.3390/en17225637
APA StyleAlmutairi, Z. A., & Eltamaly, A. M. (2024). Synergistic Effects of Energy Storage Systems and Demand-Side Management in Optimizing Zero-Carbon Smart Grid Systems. Energies, 17(22), 5637. https://doi.org/10.3390/en17225637






