A Robust-Based Home Energy Management Model for Optimal Participation of Prosumers in Competitive P2P Platforms
Abstract
:1. Introduction
1.1. Context and Motivation
1.2. Literature Review
1.3. Contributions
2. HEM Model
2.1. Power Balance
2.2. PV System
2.3. Storage Systems
2.4. HVAC
2.5. CAs
2.6. HEM Decision Variables
3. Competitive P2P Modeling
3.1. The Upper Level
3.2. The Lower Level
3.3. Mathematical Programming with Complementarity Constraints (MPCC)
- Objective function: (20)
- Subject to (25)–(29).
3.4. MILP
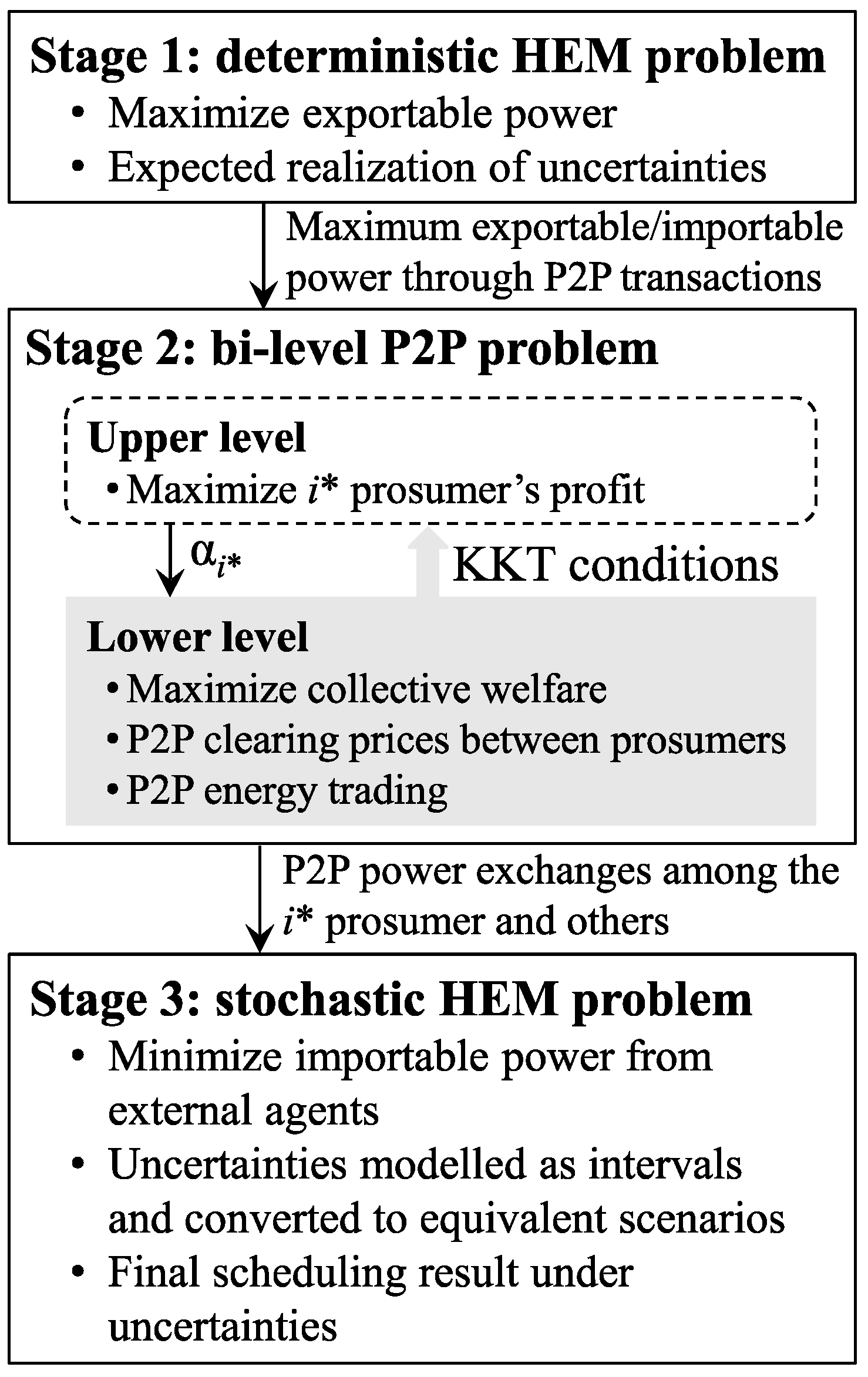
4. The Developed Solution Procedure
4.1. Stage 1
4.2. Stage 2
4.3. Stage 3
5. Case Study
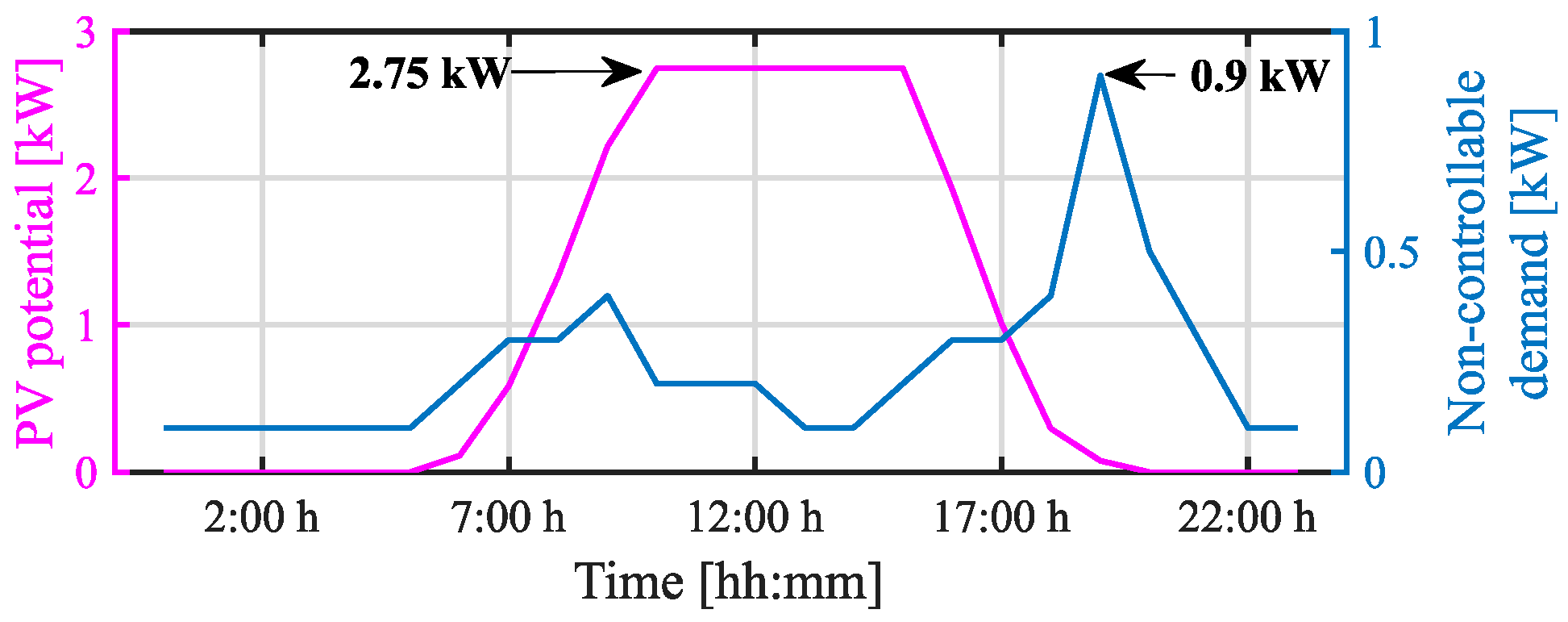
5.1. Input Data and Cases Studied
- Case 1: It is considered a low-renewable scenario in which the studied prosumer does not install onsite generators, and therefore PV potential is equal to zero.
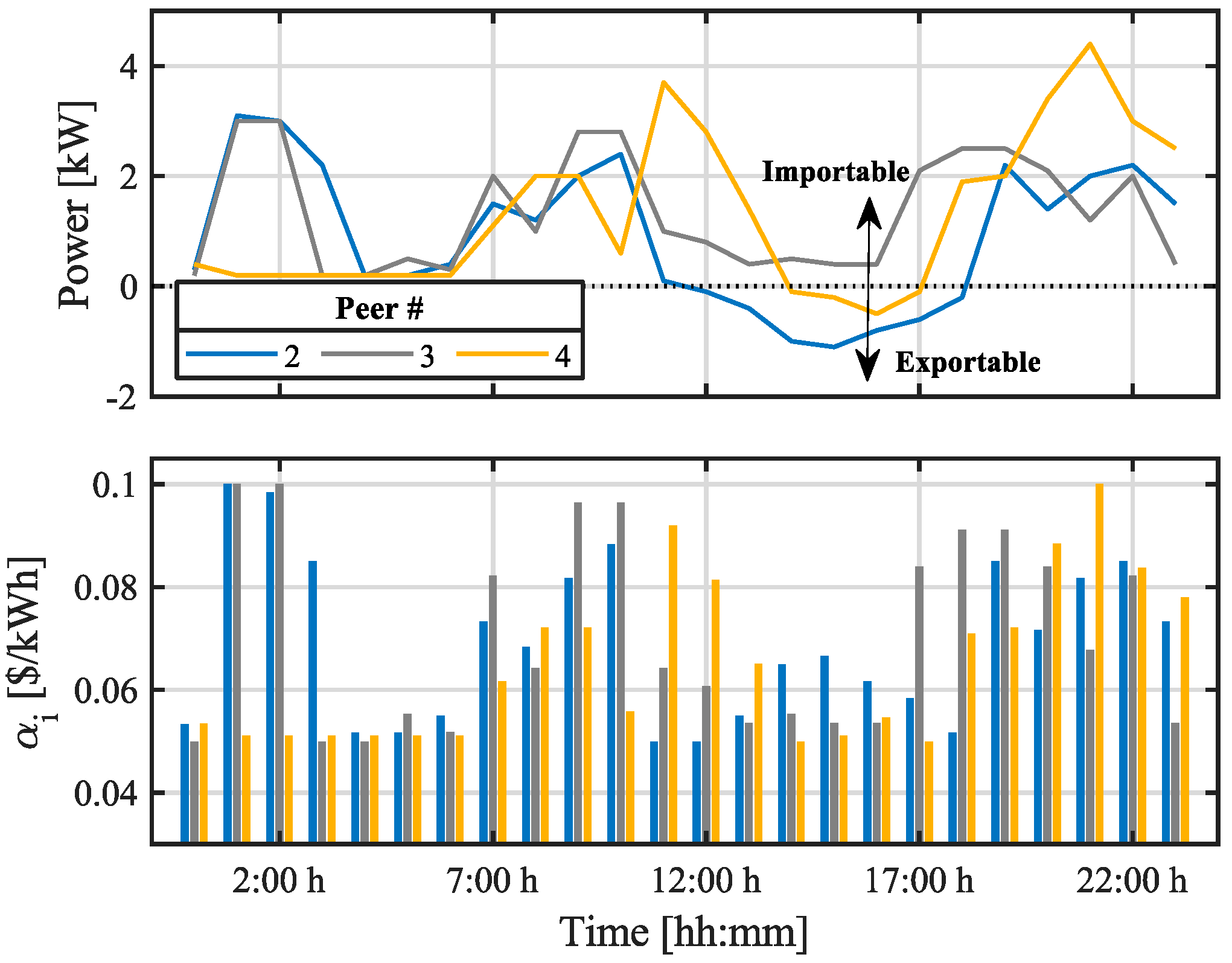
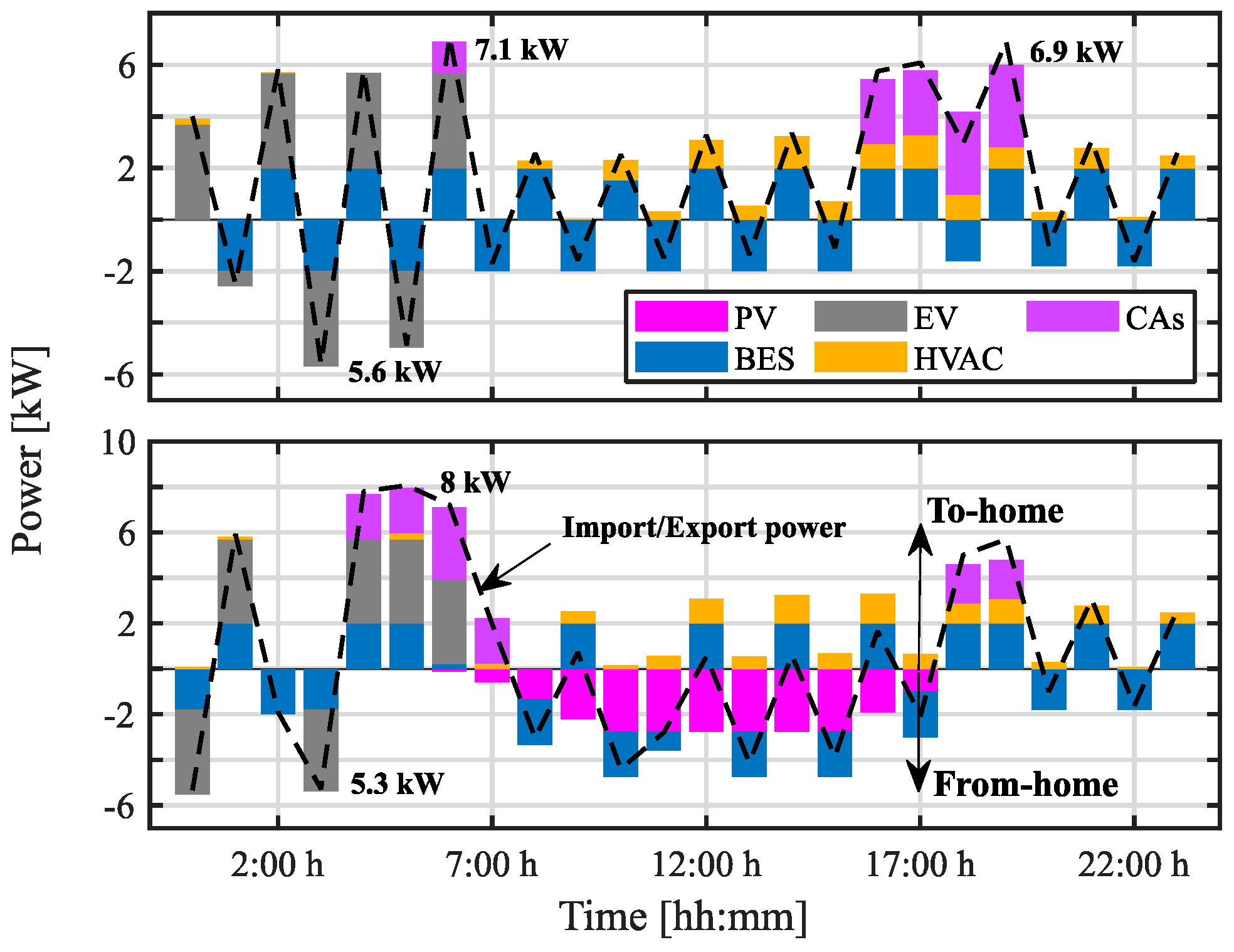
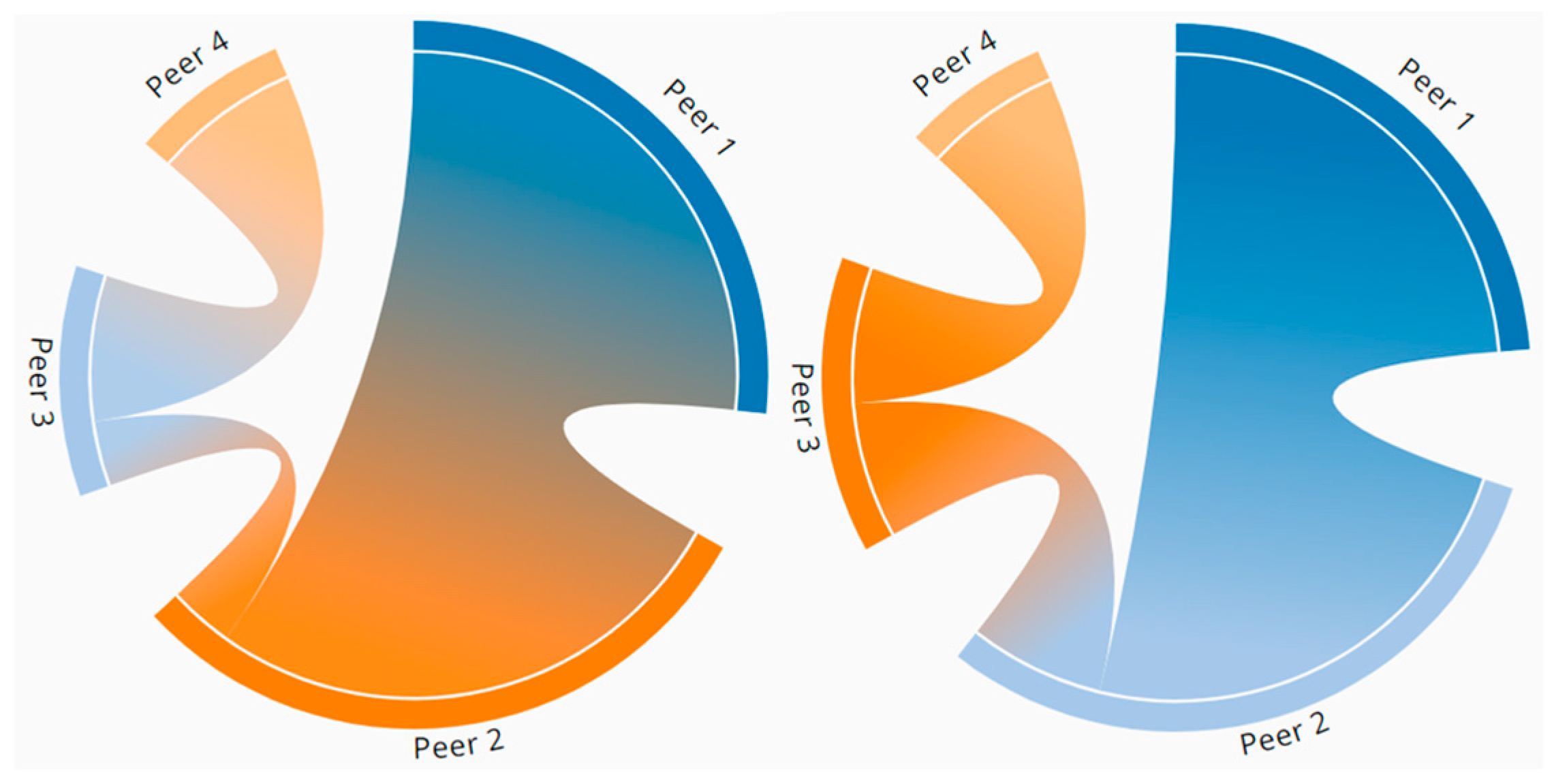
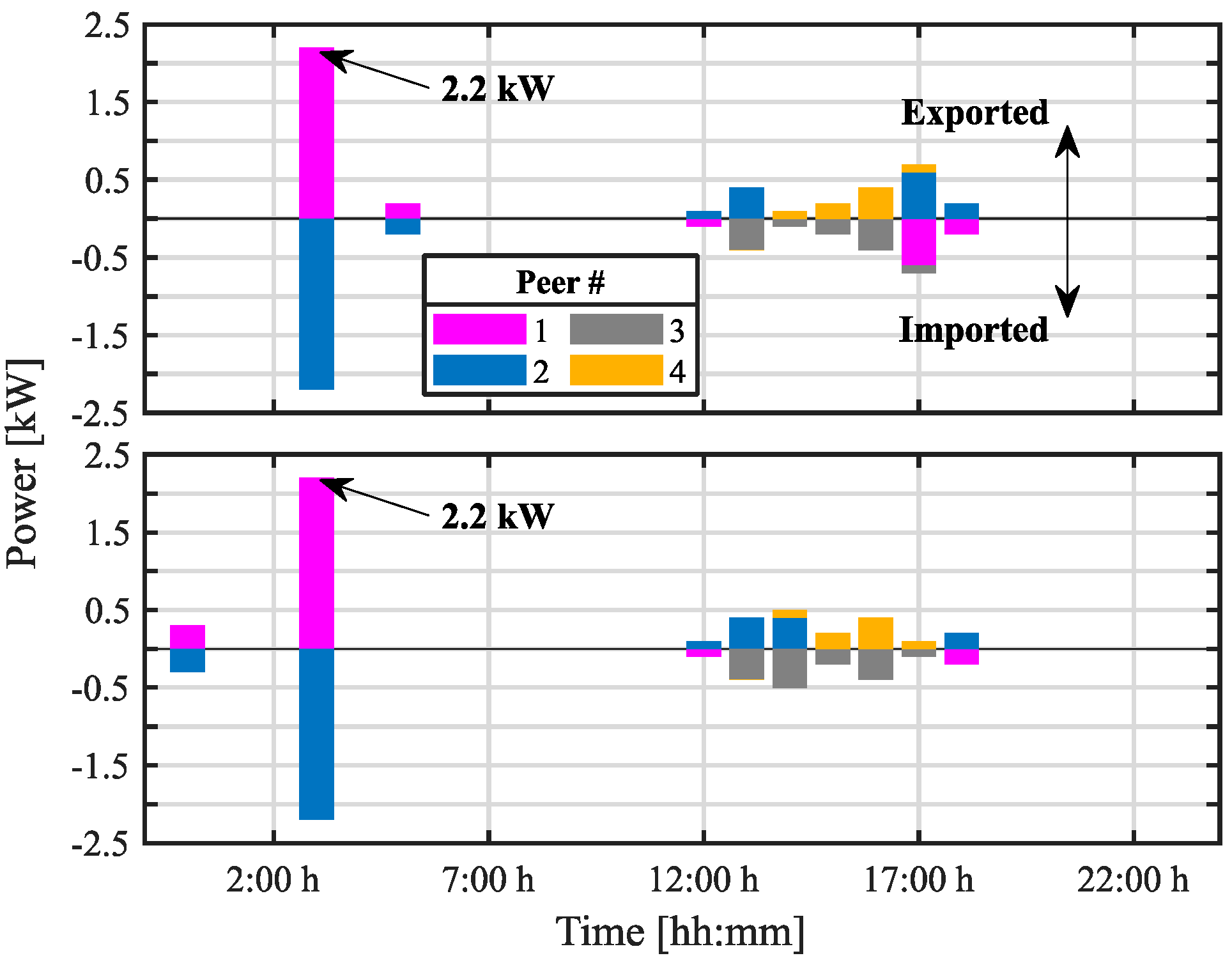
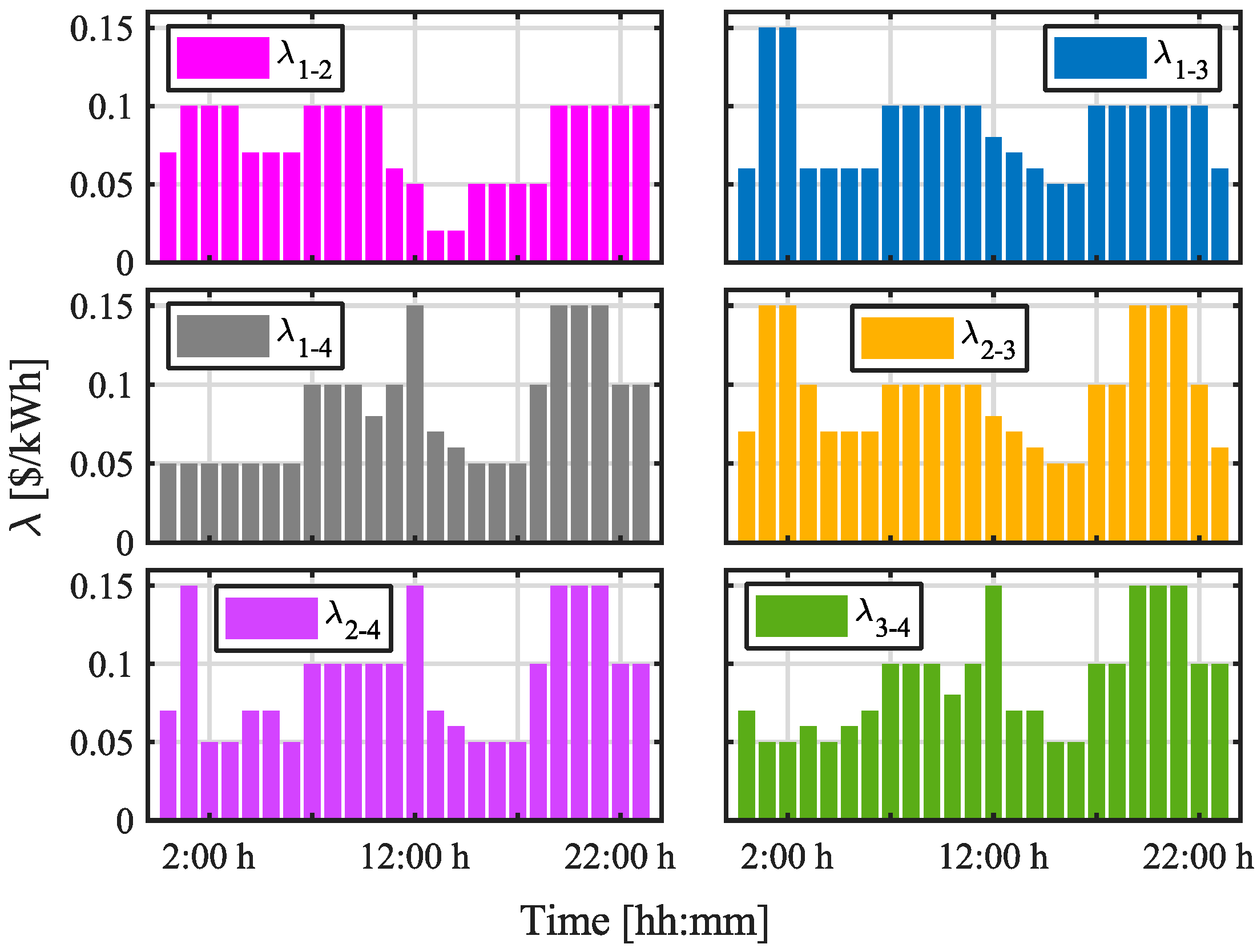
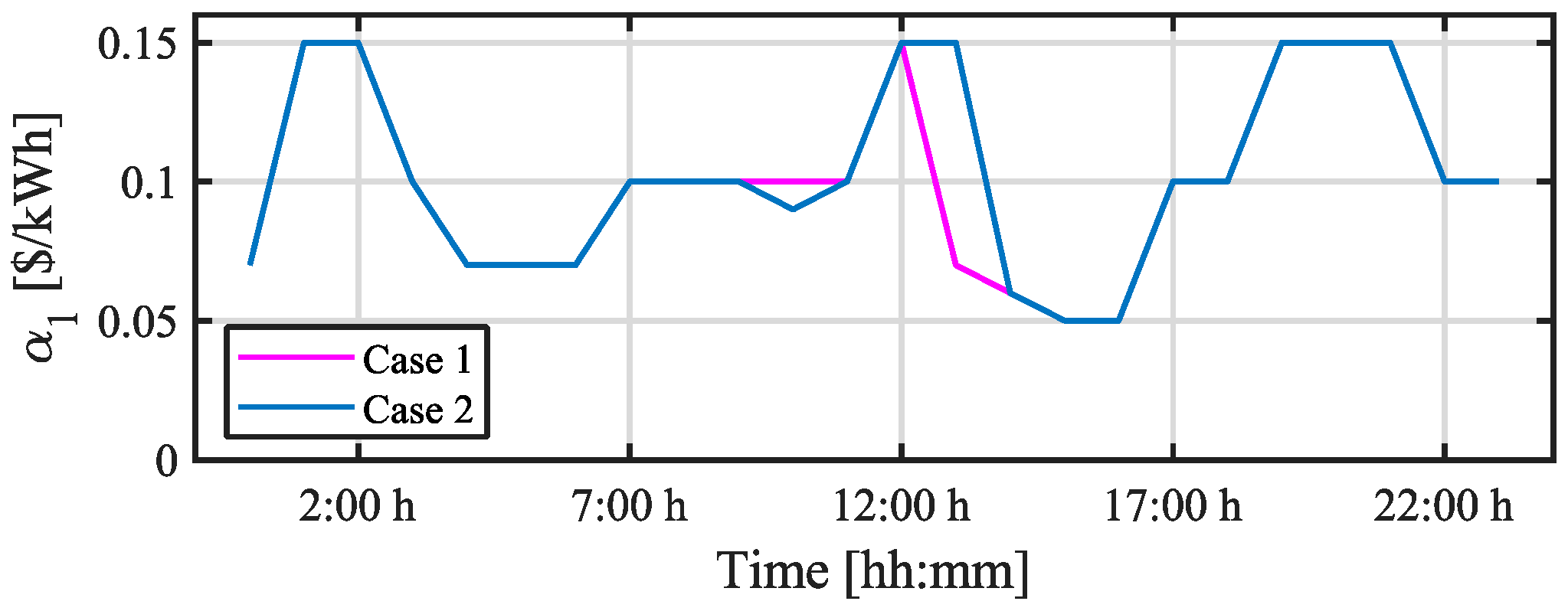
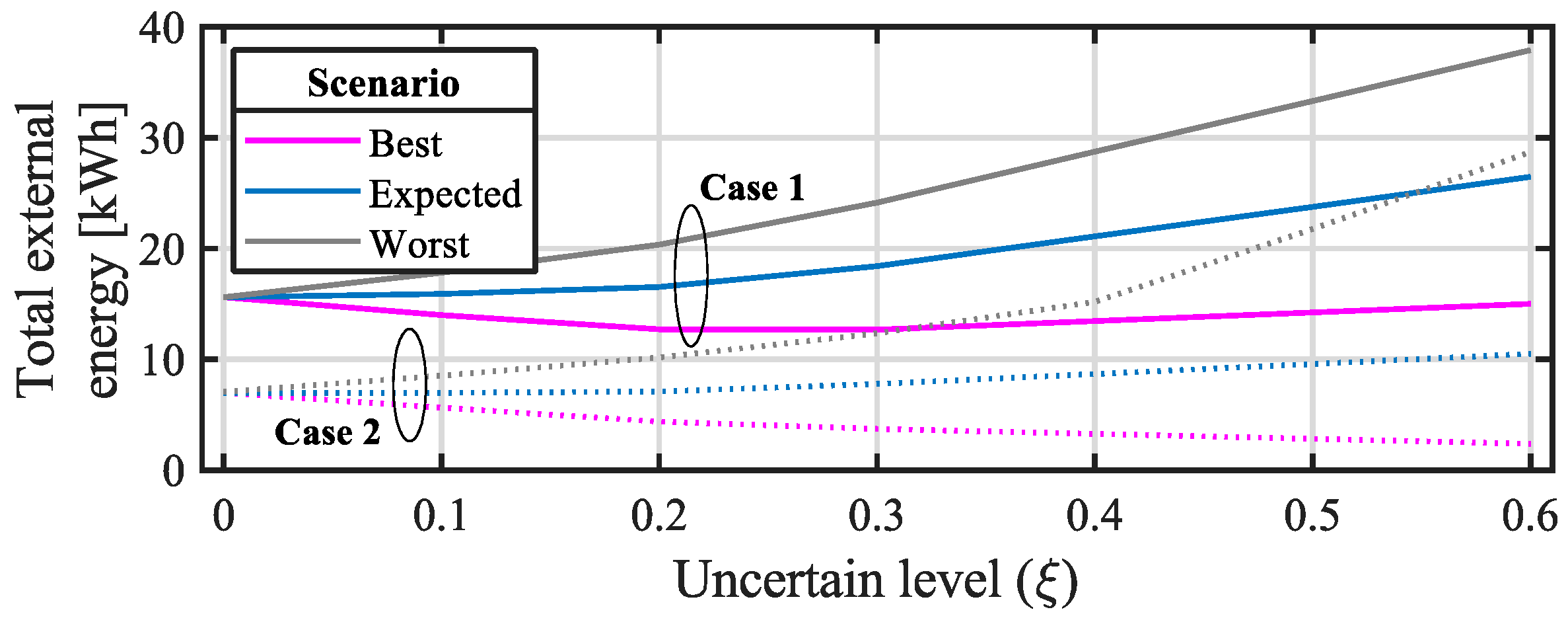
5.2. Results
5.3. Computational Burden
6. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Indices (Set) | |
| ) | Prosumer |
| ) | Time |
| ) | prosumer |
| Time window of a controllable appliance or electric vehicle | |
| ) | Scenario |
| Superscripts | |
| Photovoltaic | |
| Battery energy storage | |
| Electric vehicle | |
| Heating–ventilation–air conditioner | |
| Charging/discharging mode of storage systems | |
| Heating/cooling mode of heating–ventilation–air conditioner units | |
| Indoor/outdoor air | |
| Set-point | |
| Peer-to-peer transactions | |
| External | |
| Minimum/maximum value | |
| Constants and parameters | |
| Time step [h] | |
| Efficiency [pu] | |
| prosumer [kWh] | |
| Temperature [°C] | |
| Mass [kg] | |
| Heat capacity [kJ/(kg∙°C)] | |
| Thermal resistance of the building [J/°C] | |
| Coefficient of performance [-] | |
| Duty cycle [h] | |
| Offer/bid price [$/kWh] | |
| Large positive number (~105) [-] | |
| Decision variables | |
| Power [kW] | |
| Commitment status [Binary] | |
| Energy [kWh] | |
| On/off status of a controllable appliance [Binary] | |
| prosumer [kW] | |
| peer through peer-to-peer trade [kW] | |
| pair of prosumers [$/kWh] | |
| [$/kWh] | |
| [$/kWh] | |
| Auxiliary variable for linearization of complementarity constraints [Binary] | |
Appendix A. Derivation of the Stationary Constraints (25) and (26)
Appendix B. Linearization of (21)
References
- Guerrero, J.; Gebbran, D.; Mhanna, S.; Chapman, A.C.; Verbič, G. Towards a transactive energy system for integration of distributed energy resources: Home energy management, distributed optimal power flow, and peer-to-peer energy trading. Renew. Sustain. Energy Rev. 2020, 132, 110000. [Google Scholar] [CrossRef]
- Soriano, L.A.; Avila, M.; Ponce, P.; de Jesús Rubio, J.; Molina, A. Peer-to-peer energy trades based on multi-objective optimization. Int. J. Electr. Power Energy Syst. 2021, 131, 107017. [Google Scholar] [CrossRef]
- Lilla, S.; Orozco, C.; Borghetti, A.; Napolitano, F.; Tossani, F. Day-Ahead Scheduling of a Local Energy Community: An Alternating Direction Method of Multipliers Approach. IEEE Trans. Power Syst. 2020, 35, 1132–1142. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Kamel, S.; Hasanien, H.M.; Turky, R.A.; Jurado, F. Optimal energy management of cooperative energy communities considering flexible demand, storage and vehicle-to-grid under uncertainties. Sustain. Cities Soc. 2022, 84, 104019. [Google Scholar] [CrossRef]
- Jo, H.-C.; Byeon, G.; Kim, J.-Y.; Kim, S.-K. Optimal Scheduling for a Zero Net Energy Community Microgrid With Customer-Owned Energy Storage Systems. IEEE Trans. Power Syst. 2021, 36, 2273–2280. [Google Scholar] [CrossRef]
- Gomes, I.; Bot, K.; Ruano, M.G.; Ruano, A. Recent Techniques Used in Home Energy Management Systems: A Review. Energies 2022, 15, 2866. [Google Scholar] [CrossRef]
- Kim, H.; Lee, S.K.; Kim, H.; Kim, H. Implementing home energy management system with UPnP and mobile applications. Comput. Commun. 2012, 36, 51–62. [Google Scholar] [CrossRef]
- Chavali, P.; Yang, P.; Nehorai, A. A Distributed Algorithm of Appliance Scheduling for Home Energy Management System. IEEE Trans. Smart Grid 2014, 5, 282–290. [Google Scholar] [CrossRef]
- Rastegar, M.; Fotuhi-Firuzabad, M.; Zareipour, H. Home energy management incorporating operational priority of appliances. Int. J. Electr. Power Energy Syst. 2016, 74, 286–292. [Google Scholar] [CrossRef]
- Anvari-Moghaddam, A.; Monsef, H.; Rahimi-Kian, A. Optimal Smart Home Energy Management Considering Energy Saving and a Comfortable Lifestyle. IEEE Trans. Smart Grid 2015, 6, 324–332. [Google Scholar] [CrossRef]
- Paterakis, N.G.; Erdinç, O.; Bakirtzis, A.G.; Catalão, J.P.S. Optimal Household Appliances Scheduling Under Day-Ahead Pricing and Load-Shaping Demand Response Strategies. IEEE Trans. Ind. Inform. 2015, 11, 1509–1519. [Google Scholar] [CrossRef]
- Shafie-Khah, M.; Siano, P. A Stochastic Home Energy Management System Considering Satisfaction Cost and Response Fatigue. IEEE Trans. Ind. Inform. 2018, 14, 629–638. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Kamel, S.; Aymen, F.; Jurado, F. A novel hybrid lexicographic-IGDT methodology for robust multi-objective solution of home energy management systems. Energy 2022, 253, 124146. [Google Scholar] [CrossRef]
- Javadi, M.S.; Gough, M.; Lotfi, M.; Nezhad, A.E.; Santos, S.F.; Catalão, J.P.S. Optimal self-scheduling of home energy management system in the presence of photovoltaic power generation and batteries. Energy 2020, 210, 118568. [Google Scholar] [CrossRef]
- Javadi, M.S.; Nezhad, A.E.; Nardelli, P.H.; Gough, M.; Lotfi, M.; Santos, S.; Catalão, J.P. Self-scheduling model for home energy management systems considering the end-users discomfort index within price-based demand response programs. Sustain. Cities Soc. 2021, 68, 102792. [Google Scholar] [CrossRef]
- Wang, X.; Li, F.; Dong, J.; Olama, M.M.; Zhang, Q.; Shi, Q.; Kuruganti, T. Tri-Level Scheduling Model Considering Residential Demand Flexibility of Aggregated HVACs and EVs Under Distribution LMP. IEEE Trans. Smart Grid 2021, 12, 3990–4002. [Google Scholar] [CrossRef]
- Rücker, F.; Schoeneberger, I.; Wilmschen, T.; Sperling, D.; Haberschusz, D.; Figgener, J.; Sauer, D.U. Self-sufficiency and charger constraints of prosumer households with vehicle-to-home strategies. Appl. Energy 2022, 317, 119060. [Google Scholar] [CrossRef]
- Ali, A.; Aftab, A.; Akram, M.N.; Awan, S.; Muqeet, H.A.; Arfeen, Z.A. Residential Prosumer Energy Management System with Renewable Integration Considering Multi-Energy Storage and Demand Response. Sustainability 2024, 16, 2156. [Google Scholar] [CrossRef]
- Aljohani, T.M. Multilayer Iterative Stochastic Dynamic Programming for Optimal Energy Management of Residential Loads with Electric Vehicles. Int. J. Energy Res. 2024, 2024, 6842580. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Gurung, S.; Jurado, F. Efficient solution of many-objective Home Energy Management systems. Int. J. Electr. Power Energy Syst. 2022, 136, 107666. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, Y.; Luo, F.; Ranzi, G. Many-Objective HEMS Based on Multi-Scale Occupant Satisfaction Modelling and Second-Life BESS Utilization. IEEE Trans. Sustain. Energy 2022, 13, 934–947. [Google Scholar] [CrossRef]
- Dinh, H.T.; Lee, K.-H.; Kim, D. Supervised-learning-based hour-ahead demand response for a behavior-based home energy management system approximating MILP optimization. Appl. Energy 2022, 321, 119382. [Google Scholar] [CrossRef]
- Yang, J.; Huang, G.; Wei, C. Privacy-aware electricity scheduling for home energy management system. Peer-to-Peer Netw. Appl. 2018, 11, 309–317. [Google Scholar] [CrossRef]
- Long, C.; Wu, J.; Zhou, Y.; Jenkins, N. Peer-to-peer energy sharing through a two-stage aggregated battery control in a community Microgrid. Appl. Energy 2018, 226, 261–276. [Google Scholar] [CrossRef]
- Paudel, A.; Chaudhari, K.; Long, C.; Gooi, H.B. Peer-to-Peer Energy Trading in a Prosumer-Based Community Microgrid: A Game-Theoretic Model. IEEE Trans. Ind. Electron. 2019, 66, 6087–6097. [Google Scholar] [CrossRef]
- Feng, C.; Wen, F.; You, S.; Li, Z.; Shahnia, F.; Shahidehpour, M. Coalitional Game-Based Transactive Energy Management in Local Energy Communities. IEEE Trans. Power Syst. 2020, 35, 1729–1740. [Google Scholar] [CrossRef]
- Daneshvar, M.; Mohammadi-Ivatloo, B.; Zare, K.; Asadi, S.; Anvari-Moghaddam, A. A Novel Operational Model for Interconnected Microgrids Participation in Transactive Energy Market: A Hybrid IGDT/Stochastic Approach. IEEE Trans. Ind. Inform. 2021, 17, 4025–4035. [Google Scholar] [CrossRef]
- Mehrjerdi, H. Peer-to-peer home energy management incorporating hydrogen storage system and solar generating units. Renew. Energy 2020, 156, 183–192. [Google Scholar] [CrossRef]
- Park, D.-H.; Park, J.-B.; Lee, K.Y.; Son, S.-Y.; Roh, J.H. A Bidding-Based Peer-to-Peer Energy Transaction Model Considering the Green Energy Preference in Virtual Energy Community. IEEE Access 2021, 9, 87410–87419. [Google Scholar] [CrossRef]
- Khorasany, M.; Razzaghi, R.; Gazafroudi, A.S. Two-stage mechanism design for energy trading of strategic agents in energy communities. Appl. Energy 2021, 295, 117036. [Google Scholar] [CrossRef]
- Javadi, M.S.; Gough, M.; Nezhad, A.E.; Santos, S.F.; Shafie-Khah, M.; Catalão, J.P.S. Pool trading model within a local energy community considering flexible loads, photovoltaic generation and energy storage systems. Sustain. Cities Soc. 2022, 79, 103747. [Google Scholar] [CrossRef]
- Mu, C.; Ding, T.; Sun, Y.; Huang, Y.; Li, F.; Siano, P. Energy Block-Based Peer-to-Peer Contract Trading With Secure Multi-Party Computation in Nanogrid. IEEE Trans. Smart Grid 2022, 13, 4759–4772. [Google Scholar] [CrossRef]
- Gough, M.; Santos, S.F.; Almeida, A.; Lotfi, M.; Javadi, M.S.; Fitiwi, D.Z.; Catalão, J.P. Blockchain-Based Transactive Energy Framework for Connected Virtual Power Plants. IEEE Trans. Ind. Appl. 2022, 58, 986–995. [Google Scholar] [CrossRef]
- Nezamabadi, H.; Vahidinasab, V. Arbitrage Strategy of Renewable-Based Microgrids via Peer-to-Peer Energy-Trading. IEEE Trans. Sustain. Energy 2021, 12, 1372–1382. [Google Scholar] [CrossRef]
- Stanescu, D.; Enache, F.; Popescu, F. Smart Non-Intrusive Appliance Load-Monitoring System Based on Phase Diagram Analysis. Smart Cities 2024, 7, 1936–1949. [Google Scholar] [CrossRef]
- Mandal, S.; Das, B.K.; Hoque, N. Optimum sizing of a stand-alone hybrid energy system for rural electrification in Bangladesh. J. Clean. Prod. 2018, 200, 12–27. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Mouassa, S.; Jurado, F. A MILP framework for electricity tariff-choosing decision process in smart homes considering ‘Happy Hours’ tariffs. Int. J. Electr. Power Energy Syst. 2021, 131, 107139. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Jordehi, A.R.; Mansouri, S.A.; Jurado, F. Day-ahead scheduling of 100% isolated communities under uncertainties through a novel stochastic-robust model. Appl. Energy 2022, 328, 120257. [Google Scholar] [CrossRef]
- Negarestani, S.; Fotuhi-Firuzabad, M.; Rastegar, M.; Rajabi-Ghahnavieh, A. Optimal Sizing of Storage System in a Fast Charging Station for Plug-in Hybrid Electric Vehicles. IEEE Trans. Transp. Electrif. 2016, 2, 443–453. [Google Scholar] [CrossRef]
- Maher, K.; Bouaiza, A.; Amin, R. Understanding the heat generation mechanisms and the interplay between joule heat and entropy effects as a function of state of charge in lithium-ion batteries. J. Power Sources 2024, 623, 235504. [Google Scholar] [CrossRef]
- Liang, Z.; Chung, C.Y.; Zhang, W.; Wang, Q.; Lin, W.; Wang, C. Enabling High-Efficiency Economic Dispatch of Hybrid AC/DC Networked Microgrids: Steady-State Convex Bi-Directional Converter Models. IEEE Trans. Smart Grid, 2024; early access. [Google Scholar] [CrossRef]
- Boumaiza, A. A blockchain-centric P2P trading framework incorporating carbon and energy trades. Energy Strategy Rev. 2024, 54, 101466. [Google Scholar] [CrossRef]
- Wang, X.; Li, F.; Zhang, Q.; Shi, Q.; Wang, J. Profit-Oriented BESS Siting and Sizing in Deregulated Distribution Systems. IEEE Trans. Smart Grid. 2022, 14, 1528–1540. [Google Scholar] [CrossRef]
- Nekouei, E.; Alpcan, T.; Chattopadhyay, D. Game-Theoretic Frameworks for Demand Response in Electricity Markets. IEEE Trans. Smart Grid 2015, 6, 748–758. [Google Scholar] [CrossRef]
- Jabr, R.A.; Džafić, I.; Pal, B.C. Robust Optimization of Storage Investment on Transmission Networks. IEEE Trans. Power Syst. 2015, 30, 531–539. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, Z.; Li, Z.; Mi, Y. Energy Management for Hybrid AC/DC Distribution System With Microgrid Clusters Using Non-Cooperative Game Theory and Robust Optimization. IEEE Trans. Smart Grid 2020, 11, 1510–1525. [Google Scholar] [CrossRef]
- Kleinert, T.; Labbe, M.; Plein, F.; Schmidt, M. There’s no free lunch: On the hardness of choosing a correct big-M in bilevel optimization. Oper. Res. 2020, 68, 1716–1721. [Google Scholar] [CrossRef]
- Baringo, L.; Conejo, A.J. Strategic Offering for a Wind Power Producer. IEEE Trans. Power Syst. 2013, 28, 4645–4654. [Google Scholar] [CrossRef]
- Zhuo, Z.; Du, E.; Zhang, N.; Kang, C.; Xia, Q.; Wang, Z. Incorporating Massive Scenarios in Transmission Expansion Planning With High Renewable Energy Penetration. IEEE Trans. Power Syst. 2020, 35, 1061–1074. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Kamel, S.; Hasanien, H.M.; Arévalo, P.; Turky, R.A.; Jurado, F. A stochastic-interval model for optimal scheduling of PV-assisted multi-mode charging stations. Energy 2022, 253, 124219. [Google Scholar] [CrossRef]
- Wang, X.; Li, F.; Zhao, J.; Olama, M.; Dong, J.; Shuai, H.; Kuruganti, T. Tri-level hybrid interval-stochastic optimal scheduling for flexible residential loads under GAN-assisted multiple uncertainties. Int. J. Electr. Power Energy Syst. 2023, 146, 108672. [Google Scholar] [CrossRef]
- Nezamabadi, H.; Vahidinasab, V. Market bidding strategy of the microgrids considering demand response and energy storage potential flexibilities. IET Gener. Transm. Distrib. 2019, 13, 1346–1357. [Google Scholar] [CrossRef]
- Gurobi Optimizer Reference Manual. Available online: https://www.gurobi.com/wp-content/plugins/hd_documentations/documentation/9.1/refman.pdf (accessed on 30 October 2024).
- Vespermann, N.; Hamacher, T.; Kazempour, J. Risk Trading in Energy Communities. IEEE Trans. Smart Grid 2021, 12, 1249–1263. [Google Scholar] [CrossRef]

| Ref. | Model | Uncertainties | Remarks |
|---|---|---|---|
| [3] | MILP with alternating direction of multipliers | No | Branch losses are included as indirect costs while P2P transactions are cooperative |
| [4] | MILP, two-stage | Yes, using interval notation and iterative procedure | Domestic appliances and storage are modeled as collective assets and scheduled to maximize the collective welfare |
| [5] | MILP | No | Peers trade with storage capacity in a local market structure |
| [23] | Quadratic without explicitly modeling P2P trading | No | Focused on limiting the amount of information exchanged with the system |
| [24] | Non-linear/heuristic | No | Transaction prices are calculated using the modified supply–demand ratio method while appliances’ scheduling is performed under rule-based decisions |
| [25] | Quadratic utility functions. Evolutionary game among buyers | No | Interactions among buyers and sellers are modeled using an M-leader and N-follower Stackelberg game approach |
| [26] | MILP with Coalitional game | Yes, using probability functions | Rayleigh distribution is used to capture uncertain in renewable outputs |
| [27] | MILP with cooperative P2P trading | Yes, using a stochastic-IGDT method | The original hybrid stochastic-IGDT formulation allows to adopt risk-seeker and risk-averse operational strategies |
| [28] | MILP with coordinator-ruled P2P transactions | Yes, using renewable scenarios | An electrolyzer and fuel-cell modeling are included in the formulation. |
| [29] | MILP with coordinator-ruled P2P transactions | No | Green and normal loads and prices are included together with storage depreciation cost. |
| [30] | MILP | No | Peers can trade energy in a P2P mechanism from which energy allocation is decided on the basis of bids from prosumers |
| [31] | MILP with rule-based P2P mechanism | No | A rule-based mechanism is proposed for P2P transactions while prosumers are encouraged to participate through demand response initiatives |
| [32] | MILP with garbled circuit | No | Privacy concerns are minimized using a garbled circuit-based price comparison mechanism is proposed based on a secure multi-party computation |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| /// [kWh] | 5/1/16/3.2 | [kJ/(kg∙°C)] | 1.01 |
| // [kW] | 2/3.7/2 | [J/°C] | 3.2∙10−6 |
| // [°C] | 22.5/23.5/23 | [-] | 1.2 |
| / [%] | 95/95 | 0:00–9:00 h | |
| [kg] | 1500 | [kWh] | 9.6 |
| Power [kW] | Duty Cycle [h] | Time Window | Type |
|---|---|---|---|
| 2 | 4 | 4:00–20:00 h | Non-interruptible |
| 1.2 | 3 | 6:00–22:00 h | Interruptible |
| 0.5 | 2 | 16:00–23:00 h | Non-interruptible |
| Result | Case 1 | Case 2 |
|---|---|---|
| Total importable | 61.75 kWh | 50.80 kWh (−21.5%) |
| Total exportable | 22.86 kWh | 35.40 kWh (+35.4%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zetawi, A.A.; Tostado-Véliz, M.; Hasanien, H.M.; Jurado, F. A Robust-Based Home Energy Management Model for Optimal Participation of Prosumers in Competitive P2P Platforms. Energies 2024, 17, 5735. https://doi.org/10.3390/en17225735
Zetawi AA, Tostado-Véliz M, Hasanien HM, Jurado F. A Robust-Based Home Energy Management Model for Optimal Participation of Prosumers in Competitive P2P Platforms. Energies. 2024; 17(22):5735. https://doi.org/10.3390/en17225735
Chicago/Turabian StyleZetawi, Alaa Al, Marcos Tostado-Véliz, Hany M. Hasanien, and Francisco Jurado. 2024. "A Robust-Based Home Energy Management Model for Optimal Participation of Prosumers in Competitive P2P Platforms" Energies 17, no. 22: 5735. https://doi.org/10.3390/en17225735
APA StyleZetawi, A. A., Tostado-Véliz, M., Hasanien, H. M., & Jurado, F. (2024). A Robust-Based Home Energy Management Model for Optimal Participation of Prosumers in Competitive P2P Platforms. Energies, 17(22), 5735. https://doi.org/10.3390/en17225735









