Design and Visual Implementation of a Regional Energy Risk Superposition Model for Oil Tank Farms
Abstract
1. Introduction
2. Basic Model
2.1. Individual Risk Calculation Model
2.2. Societal Risk Calculation Model
- (1)
- Grid the risk area at an appropriate density.
- (2)
- Determine the weather conditions in the region and the frequency of leaks from each tank.
- (3)
- Consider all the types of accidents that may occur in the region and add data on the consequences of the accidents, such as thermal radiation, explosion overpressure, etc., to the grid.
- (4)
- Select one of the weather classes.
- (5)
- Select one of the accident types that may occur in that weather class.
- (6)
- Select a grid and calculate the probability of death Pd based on the consequences of the accident, and then get the number of fatalities Nx,y|o in a single grid point.
- (7)
- Repeat steps (4)–(6) until all grid deaths have been calculated.
- (8)
- Add up all the grid fatalities to get the total number of fatalities N.
- (9)
- Calculate the frequency F of the accident.
- (10)
- Repeat steps (4)–(9), considering all weather classes, wind directions, and accident types. Use the calculated N and F to plot the F-N curve.

3. Methods
3.1. Design Process
3.1.1. Evaluation Objectives and Data Collection
3.1.2. Accident Scenario Construction
3.2. Program Development
3.2.1. Individual Risk Architecture
3.2.2. Societal Risk Architecture
3.3. Outcome Visualization
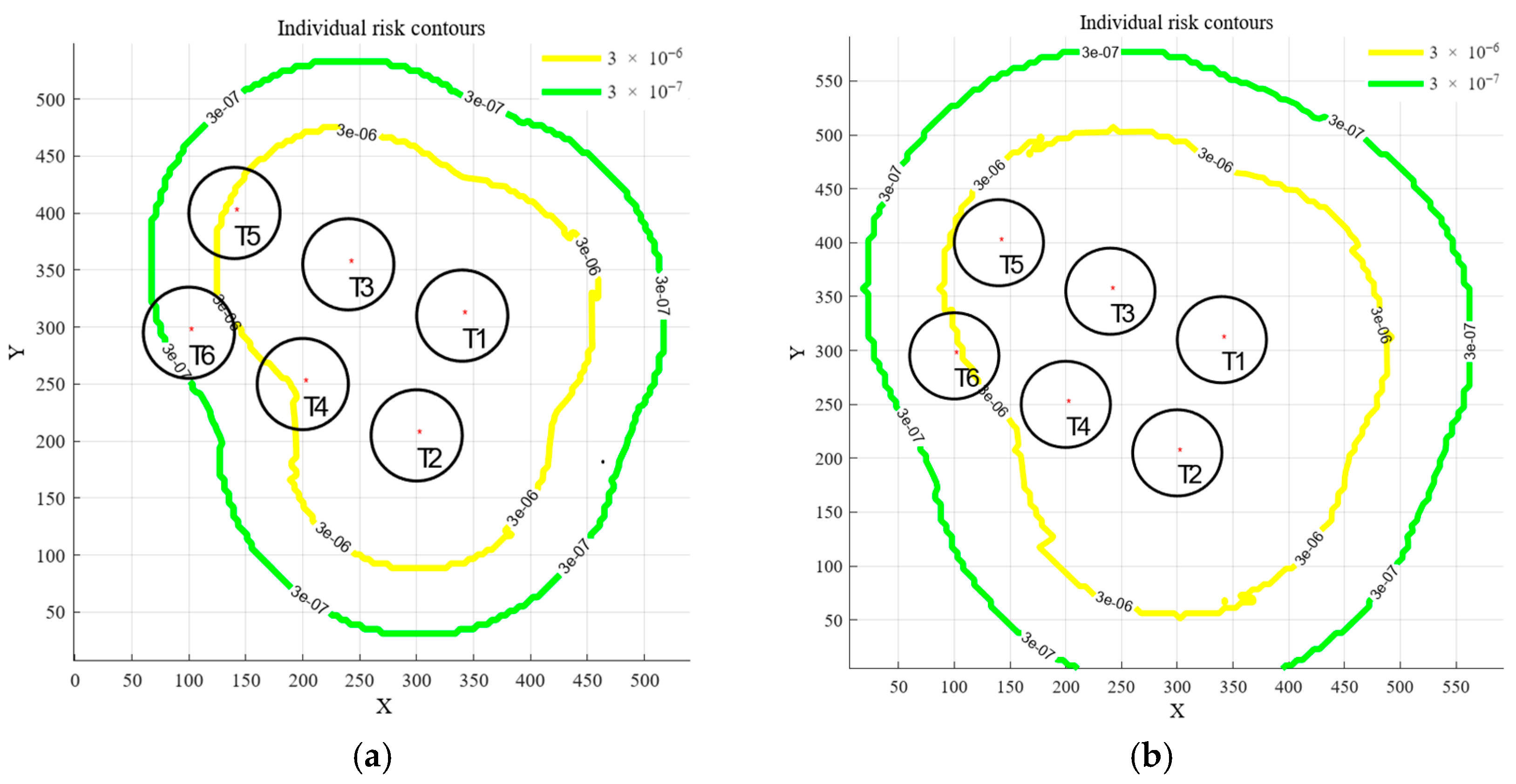
4. Case Study
5. Conclusions
- (1)
- The proposed methodology effectively incorporates diurnal variations and weather factors into the risk assessment framework, offering a more nuanced and reliable evaluation of both individual and societal risks. This approach provides a practical tool for engineering applications, particularly in environments like oil tank farms, where maintaining energy security is of paramount importance.
- (2)
- The model simplifies traditionally complex risk assessment processes, offering a user-friendly and efficient platform for risk analysis. By visually mapping risks and integrating multiple risk factors, it enhances both the accuracy and clarity of assessments, thus contributing to the safer operation of oil tank farms and supporting broader energy supply security.
- (3)
- While the application of the model to case studies has demonstrated its capability to visually display key quantitative indicators such as individual and societal risk, the accuracy of the results is dependent upon the quality and completeness of the input data. Future research should prioritize improving data acquisition and processing methods to enhance data quality and effectively manage uncertainties. Additionally, expanding the model’s application to a wider range of industrial settings will further strengthen its role in safeguarding energy infrastructure. Integrating advanced modeling techniques, such as machine learning algorithms, could also significantly improve the predictive capabilities of risk assessments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Name | Units | Description |
|---|---|---|
| n | - | Number of tanks that failed |
| fs | - | Failure frequency |
| Pi | - | Ignition probability |
| E,L | kW/m2 | Thermal radiation matrix for early pool fire and late pool fire, which can be obtained from the pool fire solid flame calculation model |
| O | bar | The shock wave overpressure matrix, which can be obtained from the vapor cloud explosion (VCE) TNO calculation model |
| B | kW/m2 | BLEVE thermal radiation matrix |
| Pday | - | Percentage of daytime |
| Pnight | - | Percentage of nighttime |
| PM | - | Select a weather class, with wind frequency matrix for 16 sectors |
| Gs | - | Grid size. Enter 100 to generate a grid space of 100 × 100 units |
| step | m | Grid step, unit length of the grid |
| population | - | Population matrix |
| Pd | - | The probability of death at the grid point |
References
- CTS News. At Least 17 Dead, 50 Injured in Oil Depot Explosion at Indonesia’s State-1un Oil Company. Available online: https://www.chinatimes.com/realtimenews/20230304001159-260408?chdtv (accessed on 27 August 2024).
- Investigation Report on the “5·1” Major Explosion and Fire Accident in Sinochem Liaocheng Luxi Hydrogen Peroxide New Material Technology, Co. Available online: http://yjt.shandong.gov.cn/zwgk/zdly/aqsc/sgxx/202404/t20240419_4720072.html (accessed on 27 August 2024).
- Swuste, P.; van Nunen, K.; Reniers, G.; Khakzad, N. Domino Effects in Chemical Factories and Clusters: An Historical Perspective and Discussion. Process. Saf. Environ. Prot. 2019, 124, 18–30. [Google Scholar] [CrossRef]
- Meng, G.; Hu, H. Research on Multi-Point Monitoring Data Grid Model and Inversion Positioning Method for Gas Leakage in Oil and Gas Stations. Sustainability 2024, 16, 1638. [Google Scholar] [CrossRef]
- Bartolozzi, V.; Bajardi, S.; Vasile, F.; Marino, S. Safety Integrated Area Analysis: A Recent Case Study. In Proceedings of the Cisap4: 4th International Conference on Safety & Environment in Process Industry, Florence, Italy, 7–10 March 2010; Buratti, S.S., Ed.; Aidic Servizi Srl: Milan, Italy; Volume 19, pp. 457–462. [Google Scholar]
- Zhang, H.; Cao, X.; Yuan, X.; Wu, F.; Wang, J.; Zhang, Y.; Li, Q.; Liu, H.; Huang, Z. Study on Thermal Radiation Characteristics and the Multi-Point Source Model of Hydrogen Jet Fire. Appl. Sci. 2024, 14, 7098. [Google Scholar] [CrossRef]
- Su, J.; Zhang, X.; Zhou, L.; Yin, Y. A Quantitative Analysis Pattern for Regional Risk Conduction. J. Phys. Conf. Ser. 2019, 1419, 012032. [Google Scholar] [CrossRef]
- Lee, K.; Kang, C. Expansion of Next-Generation Sustainable Clean Hydrogen Energy in South Korea: Domino Explosion Risk Analysis and Preventive Measures Due to Hydrogen Leakage from Hydrogen Re-Fueling Stations Using Monte Carlo Simulation. Sustainability 2024, 16, 3583. [Google Scholar] [CrossRef]
- Jonkman, S.N.; Jongejan, R.; Maaskant, B. The Use of Individual and Societal Risk Criteria Within the Dutch Flood Safety Policy—Nationwide Estimates of Societal Risk and Policy Applications. Risk Anal. Int. J. 2011, 31, 282–300. [Google Scholar] [CrossRef] [PubMed]
- Park, B.; Kim, Y.; Lee, K.; Paik, S.; Kang, C. Risk Assessment Method Combining Independent Protection Layers (IPL) of Layer of Protection Analysis (LOPA) and RISKCURVES Software: Case Study of Hydrogen Refueling Stations in Urban Areas. Energies 2021, 14, 4043. [Google Scholar] [CrossRef]
- Kwak, H.; Kim, M.; Min, M.; Park, B.; Jung, S. Assessing the Quantitative Risk of Urban Hydrogen Refueling Station in Seoul, South Korea, Using SAFETI Model. Energies 2024, 17, 867. [Google Scholar] [CrossRef]
- Abdolhamidzadeh, B.; Abbasi, T.; Rashtchian, D.; Abbasi, S.A. Corrigendum to “A New Method for Assessing Domino Effect in Chemical Process Industry” [J. Hazard. Mater. 2010, 182, 416–426]. J. Hazard. Mater. 2010, 184, 877. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Liu, X. Reprint of: Regional Risk Assessment for Urban Major Hazards Based on GIS Geoprocessing to Improve Public Safety. Saf. Sci. 2017, 97, 112–119. [Google Scholar] [CrossRef]
- Rajeev, K.; Soman, S.; Renjith, V.; George, P. Human Vulnerability Mapping of Chemical Accidents in Major Industrial Units in Kerala, India for Better Disaster Mitigation. Int. J. Disaster Risk Reduct. 2019, 39, 101247. [Google Scholar] [CrossRef]
- Tahmid, M.; Dey, S.; Syeda, S.R. Mapping Human Vulnerability and Risk Due to Chemical Accidents. J. Loss Prev. Process Ind. 2020, 68, 104289. [Google Scholar] [CrossRef]
- Dormohammadi, A.; Zarei, E.; Delkhosh, M.B.; Gholami, A. Risk Analysis by Means of a QRA Approach on a LPG Cylinder Filling Installation. Process Saf. Prog. 2014, 33, 77–84. [Google Scholar] [CrossRef]
- GB/T 37243-2019; Determination Method of External Safety Distance for Hazardous Chemicals Production Units and Storage Installations. National Standards of People’s Republic of China: Beijing, China, 2019. Available online: https://www.chinesestandard.net/Related.aspx/GBT37243-2019 (accessed on 20 September 2024).
- SH/T 3226-2024; Standards for Quantitative Analysis of Petrochemical Processes Risks. Ministry of Industry and Information Technology: Beijing, China, 2024. Available online: http://www.standardcn.com/standard_bp/BPG_ReadFile.asp?FID=20861 (accessed on 20 September 2024).
- AQ/T 3046-2013; Guidelines for Quantitative Risk Assessment of Chemical Enterprises. National Standardization Technical Committee of Safety Production Technical Committee on Chemical Safety: Beijing, China, 2013. Available online: https://www.chinesestandard.net/Related.aspx/AQT3046-2013 (accessed on 20 September 2024).
- DNV. The MPACT Risk Model Theory. Available online: https://myworkspace.dnv.com/download/public/phast/technical_documentation/09_risk/MPACT%20Risk%20Model%20Theory.pdf (accessed on 20 September 2024).
- ISO 31000:2018; Risk Management—Guidelines. ISO: Geneva, Switzerland, 2018. Available online: https://www.iso.org/standard/65694.html (accessed on 20 September 2024).
- Guelzim, A.; Chakir, B.A.; Ettahir, A.; Mbarki, A. Use of Statistical Tools for Comparison between Different Analytical and Semi-Empirical Models of the Bleve Fireball. Front. Heat Mass Transf. 2023, 21, 125–140. [Google Scholar] [CrossRef]
- Zhao, J.; Wu, M.; Lu, H.; Li, G.; Xu, Y.; Tian, M. Quantitative Risk Assessment of an Oil-Gas-Hydrogen-Electricity Integrated Energy Station in China. ACS Omega 2024, 9, 38887–38896. [Google Scholar] [CrossRef] [PubMed]
- Carboni, M.; Pio, G.; Mocellin, P.; Vianello, C.; Maschio, G.; Salzano, E. On the Flash Fire of Stratified Cloud of Liquefied Natural Gas. J. Loss Prev. Process Ind. 2022, 75, 104680. [Google Scholar] [CrossRef]
- Tsukada, R.I.; Shiguemoto, D.A.; Vianna, S.S. The TNO Multi-Energy Method Combined to Mathematical Programming and Computational Fluid Dynamics for Optimisation of Gas Detectors. J. Loss Prev. Process Ind. 2023, 83, 105035. [Google Scholar] [CrossRef]
- Shen, G.; Zhou, K.; Wu, F.; Jiang, J.; Dou, Z. A Model Considering the Flame Volume for Prediction of Thermal Radiation from Pool Fire. Fire Technol. 2019, 55, 129–148. [Google Scholar] [CrossRef]
- GB 36894-2018; Risk Criteria for Hazardous Chemicals Production Unit and Storage Installations. National Standards of People’s Republic of China: Beijing, China. Available online: https://www.chinesestandard.net/Related.aspx/GB36894-2018 (accessed on 20 September 2024).
- IEC 31010:2019; Risk Management—Risk Assessment Techniques. ISO: Geneva, Switzerland, 2019. Available online: https://www.iso.org/standard/72140.html (accessed on 30 June 2019).








| Event Tree | Branch 1 | Branch 2 | Branch 3 | Branch 4 | Po |
|---|---|---|---|---|---|
| Independent BLEVE | Pb | ||||
| Independent Pool Fire | PwssPp | ||||
| Continuous release, No Rainout | Immediate | BLEVE | PsPwssPblPi | ||
| Explosion | PsPwssPePi | ||||
| Not immediate | Delayed ignition | Explosion | (1 − Pi)PwssPePdi | ||
| Instantaneous release, No Rainout | Immediate | BLEVE | PwssPbPi | ||
| Explosion | PwssPePi | ||||
| Not immediate | Delayed ignition | Explosion | (1 − Pi)PwssPePdi | ||
| Continuous release, Rainout | Immediate | Not short | Pool fire | (1 − Ps)PwssPi | |
| Short release | BLEVE and pool fire | PsPwssPbpPi | |||
| BLEVE alone | PsPwssPblPi | ||||
| Explosion and pool fire | PsPwssPepPi | ||||
| Explosion alone | PsPwssPePi | ||||
| Pool fire alone | PsPwssPpPi | ||||
| Not immediate | Dispersion | Delayed | Explosion | (1 − Pi)PwssPePdi | |
| Residual | Pool fire | (1 − Pi)PwssPrpPirp | |||
| Instantaneous release, Rainout | Immediate | BLEVE and pool fire | PwsPbpPi | ||
| BLEVE alone | PwsPblPi | ||||
| Explosion and pool fire | PwsPepPi | ||||
| Explosion alone | PwsPePi | ||||
| Pool fire alone | PwsPpPi | ||||
| Not immediate | Dispersion | Delayed | Explosion | (1 − Pi)PwsPePdi | |
| Residual | Pool fire | (1 − Pi)PwsPrpPirp |
| Protective Target | Individual Risk Benchmark (Times/Year)< | |
|---|---|---|
| New Facilities | Using Facilities | |
| General protective targets of Category III (population < 30) | 1 × 10−5 | 3 × 10−5 |
| General protective targets of Category II (30 ≤ population < 100) | 3 × 10−6 | 1 × 10−5 |
| High sensitivity protective targets; Important protective targets; General protective targets of Category I (population ≥ 100) | 3 × 10−7 | 3 × 10−6 |
| Time Period | Weather Type | Wind Direction | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | NNE | NE | ENE | E | ESE | SE | SSE | S | SSW | SW | WSW | W | WNW | NW | NNW | ||
| Daytime | 0.1/F | 1.2 | 0.8 | 1.24 | 1.63 | 2.77 | 2.8 | 2.1 | 1.2 | 1.7 | 3.3 | 3.3 | 2.03 | 1.6 | 1.93 | 2.63 | 1.64 |
| 1.5/D | 1.2 | 0.8 | 1.24 | 1.63 | 2.77 | 2.8 | 2.1 | 1.2 | 1.7 | 3.3 | 3.3 | 2.03 | 1.6 | 1.93 | 2.63 | 1.64 | |
| 5/D | 1.2 | 0.8 | 1.24 | 1.63 | 2.77 | 2.8 | 2.1 | 1.2 | 1.7 | 3.3 | 3.3 | 2.03 | 1.6 | 1.93 | 2.63 | 1.64 | |
| Nighttime | 0.1/F | 1.2 | 0.8 | 1.24 | 1.63 | 2.77 | 2.8 | 2.1 | 1.2 | 1.7 | 3.3 | 3.3 | 2.03 | 1.6 | 1.93 | 2.63 | 1.64 |
| 1.5/D | 1.2 | 0.8 | 1.24 | 1.63 | 2.77 | 2.8 | 2.1 | 1.2 | 1.7 | 3.3 | 3.3 | 2.03 | 1.6 | 1.93 | 2.63 | 1.64 | |
| 5/D | 1.2 | 0.8 | 1.24 | 1.63 | 2.77 | 2.8 | 2.1 | 1.2 | 1.7 | 3.3 | 3.3 | 2.03 | 1.6 | 1.93 | 2.63 | 1.64 | |
| Tank Parameters | Failure Parameters | ||
|---|---|---|---|
| Height (m) | 21.8 | Leak height (m) | 10 |
| Radius (m) | 40 | Leakage hole diameter (m) | 0.025 |
| Material type | Crude oil (dodecane, N-HEXANE) | Failure probability | 0.0001 |
| Material quality (kg) | 8.65 × 107 | Immediate ignition probability | 0.065 |
| Number of failed tanks | 3 | Consequence data (early pool fire, late pool fire, blast overpressure, BLEVE) | Calculated from Algorithm |
| Hole Leakage (0~5 mm) | Medium-Sized Hole Leakage (5~50 mm) | Nozzle Leakage (50~100 mm) | |
|---|---|---|---|
| atmospheric storage tank | 4 × 10−5 | 1 × 10−4 | 1 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Zhang, X.; Xie, S.; Qu, S.; Chen, H.; Xu, Q.; Chen, G. Design and Visual Implementation of a Regional Energy Risk Superposition Model for Oil Tank Farms. Energies 2024, 17, 5775. https://doi.org/10.3390/en17225775
Yang Y, Zhang X, Xie S, Qu S, Chen H, Xu Q, Chen G. Design and Visual Implementation of a Regional Energy Risk Superposition Model for Oil Tank Farms. Energies. 2024; 17(22):5775. https://doi.org/10.3390/en17225775
Chicago/Turabian StyleYang, Yufeng, Xixiang Zhang, Shuyi Xie, Shanqi Qu, Haotian Chen, Qiming Xu, and Guohua Chen. 2024. "Design and Visual Implementation of a Regional Energy Risk Superposition Model for Oil Tank Farms" Energies 17, no. 22: 5775. https://doi.org/10.3390/en17225775
APA StyleYang, Y., Zhang, X., Xie, S., Qu, S., Chen, H., Xu, Q., & Chen, G. (2024). Design and Visual Implementation of a Regional Energy Risk Superposition Model for Oil Tank Farms. Energies, 17(22), 5775. https://doi.org/10.3390/en17225775







