Energy-Oriented Modeling of Hot Stamping Production Line: Analysis and Perspectives for Reduction
Abstract
:1. Introduction
2. Literature Review
2.1. Regulation of the Hot Stamping Process
2.2. Related Works on Energy Consumption Modeling of Hot Stamping
3. Energy Consumption Modeling of Sequential Process Stages
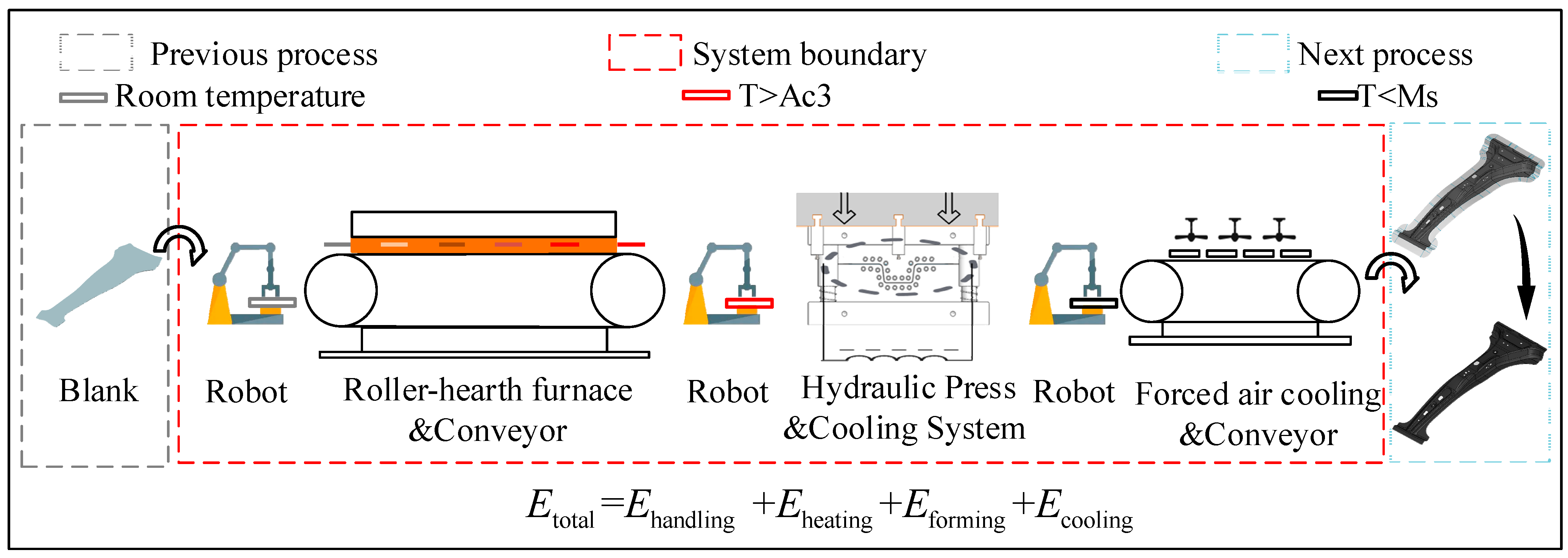
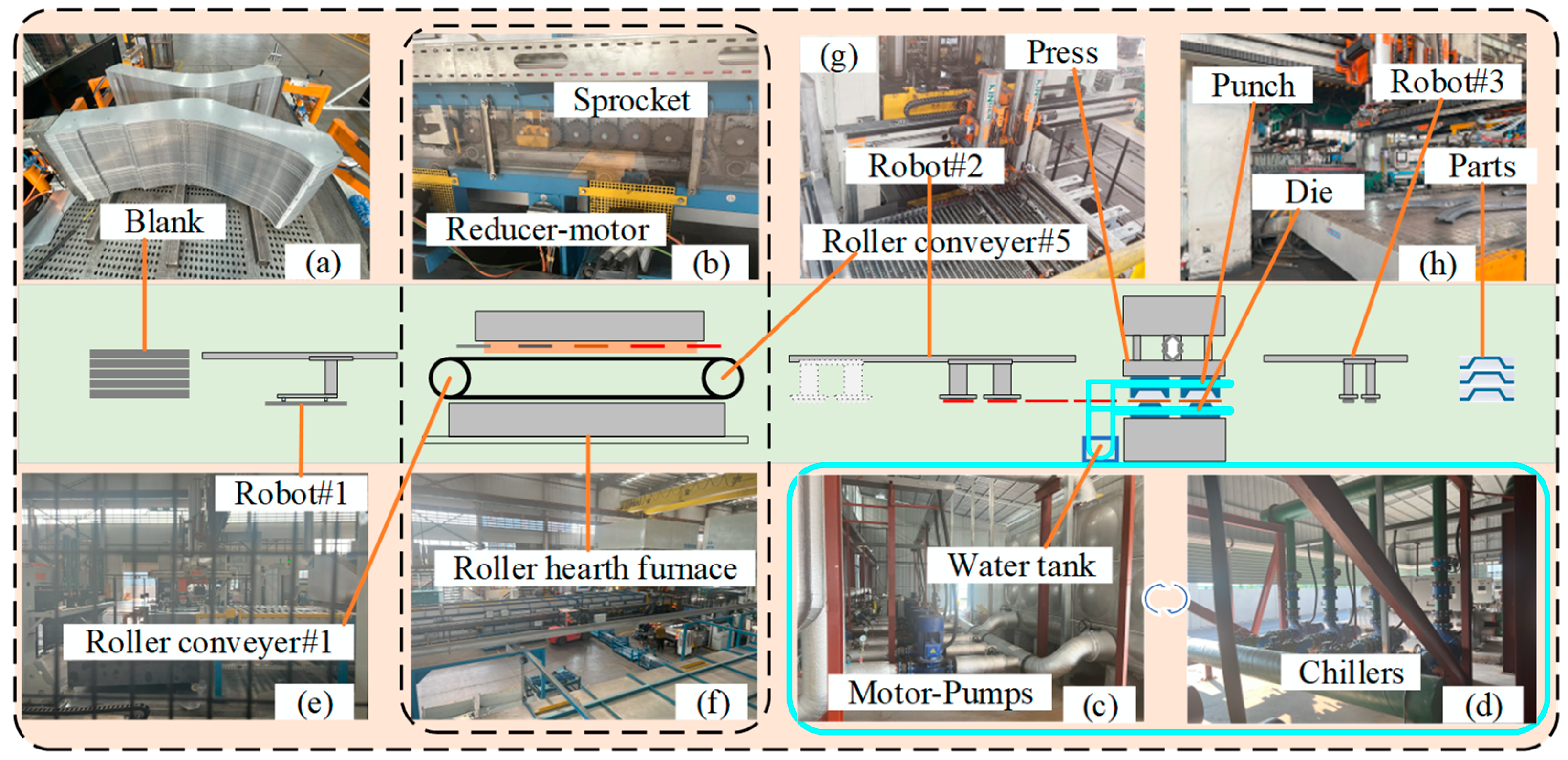
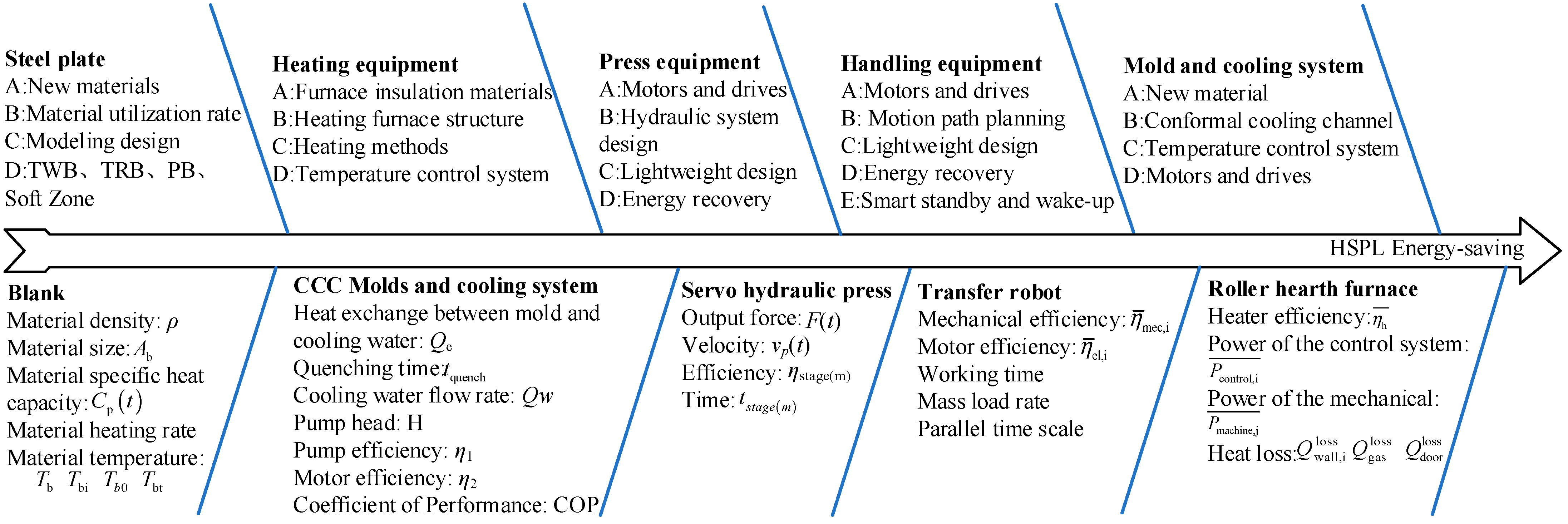
3.1. Hot Stamping Production Line and System Boundary
- (1)
- Handling: each step must be transferred from the mechanical arm to the next step, and these operations must consume energy.
- (2)
- Heating: heating the blank to the optimal temperature and maintaining it until complete austenitization is achieved constitutes a critical aspect in the energy consumption analysis of HSPL.
- (3)
- Forming: operating the hydraulic press to form and quench the blank results in significant energy consumption.
- (4)
- Cooling: the quenching process requires continuous operation of cooling pump motors and heat exchangers, resulting in substantial energy consumption.
3.2. Energy Consumption Analysis of Automatic Transfer Device for Loading and Unloading
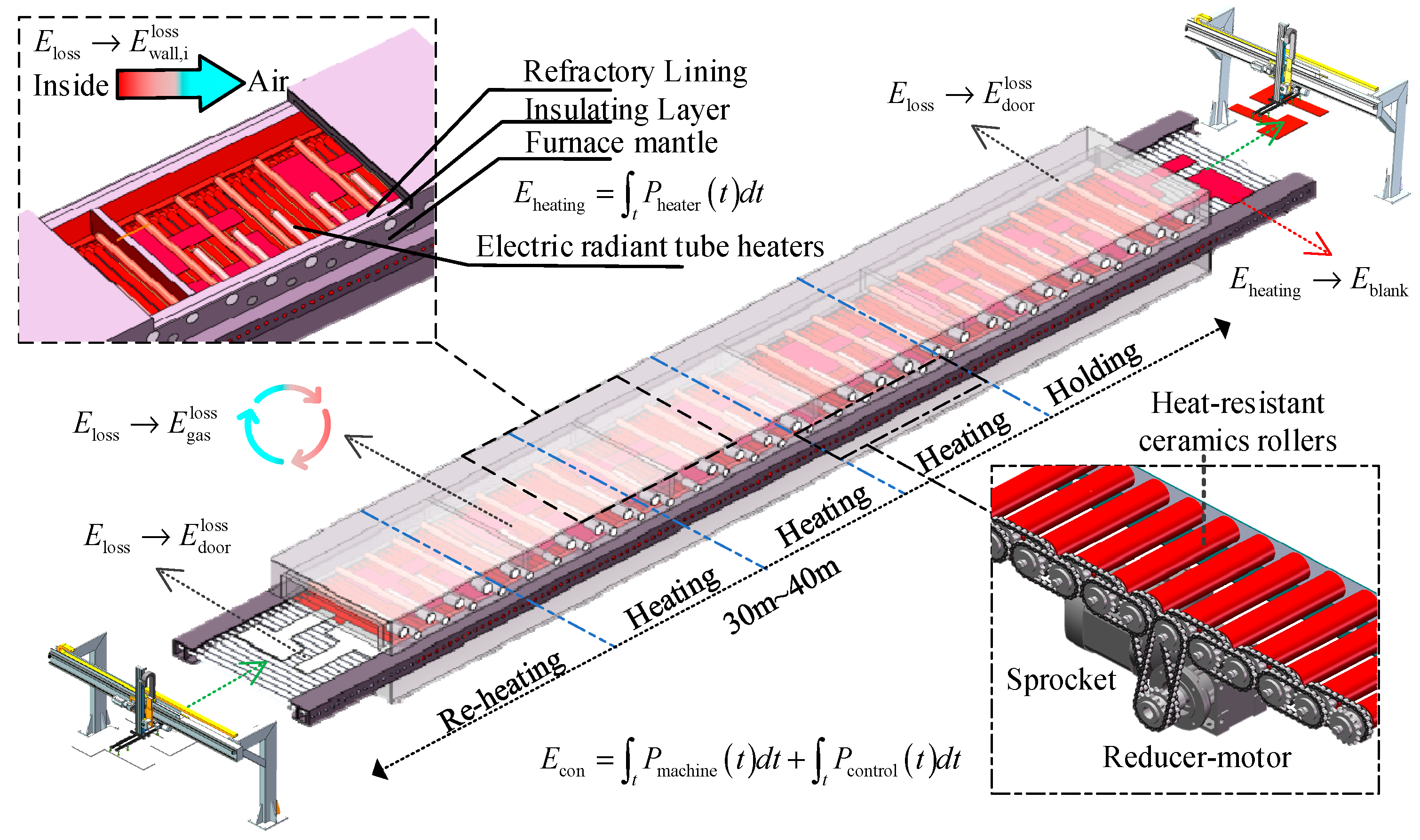
3.3. Energy Consumption Analysis of Hearth Furnace
3.3.1. Fixed Energy Consumption Model of the Roller Hearth Furnace
3.3.2. Heat Loss Model of the Roller Hearth Furnace
- (1)
- Heat exchange with the surrounding environment. Heat is transferred through the furnace’s outer walls due to temperature gradients with the environment. To minimize this heat loss, modern furnaces are equipped with a multi-layered design that includes a refractory lining, an insulating layer, and an outer wall enclosure.
- (2)
- Extended opening of furnace doors: Continuous loading of the roller-bottom heating furnace for prolonged periods with open doors can lead to heat loss.
- (3)
- Atmosphere circulation: Circulation of the furnace atmosphere is crucial for the heating process. However, releasing exhaust gases during this circulation can lead to heat loss.
3.3.3. Heating Energy Consumption Model of Blank
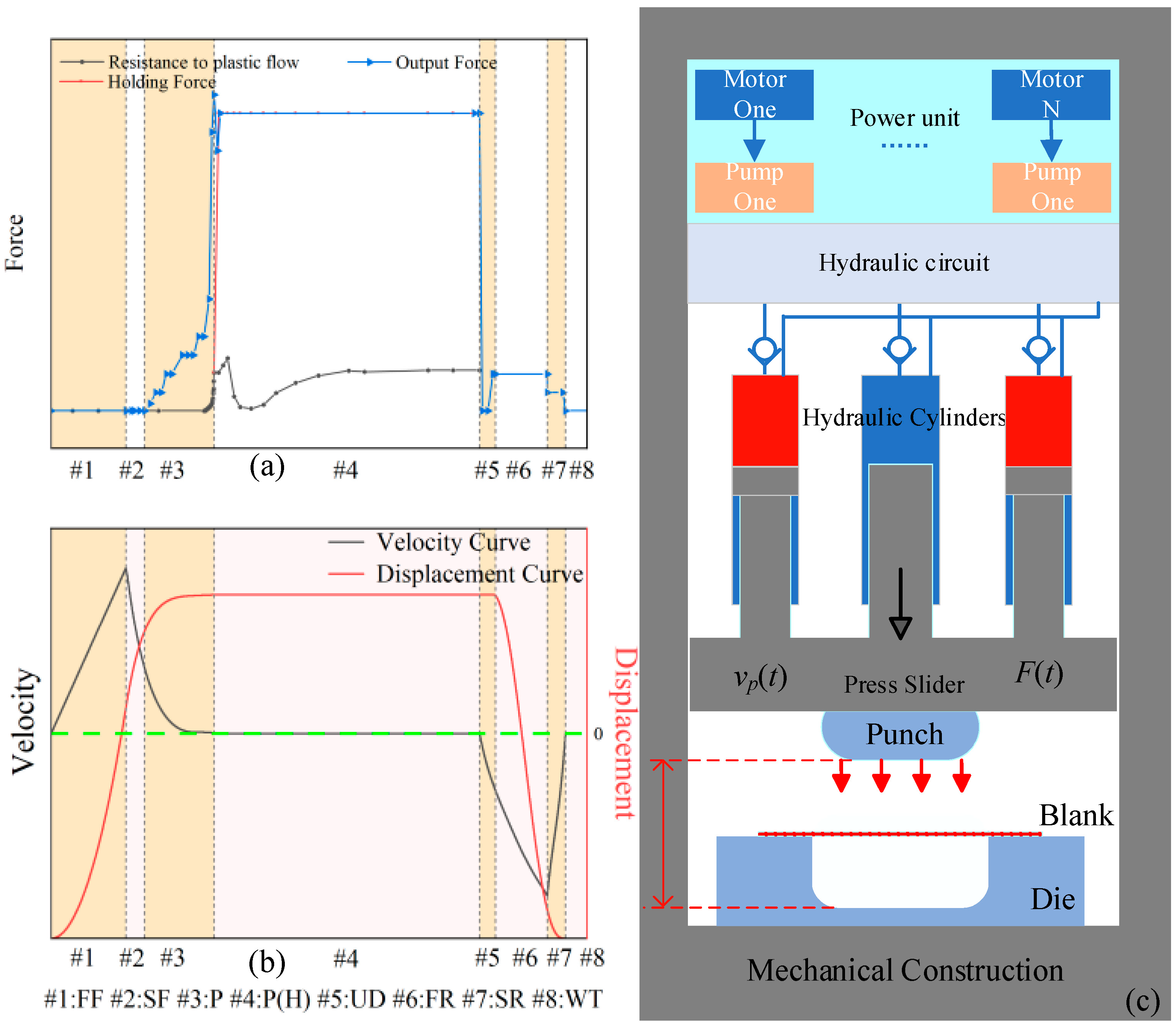
3.4. Energy Consumption Analysis of the Press During Forming
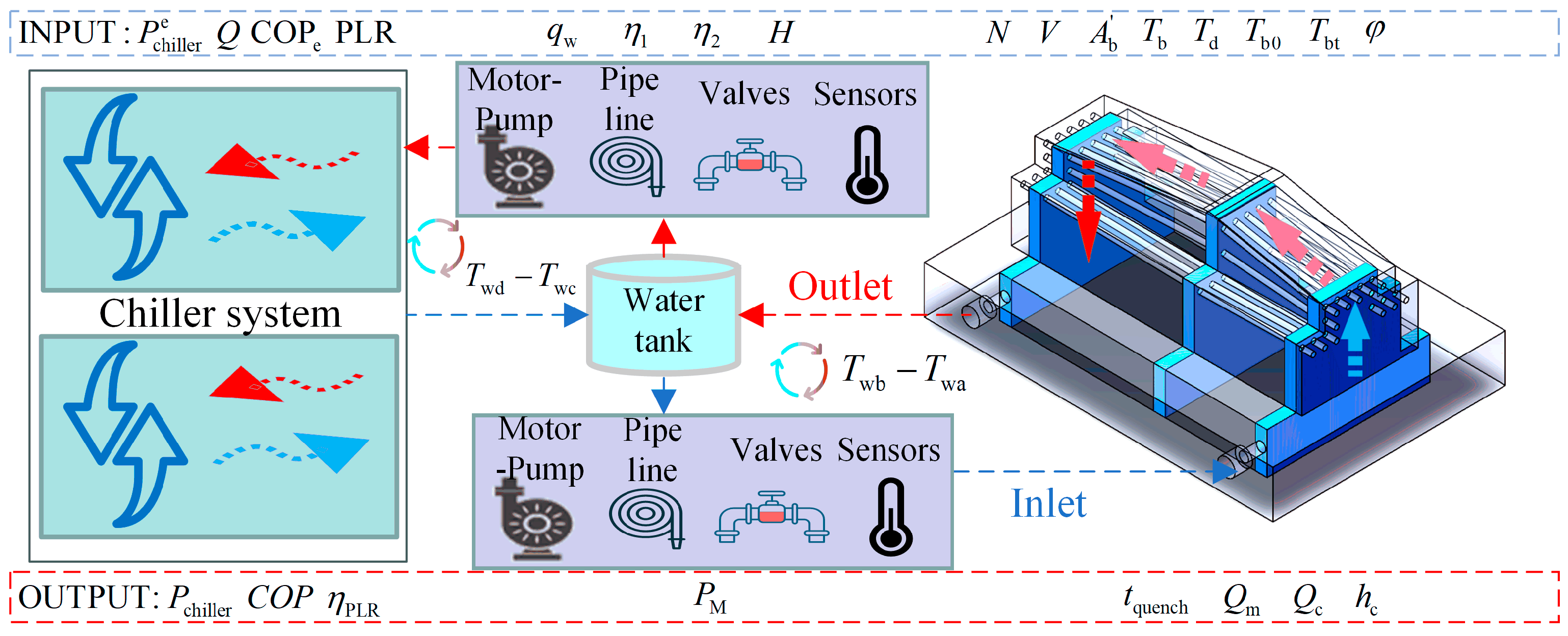
3.5. Energy Consumption Analysis of the Cooling System
4. Case Study
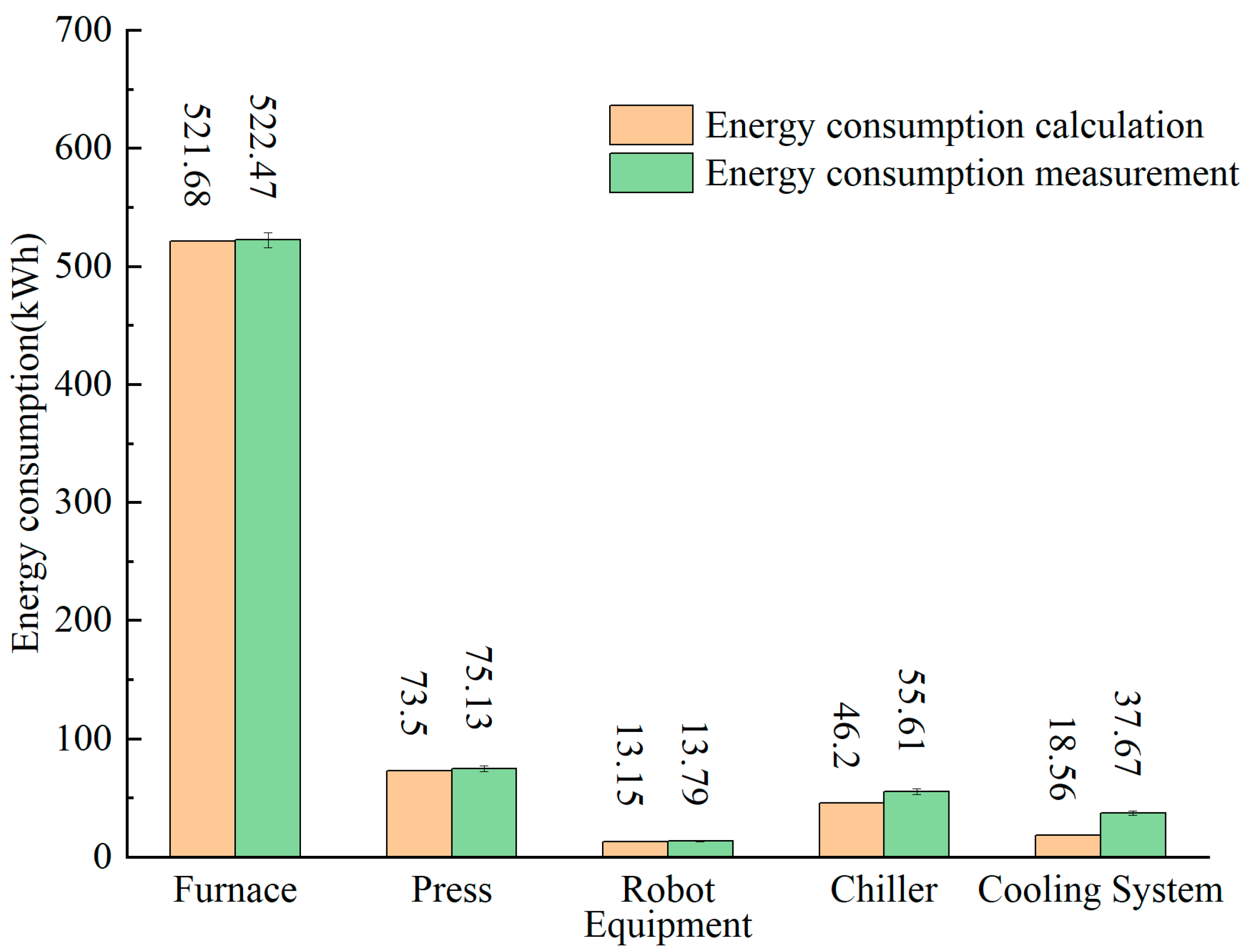
4.1. Calculation Results of Energy Consumption of Production Line
4.2. Measurement Method and Results of Energy Consumption of Production Line
4.3. Power Profiles and Analysis of Each Piece of HSPL
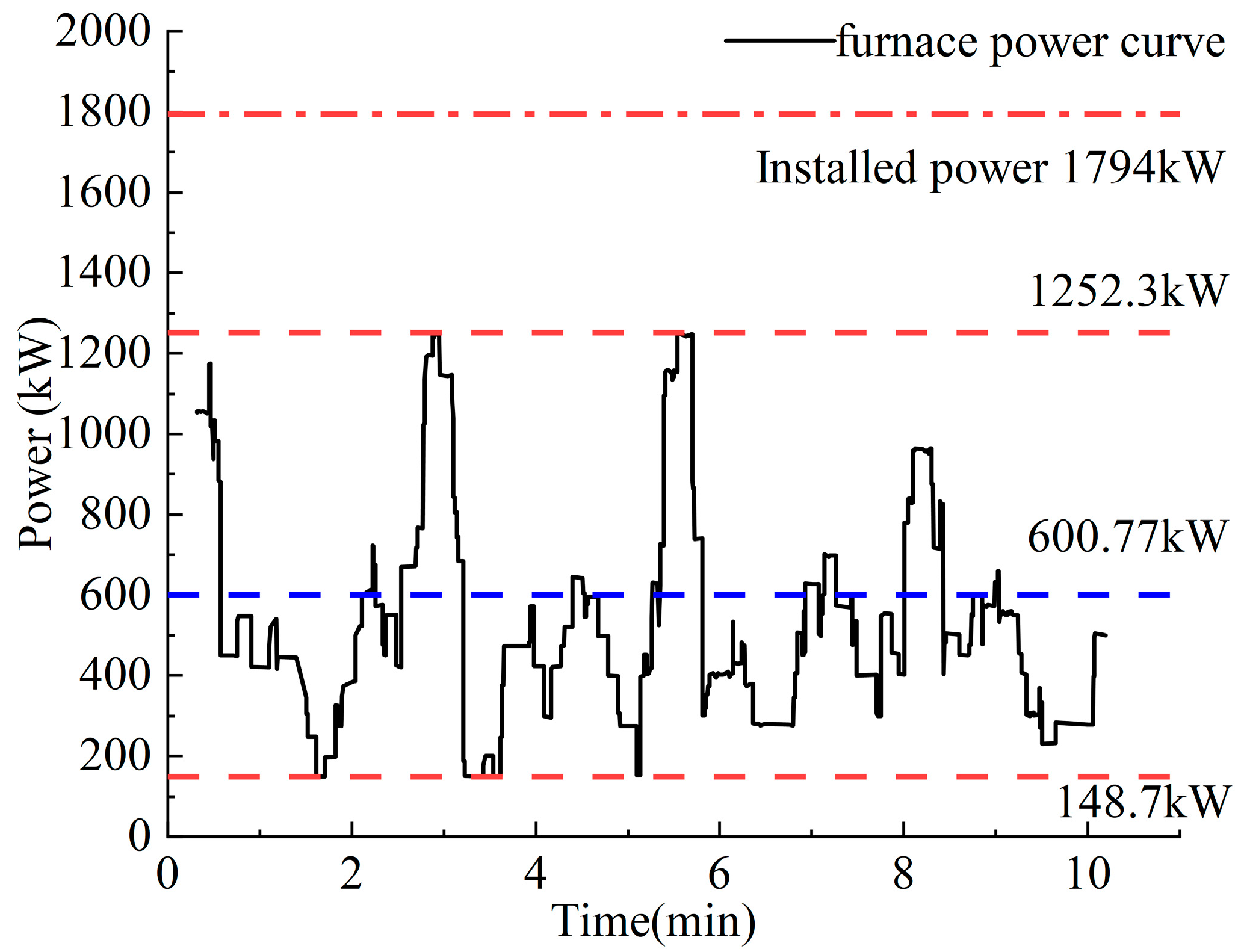
4.3.1. Power Analysis of the Roller Hearth Furnace
4.3.2. Power Analysis of the Automatic Handling Equipment
- (1)
- Rotation of 180° on the z-axis at 30 rpm under a 30 kg load.
- (2)
- Rotation of 180° on the Z-axis at 30 rpm under a 50 kg load.
- (3)
- Rotation of 180° on the Z-axis at 50 rpm under a 30 kg load.
- (4)
- Rotation of 180° on the Z-axis at 30 rpm under a 30 kg load, with simultaneous operations on the X and Y axes.
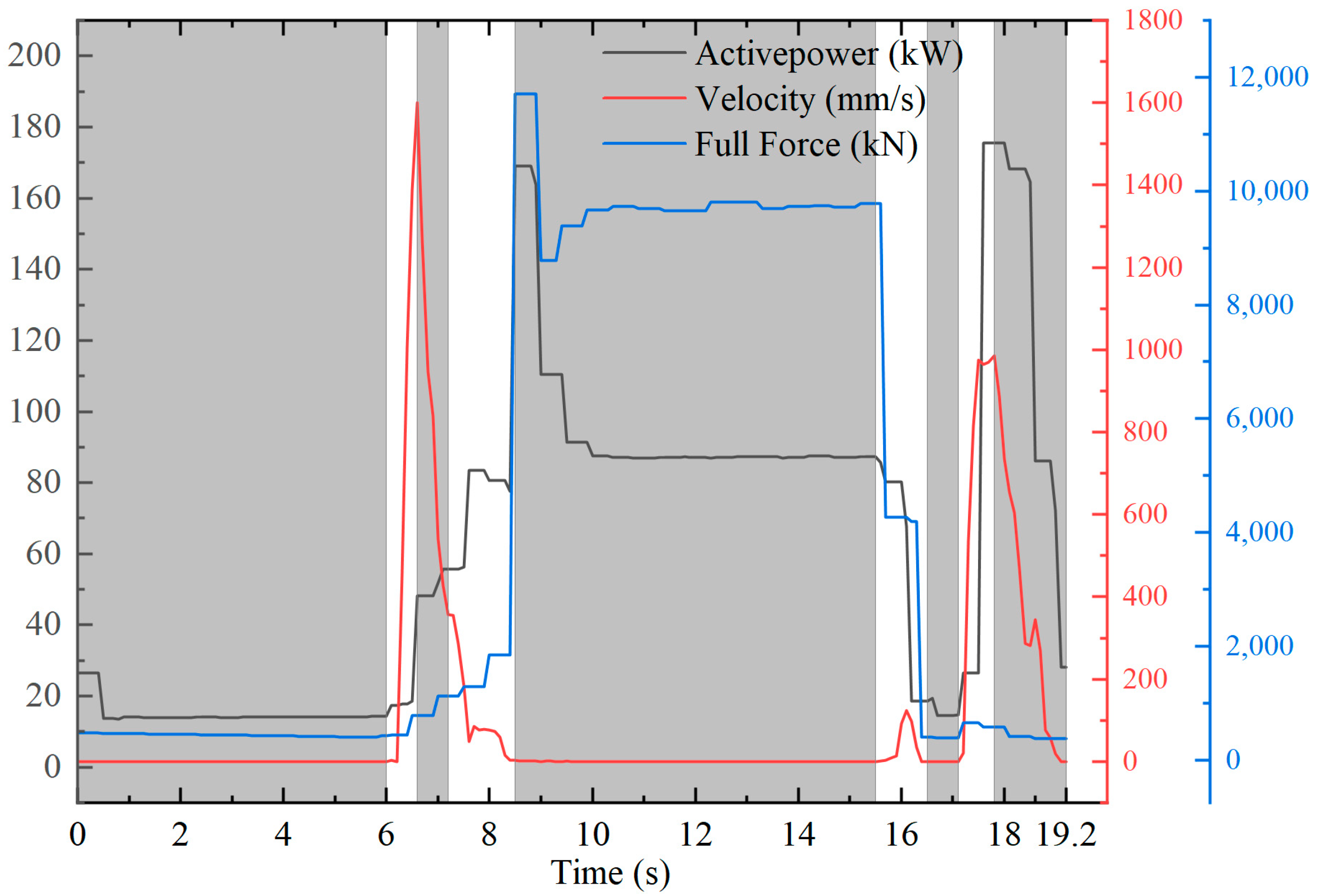
4.3.3. Power Analysis of the Servo-Hydraulic Press
4.3.4. Power Analysis of the Cooling System
4.4. Perspectives for the Reduction of Energy Consumption
5. Conclusions and Future Works
- (1)
- The analysis reveals that the roller hearth furnace is the primary contributor to the total energy consumption. The energy loss is concentrated in the heat loss, especially the large area of the furnace wall and the usually open furnace door. In actual production, the space utilization rate of the furnace is meager, but the heat loss is only positively related to the temperature setting of the region.
- (2)
- The deformation energy of the blank is supplied by the servo hydraulic press, consuming an average of 0.033 kWh/kg. However, significant energy wastage occurs during the hardening time. Compared with the locking pressure holding of the mechanical press, the overflow pressure holding of the hydraulic press is not economical.
- (3)
- Energy efficiency for automation equipment relies on modern servo control systems, superior path control methods, lightweight structural design, and optimized cycle scheduling.
- (4)
- The energy consumption calculation error of the cooling system is significant, mainly due to the wrong estimation and use of the head parameters of the pump. The extensive use of modern intelligent water pump equipment makes it effective in energy saving, and the monitoring and management of energy consumption is also in urgent need of improvement.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| SPM | Statistical parametric mapping | Econ | The fixed energy consumption of the furnace (kWh) |
| V | Volume of blank (m3) | Eloss | The furnace heat energy loss (kWh) |
| Ab | The surface area of blank, single side (m2) | Heat loss of protective atmosphere in furnace (kWh) | |
| The surface area of blank after forming, single side (m2) | Wall surface energy loss (kWh) | ||
| ρ | Density () | tstage(m) | The time consumed by each operation (s) |
| ε | Emissivity | νp(t) | Motion speed curve of servo-hydraulic press (m·s−1) |
| σ | Stefan Boltzmann constant (W·m−2·K−4) | F(t) | Punching pressure curve of the hydraulic press (kN) |
| Cp(t) | Specific heat capacity (J·kg−1·K−1) | ηstage(m) | The energy efficiency of each operation (%) |
| Tb | Tapping temperature of blank (K) | PLn | No-load power consumption of hydraulic press (kW) |
| Tair | Ambient temperature (K) | tidle | The idle time of the process (s) |
| Tf | Temperature of floor and surrounding facilities (K) | Pquench | Quench power consumption of press (kW) |
| Tbi | End temperature of blank in the transfer stage (K) | Qc | The heat transfer between blank and die (kJ) |
| Tb0 | Initial temperature of blank in the cooling stage (K) | Qe | Convection heat transfer between cooling and die (kJ) |
| Tbt | Temperature after quench (K) | Qm | The heat stored in the die (kJ) |
| Td | Temperature of tool (K) | qw | Theoretical cooling flow rate (m3·h−1) |
| tcycle | Interval time (s) | tw | Total cooling time (s) |
| tFF | Fast forming time (s) | ρw | Cooling medium density (kg·m−3) |
| tSF | Slow forming time (s) | Cw | The specific heat capacity of the water (J·kg−1·K−1) |
| tForm | Forming time (s) | Twb-Twa | Temperature difference of cooling medium (%) |
| tquench | Quenching time (s) | φ | Cooling efficiency (%) |
| tUD | Unloading time (s) | η1 | Pump efficiency (%) |
| tFR | Fast returning time (s) | η2 | Motor efficiency (%) |
| tSR | Slow returning time (s) | PM | Motor power (kW) |
| Etotal | Average total energy consumption (kWh) | g | Gravity (kg·N−1) |
| Ecooling | Average energy consumption of cooling (kWh) | H | Pump head (m) |
| Eforming | Average energy consumption of forming (kWh) | PM,i(t) | The power curve of the motor (kW) |
| Ehandling | Average energy consumption of handling (kWh) | COP | Coefficient of Performance |
| Eheating | Average energy consumption of heating (kWh) | PLR | Part load Ratio |
| Pheater | The power of heaters (kW) | Qtotal | The nominal cooling capacity (KJ) |
| Heat loss of furnace door opening (kWh) | Rated power of chillers (kW) | ||
| Erad | Radiation heat loss energy when opening the furnace door (kWh) | Twd-Twc | Temperature difference between inlet and outlet of water tank (K) |
| Econv | Convection heat loss energy when opening the furnace door (kWh) | ηPLR | The efficiency of the chiller on PLR |
| Eblank | Energy consumption of heating blanks (kWh) | Pchiller,j(t) | The power curve of the chiller (kW) |
References
- Yang, X.; Ran, R.; Chen, Y.; Zhang, J. Does Digital Government Transformation Drive Regional Green Innovation? Evidence from Cities in China. Energy Policy 2024, 187, 114017. [Google Scholar] [CrossRef]
- Khan, M.S.; Razmpoosh, M.H.; Biro, E.; Zhou, Y. A Review on the Laser Welding of Coated 22MnB5 Press-Hardened Steel and Its Impact on the Production of Tailor-Welded Blanks. Sci. Technol. Weld. Join. 2020, 25, 447–467. [Google Scholar] [CrossRef]
- Berger, R. Automotive Metal Components for Car Bodies and Chassis Global Market Study. Roland Berger. 2017. Available online: https://www.rolandberger.com/publications/publication_pdf/roland_berger_global_automotive_stamping_study_e_20170210.pdf (accessed on 10 February 2017).
- Li, L.; Huang, H.; Zhao, F.; Liu, Z. Operation Scheduling of Multi-Hydraulic Press System for Energy Consumption Reduction. J. Clean. Prod. 2017, 165, 1407–1419. [Google Scholar] [CrossRef]
- Heng, V.R.; Ganesh, H.S.; Dulaney, A.R.; Kurzawski, A.; Baldea, M.; Ezekoye, O.A.; Edgar, T.F. Energy-Oriented Modeling and Optimization of a Heat Treating Furnace. J. Dyn. Syst. Meas. Control 2017, 139, 061014. [Google Scholar] [CrossRef]
- Li, J.; Tong, C.; Zhang, R.; Shi, Z.; Lin, J. A Data-Informed Review of Scientific and Technological Developments and Future Trends in Hot Stamping. Int. J. Lightweight Mater. Manuf. 2024, 7, 327–343. [Google Scholar] [CrossRef]
- Min, J.; Lin, J.; Li, J.; Bao, W. Investigation on Hot Forming Limits of High Strength Steel 22MnB5. Comput. Mater. Sci. 2010, 49, 326–332. [Google Scholar] [CrossRef]
- Raugei, M.; El Fakir, O.; Wang, L.; Lin, J.; Morrey, D. Life Cycle Assessment of the Potential Environmental Benefits of a Novel Hot Forming Process in Automotive Manufacturing. J. Clean. Prod. 2014, 83, 80–86. [Google Scholar] [CrossRef]
- Abdulhay, B.; Bourouga, B.; Dessain, C.; Brun, G.; Wilsius, J. Development of Estimation Procedure of Contact Heat Transfer Coefficient at the Part–Tool Interface in Hot Stamping Process. Heat Transf. Eng. 2011, 32, 497–505. [Google Scholar] [CrossRef]
- Chang, Y.; Tang, X.; Zhao, K.; Hu, P.; Wu, Y. Investigation of the Factors Influencing the Interfacial Heat Transfer Coefficient in Hot Stamping. J. Mater. Process. Technol. 2016, 228, 25–33. [Google Scholar] [CrossRef]
- Fernández, B.; González, B.; Artola, G.; López De Lacalle, N.; Angulo, C. A Quick Cycle Time Sensitivity Analysis of Boron Steel Hot Stamping. Metals 2019, 9, 235. [Google Scholar] [CrossRef]
- Palmieri, M.E.; Tricarico, L. Influence of Conformal Cooling Channel Parameters on Hot Stamping Tool and Press-Hardening Process. Key Eng. Mater. 2022, 926, 645–654. [Google Scholar] [CrossRef]
- Ying, X.; Zhong-de, S. Design Parameter Investigation of Cooling Systems for UHSS Hot Stamping Dies. Int. J. Adv. Manuf. Technol. 2014, 70, 257–262. [Google Scholar] [CrossRef]
- Zhao, K.; Liu, Z.; Yu, S.; Li, X.; Huang, H.; Li, B. Analytical Energy Dissipation in Large and Medium-Sized Hydraulic Press. J. Clean. Prod. 2015, 103, 908–915. [Google Scholar] [CrossRef]
- Gao, M.; Li, L.; Wang, Q.; Liu, C. Energy Efficiency and Dynamic Analysis of a Novel Hydraulic System with Double Actuator. Int. J. Precis. Eng. Manuf.-Green Technol. 2020, 7, 643–655. [Google Scholar] [CrossRef]
- Li, L.; Huang, H.; Liu, Z.; Li, X.; Triebe, M.J.; Zhao, F. An Energy-Saving Method to Solve the Mismatch between Installed and Demanded Power in Hydraulic Press. J. Clean. Prod. 2016, 139, 636–645. [Google Scholar] [CrossRef]
- Gao, J.; Li, Q.; Lyv, Y.; Xing, J. A Quantitative Study on Energy Saving in Stamping Industry Using Servo Drive of Electric Machine. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference, Nanjing, China, 29 November–2 December 2020; pp. 79–84. [Google Scholar]
- Li, L.; Huang, H.; Zhao, F.; Zou, X.; Mendis, G.P.; Luan, X.; Liu, Z.; Sutherland, J.W. Modeling and Analysis of the Process Energy for Cylindrical Drawing. J. Manuf. Sci. Eng. 2019, 141, 021001. [Google Scholar] [CrossRef]
- Gao, M.; Huang, H.; Li, X.; Liu, Z. Carbon Emission Analysis and Reduction for Stamping Process Chain. Int. J. Adv. Manuf. Technol. 2017, 91, 667–678. [Google Scholar] [CrossRef]
- Cheng, Q.; Gong, J.; Xiao, G.; Yang, C.; Liu, Z.; Qi, B. Research on Energy-Saving Production Planning of Periodic Forging Resistance Furnace. J. Clean. Prod. 2020, 275, 122897. [Google Scholar] [CrossRef]
- Verma, M.; Ciano, M.D.; Culham, J.R.; Yau, C.; Daun, K.J. Minimizing the Cycle Time of a Roller Hearth Furnace for Hot-Forming Die-Quenching. IOP Conf. Ser. Mater. Sci. Eng. 2018, 418, 012016. [Google Scholar] [CrossRef]
- Di Ciano, M.; Field, N.; Wells, M.A.; Daun, K.J. Development of an Austenitization Kinetics Model for 22MnB5 Steel. J. Mater. Eng. Perform. 2018, 27, 1792–1802. [Google Scholar] [CrossRef]
- Chang, J.H.; Oh, J.; Lee, H. Development of a Roller Hearth Furnace Simulation Model and Performance Investigation. Int. J. Heat. Mass. Transf. 2020, 160, 120222. [Google Scholar] [CrossRef]
- Gao, M.; Wang, Q.; Li, L.; Ma, Z. Energy-Economizing Optimization of Magnesium Alloy Hot Stamping Process. Processes 2020, 8, 186. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, B.; Wang, Q.; Zhang, Y. Modeling of Hot Stamping Process Procedure Based on Finite State Machine (FSM). Int. J. Adv. Manuf. Technol. 2017, 89, 857–868. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, B.; Zhang, Y.S. A Runtime Intelligent Iterative Manufacturing System (RIIMS) for Hot Stamping. In Proceedings of the Advanced High Strength Steel and Press Hardening: Proceedings of the 2nd International Conference, Changsha, China, 15–18 October 2015; pp. 647–654.
- Paryanto; Brossog, M.; Bornschlegl, M.; Franke, J. Reducing the Energy Consumption of Industrial Robots in Manufacturing Systems. Int. J. Adv. Manuf. Technol. 2015, 78, 1315–1328. [Google Scholar] [CrossRef]
- Tong, C.; Rong, Q.; Yardley, V.A.; Li, X.; Luo, J.; Zhu, G.; Shi, Z. New Developments and Future Trends in Low-Temperature Hot Stamping Technologies: A Review. Metals 2020, 10, 1652. [Google Scholar] [CrossRef]
- Abdulhay, B.; Bourouga, B.; Dessain, C. Experimental and Theoretical Study of Thermal Aspects of the Hot Stamping Process. Appl. Therm. Eng. 2011, 31, 674–685. [Google Scholar] [CrossRef]
- Optimal Design for Cooling System of Hot Stamping Dies. Available online: https://www.jstage.jst.go.jp/article/isijinternational/56/12/56_ISIJINT-2016-191/_article (accessed on 27 February 2024).
- Shapiro, A.B. Using LS-Dyna for Hot Stamping. In Proceedings of the7th European LS-DYNA Conference, Salzburg, Austria, 14–56 May 2009. [Google Scholar]
- Pashchenko, D. Ammonia Fired Gas Turbines: Recent Advances and Future Perspectives. Energy 2024, 290, 130275. [Google Scholar] [CrossRef]


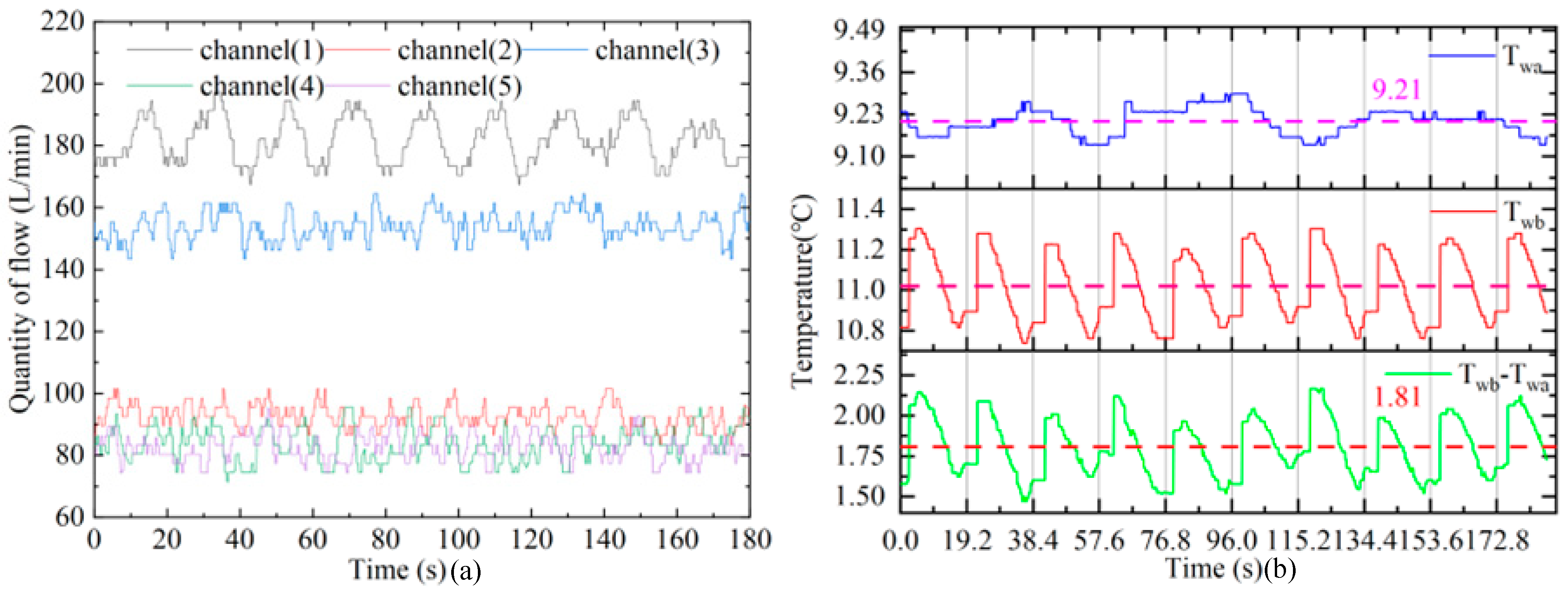

| Type | Unit | Value |
|---|---|---|
| Material | —— | 22MnB5 (Al-Si) |
| Thickness | mm | 1.7 |
| Blank Quality | kg | 6 |
| V: Volume of blank (m3) | m3 | 7.66 × 10−4 |
| Ab: cross-sectional area of blank | m2 | 0.451 |
| : cross-sectional area of the tool in contact with the blank | m2 | 0.485 |
| ρ: Density | kg/m3 | 7830 |
| ε: Emissivity | —— | 0.7 |
| σ: Stefan Boltzmann constant | Wm−2K−4 | 5.670373 × 10−8 |
| Processing Parameter | Unit | Value |
|---|---|---|
| Tair: Ambient temperature | K | 303 |
| Tf: Temperature of floor and surrounding facilities | K | 313 |
| Tb0: Initial temperature of blank in the cooling stage | K | 1024 |
| Tbt: Temperature after hardening | K | 454 |
| Td: Temperature of tool | K | 349 |
| SPM(N): Statistical parametric mapping | —— | 3.125 |
| GSPH: Gross stamping per hour | —— | 188 |
| Areas | Temperature (K) | Heater Power (kW) | (kWh) |
|---|---|---|---|
| 1 | 1023 | 200 | 18 |
| 2 | 1023 | 150 | 20 |
| 3 | 1033 | 150 | |
| 4 | 1023 | 150 | |
| 5 | 1023 | 150 | |
| 6 | 1053 | 150 | 27.7 |
| 7 | 1083 | 150 | |
| 8 | 1133 | 150 | |
| 9 | 1173 | 150 | |
| 10 | 1213 | 60 | 45 |
| 11 | 1213 | 60 | |
| 12 | 1213 | 60 | |
| 13 | 1213 | 60 | |
| 14 | 1213 | 60 | |
| 15 | 1213 | 90 | 16 |
| Total | —— | 1790 | 126.7 |
| Equipment | Working Time (s) | Holding Time (s) | Returning Time (s) | Waiting Time (s) |
|---|---|---|---|---|
| Robot#1 | 9.6 | 6 | 3.8 | 0.1 |
| Roller conveyor#5 | 6.4 | 0 | 0 | 13 |
| Robot #2 | 2.3 | 0 | 3.7 | 13.4 |
| Press | 2.5 | 7 | 3.7 | 6 |
| Robot#3 | 5.3 | 0.2 | 1.2 | 12.7 |
| Unit | Parameters | Power | Energy | |
|---|---|---|---|---|
| Cooling system | Pump-Motor | |||
| Chiller × 4 (EKSC390B3MST) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Zuo, Q.; Li, L.; Yang, C.; Yan, J.; Xu, Y. Energy-Oriented Modeling of Hot Stamping Production Line: Analysis and Perspectives for Reduction. Energies 2024, 17, 5798. https://doi.org/10.3390/en17225798
Liu Q, Zuo Q, Li L, Yang C, Yan J, Xu Y. Energy-Oriented Modeling of Hot Stamping Production Line: Analysis and Perspectives for Reduction. Energies. 2024; 17(22):5798. https://doi.org/10.3390/en17225798
Chicago/Turabian StyleLiu, Qiong, Quan Zuo, Lei Li, Chen Yang, Jianwen Yan, and Yuhang Xu. 2024. "Energy-Oriented Modeling of Hot Stamping Production Line: Analysis and Perspectives for Reduction" Energies 17, no. 22: 5798. https://doi.org/10.3390/en17225798
APA StyleLiu, Q., Zuo, Q., Li, L., Yang, C., Yan, J., & Xu, Y. (2024). Energy-Oriented Modeling of Hot Stamping Production Line: Analysis and Perspectives for Reduction. Energies, 17(22), 5798. https://doi.org/10.3390/en17225798




