Dynamic Environmental Economic Dispatch Considering the Uncertainty and Correlation of Photovoltaic–Wind Joint Power
Abstract
1. Introduction
- (1)
- It proposes a novel dynamic environmental economic dispatch model based on a multi-objective fireworks algorithm, specifically tailored to tackle the DEED problem and address the limitations observed in existing heuristic algorithms.
- (2)
- The utilization of the non-parametric kernel density estimation method to construct a joint output model for both wind and photovoltaic power sources represents a pioneering approach in capturing and integrating uncertainty and correlation factors.
- (3)
- Through the application of the Copula function, the research establishes a robust joint output probability model for photovoltaic–wind joint power, facilitating the generation of realistic joint output scenarios via the innovative combination of the Latin Hypercubic Sampling Method and the Improved K-means Clustering Algorithm.
- (4)
- The improved fireworks algorithm (IFWA) is proposed for the optimal solution of the power system planning problem. This algorithm improves the way fireworks are initially generated based on the basic fireworks algorithm. It also optimizes the explosion and mutation operators by combining adaptive operators and the idea of differential evolution algorithm and introduces a selection strategy based on fitness values for elite preservation. At the same time, the random selection method for the roulette wheel in the basic fireworks algorithm is replaced with binary search to effectively improve computational efficiency.
2. Generation and Reduction in Scenery Scenes
2.1. Output Model for Wind Power Generator
2.2. Output Model for Photovoltaic Generator
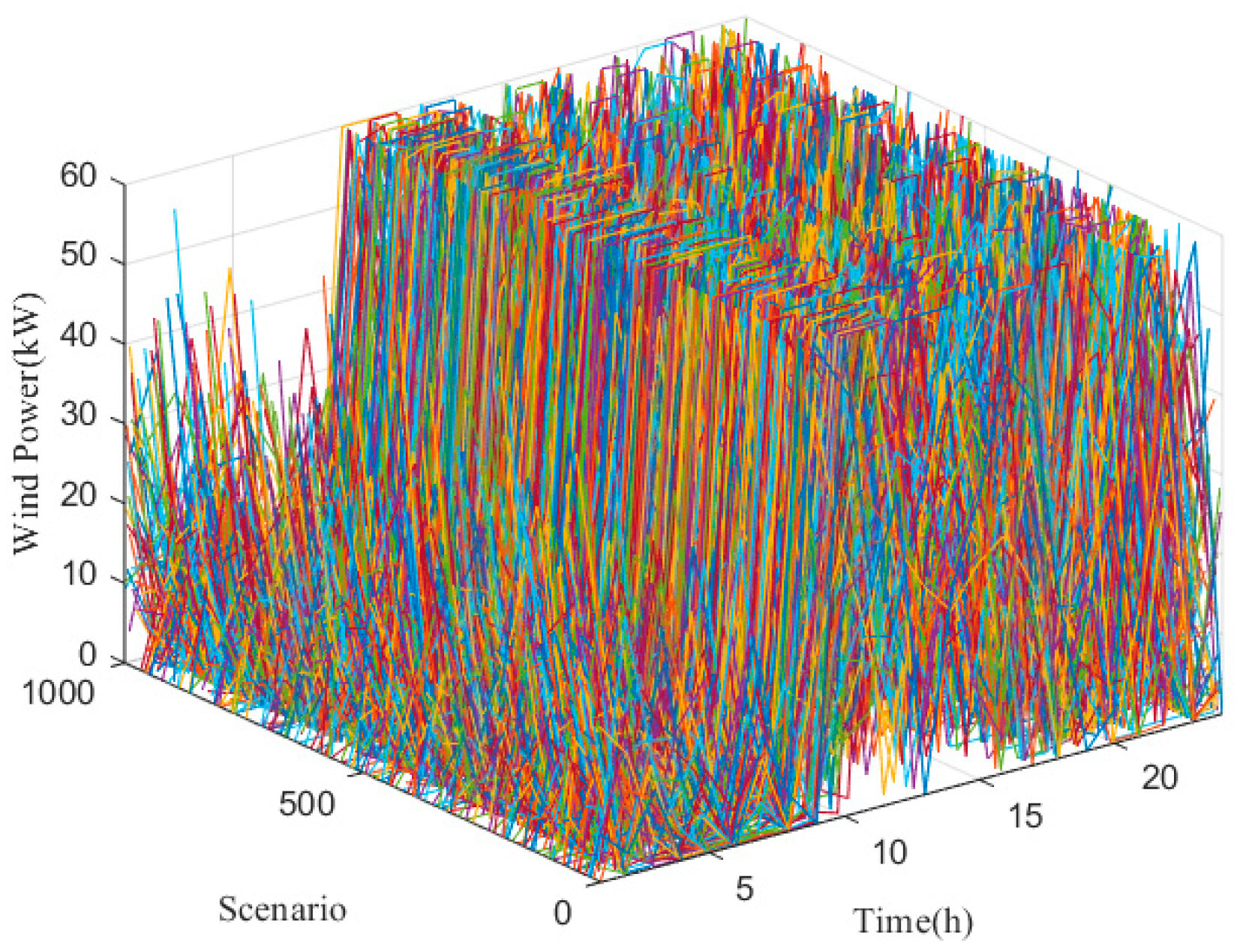
2.3. Scenario Generation and Reduction
3. DEED Model
3.1. Objective Functions
3.2. Constraint Function
3.2.1. System Power Balance Constraints
3.2.2. Power Generation Capacity Constraints
3.2.3. Ramp Rate Constraints for Thermal Power Units
3.2.4. System Spare Capacity Constraints
4. Adaptive Multi-Objective Fireworks Algorithm
4.1. Algorithm Initialization
4.2. Evolutionary Strategy
- For each solution x in the solution set obtained above, the other two solutions are randomly selected, and their differences are weighted and added to the original solution to obtain the mutation solution of the original solution ;
- Cross mutation solution and several elements in the original solution, resulting in a cross solution . The method for selecting the j-th element in the cross solution is shown:where denotes a constant between , denotes the probability of crossing, A random number is taken within ;
- Choose the cross solution and the better solution from the original solution to join the next generation. If the cross solution is selected, the fitness function is used to determine whether it is a non-dominant solution within the contemporary solution. If so, it is also needed to update NP, which is shown as:
4.3. Selecting Strategy Improvements
- The elite individuals with the best fitness from the current fireworks, explosion sparks, and mutation sparks populations are directly preserved in the next generation of explosion fireworks. This ensures that the optimal individuals are not lost. For the remaining N-1 fireworks with relatively high fitness that were not selected, it is important to note that the best few sparks may originate from a single firework. This could lead to a situation where a locally optimal firework is not easily eliminated, resulting in a weakened global search capability of the algorithm. Thus, direct selection is not feasible, and it is necessary to continue integrating subsequent selection strategies.
- Calculate the fitness difference between different fireworks and sparks . Select fireworks with an internal fitness that is superior, where is less than ( being a constant that filters for fireworks with similar fitness values).where and represent the fitness of fireworks and , respectively.
- After the second round of screening, N−1 fireworks are randomly selected to proceed to the next generation, ensuring population diversity.In addition, regarding the roulette wheel selection method of the basic fireworks algorithm, it is necessary to traverse the entire population to calculate and set the weight of each firework individual. Based on the Euclidean distance calculation method, its time complexity is . This paper improves upon this by employing a binary search method; for each query, a random number is generated for the firework individual, and then binary search is utilized for the query, resulting in a time complexity of . This approach can significantly enhance computational efficiency, especially when dealing with larger populations.

| Algorithm 1: ADMOFWA Pseudocode |
| 1. Start; |
| 2. Divide the entire solution space N equally, and randomly explode a set of initial fireworks in each population; |
| 3. Record the global optimal gBest, the set of sparkpBest for the optimal explosive sparks generated by each firework, obtain the fitness value of each firework, and form the solution set P; |
| 4. Create an empty non dominated solution set NP; |
| 5. When the number of iterations iter < max_itr; |
| 6. For each firework in solution P, calculate the number of explosive sparks for each firework according to the equation; |
| 7. Calculate the explosion radius of each firework according to the formula to generate sparks, and update SparkpBest to generate sparks for Gaussian explosions; |
| 8. Acquire the fitness values for all sparks; |
| 9. Update NP by selecting non-dominated solutions from sparks; |
| 10. Using roulette to choose n solutions from fireworks and sparks; |
| 11. Decompose each firework in the fireworks set P;12. Obtain a crossover solution based on crossover, mutation, and selection . If the fitness value of the crossover solution is better than , use to update NP; |
| 13. Select an optimal solution, and then use the roulette wheel method to select solutions to form a new fireworks solution set P; |
| 14. If the number of iterations reaches, the algorithm stops; Otherwise, skip to the fifth step of the algorithm to continue the iteration; |
| 15. End of iteration. |
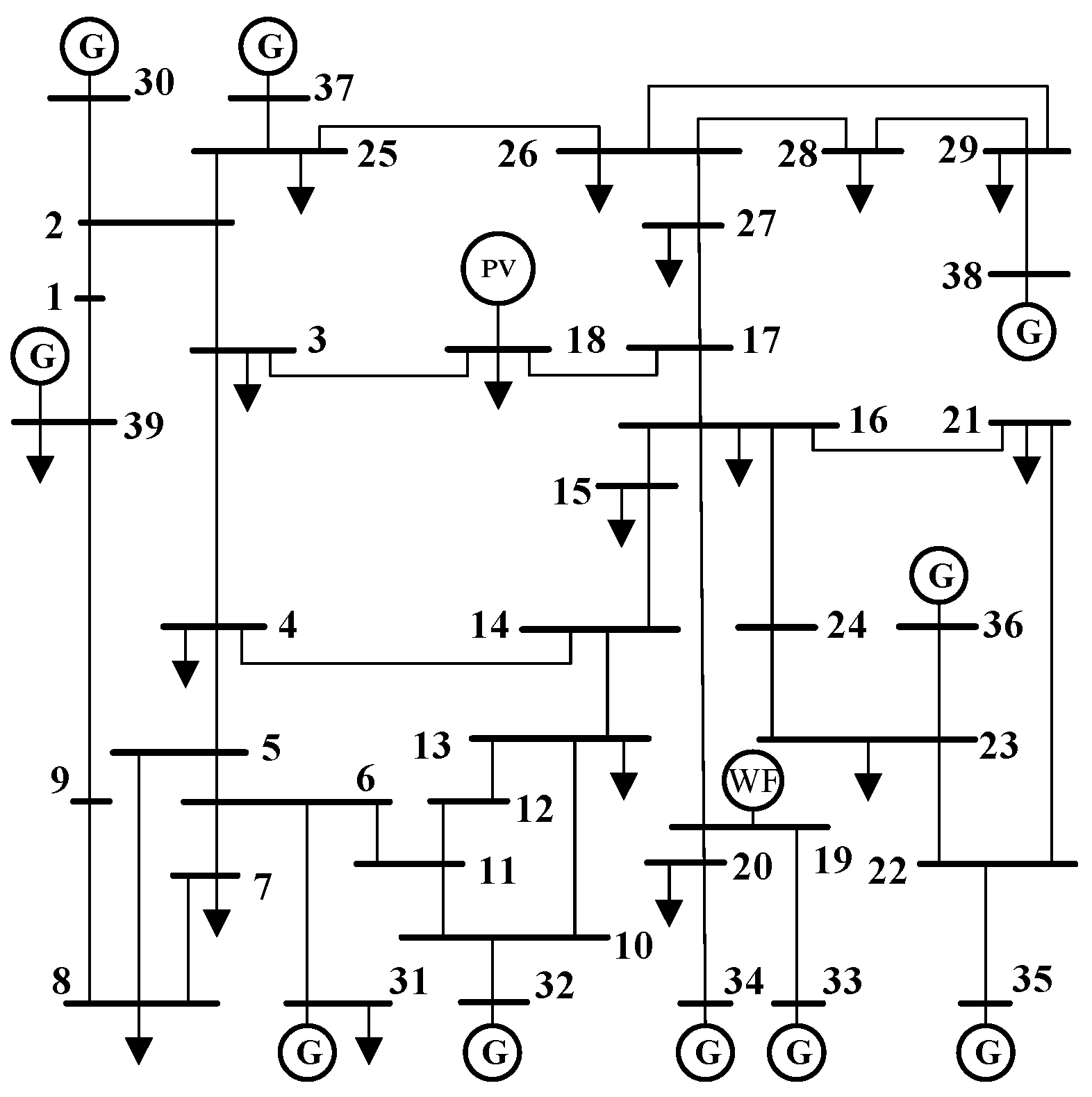
5. Case Analysis
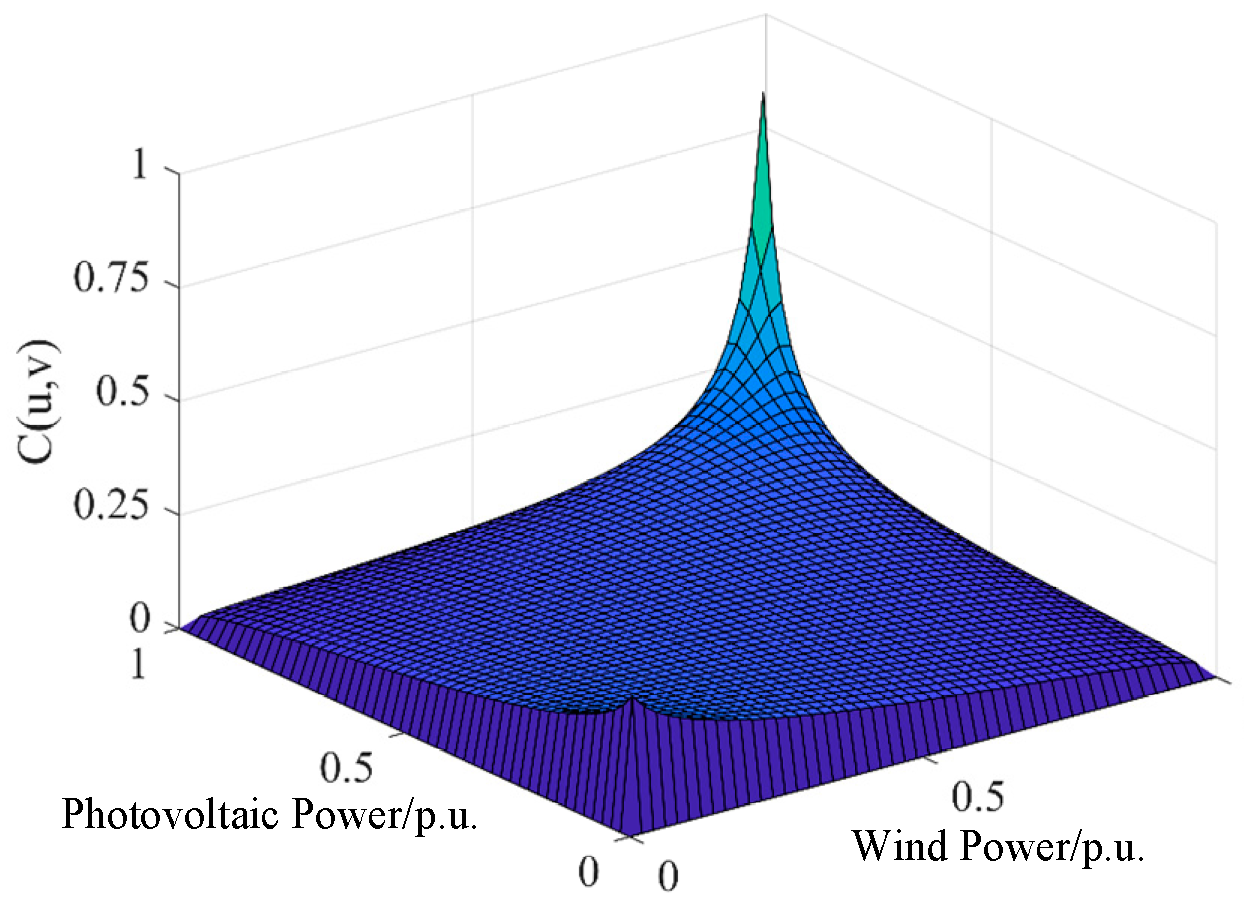
5.1. Select the Optimal Copula Function
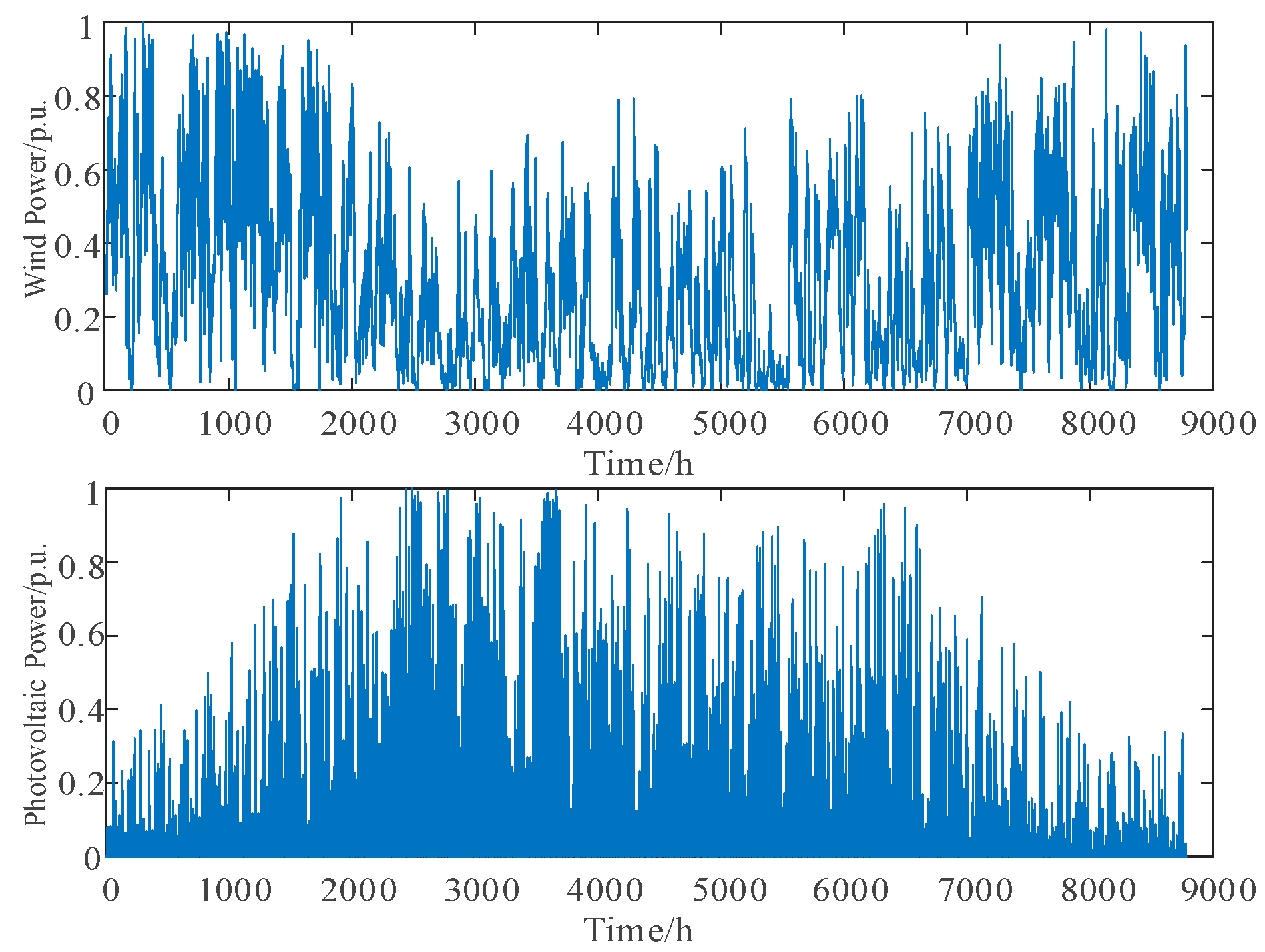
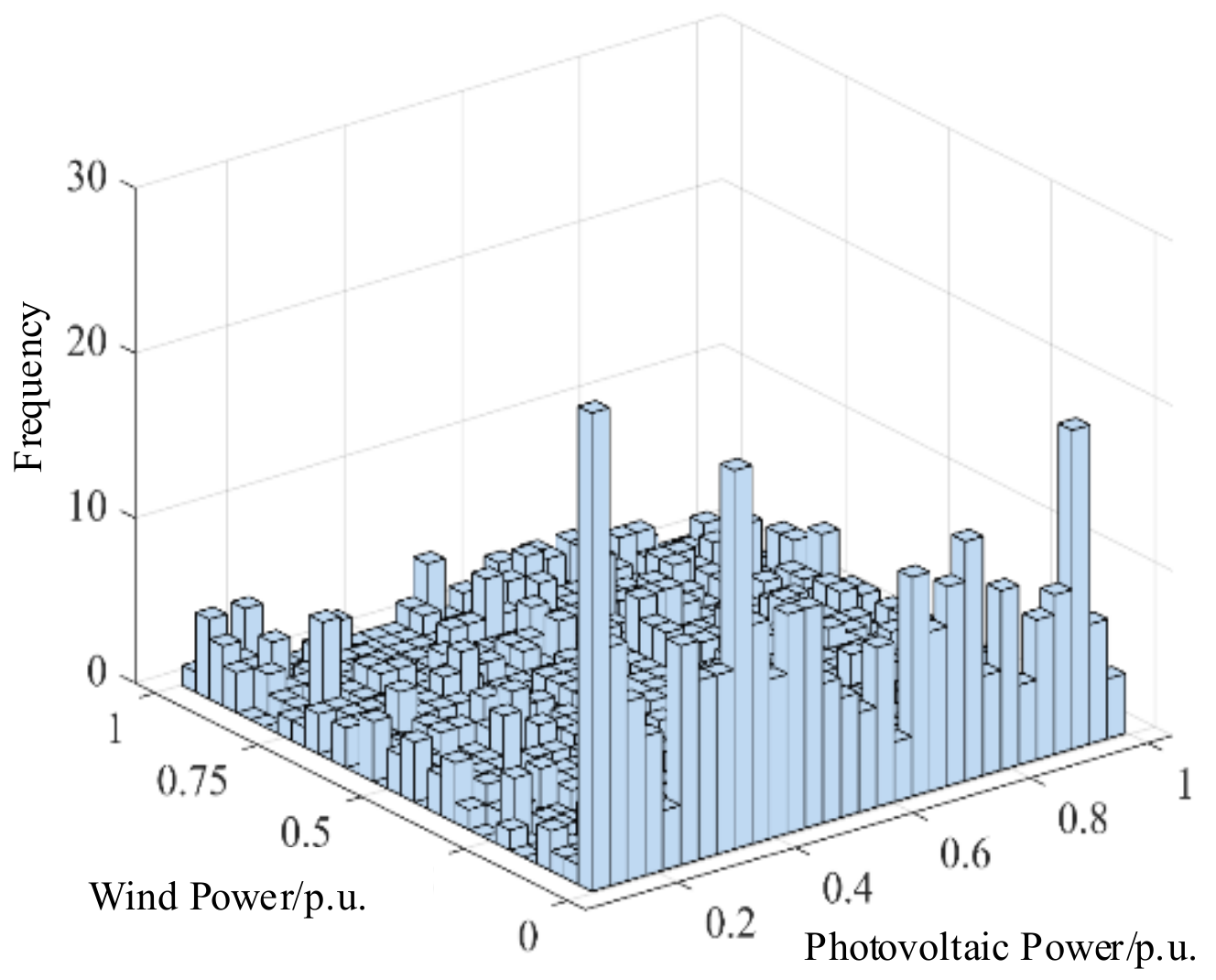
5.2. Joint Output Scenario Generation of Wind and Photovoltaic Power
5.3. Model Solving
| Algorithm | Fuel Cost /YUAN | Pollution Discharge /YUAN |
|---|---|---|
| MOPSO | 2,488,134 | 286,009 |
| MOFWA | 2,387,105 | 269,570 |
| ADMOFWA | 2,281,716 | 251,538 |
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| EED | Environmental economic dispatch | DED | Dynamic Economic Dispatch |
| DEED | Dynamic Environmental Economic Dispatch | PSO | Particle Swarm Optimization |
| RDHBO | Reactor Optimization | DE | Differential Evolution |
| ADMOFWA | Adaptive Multiple Objective Firework Algorithm | MOPSO | Multiple Objective Particle Swarm Optimization |
| MOFWA | Multiple Objective Firework Algorithm |
References
- Ramírez, V.M.D.; Paz, A.R.; Marín, J.A. Proposal for a Solution to the Environmental Economic Dispatch Problem Using Scilab. In Proceedings of the 2021 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 10–12 November 2021; pp. 1–6. [Google Scholar]
- Yin, Q.; Wang, Z.; Sun, T.; Li, W.; Chong, F. Environmental and Economic Dispatch with Photovoltaic and Wind Power. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 1108–1112. [Google Scholar]
- Wei, X.; Xiaoying, Z.; Kun, W.; Wei, C.; Xiaolan, W. Multi-source Coordination and Scheduling Strategy of New Energy with High Proportion of Wind Power, Photovoltaic and Photothermal. In Proceedings of the 2019 4th International Conference on Intelligent Green Building and Smart Grid (IGBSG), Hubei, China, 6–9 September 2019; pp. 661–665. [Google Scholar]
- Li, X.; Wang, W.; Wang, H.; Wu, J.; Fan, X.; Xu, Q. Dynamic environmental economic dispatch of hybrid renewable energy systems based on tradable green certificates. Energy. 2020, 193, 116699. [Google Scholar] [CrossRef]
- Sadoudi, S.; Boudour, M.; Kouba, N.E.Y. Optimal Combined Dynamic Economic and Emission Dispatch Including Wind and Photovoltaic Power Systems. In Proceedings of the 2018 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Algiers, Algeria, 28–31 October 2018; pp. 1–6. [Google Scholar]
- Li, K.P.; Zhang, Z.Y.; Wang, F.; Jiang, L.; Zhang, J.; Yu, Y.; Mi, Z. Stochastic optimization model of capacity configuration for stand-alone microgrid based on scenario simulation using GAN and conditional value at risk. Power Syst. Technol. 2019, 43, 1717–1725. [Google Scholar]
- Huang, C.; Wang, L.; Lai, L. Data-driven short-term solar irradiance forecasting based on information of neighboring sites. IEEE Trans. Ind. Electron. 2019, 66, 9918–9927. [Google Scholar] [CrossRef]
- Song, Y.; Li, H. Typical scene generation of wind and photovoltaic power output based on kernel density estimation and Copula function. Electr. Eng. 2022, 23, 56–63. [Google Scholar]
- Zhu, X.; Jin, H.; Wang, Y. Analysis on dependence structure among photovoltaic power outputs based on combination of copula function and gaussian mixture model. Acta Energiae Solaris Sin. 2019, 40, 1912–1919. [Google Scholar]
- Xu, J.; Wu, W.; Wang, K.; Li, G. C-Vine pair copula based wind power correlation modelling in probabilistic small signal stability analysis. IEEE/CAA J. Autom. Sin. 2020, 7, 1154–1160. [Google Scholar] [CrossRef]
- Bai, J.; Wu, X.; Xia, A. An enhanced multi-objective differential evolution algorithm for dynamic environmental economic dispatch of power system with wind power. Energy Sci. Eng. 2020, 9, 316–329. [Google Scholar] [CrossRef]
- Gherbi, Y.A.; Lakdja, F. Dynamic economic emission dispatch concidering valve point effect and variale active losse using new optimization method. In Proceedings of the 2022 IEEE International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Tunis, Tunisia, 26–28 October 2022; pp. 1–6. [Google Scholar]
- Yang, Z.; Li, K.; Niu, Q.; Xue, Y.; Foley, A. A self-learning TLBO based dynamic economic/environmental dispatch considering multiple plug-in electric vehicle loads. J. Mod. Power Syst. Clean Energy 2014, 2, 298–307. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, X.; Li, B.; Si, Q.; Zhao, M. Distributionally robust optimaldispatch for multi-community photovoltaic and energy storage system considering energy sharing. Autom. Electr. Powe Syst. 2022, 46, 21–31. [Google Scholar]
- Ju, L.; Yu, C.; Tan, Z. A two-Stage scheduling optimization model and corresponding solving algorithm for power grid containing wind farm and energy storage system considering demand response. Power Syst. Technol. 2015, 39, 1287–1293. [Google Scholar]
- Lydia, M.; Kumar, S.S.; Selvakumar, A.I.; Kumar, G.E. Wind resource estimation using wind speed and power curve models. Renew. Energy 2015, 83, 425–434. [Google Scholar] [CrossRef]
- Sheng, S.; Zhang, L. Economic dispatch of power system considering the prediction error of wind power, solar energy and load. Proc. CSU-EPSA 2017, 9, 80–85. [Google Scholar]
- Zhou, W.; Lou, C.; Li, Z.; Lu, L.; Yang, H. Current status of research on optimum sizing of stand-alone hybrid solar–wind power generation systems. Appl. Energy 2010, 87, 380–389. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, Z. Solving dynamic economic dispatch with electric vehicle based on improved heap-based optimizer algorithm. Appl. Res. Comput. 2024, 41, 3032–3037. [Google Scholar]
- Wu, H.; Qian, S.; Liu, Y.; Xu, G.; Guo, B. Multiobjective dynamic economic emission dispatch differential evolution algorithm based on elites cloning local search. J. Shandong Univ. Eng. Sci. 2021, 51, 11–23. [Google Scholar]
- Wu, H.; Lin, Y.; Zeng, X.; Qian, S. Adaptive different evolutionary algorithm and its application of dynamic emission economic dispatch problem. Appl. Res. Comput. 2021, 38, 1443–1448+1454. [Google Scholar]
- Tian, H.; Wang, K.; Yu, B.; Tian, W.; Song, C.; Wu, Z. Optimal planning method for distribution network considering multi-type load and uncertainty of wind and solar. Proc. CSU-EPSA 2021, 33, 144–150. [Google Scholar]
- Zhang, L.; Wang, X.; Wang, J.; Zheng, Y.; Ma, Q. Bi-level optimization model of inter-regional power dispatch based on regional electricity price. Electrc Power Autom Equip. 2021, 43, 195–201. [Google Scholar]
- Sheikholeslami, R.; Razavi, S. Progressive Latin Hypercube Sampling: An efficient approach for robust sampling-based analysis of environmental models. Environ. Model. Softw. 2017, 93, 109–126. [Google Scholar] [CrossRef]
- Li, J.; Lan, F.; Wei, H. A scenario optimal reduction method for wind power time series. IEEE Trans. Power Syst. 2016, 31, 1657–1658. [Google Scholar] [CrossRef]
- Beirami, A.; Vahidinasab, V.; Shafie-Khah, M.; Catalão, J.P. Multiobjective ray optimization algorithm as a solution strategy for solving non-convex problems: A power generation scheduling case study. Int. J. Electr. Power Energy Syst. 2020, 119, 105967. [Google Scholar] [CrossRef]
- Zheng, S.; Li, J.; Janecek, A.; Tan, Y. A cooperative framework for fireworks algorithm. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017, 14, 27–41. [Google Scholar] [CrossRef] [PubMed]
- Jadoun, V.K.; Pandey, V.C.; Gupta, N.; Niazi, K.R.; Swarnkar, A. Integration of renewable energy sources in dynamic economic load dispatch problem using an improved fireworks algorithm. IET Renew. Power Gener. 2018, 12, 1004–1011. [Google Scholar] [CrossRef]
- Cui, Y.; Zeng, P.; Wang, Z.; Wang, M.; Zhang, J.; Zhao, Y. Multiple time scales scheduling strategy of wind power accommodation considering energy transfer characteristics of carbon capture power plant. Proc. CSEE. 2021, 41, 946–961. [Google Scholar]
- Attaviriyanupap, P.; Kita, H.; Tanaka, E.; Hasegawa, J. A hybrid EP and SQP for dynamic economic dispatch with nonsmooth fuel cost function. IEEE Trans. Power Syst. 2002, 17, 411–416. [Google Scholar] [CrossRef]
- Liu, G.; Peng, C.; Xiang, L. Economic-environmental dispatch using improved multi-objective particle swarm optimization. Power Syst. Technol. 2011, 35, 139–144. [Google Scholar]
- Zare, M.; Narimani, M.R.; Malekpour, M.; Azizipanah-Abarghooee, R.; Terzija, V. Reserve constrained dynamic economic dispatch in multi-area power systems: An improved fireworks algorithm. Int. J. Electr. Power Energy Syst. 2021, 126, 106579. [Google Scholar] [CrossRef]




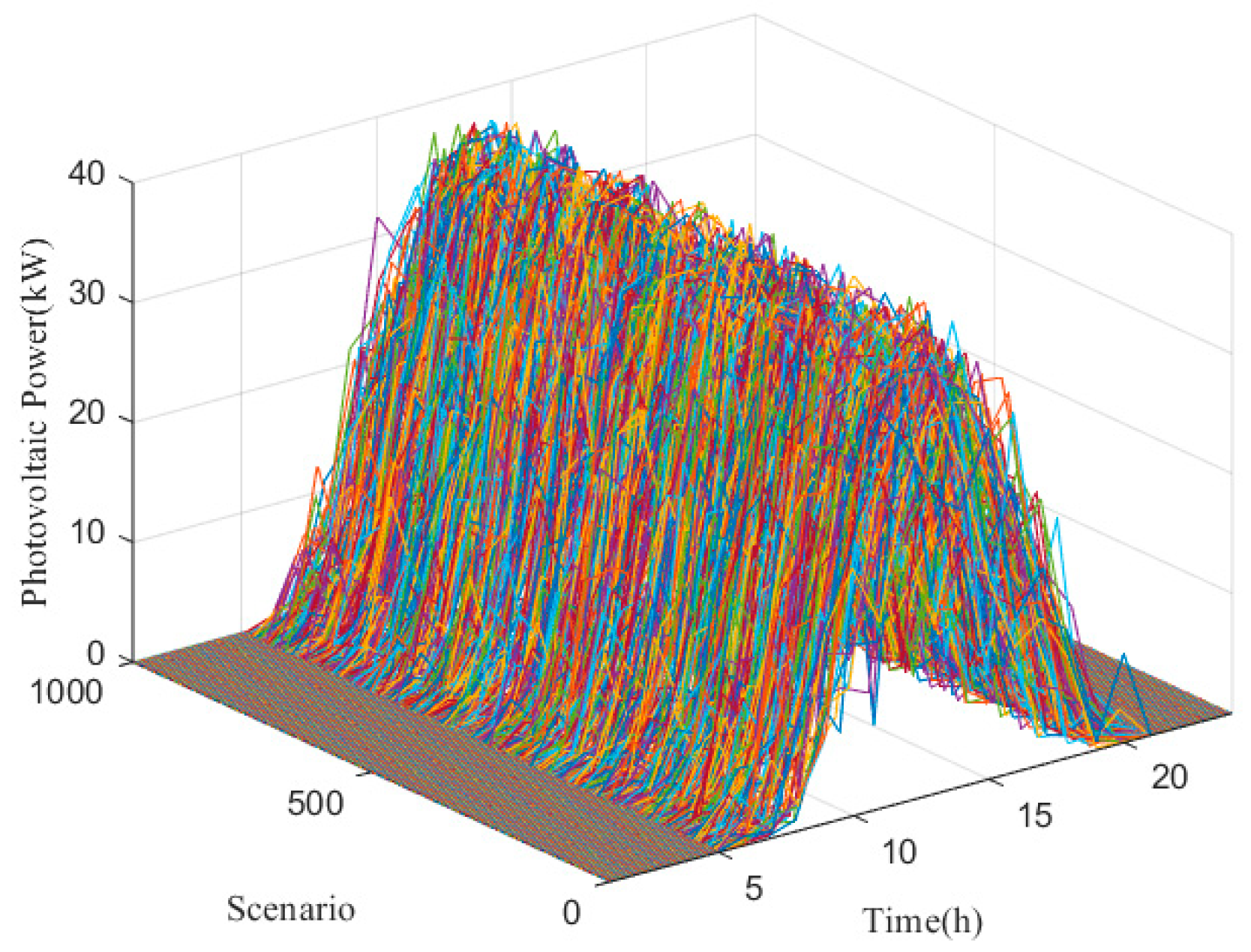

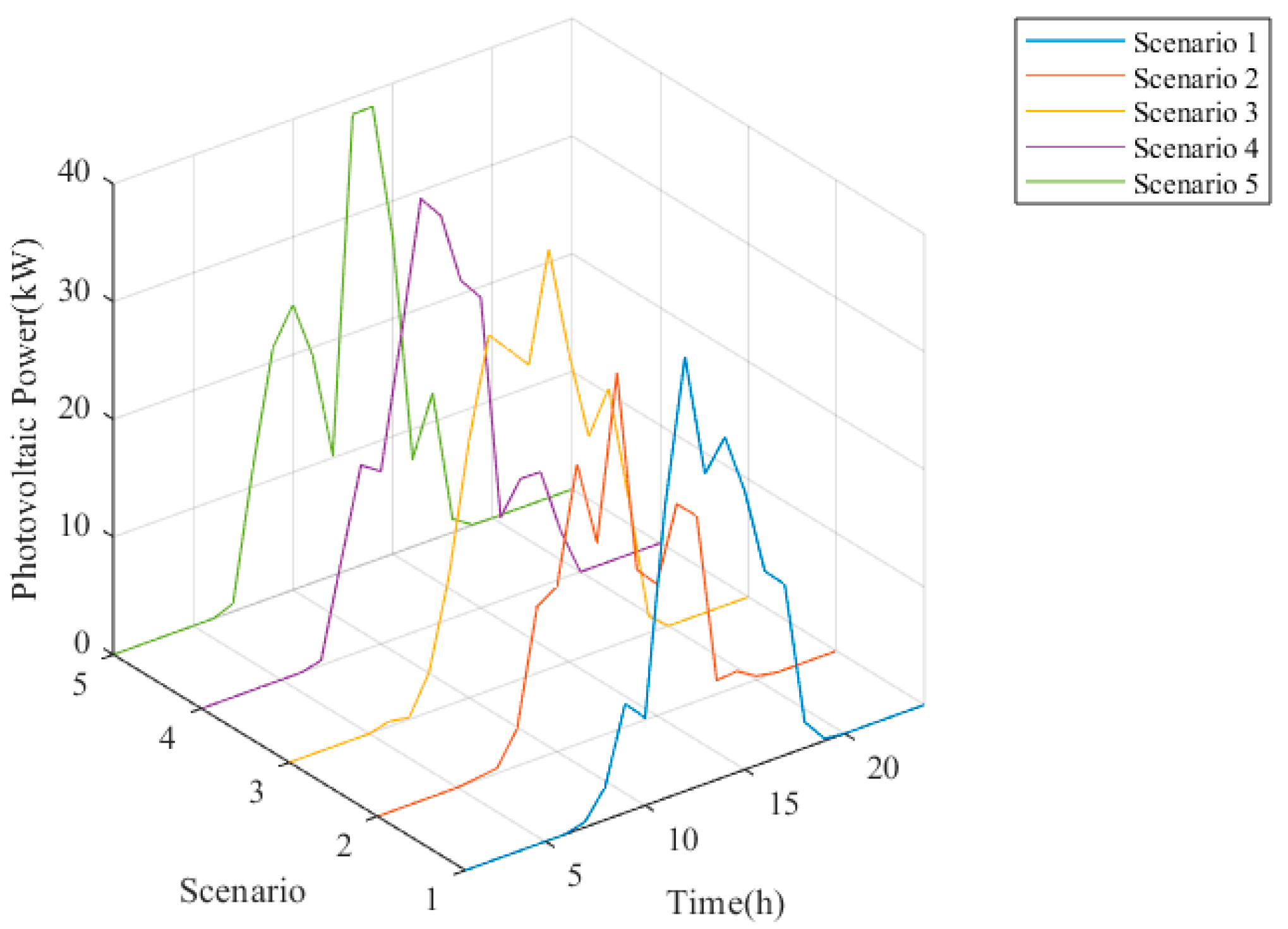



| Copula Function | Clayton | Gumbel | Frank |
|---|---|---|---|
| correlation coefficient | 0.5423 | 1.2763 | 2.5124 |
| Evaluating Indicator | Function Category | Indicator Value |
|---|---|---|
| Kendall Rank Correlation Coefficient | Raw Data | 0.2432 |
| Clayton | 0.2032 | |
| Frank | 0.2453 | |
| Gumbel | 0.2216 | |
| Spearman Rank Correlation Coefficient | Raw Data | 0.4117 |
| Clayton | 0.3254 | |
| Frank | 0.4129 | |
| Gumbel | 0.3843 | |
| Squared Euclidean Distance | Clayton | 0.9026 |
| Frank | 0.0715 | |
| Gumbel | 1.2036 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ru, Y.; Wang, Y.; Mao, W.; Zheng, D.; Fang, W. Dynamic Environmental Economic Dispatch Considering the Uncertainty and Correlation of Photovoltaic–Wind Joint Power. Energies 2024, 17, 6247. https://doi.org/10.3390/en17246247
Ru Y, Wang Y, Mao W, Zheng D, Fang W. Dynamic Environmental Economic Dispatch Considering the Uncertainty and Correlation of Photovoltaic–Wind Joint Power. Energies. 2024; 17(24):6247. https://doi.org/10.3390/en17246247
Chicago/Turabian StyleRu, Yi, Ying Wang, Weijun Mao, Di Zheng, and Wenqian Fang. 2024. "Dynamic Environmental Economic Dispatch Considering the Uncertainty and Correlation of Photovoltaic–Wind Joint Power" Energies 17, no. 24: 6247. https://doi.org/10.3390/en17246247
APA StyleRu, Y., Wang, Y., Mao, W., Zheng, D., & Fang, W. (2024). Dynamic Environmental Economic Dispatch Considering the Uncertainty and Correlation of Photovoltaic–Wind Joint Power. Energies, 17(24), 6247. https://doi.org/10.3390/en17246247






