The Windcatcher: A Renewable-Energy-Powered Device for Natural Ventilation—The Impact of Upper Wing Walls
Abstract
:1. Introduction
2. Methodology
3. Results and Discussions
3.1. Validation
3.1.1. Grid Adaption
3.1.2. Comparison between CFD and Experimental Results
3.2. Integration of UWW with the Windcatcher
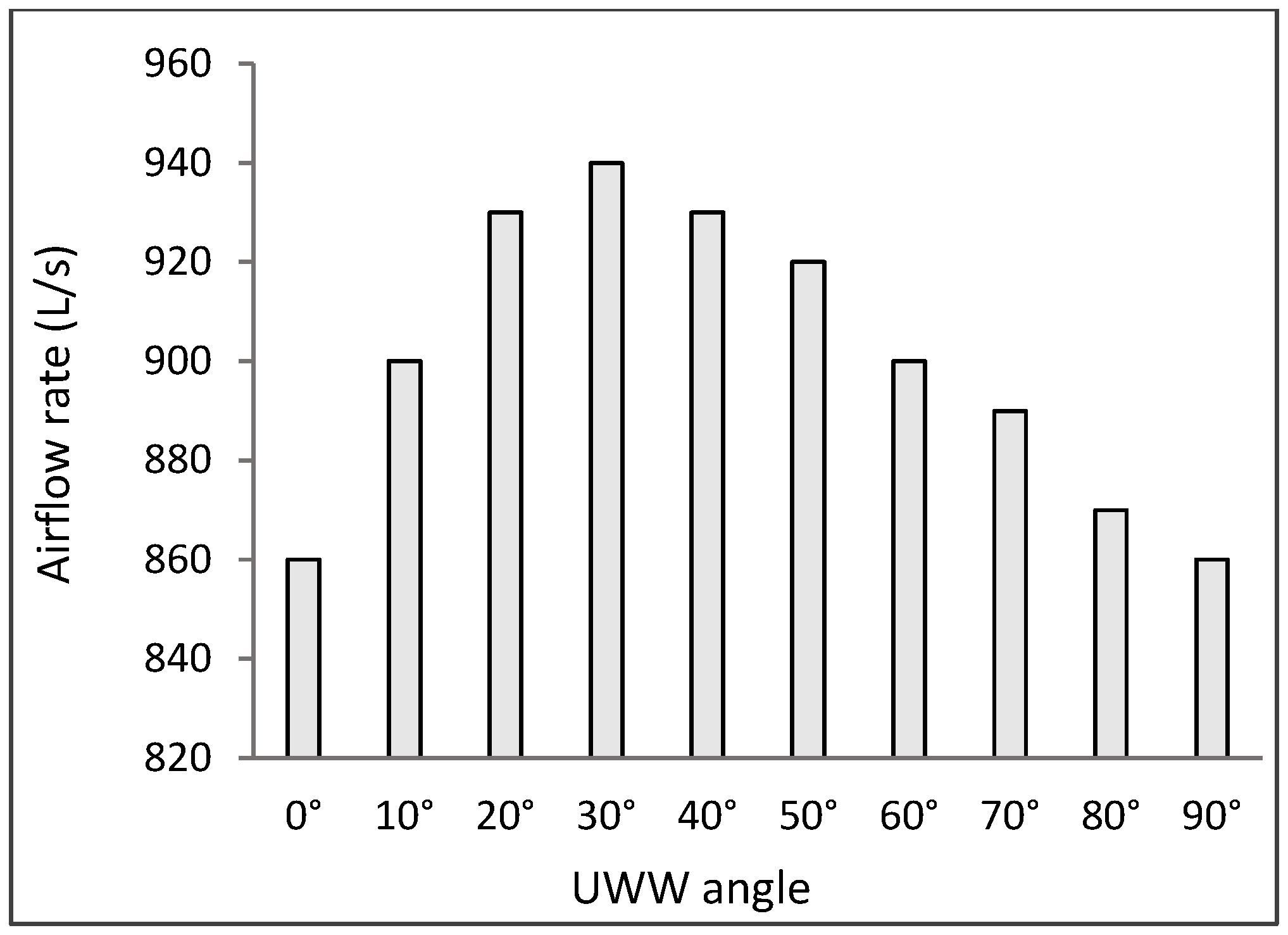
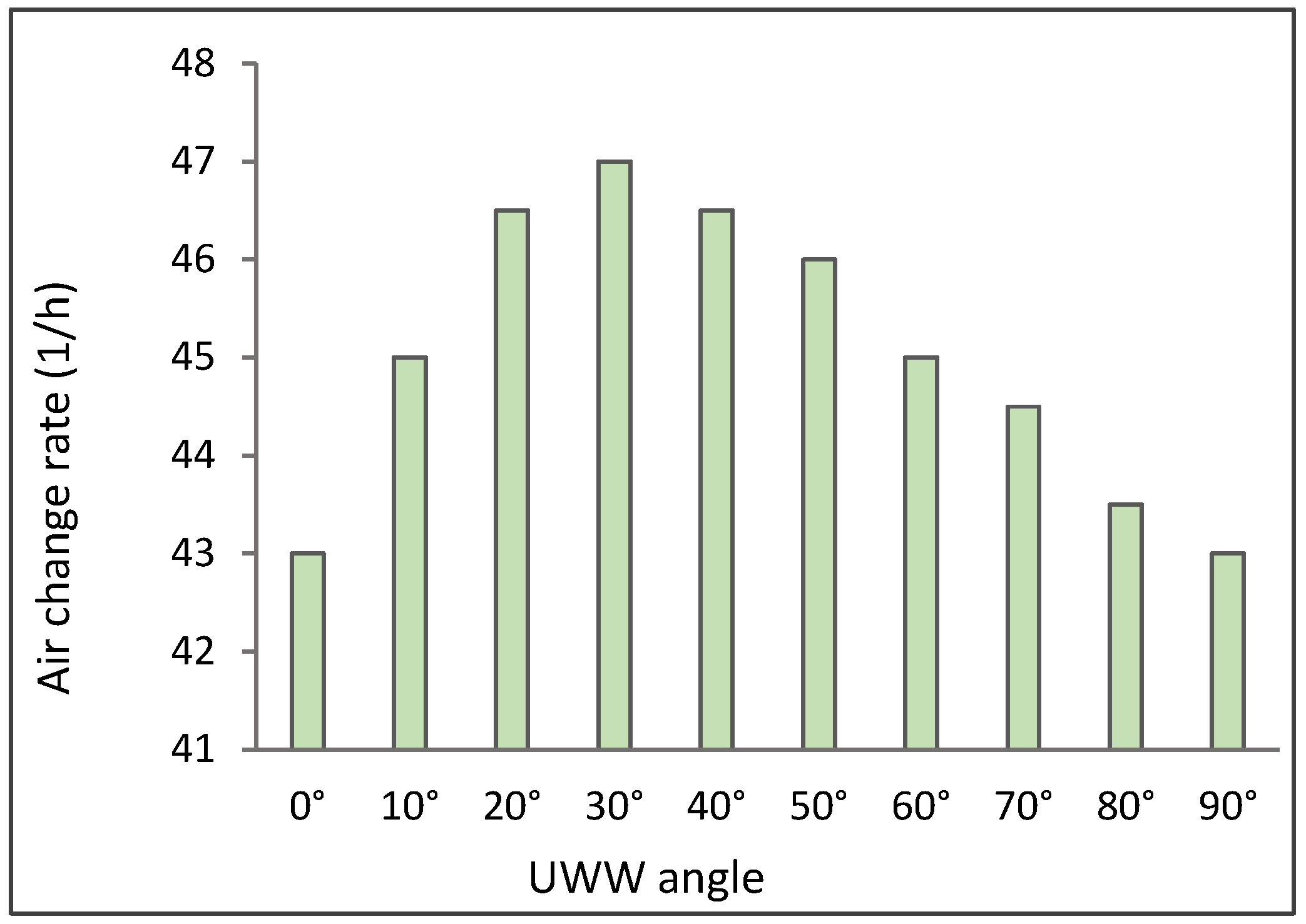
3.2.1. The Effect of the UWW Angle on the Ventilation Performance
Airflow Rate and Air Changes Per Hour (ACH)
Mean Age of Air
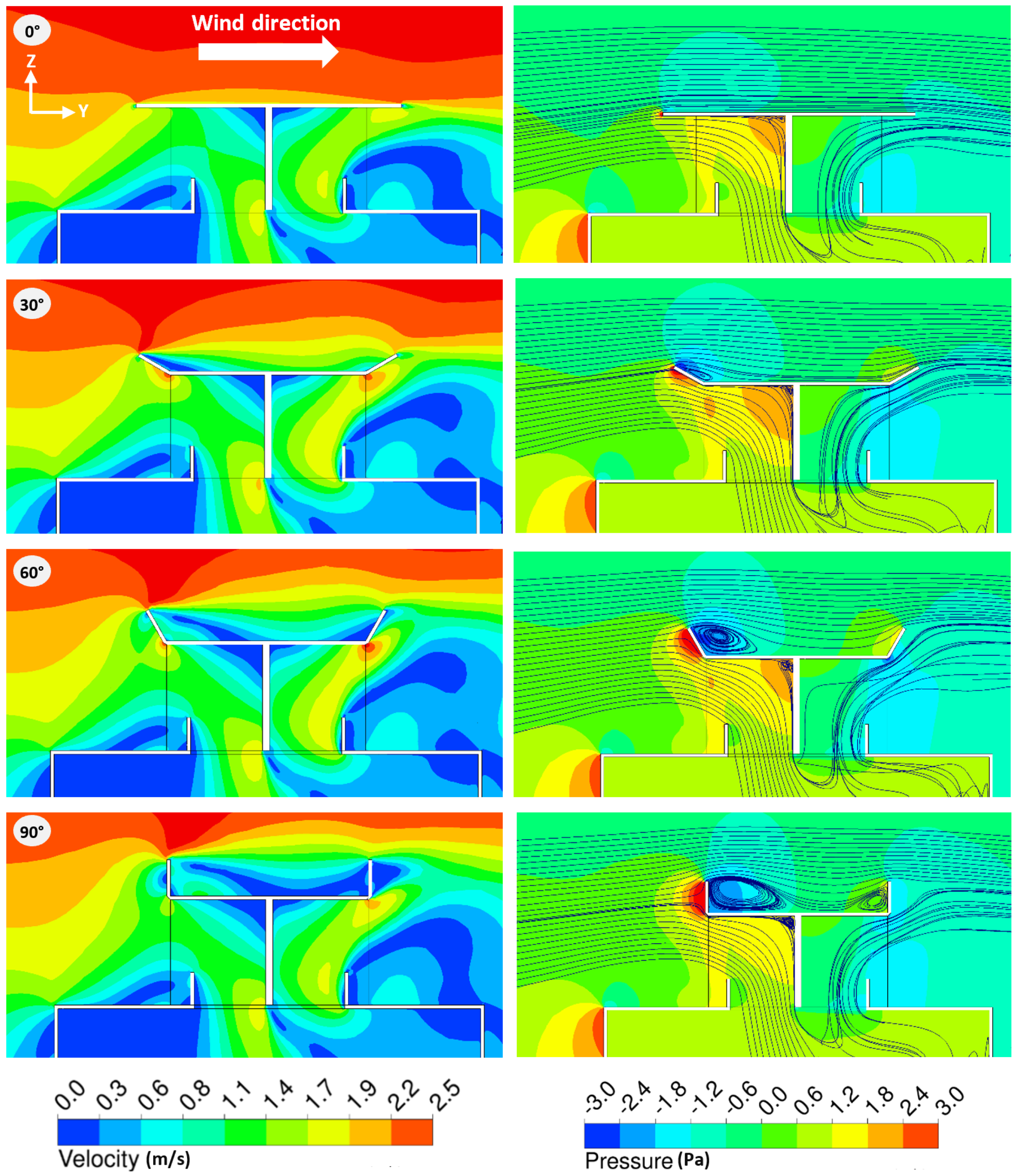
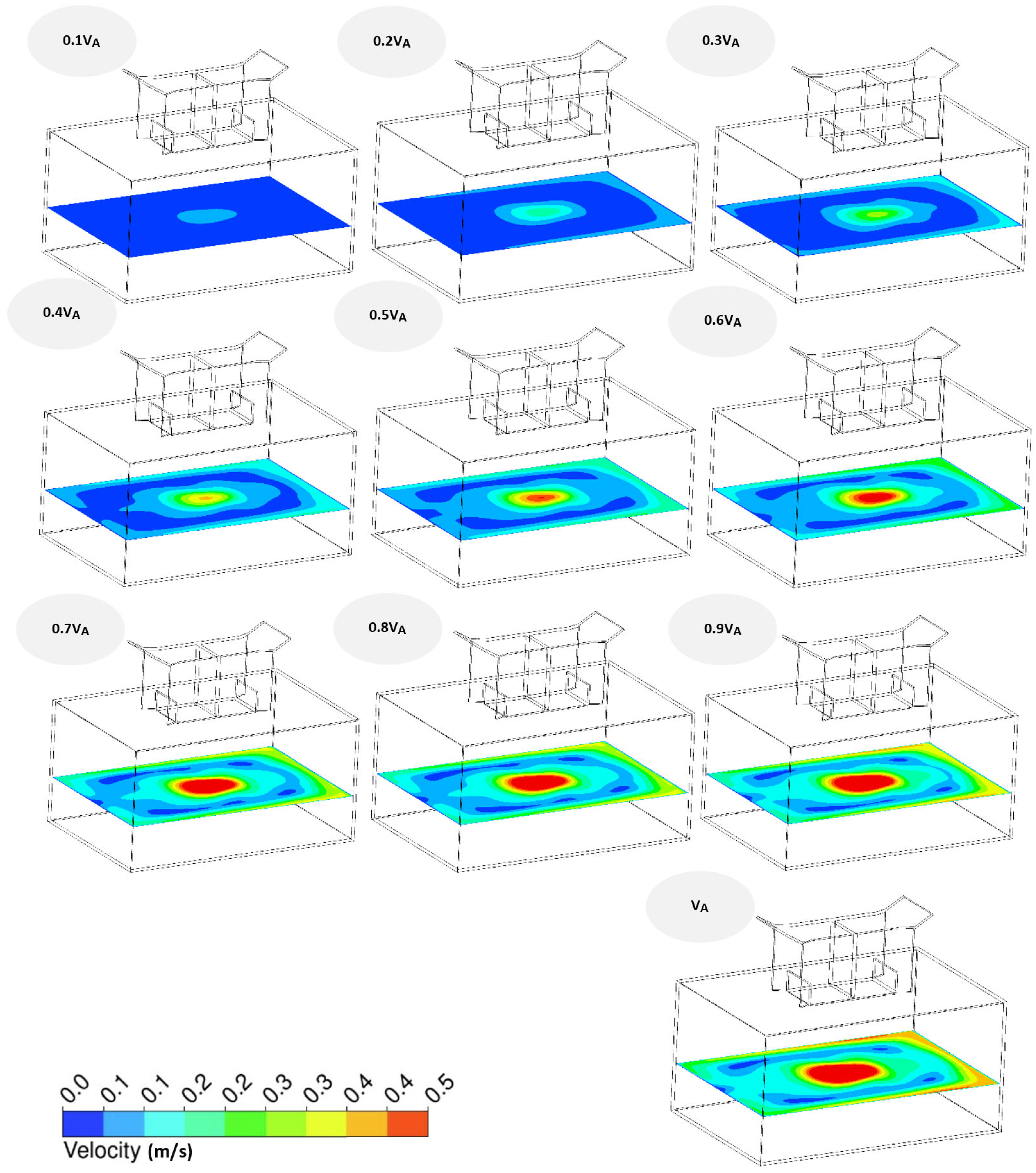
3.2.2. Qualitative Analysis of the UWW’s Impact on Aerodynamic Performance and Flow Field Pattern
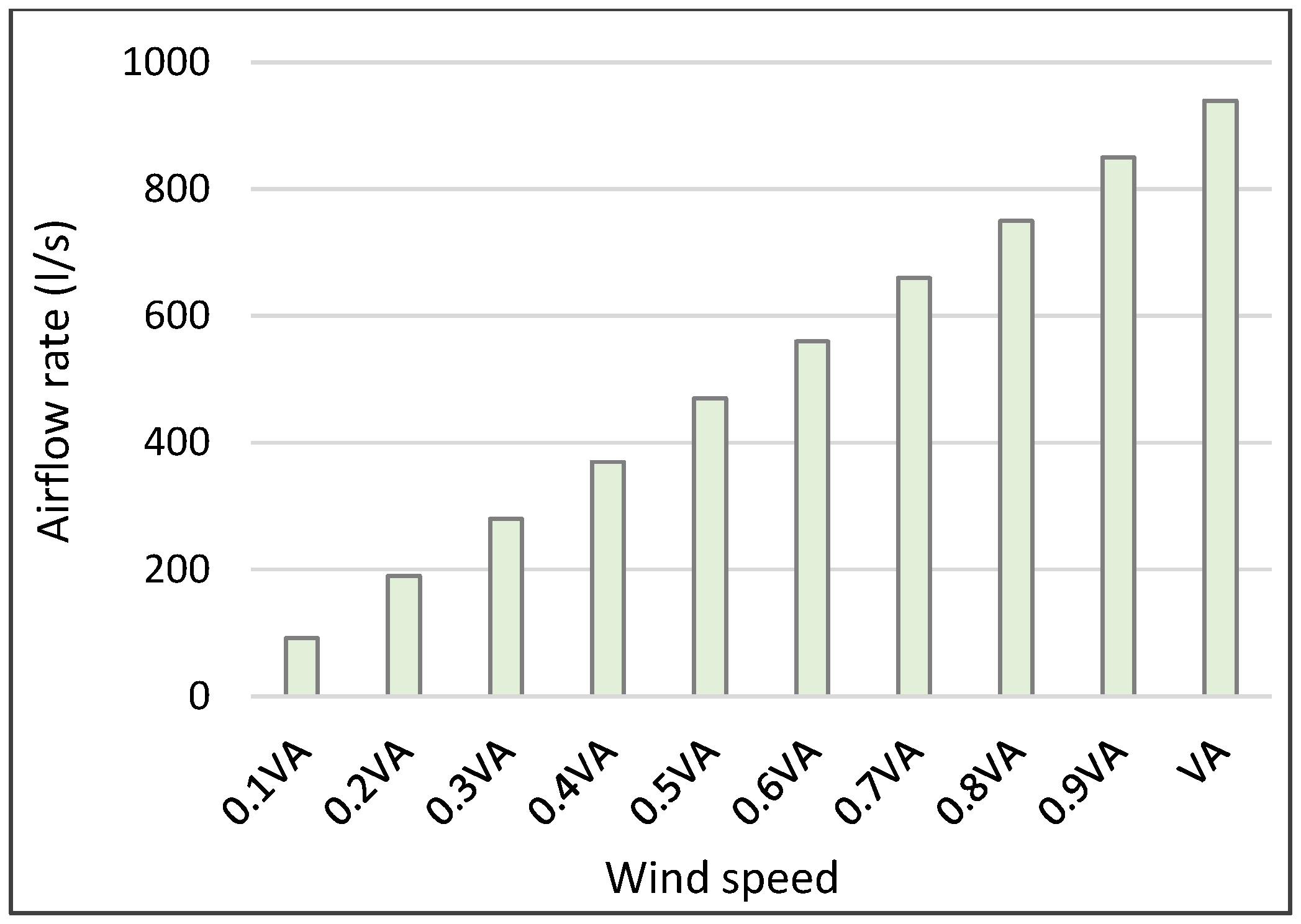
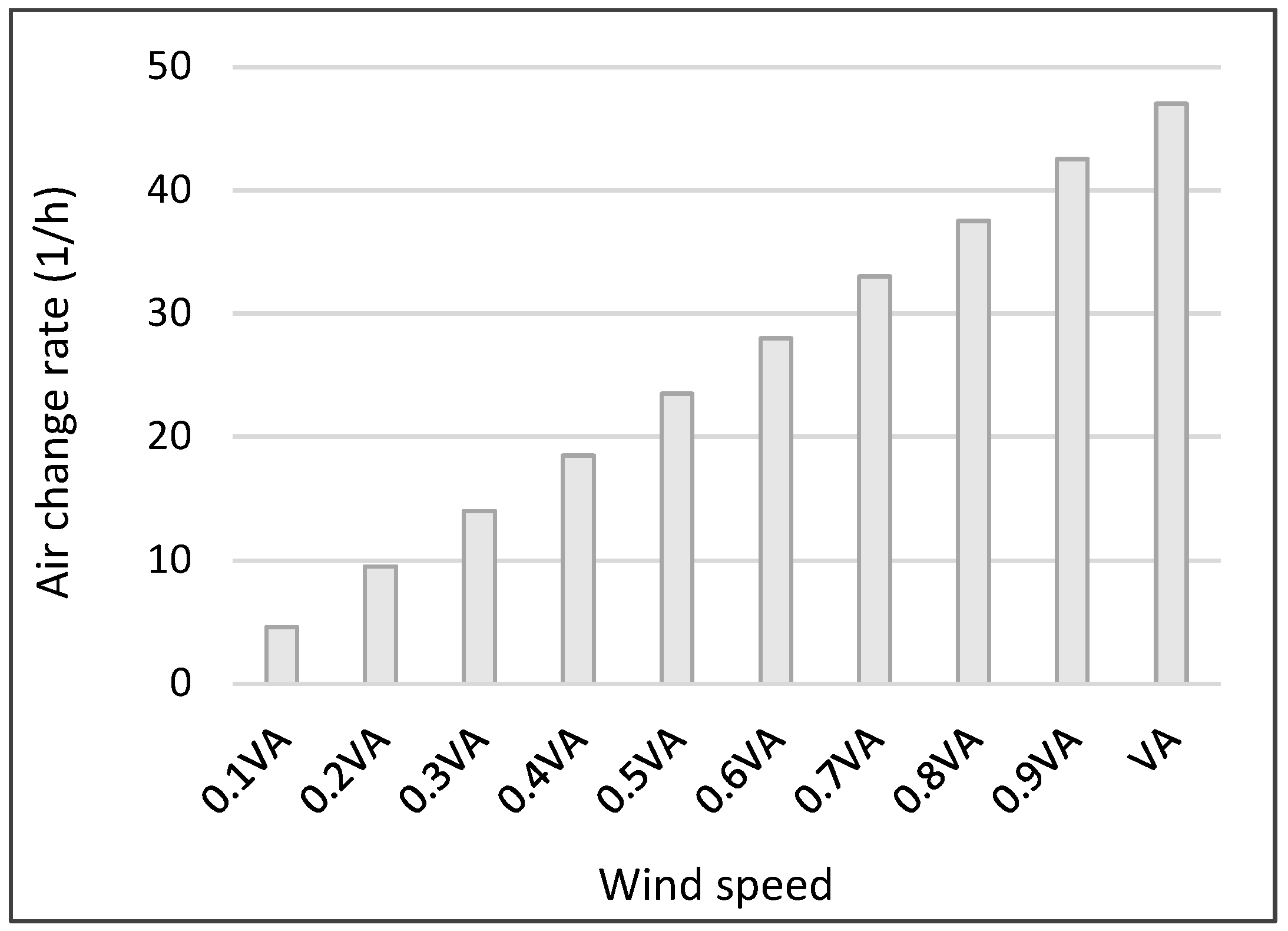
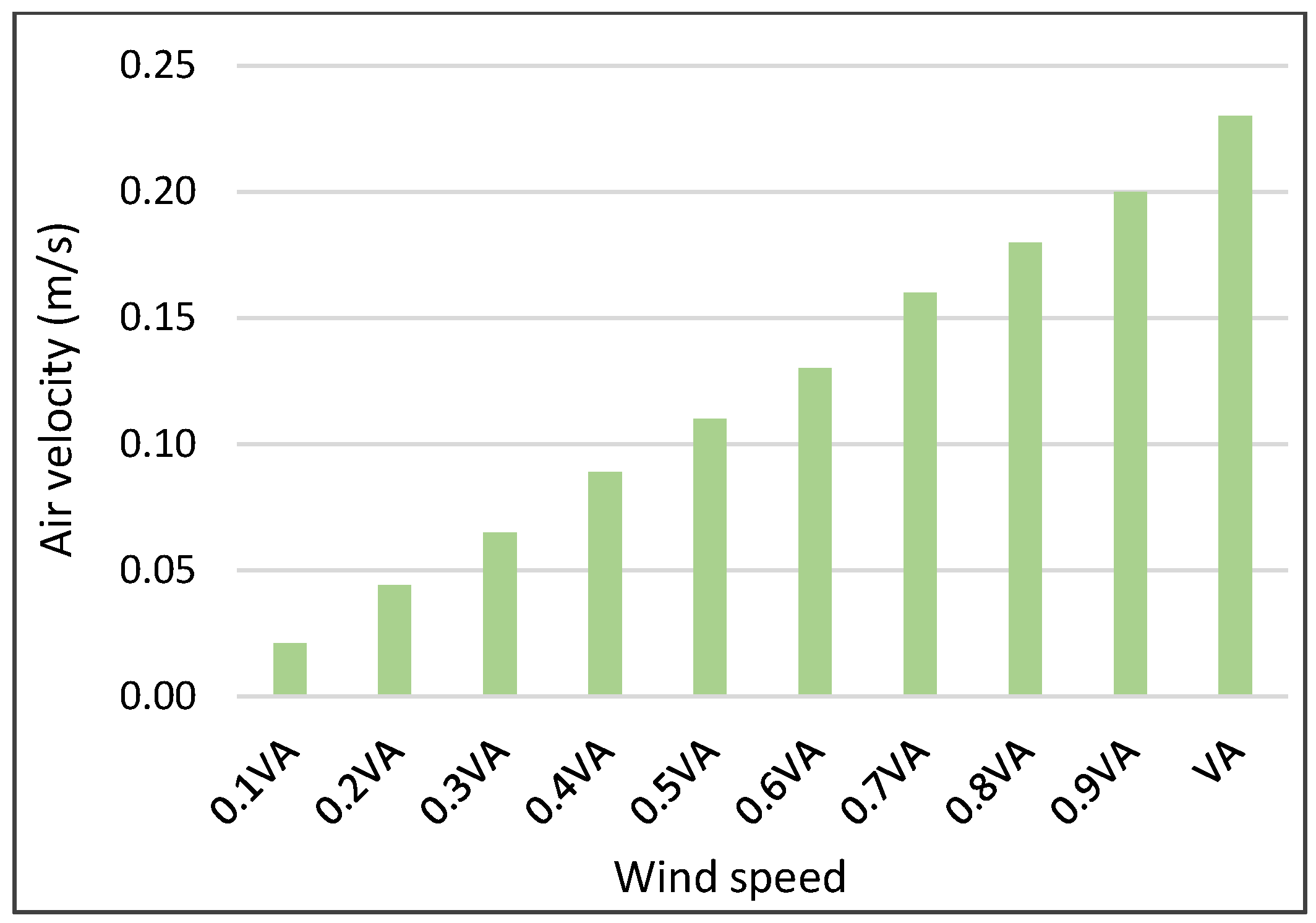
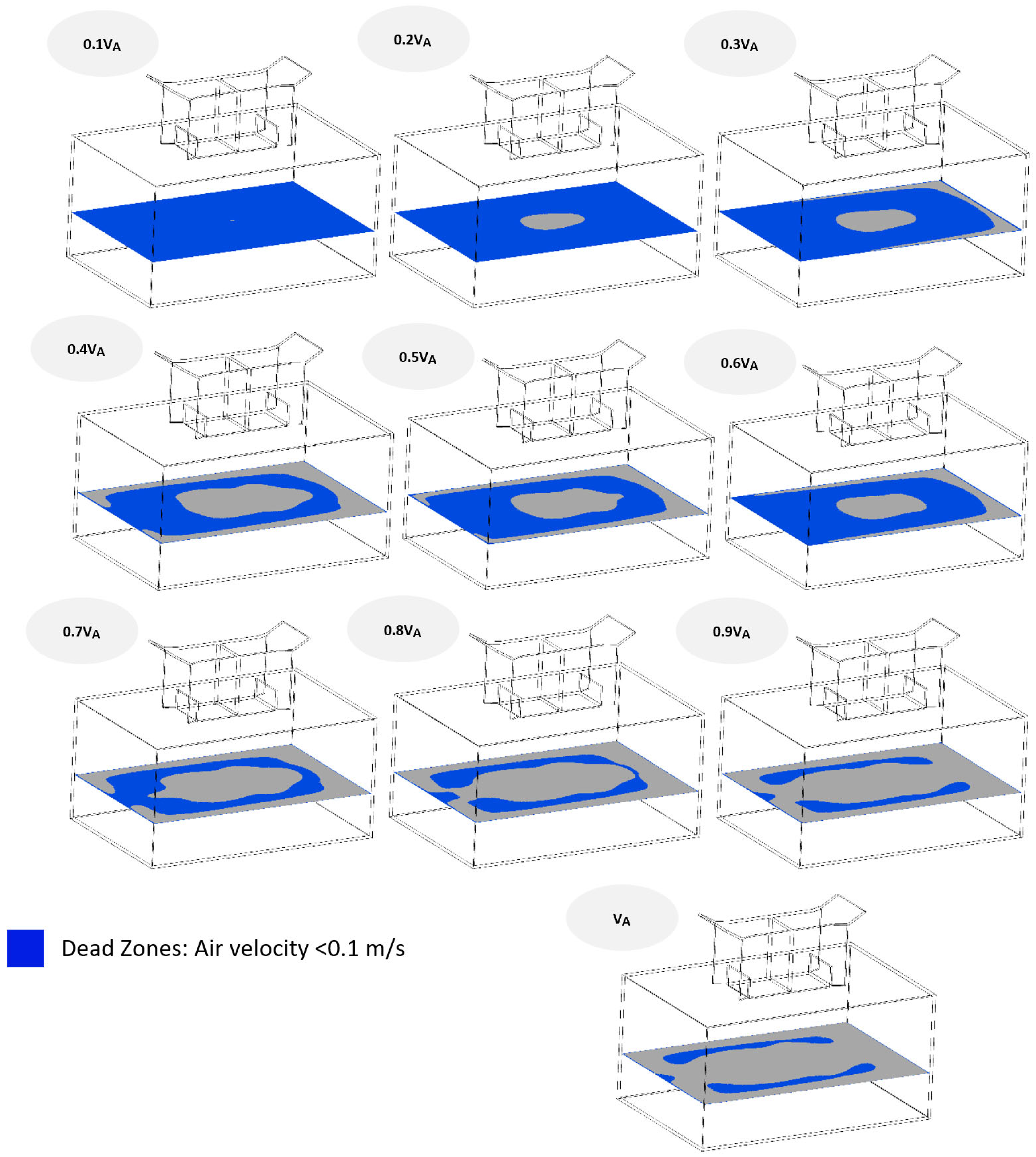
3.2.3. Ventilation Performance under Different Wind Speeds
Airflow Rate and ACH
Airflow Velocity at Head Height
Dead Zones
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, X.; Yu, H.; Sun, Q.; Tam, V.W.Y. A Critical Review of Occupant Energy Consumption Behavior in Buildings: How We Got Here, Where We Are, and Where We Are Headed. Renew. Sustain. Energy Rev. 2023, 182, 113396. [Google Scholar] [CrossRef]
- Afroz, Z.; Burak Gunay, H.; O’Brien, W. A Review of Data Collection and Analysis Requirements for Certified Green Buildings. Energy Build. 2020, 226, 110367. [Google Scholar] [CrossRef] [PubMed]
- Gomis, L.L.; Fiorentini, M.; Daly, D. Potential and Practical Management of Hybrid Ventilation in Buildings. Energy Build. 2020, 231, 110597. [Google Scholar] [CrossRef]
- Wu, Y.; Gao, N.; Niu, J.; Zang, J.; Cao, Q. Numerical Study on Natural Ventilation of the Wind Tower: Effects of Combining with Different Window Configurations in a Low-Rise House. Build. Environ. 2020, 188, 107450. [Google Scholar] [CrossRef]
- Harrouz, J.P.; Ghali, K.; Ghaddar, N.; Paul Harrouz, J.; Ghali, K.; Ghaddar, N. Integrated Solar—Windcatcher with Dew-Point Indirect Evaporative Cooler for Classrooms. Appl. Therm. Eng. 2021, 188, 116654. [Google Scholar] [CrossRef]
- Omrani, S.; Garcia-Hansen, V.; Capra, B.; Drogemuller, R. Natural Ventilation in Multi-Storey Buildings: Design Process and Review of Evaluation Tools. Build. Environ. 2017, 116, 182–194. [Google Scholar] [CrossRef]
- Calautit, J.K.; Hughes, B.R. Wind Tunnel and CFD Study of the Natural Ventilation Performance of a Commercial Multi-Directional Wind Tower. Build. Environ. 2014, 80, 71–83. [Google Scholar] [CrossRef]
- Afshin, M.; Sohankar, A.; Manshadi, M.D.; Esfeh, M.K. An Experimental Study on the Evaluation of Natural Ventilation Performance of a Two-Sided Wind-Catcher for Various Wind Angles. Renew. Energy 2016, 85, 1068–1078. [Google Scholar] [CrossRef]
- Ding, C.; Lam, K.P. Data-Driven Model for Cross Ventilation Potential in High-Density Cities Based on Coupled CFD Simulation and Machine Learning. Build. Environ. 2019, 165, 106394. [Google Scholar] [CrossRef]
- Gil-Baez, M.; Lizana, J.; Becerra Villanueva, J.A.; Molina-Huelva, M.; Serrano-Jimenez, A.; Chacartegui, R. Natural Ventilation in Classrooms for Healthy Schools in the COVID Era in Mediterranean Climate. Build. Environ. 2021, 206, 108345. [Google Scholar] [CrossRef]
- Fortenberry, C.; Walker, M.; Dang, A.; Loka, A.; Date, G.; Cysneiros de Carvalho, K.; Morrison, G.; Williams, B. Analysis of Indoor Particles and Gases and Their Evolution with Natural Ventilation. Indoor Air 2019, 29, 761–779. [Google Scholar] [CrossRef]
- Nejat, P.; Jomehzadeh, F.; Majid, Z.; Mohd Yusof, B.; Zeynali, I. Windcatcher as Sustainable Passive Cooling Solution for Natural Ventilation in Hot Humid Climate of Malaysia. IOP Conf. Ser. Mater. Sci. Eng. 2019, 620, 012087. [Google Scholar] [CrossRef]
- Carreto-Hernandez, L.G.; Moya, S.L.; Varela-Boydo, C.A.; Francisco-Hernandez, A. Numerical-Experimental Study of Mixed Convection in a Wind Tower-Room System. Build. Environ. 2023, 237, 110294. [Google Scholar] [CrossRef]
- Bahadori, M.N.N.; Mazidi, M.; Dehghani, A.R. Experimental Investigation of New Designs of Wind Towers. Renew. Energy 2008, 33, 2273–2281. [Google Scholar] [CrossRef]
- Sadeghi, M.; Wood, G.; Samali, B.; de Dear, R. Effects of Urban Context on the Indoor Thermal Comfort Performance of Windcatchers in a Residential Setting. Energy Build. 2020, 219, 110010. [Google Scholar] [CrossRef]
- Varela-Boydo, C.A.; Moya, S.L. Inlet Extensions for Wind Towers to Improve Natural Ventilation in Buildings. Sustain. Cities Soc. 2020, 53, 101933. [Google Scholar] [CrossRef]
- Bahadori, M.N.; Dehghani-sanij, A. Wind Towers: Architecture, Climate and Sustainability; Sayigh, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 3319058762. [Google Scholar]
- Vassella, C.C.; Koch, J.; Henzi, A.; Jordan, A.; Waeber, R.; Iannaccone, R.; Charrière, R. From Spontaneous to Strategic Natural Window Ventilation: Improving Indoor Air Quality in Swiss Schools. Int. J. Hyg. Environ. Health 2021, 234, 113746. [Google Scholar] [CrossRef]
- Chu, C.R.; Su, Z.Y. Natural Ventilation Design for Underground Parking Garages. Build. Environ. 2023, 227, 109784. [Google Scholar] [CrossRef]
- Kahkzand, M.; Deljouiee, B.; Chahardoli, S.; Siavashi, M. Radiative Cooling Ventilation Improvement Using an Integrated System of Windcatcher and Solar Chimney. J. Build. Eng. 2024, 83, 108409. [Google Scholar] [CrossRef]
- Carreto-Hernandez, L.G.; Moya, S.L.; Varela-Boydo, C.A.; Francisco-Hernandez, A. Studies of Ventilation and Thermal Comfort in Different Wind Tower-Room Configurations Considering Humidification for a Warm Climate of Mexico. J. Build. Eng. 2022, 46, 103675. [Google Scholar] [CrossRef]
- Nejat, P.; Calautit, J.K.; Majid, M.Z.A.; Hughes, B.R.; Zeynali, I.; Jomehzadeh, F. Wind Tunnel and Numerical Data on the Ventilation Performance of Windcatcher with Wing Wall. Data Brief 2016, 9, 448–452. [Google Scholar] [CrossRef] [PubMed]
- Nejat, P.; Hussen, H.M.; Fadli, F.; Chaudhry, H.N.; Calautit, J.; Jomehzadeh, F. Indoor Environmental Quality (IEQ) Analysis of a Two-Sided Windcatcher Integrated with Anti-Short-Circuit Device for Low Wind Conditions. Processes 2020, 8, 840. [Google Scholar] [CrossRef]
- Nejat, P.; Fekri, Y.; Gohari, M.; Alsaad, H.; Voelker, C. Short-Circuiting Reduction in Windcatchers: Shape Effect of Anti-Short-Circuit Device. In Proceedings of the BauSim Conference 2022: 9th Conference of IBPSA-Germany and Austria; IBPSA-Germany and Austria, Weimar, Germany, 20–22 September 2022; Volume 9. [Google Scholar]
- Nejat, P.; Salim Ferwati, M.; Calautit, J.; Ghahramani, A.; Sheikhshahrokhdehkordi, M. Passive Cooling and Natural Ventilation by the Windcatcher (Badgir): An Experimental and Simulation Study of Indoor Air Quality, Thermal Comfort and Passive Cooling Power. J. Build. Eng. 2021, 41, 102436. [Google Scholar] [CrossRef]
- Franke, J.; Hellsten, A.; Schlünzen, H.; Carissimo, B. COST Action 732, Best Practice Guideline for the CFD Simulation of Flows in The Urban Environment; University of Hamburg: Hamburg, Germany, 2007. [Google Scholar]
- Alsailani, M.; Montazeri, H.; Rezaeiha, A. Towards Optimal Aerodynamic Design of Wind Catchers: Impact of Geometrical Characteristics. Renew. Energy 2021, 168, 1344–1363. [Google Scholar] [CrossRef]
- Montazeri, H.; Montazeri, F. CFD Simulation of Cross-Ventilation in Buildings Using Rooftop Wind-Catchers: Impact of Outlet Openings. Renew. Energy 2018, 118, 502–520. [Google Scholar] [CrossRef]
- Zaki, A.; Richards, P.; Sharma, R. Analysis of Airflow inside a Two-Sided Wind Catcher Building. J. Wind Eng. Ind. Aerodyn. 2019, 190, 71–82. [Google Scholar] [CrossRef]
- Esfeh, M.K.; Sohankar, A.; Shahsavari, A.R.; Rastan, M.R.; Ghodrat, M.; Nili, M. Experimental and Numerical Evaluation of Wind-Driven Natural Ventilation of a Curved Roof for Various Wind Angles. Build. Environ. 2021, 205, 108275. [Google Scholar] [CrossRef]
- Varela-Boydo, C.A.; Moya, S.L.; Watkins, R. Analysis of Traditional Windcatchers and the Effects Produced by Changing the Size, Shape, and Position of the Outlet Opening. J. Build. Eng. 2021, 33, 101828. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ Guidelines for Practical Applications of CFD to Pedestrian Wind Environment around Buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Richards, P.J.; Hoxey, R.P. Appropriate Boundary Conditions for Computational Wind Engineering Models Using the K-ϵ Turbulence Model. J. Wind Eng. Ind. Aerodyn. 1993, 46, 145–153. [Google Scholar] [CrossRef]
- Berlin Climate, Weather by Month, Average Temperature (Germany)—Weather Spark. Available online: https://weatherspark.com/y/75981/Average-Weather-in-Berlin-Germany-Year-Round (accessed on 8 September 2023).
- Ferziger, J.H. Computational Methods for Fluid Dynamics, 3rd ed.; Perić, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Blocken, B.; Stathopoulos, T.; Carmeliet, J.; Blockena, B.; Stathopoulosb, T.; Carmelieta, J. CFD Simulation of the Atmospheric Boundary Layer: Wall Function Problems. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- Moosavi, L.; Zandi, M.; Bidi, M.; Behroozizade, E.; Kazemi, I. New Design for Solar Chimney with Integrated Windcatcher for Space Cooling and Ventilation. Build. Environ. 2020, 181, 106785. [Google Scholar] [CrossRef]
- Sadeghi, H.; Kalantar, V. Performance Analysis of a Wind Tower in Combination with an Underground Channel. Sustain. Cities Soc. 2018, 37, 427–437. [Google Scholar] [CrossRef]
- Benkari, N.; Fazil, I.; Husain, A. Design and Performance Comparison of Two Patterns of Wind-Catcher for a Semi-Enclosed Courtyard. Int. J. Mech. Eng. Robot. Res. 2017, 6, 396–400. [Google Scholar] [CrossRef]
- Nejat, P.; Calautit, J.K.; Fekri, Y.; Sheikhshahrokhdehkordi, M.; Alsaad, H.; Voelker, C. Influence of Terrain and Atmospheric Boundary Layer on the Ventilation and Thermal Comfort Performance of Windcatchers. J. Build. Eng. 2023, 73, 106791. [Google Scholar] [CrossRef]
- ASHRAE Standard 62.1; Ventilation for Acceptable Indoor Air Quality. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2019.
- Dehghan, A.A.A.; Esfeh, M.K.; Manshadi, M.D. Natural Ventilation Characteristics of One-Sided Wind Catchers: Experimental and Analytical Evaluation. Energy Build. 2013, 61, 366–377. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nejat, P.; Fekri, Y.; Sheikhshahrokhdehkordi, M.; Jomehzadeh, F.; Alsaad, H.; Voelker, C. The Windcatcher: A Renewable-Energy-Powered Device for Natural Ventilation—The Impact of Upper Wing Walls. Energies 2024, 17, 611. https://doi.org/10.3390/en17030611
Nejat P, Fekri Y, Sheikhshahrokhdehkordi M, Jomehzadeh F, Alsaad H, Voelker C. The Windcatcher: A Renewable-Energy-Powered Device for Natural Ventilation—The Impact of Upper Wing Walls. Energies. 2024; 17(3):611. https://doi.org/10.3390/en17030611
Chicago/Turabian StyleNejat, Payam, Yashar Fekri, Mohammadamin Sheikhshahrokhdehkordi, Fatemeh Jomehzadeh, Hayder Alsaad, and Conrad Voelker. 2024. "The Windcatcher: A Renewable-Energy-Powered Device for Natural Ventilation—The Impact of Upper Wing Walls" Energies 17, no. 3: 611. https://doi.org/10.3390/en17030611
APA StyleNejat, P., Fekri, Y., Sheikhshahrokhdehkordi, M., Jomehzadeh, F., Alsaad, H., & Voelker, C. (2024). The Windcatcher: A Renewable-Energy-Powered Device for Natural Ventilation—The Impact of Upper Wing Walls. Energies, 17(3), 611. https://doi.org/10.3390/en17030611






