Simulations of CO2 Dissolution in Porous Media Using the Volume-of-Fluid Method
Abstract
:1. Introduction
2. Theory and Background
3. Mathematical Model
3.1. Two-Phase Flow Modeling
3.2. Mass Transfer Modeling
4. Simulations
5. Results and Discussion
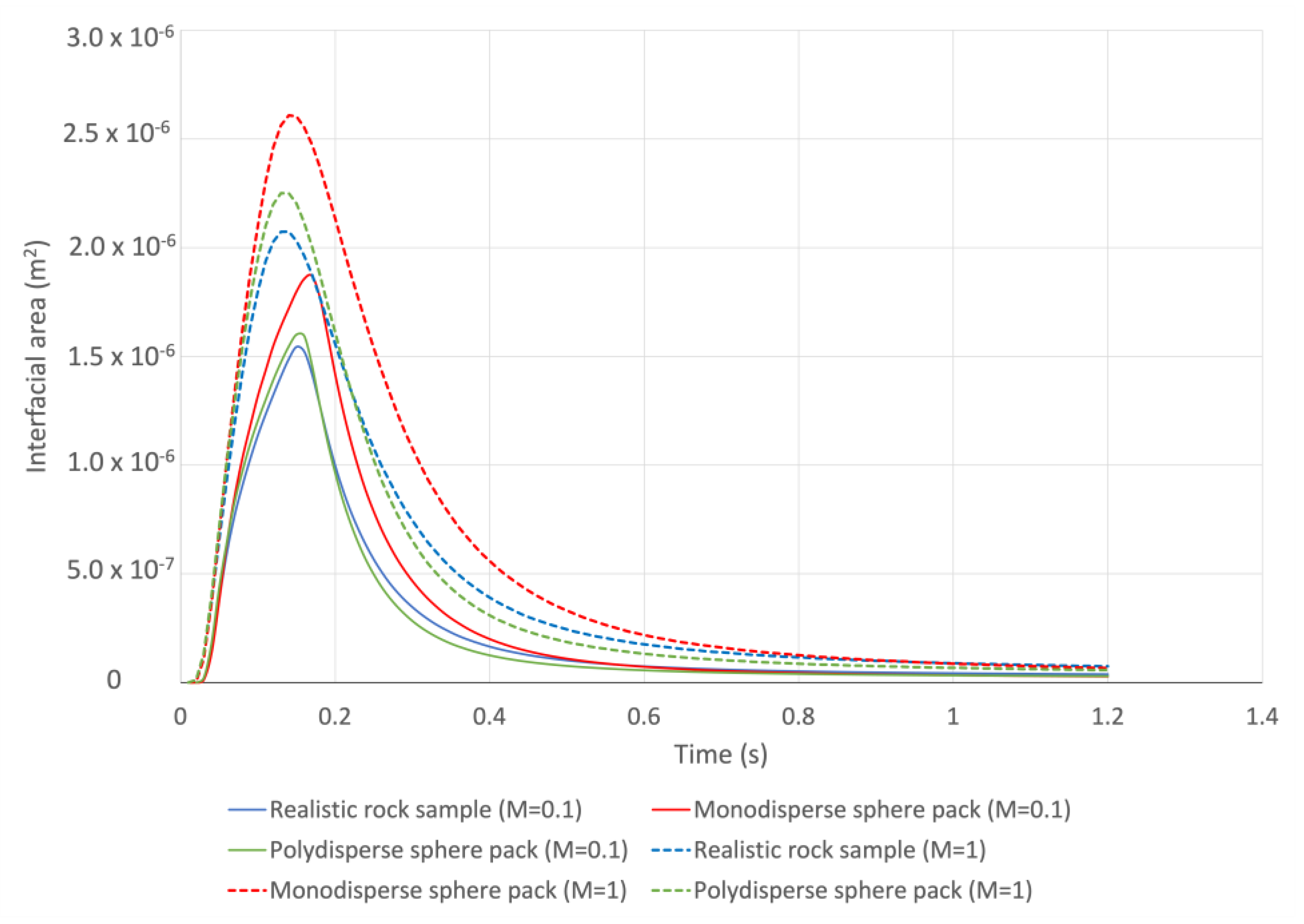
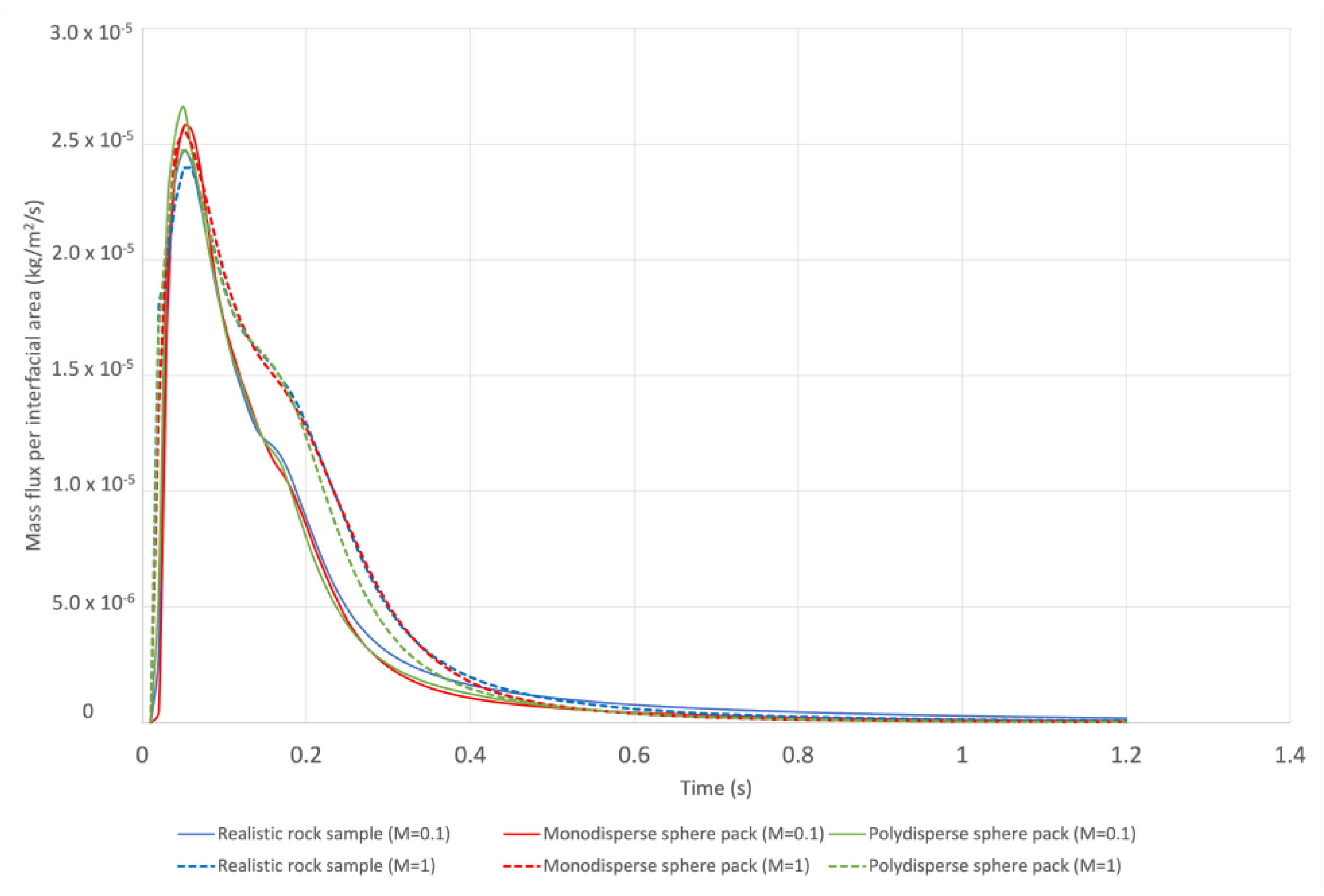
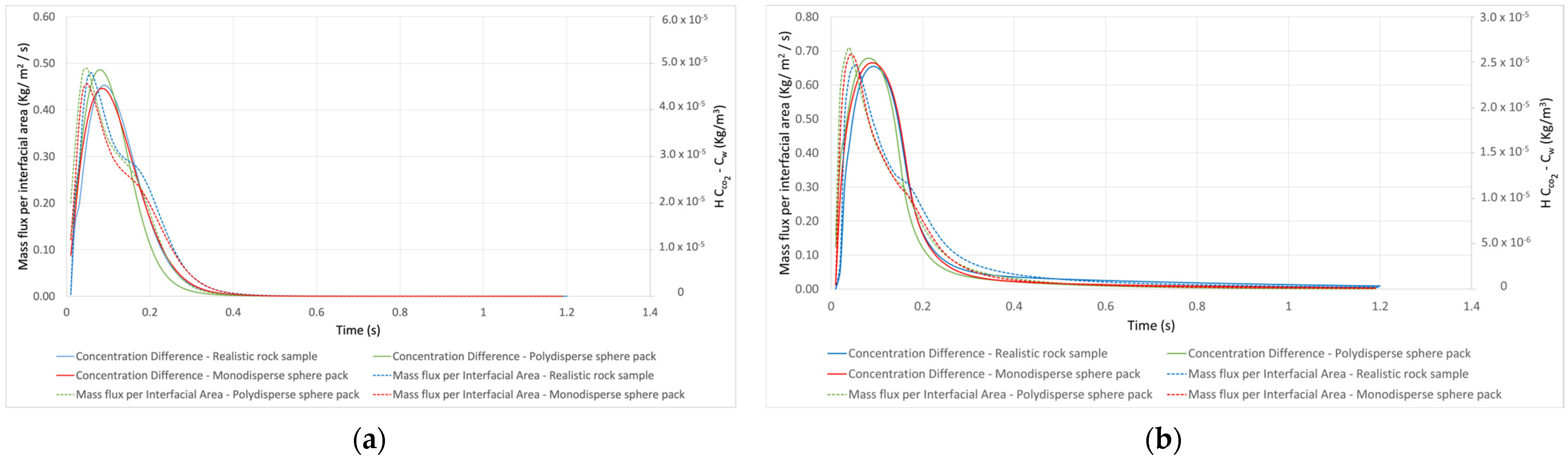
5.1. Analysis of the Simulation Resutlts
5.2. Estimation of the Mass Transfer Coefficien
5.3. Development of Sherwood Correlation with Peclet
5.4. Development of Sherwood Correlation with Reynold and Schmidt
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bultreys, T.; Boever, W.; De Cnudde, V. Imaging and image-based fluid transport modeling at the pore scale in geological materials: A practical introduction to the current state-of-the-art. Earth-Sci. Rev. 2016, 155, 93–128. [Google Scholar] [CrossRef]
- Xiong, T.; Chen, M.; Jin, Y.; Zhang, W.; Shao, H.; Wang, G.; Long, E.; Long, W. A New Multi-Scale Method to Evaluate the Porosity and MICP Curve for Digital Rock of Complex Reservoir. Energies 2023, 16, 7613. [Google Scholar] [CrossRef]
- Mobile, M.; Widdowson, M.; Stewart, L.; Nyman, J.; Deeb, R.; Kavanaugh, M.; Mercer, J.; Gallagher, D. In-situ determination of field-scale NAPL mass transfer coefficients: Performance, simulation and analysis. J. Contam. Hydrol. 2016, 187, 31–46. [Google Scholar] [CrossRef]
- Carrillo, F.J.; Bourg, I.C.; Soulaine, C. Multiphase Flow Modelling in Multiscale Porous Media: An Open-Sourced Micro-Continuum Approach. J. Comput. Phys. X 2020, 8, 100073. [Google Scholar] [CrossRef]
- Icardi, M.; Boccardo, G.; Marchisio, D.L.; Tosco, T.; Sethi, R. Pore-scale simulation of fluid flow and solute dispersion in three-dimensional porous media. Phys. Rev. E 2014, 90, 013032. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Kang, Q.; Robinson, B.A.; He, Y.-L.; Tao, W.-Q. Pore-scale modeling of multiphase reactive transport with phase transitions and dissolution-precipitation processes in closed systems. Phys. Rev. E 2013, 87, 043306. [Google Scholar] [CrossRef]
- Agaoglu, B.; Scheytt, T.; Copty, N.K. Impact of NAPL architecture on interphase mass transfer: A pore network study. Adv. Water Resour. 2016, 95, 138–151. [Google Scholar] [CrossRef]
- Niessner, J.; Hassanizadeh, S.M. Modeling Kinetic Interphase Mass Transfer for Two-Phase Flow in Porous Media Including Fluid–Fluid Interfacial Area. Transp. Porous Media 2009, 80, 329. [Google Scholar] [CrossRef]
- Illangasekare, T.H.; Smits, K.M.; Fučík, R.; Davarzani, H. From Pore to the Field: Upscaling Challenges and Opportunities in Hydrogeological and Land–Atmospheric Systems. In Pore Scale Phenomena; World Scientific Series in Nanoscience and Nanotechnology; World Scientific, 2014; Volume 10, pp. 163–202. [Google Scholar] [CrossRef]
- Chen, L.; Kang, Q.; Tang, Q.; Robinson, B.A.; He, Y.-L.; Tao, W.-Q. Pore-scale simulation of multicomponent multiphase reactive transport with dissolution and precipitation. Int. J. Heat Mass Transf. 2015, 85, 935–949. [Google Scholar] [CrossRef]
- Ehlers, W.; Häberle, K. Interfacial Mass Transfer During Gas-Liquid Phase Change in Deformable Porous Media with Heat Transfer. Transp. Porous Media 2016, 114, 525–556. [Google Scholar] [CrossRef]
- Chen, L.; Wang, M.; Kang, Q.; Tao, W. Pore scale study of multiphase multicomponent reactive transport during CO2 dissolution trapping. Adv. Water Resour. 2018, 116, 208–218. [Google Scholar] [CrossRef]
- Mwenketishi, G.T.; Benkreira, H.; Rahmanian, N. A Comprehensive Review on Carbon Dioxide Sequestration Methods. Energies 2023, 16, 7971. [Google Scholar] [CrossRef]
- Pan, X.; Sun, L.; Huo, X.; Feng, C.; Zhang, Z. Research Progress on CO2 Capture, Utilization, and Storage (CCUS) Based on Micro-Nano Fluidics Technology. Energies 2023, 16, 7846. [Google Scholar] [CrossRef]
- Kokkinaki, A.; O’Carroll, D.M.; Werth, C.J.; Sleep, B.E. An evaluation of Sherwood–Gilland models for NAPL dissolution and their relationship to soil properties. J. Contam. Hydrol. 2013, 155, 87–98. [Google Scholar] [CrossRef] [PubMed]
- Miller, C.T.; Christakos, G.; Imhoff, P.T.; McBride, J.F.; Pedit, J.A.; Trangenstein, J.A. Multiphase flow and transport modeling in heterogeneous porous media: Challenges and approaches. Adv. Water Resour. 1998, 21, 77–120. [Google Scholar] [CrossRef]
- Agaoglu, B.; Copty, N.K.; Scheytt, T.; Hinkelmann, R. Interphase mass transfer between fluids in subsurface formations: A review. Adv. Water Resour. 2015, 79, 162–194. [Google Scholar] [CrossRef]
- Held, R.J.; Celia, M.A. Pore-scale modeling and upscaling of nonaqueous phase liquid mass transfer. Water Resour. Res. 2001, 37, 539–549. [Google Scholar] [CrossRef]
- Joekar-Niasar, V.; Hassanizadeh, S.M. Analysis of Fundamentals of Two-Phase Flow in Porous Media Using Dynamic Pore-Network Models: A Review. Crit. Rev. Environ. Sci. Technol. 2012, 42, 1895–1976. [Google Scholar] [CrossRef]
- Parker, J.C.; Park, E. Modeling field-scale dense nonaqueous phase liquid dissolution kinetics in heterogeneous aquifers. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Sainz-Garcia, A.A. Dynamics of Underground Gas Storage. Insights from Numerical Models for Carbon Dioxide and Hydrogen. Ph.D. Thesis, Université Toulouse 3 Paul Sabatier (UT3 Paul Sabatier), Toulouse, France, 2017. [Google Scholar]
- Brusseau, M.L.; DiFilippo, E.L.; Marble, J.C.; Oostrom, M. Mass-removal and mass-flux-reduction behavior for idealized source zones with hydraulically poorly-accessible immiscible liquid. Chemosphere 2008, 71, 1511–1521. [Google Scholar] [CrossRef]
- Schnaar, G.; Brusseau, M.L. Pore-Scale Characterization of Organic Immiscible-Liquid Morphology in Natural Porous Media Using Synchrotron X-ray Microtomography. Environ. Sci. Technol. 2005, 39, 8403–8410. [Google Scholar] [CrossRef] [PubMed]
- Seyedabbasi, M.A.; Farthing, M.W.; Imhoff, P.T.; Miller, C.T. The influence of wettability on NAPL dissolution fingering. Adv. Water Resour. 2008, 31, 1687–1696. [Google Scholar] [CrossRef]
- Dillard, L.A.; Blunt, M.J. Development of a pore network simulation model to study nonaqueous phase liquid dissolution. Water Resour. Res. 2000, 36, 439–454. [Google Scholar] [CrossRef]
- Maes, J.; Soulaine, C. A new compressive scheme to simulate species transfer across fluid interfaces using the Volume-Of-Fluid method. Chem. Eng. Sci. 2018, 190, 405–418. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Dover publications: New York, NY, USA, 1988; ISBN 978-0-486-65675-5. [Google Scholar]
- Costanza-Robinson, M.S.; Harrold, K.H.; Lieb-Lappen, R.M. X-ray Microtomography Determination of Air−Water Interfacial Area−Water Saturation Relationships in Sandy Porous Media. Environ. Sci. Technol. 2008, 42, 2949–2956. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Rao, P.S.C.; Annable, M.D. Gaseous Tracer Technique for Estimating Air–Water Interfacial Areas and Interface Mobility. Soil Sci. Soc. Am. J. 1999, 63, 1554–1560. [Google Scholar] [CrossRef]
- Segura, L.A.; Toledo, P.G. Pore-Level Modeling of Isothermal Drying of Pore Networks Accounting for Evaporation, Viscous Flow, and Shrinking. Dry. Technol. 2005, 23, 2007–2019. [Google Scholar] [CrossRef]
- Wang, Q.; Jia, Z.; Cheng, L.; Li, B.; Jia, P.; Lan, Y.; Dong, D.; Qu, F. Characterization of Flow Parameters in Shale Nano-Porous Media Using Pore Network Model: A Field Example from Shale Oil Reservoir in Songliao Basin, China. Energies 2023, 16, 5424. [Google Scholar] [CrossRef]
- Luo, C.; Wan, H.; Chen, J.; Huang, X.; Cui, S.; Qin, J.; Yan, Z.; Qiao, D.; Shi, Z. Estimation of 3D Permeability from Pore Network Models Constructed Using 2D Thin-Section Images in Sandstone Reservoirs. Energies 2023, 16, 6976. [Google Scholar] [CrossRef]
- Sarikurt, D.A.; Gokdemir, C.; Copty, N.K. Sherwood correlation for dissolution of pooled NAPL in porous media. J. Contam. Hydrol. 2017, 206, 67–74. [Google Scholar] [CrossRef]
- van Genuchten, M.T.; Alves, W.J. Analytical Solutions of the One-Dimensional Convective-Dispersive Solute Transport Equation; United States Department of Agriculture, Economic Research Service: Washington, DC, USA, 1982. [Google Scholar]
- Hunt, J.R.; Sitar, N.; Udell, K.S. Nonaqueous phase liquid transport and cleanup: 1. Analysis of mechanisms. Water Resour. Res. 1988, 24, 1247–1258. [Google Scholar] [CrossRef]
- Al-Futaisi, A.; Patzek, T.W. Impact of wettability alteration on two-phase flow characteristics of sandstones: A quasi-static description. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Latt, J.; Malaspinas, O.; Kontaxakis, D.; Parmigiani, A.; Lagrava, D.; Brogi, F.; Belgacem, M.B.; Thorimbert, Y.; Leclaire, S.; Li, S.; et al. Palabos: Parallel Lattice Boltzmann Solver. Comput. Math. Appl. 2021, 81, 334–350. [Google Scholar] [CrossRef]
- Haroun, Y.; Legendre, D.; Raynal, L. Volume of fluid method for interfacial reactive mass transfer: Application to stable liquid film. Chem. Eng. Sci. 2010, 65, 2896–2909. [Google Scholar] [CrossRef]
- Benson, S.M.; Bennaceur, K.; Cook, P.; Davison, J.; De Coninck, H.; Farhat, K.; Ramirez, A.; Simbeck, D.; Surles, T.; Verma, P.; et al. Carbon Capture and Storage. In Global Energy Assessment (GEA); Johansson, T.B., Nakicenovic, N., Patwardhan, A., Gomez-Echeverri, L., Eds.; Cambridge University Press: Cambridge, UK, 2012; pp. 993–1068. ISBN 978-0-511-79367-7. [Google Scholar]
- Liu, B.; Mahmood, B.S.; Mohammadian, E.; Khaksar Manshad, A.; Rosli, N.R.; Ostadhassan, M. Measurement of Solubility of CO2 in NaCl, CaCl2, MgCl2 and MgCl2 + CaCl2 Brines at Temperatures from 298 to 373 K and Pressures up to 20 MPa Using the Potentiometric Titration Method. Energies 2021, 14, 7222. [Google Scholar] [CrossRef]
- Wang, H.; Kou, Z.; Ji, Z.; Wang, S.; Li, Y.; Jiao, Z.; Johnson, M.; McLaughlin, J.F. Investigation of enhanced CO2 storage in deep saline aquifers by WAG and brine extraction in the Minnelusa sandstone, Wyoming. Energy 2023, 265, 126379. [Google Scholar] [CrossRef]
- Powers, S.E.; Abriola, L.M.; Dunkin, J.S.; Weber, W.J. Phenomenological models for transient NAPL-water mass-transfer processes. J. Contam. Hydrol. 1994, 16, 1–33. [Google Scholar] [CrossRef]
- Miller, C.T.; Poirier-McNeil, M.M.; Mayer, A.S. Dissolution of Trapped Nonaqueous Phase Liquids: Mass Transfer Characteristics. Water Resour. Res. 1990, 26, 2783–2796. [Google Scholar] [CrossRef]
- Powers, S.E.; Abriola, L.M.; Weber, W.J., Jr. An experimental investigation of nonaqueous phase liquid dissolution in saturated subsurface systems: Steady state mass transfer rates. Water Resour. Res. 1992, 28, 2691–2705. [Google Scholar] [CrossRef]
- Ibrahim, M.A.A.; Kerimov, A.; Mukerji, T.; Mavko, G. Particula: A simulator tool for computational rock physics of granular media. Geophysics 2019, 84, F85–F95. [Google Scholar] [CrossRef]
- Raeini, A.Q.; Blunt, M.J.; Bijeljic, B. Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method. J. Comput. Phys. 2012, 231, 5653–5668. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Ubbink, O.; Issa, R.I. A Method for Capturing Sharp Fluid Interfaces on Arbitrary Meshes. J. Comput. Phys. 1999, 153, 26–50. [Google Scholar] [CrossRef]
- Popinet, S.; Zaleski, S. A front-tracking algorithm for accurate representation of surface tension. Int. J. Numer. Methods Fluids 1999, 30, 775–793. [Google Scholar] [CrossRef]
- Graveleau, M.; Soulaine, C.; Tchelepi, H.A. Pore-Scale Simulation of Interphase Multicomponent Mass Transfer for Subsurface Flow. Transp. Porous Media 2017, 120, 287–308. [Google Scholar] [CrossRef]
- Henry, W.; Banks, J. III. Experiments on the quantity of gases absorbed by water, at different temperatures, and under different pressures. Philos. Trans. R. Soc. Lond. 1997, 93, 29–274. [Google Scholar] [CrossRef]
- Deising, D.; Marschall, H.; Bothe, D. A unified single-field model framework for Volume-Of-Fluid simulations of interfacial species transfer applied to bubbly flows. Chem. Eng. Sci. 2016, 139, 173–195. [Google Scholar] [CrossRef]
- Jasak, H.; Jemcov, A.; Tuković, Ž. OpenFOAM: A C++ Library for Complex Physics Simulations. 2007. Available online: www.openfoam.org/ (accessed on 23 January 2024).
- Zhang, D.; Song, J. Mechanisms for Geological Carbon Sequestration. Procedia IUTAM 2014, 10, 319–327. [Google Scholar] [CrossRef]
- Seyyedi, M.; Mahmud, H.K.B.; Verrall, M.; Giwelli, A.; Esteban, L.; Ghasemiziarani, M.; Clennell, B. Pore Structure Changes Occur During CO2 Injection into Carbonate Reservoirs. Sci. Rep. 2020, 10, 3624. [Google Scholar] [CrossRef]
- Soulaine, C.; Debenest, G.; Quintard, M. Upscaling multi-component two-phase flow in porous media with partitioning coefficient. Chem. Eng. Sci. 2011, 66, 6180–6192. [Google Scholar] [CrossRef]
- Patmonoaji, A.; Suekane, T. Investigation of CO2 dissolution via mass transfer inside a porous medium. Adv. Water Resour. 2017, 110, 97–106. [Google Scholar] [CrossRef]
- Patmonoaji, A.; Hu, Y.; Zhang, C.; Suekane, T.; Patmonoaji, A.; Hu, Y.; Zhang, C.; Suekane, T. Dissolution Mass Transfer of Trapped Phase in Porous Media. In Porous Fluids—Advances in Fluid Flow and Transport Phenomena in Porous Media; IntechOpen: London, UK, 2021; ISBN 978-1-83962-712-5. [Google Scholar]
- Patmonoaji, A.; Tahta, M.A.; Tuasikal, J.A.; She, Y.; Hu, Y.; Suekane, T. Dissolution mass transfer of trapped gases in porous media: A correlation of Sherwood, Reynolds, and Schmidt numbers. Int. J. Heat Mass Transf. 2023, 205, 123860. [Google Scholar] [CrossRef]
- Donaldson, J.H.; Istok, J.D.; Humphrey, M.D.; O’Reilly, K.T.; Hawelka, C.A.; Mohr, D.H. Development and Testing of a Kinetic Model for Oxygen Transport in Porous Media in the Presence of Trapped Gas. Groundwater 1997, 35, 270–279. [Google Scholar] [CrossRef]
- Patmonoaji, A.; Hu, Y.; Nasir, M.; Zhang, C.; Suekane, T. Effects of Dissolution Fingering on Mass Transfer Rate in Three-Dimensional Porous Media. Water Resour. Res. 2021, 57, e2020WR029353. [Google Scholar] [CrossRef]


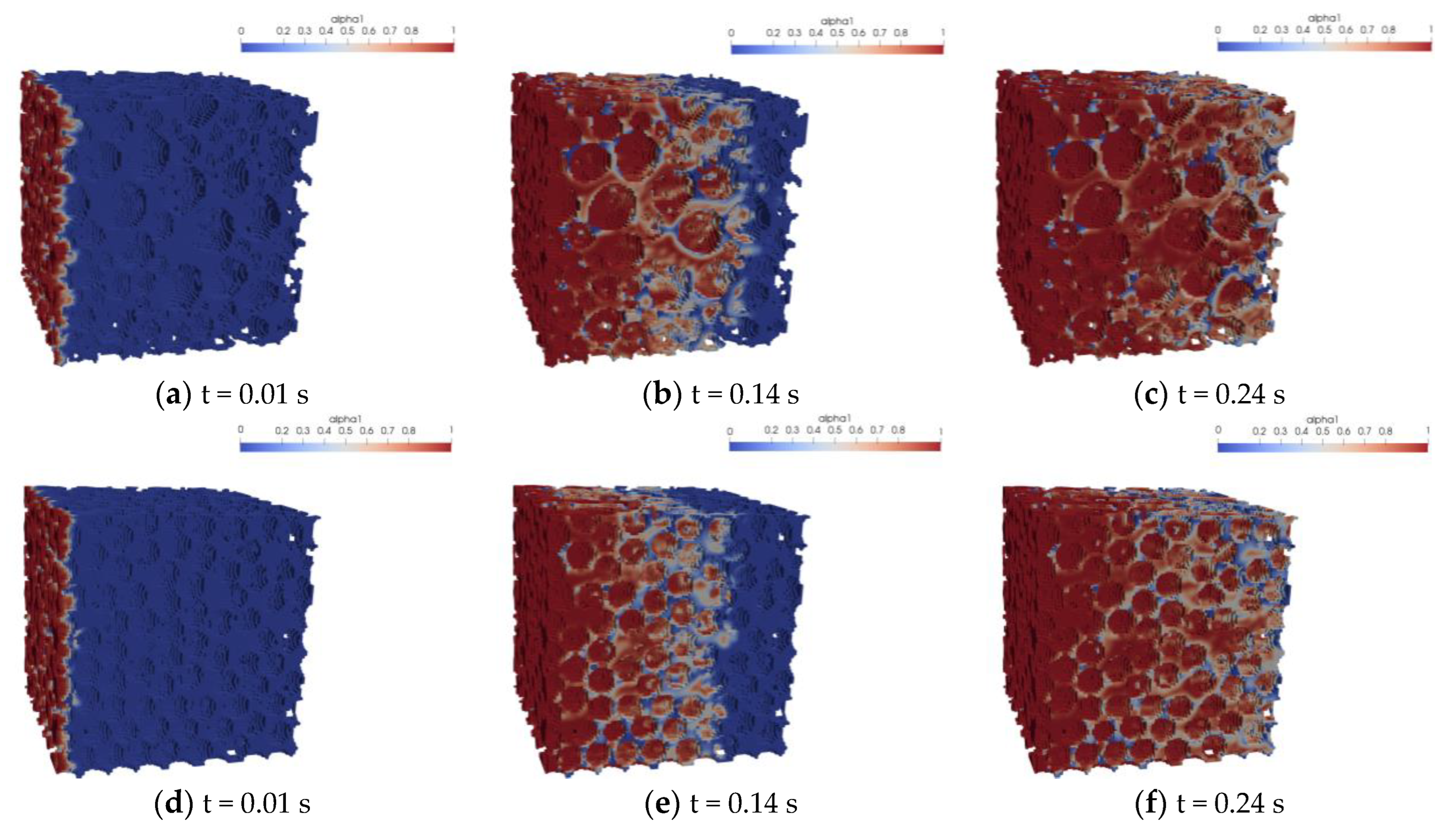


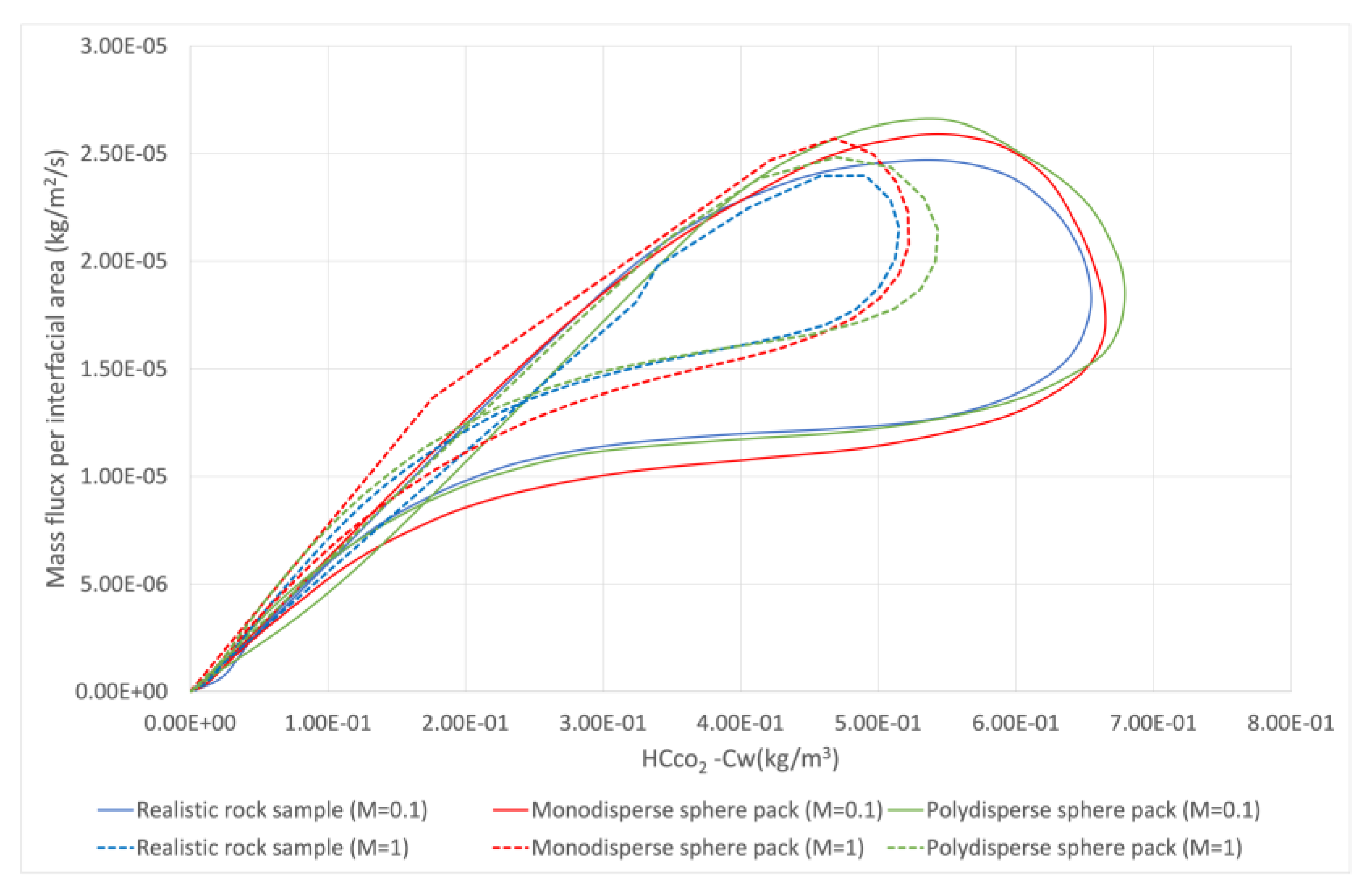

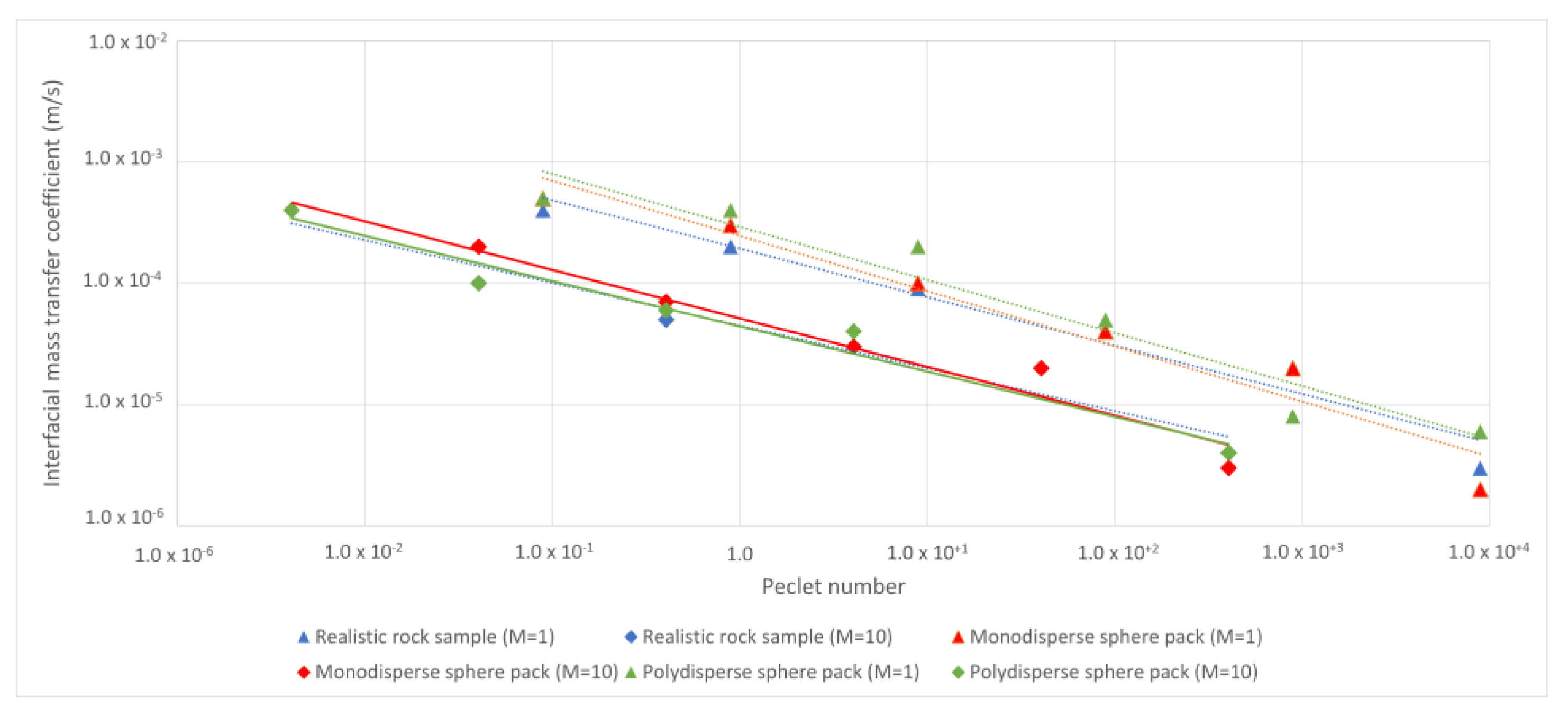
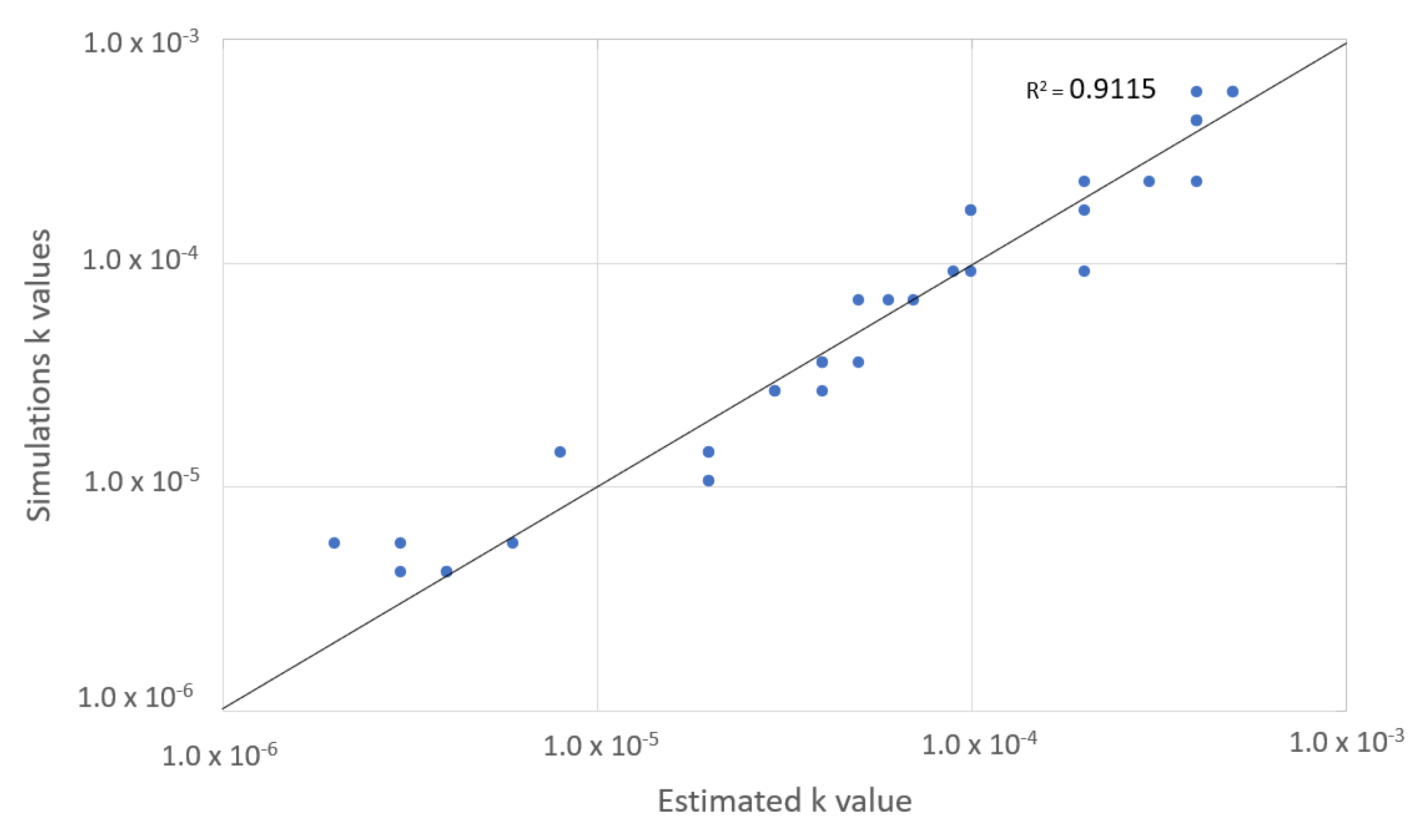
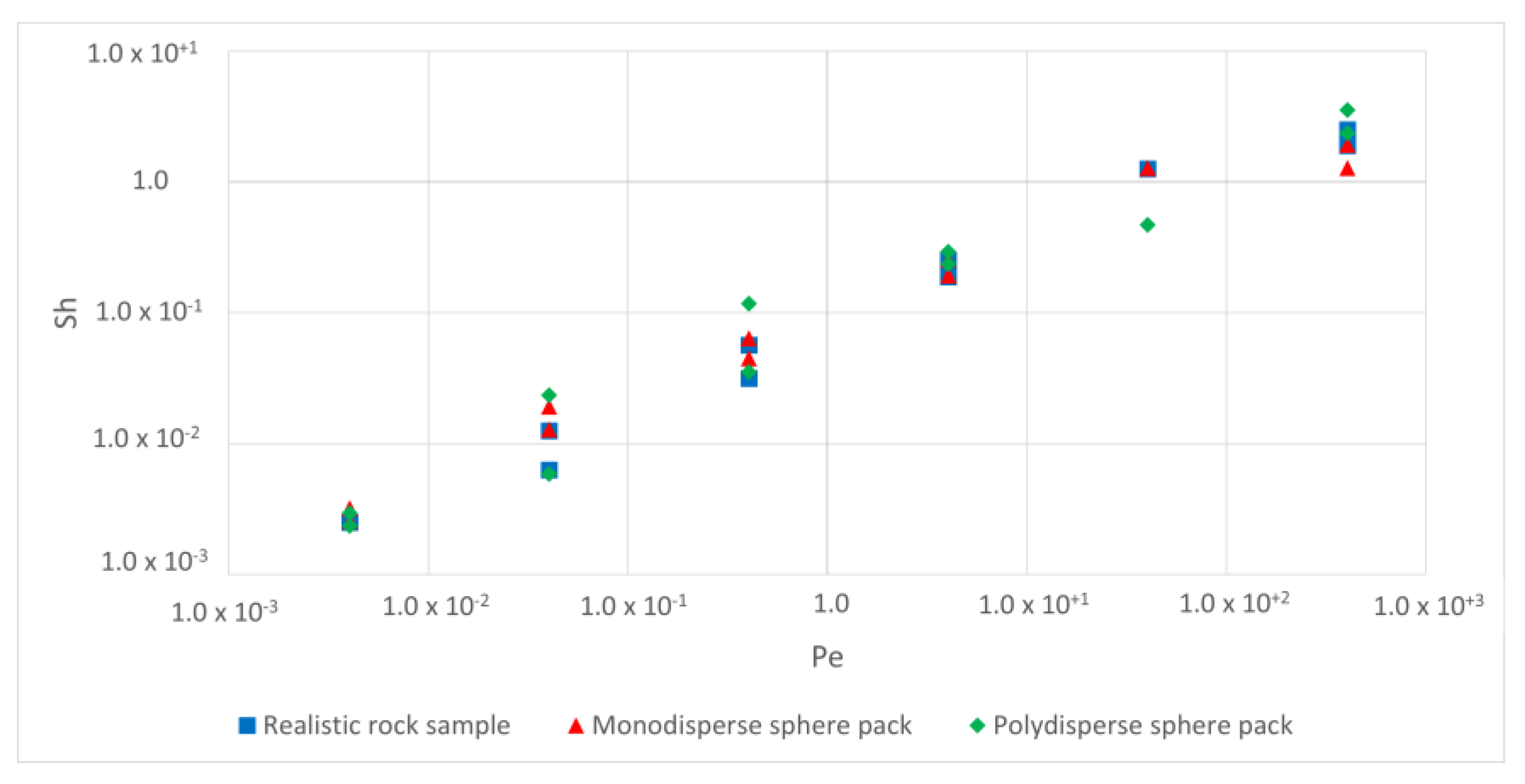

| Rock Sample | Porosity | Permeability (m2) | Voxel Size (μm) | Side Length (m) | Tortuosity | Grain Surface Area (m2) |
|---|---|---|---|---|---|---|
| Realistic rock sample | 0.29 | 3.0 | 900 | 1.22 | ||
| Monodisperse sphere pack | 0.34 | 3.0 | 900 | 1.19 | ||
| Polydisperse sphere pack | 0.34 | 3.0 | 900 | 1.20 |
| Rock Sample | M = 1 | M = 0.1 |
|---|---|---|
| Realistic rock sample | 0.9572 | |
| Monodisperse sphere pack | 0.9431 | |
| Polydisperse sphere pack | 0.8156 |
| Rock Sample | Realistic Rock Sample | Monodisperse Sphere Pack | Polydisperse Sphere Pack |
|---|---|---|---|
| Sherwood and Peclet equation |
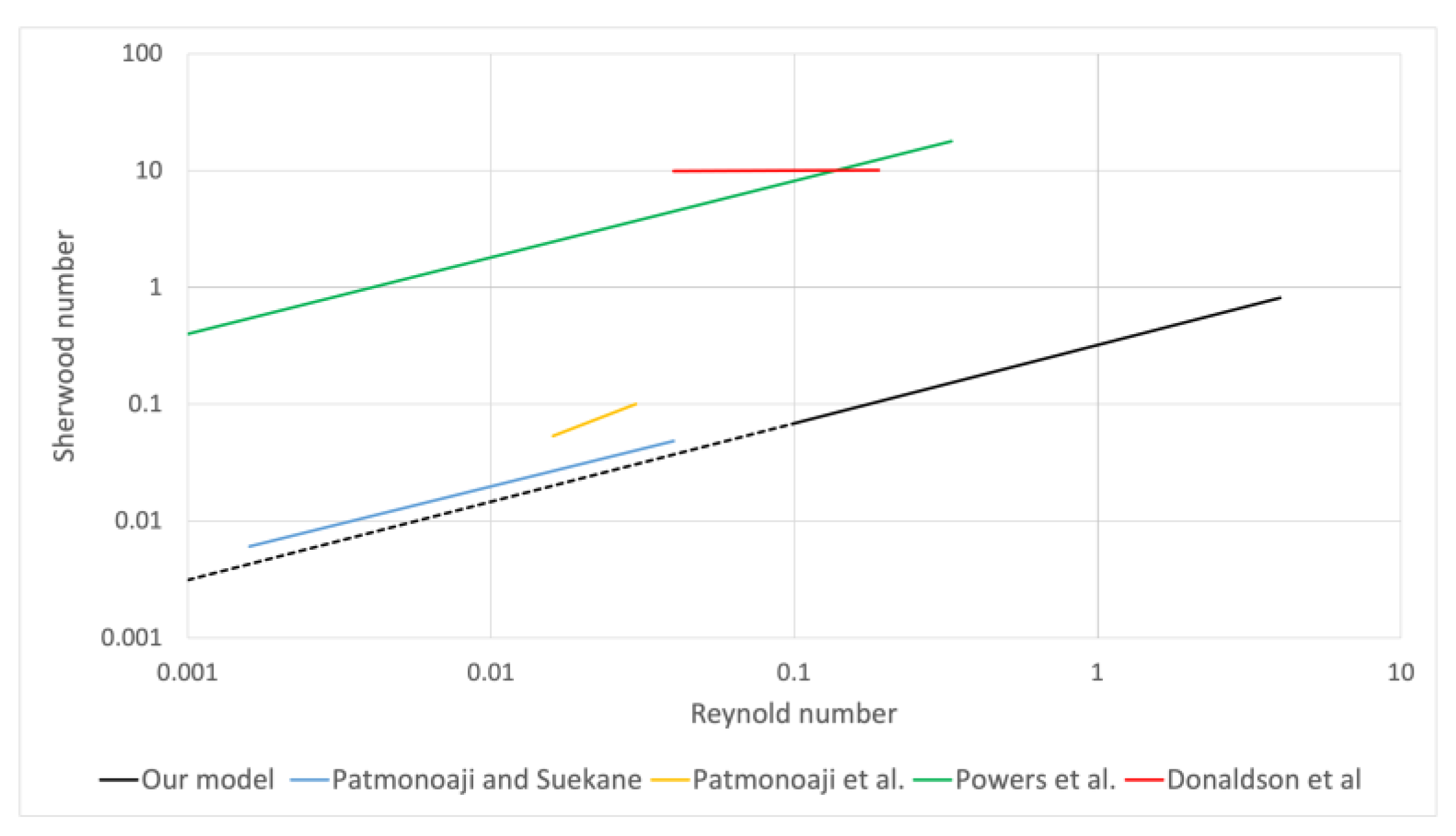
| Source | Model | Detail |
|---|---|---|
| Patmonoaji and Suekane [57] | Schmidt number of trapped CO2 gas at 532 and Reynolds numbers between 0.0016 and 0.04. | |
| Patmonoaji et al. [61] | Schmidt number of trapped N2 gas at 534 and Reynolds numbers between 0.016 and 0.03. | |
| Powers et al. [42] | Schmidt number of trapped solid Naphthalene at 1250 and Reynolds numbers between 0.001 and 0.33. | |
| Donaldson et al. [60] | Schmidt number of trapped solid N2 at 478 and Reynolds numbers between 0.04 and 0.19. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Golestan, M.H.; Berg, C.F. Simulations of CO2 Dissolution in Porous Media Using the Volume-of-Fluid Method. Energies 2024, 17, 629. https://doi.org/10.3390/en17030629
Golestan MH, Berg CF. Simulations of CO2 Dissolution in Porous Media Using the Volume-of-Fluid Method. Energies. 2024; 17(3):629. https://doi.org/10.3390/en17030629
Chicago/Turabian StyleGolestan, Mohammad Hossein, and Carl Fredrik Berg. 2024. "Simulations of CO2 Dissolution in Porous Media Using the Volume-of-Fluid Method" Energies 17, no. 3: 629. https://doi.org/10.3390/en17030629






