Optimization Method of Production System for Coalbed Methane Wells throughout Life Cycle
Abstract
:1. Introduction
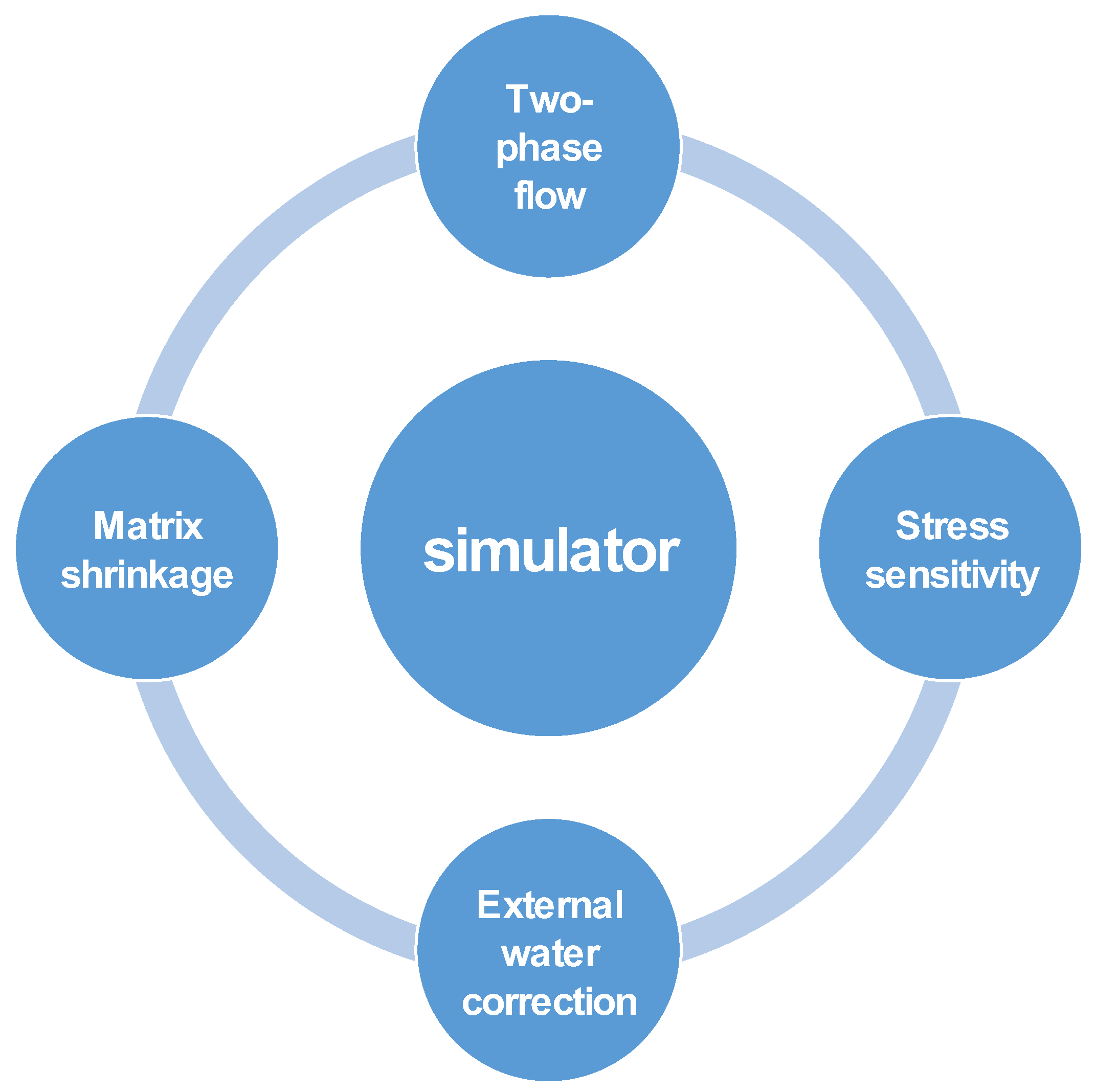
2. Production System Optimization Mechanism of Coalbed Methane Wells
2.1. Influence of Two Phase Flow on Coalbed Methane Reservoir Production
2.2. Influence of Stress Sensitivity and Matrix Shrinkage Effects on Coalbed Methane
2.3. Coal Reservoir External Water Correction
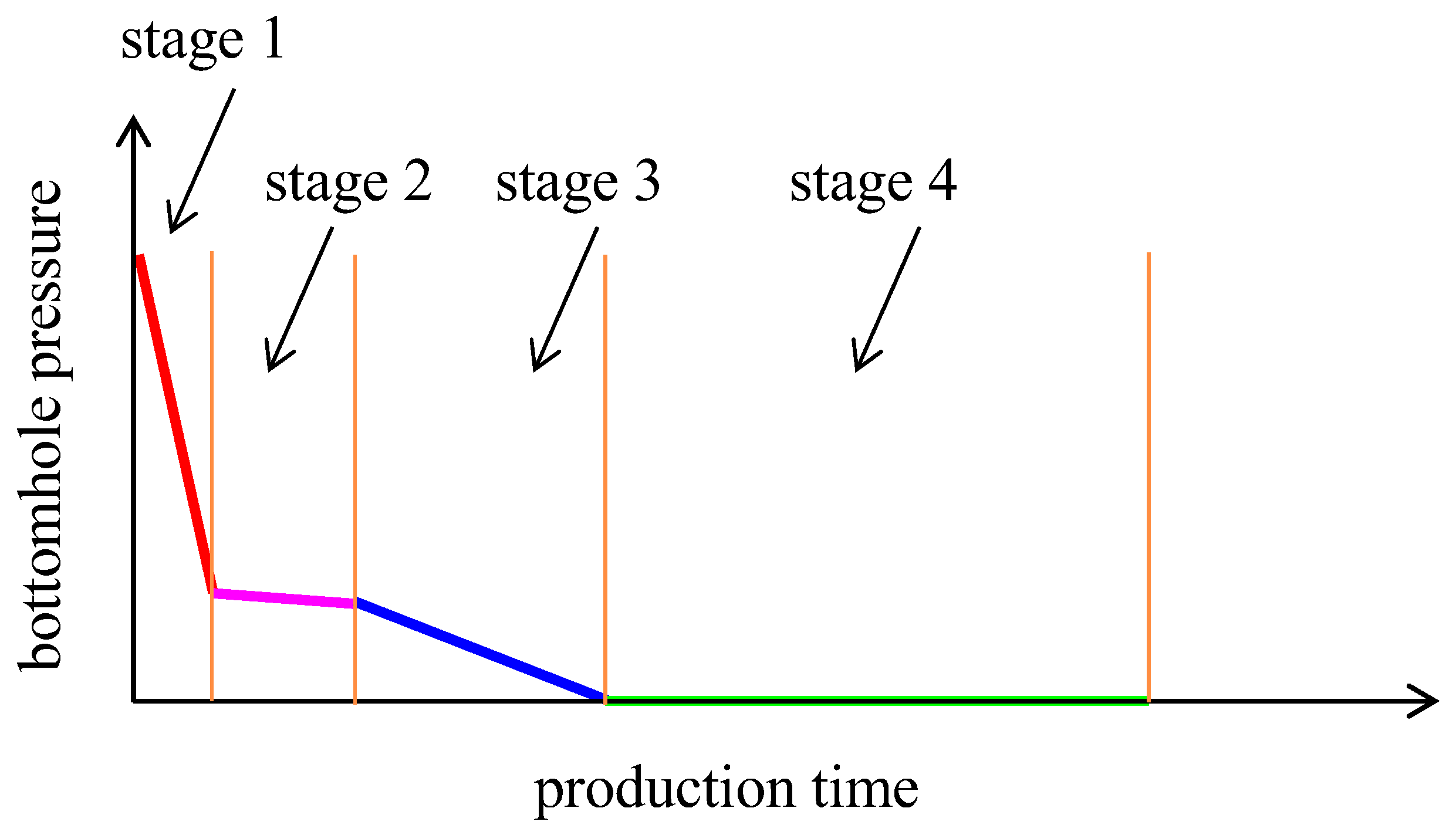
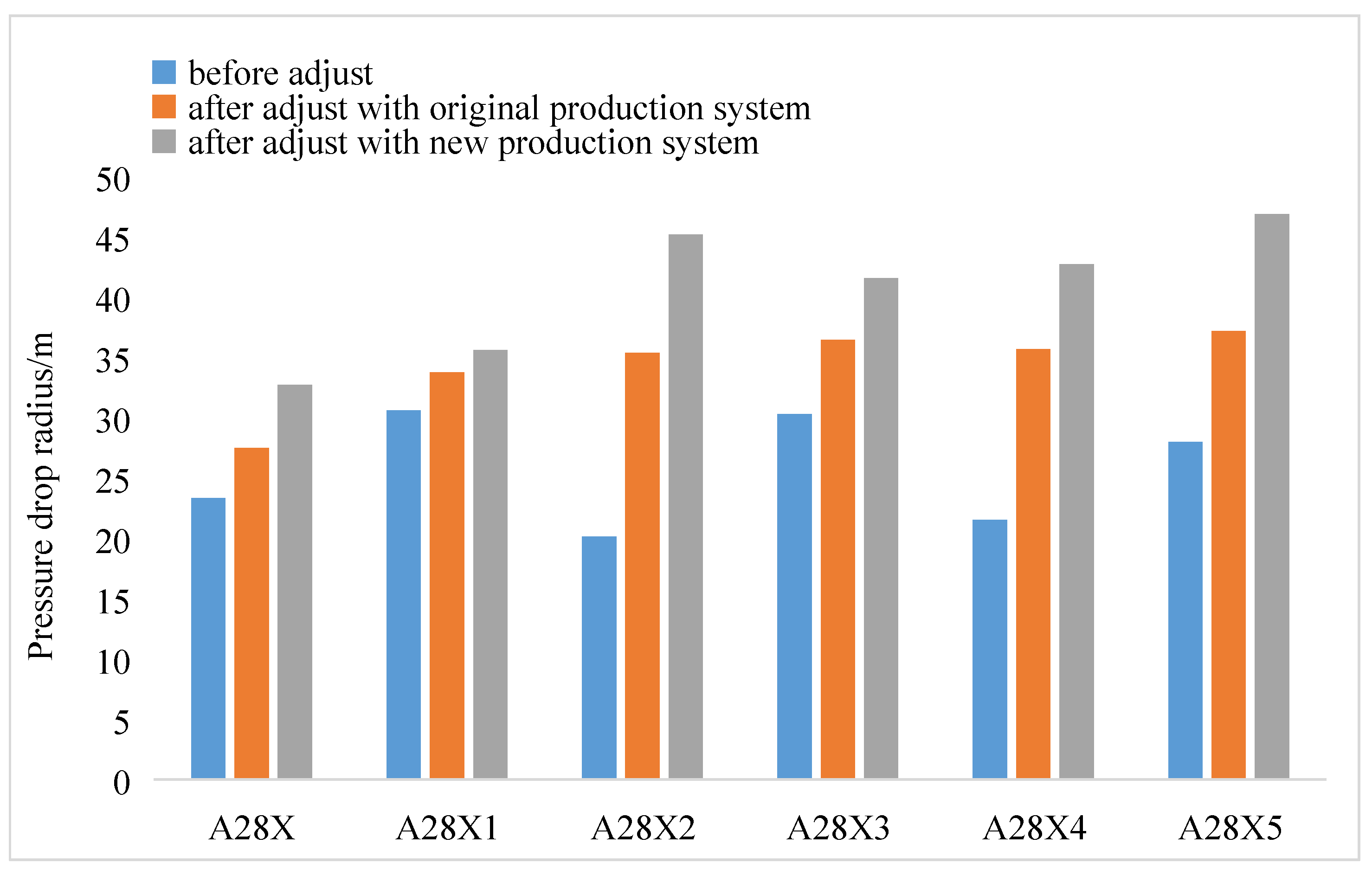
2.4. Production System Optimization for Coalbed Methane Wells
- The flow material balance equation method is used to correct the water production of gas wells. The corrected water production is input into the numerical simulation model as the actual water production of coalbed methane wells.
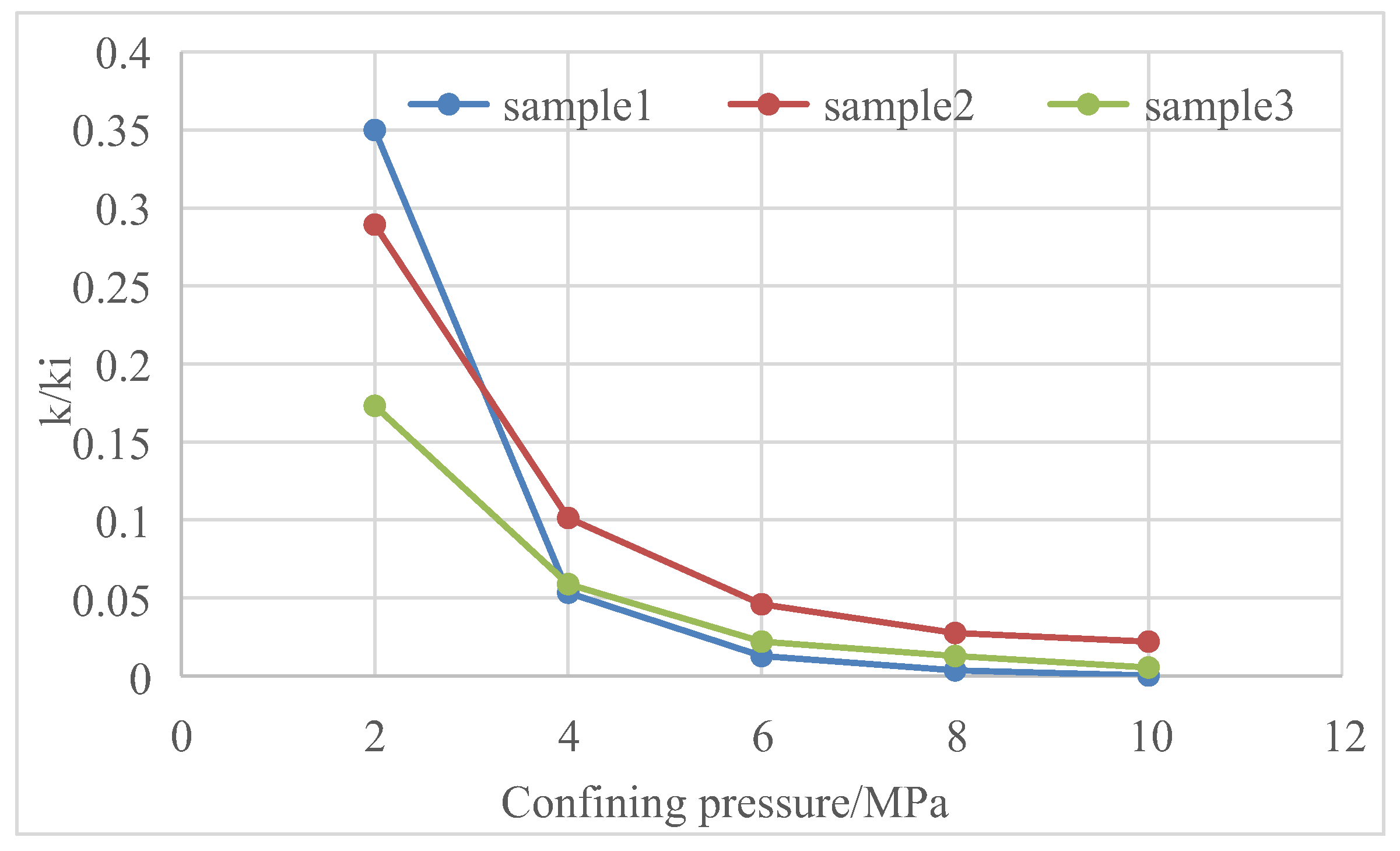
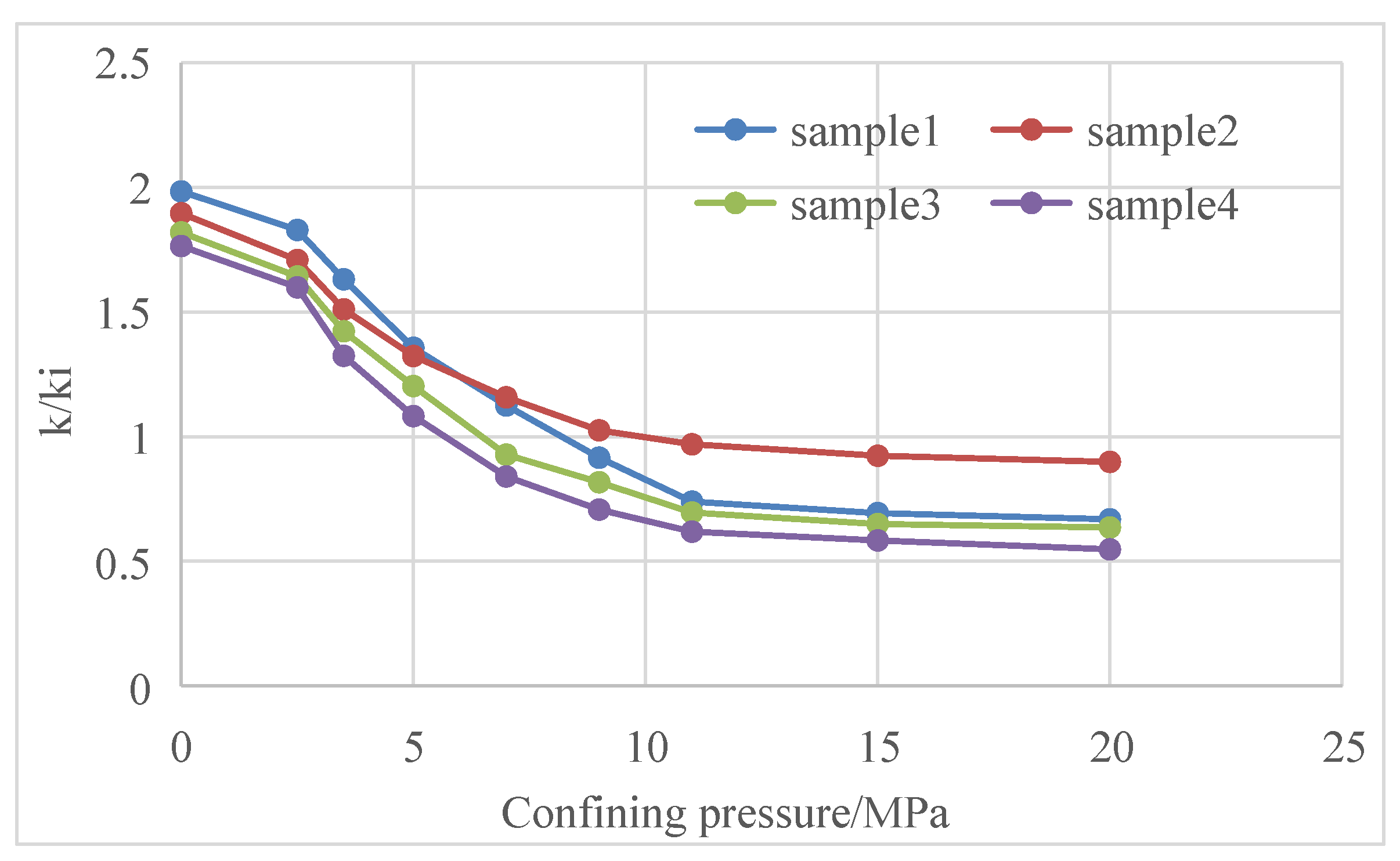
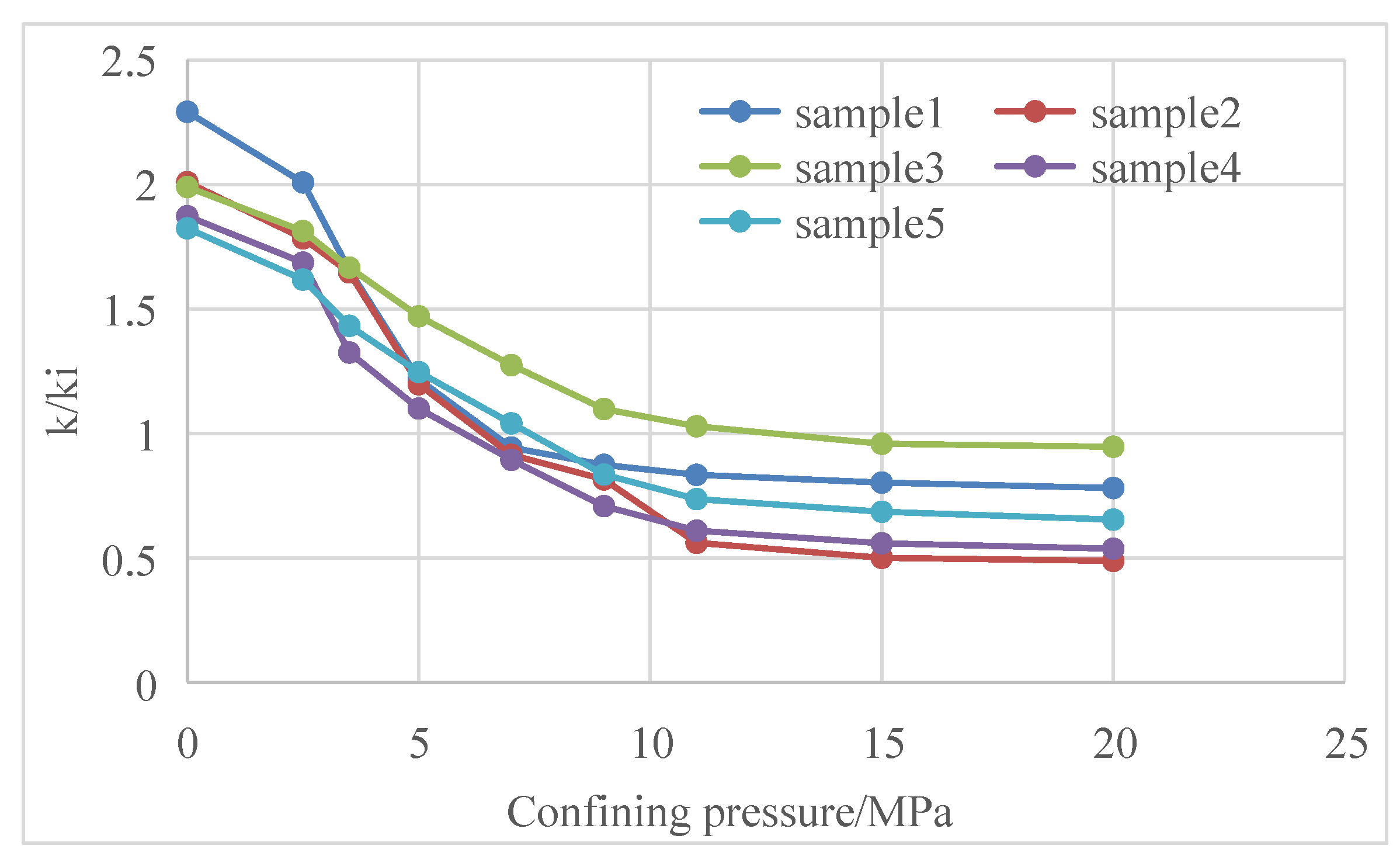
- Both the stress sensitivity effect and matrix contraction effect represent the variation in reservoir permeability with reservoir pressure. In production, they are only reflected in the relation curve between reservoir pressure and reservoir permeability. The relationship between reservoir pressure and reservoir permeability can be measured in a laboratory. If no laboratory data are available, the typical curve recommended by the software or the typical curve from the survey is selected based on the geological conditions of the reservoir. The curve is then prepared and fed into a numerical simulation model.
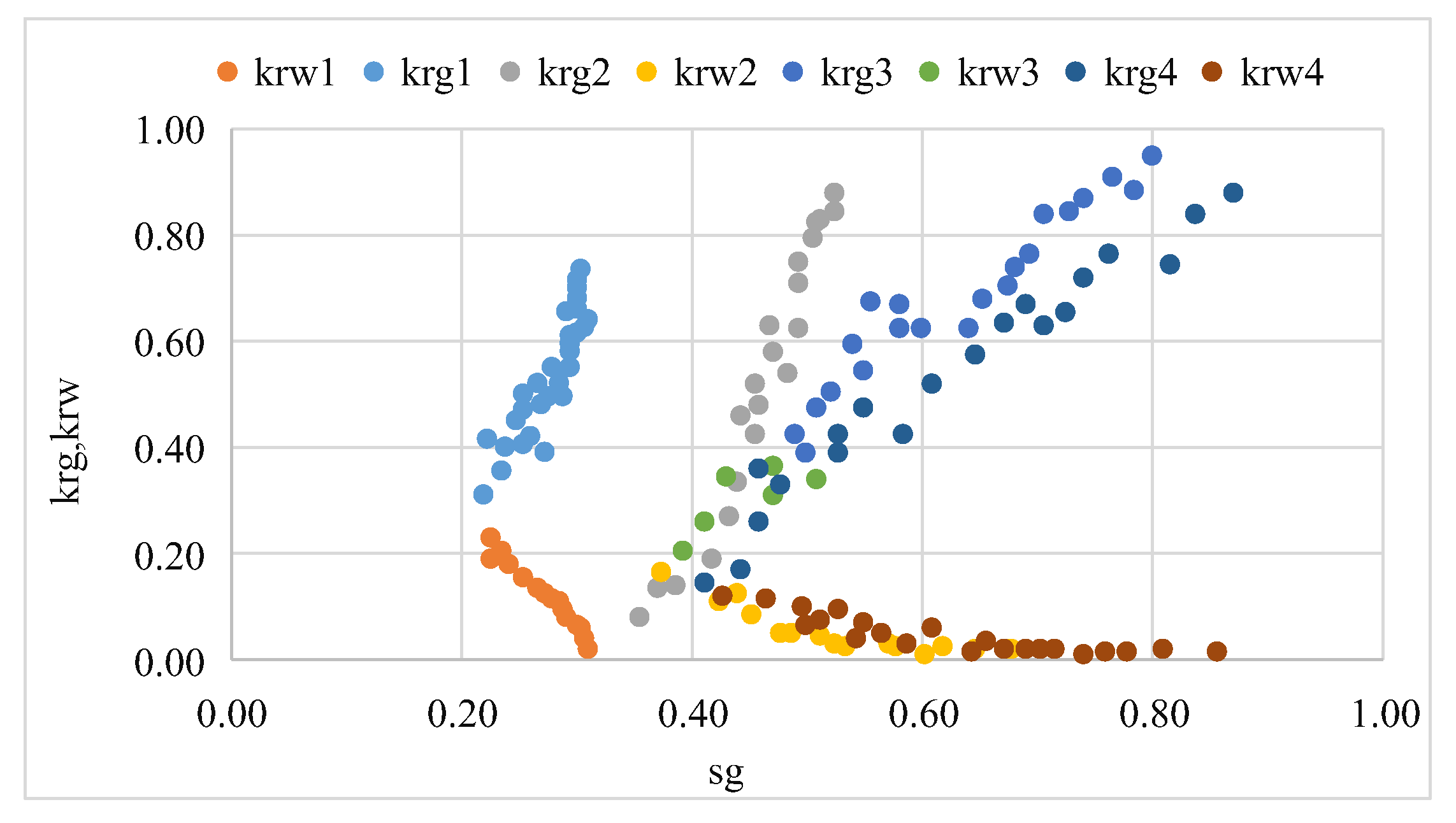
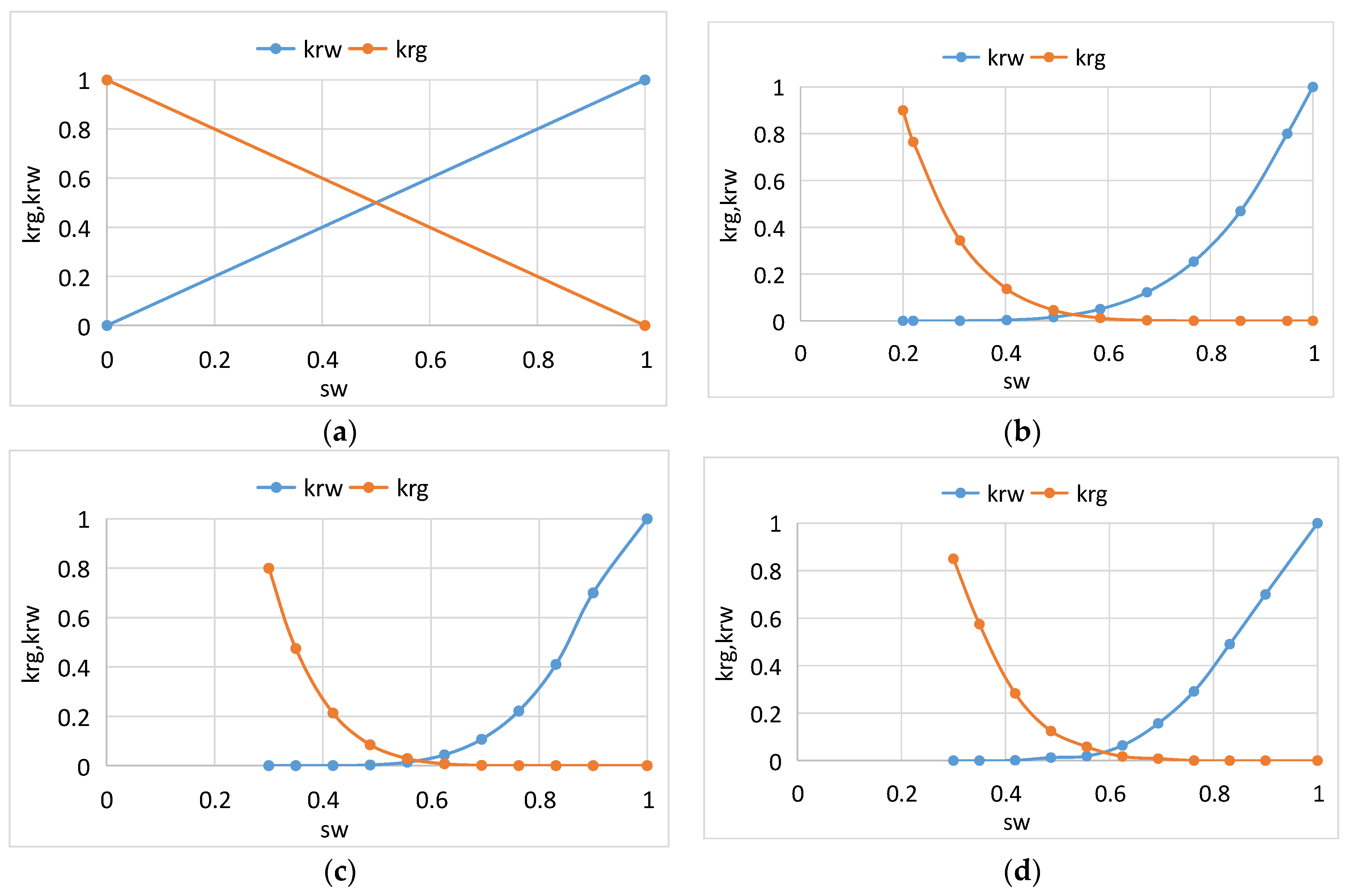
- The phase permeability curve is mainly from laboratory tests. The core permeability test data that are close to the optimized target well are selected and input into the numerical simulation model.
- In the numerical simulation model, the production system is optimized by setting different production systems and setting optimal targets (the optimal targets can be stable production time, peak gas production, cumulative gas production, etc.).
3. Discussion
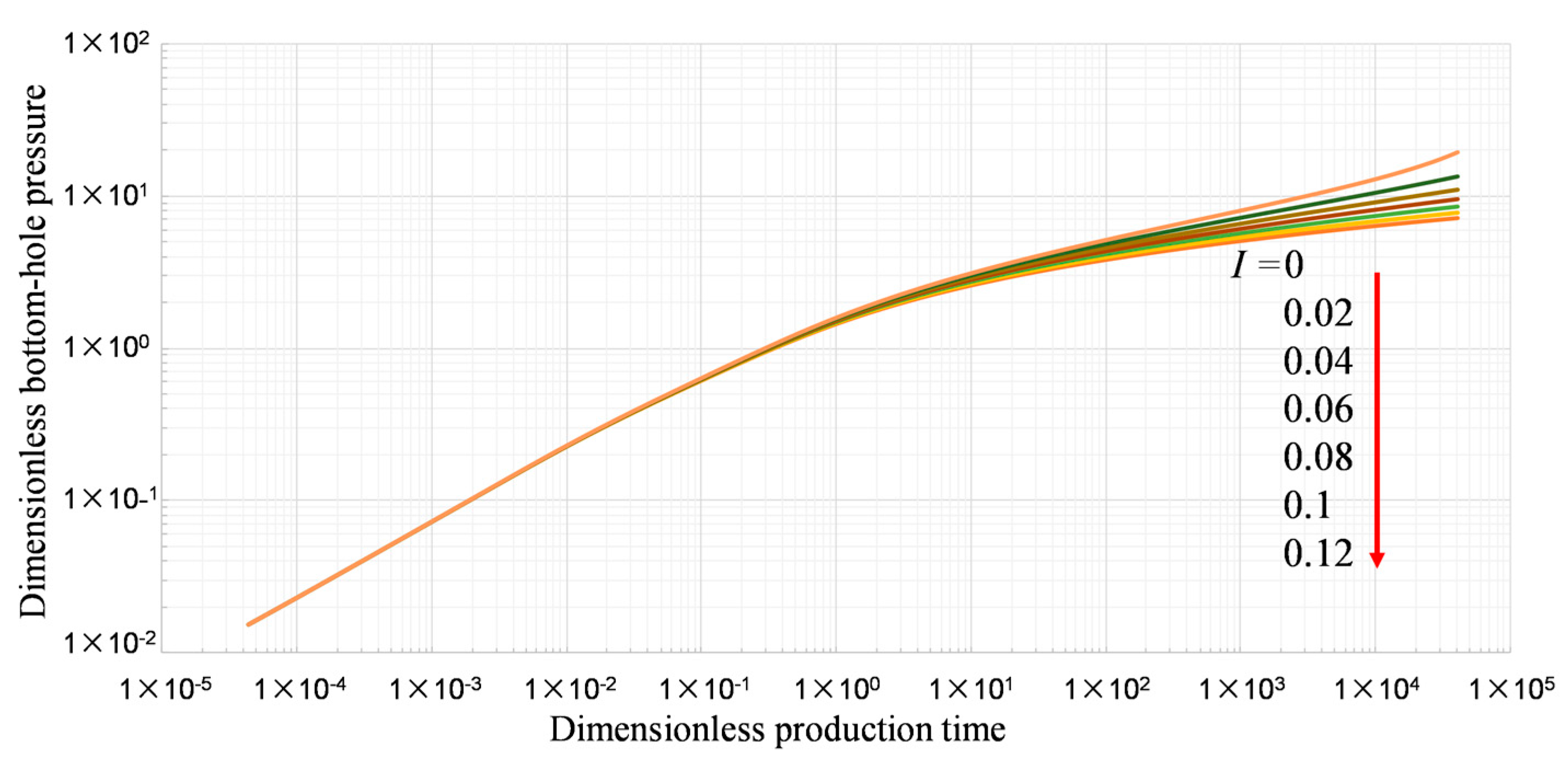
3.1. Effect of Stress Sensitivity and Matrix Shrinkage on Productivity of Coalbed Methane Wells
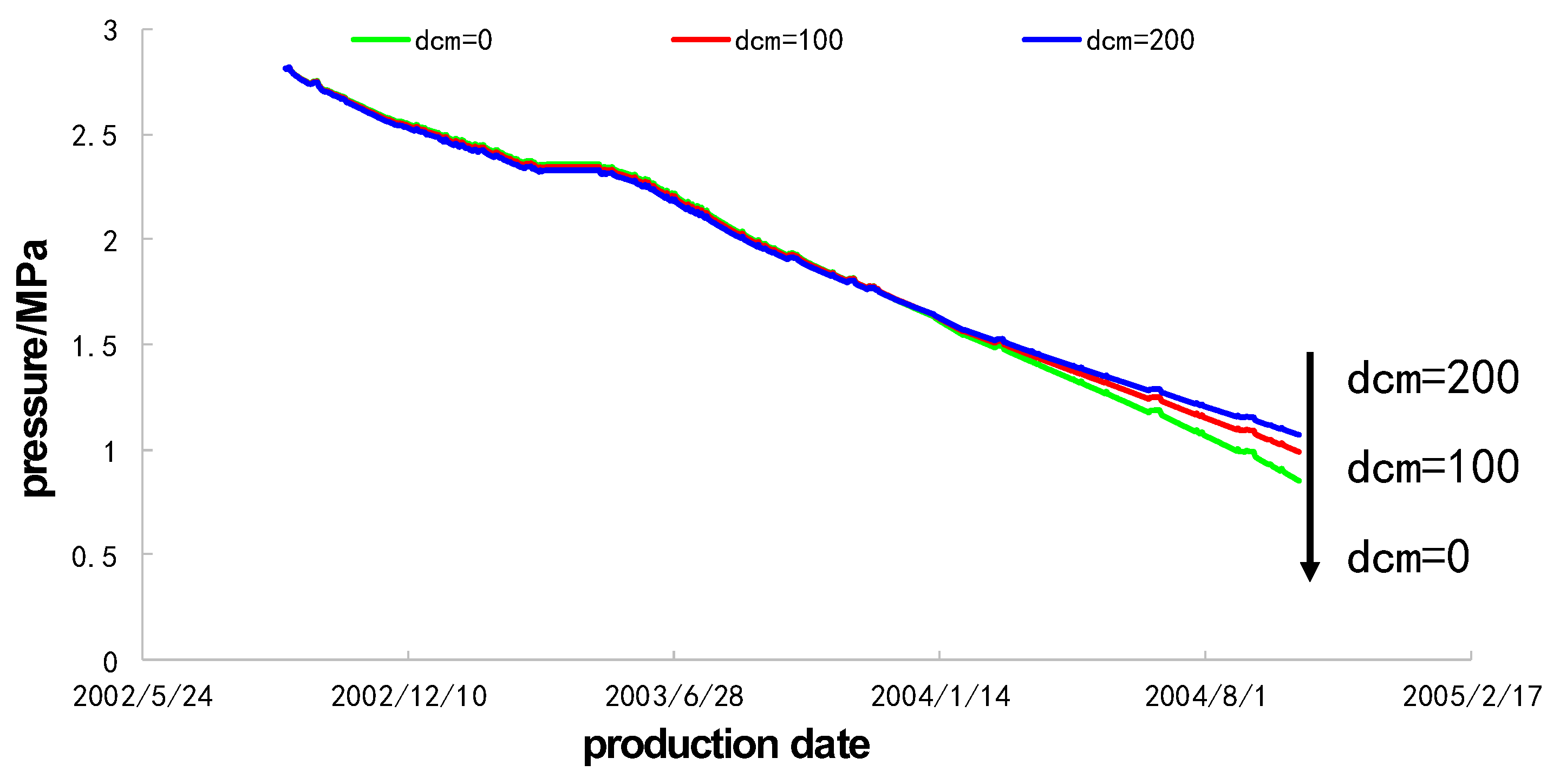
3.2. External Water Correction for Coalbed Methane Wells
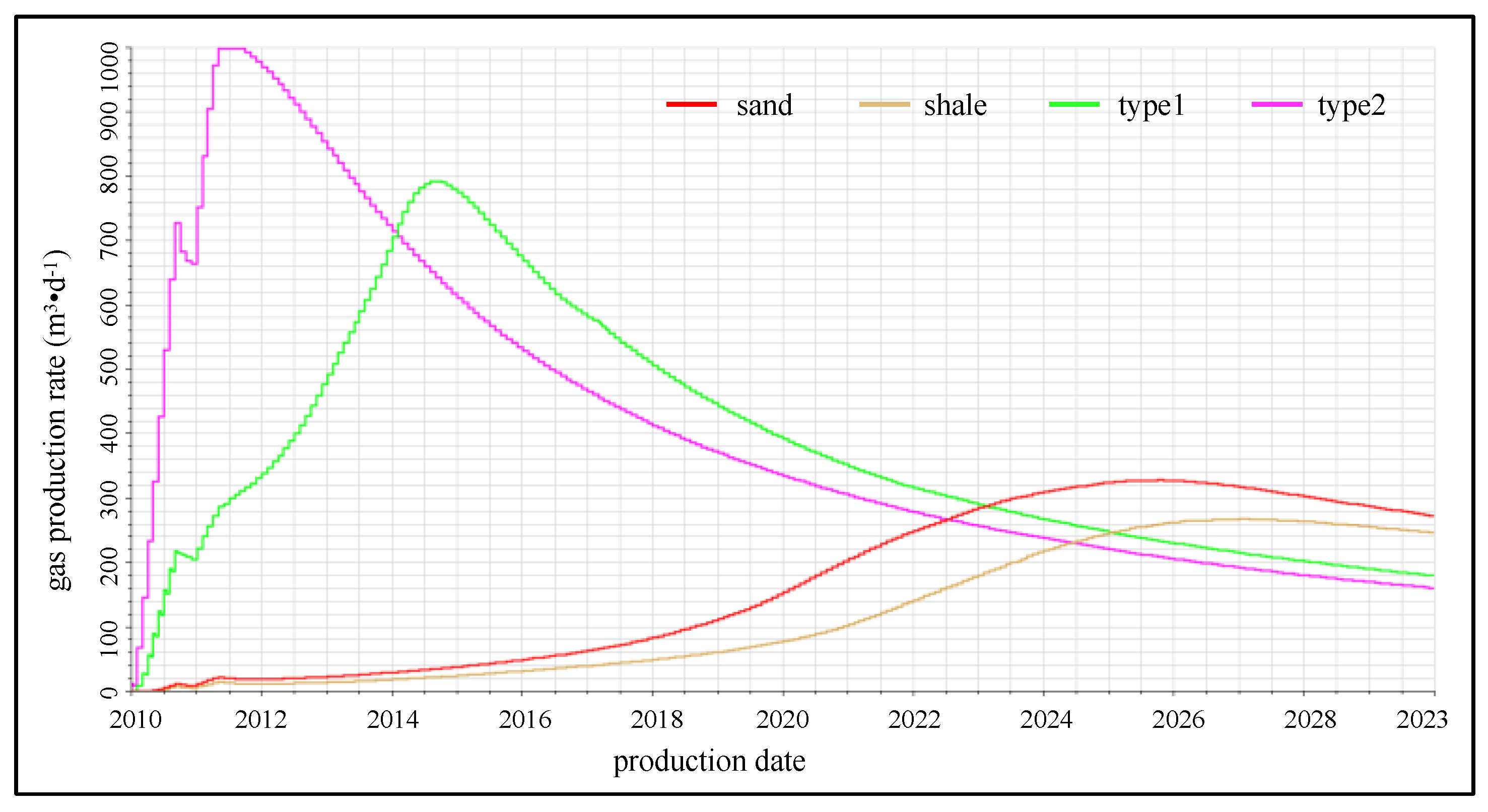
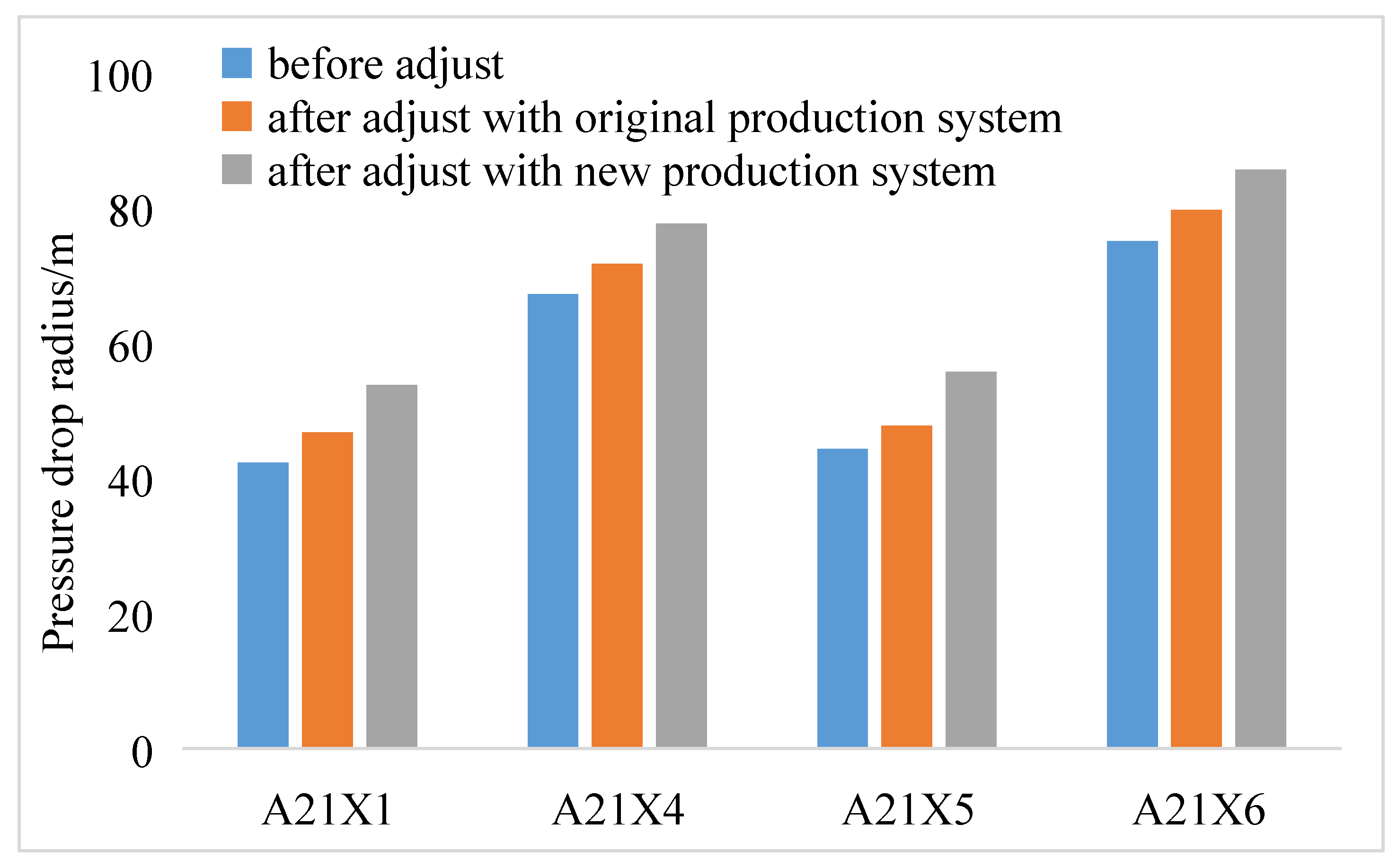
3.3. Production System Optimization for Coalbed Methane Wells
4. Conclusions
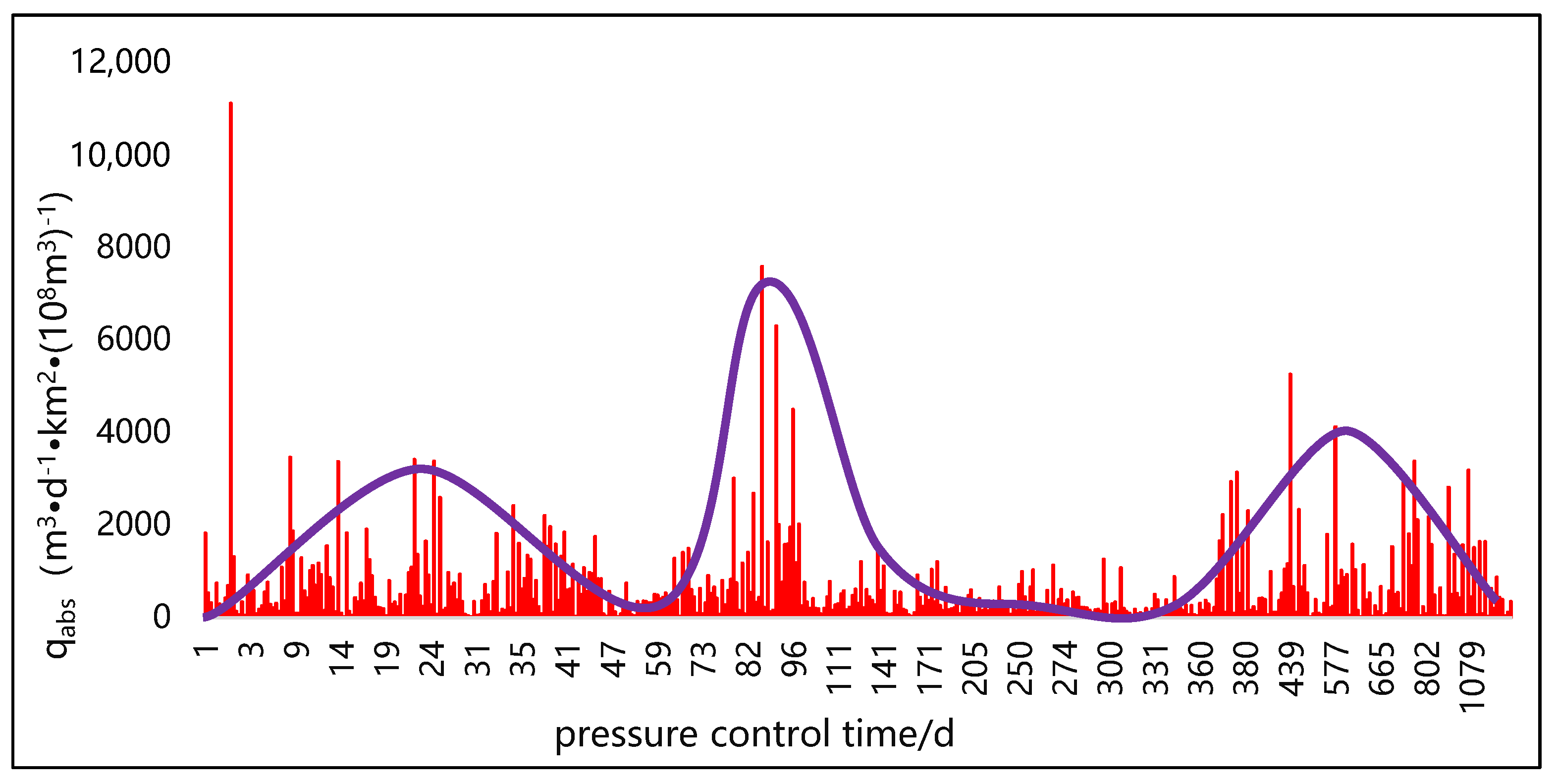
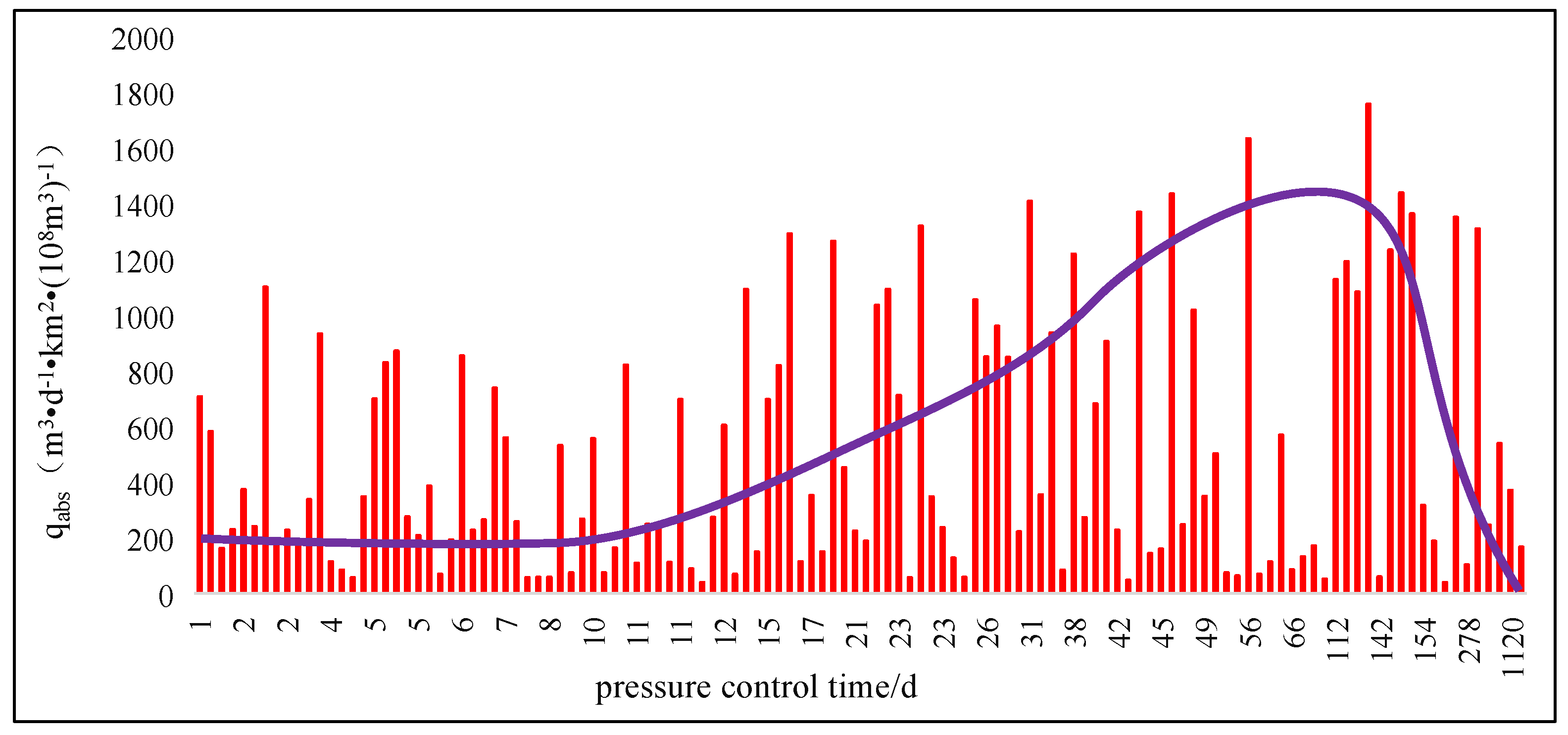
- The conversion from single-phase flow to two phase flow in a coal reservoir has a great impact on the seepage capacity of the coal reservoir. The gas phase permeability and water phase permeability near the isotonic point can drop to 0.2 times the absolute permeability. The linear phase seepage curve of the fracture system is not suitable for a coal reservoir; the core should be actually used for testing.
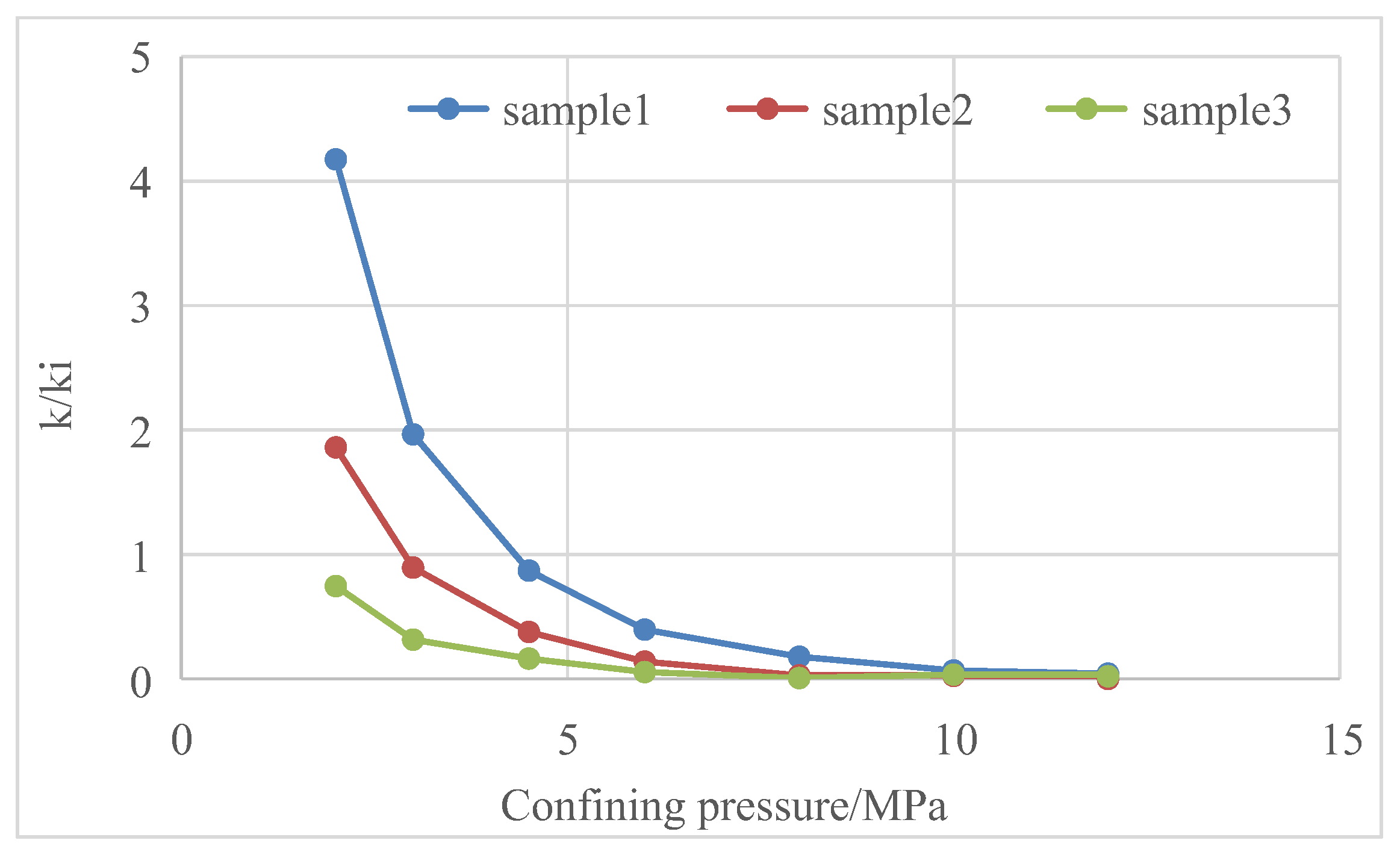
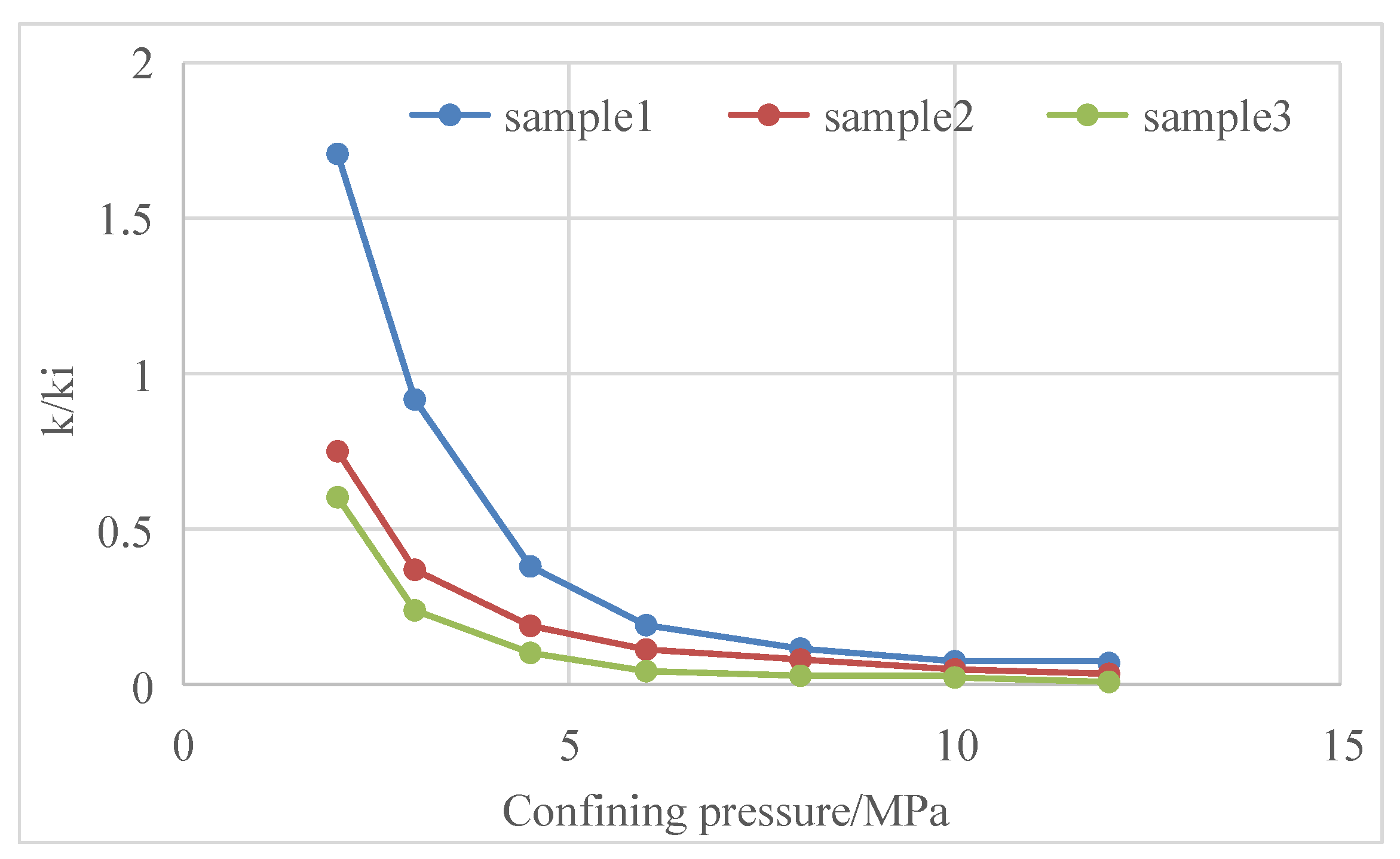
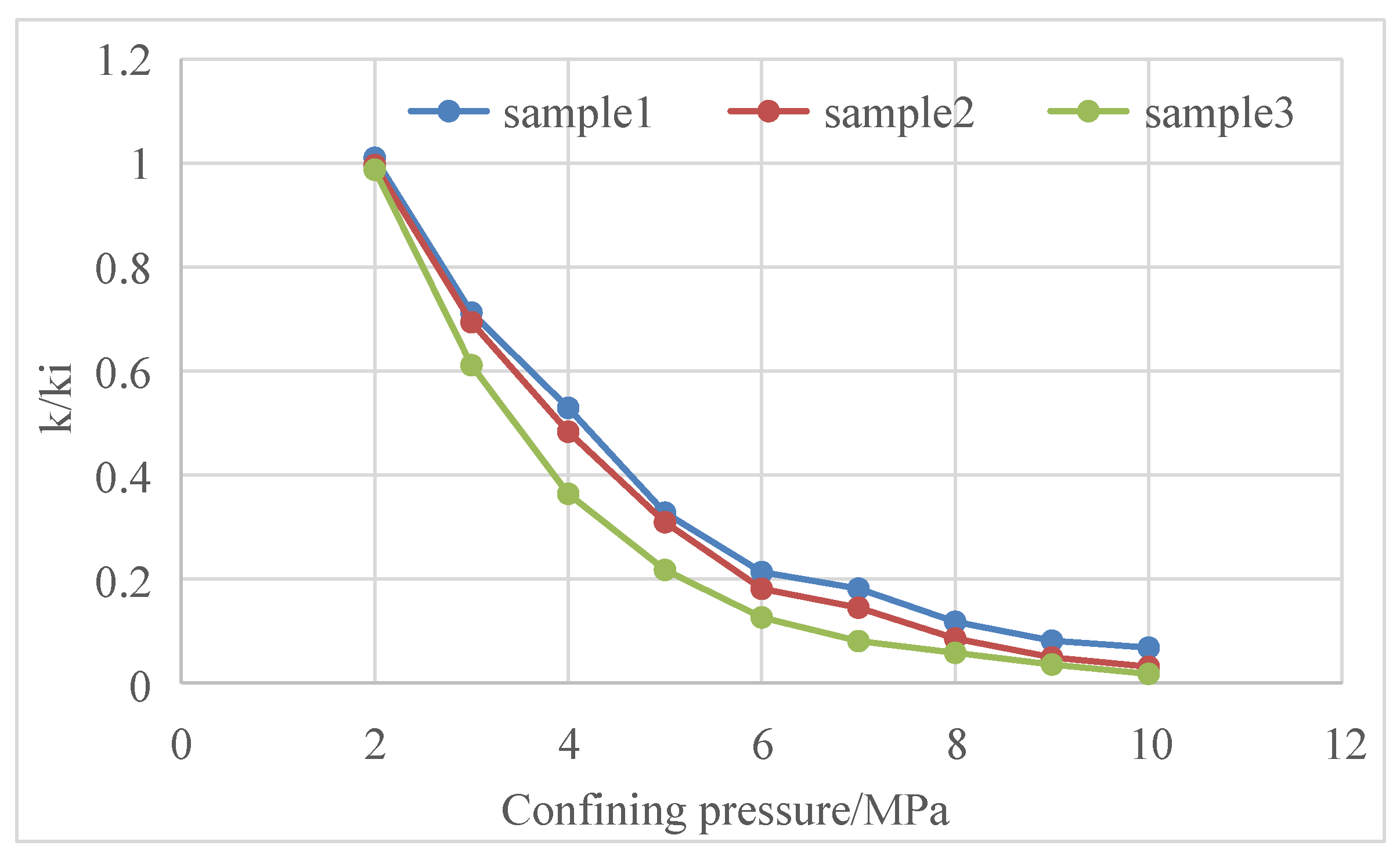
- Stress sensitivity and matrix shrinkage effects affect the permeability of coal reservoirs. Stress sensitivity mainly occurs in the early stage, and matrix shrinkage mainly acts in the late stage; the influence of the matrix shrinkage effect is greater than that of stress sensitivity. The actual test data of some coalbed methane blocks show that the permeability of the reservoir can change up to 60 times during the initial production and abandonment. The influence of stress sensitivity and matrix shrinkage effects on the productivity of coalbed methane wells should be fully considered in the formulation of production systems.
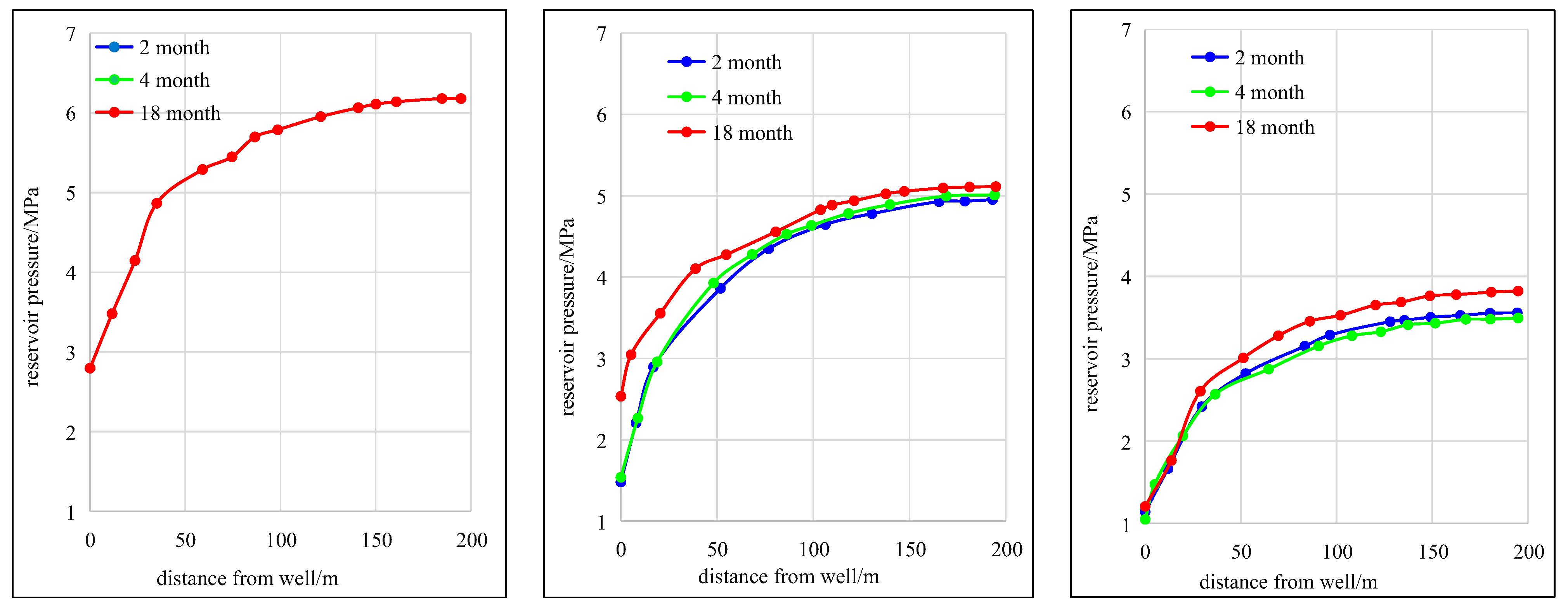
- In some coalbed methane blocks, the inflow of external and domestic water is relatively large. The amount of external water in some blocks reaches more than 70% of the produced water. It is necessary to adjust the inflow of water first in the optimization of the production system, which will make the optimized production system more suitable for the production of coalbed methane wells.
- Considering the matrix shrinkage effect, the stress sensitivity effect and external water correction in the optimization of the production system of a coalbed methane well can greatly increase the discharge area (actual field examples show that the optimized gas well has a 65% increase in drainage area) and increase the desorption area of coal reservoirs, thus increasing the production of coalbed methane wells.
- This research work can well guide the on-site production of coalbed methane and reverse the situation of the optimization of production systems of coalbed methane wells depending only on experience. At the same time, the current research on damage mechanisms is only in the experimental stage, and the damage mechanisms can be further studied in the future to form relevant formulas that can be directly used.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviation
| Symbol Explanation | |
| Symbol in Article | |
| relative permeability of gas phase in two phase flow, μm2 | |
| relative permeability of water phase in two phase flow, μm2 | |
| gas saturation in reservoir, dimensionless | |
| water saturation in reservoir, dimensionless | |
| short for coalbed methane block name | |
| gas production in coalbed methane wells with normalized reserve abundance | |
| reservoir permeability under original conditions, μm2 | |
| reservoir porosity, dimensionless | |
| reservoir porosity in the initial condition, dimensionless | |
| Langmuir volume, m3/t | |
| pressure in the original condition, MPa | |
| Langmuir pressure, MPa | |
| pressure, MPa | |
| experiment strain, dimensionless | |
| mechanical compliance coefficient, MPa−1 | |
| constrained axial modulus, MPa | |
| bulk modulus, MPa | |
| a fraction from 0 to 1, dimensionless | |
| parameters of Langmuir curve matching volumetric strain change, dimensionless | |
| reservoir permeability, D | |
| reservoir permeability in the initial condition, D | |
| compression coefficient of the matrix, MPa−1 | |
| effective stress–strain, dimensionless | |
| effective stress–strain in the initial condition, dimensionless | |
| Poisson’s ratio, dimensionless | |
| Young’s modulus, MPa−1 | |
| Langmuir-type matrix shrinkage constants, dimensionless | |
| permeability modulus, MPa−1 | |
| radius of coalbed methane reservoir, m | |
| Hussainy pseudo-pressure, MPa2·cp−1 | |
| gas viscosity, mpa·s | |
| coal compressibility, MPa−1 | |
| adsorption compression coefficient, MPa−1 | |
| time variable, h | |
| gas viscosity in the initial condition, mpa·s | |
| total adsorption compression coefficient in the original state, MPa−1 | |
| total compression coefficient, MPa−1 | |
| pressure in the standard state, MPa | |
| temperature, K | |
| gas deviation factor, dimensionless | |
| standard temperature, K | |
| dimensionless bottom-hole pressure in Laplace transform, dimensionless | |
| dimensionless length of the x coordinates, dimensionless | |
| s | Laplace variable, dimensionless |
| dimensionless flow rate in Laplace transform, dimensionless | |
| integral variable, dimensionless | |
| zero-order Bessel function | |
| zero-order Bessel function | |
| A | a constant, representing different boundaries |
| B | a constant, representing different boundaries |
| one-order Bessel function | |
| one-order Bessel function | |
| dimensionless reservoir radius, dimensionless | |
| matrix shrinkage coefficient, t/m3 | |
| critical desorption pressure, MPa | |
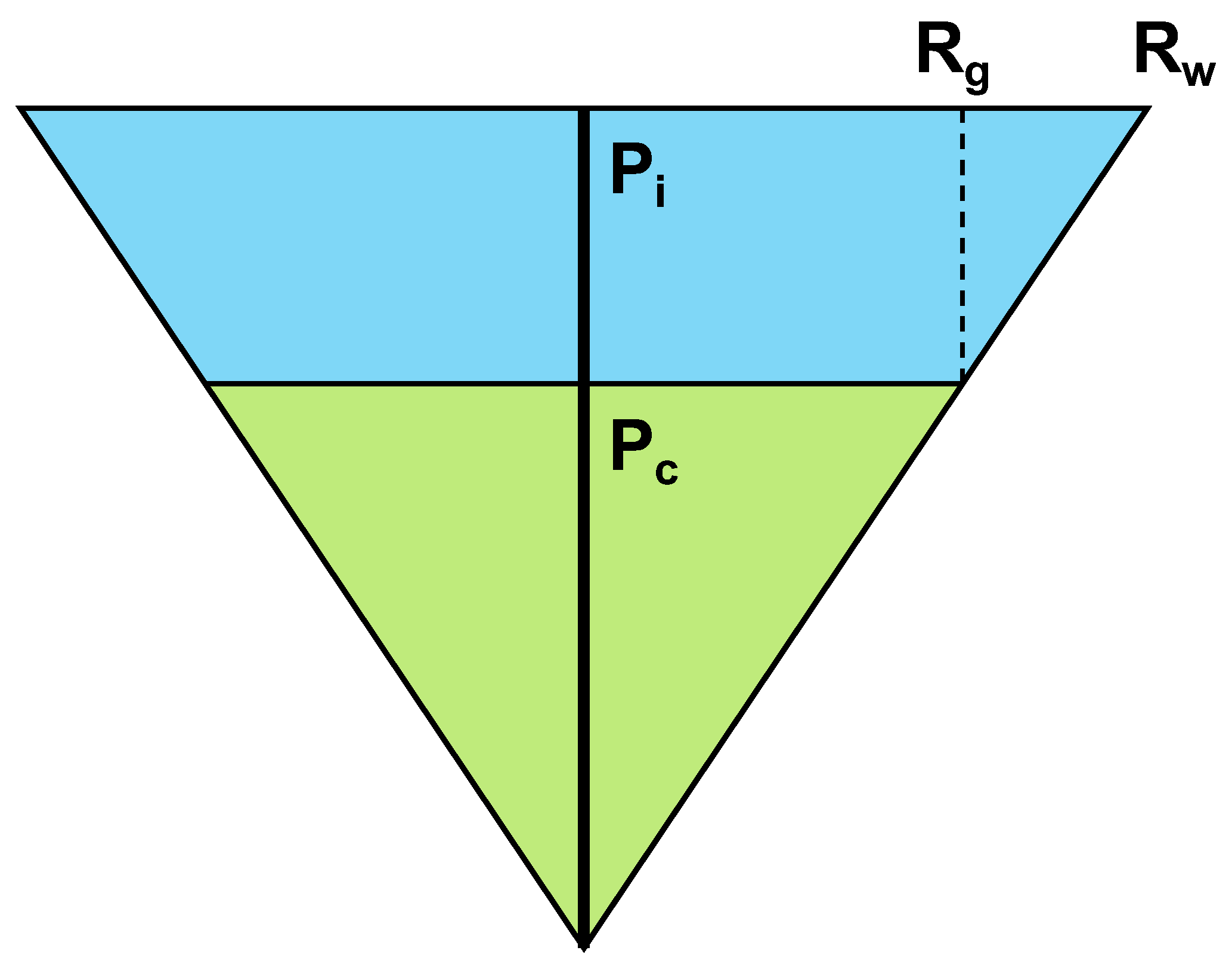
| discharge radius of water production, m | |
| discharge radius of gas production, m | |
| n | Pore permeability relation characteristic index, dimensionless |
| Intermediate Variable | |
References
- Seidle, J. Principle of Coalbed Gas Reservoir Engineering; Shi, X., Translator; Petroleum Industry Press: Beijing, China, 2016. [Google Scholar]
- Zheng, C.; Ma, D.; Chen, Y.; Ji, Y.; Ma, Z.; Wang, L.; Wang, X. Research progress micro effect of water on coalbed methane adsorption/desorption. Coal Sci. Technol. 2023, 51, 256–268. [Google Scholar]
- Reng, J. Effect of dynamic permeability variation on production of coalbed methane wells. Nat. Gas Ind. 2018, 38, 62–64. [Google Scholar]
- Yang, M.; Wang, G.; Xu, S.; Gao, C. Steady Flow Productivity Equation for Stress Sensitivity Coal-bed Methane Gas Well. Nat. Gas Geosci. 2011, 22, 347–351. [Google Scholar]
- Liu, W.; Liu, Y. Dynamic analysis on gas-water two-phase unsteady seepage flow in low-permeable coalbed gas reservoirs. Chin. J. Theor. Appl. Mech. 2017, 49, 828–835. [Google Scholar]
- Zhu, W.; Dong, H.; Song, H.; Yang, J.; Yue, M. A Mathematical Model for Gas-water Two-phase Nonlinear Flow in Low Permeability Coal Reservoirs and Calculation Analysis. Sci. Technol. Rev. 2013, 3, 36–39. [Google Scholar]
- Zhang, P.; Wang, X.; Feng, C.; Zheng, L.; Zhang, Y.; Sun, M. Evaluation method and application of gas-water two-phase unsteady inflow performance of coal reservoir based on multiple factors. Nat. Gas Geosci. 2023, 34, 1641–1651. [Google Scholar]
- Feng, Q.; Shu, C.; Zhang, X.; Zhang, J.; Wang, B. Real-time optimization of drainage schedule for coalbed methane wells at gas-water two-phase flow stage. J. China Coal Soc. 2015, 40, 142–148. [Google Scholar]
- Niu, C.; Liu, Y.; Cai, Q.; Li, H. Transient well test model for the well with gas and water distributed in coalbed. Mech. Eng. 2013, 35, 35–41. [Google Scholar]
- Han, W.; Li, Y.; Chen, X.; Zhuo, Q.; Wang, Y. Mechanism of coal fine-bubble coupling in the unsaturated flow stage of coalbed methane drainage. Coal Geol. Explor. 2023, 51, 46–53. [Google Scholar]
- Wei, Y.; Li, C.; Cao, D.; Zhang, A.; Yao, Z.; Xiong, X. The output mechanism and control measures of the pulverized coal in coalbed methane development. Coal Geol. Explor. 2018, 46, 68–73. [Google Scholar]
- Han, G.; Ling, K.; Wu, H.; Gao, F.; Zhu, F.; Zhang, M. An experimental study of coal-fines migration in Coalbed-methane production wells. J. Nat. Gas Sci. Eng. 2015, 26, 1542–1548. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, S.; Sang, S.; Pan, Z.; Zhao, W.; Yang, Y.; Hu, Q.; Yang, Y. Characteristics and generation mechanisms of coal fines in coalbed methane wells in the southern Qinshui Basin, China. J. Nat. Gas Sci. Eng. 2016, 34, 849–863. [Google Scholar] [CrossRef]
- Bai, T.; Chen, Z.; Saiied, M.; Pan, Z.; Liu, J.; Li, L. Characterization of coal fines generation: A micro-scale investigation. J. Nat. Gas Sci. Eng. 2015, 27, 862–875. [Google Scholar] [CrossRef]
- Guo, Z.; Hussain, F.; Cinar, Y. Physical and analytical modelling of permeability damage in bituminous coal caused by fines migration during water production. J. Nat. Gas Sci. Eng. 2016, 35, 331–346. [Google Scholar] [CrossRef]
- Yang, Y.; Meng, Z.; Zhang, J. Research on stress sensitivity of coal reservoir and a new method for its evaluation. Coal Geol. Explor. 2016, 44, 38–46. [Google Scholar]
- Seidle, J.; Huitt, L. Experimental Measurement of Coal Matrix Shrinkage Due to Gas Desorption and Implications for Cleat Permeability Increases. In Proceedings of the International Meeting on Petroleum Engineering, Beijing, China, 14–17 November 1995; Society of Petroleum Engineers: Beijing, China, 1995; pp. 575–582. [Google Scholar]
- Palmer, I.; Mansoori, J. How Permeability Depends on Stress and Pore Pressure in Coalbeds: A New Model. SPE Reserv. Eval. Eng. 1998, 1, 539–544. [Google Scholar] [CrossRef]
- Shi, J.Q.; Durucan, S. Drawdown Induced Changes in Permeability of Coalbeds: A New Interpretation of the Reservoir Response to Primary Recovery. Transp. Porous Media 2004, 56, 1–16. [Google Scholar] [CrossRef]
- Pedrosa, O.A. Pressure Transient Response in Stress-Sensitive Formations. In Proceedings of the SPE California Regional Meeting Society of Petroleum Engineers, Oakland, CA, USA, 2–4 April 1986; Society of Petroleum Engineers: Oakland, CA, USA, 1986; pp. 203–214. [Google Scholar]
- Jing, W.; Zhou, J.; Yang, L.; Jin, R.; Jing, L. Deformation and Failure Mechanism of Surrounding Rock in Deep Soft Rock Tunnels Considering Rock Rheology and Different Strength Criteria. Rock Mech. Rock Eng. 2023, 2024, 545–580. [Google Scholar] [CrossRef]
- Jia, Q.; Liu, D.; Cai, Y.; Fang, X.; Li, L. Petrophysics characteristics of coalbed methane reservoir: A comprehensive review. Front. Earth Sci. 2021, 15, 202–223. [Google Scholar] [CrossRef]
- Altowilib, A.; AlSaihati, A.; Alhamood, H.; Alafnan, S.; Alarifi, S. Reserves Estimation for Coalbed Methane Reservoirs: A Review. Sustainability 2020, 12, 10621. [Google Scholar] [CrossRef]
- Zhu, S.; Peng, X.; Li, C.; Deng, P.; Ma, Y.; Peng, C.; Sun, H.; Jia, H. An approximation of the relative permeability and discussion on curve shapes in coalbed methane reservoirs. Chin. J. Rock Mech. Eng. 2019, 38, 1659–1666. [Google Scholar]
- Zhang, S. Change and Stress Sensitivity of Physical Properties and Gas Content of Coal Reservoir with Depth in Qinshui Basin. China Coalbed Methane 2016, 13, 7–9. [Google Scholar]
- Wan, J.; Li, K.; Ran, C.; Hou, D. Coalbed Methane Deliverability Correlation Research Considering Stress Sensitivity. Coal Technol. 2016, 35, 311–313. [Google Scholar]
- Zhang, H.; Li, B.; Li, Z.; Reng, G. Study on dynamic curves of coalbed methane well flow rate considering stress sensitivity. Petrochem. Ind. Appl. 2012, 31, 33–34+53. [Google Scholar]
- Liu, H.; Sang, S.; Feng, Q.; Hu, B.; Hu, Y.; Xu, H.; Cheng, Q. Study on stress sensitivity of coal reservoir during drainage of coal-bed methane well in Southern Qinshui Basin. J. China Coal Soc. 2014, 39, 1873–1878. [Google Scholar]
- Kang, Y.; Chen, D.; Li, X.; Zhou, L.; Chen, F. Influence of dvilling fluid on stress sensitivity of coalbed reservoir. Coal Geol. Explor. 2014, 42, 39–43. [Google Scholar]
- Chen, Z.; Wang, Y.; Guo, K.; Sun, Q.; Zhang, Y. Stress Sensitivity of High-rank Coalbed Methane Reservoir. Acta Geol. Sin. 2008, 82, 1390–1395. [Google Scholar]





| Boundary | ||
|---|---|---|
| Infinite boundary | 1 | 0 |
| Closed boundary | 1 | |
| Constant-pressure boundary | 1 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Pi/pa | 2.83 × 106 | sk | 0 |
| k1/ | 0.001 | k2/ | 0.002 |
| rm/m | 110 | re/m | 500 |
| h/m | 19.812 | Lf/m | 110 |
| n | 3 | dcm | 0, 100, 200 |
| φ | 0.2 | sg/% | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Sun, L.; Zhao, Z.; Zhang, J.; Wang, C.; Lei, G.; Li, Y.; Meng, Y. Optimization Method of Production System for Coalbed Methane Wells throughout Life Cycle. Energies 2024, 17, 789. https://doi.org/10.3390/en17040789
Li C, Sun L, Zhao Z, Zhang J, Wang C, Lei G, Li Y, Meng Y. Optimization Method of Production System for Coalbed Methane Wells throughout Life Cycle. Energies. 2024; 17(4):789. https://doi.org/10.3390/en17040789
Chicago/Turabian StyleLi, Chen, Lichun Sun, Zhigang Zhao, Jian Zhang, Cunwu Wang, Gang Lei, Yong Li, and Yanjun Meng. 2024. "Optimization Method of Production System for Coalbed Methane Wells throughout Life Cycle" Energies 17, no. 4: 789. https://doi.org/10.3390/en17040789
APA StyleLi, C., Sun, L., Zhao, Z., Zhang, J., Wang, C., Lei, G., Li, Y., & Meng, Y. (2024). Optimization Method of Production System for Coalbed Methane Wells throughout Life Cycle. Energies, 17(4), 789. https://doi.org/10.3390/en17040789








