Optimization of Financial Indicators in Shale-Gas Wells Combining Numerical Decline Curve Analysis and Economic Data Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Physical, Mathematical, and Numerical Model of Gas Production in a Standard Shale-Gas Well
2.2. Methods for the Statistical Characterization of Financial Indicators
- •
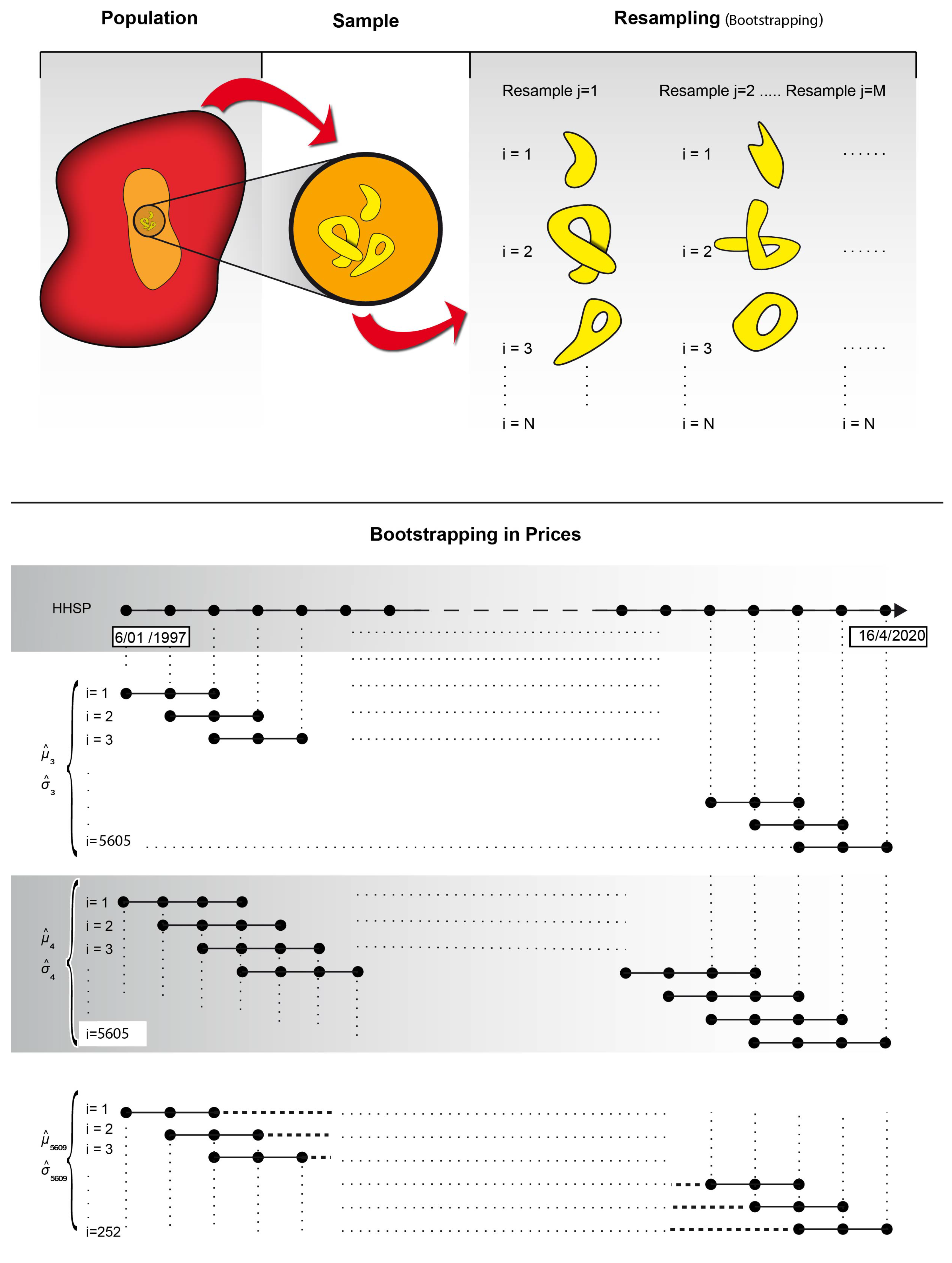
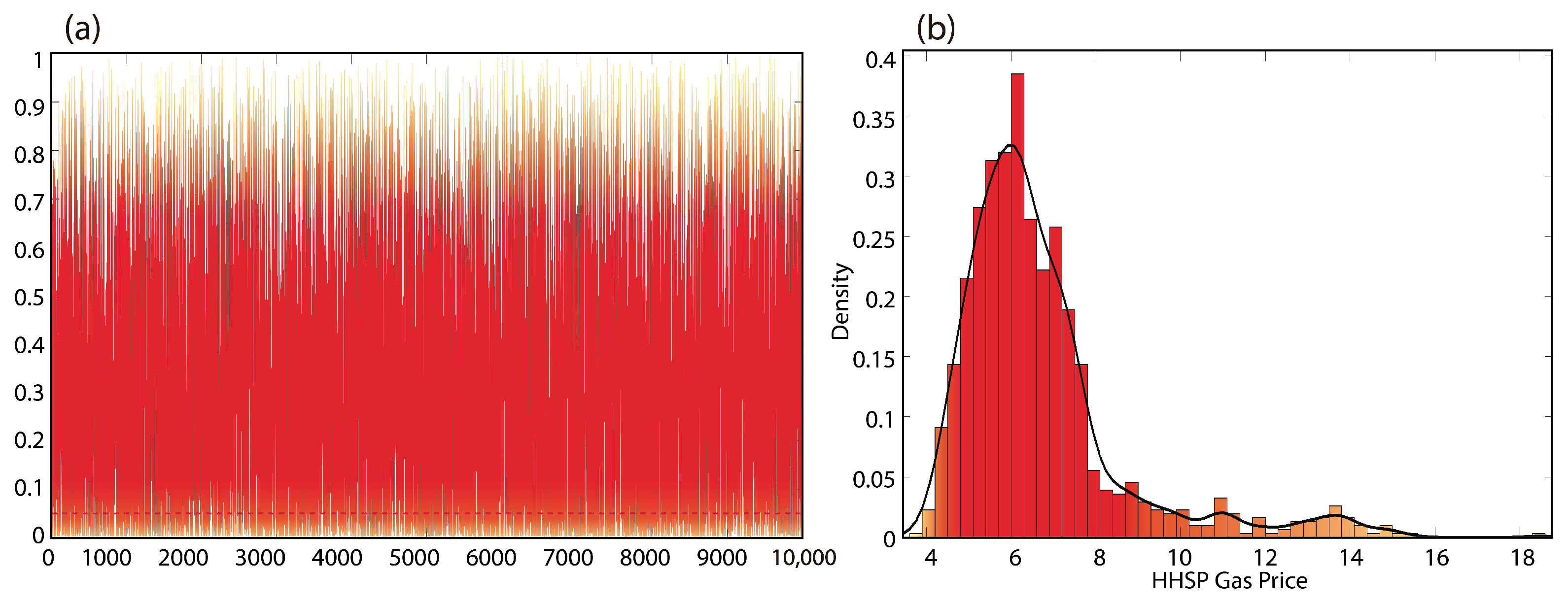
- Each subsample takes a time lapse of between 3 and 5609 days, in such a manner that each of the subsamples consists of consecutive gas price values throughout the historical series of time lapses of 3 days, 4 days, 5 days, etc. The maximum time lapse we take is 5609 days, as this is the equivalent of the historical sample 5861 minus one stock market year of 252 days. Then, for a time lapse of 5609 days, the size or total resamples will be 252, which is considered the reasonable minimum required to generate a probability distribution of a statistic.
- •
- The shorter the time lapse, the greater the number of resamples for this time lapse and vice versa.
- •
- Each time lapse will generate subsamples with elements that are not repeated and are consecutive over time. In this manner, for two subsamples from a specific time lapse, some of the elements of the subsamples will be repeated twice, at most.
- •
- The idea of taking consecutive data over time from the different subsamples comes from the perspective that there is a certain time correlation within the gas price data. It is common to find weak long-tailed or long-term correlations in historical evolution of listed assets [81].
2.3. Statistical Calculation of Financial Indicators
- CAPEX or Capital Expenditure is the financial value of the investment in the shale-gas well expressed in USD. We consider an investment of 4.8 million USD as the estimated cost of a shale-gas well of 1500 m length with 7 hydraulic fractures located at 3000 m depth.
- i is the time step.
- N represents the total time steps.
- is the gas price at the time step i, its value expressed in USD/Mscf.
- is the flow rate at time step i, its value expressed in Mscf/d. When this value is multiplied by , the gross cash flows for time step i are obtained.
- Roy refers to royalties, expressed on a unit basis, paid to the owner of the land and other agents such as county administrations in some cases. We assume a constant rate of 15% of the gross economic flow.
- OPEX or Operational Expenditures are the well operating costs. We estimate a constant cost value of 150 USD/day. It is sometimes expressed in units of USD/Mscf, showing that its importance decreases as gas production drops. In this case, we consider it fixed and constant day to day. It is assumed as a hypothesis that day-to-day operations costs (OPEX) are constant since gas extraction management is carried out in an automated manner [14].
- refers to daily inflation and depends on . That is, it depends on the annualized gas price inflation. This varies with each time step and is expressed on a unit basis. The annualized discount rate ranges from −0.1% to 1.75% over the life of the well.
- RateT represents the profit taxes expressed on a unit basis. We apply 21% tax, which is the current gross rate for corporate tax in the USA.
2.4. Optimization of Financial Indicators
- •
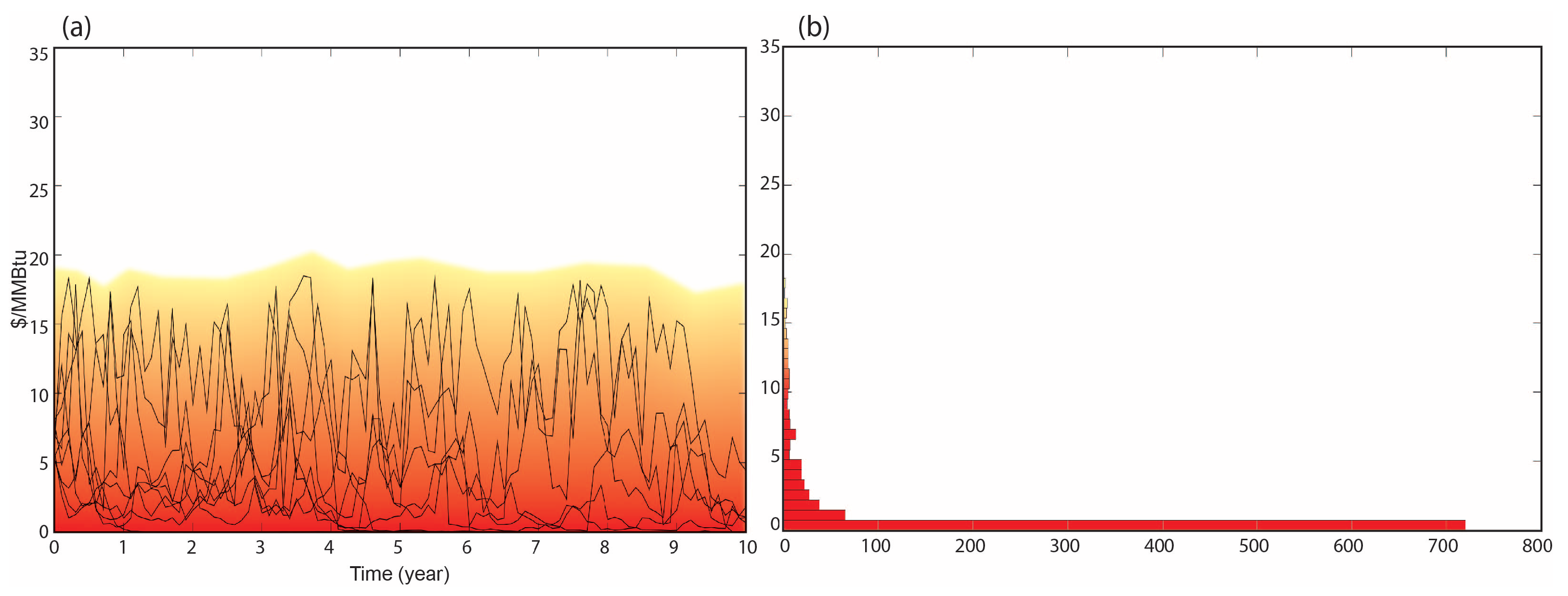
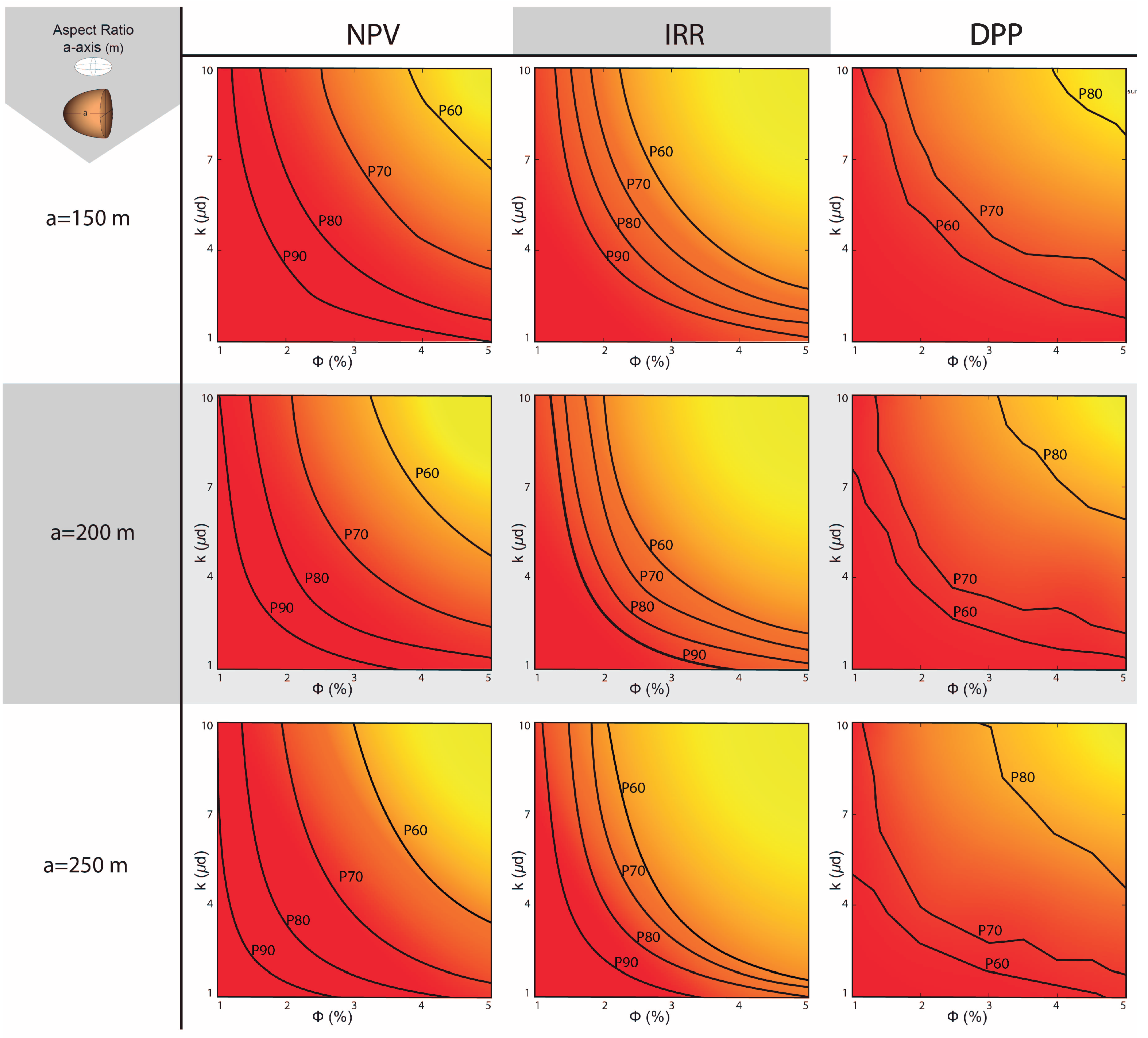
- An induced porosity–permeability field is defined in which parameter values vary between 1% and 5% for the porosity and between 1 and 10 d induced permeability in the SRV. There are 9 intervals of variation of porosity (0.5% increase per interval) and 11 intervals of variation of permeability (0.9 d of increase per interval). We generate 99 “porosity-induced permeability” pairs, calculating the corresponding production curve or flow-rate for each one.
- •
- Each production curve is combined with the 1000 price realizations. With the economic production curves (), the statistical percentiles of the financial indicators are calculated (NPV, IRR, and DPP).
- •
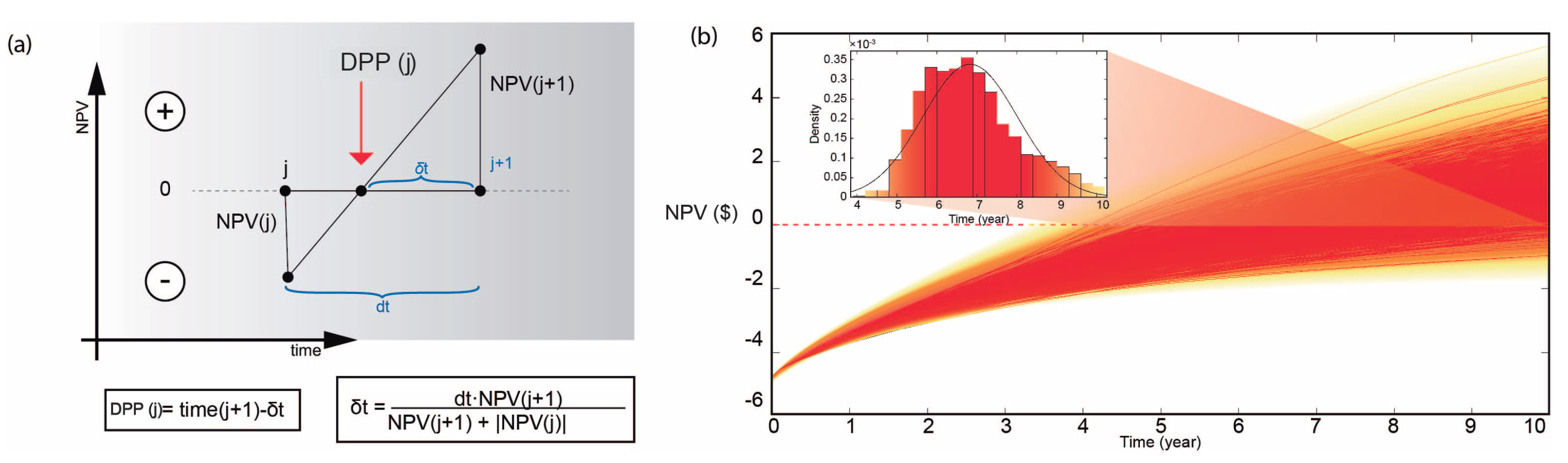
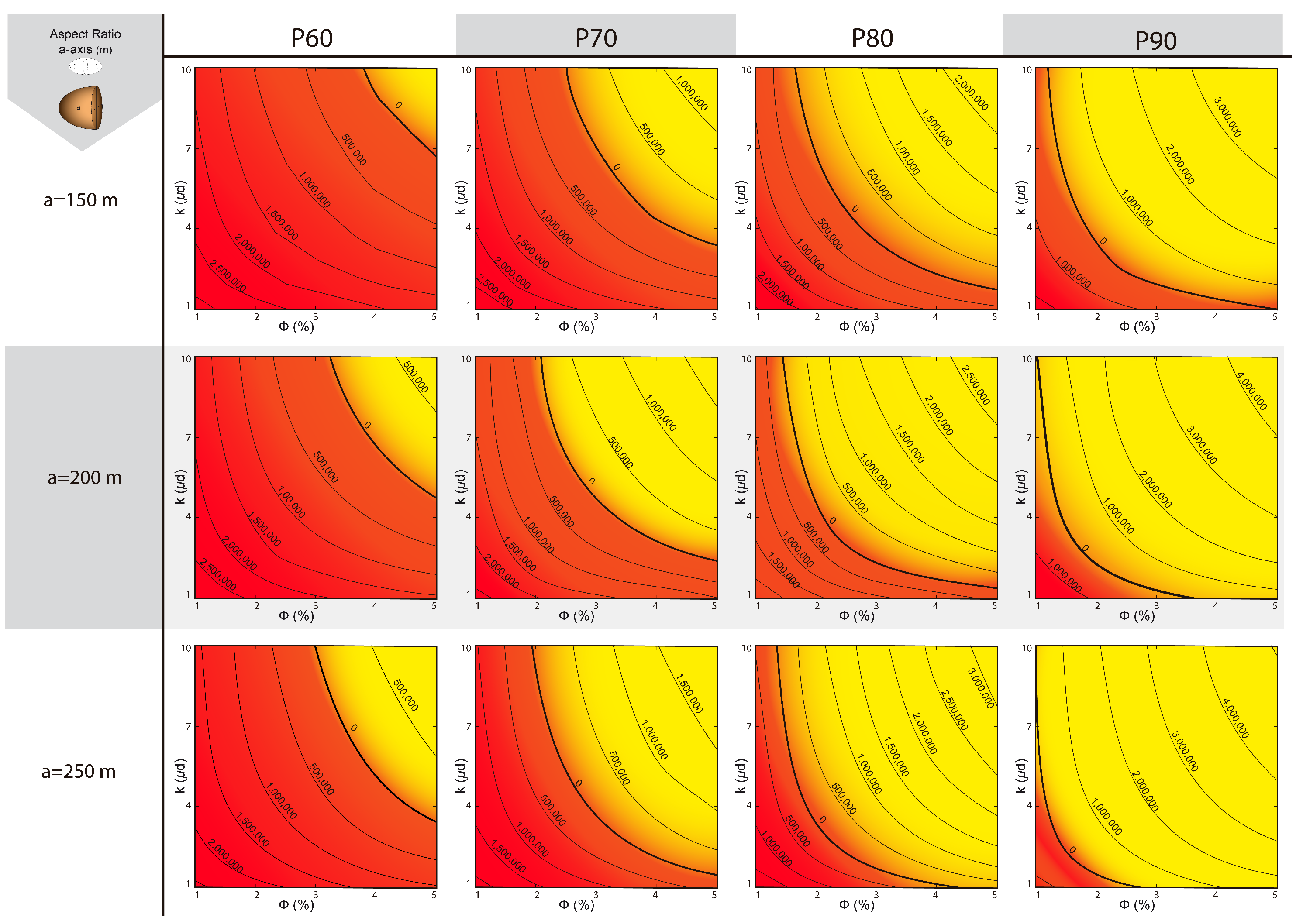
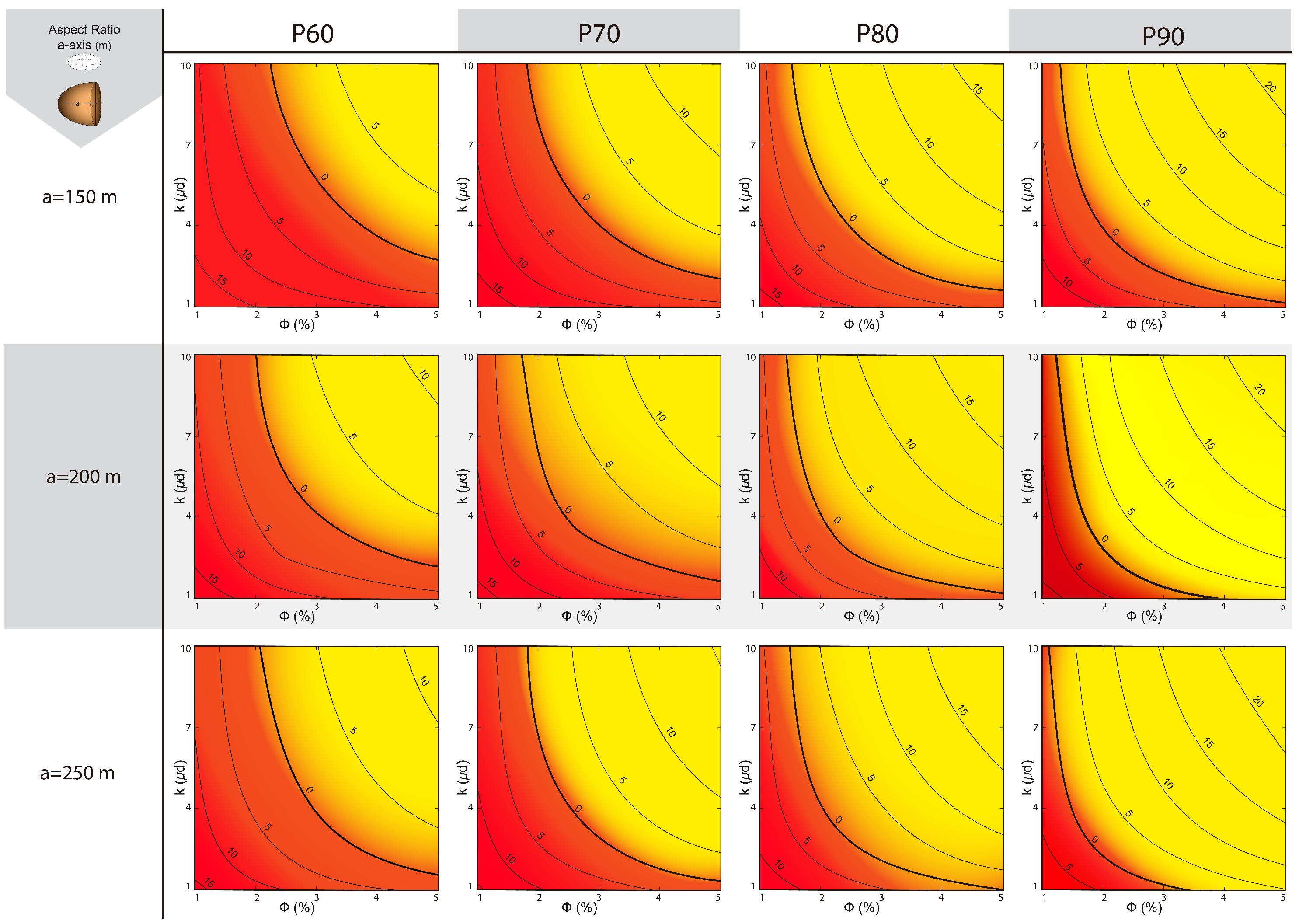
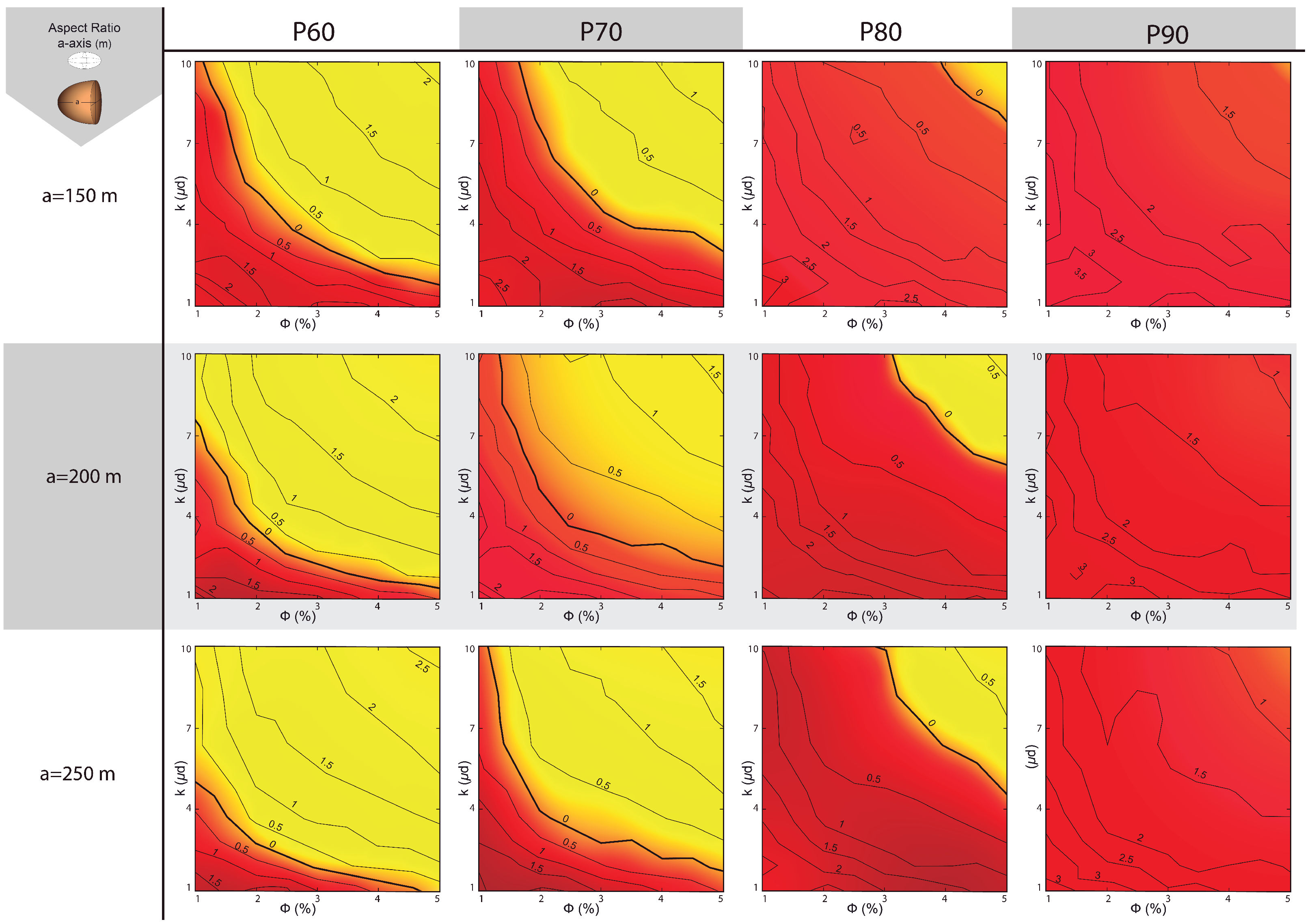
- This same operation is performed for half-length ellipsoidal fractured volumes of 150 m, 200 m, and 250 m. The longer the axis, the flatter the ellipsoids. For certain financial indicators (NPV, IRR, or DPP) and risk level (X%), we determine the threshold value for which the investment is consider admissible. For NPV and IRR, we set the threshold at 0 USD/% or higher, and for DPP in 7 years or less.
- •
- Based on the porosity–permeability combinations, we perform a minimization of the absolute NPV and IRR percentiles adopted and a minimization of the absolute value of the DPP minus 7. Thus, if we decide to assume a risk of X0%, the absolute NPV, IRR, and DPP-7 values should be minimized, and the porosity–permeability combination that generates that minimum is a curve in the porosity–permeability plane for a PX0 percentile. This combination will also define a region in this plane in which the probability of achieving a positive NPV and IRR will be at least 100–X0%, or a region where the DPP will be less than 7 years with the same probability.
2.5. Aggregate Results of Financial Indicators
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| O&G | oil and gas |
| Mscf | thousand standard cubic feet |
| CAPEX | Capital Expenditure |
| OPEX | Operational Expenditures |
| NPV | Net Present Value |
| IRR | Internal Rate of Return |
| DPP | Discounted Payback Period |
References
- Weber, C.L.; Clavin, C. Life cycle carbon footprint of shale gas: Review of evidence and implications. Environ. Sci. Technol. 2012, 46, 5688–5695. [Google Scholar] [CrossRef] [PubMed]
- Rivard, C.; Lavoie, D.; Lefebvre, R.; Séjourné, S.; Lamontagne, C.; Duchesne, M. An overview of Canadian shale gas production and environmental concerns. Int. J. Coal Geol. 2014, 126, 64–76. [Google Scholar] [CrossRef]
- Bowker, K.A. Barnett Shale gas production, Fort Worth Basin: Issues and discussion. AAPG Bull. 2014, 91, 523–533. [Google Scholar] [CrossRef]
- Chebeir, J.; Asala, H.; Manee, V.; Gupta, I.; Romagnoli, J.A. Data driven techno-economic framework for the development of shale gas resources. J. Nat. Gas Sci. Eng. 2019, 72, 103007. [Google Scholar] [CrossRef]
- Gao, J.; You, F. Game theory approach to optimal design of shale gas supply chains with consideration of economics and life cycle greenhouse gas emissions. AIChE J. 2019, 63, 2671–2693. [Google Scholar] [CrossRef]
- Rao, V. Shale Gas Drives Vertical Integration. J. Pet. Technol. 2014, 66, 18–19. [Google Scholar] [CrossRef]
- Hsu, C.S.; Robinson, P.R.; Hsu, C.S.; Robinson, P.R. Midstream transportation, storage, and processing. In Petroleum Science and Technology; Springer: Cham, Switzerland, 2019; pp. 385–394. [Google Scholar] [CrossRef]
- Quevedo-Orozco, D.R.; Ríos-Mercado, R.Z. Improving the quality of heuristic solutions for the capacitated vertex p-center problem through iterated greedy local search with variable neighborhood descent. Comput. Oper. Res. 2015, 62, 133–144. [Google Scholar] [CrossRef]
- Behrooz, H.A.; Boozarjomehry, R.B. Dynamic optimization of natural gas networks under customer demand uncertainties. Energy 2015, 134, 968–983. [Google Scholar] [CrossRef]
- Bellout, M.C.; Echeverría Ciaurri, D.; Durlofsky, L.J.; Foss, B.; Kleppe, J. Joint optimization of oil well placement and controls. Comput. Geosci. 2012, 16, 1061–1079. [Google Scholar] [CrossRef]
- Chang, C.; Liu, C.; Li, Y.; Li, X.; Yu, W.; Miao, J.; Sepehrnoori, K. A Novel Optimization Workflow Coupling Statistics-Based Methods to Determine Optimal Well Spacing and Economics in Shale Gas Reservoir with Complex Natural Fractures. Energies 2020, 13, 3965. [Google Scholar] [CrossRef]
- Gao, J.; You, F. Design and optimization of shale gas energy systems: Overview, research challenges, and future directions. Comput. Chem. Eng. 2017, 106, 699–718. [Google Scholar] [CrossRef]
- Guerra, O.J.; Calderon, A.J.; Papageorgiou, L.G.; Siirola, J.J.; Reklaitis, G.V. An optimization framework for the integration of water management and shale gas supply chain design. Comput. Chem. Eng. 2016, 92, 230–255. [Google Scholar] [CrossRef]
- Wilson, K.C.; Durlofsky, L.J. Optimization of shale gas field development using direct search tecniques and reduce-physics models. J. Pet. Sci. Eng. 2013, 108, 304–315. [Google Scholar] [CrossRef]
- Maxwell, S. Microseismic hydraulic fracture imaging: The path toward optimizing shale gas production. Lead. Edge 2011, 30, 340–346. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K. An Efficient Reservoir-Simulation Approach To Design and Optimize Unconventional Gas Production. J. Can. Pet. Technol. 2014, 53, 109–121. [Google Scholar] [CrossRef]
- Rahmanifard, H.; Plaksina, T. Application of fast analytical approach and AI optimization techniques to hydraulic fracture stage placement in shale gas reservoirs. J. Nat. Gas Sci. Eng. 2010, 52, 367–378. [Google Scholar] [CrossRef]
- Onwunalu, J.E.; Durlofsky, L.J. Application of a particle swarm optimization algorithm for determining optimum well location and type. Comput. Geosci. 2010, 14, 183–198. [Google Scholar] [CrossRef]
- Yuan, J.; Luo, D.; Feng, L. A review of the technical and economic evaluation techniques for shale gas development. Appl. Energy 2015, 148, 49–65. [Google Scholar] [CrossRef]
- Li, C.; Eason, J.P.; Drouven, M.G.; Grossmann, I.E. Shale gas pad development planning under price uncertainty. AIChE J. 2020, 66, e16933. [Google Scholar] [CrossRef]
- Tang, S.L.; John Tang, H. The variable financial indicator IRR and the constant economic indicator NPV. Eng. Econ. 2003, 48, 69–78. [Google Scholar] [CrossRef]
- Guanche, R.; De Andres, A.D.; Simal, P.D.; Vidal, C.; Losada, I.J. Uncertainty analysis of wave energy farms financial indicators. Renew. Energy 2014, 68, 570–580. [Google Scholar] [CrossRef]
- Zhang, K. Comparative Analysis of NPV and IRR Indicators Based on Practical Applications. Highlights Bus. Econ. Manag. 2023, 7, 22–28. [Google Scholar] [CrossRef]
- Rushinck, A. Capital Budgeting Techniques, the Payback Period, the Net Present Value, the Internal Rate of Return and Their Computer Applications. Manag. Financ. 1983, 9, 11–13. [Google Scholar] [CrossRef]
- Bhandari, S.B. Discounted payback period-some extensions. J. Bus. Behav. Sci. 2009, 21, 28–38. [Google Scholar]
- Gorshkov, A.S.; Vatin, N.I.; Rymkevich, P.P.; Kydrevich, O.O. Payback period of investments in energy saving. Mag. Civ. Eng. 2018, 2, 65–75. [Google Scholar]
- Mohn, K.; Misund, B. Investment and uncertainty in the international oil and gas industry. Energy Econ. 2009, 31, 240–248. [Google Scholar] [CrossRef]
- Brockway, P.E.; Owen, A.; Brand-Correa, L.I.; Hardt, L. Estimation of global final-stage energy-return- on-investment for fossil fuels with comparison to renewable energy sources. Nat. Energy 2019, 4, 616–621. [Google Scholar] [CrossRef]
- Shirangi, M.G.; Durlofsky, L.J. A general method to select representative models for decision making and optimization under uncertainty. Comput. Geosci. 2016, 96, 109–123. [Google Scholar] [CrossRef]
- Ramos, S.B.; Veiga, H. Risk factors in oil and gas industry returns: International evidence. Energy Econ. 2011, 33, 525–542. [Google Scholar] [CrossRef]
- Domnikov, A.; Khomenko, P.; Chebotareva, G.; Khodorovsky, M. Risk and Profitability Optimization of Investments in the Oil and Gas Industry. Energy 2017, 2, 263–276. [Google Scholar] [CrossRef]
- Isebor, O.J.; Durlofsky, L.J. Biobjective optimization for general oil field development. J. Pet. Sci. Eng. 2017, 119, 123–138. [Google Scholar] [CrossRef]
- Yuhua, Z.; Dongkun, L. Investment optimization in oil and gas plays. Pet. Explor. Dev. 2009, 36, 535–540. [Google Scholar] [CrossRef]
- Tan, S.H.; Barton, P.I. Optimal shale oil and gas investments in the United States. Energy 2017, 141, 398–422. [Google Scholar] [CrossRef]
- Shirangi, M.G.; Durlofsky, L.J. Closed-loop field development under uncertainty by use of optimization with sample validation. SPE J. 2017, 20, 908–922. [Google Scholar] [CrossRef]
- Boulis, A.; Jayakumar, R.; Rai, R. A New Approach for Well Spacing Optimisation and Its Application to Various Shale Gas Resources. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26–28 March 2013. [Google Scholar] [CrossRef]
- Valle-Falcones, L.M.; Grima-Olmedo, C.; Rodríguez-Pons Esparver, R.; Zamarro-Toves, E. Evaluation and Economics of Shale Gas Reserves in the Flysch-Eocene Formation of the Jaca Basin. Appl. Sci. 2023, 13, 1732. [Google Scholar] [CrossRef]
- Weijermars, R. Economic appraisal of shale gas plays in Continental Europe. Appl. Energy 2013, 106, 100–115. [Google Scholar] [CrossRef]
- Soage, A.; Juanes, R.; Colominas, I.; Cueto-Felgueroso, L. The Impact of the Geometry of the Effective Propped Volume on the Economic Performance of Shale Gas Well Production. Energies 2021, 14, 2475. [Google Scholar] [CrossRef]
- Soage, M.A. A Numerical Modelling Framework for the Optimization and Economic Analysis of Unconventional Gas Production. Doctoral Thesis, University of A Coruna, A Coruña, Spain, 2021. [Google Scholar]
- Silin, D.; Kneafsey, T. Shale Gas: Nanometer-Scale Observations and Well Modelling. J. Canadian Petro. Tech. 2012, 464–475. [Google Scholar] [CrossRef]
- Cipolla, C.L.; Lolon, E.P.; Erdle, J.C. Rubin, B. Reservoir Modeling in Shale-Gas Reservoirs. SPE Reserv. Eval. Eng. 2010, 13, 464–475. [Google Scholar] [CrossRef]
- Patzek, T.W.; Male, F.; Marder, M. Gas production in the Barnett Shale obeys a simple scaling theory. Proc. Natl. Acad. Sci. USA 2013, 110, 304–315. [Google Scholar] [CrossRef]
- Wang, X.; Sheng, J. Gas sorption and non-Darcy flow in shale reservoirs. Pet. Sci. 2017, 14, 746–754. [Google Scholar] [CrossRef]
- Haider, S.; Saputra, W.; Patzek, T. The Key Factors That Determine the Economically Viable, Horizontal Hydrofractured Gas Wells in Mudrocks. Energies 2020, 13, 2348. [Google Scholar] [CrossRef]
- Starovoitova, B.N.; Golovin, S.V.; G.V. Paderin, G.V.; Shel, E.V.; Kavunnikova, E.A.; Krivtsov, A.M. Design optimization of hydraulic fracturing. IOP Conf. Ser. Earth Environ. Sci. 2018, 193, 0120115. [Google Scholar] [CrossRef]
- Yan, X.; Sun, H.; Huang, Z.; Liu, L.; Wang, P.; Zhang, Q.; Yao, J. Hierarchical modeling of hydromechanical coupling in fractured shale gas reservoirs with multiple porosity scales. Energy Fuels 2021, 35, 5758–5776. [Google Scholar] [CrossRef]
- Vandenbroucke, M.; Largeau, C. Kerogen origin, evolution and structure. Org. Geochem. 2007, 38, 719–833. [Google Scholar] [CrossRef]
- Cheng, Y.; Jiang, S.; Zhang, D.; Liu, C. An adsorbed gas estimation model for shale gas reservoirs via statistical learning. Appl. Energy 2017, 197, 327–341. [Google Scholar] [CrossRef]
- Tan, L.; Zuo, L.; Wang, B. Methods of Decline Curve Analysis for Shale Gas Reservoirs. Energies 2018, 11, 552. [Google Scholar] [CrossRef]
- Arias Ortiz, D.A.; Klimkowski, L.; Finkbeiner, T.; Patzek, T.W. The Effect of Hydraulic Fracture Geometry on Well Productivity in Shale Oil Plays with High Pore Pressure. Energies 2021, 14, 7727. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K.; Patzek, T.W. Evaluation of gas adsorption in Marcellus Shale. In Proceedings of the Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27–29 October 2014. [Google Scholar] [CrossRef]
- Efron, B. The 1977 RIETZ lecture. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Clark, P.K. A Subordinated Stochastic Process Model with Finite Variance for Speculative Prices. Econom. J. Econom. Soc. 1973, 41, 135–155. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Zambom, A.Z.; Ronaldo, D. A review of kernel density estimation with applications to econometrics. Int. Econom. Rev. 2013, 5, 20–42. [Google Scholar]
- Wang, H.; Ma, F.; Tong, X.; Liu, Z.; Zhang, X.; Wu, Z.; Li, D.; Wang, B.; Xie, Y.; Yang, L. Assessment of global unconventional oil and gas resources. Pet. Explor. Dev. 2016, 43, 925–940. [Google Scholar] [CrossRef]
- McGlade, C.; Speirs, J.; Sorrell, S. Unconventional gas–a review of regional and global resource estimates. Energy 2013, 55, 571–584. [Google Scholar] [CrossRef]
- Dong, Z.; Holditch, S.A.A.; McVay, D.A.A.; Ayers, W.B.B. Global Unconventional Gas Resource Assessment. SPE Econ. Manag. 2012, 4, 222–234. [Google Scholar] [CrossRef]
- Pejman, T.; Javadpour, F.; Sahimi, M. Data mining and machine learning for identifying sweet spots in shale reservoirs. Expert Syst. Appl. 2017, E88, 435–447. [Google Scholar] [CrossRef]
- Qian, K.-R.; He, Z.-L.; Liu, X.-W.; Chen, Y.-Q. Intelligent prediction and integral analysis of shale oil and gas sweet spots. Pet. Sci. 2018, 15, 744–755. [Google Scholar] [CrossRef]
- Montgomery, J.B.; O’sullivan, F.M. Spatial variability of tight oil well productivity and the impact of technology. Appl. Energy 2018, 195, 344–355. [Google Scholar] [CrossRef]
- COMSOL Multiphysics. Introduction to COMSOL Multiphysics (2018); COMSOL Multiphysics: Burlington, MA, USA, 2018. [Google Scholar]
- Sakhaee-Pour, A.; Bryant, S.L. Gas permeability of shale. SPE Reserv. Eval. Eng. 2012, 15, 401–409. [Google Scholar] [CrossRef]
- Cui, G.; Liu, J.; Wei, M.; Feng, X.; Elsworth, D. Evolution of permeability during the process of shale gas extraction. J. Nat. Gas Sci. Eng. 2018, 49, 94–109. [Google Scholar] [CrossRef]
- Gao, Q.; Han, S.; Cheng, Y.; Li, Y.; Yan, C.; Han, Z. Apparent permeability model for gas transport through micropores and microfractures in shale reservoirs. Fuel 2021, 285, 119086. [Google Scholar] [CrossRef]
- Marder, M.; Chen, C.H.; Patzek, T. Simple models of the hydrofracture process. Phys. Rev. E 2015, 92, 062408. [Google Scholar] [CrossRef] [PubMed]
- Kwok, Y.K. Introduction to Derivative Instruments. In Mathematical Models of Financial Derivatives; Springer Finance: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Van Kampen, N.G. Stochastic differential equations. Phys. Rep. 1976, 24, 171–228. [Google Scholar] [CrossRef]
- Postali, F.A.; Picchetti, P. Geometric Brownian motion and structural breaks in oil prices: A quantitative analysis. Energy Econ. 2006, 28, 506–522. [Google Scholar] [CrossRef]
- Itô, K. On a formula concerning stochastic differentials. Nagoya Math. J. 1951, 3, 55–65. [Google Scholar] [CrossRef]
- Shiga, T.; Shimizu, A. Infinite dimensional stochastic differential equations and their applications. J. Math. Kyoto Univ. 1980, 20, 395–416. [Google Scholar] [CrossRef]
- Burrage, K.; Burrage, P.M.; Tian, T. Numerical methods for strong solutions of stochastic differential equations: An overview. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004, 460, 373–402. [Google Scholar] [CrossRef]
- Doob, J.L. The Brownian movement and stochastic equations. Ann. Math. 1942, 43, 351–369. [Google Scholar] [CrossRef]
- Naseer, M.; Bin Tariq, D.Y. The efficient market hypothesis: A critical review of the literature. Iup J. Financ. Risk Manag. 2015, 12, 48–63. [Google Scholar]
- Ricciardi, L.M. On the transformation of diffusion processes into the Wiener process. J. Math. Anal. Appl. 1976, 54, 185–199. [Google Scholar] [CrossRef]
- Lepskii, O.V. On a problem of adaptive estimation in Gaussian white noise. Theory Probab. Its Appl. 1991, 35, 454–466. [Google Scholar] [CrossRef]
- Itô, K. 109.Stochastic Integral. Proc. Imp. Acad. 1944, 20, 519–524. [Google Scholar] [CrossRef]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Li, J.; Wu, Q.; Tian, Y.; Fan, L. Monthly Henry Hub natural gas spot prices forecasting using variational mode decomposition and deep belief network. Energy 2021, 227, 120478. [Google Scholar] [CrossRef]
- Lidén, J. Stock Price Predictions Using a Geometric Brownian Motion. Master’s Thesis, Uppsala University, Uppsala, Sweden, 2018. [Google Scholar]
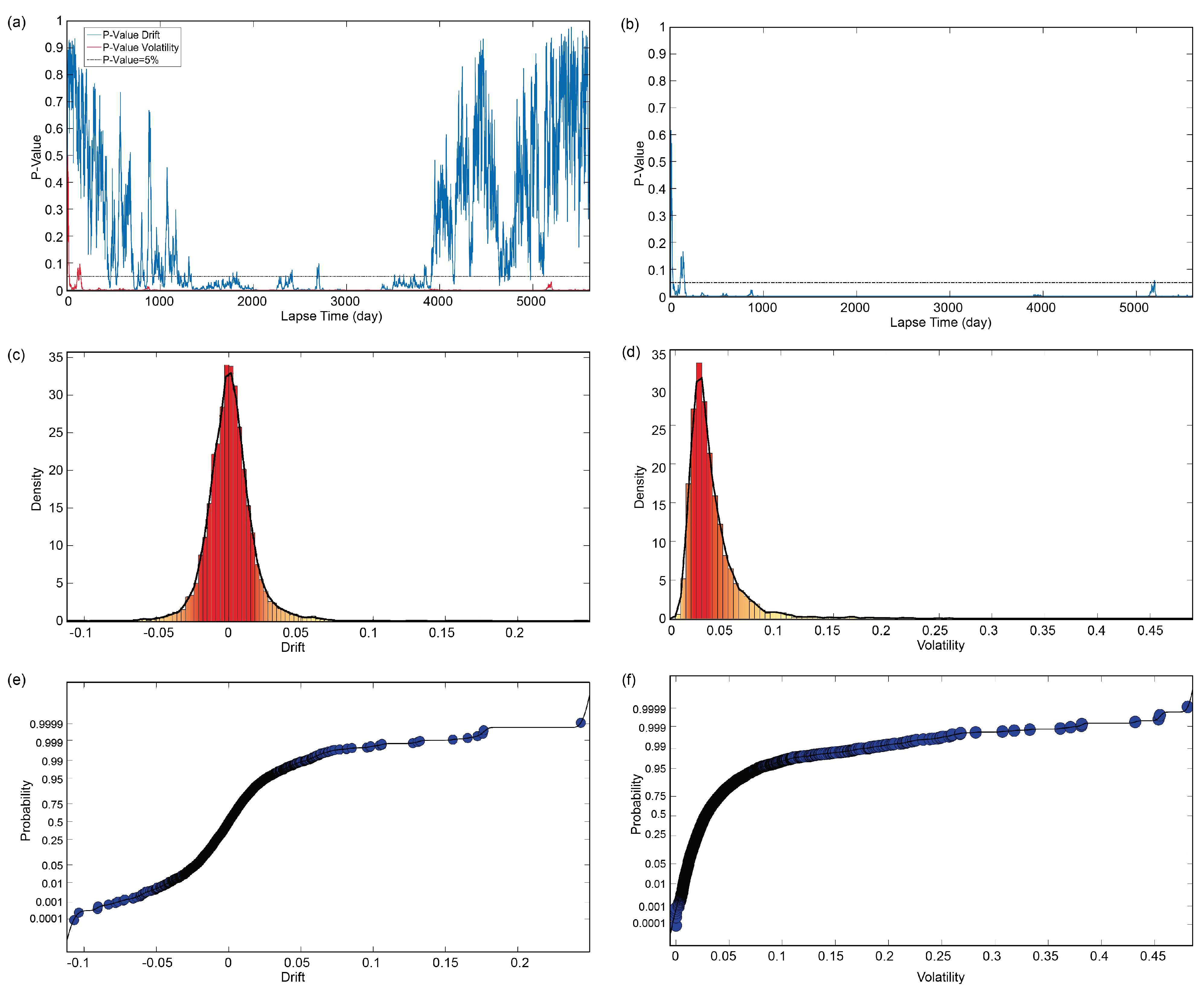
- Massey, F.J. The Kolmogorov-Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Wand, M.P.; Schucany, W.R. Gaussian-Based Kernels. Can. J. Stat. 1990, 18, 197–204. [Google Scholar] [CrossRef]
- Papadopoulos, C.E.; Yeung, H. Uncertainty estimation and Monte Carlo simulation method. Flow Meas. Instrum. 2001, 12, 291–298. [Google Scholar] [CrossRef]
- Hacura, A.; Jadamus-Hacura, M.; Kocot, A. Risk analysis in investment appraisal based on the Monte Carlo simulation technique. Eur. Phys. J. B 2001, 20, 551–553. [Google Scholar] [CrossRef]
- Bas, E. A robust approach to the decision rules of NPV and IRR for simple projects. Appl. Math. Comput. 2013, 219, 5901–5908. [Google Scholar] [CrossRef]
- Lake, L.W.; Baylor, J.M.; Ramsey, J.D.; Titman, S. A Primer on the Economics of Shale Gas Production Just How Cheap is Shale Gas? J. Appl. Corp. Financ. 2013, 25, 87–96. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K. Optimization of Multiple Hydraulically Fractured Horizontal Wells in Unconventional Gas Reservoirs. J. Pet. Eng. 2013, 2013, 151898. [Google Scholar]
- Eshkalak, M.O.; Aybar, U.; Sepehrnoori, K. An Economic Evaluation on the Re-fracturing Treatment of US Shale Gas Resources. In Proceedings of the Eastern Regional Meeting, Charleston, WV, USA, 21–23 October 2014. SPE 171009-MS. [Google Scholar]
- Du, Y.; Liu, H.; Sun, Y.; Sheng, S.; Wei, M. An Improved Integrated Numerical Simulation Method to Study Main Controlling Factors of EUR and Optimization of Development Strategy. Energies 2023, 16, 2011. [Google Scholar] [CrossRef]
- Nguyen-Le, V.; Shin, H. Development of Reservoir Economic Indicator for Barnett Shale Gas Potential Evaluation Based on the Reservoir and Hydraulic Fracturing Parameters. J. Nat. Gas Sci. Eng. 2019, 66, 159–167. [Google Scholar] [CrossRef]
- Hong, B.; Li, X.; Song, S.; Chen, S.; Zhao, C.; Gong, J. Optimal planning and modular infrastructure dynamic allocation for shale gas production. Appl. Energy 2020, 261, 114439. [Google Scholar] [CrossRef]
- Kampf, R.; Majerčák, P.; Švagr, P. Break-Even Point Analyze. NašE More Znan. čAsopis More Pomor. 2016, 63, 126–128. [Google Scholar] [CrossRef]
- Lee, D.S.; Herman, J.D.; Elsworth, D.; Kim, H.T.; Lee, H.S. A Critical Evaluation of Unconventional Gas Recovery from Marcellus Shale, Northeastern United States. KSCE J. Civ. Eng. 2018, 15, 679–687. [Google Scholar] [CrossRef]

| Variable | Meaning | Value |
|---|---|---|
| gas pressure | [30–35 MPa] | |
| initial reservoir pressure | 30 MPa | |
| bottom hole pressure | 5 MPa | |
| gas compressibility | ||
| Langmuir isotherm slope | - | |
| porosity | 1–5% | |
| methane density at standard conditions | ||
| kerogen density | ||
| kerogen relative volume | ||
| Langmuir isotherm | - | |
| Langmuir volume | ||
| Langmuir pressure | 3 MPa | |
| k | fractured shale permeability | |
| EPV permeability | ||
| methane viscosity | ||
| q | methane flux | Mscf/month |
| stimulated volume | - | |
| normal vector to contour | - |
| p-Value–Time Lapse = 7 Days | F1 Score–Time Lapse = 7 Days | |
|---|---|---|
| 0.8127 | 0.6161 | |
| 0.4961 | 0.6161 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soage, A.; Juanes, R.; Colominas, I.; Cueto-Felgueroso, L. Optimization of Financial Indicators in Shale-Gas Wells Combining Numerical Decline Curve Analysis and Economic Data Analysis. Energies 2024, 17, 864. https://doi.org/10.3390/en17040864
Soage A, Juanes R, Colominas I, Cueto-Felgueroso L. Optimization of Financial Indicators in Shale-Gas Wells Combining Numerical Decline Curve Analysis and Economic Data Analysis. Energies. 2024; 17(4):864. https://doi.org/10.3390/en17040864
Chicago/Turabian StyleSoage, Andres, Ruben Juanes, Ignasi Colominas, and Luis Cueto-Felgueroso. 2024. "Optimization of Financial Indicators in Shale-Gas Wells Combining Numerical Decline Curve Analysis and Economic Data Analysis" Energies 17, no. 4: 864. https://doi.org/10.3390/en17040864
APA StyleSoage, A., Juanes, R., Colominas, I., & Cueto-Felgueroso, L. (2024). Optimization of Financial Indicators in Shale-Gas Wells Combining Numerical Decline Curve Analysis and Economic Data Analysis. Energies, 17(4), 864. https://doi.org/10.3390/en17040864





