A Dual-Layer MPC of Coordinated Control of Battery Load Demand and Grid-Side Supply Matching at Electric Vehicle Swapping Stations
Abstract
1. Introduction
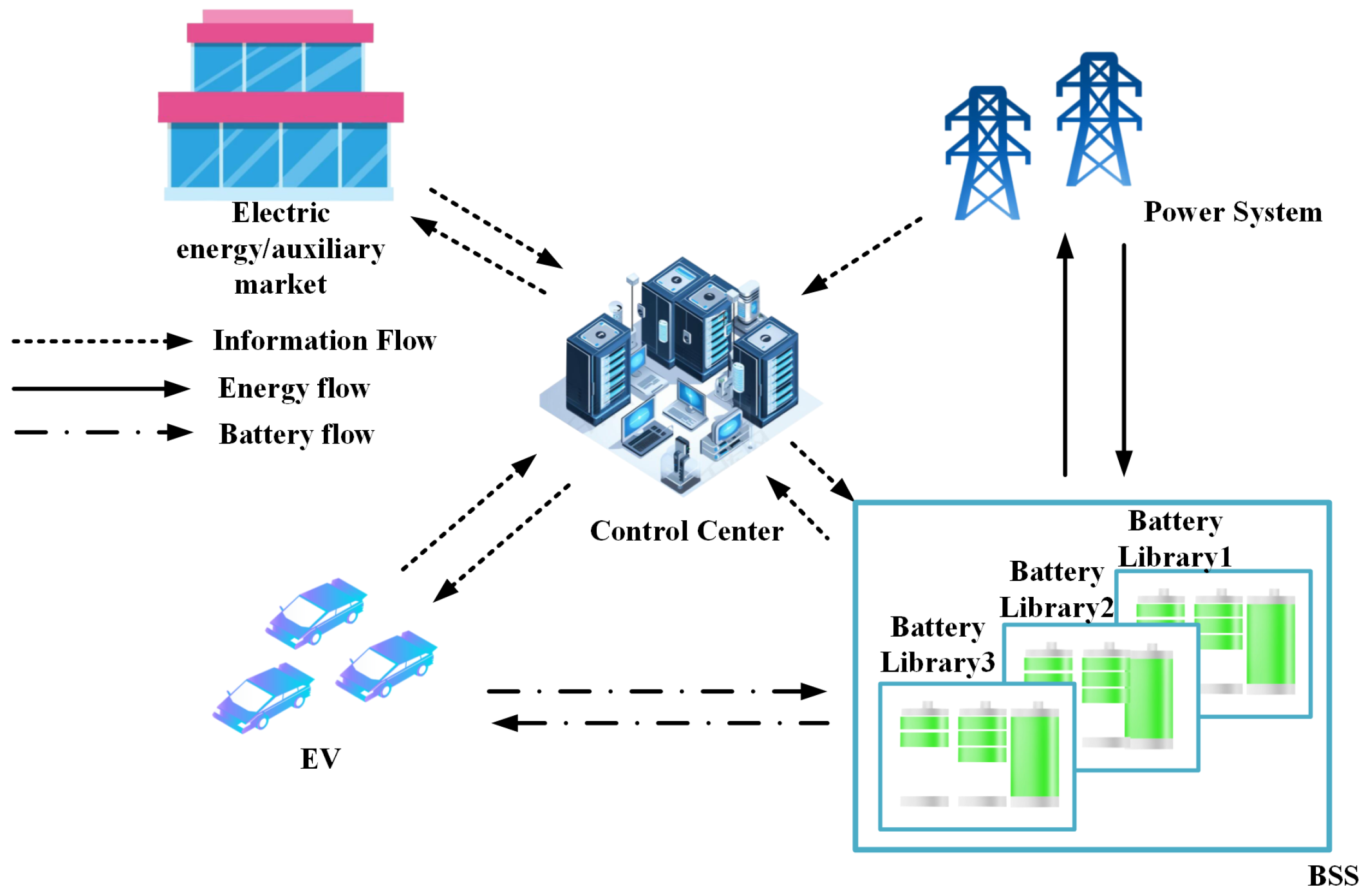
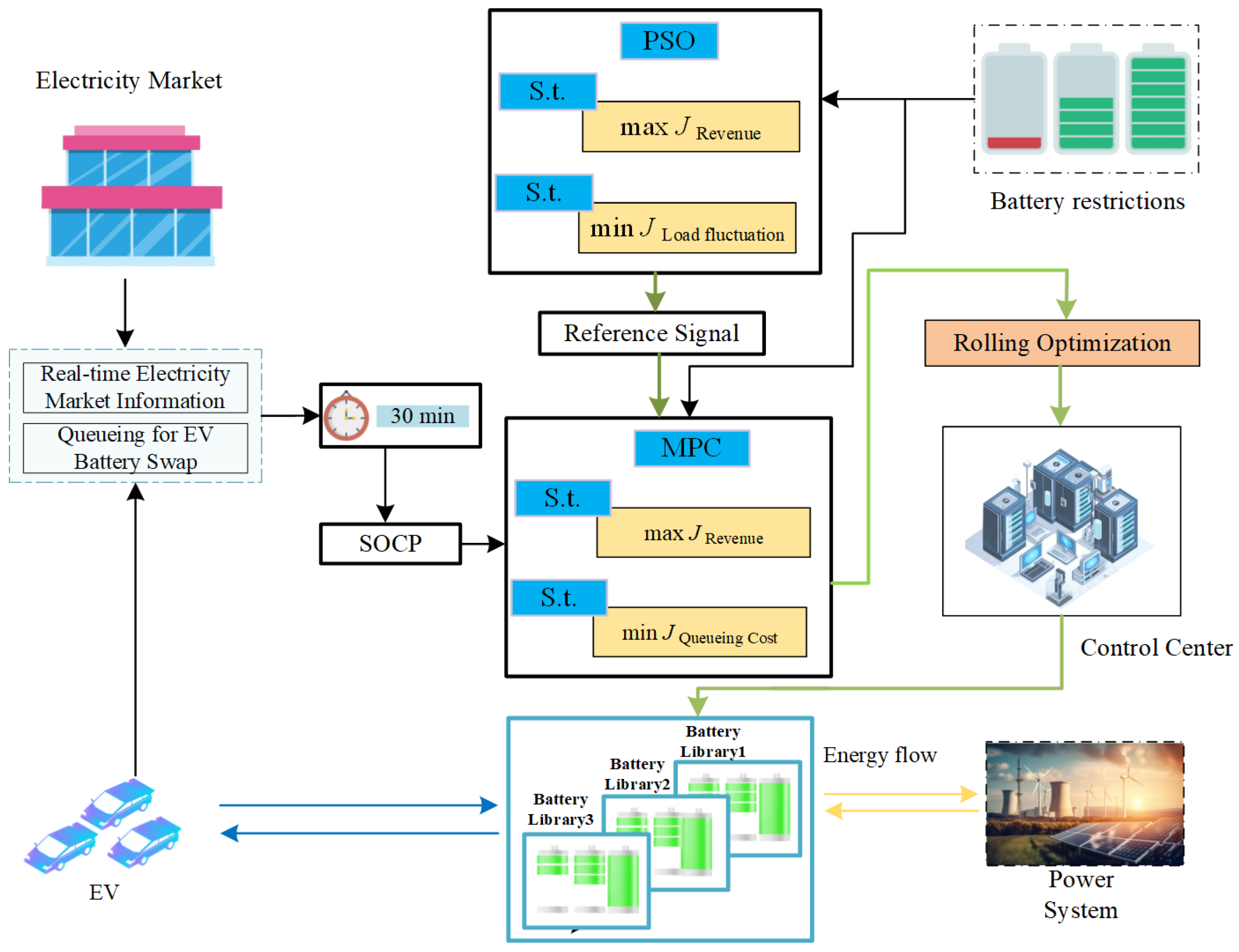
2. System Model and Allocation Strategy
2.1. System Model
2.2. Methods
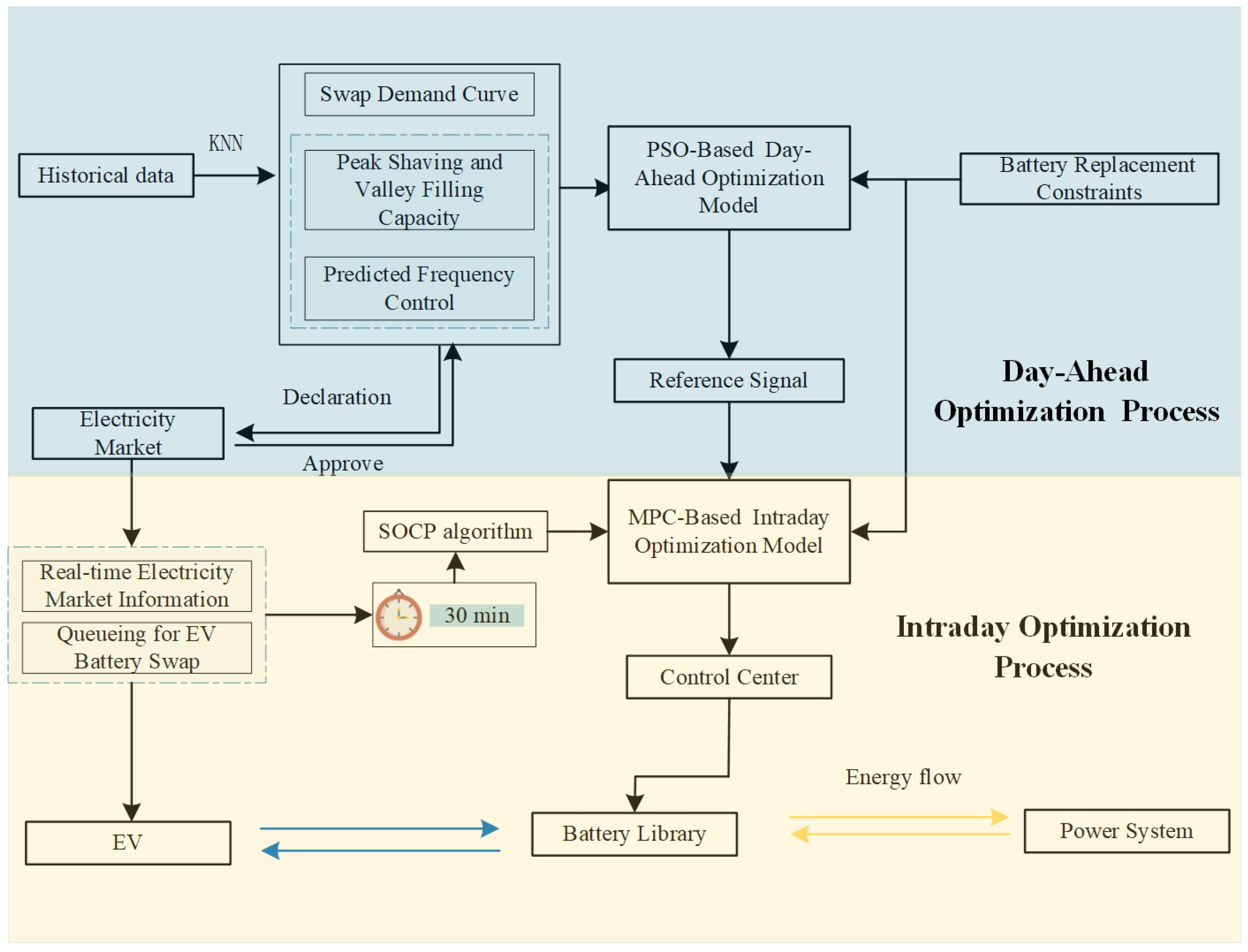
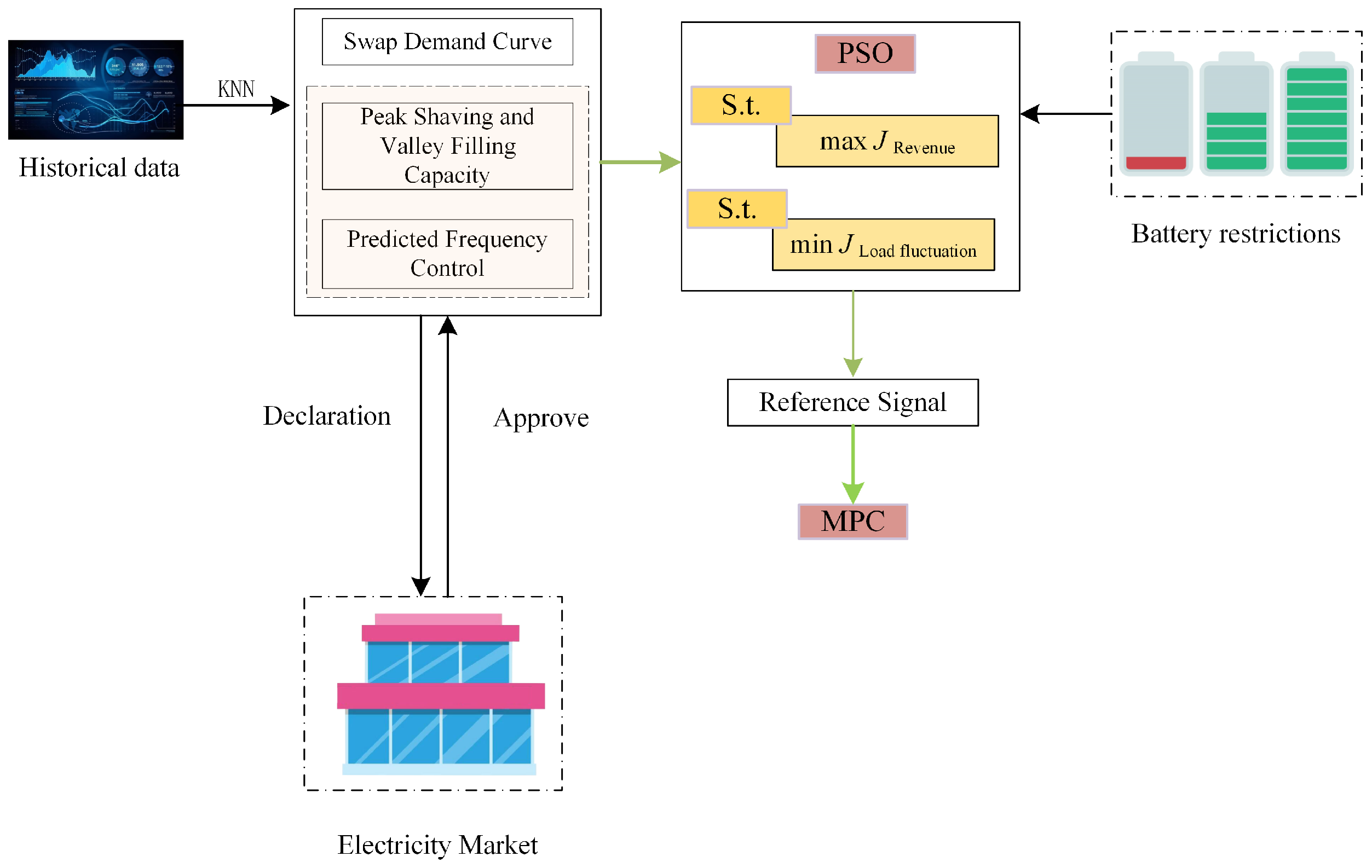
2.3. Day-Ahead Prediction-Based Optimal Scheduling Modeling
- (1)
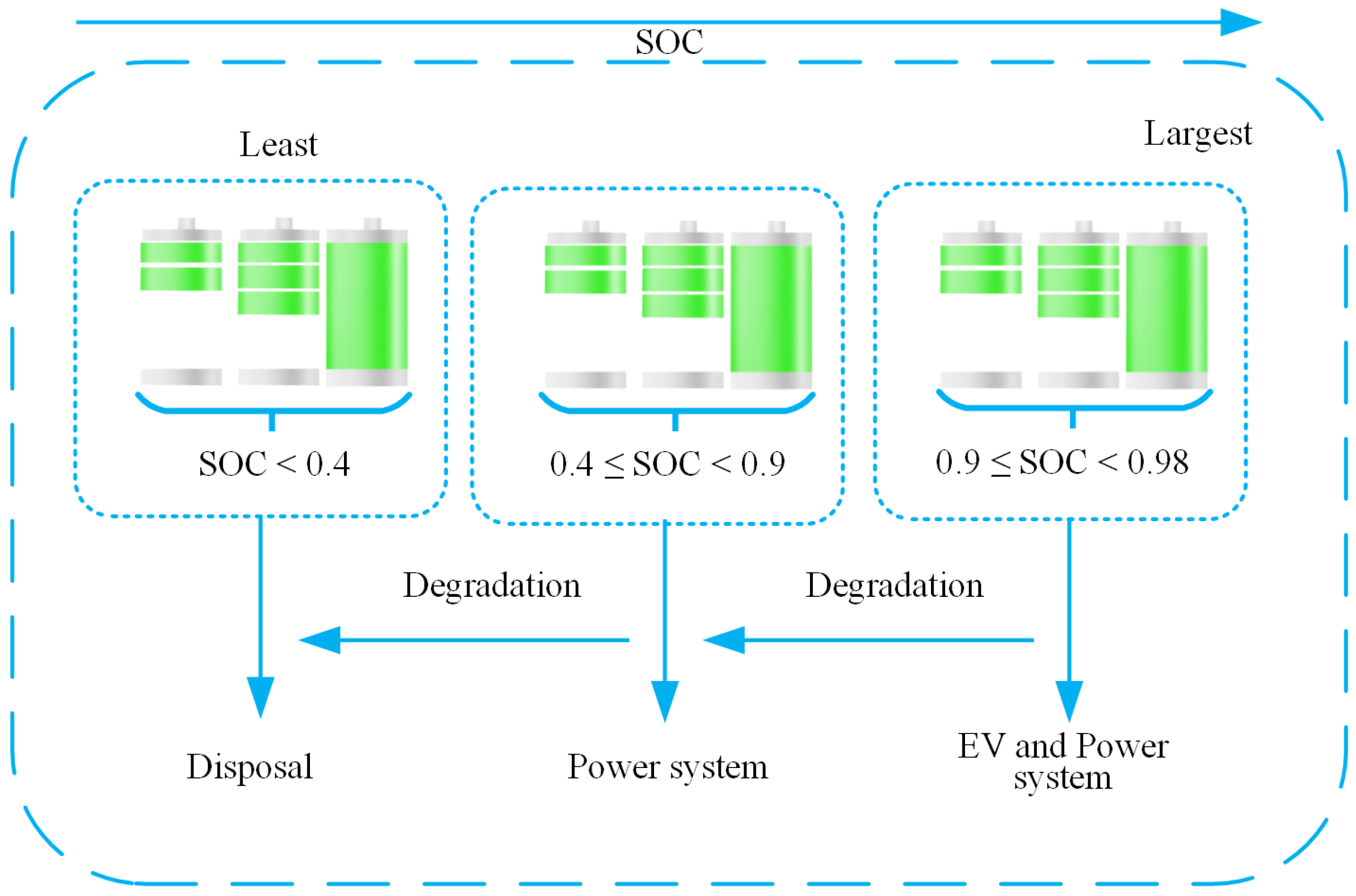
- Battery aging modeling
- (2)
- Frequency regulation assistance modeling
- (3)
- Modeling of peak shaving and valley-filling benefits
- (4)
- Swapping battery revenue modeling
- (5)
- BSS charge cost modeling
- (6)
- Constraints on charging power batteries
- (7)
- Strategies for battery power participation in peak shaving and frequency regulation assistance
- (8)
- Constraints for battery power swapping
2.4. Intraday Optimized Scheduling Model
- (1)
- The objective function
- (1)
- The day-ahead optimized charge/discharge curve is used as the reference curve for MPC for rolling optimization tracking.
- (2)
- Establish the control time interval and prediction time interval of the MPC algorithm. The shorter the time interval of the battery swapping demand, the more random and frequent regulation of the battery charging and discharging power will affect the battery lifespan. A longer the time interval leads to the control of the space being small, meaning it cannot respond to the real-time swapping demand, resulting in the vehicle not being able to carry out the orderly battery swapping. So, this paper takes 30 min as the control time interval and 4 h as the predictive.
- (3)
- Obtain the system state at the current time period t. Based on the battery swapping demand, the actual tariff, and the demand related Intraday invitations, track the reference curve in the prediction time domain. ( is the prediction step), obtain the predicted power through the online rolling optimization algorithm, and compute the control sequences in the respective control time domains ( is the control step), .
- (4)
- Because the uncertainty of real-time tariffs and swapping batter vehicles can cause vehicle queuing, the second-order cone optimization algorithm is used in each time period t to update the reference curve after time period t to improve the real-time responsiveness of the MPC algorithm.
- (5)
- Apply the first result of the control sequence to the control object and produce the output vector .
- (6)
- To time period , update the system state to feed back to the rolling optimization model to correct the prediction error.
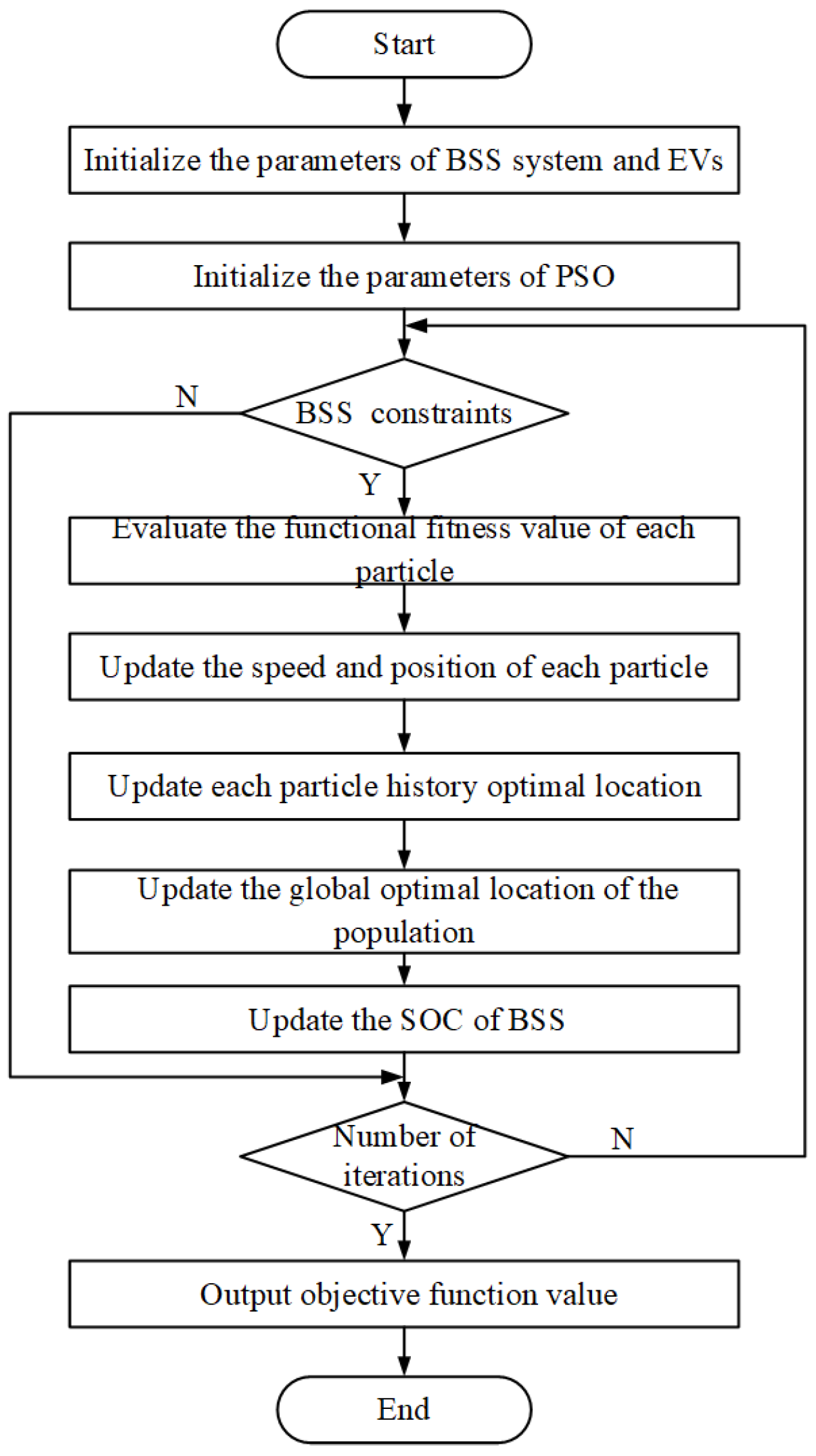
3. Optimization Algorithms
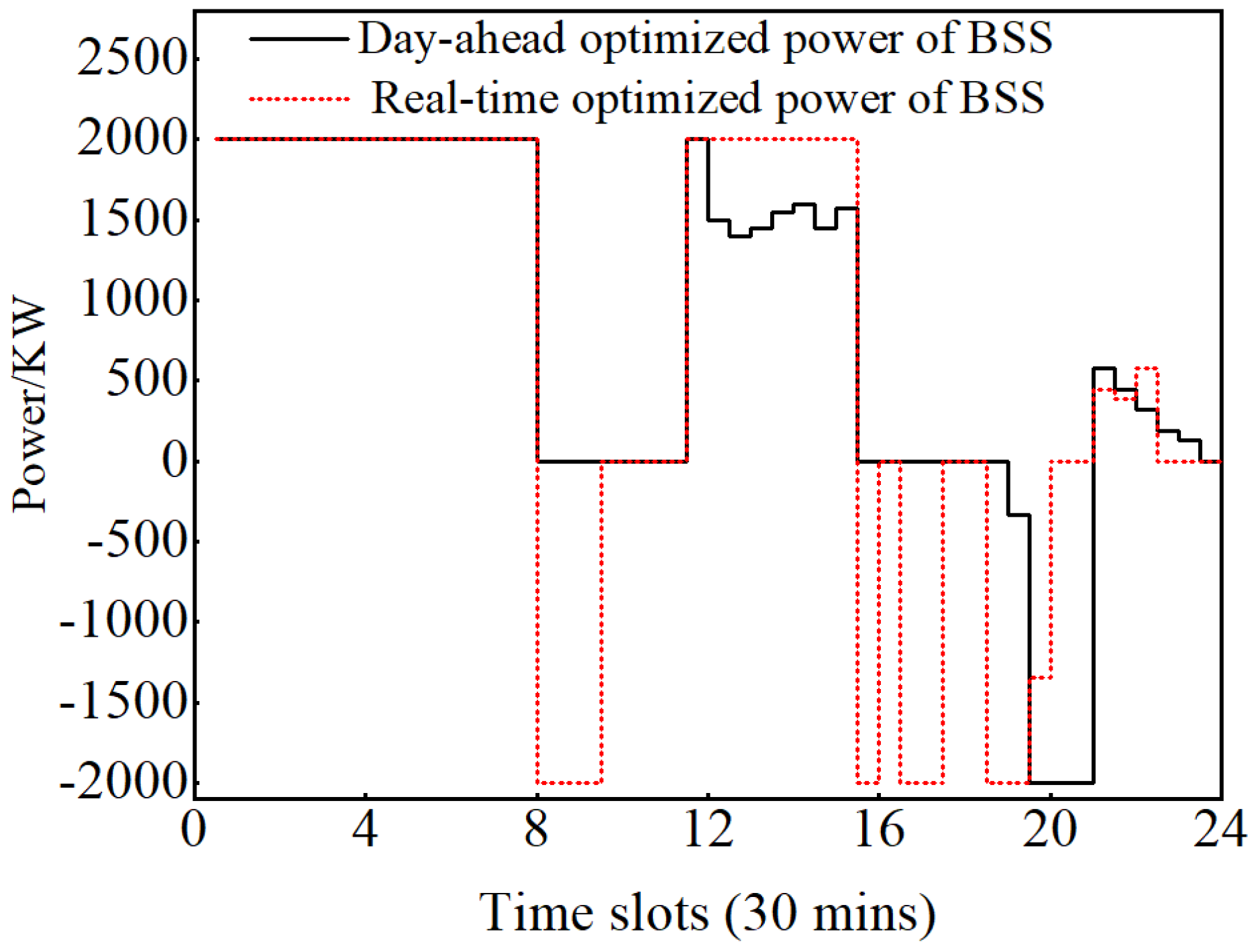
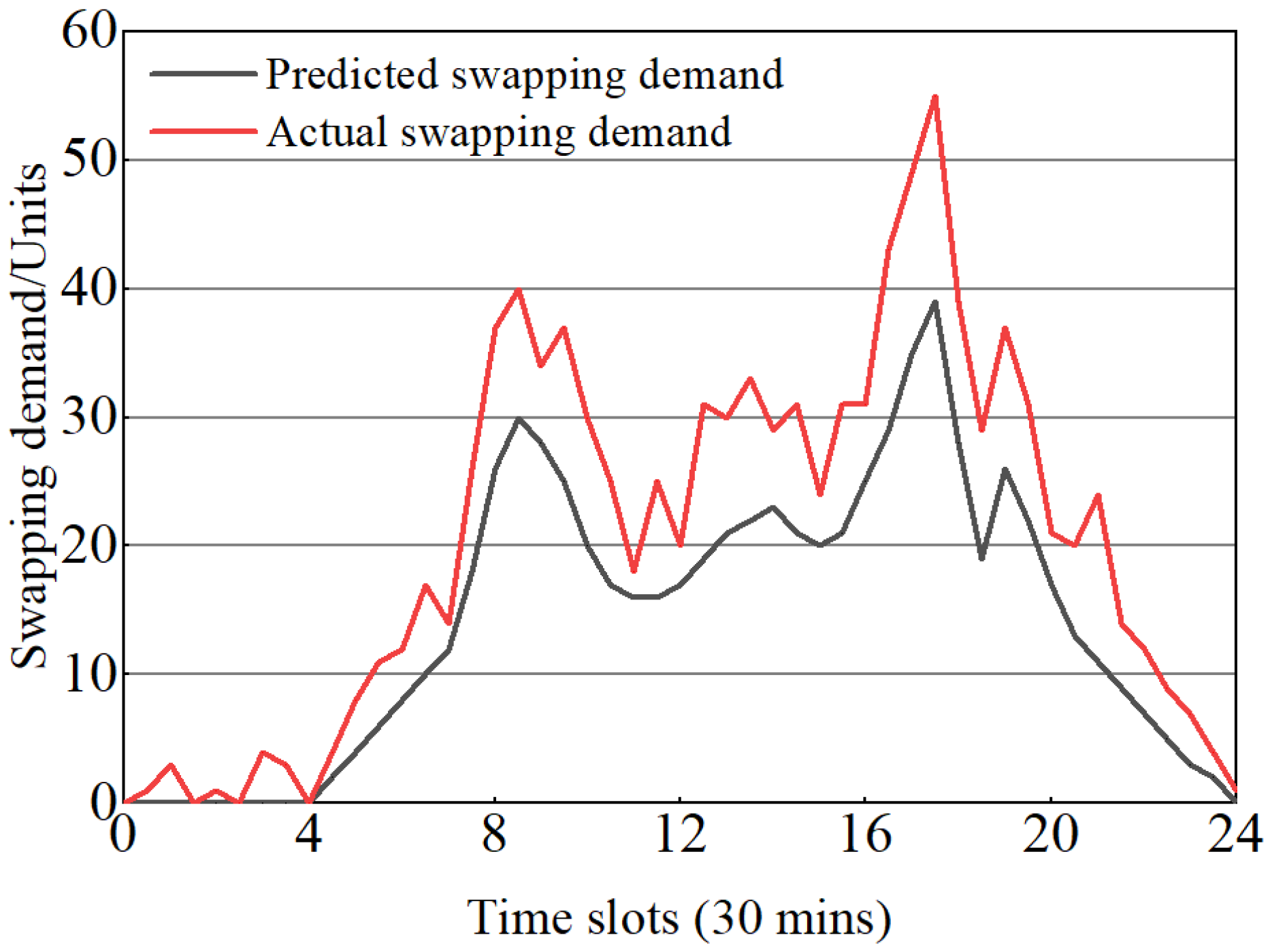
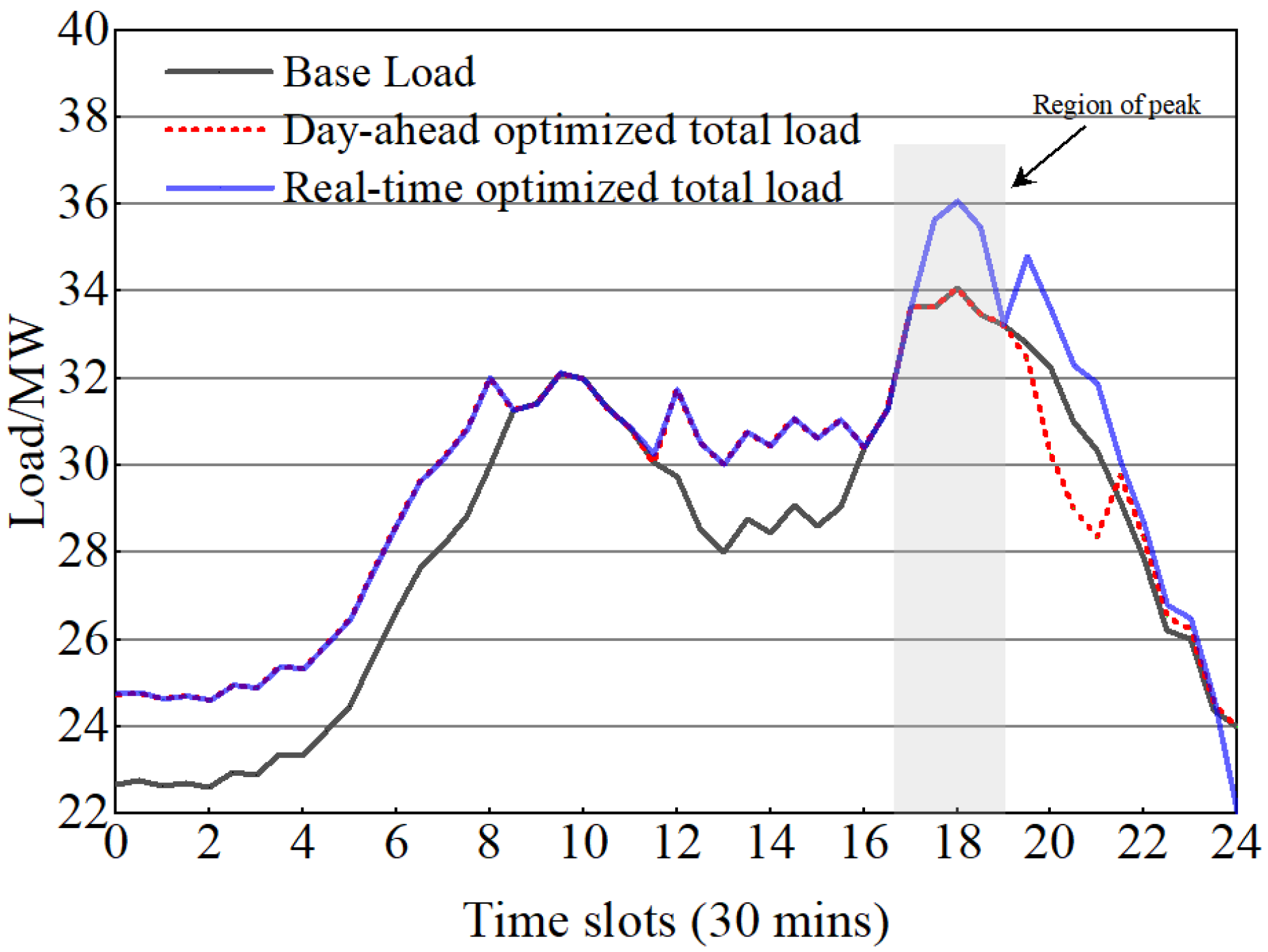
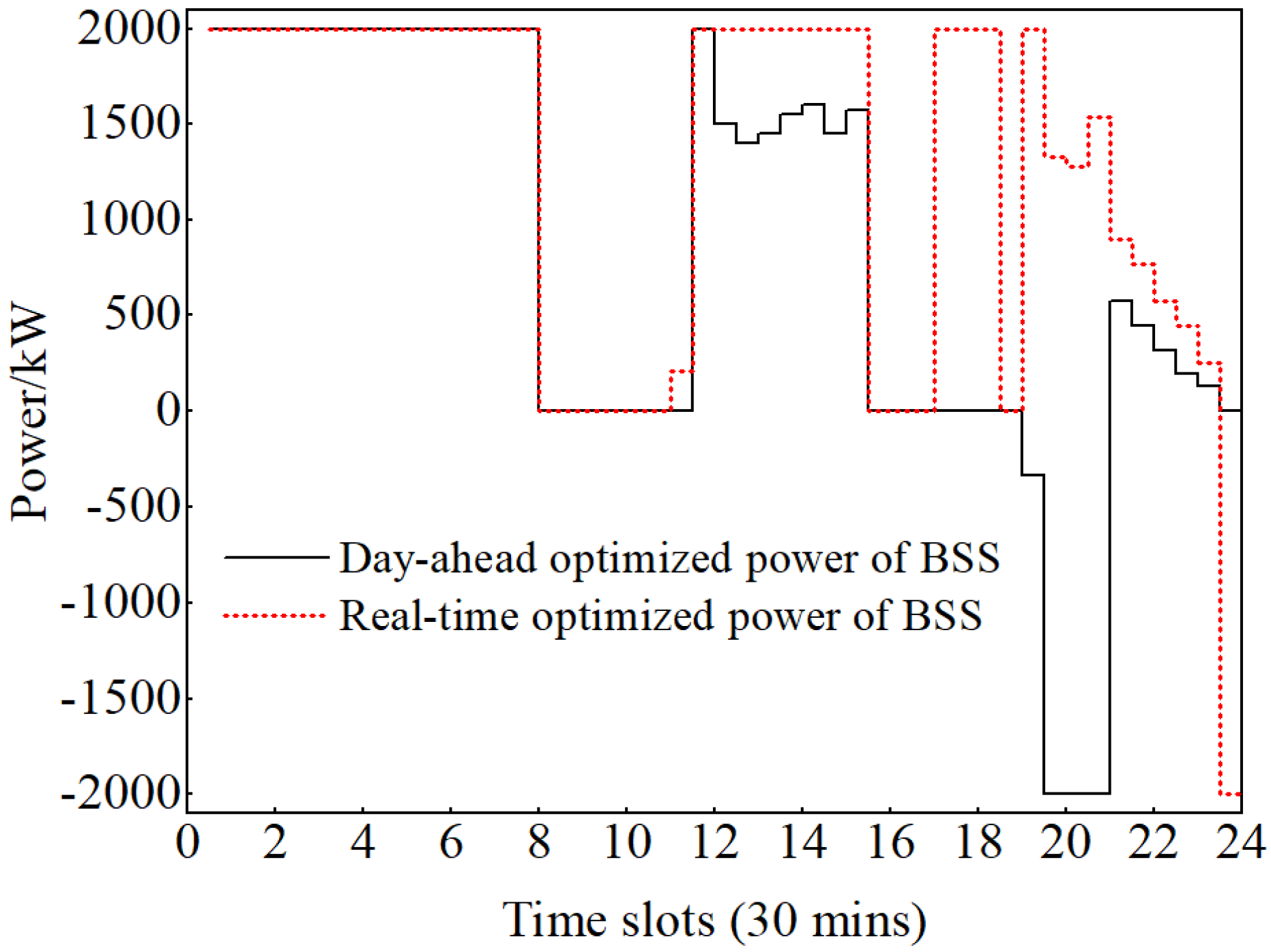
4. Simulations and Analysis
4.1. Experimental Parameters and Environment
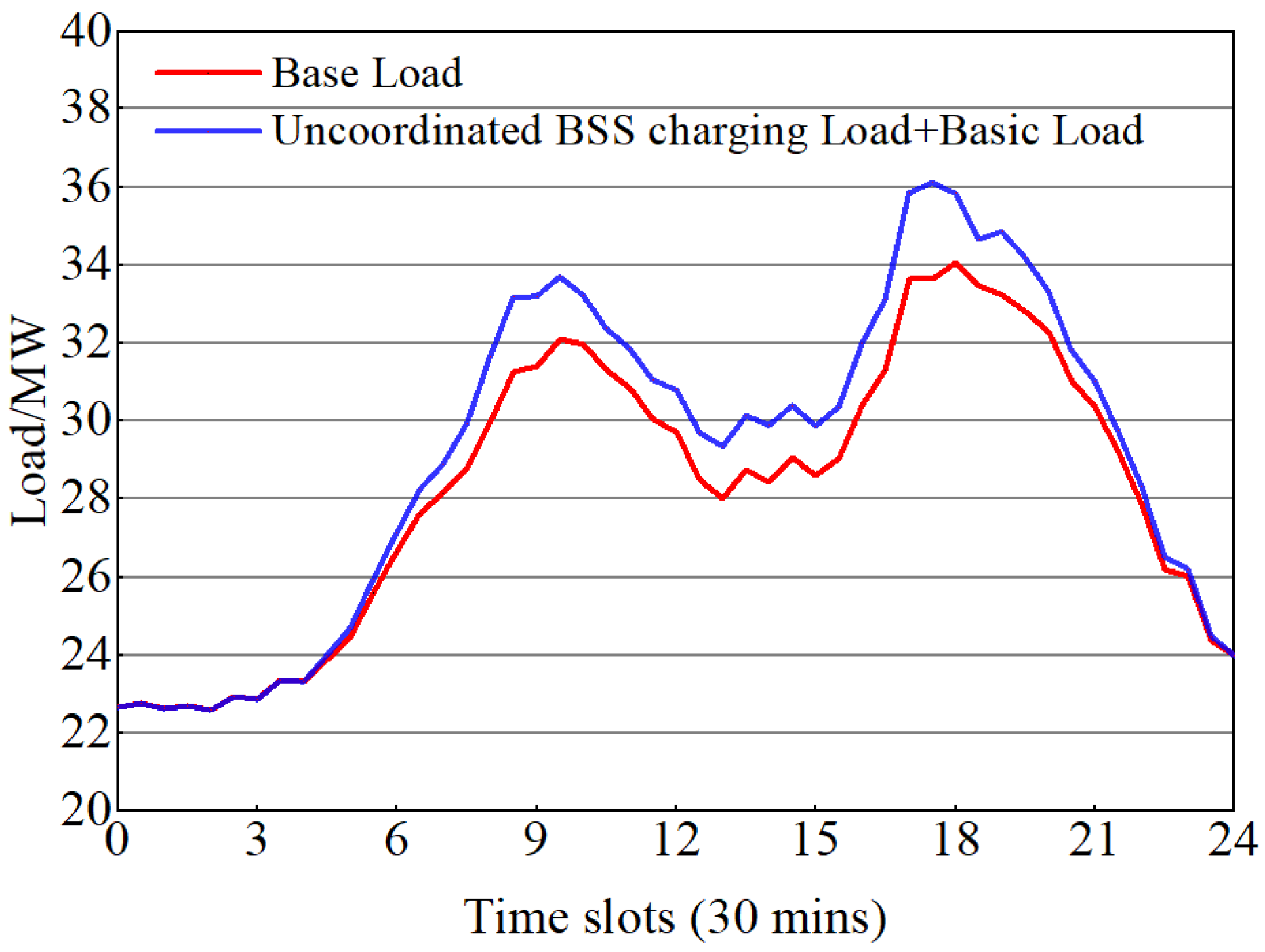
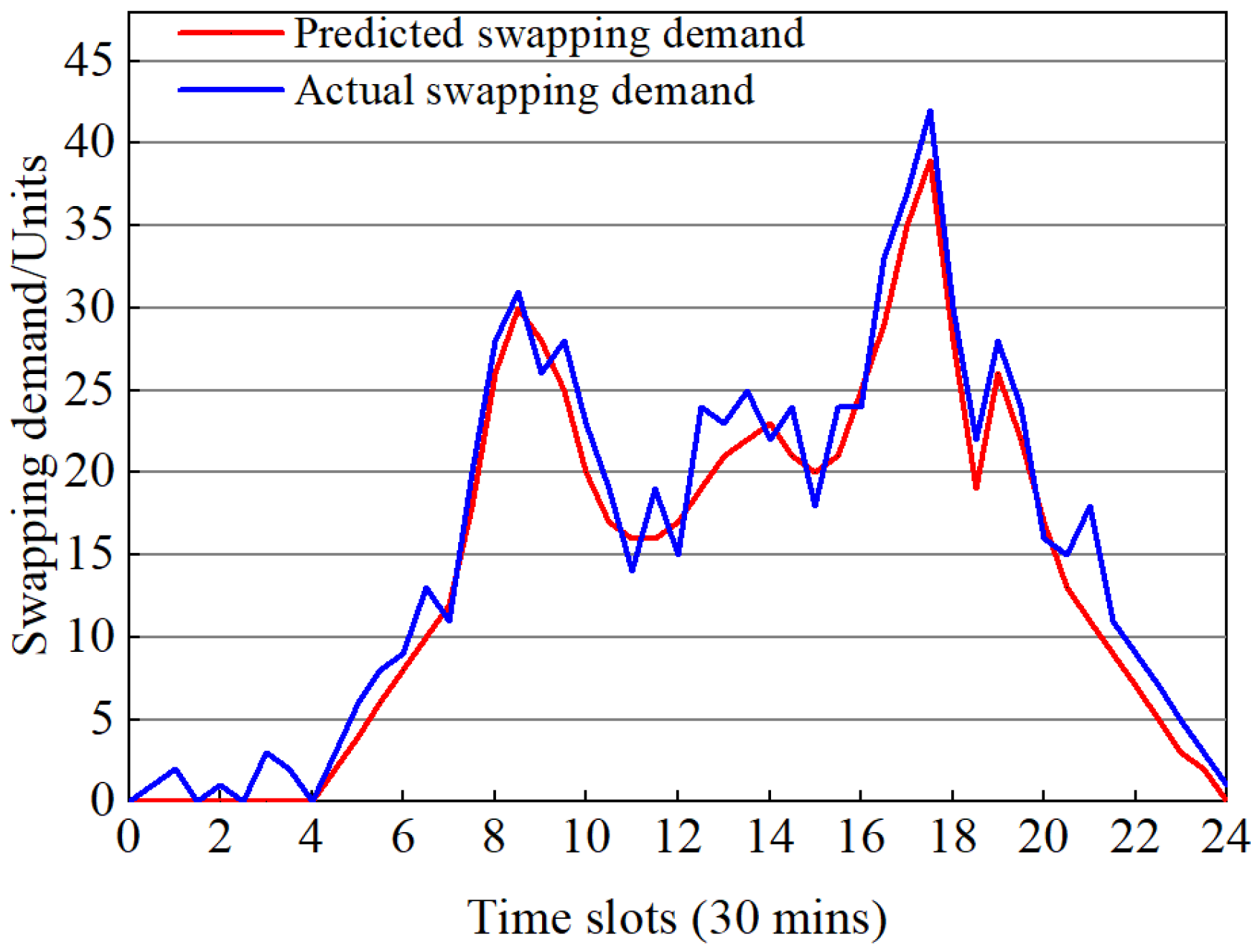
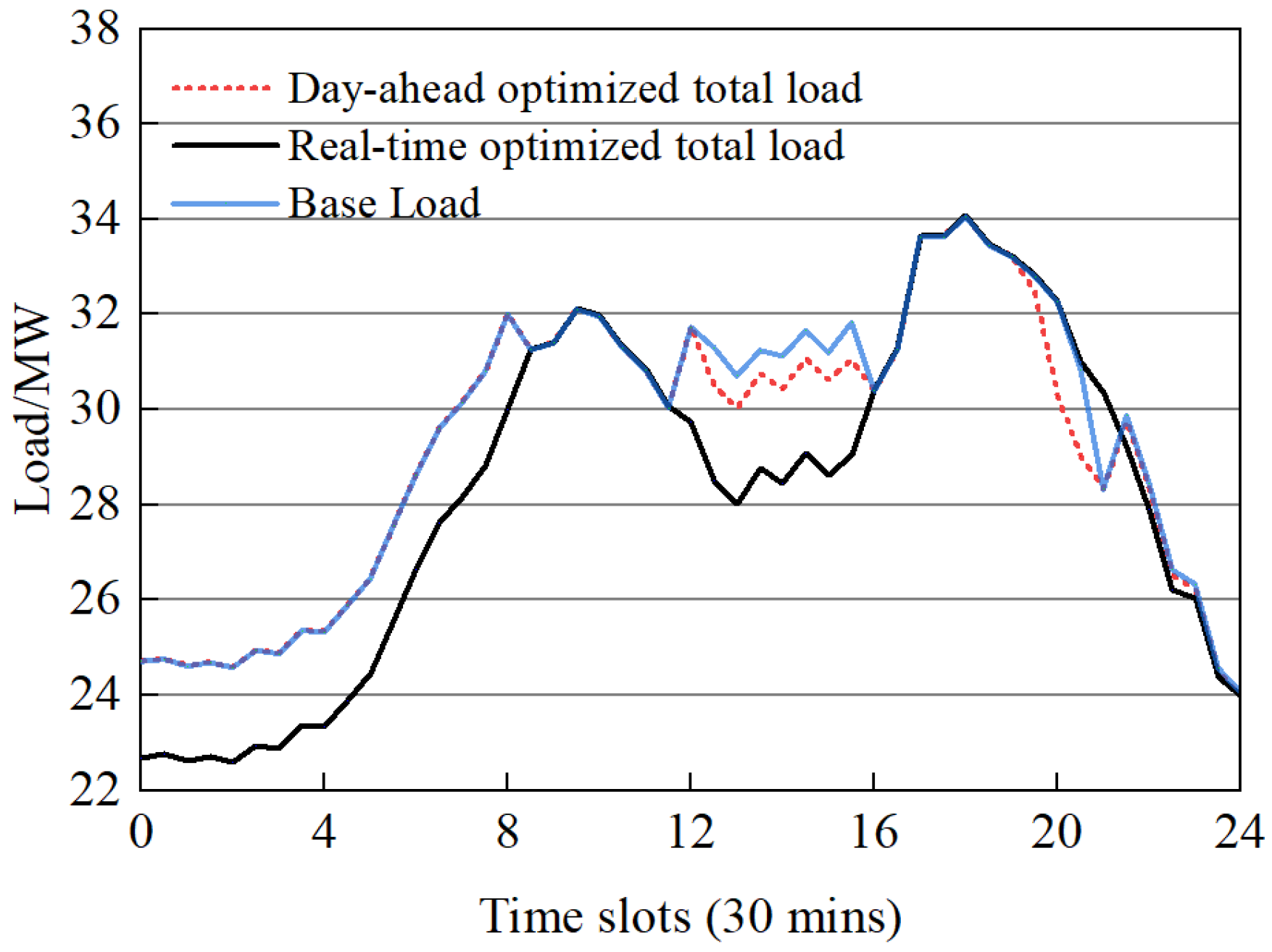
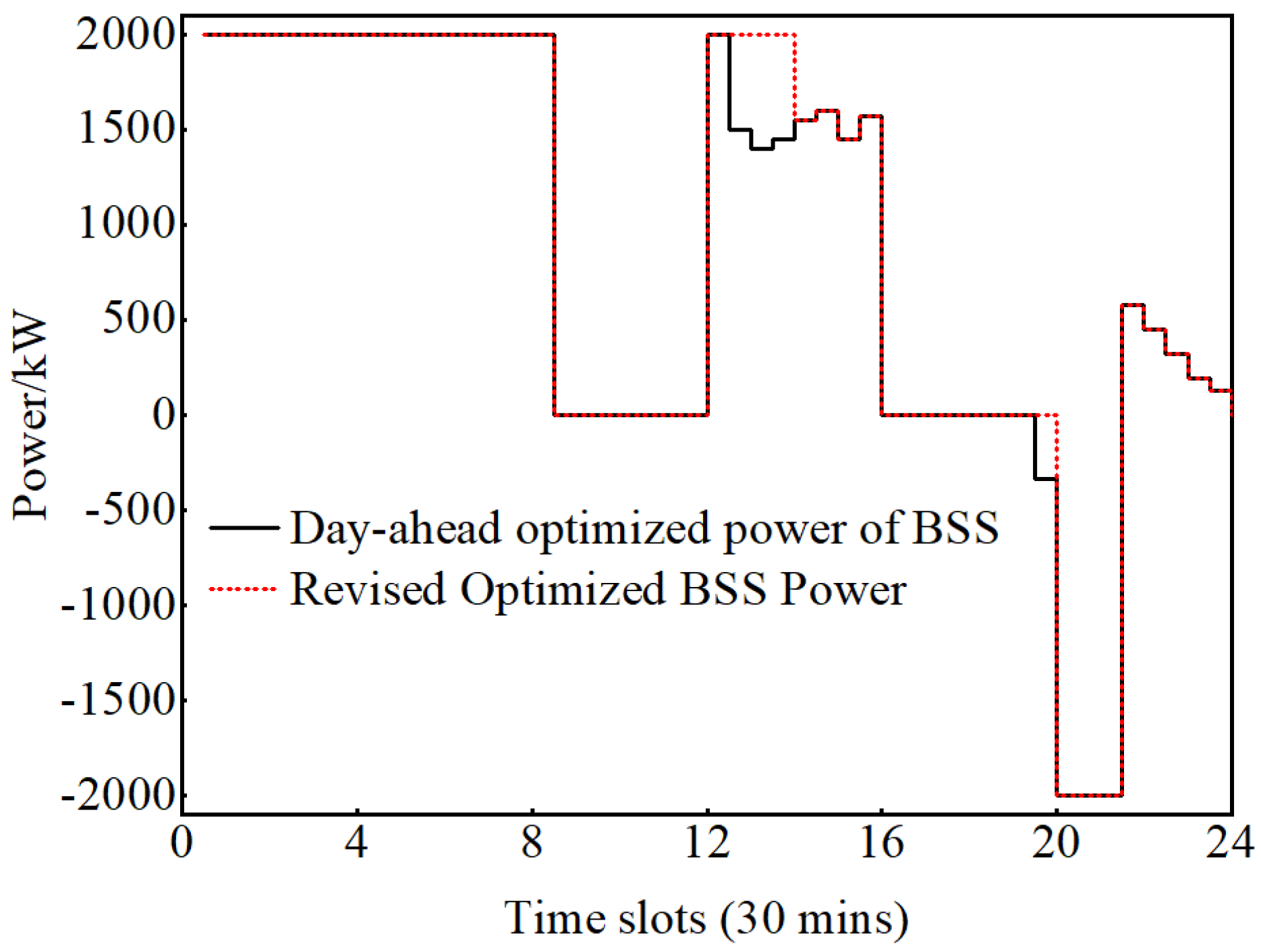
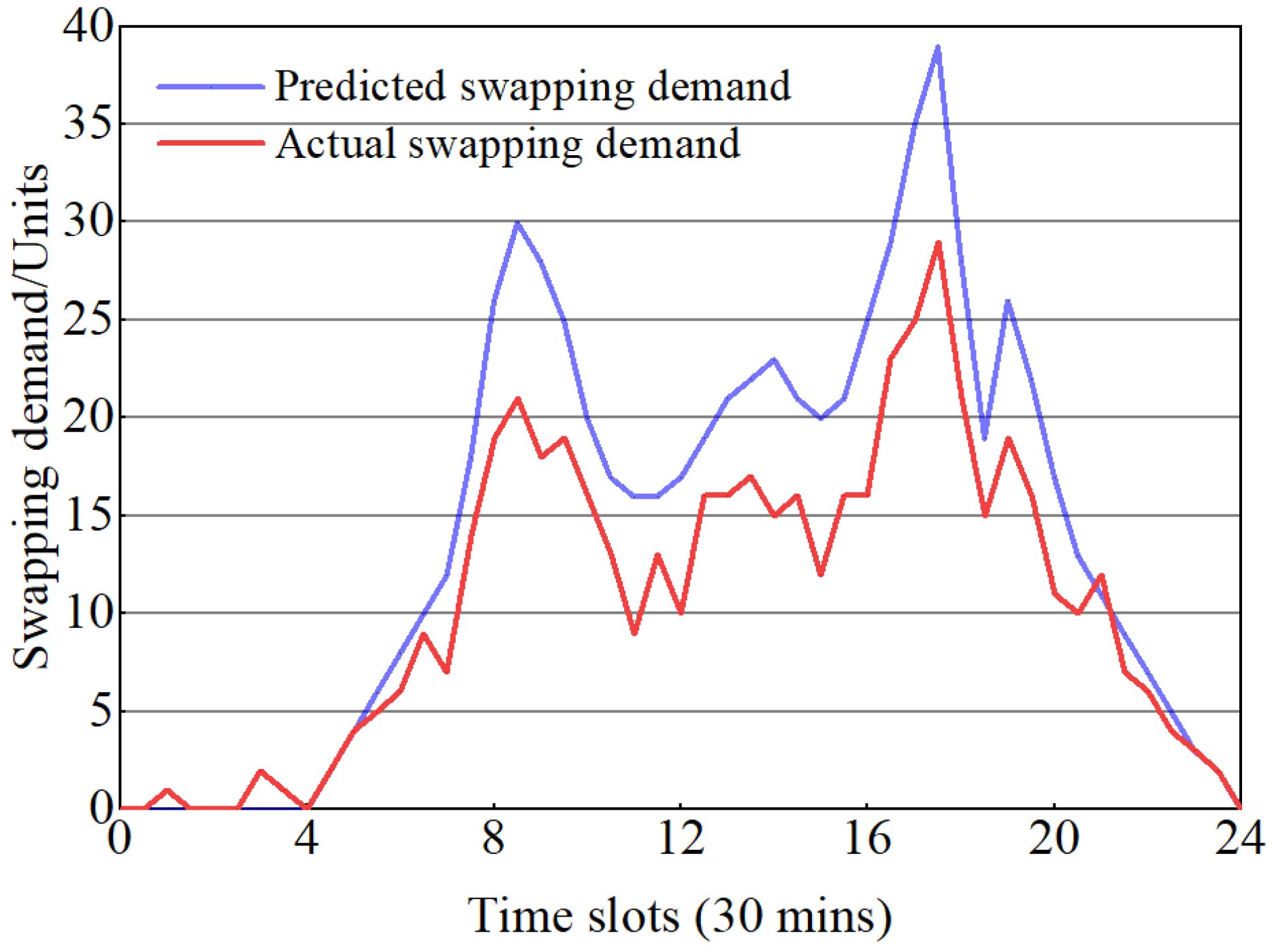
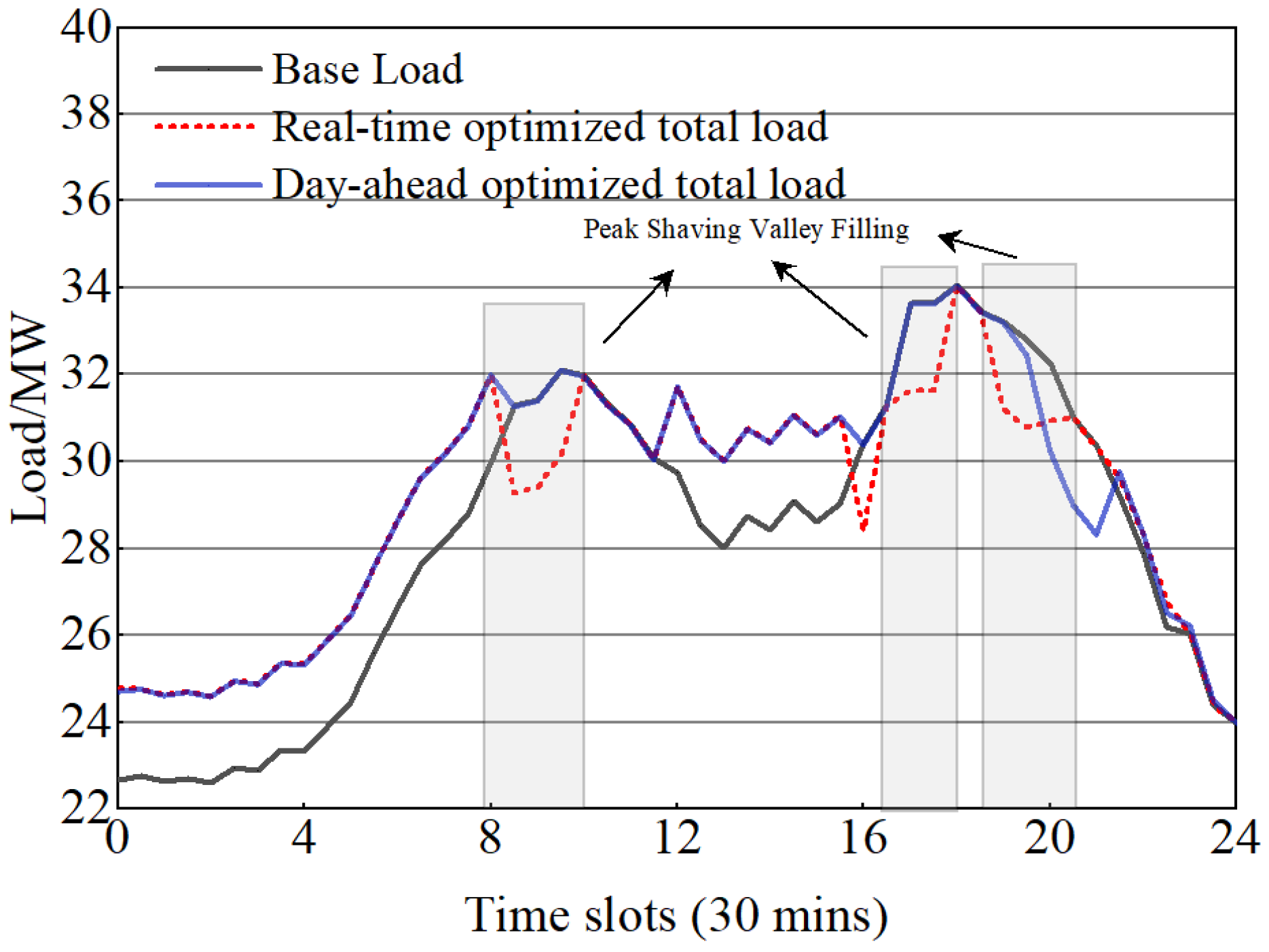
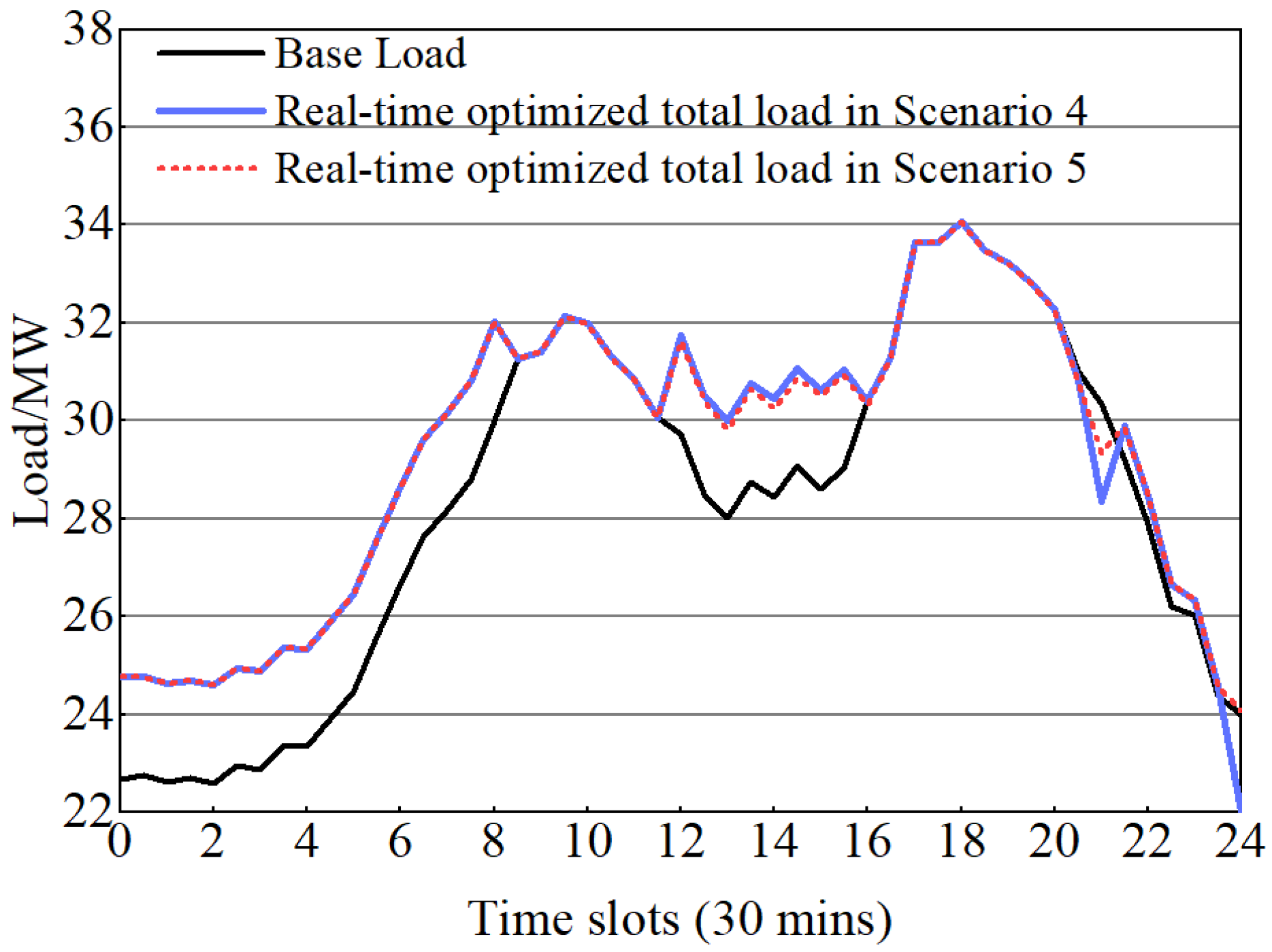
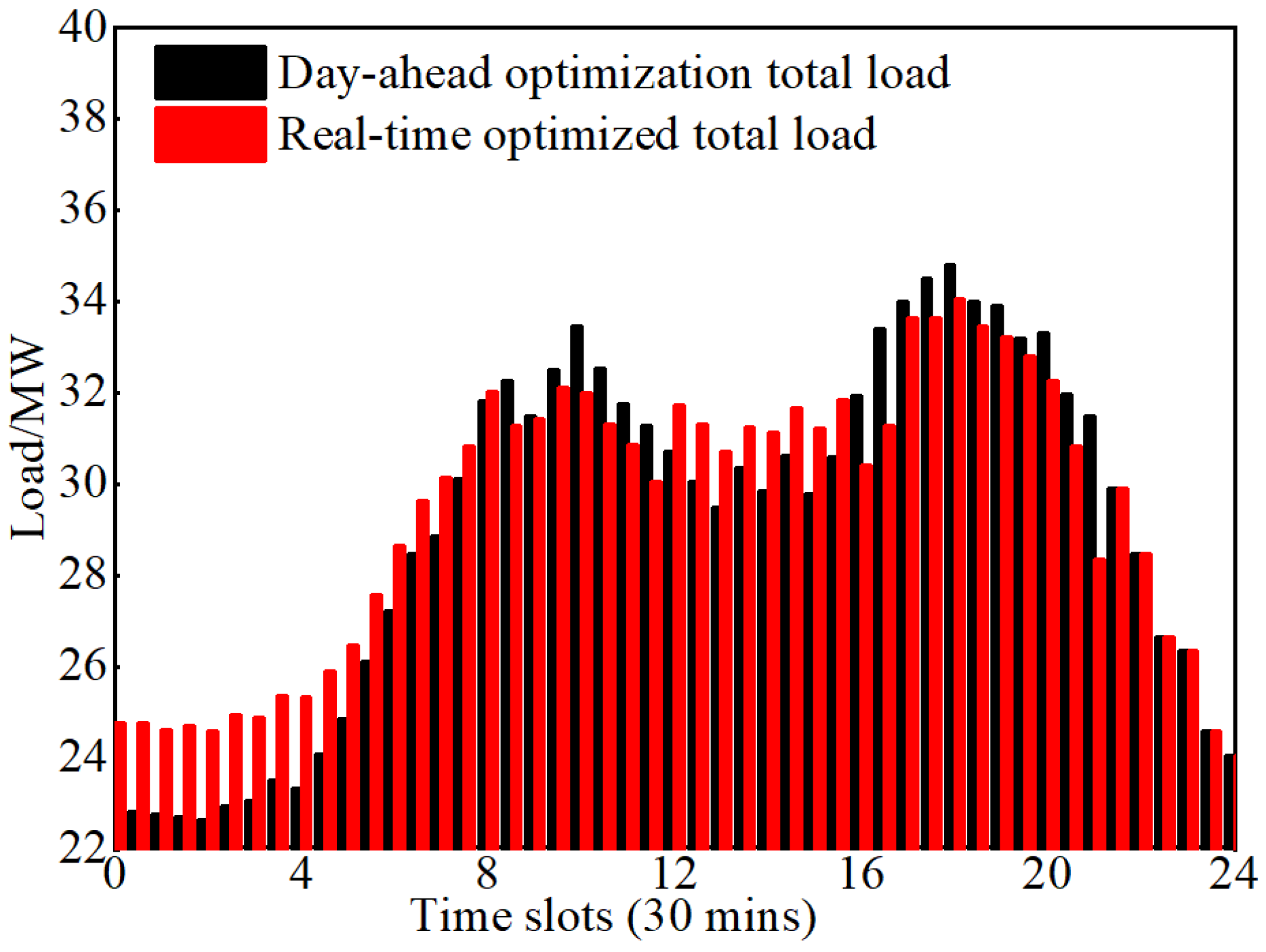
4.2. Experimental Procedure and Analysis
5. Industrial Field Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BSS | Electric Vehicle Battery Swapping Station |
| MPC | Model Predictive Control |
| PSO | Particle Swarm Optimization |
| EV | Electric Vehicle |
References
- Malozyomov, B.; Kukartsev, V.; Martyushev, N. Improvement of Hybrid Electrode Material Synthesis for Energy Accumulators Based on Carbon Nanotubes and Porous Structures. Micromachines 2023, 14, 1288. [Google Scholar] [CrossRef] [PubMed]
- Tran, M.; Khang, T.; Panchal, K. Concept review of a cloud-based smart battery management system for lithium-ion batteries: Feasibility, logistics, and functionality. Batteries 2022, 8, 19. [Google Scholar] [CrossRef] [PubMed]
- Houache, M.; Yim, C.; Karkar, Z. On the Current and Future Outlook of Battery Chemistries for Electric Vehicles—Mini Review. Batteries 2022, 8, 70. [Google Scholar] [CrossRef]
- Molaiyan, P.; Dos Reis, G.; Karuppiah, D. Recent progress in biomass-derived carbon materials for Li-ion and Na-ion batteries—A review. Batteries 2023, 9, 116. [Google Scholar] [CrossRef]
- Örüm Aydin, A.; Zajonz, F.; Günther, T. Lithium-Ion Battery Manufacturing: Industrial View on Processing Challenges, Possible Solutions and Recent Advances. Batteries 2023, 9, 555. [Google Scholar] [CrossRef]
- Lipu, M.; Mamun, A.; Ansari, S.; Miah, M. Battery management, key technologies, methods, issues, and future trends of electric vehicles: A pathway toward achieving sustainable development goals. Batteries 2022, 8, 119. [Google Scholar] [CrossRef]
- Atawi, I.; Al-Shetwi, A.; Magableh, A. Recent advances in hybrid energy storage system integrated renewable power generation: Configuration, control, applications, and future directions. Batteries 2022, 9, 29. [Google Scholar] [CrossRef]
- Benmouna, A.; Borderiou, L.; Becherif, M. Charging Stations for Large-Scale Deployment of Electric Vehicles. Batteries 2024, 10, 33. [Google Scholar] [CrossRef]
- Fan, Y.; Li, Y.; Zhao, J. Online State-of-Health Estimation for Fast-Charging Lithium-Ion Batteries Based on a Transformer–Long Short-Term Memory Neural Network. Batteries 2023, 9, 539. [Google Scholar] [CrossRef]
- Powar, V.; Singh, R. End-to-End Direct-Current-Based Extreme Fast Electric Vehicle Charging Infrastructure Using Lithium-Ion Battery Storage. Batteries 2023, 9, 169. [Google Scholar] [CrossRef]
- Horak, D.; Hainoun, A.; Neugebauer, G. Battery electric vehicle energy demand in urban energy system modeling: A stochastic analysis of added flexibility for home charging and battery swapping stations. Sustain. Energy Grids Netw. 2024, 37, 101260. [Google Scholar] [CrossRef]
- He, C.; Zhu, J.; Lan, J.; Li, S. Optimal planning of electric vehicle battery centralized charging station based on EV load forecasting. IEEE Trans. Ind. Appl. 2022, 58, 6557–6575. [Google Scholar] [CrossRef]
- He, Y.; Liu, Z.; Song, Z. Integrated charging infrastructure planning and charging scheduling for battery electric bus systems. Elsevier 2022, 111, 103437. [Google Scholar] [CrossRef]
- Alwesabi, Y.; Avishan, F.; Liu, Z. Robust strategic planning of dynamic wireless charging infrastructure for electric buses. Appl. Energy 2022, 307, 118243. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Zhi, B. Strategic investment in electric vehicle charging service: Fast charging or battery swapping. Int. J. Prod. Econ. 2024, 268, 109136. [Google Scholar] [CrossRef]
- Tan, Y.; Fukuda, H.; Li, Z.; Wang, S.; Gao, W.; Liu, Z. Does the public support the construction of battery swapping station for battery electric vehicles?-Data from Hangzhou, China. Energy Policy 2022, 163, 33–74. [Google Scholar] [CrossRef]
- Moghaddam, Z.; Ahmad, I.; Habibi, D.; Phung, Q.V. Smart charging strategy for electric vehicle charging stations. IEEE Trans. Transp. Electrif. 2017, 4, 76–88. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, X.; Yu, Z.; Zhu, X.Y.; Shi, D. A Monte Carlo simulation approach to evaluate service capacities of EV charging and battery swapping stations. IEEE Trans. Ind. Inform. 2018, 14, 3914–3923. [Google Scholar] [CrossRef]
- Wu, H. A survey of battery swapping stations for electric vehicles: Operation modes and decision scenarios. IEEE Trans. Intell. Transp. Syst. 2021, 23, 10163–10185. [Google Scholar] [CrossRef]
- Zhan, W.; Wang, Z.; Zhang, L.; Liu, P.; Cui, D.; Dorrell, D.G. A review of siting, sizing, optimal scheduling, and cost-benefit analysis for battery swapping stations. Energy 2022, 258, 124723. [Google Scholar] [CrossRef]
- Kang, Q.; Wang, J.B.; Zhou, M.C.; Ammari, A.C. Centralized charging strategy and scheduling algorithm for electric vehicles under a battery swapping scenario. IEEE Trans. Intell. Transp. Syst. 2015, 17, 659–669. [Google Scholar] [CrossRef]
- Wang, R.; Wang, P.; Xiao, G. Two-stage mechanism for massive electric vehicle charging involving renewable energy. IEEE Trans. Veh. Technol. 2016, 65, 4159–4171. [Google Scholar] [CrossRef]
- Rao, R.; Zhang, X.; Xie, J.; Ju, L. Optimizing electric vehicle users’ charging behavior in battery swapping mode. Appl. Energy 2015, 155, 547–559. [Google Scholar] [CrossRef]
- Ye, F.; Qian, Y.; Hu, R.Q. Incentive load scheduling schemes for PHEV battery exchange stations in smart grid. IEEE Syst. J. 2015, 11, 922–930. [Google Scholar] [CrossRef]
- Ding, R.; Liu, Z.; Li, X.; Hou, Y.; Sun, W.; Zhai, H.; Wei, X. Joint charging scheduling of electric vehicles with battery to grid technology in battery swapping station. Energy Rep. 2022, 8, 872–882. [Google Scholar] [CrossRef]
- Wu, H.; Pang, G.; Choy, K.; Lam, H. An optimization model for electric vehicle battery charging at a battery swapping station. IEEE Trans. Veh. Technol. 2018, 67, 881–895. [Google Scholar] [CrossRef]
- Han, S.; Han, S.; Sezaki, K. Development of an optimal vehicle-to-grid aggregator for frequency regulation. IEEE Trans. Smart Grid 2010, 1, 65–72. [Google Scholar]
- Scarabaggio, P.; Carli, R.; Cavone, G.; Dotoli, M. Smart control strategies for primary frequency regulation through electric vehicles: A battery degradation perspective. Energies 2020, 13, 4586. [Google Scholar] [CrossRef]
- Miao, B.; Deng, Q.; Zhang, L.; Huo, Z.; Liu, X. Collaborative scheduling of spare parts production and service workers driven by distributed maintenance demand. J. Manuf. Syst. 2022, 64, 261–274. [Google Scholar] [CrossRef]
- Al-Obaidi, A.; Khani, H.; Farag, H.E.Z.; Mohamed, M. Bidirectional smart charging of electric vehicles considering user preferences, peer to peer energy trade, and provision of grid ancillary services. Int. J. Electr. Power Energy Syst. 2021, 124, 106353. [Google Scholar] [CrossRef]
- Amiri, S.S.; Jadid, S.; Saboori, H. Multi-objective optimum charging management of electric vehicles through battery swapping stations. Energy 2018, 165, 549–562. [Google Scholar] [CrossRef]
- Yang, J.; Wang, W.; Ma, K. Optimal dispatching strategy for shared battery station of electric vehicle by divisional battery control. IEEE Access 2019, 7, 38224–38235. [Google Scholar] [CrossRef]
- Li, S.; He, H.; Wei, Z. Edge computing for vehicle battery management: Cloud-based online state estimation. J. Energy Storage 2022, 55, 105502. [Google Scholar] [CrossRef]
- Dreyfuss, M.; Giat, Y. Optimal allocation of spares to maximize the window fill rate in a two-echelon exchangeable-item repair system. Eur. J. Oper. Res. 2018, 270, 1053–1062. [Google Scholar] [CrossRef]
- Ahmad, F.; Saad, A.M.; Saad, A.I. Battery swapping station for electric vehicles: Opportunities and challenges. IET Smart Grid 2020, 3, 280–286. [Google Scholar] [CrossRef]
- Wu, C.; Lin, X.; Sui, Q. Two-stage self-scheduling of battery swapping station in day-ahead energy and frequency regulation markets. Appl. Energy 2021, 283, 116285. [Google Scholar] [CrossRef]
- Cui, D.; Wang, Z.; Liu, P.; Wang, S. Operation optimization approaches of electric vehicle battery swapping and charging station: A literature review. Energy 2023, 263, 126095. [Google Scholar] [CrossRef]
- Tarar, M.O.; Hassan, N.U.L.; Naqvi, I.H.; Pecht, M. Techno-Economic Framework for Electric Vehicle Battery Swapping Stations. IEEE Trans. Transp. Electrif. 2023, 9, 4458–4473. [Google Scholar] [CrossRef]
- Wu, X.; Feng, Q.; Bai, C.; Lai, C.S.; Jia, Y.; Lai, L.L. Flots d’Anosov a distributions stable et instable differentiables. Energy 2021, 224, 120106. [Google Scholar] [CrossRef]
- An, K. Battery electric bus infrastructure planning under demand uncertainty. Transp. Res. Part C Emerg. Technol. 2020, 111, 572–587. [Google Scholar] [CrossRef]
- Li, B.; Jing, D.; Zhong, H.; He, G.; Ma, Z.; Ruan, G. Centralized charging station planning for battery electric trucks considering the impacts on electricity distribution systems. Energy Rep. 2023, 9, 346–357. [Google Scholar] [CrossRef]
- Sindha, J.; Thakur, J.; Khalid, M. The economic value of hybrid battery swapping stations with second life of batteries. Clean. Energy Syst. 2023, 5, 33–74. [Google Scholar] [CrossRef]





| Parameter Type | Set Values | Parameter Type | Set Values |
|---|---|---|---|
| Charging and discharging efficiency of the charger/% | 95 | Number of Batteries/Each | 100 |
| Number of chargers/each | 100 | Battery load lower limit (SOC) | 20 |
| Charging and discharging power limit/kW | 20 | Battery Investment Cost/[yuan(kW·h)] | 1309 |
| Conversion cost of electricity exchange/[yuan(kW·h)] | 2.0 | Battery capacity/(kW·h) | 64 |
| Type of Response | Price/[yuan(kW·h)] Day-Ahead | Price/[yuan(kW·h)] Intraday |
|---|---|---|
| Peak shaving | 5 ± 0.5 | 7.5 ± 0.75 |
| Valley filling | 2 ± 0.2 | 3 ± 0.3 |
| Interval | Specific Intervals | Charging Standard |
|---|---|---|
| Peak period | 8:30–12:00; 16:00–21:00 | 1.35/yuan(kW·h) |
| Mid-peak hours | 5:00–8:30; 21:00–24:00 | 1.07/yuan(kW·h) |
| Off-peak hours | 00:00–5:00; 12:00–16:00 | 0.36/yuan(kW·h) |
| Scenario | Day-Ahead Net Income/Yuan | Day-Ahead Cost/Yuan | Intraday Net Income/Yuan | Intraday Cost/Yuan |
|---|---|---|---|---|
| 1 | 75,183 | 16,176 | 78,942 | 24,348.5 |
| 2 | 75,183 | 16,176 | 70,920 | 15,802 |
| 3 | 75,183 | 16,176 | 84,970 | 49,043 |
| 4 | 75,183 | 16,176 | 79,351 | 22,140 |
| 5 | 75,183 | 16,176 | 71,491.8 | 30,435.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, M.; Zhang, C.; Zhang, Y.; Yan, Y.; Wang, W.; An, B. A Dual-Layer MPC of Coordinated Control of Battery Load Demand and Grid-Side Supply Matching at Electric Vehicle Swapping Stations. Energies 2024, 17, 879. https://doi.org/10.3390/en17040879
Tang M, Zhang C, Zhang Y, Yan Y, Wang W, An B. A Dual-Layer MPC of Coordinated Control of Battery Load Demand and Grid-Side Supply Matching at Electric Vehicle Swapping Stations. Energies. 2024; 17(4):879. https://doi.org/10.3390/en17040879
Chicago/Turabian StyleTang, Minan, Chenchen Zhang, Yaqi Zhang, Yaguang Yan, Wenjuan Wang, and Bo An. 2024. "A Dual-Layer MPC of Coordinated Control of Battery Load Demand and Grid-Side Supply Matching at Electric Vehicle Swapping Stations" Energies 17, no. 4: 879. https://doi.org/10.3390/en17040879
APA StyleTang, M., Zhang, C., Zhang, Y., Yan, Y., Wang, W., & An, B. (2024). A Dual-Layer MPC of Coordinated Control of Battery Load Demand and Grid-Side Supply Matching at Electric Vehicle Swapping Stations. Energies, 17(4), 879. https://doi.org/10.3390/en17040879








