An Experimental and Numerical Study on the Cavitation and Spray Characteristics of Micro-Orifice Injectors under Low-Pressure Conditions
Abstract
:1. Introduction
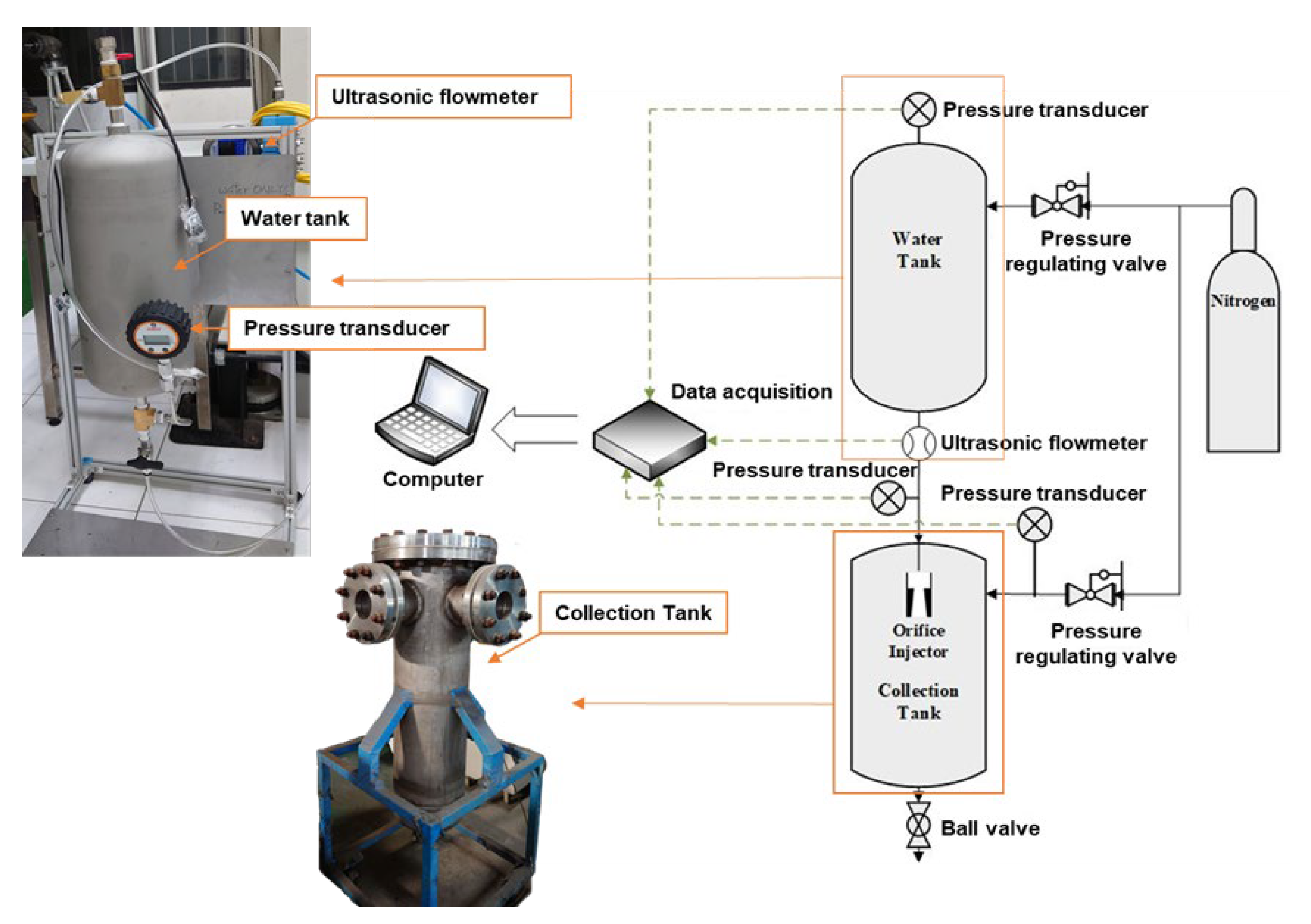
2. Experimental Setup
3. Numerical Model
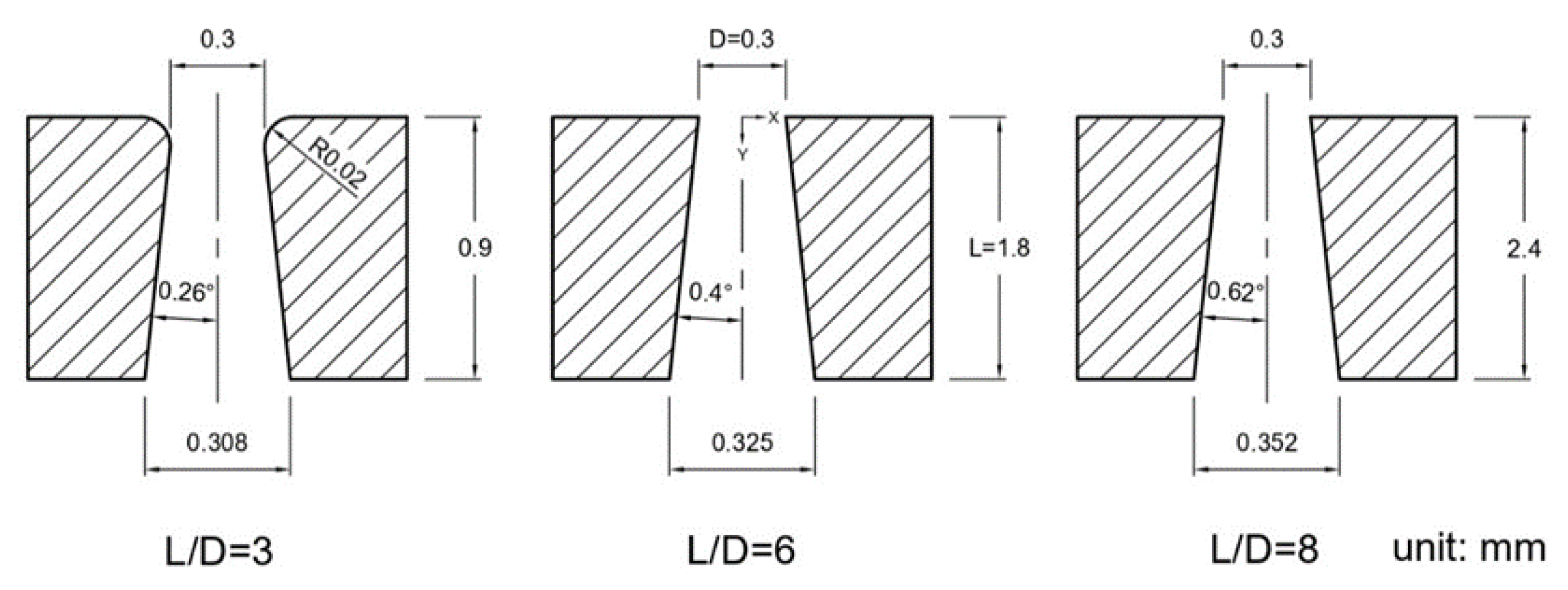
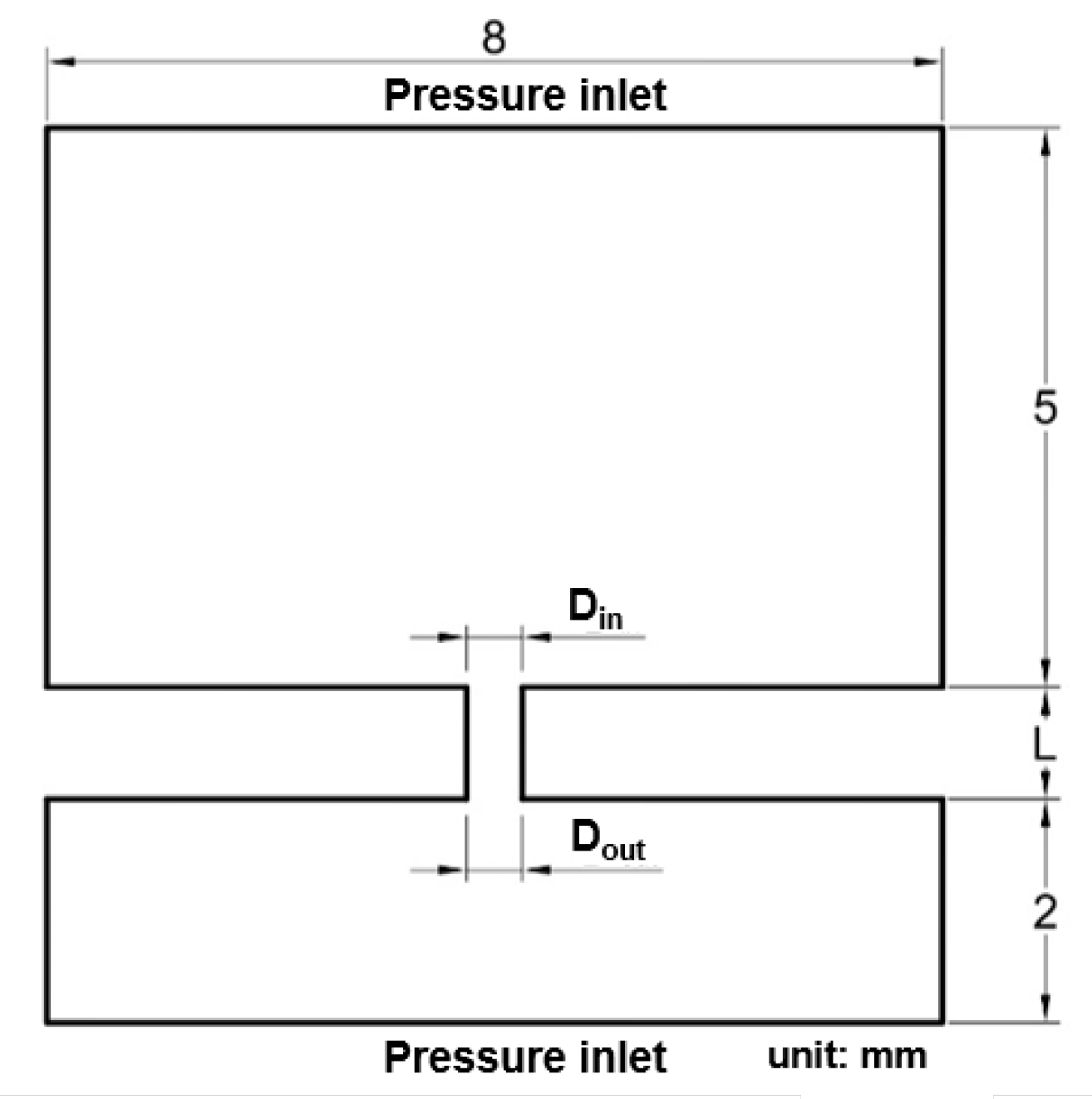
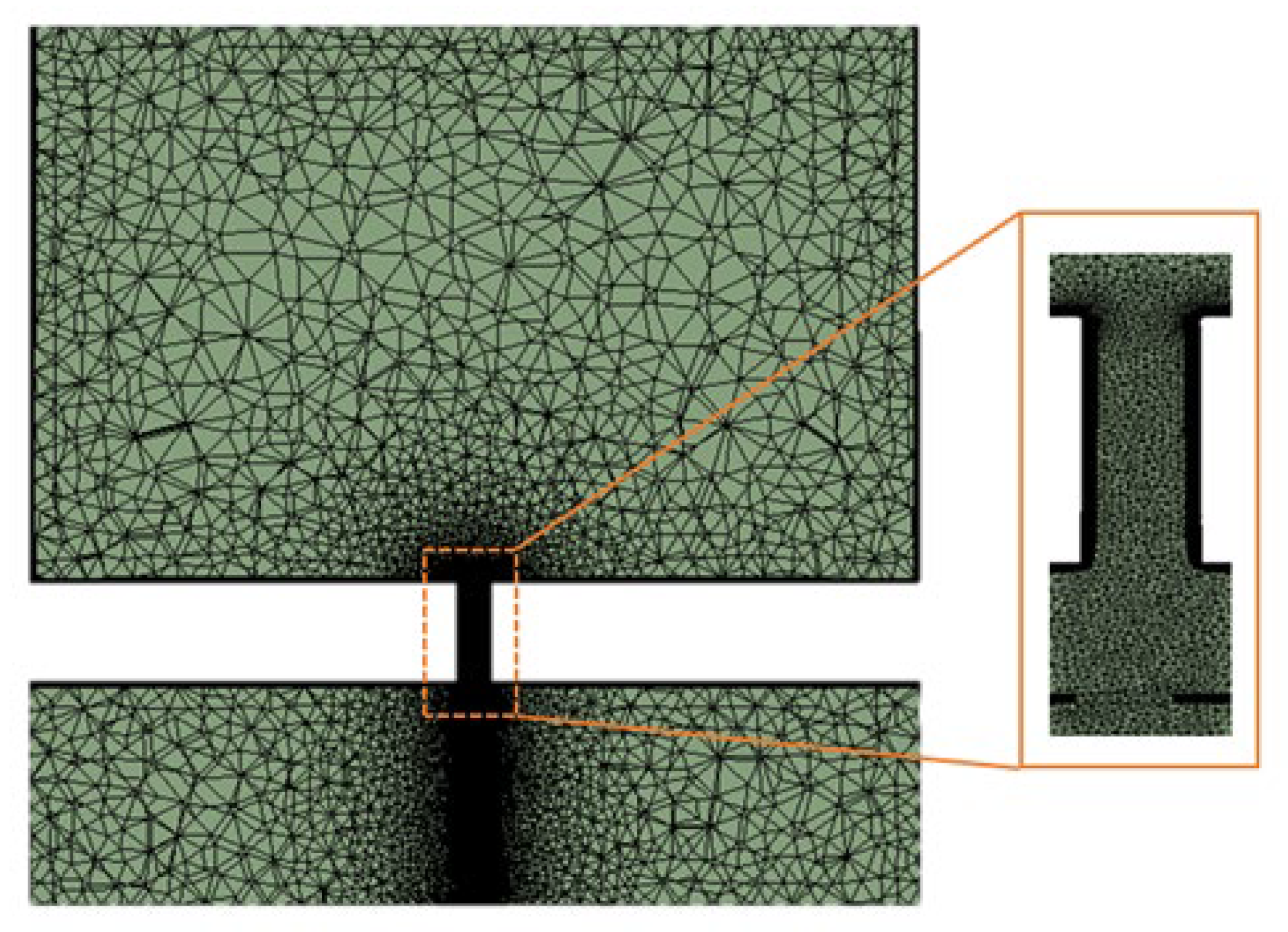
3.1. Assumptions and Computational Domain
3.2. Governing Equation
3.3. Turbulence Model
3.4. Boundary and Initial Conditions
3.5. Numerical Calculation Validation
4. Results and Discussion
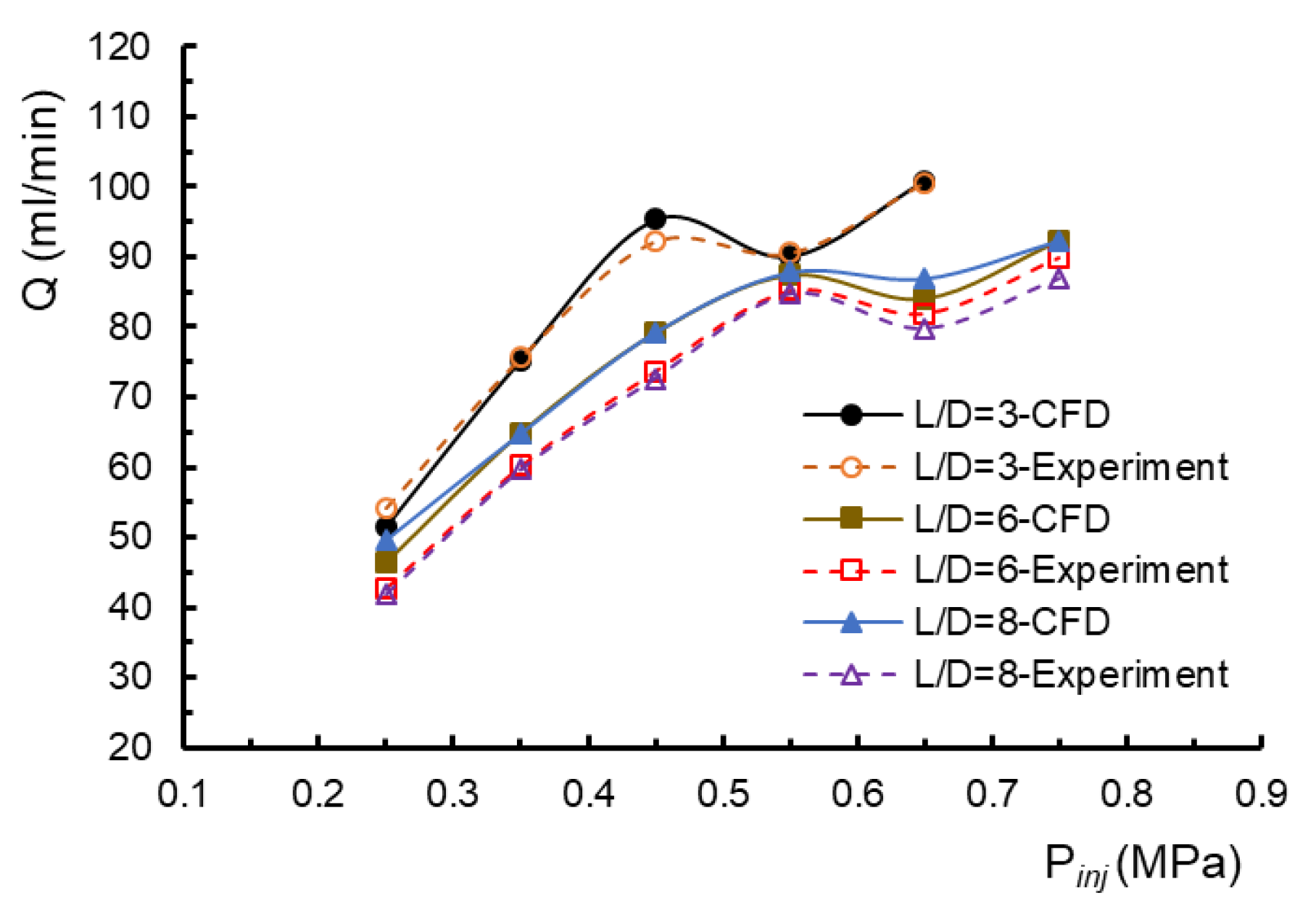
4.1. Model Validation
4.2. Results of Research on Water
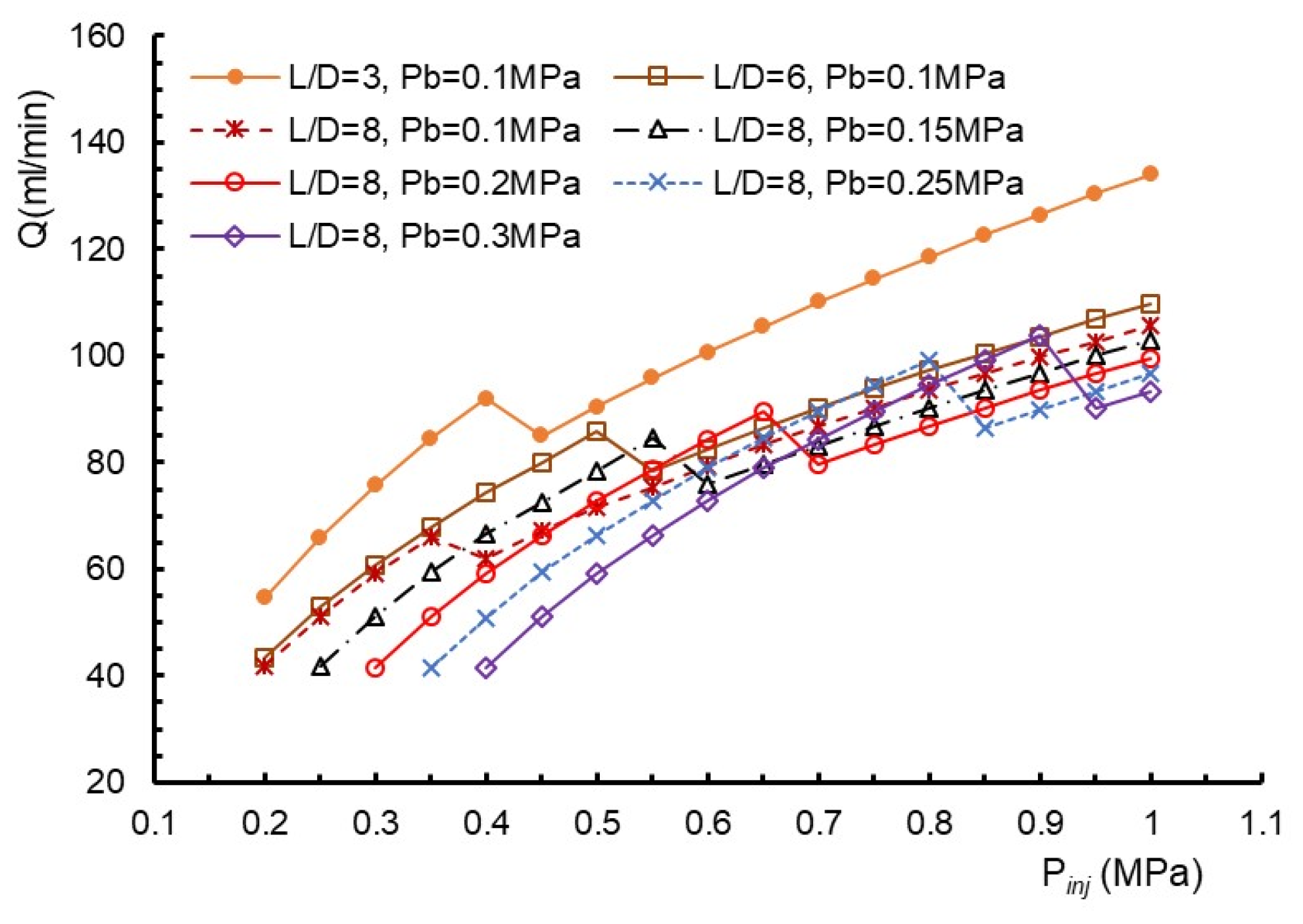
4.2.1. Experimental Results for Flow Rate Characteristics
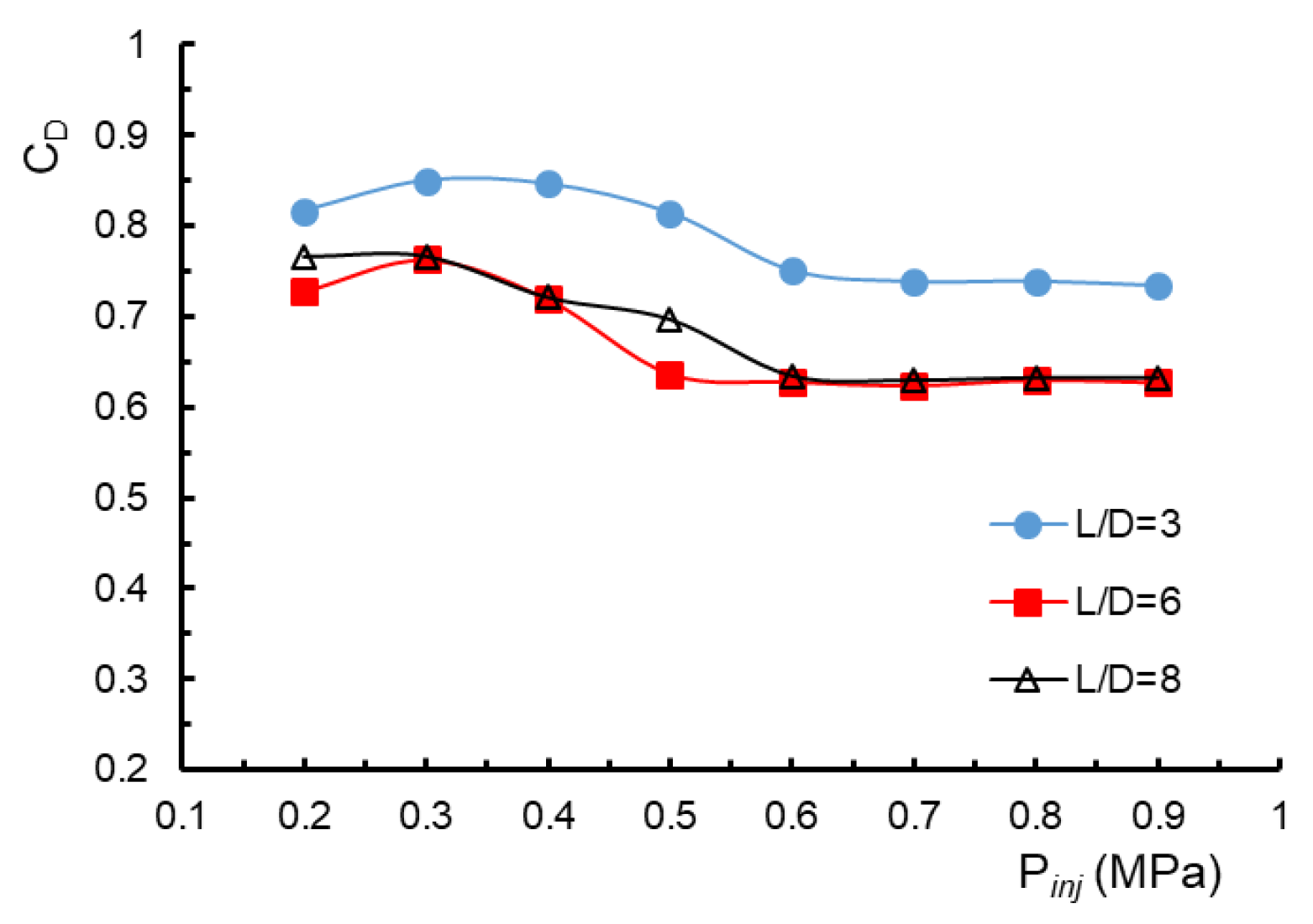
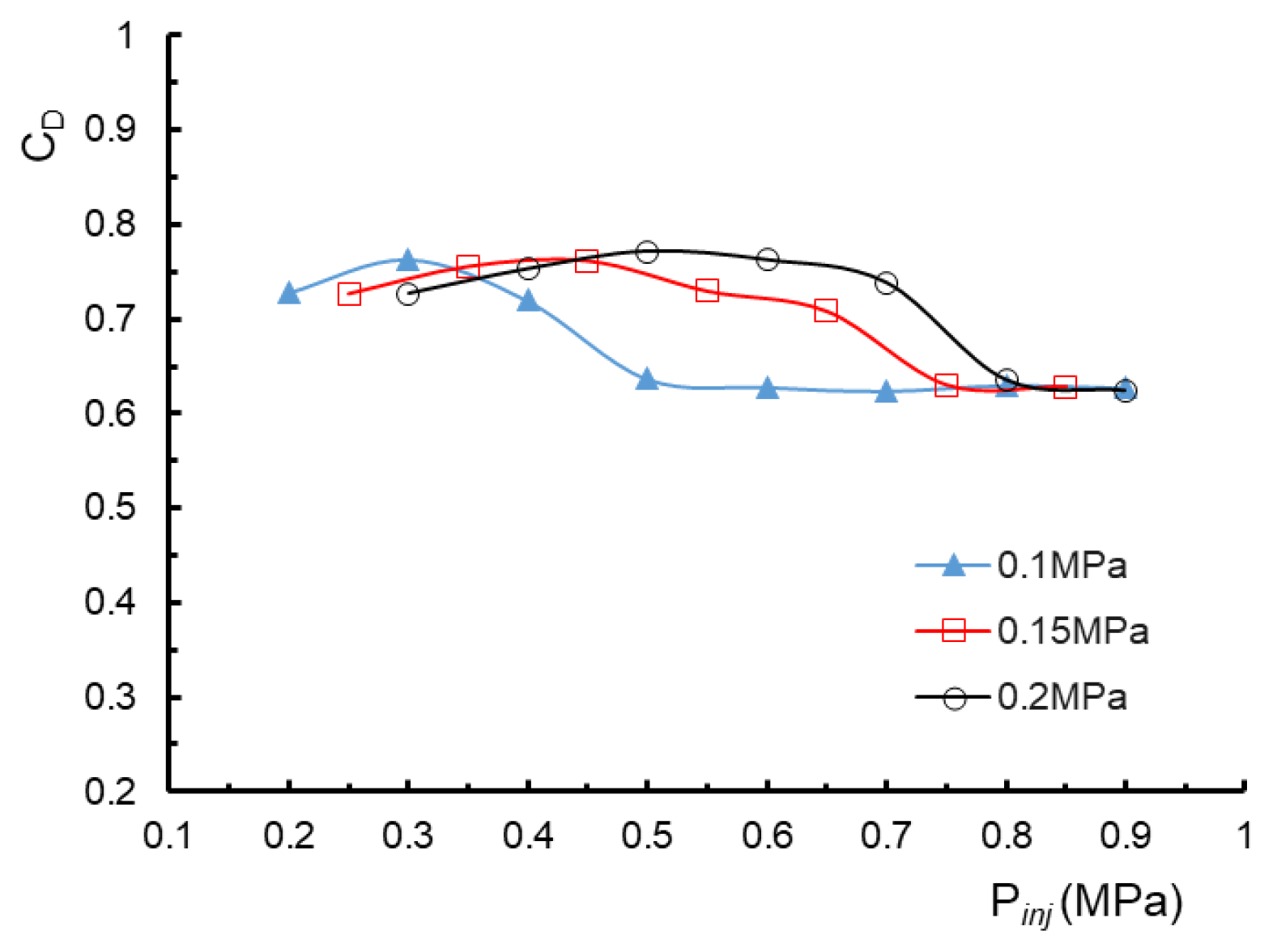
4.2.2. Characteristics of the Discharge Coefficient
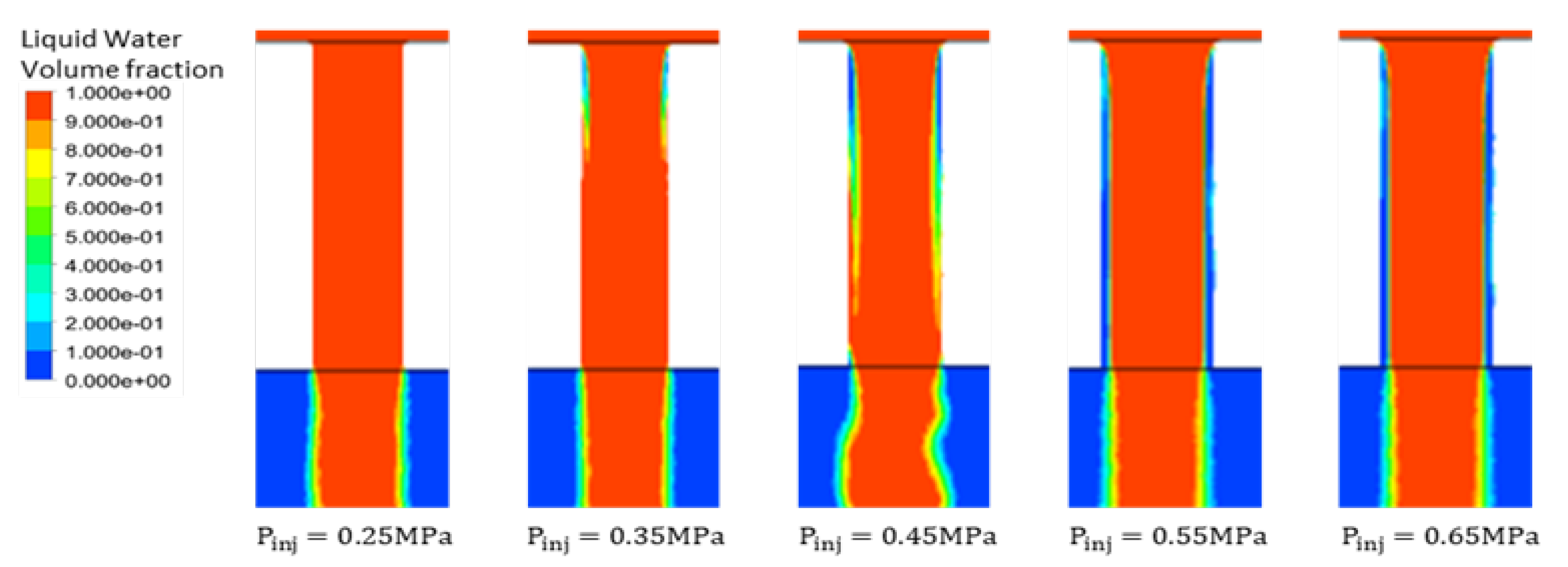
4.2.3. Numerical Results for the Internal Flow Pattern and Spray Angle
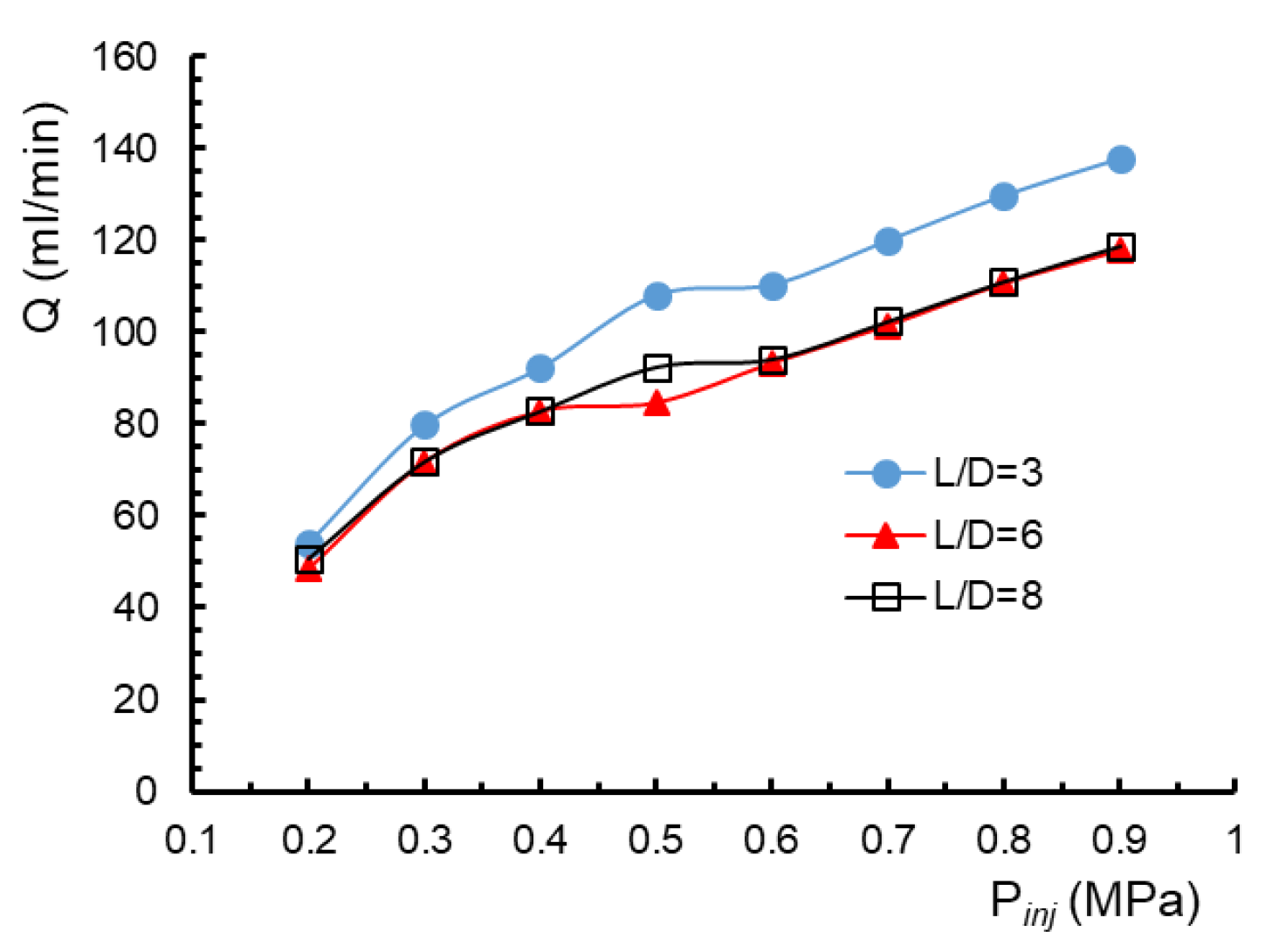
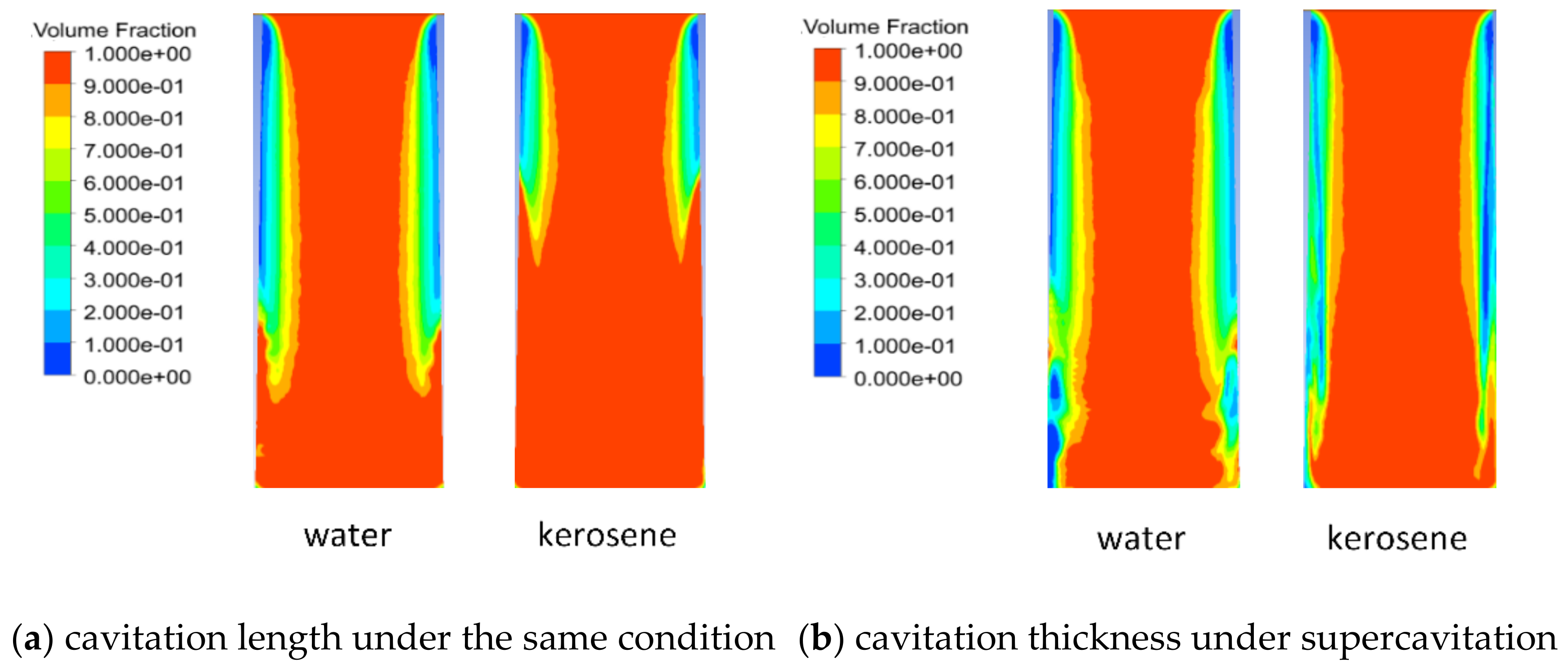
4.3. Numerical Results for Kerosene Fuel
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bergwerk, W. Flow Pattern in Diesel Nozzle Spray Holes. Proc. Inst. Mech. Eng. 1959, 173, 655–660. [Google Scholar] [CrossRef]
- Nurick, W.H. Orifice Cavitation and Its Effect on Spray Mixing. J. Fluids Eng. 1976, 98, 681–687. [Google Scholar] [CrossRef]
- Suh, H.K.; Lee, C.S. Effect of Cavitation in Nozzle Orifice on the Diesel Fuel Atomization Characteristics. Int. J. Heat Fluid Flow 2008, 29, 1001–1009. [Google Scholar] [CrossRef]
- Chemloul, N.S. Experimental Study of Cavitation and Hydraulic Flip Effects on Liquid Jet Characteristics into Crossflows. J. Appl. Fluid Mech. 2012, 5, 33–43. [Google Scholar]
- Jung, K.; Khil, T.; Yoon, Y. Effects of Orifice Internal Flow on Breakup Characteristics of like-Doublet Injectors. J. Propul. Power 2006, 22, 653–660. [Google Scholar] [CrossRef]
- Sou, A.; Hosokawa, S.; Tomiyama, A. Effects of Cavitation in a Nozzle on Liquid Jet Atomization. Int. J. Heat Mass Transf. 2007, 50, 3575–3582. [Google Scholar] [CrossRef]
- Asi, O. Failure of a Diesel Engine Injector Nozzle by Cavitation Damage. Eng. Fail. Anal. 2006, 13, 1126–1133. [Google Scholar] [CrossRef]
- Abderrezzak, B.; Huang, Y. Investigation of the Effect of Cavitation in Nozzles with Different Length to Diameter Ratios on Atomization of a Liquid Jet. J. Therm. Sci. Eng. Appl. 2017, 9, 031014. [Google Scholar] [CrossRef]
- Ro, S.; Kim, B.; Park, S.; Kim, Y.B.; Choi, B.; Jung, S.; Lee, D.W. Internal Cavitating Flow and External Spray Behavior Characteristics According to Length-to-Width Ratio of Transparent Nozzle Orifice. Int. J. Automot. Technol. 2020, 21, 181–188. [Google Scholar] [CrossRef]
- Kiaoulias, D.N.; Travis, T.A.; Moore, J.D.; Risha, G.A. Evaluation of Orifice Inlet Geometries on Single Liquid Injectors Through Cold-Flow Experiments. Exp. Therm Fluid Sci. 2019, 103, 78–88. [Google Scholar] [CrossRef]
- Fox, T.A.; Stark, J. Characteristics of Miniature Short-Tube Orifice Flows. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1989, 203, 351–358. [Google Scholar] [CrossRef]
- He, Z.; Guo, G.; Tao, X.; Zhong, W.; Leng, X.; Wang, Q. Study of the Effect of Nozzle Hole Shape on Internal Flow and Spray Characteristics. Int. Commun. Heat Mass Transfer 2016, 71, 1–8. [Google Scholar] [CrossRef]
- Simpson, A.; Ranade, V.V. Modelling of Hydrodynamic Cavitation with Orifice: Influence of different orifice designs. Chem. Eng. Res. Des. 2018, 136, 698–711. [Google Scholar] [CrossRef]
- Kim, B.; Park, S. Effect of Orifice Inlet Roundness on Internal Flow and External Spray Characteristics in Enlarged Nozzle with Single-Passage. Exp. Therm Fluid Sci. 2019, 109, 109875. [Google Scholar] [CrossRef]
- Omelyanyuk, M.; Ukolov, A.; Pakhlyan, I.; Bukharin, N.; El Hassan, M. Experimental and Numerical Study of Cavitation Number Limitations for Hydrodynamic Cavitation Inception Prediction. Fluids 2022, 7, 198. [Google Scholar] [CrossRef]
- Yu, B.; Fu, P.F.; Zhang, T.; Zhou, H.C. The Influence of Back Pressure on the Flow Discharge Coefficients of Plain Orifice Nozzle. Int. J. Heat Fluid Flow 2013, 44, 509–514. [Google Scholar] [CrossRef]
- Tharakan, T.J.; Rafeeque, T.A. The Role of Backpressure on Discharge Coefficient of Sharp Edged Injection Orifices. Aerosp. Sci. Technol. 2016, 49, 269–275. [Google Scholar] [CrossRef]
- Prasetya, R.; Sou, A.; Wada, Y.; Yokohata, H. Effects of Ambient Pressure on Cavitation in the Nozzle and the Discharged Liquid Jet. J. Fluid Sci. Technol. 2019, 14, JFST0005. [Google Scholar] [CrossRef]
- Payri, R.; Salvador, F.J.; Gimeno, J.; Venegas, O. Study of Cavitation Phenomenon Using Different Fuels in a Transparent Nozzle by Hydraulic Characterization and Visualization. Exp. Therm Fluid Sci. 2013, 44, 235–244. [Google Scholar] [CrossRef]
- He, Z.; Shao, Z.; Wang, Q.; Zhong, W.; Tao, X. Experimental Study of Cavitating Flow Inside Vertical Multi-Hole Nozzles with Different Length–Diameter Ratios Using Diesel and Biodiesel. Exp. Therm Fluid Sci. 2015, 60, 252–262. [Google Scholar] [CrossRef]
- He, Z.; Hu, B.; Wang, J.; Guo, G.; Feng, Z.; Wang, C.; Duan, L. The Cavitation Flow and Spray Characteristics of Gasoline-Diesel Blends in the nozzle of a High-Pressure Common-Rail Injector. Fuel 2023, 350, 128786. [Google Scholar] [CrossRef]
- Pratama, R.H.; Huang, W.; Moon, S.; Wang, J.; Murayama, K.; Taniguchi, H.; Arima, T.; Sasaki, Y.; Arioka, A. Hydraulic Flip in a Gasoline Direct Injection Injector and its Effect on Injected Spray. Fuel 2022, 310, 122303. [Google Scholar] [CrossRef]
- Jia, M.; Xie, M.; Liu, H.; Lam, W.-H.; Wang, T. Numerical Simulation of Cavitation in the Conical-Spray Nozzle for Diesel Premixed Charge Compression Ignition Engines. Fuel 2011, 90, 2652–2661. [Google Scholar] [CrossRef]
- Sadegharani, H.; Haghshenasfard, M.; Salimi, J. Numerical Study on the Effect of Cavitation on Flow and Diesel Fuel Atomization Characteristics. Chem. Eng. Technol. 2013, 36, 474–482. [Google Scholar] [CrossRef]
- Biçer, B.; Sou, A. Application of the Improved Cavitation Model to Turbulent Cavitating Flow in Fuel Injector Nozzle. Appl. Math. Modell. 2016, 40, 4712–4726. [Google Scholar] [CrossRef]
- Ghorbani, M.; Sadaghiani, A.K.; Yidiz, M.; Koşar, A. Experimental and Numerical Investigations on Spray Structure under the Effect of Cavitation Phenomenon in a Microchannel. J. Mech. Sci. Technol. 2017, 31, 235–247. [Google Scholar] [CrossRef]
- Mithun, M.G.; Koukouvnis, P.; Karathanassis, I.K.; Gavaises, M. Simulating the Effect of In-Nozzle Cavitation on Liquid Atomisation Using a Three-Phase Model. In Proceedings of the 10th International Symposium on Cavitation (CAV2018), Baltimore, MD, USA, 14–16 May 2018; Katz, J., Ed.; ASME Press: New York, NY, USA, 2018. [Google Scholar]
- Cristofaro, M.; Edelbauer, W.; Koukouvinis, P.; Gavaises, M. Influence of Diesel Fuel Viscosity on Cavitating Throttle Flow Simulations under Erosive Operation Conditions. ACS Omega 2020, 5, 7182–7192. [Google Scholar] [CrossRef]
- Urazmetov, O.; Cadet, M.; Teutsch, R.; Antonyuk, S. Investigation of the Flow Phenomena in High-Pressure Water Jet Nozzles. Chem. Eng. Res. Des. 2021, 165, 320–332. [Google Scholar] [CrossRef]
- Bambhania, M.; Patel, N.K. Numerical Modeling of the Cavitation Flow in Throttle Geometry. J. Appl. Fluid Mech. 2022, 16, 257–267. [Google Scholar] [CrossRef]
- Pietrykowski, K.; Karpiński, P. Simulation Study of Hydrodynamic Cavitation in the Orifice Flow. Appl. Comput. Sci. 2022, 18, 31–41. [Google Scholar] [CrossRef]
- Li, Q.; Zong, C.; Liu, F.; Xue, T.; Zhang, A.; Song, X. Numerical and Experimental Analysis of the Cavitation Characteristics of Orifice Plates under High-Pressure Conditions Based on a Modified Cavitation Model. Int. J. Heat Mass Transfer 2023, 203, 123782. [Google Scholar] [CrossRef]
- Fuchs, F.; Meidinger, V.; Neuburger, N.; Reiter, T.; Zündel, M.; Hupfer, A. Challenges in Designing very small Jet Engines-Fuel Distribution and Atomization. In Proceedings of the 16th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, HI, USA, 10–15 April 2016. [Google Scholar]
- Rahmatian, M.A.; Tari, P.H.; Mojaddam, M.; Majidi, S. Numerical and Experimental Study of the Ducted Diffuser Effect on Improving the Aerodynamic Performance of a Micro Horizontal Axis Wind Turbine. Energy 2022, 245, 123267. [Google Scholar] [CrossRef]
- Janmanee, P.; Muttamara, A. A Study of Hole Drilling on Stainless Steel AISI 431 by EDM Using Brass Tube Electrode. Int. Trans. J. Eng. Manag. Appl. Sci. Technol. 2011, 2, 471–481. [Google Scholar]
- Pramanik, A.; Basak, A.K.; Littlefair, G.; Debnath, S.; Prakash, C.; Singh, M.A.; Marla, D.; Singh, R.K. Methods and Variables in Electrical Discharge Machining of Titanium Alloy—A review. Heliyon 2020, 6, e05554. [Google Scholar] [CrossRef]
- Qiu, T.; Song, X.; Lei, Y.; Liu, X.; An, X.; Lai, M. Influence of inlet pressure on cavitation flow in diesel nozzle. Appl. Therm. Eng. 2016, 109, 364–372. [Google Scholar] [CrossRef]
- Jin, Z.J.; Gao, Z.X.; Li, X.J.; Qian, J.Y. Cavitating flow through a micro-orifice. Micromachines 2019, 10, 191. [Google Scholar] [CrossRef]
- Kumar, A.; Ghobadian, A.; Nouri, J.M. Assessment of cavitation models for compressible flows inside a nozzle. Fluids 2020, 5, 134. [Google Scholar] [CrossRef]
- Zwart, P.; Gerber, A.; Belamri, T. A Two-Phase Model for Predicting Cavitation Dynamics. In Proceedings of the ICMF 2004 International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004; pp. 1–11. [Google Scholar]
- Ansys Fluent Theory Guide; Chapter 18. Available online: https://dl.cfdexperts.net/cfd_resources/Ansys_Documentation/Fluent/Ansys_Fluent_Theory_Guide.pdf (accessed on 9 January 2024).
- Ebrahimi, B.; He, G.; Tang, Y.; Franchek, M.; Liu, D.; Pickett, J.; Springett, F.; Franklin, D. Characterization of high-pressure cavitating flow through a thick orifice plate in a pipe of constant cross section. Int. J. Therm. Sci. 2017, 114, 229–240. [Google Scholar] [CrossRef]
- Casoli, P.; Scolari, F.; Rundo, M. Modelling and Validation of Cavitating Orifice Flow in Hydraulic Systems. Sustainability 2021, 13, 7239. [Google Scholar] [CrossRef]
- Sou, A.; Hosokawa, S.; Tomiyama, A. Cavitation in Nozzles of Plain Orifice Atomizers with Various Length-to-Diameter Ratios. At. Sprays 2010, 20, 513–524. [Google Scholar] [CrossRef]
- Reitz, R.D. Atomization and Other Breakup Regimes of a Liquid Jet. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1978. [Google Scholar]







| Test Parameters | |||
|---|---|---|---|
| Length-to-diameter ratio | 3 | 6 | 8 |
| Injection pressure (MPa) | 0.2–1 | ||
| Back pressure (MPa) | 0.1–0.3 | ||
| Reynolds number | 3000–9500 (water); 1590–4800 (kerosene) | ||
| Cavitation number | 1.11–4.47 (water); 1.12–2.29 (kerosene) | ||
| Physical Properties | Water | Kerosene |
|---|---|---|
| Density (kg/m3) | 998.2 | 816 |
| Vapor pressure (Pa) | 3169.8 | 666.45 |
| Dynamic viscosity (kg/m·s) | 0.001 | 0.00175 |
| Surface tension (N/m) | 0.072 | 0.02883 |
| Ohnesorge number | 0.0068 | 0.02 |
| = 0.1 MPa | = 0.15 MPa | = 0.2 MPa | = 0.25 MPa | = 0.3 MPa | ||
|---|---|---|---|---|---|---|
| L/D = 3 | 0.45 | 0.55 | 0.9 | --- | --- | |
| 0.35 | 0.45 | 0.7 | --- | --- | ||
| L/D = 6 | 0.55 | 0.65 | 0.8 | 0.9 | --- | |
| 0.45 | 0.5 | 0.6 | 0.65 | --- | ||
| L/D = 8 | 0.4 | 0.6 | 0.7 | 0.85 | 0.95 | |
| 0.3 | 0.45 | 0.5 | 0.60 | 0.65 |
| Injector Condition | L/D = 3 | L/D = 6 | L/D = 8 |
|---|---|---|---|
| Inlet geometry | round edge (difficult) | sharp edge (easy) | sharp edge (easy) |
| Length | 0.9 mm (easy) | 1.8 mm (less difficult) | 2.4 mm (difficult) |
| Taper angle | 0.26° (difficult) | 0.4° (less difficult) | 0.62° (easy) |
| = 0.1 MPa (Water/Kerosene) | = 0.15 MPa (Water/Kerosene) | = 0.2 MPa (Water/Kerosene) | |
|---|---|---|---|
| L/D = 3 | K = 1.24/1.20 | K = 1.37/1.21 | K = 1.28/----- |
| L/D = 6 | K = 1.25/1.25 | K = 1.29/1.25 | K = 1.33/1.32 |
| L/D = 8 | K = 1.32/1.20 | K = 1.29/1.25 | K = 1.39/1.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.-Y.; Yang, C.-C.; Ouyang, K. An Experimental and Numerical Study on the Cavitation and Spray Characteristics of Micro-Orifice Injectors under Low-Pressure Conditions. Energies 2024, 17, 1045. https://doi.org/10.3390/en17051045
Chen T-Y, Yang C-C, Ouyang K. An Experimental and Numerical Study on the Cavitation and Spray Characteristics of Micro-Orifice Injectors under Low-Pressure Conditions. Energies. 2024; 17(5):1045. https://doi.org/10.3390/en17051045
Chicago/Turabian StyleChen, Tzeng-Yuan, Chih-Cheng Yang, and Kwan Ouyang. 2024. "An Experimental and Numerical Study on the Cavitation and Spray Characteristics of Micro-Orifice Injectors under Low-Pressure Conditions" Energies 17, no. 5: 1045. https://doi.org/10.3390/en17051045
APA StyleChen, T.-Y., Yang, C.-C., & Ouyang, K. (2024). An Experimental and Numerical Study on the Cavitation and Spray Characteristics of Micro-Orifice Injectors under Low-Pressure Conditions. Energies, 17(5), 1045. https://doi.org/10.3390/en17051045






