Effect of Morphological Characteristics of Aggregates on Thermal Properties of Molten Salt Nanofluids
Abstract
:1. Introduction
2. Simulation Model and Method
3. Results and Discussion
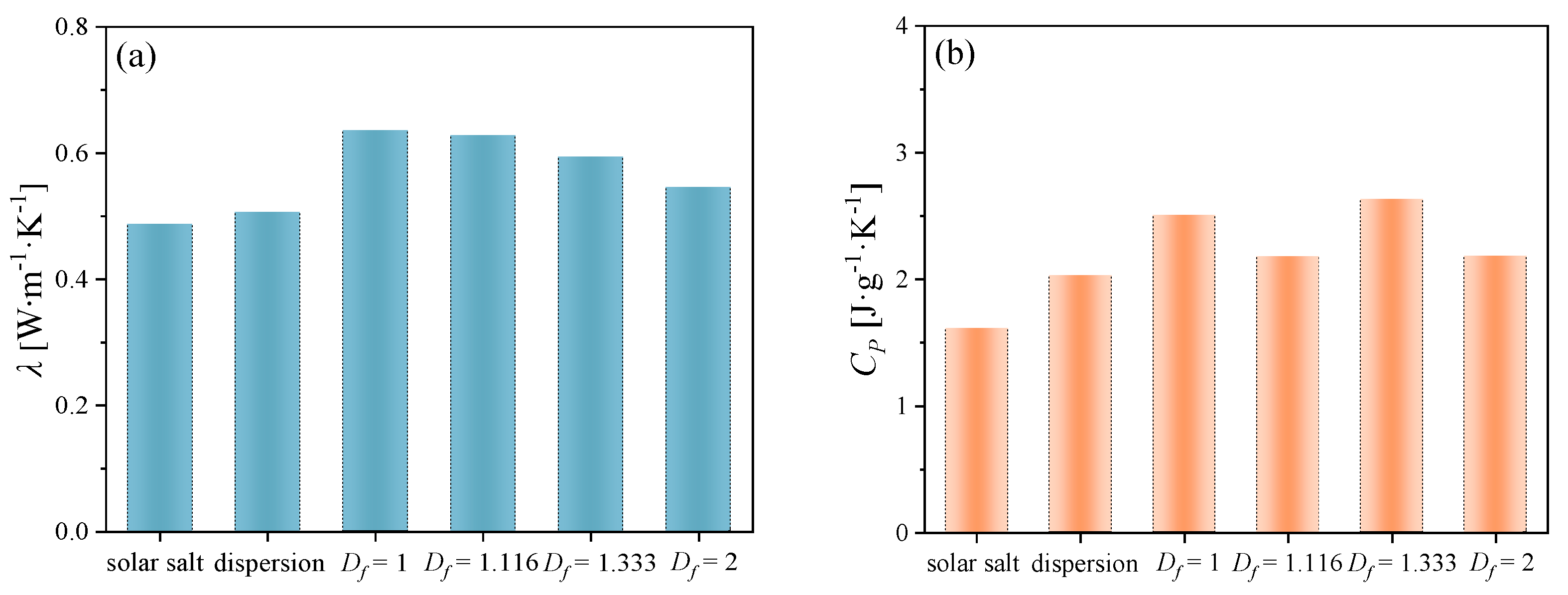
3.1. Thermal Conductivity and Specific Heat Capacity
3.2. Contributions of Different Material Components and Heat Flux Fluctuation Modes to Thermal Conductivity
3.3. Contributions of Different Energy Compositions to Specific Heat Capacity
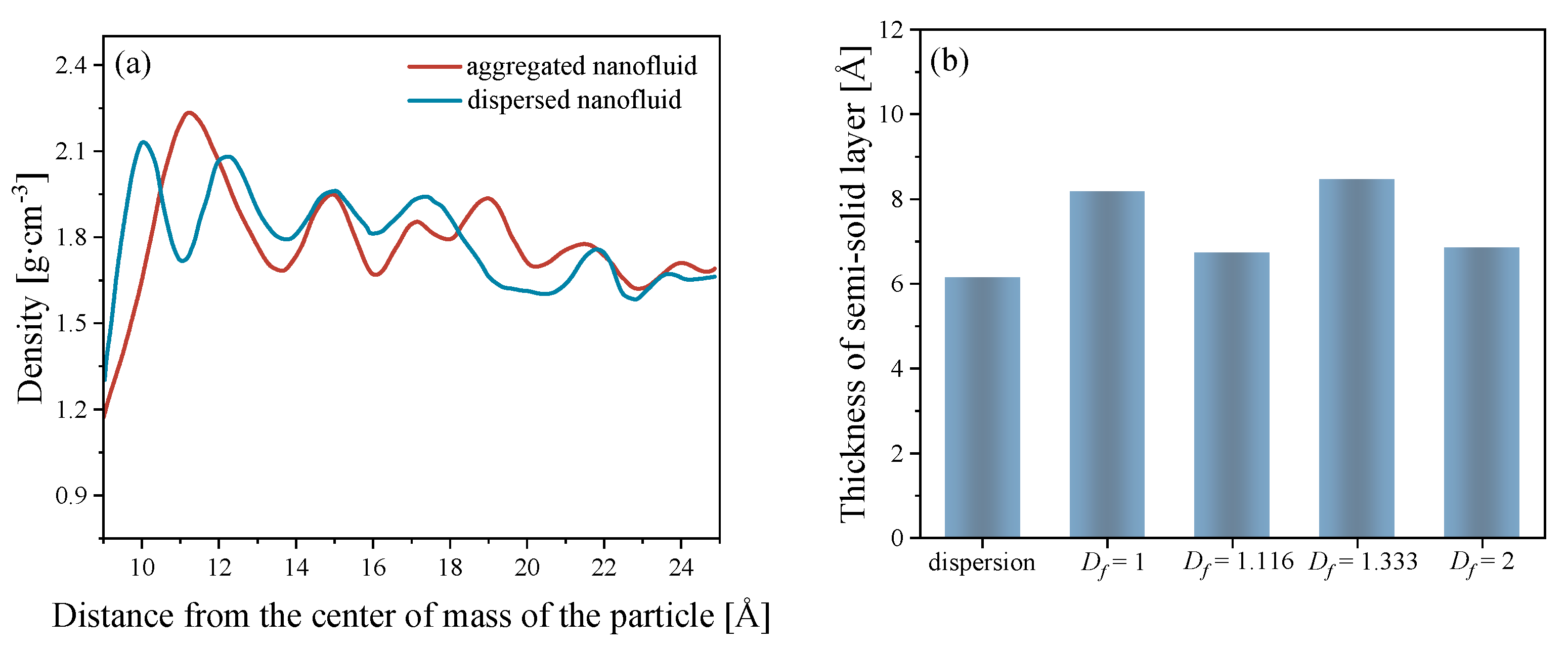
3.4. Semi-Solid Layer
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Praveen, R.; Baseer, M.A.; Sankara, N.K. Design. Performance analysis and optimization of a 100 MW concentrated solar power plant with thermal energy storage. In Proceedings of the 2018 International Conference on Current Trends towards Converging Technologies (ICCTCT), Coimbatore, India, 1–3 March 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Islam, M.T.; Huda, N.; Abdullah, A.; Saidur, R. A comprehensive review of state-of-the-art concentrating solar power (CSP) technologies: Current status and research trends. Renew. Sustain. Energy Rev. 2018, 91, 987–1018. [Google Scholar] [CrossRef]
- El Alami, K.; Asbik, M.; Agalit, H. Identification of natural rocks as storage materials in thermal energy storage (TES) system of concentrated solar power (CSP) plants—A review. Sol. Energy Mater. Sol. Cells 2020, 217, 110599. [Google Scholar] [CrossRef]
- Rao, Z.; Bai, R.; Ye, K.; Zhou, T. Effects of interfacial layer on thermal conductivity enhancement of solar salt-based nanofluids: Insights from molecular dynamics simulations. Case Stud. Therm. Eng. 2022, 35, 102087. [Google Scholar] [CrossRef]
- Nunes, V.; Queirós, C.; Lourenço, M.; Santos, F.; De Castro, C.N. Molten salts as engineering fluids—A review: Part I. Molten alkali nitrates. Appl. Energy 2016, 183, 603–611. [Google Scholar] [CrossRef]
- Da Cunha, J.P.; Eames, P. Thermal energy storage for low and medium temperature applications using phase change materials—A review. Appl. Energy 2016, 177, 227–238. [Google Scholar] [CrossRef]
- Evans, W.; Prasher, R.; Fish, J.; Meakin, P.; Phelan, P.; Keblinski, P. Effect of aggregation and interfacial thermal resistance on thermal conductivity of nanocomposites and colloidal nanofluids. Int. J. Heat Mass Transf. 2008, 51, 1431–1438. [Google Scholar] [CrossRef]
- Wu, C.; Cho, T.J.; Xu, J.; Lee, D.; Yang, B.; Zachariah, M.R. Effect of nanoparticle clustering on the effective thermal conductivity of concentrated silica colloids. Phys. Rev. E 2010, 81, 011406. [Google Scholar] [CrossRef] [PubMed]
- Karthikeyan, N.; Philip, J.; Raj, B. Effect of clustering on the thermal conductivity of nanofluids. Mater. Chem. Phys. 2008, 109, 50–55. [Google Scholar] [CrossRef]
- Suganthi, K.S.; Parthasarathy, M.; Rajan, K.S. Liquid-layering induced, temperature-dependent thermal conductivity enhancement in ZnO-propylene glycol nanofluids. Chem. Phys. Lett. 2013, 561, 120–124. [Google Scholar] [CrossRef]
- Kumar, D.H.; Patel, H.E.; Kumar, V.R.; Sundararajan, T.; Pradeep, T.; Das, S.K. Model for heat conduction in nanofluids. Phys. Rev. Lett. 2004, 93, 144301. [Google Scholar] [CrossRef]
- Nagvenkar, A.P.; Perelshtein, I.; Gedanken, A. Doping effect on the thermal conductivity of metal oxide nanofluids: Insight and mechanistic investigation. J. Phys. Chem. C 2017, 121, 26551–26557. [Google Scholar] [CrossRef]
- Prasher, R.; Bhattacharya, P.; Phelan, P.E. Brownian-motion-based convective-conductive model for the effective thermal conductivity of nanofluids. J. Heat Mass Transf. 2006, 128, 588–595. [Google Scholar] [CrossRef]
- Abbasi, M.; Heyhat, M.; Rajabpour, A. Study of the effects of particle shape and base fluid type on density of nanofluids using ternary mixture formula: A molecular dynamics simulation. J. Mol. Liq. 2020, 305, 112831. [Google Scholar] [CrossRef]
- Selvam, C.; Mohan Lal, D.; Harish, S. Thermal conductivity and specific heat capacity of water-ethylene glycol mixture-based nanofluids with graphene nanoplatelets. J. Therm. Anal. Calorim. 2017, 129, 947–955. [Google Scholar] [CrossRef]
- Hong, J.; Kim, D. Effects of aggregation on the thermal conductivity of alumina/water nanofluids. Thermochim. Acta 2012, 542, 28–32. [Google Scholar] [CrossRef]
- Wu, Z.; Sundén, B. Convective heat transfer performance of aggregate-laden nanofluids. Int. J. Heat Mass Transf. 2016, 93, 1107–1115. [Google Scholar] [CrossRef]
- Motevasel, M.; Nazar, A.R.S.; Jamialahmadi, M. The effect of nanoparticles aggregation on the thermal conductivity of nanofluids at very low concentrations: Experimental and theoretical evaluations. Heat Mass Transf. 2018, 54, 125–133. [Google Scholar] [CrossRef]
- Wensel, J.; Wright, B.; Thomas, D.; Douglas, W.; Mannhalter, B.; Cross, W.; Hong, H.; Kellar, J.; Smith, P.; Roy, W. Enhanced thermal conductivity by aggregation in heat transfer nanofluids containing metal oxide nanoparticles and carbon nanotubes. Appl. Phys. Lett. 2008, 92, 023110. [Google Scholar] [CrossRef]
- Prasher, R.; Phelan, P.E.; Bhattacharya, P. Effect of aggregation kinetics on the thermal conductivity of nanoscale colloidal solutions (nanofluid). Nano Lett. 2006, 6, 1529–1534. [Google Scholar] [CrossRef]
- Pang, C.; Jung, J.Y.; Kang, Y.T. Aggregation based model for heat conduction mechanism in nanofluids. Int. J. Heat Mass Transf. 2014, 72, 392–399. [Google Scholar] [CrossRef]
- Tahmooressi, H.; Kasaeian, A.; Tarokh, A.; Rezaei, R.; Hoorfar, M. Numerical simulation of aggregation effect on nanofluids thermal conductivity using the lattice Boltzmann method. Int. Commun. Heat Mass Transf. 2020, 110, 104408. [Google Scholar] [CrossRef]
- Wang, R.; Qian, S.; Zhang, Z. Investigation of the aggregation morphology of nanoparticle on the thermal conductivity of nanofluid by molecular dynamics simulations. Int. J. Heat Mass Transf. 2018, 127, 1138–1146. [Google Scholar] [CrossRef]
- Li, Y.; Zhai, Y.; Chen, W.; Li, Z.; Wang, H. Microscopic mechanisms of particle agglomeration to enhance transport properties of nanofluids. J. Mol. Liq. 2023, 383, 122008. [Google Scholar] [CrossRef]
- Du, J.; Su, Q.; Li, L.; Wang, R.; Zhu, Z. Evaluation of the influence of aggregation morphology on thermal conductivity of nanofluid by a new MPCD-MD hybrid method. Int. Commun. Heat Mass Transf. 2021, 127, 105501. [Google Scholar] [CrossRef]
- Awad, A.; Navarro, H.; Ding, Y.; Wen, D. Thermal-physical properties of nanoparticle-seeded nitrate molten salts. Renew. Energy 2018, 120, 275–288. [Google Scholar] [CrossRef]
- Anagnostopoulos, A.; Alexiadis, A.; Ding, Y. Molecular dynamics simulation of solar salt (NaNO3-KNO3) mixtures. Sol. Energy Mater. Sol. Cells 2019, 200, 109897. [Google Scholar] [CrossRef]
- Niégawa, A.; Takashiba, K. Transition rates of reactions in the microcanonical ensemble and the finite-size effect. Can. J. Phys. 1993, 71, 276–279. [Google Scholar] [CrossRef]
- Li, Z.; Cui, L.; Li, B.; Du, X. Enhanced heat conduction in molten salt containing nanoparticles: Insights from molecular dynamics. Int. J. Heat Mass Transf. 2020, 153, 119578. [Google Scholar] [CrossRef]
- Cui, L.; Yu, Q.; Wei, G.; Du, X. Mechanisms for thermal conduction in molten salt-based nanofluid. Int. J. Heat Mass Transf. 2022, 188, 122648. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Qiao, G.; Alexiadis, A.; Ding, Y. Simulation study of anomalous thermal properties of molten nitrate salt. Powder Technol. 2017, 314, 660–664. [Google Scholar] [CrossRef]
- Qiao, G.; Lasfargues, M.; Alexiadis, A.; Ding, Y. Simulation and experimental study of the specific heat capacity of molten salt based nanofluids. Appl. Therm. Eng. 2017, 111, 1517–1522. [Google Scholar] [CrossRef]
- Janz, G.J.; James, D.W. Raman spectra and ionic interactions in molten nitrates. J. Chem. Phys. 1961, 35, 739–745. [Google Scholar] [CrossRef]
- Hisatsune, I.; Devlin, J.; Califano, S. Urey-Bradley potential constants in nitrogen dioxide, nitrite ion and dinitrogen tetroxide. Spectrochim. Acta 1960, 16, 450–458. [Google Scholar] [CrossRef]
- Aljaerani, H.A.; Samykano, M.; Saidur, R.; Pandey, A.; Kadirgama, K. Nanoparticles as molten salts thermophysical properties enhancer for concentrated solar power: A critical review. J. Energy Storage 2021, 44, 103280. [Google Scholar] [CrossRef]
- Romero, M.; González-Aguilar, J. Solar thermal CSP technology. Wiley Interdiscip. Rev. Energy Environ. 2014, 3, 42–59. [Google Scholar] [CrossRef]
- Lv, W.; Henry, A. Direct calculation of modal contributions to thermal conductivity via Green-Kubo modal analysis. New J. Phys. 2016, 18, 013028. [Google Scholar] [CrossRef]
- Babaei, H.; Keblinski, P.; Khodadadi, J. A proof for insignificant effect of Brownian motion-induced micro-convection on thermal conductivity of nanofluids by utilizing molecular dynamics simulations. J. Appl. Phys. 2013, 113, 084302. [Google Scholar] [CrossRef]
- Li, S.; Guenther, C.L.; Kelley, M.S.; Dixon, D.A. Molecular structures, acid-base properties, and formation of group 6 transition metal hydroxides. J. Phys. Chem. C 2011, 115, 8072–8103. [Google Scholar] [CrossRef]
- Serrano-López, R.; Fradera, J.; Cuesta-López, S. Molten salts database for energy applications. Chem. Eng. Process. Process Intensif. 2013, 73, 87–102. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Wu, Y.; Lu, Y.; Zhi, R.; Wang, X.; Ma, C. Experimental study on the effect of SiO2 nanoparticle dispersion on the thermophysical properties of binary nitrate molten salt. Sol. Energy 2019, 183, 776–781. [Google Scholar] [CrossRef]
- Nasiri, A.; Shariaty-Niasar, M.; Rashidi, A.M.; Khodafarin, R. Effect of CNT structures on thermal conductivity and stability of nanofluid. Int. J. Heat Mass Transf. 2012, 55, 1529–1535. [Google Scholar] [CrossRef]
- Kazemi-Beydokhti, A.; Heris, S.Z.; Moghadam, N.; Shariati-Niasar, M.; Hamidi, A. Experimental investigation of parameters affecting nanofluid effective thermal conductivity. Chem. Eng. Commun. 2014, 201, 593–611. [Google Scholar] [CrossRef]
- Meibodi, M.E.; Vafaie-Sefti, M.; Rashidi, A.M.; Amrollahi, A.; Tabasi, M.; Kalal, H.S. The role of different parameters on the stability and thermal conductivity of carbon nanotube/water nanofluids. Int. Commun. Heat Mass Transf. 2010, 37, 319–323. [Google Scholar] [CrossRef]
- Zhang, T.; Zou, Q.; Cheng, Z.; Chen, Z.; Liu, Y.; Jiang, Z. Effect of particle concentration on the stability of water-based SiO2 nanofluid. Powder Technol. 2021, 379, 457–465. [Google Scholar] [CrossRef]
- Chieruzzi, M.; Cerritelli, G.F.; Miliozzi, A.; Kenny, J.M. Effect of nanoparticles on heat capacity of nanofluids based on molten salts as PCM for thermal energy storage. Nanoscale Res. Lett. 2013, 8, 448. [Google Scholar] [CrossRef] [PubMed]
- Shin, D.; Banerjee, D. Enhanced thermal properties of SiO2 nanocomposite for solar thermal energy storage applications. Int. J. Heat Mass Transf. 2015, 84, 898–902. [Google Scholar] [CrossRef]
- Teng, K.L.; Hsiao, P.Y.; Hung, S.W.; Chieng, C.C.; Liu, M.S.; Lu, M.C. Enhanced thermal conductivity of nanofluids diagnosis by molecular dynamics simulations. J. Nanosci. Nanotechnol. 2008, 8, 3710–3718. [Google Scholar] [CrossRef]
- Eapen, J.; Li, J.; Yip, S. Mechanism of thermal transport in dilute nanocolloids. Phys. Rev. Lett. 2007, 98, 028302. [Google Scholar] [CrossRef]
- Jo, B.; Banerjee, D. Enhanced specific heat capacity of molten salt-based nanomaterials: Effects of nanoparticle dispersion and solvent material. Acta Mater. 2014, 75, 80–91. [Google Scholar] [CrossRef]
- Gorji, T.B.; Ranjbar, A.; Mirzababaei, S. Optical properties of carboxyl functionalized carbon nanotube aqueous nanofluids as direct solar thermal energy absorbers. Sol. Energy 2015, 119, 332–342. [Google Scholar] [CrossRef]
- Fedele, L.; Colla, L.; Bobbo, S.; Barison, S.; Agresti, F. Experimental stability analysis of different water-based nanofluids. Nanoscale Res. Lett. 2011, 6, 300. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhu, D.; Wang, X. Evaluation on dispersion behavior of the aqueous copper nano-suspensions. J. Colloid Interface Sci. 2007, 310, 456–463. [Google Scholar] [CrossRef] [PubMed]



| Atom | qi/e | Aii/Kcal·mol−1 | ρii/Å | Cii/Kcal·mol−1·Å6 |
|---|---|---|---|---|
| N | 0.95 | 33,652.75 | 0.2646 | 259.1 |
| Na | 1 | 9778.06 | 0.3170 | 24.18 |
| K | 1 | 35,833.47 | 0.3370 | 349.9 |
| O (In NO3−) | −0.65 | 62,142.9 | 0.2392 | 259.4 |
| O (In SiO2) | −0.955209 | 15,170.70 | 0.386 | 617.24 |
| Si | 1.910418 | 72,460.64 | 0.351 | 14,415.29 |
| Group | Kr/eV·10−20 m | r0/10−10 m | Kθ/eV | θ0/° | KUB/eV | rUB/10−10 m |
|---|---|---|---|---|---|---|
| NO3− | 17.5344 | 1.2676 | 2.7122 | 120 | 4.9608 | 2.1955 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zhu, C.; Chen, S.; Wang, S.; Jing, Z.; Cui, L. Effect of Morphological Characteristics of Aggregates on Thermal Properties of Molten Salt Nanofluids. Energies 2024, 17, 1080. https://doi.org/10.3390/en17051080
Zhang W, Zhu C, Chen S, Wang S, Jing Z, Cui L. Effect of Morphological Characteristics of Aggregates on Thermal Properties of Molten Salt Nanofluids. Energies. 2024; 17(5):1080. https://doi.org/10.3390/en17051080
Chicago/Turabian StyleZhang, Weichao, Chaoyang Zhu, Shuanjun Chen, Shixing Wang, Zhaoshuo Jing, and Liu Cui. 2024. "Effect of Morphological Characteristics of Aggregates on Thermal Properties of Molten Salt Nanofluids" Energies 17, no. 5: 1080. https://doi.org/10.3390/en17051080
APA StyleZhang, W., Zhu, C., Chen, S., Wang, S., Jing, Z., & Cui, L. (2024). Effect of Morphological Characteristics of Aggregates on Thermal Properties of Molten Salt Nanofluids. Energies, 17(5), 1080. https://doi.org/10.3390/en17051080




