Modeling of Linearized Generator Inertia Constraints for Unit Commitment
Abstract
:1. Introduction
- We effectively secure the system inertia using the average RoCoF constraint and the minimum frequency constraint that considers changes in the PFR characteristics of the system.
- We implement linearized inertia constraints that consider the characteristics of load changes with respect to frequency changes.
- We validate the applicability of the linearized inertia constraints modeled using a single-machine frequency response model to real systems.
2. Formulation of Linearized Inertia Constraints
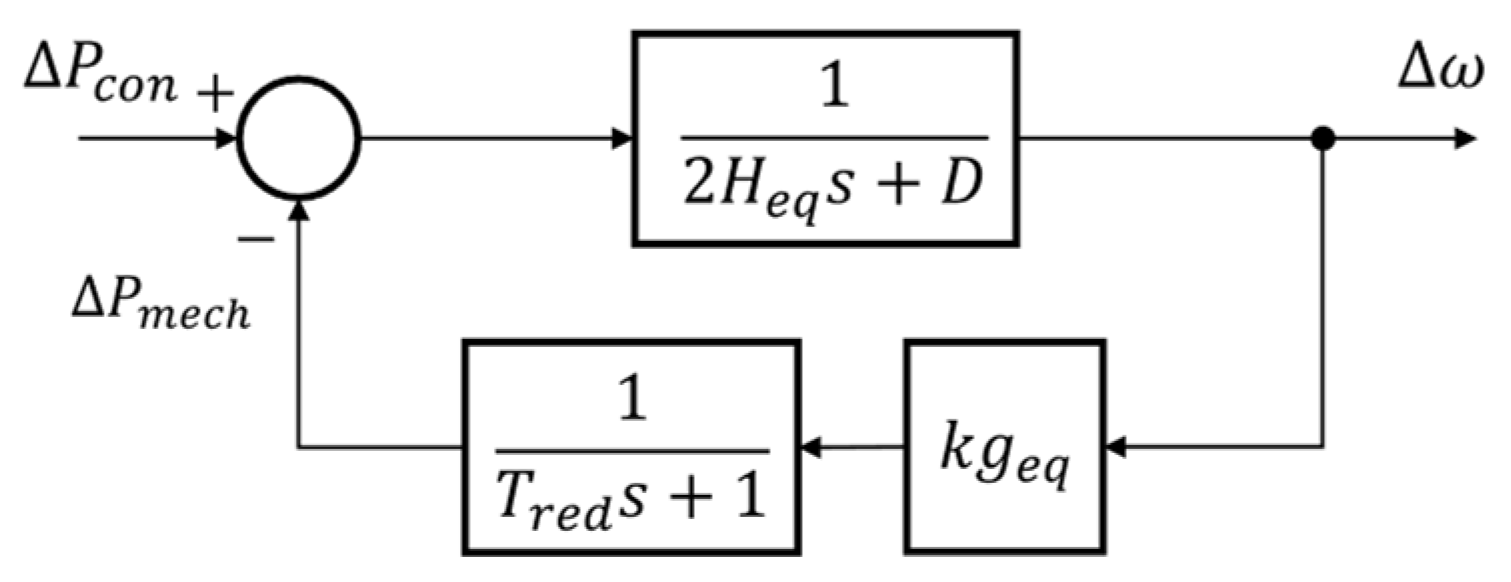
2.1. Analytical Expression of Frequency
2.2. Piecewise Linearization Technique for Linearizing the Analytical Expression
2.3. Linearized Inertia Constraint Model
2.3.1. Average Rate of Change of Frequency Constraint Model
2.3.2. Minimum Frequency Constraint Model
2.3.3. Quasi Steady State Frequency Constraint Model
2.4. Variables for Linearized Inertia Constraints
2.4.1. System Inertia
2.4.2. Generator Gain of Single Machine
2.4.3. Load-Damping Constant
2.5. Time Constant of Single Machine
3. Unit Commitment Model for Linearized Inertia Constraints
3.1. Objective Function
3.2. Unit Commitment Constraints
3.2.1. Power Balance Constraints
3.2.2. Power Limit Constraints
3.2.3. Ramp Rate Constraints
3.2.4. Minimum Up/Down Time Constraints
3.2.5. Start-Up/Shut-Down Power Output
3.2.6. Reserve Capacity Constraints
3.2.7. Constraints on Pumped Storage Hydropower Units
3.2.8. Binary Variable Constraints
4. Case Study
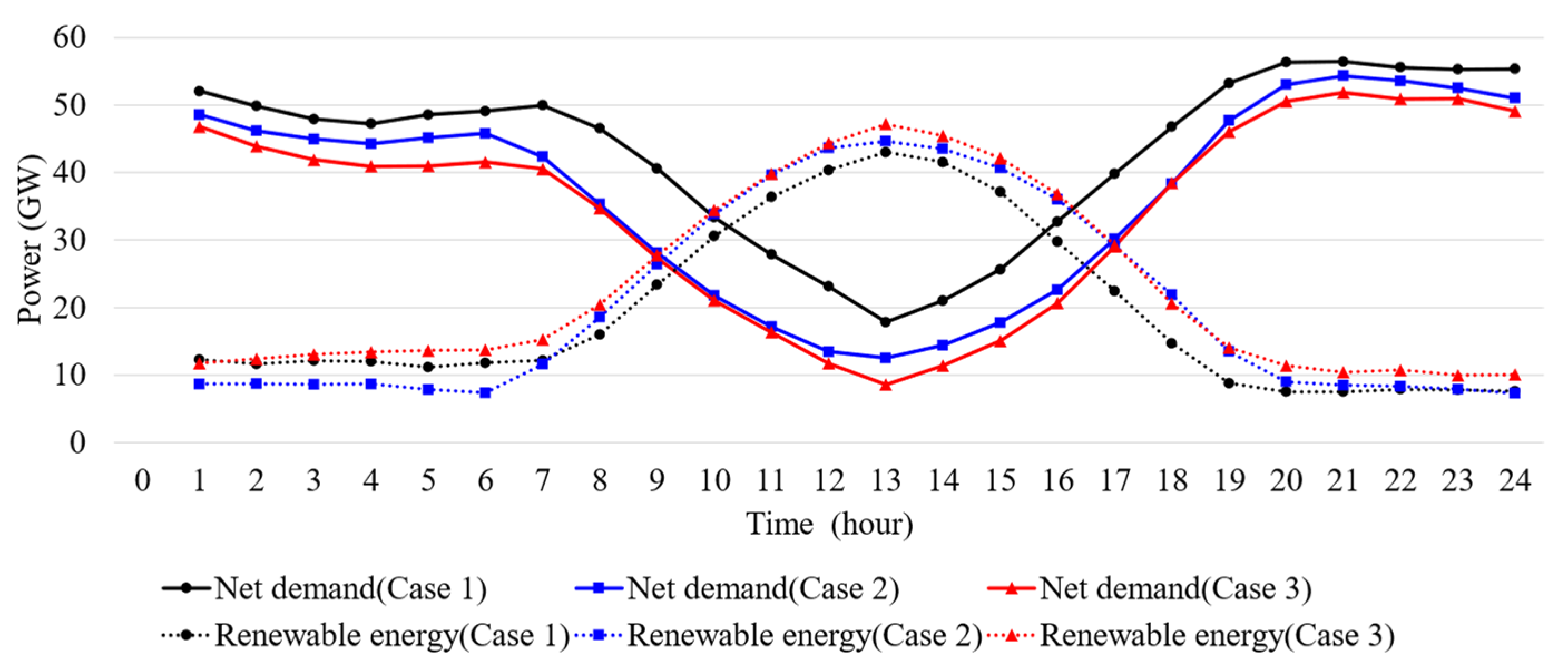
4.1. Description of System and Premises
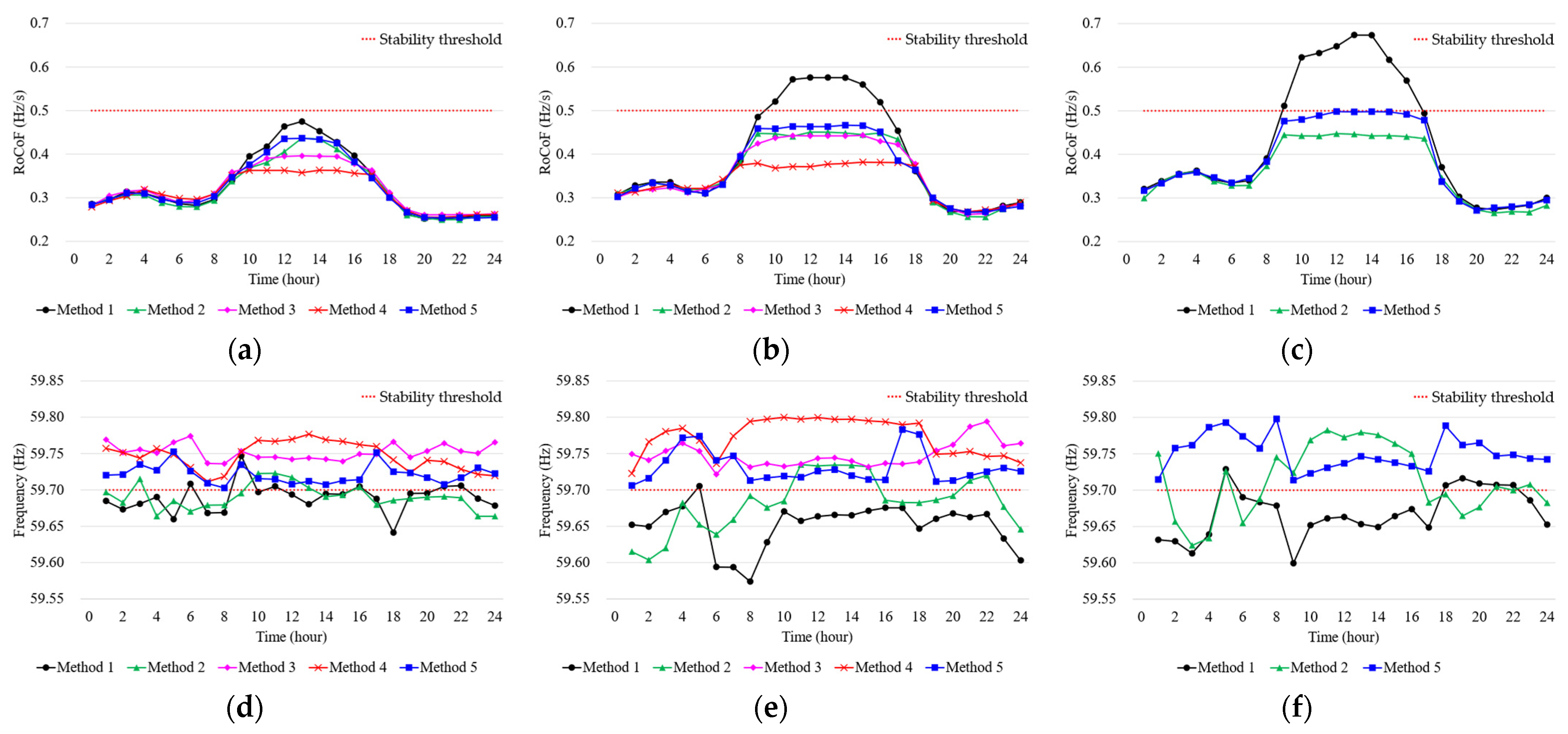
4.2. Frequency Stability Results
4.3. Effects of Linearized Inertia Constraints
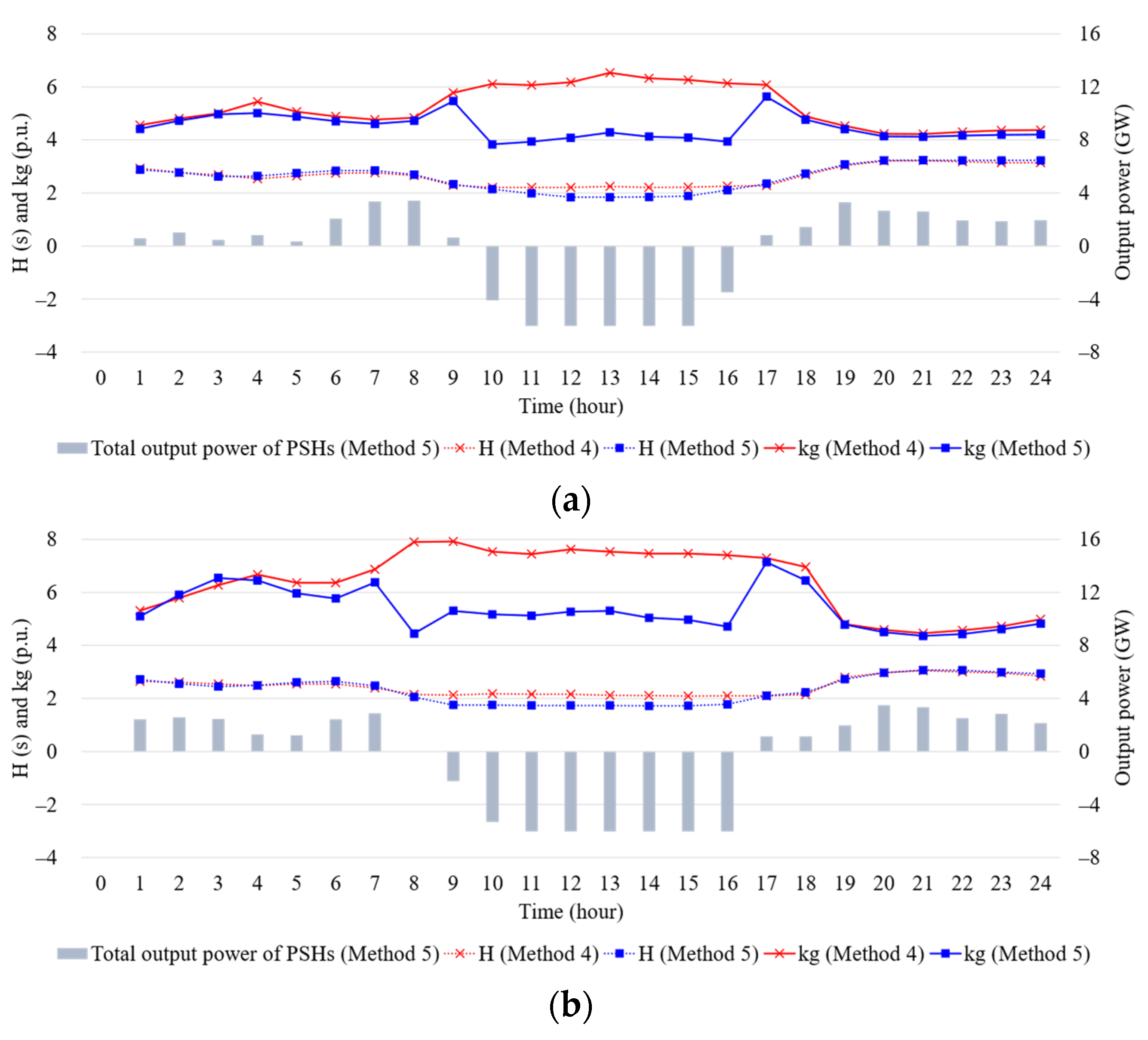
4.3.1. Securement of System Inertia
4.3.2. Efficiency of Proposed Minimum Frequency Constraint
4.3.3. Securement of Generator Gain of the Single Machine
4.3.4. Acceptance of Inflexible Generation and Total Cost
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Sets and Indices | |
| Set of time in UC, | |
| Set of synchronous units | |
| Set of PSH units, | |
| Set of tripped units of a contingency for the average RoCoF constraint, | |
| Set of tripped units of a contingency for the minimum frequency constraint, | |
| Set of segments of the average RoCoF constraint/minimum frequency constraint | |
| Parameters | |
| System nominal frequency [Hz] | |
| RoCoF limit [Hz/s] | |
| Minimum frequency deviation limit [Hz] | |
| Quasi steady-state frequency deviation limit [Hz] | |
| Parameters for the average RoCoF constraint | |
| Parameters for the average RoCoF constraint | |
| Parameters for the minimum frequency constraint (generation mode of PSH) | |
| Parameters for the minimum frequency constraint (non-generation mode of PSH) | |
| Inertia constant of unit g [s] | |
| Generator gain of unit g [p.u.] | |
| Machine base of unit g [MVA] | |
| System base [MVA] | |
| Power output of renewable energy/load on the system [MW] | |
| Load-damping constant based on [p.u.] | |
| Operating cost/no-load cost/start-up cost of unit g [USD/MWh] | |
| Maximum/minimum power output limit of unit g [MW] | |
| Maximum/minimum pumping power input of PSH unit g [MW] | |
| Ramp-up/-down rate of unit g [MW/h] | |
| Start-up/shut-down ramp rate of unit g [MW/h] | |
| Start-up/shut-down time of unit g [h] | |
| Minimum up/down time of unit g [h] | |
| Maximum primary reserve of unit g [MW] | |
| Maximum upward/downward secondary reserve of unit g [MW] | |
| Requirement of primary reserve of the system [MW] | |
| Requirement of upward/downward secondary reserve of the system [MW] | |
| Maximum storable energy for PSH unit g [MWh] | |
| Pumping efficiency of PSH unit g | |
| Variables | |
| System inertia constant of the average RoCoF constraint/the minimum frequency constraint [p.u.] | |
| Generator gain of the single machine of the average RoCoF constraint/the minimum frequency constraint [p.u.] | |
| Generator gain of unit g considering generation limits [p.u.] | |
| Power output/pumping power input of unit g/PSH unit g [MW] | |
| Start-up/shut-down power output of unit g [MW] | |
| Primary/upward secondary/downward secondary reserve of unit g [MW] | |
| Energy stored in PSH unit g [MWh] | |
| Binary variable representing commitment status of unit g | |
| Binary variable representing the operating status of PSH unit g (1 if in pumping mode and 0 if not in pumping mode) | |
| Binary variable representing start-up/shut-down status of unit g (1 if the end of start-up process/the start of the shut-down process) | |
| Binary variable representing start-up/shut-down processes of unit g (1 if while in start-up process/shut-down process) | |
| Binary variable representing generation/pumping mode of all PSH units (1 if in generation/pumping mode) | |
References
- Ørum, E.; Kuivaniemi, M.; Laasonen, M.; Bruseth, A.I.; Jansson, E.A.; Danell, A.; Elkington, K.; Modig, N. Future System Inertia; ENTSOE: Brussels, Belgium, 2018. [Google Scholar]
- ENTSOE subgroup system protection inertia TF. Inertia and Rate of Change of Frequency (RoCoF); ENTSOE: Brussels, Belgium, 2020. [Google Scholar]
- Johnson, S.C.; Papageorgiou, D.J.; Mallapragada, D.S.; Deetjen, T.A.; Rhodes, J.D.; Webber, M.E. Evaluating rotational inertia as a component of grid reliability with high penetrations of variable renewable energy. Energy 2019, 180, 258–271. [Google Scholar] [CrossRef]
- Mehigan, L.; Al Kez, D.; Collins, S.; Foley, A.; Ó’Gallachóir, B.; Deane, P. Renewables in the European power system and the impact on system rotational inertia. Energy 2020, 203, 117776. [Google Scholar] [CrossRef]
- Villamor, L.V.; Avagyan, V.; Chalmers, H. Opportunities for reducing curtailment of wind energy in the future electricity systems: Insights from modelling analysis of Great Britain. Energy 2020, 195, 116777. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Watanabe, M.; Mitani, Y.; Turschner, D.; Beck, H. Enhanced virtual inertia control based on derivative technique to emulate simultaneous inertia and damping properties for microgrid frequency regulation. IEEE Access 2019, 7, 14422–14433. [Google Scholar] [CrossRef]
- Du, P.; Mago, N.V.; Li, W.; Sharma, S.; Hu, Q.; Ding, T. New ancillary service market for ERCOT. IEEE Access 2020, 8, 178391–178401. [Google Scholar] [CrossRef]
- Chamorro, H.R.; Sevilla, F.R.S.; Gonzalez-Longatt, F.; Rouzbehi, K.; Chavez, H.; Sood, V.K. Innovative primary frequency control in low-inertia power systems based on wide-area RoCoF sharing. IET Energy Syst. Integr. 2020, 2, 151–160. [Google Scholar] [CrossRef]
- Mosca, C.; Bompard, E.; Chicco, G.; Aluisio, B.; Migliori, M.; Vergine, C.; Cuccia, P. Technical and economic impact of the inertia constraints on power plant unit commitment. IEEE Open Access J. Power Energy 2020, 7, 441–452. [Google Scholar] [CrossRef]
- Schipper, J.; Wood, A.; Edwards, C. Optimizing instantaneous and ramping reserves with different response speeds for contingencies—Part I: Methodology. IEEE Trans. Power Syst. 2020, 35, 3953–3960. [Google Scholar] [CrossRef]
- Muzhikyan, A.; Mezher, T.; Farid, A.M. Power system enterprise control with inertial response procurement. IEEE Trans. Power Syst. 2018, 33, 3735–3744. [Google Scholar] [CrossRef]
- Daly, P.; Flynn, D.; Cunniffe, N. Inertia considerations within unit commitment and economic dispatch for systems with high non-synchronous penetrations. In Proceedings of the IEEE Eindhoven Powertech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Banik, S.; Sakib, M.S.; Chowdhury, S.; Masood, N.A. Inertia constrained economic dispatch in a renewable dominated power system. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference—Latin America (ISGT Latin America), Lima, Peru, 15–17 September 2021; pp. 1–5. [Google Scholar]
- Helistö, N.; Kiviluoma, J.; Ikäheimo, J.; Rasku, T.; Rinne, E.; O’Dwyer, C.; Li, R.; Flynn, D. Backbone—An adaptable energy systems modelling framework. Energies 2019, 12, 3388. [Google Scholar] [CrossRef]
- Teng, F.; Trovato, V.; Strbac, G. Stochastic scheduling with inertia-dependent fast frequency response requirements. IEEE Trans. Power Syst. 2016, 31, 1557–1566. [Google Scholar] [CrossRef]
- Badesa, L.; Teng, F.; Strbac, G. Simultaneous scheduling of multiple frequency services in stochastic unit commitment. IEEE Trans. Power Syst. 2019, 34, 3858–3868. [Google Scholar] [CrossRef]
- Badesa, L.; Teng, F.; Strbac, G. Conditions for regional frequency stability in power system scheduling—Part I: Theory. IEEE Trans. Power Syst. 2021, 36, 5558–5566. [Google Scholar] [CrossRef]
- Badesa, L.; Teng, F.; Strbac, G. Conditions for regional frequency stability in power system scheduling—Part II: Application to unit commitment. IEEE Trans. Power Syst. 2021, 36, 5567–5577. [Google Scholar] [CrossRef]
- Wen, Y.; Li, W.; Huang, G.; Liu, X. Frequency dynamics constrained unit commitment with battery energy storage. IEEE Trans. Power Syst. 2016, 31, 5115–5125. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, L.; Cheng, H.; Liu, D.; Zhang, J.; Li, G. Frequency-constrained co-planning of generation and energy storage with high-penetration renewable energy. J. Mod. Power Syst. Clean Energy 2021, 9, 760–775. [Google Scholar] [CrossRef]
- Javadi, M.; Gong, Y.; Chung, C.Y. Frequency stability constrained microgrid scheduling considering seamless islanding. IEEE Trans. Power Syst. 2022, 37, 306–316. [Google Scholar] [CrossRef]
- Paturet, M.; Markovic, U.; Delikaraoglou, S.; Vrettos, E.; Aristidou, P.; Hug, G. Stochastic unit commitment in low-inertia grids. IEEE Trans. Power Syst. 2020, 35, 3448–3458. [Google Scholar] [CrossRef]
- Trovato, V.; Bialecki, A.; Dallagi, A. Unit commitment with inertia-dependent and multispeed allocation of frequency response services. IEEE Trans. Power Syst. 2019, 34, 1537–1548. [Google Scholar] [CrossRef]
- Ahmadi, H.; Ghasemi, H. Security-constrained unit commitment with linearized system frequency limit constraints. IEEE Trans. Power Syst. 2014, 29, 1536–1545. [Google Scholar] [CrossRef]
- Zhang, Z.; Du, E.; Teng, F.; Zhang, N.; Kang, C. Modeling frequency dynamics in unit commitment with a high share of renewable energy. IEEE Trans. Power Syst. 2020, 35, 4383–4395. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Wood, A.J.; Wollenberg, B.F.; Sheblé, G.B. Power Generation, Operation, and Control, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Kim, S.; Chun, Y. Single-machine frequency model and parameter identification for inertial constraints in unit commitment. Energies 2021, 14, 5961. [Google Scholar] [CrossRef]
- Anderson, P.M.; Mirheydar, M. A low-order system frequency response model. IEEE Trans. Power Syst. 1990, 5, 720–729. [Google Scholar] [CrossRef]
- Shi, Q.; Li, F.; Cui, H. Analytical method to aggregate multi-machine SFR model with applications in power system dynamic studies. IEEE Trans. Power Syst. 2018, 33, 6355–6367. [Google Scholar] [CrossRef]
- Magnani, A.; Boyd, S.P. Convex piecewise-linear fitting. Optim. Eng. 2009, 10, 1–17. [Google Scholar] [CrossRef]
- Operations directorate of ENA. Engineering Recommendation G59 Issue 3 Amendment 7; ENA: London, UK, 2019. [Google Scholar]

| Combined Cycle | Thermal Power | Nuclear Power | Hydroelectric Power | Pumped Storage Hydropower | |
|---|---|---|---|---|---|
| Total capacity [MW] | 47,953 | 37,871 | 20,400 | 1582 | 5500 |
| Number of units [EA] | 103 | 57 | 18 | 15 | 8 |
| Operating cost [USD/MWh] | 67 | 37 | 4 | 0 | 0 |
| No-load cost [USD] | 2766 | 3392 | 433 | 0 | 0 |
| Start-up cost [USD] | 2808 | 35,162 | - | 0 | 0 |
| Ramp rate [MW/min] | 21.2 | 16.7 | - | 31.8 | 205.6 |
| Minimum up time [h] | 4.1 | 7.8 | - | 0.5 | 0.5 |
| Minimum down time [h] | 3.5 | 13.7 | - | 0.5 | 0.6 |
| Inertia constant [s] | 5.15 | 3.99 | 4.99 | 3.71 | 4.93 |
| Generator gain [p.u.] | 13.82 | 15.39 | - | 21.85 | 24.93 |
| Method 1 (GWs) | Method 2 (GWs) | Method 3 (GWs) | Method 4 (GWs) | Method 5 (GWs) | |
|---|---|---|---|---|---|
| Case 2 | 133 | 170 | 173 | 203 | 164 |
| Case 3 | 119 | 170 | - | - | 153 |
| Method 1 (p.u.) | Method 2 (p.u.) | Method 3 (p.u.) | Method 4 (p.u.) | Method 5 (p.u.) | |
|---|---|---|---|---|---|
| Case 1 | 3.43 | 3.49 | 5.50 | 5.24 | 4.47 |
| Case 2 | 3.37 | 3.75 | 5.55 | 6.43 | 5.36 |
| Case 3 | 3.31 | 3.86 | - | - | 5.71 |
| Method 1 (GW) | Method 2 (GW) | Method 3 (GW) | Method 4 (GW) | Method 5 (GW) | |
|---|---|---|---|---|---|
| Case 1 | 15.6 | 14.6 | 12.2 | 10.2 | 14.2 |
| Case 2 | 10.2 | 7.2 | 6.2 | 3.8 | 7.2 |
| Case 3 | 5.8 | 2.8 | - | - | 2.8 |
| Method 1 (MUSD) | Method 2 (MUSD) | Method 3 (MUSD) | Method 4 (MUSD) | Method 5 (MUSD) | |
|---|---|---|---|---|---|
| Case 1 | 30.6 | 31.7 | 33.0 | 34.9 | 31.5 |
| Case 2 | 29.0 | 32.1 | 32.6 | 35.1 | 31.7 |
| Case 3 | 31.5 | 36.5 | - | - | 34.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-E.; Chun, Y.-H. Modeling of Linearized Generator Inertia Constraints for Unit Commitment. Energies 2024, 17, 1120. https://doi.org/10.3390/en17051120
Kim S-E, Chun Y-H. Modeling of Linearized Generator Inertia Constraints for Unit Commitment. Energies. 2024; 17(5):1120. https://doi.org/10.3390/en17051120
Chicago/Turabian StyleKim, Sung-Eun, and Yeong-Han Chun. 2024. "Modeling of Linearized Generator Inertia Constraints for Unit Commitment" Energies 17, no. 5: 1120. https://doi.org/10.3390/en17051120
APA StyleKim, S.-E., & Chun, Y.-H. (2024). Modeling of Linearized Generator Inertia Constraints for Unit Commitment. Energies, 17(5), 1120. https://doi.org/10.3390/en17051120






