A New Approach to Use of Traction Power Network in Poland for Charging Electric Vehicles
Abstract
1. Introduction
2. Review of Technical Solutions for Charging Electric Vehicles Using Railway Power Infrastructure
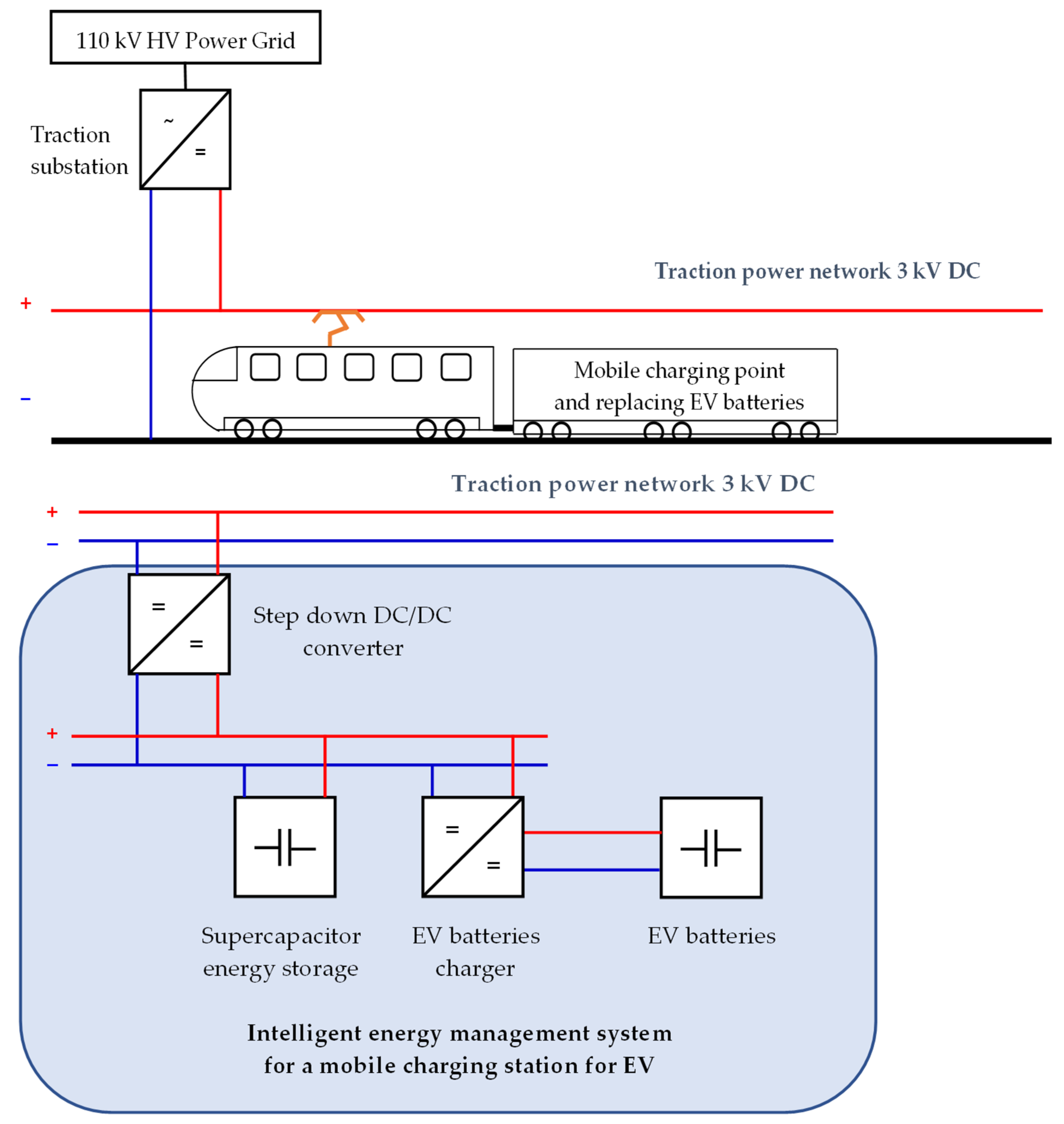
3. Description of the Developed Concept
- Popularizing electromobility by increasing the number of points and stations for charging electric vehicles using RPI;
- Achieving high energy efficiency of electric vehicle charging systems by using the potential of RPI;
- Achieving high ecological efficiency by reducing CO2 and dust emissions into the environment;
- Recovering as much electricity as possible from regenerative braking of the train and using it to charge the lithium-ion batteries of electric vehicles.
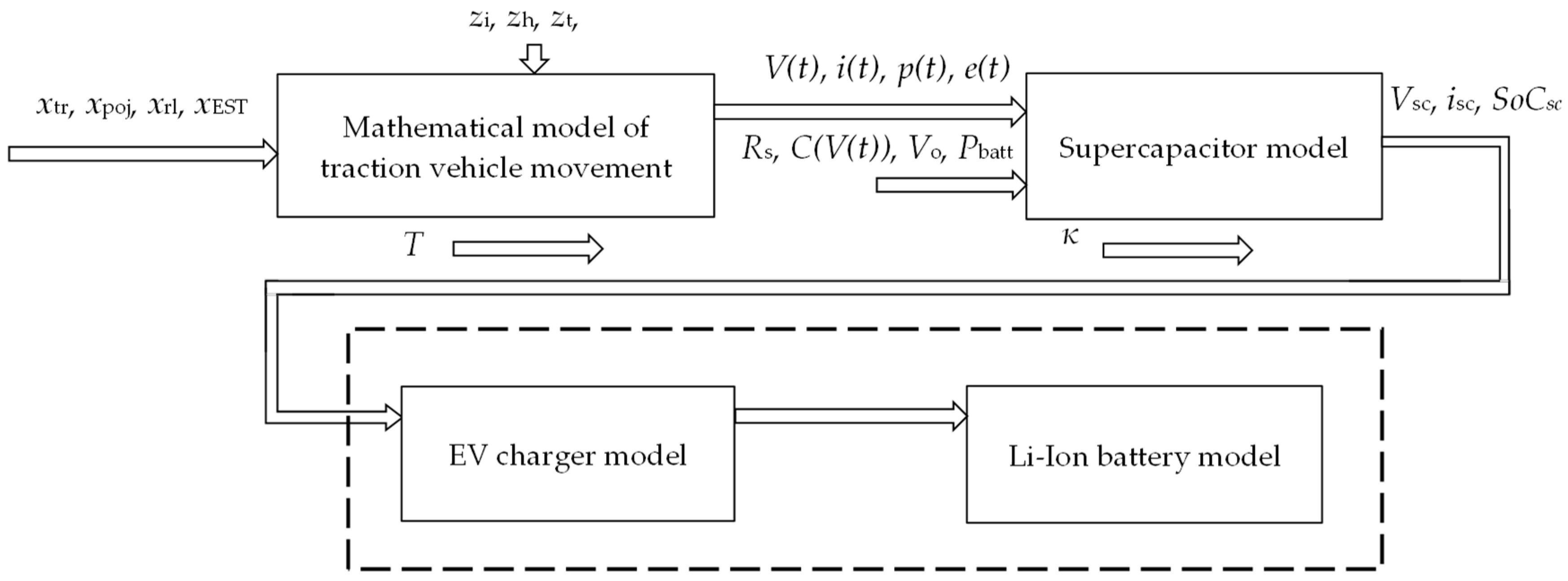
4. Materials and Methods
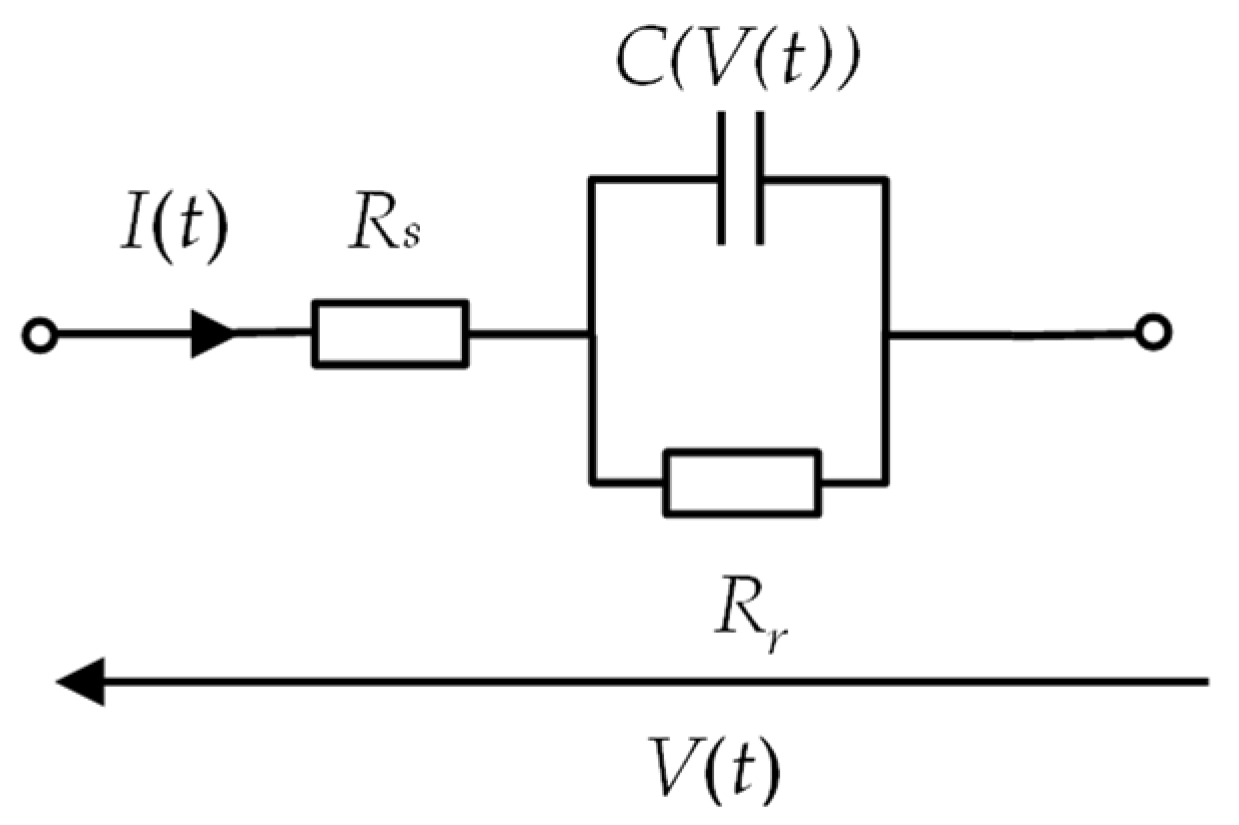
- Independent variables: xtr—traction characteristics F = f(v) (dependence of the tractive force F on the speed v), xpoj—technical data of the vehicle, xrl—technical data of the route, xEST—data on the electric traction network, Rs—equivalent resistance of the supercapacitor module, C(V(t))—capacity of the supercapacitor, V0—initial voltage of the supercapacitor module, Pbatt—charging power of Li-Ion batteries (discharging supercapacitors);
- Dependent variables: V(t)—course of changes in voltage at the pantograph, i(t)—course of changes in the intensity of current absorbed/remitted by the vehicle, p(t)—course of changes in power consumed and generated by the traction vehicle, e(t)—course of changes in electrical energy over time, Vsc—voltage of the supercapacitor module, isc—charging current of electric vehicle batteries, SoCsc—degree of charge of the supercapacitor module;
- Disturbances: zi—local terrain slope, zh—sudden braking, zt—local speed restrictions caused by maintenance work or breakdown;
- Constant values: T—temperature, κ—coefficient of the influence of voltage on the capacity of the supercapacitor.
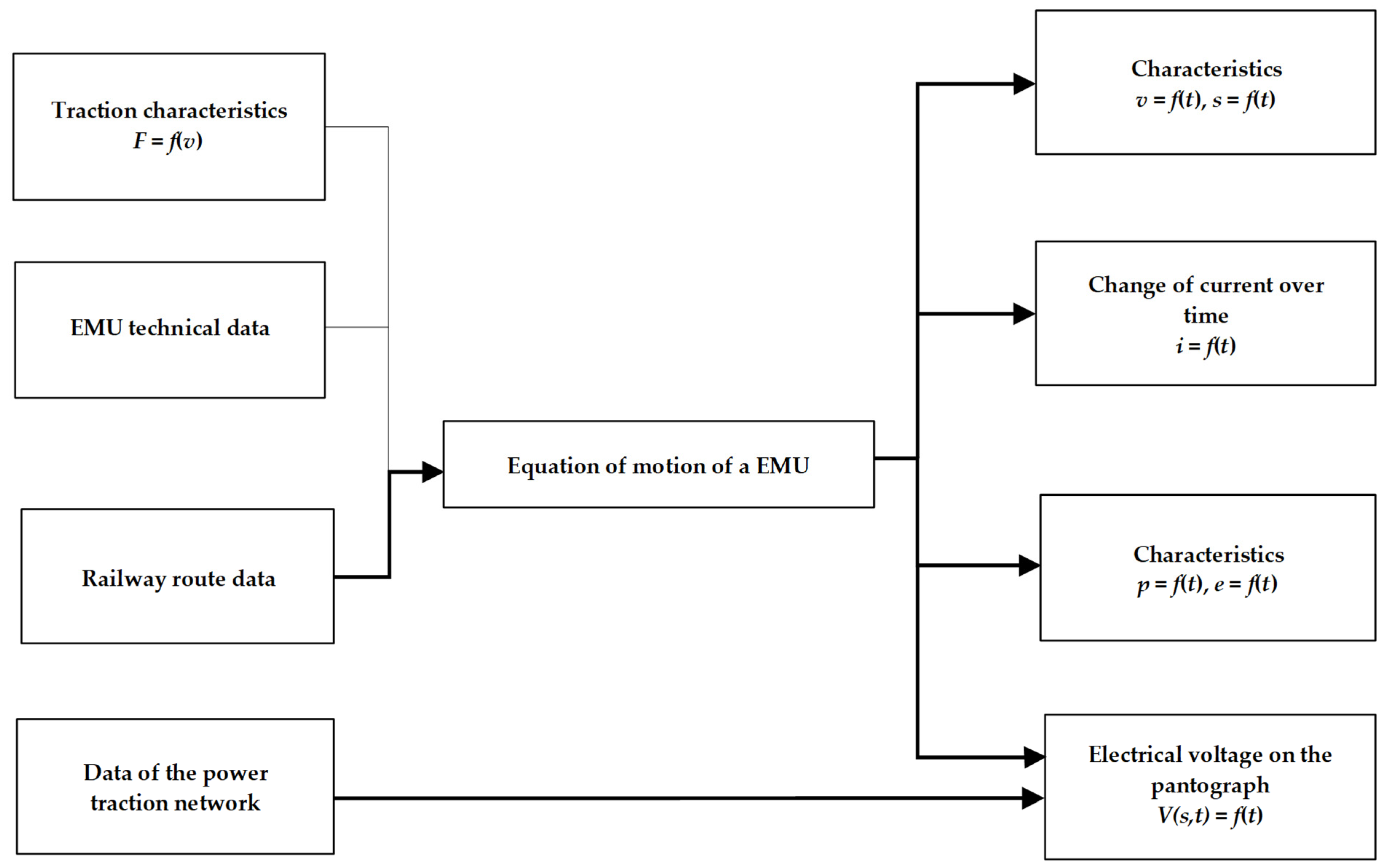
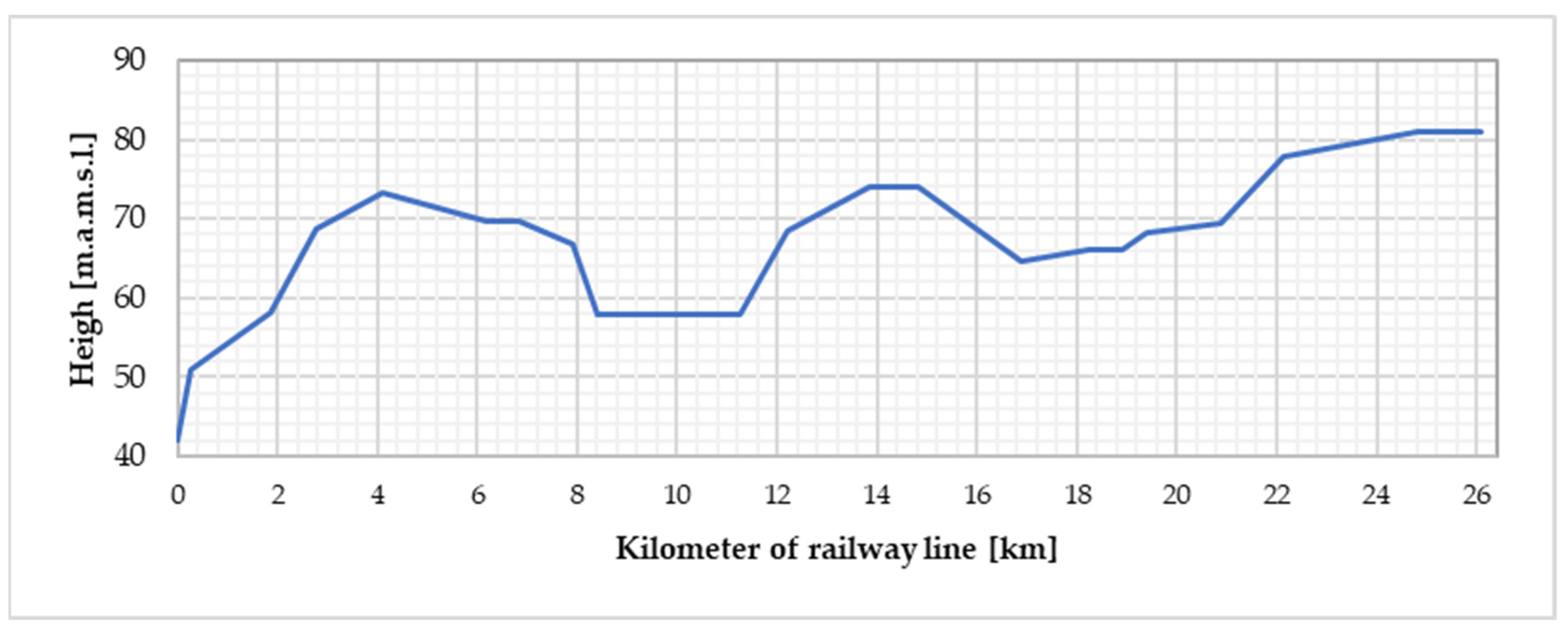
4.1. Modeling of the Theoretical Journey
4.2. Modeling of Movement Resistance
- Basic resistance Wz related to rolling resistance, aerodynamic resistance, internal friction forces, which are approximated by a second-degree polynomial; e.g., in Poland, the formula developed by the Central Center for Research and Development of Railway Technology is used, which was written using Equation (4):
- Local resistance Wi, related to the resistance of the hill, determined using Equation (5):
- Curve resistances Wr, which result from the forces acting on the vehicle while driving a curved road section and are determined using the so-called Röckel formula (6):
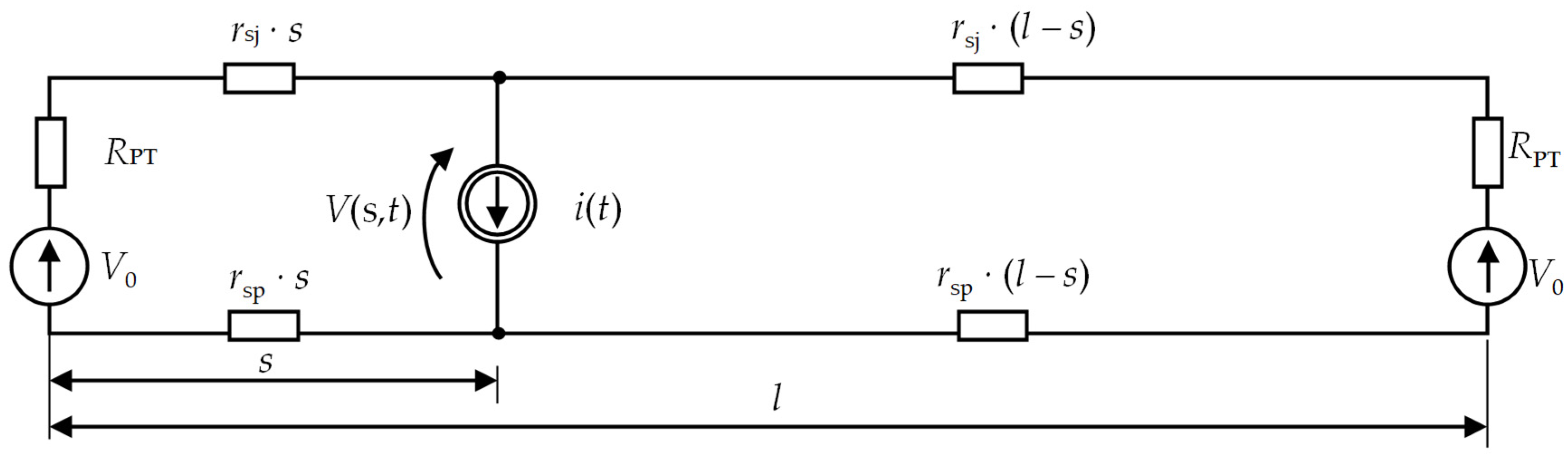
4.3. Modeling of Traction Power System
4.4. Modeling of Supercapacitor
4.5. Research Plan
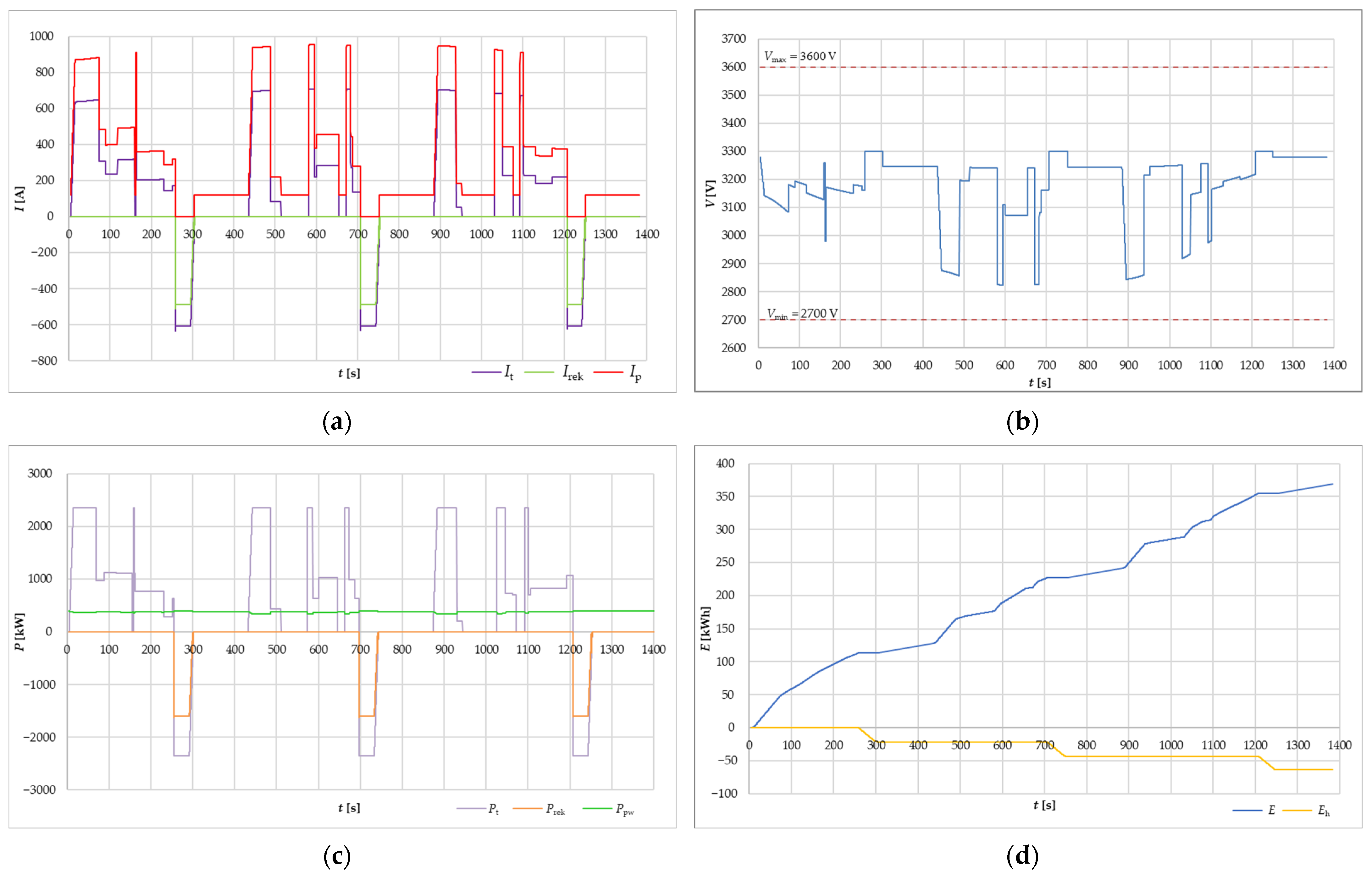
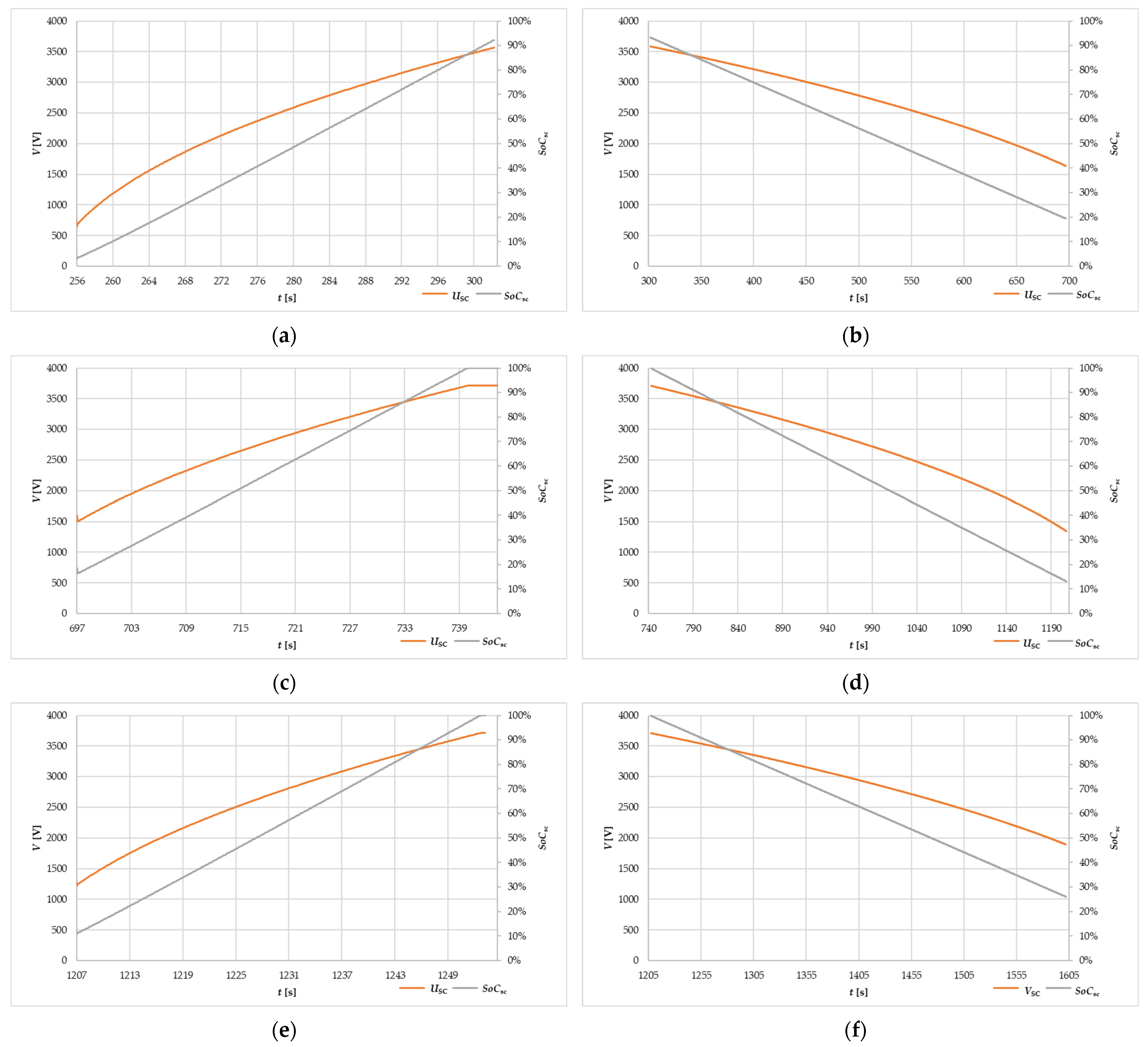
- Charging I: 255.6 s–302.0 s of simulation;
- Charging II: 696.8 s–743.2 s of simulation;
- Charging III: 1207.3 s–1253.7 s of simulation.
- Discharge I: 302.1 s–696.7 s of simulation, duration tr = 394.6 s;
- Discharge II: 743.3 s–1207.2 s of simulation, duration tr = 463.9 s;
- Discharge III: 1253.7 s–1653.7 s of simulation, duration tr = 400.0 s.
- Efficiency of electrical energy recovery from regenerative braking;
- The degree of coverage of electric energy obtained from braking the train for the purpose of charging electric vehicle batteries;
- Efficiency of the process of recovering electricity from train braking for the purpose of charging EV batteries;
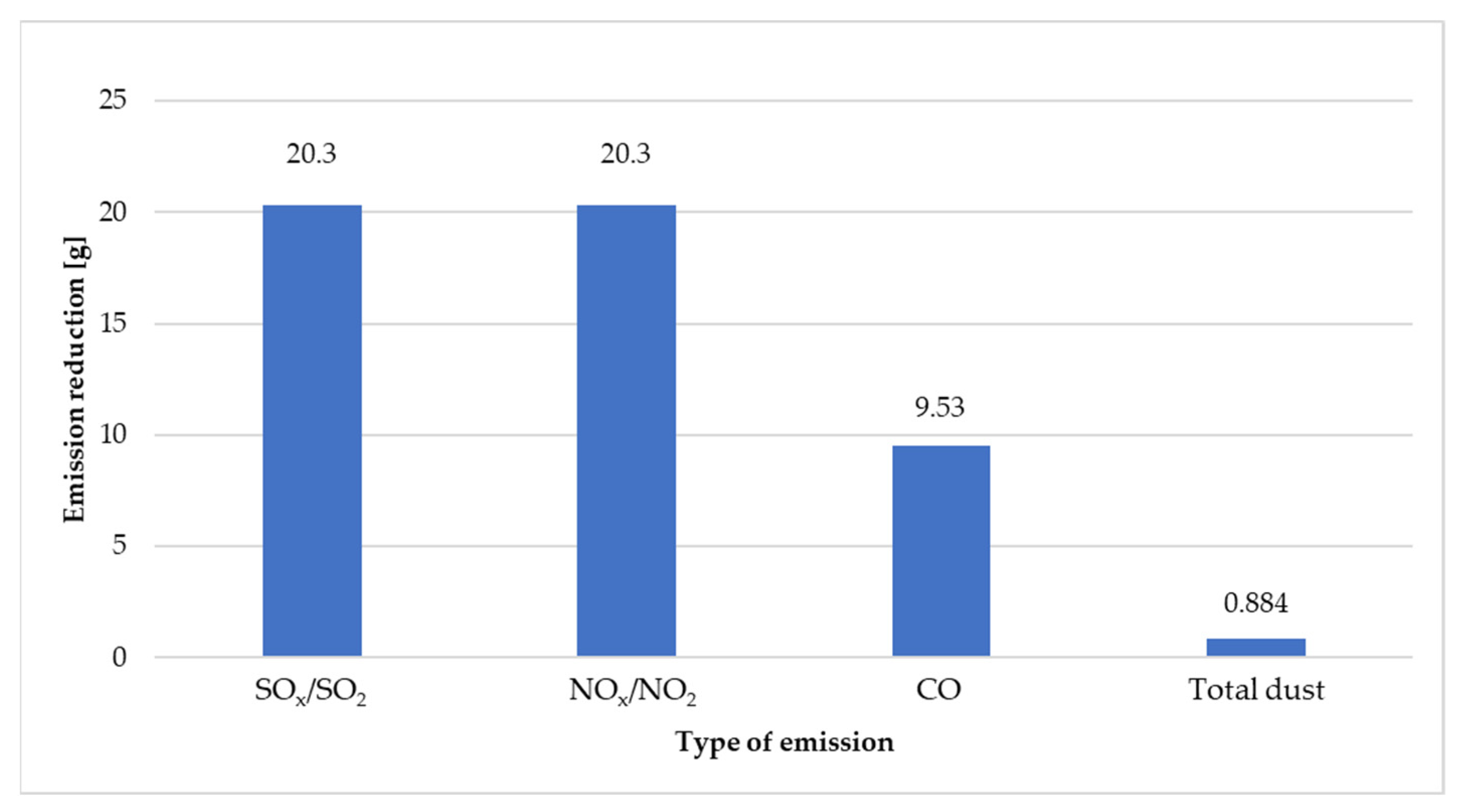
- Ecological benefits due to the reduction of pollutant emissions.
5. Results
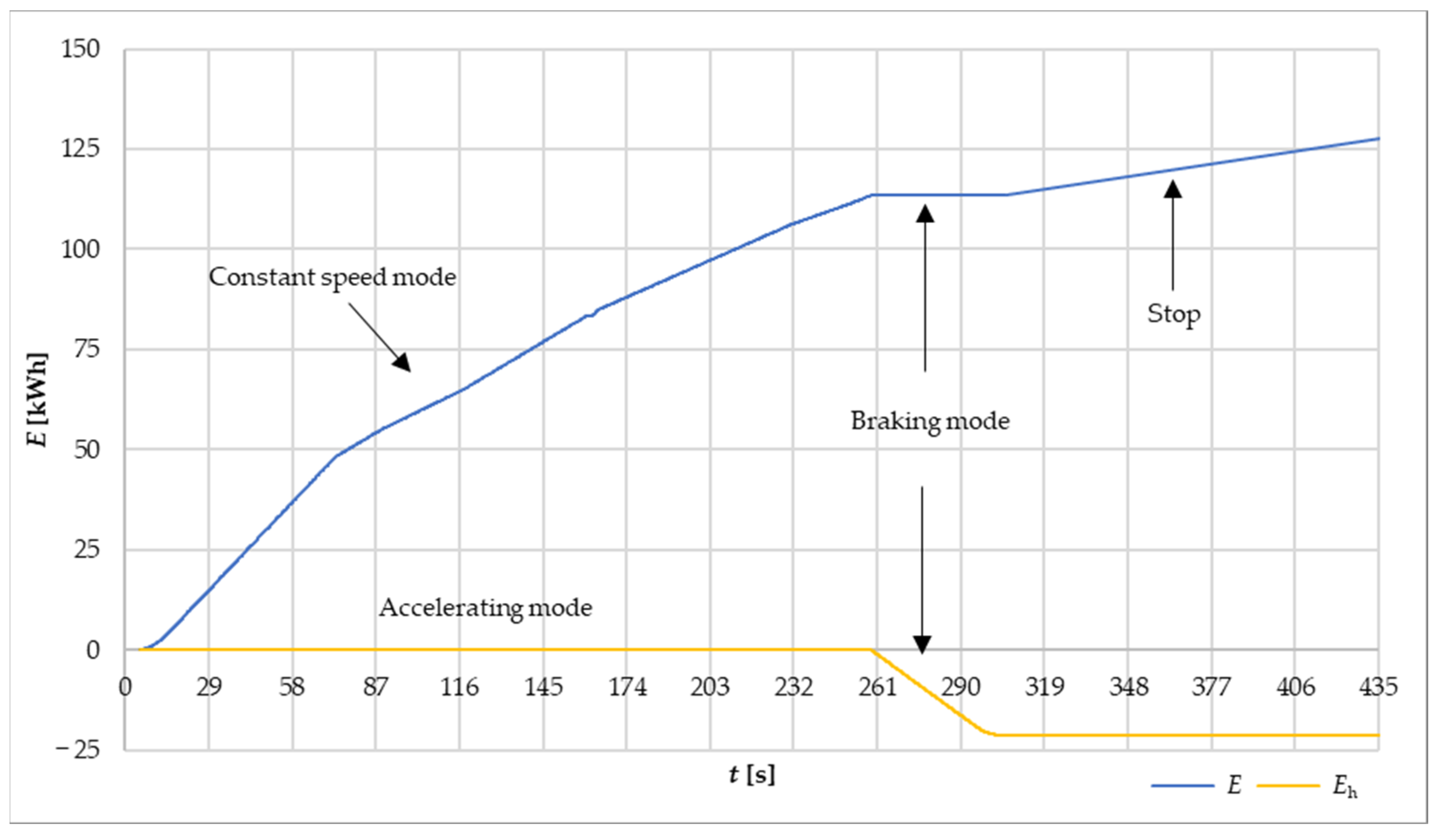
5.1. Simulation Results of the Theoretical Journey
5.2. Solution Effectiveness Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bartłomiejczyk, M.; Połom, M. The integration of urban traction power and stations of electric buses charging—Opportunity and threat? TTS Tech. Transp. Szyn. 2015, 22, 68–71. (In Polish) [Google Scholar]
- Bartłomiejczyk, M.; Połom, M. The modern concept of develepment of trolleybus transport—Slide-In project. Autobusy: Tech. Eksploat. Syst. Transp. 2015, 16, 32–35. (In Polish) [Google Scholar]
- Beister, M.; Górny, J.; Połom, M. The development of the tramway infrastructure in Poland during accession to the European Union. TTS Tech. Transp. Szyn. 2015, 22, 20–36. (In Polish) [Google Scholar]
- Benysek, G.; Jarntut, M. Application of power electronics devices in SmartGrid and V2G technologies. In Proceedings of the 2010 5th Innovative Materials and Technologies in Electrical Engineering (i-MITEL), Gorzów Wielkopolski, Poland, 21–23 April 2010; pp. 169–176. (In Polish). [Google Scholar]
- Gajewski, J.; Paprocki, W.; Pieriegud, J. Electromobility in Poland vis-à-vis the European and Global Trends; CeDeWu: Warsaw, Poland, 2019. (In Polish) [Google Scholar]
- Markowska, K.; Flizikowski, J.; Bieliński, K.; Tomporowski, A.; Kruszelnicka, W.; Kasner, R.; Bałdowska-Witos, P.; Mazur, Ł. The Comparative Assessment of Effects on the Power System and Environment of Selected Electric Transport Means in Poland. Materials 2021, 14, 4556. [Google Scholar] [CrossRef]
- Mazur, Ł.; Bieliński, K.; Flizikowski, J. Ocena ekologiczna, ekonomiczna i energetyczna transportu elektrycznego. Ekol. I Tech. 2018, 2, 41–52. (In Polish) [Google Scholar]
- IEC 61851-1:2017; Electric Vehicle Conductive Charging System—Part 1: General Requirements. International Electrotechnical Commission: Geneva, Switzerland, 2017.
- IEC 621196-1:2022; Plugs, Socket-Outlets, Vehicle Connectors and Vehicle Inlets—Conductive Charging of Electric Vehicles—Part 1: General Requirements. International Electrotechnical Commission: Geneva, Switzerland, 2022.
- Guziński, J.; Adamowicz, M.; Kamiński, J. Electric Vehicle Charging Infrastructure. Autom. Elektr. Zakłócenia 2014, 5, 74–83. (In Polish) [Google Scholar]
- Adegbohun, F.; von Jouanne, A.; Lee, K.Y. Autonomous Battery Swapping System and Methodologies of Electric Vehicles. Energies 2019, 12, 667. [Google Scholar] [CrossRef]
- Bartłomiejczyk, M. Smart grid technologies in electric power supply systems of public transport. Transport 2018, 33, 1144–1154. [Google Scholar] [CrossRef]
- Szałkowski, M.; Wróbel, R. Development of electromobility in urban public transport in Krakow. Transp. Miej. I Reg. 2018, 12, 22–29. (In Polish) [Google Scholar]
- Fernández-Rodríguez, A.; Fernández-Cardador, A.; Cucala, A.P.; Falvo, M.C. Energy Efficiency and Integration of Urban Electrical Transport Systems: EVs and Metro-Trains of Two Real European Lines. Energies 2019, 12, 366. [Google Scholar] [CrossRef]
- Sejm of the Republic Poland. Act of December 2, 2021 Amending the Act on Electromobility and Alternative Fuels and Certain Other Acts (Dz.U. 2021 poz. 2269). Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20210002269 (accessed on 7 December 2023). (In Polish)
- Mierzejewski, L.; Szeląg, A.; Gałuszewski, M. DC Electric Traction Power Supply; Wydawnictwa Politechniki Warszawskiej: Warsaw, Poland, 1989. (In Polish) [Google Scholar]
- Cipolletta, G.; Delle Femine, A.; Gallo, D.; Luiso, M.; Landi, C. Design of a Stationary Energy Recovery System in Rail Transport. Energies 2021, 14, 2560. [Google Scholar] [CrossRef]
- Bartłomiejczyk, M.; Jarzebowicz, L.; Hrbáč, R. Application of Traction Supply System for Charging Electric Cars. Energies 2022, 15, 1448. [Google Scholar] [CrossRef]
- Hernandez, J.C.; Sanchez, F. Electric Vehicle Charging Stations Fed by Renewables: PV and Train Regenerative Braking. IEEE Lat. Am. Trans. 2016, 14, 3262–3269. [Google Scholar] [CrossRef]
- Falvo, C.M.; Lamedica, R.; Bartoni, R.; Maranzano, G. Energy management in metro-transit systems: An innovative proposal toward an integrated and sustainable urban mobility system including plug-in electric vehicles. Electr. Power Syst. Res. 2011, 81, 2127–2138. [Google Scholar] [CrossRef]
- Nasr, S.; Iordache, M.; Petit, M. Smart Micro-grid integration in DC railway systems. In Proceedings of the 2014 5th IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Istanbul, Turkey, 12–15 October 2014. [Google Scholar] [CrossRef]
- Sarabi, S.; Davigny, A.; Riffonneau, Y.; Robyns, B. V2G Electric Vehicle Charging Scheduling for Railway Station Parking Lots Based on Binary Linear Programming. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016. [Google Scholar] [CrossRef]
- Małek, A.; Marciniak, A. Selection of the photovoltaic power system for the electric vehicle. Arch. Automot. Eng. 2023, 100, 44–61. [Google Scholar] [CrossRef]
- Su, S.; Wang, X.; Cao, Y.; Yin, J. An Energy-Efficient Train Operation Approach by Integrating the Metro Timetabling and Eco-Driving. IEEE Trans. Intell. Transp. Syst. 2020, 21, 4252–4268. [Google Scholar] [CrossRef]
- Dominguez, M.; Fernández-Cardador, A.; Cucala, A.P.; Pecharroman, R.R. Energy Savings in Metropolitan Railway Substations Through Regenerative Energy Recovery and Optimal Design of ATO Speed Profiles. IEEE Trans. Autom. Sci. Eng. 2012, 9, 496–504. [Google Scholar] [CrossRef]
- Witt, A. Determination of the Number of Required Charging Stations on a German Motorway Based on Real Traffic Data and Discrete Event-Based Simulation. LOGI–Sci. J. Transp. Logist. 2023, 14, 1–11. [Google Scholar] [CrossRef]
- Sejm of the Republic Poland. Act of 28 March 2003 on Railway Transport (Dz.U. 2003 no 86 poz. 789). Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=wdu20030860789 (accessed on 7 December 2023). (In Polish)
- Ministry of Energy. Regulation of the Minister of Energy of June 26, 2019 on Technical Requirements for Charging Stations and Charging Points Constituting Part of the Charging Infrastructure for Road Public Transport. (Dz.U. 2019 poz. 1316). Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20190001316 (accessed on 7 December 2023). (In Polish)
- Ministry of Climate and Environment. Regulation of the Minister of Climate and Environment of March 22, 2023 on Detailed Conditions for the Operation of the Power System. (Dz.U. 2023 poz. 819). Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20230000819 (accessed on 7 December 2023). (In Polish)
- Directive 2014/30/EU of the European Parliament and of the Council of 26 February 2014 on the Harmonisation of the Laws of the Member States Relating to Electromagnetic Compatibility. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32014L0030&rid=4 (accessed on 7 December 2023).
- PN-EN 50160:2023; Voltage Characteristics of Electricity Supplied by Public Electricity Networks. Polish Committee for Standardization: Warsaw, Poland, 2023.
- Flizikowski, J.; Bieliński, K. Design of Environmental Energy Processors; Wydawnictwa Uczelniane Akademii Techniczno-Rolniczej w Bydgoszczy: Bydgoszcz, Poland, 2000. (In Polish) [Google Scholar]
- Flizikowski, J.; Bieliński, K. Technology and Energy Sources Monitoring: Control, Efficency and Optimization; IGI GLOBAL: Hershey, PA, USA, 2013. [Google Scholar]
- Kamiński, J. Modeling of Energy Systems: General Methodology of a Model Development. Polityka Energetyczna 2010, 13, 219–226. (In Polish) [Google Scholar]
- Bartłomiejczyk, M.; Jarzębowicz, L.; Judek, S.; Karkosińska-Brzozowska, N.; Karwowski, K.; Mizan, M.; Skibicki, J.; Wilk, A. et al. Energy of Electrified Transport. In Engineer’s Quide; Wydawnictwo Politechniki Gdańskiej: Gdańsk, Poland, 2018. (In Polish) [Google Scholar]
- Jakubowski, A.; Jarzebowicz, L.; Bartłomiejczyk, M.; Skibicki, J.; Judek, S.; Wilk, A.; Płonka, M. Modeling of Electrified Transportation Systems Featuring Multiple Vehicles and Complex Power Supply Layout. Energies 2021, 14, 8196. [Google Scholar] [CrossRef]
- Kacprzak, J. Electric traction theory. In Design Materials; Oficyna Wydawnicza Politechniki Warszawskiej: Warsaw, Poland, 1996; pp. 13–32, 91–110. (In Polish) [Google Scholar]
- Arsene, S.; Ioan, S. Analysis of the resistance to motion in the passenger trains hauled by the locomotive LE 060 EA 5100kW. Incas Bull. 2014, 6, 13–21. [Google Scholar] [CrossRef]
- Krzysztoszek, K. Mathematical model of traction vehicle movement. J. Autom. Electron. Electr. Eng. 2019, 1, 37–41. [Google Scholar] [CrossRef][Green Version]
- Dębowski, A. Electric Traction Drive; Wydawnictwo Naukowe PWN: Warsaw, Poland, 2019. (In Polish) [Google Scholar]
- Moćko, W.; Szymańska, M.; Wojciechowski, A. Development and Calibration of the Mathematical Model of Traction Batteries for Electric Car. Zesz. Probl.–Masz. Elektr. 2013, 2, 25–30. (In Polish) [Google Scholar]
- Zygmanowski, M.; Grzesik, B. The supercapacitor module as a component of the power conditioning system. Śląskie Wiadomości Elektr. 2009, XV, 6, 14–18. (In Polish) [Google Scholar]
- Satpathy, S.; Debbarma, S.; Bhattacharyya, B.K. An integration of the review of electrode’s materials and a new gamma function-based charging methodology of supercapacitor for high current applications. Mater. Today Proc. 2020, 26, 2151–2156. [Google Scholar] [CrossRef]
- Ding, Y.; Zachary, P.; Yu, C.A.; Lu, J.; Chen, Z. Automotive Li-Ion Batteries: Current Status and Future Perspectives. Electrochem. Energy Rev. 2019, 2, 1–28. [Google Scholar] [CrossRef]
- Dimitrov, B.; Konaklieva, S. A Battery Cell Equalisation System Based on a Supercapacitors Tank and DC–DC Converters for Automotive Applications. World Electr. Veh. J. 2023, 14, 185. [Google Scholar] [CrossRef]
- Datasheet 125V Heavy Transportation Modules. Available online: https://datasheet.octopart.com/BMOD0063-P125-B24-Maxwell-Technologies-datasheet-11027548.pdf (accessed on 30 November 2023).
- Zhong, Y.; Zhang, J.; Li, G.; Liu, A. Research on Energy Efficiency of Supercapacitor Energy Storage System. In Proceedings of the 2006 International Conference on Power System Technology, Chongqing, China, 22–26 October 2006. [Google Scholar] [CrossRef]
- Bieliński, K.; Młodzikowski, P. Selected results of investigations of the charging process of electric vehicle batteries. Przegląd Elektrotechniczny 2019, 10, 52–55. (In Polish) [Google Scholar] [CrossRef]
- National Center for Emission Balancing and Management. Product Indicators for Electrical Energy. Electrical Energy Benchmarks for 2021 Published in DECEMBER 2022. Available online: https://www.kobize.pl/pl/fileCategory/id/28/wskazniki-emisyjnosci (accessed on 7 December 2023). (In Polish).


| Transformer type | - | TZE 4402 | - |
| Nominal power | SN | 4400 | kVA |
| Connection system | - | Yd11 | - |
| Short-circuit voltage | ΔVk% | 11 | % |
| Number of diodes connected in series | nsz | 8 | - |
| Number of diodes connected in parallel | nr | 6 | - |
| Nominal current | IN | 750 | A |
| Nominal voltage | VN | 3300 | V |
| Substation open-circuit voltage | V0 | 3600 | V |
| Substation resistance | RT | 0.200 | Ω |
| Nominal capacitance | CN | 63 | F |
| Capacitance change (% decrease from minimum initial value) | - | 20 | % |
| Nominal voltage | VN | 125 | V |
| Capacitance change coefficient due to voltage | κ | 0.00008 | F/V |
| Equivalent series resistance | Rs | 18 | mΩ |
| Mass, typical | m | 60.04 | kg |
| Length | l | 762 | mm |
| Width | h | 425 | mm |
| Height | h | 265 | mm |
| Supercapacitor Charging Cycle | Esc p | Esc k | Esc rek | Eh | ΔE | η |
|---|---|---|---|---|---|---|
| kWh | kWh | kWh | kWh | kWh | % | |
| charging I | 1.04 | 19.6 | 18.6 | 19.6 | 1.04 | 94.7% |
| charging II | 5.82 | 19.6 | 13.8 | 19.6 | 5.82 | 70.3% |
| charging III | 4.61 | 19.6 | 15.0 | 19.6 | 4.61 | 76.5% |
| EV Battery-Charging Cycle | Esc k | Esc p | ηp | Ebatt | Missing Electrical Energy |
|---|---|---|---|---|---|
| kWh | kWh | % | kWh | kWh | |
| charging I | 19.6 | 1.04 | 85% | 15.8 | 92.2 |
| charging II | 19.6 | 5.82 | 11.7 | 80.5 | |
| charging III | 19.6 | 4.61 | 12.7 | 67.8 |
| Type of Emission | Emission Rate [g/kWh] |
|---|---|
| CO2 | 708 |
| SOx/SO2 | 0.505 |
| NOx/NO2 | 0.505 |
| CO | 0.237 |
| Total dust | 0.022 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazur, Ł.; Bieliński, K.S.; Kłosowski, Z. A New Approach to Use of Traction Power Network in Poland for Charging Electric Vehicles. Energies 2024, 17, 1123. https://doi.org/10.3390/en17051123
Mazur Ł, Bieliński KS, Kłosowski Z. A New Approach to Use of Traction Power Network in Poland for Charging Electric Vehicles. Energies. 2024; 17(5):1123. https://doi.org/10.3390/en17051123
Chicago/Turabian StyleMazur, Łukasz, Kazimierz Stanisław Bieliński, and Zbigniew Kłosowski. 2024. "A New Approach to Use of Traction Power Network in Poland for Charging Electric Vehicles" Energies 17, no. 5: 1123. https://doi.org/10.3390/en17051123
APA StyleMazur, Ł., Bieliński, K. S., & Kłosowski, Z. (2024). A New Approach to Use of Traction Power Network in Poland for Charging Electric Vehicles. Energies, 17(5), 1123. https://doi.org/10.3390/en17051123







