Energy-Aware Multicriteria Control Performance Assessment
Abstract
:1. Introduction
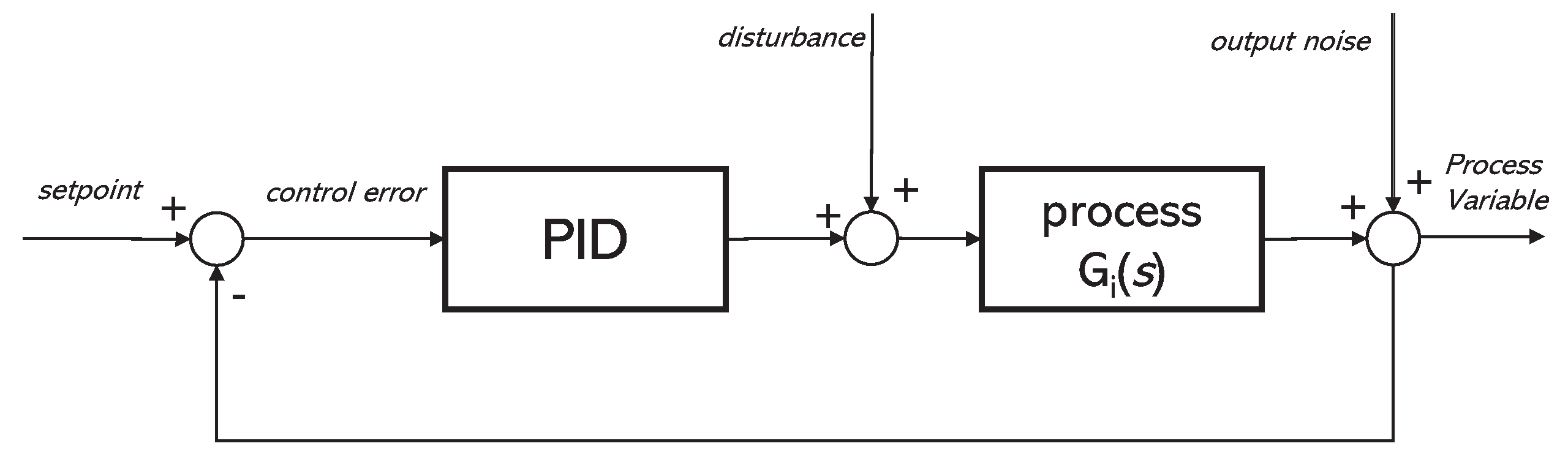
2. Methods and Measures
2.1. CPA Integral Indexes
2.2. L-Moments
2.3. Robust Statistics
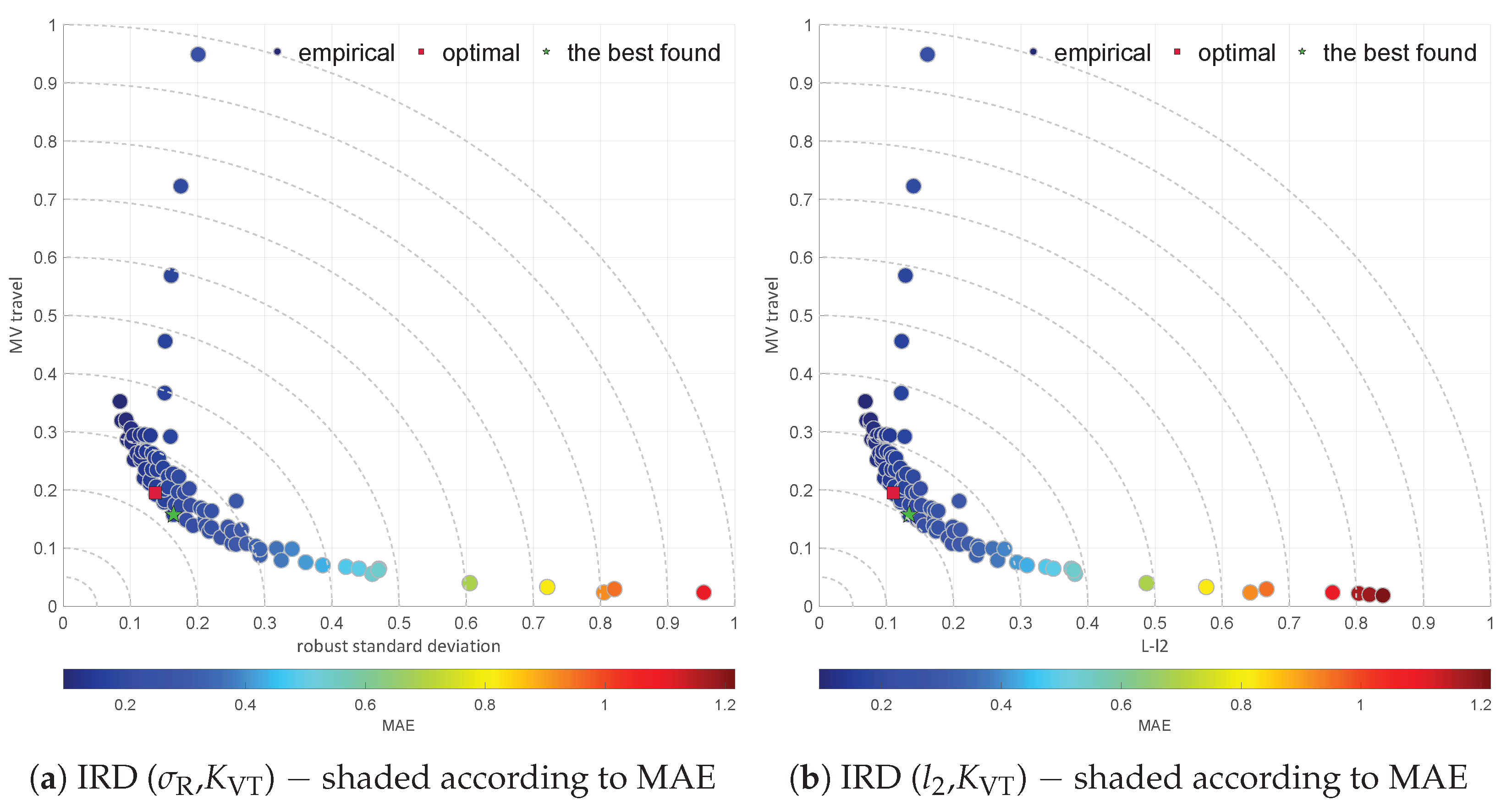
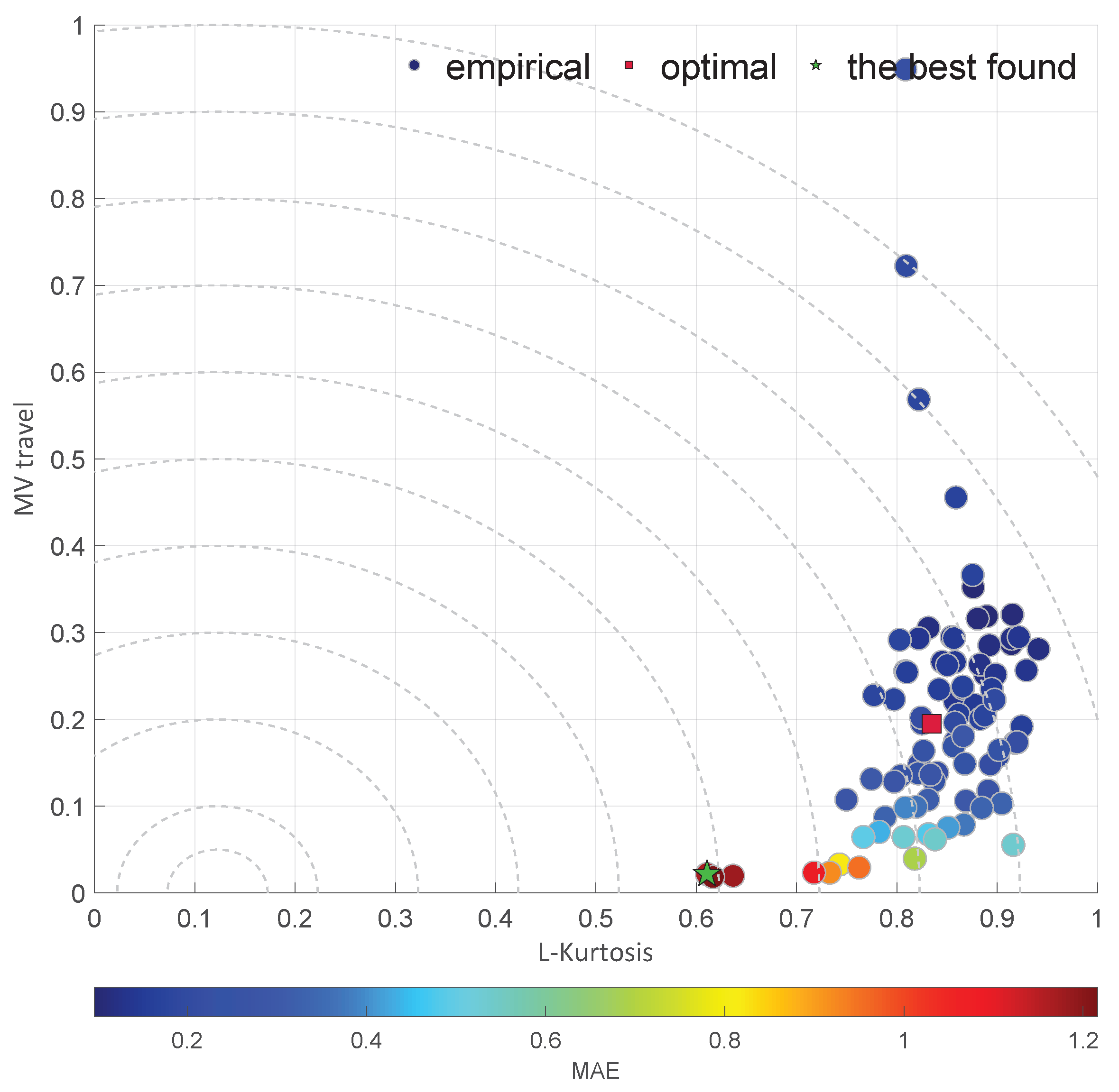
2.4. Moment Ratio Diagrams
2.5. L-Moment Ratio Diagrams
2.6. Tail Index
2.7. ARFIMA Models and Fractional Order
2.8. Quadratic Manipulated Variable
2.9. Indexes of the Valve Energy
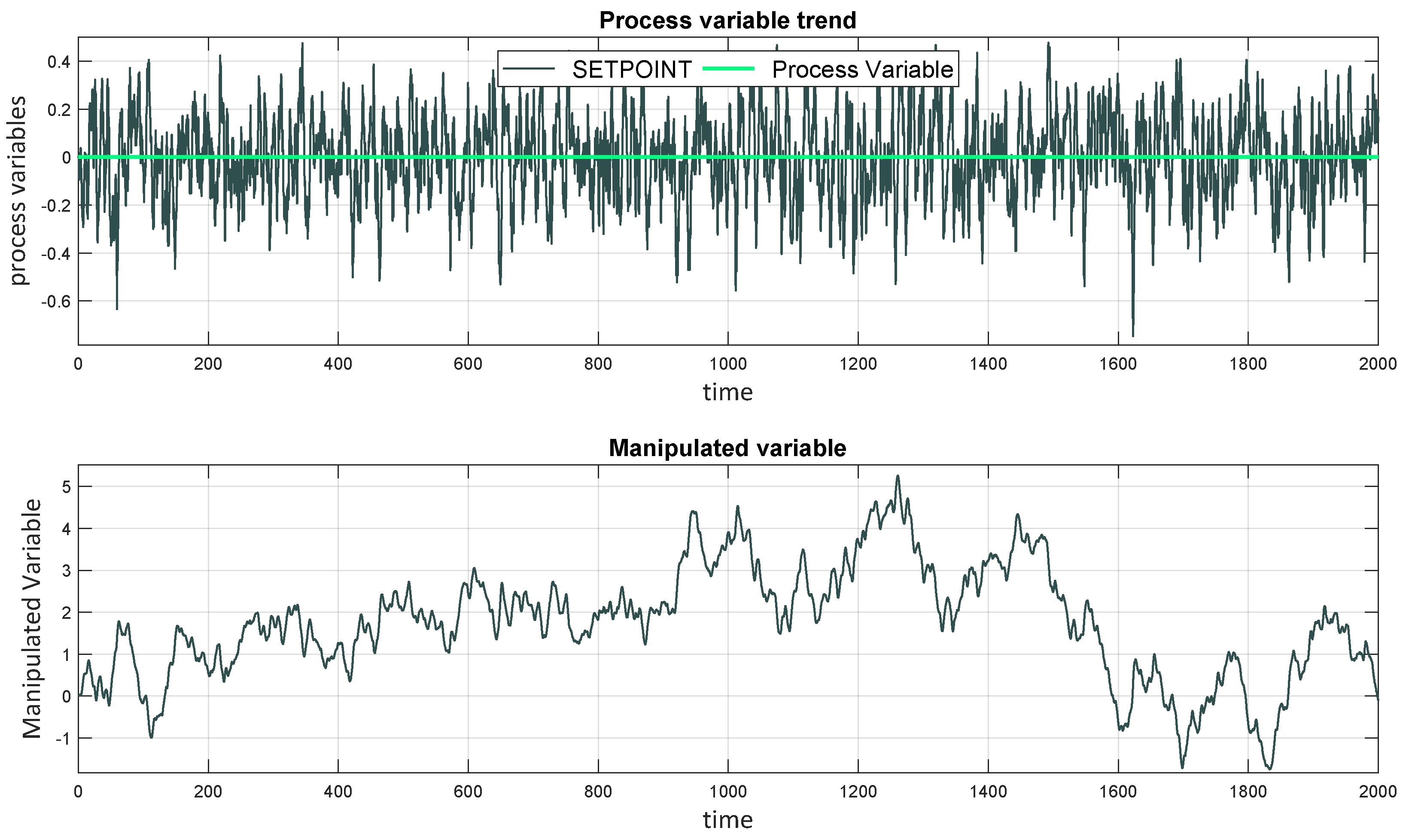
3. Simulation Analysis
- –
- System with multiple equal poles
- –
- First-order transfer function with a dead time
- –
- Fast and slow modes
- measurement noise simulated as a Gaussian process having ;
- fat-tail disturbance filtered by the inertia of the first order added before the process and simulated as an -stable distribution with , , and [36].
3.1. Simulation Results
3.2. Observations Summary
- PID loop control quality assessment is a multicriteria task.
- The overshoot and settling time indexes allow us to deliver a suitable solution, but they exhibit one significant deficiency, as they require a step response, which is not achievable in the industrial reality.
- The CPA indexes do not take into account the energy spent during control actions and the respective indicators are proposed.
- The incorporation of the energy factors into the assessment has the tendency to suggest slower controllers, which is natural.
- The MAE and robust scale estimators behave in a similar way.
- The shape factors, i.e., the stability exponent and L-kurtosis , have a tendency to indicate extremely sluggish control performance.
- The use of the fractional order evaluated as the the Geweke–Porter–Hudak estimator brings a new assessment perspective and enables us to give constructive loop tuning indications.
4. Conclusions and Further Research
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CPA | Control Performance Assessment |
| PID | Proportional-Integral-Derivative |
| KPI | Key Performance Indicators |
| QMV | Quadratic Manipulated Variable |
| MRD | Moment Ratio Diagram |
| LMRD | L-Moment Ratio Diagram |
| IRD | Index Ratio Diagram |
| MSE | Mean Square Error |
| MAE | Mean Absolute Error |
| Probability Density Function | |
| ML | Maximum Likelihood |
| GLO | Generalized Logistic distribution |
| GAM | Gamma Distribution |
| LGN | Lognormal Distribution |
| EXP | Exponential Distribution |
| WEI | Weibull Distribution |
| GEV | Generalized Extreme Value Distribution |
| GPD | Generalized Pareto Distribution |
| K4D | Four-Parameter Kappa Distribution |
| LS | Least Squares |
| QE | Quadratic Error |
References
- Bauer, M.; Horch, A.; Xie, L.; Jelali, M.; Thornhill, N. The current state of control loop performance monitoring—A survey of application in industry. J. Process Control 2016, 38, 9539. [Google Scholar] [CrossRef]
- O’Neill, Z.; Li, Y.; Williams, K. HVAC control loop performance assessment: A critical review (1587-RP). Sci. Technol. Built Environ. 2017, 23, 619–636. [Google Scholar] [CrossRef]
- Mercorelli, P. Robust Control as a Mathematical Paradigm for Innovative Engineering Applications. Mathematics 2022, 10, 4399. [Google Scholar] [CrossRef]
- Liberati, F.; Cirino, C.M.F.; Tortorelli, A. Energy-Aware Model Predictive Control of Assembly Lines. Actuators 2022, 11, 172. [Google Scholar] [CrossRef]
- Arabas, P.; Sikora, A.; Szynkiewicz, W. Energy-Aware Activity Control for Wireless Sensing Infrastructure Using Periodic Communication and Mixed-Integer Programming. Energies 2021, 14, 4828. [Google Scholar] [CrossRef]
- Krok, M.; Majewski, P.; Hunek, W.P.; Feliks, T. Energy Optimization of the Continuous-Time Perfect Control Algorithm. Energies 2022, 15, 1555. [Google Scholar] [CrossRef]
- Domański, P.D. Improving Actuator Wearing Using Noise Filtering. Sensors 2022, 22, 8910. [Google Scholar] [CrossRef]
- Grobelna, I. Intelligent Industrial Process Control Systems. Sensors 2023, 23, 6838. [Google Scholar] [CrossRef]
- Ouarda, T.; Charron, C.; Chebana, F. Review of criteria for the selection of probability distributions for wind speed data and introduction of the moment and L-moment ratio diagram methods, with a case study. Energy Convers. Manag. 2016, 124, 247–265. [Google Scholar] [CrossRef]
- Chaber, P.; Domański, P.D. Control Assessment with Moment Ratio Diagrams. In Proceedings of the Advanced, Contemporary Control; Pawelczyk, M., Bismor, D., Ogonowski, S., Kacprzyk, J., Eds.; Springer: Cham, Switzerland, 2023; pp. 3–13. [Google Scholar]
- Kaniuka, J.; Ostrysz, J.; Groszyk, M.; Bieniek, K.; Cyperski, S.; Domański, P.D. Study on Cost Estimation of the External Fleet Full Truckload Contracts. In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics, Rome, Italy, 13–15 November 2023; Volume 2, pp. 316–323. [Google Scholar]
- Huber, P.J.; Ronchetti, E.M. Robust Statistics, 2nd ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. Ser. B 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Qi, Y. On the tail index of a heavy tailed distribution. Ann. Inst. Stat. Math. 2010, 62, 277–298. [Google Scholar] [CrossRef]
- Sheng, H.; Chen, Y.; Qiu, T. Fractional Processes and Fractional-Order Signal Processing; Springer: London, UK, 2012. [Google Scholar]
- Liu, K.; Chen, Y.; Zhang, X. An Evaluation of ARFIMA (Autoregressive Fractional Integral Moving Average) Programs. Axioms 2017, 6, 16. [Google Scholar] [CrossRef]
- Samad, T. A Survey on Industry Impact and Challenges Thereof [Technical Activities]. IEEE Control Syst. Magaz. 2017, 37, 17–18. [Google Scholar]
- Åström, K.J.; Hägglund, T. Benchmark Systems for PID Control. In Proceedings of the IFAC Digital Control: Past, Present and Future of PlD Control, Terrassa, Spain, 5–7 April 2000; pp. 165–166. [Google Scholar]
- Knierim-Dietz, N.; Hanel, L.; Lehner, J. Definition and Verification of the Control Loop Performance for Different Power Plant Types; Technical Report; Institute of Combustion and Power Plant Technology, University of Stuttgart: Stuttgart, Germany, 2012. [Google Scholar]
- Rousseeuw, P.J.; Leroy, A.M. Robust Regression and Outlier Detection; John Wiley & Sons, Inc.: New York, NY, USA, 1987. [Google Scholar]
- Bílková, D. L-Moments and TL-Moments as an Alternative Tool of Statistical Data Analysis. J. Appl. Math. Phys. 2014, 2, 919–929. [Google Scholar] [CrossRef]
- Peel, M.; Wang, Q.; Mcmahon, T. The utility L-moment ratio diagrams for selecting a regional probability distribution. Hydrol. Sci. J. 2001, 46, 147–155. [Google Scholar] [CrossRef]
- Ronchetti, E. The main contributions of robust statistics to statistical science and a new challenge. In Metron; Springer: Berlin/Heidelberg, Germany, 2021; Volume 79, pp. 127–135. [Google Scholar]
- Verboven, S.; Hubert, M. LIBRA: A Matlab library for robust analysis. Chemom. Intell. Lab. Syst. 2005, 75, 127–136. [Google Scholar] [CrossRef]
- Vargo, E.; Pasupathy, R.; Leemis, L. Moment-Ratio Diagrams for Univariate Distributions. In Computational Probability Applications; Springer: Berlin/Heidelberg, Germany, 2010; Volume 42, pp. 149–164. [Google Scholar]
- Tallaksen, L.; Van Lanen, H. Hydrological Drought: Processes and Estimation Methods for Streamflow and Groundwater; Developments in Water Science; Elsevier Science B.V.: Amsterdam, The Netherlands, 2004; Volume 48. [Google Scholar]
- Kjeldsen, T.R.; Ahn, H.; Prosdocimi, I. On the use of a four-parameter kappa distribution in regional frequency analysis. Hydrol. Sci. J. 2017, 62, 1354–1363. [Google Scholar] [CrossRef]
- Taleb, N.N. Real-World Statistical Consequences of Fat Tails: Papers and Commentary; Technical Incerto Collection; STEM Academic Press: New York, NY, USA, 2018. [Google Scholar]
- Fedotenkov, I. A Review of More than One Hundred Pareto—Tail Index Estimators. Statistica 2020, 80, 245–299. [Google Scholar]
- Hill, B.M. A Simple General Approach to Inference About the Tail of a Distribution. Ann. Stat. 1975, 3, 1163–1174. [Google Scholar] [CrossRef]
- Huisman, R.; Koedijk, K.; Kool, C.; Palm, F. Tail-Index Estimates in Small Samples. J. Bus. Econ. Stat. 2001, 19, 208–216. [Google Scholar] [CrossRef]
- Burnecki, K.; Sikora, G. Identification and validation of stable ARFIMA processes with application to UMTS data. Chaos Solitons Fractals 2017, 102, 456–466. [Google Scholar] [CrossRef]
- Geweke, J.; Porter-Hudak, S. The Estimation and Application of Long Memory Time Series Models. J. Time Ser. Anal. 1983, 4, 221–238. [Google Scholar] [CrossRef]
- Beran, J. Statistics for Long-Memory Processes, 1st ed.; Routledge: New York, NY, USA, 1994. [Google Scholar]
- Unbehauen, H. Controller design in time domain. In Encyclopedia of Life Support Systems (EOLSS); Unbehauen, H., Ed.; Eolss Publishers: Oxford, UK, 2009. [Google Scholar]
- Nolan, J. Univariate Stable Distributions. Models for Heavy Tailed Data; Springer Series in Operations Research and Financial Engineering; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Swanda, A.P.; Seborg, D.E. Controller performance assessment based on setpoint response data. In Proceedings of the 1999 American Control Conference, San Diego, CA, USA, 2–4 June 1999; Volume 6, pp. 3863–3867. [Google Scholar]
- Chaber, P.; Domański, P.D. Fractional control performance assessment of the nonlinear mechanical systems. In Proceedings of the Preprints of the 3rd International Nonlinear Dynamics Conference NODYCON 2023, Rome, Italy, 18–22 June 2023. [Google Scholar]
- Spinner, T.; Srinivasan, B.; Rengaswamy, R. Data-based automated diagnosis and iterative retuning of proportional-integral (PI) controllers. Control Eng. Pract. 2014, 29, 23–41. [Google Scholar] [CrossRef]




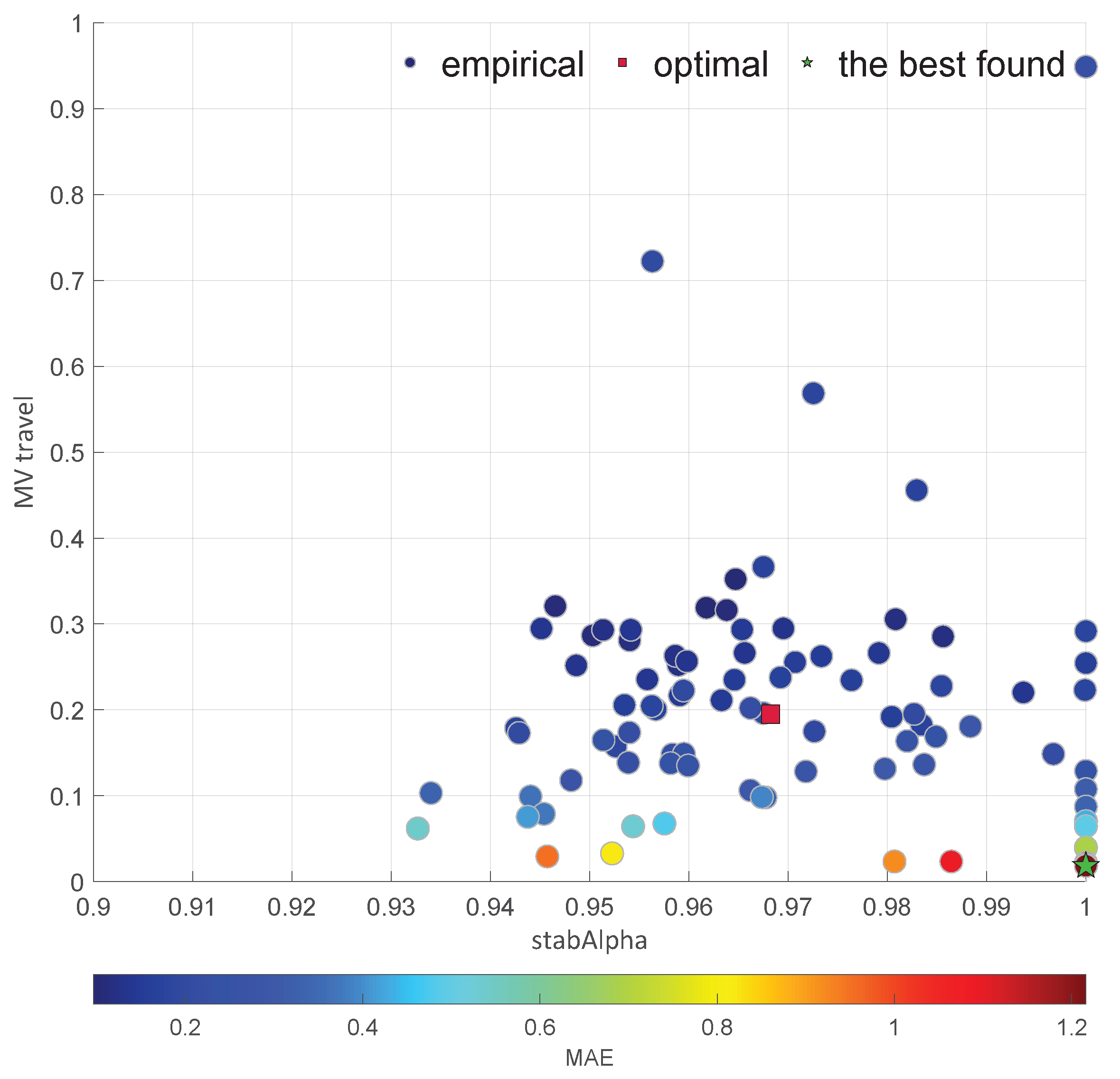
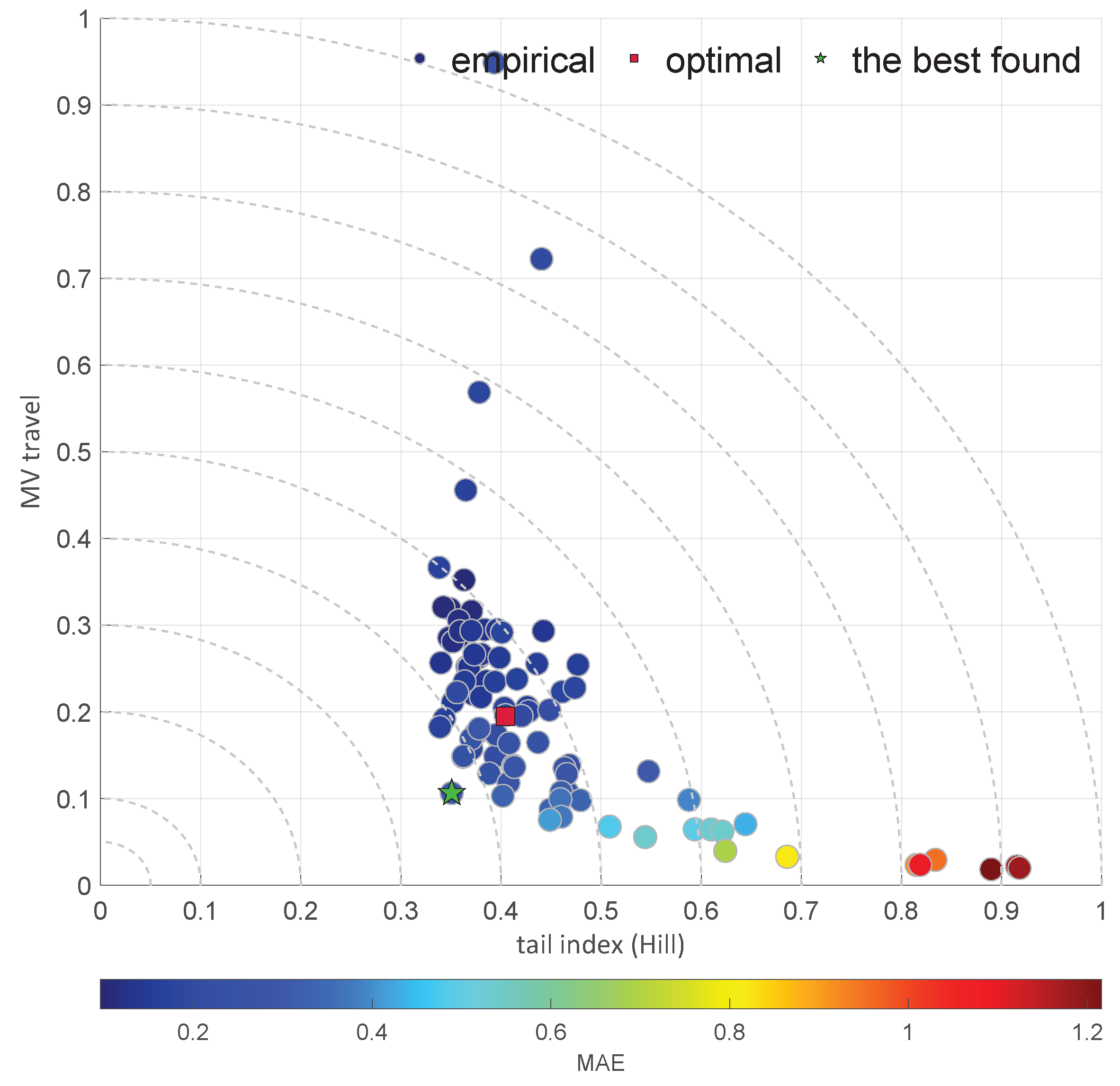

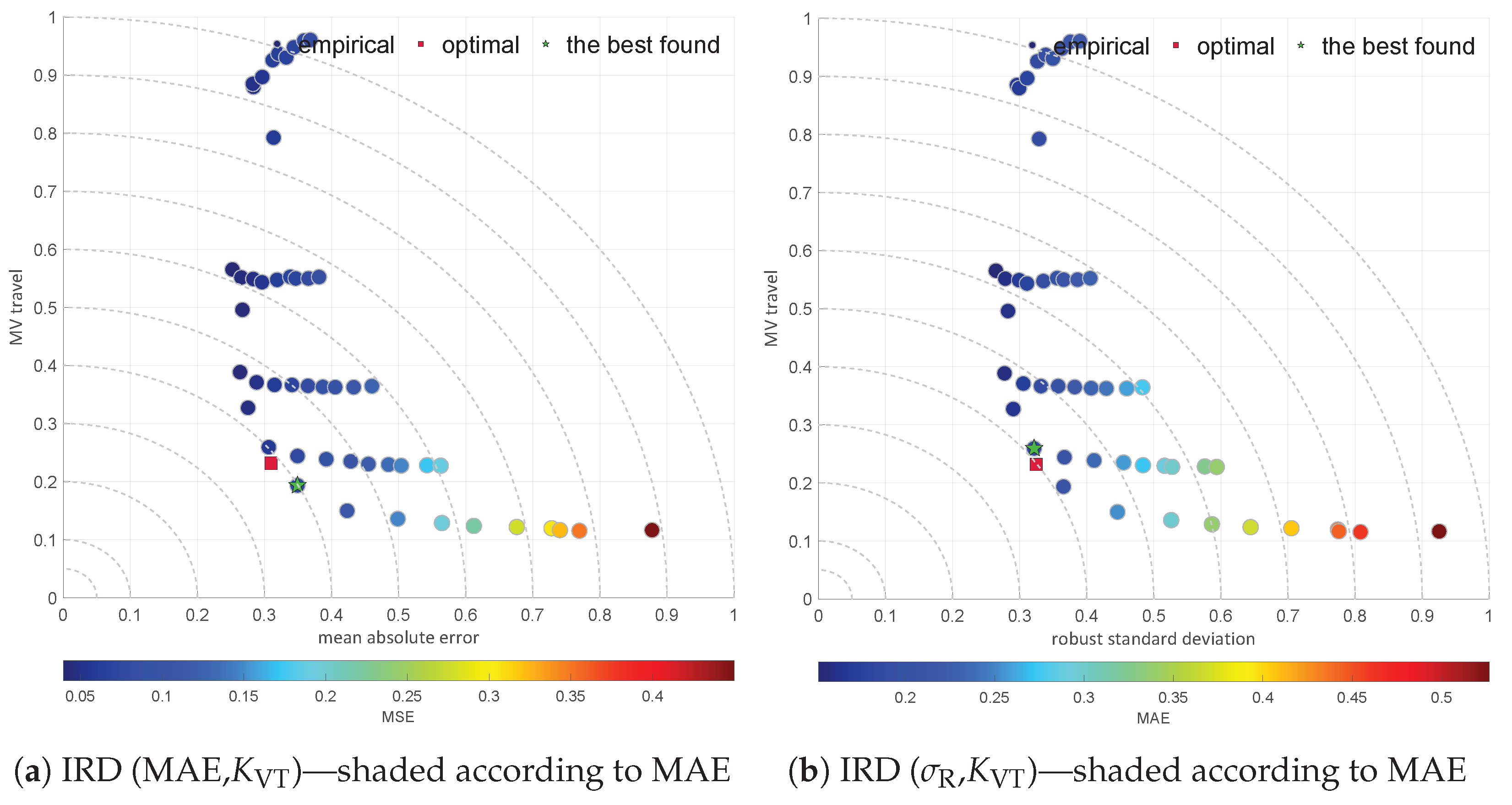

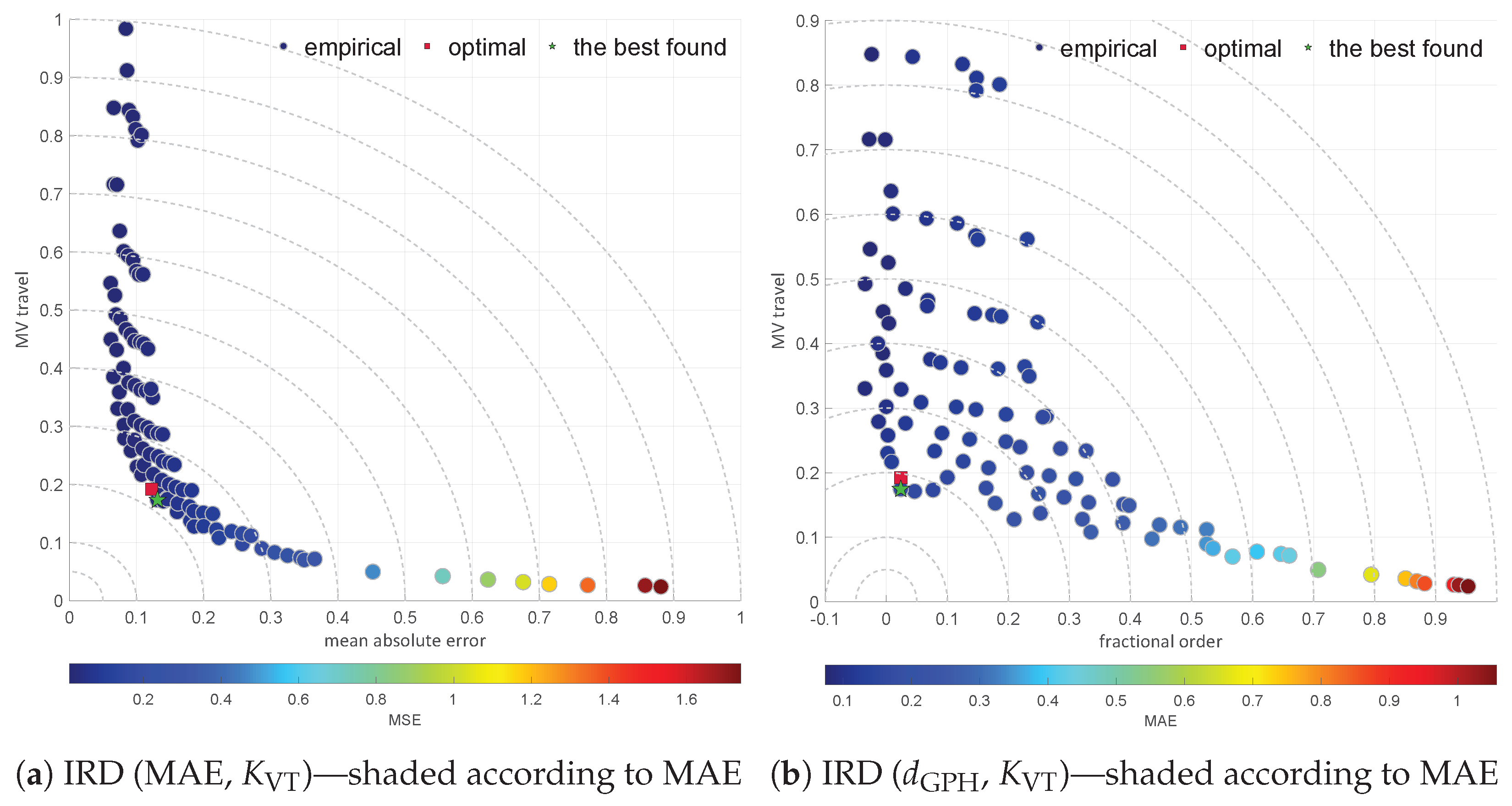
| Diagram | Characteristic | |||||
|---|---|---|---|---|---|---|
| IRD (,) | 1.05 | 3.20 | 0.9293 | 0.01 | 9.47 | good |
| IRD (MSE,) | 0.30 | 3.20 | 0.9293 | 0.00 | 38.7 | sluggish |
| IRD (MAE,) | 0.80 | 3.20 | 0.9293 | 0.00 | 12.60 | good |
| IRD (,) | ||||||
| IRD (,) | 0.05 | 7.20 | 0.9293 | 0.00 | 572 | extremely sluggish |
| IRD (,) | 0.05 | 10.20 | 0.9293 | 0.00 | 816 | extremely sluggish |
| IRD (,) | 0.30 | 2.20 | 0.9293 | 0.00 | 20.7 | good, slow |
| IRD (,) | 0.30 | 1.20 | 0.9293 | 14.98 | 25.5 | aggressive |
| Diagram | Characteristic | |||||
|---|---|---|---|---|---|---|
| IRD (,) | 0.60 | 1.10 | 0.2121 | 0.00 | 6.92 | good |
| IRD (MSE,) | 0.20 | 0.60 | 0.2121 | 0.00 | 8.73 | good |
| IRD (MAE,) | ||||||
| IRD (,) | 0.40 | 1.10 | 0.2121 | 0.00 | 10.00 | slow |
| IRD (,) | ||||||
| IRD (,) | 0.20 | 5.10 | 0.2121 | 0.00 | 111 | extremely sluggish |
| IRD (,) | 0.20 | 3.60 | 0.2121 | 0.00 | 76.9 | extremely sluggish |
| IRD (,) | 0.20 | 0.60 | 0.2121 | 0.00 | 8.73 | good |
| IRD (,) | 0.20 | 0.60 | 0.2121 | 0.00 | 8.73 | good |
| Diagram | Characteristic | |||||
|---|---|---|---|---|---|---|
| IRD (,) | 0.32 | 0.55 | 0.0808 | 1.23 | 4.56 | fast |
| IRD (MSE,) | 0.12 | 0.55 | 0.0808 | 0.00 | 16.15 | slow |
| IRD (MAE,) | 0.22 | 0.55 | 0.0808 | 0.02 | 7.84 | good |
| IRD (,) | ||||||
| IRD (,) | ||||||
| IRD (,) | 0.02 | 2.30 | 0.0808 | 0.00 | 453.00 | extremely sluggish |
| IRD (,) | ||||||
| IRD (,) | 0.22 | 0.30 | 0.0808 | 5.64 | 6.55 | aggressive |
| IRD (,) | 0.02 | 0.05 | 0.0808 | 1.66 | 5.82 | fast |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domański, P.D. Energy-Aware Multicriteria Control Performance Assessment. Energies 2024, 17, 1173. https://doi.org/10.3390/en17051173
Domański PD. Energy-Aware Multicriteria Control Performance Assessment. Energies. 2024; 17(5):1173. https://doi.org/10.3390/en17051173
Chicago/Turabian StyleDomański, Paweł D. 2024. "Energy-Aware Multicriteria Control Performance Assessment" Energies 17, no. 5: 1173. https://doi.org/10.3390/en17051173






