Low-Cost System with Transient Reduction for Automatic Power Factor Controller in Three-Phase Low-Voltage Installations
Abstract
1. Introduction
2. Materials and Methods
2.1. Analysis of Currents through Real Capacitors
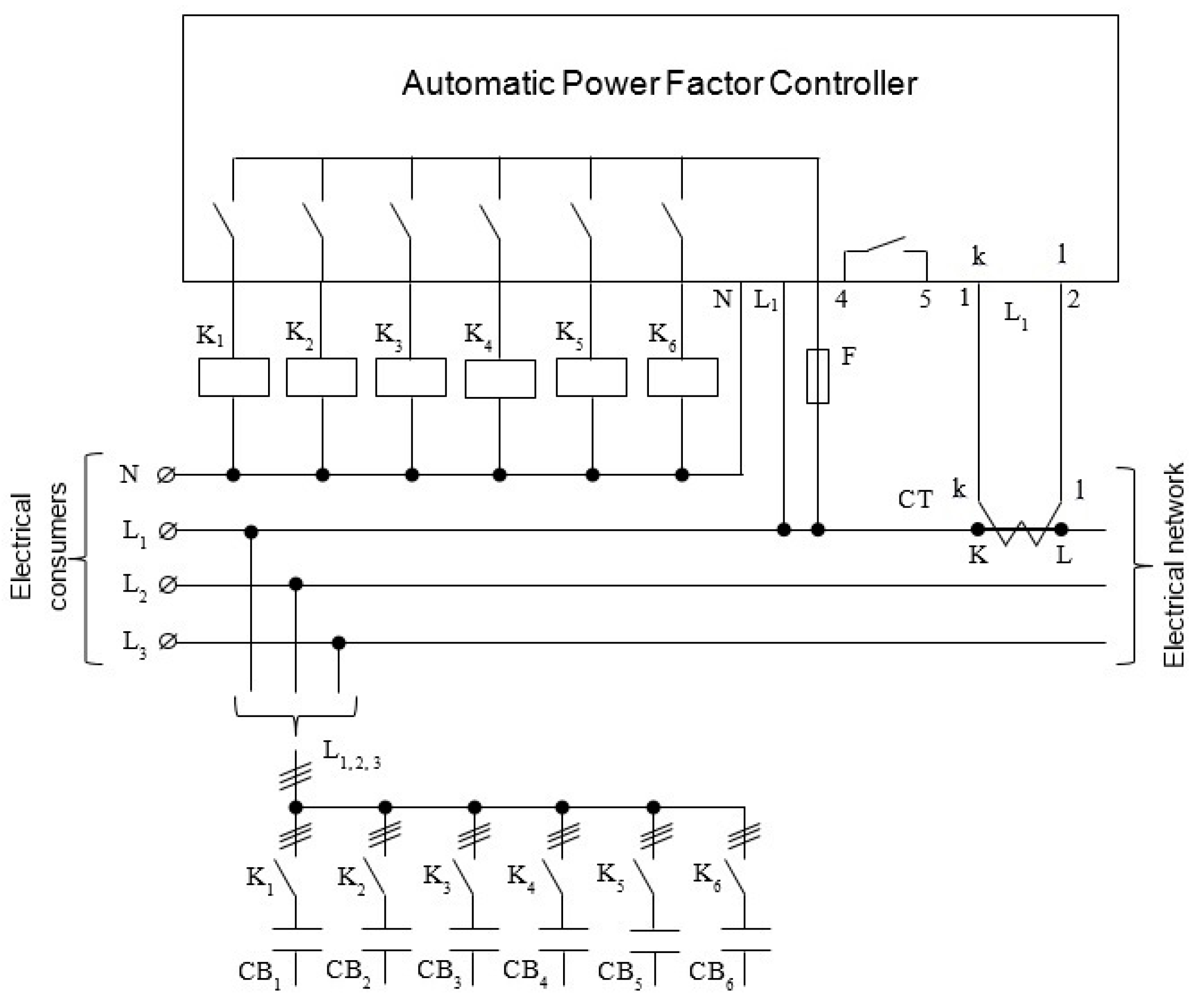
2.2. Automatic Power Factor Controller
- they have no moving parts;
- they can operate at high switching-on/switching-off frequencies;
- switching times are lower;
- the control can be applied when the voltage passes through zero, so that when starting the consumer absorbs a small current;
- they are more reliable than classic electromagnetic contactors.
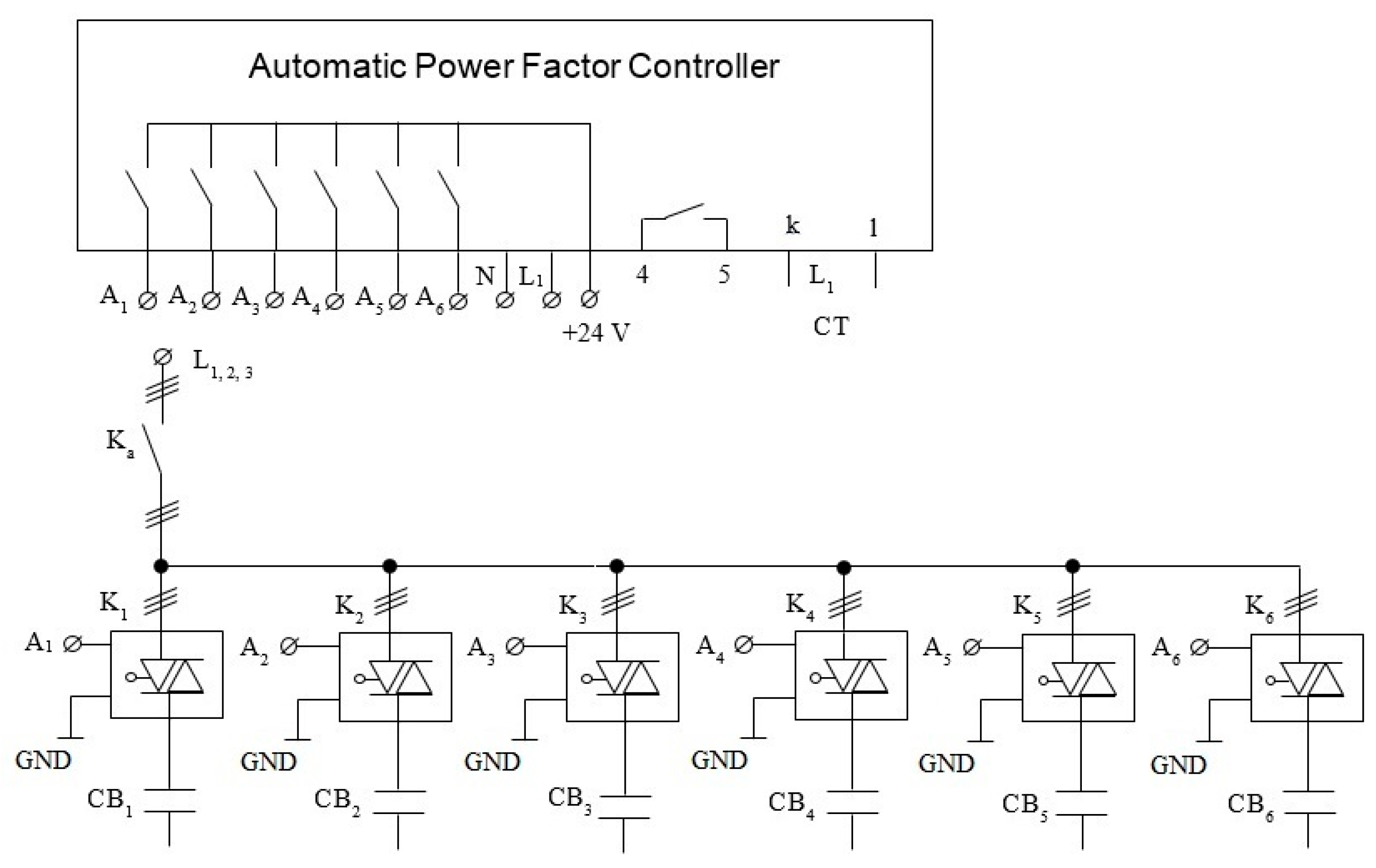
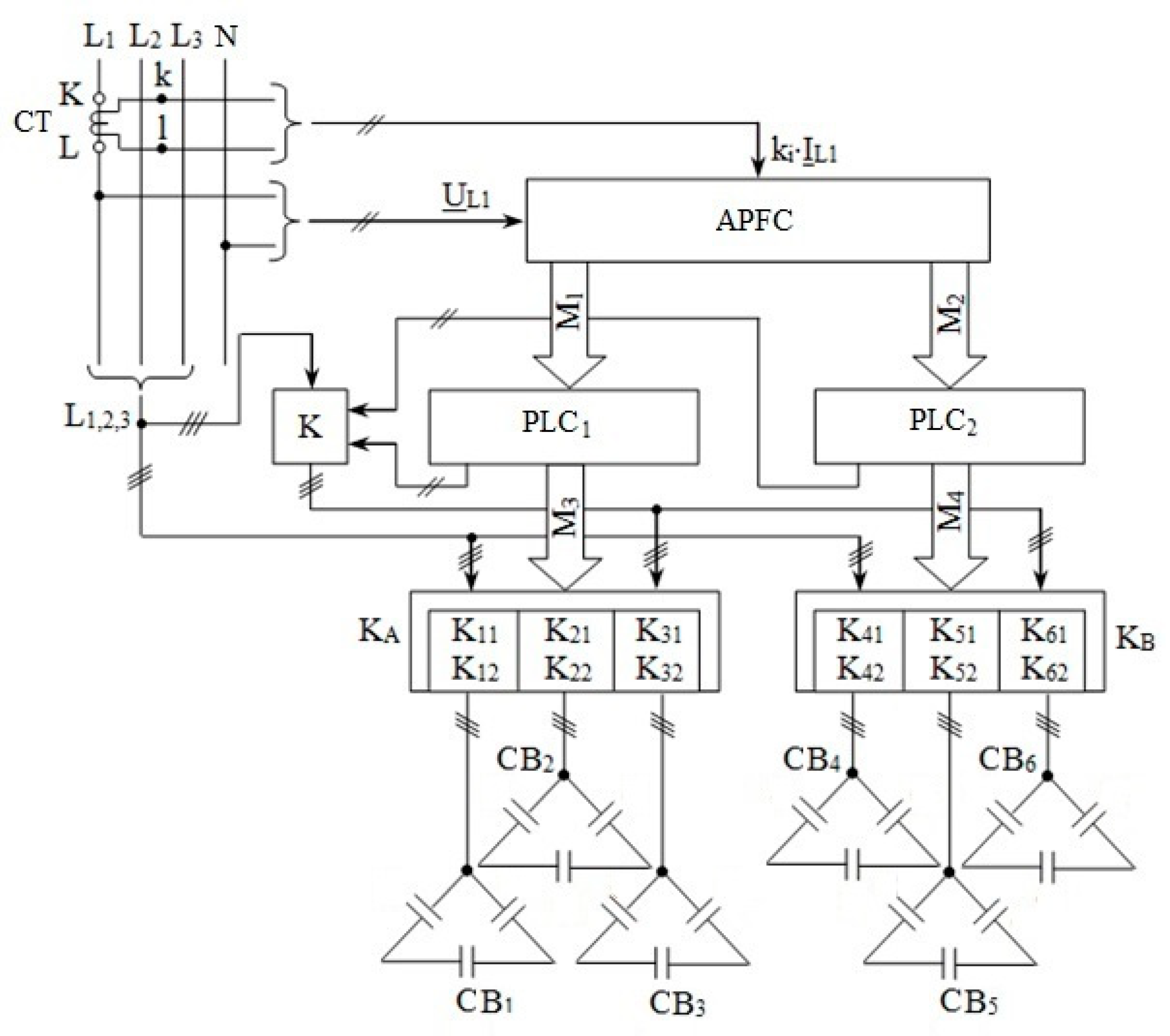
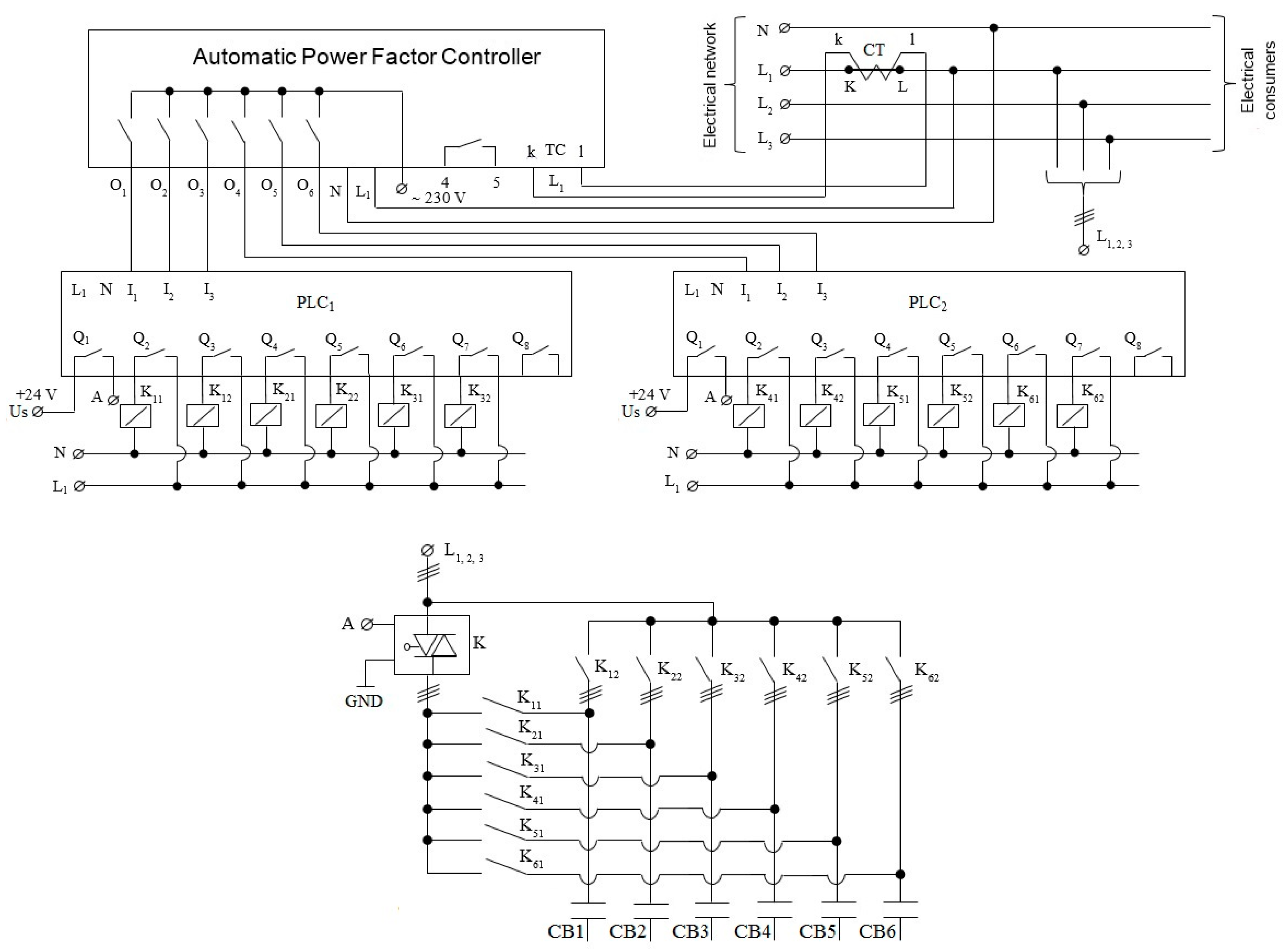
2.3. Low-Cost Automatic Power Factor Controller
- the current transformer is connected to the input terminals k and l, and the phase voltage of the L1 bar, to the terminals L1 and N of the APFC;
- the first three outputs of the APFC are connected to the first three inputs of the first PLC, and the next three outputs to the first three inputs of the second PLC;
- the first outputs of the two PLCs are connected to the command input of the three-phase power SSR, and the next six outputs of the two PLCs are connected to twelve EMCs, distributed six on each PLC;
- the EMCs are divided into six groups, each group consisting of two EMCs, which together with the common three-phase SSR are part of the circuits of the six CBs, so that the first CB in the group has the main contacts in series with the execution element (thyristors in anti-parallel) of the three-phase SSR, and the main contacts of the second EMC short-circuit the series of execution elements of the previously mentioned contactors, directly supplying the CB from the power distribution bars.
- the currents when connecting the capacitors are much reduced (from (20–50)xIn to In, where In is the nominal current);
- switch-on is performed at zero voltage;
- there is no discharge in the arc when switching;
- high reliability;
- lower costs than in the case of using a three-phase SSR for each CB;
- very high input/output isolation voltage;
- does not generate disruptive electromagnetic fields;
- superior lifetime compared to systems where CBs are connected with classical EMCs.
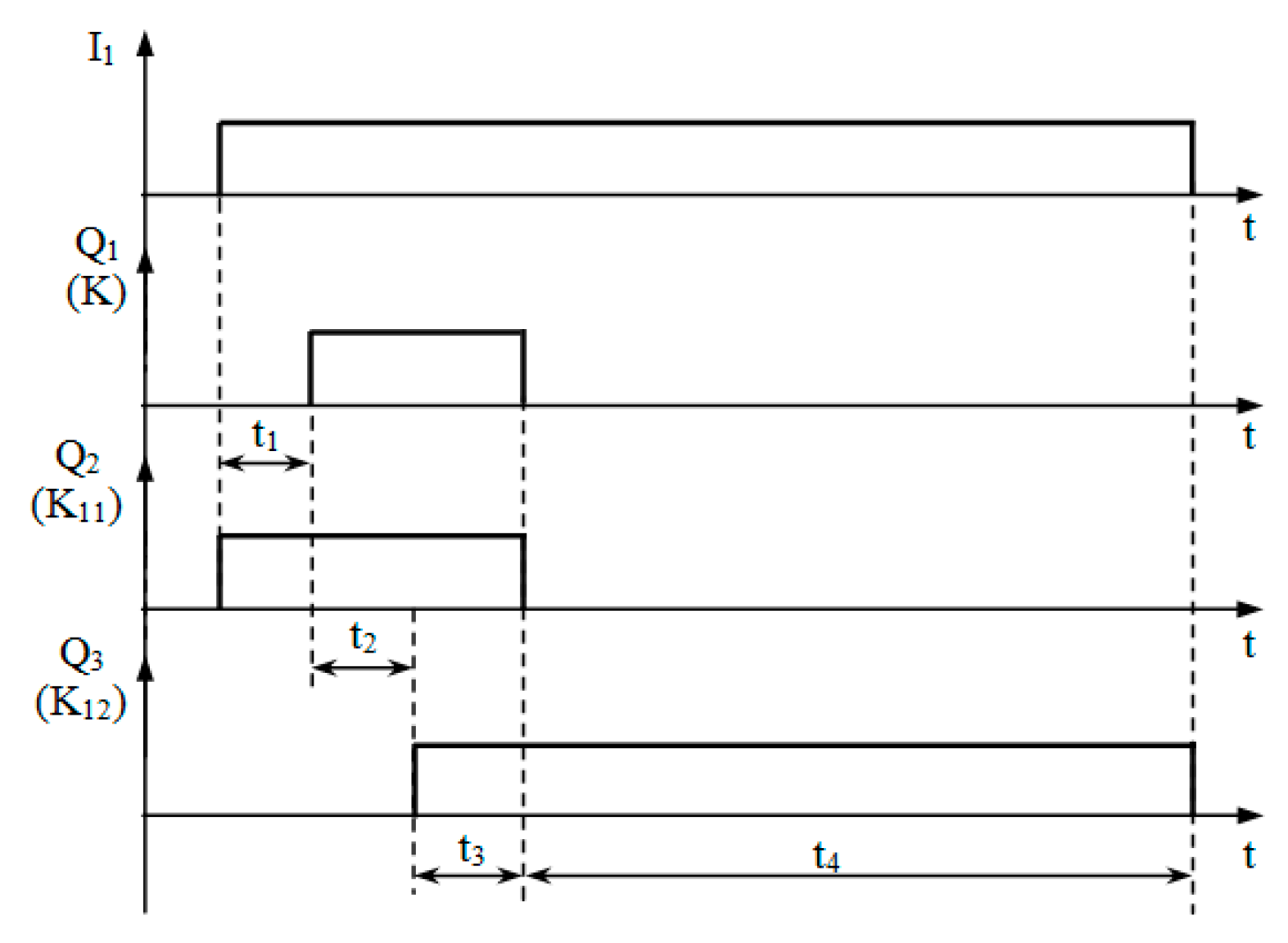
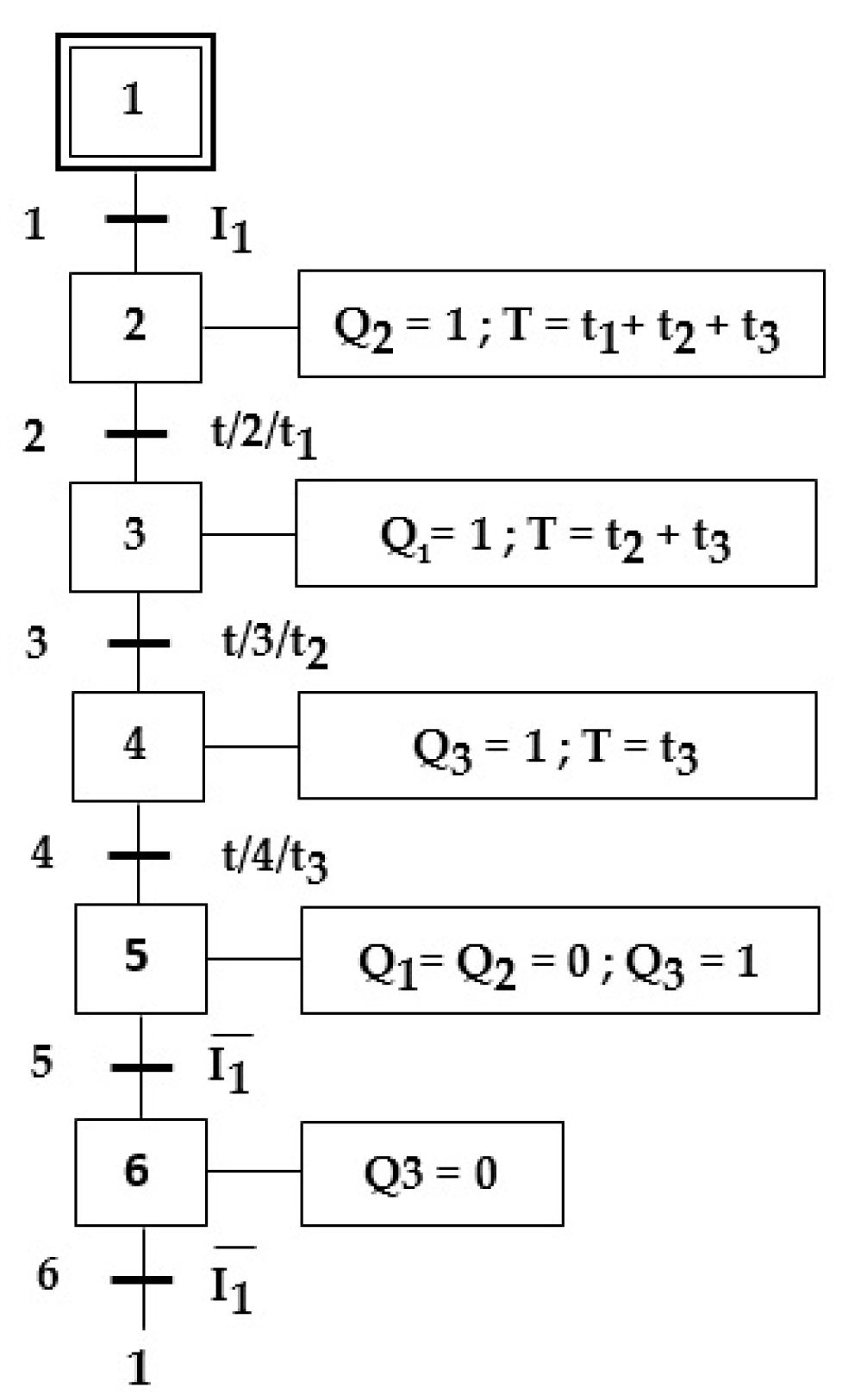
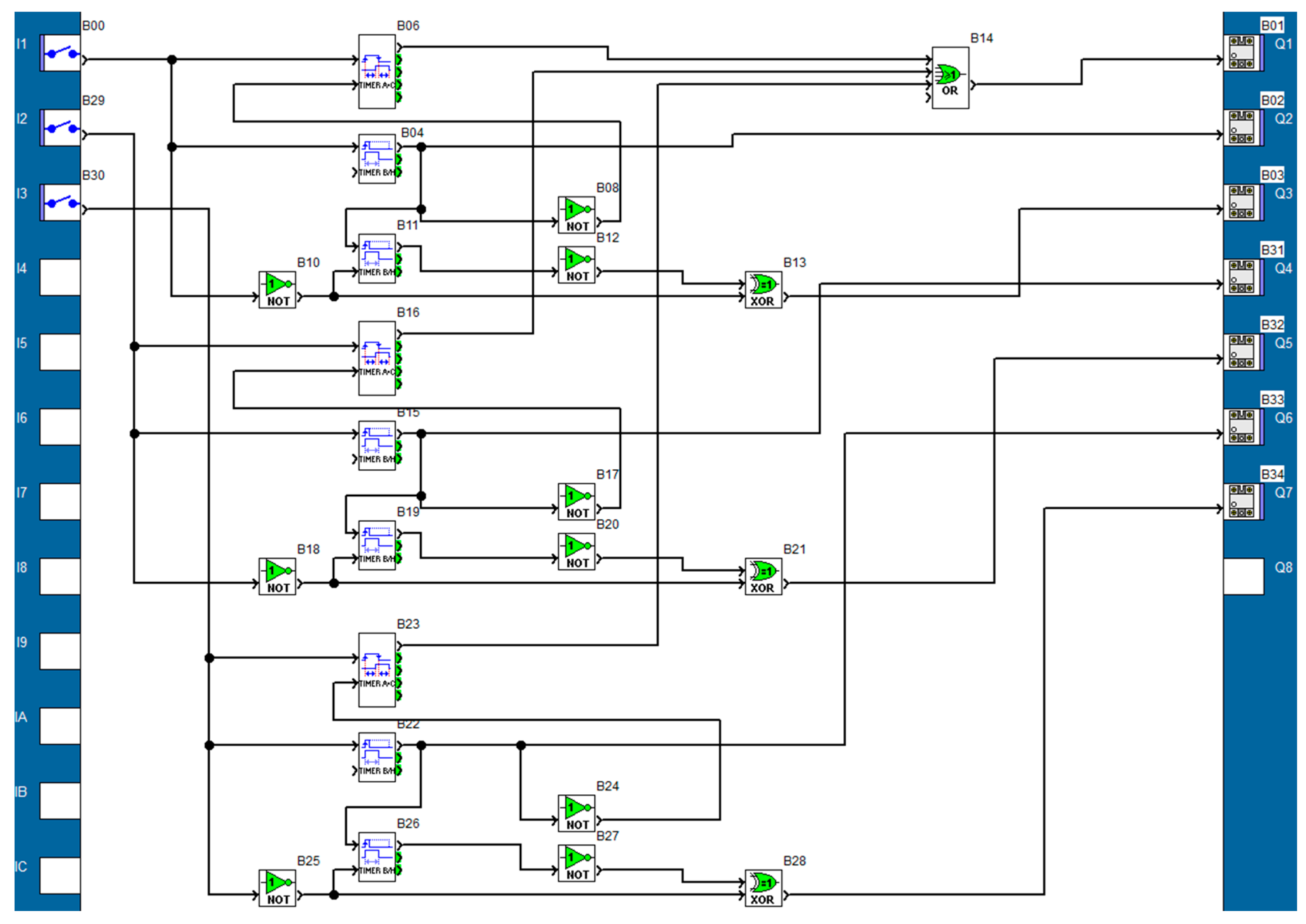
2.4. Programming the PLCs
2.5. Economical Review of Low-Cost APFC
3. Results
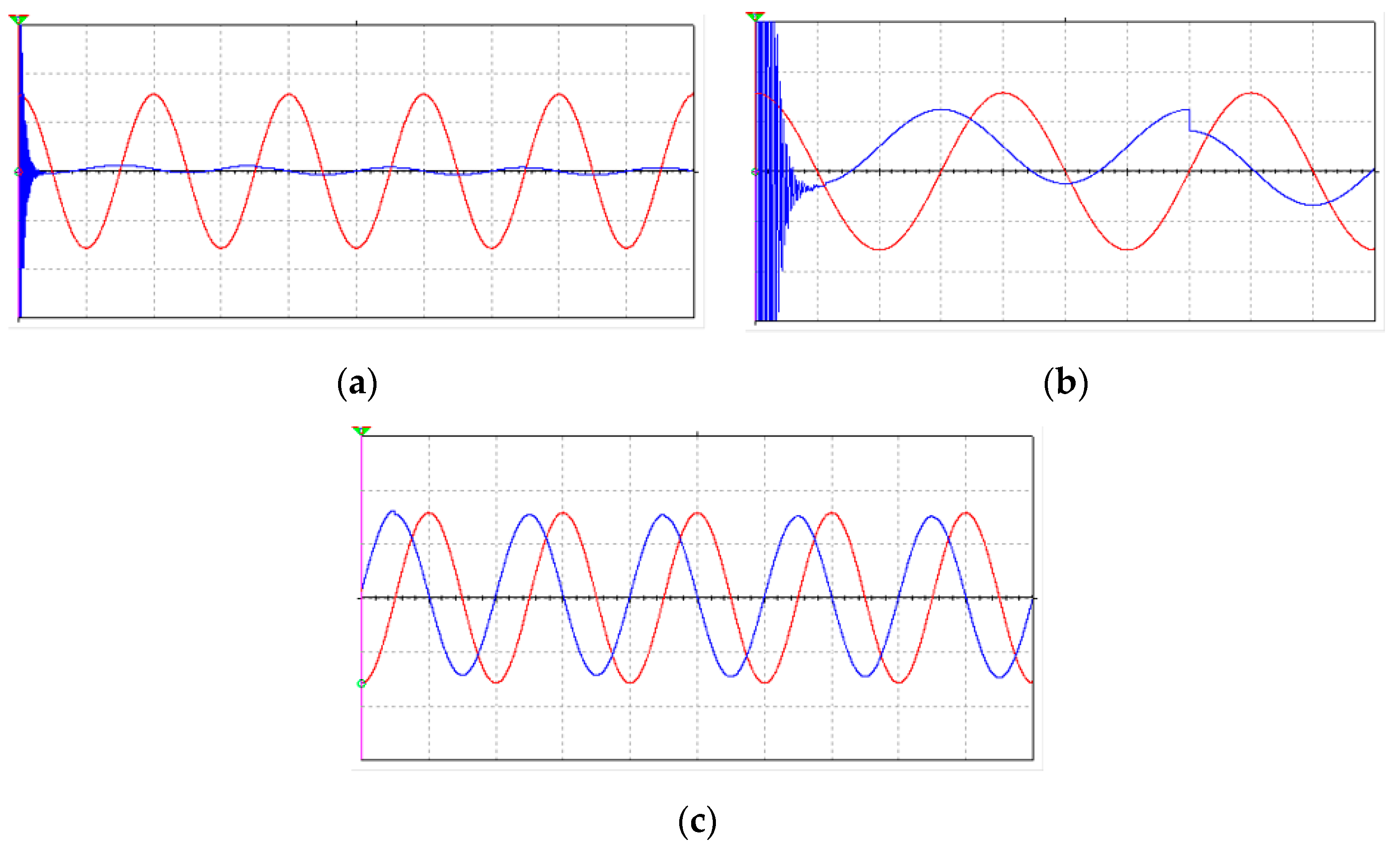
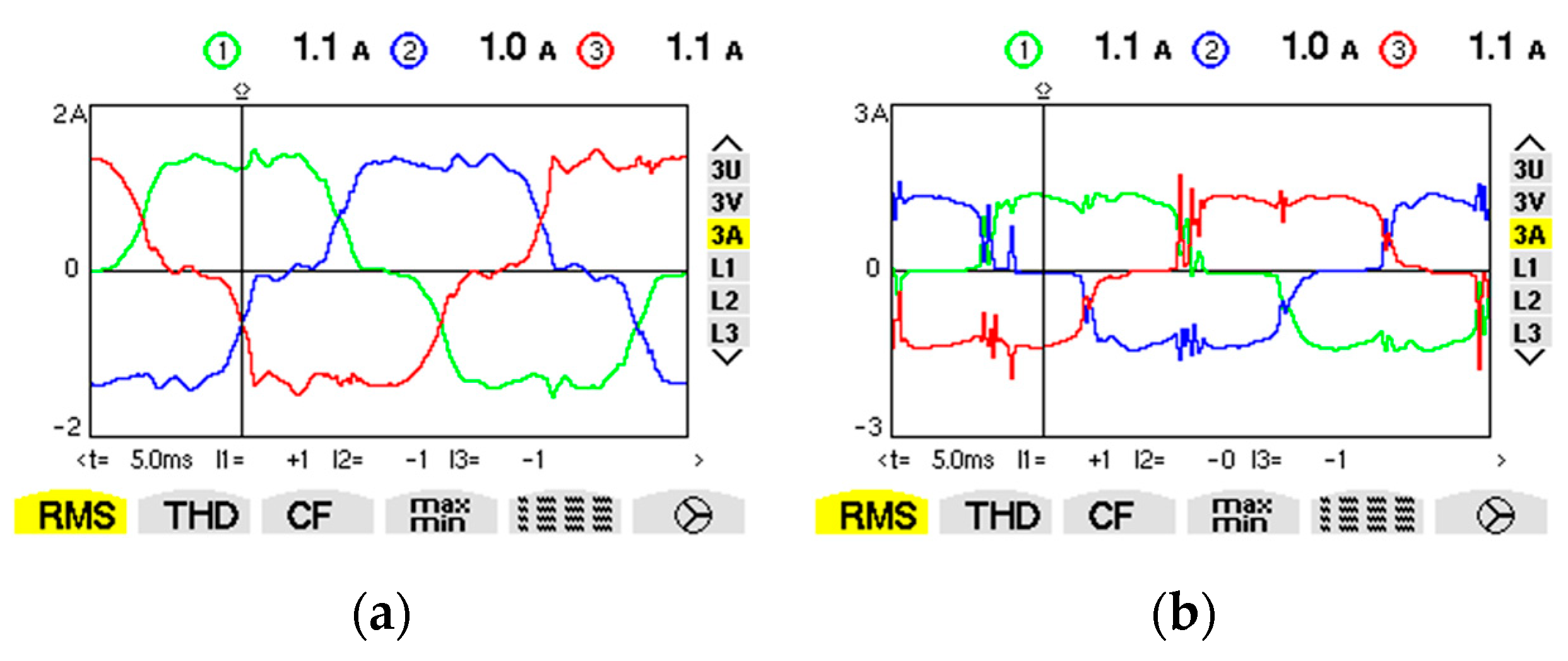
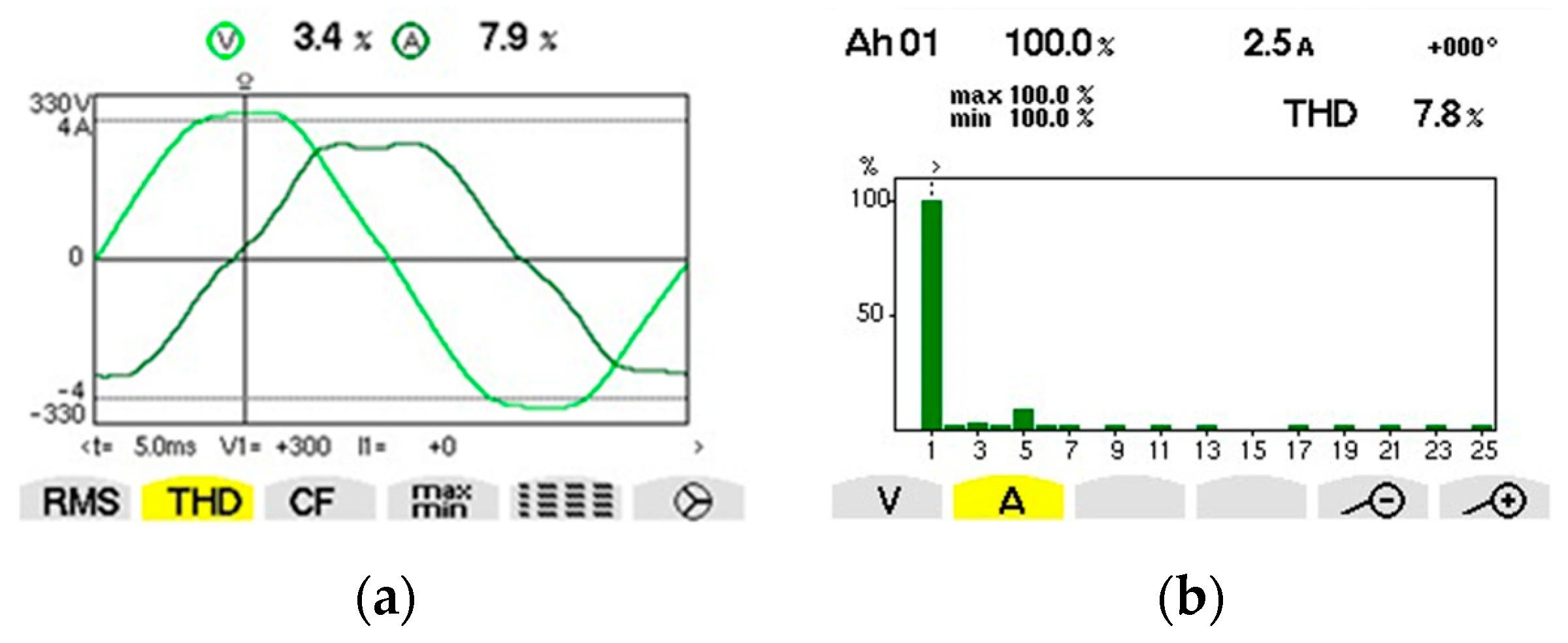
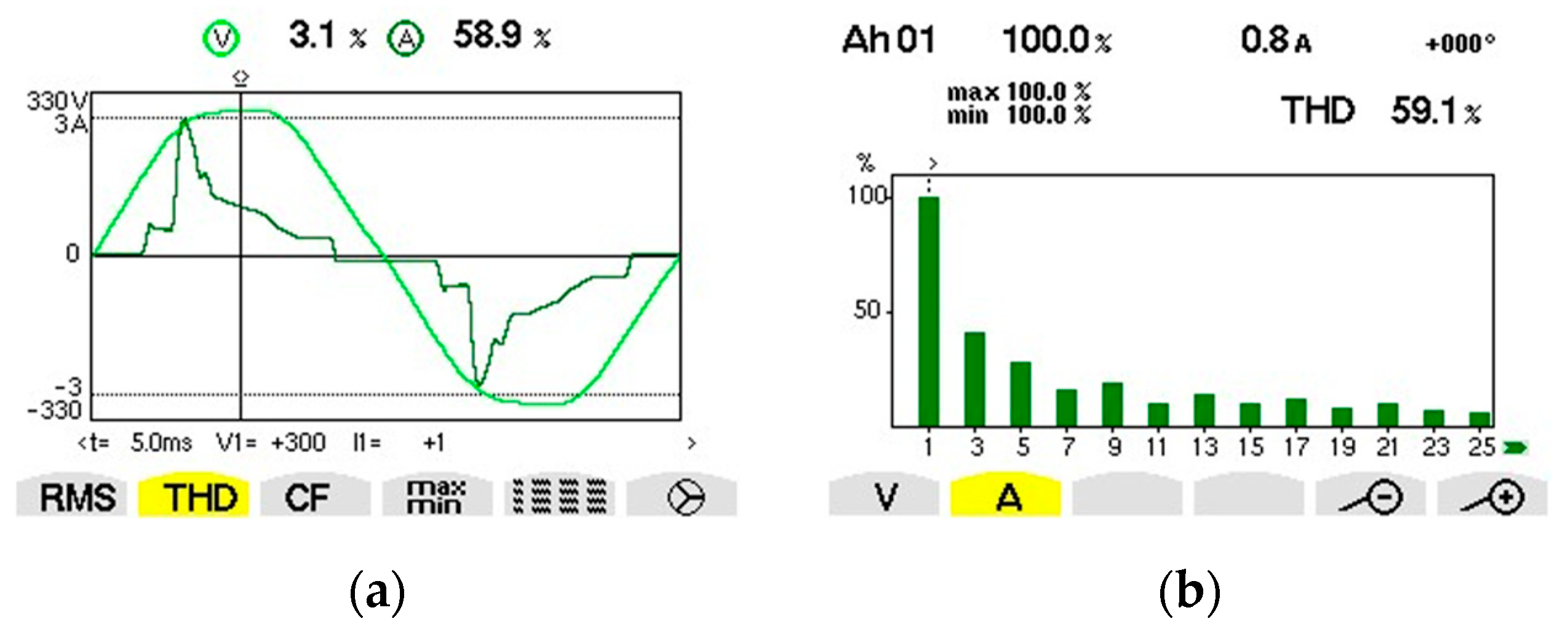
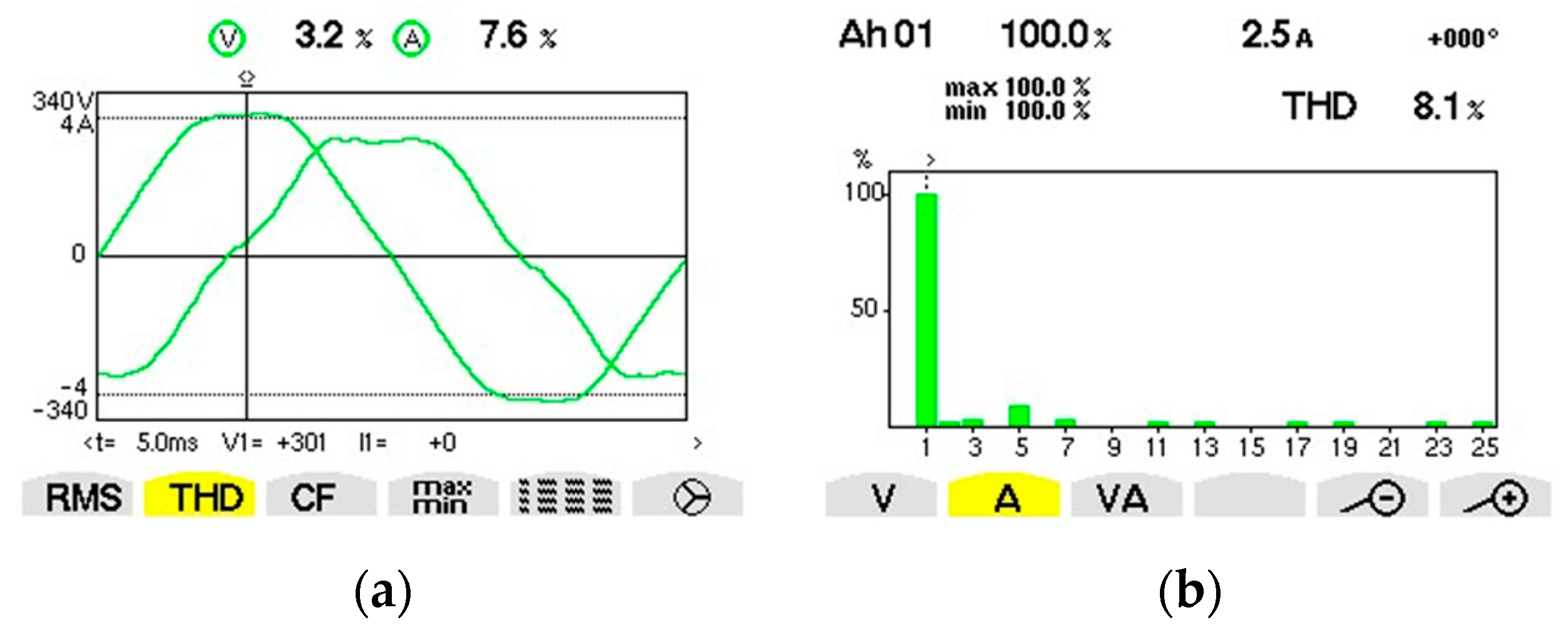
3.1. Connecting Capacitors and Capacitors Banks through Electrical Contacts and through Solid-State Relay
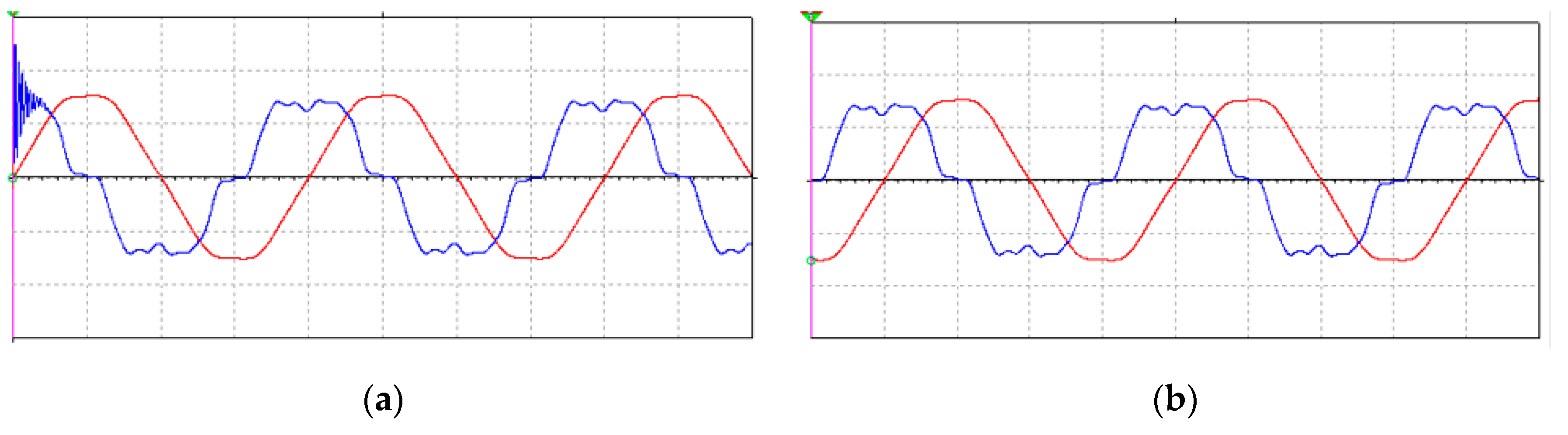
3.2. Experiments with Three-Phase Capacitors Banks
- M1, three-phase induction motor (Figure 29) with the following data (ASI 90L-24-2 type): 2.2 kW; 2780 rpm; 400 V; 4.95 A; PF = 0.855;
- M2, three-phase induction motor (Figure 30) with the following data (N 80 L type): 750 W; 1450 rpm; 400 V; 2.13 A; PF = 0.72;
- Compact fluorescent lamps (Figure 31), connected in parallel on the phase, with the following data: CFL1: 220 V, 50 Hz, 85 W, 6400 K; CFL2: 220–240 V, 50/60 Hz, 120 W, 580 mA, 4000 K.
3.3. Experiments with AC Reactors Connected in Series with Three-Phase Capacitors Banks
4. Discussion
5. Conclusions
- The realization principle of the power improvement installation with an automatic power factor controller with PLCs (one or more depending on the constructive type and the number of capacitors banks), electromagnetic contactors (two for each capacitors bank) and a three-phase SSR used to connect all the capacitors banks;
- The electrical power scheme, composed of two electromagnetic contactors, for each individual capacitors bank and a single three-phase SSR, used to connect all capacitors banks;
- The program implemented on the PLC for the control of the capacitors banks, so as to realize the switch-on at zero voltage of the capacitors banks.
6. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Power Factor Correction and Harmonic Filtering in Electrical Plants; Technical Application Papers No. 8 ABB; Electrical Engineering Portal: Belgrade, Serbia, 2010.
- Power Factor Correction and Control of Electrical Network Quality. ALPES Technologies. Available online: https://www.alpestechnologies.com/sites/all/images/pdf_EN/EX216012_AT_EN_BD.pdf (accessed on 19 January 2024).
- Power Factor Correction: A Guide for the Plant Engineer; Technical Data SA02607001E; EATON: Hampton, UK, 2022.
- Voloh, I.; Ernst, T. Review of Capacitor Bank Control Practices; GE Grid Solutions: Shanghai, China, 2015. [Google Scholar]
- Reactive Power Compensation, ABB, Santiago, Chile. 5 June 2013. Available online: https://new.abb.com/docs/librariesprovider78/chile-documentos/jornadas-tecnicas-2013---presentaciones/4-jos%C3%A9-matias---reactive-power-compensation.pdf?sfvrsn=2 (accessed on 18 January 2024).
- Riese, P. Manual of Power Factor Correction; FRAKO: Teningen, Germany, 2010. [Google Scholar]
- Koomey, J.G. Assessment of the Impacts of Power Factor Correction in Computer Power Supplies on Commercial Building Line Losses; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2006.
- Solid State Relays Common Precautions; OMRON: Tokio, Japan, 2010. Available online: https://omronfs.omron.com/en_US/ecb/products/pdf/precautions_ssr.pdf (accessed on 15 January 2024).
- Solid State Relays; Application Note AP04901001E; EATON: Hampton, UK, 2019.
- Tasker, A. Considerations for Design Using Radiation Hardened Solid State Relays; Application Note AN-1068; International Rectifier: Los Angeles, CA, USA, 2015. [Google Scholar]
- Ramos, R. Film capacitor in power applications. IEEE Power Electron. 2018, 5, 45–50. [Google Scholar] [CrossRef]
- Latt, A.Z. Power Factor Correction Using Shunt Capacitor Bank for 33/11/0.4 kV, 10 MVA Distribution Substation. Int. J. Innov. Res. Multidiscip. Field 2019, 5, 1–8. [Google Scholar]
- Tan, M.; Zhang, C.; Chen, B. Size Estimation of Bulk Capacitor Removal Using Limited Power Quality Monitors in the Distribution Network. Sustainability 2022, 14, 15153. [Google Scholar] [CrossRef]
- Power Quality Application Guide. Available online: https://www.sier.ro/ghid_aplicare.html (accessed on 24 February 2024).
- Thentral, T.M.T.; Usha, S.; Palanisamy, R.; Geetha, A.; Alkhudaydi, A.M.; Sharma, N.K.; Bajaj, M.; Ghoneim, S.S.M.; Shouran, M.; Kamel, S. An energy efficient modified passive power filter for power quality enhancement in electric drives. Front. Energy Res. 2022, 10, 989857. [Google Scholar] [CrossRef]
- Sa’ed, J.A.; Amer, M.; Bodair, A.; Baransi, A.; Favuzza, S.; Zizzo, G. A Simplified Analytical Approach for Optimal Planning of Distributed Generation in Electrical Distribution Networks. Appl. Sci. 2019, 9, 5446. [Google Scholar] [CrossRef]
- Scott, M.A. Working safely with hazardous capacitors. IEEE Ind. Appl. Mag. 2019, 25, 44–53. [Google Scholar] [CrossRef]
- Raghavendra, P.; Dattatraya, N.G. Coordinated volt-var control. IEEE Ind. Appl. Mag. 2018, 24, 14–22. [Google Scholar] [CrossRef]
- Ye, J.; Gooi, H.B. Phase Angle Control Based Three-phase DVR with Power Factor Correction at Point of Common Coupling. J. Mod. Power Syst. Clean Energy 2020, 8, 179–186. [Google Scholar] [CrossRef]
- Helmi, B.A.; D’Souza, M.; Bolz, B.A. Power factor correction capacitors. IEEE Ind. Appl. Mag. 2015, 21, 78–84. [Google Scholar] [CrossRef]
- Tariq, H.; Czapp, S.; Tariq, S.; Cheema, K.M.; Hussain, A.; Milyani, A.H.; Alghamdi, S.; Elbarbary, Z.M.S. Comparative Analysis of Reactive Power Compensation Devices in a Real Electric Substation. Energies 2022, 15, 4453. [Google Scholar] [CrossRef]
- Ahmed, M.A. Point of Common Coupling Power Factor Conditioning of Connected Loads with PWM Rectifier. WSEAS Trans. Power Syst. 2019, 14, 24–32. [Google Scholar]
- Rahimi, S.; Marinelli, M.; Silvestro, F. Evaluation of Requirements for Volt/Var Control and Optimization Function in Distribution Management Systems. In Proceedings of the 2nd IEEE ENERGYCON Conference and Exhibition, Florence, Italy, 9–12 September 2012; pp. 331–336. [Google Scholar] [CrossRef]
- Gupta, A.G.; Yadav, O.P.; DeVoto, D.; Major, J. A Review of Degradation Behavior and Modelling of Capacitors. In Proceedings of the ASME 2018 International Technical Conference and Exhibition on Packaging and Integration of Electronic and Photonic Microsystems, San Francisco, CA, USA, 27–30 August 2018; pp. 1–10. [Google Scholar] [CrossRef]
- Popa, G.N.; Dinis, C.M.; Popa, I. Economical System for Automatic Power Factor Adjustment, with Capacitors Banks, in Three-Phase Low-Voltage Installations. Patent no. A 2020 00491, 4 August 2020. (In Romanian). [Google Scholar]
- Coman, C.M.; Florescu, A.; Oancea, C.D. Improving the Efficiency and Sustainability of Power Systems Using Distributed Power Factor Correction Methods. Sustainability 2020, 12, 3134. [Google Scholar] [CrossRef]
- Stosur, M.; Sowa, K.; Kuczek, T.; Chmielewski, T.; Ruszczyk, A.; Koska, K. Overvoltage Protection of Solid State Switch for Low Voltage Applications–Simulation and Experimental Results. In Proceedings of the European EMTP-ATP Conference, Kiel, Germany, 4–6 September 2017; pp. 1–10. Available online: https://www.researchgate.net/profile/Kacper-Sowa/publication/319543888_Overvoltage_protection_of_solid_state_switch_for_low_voltage_applications_-_simulation_and_experimental_results/links/59b26e47a6fdcc3f8891c6ec/Overvoltage-protection-of-solid-state-switch-for-low-voltage-applications-simulation-and-experimental-results.pdf (accessed on 20 January 2024).
- Ruszczyk, A.; Janisz, K.; Koska, K. Solid-State Switch for Capacitors Bank Used in Reactive Power Compensation. In Proceedings of the XII International School on Nonsinusoidal Currents and Compensation, ISNCC 2015, Łagów, Poland, 15–18 June 2015; pp. 1–5. [Google Scholar]
- Technical Explanation of Solid State Relays; CSM_SSR_TG_E_9_2; OMRON: Tokio, Japan, 2018.
- From Electromechanical Relays to Robust Semiconductor Solutions: Solid-State Relays with Optimized Superjunction FET Technology; Infineon Technology: Richardson, TX, USA, 2021.

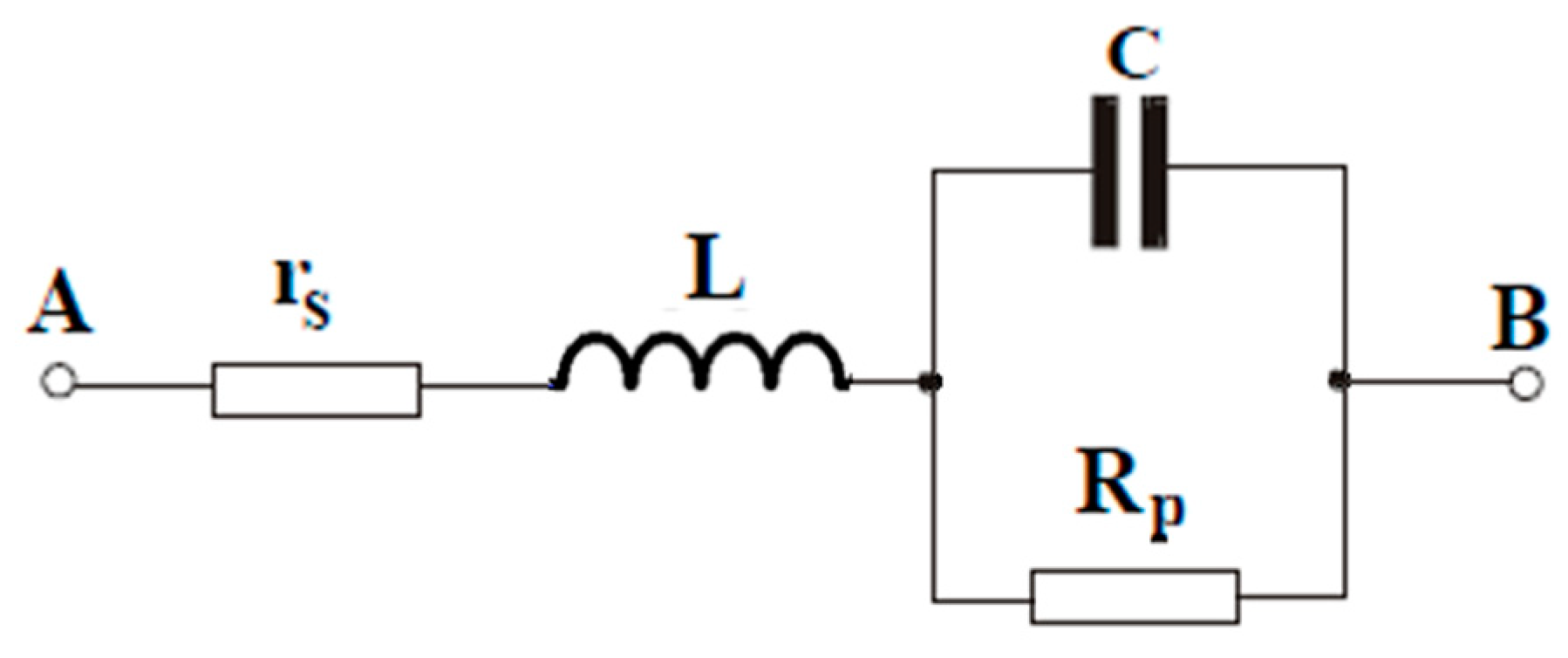
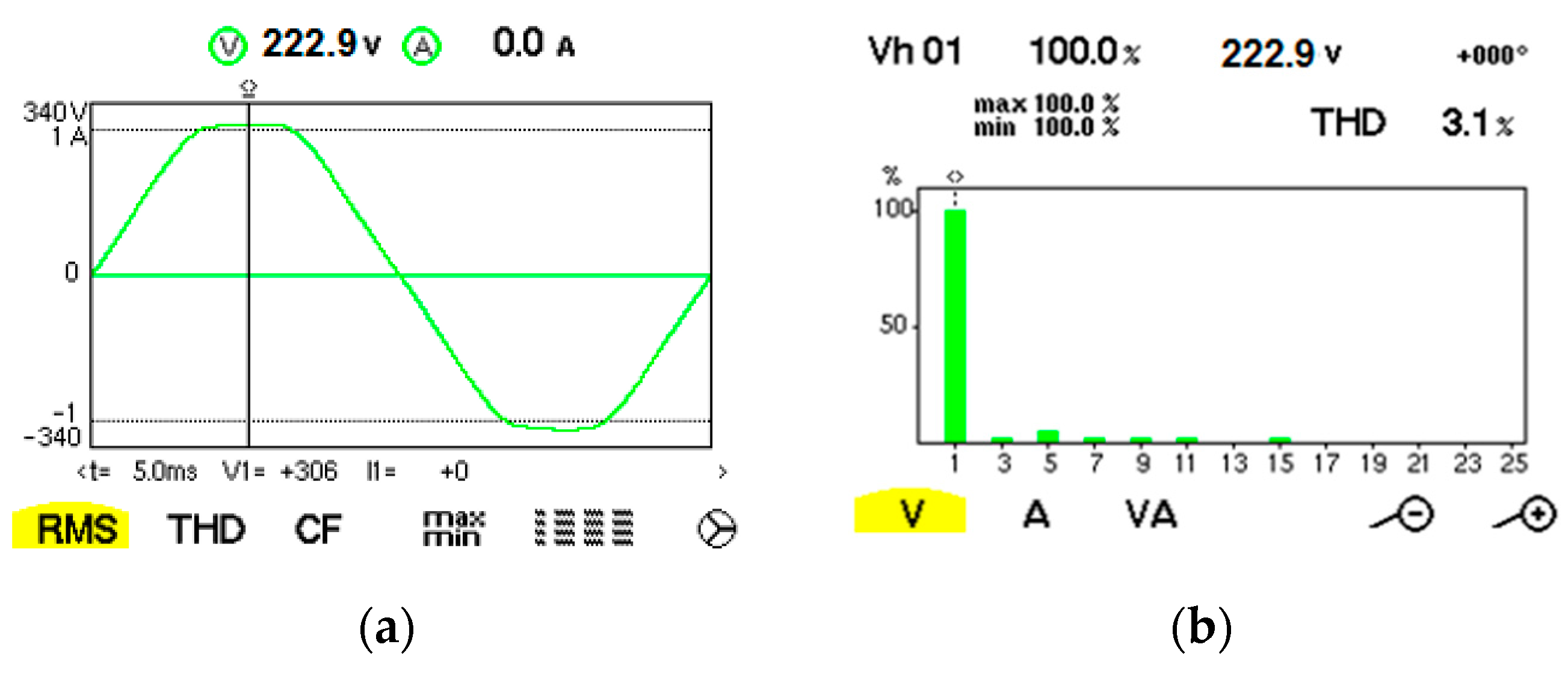

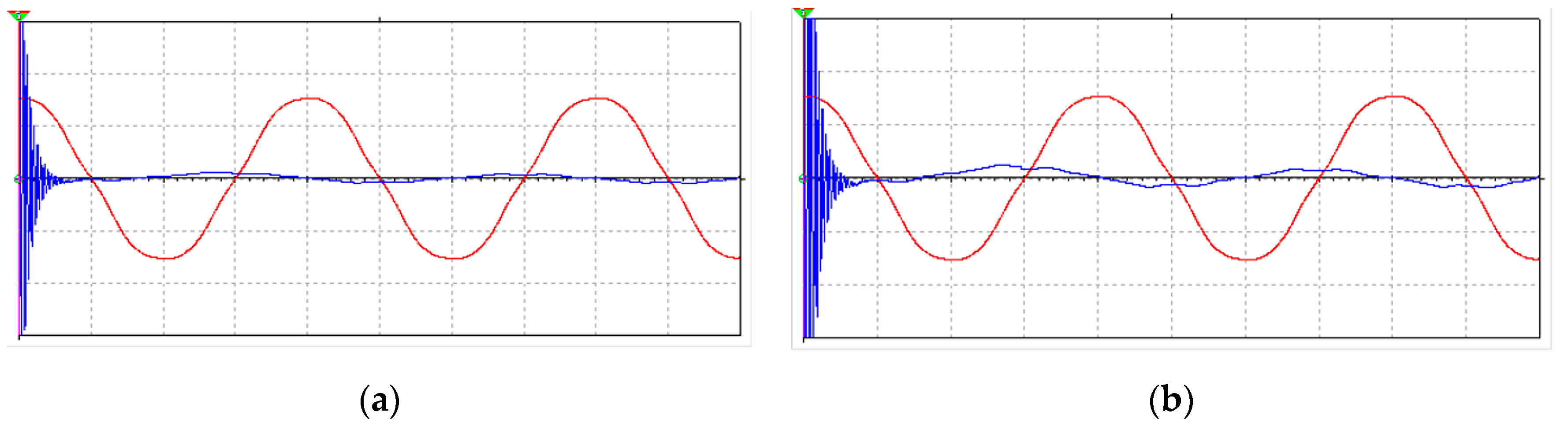
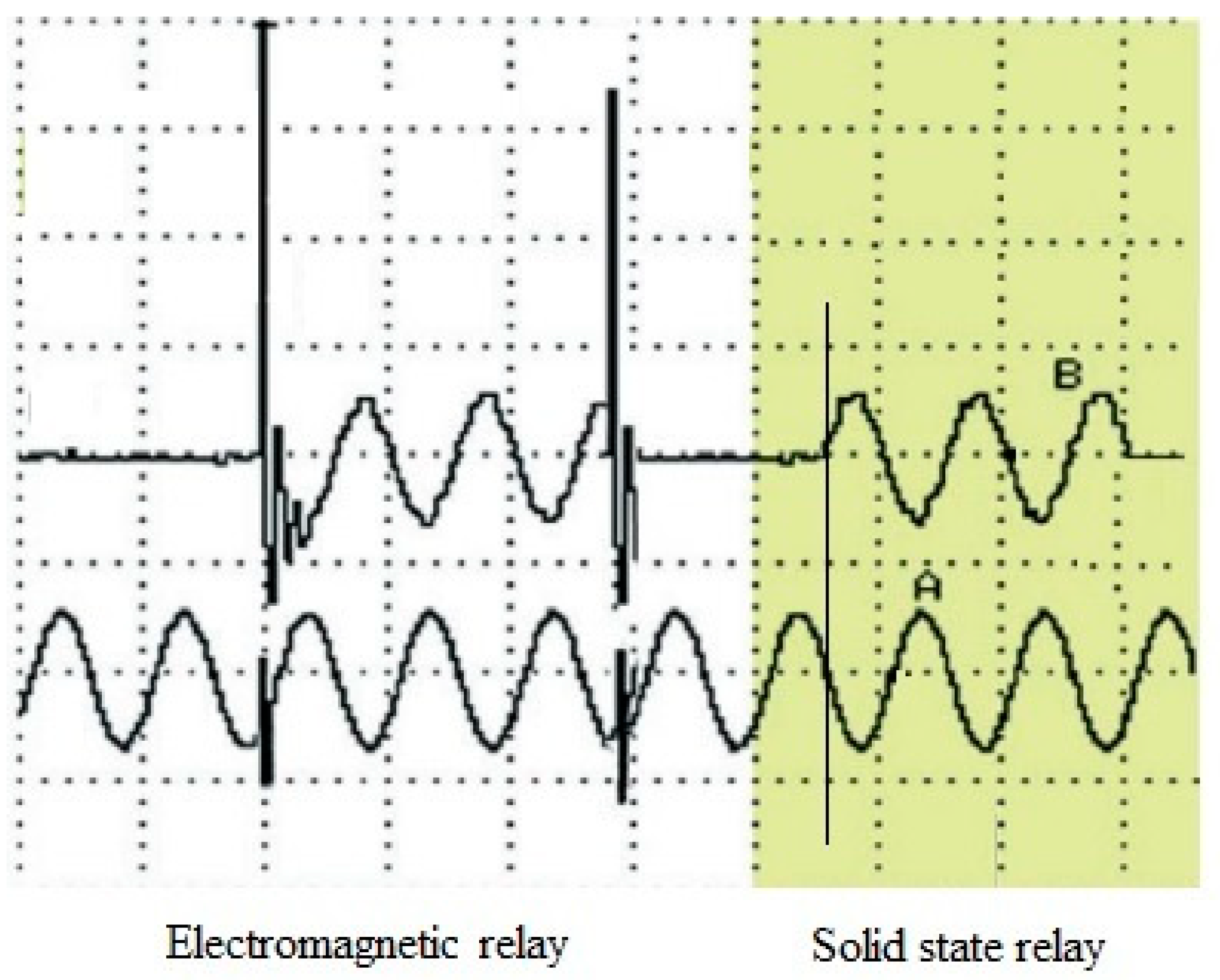

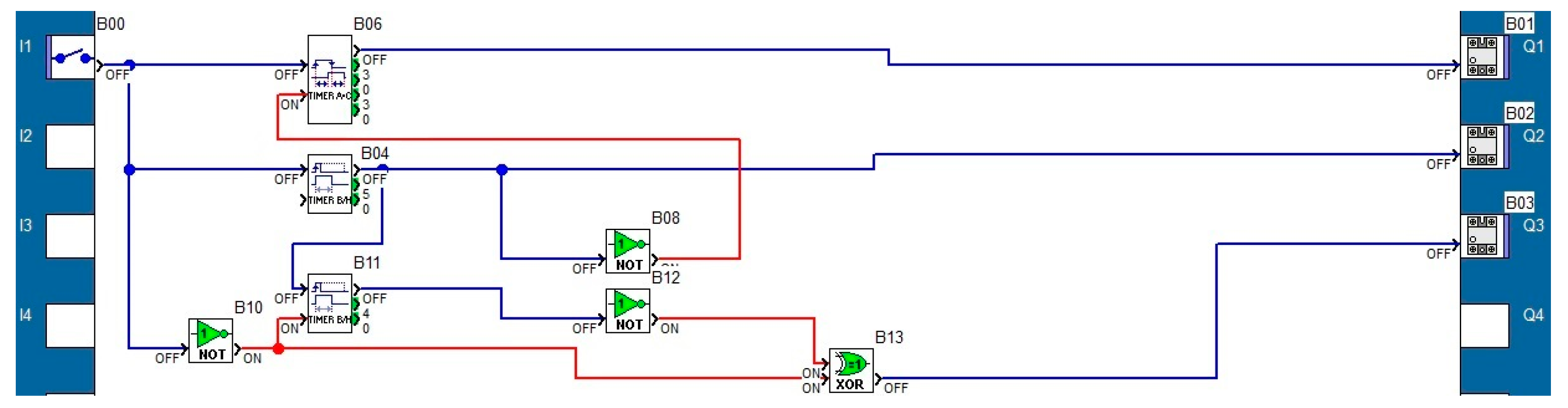

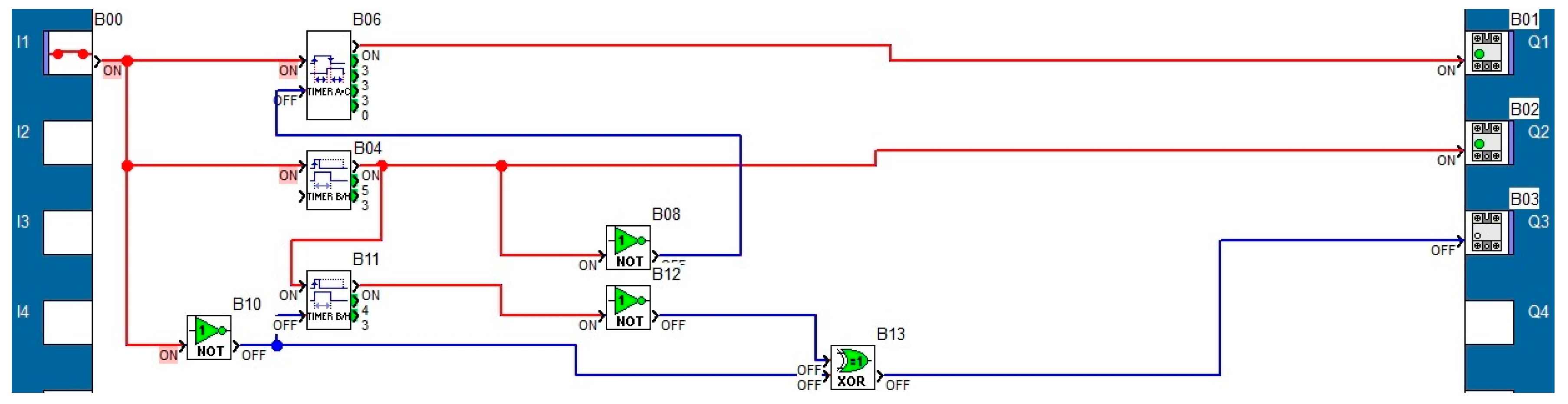
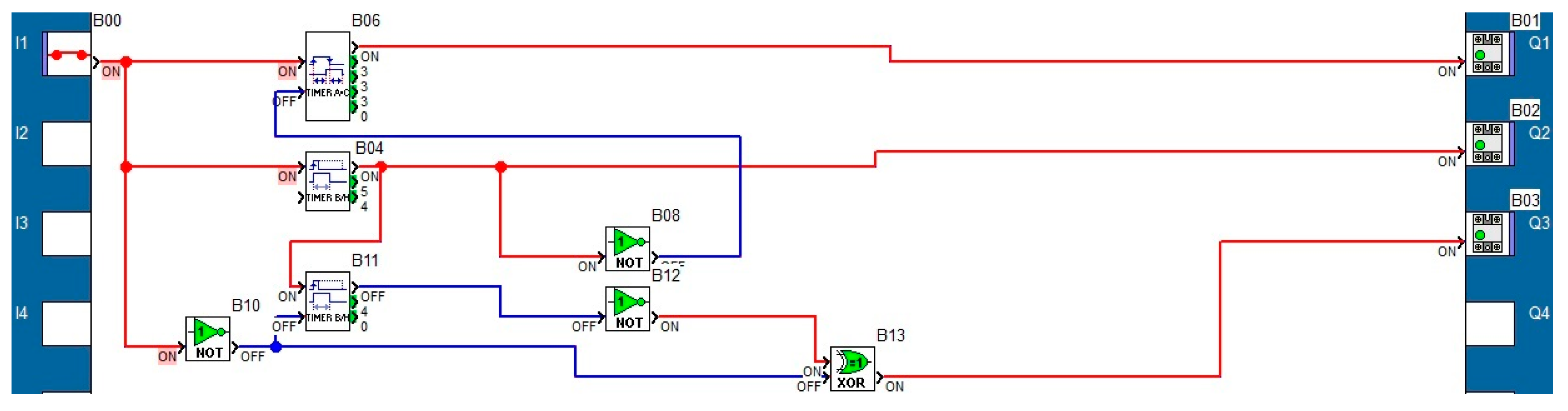
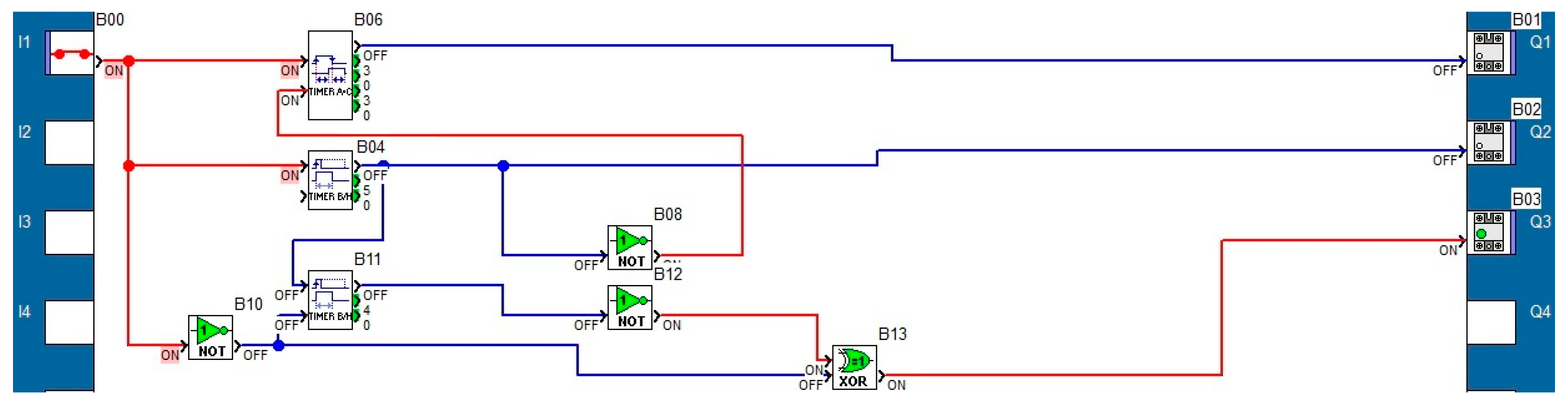

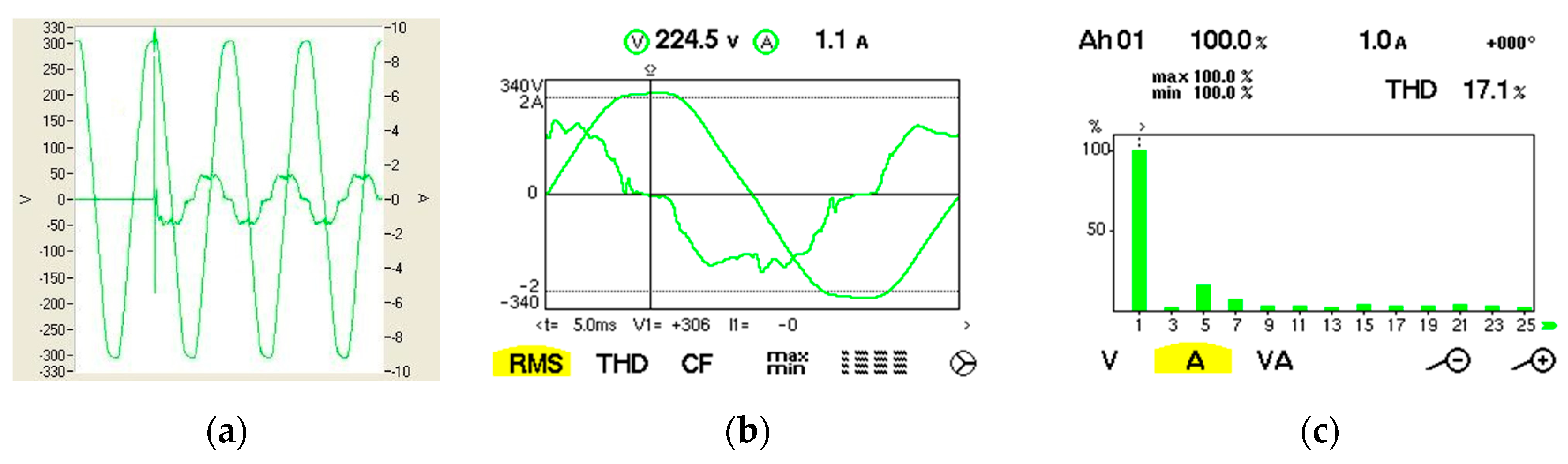
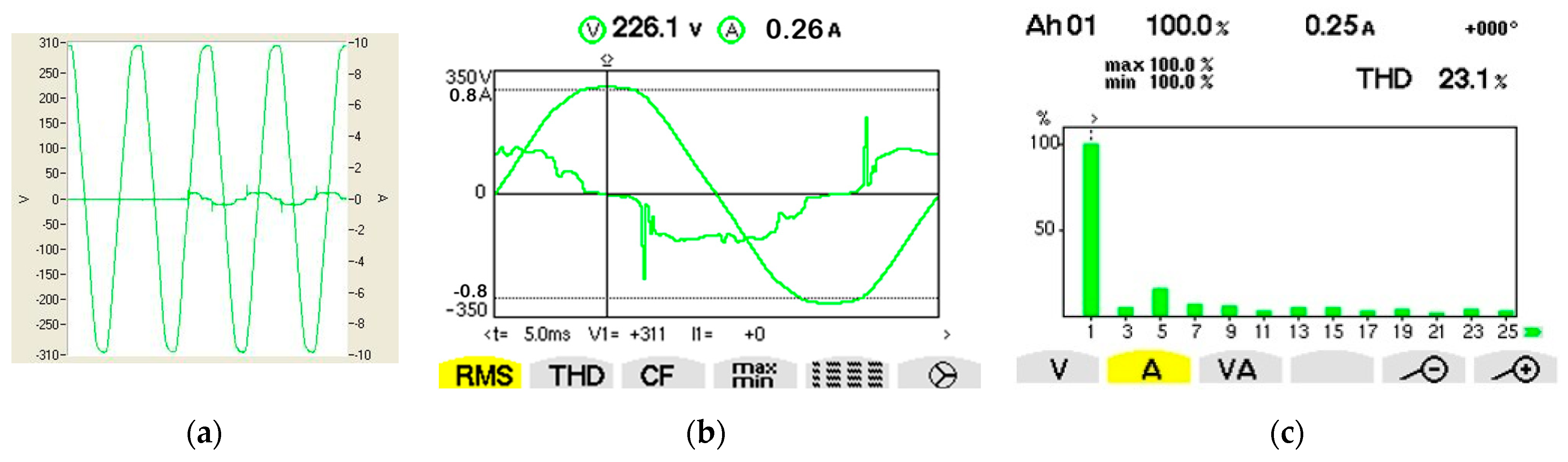
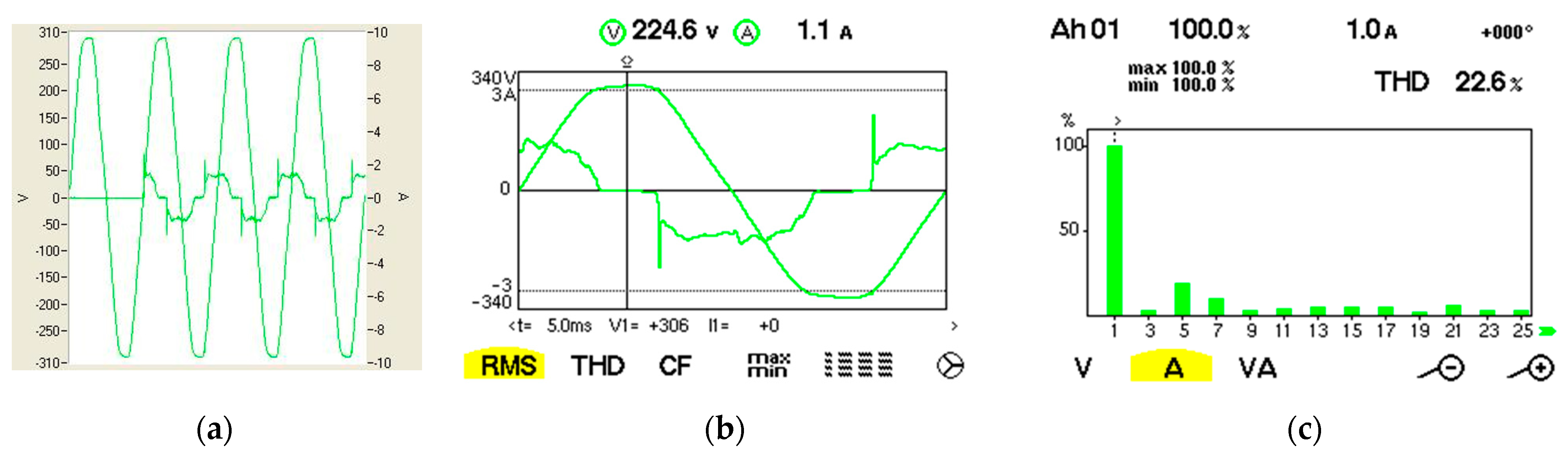



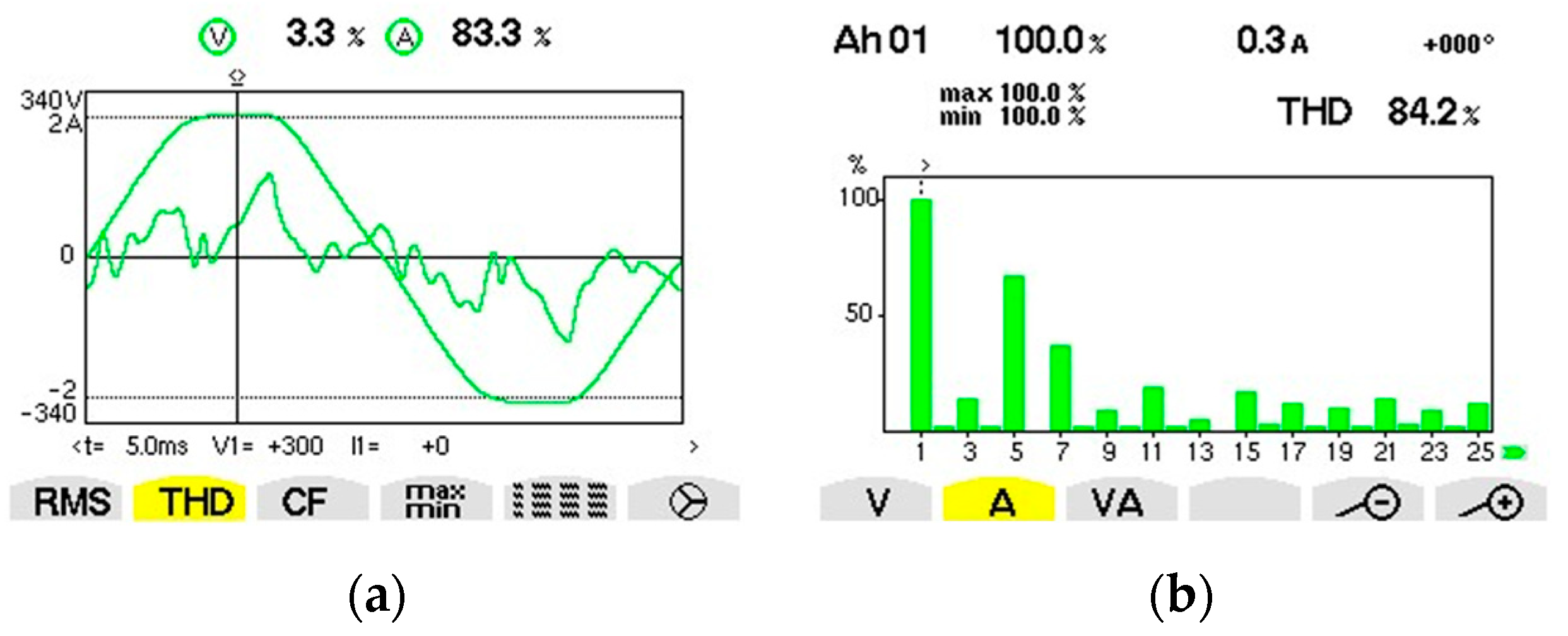
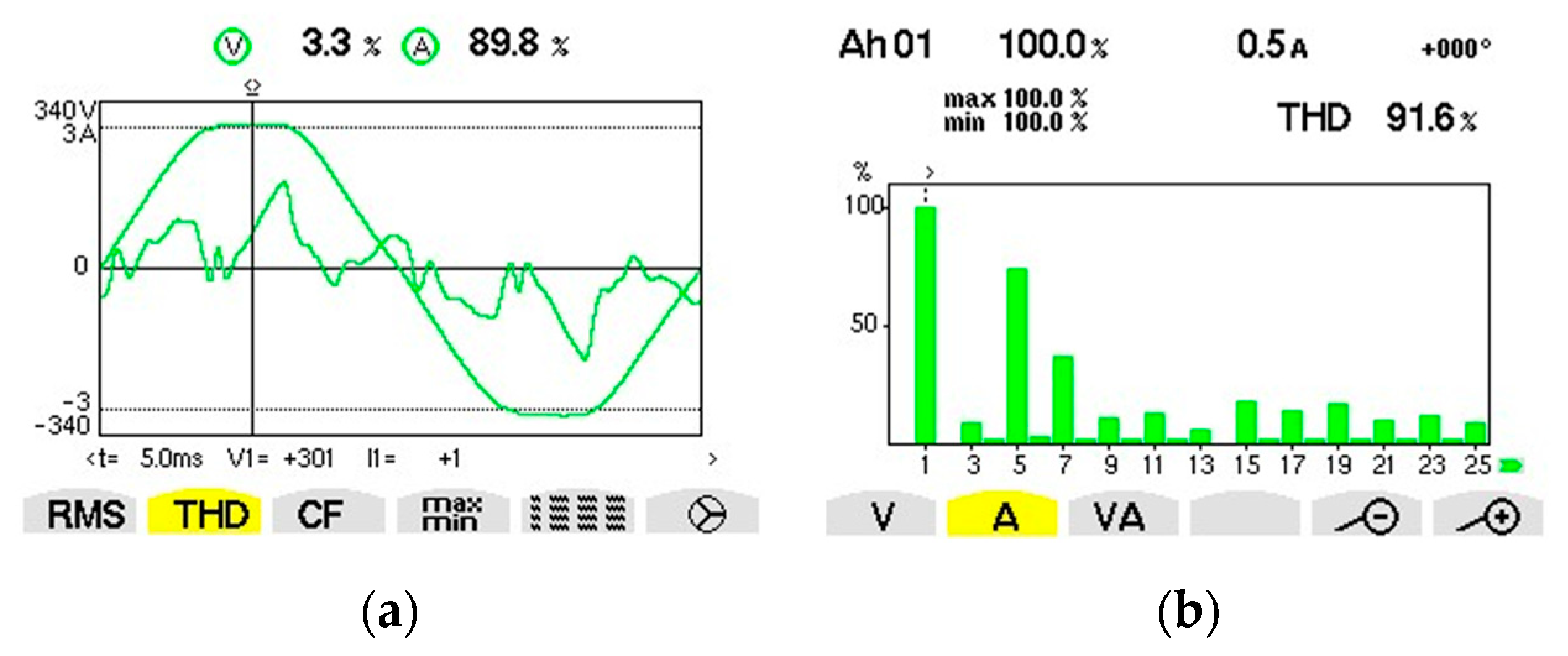
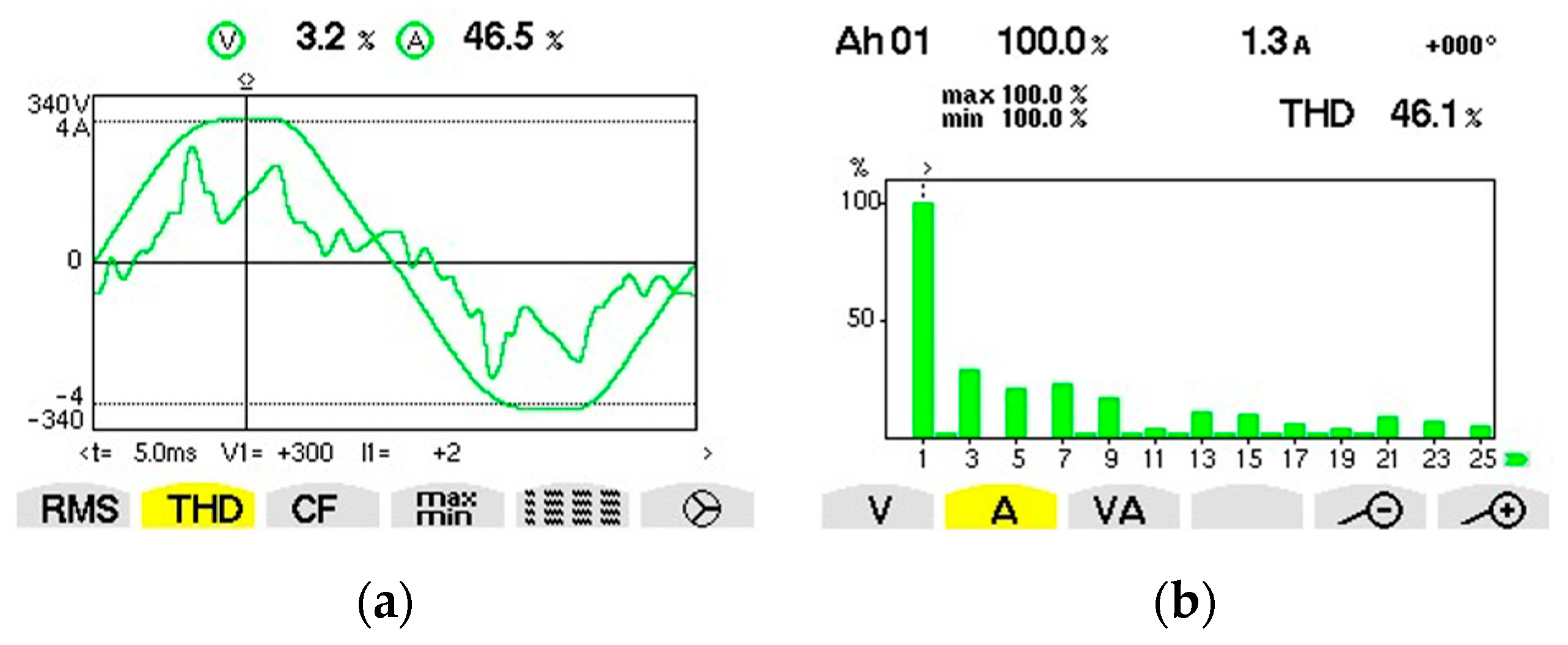
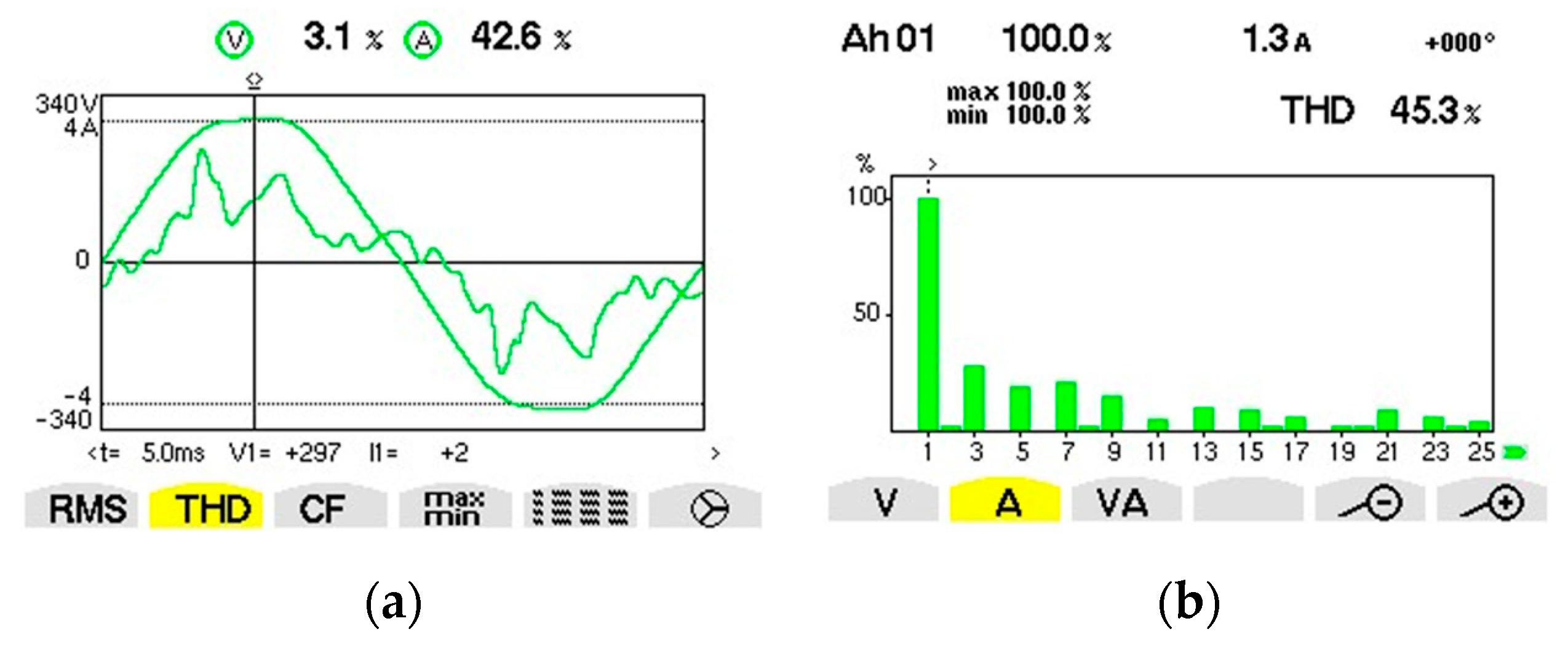
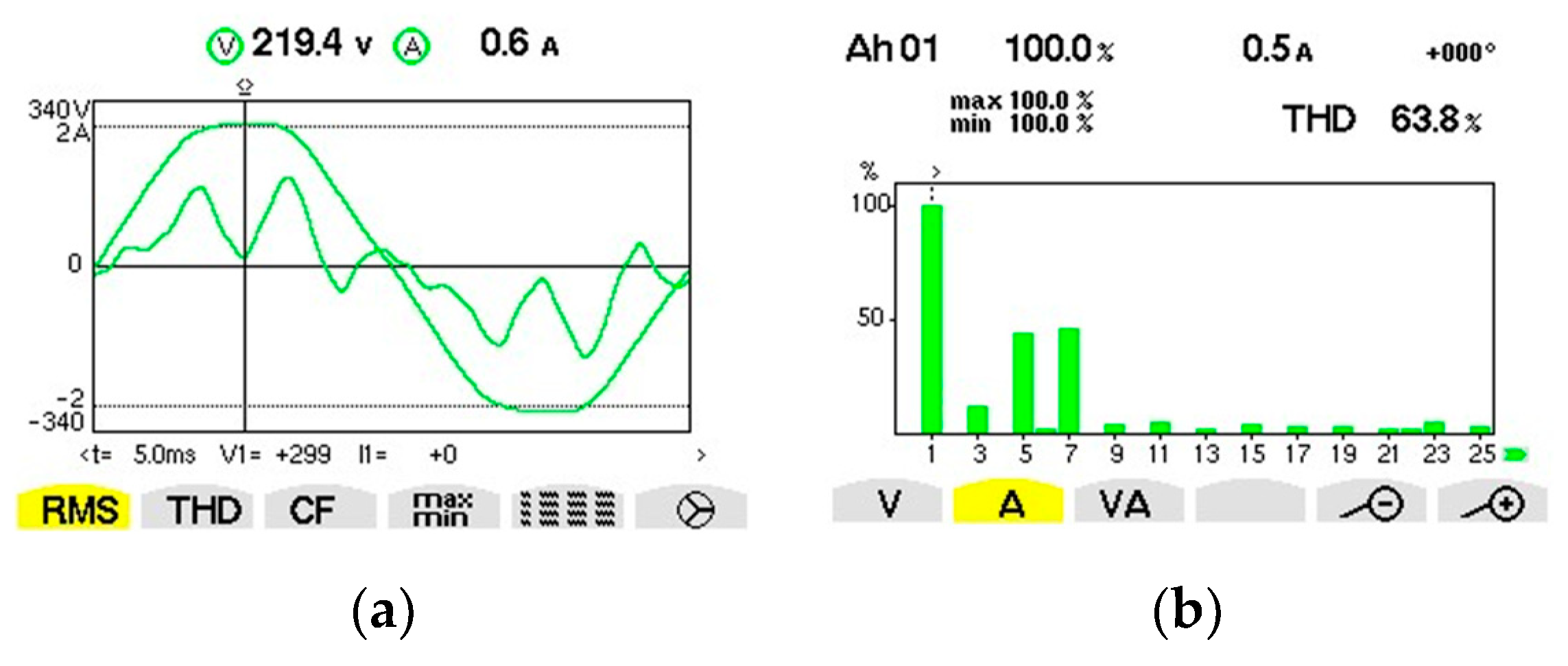
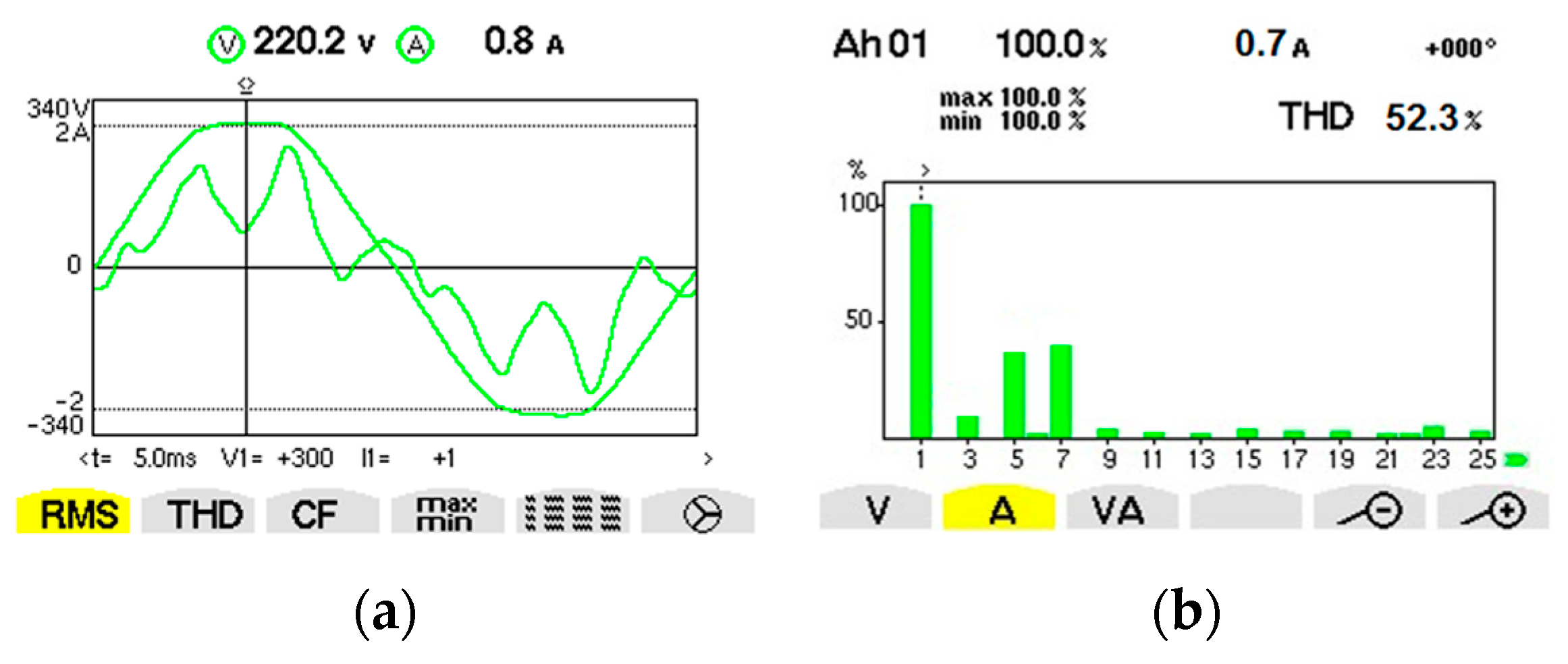

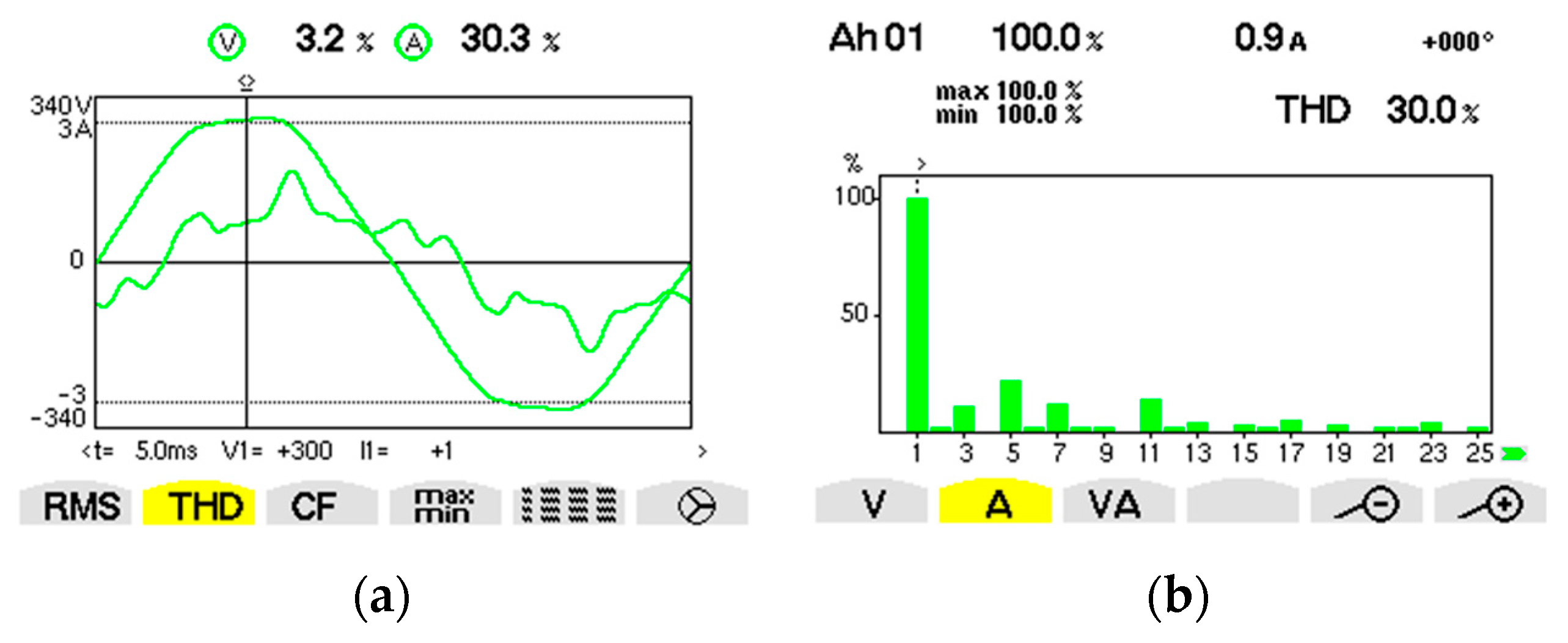
| Fundamental/Harmonic Rank | RMS (V) | The Initial Phase (°) |
|---|---|---|
| 1 | 222.8 | 0 |
| 3 | 0.4 | 160 |
| 5 | 6.9 | −172 |
| 7 | 1.8 | −5 |
| 9 | 0.4 | −149 |
| 111 | 0.4 | 173 |
| 15 | 0.4 | −140 |
| CBs | Components | Diagram from Figure 9 | Diagram from Figure 12 | Comparisons between Diagrams from Figure 12 and Figure 9 |
|---|---|---|---|---|
| 3 pcs. | APFC | 1 (EUR 600 | 1 (EUR 600) | 10.6% more expensive |
| CBs | 3 (3 × EUR 50) | 3 (3 × EUR 50) | ||
| PLCs | - | 1 (EUR 90) | ||
| EMCs | - | 6 (6 × EUR 20) | ||
| SSRs | 3 (3 × EUR 130) | 1 (EUR 130) | ||
| HS | 3 (3 × EUR 4) | 1 (EUR 4) | ||
| Total | EUR 1152 | EUR 1274 | ||
| 6 pcs. | APFC | 1 (EUR 600) | 1 (EUR 600) | 17.6% cheaper |
| CBs | 6 (3 × EUR 50) | 6 (3 × EUR 50) | ||
| PLCs | - | 2 (2 × EUR 90) | ||
| EMCs | - | 12 (12 × EUR 20) | ||
| SSRs | 6 (6 × EUR 130) | 1 (EUR 130) | ||
| HS | 6 (3 × EUR 4) | 1 (EUR 4) | ||
| Total | EUR 1704 | 1404 | ||
| 9 pcs. | APFC | 1 (EUR 600) | 1 (EUR 600) | 19.59% cheaper |
| CBs | 9 (9 × EUR 50 ) | 9 (9 × EUR 50) | ||
| PLCs | - | 3 (3 × EUR 90) | ||
| EMCs | - | 18 (18 × EUR 20) | ||
| SSRs | 9 (9 × EUR 130) | 1 (EUR 130) | ||
| HS | 9 (9 × EUR 4) | 1 (EUR 4) | ||
| Total | EUR 2256 | EUR 1814 | ||
| 12 pcs. | APFC | 1 (EUR 600) | 1 (EUR 600) | 22.57% cheaper |
| CBs | 12 (12 × EUR 50) | 12 (12 × EUR 50) | ||
| PLCs | - | 4 (4 × EUR 90 | ||
| EMCs | - | 24 (24 × EUR 20) | ||
| SSRs | 12 (12 × EUR 130) | 1 (EUR 130) | ||
| HS | 12 (12 × EUR 4) | 1 (EUR 4) | ||
| Total | EUR 2808 | EUR 2174 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popa, G.N.; Diniș, C.M. Low-Cost System with Transient Reduction for Automatic Power Factor Controller in Three-Phase Low-Voltage Installations. Energies 2024, 17, 1363. https://doi.org/10.3390/en17061363
Popa GN, Diniș CM. Low-Cost System with Transient Reduction for Automatic Power Factor Controller in Three-Phase Low-Voltage Installations. Energies. 2024; 17(6):1363. https://doi.org/10.3390/en17061363
Chicago/Turabian StylePopa, Gabriel Nicolae, and Corina Maria Diniș. 2024. "Low-Cost System with Transient Reduction for Automatic Power Factor Controller in Three-Phase Low-Voltage Installations" Energies 17, no. 6: 1363. https://doi.org/10.3390/en17061363
APA StylePopa, G. N., & Diniș, C. M. (2024). Low-Cost System with Transient Reduction for Automatic Power Factor Controller in Three-Phase Low-Voltage Installations. Energies, 17(6), 1363. https://doi.org/10.3390/en17061363






