Analysis of Increased Induced Voltages on the Sheath of Double-Circuit Underground Transmission Lines Guaranteeing Ampacity
Abstract
1. Introduction
2. Ampacity and Induced Voltages in Underground Transmission Lines
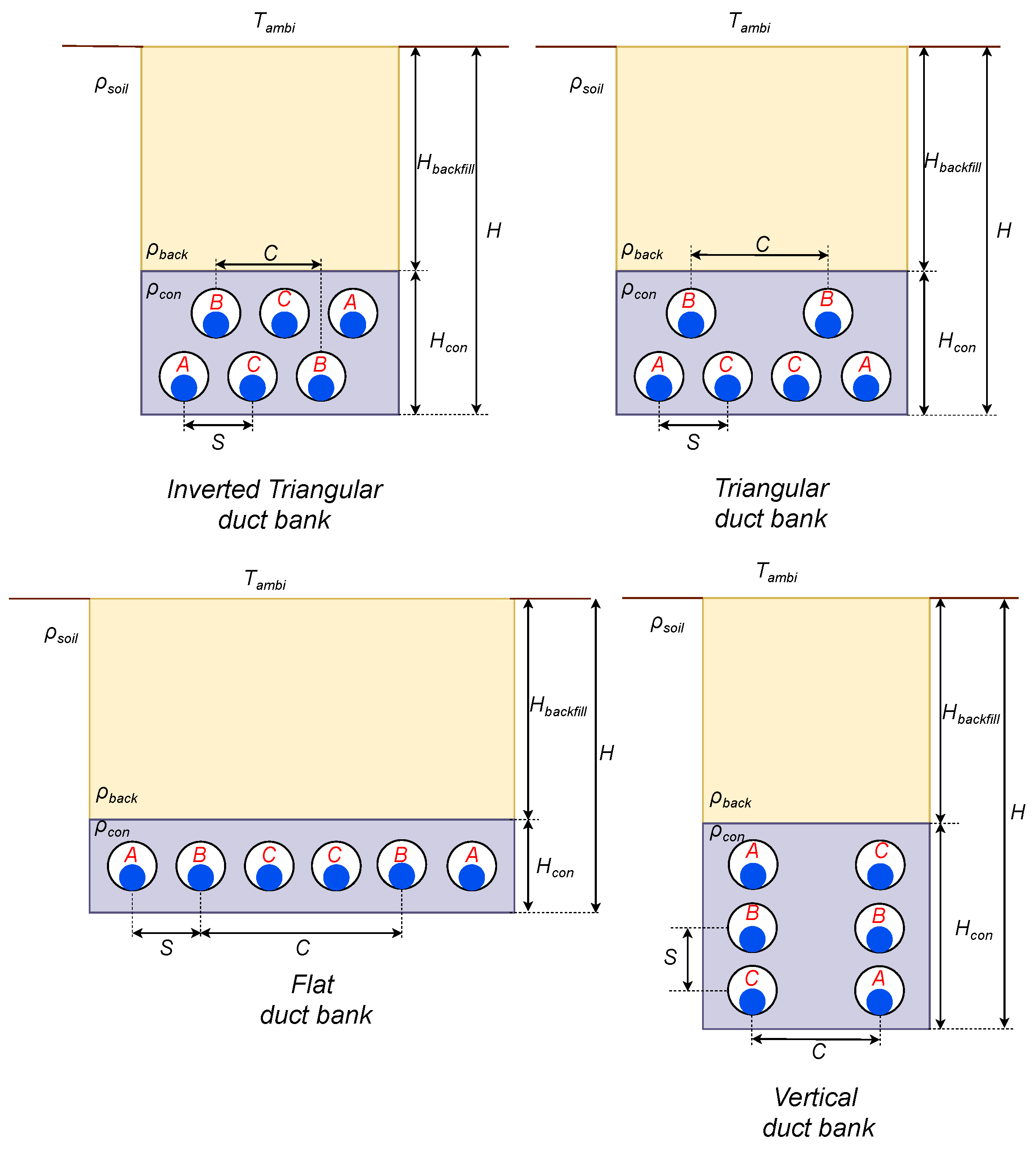
3. Situations Requiring Changes to Duct Bank Configuration and Cable Spacing
4. Results
4.1. Ampacity Calculation
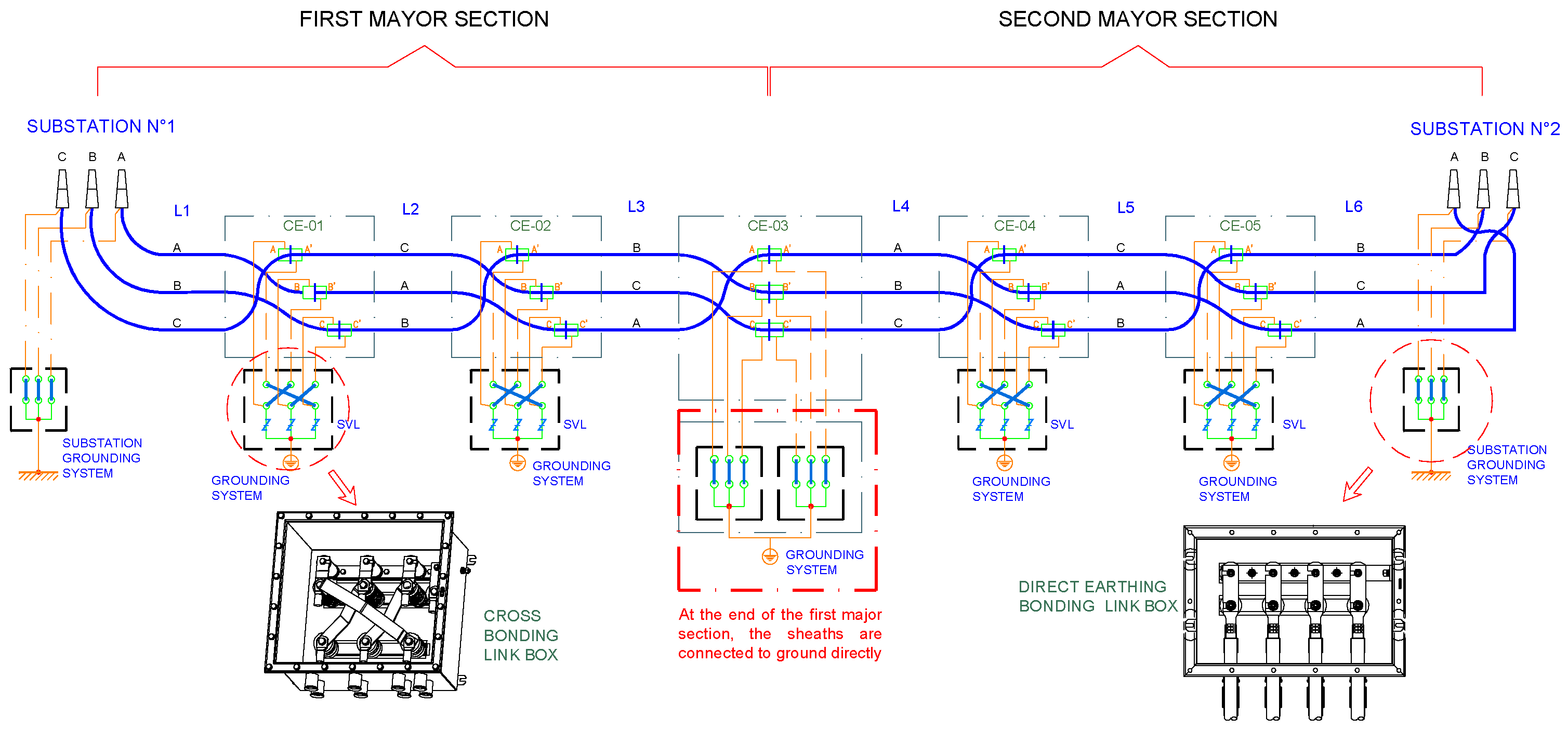
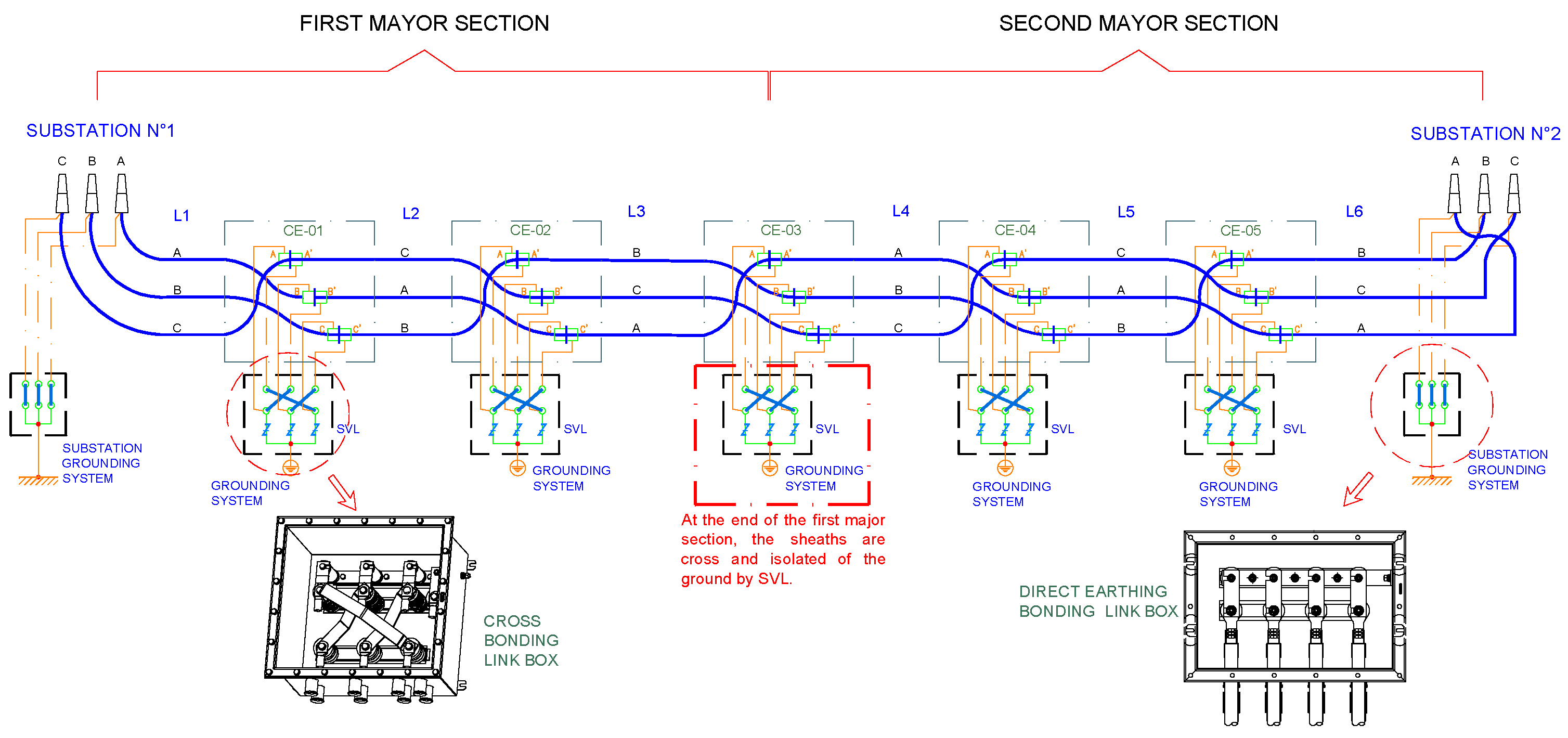
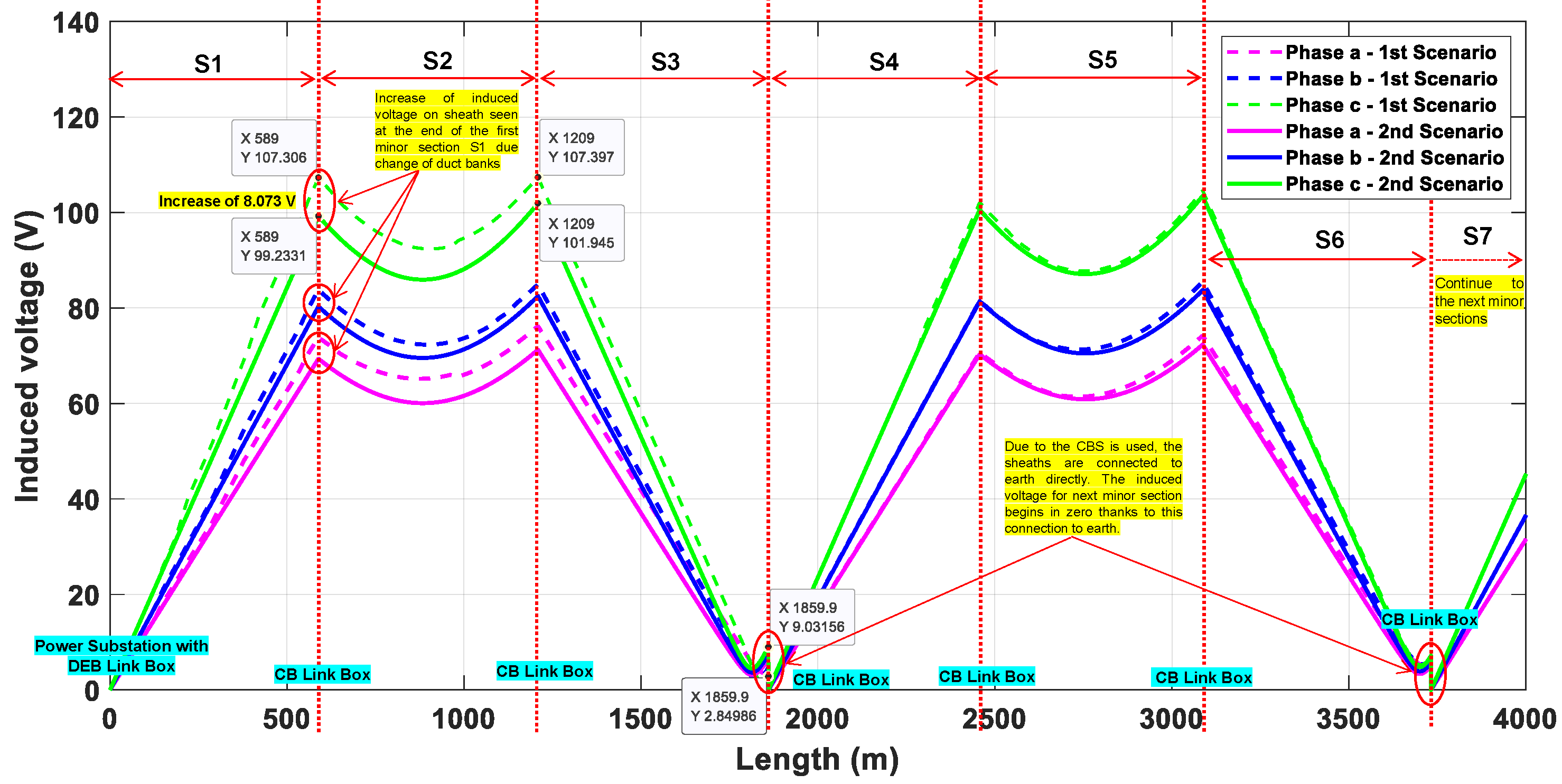
4.2. Induced Voltage on Sheath Calculation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CCB | continuous cross-bonding |
| SCB | sectionalized cross-bonding |
| GIS | gas-insulated substation |
| SVL | sheath voltage limiter |
| FEM | finite element method |
| DEB | direct earthing bonding |
| CB | cross-bonding |
References
- Moutassem, W.; Anders, G.J. Configuration Optimization of Underground Cables for Best Ampacity. IEEE Trans. Power Deliv. 2010, 25, 2037–2045. [Google Scholar] [CrossRef]
- Anders, G.J.; Electrical, I.; Engineers, E. Rating of Electric Power Cables in Unfavorable Thermal Environment; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Perović, B.; Klimenta, D.; Tasić, D.; Raičević, N.; Milovanović, M.; Tomović, M.; Vukašinović, J. Increasing the ampacity of underground cable lines by optimising the thermal environment and design parameters for cable crossings. IET Gener. Transm. Distrib. 2022, 16, 2309–2318. [Google Scholar] [CrossRef]
- Noufal, S.M.; Anders, G.J. Sheath losses correction factor for cross-bonded cable systems with unknown minor section lengths: Analytical expressions. IET Gener. Transm. Distrib. 2021, 15, 849–859. [Google Scholar] [CrossRef]
- IEEE Std 575; IEEE Guide for Bonding Shields and Sheaths of Single-Conductor Power Cables Rated 5 kV through 500 kV. IEEE: Piscataway, NJ, USA, 2014.
- CIGRE WG B1.50; Sheath Boding Systems of AC Tranmsision Cables–Design, Testing, and Maintanence. Technical Brochure 797; CIGRE: Paris, France, 2020.
- Candela, R.; Gattuso, A.; Mitolo, M.; Sanseverino, E.R.; Zizzo, G. A Model for Assessing the Magnitude and Distribution of Sheath Currents in Medium and High-Voltage Cable Lines. IEEE Trans. Ind. Appl. 2020, 56, 6250–6257. [Google Scholar] [CrossRef]
- Brakelmann, H.; Anders, G.J. Ampacity Calculations of Underground Power Cables With End Effects. IEEE Trans. Power Deliv. 2023, 38, 1968–1976. [Google Scholar] [CrossRef]
- Hoerauf, R. Ampacity application considerations for underground cables. In Proceedings of the 2015 IEEE/IAS 51st Industrial & Commercial Power Systems Technical Conference (I&CPS), Calgary, AB, Canada, 5–8 May 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Alexandrou, K.; Anders, G. Sheath circulating currents calculation in asymmetrical installation schemes for power frequency models. In Proceedings of the10th International Conference on Insulated Power Cables, Versailles, France, 23–27 June 2019. [Google Scholar]
- Ocłoń, P.; Cisek, P.; Pilarczyk, M.; Taler, D. Numerical simulation of heat dissipation processes in underground power cable system situated in thermal backfill and buried in a multilayered soil. Energy Convers. Manag. 2015, 95, 352–370. [Google Scholar] [CrossRef]
- IEC 60287-2-1; Electric Cables—Calculation of the Current Rating—Part 1-1: Current Rating Equations (100% Load Factor) and Calculation of Losses—General. IEC: Geneva, Switzerland, 1995.
- IEEE 835; IEEE Standard Power Cable Ampacity Tables. IEEE: Piscataway, NJ, USA, 1994.
- de Leon, F.; Anders, G.J. Effects of Backfilling on Cable Ampacity Analyzed With the Finite Element Method. IEEE Trans. Power Deliv. 2008, 23, 537–543. [Google Scholar] [CrossRef]
- Cymcap Version 8.1 for Windows, CYME Int. T&D, Dec. 2017 St. Bruno, QC, Canada. 2017. Available online: https://www.cyme.com/ (accessed on 17 March 2023).
- Guevara, J.E.; Colqui, J.S.L.; Bautista, J.P.; Filho, J. Analysis of Induced Voltages and Currents on the Sheath of Double-Circuit Underground Power Lines—Part II: With Phases Transposition. In Proceedings of the 2023 IEEE XXX International Conference on Electronics, Electrical Engineering and Computing (INTERCON), Lima, Peru, 2–4 November 2023. [Google Scholar]
- Candela, R.; Gattuso, A.; Mitolo, M.; Sanseverino, E.R.; Zizzo, G. A Comparison of Special Bonding Techniques for Transmission and Distribution Cables. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Guevara, J.E.; Colqui, J.S.L.; Bautista, J.P.; Filho, J.P. Analysis of Induced Voltages and Currents on the Sheath of Double-Circuit Underground Power Lines-Part I: Without Phases Transposition. In Proceedings of the 2023 IEEE XXX International Conference on Electronics, Electrical Engineering and Computing (INTERCON), Lima, Peru, 2–4 November 2023. [Google Scholar]
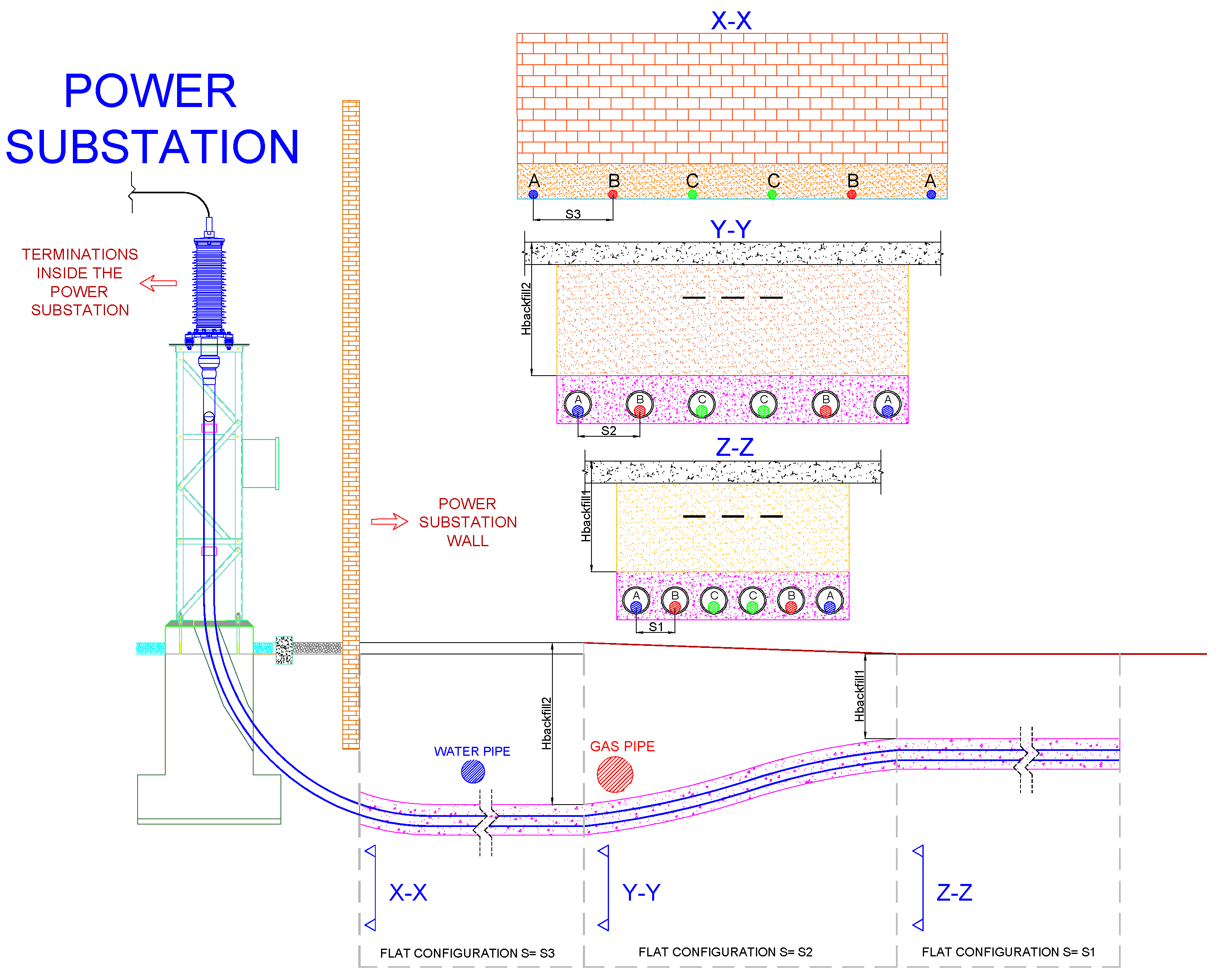
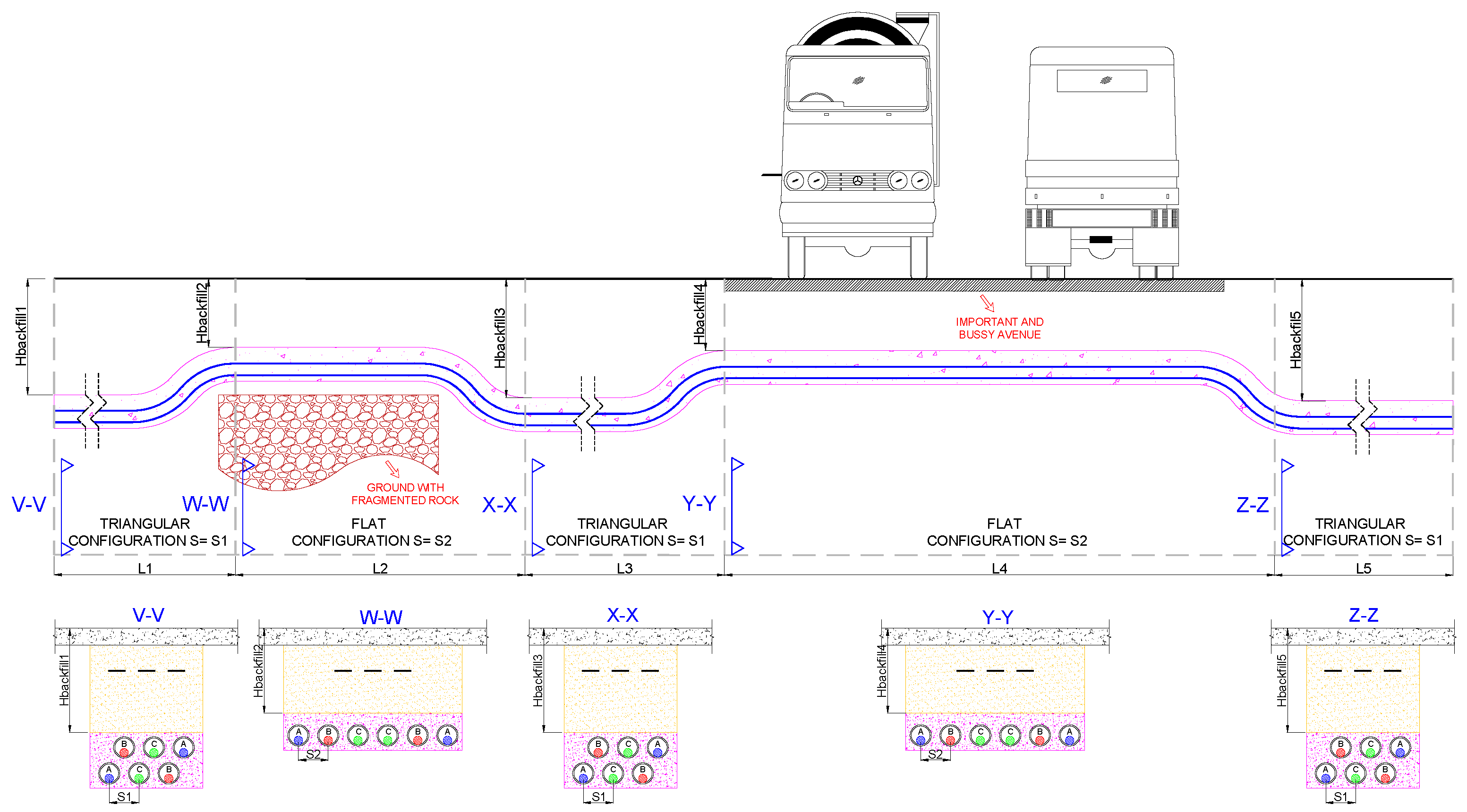
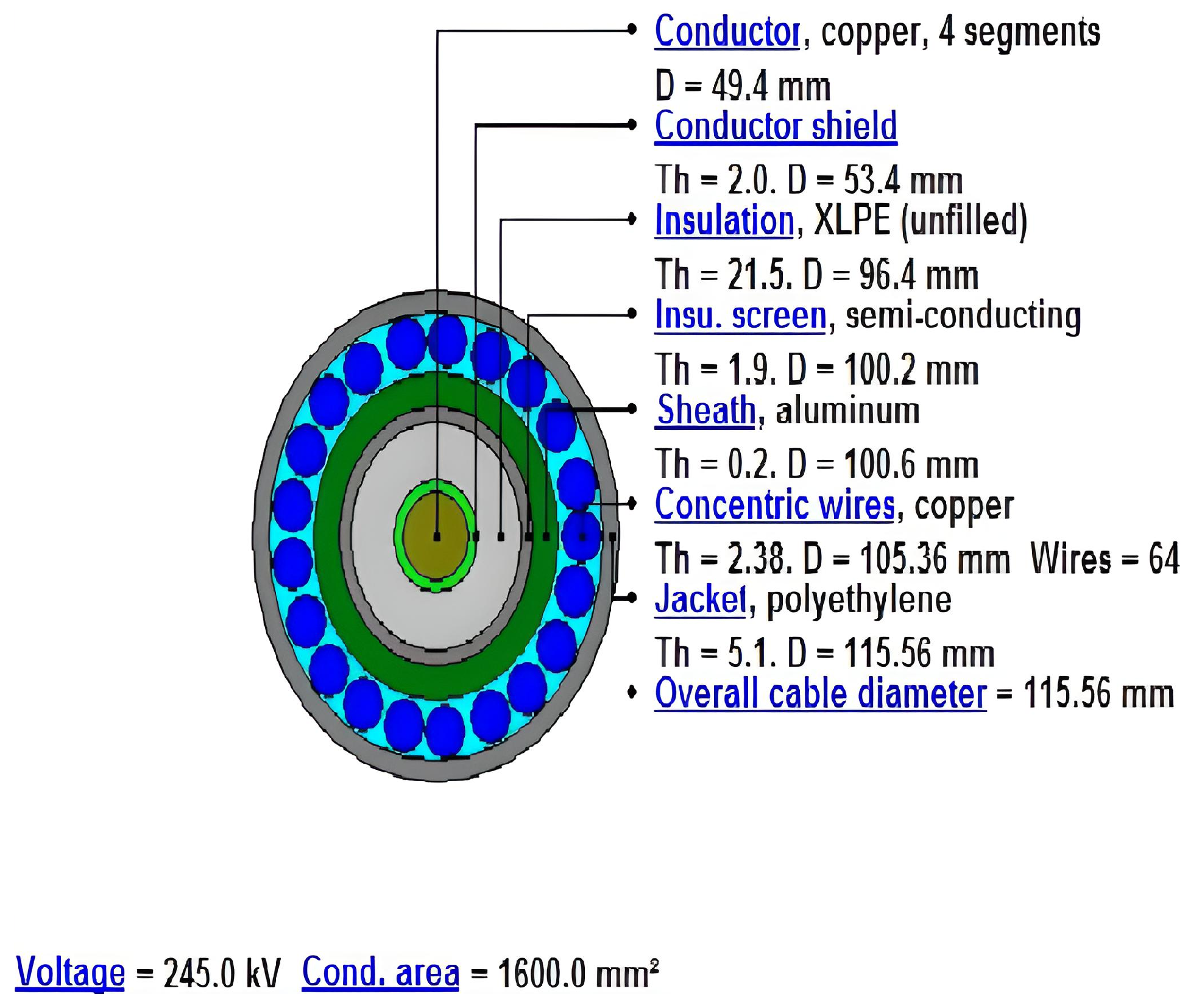
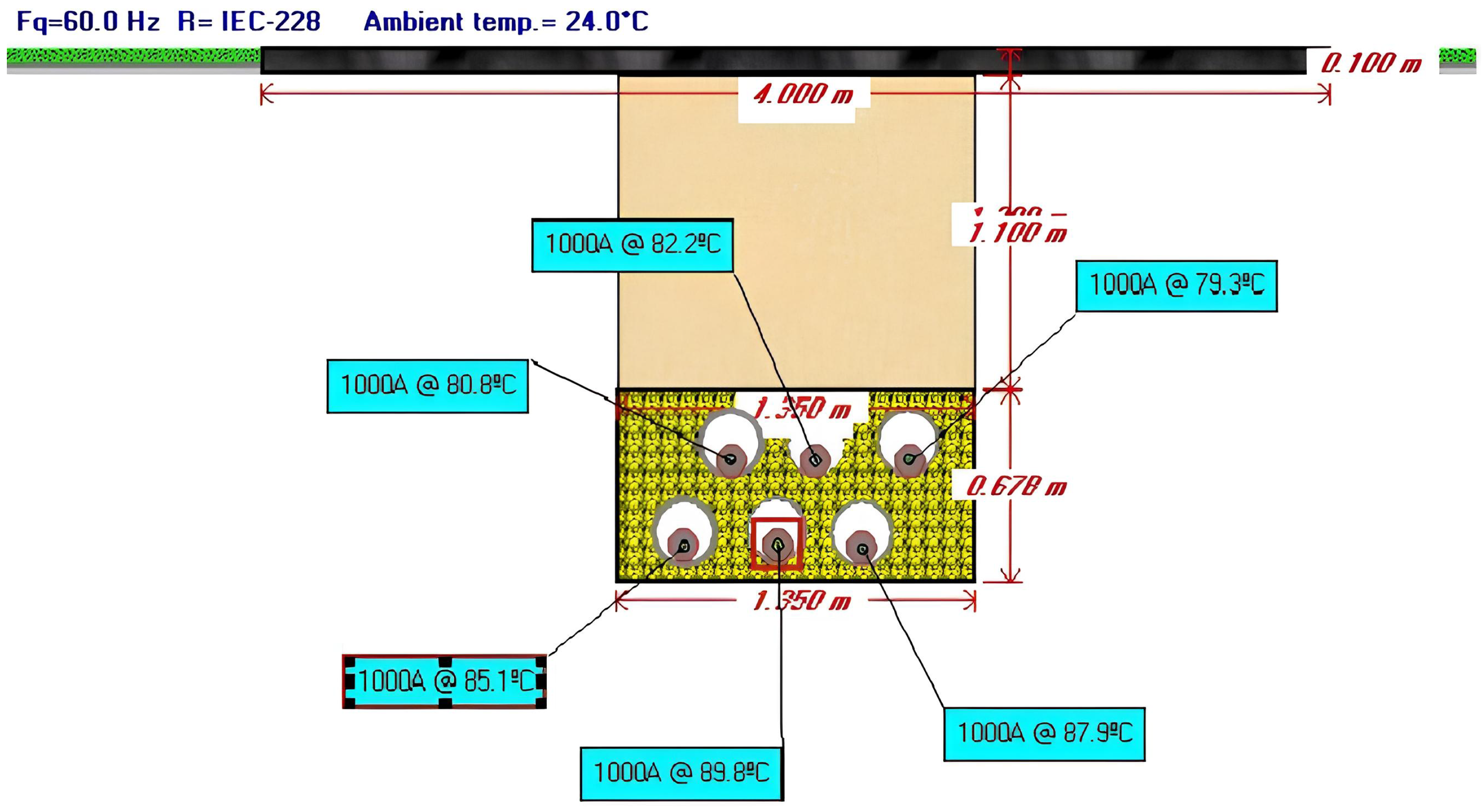
| N° Minor Section | Type of Interference | Interference Lengths | Depth of Installation (m) | Progressive (m) |
|---|---|---|---|---|
| 1 | Gas pipe | 25 | 1.5 | 0 + 150 |
| Intersection with busy avenue | 35 | 1.0 | 0 + 220 | |
| Water pipe | 13 | 1.1 | 0 + 280 | |
| Gas pipe longitudinal | 90 | 1.5 | 0 + 379 | |
| Intersection with busy avenue | 30 | 1.0 | 0 + 420 | |
| Gas pipe | 25 | 1.5 | 0 + 560 | |
| 2 | Gas pipe | 26 | 1.65 | 0 + 650 |
| MV cable | 20 | 1.4 | 0 + 830 | |
| Water pipe | 12 | 1.1 | 0 + 903 | |
| Intersection with busy avenue | 25 | 1.0 | 0 + 986 | |
| Gas pipe | 25 | 1.5 | 1 + 098 | |
| Gas pipe | 25 | 1.5 | 1 + 150 | |
| 3 | Water pipe | 15 | 1.3 | 1 + 290 |
| MV cable | 8 | 1.1 | 1 + 500 | |
| MV cable | 20 | 1.4 | 1 + 810 | |
| 4 | Water pipe | 16 | 1.3 | 1 + 990 |
| Water pipe | 12 | 1.1 | 2 + 050 | |
| Water pipe | 13 | 1.1 | 2 + 259 | |
| Intersection with busy avenue | 20 | 1.0 | 2 + 303 | |
| MV cable | 8 | 1.1 | 2 + 415 | |
| 5 | MV cable | 23 | 1.5 | 2 + 560 |
| Gas pipe longitudinal | 75 | 1.4 | 2 + 680 | |
| Water pipe | 14 | 1.3 | 2 + 750 | |
| MV cable | 8 | 1.1 | 2 + 950 | |
| Water pipe | 12 | 1.1 | 3 + 010 | |
| Water pipe | 13 | 1.1 | 3 + 050 | |
| 6 | MV cable | 19 | 1.4 | 3 + 190 |
| Gas pipe | 12 | 1.1 | 3 + 260 | |
| MV cable | 20 | 1.4 | 3 + 645 | |
| 7 | MV cable | 9 | 1.1 | 3 + 866 |
| Water pipe | 12 | 1.1 | 4 + 085 | |
| MV cable | 20 | 1.4 | 4 + 150 | |
| MV cable | 18 | 1.3 | 4 + 260 | |
| 8 | MV cable | 23 | 1.5 | 4 + 498 |
| Water pipe | 12 | 1.1 | 4 + 586 | |
| MV cable | 8 | 1.1 | 4 + 687 | |
| Water pipe | 12 | 1.1 | 4 + 802 | |
| MV cable | 22 | 1.4 | 4 + 902 | |
| 9 | Gas pipe | 25 | 1.5 | 5 + 142 |
| Water pipe | 16 | 1.3 | 5 + 269 | |
| Intersection with busy avenue | 15 | 1.0 | 5 + 345 | |
| MV cable | 10 | 1.1 | 5 + 473 | |
| 10 | Water pipe | 16 | 1.3 | 5 + 782 |
| MV cable | 20 | 1.4 | 5 + 870 | |
| MV cable | 18 | 1.3 | 5 + 994 | |
| MV cable | 9 | 1.1 | 6 + 104 | |
| 11 | Water pipe | 16 | 1.3 | 6 + 290 |
| Gas pipe longitudinal | 80 | 1.5 | 6 + 410 | |
| Water pipe | 16 | 1.3 | 6 + 558 | |
| MV cable | 22 | 1.4 | 6 + 673 | |
| MV cable | 10 | 1.1 | 6 + 773 | |
| 12 | Water pipe | 16 | 1.3 | 7 + 013 |
| High excavation cost | 150 | 1.0 | 7 + 125 | |
| MV cable | 18 | 1.3 | 7 + 344 | |
| 13 | Water pipe | 14 | 1.3 | 7 + 495 |
| Water pipe | 13 | 1.1 | 7 + 655 | |
| MV cable | 9 | 1.1 | 7 + 712 | |
| MV cable | 22 | 1.4 | 7 + 810 | |
| Water pipe | 12 | 1.1 | 7 + 940 | |
| 14 | Water pipe | 16 | 1.3 | 8 + 085 |
| Water pipe | 12 | 1.1 | 8 + 412 | |
| Water pipe | 15 | 1.3 | 8 + 553 | |
| 15 | MV cable | 9 | 1.1 | 8 + 758 |
| MV cable | 22 | 1.4 | 8 + 930 | |
| Water pipe longitudinal | 65 | 1.1 | 9 + 043 | |
| 16 | MV cable | 10 | 1.1 | 9 + 312 |
| Water pipe | 15 | 1.3 | 9 + 456 | |
| High excavation cost | 80 | 1.0 | 9 + 569 | |
| MV cable | 18 | 1.3 | 9 + 750 | |
| 17 | Water pipe | 12 | 1.1 | 9 + 969 |
| MV cable | 20 | 1.4 | 10 + 125 | |
| Water pipe | 16 | 1.3 | 10 + 307 | |
| Intersection with busy avenue | 22 | 1.0 | 10 + 375 | |
| MV cable | 9 | 1.1 | 10 + 456 | |
| 18 | MV cable | 20 | 1.4 | 10 + 595 |
| Water pipe | 15 | 1.3 | 10 + 850 | |
| MV cable | 18 | 1.3 | 11,009 |
| Type of Duct Bank | Cable Separation within the Same Circuit (mm) | Distance between Circuits (mm) | Maximum Free Depth (mm) |
|---|---|---|---|
| Triangular | 300 | 600 | 1250 |
| 350 | 700 | 1450 | |
| 400 | 800 | 1650 | |
| 450 | 900 | 1800 | |
| Inverted triangular | 350 | 525 | 1200 |
| 400 | 600 | 1400 | |
| 450 | 675 | 1550 | |
| 500 | 750 | 1700 | |
| Flat | 300 | 900 | 1850 |
| Vertical | 300 | 800 | 1150 |
| 350 | 1000 | 1500 | |
| 400 | 1200 | 1750 |
| N° Major Section | N° Minor Section | Length of Minor Section (m) |
|---|---|---|
| 1 | S1 | 589 |
| S2 | 620 | |
| S3 | 651 | |
| 2 | S4 | 597 |
| S5 | 630 | |
| S6 | 645 | |
| 3 | S7 | 620 |
| S8 | 645 | |
| S9 | 580 | |
| 4 | S10 | 605 |
| S11 | 623 | |
| S12 | 590 | |
| 5 | S13 | 610 |
| S14 | 640 | |
| S15 | 595 | |
| 6 | S16 | 640 |
| S17 | 630 | |
| S18 | 612 |
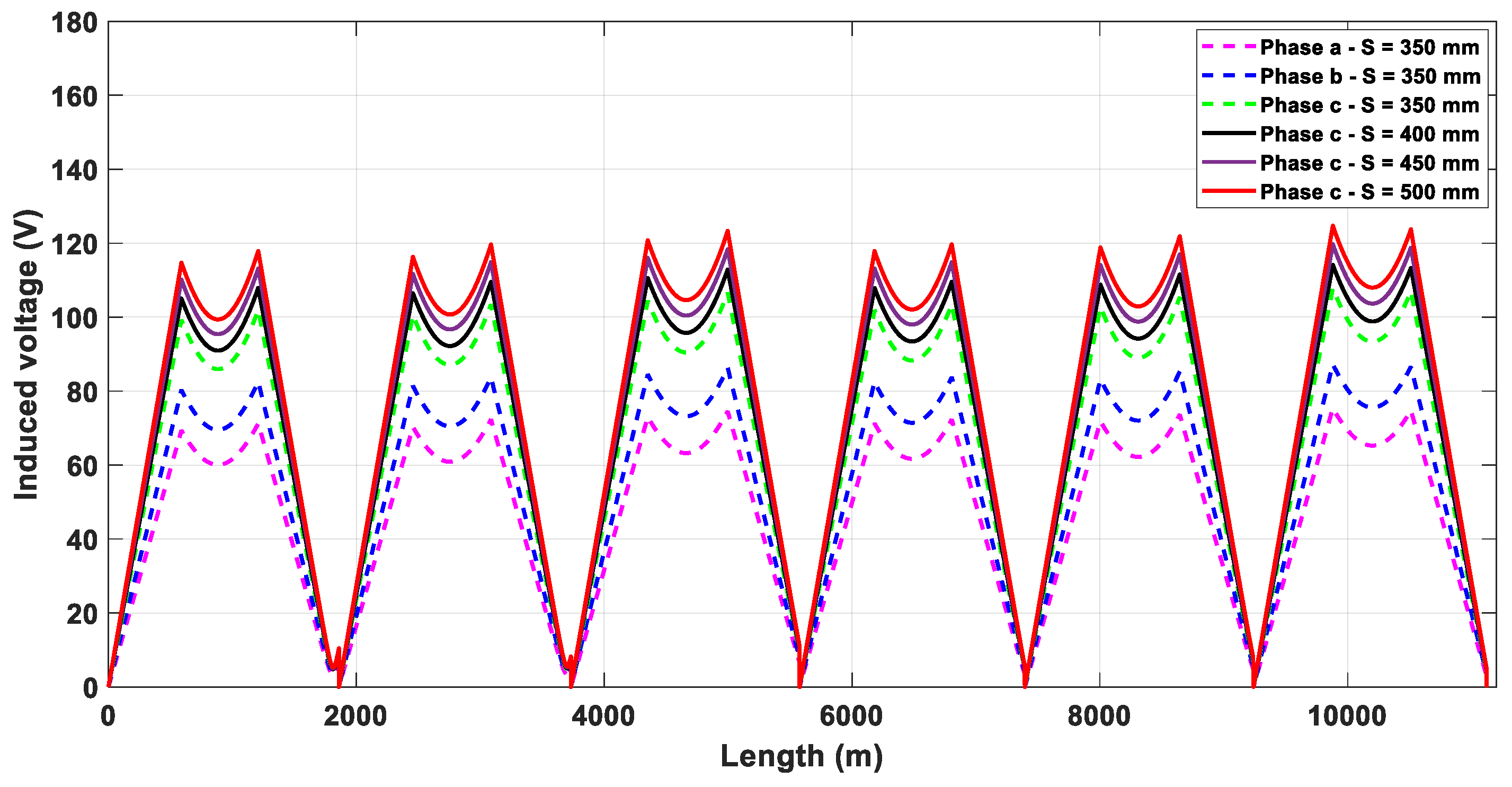
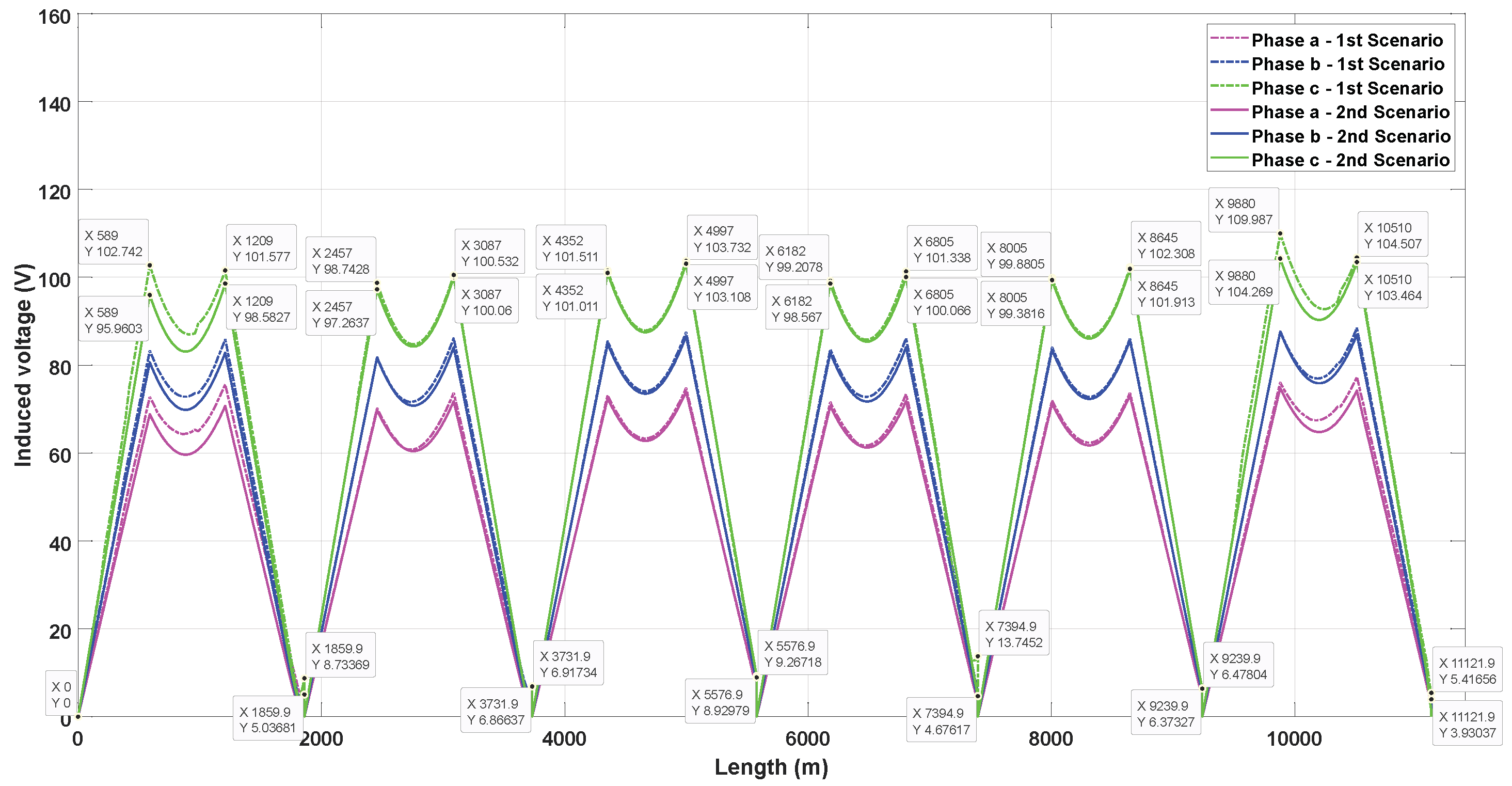
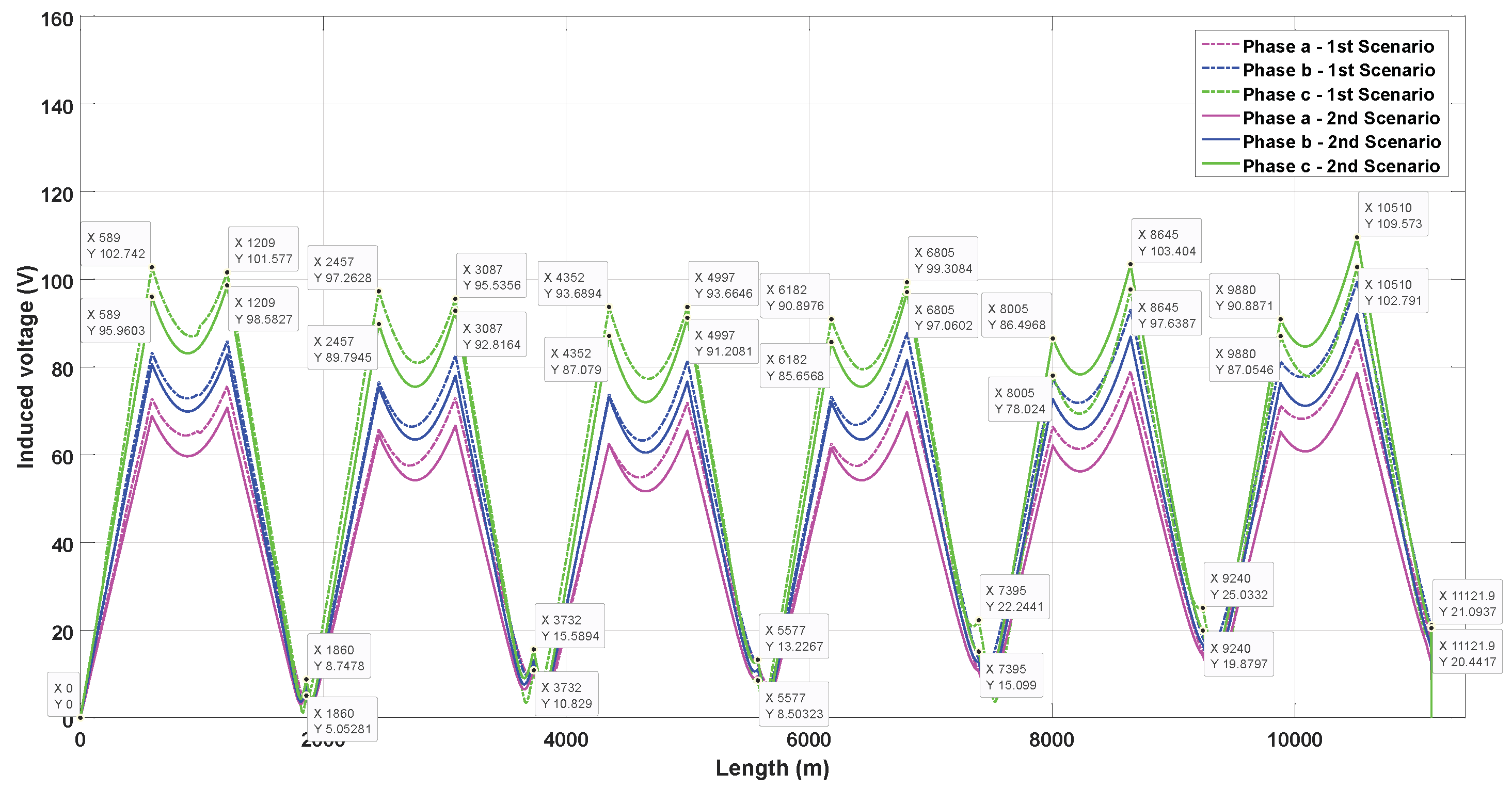
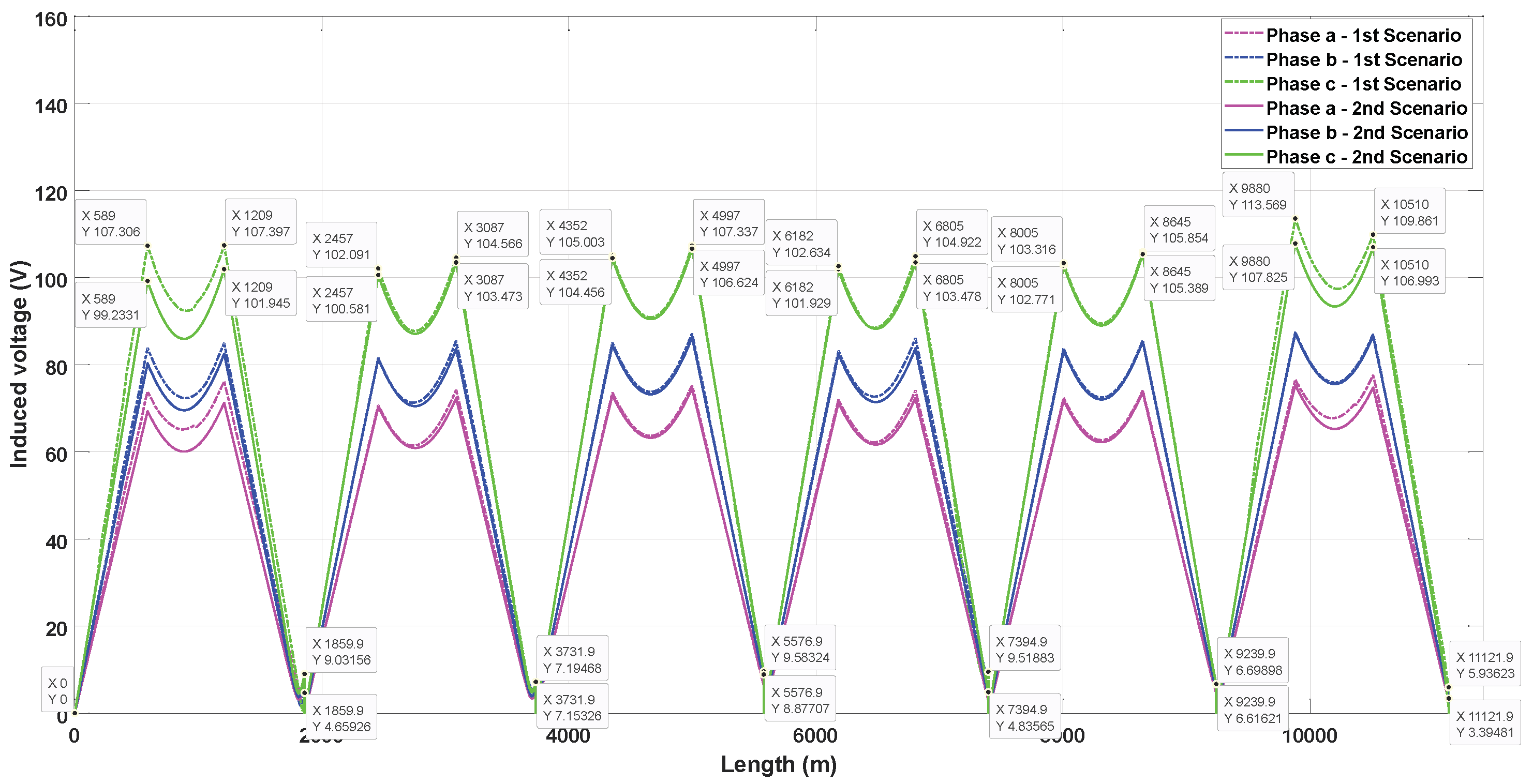
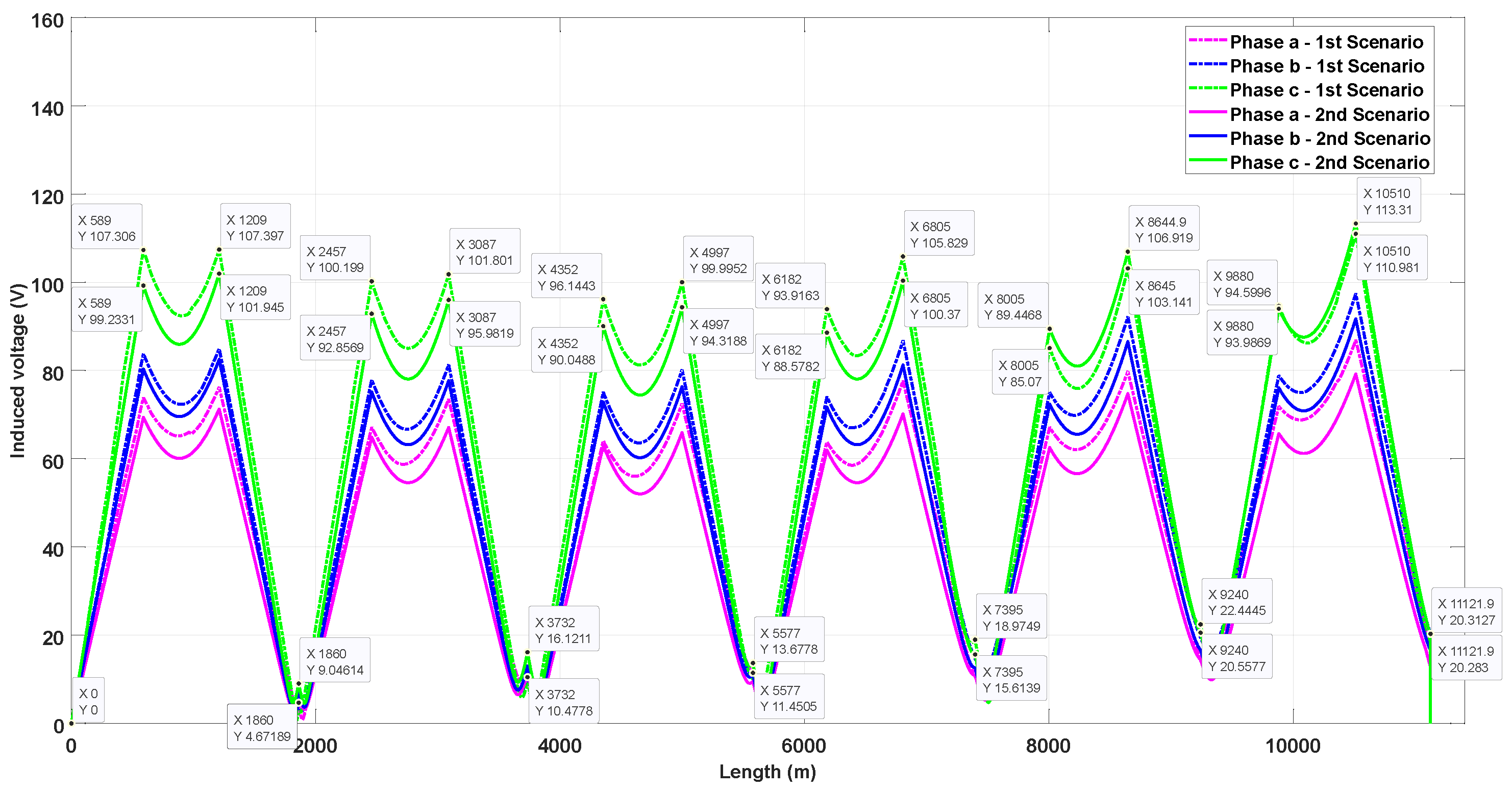
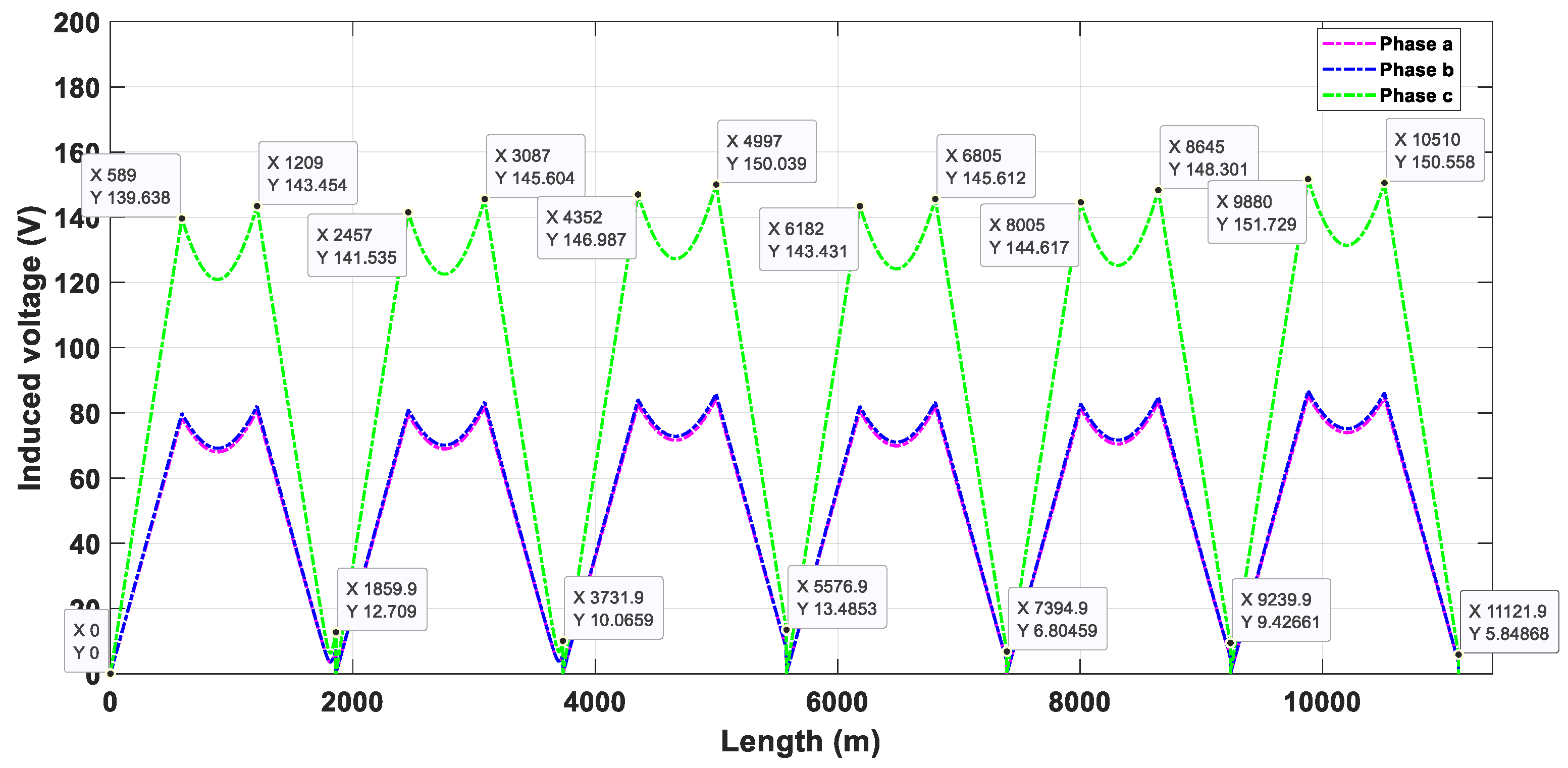
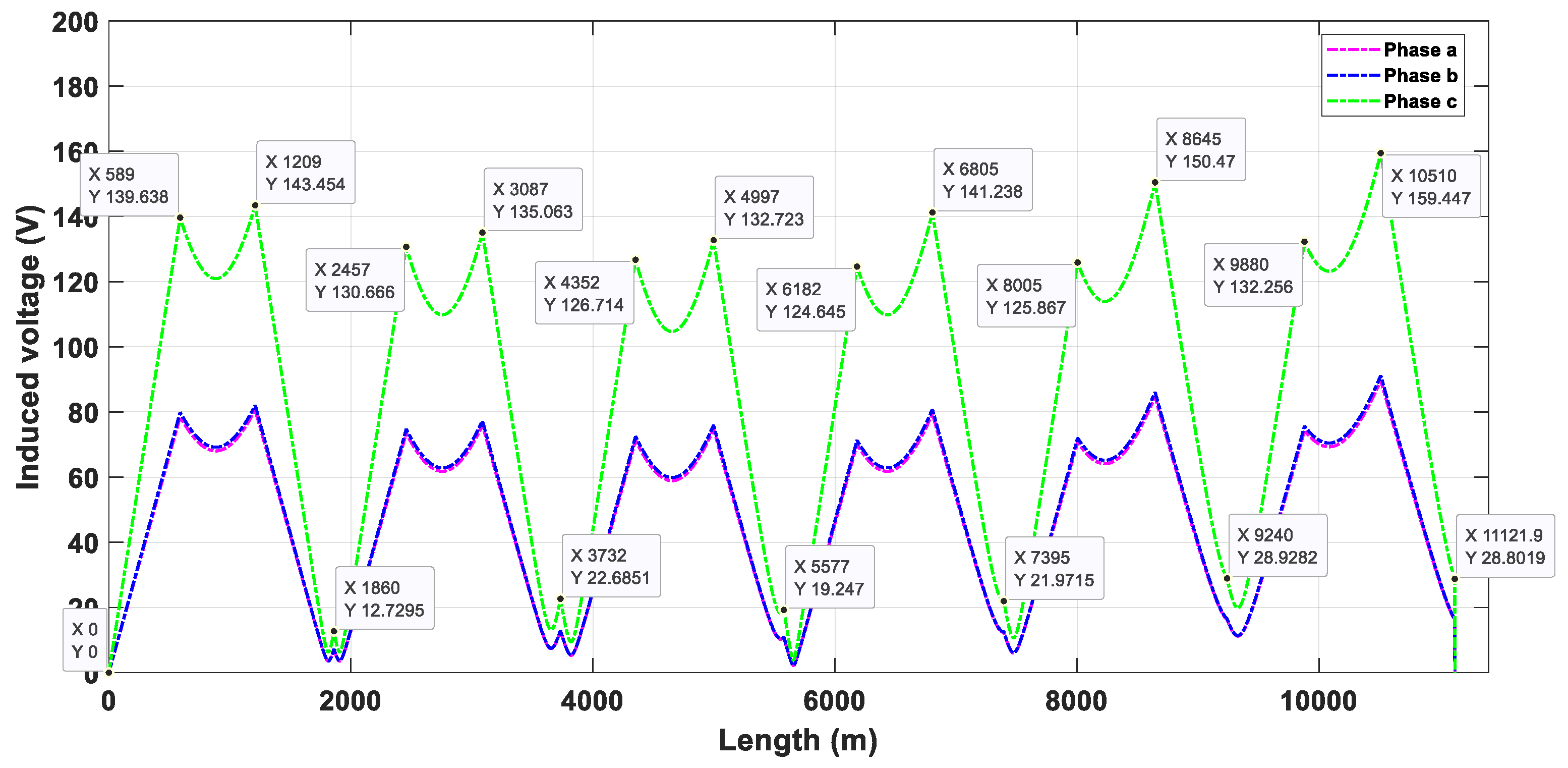
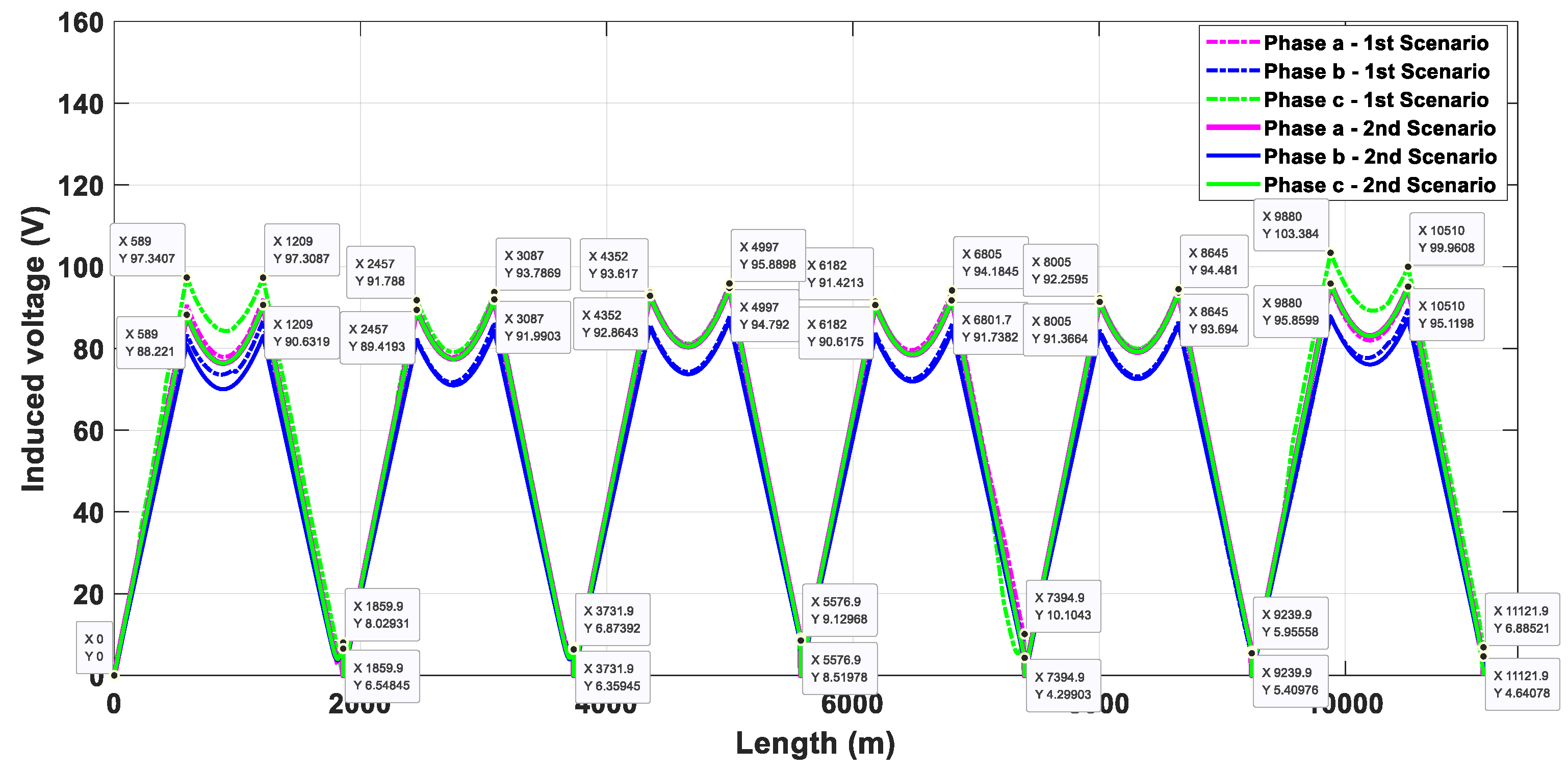
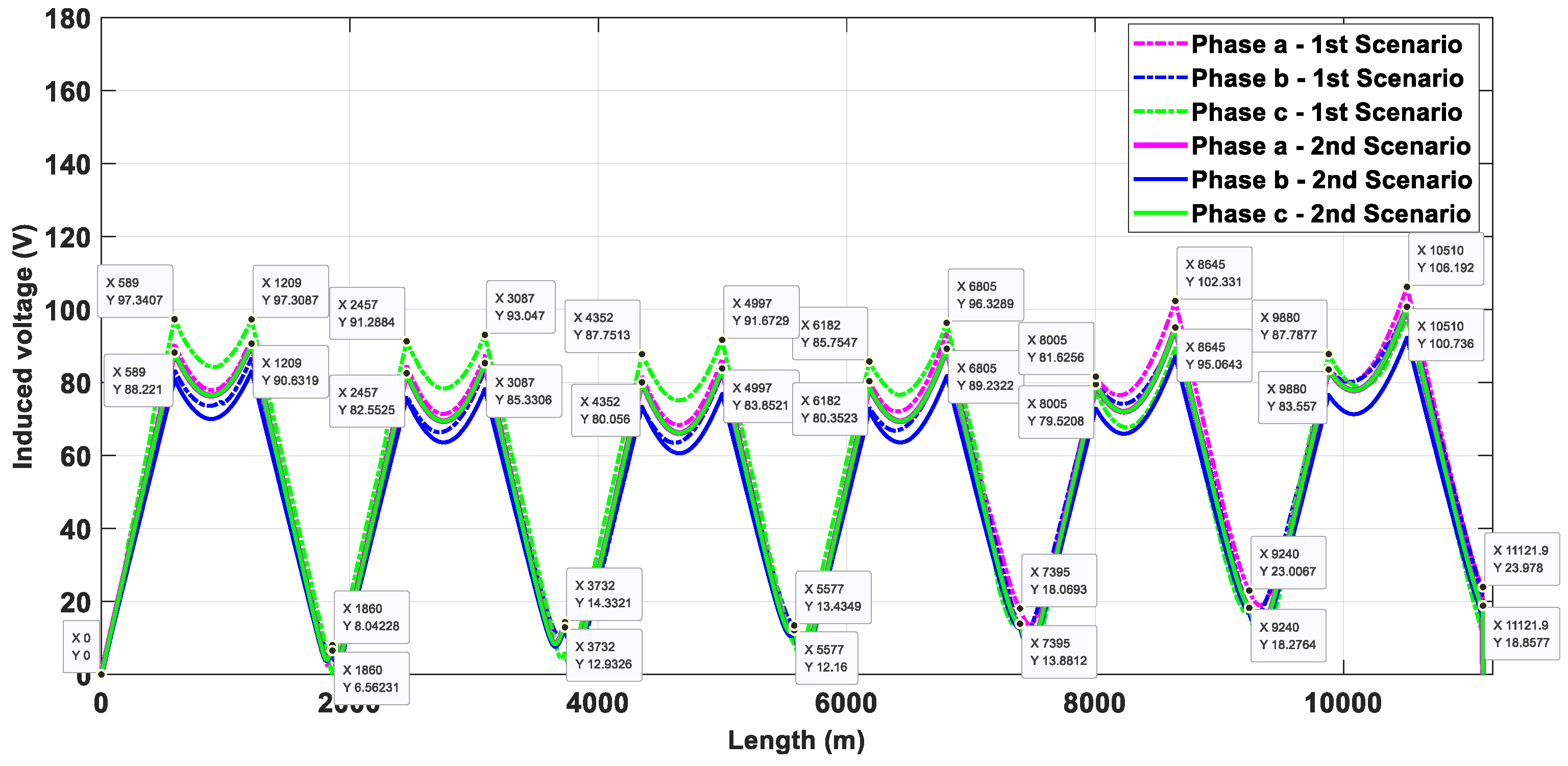
| Type of Duct Bank | Type of Cross-Bonding | Maximum Induced Voltage (Scenario 1) | Maximum Induced Voltage (Scenario 2) | Increase in Induced Voltage | Representative Phase |
|---|---|---|---|---|---|
| Triangular | SCB | 109.99 | 104.27 | 5.72 | C |
| CCB | 109.57 | 102.79 | 6.78 | C | |
| Inverted triangular | SCB | 113.57 | 107.83 | 5.74 | C |
| CCB | 113.31 | 110.98 | 2.33 | C | |
| Flat | SCB | 151.73 | 151.73 | 0.00 | C |
| CCB | 159.45 | 159.45 | 0.00 | C | |
| Vertical | SCB | 103.38 | 95.86 | 7.52 | A |
| CCB | 106.19 | 100.74 | 5.45 | A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asorza, J.E.G.; Leon Colqui, J.S.; Kurokawa, S.; Filho, J.P. Analysis of Increased Induced Voltages on the Sheath of Double-Circuit Underground Transmission Lines Guaranteeing Ampacity. Energies 2024, 17, 1637. https://doi.org/10.3390/en17071637
Asorza JEG, Leon Colqui JS, Kurokawa S, Filho JP. Analysis of Increased Induced Voltages on the Sheath of Double-Circuit Underground Transmission Lines Guaranteeing Ampacity. Energies. 2024; 17(7):1637. https://doi.org/10.3390/en17071637
Chicago/Turabian StyleAsorza, Jesus Enrique Guevara, Jaimis Sajid Leon Colqui, Sérgio Kurokawa, and José Pissolato Filho. 2024. "Analysis of Increased Induced Voltages on the Sheath of Double-Circuit Underground Transmission Lines Guaranteeing Ampacity" Energies 17, no. 7: 1637. https://doi.org/10.3390/en17071637
APA StyleAsorza, J. E. G., Leon Colqui, J. S., Kurokawa, S., & Filho, J. P. (2024). Analysis of Increased Induced Voltages on the Sheath of Double-Circuit Underground Transmission Lines Guaranteeing Ampacity. Energies, 17(7), 1637. https://doi.org/10.3390/en17071637








