Determination of an Optimal Parameter Combination for Single PEMFC Using the Taguchi Method and Orthogonal Array
Abstract
:1. Introduction
2. Materials and Methods
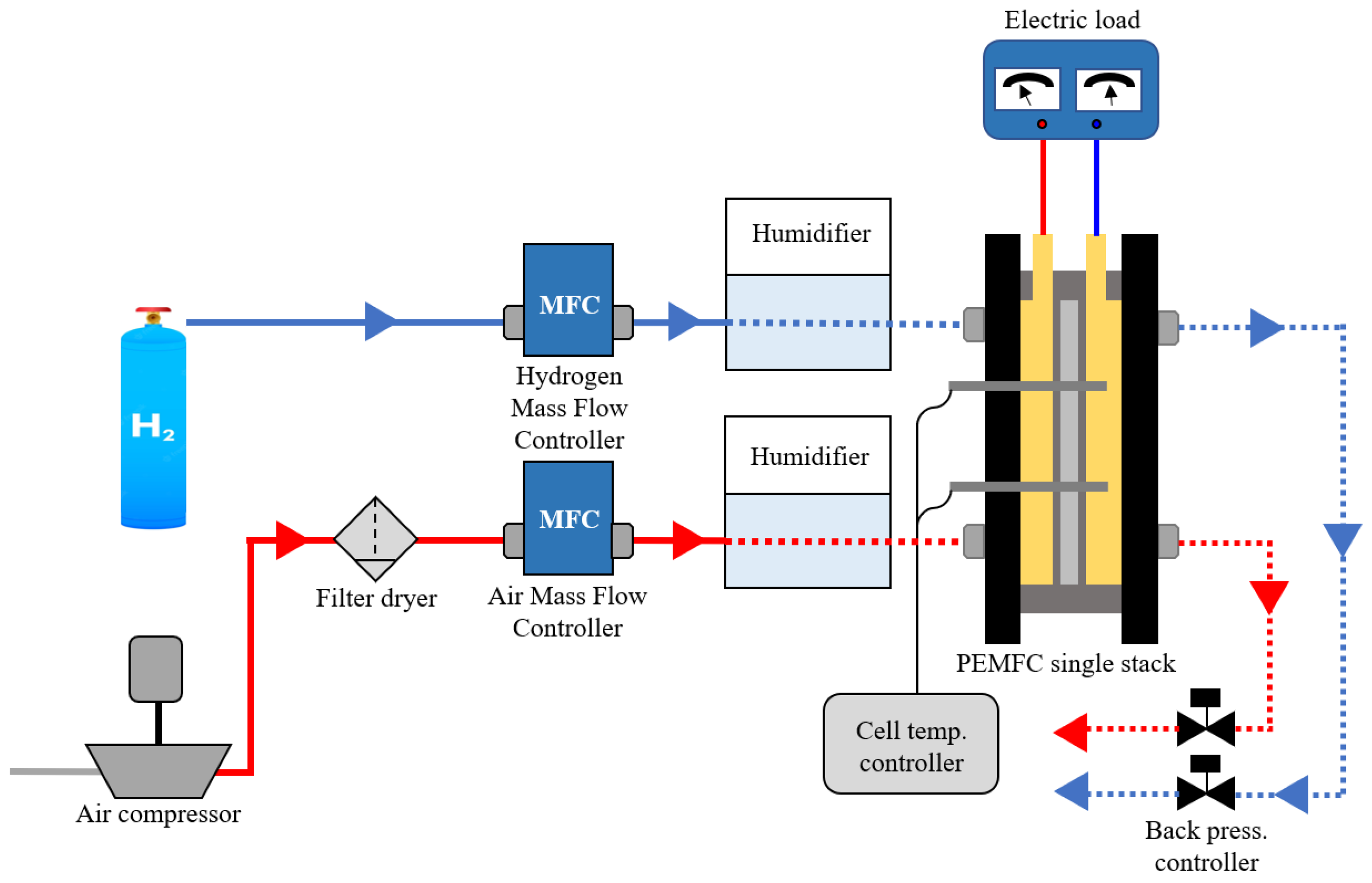
2.1. Configuration of Experiment
2.2. Taguchi Method and OA
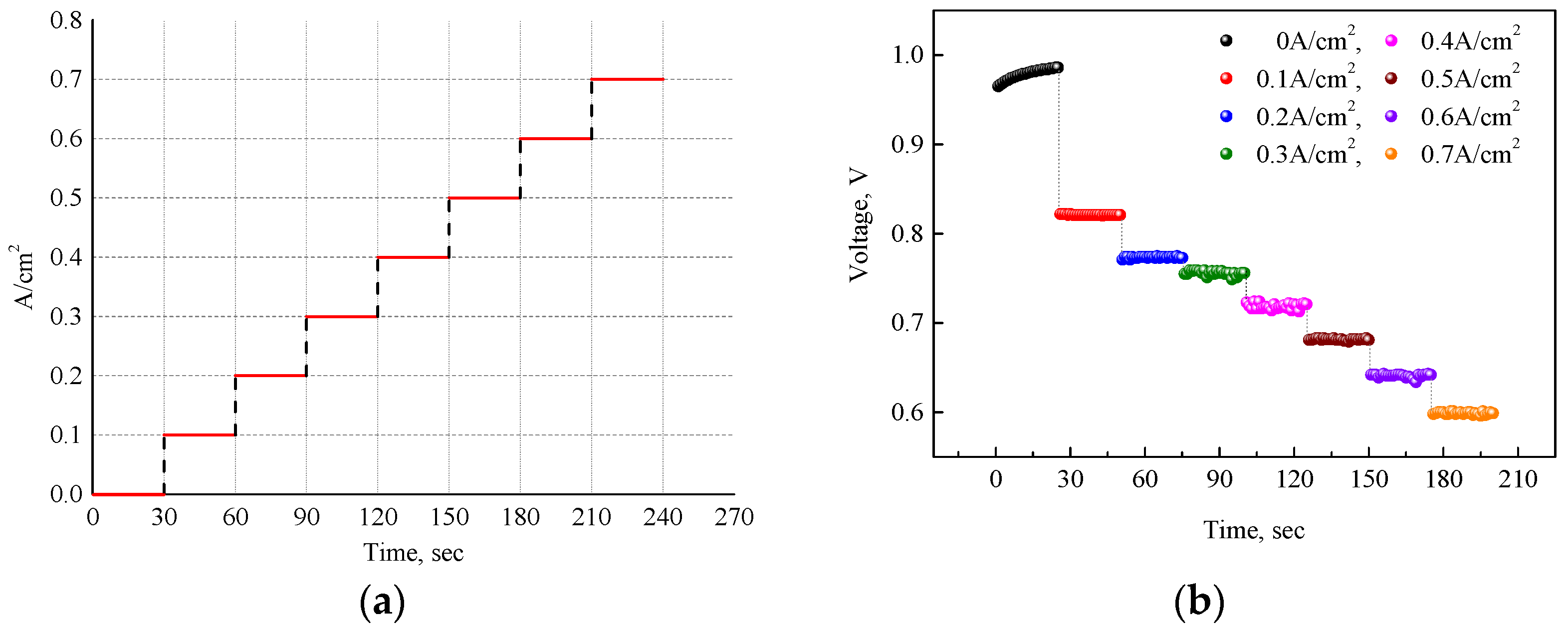
2.3. Polarization Curve
3. Results and Discussion
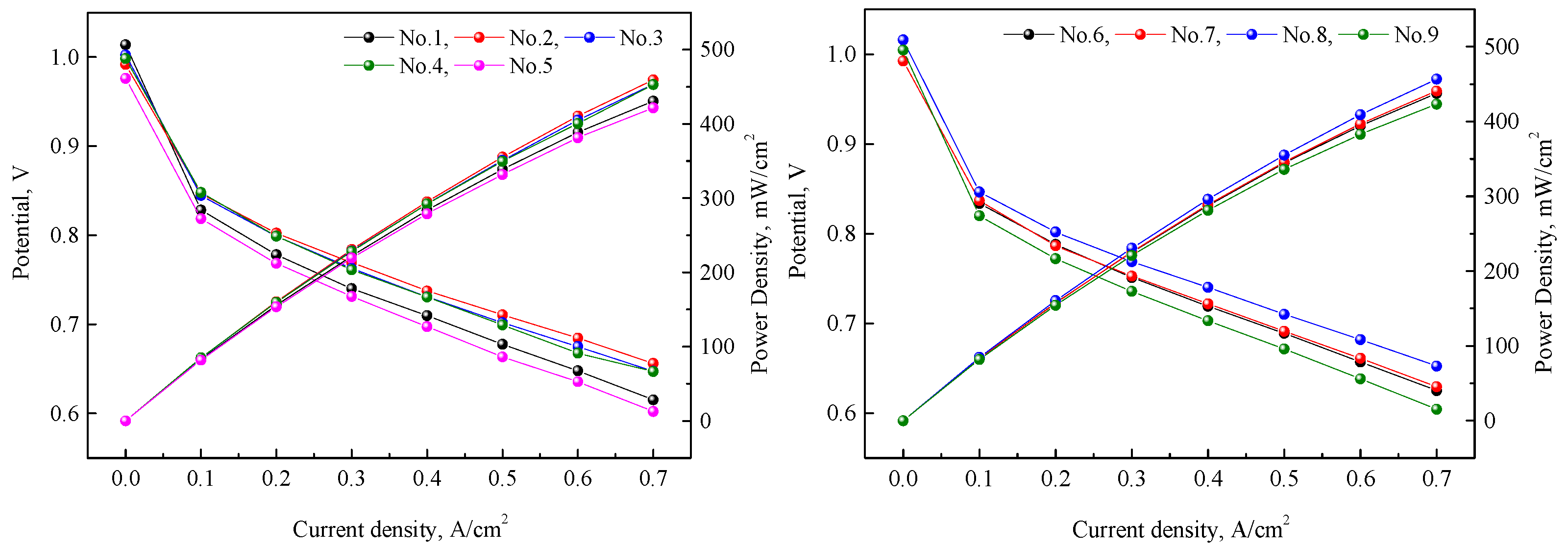
3.1. Polarization Curve
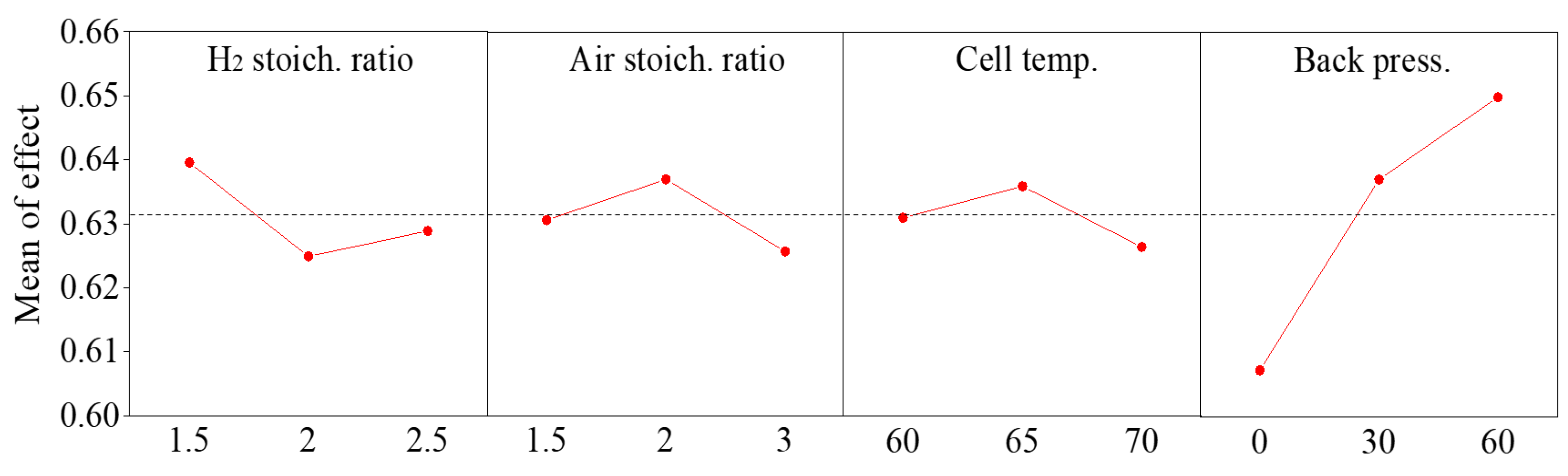
3.2. OA and Taguchi Analysis
3.3. Optimal Parameter Combination at Each Current Density
3.4. Effect of Back Pressure on Optimal Parameter Combination
3.5. Significance of Back Pressure in PEMFC Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, D.; Wang, Y.; Li, J.; Yang, Q.; Wang, J. Investigation of optimal operating temperature for the PEMFC and its tracking control for energy saving in vehicle applications. Energy Convers. Manag. 2021, 249, 114842. [Google Scholar] [CrossRef]
- Wang, B.; Lin, R.; Liu, D.; Xu, J.; Feng, B. Investigation of the effect of humidity at both electrode on the performance of PEMFC using orthogonal test method. Int. J. Hydrogen Energy 2019, 44, 13737–13743. [Google Scholar] [CrossRef]
- Jang, J.H.; Chiu, H.C.; Yan, W.M.; Sun, W.L. Effects of operating conditions on the performances of individual cell and stack of PEM fuel cell. J. Power Sources 2008, 180, 476–483. [Google Scholar] [CrossRef]
- Kim, B.; Cha, D.; Kim, Y. The effects of air stoichiometry and air excess ratio on the transient response of a PEMFC under load change conditions. Appl. Energy 2015, 138, 143–149. [Google Scholar] [CrossRef]
- Zhang, Q.; Lin, R.; Técher, L.; Cui, X. Experimental study of variable operating parameters effects on overall PEMFC performance and spatial performance distribution. Energy 2016, 115, 550–560. [Google Scholar] [CrossRef]
- Kaytakoğlu, S.; Akyalçın, L. Optimization of parametric performance of a PEMFC. Int. J. Hydrogen Energy 2007, 32, 4418–4423. [Google Scholar] [CrossRef]
- Hasanzadeh, R.; Mojaver, P.; Chitsaz, A.; Mojaver, M.; Jalili, M.; Rosen, M.A. Biomass and low-density polyethylene waste composites gasification: Orthogonal array design of Taguchi technique for analysis and optimization. Int. J. Hydrogen Energy 2022, 47, 28819–28832. [Google Scholar] [CrossRef]
- Awolusi, T.; Taiwo, A.; Aladegboye, O.; Oguntayo, D.; Akinkurolere, O. Optimization of quinary blended supplementary cementitious material for eco-friendly paving unit using taguchi orthogonal array design. Mater. Today Proc. 2022, 65, 2221–2227. [Google Scholar] [CrossRef]
- Taiwo, A.E.; Madzimbamuto, T.N.; Ojumu, T.V. Optimization of process variables for acetoin production in a bioreactor using Taguchi orthogonal array design. Heliyon 2020, 6, e05103. [Google Scholar] [CrossRef]
- Deresse, N.C.; Deshpande, V.; Taifa, I.W. Experimental investigation of the effects of process parameters on material removal rate using Taguchi method in external cylindrical grinding operation. Eng. Sci. Technol. Int. J. 2020, 23, 405–420. [Google Scholar] [CrossRef]
- Chang, K.Y.; Lin, H.J.; Chen, P.C. The optimal performance estimation for an unknown PEMFC based on the Taguchi method and a generic numerical PEMFC model. Int. J. Hydrogen Energy 2009, 34, 1990–1998. [Google Scholar] [CrossRef]
- Chang, K.Y. The optimal design for PEMFC modeling based on Taguchi method and genetic algorithm neural networks. Int. J. Hydrogen Energy 2011, 36, 13683–13694. [Google Scholar] [CrossRef]
- Wu, H.W.; Ku, H.W. The optimal parameters estimation for rectangular cylinders installed transversely in the flow channel of PEMFC from a three-dimensional PEMFC model and the Taguchi method. Appl. Energy 2011, 88, 4879–4890. [Google Scholar] [CrossRef]
- Karthikeyan, P.; Muthukumar, M.; Shanmugam, S.V.; Kumar, P.P.; Murali, S.; Kumar, A.S. Optimization of operating and design parameters on proton exchange membrane fuel cell by using Taguchi method. Procedia Eng. 2013, 64, 409–418. [Google Scholar] [CrossRef]
- Lin, C.; Yan, X.; Wei, G.; Ke, C.; Shen, S.; Zhang, J. Optimization of configurations and cathode operating parameters on liquid-cooled proton exchange membrane fuel cell stacks by orthogonal method. Appl. Energy 2019, 253, 113496. [Google Scholar] [CrossRef]
- Xia, S.; Lin, R.; Cui, X.; Shan, J. The application of orthogonal test method in the parameters optimization of PEMFC under steady working condition. Int. J. Hydrogen Energy 2016, 41, 11380–11390. [Google Scholar] [CrossRef]
- Santarelli, M.G.; Torchio, M.F. Experimental analysis of the effects of the operating variables on the performance of a single PEMFC. Energy Convers. Manag. 2007, 48, 40–51. [Google Scholar] [CrossRef]
- Chugh, S.; Chaudhari, C.; Sonkar, K.; Sharma, A.; Kapur, G.S.; Ramakumar, S.S.V. Experimental and modelling studies of low temperature PEMFC performance. Int. J. Hydrogen Energy 2020, 45, 8866–8874. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, Y.; Xu, S. Experimental study of PEM fuel cell temperature characteristic and corresponding automated optimal temperature calibration model. Energy 2023, 283, 128456. [Google Scholar] [CrossRef]
- Niya, S.M.R.; Hoorfar, M. Process modeling of the ohmic loss in proton exchange membrane fuel cells. Electrochim. Acta 2014, 120, 193–203. [Google Scholar] [CrossRef]
- Salva, J.A.; Iranzo, A.; Rosa, F.; Tapia, E.; Lopez, E.; Isorna, F. Optimization of a PEM fuel cell operating conditions: Obtaining the maximum performance polarization curve. Int. J. Hydrogen Energy 2016, 41, 19713–19723. [Google Scholar] [CrossRef]
- Reshetenko, T.V.; Bender, G.; Bethune, K.; Rocheleau, R. Systematic study of back pressure and anode stoichiometry effects on spatial PEMFC performance distribution. Electrochim. Acta 2011, 56, 8700–8710. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Zhang, J. Effect of operating backpressure on PEM fuel cell performance. ECS Trans. 2019, 19, 65. [Google Scholar] [CrossRef]
- Soomro, I.A.; Memon, F.H.; Mughal, W.; Khan, M.A.; Ali, W.; Liu, Y.; Choi, K.H.; Thebo, K.H. Influence of operating and electrochemical parameters on PEMFC performance. A simulation study. Membranes 2023, 13, 259. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.B.; Wei, G.H.; Zhu, F.J.; Yan, X.H.; Zhang, J.L. Pressure effect on the PEMFC performance. Fuel Cells 2019, 19, 211–220. [Google Scholar] [CrossRef]
- Cai, C.; Rao, Y.; Zhang, Y.; Wu, F.; Li, S.; Pan, M. Failure mechanism of PEM fuel cell under high back pressures operation. Int. J. Hydrogen Energy 2019, 44, 13786–13793. [Google Scholar] [CrossRef]
- Rohendi, D.; Majlan, E.H.; Mohamad, A.B.; Daud, W.R.W.; Kadhum, A.A.H.; Shyuan, L.K. Effects of temperature and backpressure on the performance degradation of MEA in PEMFC. Int. J. Hydrogen Energy 2015, 40, 10960–10968. [Google Scholar] [CrossRef]



| Factors | Level | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| A: H2 stoichiometry | 1.5 | 2.0 | 2.5 |
| B: Air stoichiometry | 1.5 | 2.0 | 2.5 |
| C: Cell temperature (Tc), °C | 60 | 65 | 70 |
| D: Back pressure (Pb), kPa | 0 | 30 | 60 |
| Test | Factors | |||
|---|---|---|---|---|
| A | B | C | D | |
| 1 | 1 (1.5) | 1 (1.5) | 1 (60) | 1 (0) |
| 2 | 1 (1.5) | 2 (2.0) | 2 (65) | 2 (30) |
| 3 | 1 (1.5) | 3 (2.5) | 3 (70) | 3 (60) |
| 4 | 2 (2.0) | 1 (1.5) | 2 (65) | 3 (60) |
| 5 | 2 (2.0) | 2 (2.0) | 3 (70) | 1 (0) |
| 6 | 2 (2.0) | 3 (2.5) | 2 (60) | 2 (30) |
| 7 | 3 (2.5) | 1 (1.5) | 3 (70) | 2 (30) |
| 8 | 3 (2.5) | 2 (2.0) | 2 (60) | 3 (60) |
| 9 | 3 (2.5) | 3 (2.5) | 3 (65) | 1 (0) |
| Test Number | Current Density, A/cm2 | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | |
| 1 | 1.014 | 0.828 | 0.778 | 0.740 | 0.709 | 0.677 | 0.647 | 0.615 |
| 2 | 0.991 | 0.846 | 0.802 | 0.769 | 0.737 | 0.71 | 0.684 | 0.656 |
| 3 | 1.002 | 0.844 | 0.798 | 0.762 | 0.73 | 0.701 | 0.675 | 0.647 |
| 4 | 0.998 | 0.848 | 0.799 | 0.761 | 0.73 | 0.699 | 0.667 | 0.647 |
| 5 | 0.976 | 0.818 | 0.768 | 0.731 | 0.697 | 0.663 | 0.635 | 0.602 |
| 6 | 1.017 | 0.833 | 0.788 | 0.751 | 0.719 | 0.688 | 0.657 | 0.625 |
| 7 | 0.992 | 0.836 | 0.786 | 0.752 | 0.722 | 0.691 | 0.661 | 0.629 |
| 8 | 1.015 | 0.846 | 0.801 | 0.768 | 0.74 | 0.71 | 0.681 | 0.652 |
| 9 | 1.004 | 0.82 | 0.772 | 0.735 | 0.703 | 0.671 | 0.638 | 0.604 |
| Level | Factors | |||
|---|---|---|---|---|
| A | B | C | D | |
| 1 | 0.6396 | 0.6306 | 0.631 | 0.6073 |
| 2 | 0.6249 | 0.637 | 0.6359 | 0.6371 |
| 3 | 0.6289 | 0.6257 | 0.6265 | 0.649 |
| Delta | 0.0147 | 0.0112 | 0.0095 | 0.0417 |
| Rank | 2 | 3 | 4 | 1 |
| Current Density, A/cm2 | Influence Rank | Optimal Parameter |
|---|---|---|
| 0.1 | D > A > B > C | A1B1C2D3 |
| 0.2 | D > A > C > B | A1B2C2D3 |
| 0.3 | D > A > C > B | A1B2C2D3 |
| 0.4 | D > A > B > C | A1B2C2D3 |
| 0.5 | D > A > C > B | A1B2C2D3 |
| 0.6 | D > A > B > C | A1B2C2D3 |
| 0.7 | D > A > B > C | A1B2C2D3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, K.-H.; Lee, J.-H. Determination of an Optimal Parameter Combination for Single PEMFC Using the Taguchi Method and Orthogonal Array. Energies 2024, 17, 1690. https://doi.org/10.3390/en17071690
Jung K-H, Lee J-H. Determination of an Optimal Parameter Combination for Single PEMFC Using the Taguchi Method and Orthogonal Array. Energies. 2024; 17(7):1690. https://doi.org/10.3390/en17071690
Chicago/Turabian StyleJung, Kwang-Hu, and Jung-Hyung Lee. 2024. "Determination of an Optimal Parameter Combination for Single PEMFC Using the Taguchi Method and Orthogonal Array" Energies 17, no. 7: 1690. https://doi.org/10.3390/en17071690
APA StyleJung, K.-H., & Lee, J.-H. (2024). Determination of an Optimal Parameter Combination for Single PEMFC Using the Taguchi Method and Orthogonal Array. Energies, 17(7), 1690. https://doi.org/10.3390/en17071690






