Energy Management Systems’ Modeling and Optimization in Hybrid Electric Vehicles
Abstract
:1. Introduction
2. Hybrid Electric Vehicle Modeling
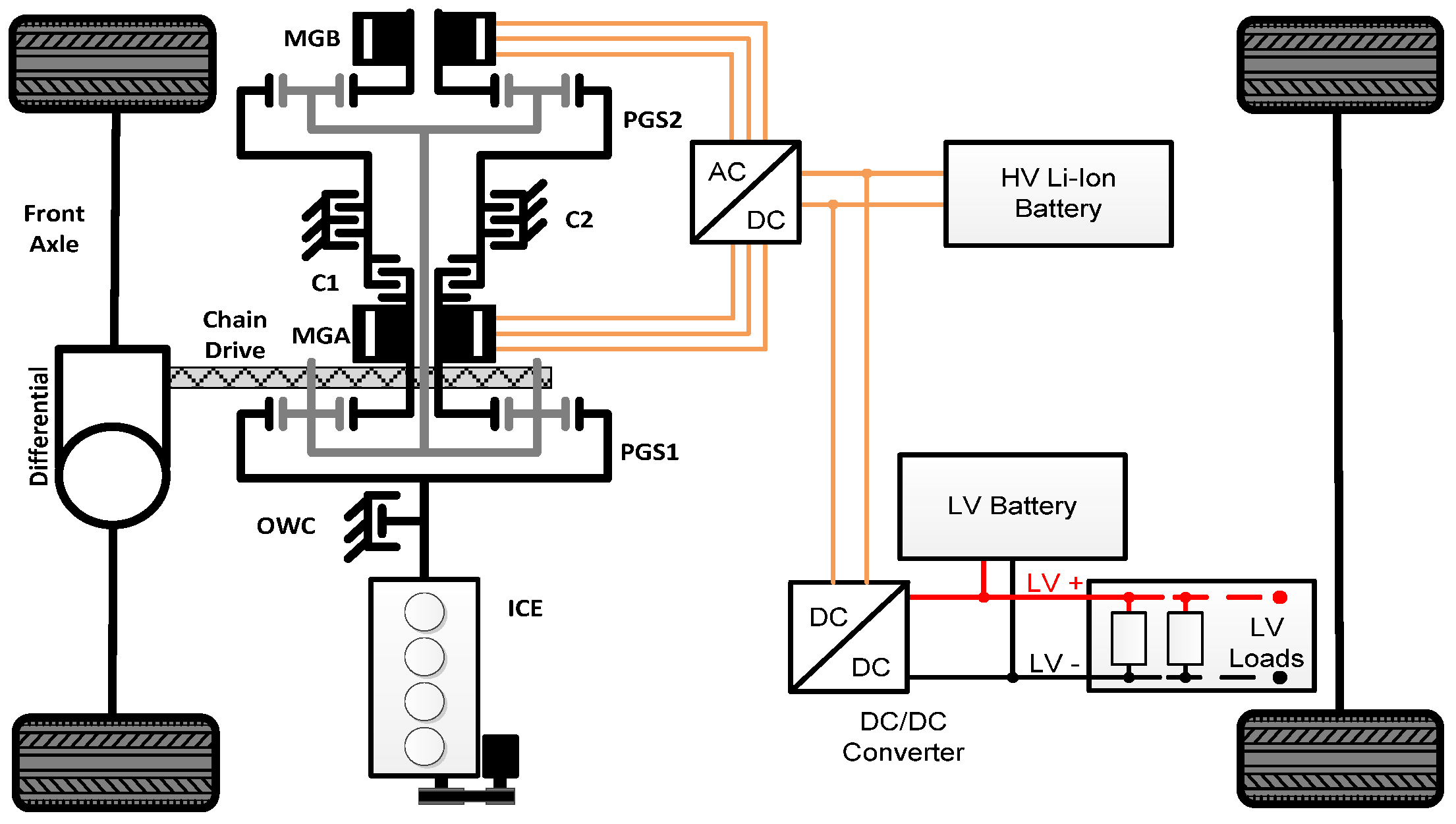
2.1. Hybrid Electric Vehicle Configuration
2.2. Hybrid Electric Vehicle Parameters
2.3. Hybrid Electric Vehicle Operating Modes
2.4. Hybrid Electric Vehicle Modeling
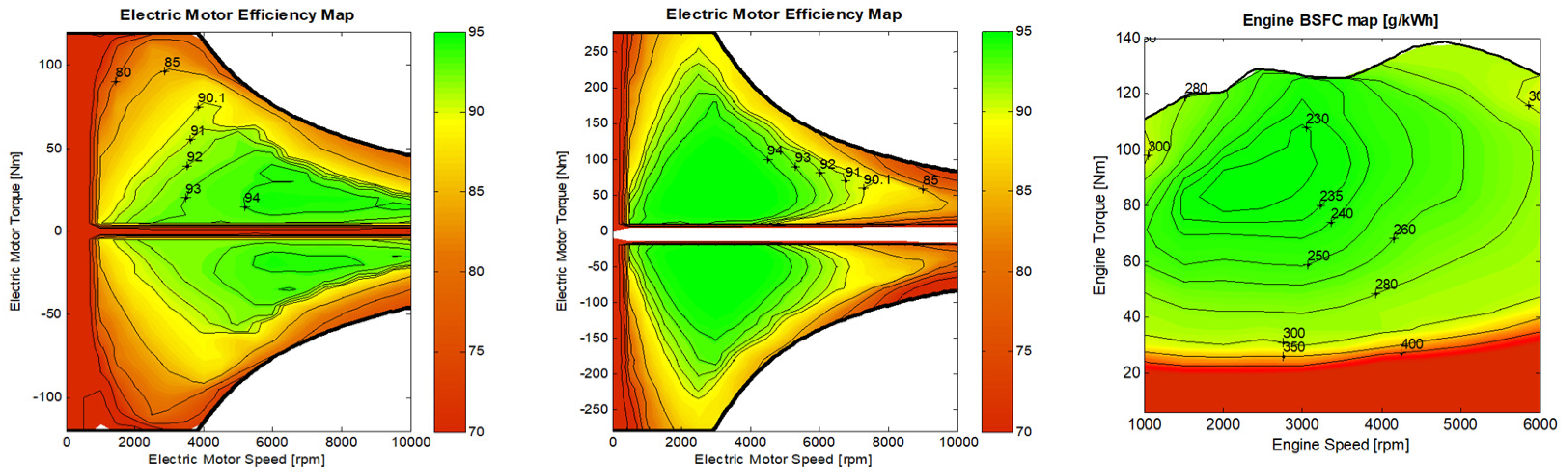
2.4.1. Internal Combustion Engine Model
2.4.2. Electric Motor Model
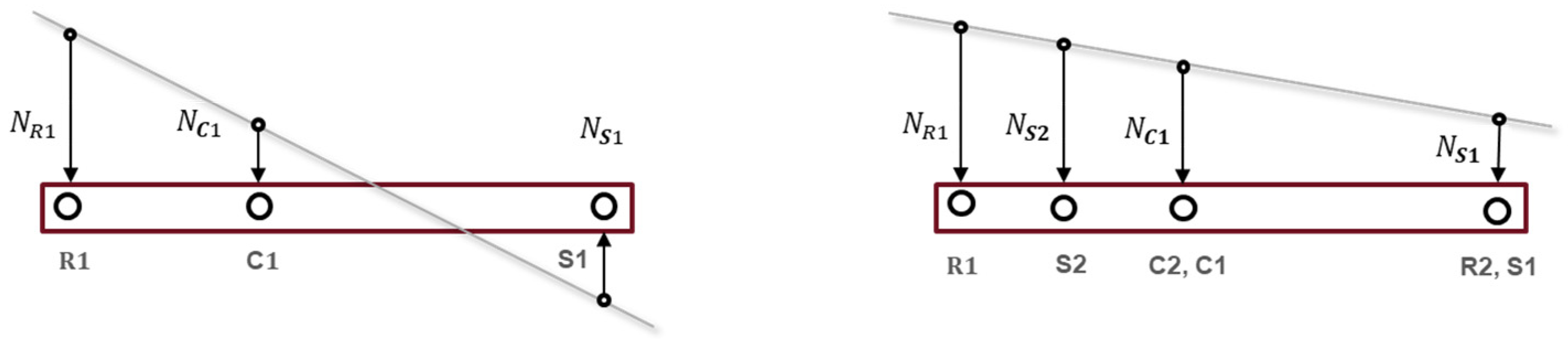
2.4.3. Transmission Model
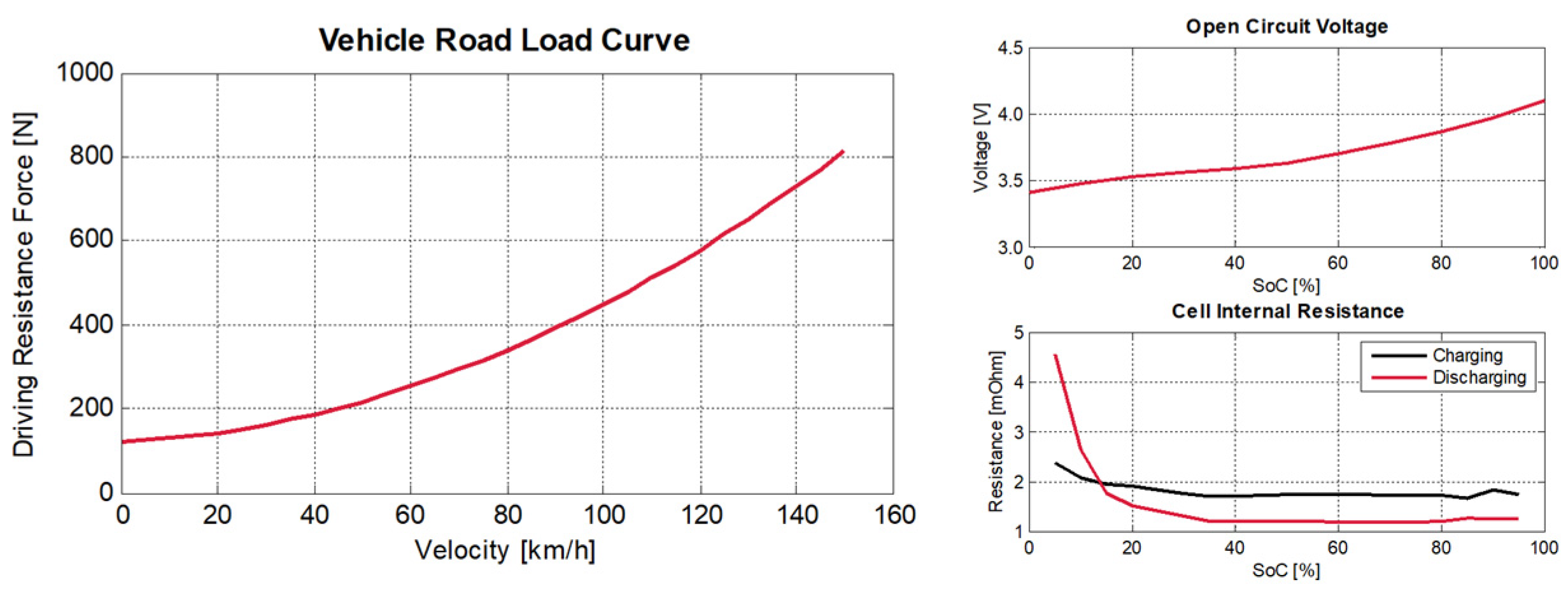
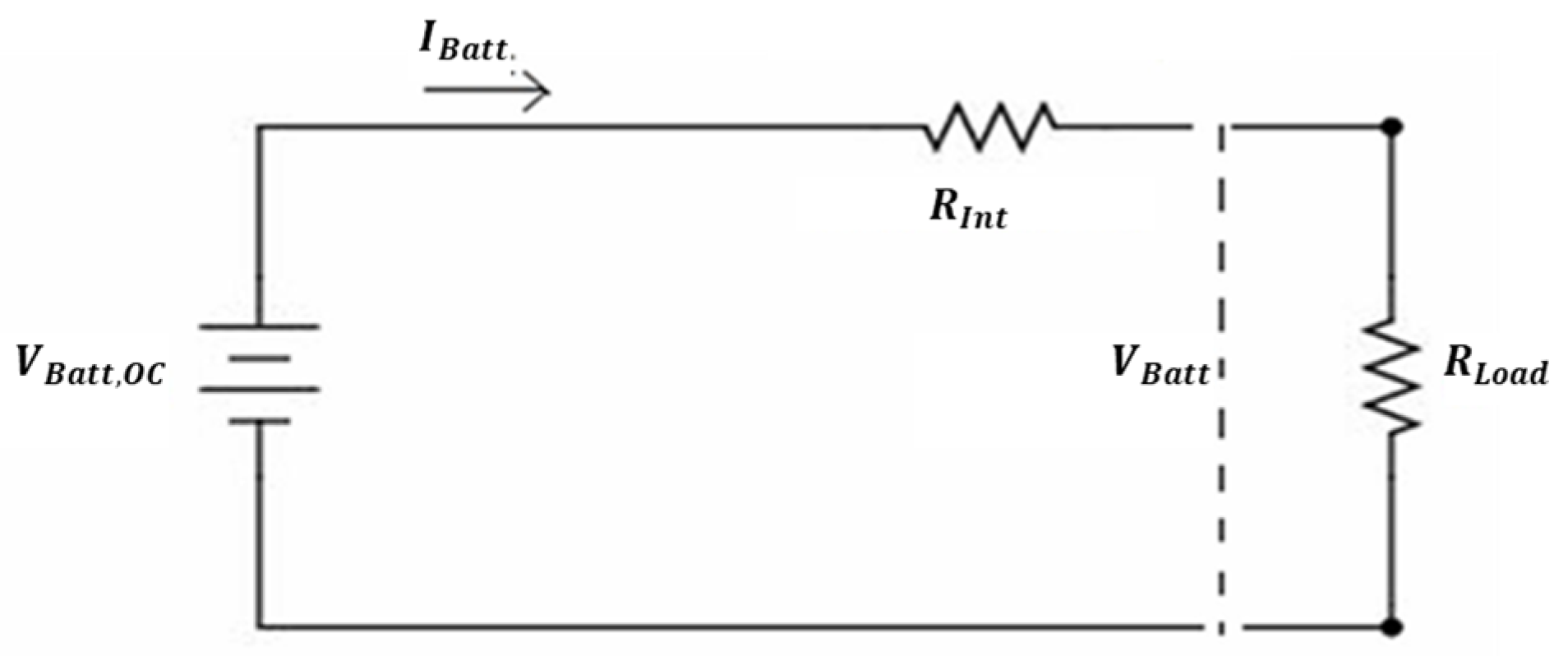
2.4.4. Battery Model
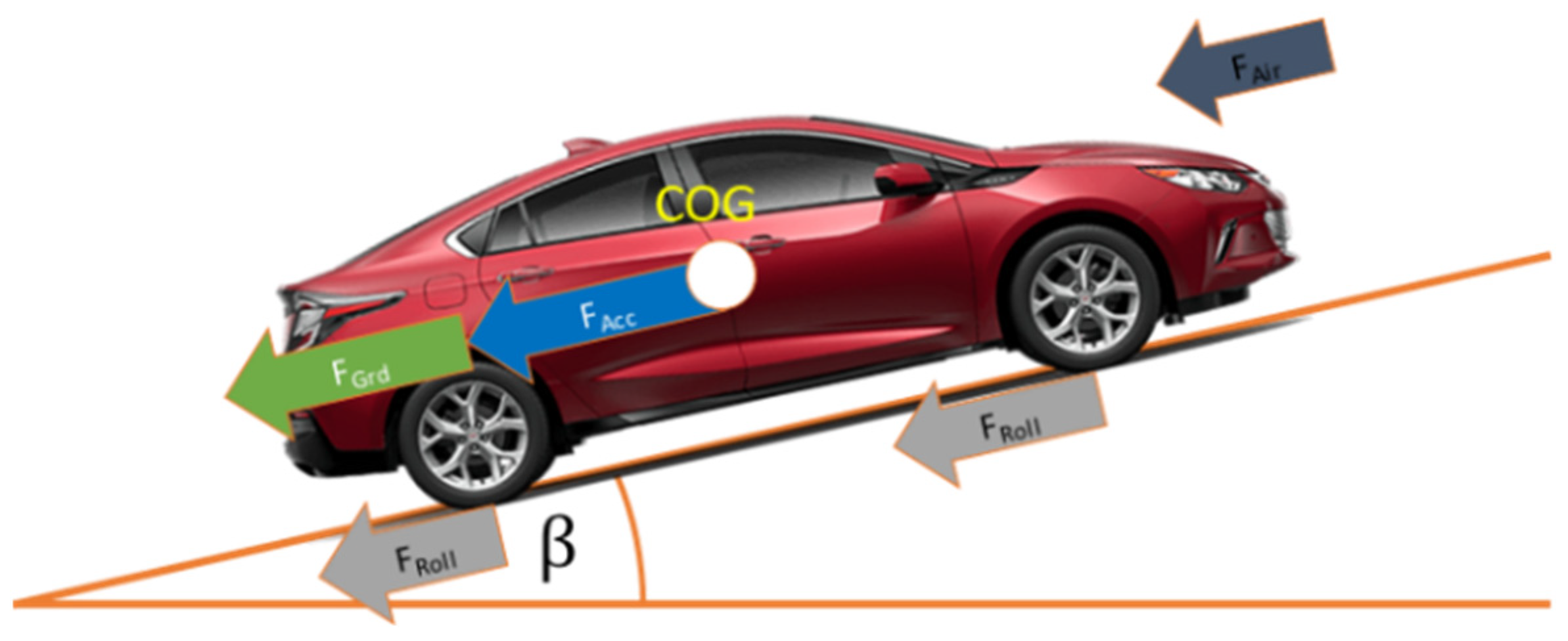
2.4.5. Vehicle Model
2.4.6. Driver Model
2.5. Drive Cycles
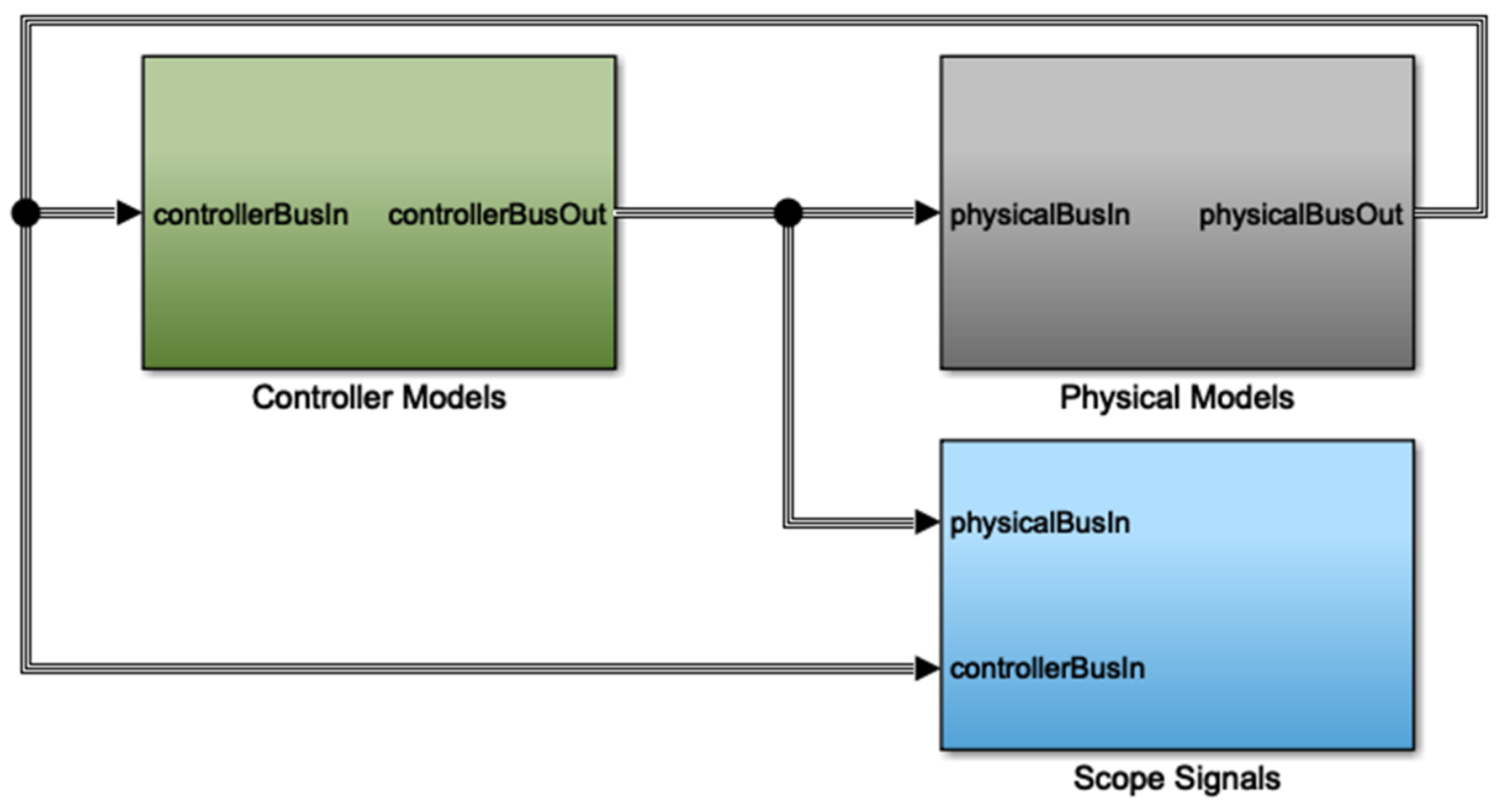
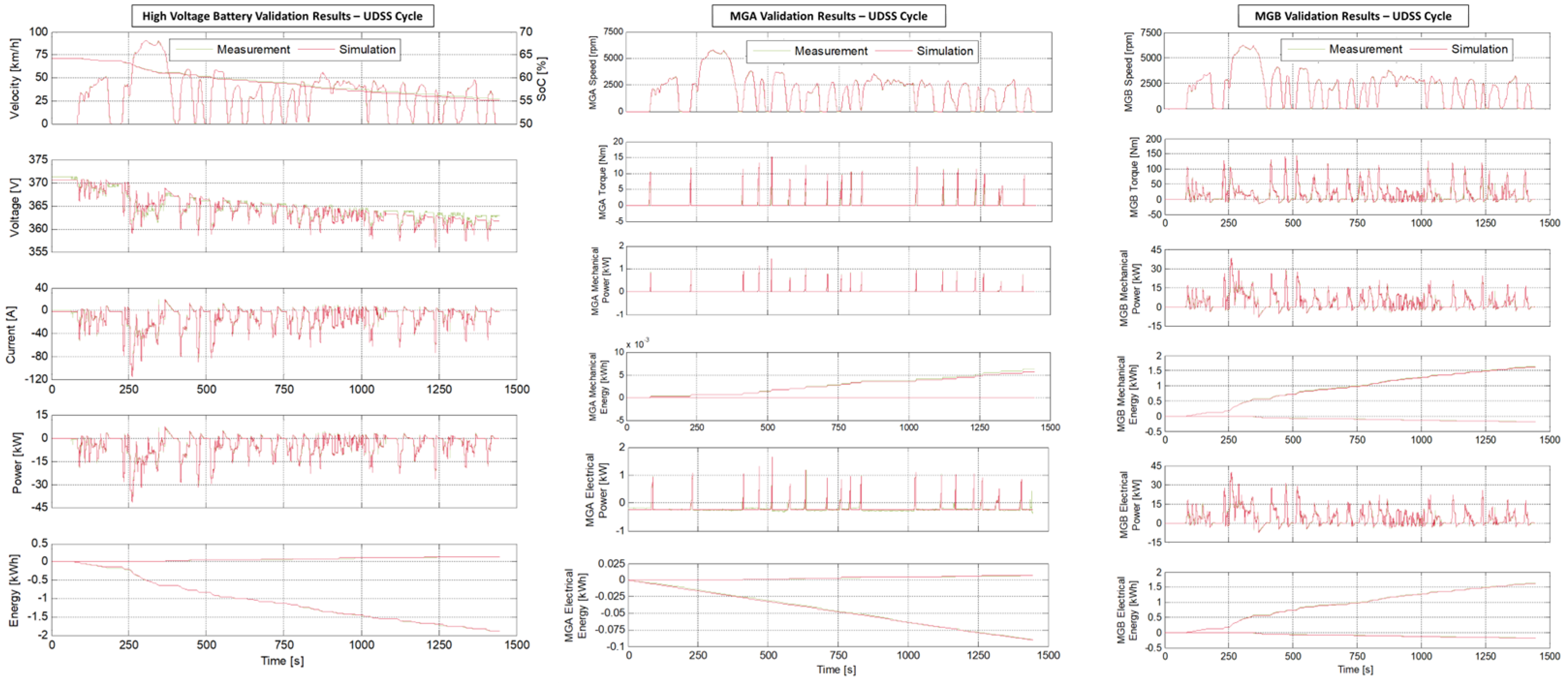
3. Hybrid Electric Vehicle Model Validation
4. Hybrid Electric Vehicle Energy Management Systems
4.1. Energy Management Systems Objectives
4.2. Classification of Energy Management Systems
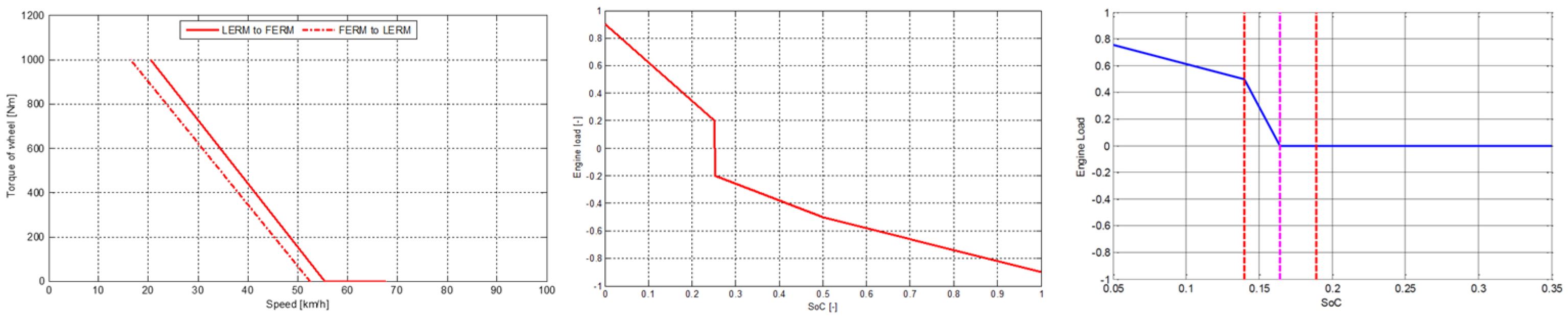
4.3. Rule-Based Energy Management System
4.4. Discrete Dynamic Programming (DDP)-Based Energy Management System
4.5. Pontryagin’s Minimum Principle (PMP) based Energy Management System
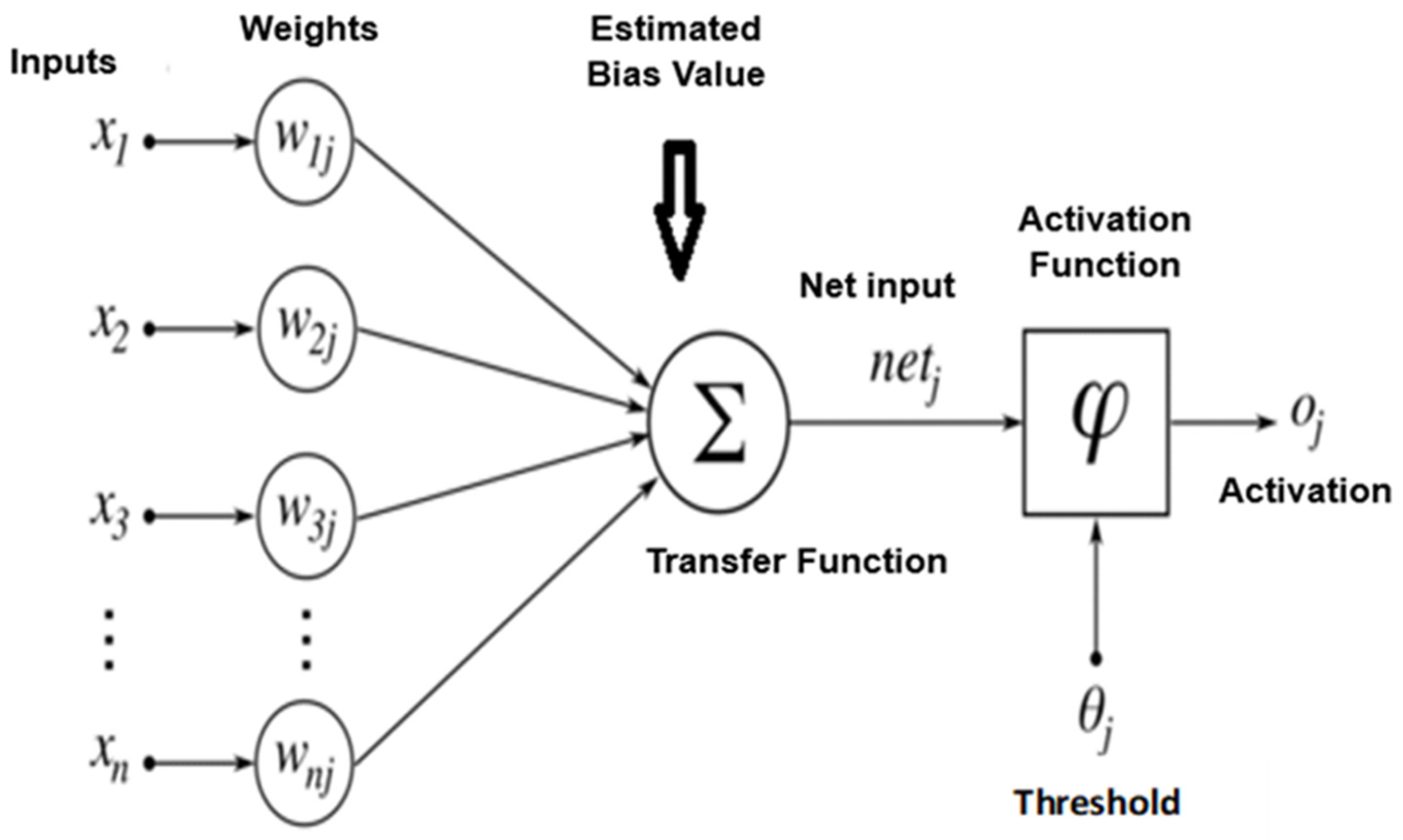
4.6. Artificial Neural Network (ANN)-Based Energy Management System
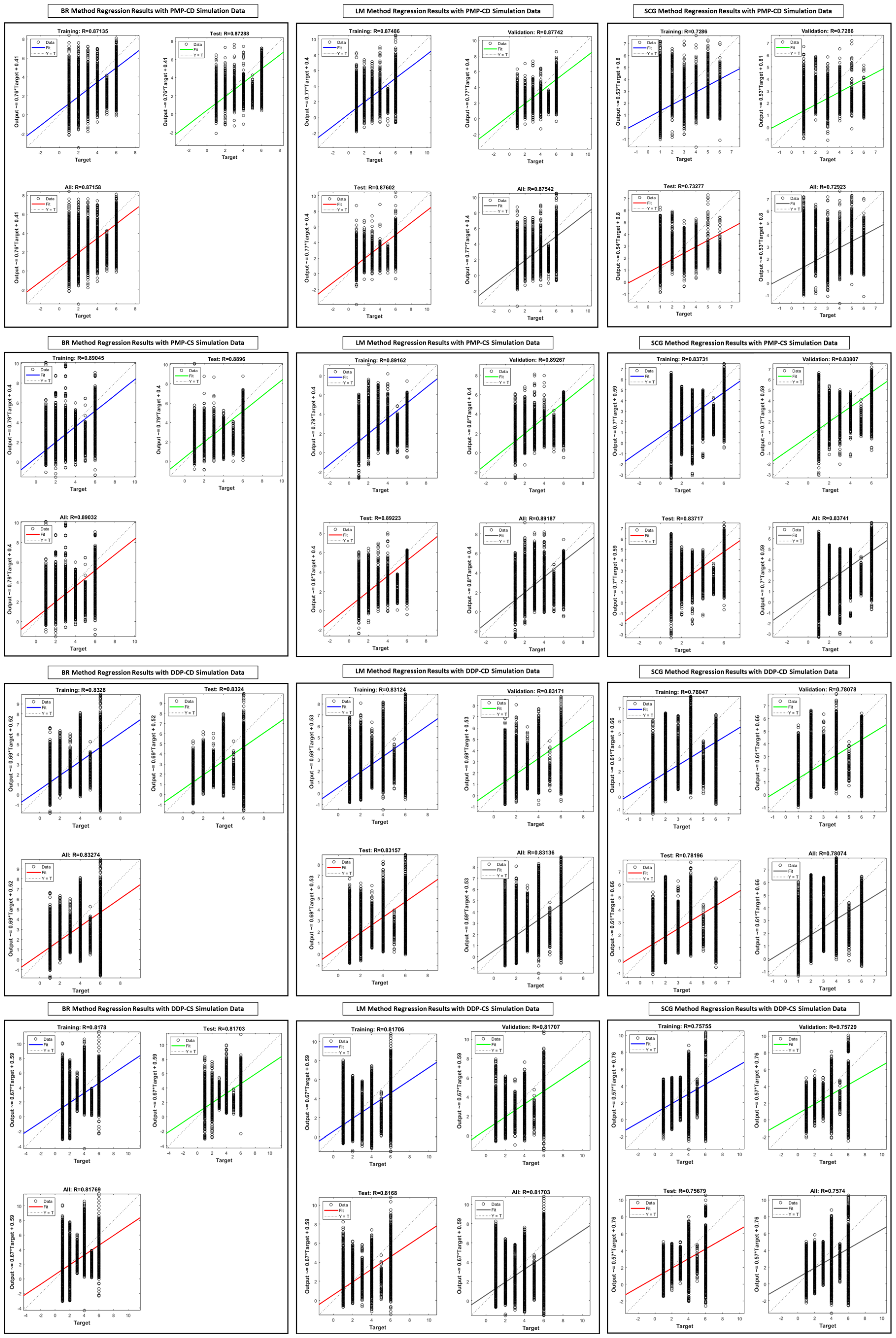
4.6.1. Artificial Neural Network (ANN) Training Method
4.6.2. Artificial Neural Network (ANN)-Based Energy Management System Design
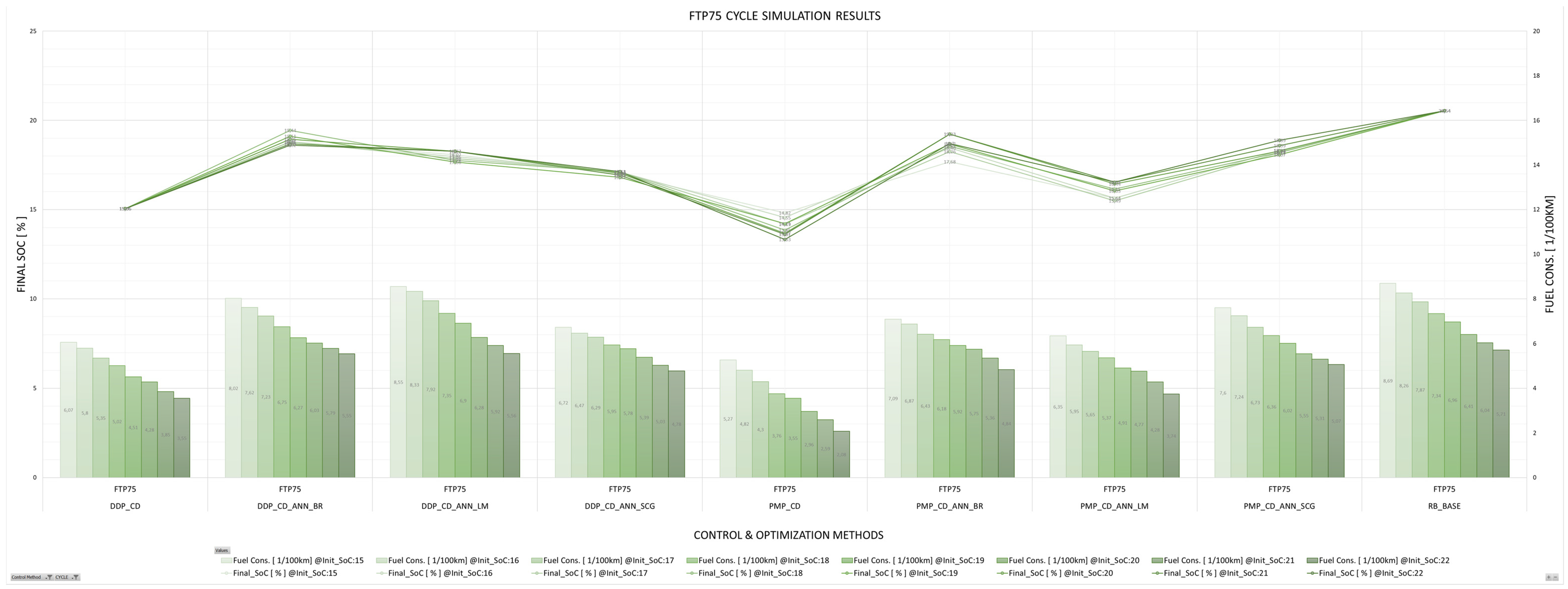
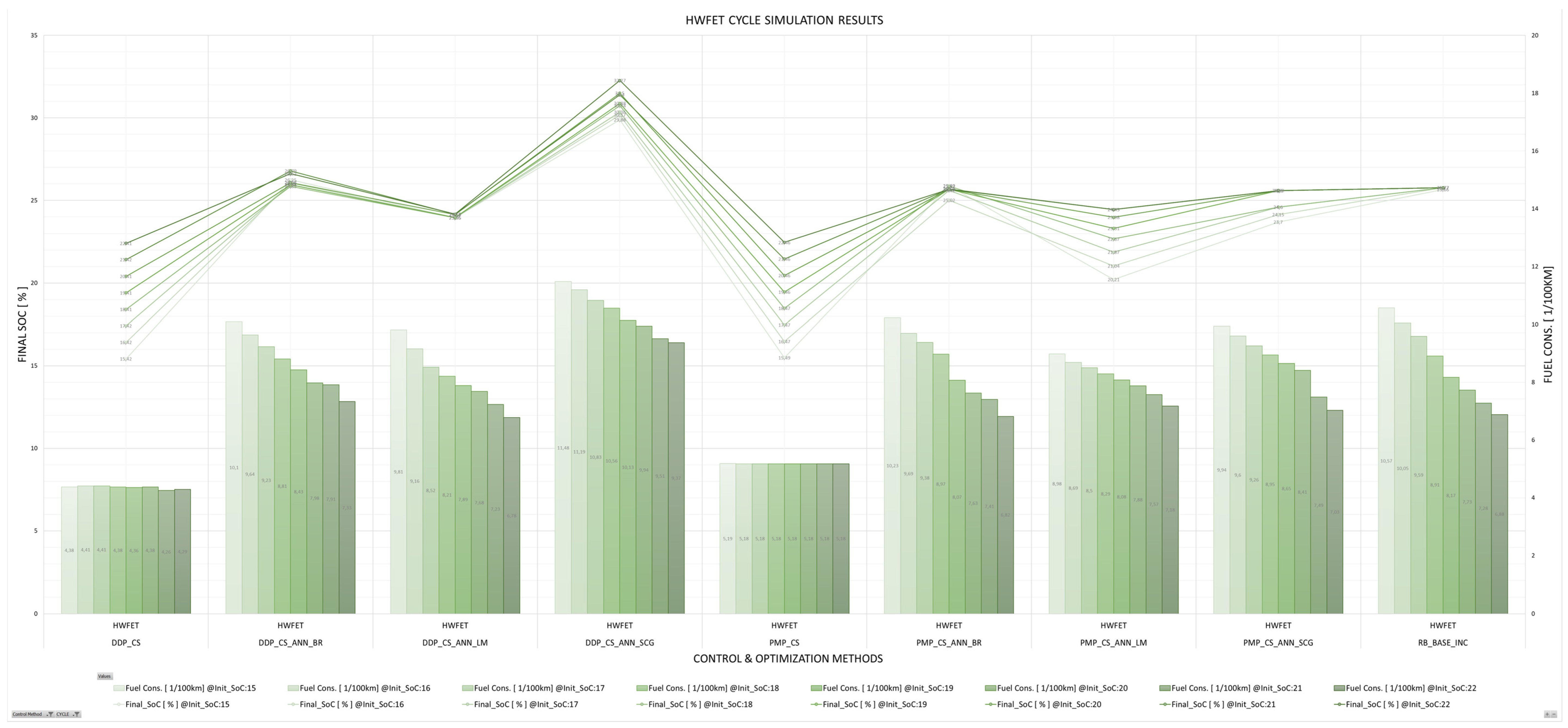
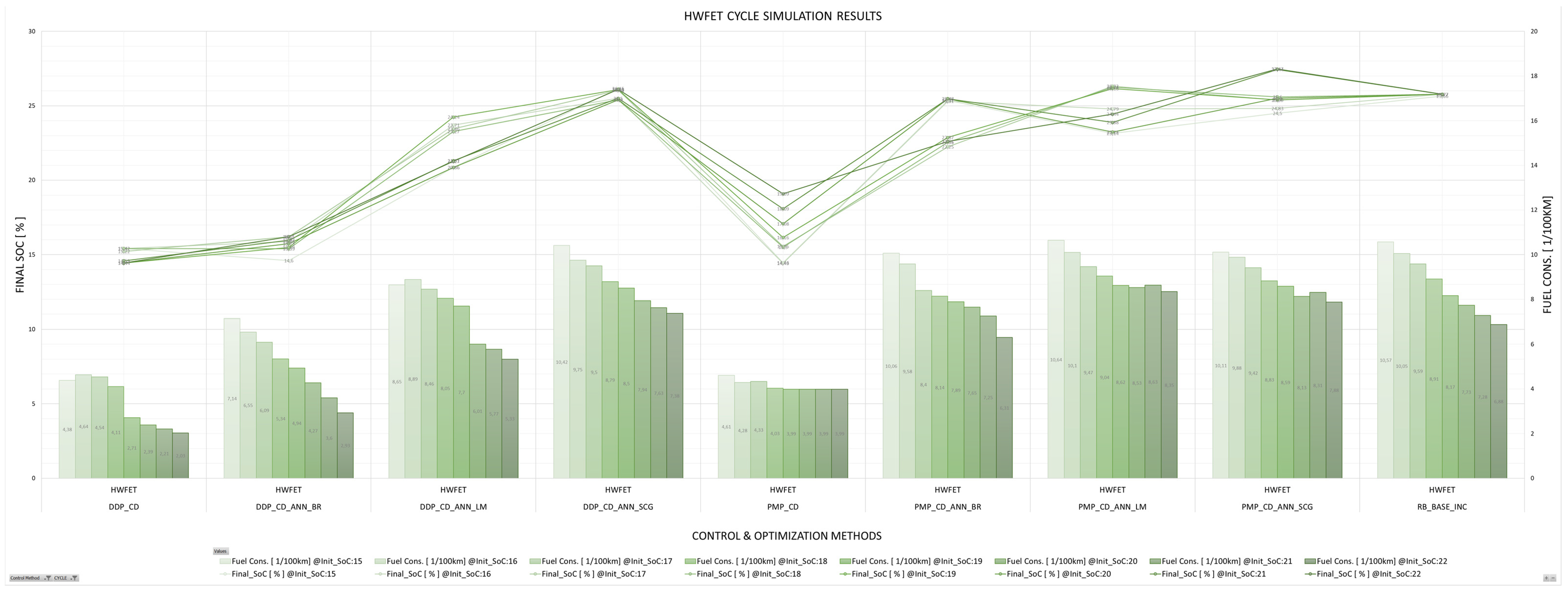
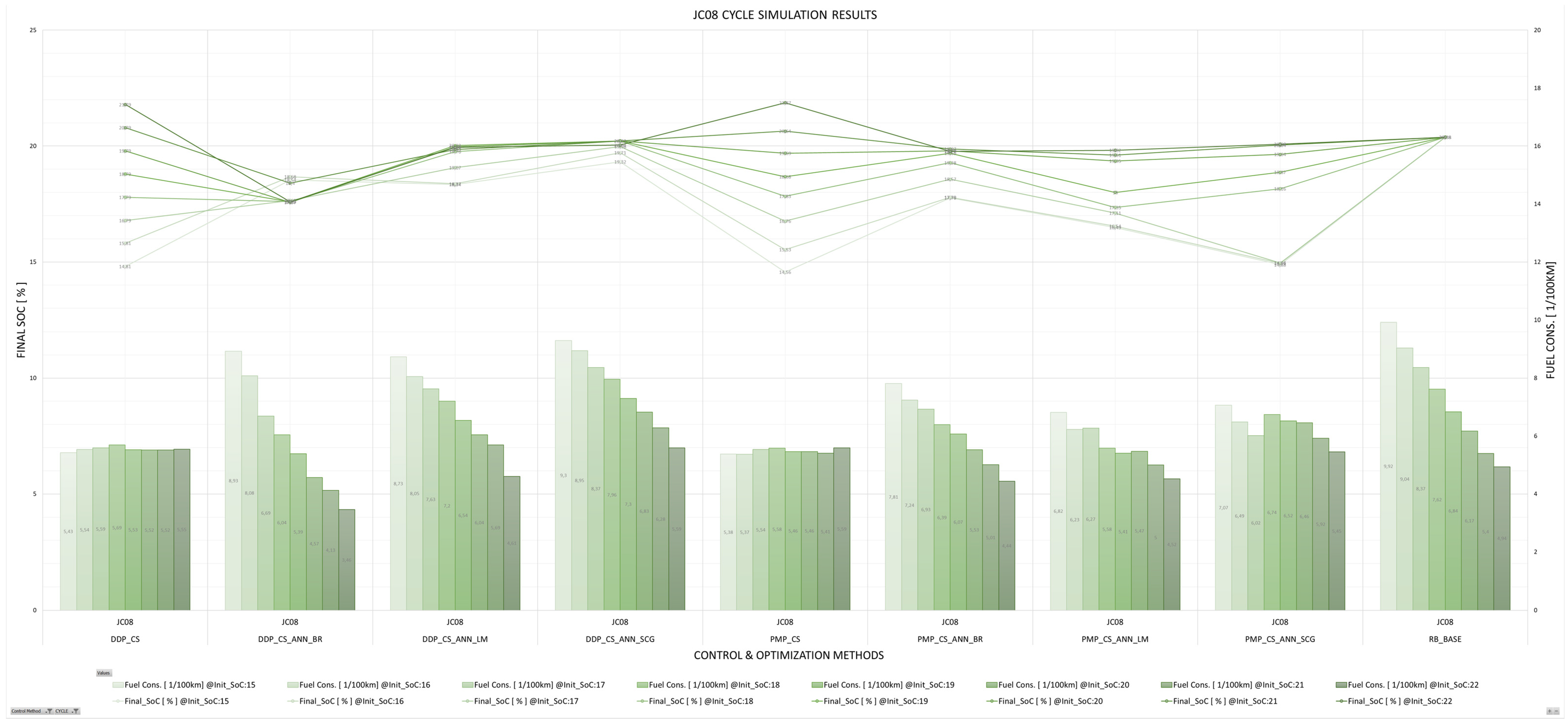
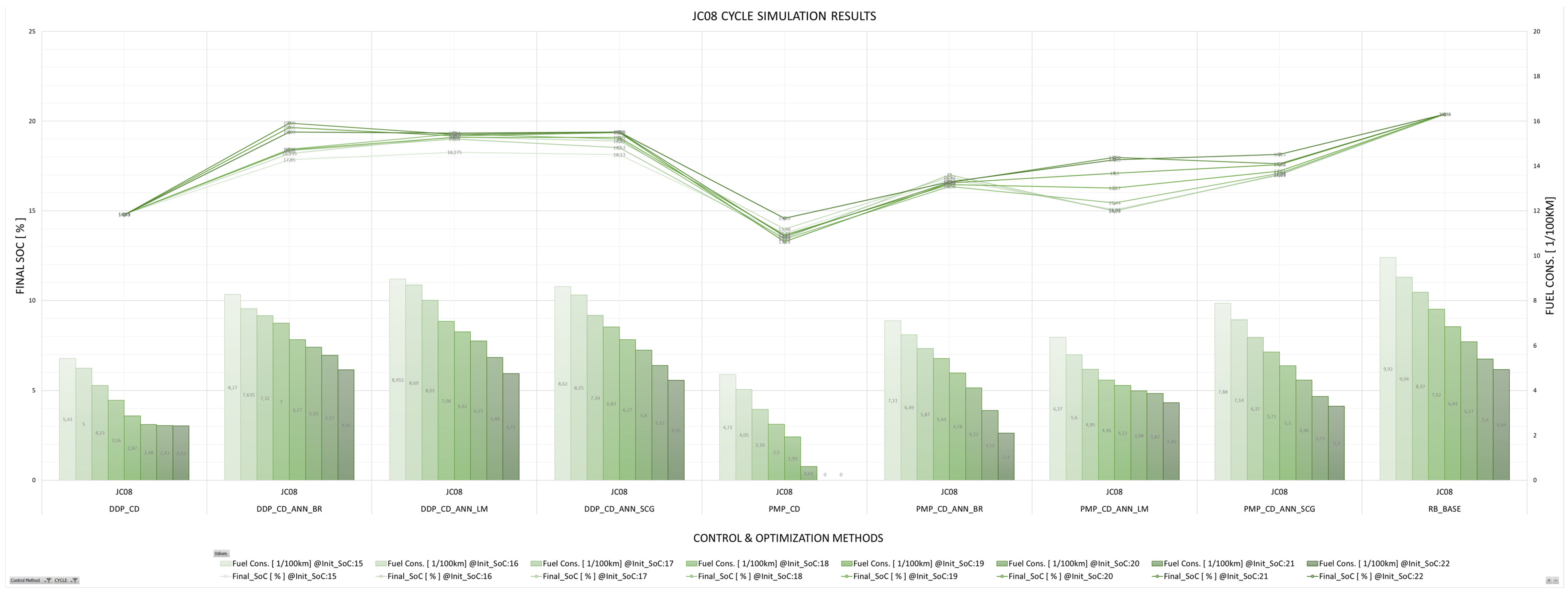
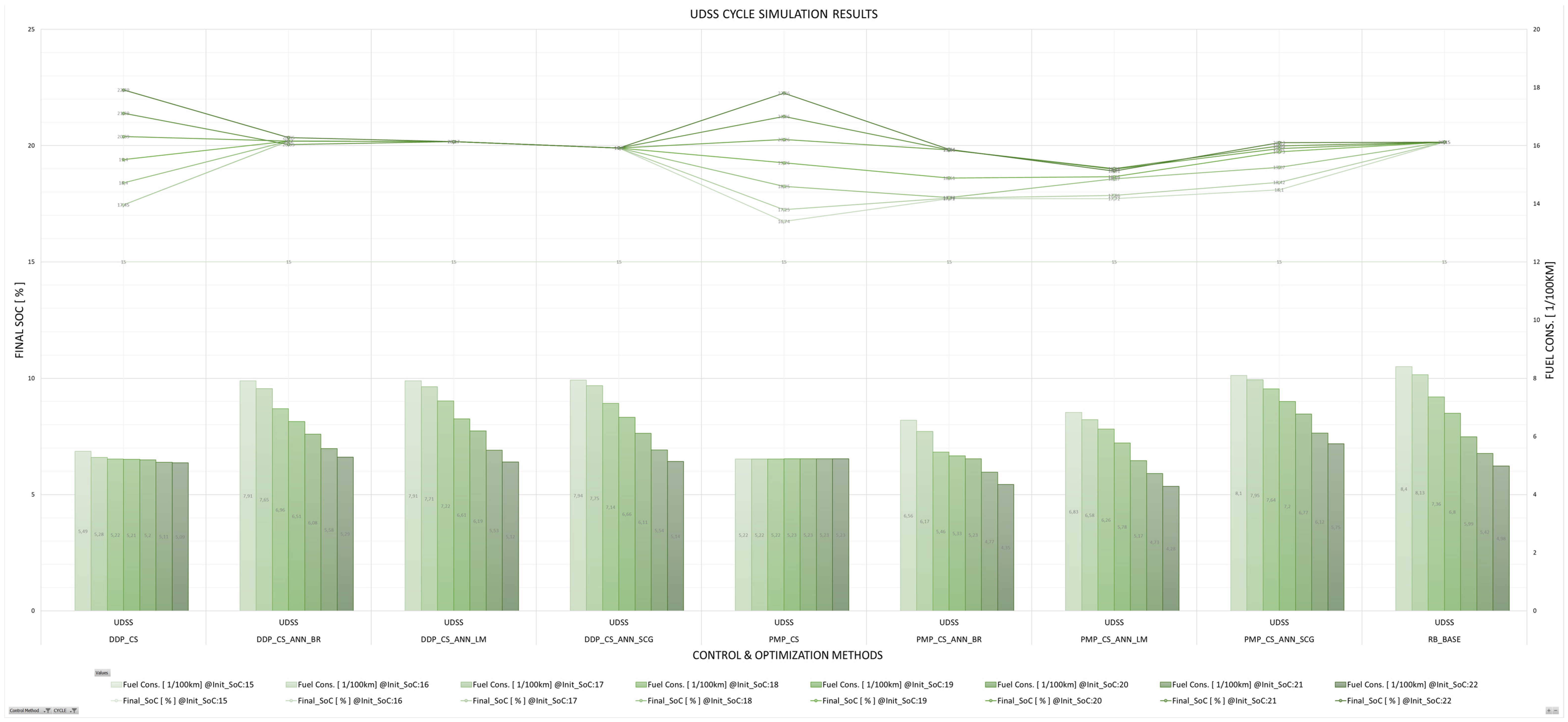
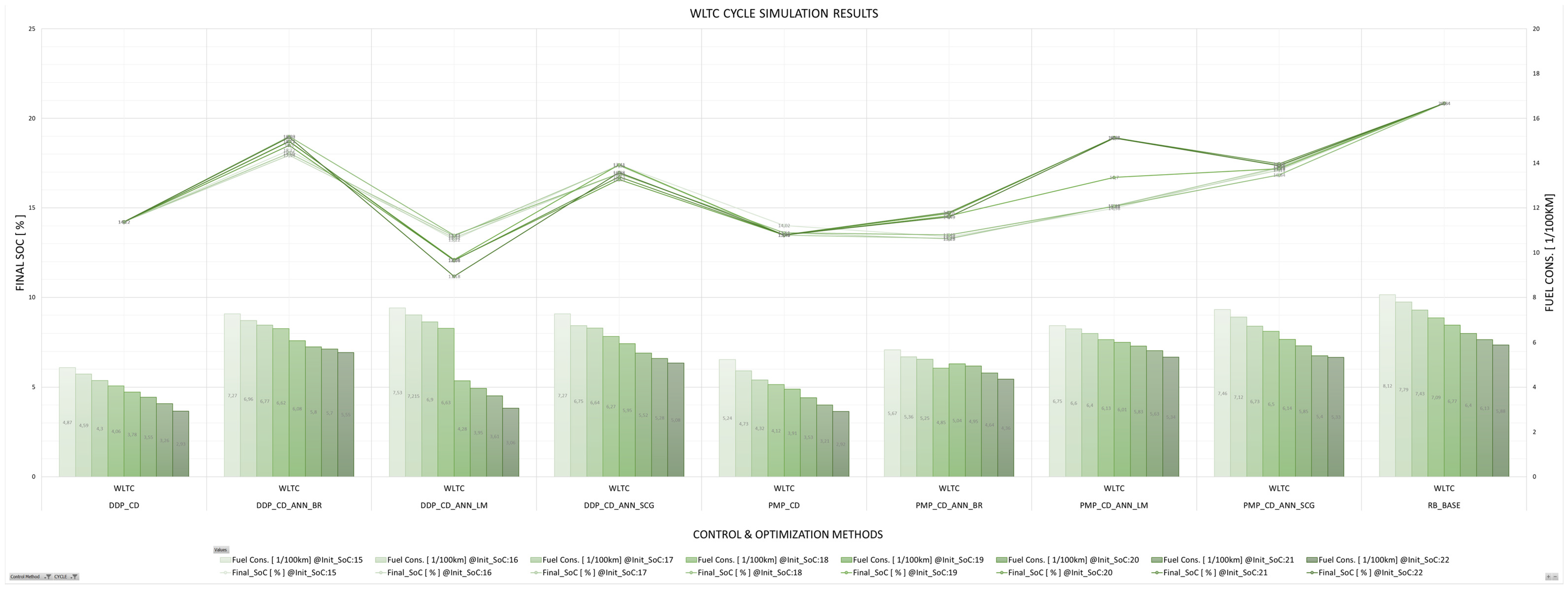
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
Appendix A
| Technical Specifications | Unit | Value | |
|---|---|---|---|
| Vehicle | Vehicle Weight | Kg | 1757.67 |
| Deceleration Factor-F0 | Nm | 120.55 | |
| Deceleration Factor-F1 | Nm/(km/h) | 0.6006 | |
| Deceleration Factor-F2 | Nm/(km/h)2 | 0.026775 | |
| Wheel Diameter | m | 0.32 | |
| MGA | Motor type | [-] | Ferrite Magnet |
| Maximum Power | kW | 48 | |
| Maximum Torque | Nm | 118 | |
| Maximum Speed | rpm | 11,000 | |
| MGB | Motor type | [-] | NdFeB Magnet |
| Maximum Power | kW | 87 | |
| Maximum Torque | Nm | 280 | |
| Maximum Speed | rpm | 11000 | |
| Battery | Battery Type | [-] | Lithium-Ion |
| Total Energy | kWh | 18.8 | |
| Nominal Voltage | V | 355 | |
| Maximum Power | kW | 120 | |
| Battery Pack Capacity | Ah | 26 | |
| Configuration (Serial/Parallel) | [-] | (2/96) | |
| Battery Pack Weight | kg | 183 | |
| Battery Pack Volume | l | 148 | |
| Cooling System | [-] | Liquid | |
| Internal Combustion Engine | Engine Volume | cm3 | 1490 |
| Cylinder Number | [-] | 4 | |
| Diameter/Stroke Ratio | [-] | 74/86.6 | |
| Maximum Power | kW | 75 @ 5600 rpm | |
| Maximum Torque | Nm | 140 @ 4300 rpm | |
| Compression Ratio | [-] | 12.5:1 | |
| Planetary Gear System 1 | Sun/Ring Gear Ratio | [-] | 0.535 |
| Sun/Carrier Gear Ratio | [-] | 2.299 | |
| Carrier/Ring Gear Ratio | [-] | 0.233 | |
| Planetary Gear System 2 | Sun/Ring Gear Ratio | [-] | 0.481 |
| Sun/Carrier Gear Ratio | [-] | 1.857 | |
| Carrier/Ring Gear Ratio | [-] | 0.259 | |
| Differential | Final Drive Ratio | [-] | 2.64 |
References
- Hwang, H.-Y.; Chen, J.-S. Optimized Fuel Economy Control of Power-Split Hybrid Electric Vehicle with Particle Swarm Optimization. Energies 2020, 13, 2278. [Google Scholar] [CrossRef]
- Gautam, A.K.; Tariq, M.; Pandey, J.P.; Verma, K.S.; Urooj, S. Hybrid Sources Powered Electric Vehicle Configuration and Integrated Optimal Power Management Strategy. IEEE Access 2022, 10, 121684–121711. [Google Scholar] [CrossRef]
- Galang, A. Predicting Hybrid Vehicle Fuel Economy and Emissions with Neural Network Models Trained with Real World Data. Master’s Thesis, Colorado State University, Fort Collins, CO, USA, 2017. Available online: https://mountainscholar.org/bitstream/handle/10217/181369/Galang_colostate_0053N_14096.pdf (accessed on 12 February 2024).
- Tribioli, L.; Onori, S. Analysis of Energy Management Strategies in Plug-in Hybrid Electric Vehicles: Application to the GM Chevrolet Volt. In Proceedings of the 013 American Control Conference, Washington, DC, USA, 17–19 June 2013. [Google Scholar] [CrossRef]
- Yuan, Z.; Teng, L.; Fengchun, S.; Peng, H. Comparative Study of Dynamic Programming and Pontryagin’s Minimum Principle on Energy Management for a Parallel Hybrid Electric Vehicle. Energies 2013, 6, 2305–2318. [Google Scholar] [CrossRef]
- Enang, W.; Bannister, C. Modelling and Control of Hybrid Electric Vehicles (a Comprehensive Review). Renew. Sustain. Energy Rev. 2017, 74, 1210–1239. [Google Scholar] [CrossRef]
- Surresh, K. Modelling and Analysis of Chevy Volt Gen II Hybrid Vehicle in Electric Mode. Master’s Thesis, Michigan Technological University, Houghton, MI, USA, 2018. [Google Scholar] [CrossRef]
- Muhammad, A.; Haruna, I.S. Hybrid Electric Vehicles: A Mini Overview. J. Mod. Manuf. Syst. Technol. 2021, 5, 27–36. [Google Scholar] [CrossRef]
- Barmaki, R.; Ilkhani, M.; Salehpour, S. Investigation of energy usage and emissions on plug-in and hybrid electric vehicle. Tech. Gaz. 2016, 23, 899–906. [Google Scholar]
- Millo, F.; Rolando, L.; Fuso, R.; Bergshoeff, E.; Shafiabady, F. Analysis of Different Energy Management Strategies for Complex Hybrid Electric Vehicles. Comput. Aided Des. Appl. 2014, 11 (Suppl. S1), S1–S10. [Google Scholar] [CrossRef]
- Singh, K.V.; Bansal, H.O.; Singh, D. A Comprehensive Review on Hybrid Electric Vehicles: Architectures and Components. J. Mod. Transp. 2019, 27, 77–107. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, L.; Coskun, S.; Pang, H.; Cui, Y.; Xi, J. Energy Management Strategies for Hybrid Electric Vehicles: Review, Classification, Comparison, and Outlook. Energies 2020, 13, 3352. [Google Scholar] [CrossRef]
- Chan, C.C. The State of the Art of Electric, Hybrid, and Fuel Cell Vehicles. Proc. IEEE 2007, 95, 704–718. [Google Scholar] [CrossRef]
- Benajes, J.; García, A.; Monsalve-Serrano, J.; Martínez-Boggio, S. Emissions Reduction from Passenger Cars with RCCI Plug-in Hybrid Electric Vehicle Technology. Appl. Therm. Eng. 2020, 164, 114430. [Google Scholar] [CrossRef]
- Bhasme, S.; Hemmati, S.; Robinette, D.L.; Shahbakhti, M. Modelling of Chevy Volt Gen II Supervisory Controller in Charge Sustaining Mode. In Proceedings of the 2019 International Conference on Advanced Vehicle Powertrains, ICAVP, Hefei, China, 25–27 August 2019. [Google Scholar]
- Liu, T.; Yu, H.; Hu, X. Robust Energy Management Strategy for a Range Extender Electric Vehicle via Genetic Algorithm. In Proceedings of the IEEE Vehicle Power Propulsion Conference (IEEE VPPC), Chicago, IL, USA, 27–30 August 2018; pp. 1–6. [Google Scholar]
- Sharma, R.D.; Sharma, D.; Awasthi, K.; Shamsi, N.A. Power Management and Energy Optimization in Hybrid Electric Vehicle—A Review. In Advances in Fluid and Thermal Engineering, Lecture Notes in Mechanical Engineering; Springer: Singapore, 2019; pp. 585–594. [Google Scholar] [CrossRef]
- Cheng, M.; Sun, L.; Buja, G.; Song, L. Advanced Electrical Machines and Machine-Based Systems for Electric and Hybrid Vehicles. Energies 2015, 8, 9541–9564. [Google Scholar] [CrossRef]
- Zhang, X.; Eben Li, S.; Peng, H.; Sun, J. Efficient Exhaustive Search of Power-Split Hybrid Powertrains with Multiple Planetary Gears and Clutches. J. Dyn. Syst. Meas. Control 2015, 137, 121006. [Google Scholar] [CrossRef]
- Zhang, F.; Tribioli, L. Energy-based Design of Powertrain for a Re-engineered Post-transmission Hybrid Electric Vehicle. Energies 2017, 7, 918. [Google Scholar] [CrossRef]
- Yadav, R. Modeling and Analysis of Energy Consumption in Chevrolet Volt Gen II Hybrid Electric Vehicle. Master’s Thesis, Michigan Technological University, Houghton, MI, USA, 2021. [Google Scholar] [CrossRef]
- Zhao, J.; Odeim, F.; Chen, B.; Maiterth, J.M.; Birmes, G. FEV Simulation and Optimization Tools and Their Usage for Hybrid Powertrain Sizing. In Der Antrieb von Morgen 2019: Diversifizierung Konsequent Vorantreiben 13. Internationale MTZ-Fachtagung Zukunftsantriebe; Springer Vieweg: Wiesbaden, Germany, 2019; pp. 191–206. [Google Scholar] [CrossRef]
- Morra, E.; Lenz, M.; Glados, F.; Espig, M.; Awarke, A.; Stapelbroek, M. FEV Hybrid System Benchmarking: Synergetic Testing, Simulation and Design Assessment; FEV Group GmbH: Aachen, Germany, 2016. [Google Scholar]
- Zhang, X.; Li, C.-T.; Kum, D.; Peng, H. Prius+ and Volt−: Configuration Analysis of Power-Split Hybrid Vehicles with a Single Planetary Gear. IEEE Trans. Veh. Technol. 2012, 61, 3544–3552. [Google Scholar] [CrossRef]
- Liu, J.; Peng, H. Modeling and Control of a Power-Split Hybrid Vehicle. IEEE Trans. Control Syst. Technol. 2008, 16, 1242–1251. [Google Scholar] [CrossRef]
- Cai, W.; Wu, X.; Zhou, M.; Liang, Y.; Wang, Y. Review and Development of Electric Motor Systems and Electric Powertrains for New Energy Vehicles. Automot. Innov. 2021, 4, 3–22. [Google Scholar] [CrossRef]
- Kabalan, B.; Vinot, E.; Yuan, C.; Trigui, R.; Dumand, C.; Hajji, T.E. Efficiency Improvement of a Series–Parallel Hybrid Electric Powertrain by Topology Modification. IEEE Trans. Veh. Technol. 2019, 68, 11523–11531. [Google Scholar] [CrossRef]
- Castellano, A.; Cammalleri, M. Power Losses Minimization for Optimal Operating Maps in Power-Split HEVs: A Case Study on the Chevrolet Volt. Appl. Sci. 2021, 11, 7779. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Y.; Li, G.; Shen, J.; Chen, Z.; Liu, Y. A Predictive Energy Management Strategy for Multi-Mode Plug-in Hybrid Electric Vehicles Based on Multi Neural Networks. Energy 2020, 208, 118366. [Google Scholar] [CrossRef]
- Conlon, B.M.; Blohm, T.; Harpster, M.; Holmes, A.; Palardy, M.; Tarnowsky, S.; Zhou, L. The next Generation “Voltec” Extended Range EV Propulsion System. SAE Int. J. Altern. Powertrains 2015, 4, 248–259. [Google Scholar] [CrossRef]
- Kim, N.; Choi, S.; Jeong, J.; Vijayagopal, R.; Stutenberg, K.; Rousseau, A. Vehicle Level Control Analysis for Voltec Powertrain. World Electr. Veh. J. 2018, 9, 29. [Google Scholar] [CrossRef]
- Onori, S.; Tribioli, L. Adaptive Pontryagin’s Minimum Principle Supervisory Controller Design for the Plug-in Hybrid GM Chevrolet Volt. Appl. Energy 2015, 147, 224–234. [Google Scholar] [CrossRef]
- Bianchi, D.; Rolando, L.; Serrao, L.; Onori, S.; Rizzoni, G.; Al-Khayat, N.; Hsieh, T.-M.; Kang, P. A Rule-Based Strategy for a Series/Parallel Hybrid Electric Vehicle: An Approach Based on Dynamic Programming. In Proceedings of the ASME 2010 Dynamic Systems and Control Conference, Cambridge, MA, USA, 12–15 September 2010; Volume 1. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, Y.G.; Lai, M.-C. Fuel Economy Improvement and Emission Reduction of 48 V Mild Hybrid Electric Vehicles with P0, P1, and P2 Architectures with Lithium Battery Cell Experimental Data. Adv. Mech. Eng. 2021, 13. [Google Scholar] [CrossRef]
- Mansour, C.J. Trip-Based Optimization Methodology for a Rule-Based Energy Management Strategy Using a Global Optimization Routine: The Case of the Prius Plug-in Hybrid Electric Vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 1529–1545. [Google Scholar] [CrossRef]
- Sciarretta, A.; Serrao, L.; Dewangan, P.C.; Tona, P.; Bergshoeff, E.N.D.; Bordons, C.; Charmpa, L.; Elbert, P.; Eriksson, L.; Hofman, T.; et al. A Control Benchmark on the Energy Management of a Plug-in Hybrid Electric Vehicle. Control Eng. Pract. 2014, 29, 287–298. [Google Scholar] [CrossRef]
- Enang, W.; Bannister, C.; Brace, C.; Vagg, C. Modelling and Heuristic Control of a Parallel Hybrid Electric Vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2015, 229, 1494–1513. [Google Scholar] [CrossRef]
- Heywood, J.B. Internal Combustion Engine Fundamentals; McGraw-Hill Education: Singapore, 2018. [Google Scholar]
- Stone, R. Introduction to Internal Combustion Engines; Palgrave Macmillan: Basingstoke, UK, 2012. [Google Scholar]
- Pulkrabek, W.W. Engineering Fundamentals of the Internal Combustion Engine; Pearson: Harlow, UK, 2014. [Google Scholar]
- Yurdaer, T.K.-E. Comparison of Energy Consumption of Different Electric Vehicle Power Systems Using Fuzzy Logic-Based Regenerative Braking. Eng. Perspect. 2021, 1, 11–21. [Google Scholar] [CrossRef]
- Chapman, S.J. Electric Machinery Fundamentals, 5th ed.; McGraw-Hill: New York, NY, USA, 2012. [Google Scholar]
- Sezer, V. Modeling, and Optimal Power Management of a Parallel Hybrid Electric Vehicle. Master’s Thesis, Istanbul Technical University, Institute of Science and Technology, Istanbul, Turkey, 2008. [Google Scholar]
- Arnaudov, K.; Karaivanov, D.P. Planetary Gear Trains; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Miri, I.; Fotouhi, A.; Ewin, N. Electric Vehicle Energy Consumption Modelling and Estimation—A Case Study. Int. J. Energy Res. 2020, 45, 501–520. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, C. Fundamentals and Applications of Lithium-Ion Batteries in Electric Drive Vehicles; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Ali, A.; Kamel, H.; Sharaf, A.; Hegazy, S. Modeling and simulation of hybrid electric vehicles. Int. Conf. Appl. Mech. Mech. Eng. 2014, 16, 1–12. [Google Scholar] [CrossRef]
- Schramm, D.; Hiller, M.; Bardini, R. VEHICLE DYNAMICS: Modeling and Simulation; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Gillespie, T.D. Fundamentals of Vehicle Dynamics; SAE International: Warrendale, PA, USA, 2021. [Google Scholar]
- Felix, R.; Economou, J.T.; Knowles, K. Modelling and Simulation of a Fuel Cell Powered Medium Duty Vehicle Platform; Elsevier: Amsterdam, The Netherlands, 2012; pp. 215–223. [Google Scholar] [CrossRef]
- Feng, L.; Liu, W.; Chen, B. Driving Pattern Recognition for Adaptive Hybrid Vehicle Control. SAE Int. J. Altern. Powertrains 2012, 1, 169–179. [Google Scholar] [CrossRef]
- Lei, Z.; Cheng, D.; Liu, Y.; Qin, D.; Zhang, Y.; Xie, Q. A Dynamic Control Strategy for Hybrid Electric Vehicles Based on Parameter Optimization for Multiple Driving Cycles and Driving Pattern Recognition. Energies 2017, 10, 54. [Google Scholar] [CrossRef]
- Zhang, Q.; Fu, X. A Neural Network Fuzzy Energy Management Strategy for Hybrid Electric Vehicles Based on Driving Cycle Recognition. Appl. Sci. 2020, 10, 696. [Google Scholar] [CrossRef]
- Divakarla, K.P.; Emadi, A.; Razavi, S.N. Journey Mapping—A New Approach for Defining Automotive Drive Cycles. IEEE Trans. Ind. Appl. 2016, 52, 5121–5129. [Google Scholar] [CrossRef]
- Armenta-Déu, C.; Cattin, E. Real Driving Range in Electric Vehicles: Influence on Fuel Consumption and Carbon Emissions. World Electr. Veh. J. 2021, 12, 166. [Google Scholar] [CrossRef]
- Liu, H.; Chen, F.; Tong, Y.; Wang, Z.; Yu, X.; Huang, R. Impacts of Driving Conditions on EV Battery Pack Life Cycle. World Electr. Veh. J. 2020, 11, 17. [Google Scholar] [CrossRef]
- Huang, Y.; Surawski, N.C.; Organ, B.; Zhou, J.L.; Tang, O.H.H.; Chan, E.F.C. Fuel Consumption and Emissions Performance under Real Driving: Comparison between Hybrid and Conventional Vehicles. Sci. Total Environ. 2019, 659, 275–282. [Google Scholar] [CrossRef] [PubMed]
- Awadallah, M.; Tawadros, P.; Walker, P.; Zhang, N. Impact of Low and High Congestion Traffic Patterns on a Mild-HEV Performance. SAE Tech. Pap. 2017. [Google Scholar] [CrossRef]
- Degraeuwe, B.; Weiss, M. Does the New European Driving Cycle (NEDC) Really Fail to Capture the NOX Emissions of Diesel Cars in Europe? Environ. Pollut. 2017, 222, 234–241. [Google Scholar] [CrossRef]
- Sulaiman, N.; Hannan, M.A.; Mohamed, A.; Majlan, E.H.; Wan Daud, W.R. A Review on Energy Management System for Fuel Cell Hybrid Electric Vehicle: Issues and Challenges. Renew. Sustain. Energy Rev. 2015, 52, 802–814. [Google Scholar] [CrossRef]
- Kaya, T.; Kutlar, O.A.; Taskiran, O.O. Evaluation of the Effects of Biodiesel on Emissions and Performance by Comparing the Results of the New European Drive Cycle and Worldwide Harmonized Light Vehicles Test Cycle. Energies 2018, 11, 2814. [Google Scholar] [CrossRef]
- Lee, H.; Lee, K. Comparative Evaluation of the Effect of Vehicle Parameters on Fuel Consumption under NEDC and WLTP. Energies 2020, 13, 4245. [Google Scholar] [CrossRef]
- Giakoumis, E.G.; Zachiotis, A.T. Investigation of a Diesel-Engined Vehicle’s Performance and Emissions during the WLTC Driving Cycle—Comparison with the NEDC. Energies 2017, 10, 240. [Google Scholar] [CrossRef]
- Yang, S.; Xie, H.; Chen, F.; Liu, J.; Feng, S.; Zhang, J. Research on Energy Management Strategy of Hybrid Electric Vehicles Based on Hierarchical Control in the Connected Environment. In Proceedings of the Applied Energy Symposium: MIT A + B (MITAB), Cambridge, MA, USA, 12–14 August 2020. [Google Scholar] [CrossRef]
- Lin, X.; Wang, Z.; Wu, J. Energy Management Strategy Based on Velocity Prediction Using Back Propagation Neural Network for a Plug-in Fuel Cell Electric Vehicle. Int. J. Energy Res. 2021, 45, 2629–2643. [Google Scholar] [CrossRef]
- Serrao, L.; Onori, S.; Rizzoni, G. A Comparative Analysis of Energy Management Strategies for Hybrid Electric Vehicles. J. Dyn. Syst. Meas. Control 2011, 133, 031012. [Google Scholar] [CrossRef]
- Opila, D.F.; Wang, X.; McGee, R.; Gillespie, R.B.; Cook, J.A.; Grizzle, J.W. An Energy Management Controller to Optimally Trade off Fuel Economy and Drivability for Hybrid Vehicles. IEEE Trans. Control Syst. Technol. 2012, 20, 1490–1505. [Google Scholar] [CrossRef]
- Panday, A.; Bansal, H.O. A Review of Optimal Energy Management Strategies for Hybrid Electric Vehicle. Int. J. Veh. Technol. 2014, 2014, 160510. [Google Scholar] [CrossRef]
- Benajes, J.; García, A.; Monsalve-Serrano, J.; Martínez-Boggio, S. Optimization of the Parallel and Mild Hybrid Vehicle Platforms Operating under Conventional and Advanced Combustion Modes. Energy Convers. Manag. 2019, 190, 73–90. [Google Scholar] [CrossRef]
- Qi, X.; Wu, G.; Boriboonsomsin, K.; Barth, M.J. Development and Evaluation of an Evolutionary Algorithm-Based OnLine Energy Management System for Plug-in Hybrid Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2181–2191. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, R.; Ding, R. Energy Optimization for Intelligent Hybrid Electric Vehicles Based on Hybrid System Approach in a Car-Following Process. Optim. Control Appl. Methods 2022, 43, 1020–1046. [Google Scholar] [CrossRef]
- Sorlei, I.; Bizon, N.; Thounthong, P.; Varlam, M.; Raboaca, M.S.; Raceanu, M. Fuel Cell Electric Vehicles—a Brief Review of Current Topologies and Energy Management Strategies. Energies 2021, 1, 252. [Google Scholar] [CrossRef]
- Li, J.; Zhou, Q.; Williams, H.; Xu, H. Back-To-Back Competitive Learning Mechanism for Fuzzy Logic Based Supervisory Control System of Hybrid Electric Vehicles. IEEE Trans. Ind. Electron. 2020, 67, 8900–8909. [Google Scholar] [CrossRef]
- Aziz, A.; Tajuddin, M.; Adzman, M.; Ramli, M.; Mekhilef, S. Energy Management and Optimization of a PV/Diesel/Battery Hybrid Energy System Using a Combined Dispatch Strategy. Sustainability 2019, 11, 683. [Google Scholar] [CrossRef]
- Dizqah, A.M.; Ballard, B.L.; Blundell, M.V.; Kanarachos, S.; Innocente, M.S. A Non-Convex Control Allocation Strategy as Energy-Efficient Torque Distributors for On-Road and Off-Road Vehicles. Control Eng. Pract. 2020, 95, 104256. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, H.; Huang, K.; Qiu, M.; Geng, L. Hybrid Optimization and Its Applications for Multi-Mode Plug-in Hybrid Electric Vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 234, 228–244. [Google Scholar] [CrossRef]
- Yi, F.; Lu, D.; Wang, X.; Pan, C.; Tao, Y.; Zhou, J.; Zhao, C. Energy Management Strategy for Hybrid Energy Storage Electric Vehicles Based on Pontryagin’s Minimum Principle Considering Battery Degradation. Sustainability 2022, 14, 1214. [Google Scholar] [CrossRef]
- Karbaschian, M.A.; Söffker, D. Review and Comparison of Power Management Approaches for Hybrid Vehicles with Focus on Hydraulic Drives. Energies 2014, 6, 3512–3536. [Google Scholar] [CrossRef]
- Han, L.; Jiao, X.; Zhang, Z. Recurrent Neural Network-Based Adaptive Energy Management Control Strategy of Plug-In Hybrid Electric Vehicles Considering Battery Aging. Energies 2020, 13, 202. [Google Scholar] [CrossRef]
- Zou, Y.; Huang, R.; Wu, X.; Zhang, B.; Zhang, Q.; Wang, N.; Qin, T. Modeling and Energy Management Strategy Research of a Power-Split Hybrid Electric Vehicle. Adv. Mech. Eng. 2020, 12. [Google Scholar] [CrossRef]
- Hu, X.; Liu, T.; Qi, X.; Barth, M. Reinforcement Learning for Hybrid and Plug-in Hybrid Electric Vehicle Energy Management: Recent Advances and Prospects. IEEE Ind. Electron. Mag. 2019, 13, 16–25. [Google Scholar] [CrossRef]
- Moulik, B.; Söffker, D. Online Power Management with Embedded Offline-Optimized Parameters for a Three-Source Hybrid Powertrain with an Experimental Emulation Application. Energies 2016, 9, 439. [Google Scholar] [CrossRef]
- Malikopoulos, A.A. Supervisory Power Management Control Algorithms for Hybrid Electric Vehicles: A Survey. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1869–1885. [Google Scholar] [CrossRef]
- Wang, W.; Cai, Z.; Liu, S. Study on Real-Time Control Based on Dynamic Programming for Plug-in Hybrid Electric Vehicles. SAE Int. J. Elec. Veh. 2021, 10, 167–176. [Google Scholar] [CrossRef]
- Hu, J.; Wu, Z.; Li, C. Research on Energy Management Strategy of Range Extender Electric Vehicle Considering Temperature Effect under Different Heat Demands. Int. J. Energy Res. 2023. [Google Scholar] [CrossRef]
- Torreglosa, J.P.; Garcia-Triviño, P.; Vera, D.; López-García, D.A. Analyzing the Improvements of Energy Management Systems for Hybrid Electric Vehicles Using a Systematic Literature Review: How Far Are These Controls from Rule-Based Controls Used in Commercial Vehicles? Appl. Sci. 2020, 10, 8744. [Google Scholar] [CrossRef]
- Dedes, E.K.; Hudson, D.A.; Turnock, S.R. Investigation of Diesel Hybrid Systems for Fuel Oil Reduction in Slow Speed Ocean Going Ships. Energy 2016, 114, 444–456. [Google Scholar] [CrossRef]
- Zhang, Y.-T.; Hu, M.-B. Research on Energy Management for Hybrid Electric Vehicles in WLTP Driving Cycle. In Proceedings of the International Conference on Computer, Artificial Intelligence, and Control Engineering (CAICE 2023), Hangzhou, China, 17–19 February 2023. [Google Scholar] [CrossRef]
- Bagwe, R.M.; Byerly, A.; dos Santos, E.C., Jr.; Ben-Miled, Z. Adaptive Rule-Based Energy Management Strategy for a Parallel HEV. Energies 2019, 12, 4472. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, C. Real-Time Optimization Power-Split Strategy for Hybrid Electric Vehicles. Sci. China Technol. Sci. 2016, 59, 814–824. [Google Scholar] [CrossRef]
- Kim, N.; Cha, S.; Peng, H. Optimal Control of Hybrid Electric Vehicles Based on Pontryagin’s Minimum Principle. IEEE Trans. Control Syst. Technol. 2011, 19, 1279–1287. [Google Scholar] [CrossRef]
- Qiu, L.; Qian, L.; Zomorodi, H.; Pisu, P. Global Optimal Energy Management Control Strategies for Connected Four-Wheel-Drive Hybrid Electric Vehicles. IET Intell. Transp. Syst. 2017, 11, 264–272. [Google Scholar] [CrossRef]
- Sharma, O.P. A Practical Implementation of a Near Optimal Energy Management Strategy Based on the Pontryagin’s Minimum Principle in a PHEV. Master’s Thesis, Ohio State University, Electrical and Computer Engineering, Columbus, OH, USA, 2012. Available online: http://rave.ohiolink.edu/etdc/view?acc_num=osu1337626310 (accessed on 13 February 2024).
- Xie, S.; Li, H.; Xin, Z.; Liu, T.; Wei, L. A Pontryagin Minimum Principle-Based Adaptive Equivalent Consumption Minimum Strategy for a Plug-in Hybrid Electric Bus on a Fixed Route. Energies 2017, 10, 1379. [Google Scholar] [CrossRef]
- Öztürk, K.; Şahin, M.E. Yapay sinir ağları ve yapay zekâ’ya genel bir bakış. Takvim-I Vekayi 2018, 6, 25–36. [Google Scholar]
- Ataseven, B. Yapay sinir ağlari ile öngörü modellemesi. Öneri 2013, 10, 101–115. [Google Scholar] [CrossRef]
- Aşkın, D.; İskender, İ.; Mamızadeh, A. Farklı Yapay Sinir Ağları Yöntemlerini Kullanarak Kuru Tip Transformatör Sargısının Termal Analizi. J. Fac. Eng. Gazi Univ. 2011, 26, 905–913. [Google Scholar]
- Vinot, E.; Trigui, R. Optimal Energy Management of HEVs with Hybrid Storage System. Energy Convers. Manag. 2013, 76, 437–452. [Google Scholar] [CrossRef]
- Li, K.; Jia, C.; Han, X.; He, H. A Novel Minimal-Cost Power Allocation Strategy for Fuel Cell Hybrid Buses Based on Deep Reinforcement Learning Algorithms. Sustainability 2023, 15, 7967. [Google Scholar] [CrossRef]
- Guo, X.; Liu, T.; Tang, B.; Tang, X.; Zhang, J.; Tan, W.; Jin, S. Transfer Deep Reinforcement Learning-Enabled Energy Management Strategy for Hybrid Tracked Vehicle. IEEE Access 2020, 8, 165837–165848. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Haykin, S. The Neural Networks a Comprehensive Foundation; Macmillan College Publishing Company: New York, NY, USA, 1998. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Martinez, C.M.; Hu, X.; Cao, D.; Velenis, E.; Gao, B.; Wellers, M. Energy Management in Plug-in Hybrid Electric Vehicles: Recent Progress and a Connected Vehicles Perspective. IEEE Trans. Veh. Technol. 2017, 66, 4534–4549. [Google Scholar] [CrossRef]
- Zhang, R.; Tao, J.; Zhou, H. Fuzzy Optimal Energy Management for Fuel Cell and Supercapacitor Systems Using Neural Network Based Driving Pattern Recognition. IEEE Trans. Fuzzy Syst. 2019, 27, 45–57. [Google Scholar] [CrossRef]
- Yang, X.; Jiang, C.; Zhou, M.; Hu, H. Bi-Level Energy Management Strategy for Power-Split Plug-in Hybrid Electric Vehicles: A Reinforcement Learning Approach for Prediction and Control. Front. Energy Res. 2023, 11. [Google Scholar] [CrossRef]
- Feldkamp, L.; Abou-Nasr, M.; Kolmanovsky, I.V. Recurrent Neural Network Training for Energy Management of a Mild Hybrid Electric Vehicle with an Ultra-Capacitor. In Proceedings of the 2009 IEEE Workshop on Computational Intelligence in Vehicles and Vehicular Systems, Nashville, TN, USA, 30 March–2 April 2009. [Google Scholar] [CrossRef]
- Hernández, J.A.; Fernández, E.; Torres, H. Electric Vehicle NiMH Battery State of Charge Estimation Using Artificial Neural Networks of Backpropagation and Radial Basis. World Electr. Veh. J. 2023, 14, 312. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Hagan, M.T.; Demuth, H.; Beale, M. Neural Network Design; PWS Publishing Co.: Worcester, UK, 2003. [Google Scholar]
- Li, A.; Yuen, A.C.Y.; Wang, W.; Chen, T.B.Y.; Lai, C.S.; Yang, W.; Wu, W.; Chan, Q.N.; Kook, S.; Yeoh, G.H. Integration of Computational Fluid Dynamics and Artificial Neural Network for Optimization Design of Battery Thermal Management System. Batteries 2022, 8, 69. [Google Scholar] [CrossRef]
- Neal, R.M. Bayesian Learning for Neural Networks; Springer: New York, NY, USA, 1996. [Google Scholar] [CrossRef]
- Veerappan, P.M.; Dineshraj, V.; Elangovan, S.; Deepika, V.; Ramachandran, M.; Panchal, H.; Lamba, R.; Thangaraj, K.; Muthusamy, S. A Novel Method of Bayesian Regularization Based Solar Charging Station Employing Maximum Power Point Tracking for Electric Vehicle Applications. Res. Sq. 2022. [Google Scholar] [CrossRef]
- Møller, M.F. A Scaled Conjugate Gradient Algorithm for Fast Supervised Learning. Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M.B. Training Feedforward Networks with the Marquardt Algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]
- Norgaard, M. Neural Networks for Modelling and Control of Dynamic Systems; Springer: London, UK, 2003. [Google Scholar]
- Nielsen, M.A. Neural Networks and Deep Learning; Determination Press. 2015. Available online: https://static.latexstudio.net/article/2018/0912/neuralnetworksanddeeplearning.pdf (accessed on 1 February 2024).











Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altun, Y.E.; Kutlar, O.A. Energy Management Systems’ Modeling and Optimization in Hybrid Electric Vehicles. Energies 2024, 17, 1696. https://doi.org/10.3390/en17071696
Altun YE, Kutlar OA. Energy Management Systems’ Modeling and Optimization in Hybrid Electric Vehicles. Energies. 2024; 17(7):1696. https://doi.org/10.3390/en17071696
Chicago/Turabian StyleAltun, Yavuz Eray, and Osman Akın Kutlar. 2024. "Energy Management Systems’ Modeling and Optimization in Hybrid Electric Vehicles" Energies 17, no. 7: 1696. https://doi.org/10.3390/en17071696
APA StyleAltun, Y. E., & Kutlar, O. A. (2024). Energy Management Systems’ Modeling and Optimization in Hybrid Electric Vehicles. Energies, 17(7), 1696. https://doi.org/10.3390/en17071696






