Dynamic Modeling and Simulation of a Facade-Integrated Adsorption System for Solar Cooling of Lightweight Buildings
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Subject Matter
1.4. Objectives of Study
- What is the achievable cooling power and cooling energy capacity?
- What is a suitable size ratio of the components?
- How can the system performance be optimized?
2. Model Description
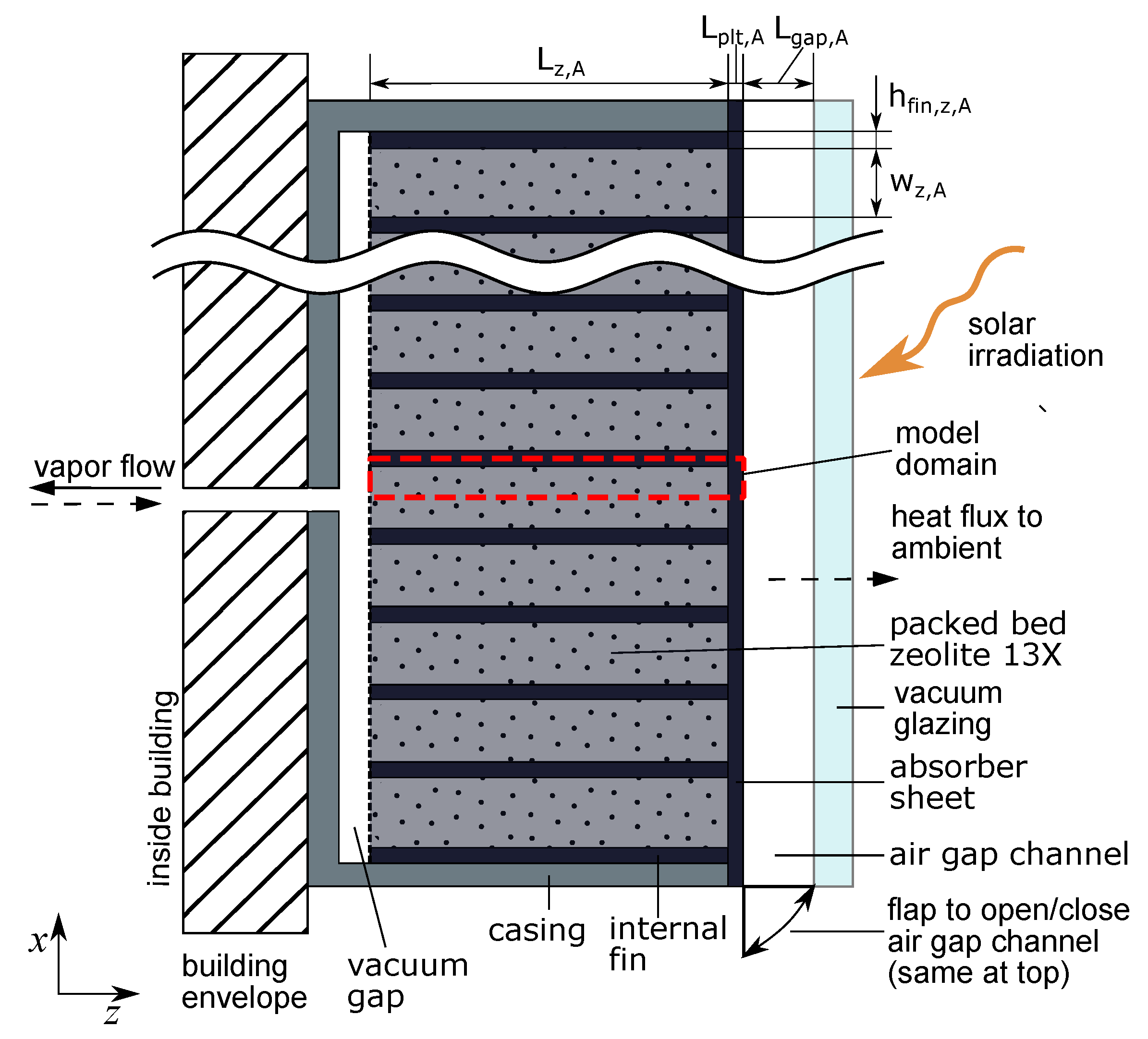
2.1. Adsorber
- The vapor is an ideal gas and viscous Newton-fluid;
- Local thermal equilibrium is assumed;
- Due to the low pressure, rarefaction effects in the mass and heat transport in the adsorbent bulk are considered;
- The adsorption kinetics can be described by the linear-driving-force approximation;
- The heat of adsorption depends on the water uptake;
- The temperature dependencies of the material parameters (viscosity, heat capacity, density, etc.) are accounted for.
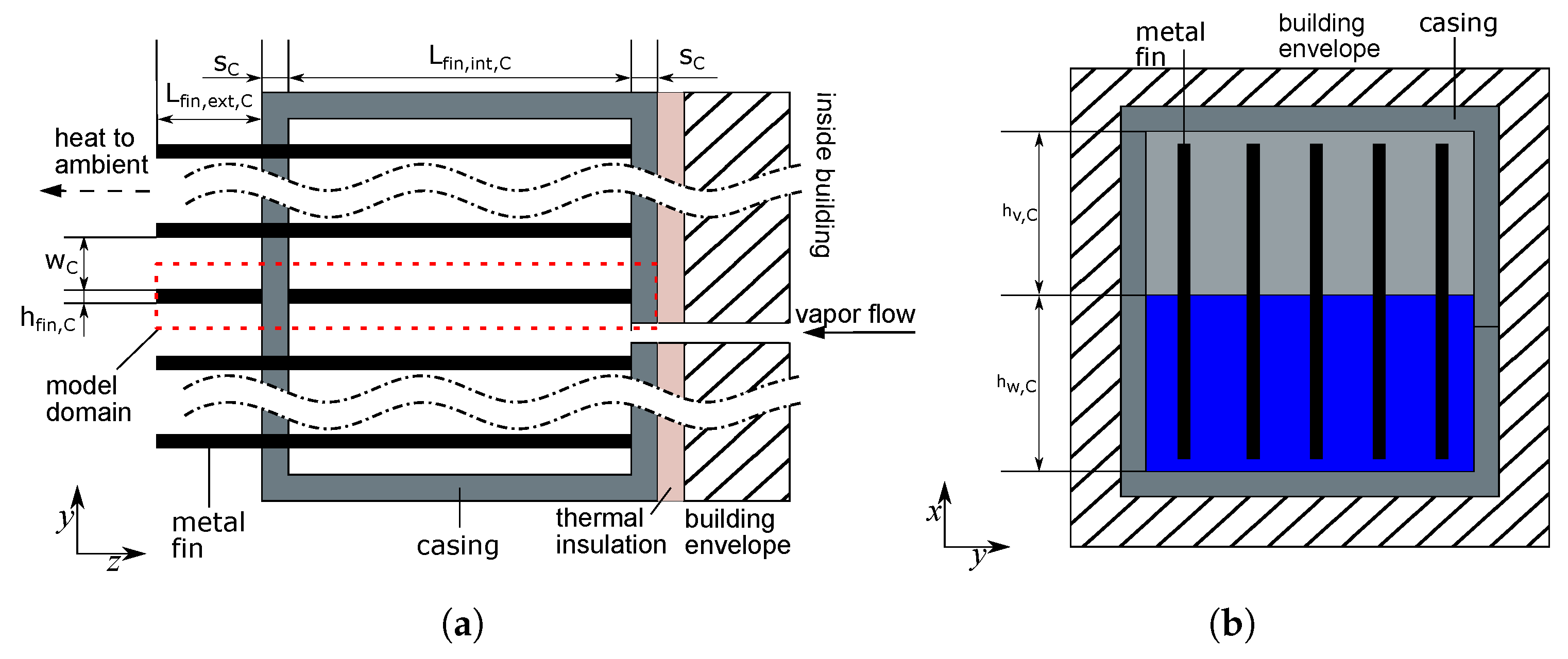
2.2. Condenser
- The energy and mass of the vapor are neglectable;
- The vapor is an ideal gas;
- The vapor is always saturated;
- Incoming vapor fully condenses;
- The water is incompressible;
- Temperature variations in the condensed water are negligibly small, but natural convection is indirectly captured through correlations for the heat transfer;
- Temperature variations in height direction of the walls are negligibly small;
- Boundary effects of the top and bottom of the casing are neglected;
- The temperature dependencies of the water (density, heat capacity, enthalpy of evaporation, etc.) are accounted for.
- The condensate film flow is always laminar and steady;
- The surface temperatures of fins and walls are isotherm;
- The vapor bulk is stagnant.
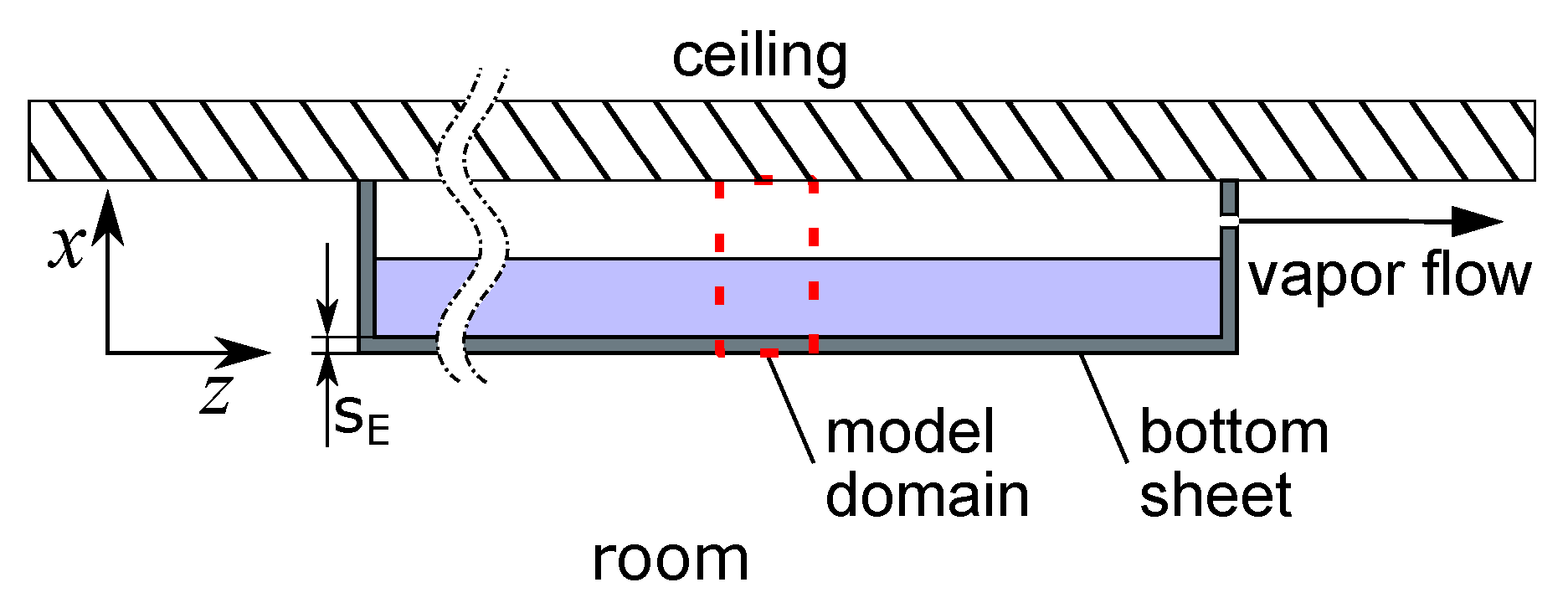
2.3. Evaporator
- Energy and mass of the vapor phase are neglectable;
- The vapor is an ideal gas;
- The water is incompressible;
- Vapor pressure in the evaporator is assumed to be equal to saturation pressure;
- Outflowing vapor instantly evaporates;
- The temperature dependencies of the water (density, heat capacity, enthalpy of evaporation, etc.) are accounted for.
2.4. Coupling and Boundary Conditions
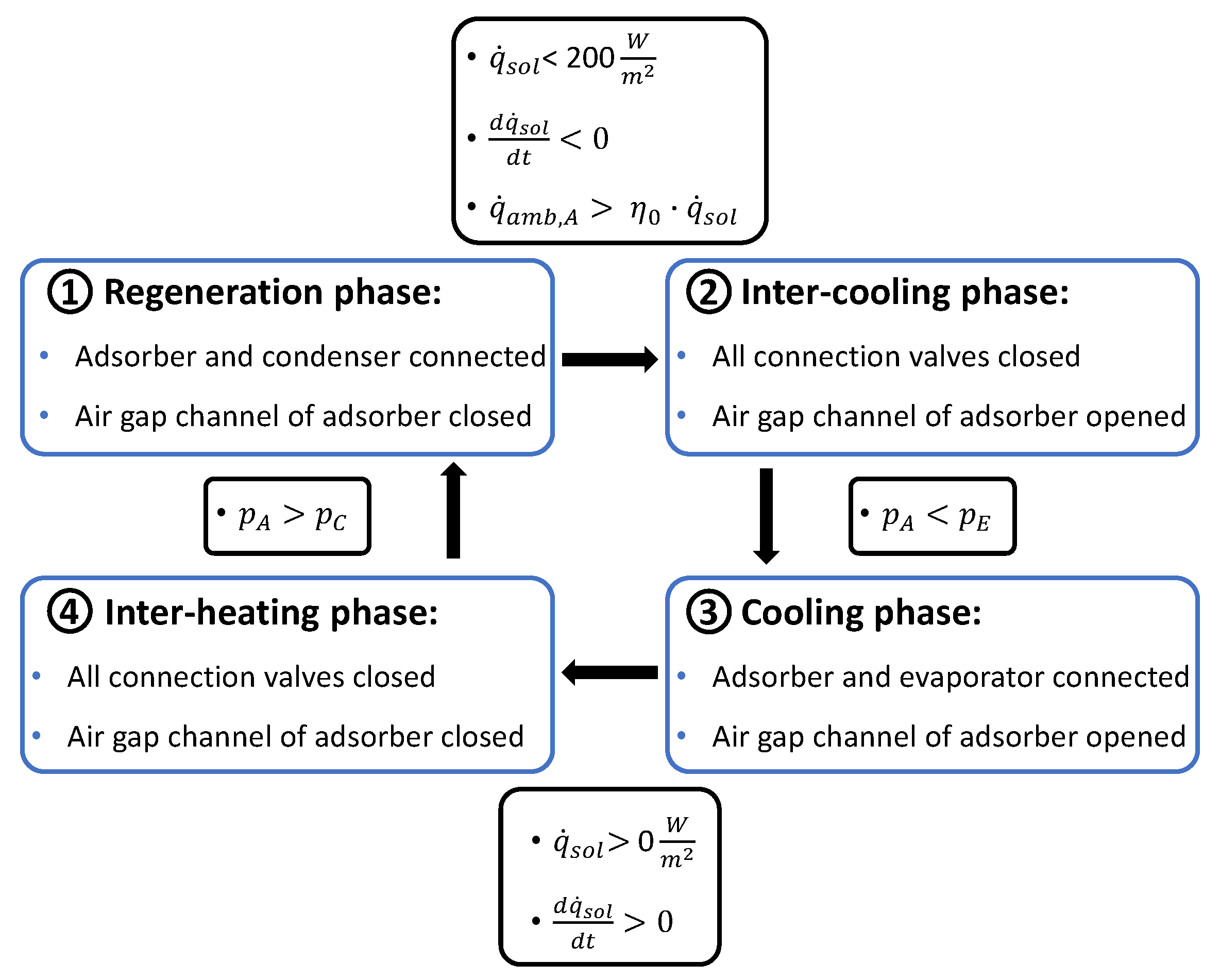
2.5. Operating Phases and Switching Criteria
2.6. Cooling Power Control
3. Numerical Implementation
4. Results and Discussion
4.1. Simulation Case Set-Up and Procedure
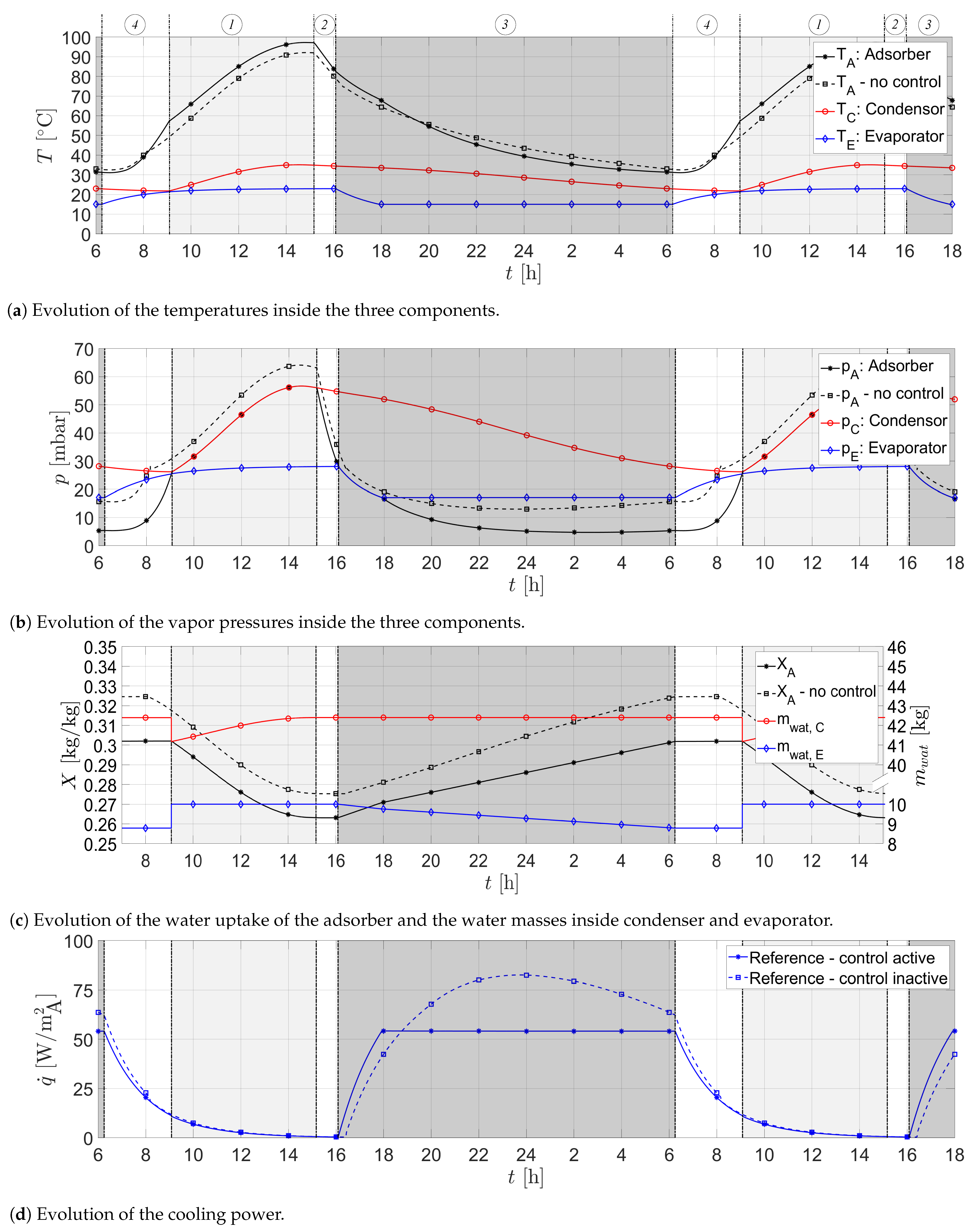
4.2. Reference Case
4.3. Parametric Studies
4.3.1. Adsorber
4.3.2. Condenser
| Control Active | Control Inactive | ||||
|---|---|---|---|---|---|
| Variation | Cooling Energy | Dynamic | Max. Cooling | Cooling Energy | |
| [Wh] | [min] | Power [W] | [Wh] | ||
| Reference | / | 823 | 112 | 1043 | |
| Adsorber | |||||
| Collector efficiency | High | ||||
| Collector efficiency | Low | ||||
| External adsorber fins | |||||
| ( × | × | ||||
| External adsorber fins | |||||
| ( × | × | ||||
| External adsorber fins | |||||
| ( × | × | ||||
| External adsorber fins | |||||
| ( × | × | ||||
| External adsorber fins | |||||
| ( × | no fins | ||||
| Material of metal structures | Copper | ||||
| Material of metal structures | Steel | ||||
| Condenser | |||||
| Length of outer fins | |||||
| Length of outer fins | |||||
| Width between fins | |||||
| Width between fins | |||||
| Heat transfer coefficient | |||||
| Heat transfer coefficient | |||||
| Facade area | |||||
| Facade area | |||||
| Evaporator | |||||
| Surface area | / | / | |||
| Surface area | / | / | |||
| Surface area | / | / | |||
| Surface area | / | / | |||
| Surface area | / | / | |||
| Surface area | / | / | |||
| Surface area | / | / | |||
| Set point temperature | / | / | |||
| Set point temperature | / | / | |||
| Heat transfer coefficient | |||||
| Building | |||||
| Compass orientation | |||||
| of adsorber facade | |||||
| Compass orientation | |||||
| of adsorber facade | |||||
| Compass orientation | |||||
| of adsorber facade | |||||
| Compass orientation | |||||
| of adsorber facade | |||||
4.3.3. Evaporator
4.3.4. Building
4.4. Optimum Cases
4.4.1. Practical Optimum Case
4.4.2. Ideal Optimum Case
5. Conclusions and Outlook
- It was found that cooling power levels of up to can be reached with a practical best-case configuration. This compares well to the values of state-of-the-art cooling ceilings. The current system is able to provide constant cooling powers of around for more than 13 hours. Nevertheless, the system is not able to provide constant power levels higher than around due to the finite adsorption rate of the adsorber.
- The optimal surface ratio of the component adsorber and evaporator strongly depends on the heat transfer that can be realized between room and the evaporator, which depends on the heat transfer coefficient and the set-point temperature of the evaporator. With the configuration of the reference case with a determined cooling rate of , the adsorber can be connected to up to of evaporator area. For higher cooling rates, the ratio should be 1:1, as the adsorption rate of the adsorber is limited. The surface area of the condenser has only minor influence on the cooling performance.
- The parameters with the highest impact on the cooling power and cooling energy, respectively, are the solar collector efficiency of the adsorber, the surface ratios, the orientation of the facade carrying the adsorber, the configuration of the external fins on the absorber sheet and the maximum heat flux between evaporator and adjacent room determined by the heat transfer coefficient and the temperature difference.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United Nations Environment Programme. 2020 Global Status Report for Buildings and Construction; United Nations Environment Programme: Nairobi, Kenya, 2020. [Google Scholar]
- Mutschler, R.; Rüdisüli, M.; Heer, P.; Eggimann, S. Benchmarking cooling and heating energy demands considering climate change, population growth and cooling device uptake. Appl. Energy 2021, 288, 116636. [Google Scholar] [CrossRef]
- Larsen, M.; Petrović, S.; Radoszynski, A.M.; McKenna, R.; Balyk, O. Climate change impacts on trends and extremes in future heating and cooling demands over Europe. Energy Build. 2020, 226, 110397. [Google Scholar] [CrossRef]
- Blandini, L.; Haase, W.; Weidner, S.; Böhm, M.; Burghardt, T.; Roth, D.; Sawodny, O.; Sobek, W. D1244: Design and Construction of the First Adaptive High-Rise Experimental Building. Front. Built Environ. 2022, 8, 814911. [Google Scholar] [CrossRef]
- Cristino, T.M.; Neto, A.F.; Wurtz, F.; Delinchant, B. The Evolution of Knowledge and Trends within the Building Energy Efficiency Field of Knowledge. Energies 2022, 15, 691. [Google Scholar] [CrossRef]
- Gupta, N.; Tiwari, G.N. Review of passive heating/cooling systems of buildings. Energy Sci. Eng. 2016, 4, 305–333. [Google Scholar] [CrossRef]
- Akeiber, H.; Nejat, P.; Majid, M.Z.A.; Wahid, M.A.; Jomehzadeh, F.; Zeynali Famileh, I.; Calautit, J.K.; Hughes, B.R.; Zaki, S.A. A review on phase change material (PCM) for sustainable passive cooling in building envelopes. Renew. Sustain. Energy Rev. 2016, 60, 1470–1497. [Google Scholar] [CrossRef]
- Internation Energy Agency. The Future of Cooling; IEA Publications: Paris, France, 2018. [Google Scholar]
- Sarbu, I.; Sebarchievici, C. Review of solar refrigeration and cooling systems. Energy Build. 2013, 67, 286–297. [Google Scholar] [CrossRef]
- Huang, B.J.; Hou, T.F.; Hsu, P.C.; Lin, T.H.; Chen, Y.T.; Chen, C.W.; Li, K.; Lee, K.Y. Design of direct solar PV driven air conditioner. Renew. Energy 2016, 88, 95–101. [Google Scholar] [CrossRef]
- Henning, H.M. Solar assisted air conditioning of buildings—An overview. Appl. Therm. Eng. 2007, 27, 1734–1749. [Google Scholar] [CrossRef]
- Ullah, K.R.; Saidur, R.; Ping, H.W.; Akikur, R.K.; Shuvo, N.H. A review of solar thermal refrigeration and cooling methods. Renew. Sustain. Energy Rev. 2013, 24, 499–513. [Google Scholar] [CrossRef]
- Settino, J.; Sant, T.; Micallef, C.; Farrugia, M.; Spiteri Staines, C.; Licari, J.; Micallef, A. Overview of solar technologies for electricity, heating and cooling production. Renew. Sustain. Energy Rev. 2018, 90, 892–909. [Google Scholar] [CrossRef]
- Ghafoor, A.; Munir, A. Worldwide overview of solar thermal cooling technologies. Renew. Sustain. Energy Rev. 2015, 43, 763–774. [Google Scholar] [CrossRef]
- Almasri, R.A.; Abu-Hamdeh, N.H.; Esmaeil, K.K.; Suyambazhahan, S. Thermal solar sorption cooling systems - A review of principle, technology, and applications. Alex. Eng. J. 2022, 61, 367–402. [Google Scholar] [CrossRef]
- Goyal, P.; Baredar, P.; Mittal, A.; Siddiqui, A.R. Adsorption refrigeration technology—An overview of theory and its solar energy applications. Renew. Sustain. Energy Rev. 2016, 53, 1389–1410. [Google Scholar] [CrossRef]
- Wang, R. Performance improvement of adsorption cooling by heat and mass recovery operation. Int. J. Refrig. 2001, 24, 602–611. [Google Scholar] [CrossRef]
- Chan, K.C.; Tso, C.Y.; Chao, C.Y.H.; Wu, C.L. Experiment verified simulation study of the operating sequences on the performance of adsorption cooling system. Build. Simul. 2015, 8, 255–269. [Google Scholar] [CrossRef]
- Hu, T.; Kwan, T.H.; Pei, G. An all-day cooling system that combines solar absorption chiller and radiative cooling. Renew. Energy 2022, 186, 831–844. [Google Scholar] [CrossRef]
- Prieto, A.; Knaack, U.; Auer, T.; Klein, T. Solar coolfacades: Framework for the integration of solar cooling technologies in the building envelope. Energy 2017, 137, 353–368. [Google Scholar] [CrossRef]
- Noaman, D.S.; Moneer, S.A.; Megahed, N.A.; El-Ghafour, S.A. Integration of active solar cooling technology into passively designed facade in hot climates. J. Build. Eng. 2022, 56, 104658. [Google Scholar] [CrossRef]
- Blackman, C.; Hallström, O.; Bales, C. Demonstration of Solar Heating and Cooling System Using Sorption Integrated Solar Thermal Collectors. In Proceedings of the EuroSun 2014 Conference, Aix-les-Bains, France, 16–19 September 2014; Frank, E., Papillon, P., Eds.; ISES: Freiburg, Germany, 2015; pp. 1–10. [Google Scholar] [CrossRef]
- Allouhi, A.; Kousksou, T.; Jamil, A.; El Rhafiki, T.; Mourad, Y.; Zeraouli, Y. Optimal working pairs for solar adsorption cooling applications. Energy 2015, 79, 235–247. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Solé, A.; Barreneche, C. Review on sorption materials and technologies for heat pumps and thermal energy storage. Renew. Energy 2017, 110, 3–39. [Google Scholar] [CrossRef]
- Rezk, A.; Gediz Ilis, G.; Demir, H. Experimental study on silica gel/ethanol adsorption characteristics for low-grade thermal driven adsorption refrigeration systems. Therm. Sci. Eng. Prog. 2022, 34, 101429. [Google Scholar] [CrossRef]
- Mette, B.; Kerskes, H.; Drück, H.; Müller-Steinhagen, H. Experimental and numerical investigations on the water vapor adsorption isotherms and kinetics of binderless zeolite 13X. Int. J. Heat Mass Transf. 2014, 71, 555–561. [Google Scholar] [CrossRef]
- Semprini, S.; Asenbeck, S.; Kerskes, H.; Drück, H. Experimental and numerical investigations of an adsorption water-zeolite heat storage for refrigeration applications. Energy Procedia 2017, 135, 513–521. [Google Scholar] [CrossRef]
- Pesaran, A.; Lee, H.; Hwang, Y.; Radermacher, R.; Chun, H.H. Review article: Numerical simulation of adsorption heat pumps. Energy 2016, 100, 310–320. [Google Scholar] [CrossRef]
- Schreiber, H.; Lanzerath, F.; Bardow, A. Predicting performance of adsorption thermal energy storage: From experiments to validated dynamic models. Appl. Therm. Eng. 2018, 141, 548–557. [Google Scholar] [CrossRef]
- Thomas, S.; André, P. Numerical simulation and performance assessment of an absorption solar air-conditioning system coupled with an office building. Build. Simul. 2012, 5, 243–255. [Google Scholar] [CrossRef]
- Tso, C.Y.; Fu, S.C.; Chao, C.Y.H. Modeling a solar-powered double bed novel composite adsorbent (silica activated carbon/CaCl2)-water adsorption chiller. Build. Simul. 2014, 7, 185–196. [Google Scholar] [CrossRef]
- Schaefer, M.; Thess, A. Modeling and simulation of closed low-pressure zeolite adsorbers for thermal energy storage. Int. J. Heat Mass Transf. 2019, 139, 685–699. [Google Scholar] [CrossRef]
- Schaefer, M. Modeling and Simulation of Closed Low-Pressure Adsorbers for Thermal Energy Storage. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2019. [Google Scholar] [CrossRef]
- Schaefer, M.; Raab, A.; Gerle, M.; Pfeiler, D.; Vogel, J.; Thess, A. Development of a zero-energy-sauna: Simulation study of thermal energy storage. Energy Build. 2022, 256, 111659. [Google Scholar] [CrossRef]
- Gao, D.; Gao, G.; Cao, J.; Zhong, S.; Ren, X.; Dabwan, Y.N.; Hu, M.; Jiao, D.; Kwan, T.H.; Pei, G. Experimental and numerical analysis of an efficiently optimized evacuated flat plate solar collector under medium temperature. Appl. Energy 2020, 269, 115129. [Google Scholar] [CrossRef]
- Baehr, H.D.; Stephan, K. Heat and Mass Transfer, 3rd ed.; Springer: Berlin, Germany, 2011. [Google Scholar]
- Alexopoulos, S.; Kalogirou, S.A. Solar Thermal Energy; Springer: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- VDI. Heat Atlas; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Nusselt, W. Die Oberflaechenkondensation des Wasserdampfes; VDI-Z: Düsseldorf, Germany, 1916; Volume 60, pp. 541–546+569–575. [Google Scholar]
- European Commission. Photovoltaic Geographical Information System. Available online: https://joint-research-centre.ec.europa.eu/pvgis-photovoltaic-geographical-information-system_en (accessed on 1 June 2022).
- Huld, T.; Müller, R.; Gambardella, A. A new solar radiation database for estimating PV performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- SPF Institute for Solar Technology. Solar Collector Factsheet Tancredi TAN 2504. 2016. Available online: https://serv.spf.ch/spftesting/collectors/pdfs/scf1858en.pdf (accessed on 1 June 2022).
- SWT Technologie. Test Report Thermal Performance of a Solar Collector. 2017. Available online: https://www.tvpsolar.com/attach/20170614_%20TVP_MT_Power_v4_Solar_Keymark_Test_Report.pdf (accessed on 1 June 2022).
- Liu, Y.; Leong, K.C. Numerical modeling of a zeolite/water adsorption cooling system with non-constant condensing pressure. Int. Commun. Heat Mass Transf. 2008, 35, 618–622. [Google Scholar] [CrossRef]
- Sapienza, A.; Velte, A.; Girnik, I.; Frazzica, A.; Füldner, G.; Schnabel, L.; Aristov, Y. “Water - Silica Siogel” working pair for adsorption chillers: Adsorption equilibrium and dynamics. Renew. Energy 2017, 110, 40–46. [Google Scholar] [CrossRef]


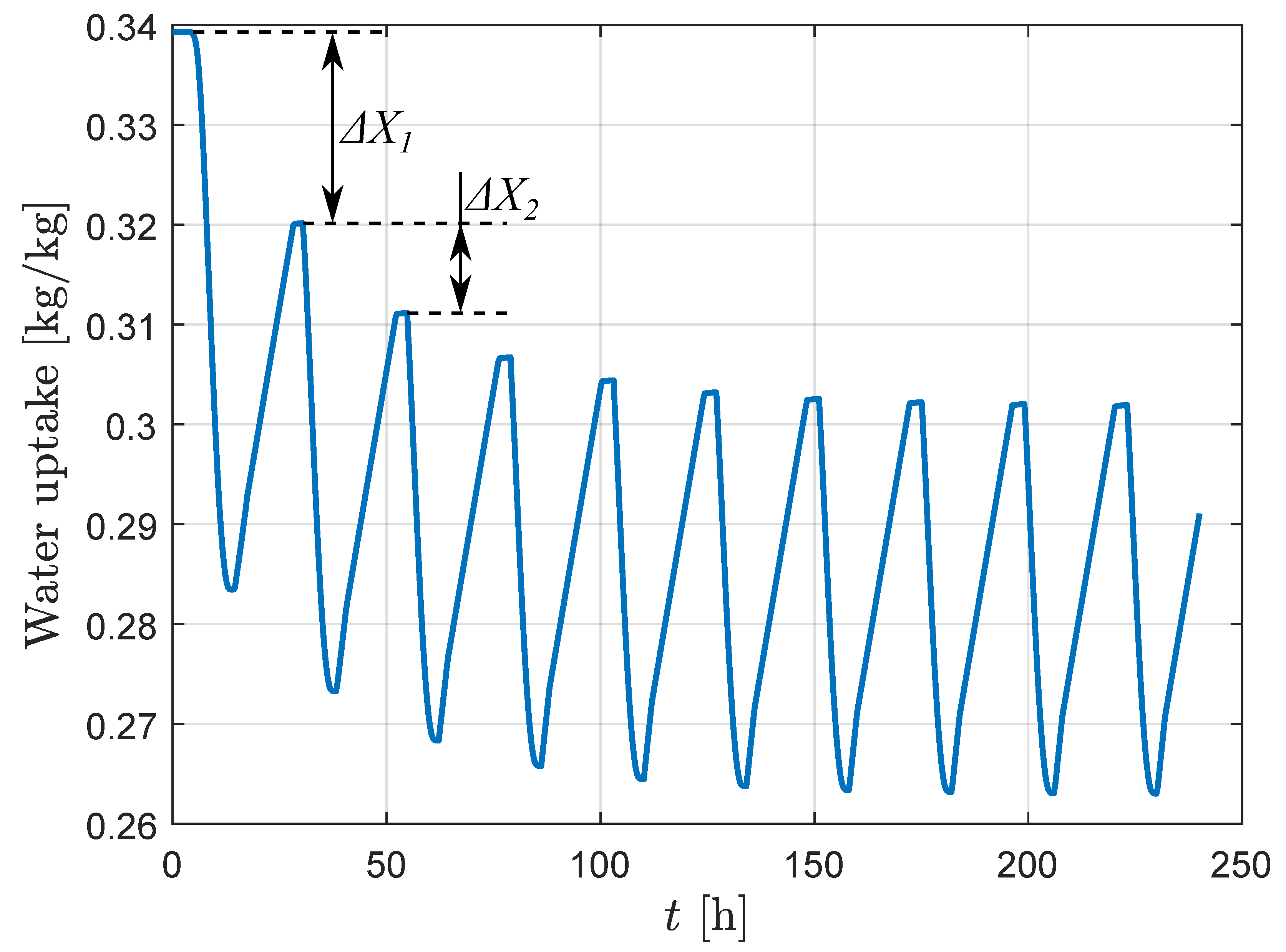


| Previous Works by co-Author Schaefer | |||
|---|---|---|---|
| Model Aspect | Fundamental Adsorber Model [32,33] | Sauna Oven Application [34] | This Work |
| Mass transfer inside the adsorber | ✓ | ✓ | ✓ |
| Heat transfer inside the adsorber | ✓ | ✓ | ✓ |
| Heat transfer fluid inside the adsorber | ✓ | - | - |
| Metal plate to absorb heat | - | ✓ | ✓ |
| Metal fins inside the adsorber | - | ✓ | ✓ |
| Solar collector | - | ✓ | - |
| Evaporator | - | - | ✓ |
| Condenser | - | - | ✓ |
| Operation strategy for building application | - | - | ✓ |
| Parameter | Evacuated Flat | Flat Plate Collector | Average |
|---|---|---|---|
| Plate Collector | |||
| 0.791 | 0.764 | ||
| Parameter | Value |
|---|---|
| Geometry—Adsorber, see Figure 2 | |
| width between internal fins | |
| length of internal fins | |
| thickness of internal fins | |
| thickness of absorber sheet | |
| width of air gap channel | |
| width between external fins | |
| Geometry—Condenser, see Figure 3 | |
| width between fins | |
| length of inner fins | |
| length of outer fins | |
| thickness of fins | |
| thickness of casing | |
| Geometry—Evaporator, see Figure 4 | |
| thickness of bottom sheet |
| Parameter | Value | Unit |
|---|---|---|
| Boundary conditions | ||
| 23 | °C | |
| 15 | °C | |
| time-dependent, see Figure 5 | °C | |
| time-dependent, see Figure 5 | ||
| average, see Table 2 | - | |
| Initial conditions | ||
| 23 | °C | |
| 21 | °C | |
| 23 | °C | |
| 40 | ||
| 10 |
| Parameter | Ref. Case | Pract. Optimum | Ideal Optimum | Unit |
|---|---|---|---|---|
| Adsorber | ||||
| Average | Average | High | % | |
| 10 | 20 | 20 | ||
| 20 | 10 | 10 | ||
| Condenser | ||||
| 50 | 50 | 25 | ||
| 45 | 45 | |||
| 4 | 8 | 16 | ||
| Evaporator | ||||
| 15 | °C | |||
| 7 | 7 | 14 | ||
| 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boeckmann, O.; Marmullaku, D.; Schaefer, M. Dynamic Modeling and Simulation of a Facade-Integrated Adsorption System for Solar Cooling of Lightweight Buildings. Energies 2024, 17, 1706. https://doi.org/10.3390/en17071706
Boeckmann O, Marmullaku D, Schaefer M. Dynamic Modeling and Simulation of a Facade-Integrated Adsorption System for Solar Cooling of Lightweight Buildings. Energies. 2024; 17(7):1706. https://doi.org/10.3390/en17071706
Chicago/Turabian StyleBoeckmann, Olaf, Drin Marmullaku, and Micha Schaefer. 2024. "Dynamic Modeling and Simulation of a Facade-Integrated Adsorption System for Solar Cooling of Lightweight Buildings" Energies 17, no. 7: 1706. https://doi.org/10.3390/en17071706
APA StyleBoeckmann, O., Marmullaku, D., & Schaefer, M. (2024). Dynamic Modeling and Simulation of a Facade-Integrated Adsorption System for Solar Cooling of Lightweight Buildings. Energies, 17(7), 1706. https://doi.org/10.3390/en17071706





