Pressure Transient Test Analysis for Deep Fractured Gas Reservoirs in Tarim Basin
Abstract
:1. Introduction
2. Development of Well-Testing Models
2.1. Development of Models
2.2. Model Assumptions and Mathematical Models
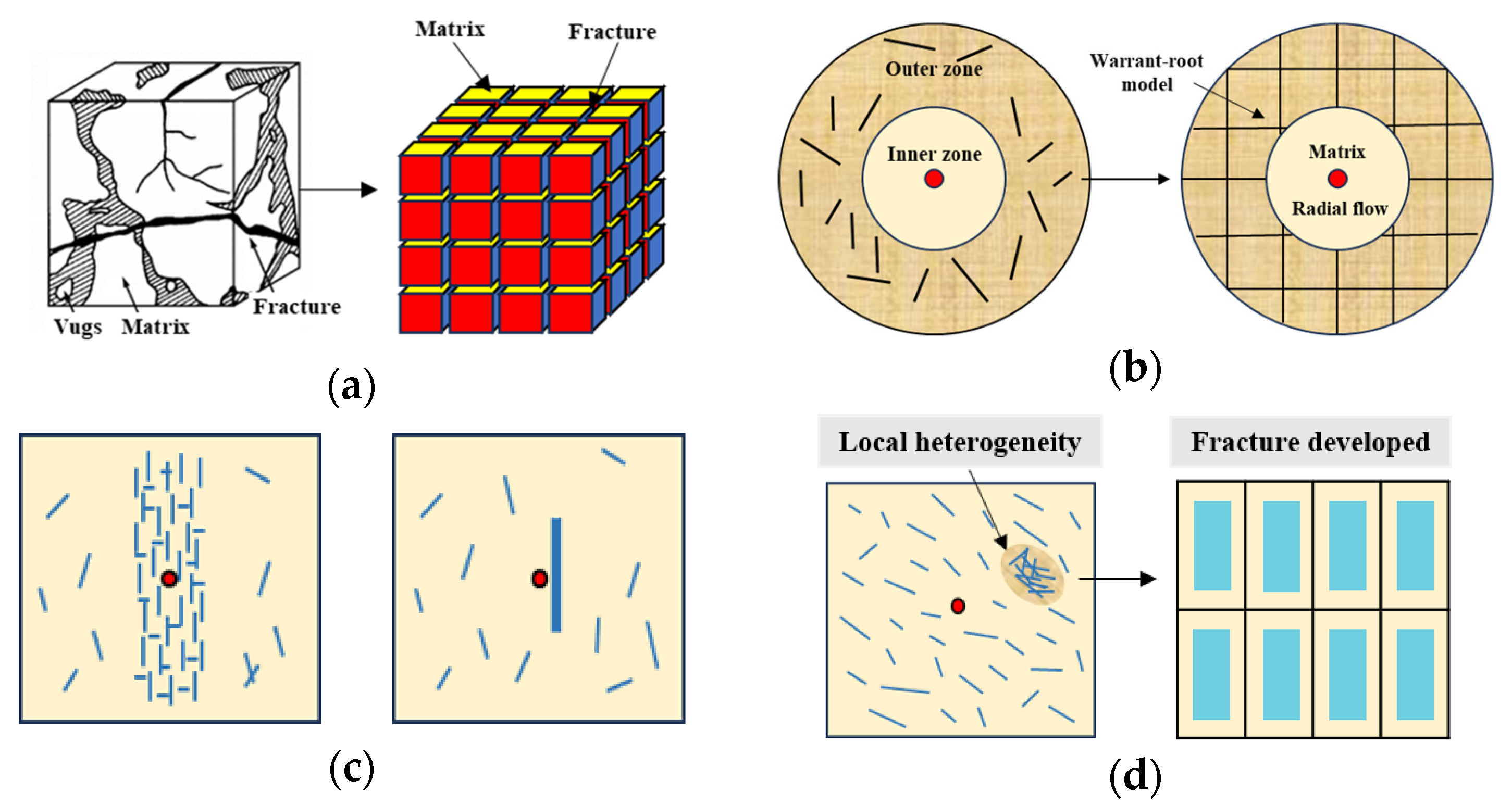
- The matrix is cut into equal-sized hexahedra in the fracture development zone, which conforms to the Warren–Root model;
- The reservoir is sealed up and down with equal thickness;
- The fluid is single-phase compressible and pseudo-pressure is applied to linearize the flowing equation;
- The influences of capillary force and gravity are ignored, and the temperature during the seepage process remains constant;
- The reservoir fluid follows the Darcy flow law.
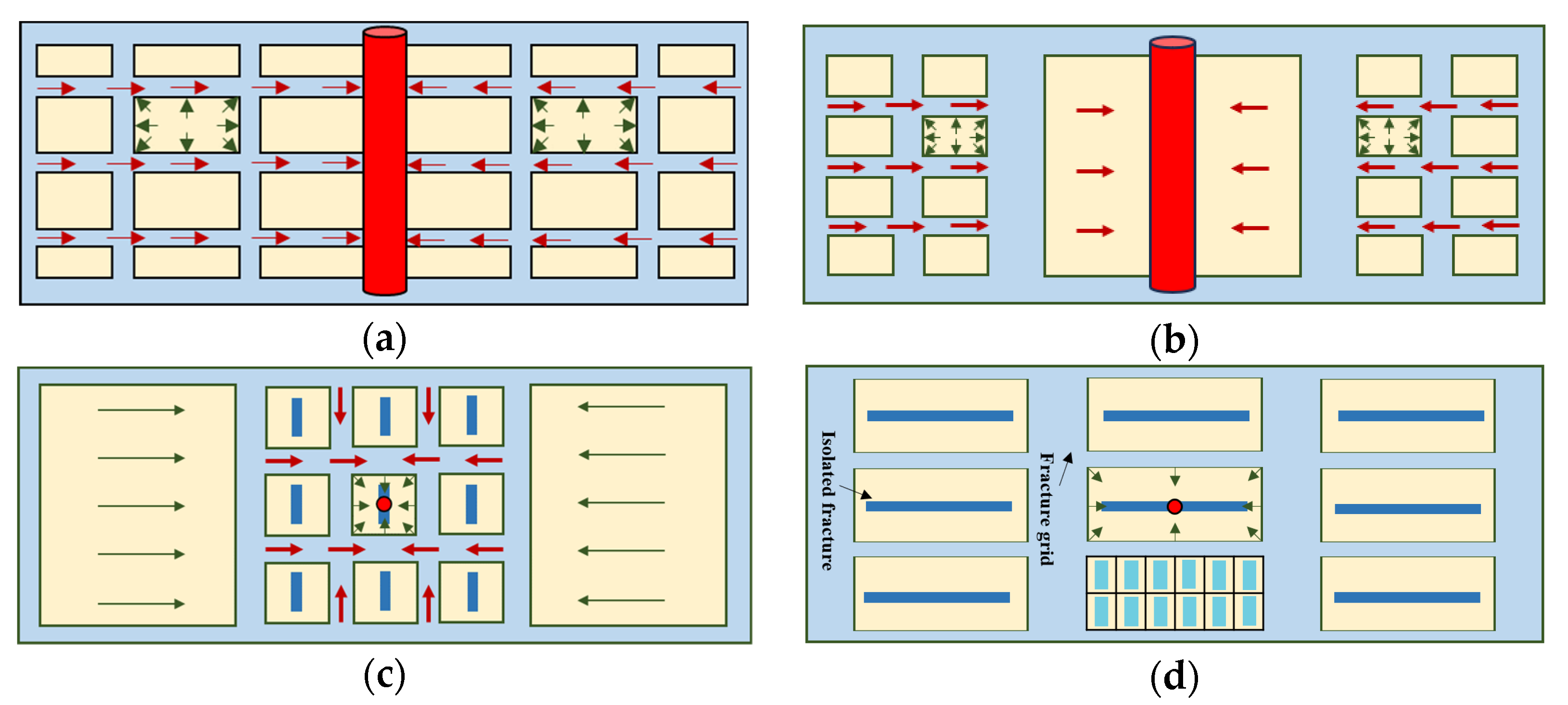
2.2.1. Warren–Root Model
2.2.2. Radial Composite Model
2.2.3. Dual-Flow-State Model
2.2.4. Local Heterogeneity Model
- Inner flow process of matrix
- 2.
- Flow process from matrix to fracture and then to matrix and finally to the wellbore
3. Results of Models
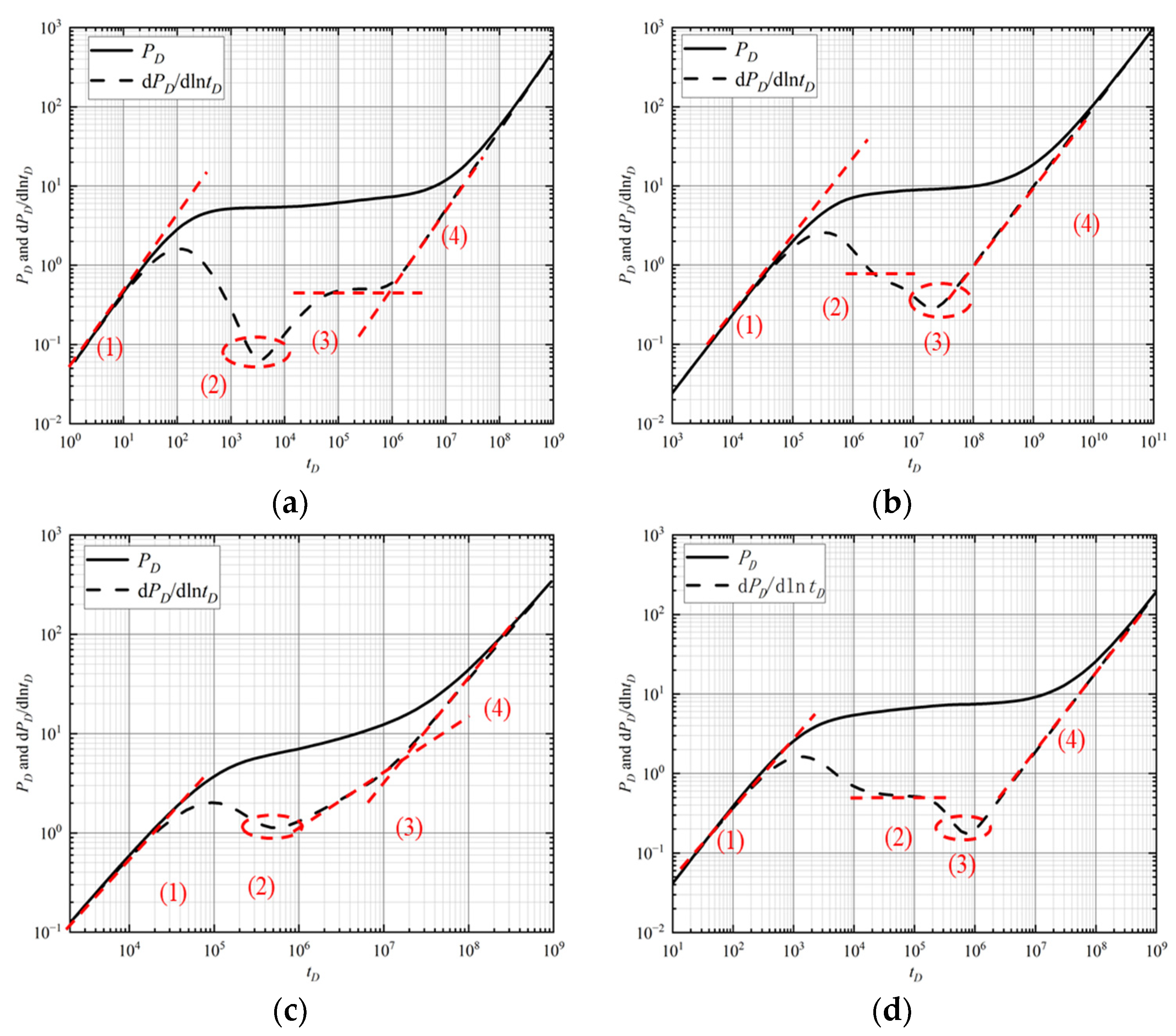
3.1. Typical Well-Testing Curve Chart and Flow Stage Division
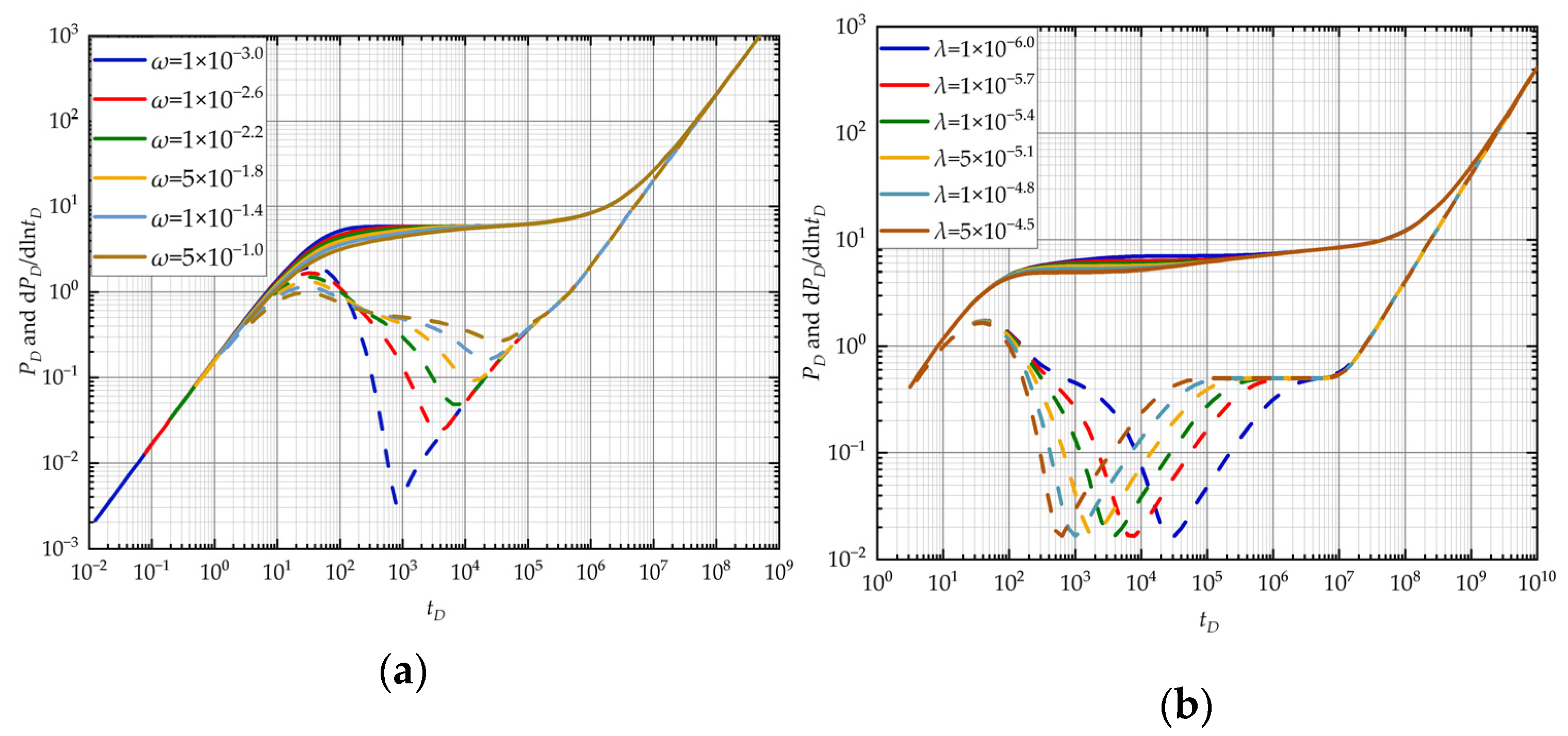
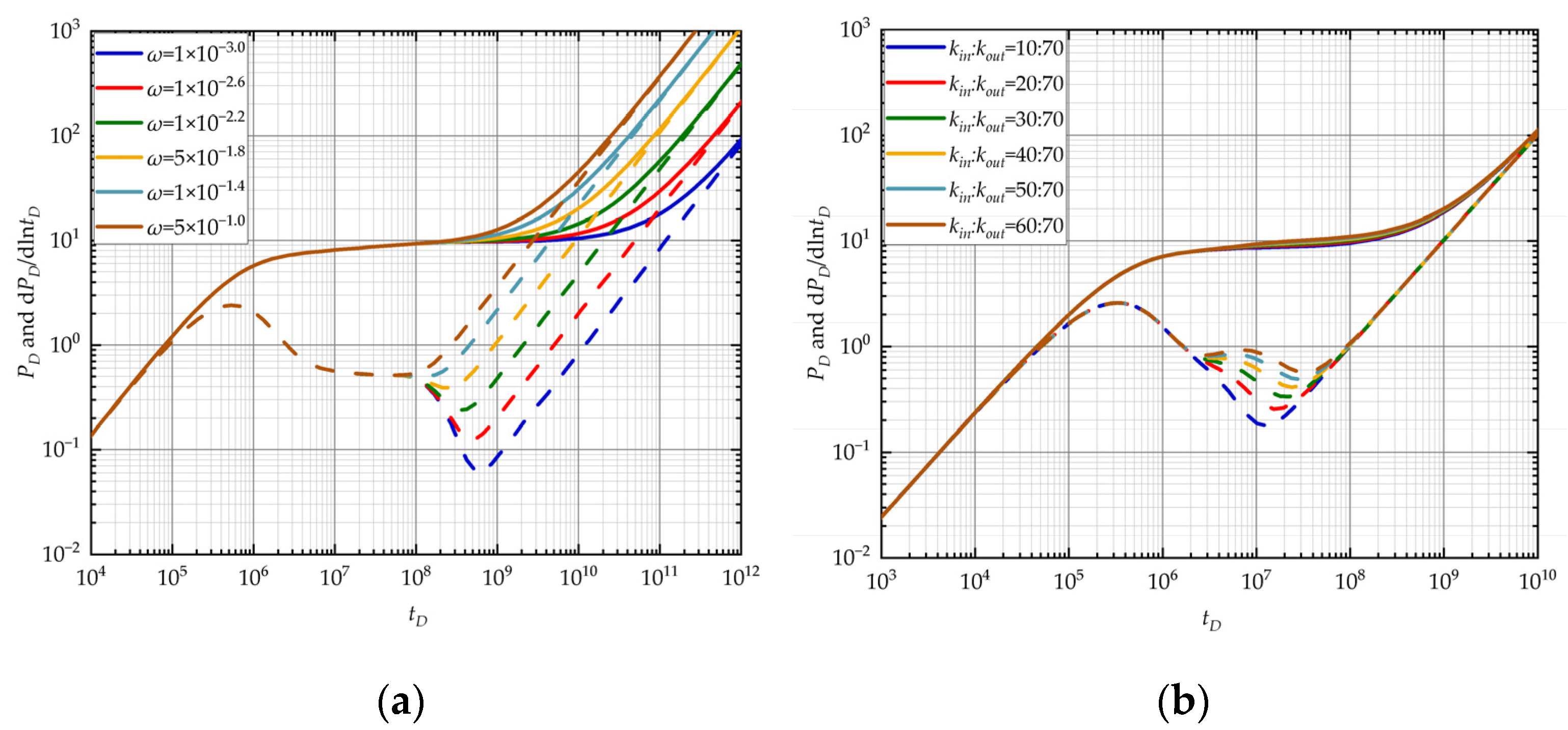
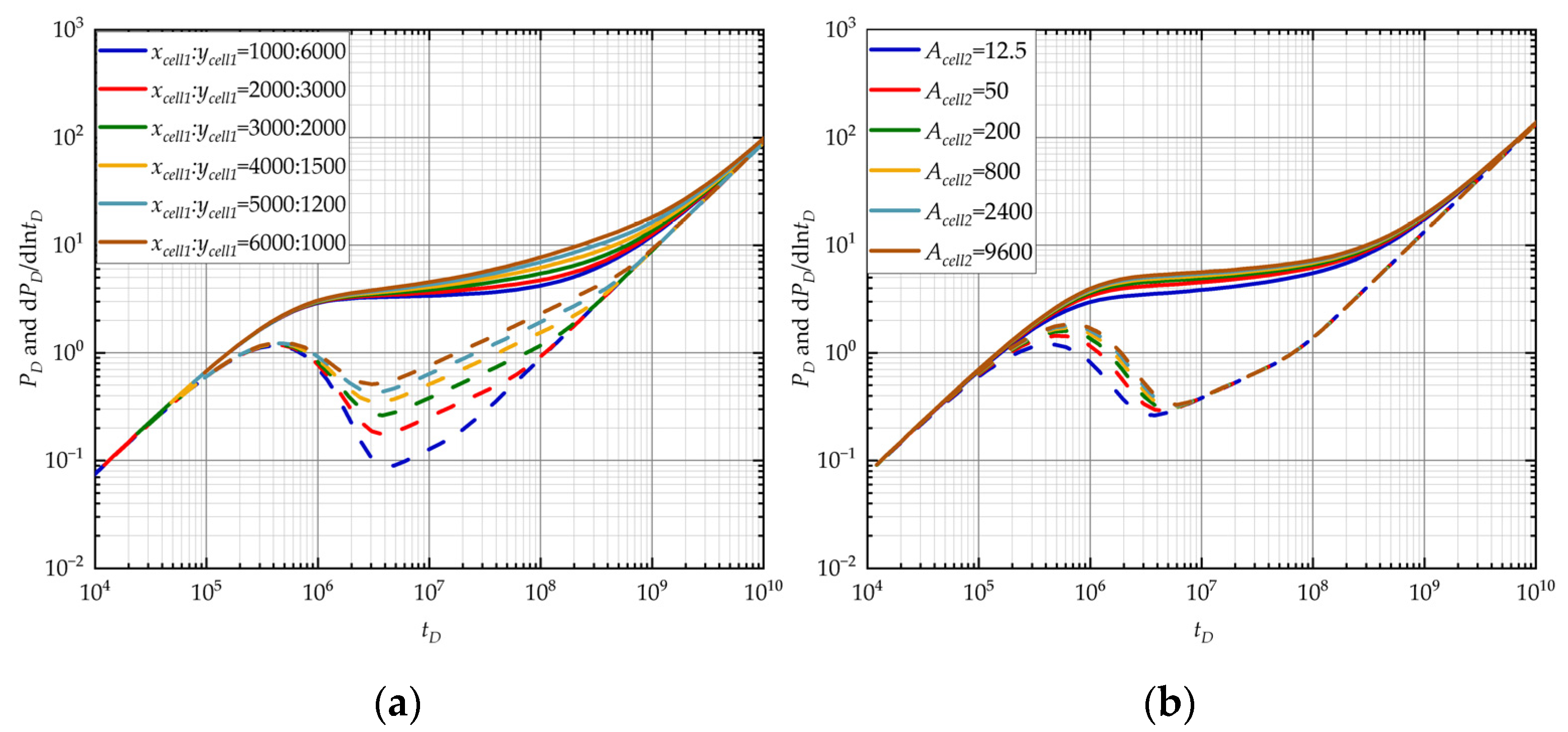
3.2. Sensitivity Analysis of Well-Testing Curves
3.2.1. Warren–Root Model
3.2.2. Radial Composite Model
3.2.3. Dual-Flow-State Model
3.2.4. Local Heterogeneity Model
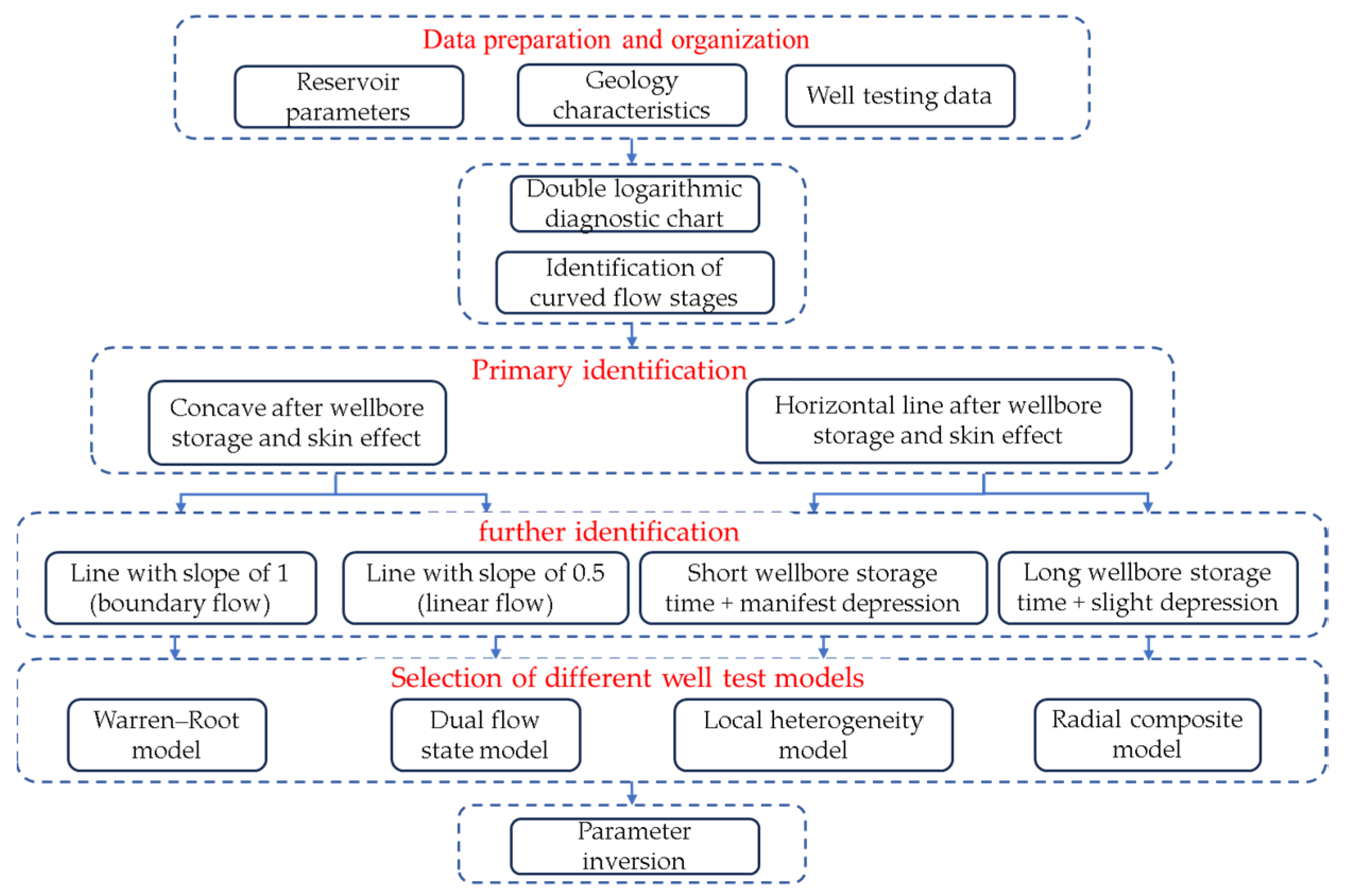
4. Identification Procedure of Well-Testing Model
- Based on the basic parameters of the reservoir, geology characteristics, and well-testing data, we first plot the pressure and its derivatives in a log–log coordinate, namely pressure transient analysis (PTA) curves;
- According to the analysis of the characteristics of the flow stages in the well-testing curve, when a concave curve appears after the wellbore storage and skin effect stage, followed by a horizontal line and boundary flow which manifests as a line with a slope of 1 on the derivative curve, the Warren–Root model should be used for well-testing analysis. However, due to the fracture development heterogeneity, the area of the “Warren–Root system” is small and the horizonal line is always covered by a boundary line which leads to the “disappearance” of the radial flow stage;
- When linear flow characteristics with a slope of 0.5 and a boundary flow stage with a slope of 1 appear after concavity on the well-testing curve, the dual-flow-state model should be used for well-testing analysis. For most cases, there is only the line with a slope of 0.5 and the line with a slope of 1 does not coexist with it. So, the line with a slope of 0.5 can serve as a sign for choosing the dual-flow-state model for parameter inversion.
- If the time of the wellbore storage effect stage is short and radial flow characteristics appear on the curve after it and subsequently a concave line appears, the local heterogeneity model should be used for well-testing analysis;
- However, the time of wellbore storage effect stage may be difficult to identify which can lead to misjudgment of the well-testing model. So, the geology characteristics and curve analysis are needed to help choose the appropriate model. If the reservoir geology characteristics near the well show local heterogeneity with high fracture development, the local heterogeneity should be considered first. Furthermore, from parameter sensitivity analysis, we can obtain that the elastic storage ratio can influence the degree of depression for the radial composite model while it has a slight influence on the local heterogeneity model due to its local fracture development. So, if the degree of concavity on the curve is not significant, the radial composite model is more appropriate for parameter inversion.
5. Model Application
5.1. Field Case
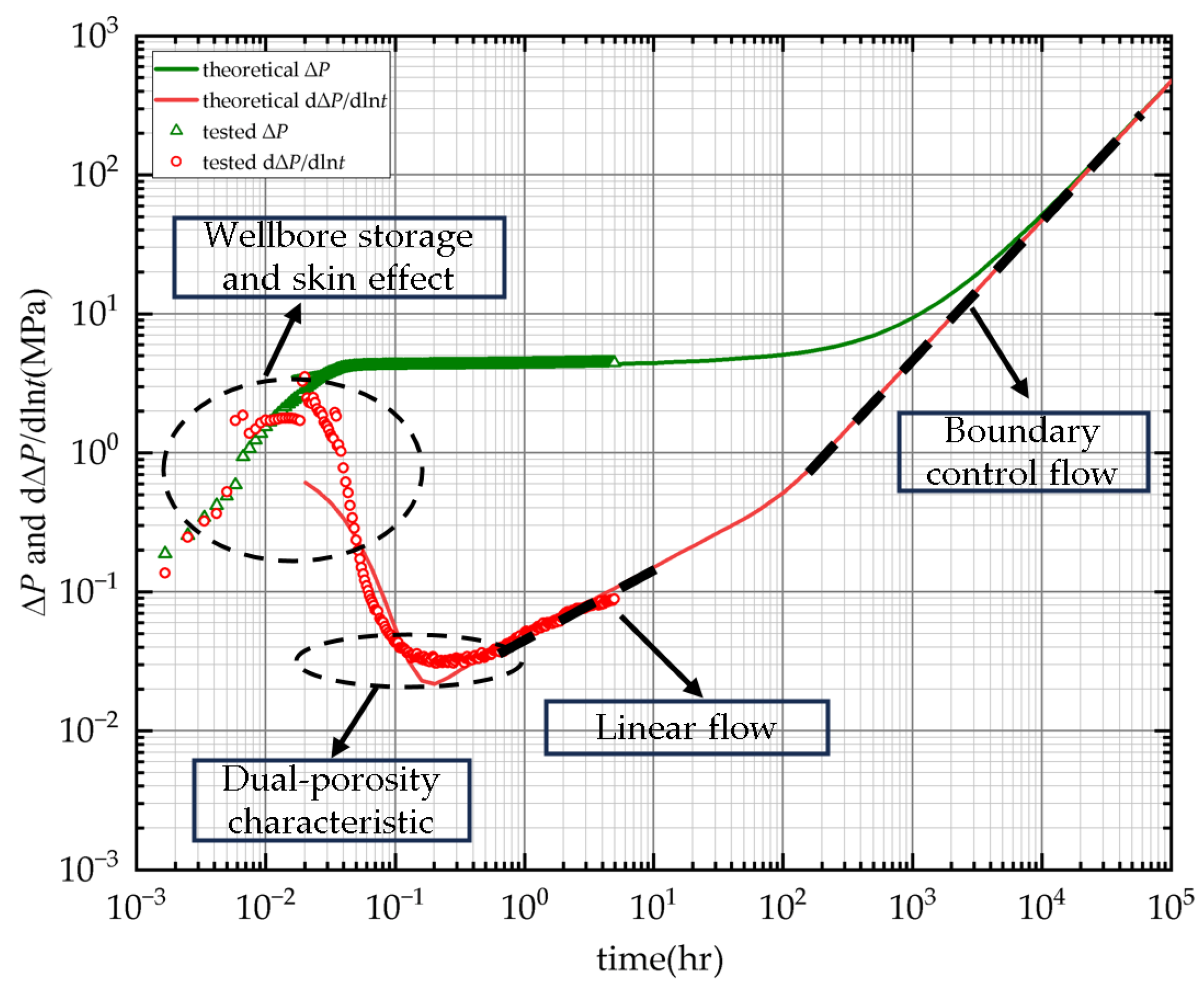
- Parameter import and curve plot in log–log coordinate. Input the sorted gas reservoir and gas parameters and import the data from the shut-in wellbore pressure recovery test. Plot the pressure and its derivatives in a log–log coordinate (Figure 10);
- Determine the analyzing model based on the curve shape. According to the identification procedure of different well-testing models and combined with the analysis of the well’s surrounding formation, the derivative curve exhibits characteristics of concavity and a slope of 0.5. Thus, the seepage characteristics conform to the dual-flow-state model. This model is used for this pressure recovery analysis, and the fitting results are shown in Figure 11;
- Division of flow stages and inversion results. The well-testing curve can be categorized into four stages: ① well storage and continuation flow stage: including wellbore storage and skin effect; ② dual-porosity characteristics. The curve exhibits a “concave” characteristic, representing dual-porosity features; ③ linear flow stage: the derivative curve shows a linear upward trend with a slope of 0.5; ④ boundary flow stage: it shows an upward trend due to obstructed flow, indicating a boundary flow with a slope of 1 (as the testing time was short, the results did not fully manifest the boundary flow characteristics). The curve-fitting rate is 85% calculated by the following method and inversion parameter results derived from the model are presented in Table 3.
5.2. Discussion
6. Conclusions
- Based on the characteristics of fracture development in the Tarim Basin and Warren–Root model, we established a set of identification methods of multi-scale media well-testing models suitable for different matrix–fracture patterns and conducted parameter sensitivity analysis for each of the four models, which can be used for the selection of well-testing models and inversion of formation parameters. Different from numerical well-testing methods, this is less time consuming and fewer parameters are needed.
- The application to the well in the Tarim Basin demonstrated that the theoretical curve in the log–log coordinate was consistent with the actual curve, with a curve-fitting rate exceeding 85%, which showed the accuracy of the identification procedure.
- Pseudo-pressure was used for the solution in this article that conforms to the properties of gas and formation heterogeneity considered in the local heterogeneity model by using a depth of investigation (DOI) method.
- A field case study shows it can be feasibly used for parameter inversion in the Tarim Basin. Combined with dynamic data, strategies for water prevention and control which are of great significance to production can be proposed. So, the procedure established in this paper can be widely used in the Tarim Basin to help guide gas development.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chang, B.; Tang, Y.; Zhu, S.; Li, S.; Cao, W. Well test characteristics and understandings of the ultra-deep fractured tight sandstone gas reservoirs: A case study on Keshen Gas Field in Tarim Basin. Petrol. Geol. Oilfield Dev. Daqing. 2021, 40, 167–174. [Google Scholar]
- Jia, C.; Li, Q. Petroleum geology of Kela-2, the most productive gas field in China. Mar. Pet. Geol. 2008, 25, 335–343. [Google Scholar]
- Li, B.; Zhu, Z.; Xia, J.; Ma, C. Development patterns and key techniques of coal-formed Kela 2 gas field. Pet. Explor. Dev. 2009, 36, 392–397. [Google Scholar]
- Han, D.; Xiong, W.; Jiang, T.; Gao, S.; Liu, H.; Ye, L.; Zhu, W.; An, W. Investigation of the Water-Invasion Gas Efficiency in the Kela-2 Gas Field Using Multiple Experiments. Energies 2023, 16, 7216. [Google Scholar] [CrossRef]
- Zhu, G.; Cui, L.; Zhang, Z.; Li, T.; Yang, H.; Chen, W.; Zhao, K.; Yan, H. Composition and origin of molecular compounds in the condensate oils of the Dabei gas field, Tarim Basin, NW China. Pet. Explor. Dev. 2019, 46, 504–517. [Google Scholar] [CrossRef]
- Yang, X.; Wang, Q.; Li, Y.; Lü, X.; Xie, H.; Wu, C.; Wang, C.; Wang, X.; Mo, T.; Wang, R. Formation mechanism of the Bozi-Dabei trillion cubic natural gas field, Kuqa foreland thrust belt. Earth Sci. Front. 2022, 29, 175–187. [Google Scholar]
- Zhu, W.; Mo, T.; Chen, C.; Hu, C.; Wang, C.; Shi, C.; Shi, L.; Li, P. Characteristics and Effects of Laminae on a Cretaceous Reservoir in the Bozi–Dabei Area of the Tarim Basin, China. Processes 2023, 11, 2472. [Google Scholar] [CrossRef]
- Jia, C. Key scientific and technological problems of petroleum exploration and development in deep and ultra-deep formation. J. China Univ. Pet. Ed. Nat. Sci. 2023, 47, 1–12. [Google Scholar]
- Jiang, T.; Teng, X.; Yang, X. Integrated techniques for rapid and highly-efficient development and production of ultra-deep tight sand gas reservoirs of Keshen 8 Block in the Tarim Basin. Nat. Gas. Ind. B 2016, 36, 30–38. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, S.; Zhou, B.; Liao, X.; Yu, W. A new numerical well testing model considering discrete fractures for heterogeneous fractured gas reservoirs. Nat. Gas. Ind. 2023, 43, 77–86. [Google Scholar]
- Barenblatt, G.; Zheltov, I.; Kochina, I. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks[strata]. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- Warren, J.; Root, P. The behavior of naturally fractured reservoirs. SPE J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Kazemi, H. Pressure transient analysis of naturally fractured reservoirs with uniform fracture distribution. SPE J. 1969, 9, 451–462. [Google Scholar] [CrossRef]
- De Swaan, O.A. Analytic solutions for determining naturally fractured reservoir properties by well testing. SPE J. 1976, 16, 117–122. [Google Scholar] [CrossRef]
- Raghavan, R.; Ohaeri, C. Unsteady flow to a well produced at constant pressure in a fractured reservoir. In Proceedings of the SPE California Regional Meeting, Bakersfield, CA, USA, 25–26 March 1981. [Google Scholar]
- Luan, Z. Analytical solution for transient flow of non-newtonian fluids in naturally fractured reservoirs. Acta Pet. Sin. 1981, 2, 75–79. [Google Scholar]
- Jia, Y. Considering skin factor, dual medium of wellbore storage effect, effective hole diameter model of confined strata and typical curve. Nat. Gas. Ind. 1994, 5, 48–51. [Google Scholar]
- Yao, J.; Dai, W.; Wang, Z. Well test interpretation method for triple medium reservoir with variable wellbore storage. J. China Univ. Pet. Ed. Nat. Sci. 2004, 28, 46–51. [Google Scholar]
- Jiang, R.; Gao, Y.; Sun, Z.; Gao, Y.; He, S. Bottom pressure characteristics for eccentric fracture vertical well in dual-medium low-permeability reservoir. Fault-Block Oil Gas Field 2020, 27, 778–783. [Google Scholar]
- Martyushev, D.; Yurikov, A. Evaluation of opening of fractures in the Logovskoye carbonate reservoir, Perm Krai, Russia. Pet. Res. 2021, 6, 137–143. [Google Scholar] [CrossRef]
- Gao, Y.; Rahman, M.; Lu, J. Novel mathematical model for transient pressure analysis of multi-fractured horizontal wells in naturally fractured oil reservoirs. ACS Omega 2021, 6, 15205–15221. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Li, T.; Zhao, G.; Zhao, J.; Cai, J. Well test model for horizontal well in dual-porosity three-zone composite reservoir. Well Test. 2022, 31, 6–12. [Google Scholar]
- Martyushev, D.; Yang, Y.; Kazemzadeh, Y.; Wang, D.; Li, Y. Understanding the mechanism of hydraulic fracturing in naturally fractured carbonate reservoirs: Microseismic monitoring and well testing. Arabian J. Sci. Eng. 2023, 1–14. [Google Scholar] [CrossRef]
- Martyushev, D.; Ponomareva, I.; Chukhlov, A.; Davoodi, S.; Osovetsky, B.; Kazymov, K.; Yang, Y. Study of void space structure and its influence on carbonate reservoir properties: X-ray microtomography, electron microscopy, and well testing. Mar. Pet. Geol. 2023, 151, 106192. [Google Scholar] [CrossRef]
- Sun, H.; Ouyang, W.; Zhu, S.; Wan, Y.; Tang, Y.; Cao, W. A new numerical well test method of multi-scale discrete fractured tight sandstone gas reservoirs and its application in the Kelasu Gas Field of the Tarim Basin. Nat. Gas. Ind. 2022, 42, 55–64. [Google Scholar] [CrossRef]
- Huang, L.; Liu, Q. Percolation mathematic model in compound gas reservoir with dual medium of excessive sections. Well Test. 2006, 15, 11–14. [Google Scholar]
- Al-Hussainy, R.; Ramey, H., Jr.; Crawford, P. The Flow of Real Gases through Porous Media. J. Pet. Technol. 1966, 18, 624–636. [Google Scholar] [CrossRef]
- Chen, Z.; Li, D.; Zhang, S.; Liao, X.; Zhou, B.; Chen, D. A well-test model for gas hydrate dissociation considering a dynamic interface. Fuel 2022, 314, 123053. [Google Scholar] [CrossRef]
- Cai, M.; Wu, Y.; Wu, Y.; Tan, J.; Fang, J. Analysis on pressure behavior of trilinear flow model of vertical fracture wells in triple porosity reservoir. Fault-Block Oil Gas Field 2008, 01, 58–60. [Google Scholar]
- Liu, J.; Liu, X.; Zhu, H.; Ma, X.; Zhang, Y.; Zeng, J.; Luo, W.; Teng, B.; Li, Y.; Wan, N. A decomposed fracture network model for characterizing well performance of fracture networks on the basis of an approximated flow equation. Lithosphere 2021, 2021, 5558746. [Google Scholar] [CrossRef]



| Parameters | Values |
|---|---|
| Wellbore radius/m | 0.08414 |
| Reservoir top depth/m | 6185 |
| Reservoir effective thickness/m | 12 |
| Porosity/% | 7.15 |
| Reservoir pressure/MPa | 92.81 |
| Rock compressibility/MPa−1 | 8.1675 × 10−5 |
| Reservoir temperature/°C | 117.56 |
| Gas relative density/dim | 0.6377 |
| Gas deviation factor/dim | 1.652 |
| Gas viscosity/(mPa·s) | 0.0401 |
| Gas volume coefficient/dim | 0.00244 |
| Gas compressibility/MPa−1 | 0.00397 |
| Parameters | Measuring Time/h | Pressure/MPa |
|---|---|---|
| Data 1 | 0.000000000 | 88.211504 |
| Data 2 | 0.004166667 | 88.580317 |
| Data 3 | 0.008333333 | 89.305794 |
| Data 4 | 0.012500000 | 89.900153 |
| Data 5 | 0.016666667 | 90.350214 |
| Data 6 | 0.020833333 | 90.825350 |
| Data 7 | 0.025000000 | 91.203580 |
| Data 8 | 0.029166667 | 91.458737 |
| Data 9 | 0.033333333 | 91.625746 |
| Data 10 | 0.037500000 | 91.779463 |
| Data 11 | 0.041666667 | 91.858774 |
| Data 12 | 0.045833333 | 91.900357 |
| Data 13 | 0.050000000 | 91.923355 |
| Parameters | Values |
|---|---|
| Elastic energy storage ratio/dim | 0.0927 |
| Wellbore storage coefficient/(m3/MPa) | 0.23 |
| Skin factor/dim | 3 |
| Effective permeability of outer matrix/mD | 62 |
| Effective permeability of the surrounding finely cut matrix/mD | 33 |
| Effective permeability of the matrix where the well is located/mD | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Wang, X.; Yang, F.; Chang, B.; Liu, L.; Wang, J.; Zhou, W. Pressure Transient Test Analysis for Deep Fractured Gas Reservoirs in Tarim Basin. Energies 2024, 17, 1717. https://doi.org/10.3390/en17071717
Chen D, Wang X, Yang F, Chang B, Liu L, Wang J, Zhou W. Pressure Transient Test Analysis for Deep Fractured Gas Reservoirs in Tarim Basin. Energies. 2024; 17(7):1717. https://doi.org/10.3390/en17071717
Chicago/Turabian StyleChen, Dong, Xin Wang, Fenglai Yang, Baohua Chang, Lei Liu, Junlei Wang, and Wenzhuo Zhou. 2024. "Pressure Transient Test Analysis for Deep Fractured Gas Reservoirs in Tarim Basin" Energies 17, no. 7: 1717. https://doi.org/10.3390/en17071717
APA StyleChen, D., Wang, X., Yang, F., Chang, B., Liu, L., Wang, J., & Zhou, W. (2024). Pressure Transient Test Analysis for Deep Fractured Gas Reservoirs in Tarim Basin. Energies, 17(7), 1717. https://doi.org/10.3390/en17071717







