School Electricity Consumption in a Small Island Country: The Case of Fiji
Abstract
1. Introduction
Building Energy Use in Fiji
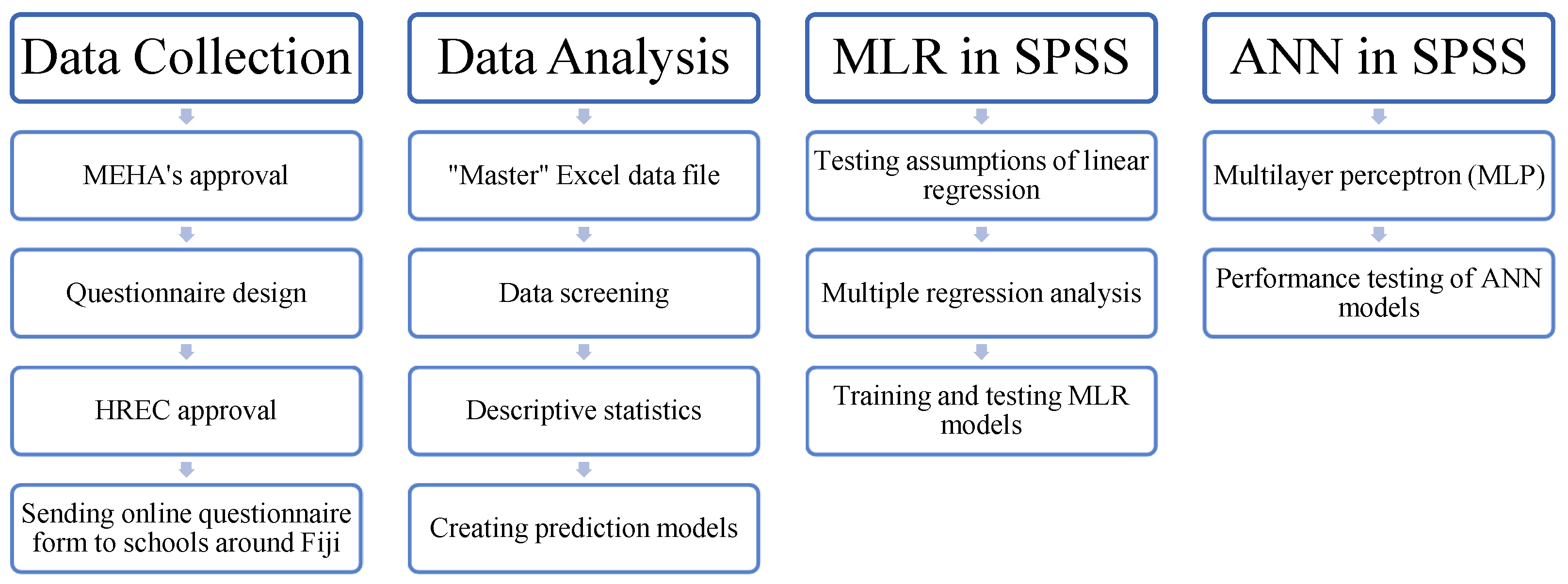
2. Materials and Methods
2.1. Questionnaire Design
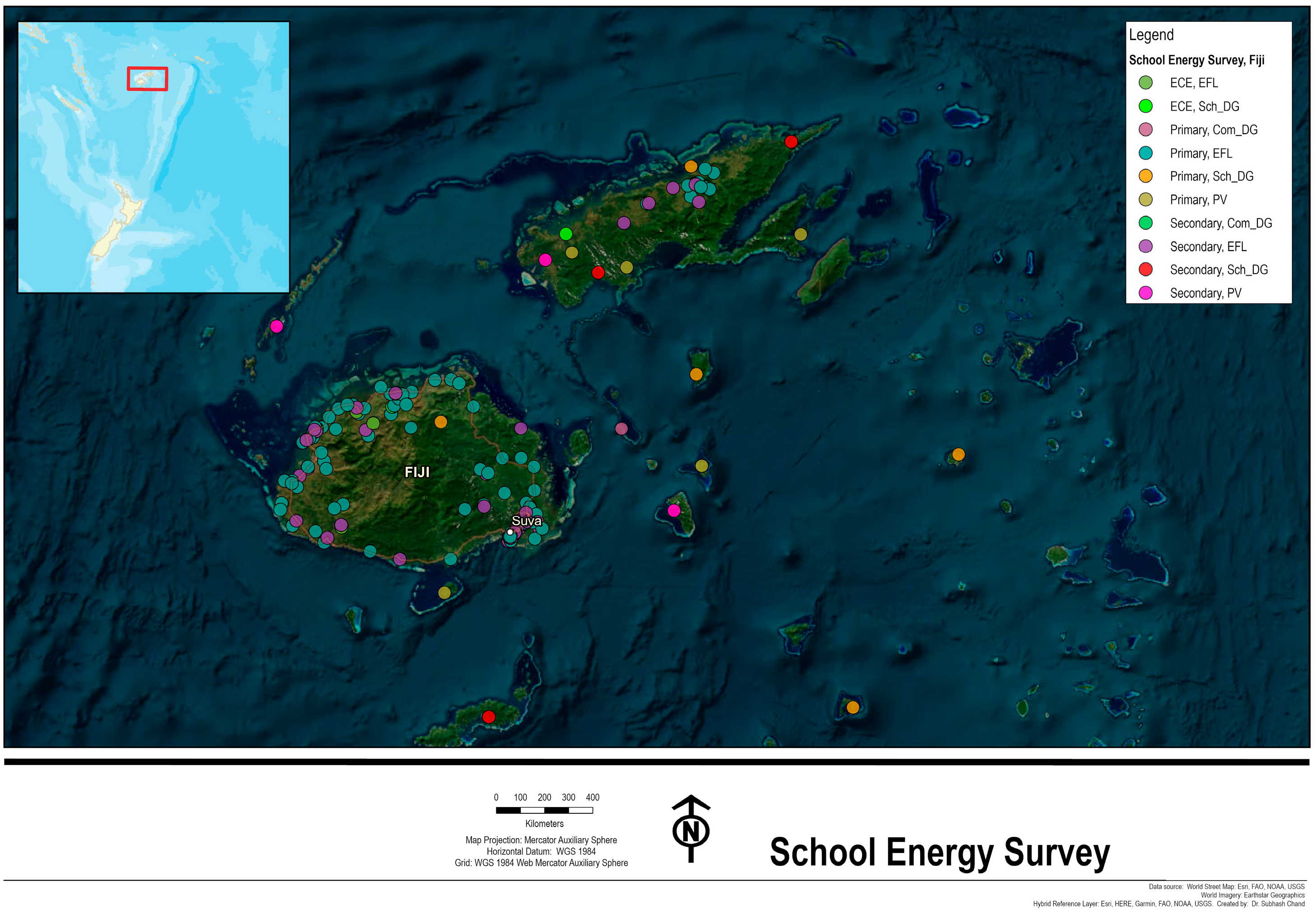
2.2. Running the Questionnaire Survey
2.3. Data Screening and Analysis
2.4. Regression Analysis
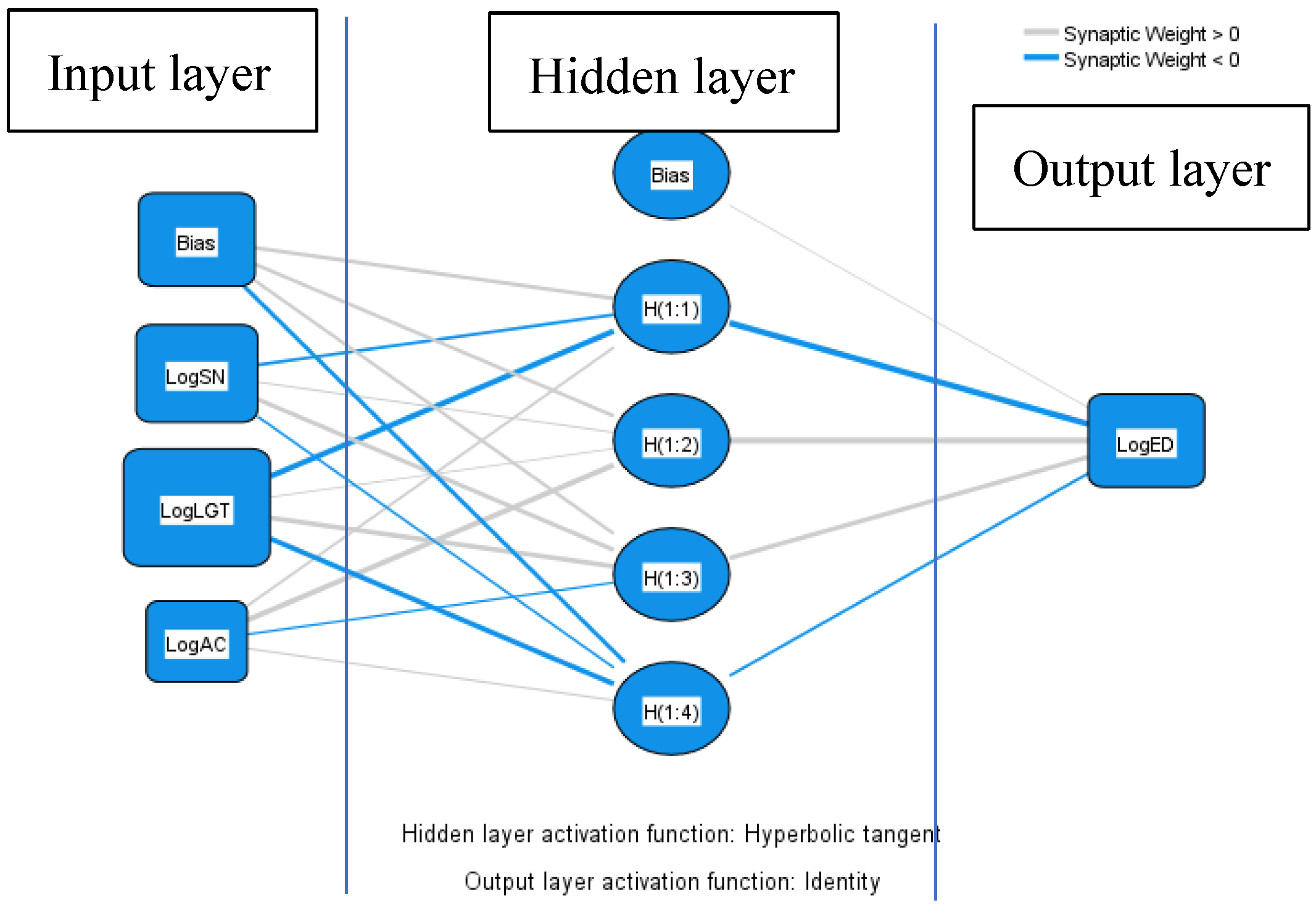
2.5. ANN Model
2.6. Testing Model Performance
3. Results
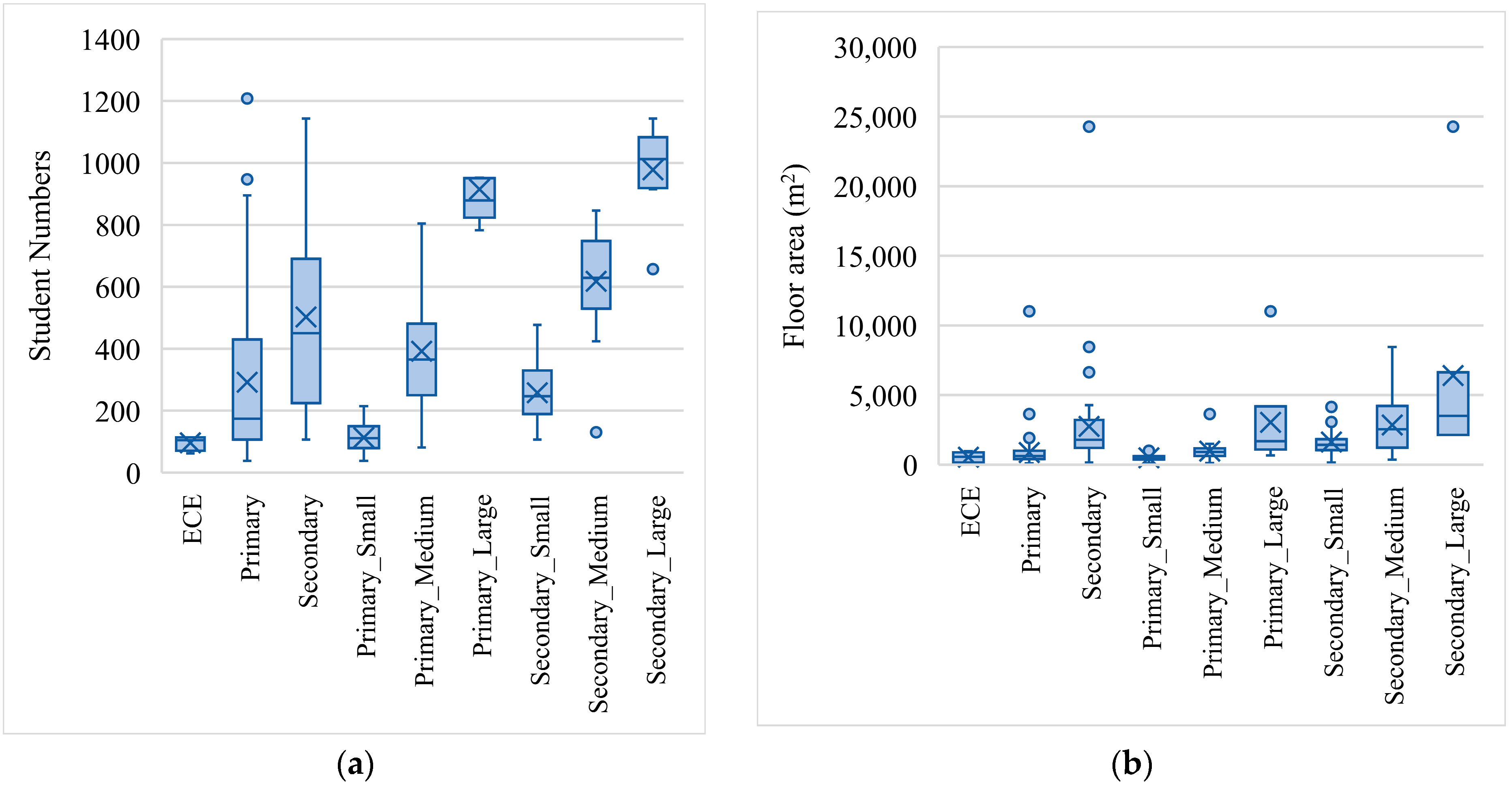
3.1. Descriptive Statistics of the Sampled Schools
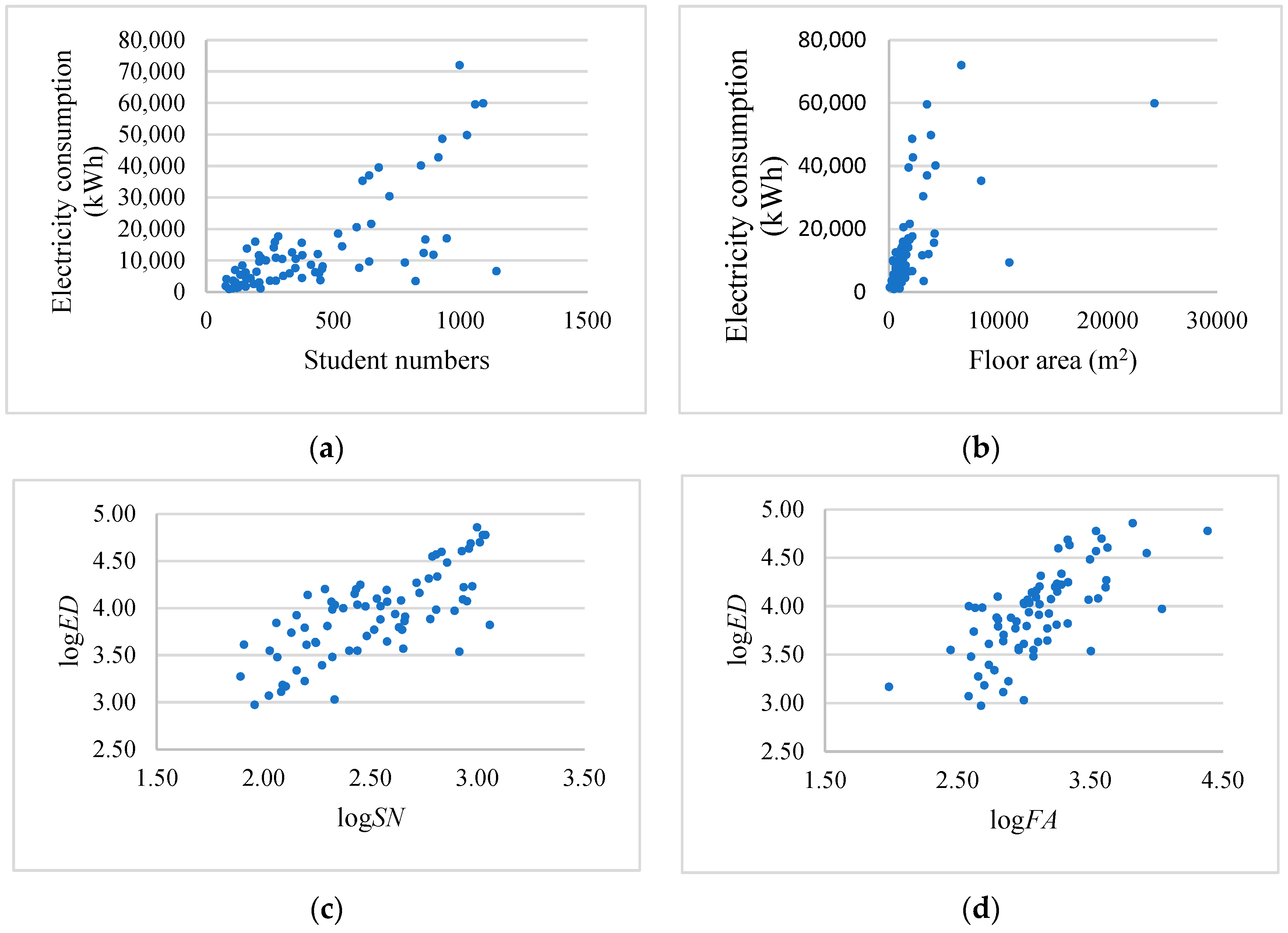
3.1.1. Electricity Consumption of Schools Connected to the Grid
3.1.2. Building Characteristics for Fijian Schools
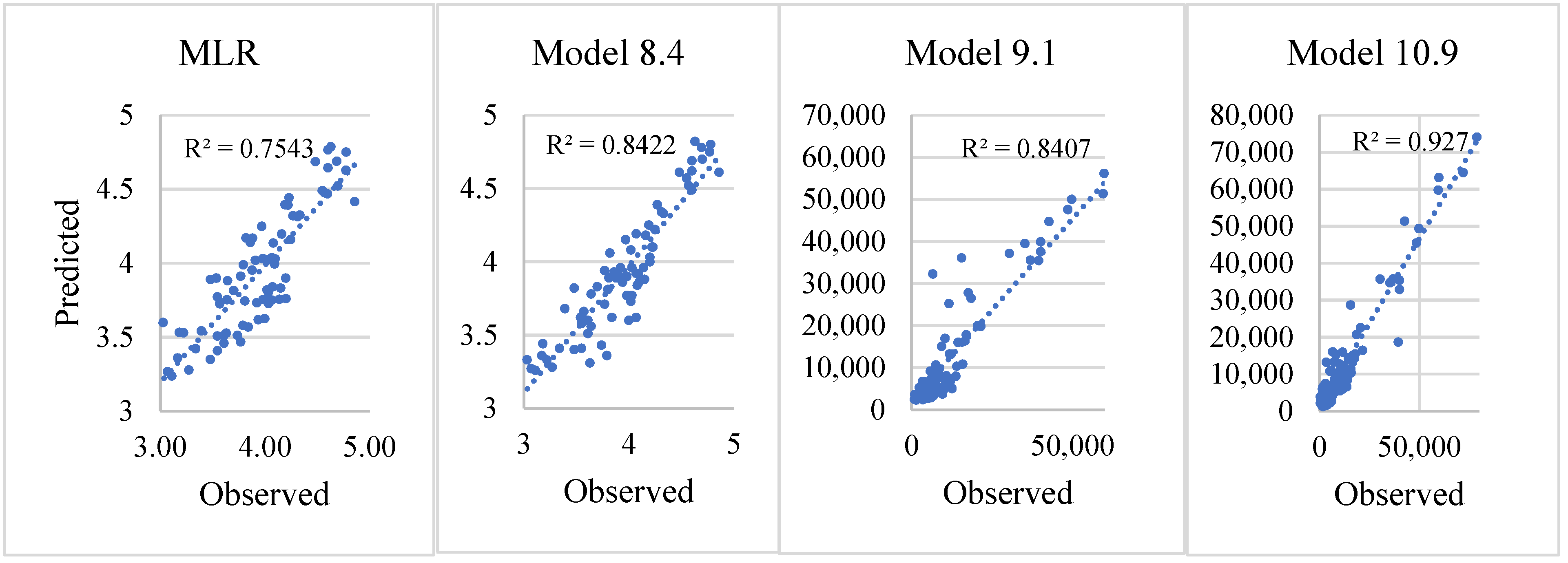
3.2. MLR Models for Predicting Electricity Demand for Grid-Connected Schools
3.3. ANN Models for Predicting Electricity Demand and Performance Testing
3.3.1. Testing Performance of MLR and ANN Models
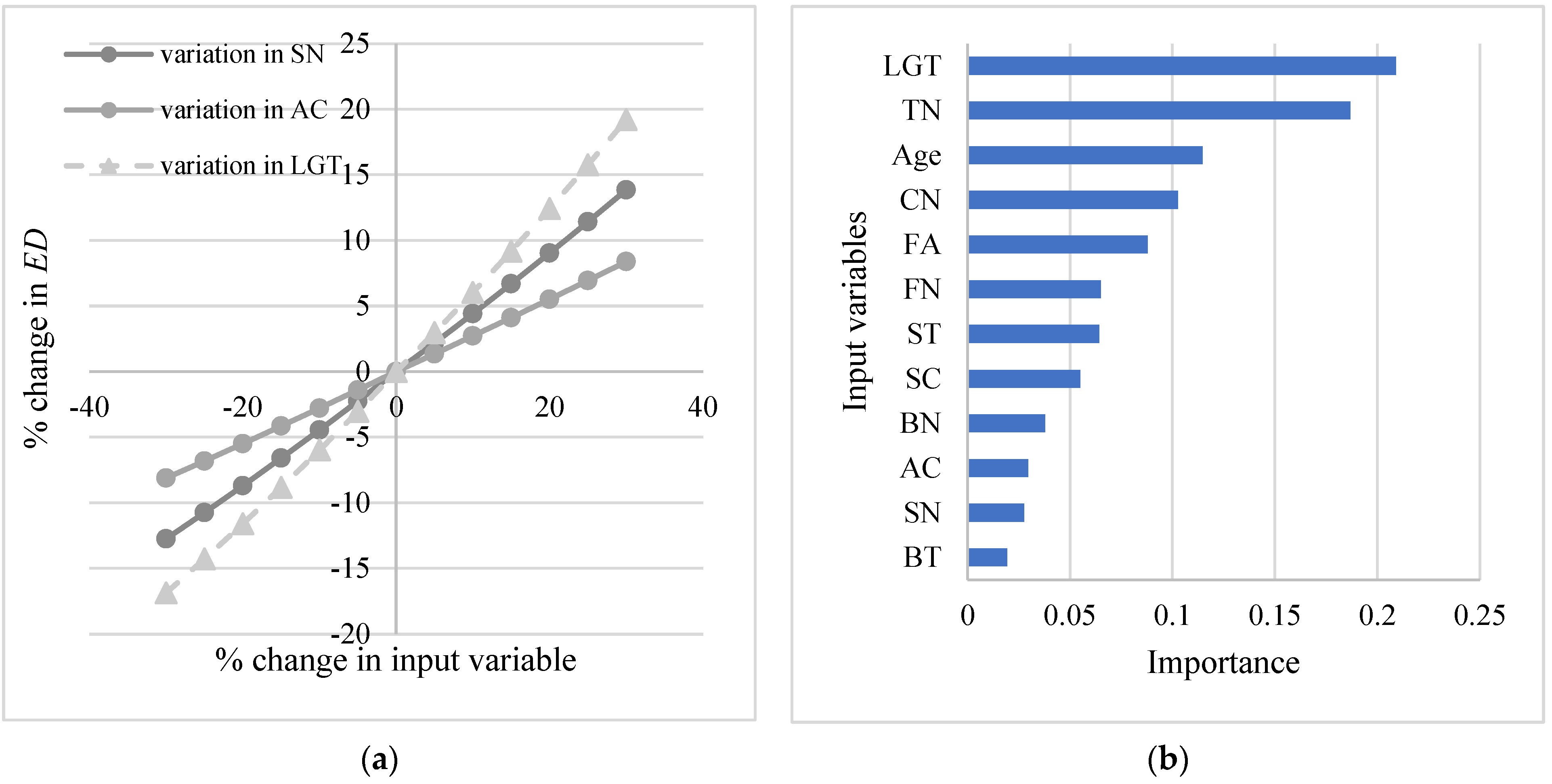
3.3.2. Importance of IVs That Affect School Electricity Demand
4. Discussions
4.1. Implications of the Current Study
4.2. Study Scope, Limitations of Present Study, and Recommendations for Future Study
5. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, X.; Shi, Y.; Xia, L.; Pan, S.; Wu, J.; Han, M.; Zhao, X. A review of data-driven approaches for prediction and classification of building energy consumption. Renew. Sustain. Energy Rev. 2018, 82, 1027–1047. [Google Scholar] [CrossRef]
- Chemingui, Y.; Gastli, A.; Ellabban, O. Reinforcement learning-based school energy management system. Energies 2020, 13, 6354. [Google Scholar] [CrossRef]
- Guo, Y.-Y. Revisiting the building energy consumption in China: Insights from a large-scale national survey. Energy Sustain. Dev. 2022, 68, 76–93. [Google Scholar] [CrossRef]
- Dias Pereira, L.; Raimondo, D.; Corgnati, S.P.; Gameiro da Silva, M. Energy consumption in schools—A review paper. Renew. Sustain. Energy Rev. 2014, 40, 911–922. [Google Scholar] [CrossRef]
- Airaksinen, M. Energy use in day care centers and schools. Energies 2011, 4, 998–1009. [Google Scholar] [CrossRef]
- Chung, W.; Yeung, I.M. A two-stage regression-based benchmarking approach to evaluate school’s energy efficiency in different tariff regions. Energy Sustain. Dev. 2021, 61, 15–27. [Google Scholar] [CrossRef]
- Wang, J.C. Energy consumption in elementary and high schools in Taiwan. J. Clean. Prod. 2019, 227, 1107–1116. [Google Scholar] [CrossRef]
- Chung, W.; Yeung, I.M.H. A study of energy consumption of secondary school buildings in Hong Kong. Energy Build. 2020, 226, 110388. [Google Scholar] [CrossRef]
- Ouf, M.M.; Issa, M.H. Energy consumption analysis of school buildings in Manitoba, Canada. Int. J. Sustain. Built Environ. 2017, 6, 359–371. [Google Scholar] [CrossRef]
- Thewes, A.; Maas, S.; Scholzen, F.; Waldmann, D.; Zürbes, A. Field study on the energy consumption of school buildings in Luxembourg. Energy Build. 2014, 68, 460–470. [Google Scholar] [CrossRef]
- Stuart, G.; Fleming, P.; Ferreira, V.; Harris, P. Rapid analysis of time series data to identify changes in electricity consumption patterns in UK secondary schools. Build. Environ. 2007, 42, 1568–1580. [Google Scholar] [CrossRef]
- Samuels, J.A.; Booysen, M.J. Chalk, talk, and energy efficiency: Saving electricity at South African schools through staff training and smart meter data visualisation. Energy Res. Soc. Sci. 2019, 56, 101212. [Google Scholar] [CrossRef]
- Agarwal, S.; Rengarajan, S.; Sing, T.F.; Yang, Y. Nudges from school children and electricity conservation: Evidence from the “Project Carbon Zero” campaign in Singapore. Energy Econ. 2017, 61, 29–41. [Google Scholar] [CrossRef]
- Mohamed, S.; Smith, R.; Rodrigues, L.; Omer, S.; Calautit, J. The correlation of energy performance and building age in UK schools. J. Build. Eng. 2021, 43, 103141. [Google Scholar] [CrossRef]
- Corrado, V.; Ballarini, I.; Paduos, S.; Tulipano, L. A new procedure of energy audit and cost analysis for the transformation of a school into a nearly zero-energy building. Energy Procedia 2017, 140, 325–338. [Google Scholar] [CrossRef]
- Shailesh, K.; Tanuja, S.; Kumar, M.; Krishna, R.A. Energy consumption optimisation in classrooms using lighting energy audit. In Proceedings of the National Conference on Challenges in Research & Technology in the Coming Decades (CRT 2013), Ujire, India, 27–28 September 2013. [Google Scholar]
- Borgstein, E.H.; Lamberts, R. Developing energy consumption benchmarks for buildings: Bank branches in Brazil. Energy Build. 2014, 82, 82–91. [Google Scholar] [CrossRef]
- Vaisi, S.; Varmazyari, P.; Esfandiari, M.; Sharbaf, S.A. Developing a multi-level energy benchmarking and certification system for office buildings in a cold climate region. Appl. Energy 2023, 336, 120824. [Google Scholar] [CrossRef]
- Quevedo, T.C.; Geraldi, M.S.; Melo, A.P. Applying machine learning to develop energy benchmarking for university buildings in Brazil. J. Build. Eng. 2023, 63, 105468. [Google Scholar] [CrossRef]
- Kim, T.; Kang, B.; Kim, H.; Park, C.; Hong, W.-H. The study on the Energy Consumption of middle school facilities in Daegu, Korea. Energy Rep. 2019, 5, 993–1000. [Google Scholar] [CrossRef]
- Mohammed, A.; Alshibani, A.; Alshamrani, O.; Hassanain, M. A regression-based model for estimating the energy consumption of school facilities in Saudi Arabia. Energy Build. 2021, 237, 110809. [Google Scholar] [CrossRef]
- Bourdeau, M.; Zhai, X.q.; Nefzaoui, E.; Guo, X.; Chatellier, P. Modeling and forecasting building energy consumption: A review of data-driven techniques. Sustain. Cities Soc. 2019, 48, 101533. [Google Scholar] [CrossRef]
- Hong, S.-M.; Paterson, G.; Mumovic, D.; Steadman, P. Improved benchmarking comparability for energy consumption in schools. Build. Res. Inf. 2014, 42, 47–61. [Google Scholar] [CrossRef]
- Almeida, A.P.; Sousa, V.; Silva, C.M. Methodology for estimating energy and water consumption patterns in university buildings: Case study, Federal University of Roraima (UFRR). Heliyon 2021, 7, e08642. [Google Scholar] [CrossRef]
- Nematchoua, M.K.; Yvon, A.; Roy, S.E.J.; Ralijaona, C.G.; Mamiharijaona, R.; Razafinjaka, J.N.; Tefy, R. A review on energy consumption in the residential and commercial buildings located in tropical regions of Indian Ocean: A case of Madagascar island. J. Energy Storage 2019, 24, 100748. [Google Scholar] [CrossRef]
- Ma, H.; Lai, J.; Li, C.; Yang, F.; Li, Z. Analysis of school building energy consumption in Tianjin, China. Energy Procedia 2019, 158, 3476–3481. [Google Scholar] [CrossRef]
- Geraldi, M.S.; Ghisi, E. Mapping the energy usage in Brazilian public schools. Energy Build. 2020, 224, 110209. [Google Scholar] [CrossRef]
- Wu, J.; Lian, Z.; Zheng, Z.; Zhang, H. A method to evaluate building energy consumption based on energy use index of different functional sectors. Sustain. Cities Soc. 2020, 53, 101893. [Google Scholar] [CrossRef]
- Jeong, K.; Koo, C.; Hong, T. An estimation model for determining the annual energy cost budget in educational facilities using SARIMA (seasonal autoregressive integrated moving average) and ANN (artificial neural network). Energy 2014, 71, 71–79. [Google Scholar] [CrossRef]
- Yuan, J.; Farnham, C.; Azuma, C.; Emura, K. Predictive artificial neural network models to forecast the seasonal hourly electricity consumption for a University Campus. Sustain. Cities Soc. 2018, 42, 82–92. [Google Scholar] [CrossRef]
- Alshibani, A. Prediction of the Energy Consumption of School Buildings. Appl. Sci. 2020, 10, 5885. [Google Scholar] [CrossRef]
- Nsangou, J.C.; Kenfack, J.; Nzotcha, U.; Ngohe Ekam, P.S.; Voufo, J.; Tamo, T.T. Explaining household electricity consumption using quantile regression, decision tree and artificial neural network. Energy 2022, 250, 123856. [Google Scholar] [CrossRef]
- Zhao, D.; Zhong, M.; Zhang, X.; Su, X. Energy consumption predicting model of VRV (Variable refrigerant volume) system in office buildings based on data mining. Energy 2016, 102, 660–668. [Google Scholar] [CrossRef]
- Panklib, K.; Prakasvudhisarn, C.; Khummongkol, D. Electricity consumption forecasting in Thailand using an artificial neural network and multiple linear regression. Energy Sources Part B Econ. Plan. Policy 2015, 10, 427–434. [Google Scholar] [CrossRef]
- Chen, S.; Ren, Y.; Friedrich, D.; Yu, Z.; Yu, J. Prediction of office building electricity demand using artificial neural network by splitting the time horizon for different occupancy rates. Energy AI 2021, 5, 100093. [Google Scholar] [CrossRef]
- EFL. 2022 Annual Report; Energy Fiji Limited: Suva, Fiji, 2023. [Google Scholar]
- Joseph, L.P.; Prasad, R. Assessing the sustainable municipal solid waste (MSW) to electricity generation potentials in selected Pacific Small Island Developing States (PSIDS). J. Clean. Prod. 2020, 248, 119222. [Google Scholar] [CrossRef]
- Prasad, R.D.; Raturi, A. Low carbon alternatives and their implications for Fiji’s electricity sector. Util. Policy 2019, 56, 1–19. [Google Scholar] [CrossRef]
- Prasad, R.D. Long-Term Energy Planning for Fiji. Ph.D. Thesis, The University of the South Pacific, Suva, Fiji, 2020. [Google Scholar]
- GoF. Republic of Fiji National Adaptation Plan: A Pathway towards Climate Resilience. Available online: https://www4.unfccc.int/sites/NAPC/Documents/Parties/National%20Adaptation%20Plan_Fiji.pdf (accessed on 24 March 2021).
- GoF. Fiji’s Updated Nationally Determined Contribution; Government of Fiji. Available online: https://www4.unfccc.int/sites/ndcstaging/PublishedDocuments/Fiji%20First/Republic%20of%20Fiji%27s%20Updated%20NDC%2020201.pdf (accessed on 17 December 2021).
- Siwatibau, S. Urban Energy in Fiji: A Survey of Suva’s Household, Industrial, and Commercial Sectors; International Development Research Centre: Ottawa, ON, Canada, 1987; Available online: https://idl-bnc-idrc.dspacedirect.org/bitstream/handle/10625/9494/IDL-9494.pdf?sequence=1 (accessed on 20 January 2022).
- Prasad, R.D.; Raturi, A. Grid electricity for Fiji islands: Future supply options and assessment of demand trends. Energy 2017, 119, 860–871. [Google Scholar] [CrossRef]
- MEHA. Statistics. Ministry of Education, Heritage and Arts. Available online: https://www.education.gov.fj/statistics/ (accessed on 6 May 2021).
- Rinaldi, A.; Schweiker, M.; Iannone, F. On uses of energy in buildings: Extracting influencing factors of occupant behaviour by means of a questionnaire survey. Energy Build. 2018, 168, 298–308. [Google Scholar] [CrossRef]
- Groves, R.M.; Fowler, F.J., Jr.; Couper, M.P.; Lepkowski, J.M.; Singer, E.; Tourangeau, R. Survey Methodology; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 561. [Google Scholar]
- Zhou, T.; Luo, X.; Liu, X.; Liu, G.; Li, N.; Sun, Y.; Xing, M.; Liu, J. Analysis of the influence of the stay-at-home order on the electricity consumption in Chinese university dormitory buildings during the COVID-19 pandemic. Energy Build. 2022, 277, 112582. [Google Scholar] [CrossRef]
- Al Qadi, S.; Sodagar, B.; Elnokaly, A. Estimating the heating energy consumption of the residential buildings in Hebron, Palestine. J. Clean. Prod. 2018, 196, 1292–1305. [Google Scholar] [CrossRef]
- Bennett, D.A. How can I deal with missing data in my study? Aust. N. Z. J. Public Health 2001, 25, 464–469. [Google Scholar] [CrossRef] [PubMed]
- Carpino, C.; Fajilla, G.; Gaudio, A.; Mora, D.; Simone, M.D. Application of survey on energy consumption and occupancy in residential buildings. An experience in Southern Italy. Energy Procedia 2018, 148, 1082–1089. [Google Scholar] [CrossRef]
- Troup, L.; Phillips, R.; Eckelman, M.J.; Fannon, D. Effect of window-to-wall ratio on measured energy consumption in US office buildings. Energy Build. 2019, 203, 109434. [Google Scholar] [CrossRef]
- Im, H.; Srinivasan, R.; Fathi, S. Building energy use prediction owing to climate change: A case study of a university campus. In Proceedings of the 1st ACM International Workshop on Urban Building Energy Sensing, Controls, Big Data Analysis, and Visualization, New York, NY, USA, 13–14 November 2019; pp. 43–50. [Google Scholar]
- Wang, Y.; Wang, F.; Wang, H. Heating Energy Consumption Questionnaire and Statistical Analysis of Rural Buildings in China. Procedia Eng. 2016, 146, 380–385. [Google Scholar] [CrossRef]
- Washburn, A.; Matsumoto, S.; Riek, L.D. Trust-aware control in proximate human-robot teaming. In Trust in Human-Robot Interaction; Elsevier: Amsterdam, The Netherlands, 2021; pp. 353–377. [Google Scholar]
- Shao, M.; Wang, X.; Bu, Z.; Chen, X.; Wang, Y. Prediction of energy consumption in hotel buildings via support vector machines. Sustain. Cities Soc. 2020, 57, 102128. [Google Scholar] [CrossRef]
- Veiga, R.K.; Veloso, A.C.; Melo, A.P.; Lamberts, R. Application of machine learning to estimate building energy use intensities. Energy Build. 2021, 249, 111219. [Google Scholar] [CrossRef]
- SurveyMonkey. Margin of Error Calculator, Formula, and Examples. Available online: https://www.surveymonkey.com/mp/margin-of-error-calculator/ (accessed on 20 March 2024).
- Amber, K.P.; Aslam, M.W.; Mahmood, A.; Kousar, A.; Younis, M.Y.; Akbar, B.; Chaudhary, G.Q.; Hussain, S.K. Energy Consumption Forecasting for University Sector Buildings. Energies 2017, 10, 1579. [Google Scholar] [CrossRef]
- Osborne, J.W.; Waters, E. Four assumptions of multiple regression that researchers should always test. Pract. Assess. Res. Eval. 2002, 8, 2. [Google Scholar] [CrossRef]
- Attoue, N.; Shahrour, I.; Younes, R. Smart building: Use of the artificial neural network approach for indoor temperature forecasting. Energies 2018, 11, 395. [Google Scholar] [CrossRef]
- Zeng, A.; Liu, S.; Yu, Y. Comparative study of data driven methods in building electricity use prediction. Energy Build. 2019, 194, 289–300. [Google Scholar] [CrossRef]
- Sharp, T. Energy benchmarking in commercial office buildings. In Proceedings of the ACEEE, Pacific Grove, CA, USA, 25 August 1996; pp. 321–329. [Google Scholar]
- Smith, G. Step away from stepwise. J. Big Data 2018, 5, 1–12. [Google Scholar] [CrossRef]
- Islam, M.S.; Rayhan, M.A.I.; Mojumder, T.H. Behavioral factors underlying energy consumption pattern: A cross-sectional study on industrial sector of Bangladesh. Heliyon 2022, 8, e11523. [Google Scholar] [CrossRef]
- C3.ai. Glossary. Available online: https://c3.ai/glossary/data-science/root-mean-square-error-RMSE/#:~:text=Root%20mean%20square%20error%20or,true%20values%20using%20Euclidean%20distance (accessed on 30 June 2023).
- Litardo, J.; Hidalgo-Leon, R.; Soriano, G. Energy Performance and Benchmarking for University Classrooms in Hot and Humid Climates. Energies 2021, 14, 7013. [Google Scholar] [CrossRef]
- Yuan, Y.; Gao, L.; Zeng, K.; Chen, Y. Space-Level air conditioner electricity consumption and occupant behavior analysis on a university campus. Energy Build. 2023, 300, 113646. [Google Scholar] [CrossRef]
- Dimoudi, A.; Kostarela, P. Energy monitoring and conservation potential in school buildings in the C′ climatic zone of Greece. Renew. Energy 2009, 34, 289–296. [Google Scholar] [CrossRef]
- Lourenço, P.; Pinheiro, M.D.; Heitor, T. Light use patterns in Portuguese school buildings: User comfort perception, behaviour and impacts on energy consumption. J. Clean. Prod. 2019, 228, 990–1010. [Google Scholar] [CrossRef]
- Pietrapertosa, F.; Tancredi, M.; Salvia, M.; Proto, M.; Pepe, A.; Giordano, M.; Afflitto, N.; Sarricchio, G.; Di Leo, S.; Cosmi, C. An educational awareness program to reduce energy consumption in schools. J. Clean. Prod. 2021, 278, 123949. [Google Scholar] [CrossRef]
- AlFaris, F.; Juaidi, A.; Manzano-Agugliaro, F. Improvement of efficiency through an energy management program as a sustainable practice in schools. J. Clean. Prod. 2016, 135, 794–805. [Google Scholar] [CrossRef]
- SPC. Framework for Energy Security and Resilience in the Pacific (FESRIP) 2021–2030; Pacific Community: Noumea, New Caledonia, 2021. [Google Scholar]
- Dumitru, C.; Maria, V. Advantages and Disadvantages of Using Neural Networks for Predictions. Ovidius Univ. Ann. Ser. Econ. Sci. 2013, 13, 444. [Google Scholar]
- Mijwel, M.M. Artificial Neural Networks Advantages and Disadvantages. 2018. Available online: https://www.linkedin.com/pulse/artificial-neural-networks-advantages-disadvantages-maad-m-mijwel (accessed on 10 July 2023).
- Zhang, D.; Bluyssen, P.M. Energy consumption, self-reported teachers’ actions and children’s perceived indoor environmental quality of nine primary school buildings in the Netherlands. Energy Build. 2021, 235, 110735. [Google Scholar] [CrossRef]
- Barbosa, F.C.; de Freitas, V.P.; Almeida, M. School building experimental characterization in Mediterranean climate regarding comfort, indoor air quality and energy consumption. Energy Build. 2020, 212, 109782. [Google Scholar] [CrossRef]
- Mariano-Hernández, D.; Hernández-Callejo, L.; Zorita-Lamadrid, A.; Duque-Pérez, O.; Santos García, F. A review of strategies for building energy management system: Model predictive control, demand side management, optimization, and fault detect & diagnosis. J. Build. Eng. 2021, 33, 101692. [Google Scholar] [CrossRef]
- Li, Z.; Su, S.; Jin, X.; Xia, M.; Chen, Q.; Yamashita, K. Stochastic and distributed optimal energy management of active distribution network with integrated office buildings. CSEE J. Power Energy Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Yoon, S.-H.; Kim, S.-Y.; Park, G.-H.; Kim, Y.-K.; Cho, C.-H.; Park, B.-H. Multiple power-based building energy management system for efficient management of building energy. Sustain. Cities Soc. 2018, 42, 462–470. [Google Scholar] [CrossRef]
- Mokhtari, R.; Arabkoohsar, A. Feasibility study and multi-objective optimization of seawater cooling systems for data centers: A case study of Caspian Sea. Sustain. Energy Technol. Assess. 2021, 47, 101528. [Google Scholar] [CrossRef]
- Schibuola, L.; Tambani, C. Performance assessment of seawater cooled chillers to mitigate urban heat island. Appl. Therm. Eng. 2020, 175, 115390. [Google Scholar] [CrossRef]
- Li, X.; Wong, W.; Lamoureux, E.L.; Wong, T.Y. Are linear regression techniques appropriate for analysis when the dependent (outcome) variable is not normally distributed? Investig. Ophthalmol. Vis. Sci. 2012, 53, 3082–3083. [Google Scholar] [CrossRef]
- OU. Assumptions of Multiple Regression. The Open University. 2022. Available online: https://www.open.ac.uk/socialsciences/spsstutorial/files/tutorials/assumptions.pdf (accessed on 3 October 2022).



| ED | Age | SN | FA | CN | BN | LGT | AC | TN | |
|---|---|---|---|---|---|---|---|---|---|
| ED | 1.000 | 0.003 | 0.735 | 0.601 | 0.708 | 0.216 | 0.793 | 0.746 | 0.854 |
| Age | 0.003 | 1.000 | 0.050 | −0.076 | −0.037 | −0.175 | −0.106 | −0.070 | −0.068 |
| SN | 0.735 | 0.050 | 1.000 | 0.509 | 0.884 | 0.196 | 0.672 | 0.643 | 0.828 |
| FA | 0.601 | −0.076 | 0.509 | 1.000 | 0.573 | 0.150 | 0.495 | 0.543 | 0.534 |
| CN | 0.708 | −0.037 | 0.884 | 0.573 | 1.000 | 0.220 | 0.657 | 0.697 | 0.853 |
| BN | 0.216 | −0.175 | 0.196 | 0.150 | 0.220 | 1.000 | 0.218 | 0.138 | 0.304 |
| LGT | 0.793 | −0.106 | 0.672 | 0.495 | 0.657 | 0.218 | 1.000 | 0.699 | 0.755 |
| AC | 0.746 | −0.070 | 0.643 | 0.543 | 0.697 | 0.138 | 0.699 | 1.000 | 0.763 |
| TN | 0.854 | −0.068 | 0.828 | 0.534 | 0.853 | 0.304 | 0.755 | 0.763 | 1.000 |
| Method | Number of Cases | Input Variables, IVs | Model Summary | ANOVA | ||||
|---|---|---|---|---|---|---|---|---|
| Equation Number | R2 | Durbin–Watson | ε | F—Ratio Regression df Residual df | p-Value | |||
| Enter | 55 | IVs: logLGT, logSN, logAC, and logFA | (6) | 0.733 | 1.666 | 0.23903 | 34.366 4 50 | 0.000 |
| Backward | 55 | IVs: logLGT, logSN, and logAC | (7) | 0.733 | 1.676 | 0.23697 | 46.579 3 51 | 0.000 |
| Stepwise | 55 | IV: logLGT | (8a) | 0.624 | 0.27571 | 87.908 1 53 | 0.000 | |
| 55 | IVs: logLGT, logSN | (8b) | 0.705 | 0.24659 | 62.076 2 52 | 0.000 | ||
| 55 | IVs: logLGT, logSN, and logAC | (8c) | 0.733 | 1.676 | 0.23697 | 46.579 3 51 | 0.000 | |
| Enter | 55 | IV: logSN | (9) | 0.504 | 1.840 | 0.31665 | 53.825 1 53 | 0.000 |
| 55 | IVs: logSN and logFA | (10) | 0.587 | 1.736 | 0.29166 | 36.959 2 52 | 0.000 | |
| 55 | IVs: logSN, logFA, and logLGT | (11) | 0.706 | 1.502 | 0.24843 | 40.848 3 51 | 0.000 | |
| Equation | Max Cook’s Distance | β0 | β1 (logSN) | β2 (logFA) | β3 (logAC) | β4 (logLGT) | |
|---|---|---|---|---|---|---|---|
| Enter | |||||||
| Unstandardized | (6) | 1.609 | 0.423 | 0.045 | 0.272 | 0.571 | |
| t-stat | 5.116 | 2.929 | 0.353 | 2.256 | 3.447 | ||
| p-value | 0.000 | 0.005 | 0.725 | 0.028 | 0.001 | ||
| Standardized coefficient Beta | 0.263 | 0.113 | 0.236 | 0.390 | |||
| Cook’s distance | 0.191 | ||||||
| Backward | |||||||
| Unstandardized | (7) | 1.646 | 0.443 | 0.275 | 0.600 | ||
| t-stat | 5.616 | 3.364 | 2.303 | 4.232 | |||
| p-value | 0.000 | 0.001 | 0.025 | 0.000 | |||
| Standardized coefficient Beta | 0.316 | 0.226 | 0.447 | ||||
| Cook’s distance | 0.233 | ||||||
| Stepwise | |||||||
| Unstandardized | (8a) | 2.096 | 1.060 | ||||
| t-stat | 10.639 | 9.376 | |||||
| p-value | 0.000 | 0.000 | |||||
| Standardized coefficient Beta | 0.790 | ||||||
| Unstandardized | (8b) | 1.328 | 0.506 | 0.762 | |||
| t-stat | 4.937 | 3.776 | 5.949 | ||||
| p-value | 0.000 | 0.000 | 0.000 | ||||
| Standardized coefficient Beta | 0.361 | 0.568 | |||||
| Unstandardized | (8c) | 1.646 | 0.443 | 0.275 | 0.600 | ||
| t-stat | 5.616 | 3.364 | 2.303 | 4.232 | |||
| p-value | 0.000 | 0.001 | 0.025 | 0.000 | |||
| Standardized coefficient Beta | 0.316 | 0.226 | 0.447 | ||||
| Cook’s distance | 0.233 | ||||||
| Enter | |||||||
| Unstandardized | (9) | 1.397 | 0.996 | ||||
| t-stat | 4.047 | 7.337 | |||||
| p-value | 0.000 | 0.000 | |||||
| Standardized coefficient Beta | 0.710 | ||||||
| Cook’s distance | 0.167 | ||||||
| Enter | |||||||
| Unstandardized | (10) | 1.056 | 0.626 | 0.410 | |||
| t-stat | 3.154 | 3.695 | 3.236 | ||||
| p-value | 0.003 | 0.001 | 0.002 | ||||
| Standardized coefficient Beta | 0.446 | 0.391 | |||||
| Cook’s distance | 0.170 | ||||||
| Enter | |||||||
| Unstandardized | (11) | 1.279 | 0.477 | 0.063 | 0.719 | ||
| t-stat | 4.420 | 3.223 | 0.479 | 4.546 | |||
| p-value | 0.000 | 0.002 | 0.634 | 0.000 | |||
| Standardized coefficient Beta | 0.340 | 0.060 | 0.536 | ||||
| Cook’s distance | 0.142 |
| Model | Model No. | Total Data Points | Inputs | Neurons in Hidden Layer | Output Variable | R2 | RMSE |
|---|---|---|---|---|---|---|---|
| MLR | 75 | logSN, logAC, logLGT | logED | 0.7522 | 0.2248 | ||
| ANN | 12.1 | 75 | logSN, logAC, logLGT | 4 | logED | 0.7440 | 0.2285 |
| ANN | 12.2 | 75 | logSN, logAC, logLGT, logFA | 3 | logED | 0.7541 | 0.2240 |
| ANN | 12.3 | 75 | ST, SC, logLGT, logFA, logAC, logSN, Age | 3 | logED | 0.7195 | 0.2392 |
| ANN | 12.4 | 75 | ST, SC, logLGT, logFA, logAC, logSN | 2 | logED | 0.8400 | 0.1807 |
| ANN | 12.5 | 75 | ST, SC, logLGT, logAC, logSN, Age | 5 | logED | 0.8228 | 0.1902 |
| ANN | 12.6 | 75 | ST, SC, logLGT, logAC, logSN | 4 | logED | 0.7769 | 0.2133 |
| ANN | 13.1 | 75 | ST, SC, LGT, FA, AC, SN, Age | 3 | ED | 0.8398 | 6203.7 |
| ANN | 13.2 | 75 | ST, SC, LGT, FA, AC, SN | 3 | ED | 0.8180 | 6612.2 |
| ANN | 13.3 | 75 | ST, SC, LGT, AC, SN | 4 | ED | 0.8026 | 6886.2 |
| ANN | 13.4 | 75 | ST, SC, LGT, AC, SN, Age | 3 | ED | 0.8365 | 6266.9 |
| ANN | 14.1 | 100 | ST, SC, LGT, FA, AC, SN, Age, TN, FN, CN, BN | 5 | ED | 0.8905 | 280.51 |
| ANN | 14.2 | 100 | ST, SC, LGT, FA, AC, SN, Age, TN, FN, CN, BN, BT | 4 | ED | 0.9350 | 150.33 |
| ANN | 14.3 | 100 | ST, SC, LGT, FA, AC, Age, TN, FN, CN, BN, BT | 2 | ED | 0.9147 | 105.73 |
| ANN | 14.4 | 100 | SC, LGT, FA, AC, SN, Age, TN, BT, FN, CN, BN | 3 | ED | 0.8856 | 170.37 |
| ANN | 14.5 | 100 | ST, SC, LGT, FA, AC, SN, Age, TN, BT, FN, CN | 2 | ED | 0.9196 | 86.231 |
| ANN | 14.6 | 100 | ST, SC, LGT, FA, AC, Age, TN, FN, CN, BN | 2 | ED | 0.9467 | 36.769 |
| ANN | 14.7 | 100 | ST, SC, LGT, FA, Age, TN, FN, CN, BN | 5 | ED | 0.9526 | 109.26 |
| ANN | 14.8 | 100 | ST, SC, LGT, FA, AC, SN, TN, BT, FN, CN, BN | 6 | ED | 0.9282 | 233.00 |
| ANN | 14.9 | 100 | ST, SC, LGT, FA, TN, FN, CN, BN | 4 | ED | 0.9528 | 59.358 |
| ANN | 14.10 | 100 | ST, SC, LGT, FA, Age, TN, FN, CN | 4 | ED | 0.9261 | 4.1990 |
| ANN | 14.11 | 100 | ST, SC, LGT, FA, AC, Age, TN, FN, CN | 2 | ED | 0.9541 | 447.56 |
| ANN | 14.12 | 100 | LGT, FA, SN, AC | 4 | ED | 0.8576 | 356.17 |
| ANN | 14.13 | 100 | LGT, FA, AC, SN, Age, TN, FN, CN, BN, BT | 3 | ED | 0.9412 | 124.55 |
| ANN | 14.14 | 100 | LGT, FA, AC, SN, Age, TN, FN, CN | 4 | ED | 0.9215 | 326.66 |
| ANN | 14.15 | 100 | ST, SC, LGT, FA, AC, SN, Age, TN, FN, CN | 3 | ED | 0.9000 | 66.799 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prasad, R.D. School Electricity Consumption in a Small Island Country: The Case of Fiji. Energies 2024, 17, 1727. https://doi.org/10.3390/en17071727
Prasad RD. School Electricity Consumption in a Small Island Country: The Case of Fiji. Energies. 2024; 17(7):1727. https://doi.org/10.3390/en17071727
Chicago/Turabian StylePrasad, Ravita D. 2024. "School Electricity Consumption in a Small Island Country: The Case of Fiji" Energies 17, no. 7: 1727. https://doi.org/10.3390/en17071727
APA StylePrasad, R. D. (2024). School Electricity Consumption in a Small Island Country: The Case of Fiji. Energies, 17(7), 1727. https://doi.org/10.3390/en17071727






