Design of Broadband Doherty Power Amplifier Based on Misaligned Current Phase
Abstract
:1. Introduction
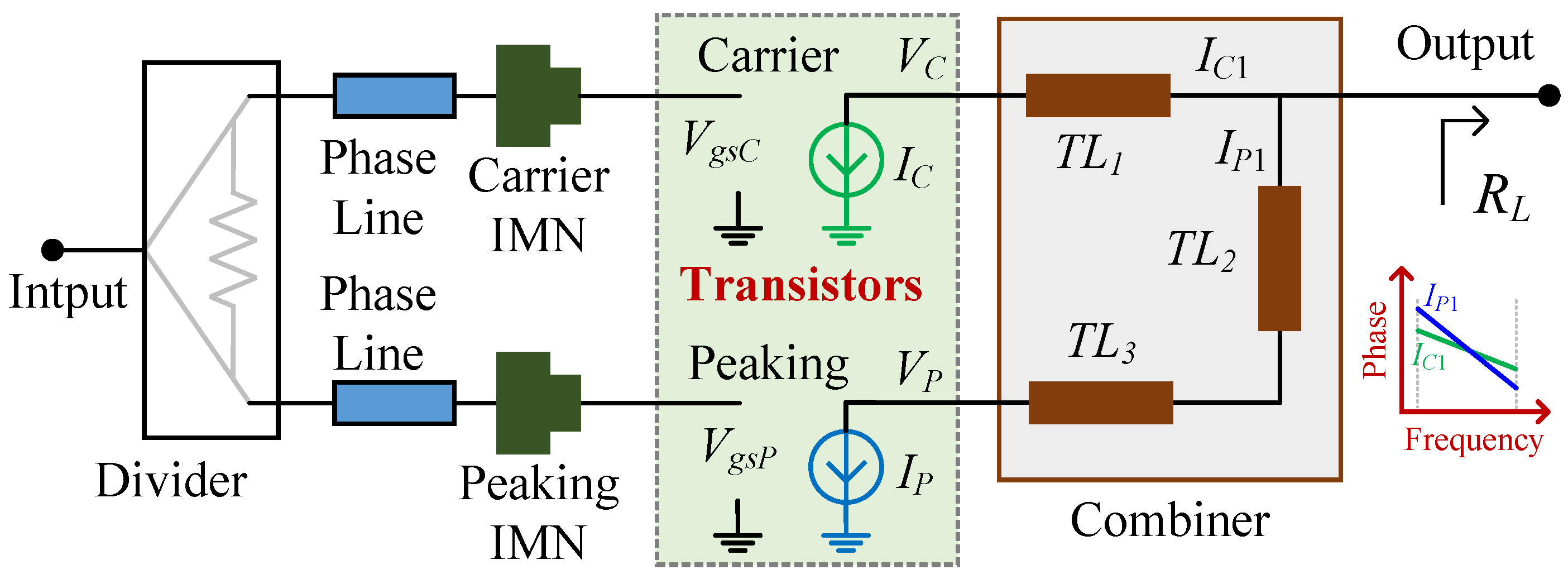
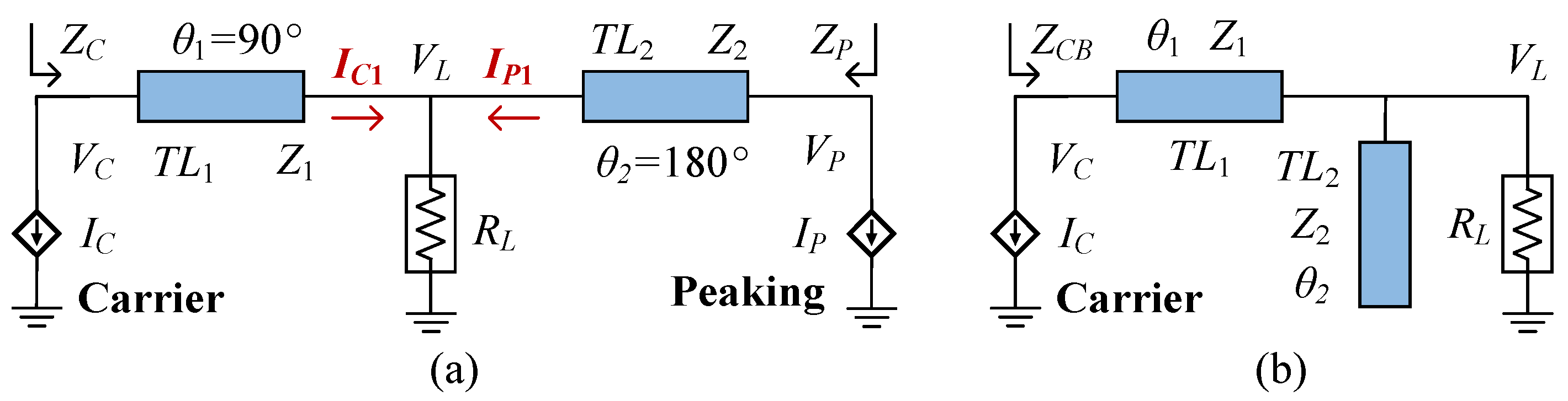
2. Theoretical Analysis
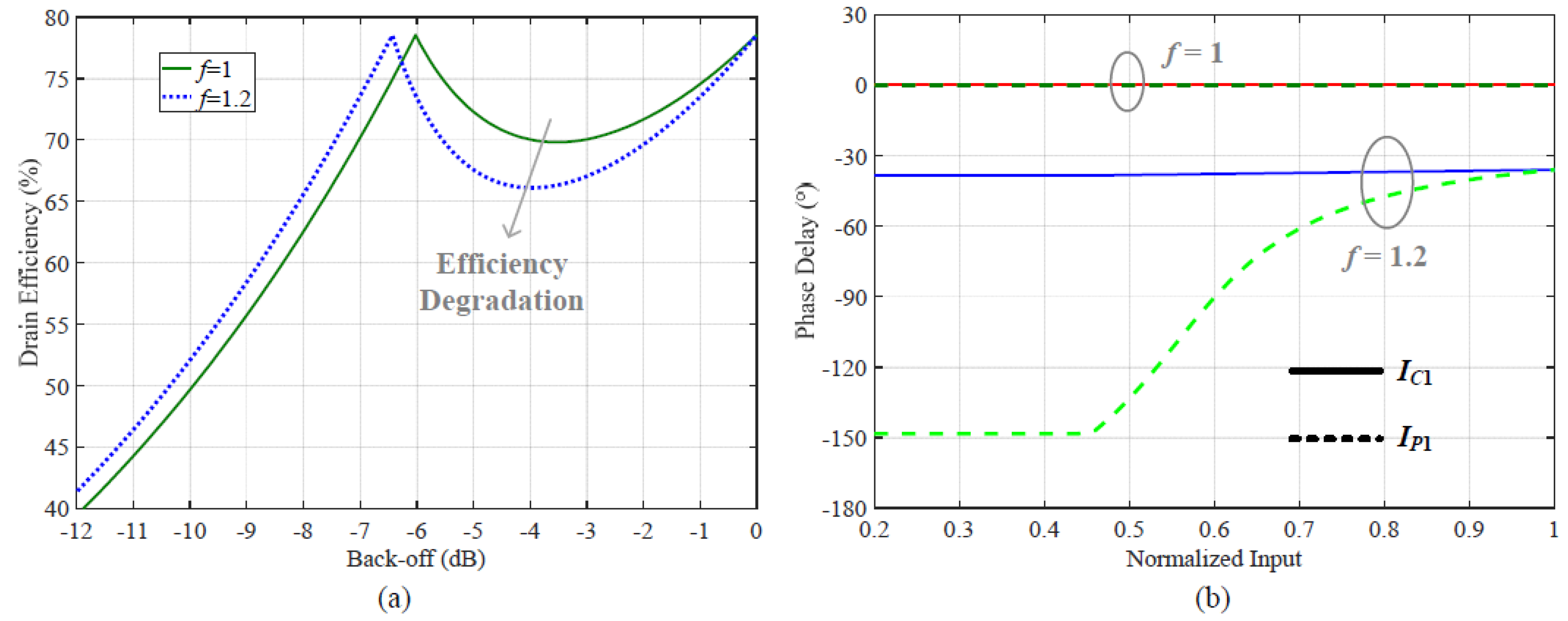
2.1. Load Modulation at Low Power Region
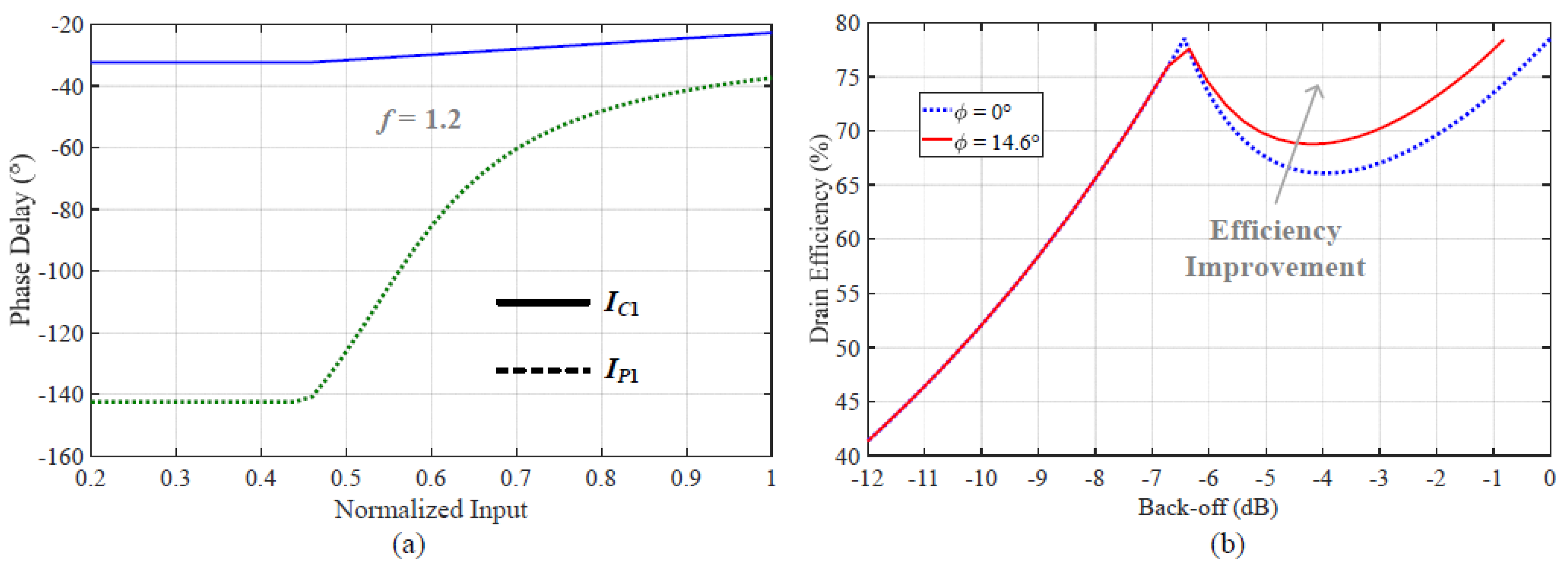
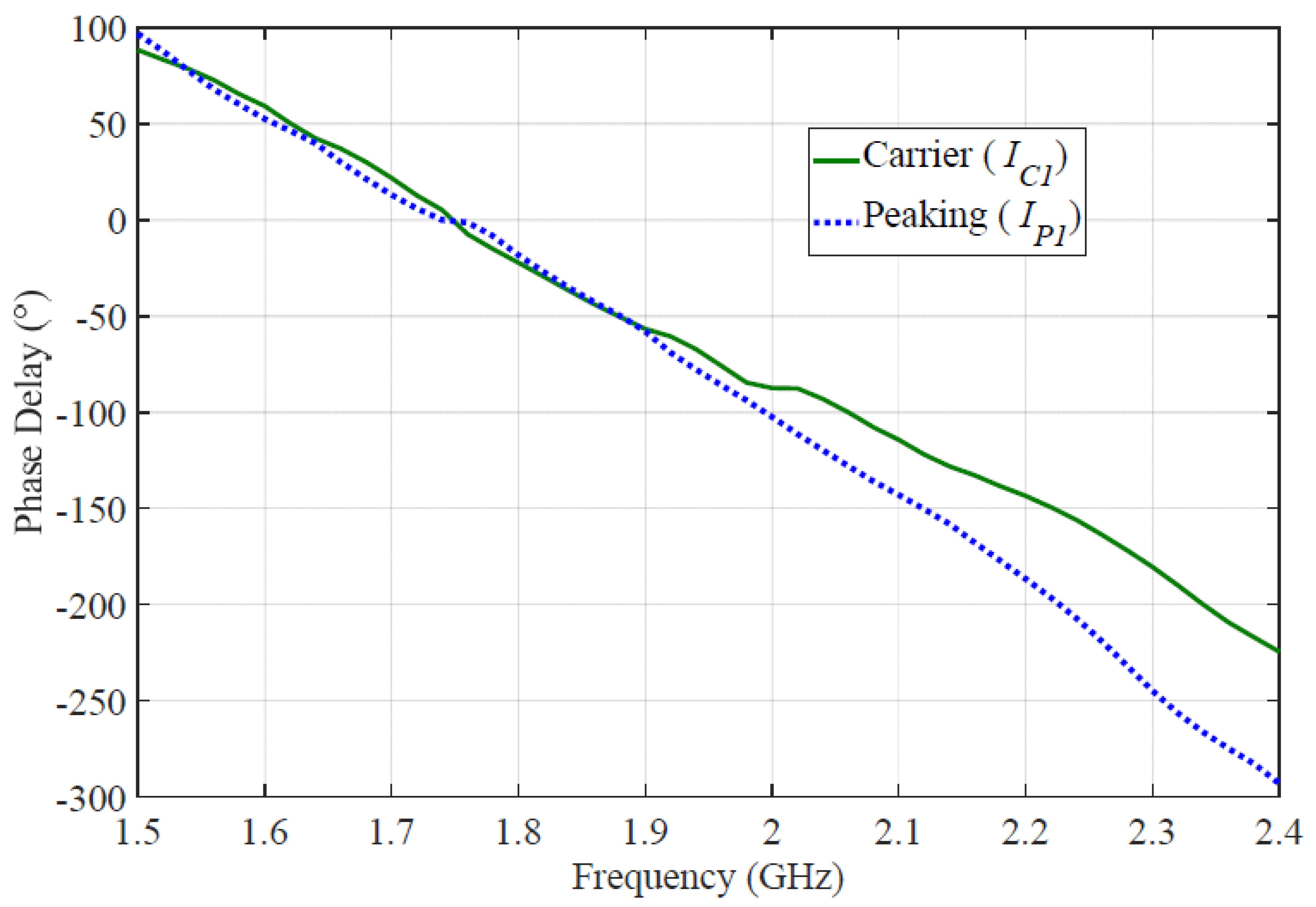
2.2. Drain Efficiency Analysis
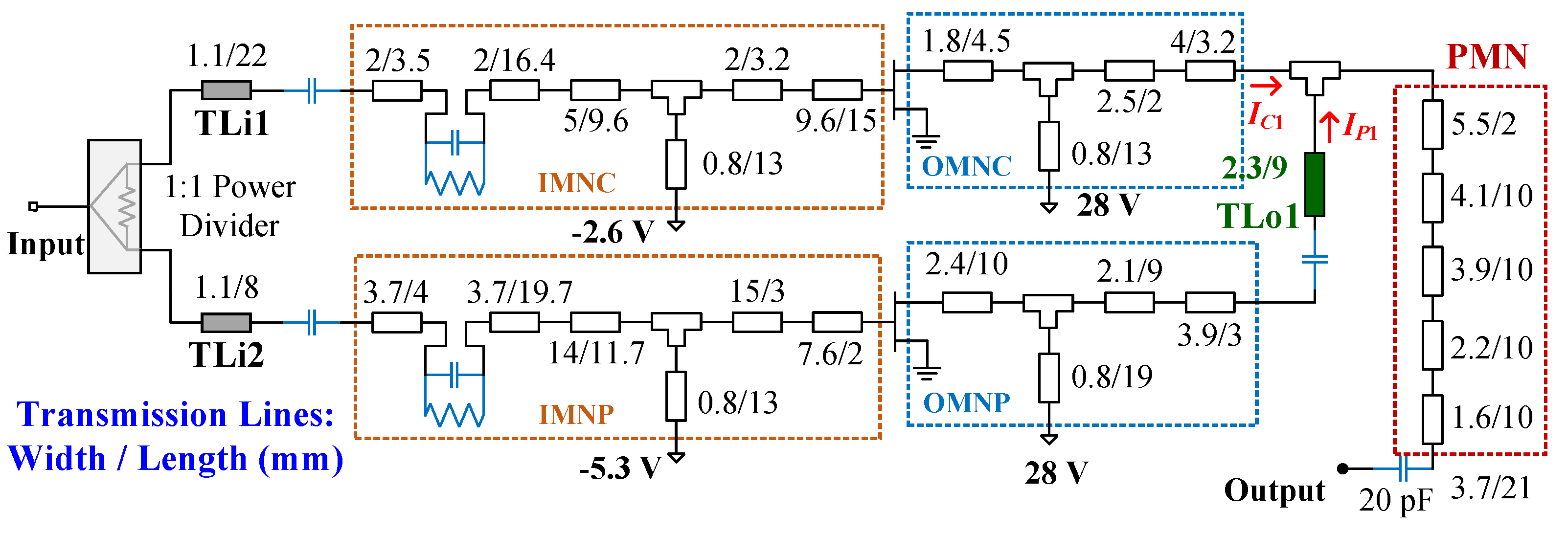
3. Construction of a Broadband DPA
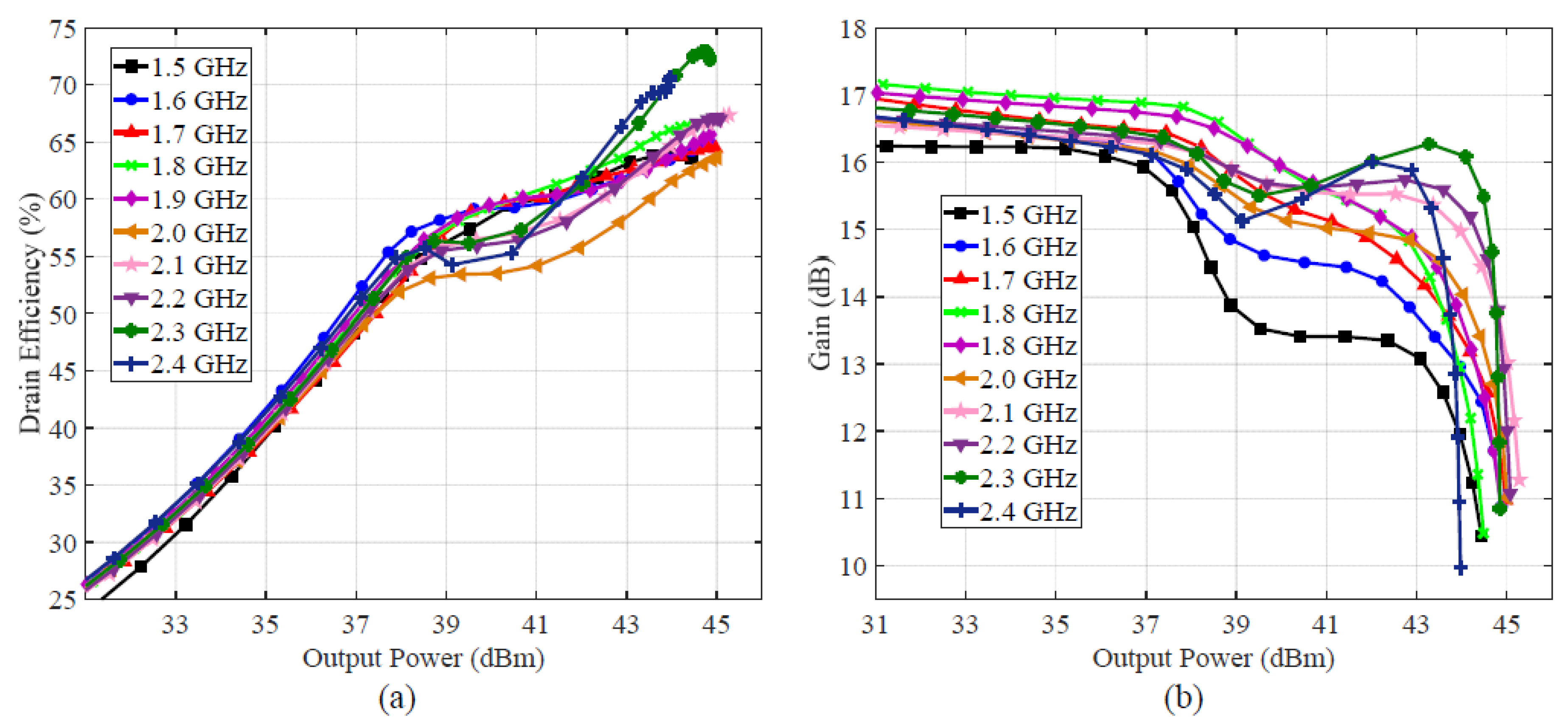
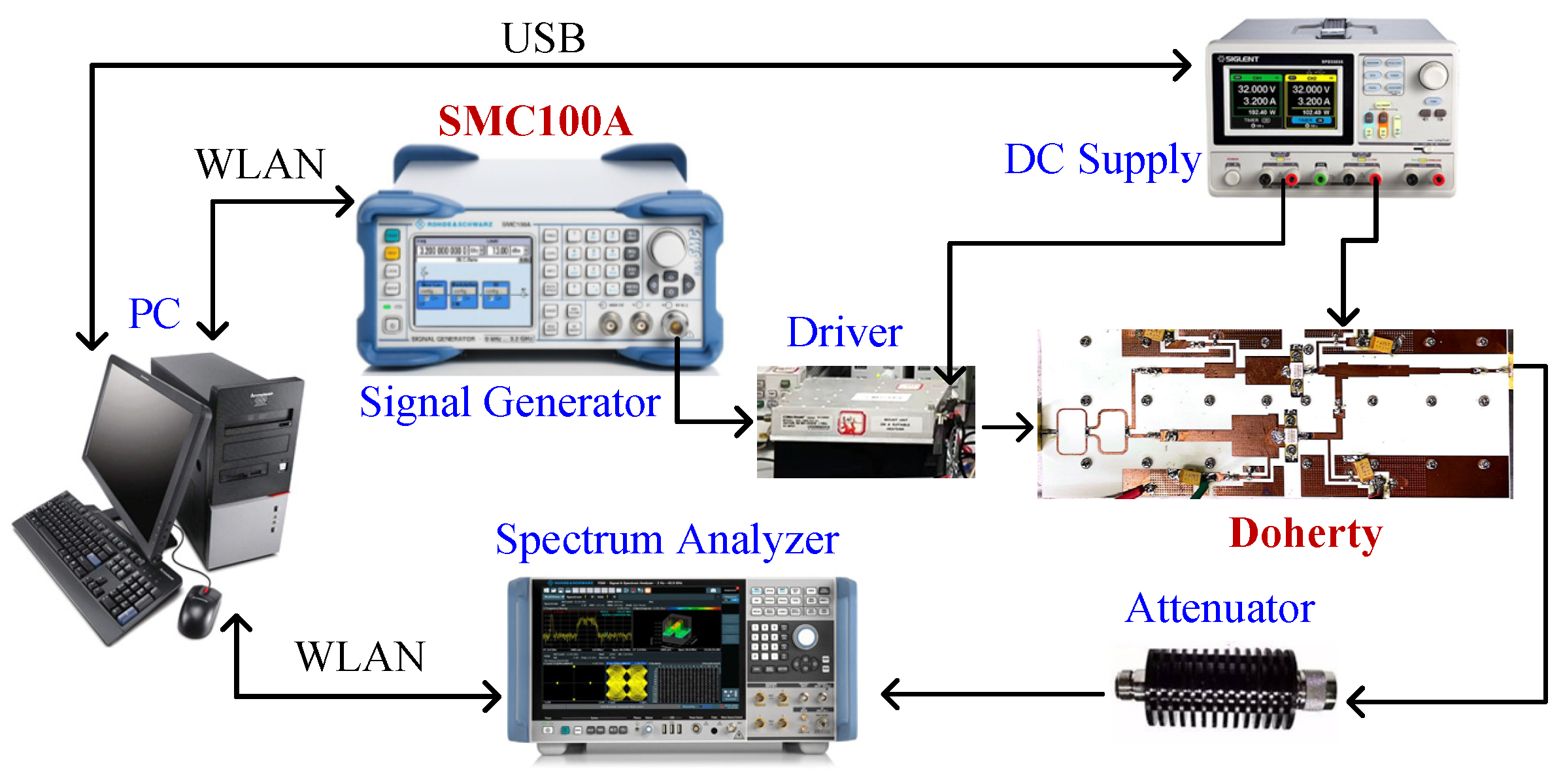
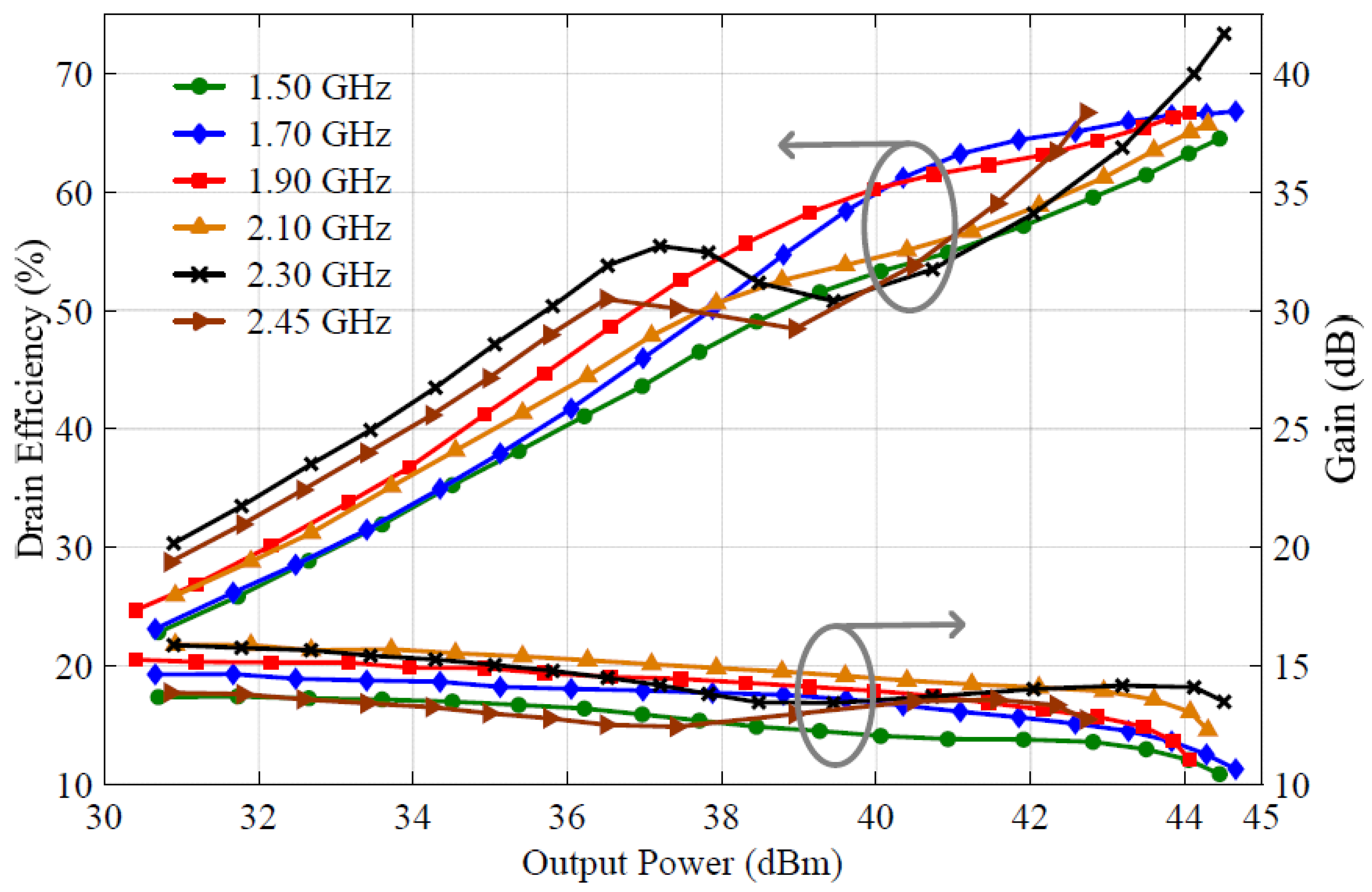
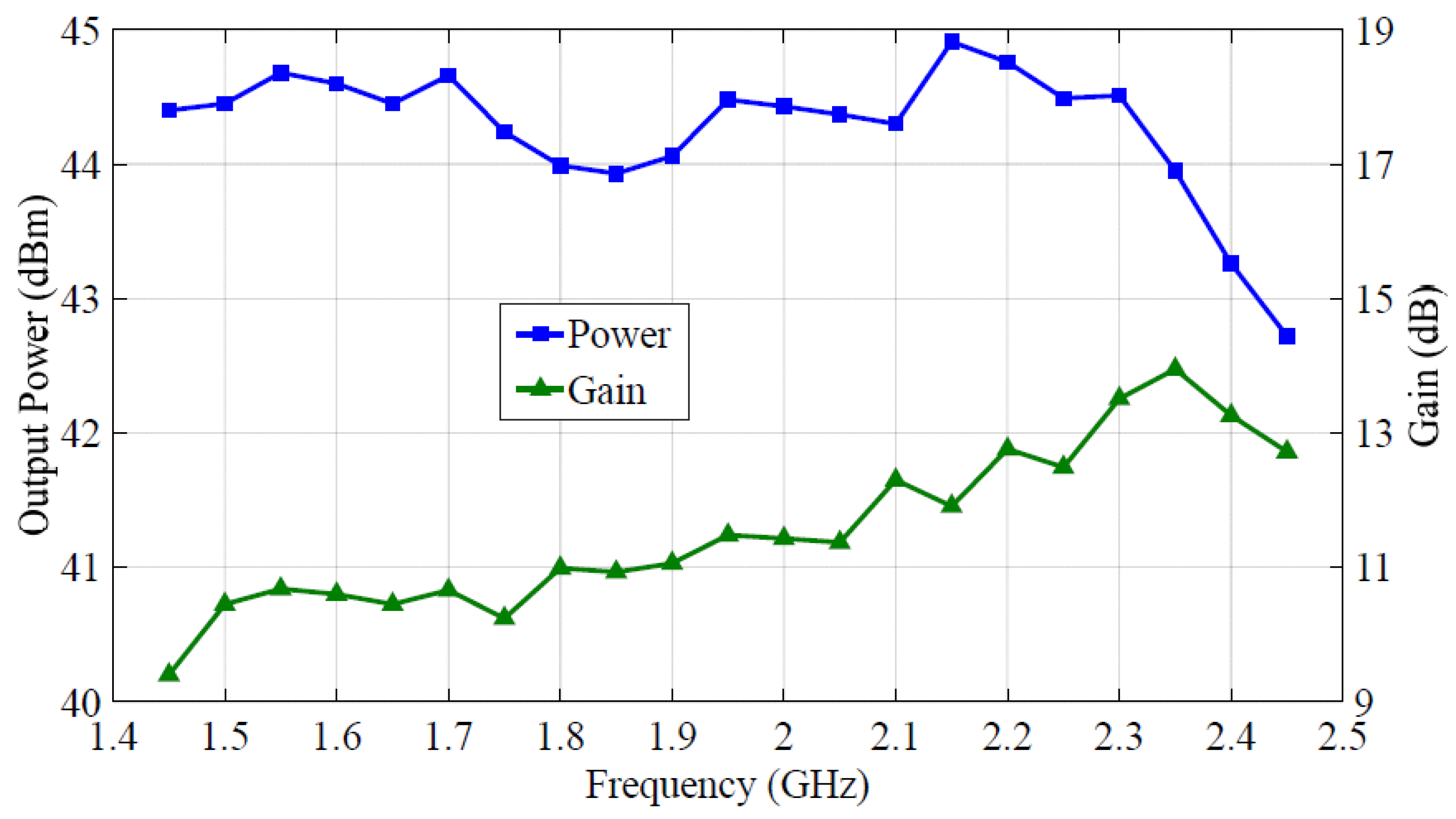
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chataut, R.; Nankya, M.; Akl, R. 6G Networks and the AI Revolution—Exploring Technologies, Applications, and Emerging Challenges. Sensors 2024, 24, 1888. [Google Scholar] [CrossRef] [PubMed]
- Carcangiu, S.; Fanni, A.; Montisci, A. A closed form selected mapping algorithm for PAPR reduction in OFDM multicarrier transmission. Energies 2022, 15, 1938. [Google Scholar] [CrossRef]
- Yang, K.; Yang, R.; Zhang, P.; Shi, W.; Hu, C.; Shi, W. Development review of highly efficient sequential power amplifier with extended back-off range for broadband application. Energies 2024, 17, 161. [Google Scholar] [CrossRef]
- Popovic, Z. Amping up the PA for 5G: Efficient GaN power amplifiers with dynamic supplies. IEEE Microw. Mag. 2017, 18, 137–149. [Google Scholar] [CrossRef]
- Nasri, A.; Estebsari, M.; Toofan, S.; Piacibello, A.; Pirola, M.; Camarchia, V.; Ramella, C. Design of a Wideband Doherty Power Amplifier with High Efficiency for 5G Application. Electronics 2021, 10, 873. [Google Scholar] [CrossRef]
- Ramella, C.; Piacibello, A.; Quaglia, R.; Camarchia, V.; Pirola, M. High Efficiency Power Amplifiers for Modern Mobile Communications: The Load-Modulation Approach. Electronics 2017, 6, 96. [Google Scholar] [CrossRef]
- Martin, D.N.; Barton, T.W. Inphasing signal component separation for an X-Band Outphasing power amplifier. IEEE Trans. Microw. Theory Tech. 2021, 69, 1661–1674. [Google Scholar] [CrossRef]
- Choi, H. A Doherty Power Amplifier for Ultrasound Instrumentation. Sensors 2023, 23, 2406. [Google Scholar] [CrossRef] [PubMed]
- Bathich, K.; Markos, A.Z.; Boeck, G. Frequency response analysis and bandwidth extension of the Doherty amplifier. IEEE Trans. Microw. Theory Tech. 2011, 59, 934–944. [Google Scholar] [CrossRef]
- Cidronali, A.; Maddio, S.; Giovannelli, N.; Collodi, G. Frequency analysis and multiline implementation of compensated impedance inverter for wideband Doherty high-power amplifier design. IEEE Trans. Microw. Theory Tech. 2016, 64, 1359–1372. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, Z.; Gu, C.; Xuan, X. A High-Relative-Bandwidth Doherty Power Amplifier with Modified Load Modulation Network for Wireless Communications. Sensors 2023, 23, 2767. [Google Scholar] [CrossRef] [PubMed]
- Darraji, R.; Bhaskar, D.; Sharma, T.; Helaoui, M.; Mousavi, P.; Ghannouchi, F.M. Generalized theory and design methodology of wideband Doherty amplifiers applied to the realization of an octave-bandwidth prototype. IEEE Trans. Microw. Theory Tech. 2017, 65, 3014–3023. [Google Scholar] [CrossRef]
- Li, M.; Pang, J.; Li, Y.; Zhu, A. Bandwidth Enhancement of Doherty Power Amplifier Using Modified Load Modulation Network. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 1824–1834. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Chan, W.S.; Feng, W.; Fang, X.; Sharma, T.; Chen, S. Broadband Doherty Power Amplifier Based on Coupled Phase Compensation Network. IEEE Trans. Microw. Theory Tech. 2022, 70, 210–221. [Google Scholar] [CrossRef]
- Xu, Y.; Pang, J.; Wang, X.; Zhu, A. Enhancing Bandwidth and Back-Off Range of Doherty Power Amplifier With Modified Load Modulation Network. IEEE Trans. Microw. Theory Tech. 2021, 69, 2291–2303. [Google Scholar] [CrossRef]
- Xu, J.X.; Chen, H.; Chen, W.; Zhang, X.Y. Broadband Doherty Power Amplifier Using Short Ended λ-4 Transmission Lines Based on the Analysis of Negative Characteristic Impedance. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 545–555. [Google Scholar] [CrossRef]
- Chen, X.; Chen, W. A novel broadband Doherty power amplifier with post-matching structure. In Proceedings of the 2012 Asia Pacific Microwave Conference (APMC), Kaohsiung, Taiwan, 4–7 December 2012; pp. 370–372. [Google Scholar] [CrossRef]
- Pang, J.; He, S.; Huang, C.; Dai, Z.; Peng, J.; You, F. A post-matching Doherty power amplifier employing low-order impedance inverters for broadband applications. IEEE Trans. Microw. Theory Tech. 2015, 63, 4061–4071. [Google Scholar] [CrossRef]
- Xia, J.; Yang, M.; Zhu, A. Improved Doherty amplifier design with minimum phase delay in output matching network for wideband application. IEEE Microw. Wirel. Components Lett. 2016, 26, 915–917. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Zheng, S.Y.; Chan, W.S.; Chen, S.; Ho, D. Broadband efficiency-enhanced mutually coupled harmonic postmatching Doherty power amplifier. IEEE Trans. Circuits Syst. Regul. Pap. 2017, 64, 1758–1771. [Google Scholar] [CrossRef]
- Chen, S.; Wang, G.; Cheng, Z.; Xue, Q. A bandwidth enhanced Doherty power amplifier with a compact output combiner. IEEE Microw. Wirel. Components Lett. 2016, 26, 434–436. [Google Scholar] [CrossRef]
- Shi, W.; He, S.; You, F.; Xie, H.; Naah, G.; Liu, Q.-A.; Li, Q. The Influence of the Output Impedances of Peaking Power Amplifier on Broadband Doherty Amplifiers. IEEE Trans. Microw. Theory Tech. 2017, 65, 3002–3013. [Google Scholar] [CrossRef]
- Xia, J.; Yang, M.; Guo, Y.; Zhu, A. A broadband high-efficiency Doherty power amplifier with integrated compensating reactance. IEEE Trans. Microw. Theory Tech. 2016, 64, 2014–2024. [Google Scholar] [CrossRef]
- Shi, W.; He, S.; Zhu, X.; Song, B.; Zhu, Z.; Naah, G.; Zhang, M. Broadband continuous-mode Doherty power amplifiers with noninfinity peaking impedance. IEEE Trans. Microw. Theory Tech. 2018, 66, 1034–1046. [Google Scholar] [CrossRef]
- Chen, X.; Chen, W.; Ghannouchi, F.M.; Feng, Z.; Liu, Y. A broadband Doherty power amplifier based on continuous-mode technology. IEEE Trans. Microw. Theory Tech. 2016, 64, 4505–4517. [Google Scholar] [CrossRef]
- Ghosh, S.; Rawat, K. Hybrid analog digital continuous class B/J mode for broadband Doherty power amplifiers. IEEE Access 2019, 7, 74986–74995. [Google Scholar] [CrossRef]
- Li, Y.; Fang, X.; Jundi, A.; Huang, H.; Boumaiza, S. Two-port network theory-based design method for broadband class J Doherty amplifiers. IEEE Access 2019, 7, 51028–51038. [Google Scholar] [CrossRef]
- Nasri, A.; Estebsari, M.; Toofan, S.; Piacibello, A.; Pirola, M.; Camarchia, V.; Ramella, C. Broadband Class-J GaN Doherty Power Amplifier. Electronics 2022, 11, 552. [Google Scholar] [CrossRef]
- Shi, W.; Shi, W.; Peng, J.; Feng, L.; Gao, Y.; He, S.; Yue, C.P. Design and Analysis of Continuous-Mode Doherty Power Amplifier With Second Harmonic Control. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2247–2251. [Google Scholar] [CrossRef]
- Giofrè, R.; Piazzon, L.; Colantonio, P.; Giannini, F. A closed-form design technique for ultra-wideband Doherty power amplifiers. IEEE Trans. Microw. Theory Tech. 2014, 62, 3414–3424. [Google Scholar] [CrossRef]
- Barakat, A.; Thian, M.; Fusco, V.; Bulja, S.; Guan, L. Toward a More Generalized Doherty Power Amplifier Design for Broadband Operation. IEEE Trans. Microw. Theory Tech. 2017, 65, 846–859. [Google Scholar] [CrossRef]
- Moreno Rubio, J.J.; Camarchia, V.; Pirola, M.; Quaglia, R. Design of an 87% Fractional Bandwidth Doherty Power Amplifier Supported by a Simplified Estimation Method. IEEE Trans. Microw. Theory Tech. 2018, 66, 1319–1327. [Google Scholar] [CrossRef]
- Yang, Z.; Yao, Y.; Li, M.; Jin, Y.; Li, T.; Dai, Z.; Tang, F.; Li, Z. Bandwidth extension of Doherty power amplifier using complex combining load with noninfinity peaking impedance. IEEE Trans. Microw. Theory Tech. 2019, 67, 765–777. [Google Scholar] [CrossRef]
- Park, Y.; Lee, J.; Jee, S.; Kim, S.; Kim, B. Gate Bias Adaptation of Doherty Power Amplifier for High Efficiency and High Power. IEEE Microw. Wirel. Compon. Lett. 2015, 25, 136–138. [Google Scholar] [CrossRef]
- Kalyan, R.; Rawat, K.; Koul, S.K. A Digitally Assisted Dual-Input Dual-Band Doherty Power Amplifier With Enhanced Efficiency and Linearity. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 297–301. [Google Scholar] [CrossRef]
- Fang, X.-H.; Liu, H.-Y.; Cheng, K.-K.M.; Boumaiza, S. Two-Way Doherty Power Amplifier Efficiency Enhancement by Incorporating Transistors’ Nonlinear Phase Distortion. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 168–170. [Google Scholar] [CrossRef]
- Zhong, K.; Dai, Z.; Xiao, F.; Gao, R.; Shi, W.; Pang, J.; Li, M. Design of dual-band Doherty power amplifier using a new phase compensation technique. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 1794–1798. [Google Scholar] [CrossRef]

| Ref., Year | Freq. (GHz) | BW. (GHz/%) | Pmax (dBm) | DE@Sat (%) | DE@OBO (%) | Gain@Sat (dB) |
|---|---|---|---|---|---|---|
| [5] 2021 | 2.8–3.6 | 1.2/25 | 43–44.2 | 62–76.5 | 44–56 | 8–13.5 |
| [11] 2023 | 1.0–2.5 | 1.5/86 | 43.9–44.5 | 63.7–71.6 | 45.2–53.7 | 9.6–10.3 |
| [13] 2020 | 2.80–3.55 | 0.75/23.6 | 43.0–45.0 | 66.0–78.0 | 50.0–60.6 | 6.5–8.1 * |
| [14] 2022 | 1.3–2.3 | 1.0/55.5 | 42.2–43.9 | 61.6–75.2 | 41.0–65.0 | 6.5–8.0 * |
| [23] 2016 | 1.7–2.8 | 1.1/49 | 44.0–44.5 | 57.0–71.0 | 50.0–55.0 | >12 |
| [28] 2022 | 3.0–3.7 | 0.7/21 | 43.0–44.2 | 60.0–74.0 | 46.0–50.0 | 7.0–7.5 * |
| [29] 2021 | 1.5–2.55 | 1.05/51.8 | 42.6–44.4 | 50.7–69.7 | 43.3–57 | 7.2–11.6 |
| [32] 2018 | 1.5–3.8 | 2.3/87 | 42.3–43.4 | 42.0–63.0 | 33.0–55.0 | N/A |
| This Work | 1.45–2.45 | 1/51.2 | 42.7–44.9 | 62.4–74.1 | 40.5–59.8 | 9.4–13.9 |
| 1.5–2.45 | 0.95/48.1 | 42.7–44.9 | 63.6–74.1 | 49.1–59.8 | 10.2–13.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Gan, D.; Shi, W. Design of Broadband Doherty Power Amplifier Based on Misaligned Current Phase. Energies 2024, 17, 2006. https://doi.org/10.3390/en17092006
Hu Y, Gan D, Shi W. Design of Broadband Doherty Power Amplifier Based on Misaligned Current Phase. Energies. 2024; 17(9):2006. https://doi.org/10.3390/en17092006
Chicago/Turabian StyleHu, Yinlong, Decheng Gan, and Weimin Shi. 2024. "Design of Broadband Doherty Power Amplifier Based on Misaligned Current Phase" Energies 17, no. 9: 2006. https://doi.org/10.3390/en17092006
APA StyleHu, Y., Gan, D., & Shi, W. (2024). Design of Broadband Doherty Power Amplifier Based on Misaligned Current Phase. Energies, 17(9), 2006. https://doi.org/10.3390/en17092006







