Value Evaluation Model of Multi-Temporal Energy Storage for Flexibility Provision in Microgrids
Abstract
:1. Introduction
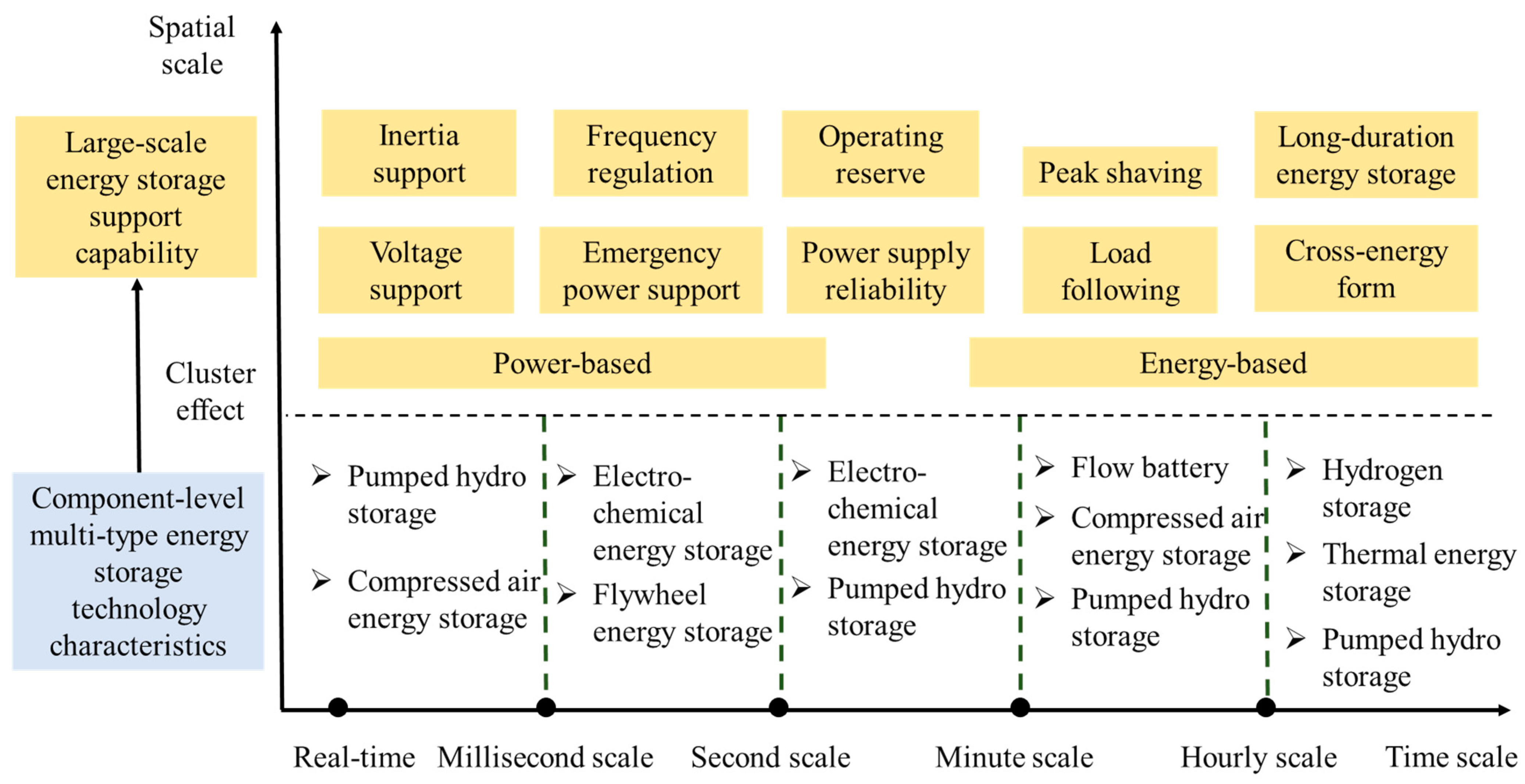
2. Analysis of the Indicators of the Flexible Regulation of Utility
2.1. Utility of Energy Storage
2.1.1. The System’s Energy Storage Investment Cost
2.1.2. The System’s Energy Storage Operational Cost
2.1.3. Cumulative Amount of Energy Storage
2.1.4. Cumulative Operational Duration of Energy Storage
2.1.5. Number of Energy Storage Discharges
2.2. Social Welfare Outcomes
2.2.1. Effectiveness of Reducing Carbon Emissions
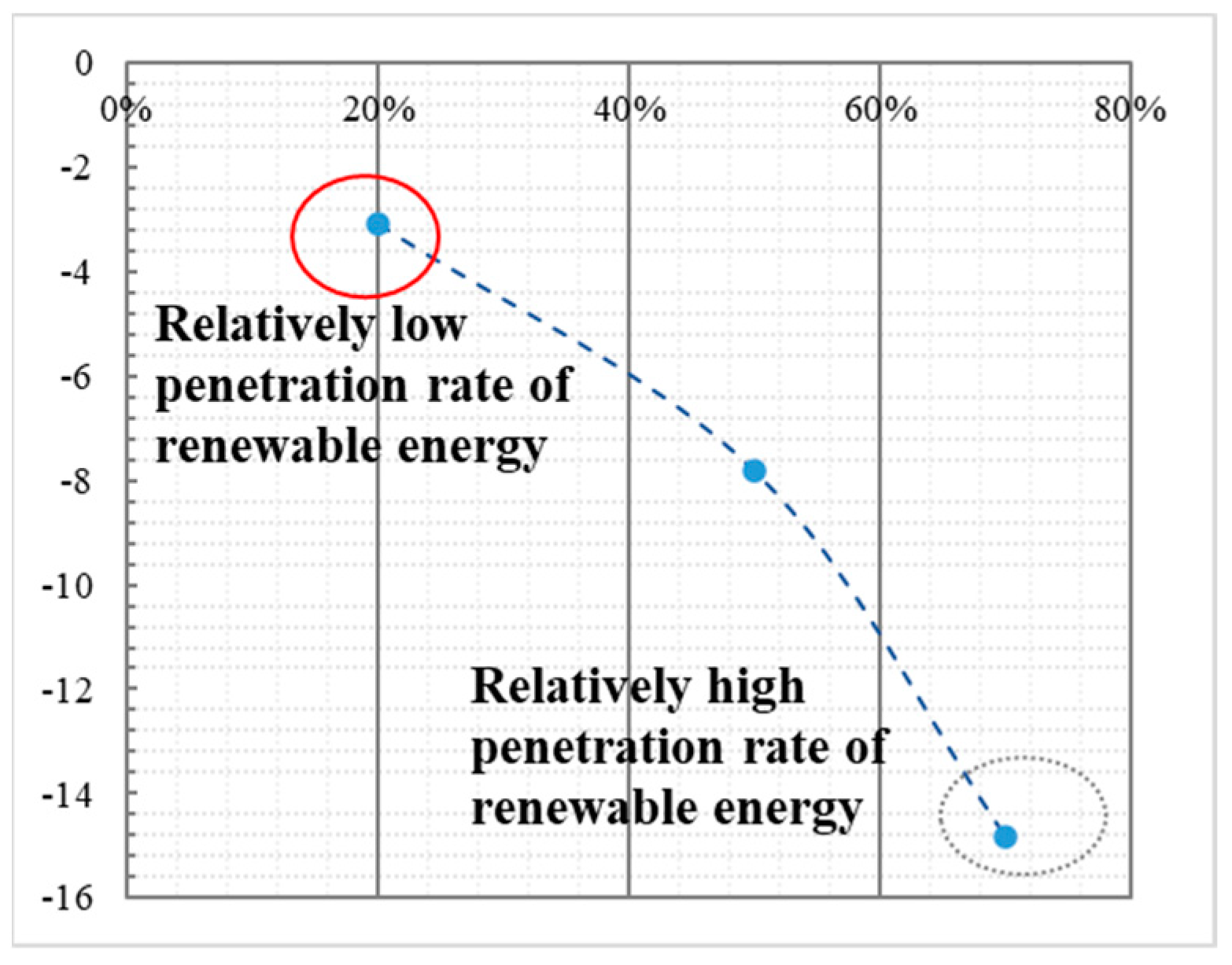
2.2.2. Absorption Rate of Renewable Energy
2.2.3. Government Subsidy Benefits
2.3. Enhancement of the Power System’s Revenue
2.3.1. Delaying Investment in Equipment
2.3.2. Expected Benefits from Peak Shaving and Valley Filling
3. Framework of Composite Weights Based on TODIM Utility Evaluation
3.1. Method for Combining Weights in Assessments of the Utility of Energy Storage
3.2. Method of Evaluating the Utility of Energy Storage—The TODIM Method
3.3. Quantification Method for the Evaluation Indicators of the Utility of Energy Storage
3.4. Process of Evaluating the Utility of Energy Storage
3.5. Analysis of the Error Sources of the Comprehensive Evaluation Method
- (1)
- The construction of assessment indicators for the value of storage and the computation of weights in this study involved subjective elements. Variations among decision-makers in determining the subjective indicators and weights may lead to discrepancies in the evaluation’s outcomes, which can be interpreted as a form of error.
- (2)
- In the operational-level assessment model of the value of storage, simplifications related to modeling storage and simulation of the system’s operation may be necessary to ensure the model’s solvability, potentially affecting the results of quantifying the value of storage at the operational level.
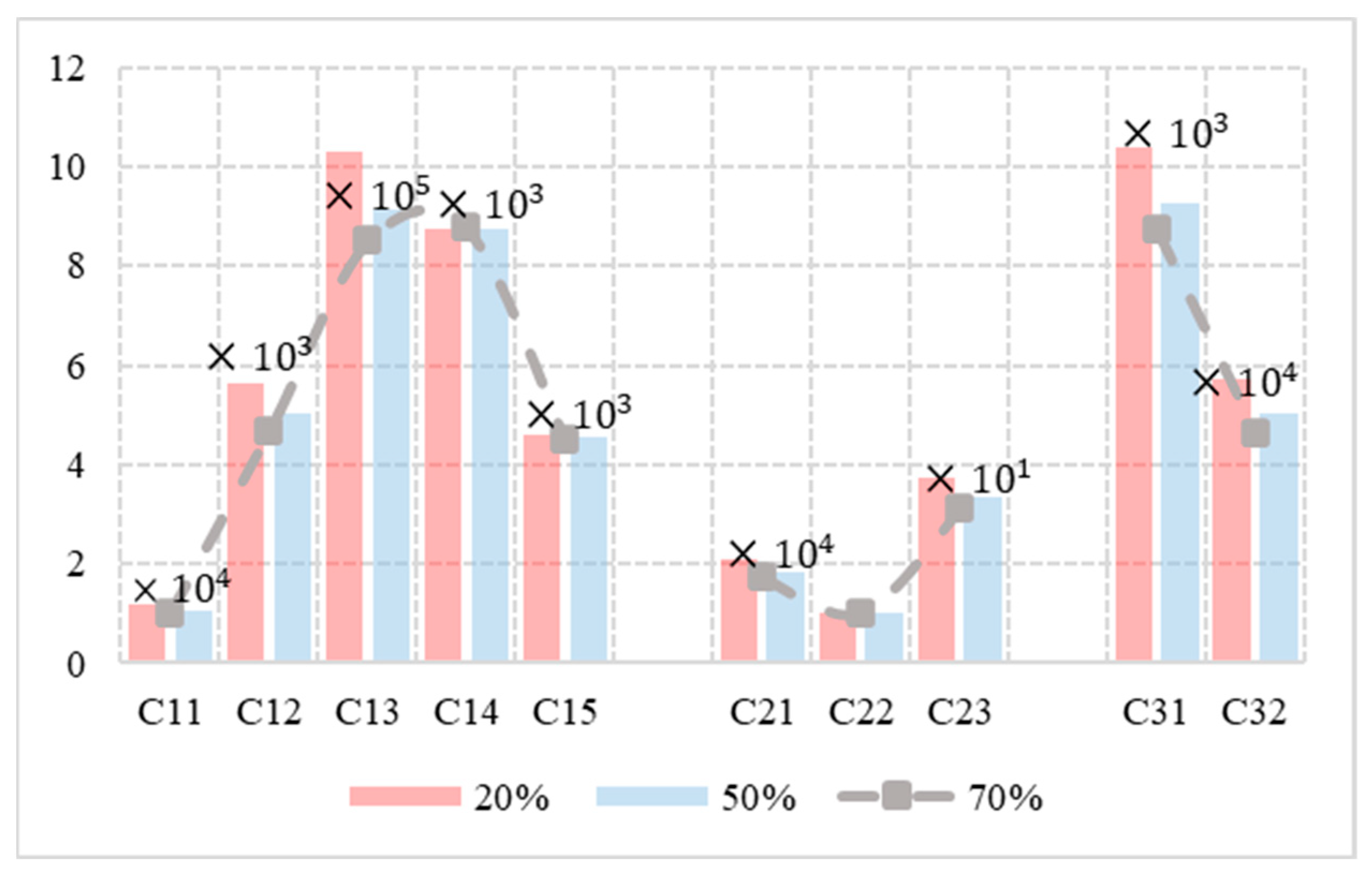
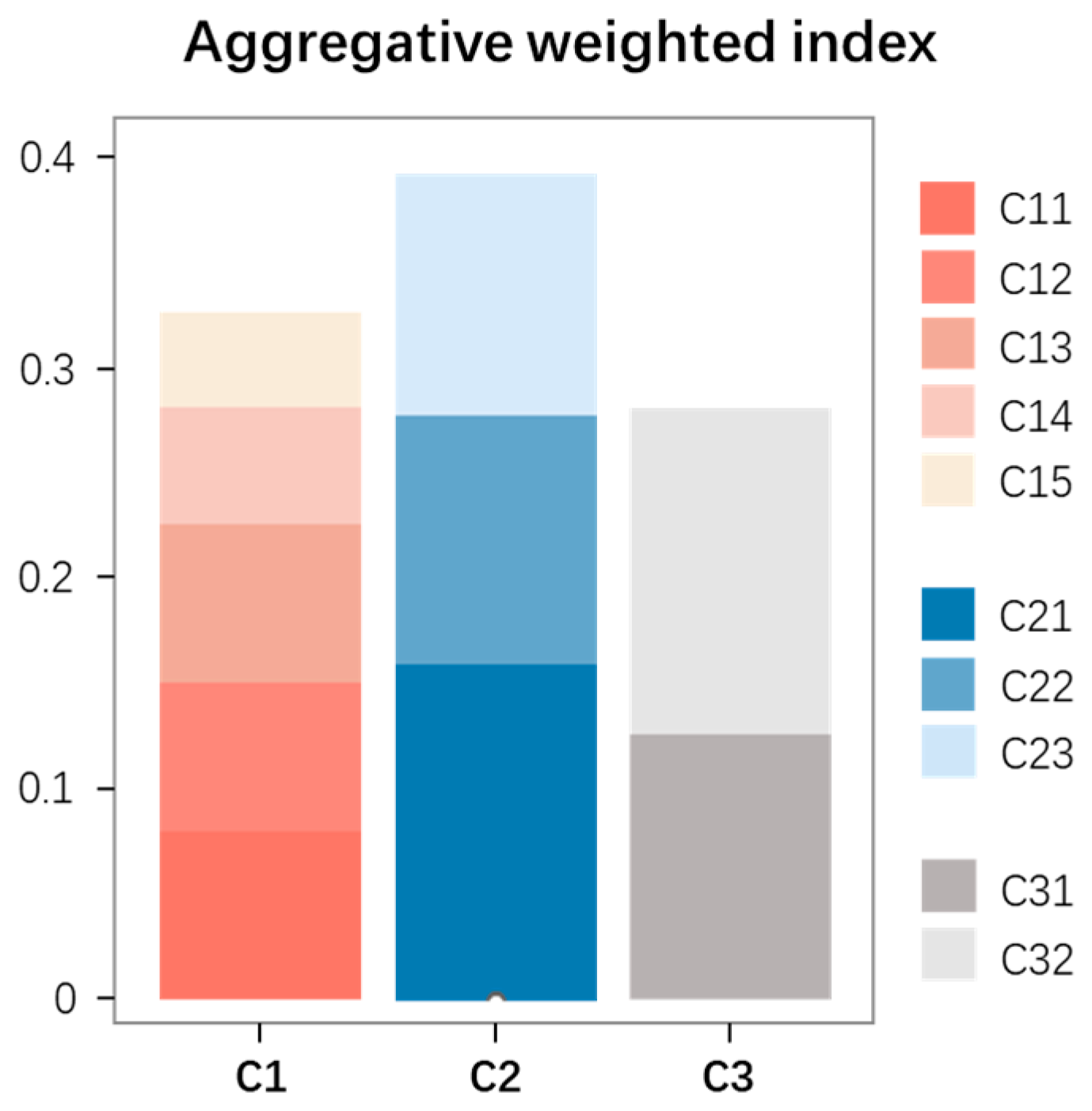
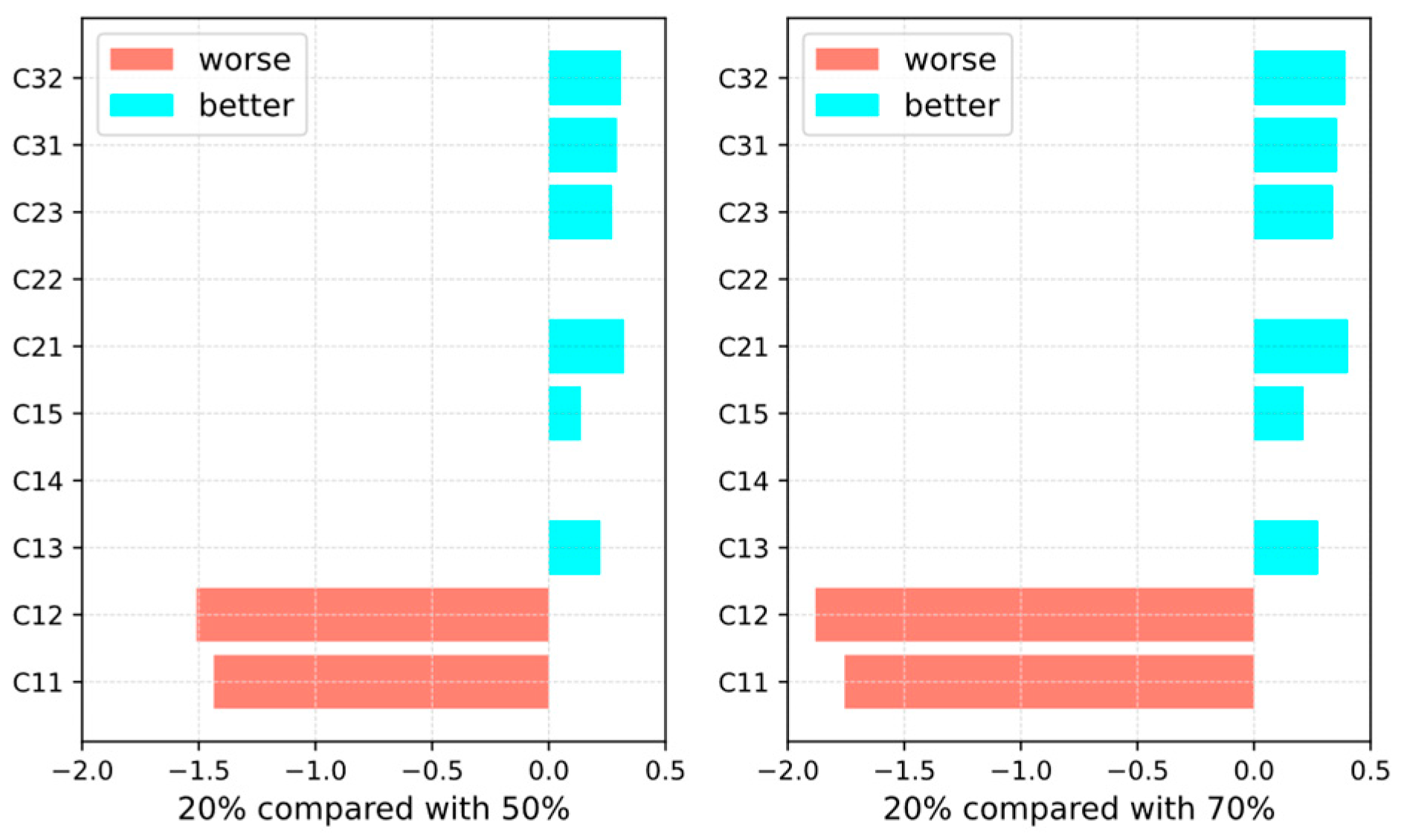
4. Case Study
- (1)
- Technologically enhance the flexibility and response speed of energy storage while reducing its self-discharge rate. From a cost perspective, lower the costs associated with adjustment to alleviate the economic pressure of the initial investments in constructing energy storage stations, and develop diverse financing models, such as public–private partnerships (PPP) and build–operate–transfer (BOT) schemes. In terms of profit, expand the methods for recovering energy storage costs by reasonably allocating market profits through assessments of the value of flexibility.
- (2)
- Considering resource endowments, exploit the complementary advantages of multiple flexibility resources, including traditional power units, energy storage stations, thermal storage facilities, gas storage facilities, appropriate wind and solar curtailment strategies, and demand response strategies, to build a clean, reliable, and convenient flexible adjustment system, and establish effective incentive mechanisms.
- (3)
- Promote the large-scale construction of renewable energy sources, harness the complementary capabilities of wind and solar generation curves to stabilize the scale of construction of energy storage stations, and reduce the decline in resource utilization caused by excessive and disorderly construction. Thus, from the perspective of external environmental changes, enhance the utility of energy storage in applications.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, Z.; Wang, J.; Zhou, M.; Xia, Q.; Tan, C.-W.; Li, G. Incentivizing frequency provision of power-to-hydrogen toward grid resiliency enhancement. IEEE Trans. Ind. Inform. 2022, 19, 9370–9381. [Google Scholar] [CrossRef]
- Ali, Z.M.; Calasan, M.; Aleem, S.H.E.A.; Jurado, F.; Gandoman, F.H. Applications of Energy Storage Systems in Enhancing Energy Management and Access in Microgrids: A Review. Energies 2023, 16, 5930. [Google Scholar] [CrossRef]
- Haas, J.; Cebulla, F.; Cao, K.; Nowak, W.; Palma-Behnke, R.; Rahmann, C.; Mancarella, P. Challenges and trends of energy storage expansion planning for flexibility provision in low-carbon power systems—A review. Renew. Sustain. Energy Rev. 2017, 80, 603–619. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, J.; Zhong, H.; Gao, F.; Pu, T.; Tan, C.-W.; Chen, X.; Li, G.; Zhao, H.; Zhou, M.; et al. Sharing economy in local energy markets. J. Mod. Power Syst. Clean Energy 2022, 11, 714–726. [Google Scholar] [CrossRef]
- Tabosa da Silva, P.L.; Rosas, P.A.C.; Castro, J.F.C.; Marques, D.d.C.; Aquino, R.R.B.; Rissi, G.F.; Neto, R.C.; Barbosa, D.C.P. Power smoothing strategy for wind generation based on fuzzy control strategy with battery energy storage system. Energies 2023, 16, 6017. [Google Scholar] [CrossRef]
- Nguyen Hong, N.; Nguyen Duc, H. Virtual Power Plant’s Optimal Scheduling Strategy in Day-Ahead and Balancing Markets Considering Reserve Provision Model of Energy Storage System. Appl. Sci. 2024, 14, 2175. [Google Scholar] [CrossRef]
- Liu, J.; Lin, S.; He, S.; Liu, W.; Liu, M. Multi-objective Optimal Dispatch of Mobile Energy Storage Vehicles in Active Distribution Networks. IEEE Syst. J. 2023, 17, 804–815. [Google Scholar] [CrossRef]
- Chang, X.; Wu, Z.; Wang, J.; Zhang, X.; Zhou, M.; Yu, T.; Wang, Y. The coupling effect of carbon emission trading and tradable green certificates under electricity marketization in China. Renew. Sustain. Energy Rev. 2023, 187, 113750. [Google Scholar] [CrossRef]
- Wang, D.; Sun, H.; Ge, Y.; Cheng, J.; Li, G.; Cao, Y.; Liu, W.; Meng, J. Operation effect evaluation of grid side energy storage power station based on combined weight TOPSIS model. Energy Rep. 2024, 11, 1993–2002. [Google Scholar] [CrossRef]
- Yun, P.; Ren, Y.; Xue, Y. Energy-Storage Optimization Strategy for Reducing Wind Power Fluctuation via Markov Prediction and PSO Method. Energies 2023, 11, 3393. [Google Scholar] [CrossRef]
- Zhou, H.; Lu, L.; Wei, M.; Shen, L.; Liu, Y. Robust Scheduling of a Hybrid Hydro/Photovoltaic/Pumped-Storage System for Multiple Grids Peak-Shaving and Congestion Management. IEEE Access 2024, 12, 22230–22242. [Google Scholar] [CrossRef]
- Pang, N.; Meng, Q.; Nan, M. Multi-Criteria Evaluation and Selection of Renewable Energy Battery Energy Storage System—A Case Study of Tibet, China. IEEE Access 2021, 9, 119857–119870. [Google Scholar] [CrossRef]
- Tan, Y.; Xie, G.; Xiao, Y.; Luo, Y.; Xie, X.; Wen, M. Comprehensive Benefit Evaluation of Hybrid Pumped-Storage Power Stations Based on Improved Rank Correlation-Entropy Weight Method. Energies 2022, 15, 8414. [Google Scholar] [CrossRef]
- Han, X.; Zhao, S.; Wei, Z.; Bai, W. Planning and overall economic evaluation of photovoltaic-energy storage station based on game theory and analytic hierarchy process. IEEE Access 2019, 7, 110972–110981. [Google Scholar] [CrossRef]
- Oening, A.P.; Marcilio, D.C.; Andrade, J.D.; Impinnisi, P.R. Analytic Hierarchy Process Algorithm Applied to Battery Energy Storage System Selection for Grid Applications. Braz. Arch. Biol. Technol. 2021, 64, e21210148. [Google Scholar] [CrossRef]
- Algarín, C.R.; Llanos, A.P.; Castro, A.O. An analytic hierarchy process based approach for evaluating renewable energy sources. Int. J. Energy Econ. Policy 2017, 7, 38–47. [Google Scholar]
- Qi, Y.; Wen, F.; Wang, K.; Li, L.; Singh, S. A fuzzy comprehensive evaluation and entropy weight decision-making based method for power network structure assessment. Int. J. Eng. Sci. Technol. 2010, 2, 92–99. [Google Scholar] [CrossRef]
- He, Z.; Gao, S.; Chen, X.; Zhang, J.; Bo, Z.; Qian, Q. Study of a new method for power system transients classification based on wavelet entropy and neural network. Int. J. Electr. Power Energy Syst. 2011, 33, 402–410. [Google Scholar]
- Liu, Y.; Wang, Y.; Li, T.; Ma, R.; Xu, K.; Xu, W. Evaluation of New Power System Based on Entropy Weight-TOPSIS Method. Math. Probl. Eng. 2022, 2022, 7669139. [Google Scholar] [CrossRef]
- Llamazares, B. An analysis of the generalized TODIM method. Eur. J. Oper. Res. 2018, 269, 1041–1049. [Google Scholar] [CrossRef]
- Yuan, J.; Li, X.; Xu, C.; Zhao, C.; Liu, Y. Investment risk assessment of coal-fired power plants in countries along the Belt and Road initiative based on ANP-Entropy-TODIM method. Energy 2019, 176, 623–640. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Peng, H.-M.; Wang, T.-L.; Wang, X.-K.; Wang, J.-Q. Supplier selection in the nuclear power industry with an integrated ANP-TODIM method under Z-number circumstances. Symmetry 2020, 12, 1357. [Google Scholar] [CrossRef]
- Leoneti, A.B.; Gomes, L.F.A.M. A novel version of the TODIM method based on the exponential model of prospect theory: The ExpTODIM method. Eur. J. Oper. Res. 2021, 295, 1042–1055. [Google Scholar] [CrossRef]
- Zhang, C.; Xia, P.; Zhang, X. Multi-attribute decision-making method of pumped storage capacity planning considering wind power uncertainty. J. Clean. Prod. 2024, 449, 141655. [Google Scholar] [CrossRef]
- Alvarez, G.E. Operation of pumped storage hydropower plants through optimization for power systems. Energy 2020, 202, 117797. [Google Scholar] [CrossRef]



| Definition | |
|---|---|
| 1 | Factor is equally important to factor |
| 3 | Factor is slightly more important than factor |
| 5 | Factor is moderately more important than factor |
| 7 | Factor is significantly more important than factor |
| 9 | Factor is absolutely more important than factor |
| 2, 4, 6, 8 | Intermediate scaling values between the two judgments |
| Reciprocal | If the judgment value of factor compared with factor is , then |
| … | ||||
|---|---|---|---|---|
| 1 | … | |||
| 1 | … | |||
| … | … | … | … | … |
| … | 1 |
| Order | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| RI Value | 0.00 | 0.00 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, Z.; Zhang, Y.; Wei, L.; Liu, J.; Lu, Y.; Tian, C.; Wu, Z. Value Evaluation Model of Multi-Temporal Energy Storage for Flexibility Provision in Microgrids. Energies 2024, 17, 2026. https://doi.org/10.3390/en17092026
Chai Z, Zhang Y, Wei L, Liu J, Lu Y, Tian C, Wu Z. Value Evaluation Model of Multi-Temporal Energy Storage for Flexibility Provision in Microgrids. Energies. 2024; 17(9):2026. https://doi.org/10.3390/en17092026
Chicago/Turabian StyleChai, Zhe, Yihan Zhang, Lanyi Wei, Junhui Liu, Yao Lu, Chunzheng Tian, and Zhaoyuan Wu. 2024. "Value Evaluation Model of Multi-Temporal Energy Storage for Flexibility Provision in Microgrids" Energies 17, no. 9: 2026. https://doi.org/10.3390/en17092026
APA StyleChai, Z., Zhang, Y., Wei, L., Liu, J., Lu, Y., Tian, C., & Wu, Z. (2024). Value Evaluation Model of Multi-Temporal Energy Storage for Flexibility Provision in Microgrids. Energies, 17(9), 2026. https://doi.org/10.3390/en17092026







