The Impact of System Sizing and Water Temperature on the Thermal Characteristics of Floating Photovoltaic Systems
Abstract
:1. Introduction
1.1. Floating PV and Heat Loss Coefficients
1.2. Objectives
2. FPV Systems and Measurement Setup
2.1. Demonstrator-Scale FPV Systems
2.1.1. Solarisfloat FPV System: Open Structure
2.1.2. Solar Float: Closed Structure
2.2. Groenleven Commercial Scale FPV System: Closed Structure
3. Analytical Methods
3.1. Datasets and Filtering
3.2. Wind Speed Height
3.3. Temperature Model including Water Temperature as a Variable
4. Results and Discussion
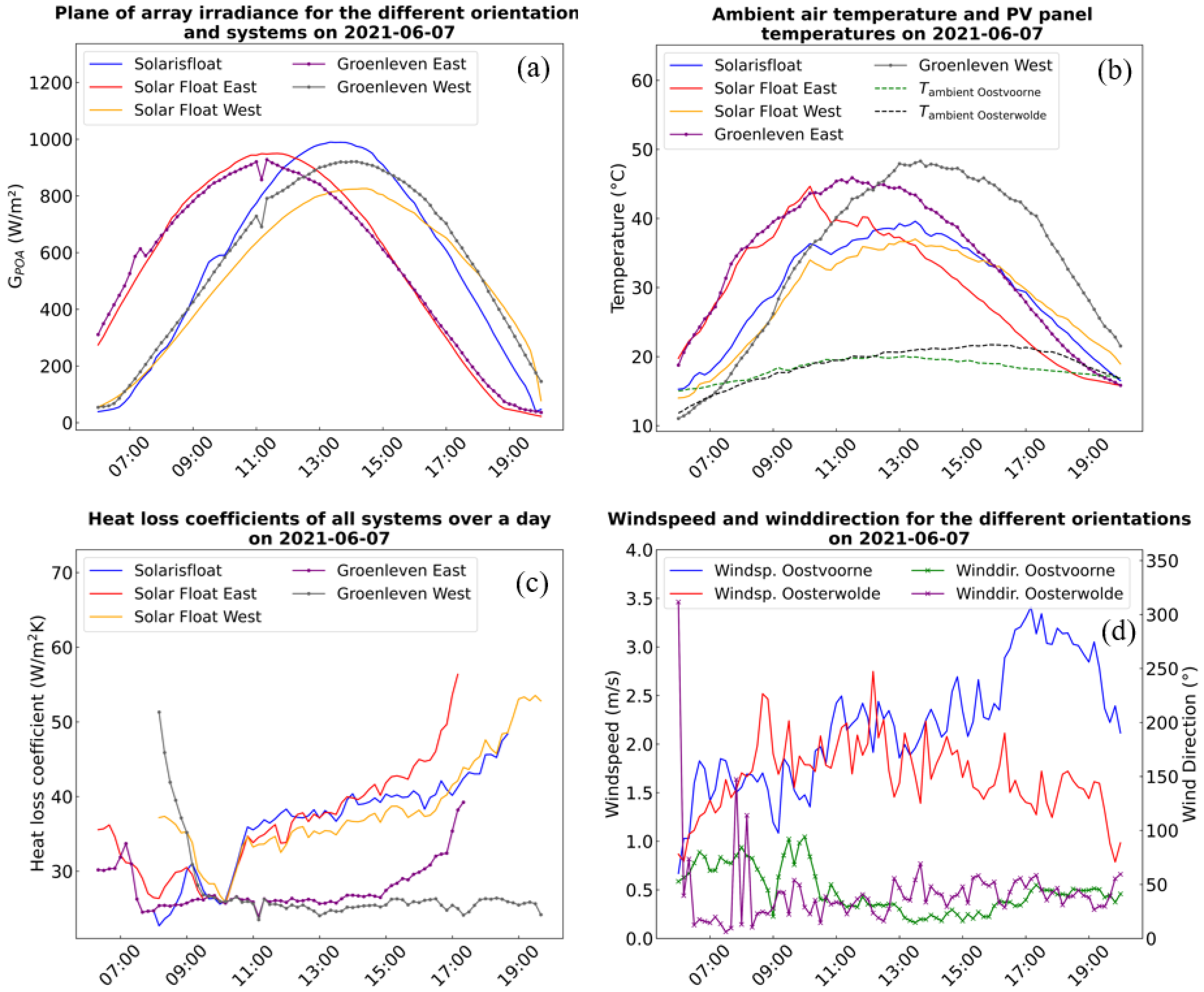
4.1. Thermal Behavior of the Different Systems on a Clear Sky Day
4.2. Heat Loss Coefficient
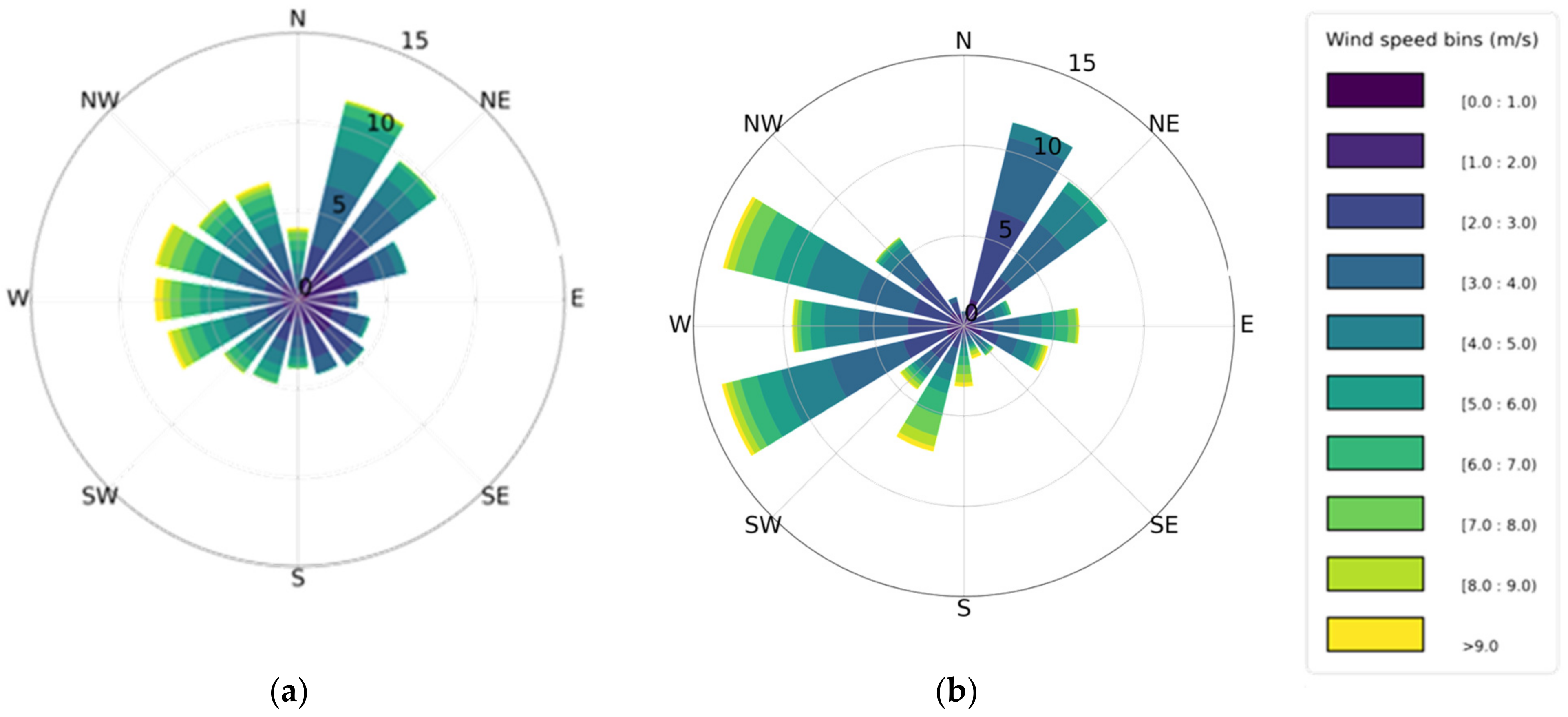
4.2.1. Wind Direction Independent
4.2.2. Wind Direction Dependency
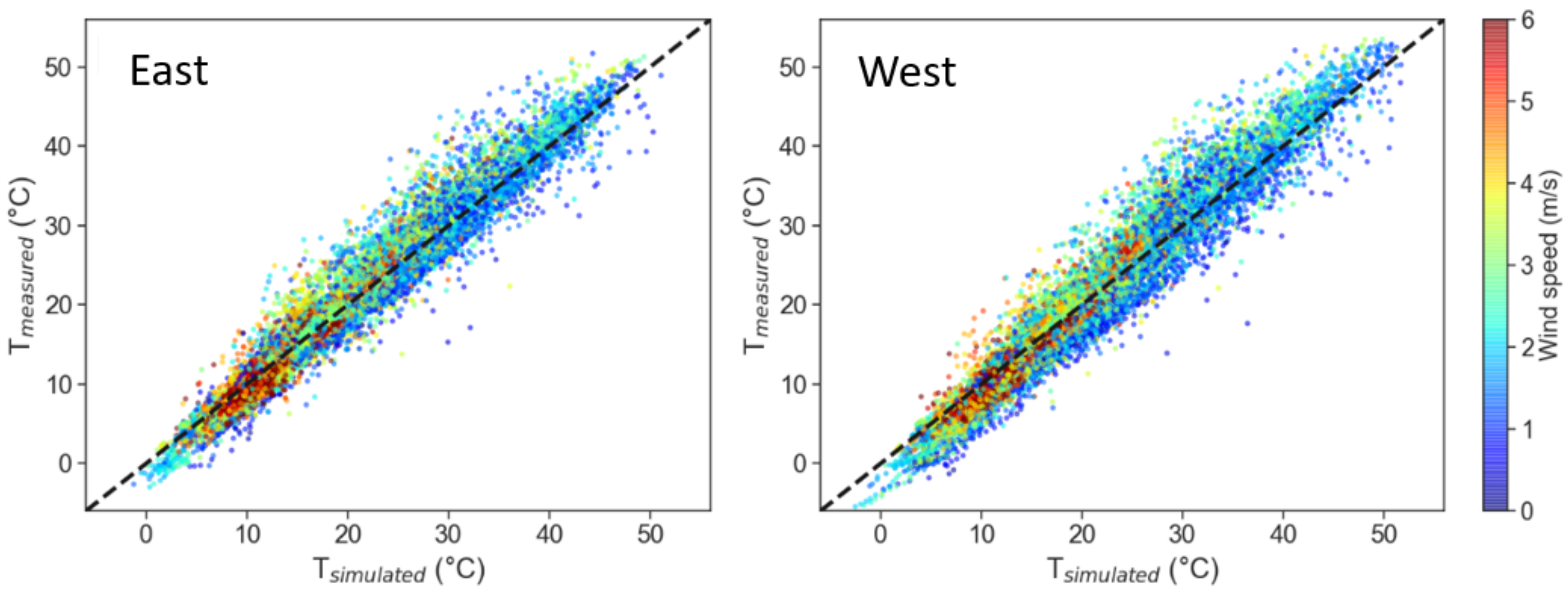
4.3. Thermal Model with Water Temperature
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- SolarPower Europe. Floating PV Best Practice Guidelines V1.0; SolarPower Europe: Brussels, Belgium, 2023; ISBN 978-9-464-66914-5. [Google Scholar]
- Chowdhury, G.; Haggag, M.; Poortmans, J. How cool is floating PV? A state-of-the-art review of floating PV’s potential gain and computational fluid dynamics modeling to find its root cause. EPJ Photovolt. 2023, 14, 24. [Google Scholar] [CrossRef]
- Woyte, A.; Richter, M.; Moser, D.; Reich, N.; Green, M.; Mau, S.; Beyer, H.G. Analytical Monitoring of Grid-Connected Photovoltaic Systems; IEA PVPS T13-03; IEA: Paris, France, 2014. [Google Scholar]
- IEC61215-2; Terrestrial Photovoltaic (PV) Modules—Design Qualification and Type Approval—Part 2: Test Procedures. IEC: Geneva, Switzerland, 2021.
- Skoplaki, E.; Palyvos, J.A. On the temperature dependence of photovoltaic module electrical performance: A review of efficiency/power correlations. Sol. Energy 2008, 83, 614–624. [Google Scholar] [CrossRef]
- King, D.L.; Boyson, W.E.; Kratochvill, J.A. Photovoltaic Array Performance Model; Sandia National Laboratories (SNL): Albuquerque, NM, USA, 2004. [Google Scholar] [CrossRef]
- Faiman, D. Assessing the outdoor operating temperature of photovoltaic modules. Prog. Photovolt. Res. Appl. 2008, 16, 307–315. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 4th ed.; Wiley: Hoboken, NJ, USA, 2014; pp. 757–759. ISBN 978-0-470-87366-3. [Google Scholar]
- PVsyst: Array Thermal Losses. 1996. Available online: https://www.pvsyst.com/help/thermal_loss.htm (accessed on 21 February 2024).
- Liu, H.; Krishna, V.; Lun Leung, J.; Reindl, T.; Zhao, L. Field experience and performance analysis of floating PV technologies in the tropics. Prog. Photovolta. Res. Appl. 2018, 26, 957–967. [Google Scholar] [CrossRef]
- Dörenkämper, M.; Wahed, A.; Kumar, A.; De Jong, M.M.; Kroon, J.; Reindl, T. The cooling effect of floating PV in two different climate zones: A comparison of field test data from the Netherlands and Singapore. Sol. Energy 2021, 214, 229–247. [Google Scholar] [CrossRef]
- Lindholm, D.; Kjeldstad, T.; Selj, J.; Marstein, E.S.; Fjær, H.G. Heat loss coefficients computed for floating PV modules. Prog. Photovolt. Res. Appl. 2021, 29, 1262–1273. [Google Scholar] [CrossRef]
- Kjeldstad, T.; Lindholm, D.; Marstein, E.; Selj, J. Cooling of floating photovoltaics and the importance of water temperature. Sol. Energy 2021, 218, 544–551. [Google Scholar] [CrossRef]
- Tina, G.M.; Bontempo Scavo, F.; Merlo, L.; Bizzarri, F. Comparative analysis of monofacial and bifacial photovoltaic modules for floating power plants. Appl. Energy 2021, 28, 116084. [Google Scholar] [CrossRef]
- Dörenkämper, M.; de Jong, M.M.; Kroon, J.; Nysted, V.S.; Selj, J.; Kjeldstad, T. Modeled and Measured Operating Temperatures of Floating PV Modules: A Comparison. Energies 2023, 16, 7153. [Google Scholar] [CrossRef]
- Fieldlab Westvoorne. Available online: https://www.fieldlabwestvoorne.nl/ (accessed on 21 February 2024).
- TNO. Project Oostvoornse Meer; TNO: Delft, The Netherlands, 2022. [Google Scholar]
- Groenleven. 2024. Available online: https://groenleven.nl/projecten/drijvend-zonnepark-oosterwolde/ (accessed on 21 March 2024).
- Holton, J.R.; Hakim, G.J. Wind and Wind Systems. In Introduction to Dynamic Meteorology; Elsevier Academic Press: Amsterdam, The Netherlands, 2013; ISBN 9780123848666. [Google Scholar]





| System | Uc [W/m2K] | Uv [W/m3Ks] | Reference |
|---|---|---|---|
| LPV (Open rack, wind independent) | 29 | 0 | PVsyst, 1996 [9] |
| LPV (Fully insulated backside, wind independent) | 15 | 0 | PVsyst, 1996 [9] |
| LPV (Open rack, with wind dependency) | 25 | 1.2 | PVsyst, 1996 [9] |
| FPV (Open structure, The Netherlands) | 24.4 | 6.5 | Dörenkämper et al., 2021 [11] |
| FPV (Closed structure, The Netherlands) | 25.2 | 3.7 | Dörenkämper et al., 2021 [11] |
| LPV (Open structure, The Netherlands) | 18.6 | 4.4 | Dörenkämper et al., 2021 [11] |
| FPV (Membrane in contact with water) | 86.5 | 0 | Lindholm et al., 2021 [12] |
| FPV (Monofacial module, open structure) | 31.9 | 1.5 | Tina et al., 2021 [14] |
| FPV (Bifacial module, open structure) | 35.2 | 1.5 | Tina et al., 2021 [14] |
| System | Uc-Value [W/m2K] | Uv-Value [W/m3Ks] |
|---|---|---|
| Solarisfloat | 24.3 | 3.2 |
| Groenleven (East) | 23.4 | 2.7 |
| Solar Float (East) | 27.2 | 4.0 |
| Groenleven (West) | 22.8 | 2.8 |
| Solar Float (West) | 23.7 | 5.1 |
| Wind Direction | Solarisfloat [W/m3Ks] | Groenleven (East) [W/m3Ks] | Solar Float (East) [W/m3Ks] | Groenleven (West) [W/m3Ks] | Solar Float (West) [W/m3Ks] |
|---|---|---|---|---|---|
| North | 4.1 | 1.7 | 5.0 | 1.6 | 6.0 |
| East | 2.6 | 2.4 | 3.3 | 1.8 | 4.1 |
| South | 3.5 | 2.6 | 3.6 | 3.9 | 4.1 |
| West | 3.0 | 3.0 | 4.2 | 3.2 | 4.9 |
| Orientation | Uc [W/m2K] | Uv [W/m3Ks] | Uw [W/m2K] |
|---|---|---|---|
| East | 23.4 | 4.7 | −0.3 |
| West | 20.6 | 5.1 | 1.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dörenkämper, M.; Villa, S.; Kroon, J.; de Jong, M.M. The Impact of System Sizing and Water Temperature on the Thermal Characteristics of Floating Photovoltaic Systems. Energies 2024, 17, 2027. https://doi.org/10.3390/en17092027
Dörenkämper M, Villa S, Kroon J, de Jong MM. The Impact of System Sizing and Water Temperature on the Thermal Characteristics of Floating Photovoltaic Systems. Energies. 2024; 17(9):2027. https://doi.org/10.3390/en17092027
Chicago/Turabian StyleDörenkämper, Maarten, Simona Villa, Jan Kroon, and Minne M. de Jong. 2024. "The Impact of System Sizing and Water Temperature on the Thermal Characteristics of Floating Photovoltaic Systems" Energies 17, no. 9: 2027. https://doi.org/10.3390/en17092027
APA StyleDörenkämper, M., Villa, S., Kroon, J., & de Jong, M. M. (2024). The Impact of System Sizing and Water Temperature on the Thermal Characteristics of Floating Photovoltaic Systems. Energies, 17(9), 2027. https://doi.org/10.3390/en17092027







