Study of Phase Changes in Operational Risk for Trucks
Abstract
:1. Introduction
2. Risk Analysis Method
2.1. Model of the System of Transport Services
2.2. Integrated Risk of the Operational Incapacity of the Vehicle
2.3. Phase Risk of the Operational Incapacity of the Vehicle
3. Experimental Research
3.1. Research Objects and Conditions
3.2. Research Results—Integrated Phase Risk
4. Phase Risk Statistical Analysis
4.1. Hypotheses
- First research hypothesis there is no significant difference in the average integrated operational risk between the mileage phases for the vehicles of brand , expressed in the following form (18):
- Second research hypothesis there is no significant difference in the average integrated operational risk between the mileage phases for the vehicles of brand , expressed formulaically in the following form (19):
- If the former is true, the mean square for phases will be an estimator of homogeneous variance for all phases.
- If, on the other hand, the differences between the means are systematic, it is necessary to consider the contribution of this systematic difference in the inter-phase variability.
- The authors verified Equations (18) and (19) using statistic (23):
- The random components of the model should be independent random variables with normal distribution ;
- Variances for the phases should be equal, i.e., ;
- Random variables and should be independent.
4.2. Analysis of Descriptive Statistics of Phase Risk ( Thousand km)
4.3. Analysis of Phase Risk Differences’ Significance ( Thousand km)
4.4. Analysis of Phase Risk Descriptive Statistics ( Thousand km)
4.5. Analysis of Phase Risk Differences’ Significance ( Thousand km)
5. Discussion of the Results
6. Conclusions
- Analysis of the phase risk descriptive statistics of vehicles’ operational incapacity, including, in particular, the assessment of differences in average risk and differences in the variation coefficient in the time series of vehicle mileage phases;
- Indicating the outliers and extremes of phase risk and identifying their physical (technical) causes;
- Analysis of the differences’ statistical significance in phase risk.
- It focuses on the practical needs of the carrier (service provider) regarding the methods of ensuring the continuity of operation;
- There is a short calculation time thanks to simple calculation procedures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pintelon, L.; Pinjala, S.K.; Vereecke, A. Evaluating the effectiveness of maintenance strategies. J. Qual. Maint. Eng. 2006, 12, 7–20. [Google Scholar] [CrossRef]
- Jardine, A.K.S. Optimizing Maintenance and Replacement Decisions. In Asset Management Excellence: Optimizing Life—Cycle Decision, 2nd ed.; Campbell, J.D., Jardine, A.K.S., McGlynn, J., Eds.; CRC Press—Taylor and Francis Group: Boca Raton, FL, USA, 2011; pp. 259–300. [Google Scholar]
- Chan, W.C.; Ibrahim, W.H.W.; Lo, M.C.; Suaidi, M.K.; Ha, S.T. Determinants of Customer Satisfaction and Loyalty in Public Transport: A PLS-SEM Approach. Sustain. Econ. Dev. Pattern Perspect. 2021, 39, 1–23. [Google Scholar] [CrossRef]
- Wiśniewski, M.; Grudzień, Ł. Metodyka Oceny Ryzyka w Świetle Wymagań Normy ISO 9001:2015. In Innowacje w Zarządzaniu i Inżynierii Produkcji: Volume 2; Knosala, R., Ed.; Oficyna Wydawnicza Polskiego Towarzystwa Zarządzania Produkcją: Opole, Poland, 2017; pp. 388–399. [Google Scholar]
- Dahlgren, S.; Ammenberg, J. Sustainability Assessment of Public Transport, Part II—Applying a Multi-Criteria Assessment Method to Compare Different Bus Technologies. Sustainability 2021, 13, 1273. [Google Scholar] [CrossRef]
- Nowakowski, T. From reliability to resilience: Modern challenges of safety and reliability theory and applications. J. KONBiN 2015, 33, 151–158. [Google Scholar] [CrossRef]
- Jamroz, K.; Kadziński, A.; Chruzik, K.; Szymanek, A.; Gucma, L.; Skorupski, J. Trans-Risk—An integrated method for risk management in transport. J. KONBiN 2010, 13, 210–220. [Google Scholar] [CrossRef]
- Tubis, A. Metoda Zarządzania Ryzykiem Operacyjnym w Transporcie Drogowym; Oficyna Wydawnicza Politechniki Wrocławskiej: Wrocław, Poland, 2018. [Google Scholar]
- Smalko, Z.; Nowakowski, T.; Tubis, A. Zarys Niezawodnościowej Teorii Zagrożeń; Oficyna Wydawnicza Politechniki Wrocławskiej: Wrocław, Poland, 2020. [Google Scholar]
- Andrzejczak, K. Metody Prognozowania w Modelowaniu Eksploatacji Środków Transportu; Wydawnictwo Politechniki Poznańskiej: Poznań, Poland, 2013. [Google Scholar]
- Borucka, A. Seasonal Methods of Demand Forecasting in the Supply Chain as Support for the Company’s Sustainable Growth. Sustainability 2023, 15, 7399. [Google Scholar] [CrossRef]
- Młynarski, S. Problemy Prognozowania Niezawodności Pojazdów Eksploatowanych w Transporcie Drogowym; Wydawnictwo Politechniki Krakowskiej: Kraków, Poland, 2018. [Google Scholar]
- Li, J.; Wang, Z.; Liu, C.; Qiu, M. Accelerated degradation analysis based on a random-effect Wiener process with one-order autoregressive errors. Eksploat. Niezawodn. Maint. Reliab. 2019, 21, 246–255. [Google Scholar] [CrossRef]
- Sobral, J.; Ferreira, L. Establishment of optimal physical assets inspection frequency based on risk principles. Eksploat. Niezawodn. Maint. Reliab. 2015, 17, 243–249. [Google Scholar] [CrossRef]
- Hlatká, M.; Stopka, O.; Bartuška, L.; Stopková, M.; Yordanova, D.N.; Gross, P.; Sádlo, P. Draft Methodology of the Age Management Implementation in Human Resource Management in a Transport Company. J. Risk Financ. Manag. 2021, 14, 183. [Google Scholar] [CrossRef]
- Salonen, A.; Bengtsson, M. The potential in strategic maintenance development. J. Qual. Maint. Eng. 2011, 17, 337–350. [Google Scholar] [CrossRef]
- Wu, F.; Niknam, S.A.; Kobza, J.E. A cost-effective degradation-based maintenance strategy under imperfect repair. Reliab. Eng. Syst. Saf. 2015, 144, 234–243. [Google Scholar] [CrossRef]
- Niewczas, A.; Mórawski, Ł.; Dębicka, E.; Borucka, A. Commercial vehicles incapacity risk analysis in the transport company. J. KONBiN 2019, 49, 321–340. [Google Scholar] [CrossRef]
- Rymarz, J.; Borucka, A.; Niewczas, A. Evaluation of impact of the operational and technical factors on downtime of municipal buses based on a linear regression model. Commun. Sci. Lett. Univ. Žilina 2021, 4, 241–247. [Google Scholar] [CrossRef]
- Niewczas, A.; Mórawski, Ł.; Rymarz, J.; Dębicka, E.; Hołyszko, P. Operational risk assessment model for city buses. Eksploat. Niezawodn. Maint. Reliab. 2023, 25, 14. [Google Scholar] [CrossRef]
- Mcgowran, P.; Donovan, A. Assemblage theory and disaster risk management. Progress. Human. Geogr. 2021, 45, 1601–1624. [Google Scholar] [CrossRef]
- Ammenberg, J.; Dahlgren, S. Sustainability Assessment of Public Transport, Part I—A Multi-Criteria Assessment Method to Compare Different Bus Technologies. Sustainability 2021, 13, 825. [Google Scholar] [CrossRef]
- Veeneman, W.; Wilschut, J.; Urlings, T.; Blank, J.; Velde, D. Efficient frontier analysis of Dutch public transport tendering: A first analysis. Res. Transp. Econ. 2014, 48, 101–108. [Google Scholar] [CrossRef]
- Raposo, H.; Farinha, J.T.; Ferreira, L.; Galar, D.P. An integrated econometric model for bus replacement and determination of reserve fleet size based on predictive maintenance. Eksploat. Niezawodn. Maint. Reliab. 2017, 19, 358–368. [Google Scholar] [CrossRef]
- Laskowski, D.; Łubkowski, P.; Pawlak, E.; Stańczyk, P. Antropo-technical systems reliability. In Safety and Reliability: Methodology and Applications; Nowakowski, T., Mlynczak, M., Jodejko-Pietruczuk, A., Werbinska-Wojciechowska, S., Eds.; CRC Press: London, UK, 2014; pp. 399–407. [Google Scholar]
- Rymarz, J. Badania Efektywności Eksploatacyjnej Autobusów Komunikacji Miejskiej; Wydawnictwo Politechniki Lubelskiej: Lublin, Poland, 2021. [Google Scholar]
- Selech, J. Prognozowanie Kosztów Obsługiwania Korekcyjnego Pojazdów Transportu Masowego; Wydawnictwo Instytutu Technologii Eksploatacji-PIB: Radom, Poland, 2019. [Google Scholar]



| Characteristic | Vehicle Brand | |
|---|---|---|
| M | I | |
| General specifications | two-axle, closed-box | |
| Type-approval category | N2 | |
| Engine type | compression ignition | |
| Engine displacement (dm3) | 5.1 | 3.9 |
| Max. engine power (kW) | 130 | 134 |
| Maximum grossweight (kg) | 12,000 | |
| Load capacity (kg) | 5.250 | 5.395 |
| Cost of acquisition (PLN thousand) | 208 | 175 |
| Parameter | Brand | |
|---|---|---|
| M | I | |
| Size (numerousness) of the sample [-] | 20 | 20 |
| Average mileage in the examined period (thousand km) | 242.6 | 240.1 |
| Standard deviation (thousand km) | 14.0 | 11.6 |
| Maximum mileage (thousand km) | 326.3 | 280.4 |
| Average annual mileage (thousand km) | 52.6 | 47.2 |
| Average monthly mileage (thousand km) | 4.4 | 3.8 |
| Average observation time (calendar months) | 56 | 60 |
| Standard deviation of average observation time (calendar months) | 2.2 | 2.1 |
| Repair Description | Amount (PLN) | Mileage (km) |
|---|---|---|
| Tyre inspection | 18.00 | 5585 |
| Leaf spring pads, 2 pcs.—replacement | 110.26 | 28,000 |
| Overspeed limitation devices inspection | 180.36 | 33,059 |
| Flexible hose + hanger—replacement | 605.18 | 36,410 |
| Right direction indicator—replacement | 100.55 | 46,834 |
| Tyre inspection | 144.00 | 47,528 |
| Wheel balancing | 90.00 | 47,528 |
| Right side window—replacement | 322.65 | 57,021 |
| Brake system bleeding | 40.00 | 99,185 |
| Leaf spring pad (rear right)—replacement | 195.11 | 99,800 |
| Leaf spring pad (rear left)—replacement | 195.11 | 105,978 |
| Brake system—bleeding | 40.00 | 106,352 |
| Pneumatic hose—replacement | 318.8 | 112,812 |
| Repair of the electrical system of the lighting + replacing missing elements | 104.3 | 128,532 |
| Water pump + in-warranty replacement | 0.00 | 128,532 |
| Reverse sensor—replacement | 262.98 | 128,532 |
| Mileage Phase [thsnd. km] | Vehicle Number j | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
| [0–30] | 0.66 | 0.39 | 1.06 | 0.87 | 0.81 | 2.94 | 0.62 | 1.03 | 2.33 | 0.76 | 0.76 | 1.26 | 2.10 | 1.50 | 0.94 | 0.78 | 2.27 | 0.92 | 0.87 | 1.31 | |
| [30–60] | 2.49 | 2.57 | 3.00 | 2.22 | 2.64 | 3.67 | 4.73 | 3.63 | 0.88 | 3.18 | 3.78 | 3.71 | 3.21 | 0.87 | 5.14 | 3.39 | 8.83 | 3.95 | 3.67 | 3.12 | |
| [60–90] | 3.63 | 2.18 | 3.35 | 5.39 | 2.96 | 0.62 | 0.00 | 0.00 | 4.54 | 0.00 | 0.00 | 1.17 | 0.00 | 5.19 | 1.80 | 8.17 | 3.41 | 0.00 | 0.00 | 0.00 | |
| [90–120] | 1.32 | 0.00 | 1.99 | 0.00 | 0.49 | 2.79 | 2.38 | 1.37 | 3.72 | 0.20 | 1.08 | 5.17 | 0.00 | 4.64 | 5.81 | 0.00 | 0.00 | 7.75 | 15.24 | 0.00 | |
| [120–150] | 8.74 | 5.56 | 0.00 | 1.16 | 0.45 | 5.82 | 5.84 | 6.25 | 4.26 | 3.29 | 8.29 | 5.86 | 3.47 | 3.38 | 1.93 | 0.28 | 0.65 | 7.80 | 2.24 | 7.48 | |
| [150–180] | 2.52 | 3.31 | 2.96 | 0.00 | 3.18 | 19.69 | 1.44 | 3.35 | 1.87 | 1.51 | 5.98 | 11.84 | 6.54 | 1.39 | 4.83 | 3.46 | 5.23 | 9.64 | 3.29 | 5.43 | |
| [180–210] | 11.06 | 17.01 | 12.93 | 8.47 | 5.06 | 7.88 | 8.34 | 10.71 | 9.68 | 4.50 | 5.67 | 7.69 | 8.38 | 1.41 | 3.63 | 0.81 | 1.62 | 3.91 | 3.33 | 4.66 | |
| [210–240] | 5.61 | 6.02 | 2.96 | 1.22 | 16.05 | 0.89 | 7.15 | 3.34 | 7.06 | 2.44 | 1.98 | 9.77 | 12.45 | 1.12 | 3.55 | 5.78 | 4.25 | 1.72 | 1.65 | 1.25 | |
| Mileage Phase [thsnd. km] | Vehicle Number j | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
| [0–30] | 0.50 | 2.15 | 1.33 | 1.72 | 1.50 | 1.69 | 2.15 | 2.31 | 1.13 | 2.18 | 6.32 | 20.80 | 2.59 | 1.54 | 5.75 | 3.55 | 2.16 | 0.63 | 1.24 | 0.62 | |
| [30–60] | 2.28 | 2.09 | 6.25 | 1.35 | 2.88 | 1.93 | 2.09 | 6.66 | 7.74 | 2.22 | 2.06 | 2.09 | 3.41 | 4.69 | 4.38 | 1.72 | 0.00 | 0.00 | 0.42 | 0.00 | |
| [60–90] | 0.00 | 15.51 | 18.13 | 14.21 | 10.30 | 6.98 | 15.51 | 3.74 | 0.00 | 0.00 | 4.18 | 12.31 | 2.18 | 2.97 | 1.74 | 3.36 | 4.72 | 1.52 | 7.33 | 0.54 | |
| [90–120] | 3.12 | 1.85 | 14.07 | 11.98 | 0.00 | 0.00 | 1.85 | 15.98 | 12.06 | 9.05 | 0.00 | 12.89 | 6.28 | 43.03 | 12.98 | 20.77 | 6.77 | 3.80 | 1.48 | 5.00 | |
| [120–150] | 8.48 | 27.23 | 24.17 | 8.62 | 7.74 | 22.02 | 27.23 | 10.08 | 7.43 | 11.04 | 6.49 | 4.75 | 7.97 | 25.11 | 35.63 | 13.94 | 5.75 | 1.02 | 7.48 | 6.42 | |
| [150–180] | 18.69 | 14.65 | 16.49 | 14.04 | 8.38 | 30.74 | 14.65 | 5.29 | 3.38 | 9.06 | 13.39 | 3.99 | 13.45 | 4.36 | 7.87 | 3.66 | 6.65 | 5.14 | 1.59 | 11.40 | |
| [180–210] | 15.41 | 9.01 | 47.23 | 4.58 | 24.99 | 16.15 | 3.30 | 13.38 | 14.10 | 11.42 | 8.73 | 8.21 | 6.23 | 8.55 | 6.35 | 4.44 | 5.16 | 2.03 | 5.91 | 11.81 | |
| [210–240] | 6.08 | 14.72 | 13.72 | 6.35 | 9.45 | 26.18 | 30.07 | 29.45 | 13.96 | 13.35 | 8.83 | 1.84 | 7.23 | 5.57 | 3.73 | 6.33 | 1.81 | 10.45 | 2.22 | 7.87 | |
| Mileage Phase [thsnd. km] | Vehicle Number j | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
| [0–60] | 3.15 | 2.97 | 4.06 | 3.09 | 3.45 | 6.61 | 5.35 | 4.66 | 3.20 | 3.94 | 4.53 | 4.96 | 5.31 | 2.37 | 6.08 | 4.16 | 7.42 | 4.87 | 4.53 | 4.43 | |
| [60–120] | 4.94 | 2.18 | 5.35 | 4.35 | 3.45 | 3.41 | 2.38 | 1.37 | 8.26 | 0.20 | 1.08 | 6.34 | 0.00 | 9.83 | 7.62 | 8.17 | 3.41 | 7.75 | 15.24 | 0.00 | |
| [120–180] | 11.26 | 8.87 | 2.96 | 1.16 | 3.62 | 25.51 | 7.28 | 9.60 | 6.13 | 4.79 | 14.27 | 17.70 | 10.02 | 4.77 | 6.77 | 3.74 | 5.88 | 17.43 | 5.53 | 12.91 | |
| [180–240] | 16.67 | 23.03 | 15.89 | 9.69 | 21.10 | 8.77 | 15.49 | 14.05 | 16.74 | 6.94 | 7.66 | 17.45 | 20.83 | 2.52 | 7.18 | 6.60 | 5.87 | 5.63 | 4.98 | 5.92 | |
| Mileage Phase [thsnd. km] | Vehicle Number j | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
| [0–60] | 2.78 | 4.24 | 7.58 | 3.07 | 4.38 | 3.62 | 4.24 | 8.97 | 8.87 | 4.40 | 8.38 | 22.89 | 6.01 | 6.23 | 10.13 | 5.27 | 2.16 | 0.63 | 1.65 | 0.62 | |
| [60–120] | 3.12 | 17.36 | 32.20 | 26.19 | 10.30 | 6.98 | 17.36 | 19.72 | 12.06 | 9.05 | 4.18 | 25.20 | 8.46 | 46.01 | 14.72 | 24.14 | 11.49 | 5.31 | 8.81 | 5.54 | |
| [120–180] | 27.16 | 41.88 | 40.65 | 22.66 | 16.13 | 52.76 | 41.88 | 15.37 | 10.81 | 20.10 | 19.88 | 8.74 | 21.42 | 29.47 | 43.50 | 17.60 | 12.40 | 6.16 | 9.08 | 17.82 | |
| [180–240] | 21.48 | 23.73 | 60.95 | 10.93 | 34.44 | 42.33 | 33.37 | 42.83 | 28.06 | 24.77 | 17.56 | 10.05 | 13.46 | 14.11 | 10.09 | 10.78 | 6.97 | 12.49 | 8.14 | 19.68 | |
| Statistic | ||||||||
|---|---|---|---|---|---|---|---|---|
| Average (thousand PLN) | 1.21 | 3.25 | 2.07 | 2.70 | 4.14 | 4.87 | 6.84 | 4.81 |
| Median (thousand PLN) | 0.93 | 3.30 | 1.49 | 1.34 | 3.87 | 3.33 | 6.68 | 3.45 |
| Std. deviation (thousand PLN) | 0.68 | 1.14 | 2.32 | 3.74 | 2.86 | 4.50 | 4.16 | 4.09 |
| Minimum (thousand PLN) | 0.39 | 0.87 | 0.00 | 0.00 | 0.00 | 0.00 | 0.81 | 0.89 |
| Maximum (thousand PLN) | 2.94 | 5.15 | 8.17 | 15.24 | 8.74 | 19.69 | 17.01 | 16.05 |
| Interquartile range (thousand PLN) | 0.69 | 1.17 | 3.57 | 4.41 | 4.80 | 3.81 | 5.68 | 5.14 |
| Variation coefficient (%) | 56.2 | 35.1 | 112.1 | 138.5 | 69.1 | 92.4 | 60.8 | 85.0 |
| Kolmogorov–Smirnov | Shapiro–Wilk | |||||
|---|---|---|---|---|---|---|
| Statistic | df | Significance p | Statistic | df | Significance p | |
| 0.238 | 20 | 0.004 | 0.837 | 20 | 0.003 | |
| 0.122 | 20 | 0.200 * | 0.939 | 20 | 0.232 | |
| 0.214 | 20 | 0.017 | 0.846 | 20 | 0.005 | |
| 0.235 | 20 | 0.005 | 0.738 | 20 | <0.001 | |
| 0.140 | 20 | 0.200 * | 0.936 | 20 | 0.205 | |
| 0.223 | 20 | 0.010 | 0.775 | 20 | <0.001 | |
| 0.116 | 20 | 0.200 * | 0.957 | 20 | 0.486 | |
| 0.171 | 20 | 0.126 | 0.845 | 20 | 0.004 | |
| Kolmogorov–Smirnov | Shapiro–Wilk | |||||
|---|---|---|---|---|---|---|
| Statistic | df | Significance p | Statistic | df | Significance p | |
| 0.345 | 20 | <0.001 | 0.506 | 20 | <0.001 | |
| 0.228 | 20 | 0.008 | 0.896 | 20 | 0.035 | |
| 0.202 | 20 | 0.031 | 0.873 | 20 | 0.013 | |
| 0.181 | 20 | 0.085 | 0.787 | 20 | <0.001 | |
| 0.248 | 20 | 0.002 | 0.849 | 20 | 0.005 | |
| 0.123 | 20 | 0.200 * | 0.892 | 20 | 0.029 | |
| 0.217 | 20 | 0.015 | 0.717 | 20 | <0.001 | |
| 0.181 | 20 | 0.086 | 0.839 | 20 | 0.003 | |
| Brand | M | I |
|---|---|---|
| Total N | 160 | 160 |
| Test statistics | 44.599 | 49.493 |
| Degree of freedom | 7 | 7 |
| Asymptotic significance (two-sided test) | <0.001 | <0.001 |
| Tested Phase Pair | Significance a,b | |
|---|---|---|
| Brand | ||
| M | I | |
| <0.001 | 0.819 | |
| 0.013 | 0.172 | |
| 0.978 | 0.819 | |
| 0.172 | 0.172 | |
| 0.819 | 0.560 | |
| 0.082 | 0.978 | |
| 0.172 | 1.000 | |
| Brand | Difference in Means (I–J) | Significance | 95% Confidence Interval | |||
|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | |||||
| M | −2.0403 | 0.488 | −5.1819 | 1.1012 | ||
| −0.8602 | 0.990 | −4.0017 | 2.2814 | |||
| −1.4889 | 0.829 | −4.6304 | 1.6527 | |||
| −2.9296 | 0.087 | −6.0712 | 0.2120 | |||
| −3.6635 | 0.011 | −6.8051 | −0.5219 | |||
| −5.6283 | <0.001 | −8.7699 | −2.4867 | |||
| −3.6045 | 0.013 | −6.7460 | −0.4629 | |||
| 1.1802 | 0.943 | −1.9614 | 4.3217 | |||
| 0.5515 | 0.999 | −2.5901 | 3.6930 | |||
| −0.8893 | 0.988 | −4.0308 | 2.2523 | |||
| −1.6232 | 0.757 | −4.7647 | 1.5184 | |||
| −3.5880 | 0.013 | −6.7295 | −0.4464 | |||
| −1.5642 | 0.790 | −4.7057 | 1.5774 | |||
| −0.6287 | 0.999 | −3.7702 | 2.5129 | |||
| −2.0694 | 0.469 | −5.2110 | 1.0721 | |||
| −2.8033 | 0.118 | −5.9449 | 0.3382 | |||
| −4.7681 | <0.001 | −7.9097 | −1.6266 | |||
| −2.7443 | 0.135 | −5.8859 | 0.3973 | |||
| −1.4407 | 0.852 | −4.5823 | 1.7008 | |||
| −2.1746 | 0.402 | −5.3162 | 0.9669 | |||
| −4.1394 | 0.002 | −7.2810 | −0.9979 | |||
| −2.1156 | 0.439 | −5.2572 | 1.0259 | |||
| −0.7339 | 0.996 | −3.8754 | 2.4077 | |||
| −2.6987 | 0.150 | −5.8402 | 0.4429 | |||
| −0.6749 | 0.998 | −3.8164 | 2.4667 | |||
| −1.9648 | 0.538 | −5.1064 | 1.1768 | |||
| 0.0590 | 1.000 | −3.0826 | 3.2006 | |||
| 2.0238 | 0.499 | −1.1178 | 5.1654 | |||
| I | 0.3796 | 1.000 | −7.1276 | 7.8868 | ||
| −3.1691 | .899 | −10.6763 | 4.3381 | |||
| −6.0557 | 0.212 | −13.5629 | 1.4515 | |||
| −10.3367 | 0.001 | −17.8439 | −2.8295 | |||
| −7.2511 | 0.067 | −14.7583 | 0.2562 | |||
| −8.2580 | 0.020 | −15.7652 | −0.7508 | |||
| −7.8674 | 0.033 | −15.3746 | −0.3602 | |||
| −3.5487 | 0.831 | −11.0559 | 3.9585 | |||
| −6.4353 | 0.152 | −13.9426 | 1.0719 | |||
| −10.7163 | <0.001 | −18.2235 | −3.2091 | |||
| −7.6307 | 0.043 | −15.1379 | −0.1235 | |||
| −8.6376 | 0.012 | −16.1448 | −1.1304 | |||
| −8.2470 | 0.020 | −15.7542 | −0.7398 | |||
| −2.8866 | 0.936 | −10.3939 | 4.6206 | |||
| −7.1676 | 0.073 | −14.6748 | 0.3396 | |||
| −4.0820 | 0.706 | −11.5892 | 3.4252 | |||
| −5.0889 | 0.430 | −12.5961 | 2.4183 | |||
| −4.6983 | 0.537 | −12.2055 | 2.8089 | |||
| −4.2810 | 0.653 | −11.7882 | 3.2262 | |||
| −1.1953 | 1.000 | −8.7025 | 6.3119 | |||
| −2.2023 | 0.986 | −9.7095 | 5.3049 | |||
| −1.8116 | 0.996 | −9.3189 | 5.6956 | |||
| 3.0857 | 0.911 | −4.4215 | 10.5929 | |||
| 2.0787 | 0.990 | −5.4285 | 9.5859 | |||
| 2.4693 | 0.972 | −5.0379 | 9.9766 | |||
| −1.0070 | 1.000 | −8.5142 | 6.5003 | |||
| −0.6163 | 1.000 | −8.1235 | 6.8909 | |||
| 0.3906 | 1.000 | −7.1166 | 7.8978 | |||
| Statistic | ||||||||
|---|---|---|---|---|---|---|---|---|
| Brand M | Brand I | |||||||
| Average (thousand PLN) | 4.46 | 4.77 | 9.01 | 11.65 | 5.81 | 15.41 | 23.77 | 22.31 |
| Median (thousand PLN) | 4.48 | 3.90 | 7.02 | 9.23 | 4.39 | 11.78 | 19.99 | 18.62 |
| Std. deviation (thousand PLN) | 1.28 | 3.90 | 6.06 | 6.29 | 4.89 | 10.92 | 13.58 | 14.32 |
| Minimum (thousand PLN) | 2.37 | 0.00 | 1.16 | 2.52 | 0.62 | 3.12 | 6.16 | 6.97 |
| Maximum (thousand PLN) | 7.42 | 15.24 | 25.51 | 23.03 | 22.89 | 46.01 | 52.76 | 60.95 |
| Interquartile range (thousand PLN) | 1.96 | 6.15 | 7.72 | 10.64 | 5.33 | 15.69 | 24.71 | 21.23 |
| Coefficient of variation (%) | 28.80 | 81.75 | 67.22 | 54.02 | 84.26 | 70.86 | 57.10 | 64.19 |
| Brand | Kolmogorov–Smirnov | Shapiro–Wilk | |||||
|---|---|---|---|---|---|---|---|
| Statistic | df | Significance p | Statistic | df | Significance p | ||
| M | 0.345 | 20 | <0.001 | 0.506 | 20 | <0.001 | |
| 0.228 | 20 | 0.008 | 0.896 | 20 | 0.035 | ||
| 0.202 | 20 | 0.031 | 0.873 | 20 | 0.013 | ||
| 0.181 | 20 | 0.085 | 0.787 | 20 | <0.001 | ||
| I | 0.248 | 20 | 0.002 | 0.849 | 20 | 0.005 | |
| 0.123 | 20 | 0.200 * | 0.892 | 20 | 0.029 | ||
| 0.217 | 20 | 0.015 | 0.717 | 20 | <0.001 | ||
| 0.181 | 20 | 0.086 | 0.839 | 20 | 0.003 | ||
| Brand | Source | Sum of Squares | Degrees of Freedom | Mean Squares | F Ratio | Significance |
|---|---|---|---|---|---|---|
| M | Inter-phase | 724.600 | 3 | 241.533 | 10.376 | <0.001 |
| Intra-phase | 1769.218 | 76 | 23.279 | |||
| Total | 2493.818 | 79 | ||||
| I | Inter-phase | 4035.914 | 3 | 1345.305 | 10.105 | <0.001 |
| Intra-phase | 10,117.931 | 76 | 133.131 | |||
| Total | 14,153.845 | 79 |
| Statistic | ||||||||
|---|---|---|---|---|---|---|---|---|
| Average (thousand PLN) | 3.09 | 2.71 | 6.26 | 9.15 | 13.43 | 10.34 | 11.35 | 10.96 |
| Median (thousand PLN) | 1.93 | 2.09 | 3.96 | 6.53 | 8.55 | 8.72 | 8.64 | 8.35 |
| Std. deviation (thousand PLN) | 4.43 | 2.22 | 5.95 | 10.03 | 9.69 | 6.95 | 10.05 | 8.57 |
| Minimum (thousand PLN) | 0.50 | 0.00 | 0.00 | 0.00 | 1.02 | 1.59 | 2.03 | 1.81 |
| Maximum (thousand PLN) | 20.80 | 7.74 | 18.13 | 43.03 | 35.63 | 30.74 | 47.23 | 30.07 |
| Interquartile range (thousand PLN) | 1.26 | 2.69 | 10.24 | 11.10 | 16.90 | 9.94 | 8.57 | 8.20 |
| Variation coefficient (%) | 143.4 | 81.9 | 95.0 | 109.6 | 72.1 | 67.2 | 88.6 | 78.2 |
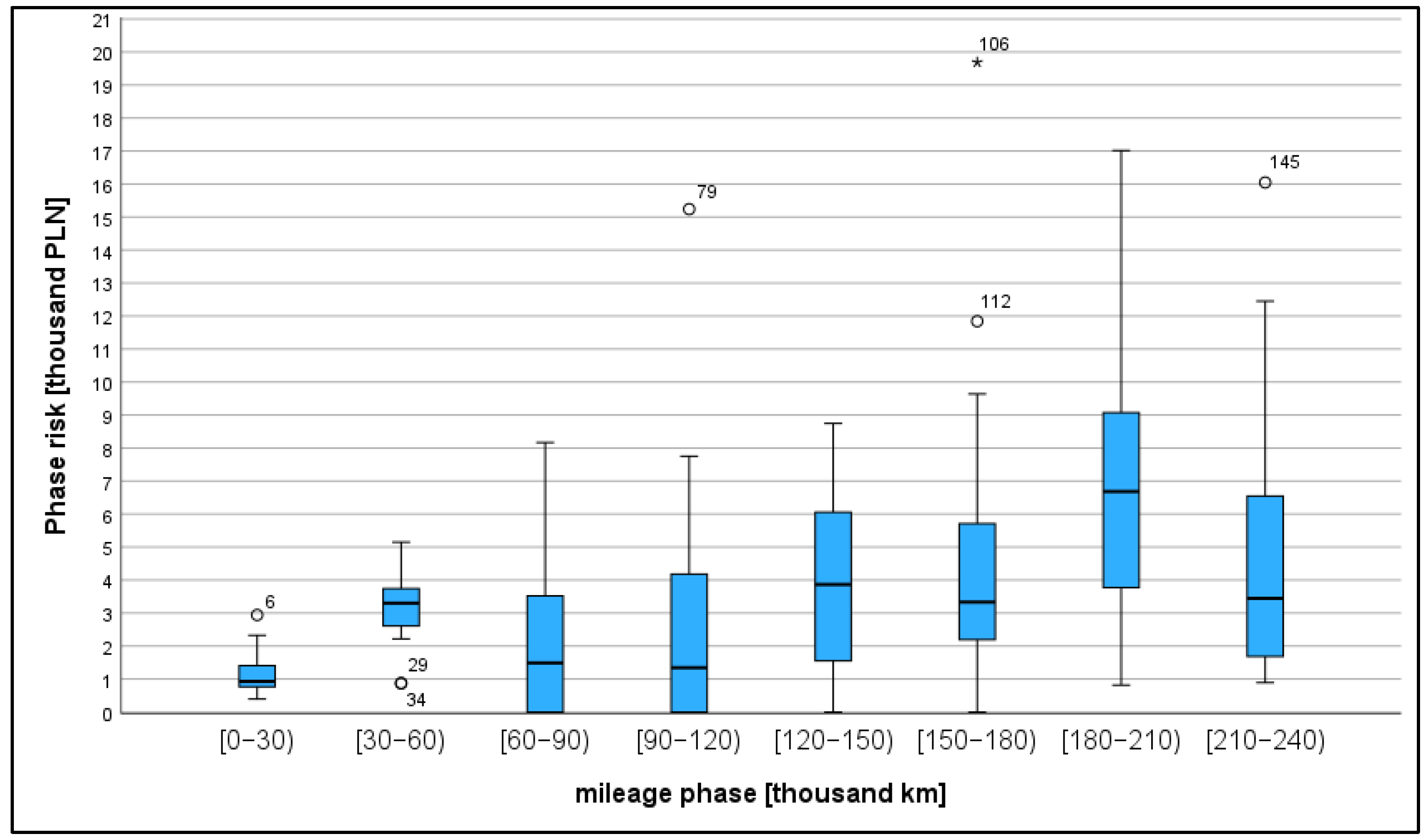
| Point in Figure 2 | Causes of the Outliers | |
|---|---|---|
| point 6 | road collision | |
| point 29 | virtually no repairs for vehicles in this phase | |
| point 34 | virtually no repairs for vehicles in this phase | |
| point 79 | the vehicle required repair and towing | |
| point 106 | many repairs connected with the driving system (wheels, hubs, bearings) | |
| point 112 | many different individual repairs | |
| point 145 | unscheduled tyre change |
| Point in Figure 3 | Causes of the Outliers | |
|---|---|---|
| point 11 | vehicle towing | |
| point 12 | repairs indicating a road collision | |
| point 15 | many repairs of the exhaust system and exhaust gas treatment system | |
| point 29 | numerous repairs | |
| point 74 | numerous repairs of the exhaust system and exhaust gas treatment system, body and paint repair | |
| point 106 | numerous expensive repairs | |
| point 123 | numerous expensive repairs, gearbox replacement | |
| point 146 | vehicle repair due to a road collision | |
| point 147 | expensive gearbox repair and another expensive repair | |
| point 148 | expensive gearbox repair |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niewczas, A.; Andrzejczak, K.; Mórawski, Ł.; Dębicka, E. Study of Phase Changes in Operational Risk for Trucks. Energies 2024, 17, 2143. https://doi.org/10.3390/en17092143
Niewczas A, Andrzejczak K, Mórawski Ł, Dębicka E. Study of Phase Changes in Operational Risk for Trucks. Energies. 2024; 17(9):2143. https://doi.org/10.3390/en17092143
Chicago/Turabian StyleNiewczas, Andrzej, Karol Andrzejczak, Łukasz Mórawski, and Ewa Dębicka. 2024. "Study of Phase Changes in Operational Risk for Trucks" Energies 17, no. 9: 2143. https://doi.org/10.3390/en17092143
APA StyleNiewczas, A., Andrzejczak, K., Mórawski, Ł., & Dębicka, E. (2024). Study of Phase Changes in Operational Risk for Trucks. Energies, 17(9), 2143. https://doi.org/10.3390/en17092143






