Novel Advanced Artificial Neural Network-Based Online Stator and Rotor Resistance Estimator for Vector-Controlled Speed Sensorless Induction Motor Drives
Abstract
1. Introduction
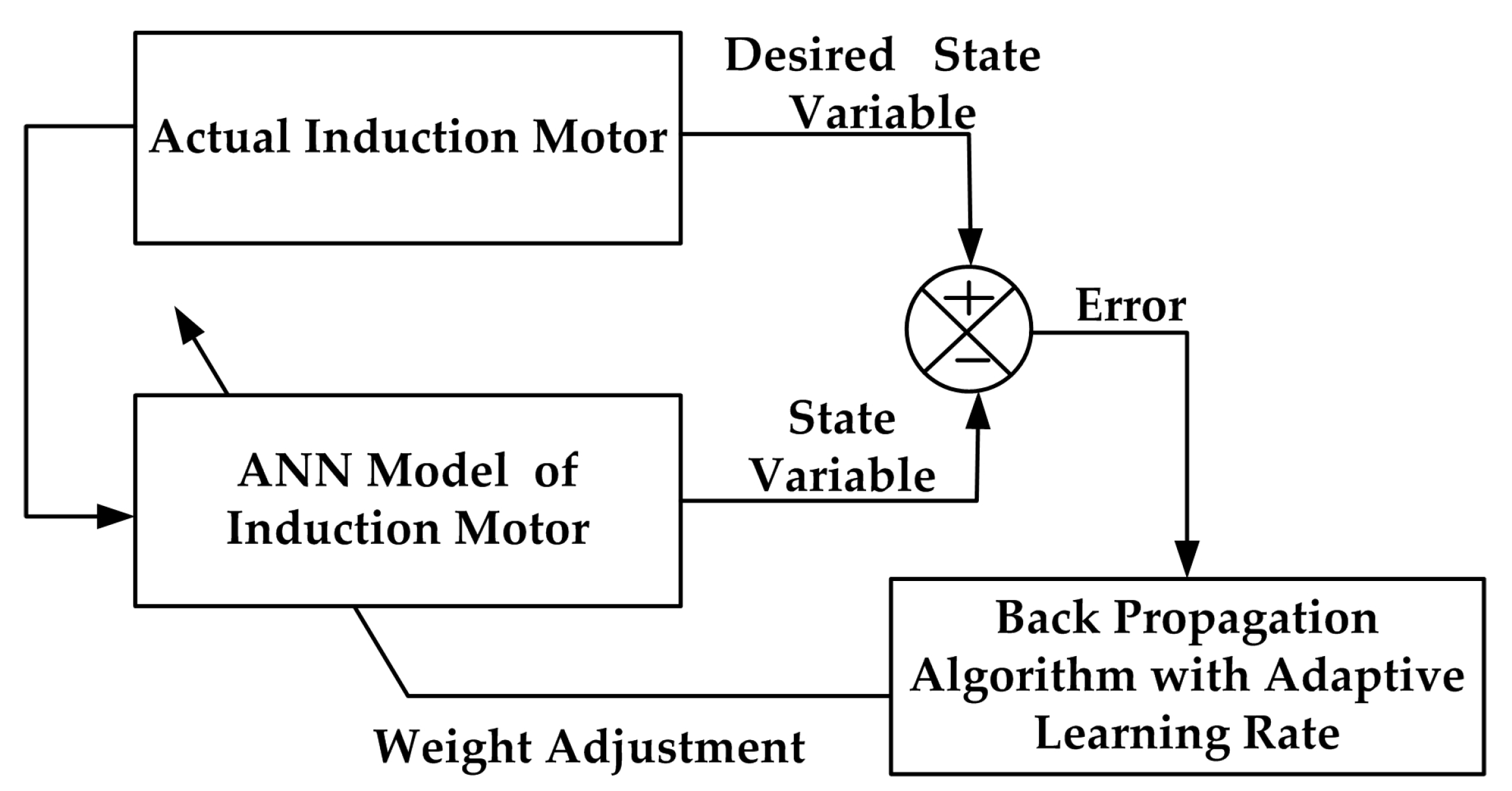
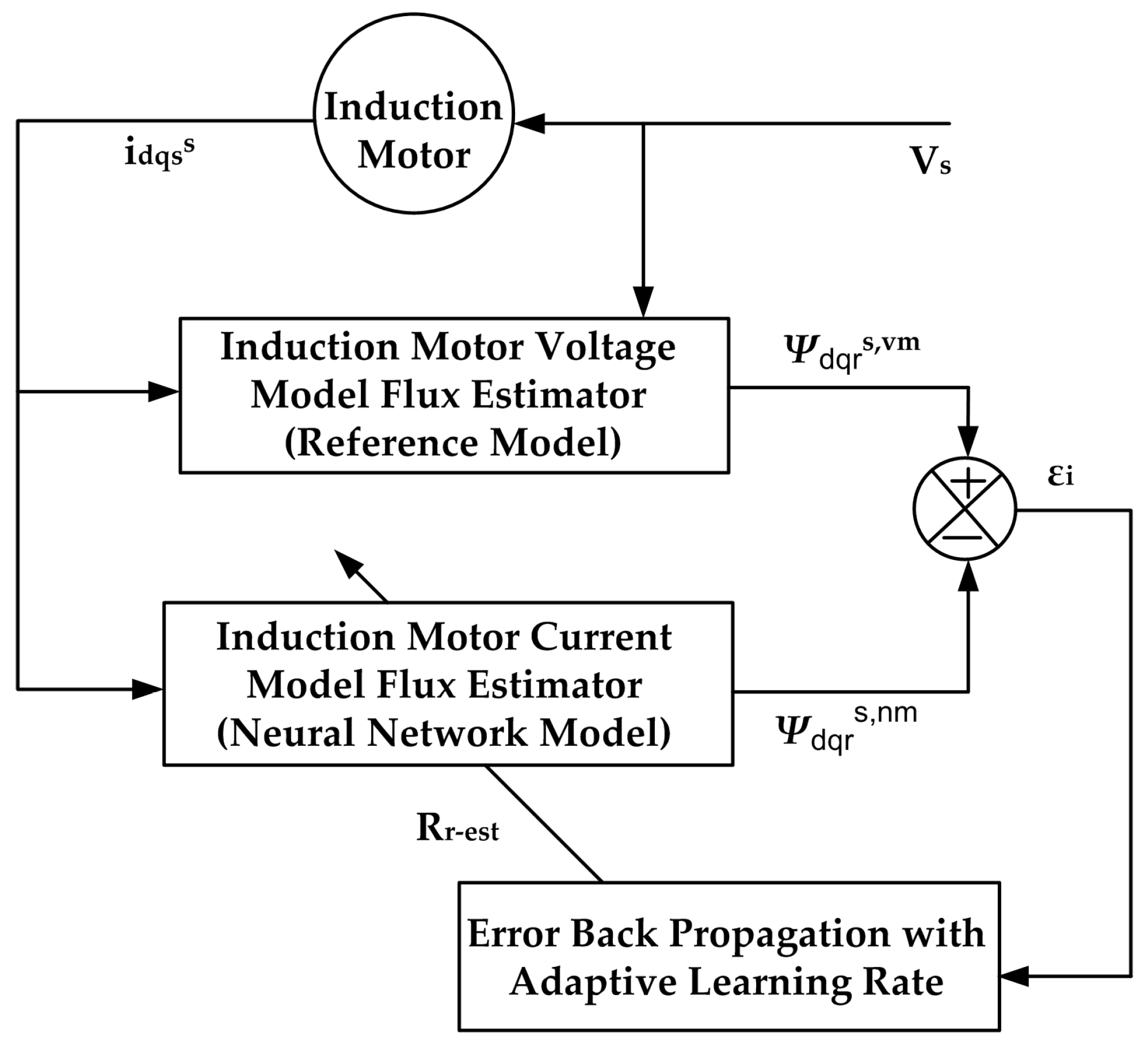
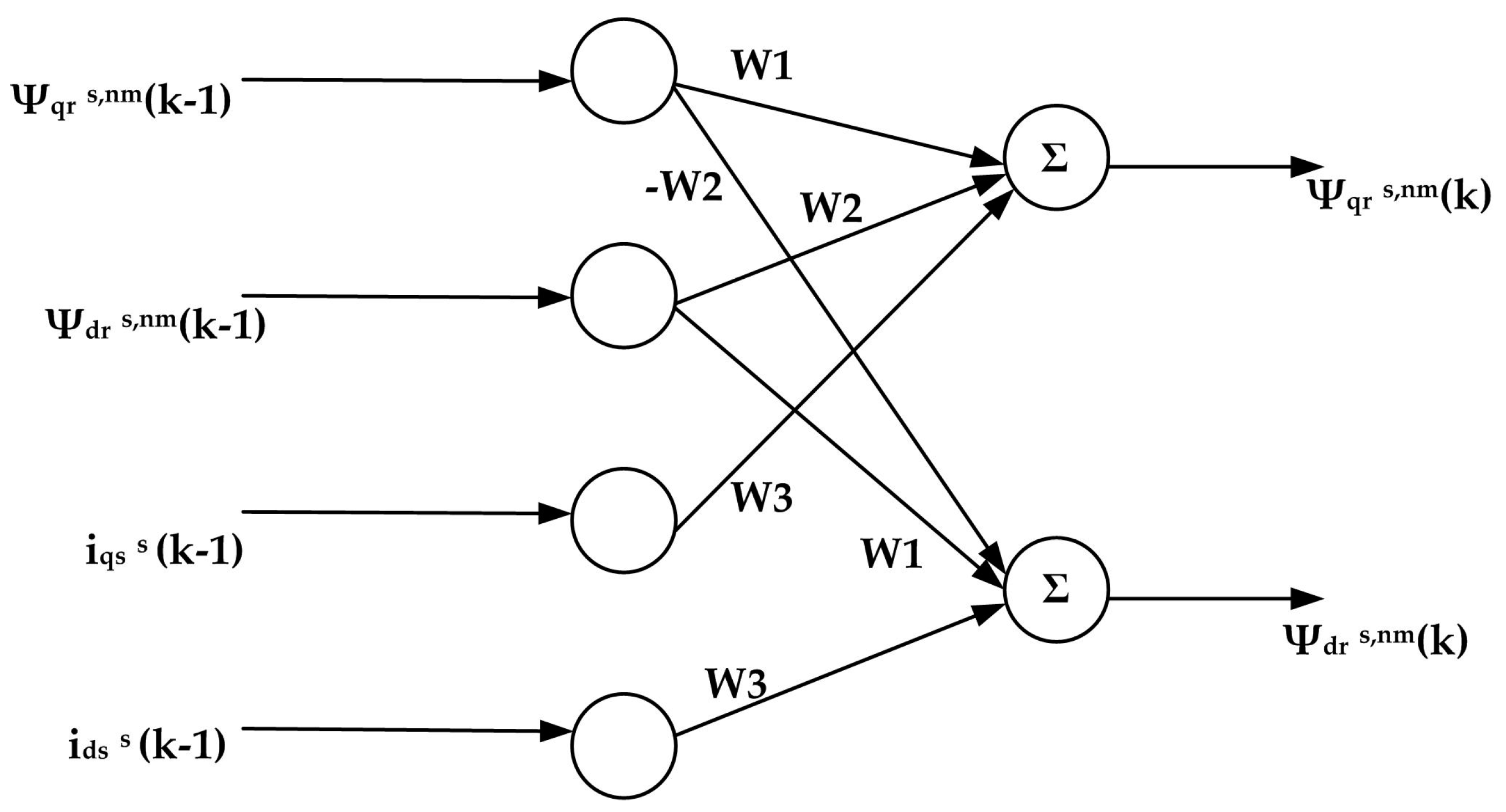
2. Artificial Neural Network-Based Rotor Resistance Estimator
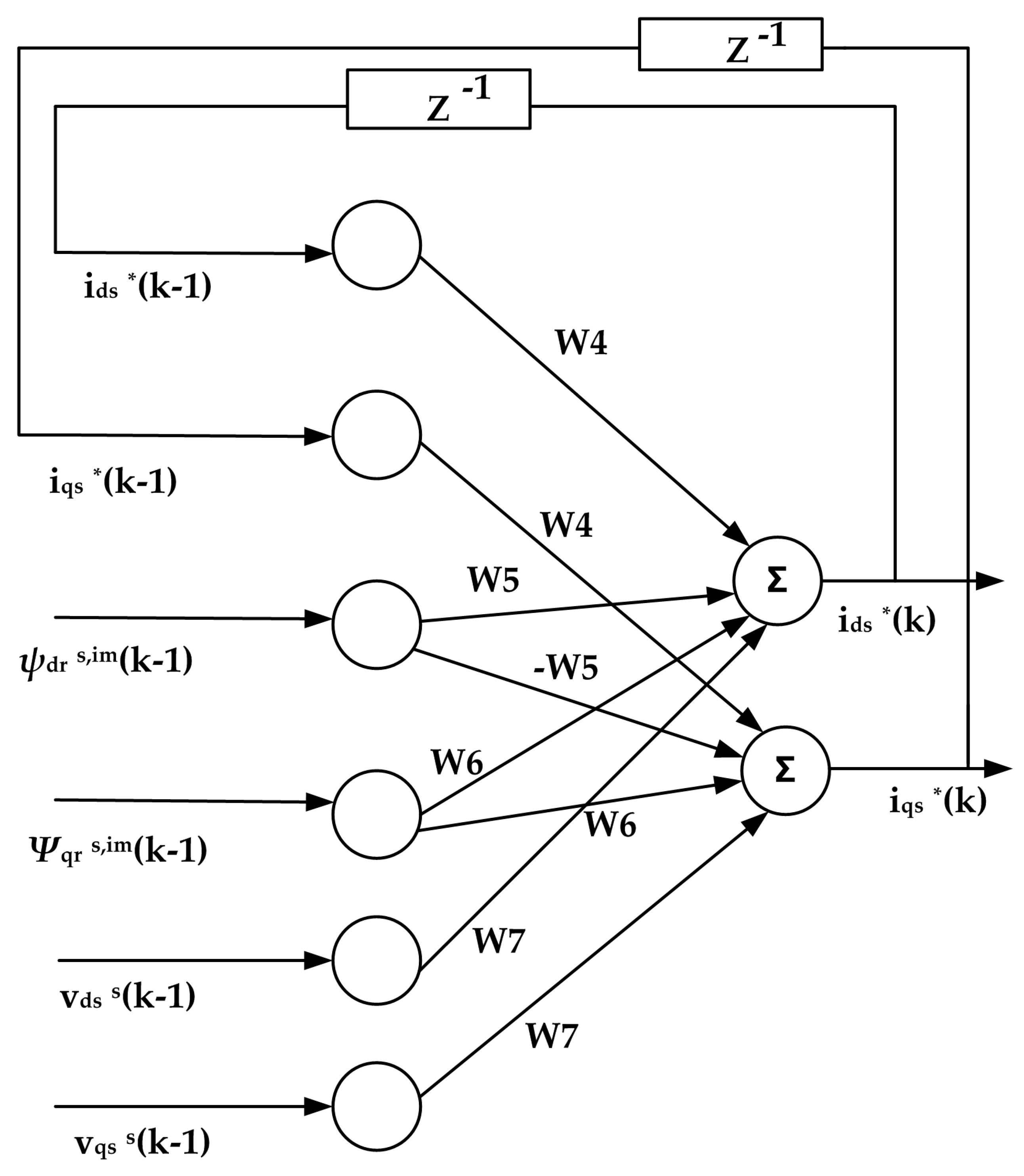
3. Artificial Neural Network-Based Stator Resistance Estimator
4. Results and Discussion
4.1. Tests for Identification of Machine Parameters
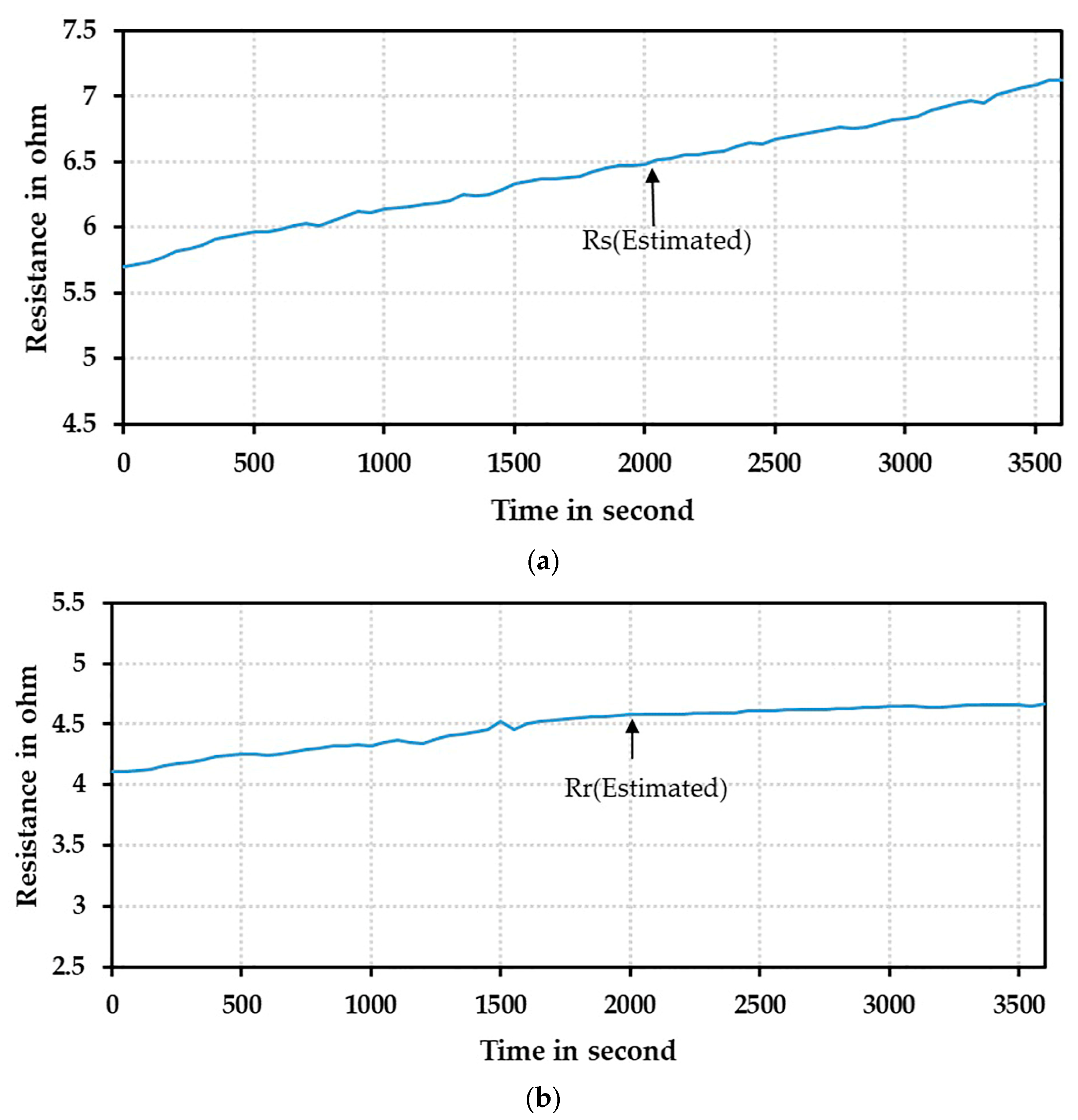
4.1.1. Stator Winding Resistance Estimation
4.1.2. No-Load Test
4.1.3. Locked Rotor or Short Circuit Test
4.1.4. Locked Rotor or Short Circuit Test
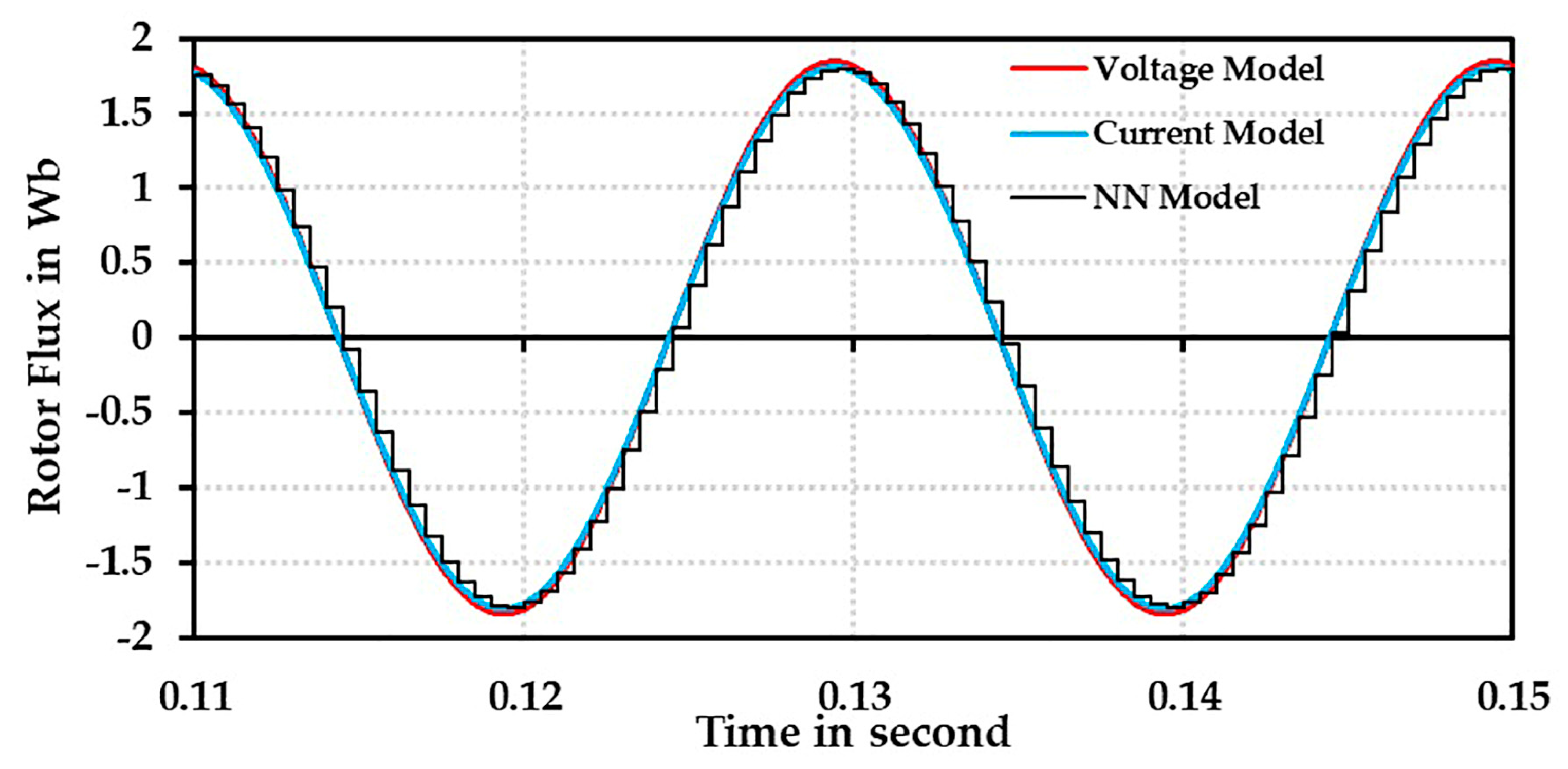
4.2. Modeling Analysis
- With the sampled terminal voltages and currents and by using the developed neural network model as presented in Section 3, stator resistance is estimated online.
- Using the obtained stator resistance, rotor fluxes are estimated. Using the neural network model as presented in Section 2, rotor resistance is determined.
- The speed is evaluated by using the obtained stator resistance, rotor resistance, and rotor fluxes as presented in Section 3.
4.2.1. Simulation Results of the Performance of the Rotor Resistance Estimator and Analysis
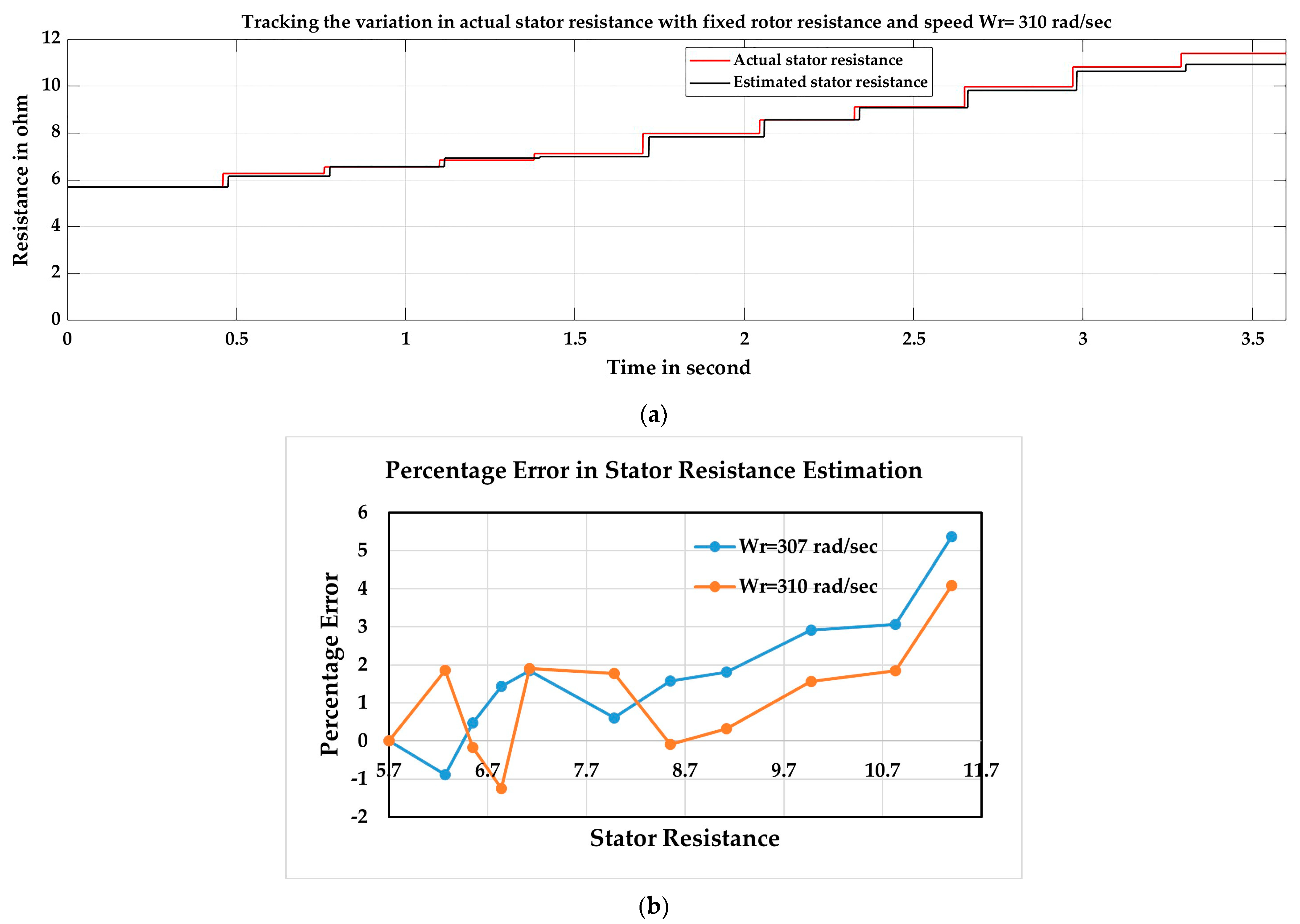
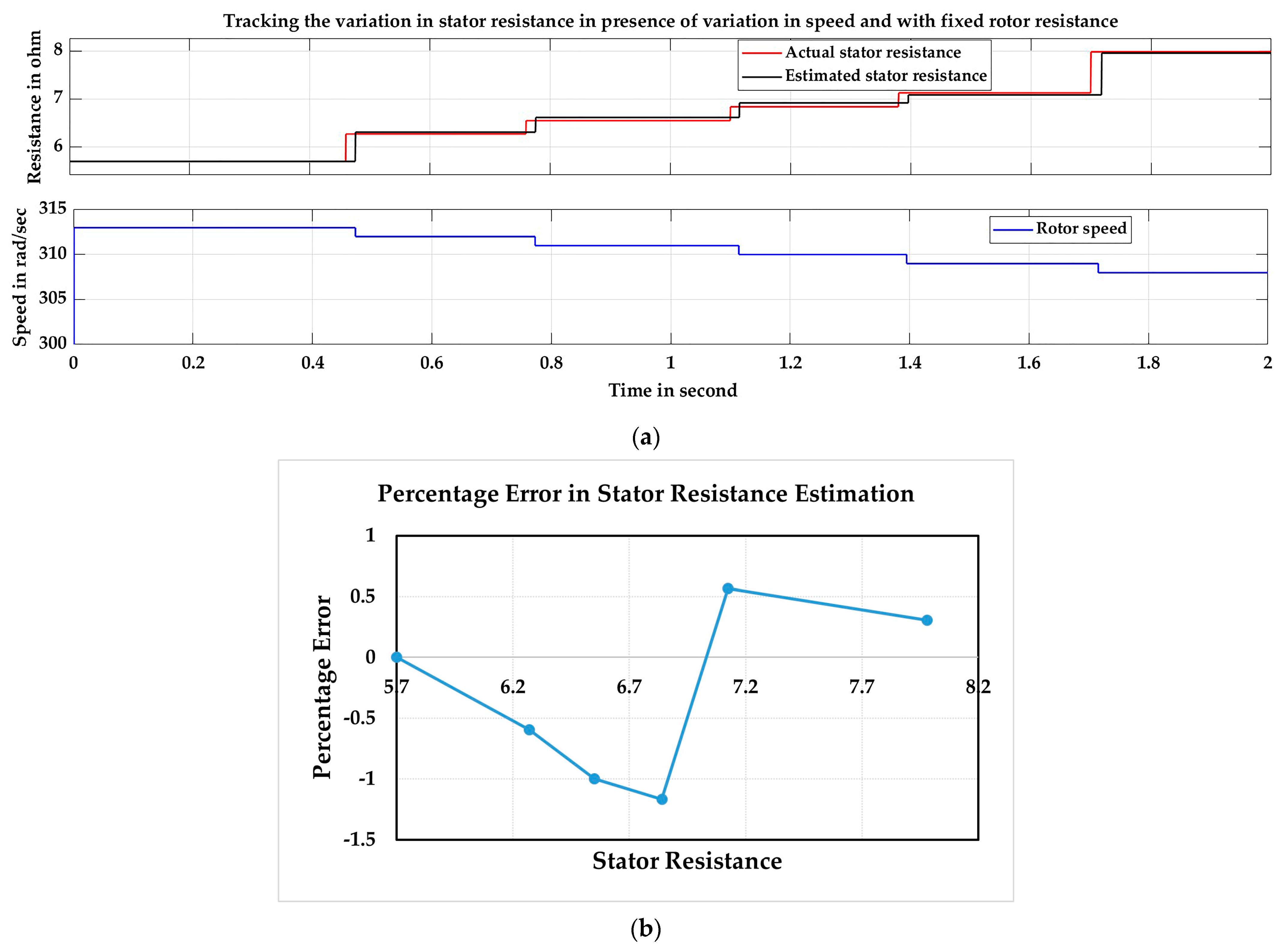
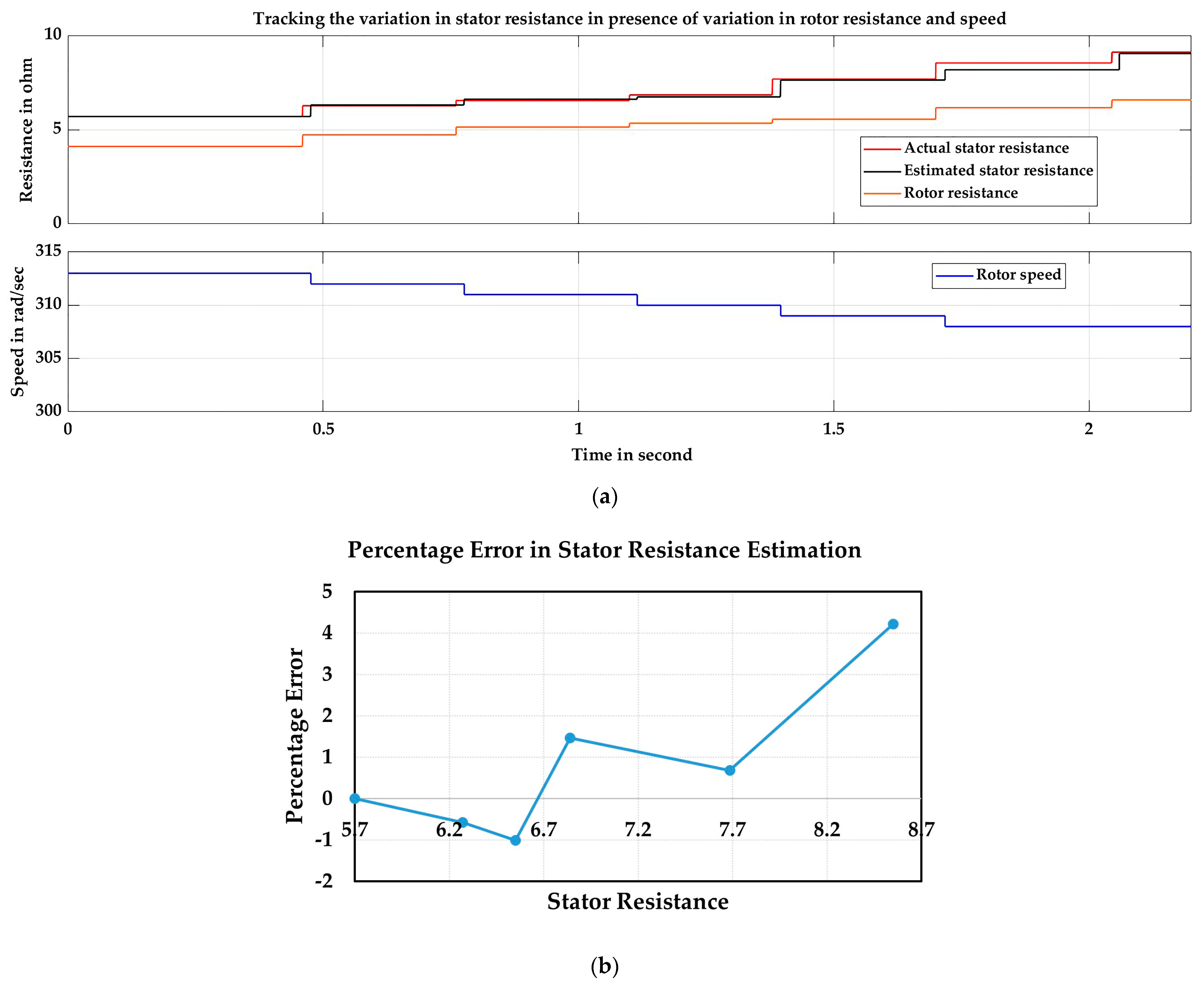
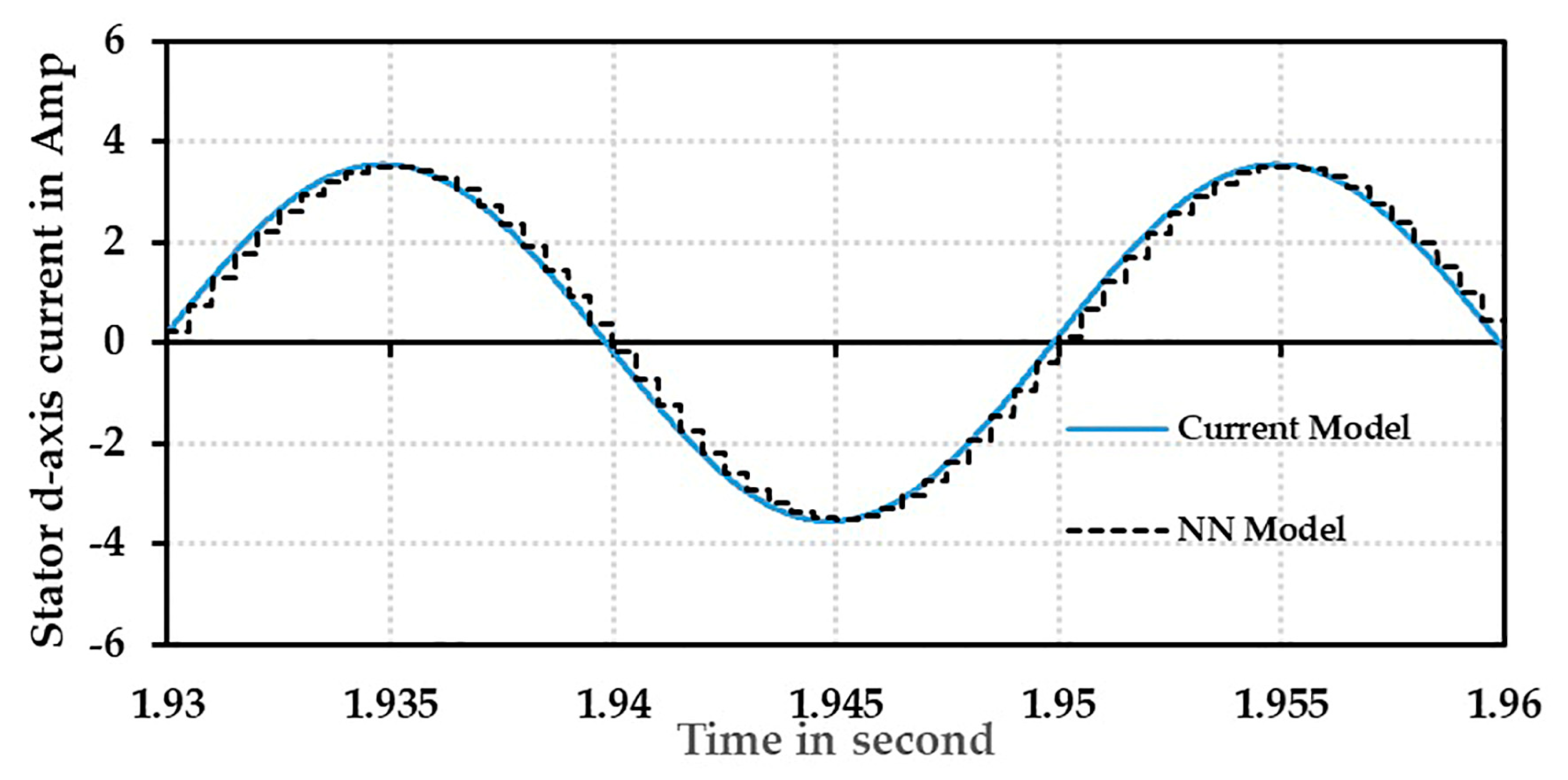
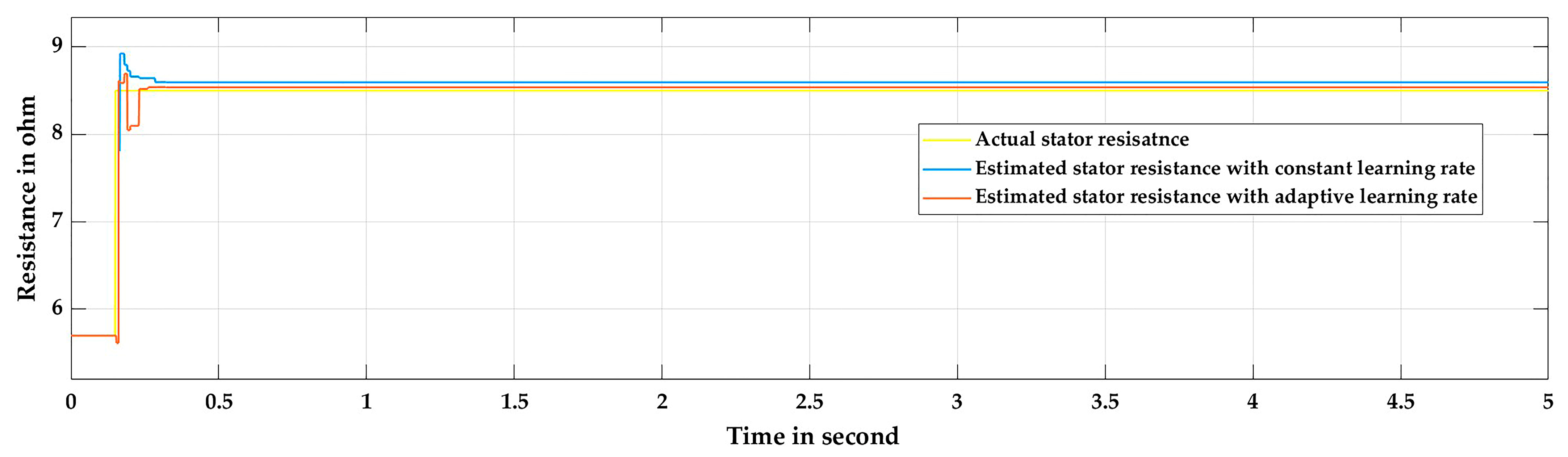
4.2.2. Simulation Results of Performance of Stator Resistance Estimator and Analysis
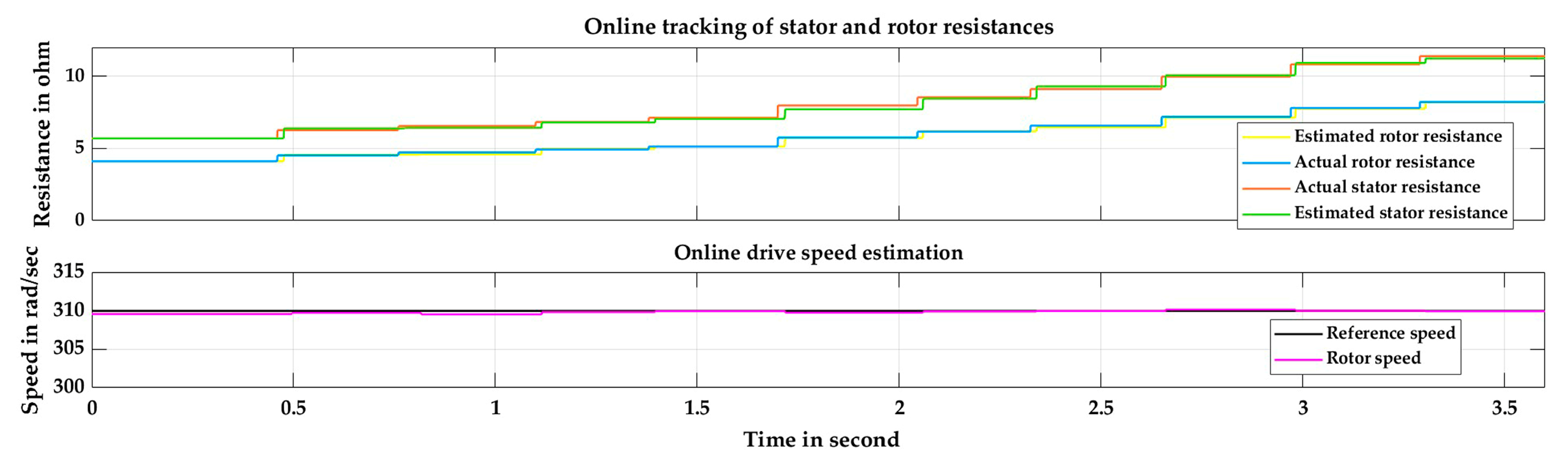
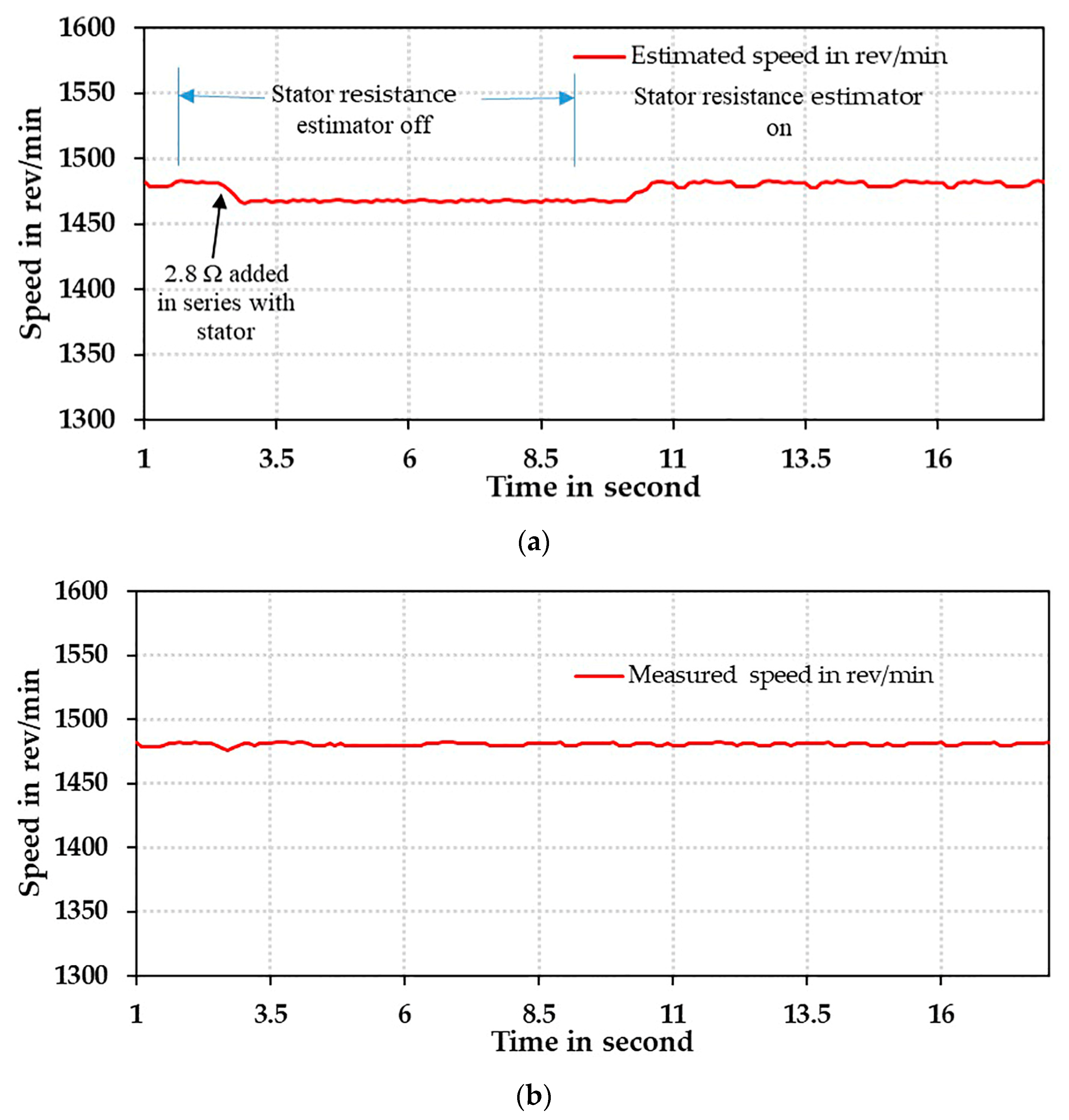
4.2.3. Speed Estimation with Integrated Online Rotor and Stator Resistance Estimation
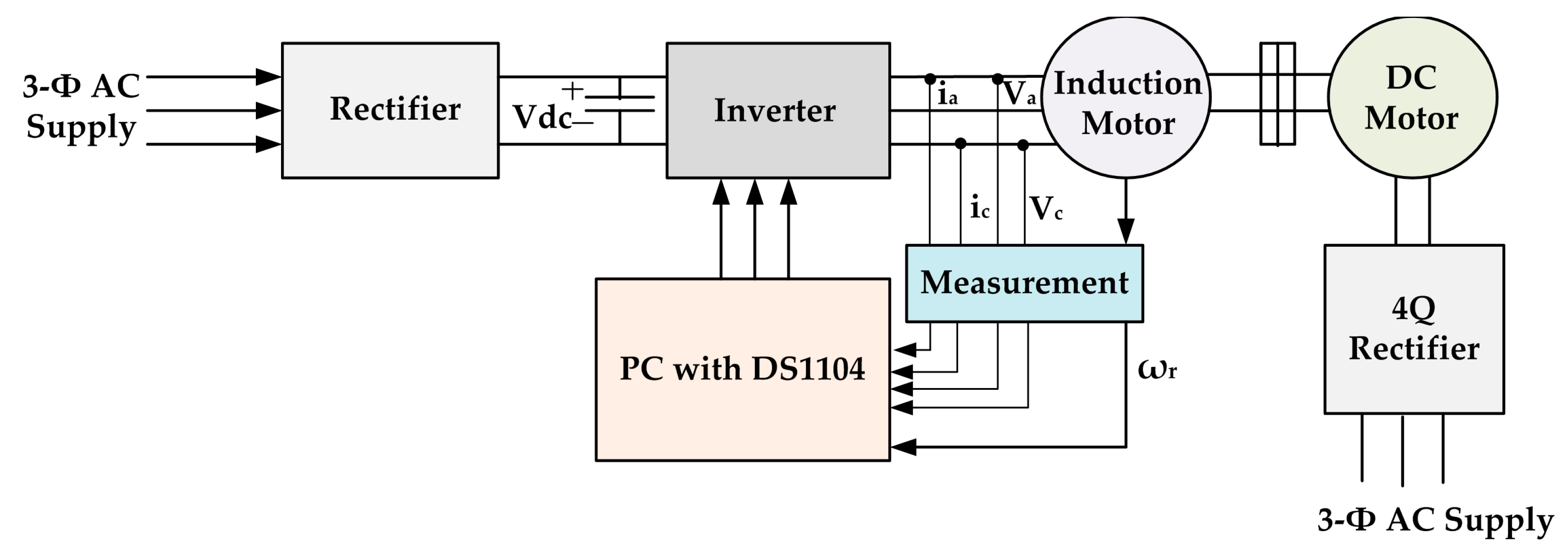
4.3. Experimental Evaluation and Results
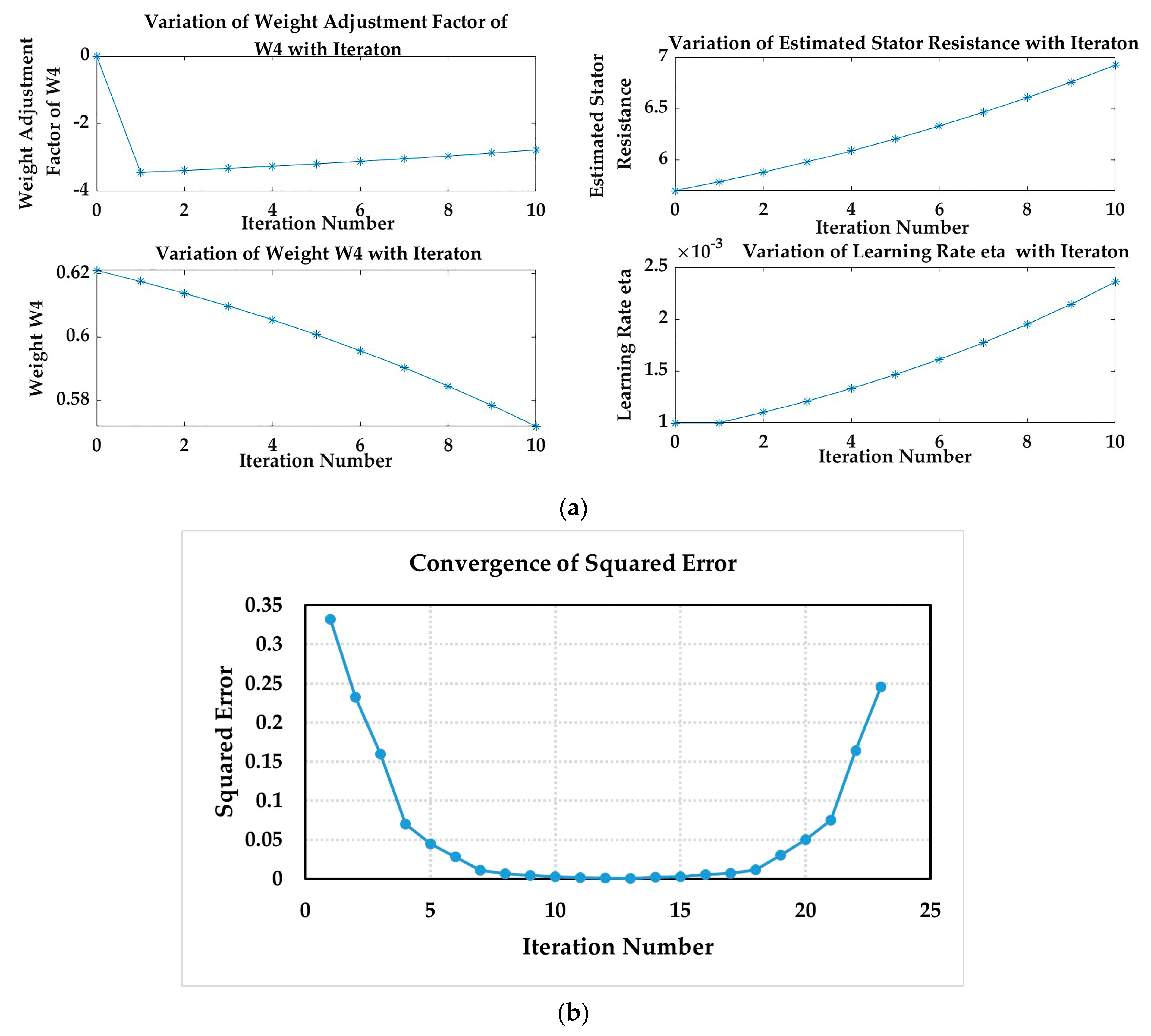
4.4. Discussion
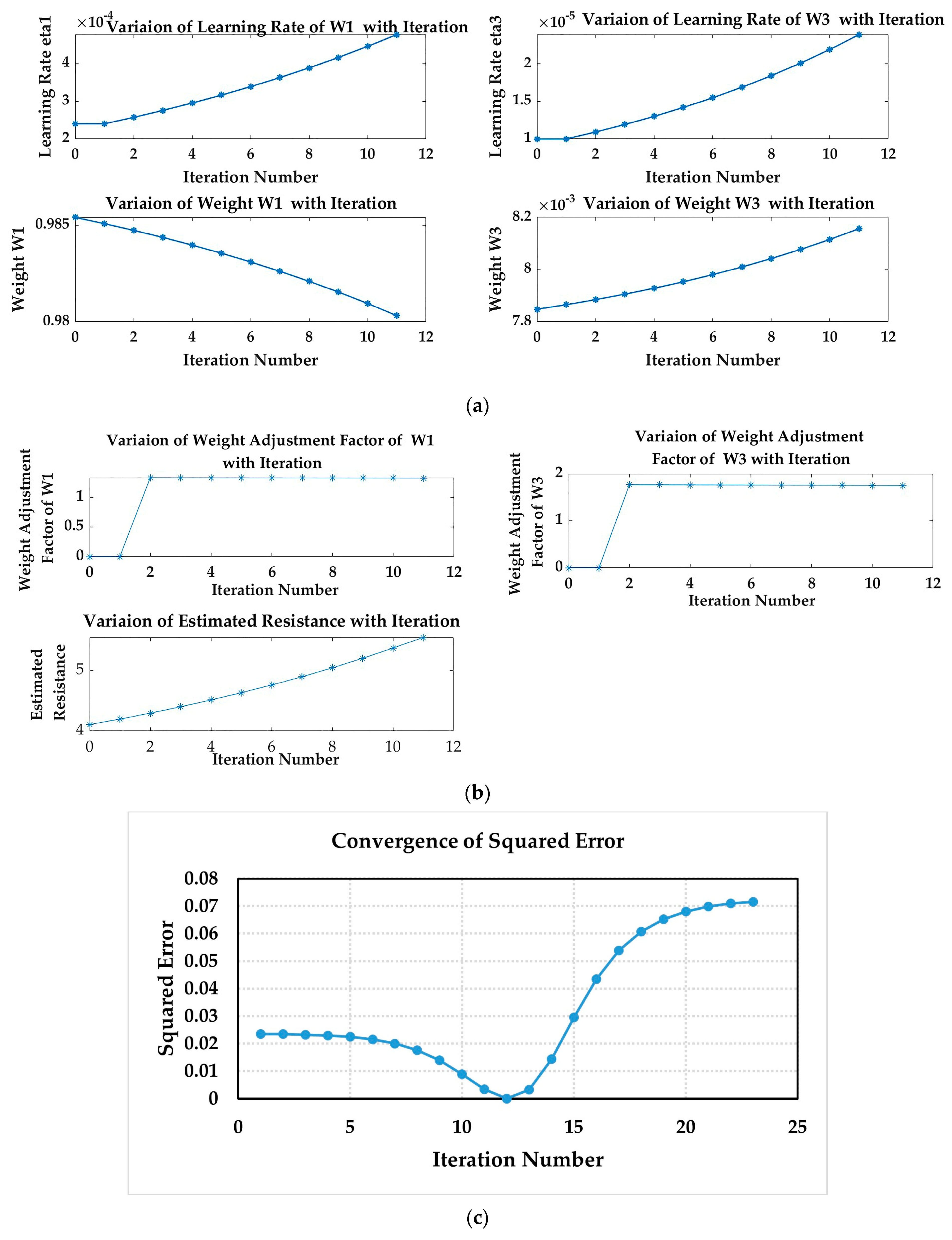
- As the number of iterations needed for the estimation of stator and rotor resistances is reduced with the proposed algorithm, the quick estimation of stator and rotor resistances is obtained as compared to the conventional constant learning rate approach. For the step change in the stator resistance, with the proposed approach, estimated stator resistance converges with the minimum error of estimation within 150 ms as compared to 250 ms obtained from the conventional constant learning rate approach [7].
- The proposed algorithm ensures the reduction in error of estimated resistances. For the step change in stator resistance, with the proposed approach, the estimation error is 0.48%, which is superior to the conventional constant learning rate approach of around 2%.
- The proposed algorithm tracks the stator resistance smoothly with the pulsation in estimated resistance within 0.35%, which is better than the constant learning rate or other function-based learning rate approach [8].
- The smooth estimation of speed is obtained with the developed algorithm where pulsation is within 0.4% which is much lower than that obtained by a conventional constant learning rate algorithm [24].
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols
| Voltage model d-axis rotor flux linkages in the stator reference frame | |
| Voltage model q-axis rotor flux linkages in the stator reference frame | |
| d-axis stator current in the stator reference frame | |
| q-axis stator current in the stator reference frame | |
| d-axis stator voltage in the stator reference frame | |
| q-axis stator voltage in the stator reference frame | |
| Neural network model d-axis rotor flux linkages in the stator reference frame | |
| Neural network model q-axis rotor flux linkages in the stator reference frame | |
| Induction motor current model d-axis rotor flux linkages in the stator reference frame | |
| Induction motor current model q-axis rotor flux linkages in the stator reference frame | |
| Rs | Stator resistance |
| Rr | Rotor resistance |
| Ls | Stator self-inductance |
| Lr | Rotor self-inductance |
| Lm | Magnetizing inductance |
References
- Dianov, A.; Anuchin, A. Offline Measurement of Stator Resistance and Inverter Voltage Drop Using Least Squares. IEEE Access 2023, 11, 17053–17065. [Google Scholar] [CrossRef]
- Dinolova, P.; Ruseva, V.; Dinolov, O. Energy Efficiency of Induction Motor Drives: State of the Art, Analysis and Recommendations. Energies 2023, 16, 7136. [Google Scholar] [CrossRef]
- Montano, J.; Garzón, O.D.; Herrera-Jaramillo, D.A.; Montoya, O.D.; Andrade, F.; Tobon, A. Estimating the Parameters of a Three-Phase Induction Motor Using the Vortex Search Algorithm. Iran. J. Sci. Technol. Trans. Electr. Eng. 2024, 48, 337–347. [Google Scholar] [CrossRef]
- Abbasi, M.A.; Bin Husain, A.R. Model Predictive Control of a Dual Induction Motor Drive Fed by a Single Voltage Source Inverter. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 1623–1637. [Google Scholar] [CrossRef]
- Çanakoǧlu, A.I.; Yetgin, A.G.; Temurtaş, H.; Turan, M. Induction Motor Parameter Estimation Using Metaheuristic Methods. Turk. J. Electr. Eng. Comput. Sci. 2014, 22, 1177–1192. [Google Scholar] [CrossRef]
- Jisha, L.K.; Thomas, A.A.P. A Comparative Study on Scalar and Vector Control of Induction Motor Drives. In Proceedings of the 2013 International Conference on Circuits, Controls and Communications (CCUBE), Bengaluru, India, 27–28 December 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Karanayil, B.; Rahman, M.F.; Grantham, C. Online Stator and Rotor Resistance Estimation Scheme Using Artificial Neural Networks for Vector Controlled Speed Sensorless Induction Motor Drive. IEEE Trans. Ind. Electron. 2007, 54, 167–176. [Google Scholar] [CrossRef]
- Van, T.P.; Tien, D.V.; Leonowicz, Z.; Jasinski, M.; Sikorski, T.; Chakrabarti, P. Online Rotor and Stator Resistance Estimation Based on Artificial Neural Network Applied in Sensorless Induction Motor Drive. Energies 2020, 13, 4946. [Google Scholar] [CrossRef]
- Kim, Y.-R.; Sul, S.-K.; Park, M.-H. Speed Sensorless Vector Control of Induction Motor Using Extended Kalman Filter. IEEE Trans. Ind. Appl. 1994, 30, 1225–1233. [Google Scholar] [CrossRef]
- Noori, O.B.; Mustafa, M.O. Flux and Speed Estimation of Induction Motors Using Extended Kalman Filter. Int. J. Comput. Appl. 2018, 181, 975–8887. [Google Scholar]
- Moaveni, B.; Masoumi, Z.; Rahmani, P. Introducing Improved Iterated Extended Kalman Filter (IIEKF) to Estimate the Rotor Rotational Speed, Rotor and Stator Resistances of Induction Motors. IEEE Access 2023, 11, 17584–17593. [Google Scholar] [CrossRef]
- Horváth, K.; Kuslits, M. Dynamic Performance of Estimator-Based Speed Sensorless Control of Induction Machines Using Extended and Unscented Kalman Filters. Power Electron. Drives 2018, 3, 129–144. [Google Scholar] [CrossRef]
- Strandt, A.R.; Strandt, A.P.; Schneider, S.C.; Yaz, E.E. Stator Resistance Estimation Using Adaptive Estimation via a Bank of Kalman Filters. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1078–1083. [Google Scholar]
- Karthikeyan, A.; Prabhakaran, K.K.; Nagamani, C. Stator Flux Based MRAS Speed and Stator Resistance Estimator for Sensorless PMSM Drive. In Proceedings of the 2017 14th IEEE India Council International Conference (INDICON), Roorkee, India, 15–17 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Hasanzadeh, A.; Reed, D.M.; Hofmann, H.F. Rotor Resistance Estimation for Induction Machines Using Carrier Signal Injection With Minimized Torque Ripple. IEEE Trans. Energy Convers. 2019, 34, 942–951. [Google Scholar] [CrossRef]
- Agrebi, Y.; Koubaa, Y.; Boussak, M. Rotor Resistance Estimation for Indirect Stator Oriented Induction Motor Drive Based on MRAS Scheme. In Proceedings of the 10th International Conference on Sciences and Techniques of Automatic Control & Computer Engineering, Hammamet, Tunisia, 20–22 December 2009; Academic Publication Center of Tunis: Hammamet, Tunisia, 2009. [Google Scholar]
- Parasiliti, F.; Petrella, R.; Tursini, M. Adaptive Sliding Mode Observer for Speed Sensorless Control of Induction Motors. In Proceedings of the Conference Record of the 1999 IEEE Industry Applications Conference. Thirty-Forth IAS Annual Meeting (Cat. No.99CH36370), Phoenix, AZ, USA, 3–7 October 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 4, pp. 2277–2283. [Google Scholar]
- Sahraoui, K.; Kouzi, K.; Ameur, A. Neural Networks Trained with Sliding Mode Control for DSIM Supplied by Two Voltage Inverters on Three Levels. In Proceedings of the 2018 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Algiers, Algeria, 28–31 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Yang, S.; Sun, R.; Cao, P.; Xie, Z.; Zhang, X. Sliding-Mode Observer Based Rotor Resistance Updating Method for Indirect Vector Controlled Induction Motor. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Harbin, China, 7–10 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–5. [Google Scholar]
- Kubota, H.; Matsuse, K.; Nakano, T. DSP-Based Speed Adaptive Flux Observer of Induction Motor. IEEE Trans. Ind. Appl. 1993, 29, 344–348. [Google Scholar] [CrossRef]
- Jouili, M.; Agrebi, Y.; Koubaa, Y.; Boussak, M. A Luenberger State Observer for Simultaneous Estimation of Speed and Stator Resistance in Sensorless IRFOC Induction Motor Drives. In Proceedings of the 2015 16th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Monastir, Tunisia, 21–23 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 898–904. [Google Scholar]
- Azzoug, Y.; Menacer, A.; Ameid, T.; Ammar, A. Performance Improvement of Sensorless Vector Control for Induction Motor Drives Using Fuzzy-Logic Luenberger Observer: Experimental Investigation. In Proceedings of the 2019 International Conference on Applied Automation and Industrial Diagnostics (ICAAID), Elazig, Turkey, 25–27 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Wlas, M.; Krzeminski, Z.; Toliyat, H.A. Neural-Network-Based Parameter Estimations of Induction Motors. IEEE Trans. Ind. Electron. 2008, 55, 1783–1794. [Google Scholar] [CrossRef]
- Cirrincione, M.; Pucci, M.; Cirrincione, G.; Capolino, G.A. A New Experimental Application of Least-Squares Techniques for the Estimation of the Induction Motor Parameters. IEEE Trans. Ind. Appl. 2003, 39, 1247–1256. [Google Scholar] [CrossRef]
- Karanayil, B.; Rahman, M.F.; Grantham, C. Stator and Rotor Resistance Observers for Induction Motor Drive Using Fuzzy Logic and Artificial Neural Networks. In Proceedings of the 38th IAS Annual Meeting on Conference Record of the Industry Applications Conference, 2003, Salt Lake City, UT, USA, 12–16 October 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 1, pp. 124–131. [Google Scholar]
- Gadoue, S.M.; Giaouris, D.; Finch, J.W. Sensorless Control of Induction Motor Drives at Very Low and Zero Speeds Using Neural Network Flux Observers. IEEE Trans. Ind. Electron. 2009, 56, 3029–3039. [Google Scholar] [CrossRef]
- Haddoun, A.; Benbouzid, M.E.H.; Diallo, D.; Abdessemed, R.; Ghouili, J.; Srairi, K. Comparative Analysis of Estimation Techniques of SFOC Induction Motor for Electric Vehicles. In Proceedings of the 2008 18th International Conference on Electrical Machines, Vilamoura, Portugal, 6–9 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–6. [Google Scholar]
- Gadoue, S.M.; Giaouris, D.; Finch, J.W. Performance Evaluation of a Sensorless Induction Motor Drive at Very Low and Zero Speed Using a MRAS Speed Observer. In Proceedings of the 2008 IEEE Region 10 and the Third international Conference on Industrial and Information Systems, Kharagpur, India, 8–10 December 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–6. [Google Scholar]
- Peng, F.Z.; Fukao, T. Robust Speed Identification for Speed-Sensorless Vector Control of Induction Motors. IEEE Trans. Ind. Appl. 1994, 30, 1234–1240. [Google Scholar] [CrossRef]
- Nitayotan, C.; Sangwongwanich, S. A Filtered Back EMF Based Speed-Sensorless Induction Motor Drive. In Proceedings of the Conference Record of the 2001 IEEE Industry Applications Conference. 36th IAS Annual Meeting (Cat. No.01CH37248), Chicago, IL, USA, 30 September–4 October 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 2, pp. 1224–1231. [Google Scholar]
- Maiti, S.; Chakraborty, C. A New Instantaneous Reactive Power Based MRAS for Sensorless Induction Motor Drive. Simul. Model. Pract. Theory 2010, 18, 1314–1326. [Google Scholar] [CrossRef]
- Manohar, M.; Das, S. Combined Speed and Rotor Resistance Estimation for Speed Sensorless Induction Motor Drive Using Reactive Power Based MRAS. In Proceedings of the Michael Faraday IET International Summit 2015, Kolkata, India, 12–13 September 2015; Institution of Engineering and Technology: Stevenage, UK, 2015; pp. 56–57. [Google Scholar]
- Kiran, K.; Das, S. Implementation of Reactive Power-based MRAS for Sensorless Speed Control of Brushless Doubly Fed Reluctance Motor Drive. IET Power Electron. 2018, 11, 192–201. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Dybkowski, M. Stator-Current-Based MRAS Estimator for a Wide Range Speed-Sensorless Induction-Motor Drive. IEEE Trans. Ind. Electron. 2010, 57, 1296–1308. [Google Scholar] [CrossRef]
- Asfu, W.T. Stator Current-Based Model Reference Adaptive Control for Sensorless Speed Control of the Induction Motor. J. Control Sci. Eng. 2020, 2020, 8954704. [Google Scholar] [CrossRef]
- Ravi Teja, A.V.; Chakraborty, C.; Maiti, S.; Hori, Y. A New Model Reference Adaptive Controller for Four Quadrant Vector Controlled Induction Motor Drives. IEEE Trans. Ind. Electron. 2012, 59, 3757–3767. [Google Scholar] [CrossRef]
- Das, S.; Kumar, R.; Chattopadhyay, A.K. Comparison of Q- and X-MRAS for Speed Sensor Less Induction Motor Drive On. In Proceedings of the Michael Faraday IET International Summit 2015, Kolkata, India, 12–13 September 2015; Institution of Engineering and Technology: Stevenage, UK, 2015; pp. 319–324. [Google Scholar]
- Ide, K.; Ha, J.I.; Sawamura, M.; Iura, H.; Yamamoto, Y. High Frequency Injection Method Improved by Flux Observer for Sensorless Control of an Induction Motor. In Proceedings of the Power Conversion Conference-Osaka 2002 (Cat. No.02TH8579), Osaka, Japan, 2–5 April 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 2, pp. 516–521. [Google Scholar]
- Xu, Z.; Shao, C.; Feng, D. An MRAS Method for Sensorless Control of Induction Motor over a Wide Speed Range. J. Control Theory Appl. 2011, 9, 203–209. [Google Scholar] [CrossRef]
- Xu, L.; Inoa, E.; Liu, Y.; Guan, B. A New High Frequency Injection Method for Sensorless Control of Doubly-Fed Induction Machines. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1758–1764. [Google Scholar]
- Kojabadi, H.M.; Abarzadeh, M.; Chang, L. A Comparative Study of Various Methods of IM’s Rotor Resistance Estimation. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2884–2891. [Google Scholar]
- Kumar, R.; Das, S.; Syam, P.; Chattopadhyay, A.K. Review on Model Reference Adaptive System for Sensorless Vector Control of Induction Motor Drives. IET Electr. Power Appl. 2015, 9, 496–511. [Google Scholar] [CrossRef]
- Tiwari, A.; Kumar, B.; Chauhan, Y.K. ANN Based RF-MRAS Speed Estimation of Induction Motor Drive at Low Speed. In Proceedings of the 2017 International conference of Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 20–22 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 176–179. [Google Scholar]
- Dehghan-Azad, E.; Gadoue, S.; Atkinson, D.; Slater, H.; Barrass, P.; Blaabjerg, F. Sensorless Control of IM Based on Stator-Voltage MRAS for Limp-Home EV Applications. IEEE Trans. Power Electron. 2018, 33, 1911–1921. [Google Scholar] [CrossRef]
- Gadoue, S.M.; Giaouris, D.; Finch, J.W. A Neural Network Based Stator Current MRAS Observer for Speed Sensorless Induction Motor Drives. In Proceedings of the 2008 IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 650–655. [Google Scholar]
- Venkadesan, A.; Himavathi, S.; Muthuramalingam, A.; Sedhuraman, K. ANN Based Flux Estimator for Rotor Resistance Estimation in Vector Controlled IM Drives. In Proceedings of the 2018 IEEE International Conference on System, Computation, Automation and Networking (ICSCAN), Pondicherry, India, 6–7 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Krishnan, R. Electric Motor Drives: Modeling, Analysis and Control; Pearson Prentice Hall: Hoboken, NJ, USA, 2013. [Google Scholar]
- Ajithanjaya Kumar, M.K.; Ballal, R.; Saralaya, S.; Bhat, J.S. Novel Adaptive Learning Rate Back Propagation Neural Network-Based Online Rotor and Stator Resistance Estimator for Sensorless Induction Motor Drives. In Advances in Communication and Applications; Shetty, N.R., Prasad, N.H., Nagaraj, H.C., Eds.; Springer Nature Singapore: Singapore, 2024; pp. 557–573. [Google Scholar]
- Kumar, A.; Bhat, S.; Ballal, R. Experimental Investigations of Load Characteristics of Induction Motor Drive. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1065, 012046. [Google Scholar] [CrossRef]
- Sengamalai, U.; Anbazhagan, G.; Thamizh Thentral, T.M.; Vishnuram, P.; Khurshaid, T.; Kamel, S. Three Phase Induction Motor Drive: A Systematic Review on Dynamic Modeling, Parameter Estimation, and Control Schemes. Energies 2022, 15, 8260. [Google Scholar] [CrossRef]
- Da Silva, L.E.B.; Bose, B.K.; Pinto, J.O.P. Recurrent-Neural-Network-Based Implementation of a Programmable Cascaded Low-Pass Filter Used in Stator Flux Synthesis of Vector-Controlled Induction Motor Drive. IEEE Trans. Ind. Electron. 1999, 46, 662–665. [Google Scholar] [CrossRef]
- Wang, Z.S.; Ho, S.L. Indirect Rotor Field Orientation Vector Control for Induction Motor Drives in the Absence of Current Sensors. In Proceedings of the 2006 CES/IEEE 5th International Power Electronics and Motion Control Conference, Shanghai, China, 14–16 August 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 1–5. [Google Scholar]


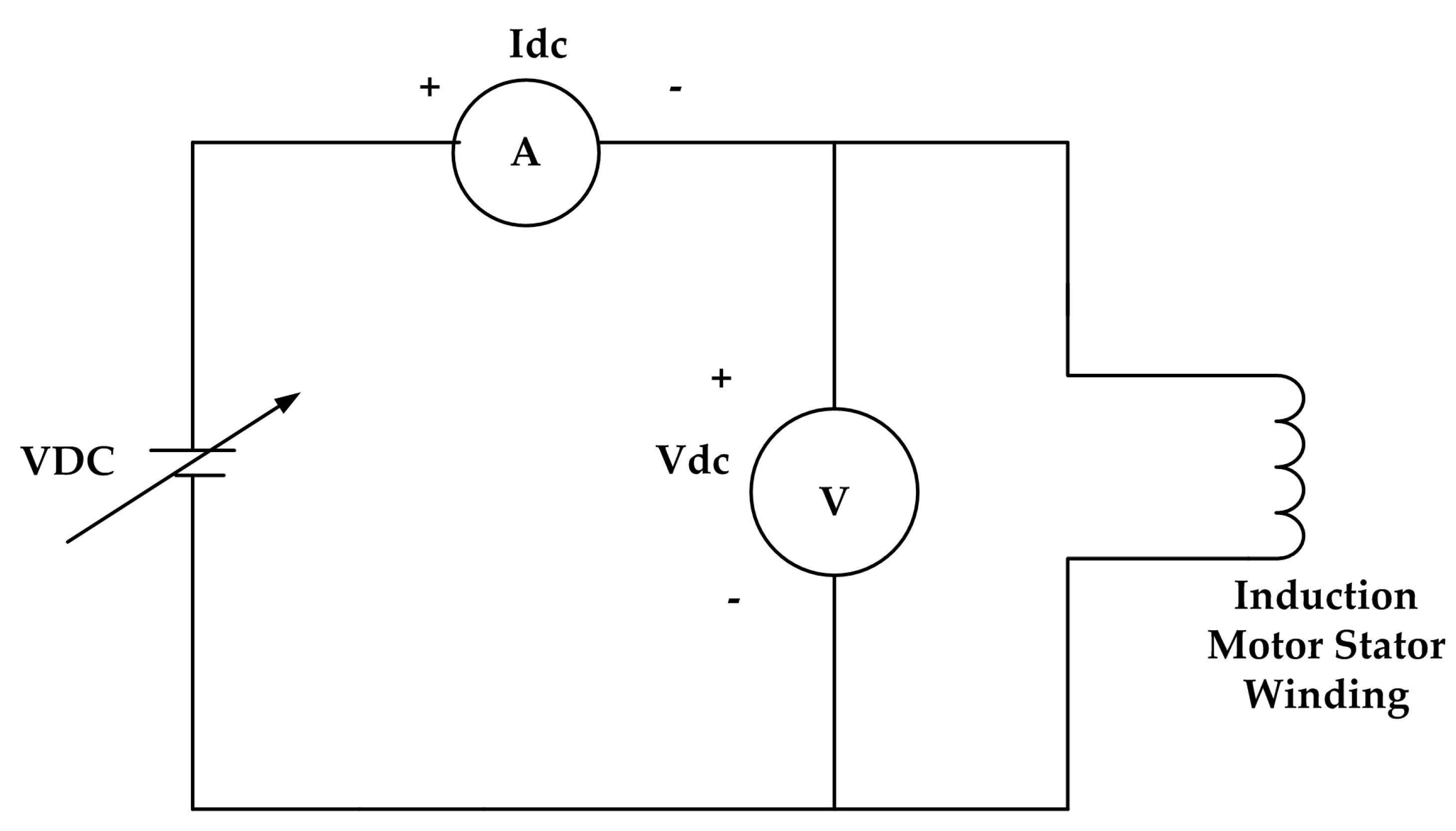
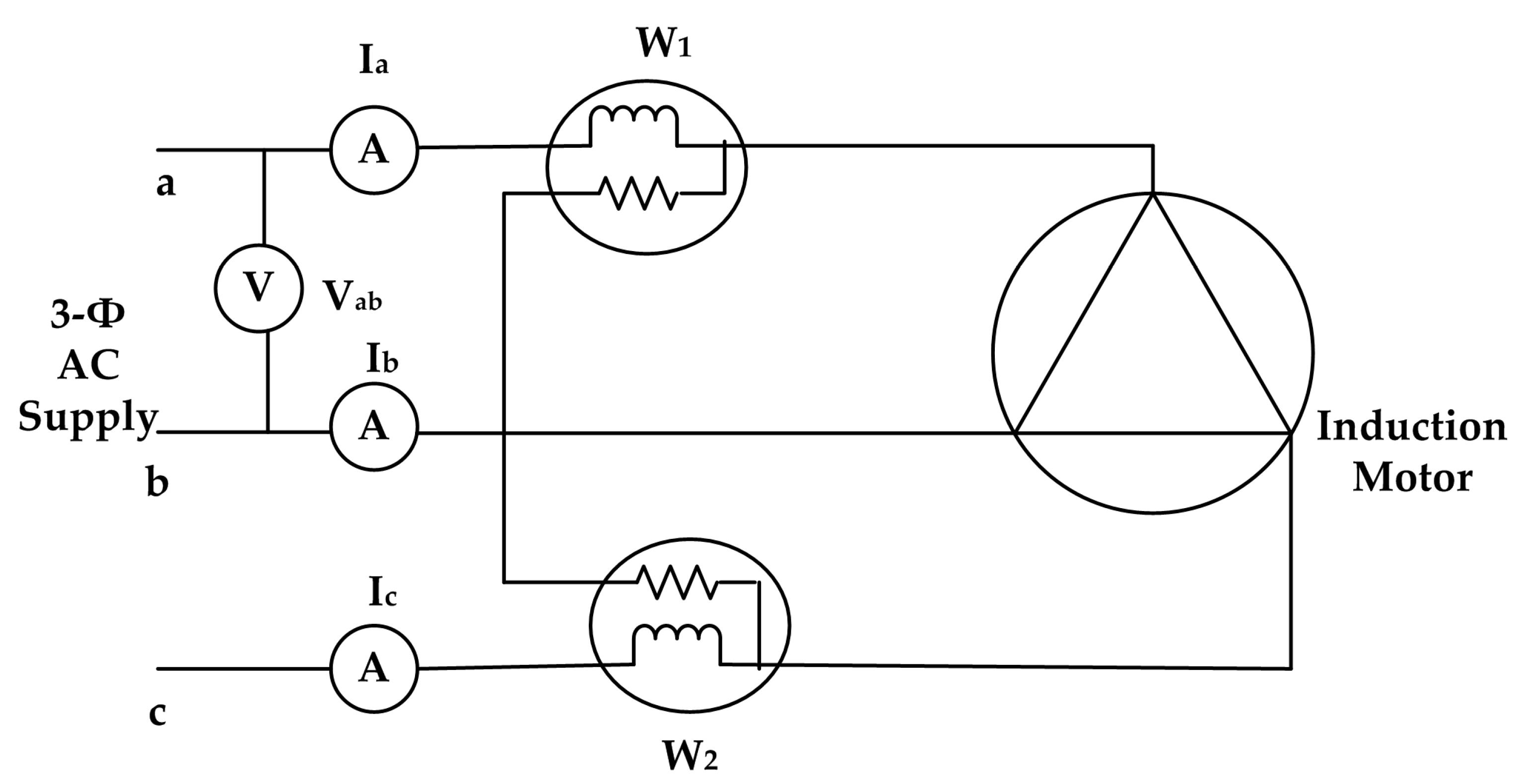
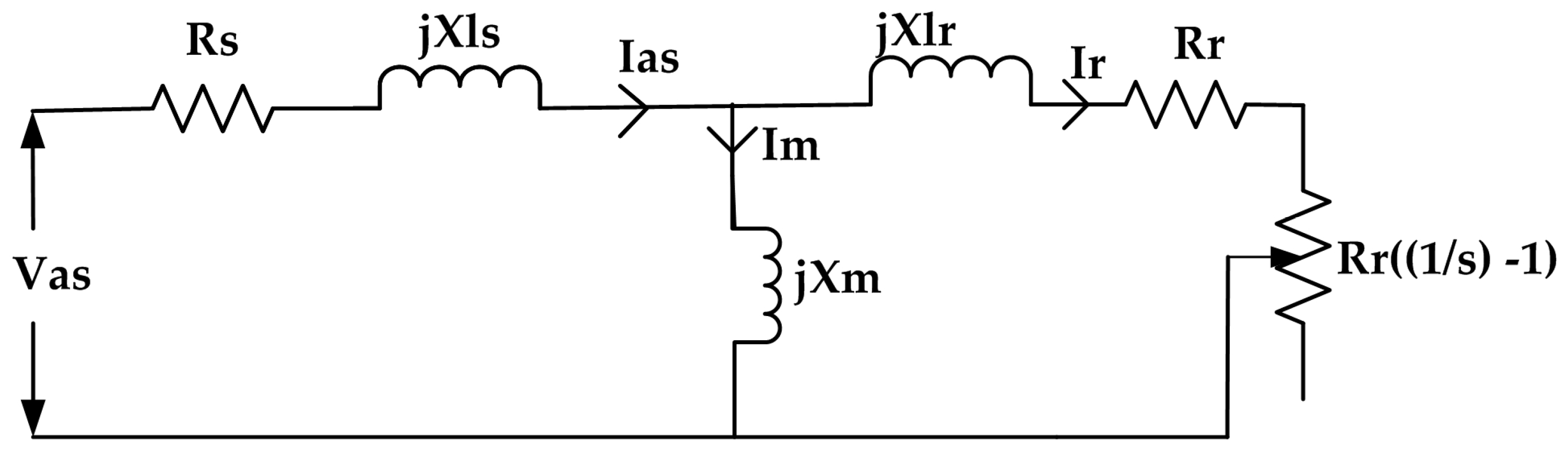
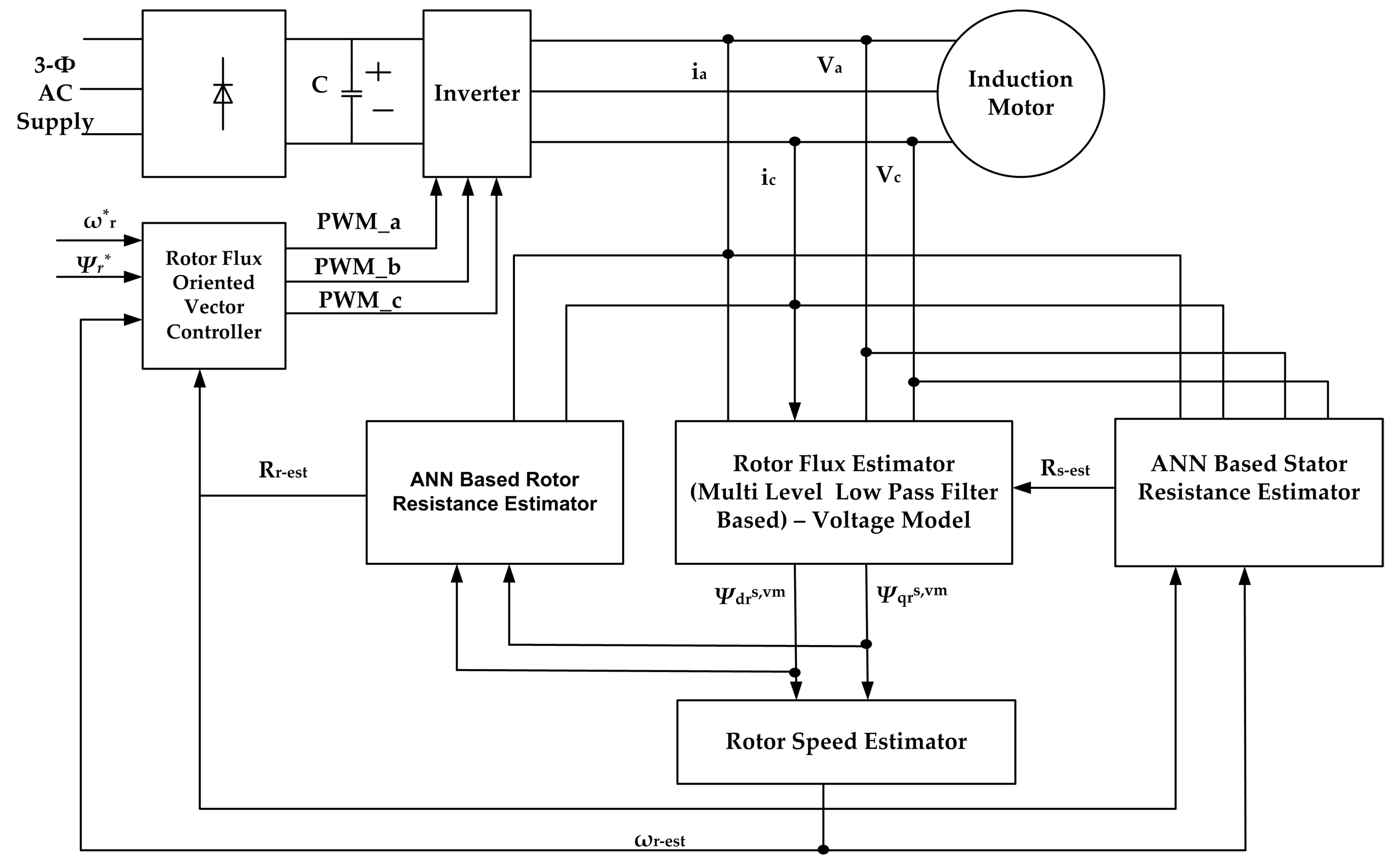


| Power (HP) | 3.7 kW |
| Current (Amps) | 7.5 |
| Terminal voltage (Volts) | 415 |
| Frequency (Hz) | 50 |
| Poles | 4 |
| No-load speed (RPM) | 1498 |
| Stator connection | Delta |
| Sl No. | Applied Voltage (volt) | Current (amp) | DC Resistance (ohm) | Average dc Resistance (ohm) | Stator ac Resistance (ohm) |
|---|---|---|---|---|---|
| 1 | 6.82 | 1.5 | 4.55 | ||
| 2 | 9.34 | 2 | 4.67 | 4.57 | 5.71 |
| 3 | 11.21 | 2.5 | 4.484 |
| Voltage Vas (volt) | Ia (amp) | Ib (amp) | Ic (amp) | No-Load Current Io (amp) | W1 (watts) | W2 (watts) | Power Input Poc (watts) | Speed (rpm) |
|---|---|---|---|---|---|---|---|---|
| 415 | 4.15 | 4.1 | 4.1 | 4.12 | −672 | 1080 | 408 | 1498 |
| SC Voltage Vsc (volt) | SC Current Isc (Amp) | W1 (watts) | W2 (watts) | SC Power Input Psc (watts) |
|---|---|---|---|---|
| 82 | 7.5 | −11 | 510 | 499 |
| Rs (ohm) | Rr (ohm) | Ls = (Lls + Lm) (Henry) | Lr = (Llr + Lm) (Henry) | Lm (Henry) |
|---|---|---|---|---|
| 5.7 | 4.11 | 0.5634 | 0.5634 | 0.5379 |
| Parameters | Values |
|---|---|
| Rated power | 3.7 kW |
| Rated frequency | 50 Hz |
| Rated voltage | 415 V |
| Rated current | 7.5 A |
| Number of poles | 4 |
| Type of stator connection | Delta |
| No-load speed | 1498 rpm |
| Rotor resistance | 4.11 Ohm |
| Stator resistance | 5.7 Ohm |
| Rotor inductance (Lr) | 0.5634 H |
| Stator inductance (Ls) | 0.5634 H |
| Magnetizing inductance (Lm) | 0.5379 H |
| Moment of inertia (Jr) | 0.01542 kg-m2 |
| Parameter | Value |
|---|---|
| The initial learning rate for weight W1 | 2.4 × 10−4 |
| The initial learning rate for weight W3 | 10 × 10−6 |
| Steepness factor of bipolar sigmoid function s1 and s3 | 1 |
| α1, α3 | 0.1 |
| Sampling time Ts | 2 ms |
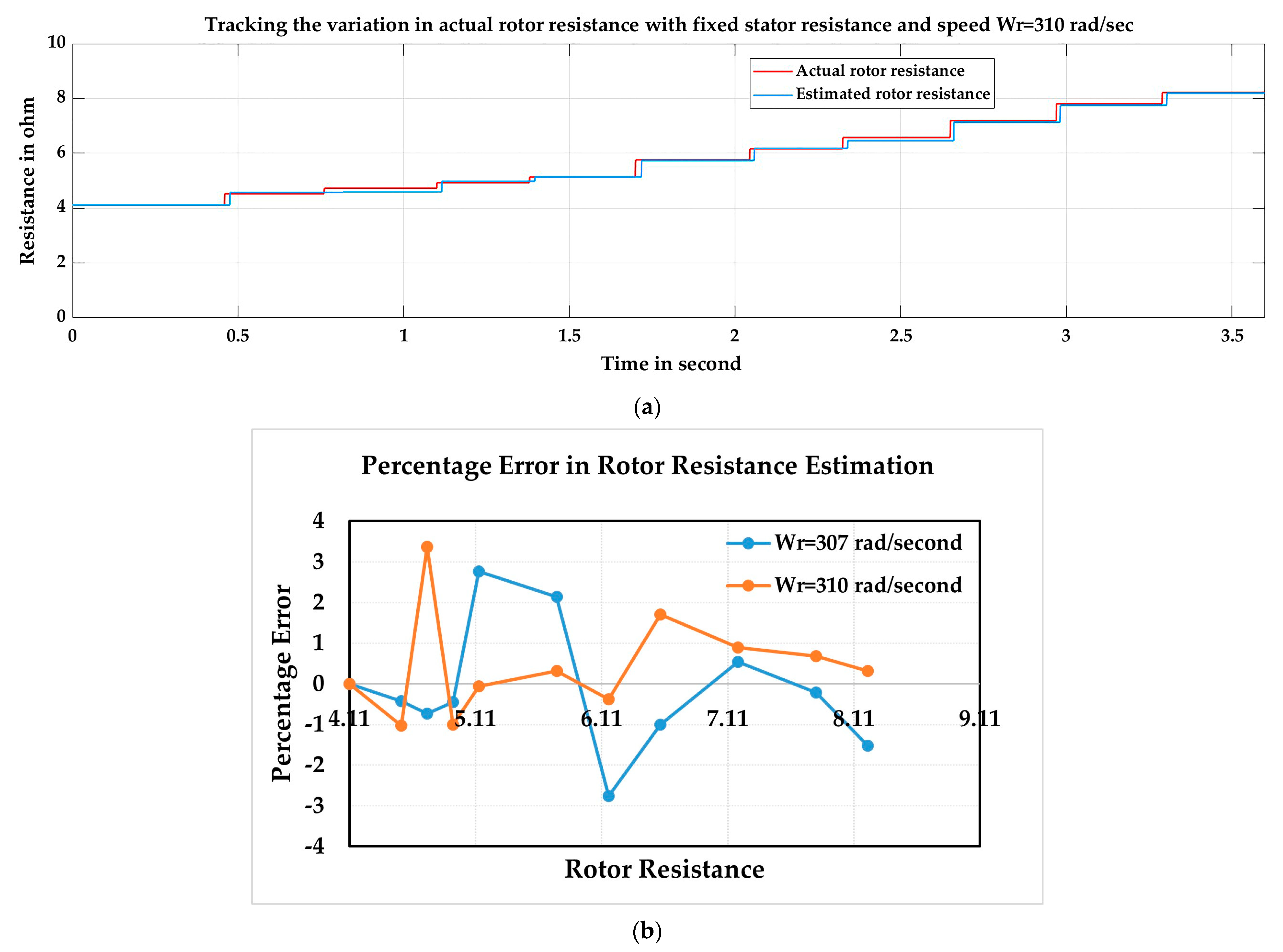
| Actual Rotor Resistance | Wr = 307 Radian/Second | Wr = 310 Radian/Second | ||||
|---|---|---|---|---|---|---|
| Estimated Resistance | Percentage Error | Number of Iterations | Estimated Resistance | Percentage Error | Number of Iterations | |
| 4.11 | 4.11 | 0 | 1 | 4.11 | 0 | 1 |
| 4.521 | 4.54 | −0.4242 | 6 | 4.568 | −1.033 | 6 |
| 4.7265 | 4.761 | −0.7391 | 8 | 4.59 | 3.36 | 6 |
| 4.932 | 4.954 | −0.4538 | 10 | 4.982 | −1.01 | 9 |
| 5.1375 | 4.995 | 2.765 | 10 | 5.141 | −0.06854 | 10 |
| 5.754 | 5.631 | 2.14 | 14 | 5.736 | 0.3159 | 13 |
| 6.165 | 6.335 | −2.754 | 9 | 6.188 | −0.3811 | 15 |
| 6.576 | 6.642 | −1.008 | 10 | 6.464 | 1.709 | 16 |
| 7.1925 | 7.154 | 0.5389 | 12 | 7.129 | 0.8871 | 18 |
| 7.809 | 7.826 | −0.219 | 16 | 7.756 | 0.68 | 19 |
| 8.22 | 8.345 | −1.525 | 17 | 8.194 | 0.3145 | 20 |
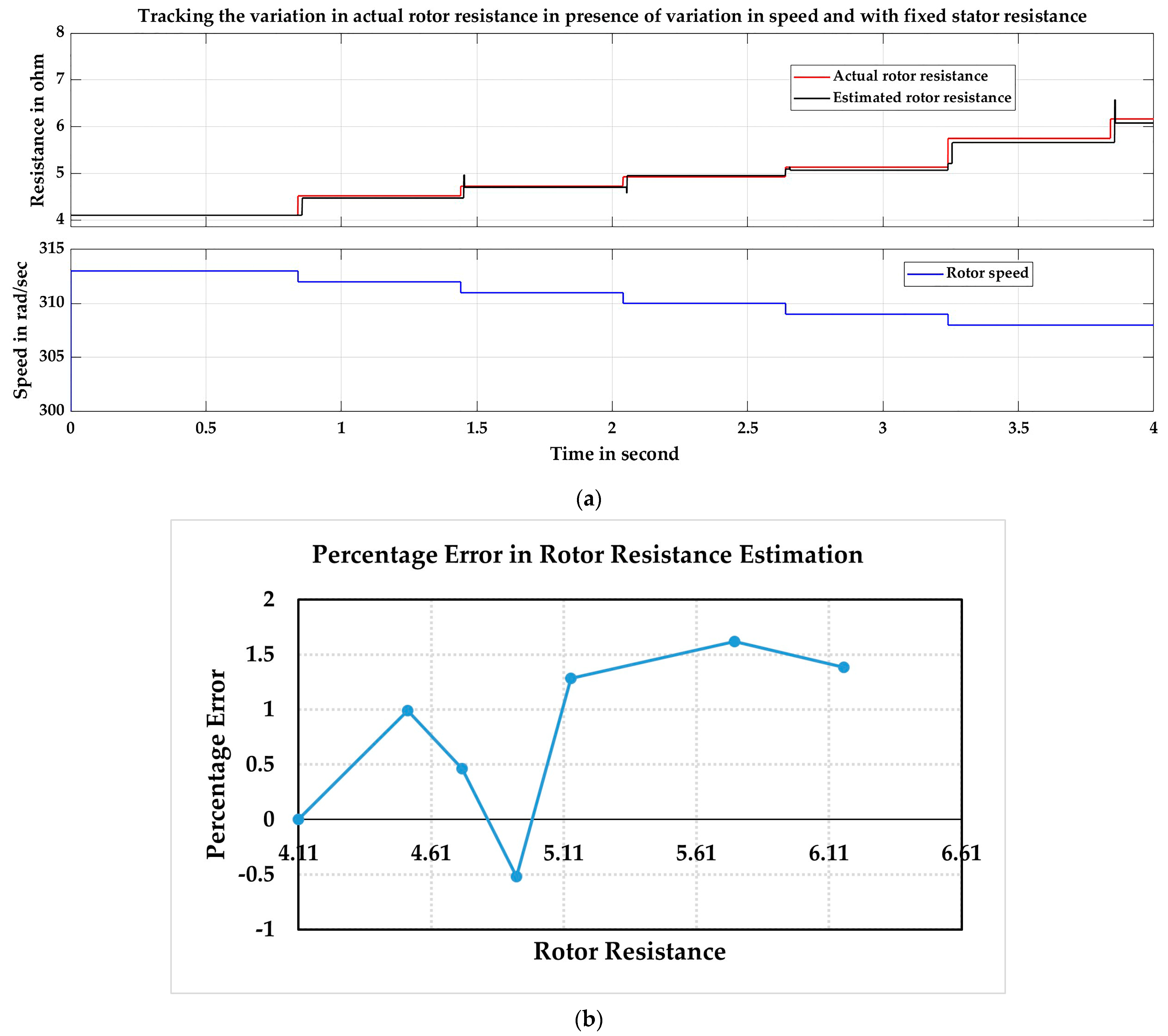
| Actual Rotor Resistance | Speed Wr (rad/s) | Estimated Rotor Resistance | Percentage Error | Number of Iterations |
|---|---|---|---|---|
| 4.11 | 313 | 4.11 | 0 | 1 |
| 4.521 | 312 | 4.476 | 0.9889 | 5 |
| 4.7265 | 311 | 4.705 | 0.4627 | 7 |
| 4.932 | 310 | 4.958 | −0.5192 | 9 |
| 5.137 | 309 | 5.072 | 1.283 | 10 |
| 5.754 | 308 | 5.661 | 1.62 | 14 |
| 6.165 | 308 | 6.08 | 1.385 | 16 |
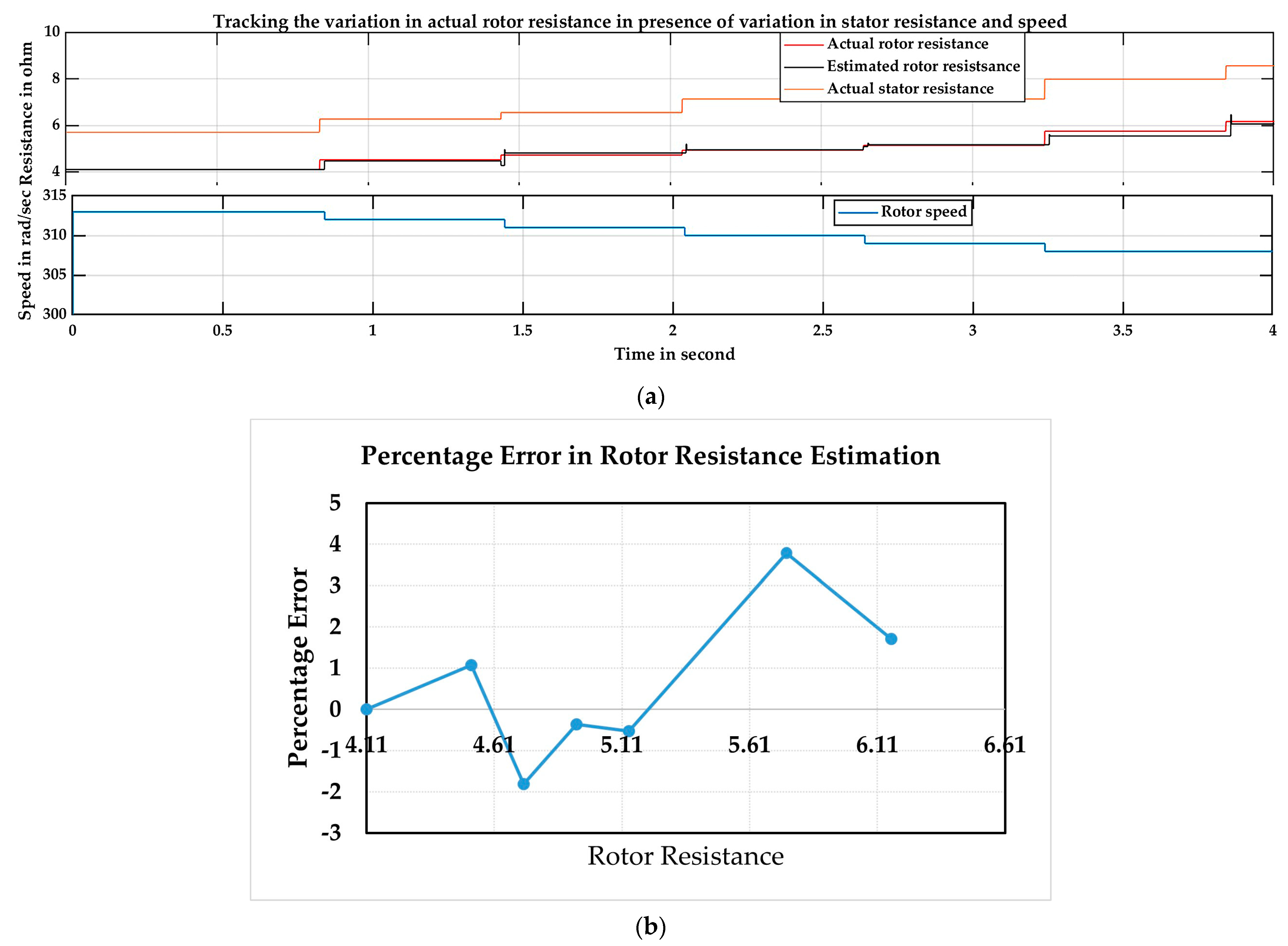
| Actual Rotor Resistance | Actual Stator Resistance | Speed (rad/s) | Estimated Resistance | Percentage Error | Number of Iterations |
|---|---|---|---|---|---|
| 4.11 | 5.7 | 313 | 4.11 | 0 | 1 |
| 4.521 | 6.27 | 312 | 4.472 | 1.077 | 5 |
| 4.726 | 6.55 | 311 | 4.812 | −1.817 | 8 |
| 4.932 | 6.84 | 310 | 4.95 | −0.3642 | 9 |
| 5.137 | 7.125 | 309 | 5.165 | −0.5305 | 11 |
| 5.754 | 7.98 | 308 | 5.537 | 3.78 | 14 |
| 6.165 | 8.55 | 308 | 6.06 | 1.705 | 17 |
| Parameter | Value |
|---|---|
| The initial learning rate for weight W4 | 0.001 |
| Steepness factor of bipolar sigmoid function s4 | 0.01 |
| α4 | 4 |
| Sampling time Ts | 4 ms |
| Actual Stator Resistance | Wr = 307 rad/s | Wr = 310 rad/s | ||||
|---|---|---|---|---|---|---|
| Estimated Resistance | Percentage Error | Number of Iterations | Estimated Resistance | Percentage Error | Number of Iterations | |
| 5.7 | 5.7 | 0 | 1 | 5.7 | 0 | 1 |
| 6.27 | 6.325 | −0.8841 | 5 | 6.154 | 1.857 | 6 |
| 6.55 | 6.519 | 0.4765 | 7 | 6.561 | −0.1756 | 8 |
| 6.84 | 6.742 | 1.437 | 7 | 6.926 | −1.25 | 10 |
| 7.125 | 6.994 | 1.838 | 8 | 6.99 | 1.901 | 10 |
| 7.98 | 7.932 | 0.6067 | 11 | 7.838 | 1.778 | 13 |
| 8.55 | 8.415 | 1.578 | 12 | 8.558 | −0.091 | 15 |
| 9.12 | 8.955 | 1.807 | 13 | 9.091 | 0.3181 | 16 |
| 9.975 | 9.684 | 2.916 | 15 | 9.819 | 1.566 | 17 |
| 10.83 | 10.5 | 3.068 | 16 | 10.63 | 1.848 | 18 |
| 11.4 | 10.79 | 5.366 | 16 | 10.94 | 4.078 | 19 |
| Actual Stator Resistance | Speed Wr (rad/s) | Estimated Stator Resistance | Percentage Error | Number of Iterations |
|---|---|---|---|---|
| 5.7 | 313 | 5.7 | 0 | 1 |
| 6.27 | 312 | 6.307 | −0.5941 | 8 |
| 6.55 | 311 | 6.615 | −0.9972 | 9 |
| 6.84 | 310 | 6.92 | −1.166 | 10 |
| 7.125 | 309 | 7.085 | 0.566 | 11 |
| 7.98 | 308 | 7.956 | 0.3065 | 12 |
| Actual Stator Resistance | Actual Rotor Resistance | Speed Wr (rad/s) | Estimated Stator Resistance | Percentage Error | Number of Iterations |
|---|---|---|---|---|---|
| 5.7 | 4.11 | 313 | 5.7 | 0 | 1 |
| 6.27 | 4.727 | 312 | 6.306 | −0.5775 | 6 |
| 6.55 | 5.138 | 311 | 6.616 | −1.009 | 11 |
| 6.84 | 5.343 | 310 | 6.74 | 1.456 | 10 |
| 7.685 | 5.548 | 309 | 7.633 | 0.6825 | 14 |
| 8.55 | 6.165 | 308 | 8.18 | 4.21 | 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanakabettu, A.K.M.; Irvathoor, R.B.; Saralaya, S.; Jodumutt, S.B.; Singh, A.B. Novel Advanced Artificial Neural Network-Based Online Stator and Rotor Resistance Estimator for Vector-Controlled Speed Sensorless Induction Motor Drives. Energies 2024, 17, 2150. https://doi.org/10.3390/en17092150
Kanakabettu AKM, Irvathoor RB, Saralaya S, Jodumutt SB, Singh AB. Novel Advanced Artificial Neural Network-Based Online Stator and Rotor Resistance Estimator for Vector-Controlled Speed Sensorless Induction Motor Drives. Energies. 2024; 17(9):2150. https://doi.org/10.3390/en17092150
Chicago/Turabian StyleKanakabettu, Ajithanjaya Kumar Mijar, Rajkiran Ballal Irvathoor, Sanath Saralaya, Sathyendra Bhat Jodumutt, and Athokpam Bikramjit Singh. 2024. "Novel Advanced Artificial Neural Network-Based Online Stator and Rotor Resistance Estimator for Vector-Controlled Speed Sensorless Induction Motor Drives" Energies 17, no. 9: 2150. https://doi.org/10.3390/en17092150
APA StyleKanakabettu, A. K. M., Irvathoor, R. B., Saralaya, S., Jodumutt, S. B., & Singh, A. B. (2024). Novel Advanced Artificial Neural Network-Based Online Stator and Rotor Resistance Estimator for Vector-Controlled Speed Sensorless Induction Motor Drives. Energies, 17(9), 2150. https://doi.org/10.3390/en17092150






