Health State Assessment of Lithium-Ion Batteries Based on Multi-Health Feature Fusion and Improved Informer Modeling
Abstract
:1. Introduction
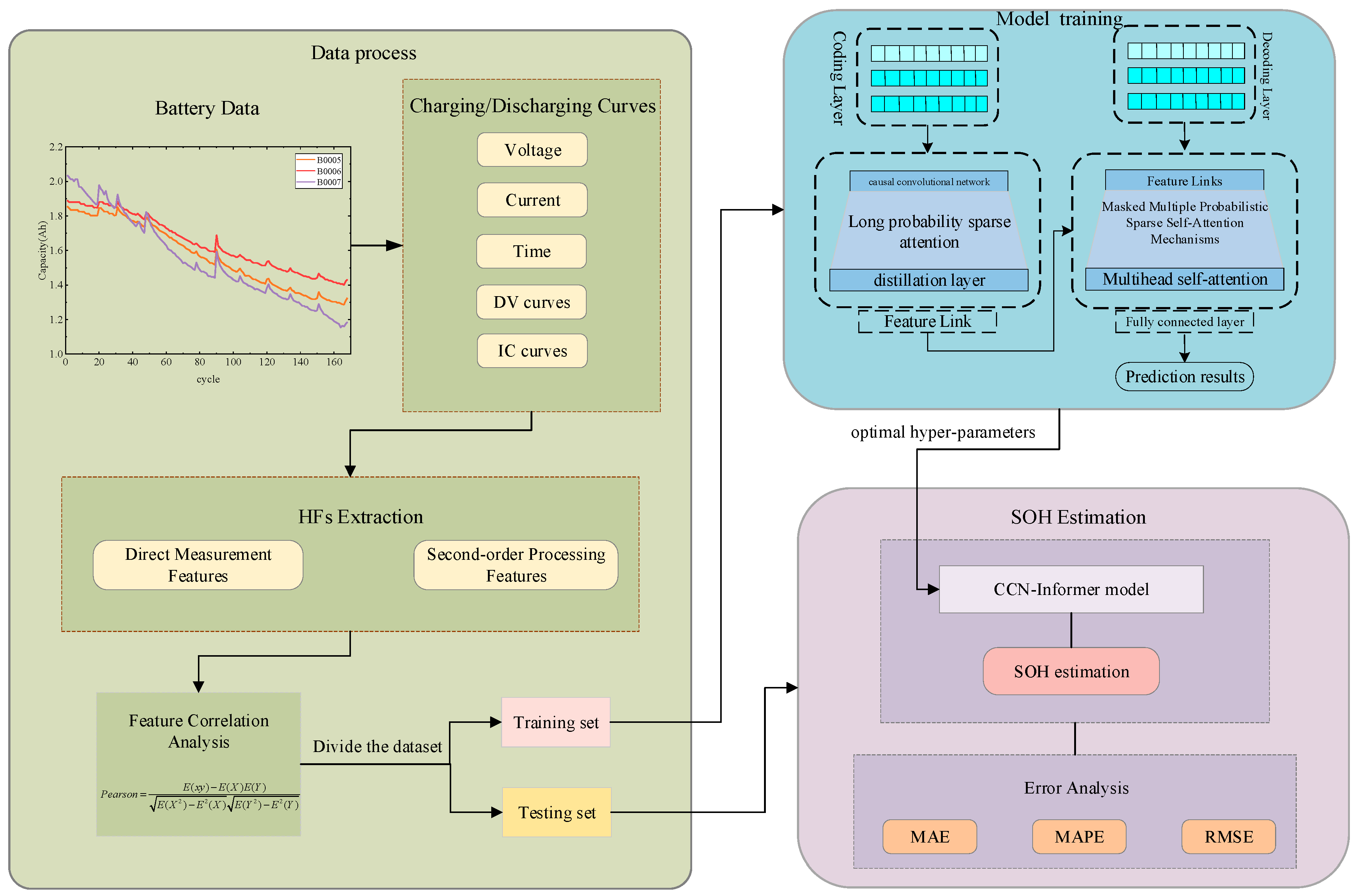
- In order to accurately characterize the battery aging process, eight features were extracted from the battery data and classified into two categories: direct measurement features and second-order processing features.
- An SOH estimation model for lithium-ion batteries based on causal convolutional neural network and the Informer model is established, which enhances the local information extraction capability of the Informer model, and is able to well capture the nonlinear relationship reflected by different features in the aging process of lithium-ion batteries.
2. Health Feature Extraction Based on Battery Charging Profile
2.1. Health Feature Extraction Framework
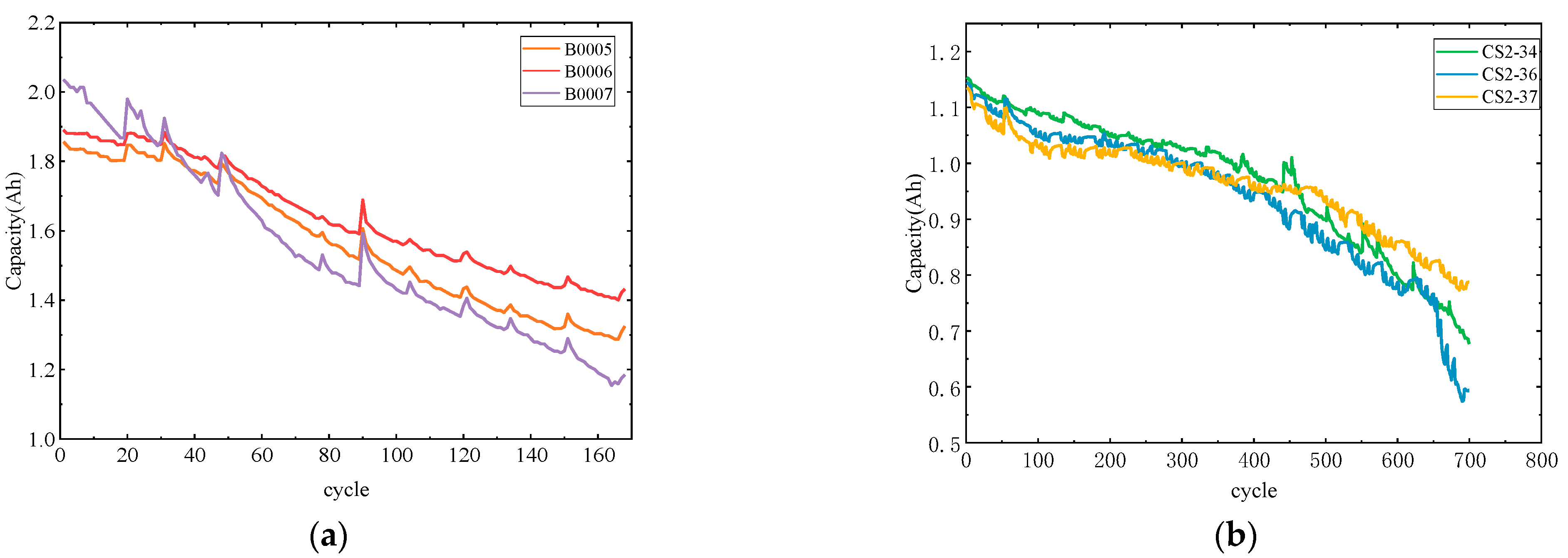
2.2. Experimental Dataset
2.3. Direct Measurement Feature Extraction
2.4. Second-Order Processing Feature Extraction
2.5. Feature Correlation Analysis
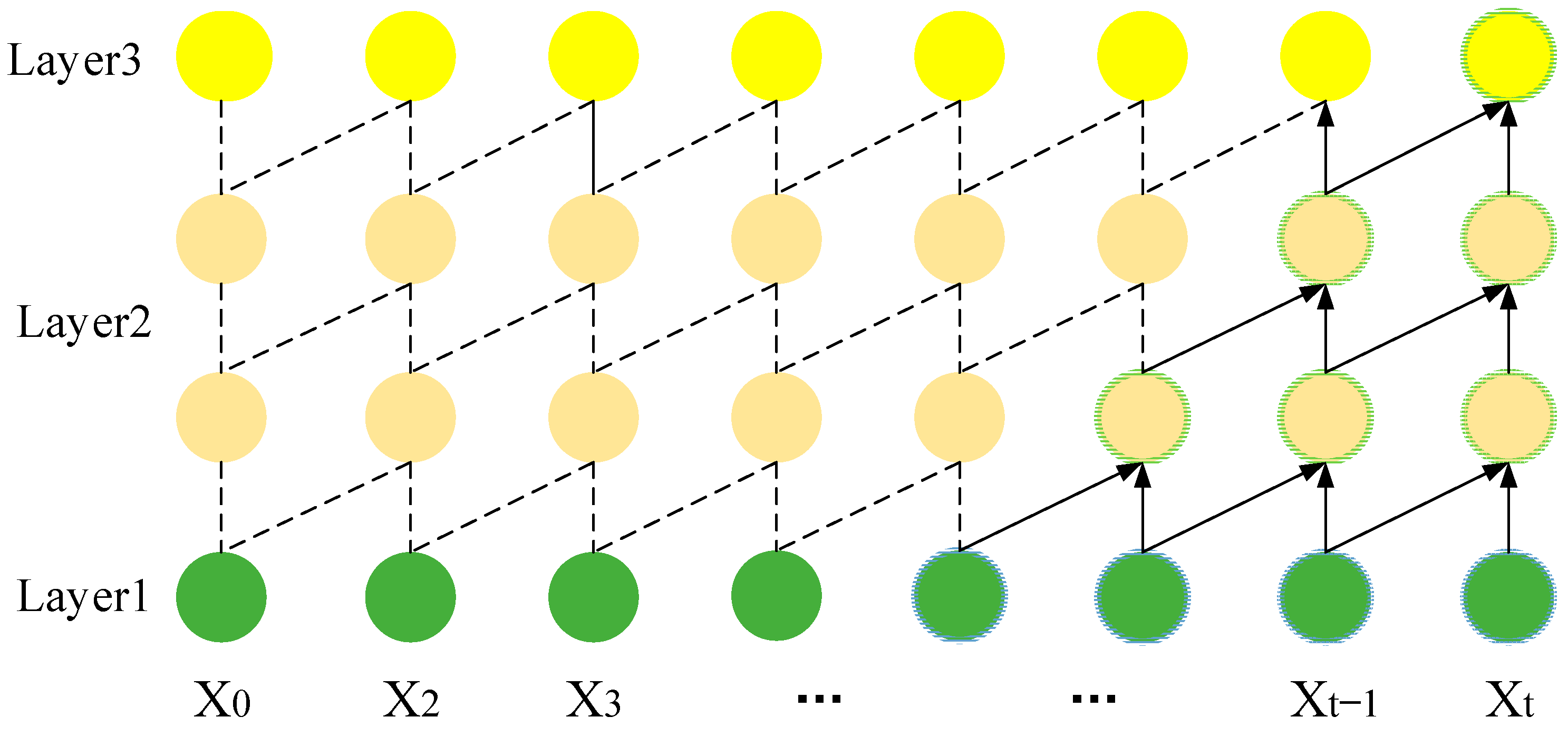
3. Causal Convolutional Self-Attention-Based Health State Prediction Model for CCN-Informer Batteries
3.1. Causal Convolutional Neural Network
3.2. Self-Attention Mechanisms Incorporating Causal Convolutions
- (1)
- Using the feature that causal convolution can capture local features, the input time series is subjected to a one-dimensional convolution operation, the one-dimensional convolution kernel parameter is set to k, which is used to set the sampling frequency of the network, and the number of convolution kernels is gn, which yields the query vector and the key value .
- (2)
- Q and K for similarity calculation, which is Softmax-normalized to obtain the weights on the time series as shown in Equation (8).
- (3)
- After the fully connected layer is converted into a value vector V with the same shape as the result of the weight calculation, it is subjected to matrix dot product to obtain the data with attention features.
3.3. Informer Model Structure
4. Calculation Validation and Analysis
4.1. Evaluation Indicators
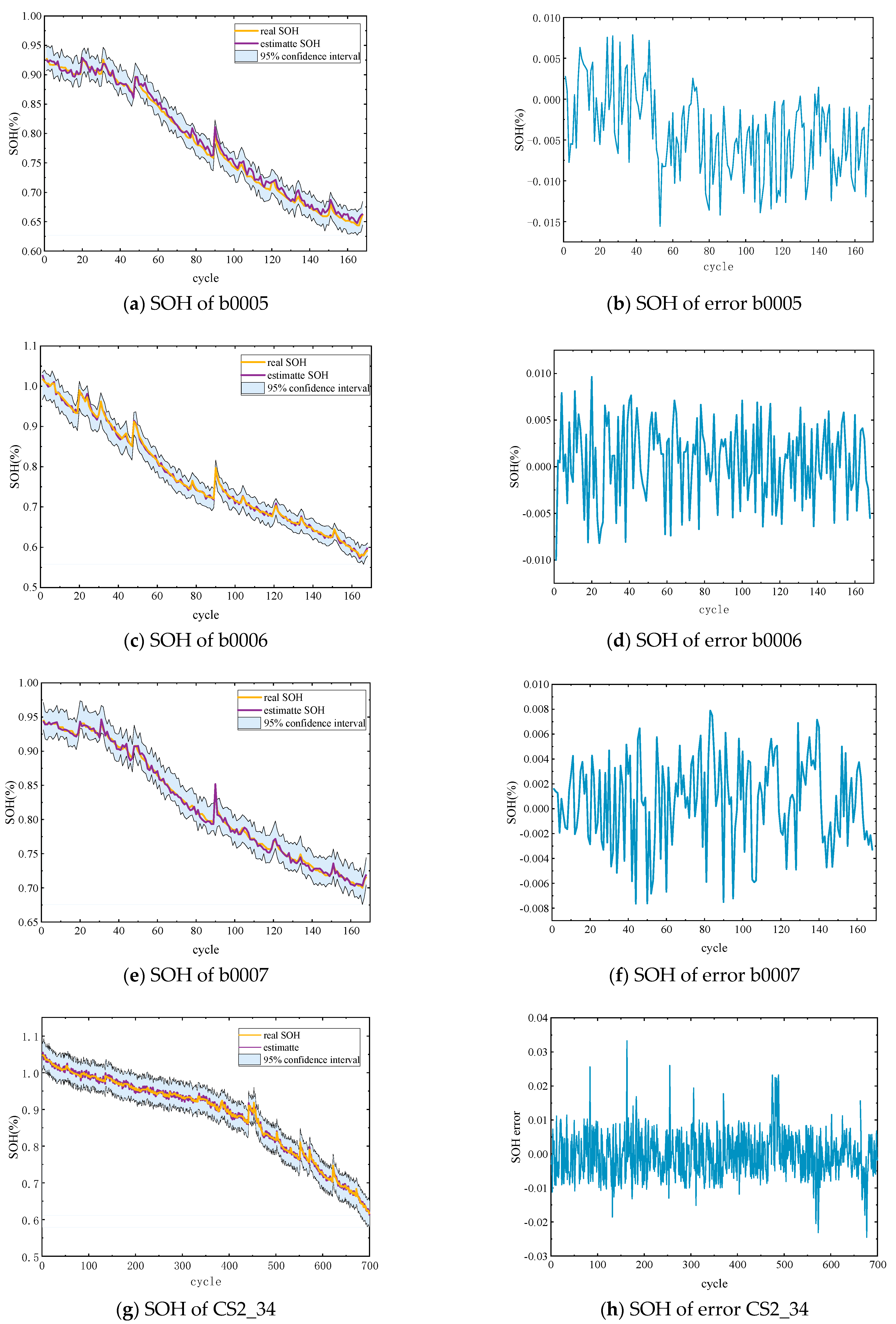
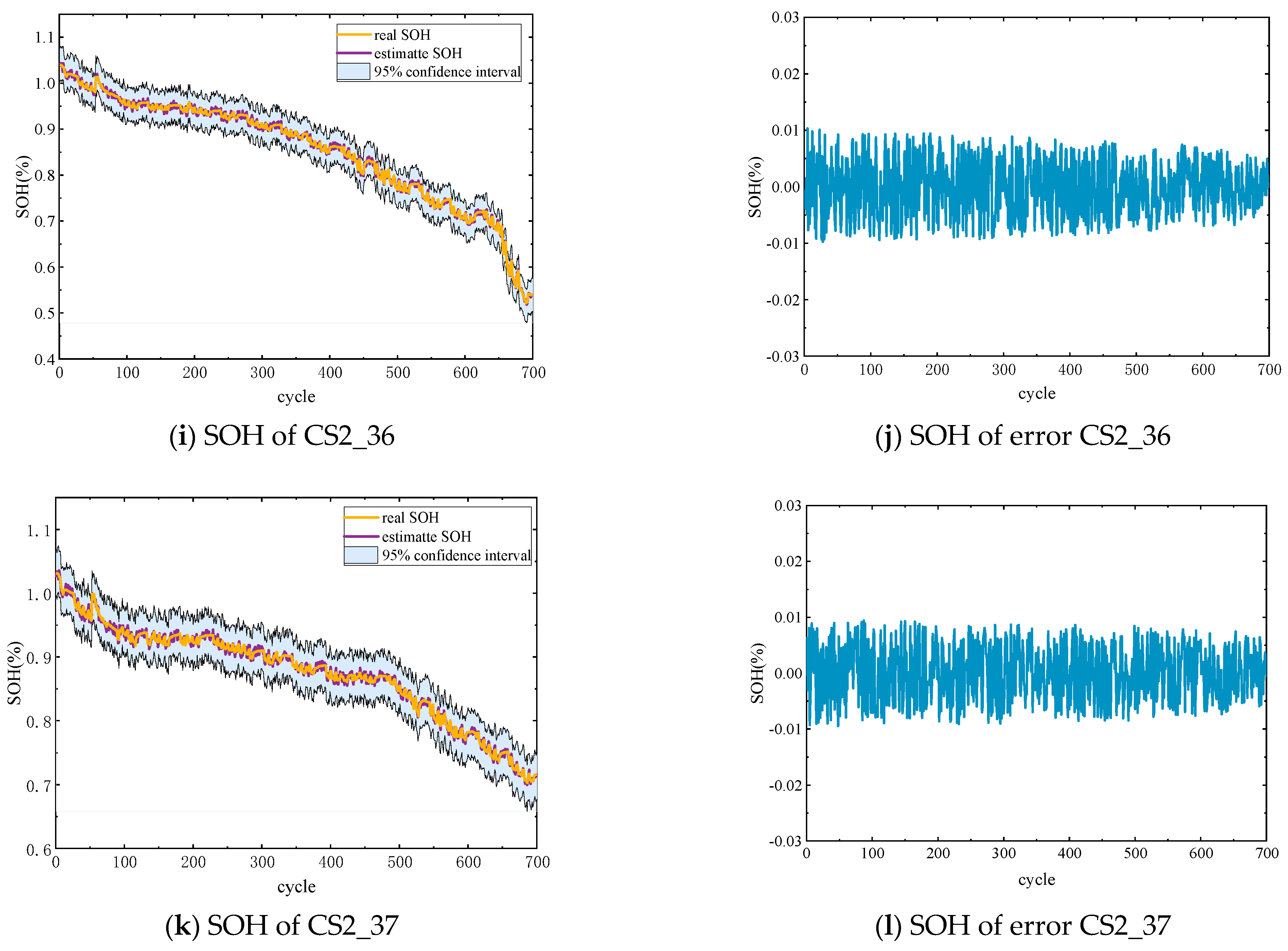
4.2. Analyzing and Validating the Prediction Results of Different Datasets
4.3. Comparative Analysis of Different SOH Prediction Models
5. Conclusions
- Eight features that can reflect the health state of the battery are extracted from the battery charge/discharge data, which are categorized into direct measurement features and second-order processing features to effectively and comprehensively describe the degradation of the battery.
- Improved the Informer model. Add causal convolutional neural network to the self-attention mechanism to enhance the ability of local information extraction, so that the CCN-Informer model has the function of capturing both global and local information, avoiding gradient explosion, and optimizing the model prediction performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abdul, D.; Wenqi, J.; Tanveer, A. Prioritization of renewable energy source for electricity generation through AHP-VIKOR integrated methodology. Renew. Energy 2022, 184, 1018–1032. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Solangi, Y.A. A sustainable solution for electricity crisis in Pakistan: Opportunities, barriers, and policy implications for 100% renewable energy. Environ. Sci. Pollut. Res. 2019, 26, 29687–29703. [Google Scholar] [CrossRef] [PubMed]
- Wen, J.; Zhao, D.; Zhang, C. An overview of electricity powered vehicles: Lithium-ion battery energy storage density and energy conversion efficiency. Renew. Energy 2020, 162, 1629–1648. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Q.; Huang, H.; Yang, B.; Dong, H.; Zhang, J. An electrochemical–thermal model of lithium-ion battery and state of health estimation. J. Energy Storage 2022, 47, 103528. [Google Scholar] [CrossRef]
- Song, Z.; Hou, J.; Li, X.; Wu, X.; Hu, X.; Hofmann, H.; Sun, J. The sequential algorithm for combined state of charge and state of health estimation of lithium-ion battery based on active current injection. Energy 2020, 193, 116732. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, J.; Li, L.; Gu, J. Fractional modeling and parameter identification of lithium-ion battery. Ionics 2022, 28, 4135–4148. [Google Scholar] [CrossRef]
- Guo, X.; Kang, L.; Yao, Y.; Huang, Z.; Li, W. Joint estimation of the electric vehicle power battery state of charge based on the least squares method and the Kalman filter algorithm. Energies 2016, 9, 100. [Google Scholar] [CrossRef]
- Hongwen, H.; Rui, X.; Hongqiang, G. Online estimation of model parameters and state-of-charge of LiFePO4 batteries in electric vehicles. Appl. Energy 2012, 89, 413–420. [Google Scholar]
- Wei, Z.; Ruan, H.; Li, Y.; Li, J.; Zhang, C.; He, H. Multistage state of health estimation of lithium-ion battery with high tolerance to heavily partial charging. IEEE Trans. Power Electron. 2022, 37, 7432–7442. [Google Scholar] [CrossRef]
- Fan, Y.; Xiao, F.; Li, C.; Yang, G.; Tang, X. A novel deep learning framework for state of health estimation of lithium-ion battery. J. Energy Storage 2020, 32, 10–41. [Google Scholar] [CrossRef]
- Zhao, G.; Kang, Y.; Huang, P.; Duan, B.; Zhang, C. Chenghui Battery health prognostic using efficient and robust aging trajectory matching with ensemble deep transfer learning. Energy 2023, 282, 128228. [Google Scholar] [CrossRef]
- Wu, J.; Fang, L.; Dong, G.; Lin, M. State of health estimation of lithium-ion battery with improved radial basis function neural network. Energy 2023, 262, 125380. [Google Scholar] [CrossRef]
- Wei, J.; Dong, G.; Chen, Z. Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression. IEEE Trans. Ind. Electron. 2017, 65, 5634–5643. [Google Scholar] [CrossRef]
- Liu, Q.; Kang, Y.; Qu, S.; Duan, B.; Wen, F.; Zhang, C. An online SOH estimation method based on the fusion of improved ICA and LSTM. In Proceedings of the 2020 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Weihai, China, 13–15 July 2020; pp. 1163–1167. [Google Scholar]
- Xiong, W.; Xu, G.; Li, Y.; Zhang, F.; Ye, P.; Li, B. Early prediction of lithium-ion battery cycle life based on voltage-capacity discharge curves. J. Energy Storage 2023, 62, 106790. [Google Scholar] [CrossRef]
- Choi, S.; Wang, G. Advanced lithium-ion batteries for practical applications: Technology, development, and future perspectives. Adv. Mater. Technol. 2018, 3, 1700376. [Google Scholar] [CrossRef]
- Sui, X.; He, S.; Vilsen, S.B.; Meng, J.; Teodorescu, R.; Stroe, D.-I. A review of nonprobabilistic machine learning-based state of health estimation techniques for lithium-ion battery. Appl. Energy 2021, 300, 117346. [Google Scholar] [CrossRef]
- Bian, X.; Wei, Z.; Li, W.; Pou, J.; Sauer, D.U.; Liu, L. State-of-health estimation of lithium-ion batteries by fusing an open circuit voltage model and incremental capacity analysis. IEEE Trans. Power Electron. 2022, 37, 2226–2236. [Google Scholar] [CrossRef]
- Dong, J.X.; Yu, Z.S.; Zhang, X.K.; Luo, J.J.; Zou, Q.H.; Feng, C.; Ma, X.Q. Data-driven predictive prognostic model for power batteries based on machine learning. Process Saf. Environ. Prot. 2023, 172, 894–907. [Google Scholar] [CrossRef]
- Zheng, L.F.; Zhu, J.G.; Lu, D.D.C.; Wang, G.X.; He, T.T. Incremental capacity analysis and differential voltage analysis based state of charge and capacity estimation for lithium-ion batteries. Energy 2018, 150, 759–769. [Google Scholar] [CrossRef]
- Agudelo, B.O.; Zamboni, W.; Monmasson, E. Application domain extension of incremental capacity-based battery SoH indicators. Energy 2021, 234, 121224. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Zhang, L.; Zou, C.; Dorrell, D.D. State-ofhealth estimation for Li-ion batteries by combing the incremental capacity analysis method with grey relational analysis. J. Power Sources 2019, 410, 106–114. [Google Scholar] [CrossRef]
- Chen, D.H.; Zhang, W.G.; Zhang, C.P.; Sun, B.X.; Zhang, L.J.; Cong, X.W. Data-driven rapid lifetime prediction method for lithium-ion batteries under diverse fast charging protocols. J. Energy Storage 2023, 74, 109285. [Google Scholar] [CrossRef]
- Su, X.; Sun, B.; Wang, J.; Zhang, W.; Ma, S.; He, X.; Ruan, H. Fast capacity estimation for lithium-ion battery based on online identification of low-frequency electrochemical impedance spectroscopy and Gaussian process regression. Appl. Energy 2022, 322, 119516. [Google Scholar] [CrossRef]
- Wang, Z.; Yuan, C.; Li, X. Lithium battery state-of-health estimation via differential thermal voltammetry with Gaussian process regression. IEEE Trans. Transp. Electrif. 2021, 7, 16–25. [Google Scholar] [CrossRef]
- Richardson, R.R.; Birkl, C.R.; Osborne, M.A.; Howey, D.A. Gaussian Process Regression for In Situ Capacity Estimation of Lithium-Ion Batteries. IEEE Trans. Ind. Inform. 2019, 15, 127–138. [Google Scholar] [CrossRef]
- Montaru, M.; Fiette, S.; Kon’e, J.-L.; Bultel, Y. Calendar ageing model of Li-ion battery combining physics-based and empirical approaches. J. Energy Storage 2022, 51, 104544. [Google Scholar] [CrossRef]
- Gong, D.; Gao, Y.; Kou, Y.; Wang, Y. State of health estimation for lithium-ion battery based on energy features. Energy 2022, 257, 124812. [Google Scholar] [CrossRef]
- Li, Y.; Stroe, D.-I.; Cheng, Y.; Sheng, H.; Sui, X.; Teodorescu, R. On the feature selection for battery state of health estimation based on charging–discharging profiles. Energy Storage 2021, 33, 102–122. [Google Scholar] [CrossRef]
- Liu, W.; Xu, Y. Data-driven online health estimation of Li-ion batteries using a novel energy-based health indicator. IEEE Trans. Energy Convers. 2020, 35, 1715–1718. [Google Scholar] [CrossRef]
- Pang, X.; Liu, X.; Jia, J.; Wen, J.; Shi, Y.; Zeng, J.; Zhao, Z. A lithium-ion battery remaining useful life prediction method based on the incremental capacity analysis and Gaussian process regression. Microelectron. Reliab. 2021, 127, 114405. [Google Scholar] [CrossRef]
- Damianou, A.; Lawrence, N.D. Deep gaussian processes. In Artificial Intelligence and Statistics; PMLR: New York City, NY, USA, 2013; pp. 207–215. [Google Scholar]
- Xing, Y.; Ma, E.W.M.; Tsui, K.-L.; Pecht, M. An ensemble model for predicting the remaining useful performance of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 811–820. [Google Scholar] [CrossRef]
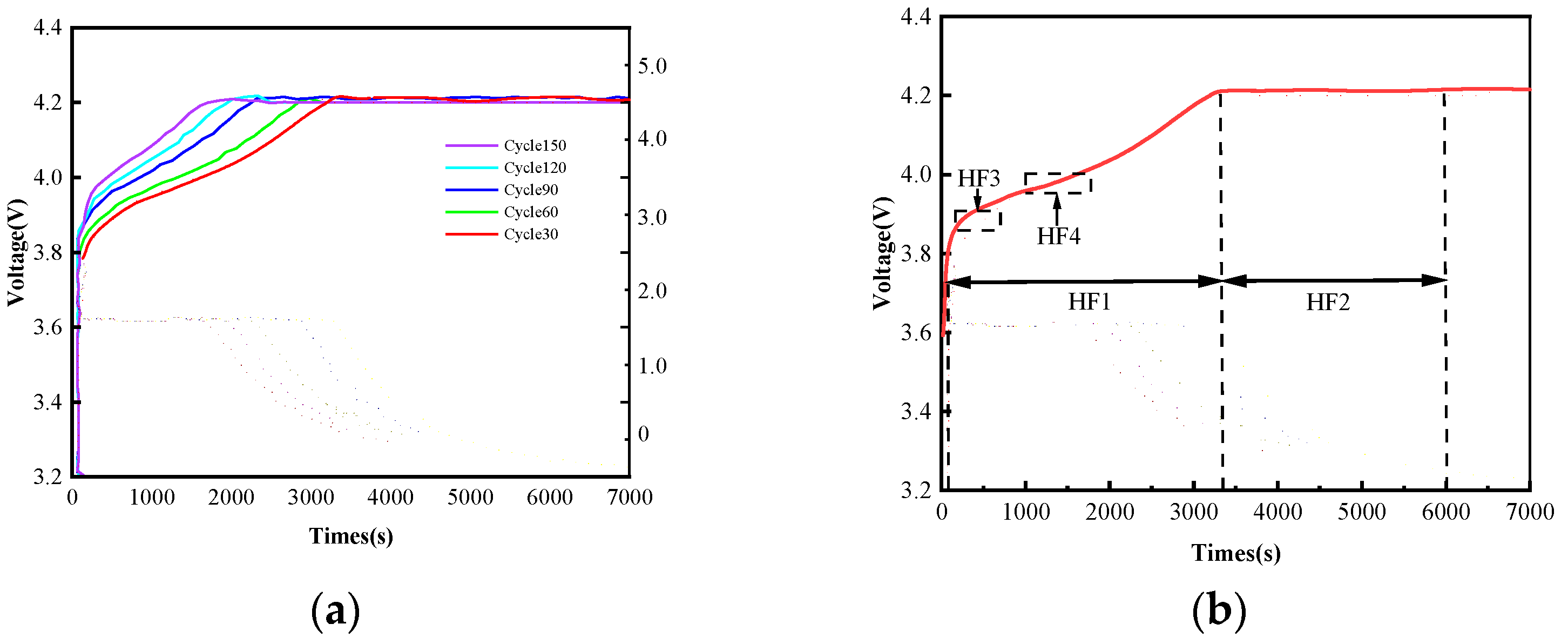
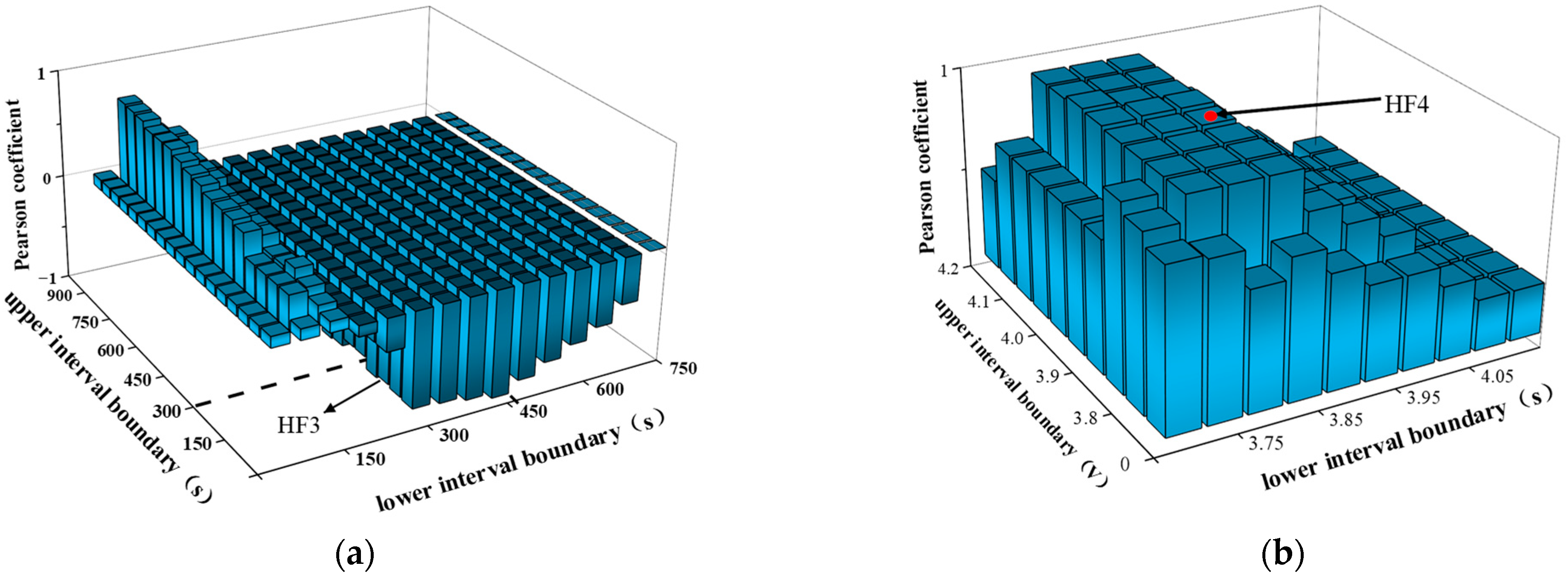
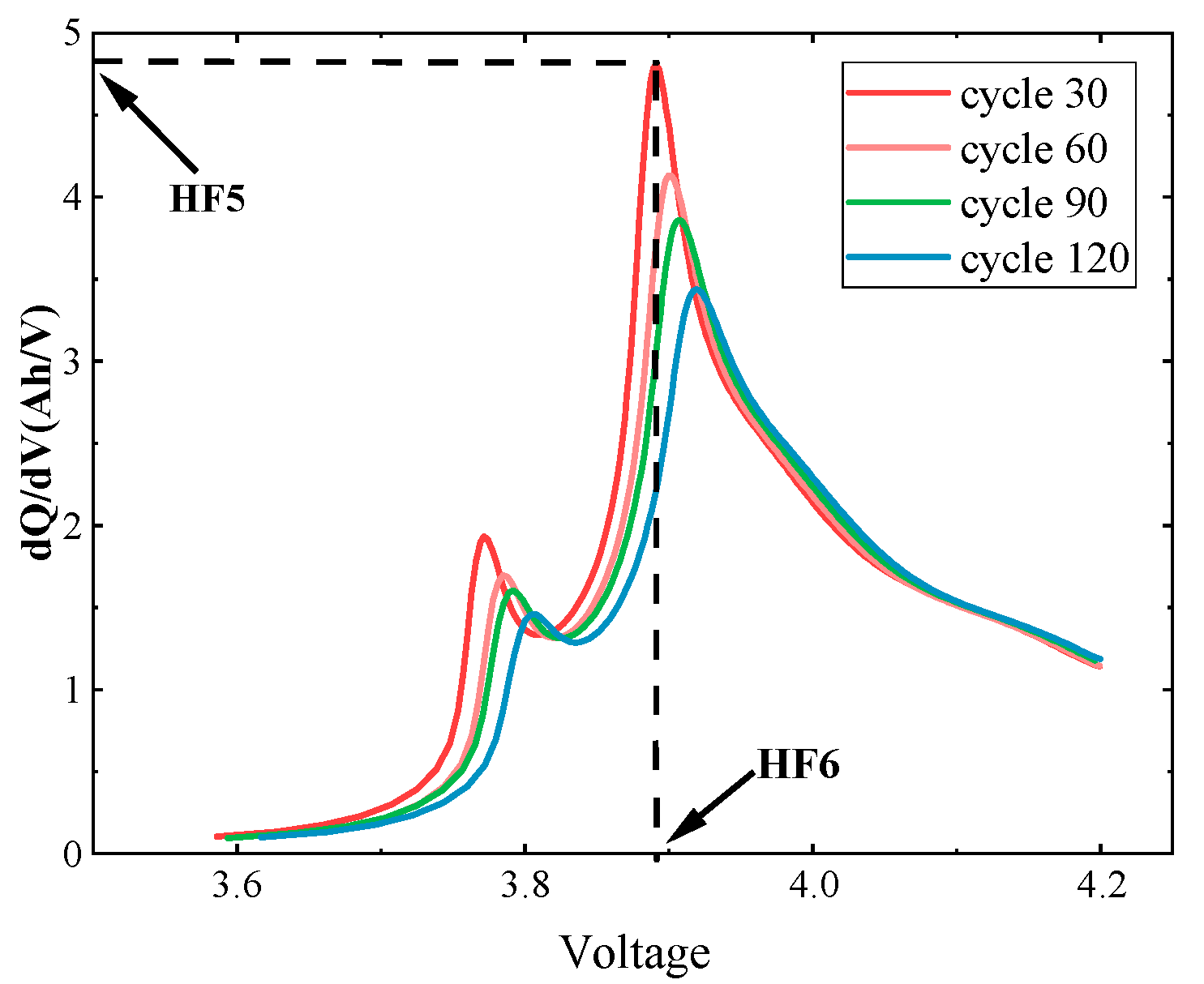



| HF1 | HF2 | HF3 | HF4 | HF5 | HF6 | HF7 | HF8 | ||
|---|---|---|---|---|---|---|---|---|---|
| CALCE | CS2_34 | 0.9238 | 0.8630 | 0.9789 | 0.9686 | 0.9984 | 0.9265 | 0.8677 | 0.9739 |
| CS2_36 | 0.6109 | 0.5398 | 0.8283 | 0.9791 | 0.9884 | 0.7177 | 0.6233 | 0.8001 | |
| CS2_37 | 0.9245 | 0.8215 | 0.9730 | 0.9287 | 0.9927 | 0.8243 | 0.9281 | 0.9656 | |
| NASA | B0005 | 0.9303 | 0.8715 | 0.9731 | 0.9516 | 0.9947 | 0.8725 | 0.9321 | 0.9668 |
| B0006 | 0.9282 | 0.9799 | 0.9724 | 0.9818 | 0.9455 | 0.8487 | 0.9439 | 0.9754 | |
| B0007 | 0.9686 | 0.9491 | 0.9809 | 0.9756 | 0.9211 | 0.8977 | 0.9502 | 0.9234 |
| MAE | MAPE | RSME | R2 | ||
|---|---|---|---|---|---|
| CALCE | CS2_34 | 0.0051 | 0.0153 | 0.0069 | 0.9977 |
| CS2_36 | 0.0040 | 0.0150 | 0.0065 | 0.9987 | |
| CS2_37 | 0.0043 | 0.0167 | 0.0066 | 0.9986 | |
| NASA | B0005 | 0.0027 | 0.0131 | 0.0032 | 0.9988 |
| B0006 | 0.0044 | 0.0161 | 0.0011 | 0.9854 | |
| B0007 | 0.0027 | 0.0127 | 0.0023 | 0.9989 |
| Battery | Method | MAE | MAPE | RSME | R2 |
|---|---|---|---|---|---|
| B0005 | CCN-Informer | 0.0027 | 0.0131 | 0.0032 | 0.9988 |
| Informer | 0.0054 | 0.0283 | 0.0069 | 0.9971 | |
| LSTM | 0.0090 | 0.0492 | 0.0079 | 0.9967 | |
| B0006 | CCN-Informer | 0.0044 | 0.0161 | 0.0011 | 0.9854 |
| Informer | 0.0063 | 0.0237 | 0.0040 | 0.9854 | |
| LSTM | 0.0108 | 0.0442 | 0.0045 | 0.9845 | |
| B0007 | CCN-Informer | 0.0027 | 0.0127 | 0.0023 | 0.9989 |
| Informer | 0.0056 | 0.0323 | 0.0097 | 0.9821 | |
| LSTM | 0.0088 | 0.0486 | 0.0133 | 0.9788 | |
| CS2_34 | CCN-Informer | 0.0051 | 0.0153 | 0.0065 | 0.9986 |
| Informer | 0.0077 | 0.0384 | 0.0079 | 0.9902 | |
| LSTM | 0.0102 | 0.0510 | 0.0119 | 0.9799 | |
| CS2_36 | CCN-Informer | 0.0040 | 0.0150 | 0.0069 | 0.9977 |
| Informer | 0.0066 | 0.0412 | 0.0089 | 0.9921 | |
| LSTM | 0.0093 | 0.0633 | 0.0132 | 0.9798 | |
| CS2_37 | CCN-Informer | 0.0043 | 0.0167 | 0.0066 | 0.9986 |
| Informer | 0.0066 | 0.0348 | 0.0141 | 0.9801 | |
| LSTM | 0.0087 | 0.0433 | 0.0135 | 0.9659 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Liu, X.; Huang, W.; Zhang, B.; Zhang, Z.; Shao, Z.; Mao, Z. Health State Assessment of Lithium-Ion Batteries Based on Multi-Health Feature Fusion and Improved Informer Modeling. Energies 2024, 17, 2154. https://doi.org/10.3390/en17092154
He J, Liu X, Huang W, Zhang B, Zhang Z, Shao Z, Mao Z. Health State Assessment of Lithium-Ion Batteries Based on Multi-Health Feature Fusion and Improved Informer Modeling. Energies. 2024; 17(9):2154. https://doi.org/10.3390/en17092154
Chicago/Turabian StyleHe, Jun, Xinyu Liu, Wentao Huang, Bohan Zhang, Zuoming Zhang, Zirui Shao, and Zimu Mao. 2024. "Health State Assessment of Lithium-Ion Batteries Based on Multi-Health Feature Fusion and Improved Informer Modeling" Energies 17, no. 9: 2154. https://doi.org/10.3390/en17092154
APA StyleHe, J., Liu, X., Huang, W., Zhang, B., Zhang, Z., Shao, Z., & Mao, Z. (2024). Health State Assessment of Lithium-Ion Batteries Based on Multi-Health Feature Fusion and Improved Informer Modeling. Energies, 17(9), 2154. https://doi.org/10.3390/en17092154





