Application of Machine Learning for Shale Oil and Gas “Sweet Spots” Prediction
Abstract
1. Introduction
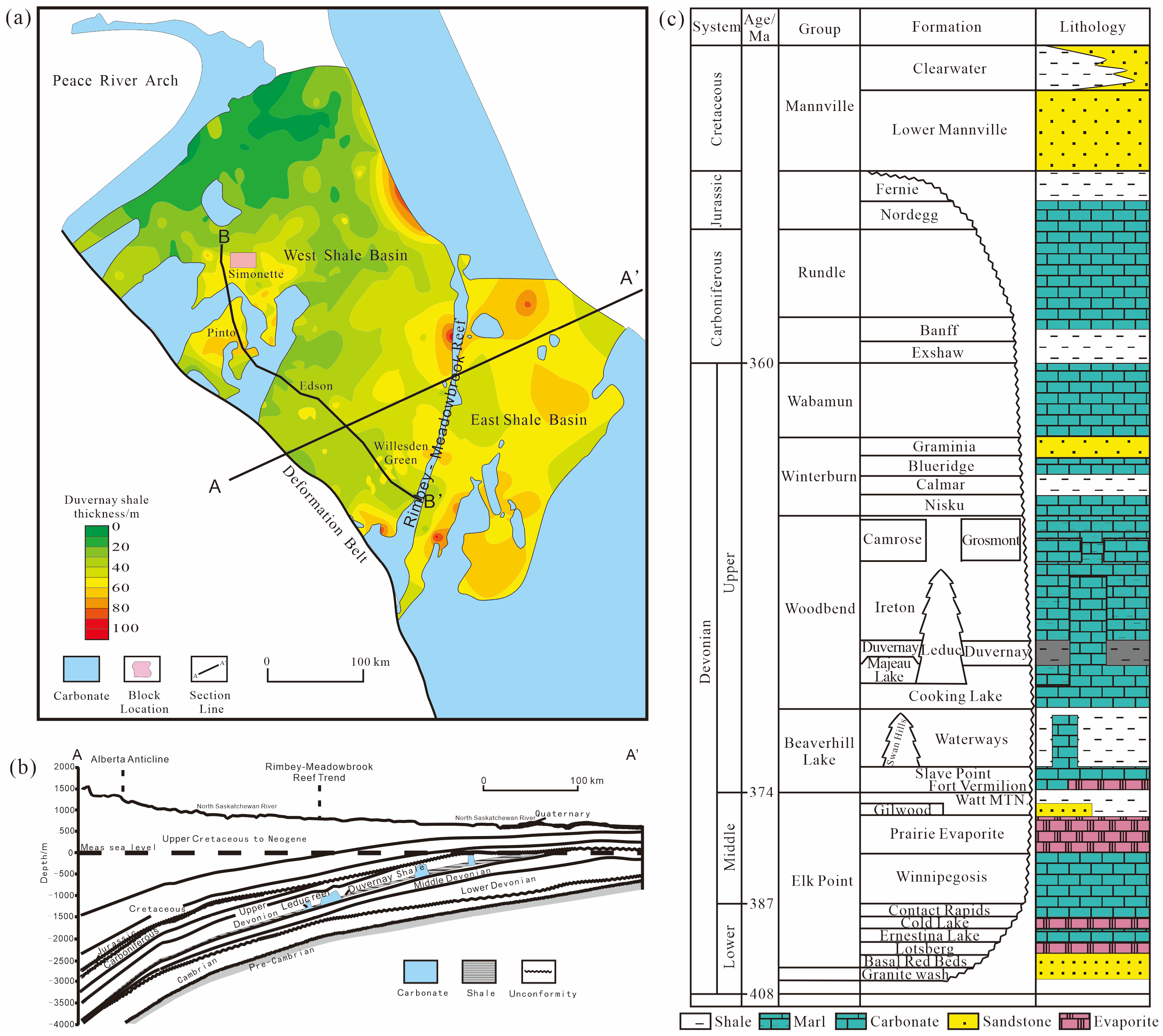
2. Background of the Study Area
3. Research Approach and Technology Roadmap
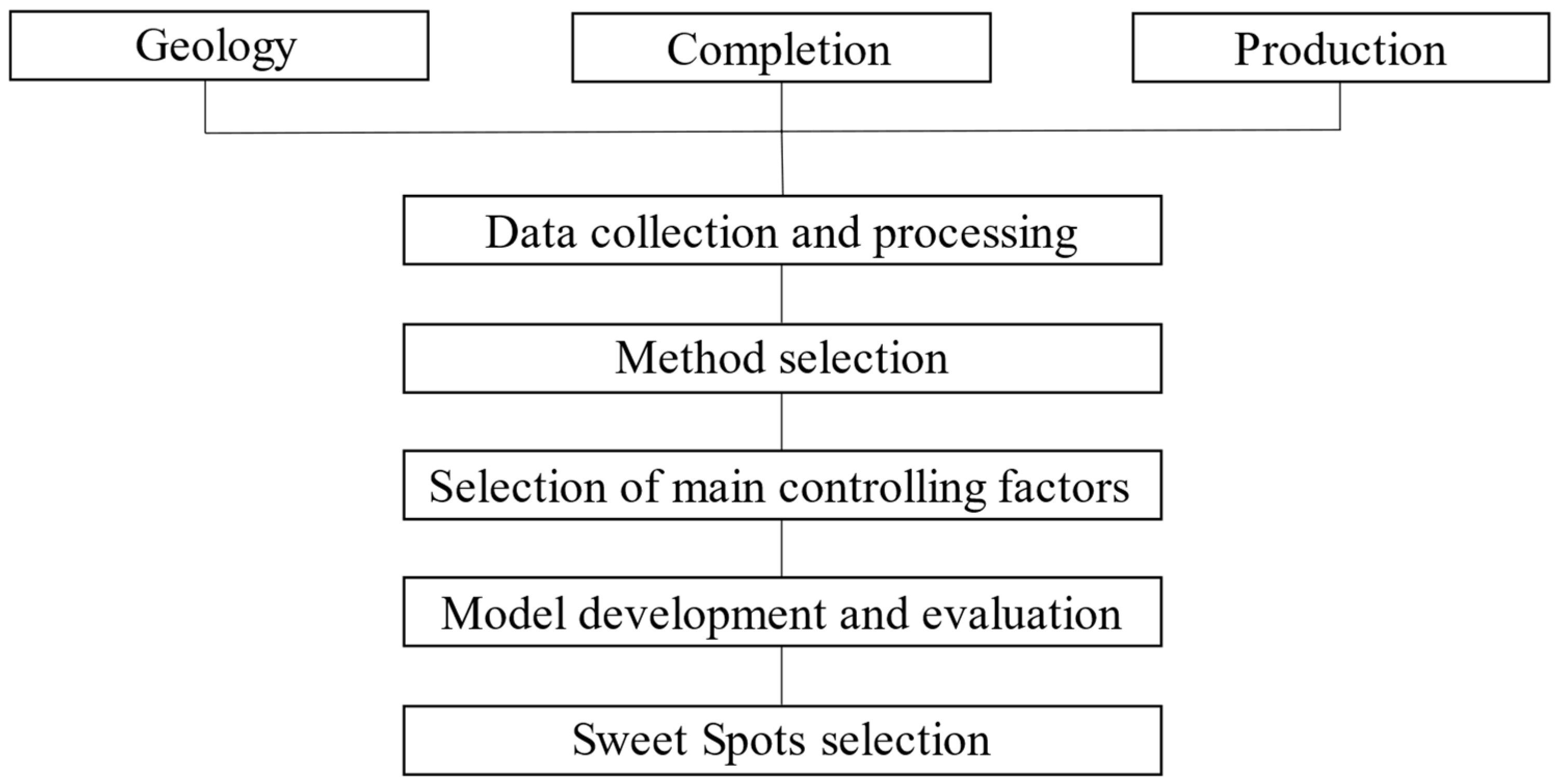
3.1. Technology Roadmap
3.2. Random Forest
3.3. Support Vector Machine
3.4. Artificial Neural Networks
3.5. Data Preprocessing
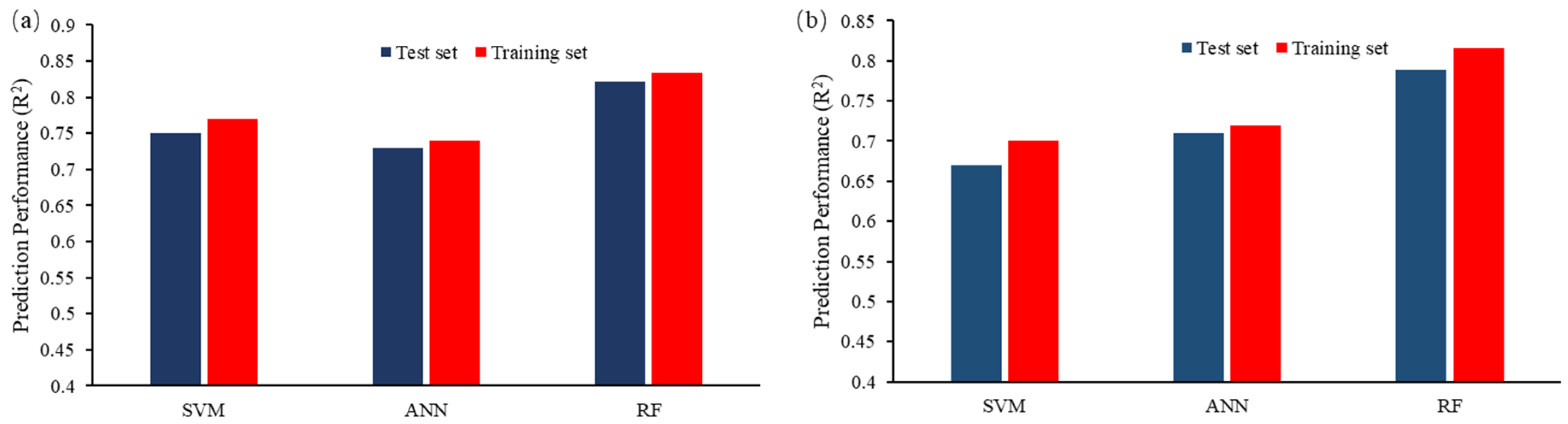
3.6. Model Selection and Evaluation
4. Data Integration and Analysis
4.1. Analysis of Geological Main Controlling Factors
4.2. Analysis of Engineering Main Controlling Factors
5. Discussion
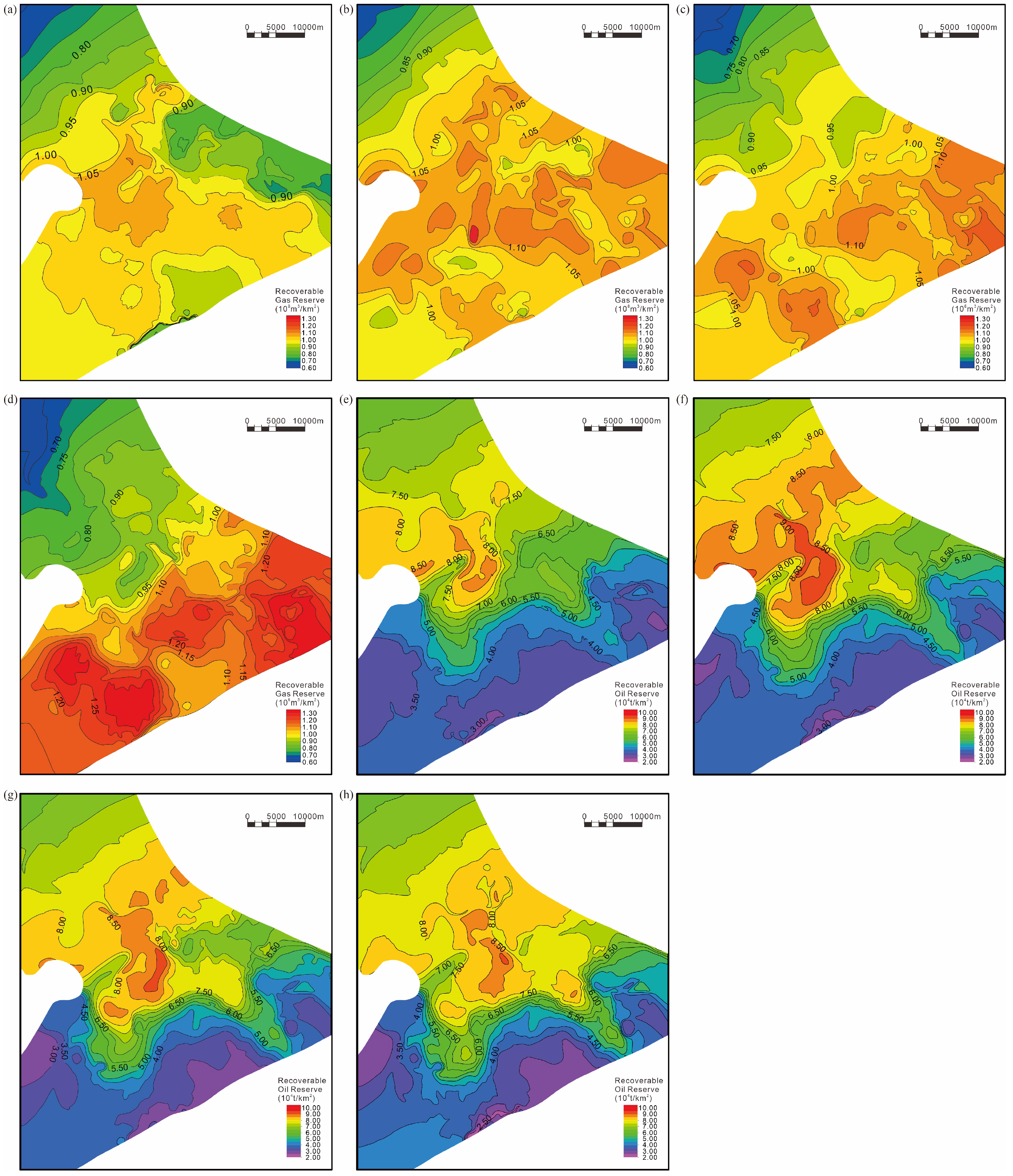
6. Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation | Full Name |
| R2 | Determination coefficient |
| RMSE | Root mean square error |
| RF | Random Forest |
| EUR | Estimated Ultimate Recovery |
| TOC | Total Organic Carbon Content (%) |
References
- Wang, H.; Ma, F.; Tong, X.; Liu, Z.; Zhang, X.; Wu, Z.; Li, D.; Wang, B.; Xie, F.; Yang, L. Assessment of global unconventional oil and gas resources. Pet. Explor. Dev. 2016, 43, 925–940. [Google Scholar] [CrossRef]
- Zhang, X.S.; Wang, H.J.; Ma, F.; Sun, X.C.; Zhang, Y.; Song, Z.H. Classification and characteristics of tight oil plays. Pet. Sci. 2016, 13, 18–33. [Google Scholar] [CrossRef]
- Shelley, B.; Grieser, B.; Johnson, B.J.; Fielder, E.O.; Heinze, J.R.; Werline, J.R. Data analysis of Barnett shale completions. SPE J. 2008, 13, 366–374. [Google Scholar] [CrossRef]
- Baihly, J.; Altman, R.; Aviles, I. Has the economic stage count been reached in the Bakken shale? In Proceedings of the SPE Hydrocarbon Economics and Evaluation Symposium, Calgary, AB, Canada, 24–25 September 2012. [Google Scholar]
- Lafollette, R.F.; Holcomb, W.D.; Aragon, J. Practical Data Mining: Analysis of Barnett Shale Production Results with Emphasis on Well Completion and Fracture Stimulation. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 6–8 February 2012. [Google Scholar]
- Shelley, R.; Guliyev, N.; Nejad, A. A Novel Method to Optimize Horizontal Bakken Completions in a Factory Mode Development Program. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–10 October 2012. [Google Scholar]
- Pearson, C.M.; Griffin, L.; Wright, C.; Weijers, L. Breaking Up is Hard to Do: Creating Hydraulic Fracture Complexity in the Bakken Central Basin. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 5 February 2013; p. D021S006R005. [Google Scholar]
- Newgord, C.; Mediani, M.; Ouenes, A.; O’Conor, P. Predicting Middle Bakken Well Performance with Shale Capacity. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015; p. D011S001R003. [Google Scholar]
- Schuetter, J.; Mishra, S.; Zhong, M.; LaFollette, R. Data Analytics for Production Optimization in Unconventional Reservoirs. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, San Antonio, TX, USA, 20–22 July 2015. [Google Scholar]
- Lolon, E.; Hamidieh, K.; Weijers, L.; Mayerhofer, M.; Melcher, H.; Oduba, O. Evaluating the Relationship between Well Parameters and Production Using Multivariate Statistical Models: A Middle Bakken and Three Forks Case History. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 9–11 February 2016; p. D031S007R003. [Google Scholar]
- Wang, S.; Chen, S. A Comprehensive Evaluation of Well Completion and Production Performance in Bakken Shale Using Data-Driven Approaches. In Proceedings of the SPE Asia Pacific Hydraulic Fracturing Conference, Beijing, China, 24–26 August 2016; p. D011S002R005. [Google Scholar]
- Mohaghegh, S.D.; Gaskari, R.; Maysami, M. Shale Analytics: Making Production and Operational Decisions Based on Facts: A Case Study in Marcellus Shale. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 24–26 January 2017; p. D031S007R004. [Google Scholar]
- Tian, Y.; Ayers, W.B.; Sang, H.; McCain, W.D., Jr.; Ehlig-Economides, C. Quantitative Evaluation of Key Geological Controls on Regional Eagle Ford Shale Production Using Spatial Statistics. SPE Reserv. Eval. Eng. 2018, 21, 238–256. [Google Scholar] [CrossRef]
- He, Q.; Bruno, J.; Zhong, Z. Controlling Factors of Shale Gas Production: What Can Artificial Intelligence Tell Us? In Proceedings of the SPE Eastern Regional Meeting, Charleston, WV, USA, 16 October 2019; p. D021S002R004. [Google Scholar]
- Ahmed, A.A.; Elkatatny, S.; Abdulraheem, A.; Mahmoud, M. Application of artificial intelligence techniques in estimating oil recovery factor for water derive sandy reservoirs. In Proceedings of the SPE Kuwait Oil and Gas Show and Conference, Mishref, Kuwait, 2–5 October 2017. [Google Scholar]
- Mahmoud, A.A.; Elkatatny, S.; Chen, W.; Abdulraheem, A. Estimation of oil recovery factor for water drive sandy reservoirs through applications of artificial intelligence. Energies 2019, 12, 3671. [Google Scholar] [CrossRef]
- Qin, Z.; Xu, T. Shale gas geological “sweet spot” parameter prediction method and its application based on convolutional neural network. Sci. Rep. 2022, 12, 15405. [Google Scholar] [CrossRef] [PubMed]
- Zhai, G.; Li, J.; Jiao, Y.; Wang, Y.; Liu, G.; Xu, Q.; Wang, C.; Chen, R.; Guo, X. Applications of chemostratigraphy in a characterization of shale gas Sedimentary Microfacies and predictions of sweet spots—Taking the Cambrian black shales in Western Hubei as an example. Mar. Pet. Geol. 2019, 109, 547–560. [Google Scholar] [CrossRef]
- Jiachen, H. Production Forecast Modeling and Application Based on Machine Learning. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2020. [Google Scholar]
- Song, X.; Liu, Y.; Ma, J.; Wang, J.; Kong, X.; Ren, X. Productivity forecast based on support vector machine optimized by grey wolf optimizer. Lithol. Reserv. 2020, 32, 134–140. [Google Scholar]
- Luo, G.; Tian, Y.; Bychina, M.; Ehlig-Economides, C. Production-Strategy Insights Using Machine Learning: Application for Bakken Shale. SPE Reserv. Eval. Eng. 2019, 22, 800–816. [Google Scholar] [CrossRef]
- Maucec, M.; Garni, S. Application of Automated Machine Learning for Multi-Variate Prediction of Well Production. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 18–21 March 2019; p. D032S069R003. [Google Scholar]
- Guo, Z.; Wang, H.; Kong, X.; Shen, L.; Jia, Y. Machine Learning-Based Production Prediction Model and Its Application in Duvernay Formation. Energies 2021, 14, 5509. [Google Scholar] [CrossRef]
- Whalen, M.T.; Day, J.E. Cross-Basin Variations in Magnetic Susceptibility Influenced by Changing Sea Level, Paleogeography, and Paleoclimate: Upper Devonian, Western Canada Sedimentary Basin. J. Sediment. Res. 2010, 80, 1109–1127. [Google Scholar] [CrossRef]
- Egenhoff, S.O.; Fishman, N.S. Traces In the Dark—Sedimentary Processes and Facies Gradients In the Upper Shale Member of the Upper Devonian-Lower Mississippian Bakken Formation, Williston Basin, North Dakota, U.S.A. J. Sediment. Res. 2013, 83, 803–824. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Haghshenas, B.; Ghanizadeh, A.; Qanbari, F.; Williams-Kovacs, J.D.; Riazi, N.; Debuhr, C.; Deglint, H.J. Nanopores to megafractures: Current challenges and methods for shale gas reservoir and hydraulic fracture characterization. J. Nat. Gas Sci. Eng. 2016, 31, 612–657. [Google Scholar] [CrossRef]
- Wang, P.; Chen, Z.; Jin, Z.; Jiang, C.; Sun, M.; Guo, Y.; Chen, X.; Jia, Z. Shale oil and gas resources in organic pores of the Devonian Duvernay Shale, Western Canada Sedimentary Basin based on petroleum system modeling. J. Nat. Gas Sci. Eng. 2018, 50, 33–42. [Google Scholar] [CrossRef]
- Kong, X.; Wang, P.; Xia, Z.; Zhang, X.; Qu, L.; Guo, Z. Geological characteristics and fluid distribution of the Upper Devonian Duvernay shale in Simonette block in the Western Canada Sedimentary Basin. China Pet. Explor. 2022, 27, 93–107. [Google Scholar]
- Lyster, S.; Corlett, H.; Berhane, H. Hydrocarbon Resource Potential of the Duvernay Formation in Alberta-Update; AER/AGS Open File Report 2017-02; Alberta Geological Survey/Alberta Energy Regulator: Edmonton, AB, Canada, 2017; pp. 31–43. [Google Scholar]
- Price, R. Cordilleran tectonics and the evolution of the Western Canada Sedimentary Basin. Bull. Can. Pet. Geol. 1990, 38, 176–177. [Google Scholar]
- Porter, J.; Price, R.; Mccrossan, R. The western Canada sedimentary basin. Philos. Trans. R. Soc. Lond. Ser. A Math. 1982, 305, 169–192. [Google Scholar]
- Anfort, S.; Bachu, S.; Bentley, L. Regional-scale hydrogeology of the Upper Devonian-Lower Cretaceous sedimentary succession, south-central Alberta basin, Canada. AAPG Bull. 2001, 85, 637–660. [Google Scholar]
- Green, D.G.; Mountjoy, E.W. Fault and conduit controlled burial dolomitization of the Devonian west-central Alberta Deep Basin. Bull. Can. Pet. Geol. 2005, 53, 101–129. [Google Scholar] [CrossRef]
- Li, G.; Luo, K.; Shi, D. Key technologies, engineering management and important suggestions of shale oil/gas development: Case study of a Duvernay shale project in Western Canada Sedimentary Basin. Pet. Explor. Dev. 2020, 47, 739–749. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning with Applications in R, 6th ed.; Springer Texts in Statistics; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C.; Villa-Vialaneix, N. Random forests for big data. Big Data Res. 2017, 9, 28–46. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 2000; pp. 1–15. [Google Scholar]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Zou, C.; Dong, D.; Wang, Y.; Li, X.; Huang, J.; Wang, S.; Gaun, Q.; Zhang, C.; Wang, H.; Liu, H.; et al. Shale gas in China: Characteristics, challenges and prospects (I). Pet. Explor. Dev. 2015, 42, 689–701. [Google Scholar] [CrossRef]
- Zhao, X.; Zhou, L.; Pu, X.; Jin, F.; Shi, Z.; Han, W.; Jiang, W.; Han, G.; Zhang, W.; Wang, H.; et al. Formation conditions and enrichment model of retained petroleum in lacustrine shale: A case study of the Paleogene in Huanghua depression, Bohai Bay Basin, China. Pet. Explor. Dev. 2020, 47, 856–869. [Google Scholar] [CrossRef]
- Liu, C.; Lu, S.F.; Xue, H.T. Variable-coefficient ΔlogR model and its application in shale organic evaluation. Prog. Geophys. 2014, 29, 312–317. [Google Scholar]
- Zou, C.N.; Ma, F.; Pan, S.Q. Formation and distribution potential of global shale oil and the theoretical and technological progress of continental shale oil in China. Earth Sci. Front. 2023, 30, 128–142. [Google Scholar]
- Zou, C.; Dong, D.; Wang, Y.; Li, X.; Huang, J.; Wang, S.; Guan, Q.; Zhang, C.; Wang, H.; Liu, H.; et al. Shale gas in China: Characteristics, challenges and prospects (II). Pet. Explor. Dev. 2016, 43, 166–178. [Google Scholar] [CrossRef]
- Zou, C.; Dong, D.; Wang, S.; Li, J.; Li, X.; Wang, Y.; Li, D.; Cheng, K. Geological characteristics, formation mechanism and resource potential of shale gas in China. Pet. Explor. Dev. 2010, 37, 641–653. [Google Scholar] [CrossRef]
- Liao, L.; Li, G.; Zhang, H.; Feng, J.; Zeng, Y.; Ke, K.; Wang, Z. Well Completion Optimization in Canada Tight Gas Fields Using Ensemble Machine Learning. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 9–12 November 2020. [Google Scholar]
- Sheikhi Garjan, Y.; Ghaneezabadi, M. Machine Learning Interpretability Application to Optimize Well Completion in Montney. In Proceedings of the SPE Canada Unconventional Resources Conference, Virtual, 28 September–2 October 2020; p. D033S004R003. [Google Scholar]
- Kong, B.; Chen, Z.; Chen, S.; Qin, T. Machine learning-assisted production data analysis in liquid-rich Duvernay Formation. J. Pet. Sci. Eng. 2021, 200, 108377. [Google Scholar] [CrossRef]
- Wang, S.; Chen, S. Insights to fracture stimulation design in unconventional reservoirs based on machine learning modeling. J. Pet. Sci. Eng. 2019, 174, 682–695. [Google Scholar] [CrossRef]








| Item | Thickness (m) | Porosity (%) | Permeability (mD) | Water Saturation (%) | TOC (%) | OGR (t/104m3) |
|---|---|---|---|---|---|---|
| count | 165 | 165 | 165 | 165 | 165 | 165 |
| mean | 34.2 | 4.3 | 1.469 × 10−3 | 3.2 | 3.1 | 9.8 |
| std | 8.6 | 0.4 | 1.885 × 10−3 | 0.8 | 0.8 | 5.3 |
| min | 16.7 | 3.6 | 6.150 × 10−6 | 1.9 | 1.9 | 0.2 |
| 25% | 26.5 | 3.9 | 5.780 × 10−5 | 2.6 | 2.4 | 7.0 |
| 50% | 36.1 | 4.4 | 6.410 × 10−4 | 3.2 | 2.9 | 9.0 |
| 75% | 41.1 | 4.6 | 2.150 × 10−3 | 3.6 | 3.6 | 11.3 |
| max | 48.8 | 5.6 | 7.611 × 10−3 | 8.6 | 5.2 | 41.6 |
| Item | Well Spacing | Total Fracturing Fluid (m3) | Total Proppant (t) | Total Clusters | Stages | Lateral Length (m) |
|---|---|---|---|---|---|---|
| count | 165 | 165 | 165 | 165 | 165 | 165 |
| mean | 344.8 | 50,175.0 | 7651.6 | 213.7 | 40.6 | 2522.8 |
| std | 231.5 | 15,239.4 | 2708.7 | 144.0 | 15.6 | 558.6 |
| min | 100 | 16,145.5 | 1763.0 | 32 | 10 | 975 |
| 25% | 200 | 39,222.0 | 5980.0 | 124 | 31 | 2084 |
| 50% | 300 | 47,277.0 | 7330.3 | 152 | 37 | 2551 |
| 75% | 400 | 60,531.9 | 8986.3 | 232 | 44 | 2874 |
| max | 999 | 84,414.0 | 16,493.0 | 595 | 85 | 3851 |
| Hyperparameter | One-Year Cumulative Gas Production | One-Year Cumulative Oil Production | ||
|---|---|---|---|---|
| Grid Research Range | Final Results | Grid Research Range | Final Results | |
| Number of decision trees | [400,500,600,700] | 500 | [400,500,600,700] | 500 |
| Minimum number of samples for leaf nodes | [2,3,4,5] | 3 | [2,3,4,5] | 3 |
| Minimum number of samples for split nodes | [2,3,4,5] | 3 | [2,3,4,5] | 3 |
| Number of attributes in the attribute subset | [2,3,4,5] | 3 | [2,3,4,5] | 3 |
| Hyperparameter | One-Year Cumulative Gas Production | One-Year Cumulative Oil Production | ||
|---|---|---|---|---|
| Grid Research Range | Final Results | Grid Research Range | Final Results | |
| C | [950,1000,1050,1100] | 1000 | [950,1000,1050,1100] | 1000 |
| Kernel functions | [Gaussian; Linear; Polynomial] | Gaussian | [Gaussian; Linear; Polynomial] | Gaussian |
| Epsilon | [0.9,1.0,1.1,1.2] | 1.1 | [0.9,1.0,1.1,1.2] | 1.2 |
| Hyperparameter | One-Year Cumulative Gas Production | One-Year Cumulative Oil Production | ||
|---|---|---|---|---|
| Grid Research Range | Final Results | Grid Research Range | Final Results | |
| Number of fully connected layers | [1,2,3] | 2 | [1,2,3] | 3 |
| First layer size | [10,12,14,16] | 12 | [4,5,6,7,8] | 5 |
| Second layer size | [10,15,20,25] | 20 | [4,5,6,7,8] | 5 |
| Third layer size | [10,15,20,25] | / | [4,5,6,7,8] | 5 |
| Activation | [ReLU, Tanh, Sigmoid] | Tanh | [ReLU, Tanh, Sigmoid] | Tanh |
| Training Set | Testing Set | |||||
|---|---|---|---|---|---|---|
| SVM | ANN | RF | SVM | ANN | RF | |
| R2 | 0.77 | 0.74 | 0.83 | 0.75 | 0.73 | 0.821 |
| RMSE | 445 | 485 | 397 | 460.6 | 487.94 | 404.68 |
| Training Set | Testing Set | |||||
|---|---|---|---|---|---|---|
| SVM | ANN | RF | SVM | ANN | RF | |
| R2 | 0.7 | 0.72 | 0.82 | 0.67 | 0.71 | 0.79 |
| RMSE | 4233 | 3980 | 3169.83 | 4478 | 4198 | 3300.58 |
| Item | Scheme 1 | Scheme 2 | Scheme 3 | Scheme 4 |
|---|---|---|---|---|
| Total fracturing fluid volume (m3) | 78,210 | 65,760 | 59,760 | 58,590 |
| Total proppant volume (t) | 5970 | 8970 | 9750 | 11,160 |
| Total clusters | 125 | 176.4706 | 272.7273 | 428.5714 |
| Horizontal lateral length (m) | 3000 | 3000 | 3000 | 3000 |
| Total stages | 22 | 32 | 50 | 64 |
| Fracturing fluid type | Slick water | Composite fracturing fluid | High viscosity composite fracturing fluid | High viscosity composite fracturing fluid |
| Well spacing (m) | 250 | 250 | 300 | 300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Guo, Z.; Kong, X.; Zhang, X.; Wang, P.; Shan, Y. Application of Machine Learning for Shale Oil and Gas “Sweet Spots” Prediction. Energies 2024, 17, 2191. https://doi.org/10.3390/en17092191
Wang H, Guo Z, Kong X, Zhang X, Wang P, Shan Y. Application of Machine Learning for Shale Oil and Gas “Sweet Spots” Prediction. Energies. 2024; 17(9):2191. https://doi.org/10.3390/en17092191
Chicago/Turabian StyleWang, Hongjun, Zekun Guo, Xiangwen Kong, Xinshun Zhang, Ping Wang, and Yunpeng Shan. 2024. "Application of Machine Learning for Shale Oil and Gas “Sweet Spots” Prediction" Energies 17, no. 9: 2191. https://doi.org/10.3390/en17092191
APA StyleWang, H., Guo, Z., Kong, X., Zhang, X., Wang, P., & Shan, Y. (2024). Application of Machine Learning for Shale Oil and Gas “Sweet Spots” Prediction. Energies, 17(9), 2191. https://doi.org/10.3390/en17092191






