Design and Implementation of Hybrid GA-PSO-Based Harmonic Mitigation Technique for Modified Packed U-Cell Inverters
Abstract
1. Introduction
1.1. Background on Multilevel Inverters and Their Significance in Power Systems
1.2. Challenges with Harmonics in Multilevel Inverters
1.3. Overview of Optimization Techniques Used for Harmonic Mitigation
1.4. Motivation for Combining GA and PSO for Selective Harmonic Mitigation (SHM)
1.5. Objectives of the Study
- Formulate the harmonic mitigation problem as a multi-objective optimization problem with minimum THD serving as the primary objective, while keeping voltage stress and switching loss constraints.
- Design a hybrid GA-PSO algorithm that combines the exploratory power of the GA with the convergence efficiency of PSO.
- Simulate the proposed approach in MATLAB/Simulink 2023b to evaluate its effectiveness in reducing harmonic content in five-level and seven-level PUC inverters.
- Offer a real-time implementation of the proposed system using the OPAT-RT OP5700 platform to evaluate the performance in real-time.
- Benchmark the hybrid algorithm against standalone GA and PSO methods to demonstrate its superiority.
- Explore the feasibility of hardware implementation to validate the algorithm’s performance under practical conditions.
2. Literature Review
2.1. Existing Multilevel Inverter Topologies
2.1.1. Cascaded H-Bridge (CHB) Inverter
2.1.2. Flying Capacitor (FC) Inverter
2.1.3. Neutral Point Clamped (NPC) Inverter
2.1.4. Packed U-Cell (PUC) Inverter
2.2. Existing Harmonic Mitigation Techniques in MLIs
2.2.1. Passive Filtering Techniques
2.2.2. Active Harmonic Control
2.2.3. Optimization-Based Techniques
- Genetic Algorithm (GA): The genetic algorithm is a robust evolutionary technique inspired by natural selection principles. The GA has been extensively used for Selective Harmonic Elimination (SHE) in MLIs, where the objective is to eliminate specific lower-order harmonics while preserving the fundamental frequency. The GA’s ability to explore a broad solution space makes it effective in handling nonlinear problems like THD minimization. However, the GA can sometimes suffer from slow convergence and premature stagnation, especially when dealing with highly complex or multi-modal problems [14,21].
- Particle Swarm Optimization (PSO): PSO is a population-based optimization technique inspired by the social behavior of birds and fish. It is widely used in MLIs for optimizing switching angles to reduce THD. PSO’s key advantage lies in its simplicity and rapid convergence to near-optimal solutions. However, its tendency to become trapped in local optima, particularly in high-dimensional search spaces, can limit its effectiveness in achieving the best possible harmonic suppression [22,23,24].
- Differential Evolution (DE): Another robust and efficient evolutionary optimization technique for nonlinear and multi-modal problems is DE. In harmonic mitigation, DE has also been applied for the optimization of MLI parameters with often competitive results. Simplicity in mutation and selection further makes it particularly appealing for high-dimensional problems. However, optimal results may be obtained from DE after extensive tuning of its parameters [25].
- Simulated Annealing (SA): SA is a probabilistic technique that simulates the annealing process in metallurgy. It has been applied to MLIs for the minimization of THD, where switching angles are progressively improved. In particular, SA has proved very effective in escaping local optima, although convergence rates are generally slower compared to PSO or GA methods [23,26].
- Multi-Objective Optimization (MOO): There are multi-objective techniques, such as the Non-Dominated Sorting Genetic Algorithm-II (NSGA-II), which are applied to handle the conflict of objectives in harmonic mitigation, like minimization of THD at reduced switching losses or voltage stress. They offer a Pareto-optimal front that empowers the designer with several trade-off solutions, depending on the requirements of the application [27,28].
2.2.4. Limitations of Single Optimization Techniques
- GA: Slow convergence and prematurely converges into local optima.
- PSO: Premature convergence problem, especially in multi-modal search spaces.
- SA and DE: Usually require extensive parameter tuning, which can be computationally expensive.
3. Packed U-Cell Inverters
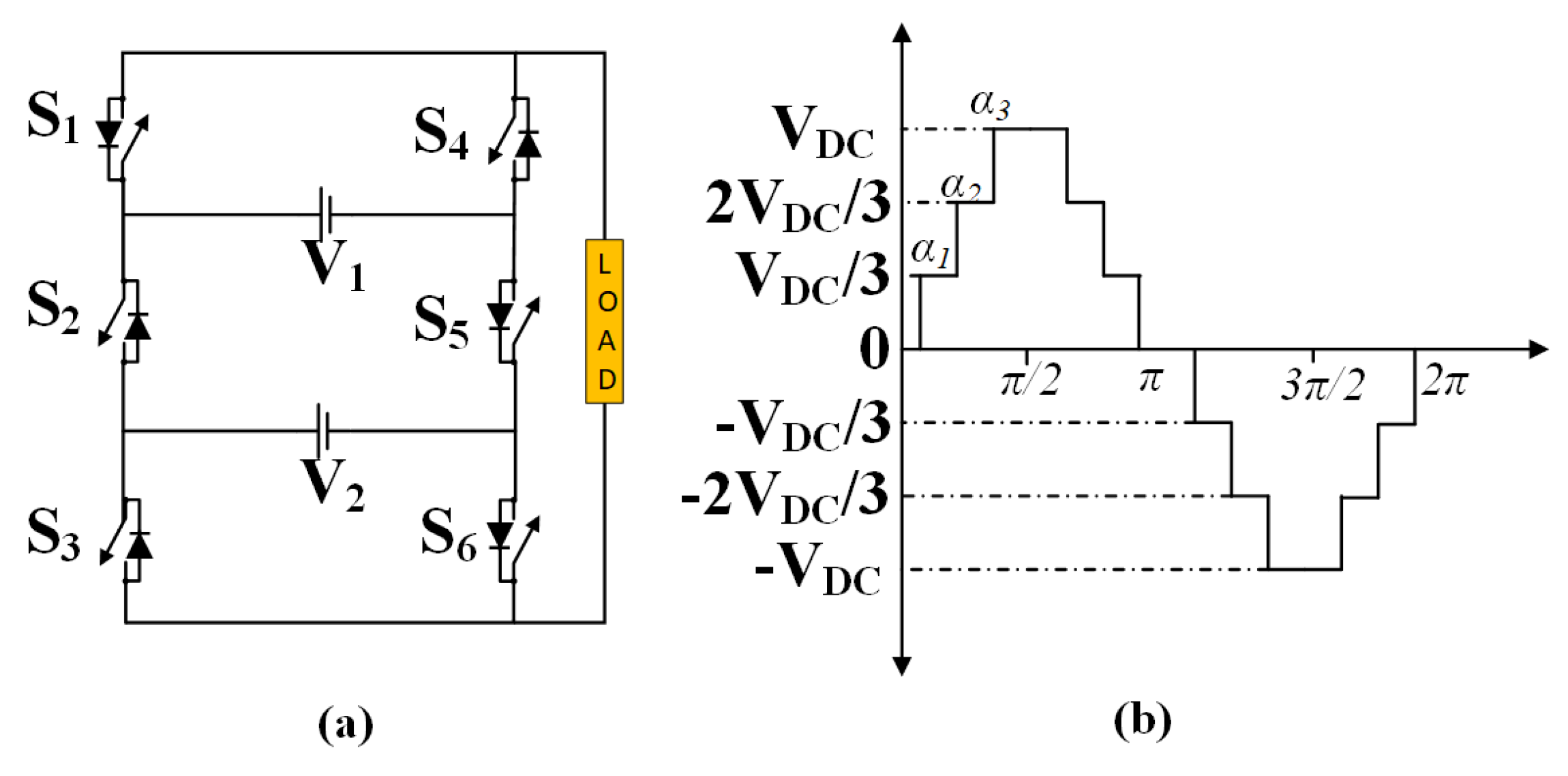
3.1. Seven-Level Modified Packed U-Cell Inverter Topology
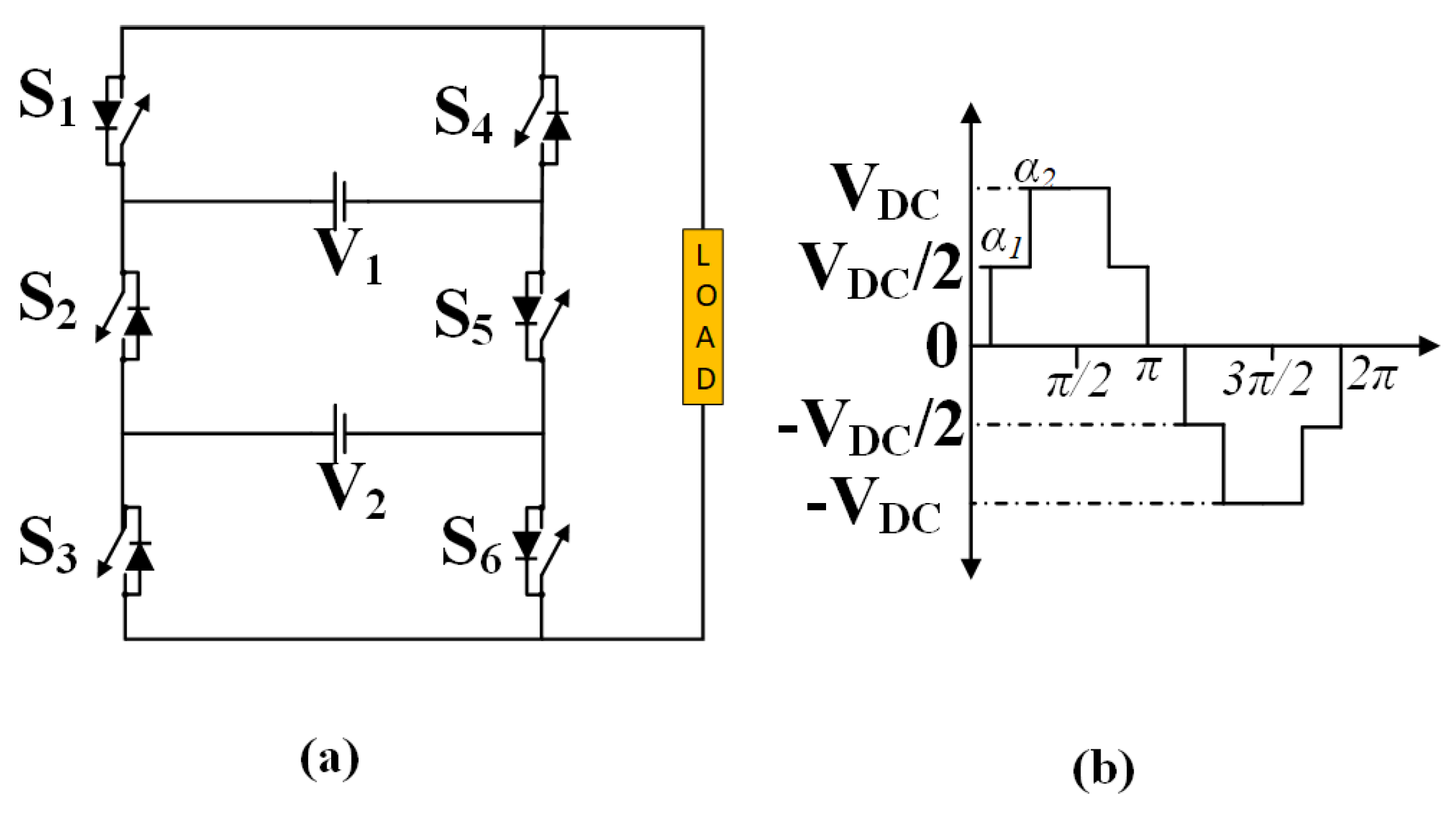
3.2. Five-Level Modified Packed U-Cell Inverter Topology
4. Problem Formulation for Harmonic Mitigation
4.1. Objective of Harmonic Mitigation
- The fundamental component is maintained at a specified reference value ,
- The 3rd, 5th, 7th, 9th, and 11th harmonics are mitigated.
4.2. Formulating the Harmonic Equations
- Fundamental Component Equation:Rearranging to express the relationship in terms of the modulation index m,
- Harmonic Component Equations for Mitigation: To minimize the 3rd, 5th, 7th, 9th, and 11th harmonics, we set their components to zero:
4.3. Defining the Cost Function for Harmonic Mitigation
- and are the amplitudes of the fundamental, 3rd, 5th, 7th, 9th, and 11th harmonics, respectively,
- and are weighting factors that determine the importance of each harmonic in the cost function.
5. Proposed Methodology
5.1. Optimization Problem for Harmonic Elimination
- Objective Function
- are the harmonic orders to consider.
- corresponds to the fundamental component equation.
- for corresponds to the harmonic elimination equations.
5.1.1. Constraints
- Inequality Constraints:
- Modulation Index Constraint:
5.1.2. Penalty Function Approach
5.2. Algorithm Steps for SHM Using GA-PSO
5.2.1. Step 1: Initialize Population
- (a)
- The population size N is defined.
- (b)
- The initial positions for N particles within the constraints can be generated as follows:where is a small random increment ensuring constraints are met.
- (c)
- Finally, the velocities are initialized to zero or small random values.
5.2.2. Step 2: Evaluate Fitness
- (a)
- Calculation of for is carried out.
- (b)
- Then, the objective function is computed:
- (c)
- Then, the personal best position is stored if improves the current best.
- (b)
- Finally, the global best position is updated if is better than the current global best.
5.2.3. Step 3: Apply Genetic Algorithm Operators
- (a)
- Selection: The tournament selection is used to choose pairs of particles based on fitness.
- (b)
- Crossover: We applied single-point crossover at a random point c:
- (c)
- Mutation: Then, a randomly selected gene is mutated:Mutation introduces diversity into the population by modifying a randomly selected gene . The parameter represents the magnitude of change applied during mutation and is randomly chosen from the range times the modulation index. This ensures that the mutation is significant enough to escape local optima but not so large as to violate constraints. The new value of is calculated as , where can be positive or negative. To ensure feasibility, the mutated is checked to remain within the constraint bounds .
5.2.4. Step 4: Update Velocities and Positions (PSO Operators)
- (a)
- Update Velocity:
- (b)
- Update Position:
- (c)
- It is important to ensure remains within constraints:Enforce ordering:
5.2.5. Step 5: Update Personal and Global Bests
- (a)
- Evaluating fitness .
- (b)
- Updating the personal best if improves the current personal best.
- (c)
- Updating the global best if improves the current global best.
5.2.6. Step 6: Termination Criteria
- (a)
- Stopping after a predefined number of iterations.
- (b)
- Stopping if the change in global best fitness is below a small threshold for consecutive iterations.
- (c)
- Stopping if is less than a predefined acceptable error.
5.2.7. Step 7: Output Results
- (a)
- Thus, the optimal switching angles are obtained.
- (b)
- Just to make sure, the optimal switching angles need to be verified:
5.3. Hybrid GA-PSO Algorithm Design
5.3.1. Hybrid GA-PSO Algorithm for MPUC7
5.3.2. Hybrid GA-PSO Algorithm for MPUC5
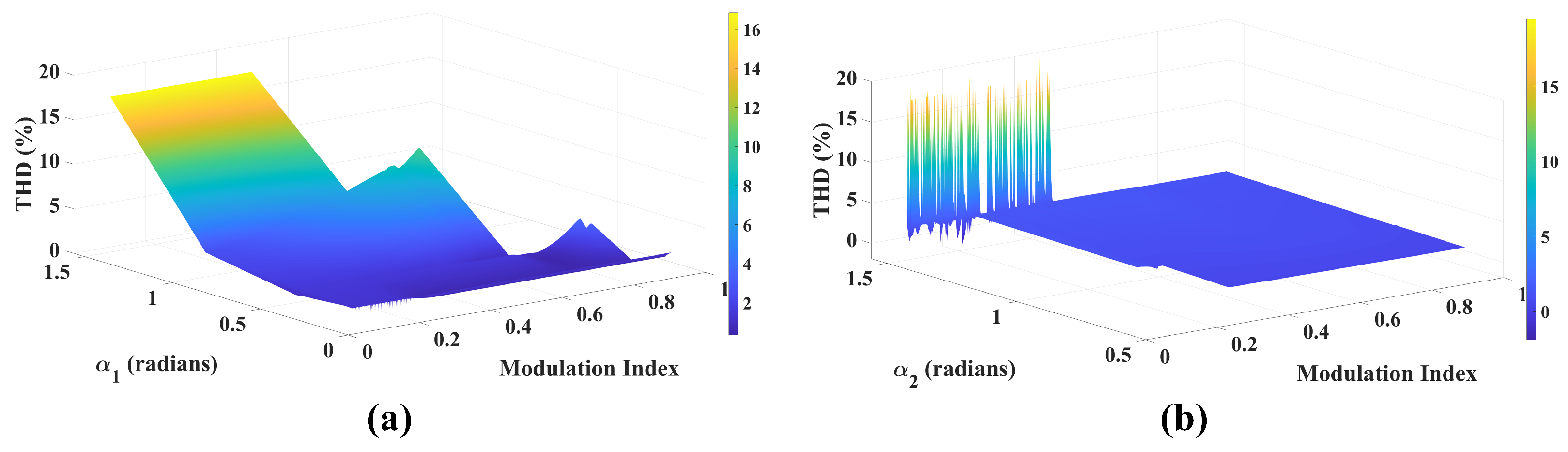
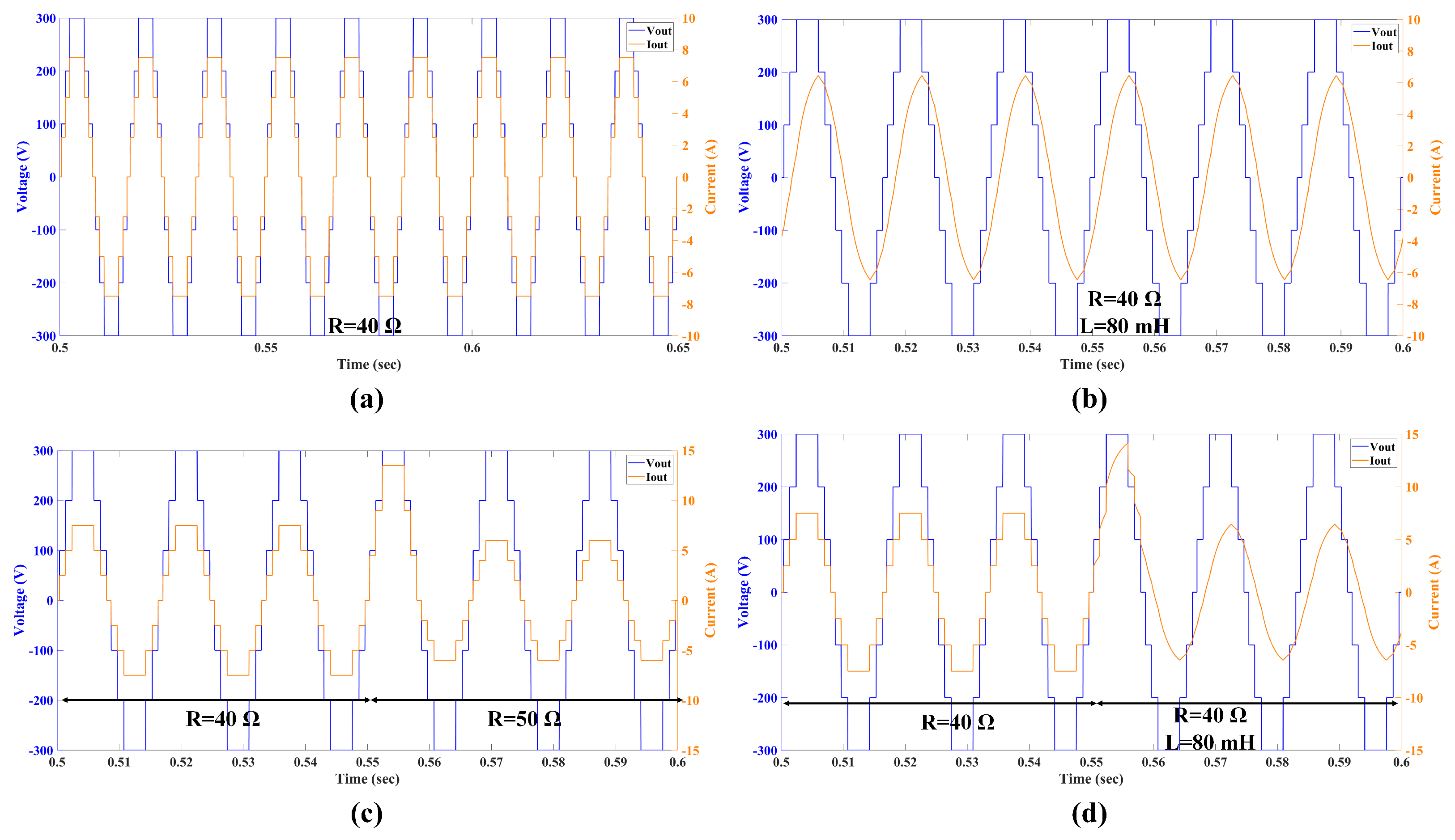
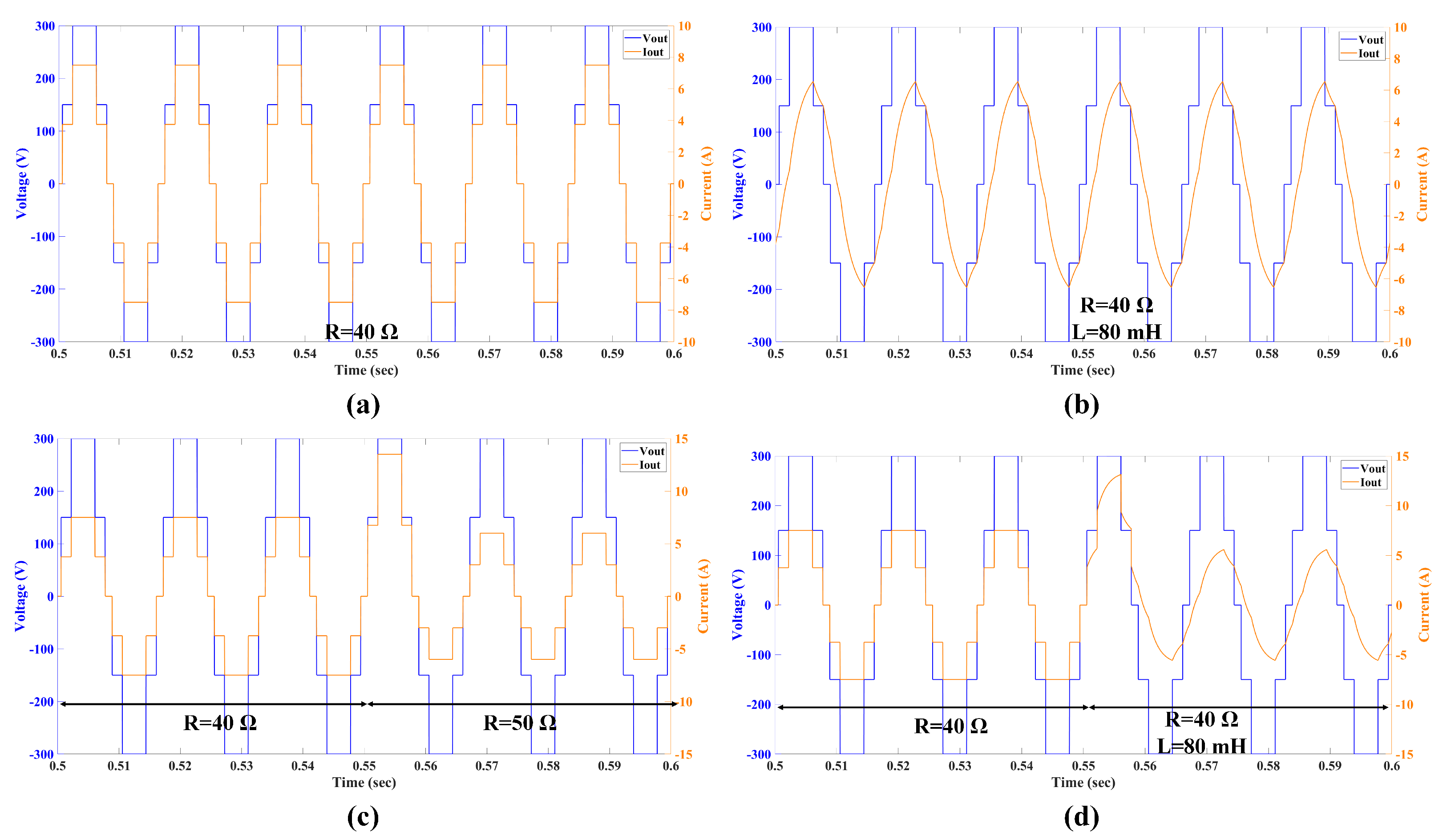
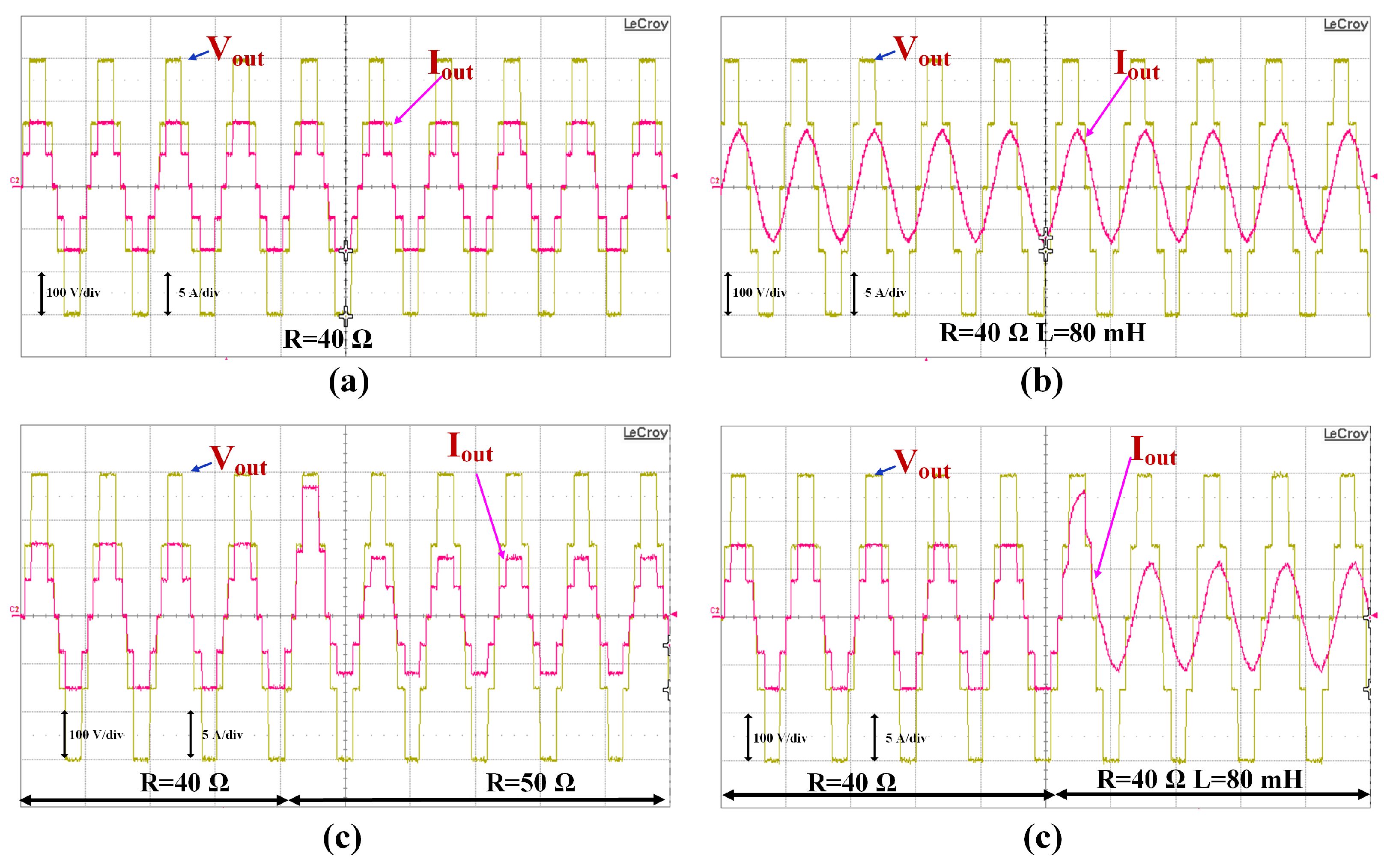
6. Results and Discussion
6.1. Simulation Results
6.2. Real-Time Simulation Results
Digital Implementation
6.3. Application
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CHB | Cascaded H-Bridge |
| DC | Direct Current |
| DE | Differential Evolution |
| FC | Flying Capacitor |
| FFT | Fast Fourier Transform |
| GA | Genetic Algorithm |
| HIL | Hardware-in-the-Loop |
| MLI | Multilevel Inverter |
| MOO | Multi-Objective Optimization |
| MPUC5 | Modified Five-Level Packed U-Cell Inverter |
| MPUC7 | Modified Seven-Level Packed U-Cell Inverter |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm-II |
| NPC | Neutral Point Clamped |
| PSO | Particle Swarm Optimization |
| PUC | Packed U-Cell |
| RL | Resistive-Inductive |
| SA | Simulated Annealing |
| SHM | Selective Harmonic Mitigation |
| THD | Total Harmonic Distortion |
References
- Srinivasan, G.K.; Rivera, M.; Loganathan, V.; Ravikumar, D.; Mohan, B. Trends and challenges in multi-level inverter with reduced switches. Electronics 2021, 10, 368. [Google Scholar] [CrossRef]
- Bughneda, A.; Salem, M.; Richelli, A.; Ishak, D.; Alatai, S. Review of multilevel inverters for PV energy system applications. Energies 2021, 14, 1585. [Google Scholar] [CrossRef]
- Mehta, S.; Puri, V. A review of different multi-level inverter topologies for grid integration of solar photovoltaic system. Renew. Energy Focus 2022, 43, 263–276. [Google Scholar] [CrossRef]
- Ali Khan, M.Y.; Liu, H.; Yang, Z.; Yuan, X. A comprehensive review on grid connected photovoltaic inverters, their modulation techniques, and control strategies. Energies 2020, 13, 4185. [Google Scholar] [CrossRef]
- Villanueva, E.; Correa, P.; Rodríguez, J.; Pacas, M. Control of a single-phase cascaded H-bridge multilevel inverter for grid-connected photovoltaic systems. IEEE Trans. Ind. Electron. 2009, 56, 4399–4406. [Google Scholar] [CrossRef]
- Rana, R.A.; Patel, S.A.; Muthusamy, A.; Lee, C.W.; Kim, H.J. Review of multilevel voltage source inverter topologies and analysis of harmonics distortions in FC-MLI. Electronics 2019, 8, 1329. [Google Scholar] [CrossRef]
- Taghvaie, A.; Haque, M.E.; Saha, S.; Mahmud, M.A. A new step-up switched-capacitor voltage balancing converter for NPC multilevel inverter-based solar PV system. IEEE Access 2020, 8, 83940–83952. [Google Scholar] [CrossRef]
- Chenchireddy, K.; Jegathesan, V. A Review Paper on the Elimination of Low-Order Harmonics in Multilevel Inverters Using Different Modulation Techniques. In Inventive Communication and Computational Technologies: Proceedings of ICICCT 2020; Springer: Berlin/Heidelberg, Germany, 2021; pp. 961–971. [Google Scholar]
- Singhal, A.; Vu, T.L.; Du, W. Consensus control for coordinating grid-forming and grid-following inverters in microgrids. IEEE Trans. Smart Grid 2022, 13, 4123–4133. [Google Scholar] [CrossRef]
- Vairavasundaram, I.; Varadarajan, V.; Pavankumar, P.J.; Kanagavel, R.K.; Ravi, L.; Vairavasundaram, S. A review on small power rating PV inverter topologies and smart PV inverters. Electronics 2021, 10, 1296. [Google Scholar] [CrossRef]
- Iqbal, H.; Khalid, A.; Riggs, H.; Sarwat, A. Kalman Filter-Based Harmonic Distortion Mitigation Technique for Microgrid Applications. In Applications and Optimizations of Kalman Filter and Their Variants; IntechOpen: London, UK, 2024; Chapter 1. [Google Scholar]
- Poorfakhraei, A.; Narimani, M.; Emadi, A. A review of multilevel inverter topologies in electric vehicles: Current status and future trends. IEEE Open J. Power Electron. 2021, 2, 155–170. [Google Scholar] [CrossRef]
- Iqbal, H.; Tariq, M.; Sarfraz, M.; Anees, M.A.; Alhosaini, W.; Sarwar, A. Model predictive control of Packed U-Cell inverter for microgrid applications. Energy Rep. 2022, 8, 813–830. [Google Scholar] [CrossRef]
- Iqbal, H.; Tariq, M.; Sarfraz, M.; Sarwat, A.I.; Alhosaini, W.; Aldosari, O.; Aziz, A. Selective harmonic mitigation based two-scale frequency control of cascaded modified packed U-Cell inverters. Energy Rep. 2022, 8, 1009–1020. [Google Scholar] [CrossRef]
- IEEE Std 519-2022; IEEE Standard for Harmonic Control in Electric Power Systems. IEEE: Piscataway, NJ, USA, 2022; pp. 1–31. Available online: https://ieeexplore.ieee.org/document/9848440 (accessed on 14 November 2024).
- Duc, M.L.; Hlavaty, L.; Bilik, P.; Martinek, R. Harmonic mitigation using meta-heuristic optimization for shunt adaptive power filters: A review. Energies 2023, 16, 3998. [Google Scholar] [CrossRef]
- Eroğlu, H.; Cuce, E.; Cuce, P.M.; Gul, F.; Iskenderoğlu, A. Harmonic problems in renewable and sustainable energy systems: A comprehensive review. Sustain. Energy Technol. Assess. 2021, 48, 101566. [Google Scholar] [CrossRef]
- Memon, M.A.; Siddique, M.D.; Mekhilef, S.; Mubin, M. Asynchronous particle swarm optimization-genetic algorithm (APSO-GA) based selective harmonic elimination in a cascaded H-bridge multilevel inverter. IEEE Trans. Ind. Electron. 2021, 69, 1477–1487. [Google Scholar] [CrossRef]
- Adak, S. Harmonics mitigation of stand-alone photovoltaic system using LC passive filter. J. Electr. Eng. Technol. 2021, 16, 2389–2396. [Google Scholar] [CrossRef]
- Raman, R.; Sadhu, P.K.; Kumar, R.; Rangarajan, S.S.; Subramaniam, U.; Collins, E.R.; Senjyu, T. Feasible Evaluation and Implementation of Shunt Active Filter for Harmonic Mitigation in Induction Heating System. Electronics 2022, 11, 3464. [Google Scholar] [CrossRef]
- Iqbal, H.; Tufail, S.; Tariq, M.; Sarwat, A.I.; Sarwar, A. GA-based Integrated SHM-NLC Control for a Single Sourced Switched Capacitor Multi-Level Inverter with Boosting Capability for Microgrid. In Proceedings of the 2023 IEEE International Conference on Energy Technologies for Future Grids (ETFG), Wollongong, Australia, 3–6 December 2023; pp. 1–6. [Google Scholar]
- Gad, A.G. Particle swarm optimization algorithm and its applications: A systematic review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Fontes, D.B.; Homayouni, S.M.; Gonçalves, J.F. A hybrid particle swarm optimization and simulated annealing algorithm for the job shop scheduling problem with transport resources. Eur. J. Oper. Res. 2023, 306, 1140–1157. [Google Scholar] [CrossRef]
- Li, G.; Wang, W.; Zhang, W.; Wang, Z.; Tu, H.; You, W. Grid search based multi-population particle swarm optimization algorithm for multimodal multi-objective optimization. Swarm Evol. Comput. 2021, 62, 100843. [Google Scholar] [CrossRef]
- Deng, W.; Shang, S.; Cai, X.; Zhao, H.; Song, Y.; Xu, J. An improved differential evolution algorithm and its application in optimization problem. Soft Comput. 2021, 25, 5277–5298. [Google Scholar] [CrossRef]
- Guilmeau, T.; Chouzenoux, E.; Elvira, V. Simulated annealing: A review and a new scheme. In Proceedings of the 2021 IEEE Statistical Signal Processing Workshop (SSP), Rio de Janeiro, Brazil, 11–14 July 2021; pp. 101–105. [Google Scholar]
- Sharma, S.; Kumar, V. A comprehensive review on multi-objective optimization techniques: Past, present and future. Arch. Comput. Methods Eng. 2022, 29, 5605–5633. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Mirjalili, S. A novel whale optimization algorithm integrated with Nelder–Mead simplex for multi-objective optimization problems. Knowl.-Based Syst. 2021, 212, 106619. [Google Scholar] [CrossRef]






| Components | NPC5 | FLC5 | CHB5 | PUC5 | PUC7 |
|---|---|---|---|---|---|
| Switches | 8 | 8 | 8 | 6 | 6 |
| Capacitor | 4 | 7 | 2 | 1 | 1 |
| Clamping Diode | 6 | 0 | 0 | 0 | 0 |
| Control Complexity | Very High | Very High | Low | Low | High |
| Switching States | S1 | S2 | S3 | Vab |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | |
| 2 | 1 | 0 | 1 | |
| 3 | 1 | 1 | 0 | |
| 4 | 1 | 1 | 1 | 0 |
| 5 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 1 | |
| 7 | 0 | 1 | 0 | |
| 8 | 0 | 1 | 1 |
| Switching States | S1 | S2 | S3 | Vab |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | |
| 2 | 1 | 0 | 1 | |
| 3 | 1 | 1 | 1 | 0 |
| 4 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 1 | |
| 6 | 0 | 1 | 1 |
| Parameters | Values |
|---|---|
| 300 V | |
| 100 V (for MPUC7), 150 V for (MPUC5) | |
| Capacitors | 2200 μF, 200 V; 2200 μF, 200 V |
| Resistance at load | 40 , 50 |
| Inductance at load | 80 mH |
| Frequency | 60 Hz |
| Optimization Algorithm | Third (%) | Fifth (%) | Seventh (%) | THD (%) |
|---|---|---|---|---|
| GWO | 1.33 | 25.29 | 1.50 | 30.20 |
| DE | 1.93 | 16.06 | 18.36 | 29.99 |
| GA | 0.57 | 22.67 | 1.45 | 27.26 |
| GA-PSO (This work) | 0.23 | 0.46 | 0.87 | 17.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iqbal, H.; Sarwat, A. Design and Implementation of Hybrid GA-PSO-Based Harmonic Mitigation Technique for Modified Packed U-Cell Inverters. Energies 2025, 18, 124. https://doi.org/10.3390/en18010124
Iqbal H, Sarwat A. Design and Implementation of Hybrid GA-PSO-Based Harmonic Mitigation Technique for Modified Packed U-Cell Inverters. Energies. 2025; 18(1):124. https://doi.org/10.3390/en18010124
Chicago/Turabian StyleIqbal, Hasan, and Arif Sarwat. 2025. "Design and Implementation of Hybrid GA-PSO-Based Harmonic Mitigation Technique for Modified Packed U-Cell Inverters" Energies 18, no. 1: 124. https://doi.org/10.3390/en18010124
APA StyleIqbal, H., & Sarwat, A. (2025). Design and Implementation of Hybrid GA-PSO-Based Harmonic Mitigation Technique for Modified Packed U-Cell Inverters. Energies, 18(1), 124. https://doi.org/10.3390/en18010124








