Integrated Stochastic Approach for Instantaneous Energy Performance Analysis of Thermal Energy Systems
Abstract
1. Introduction
2. Overview of Gas Turbine Systems Analysis
2.1. Reliability Approach for Gas Turbine Systems
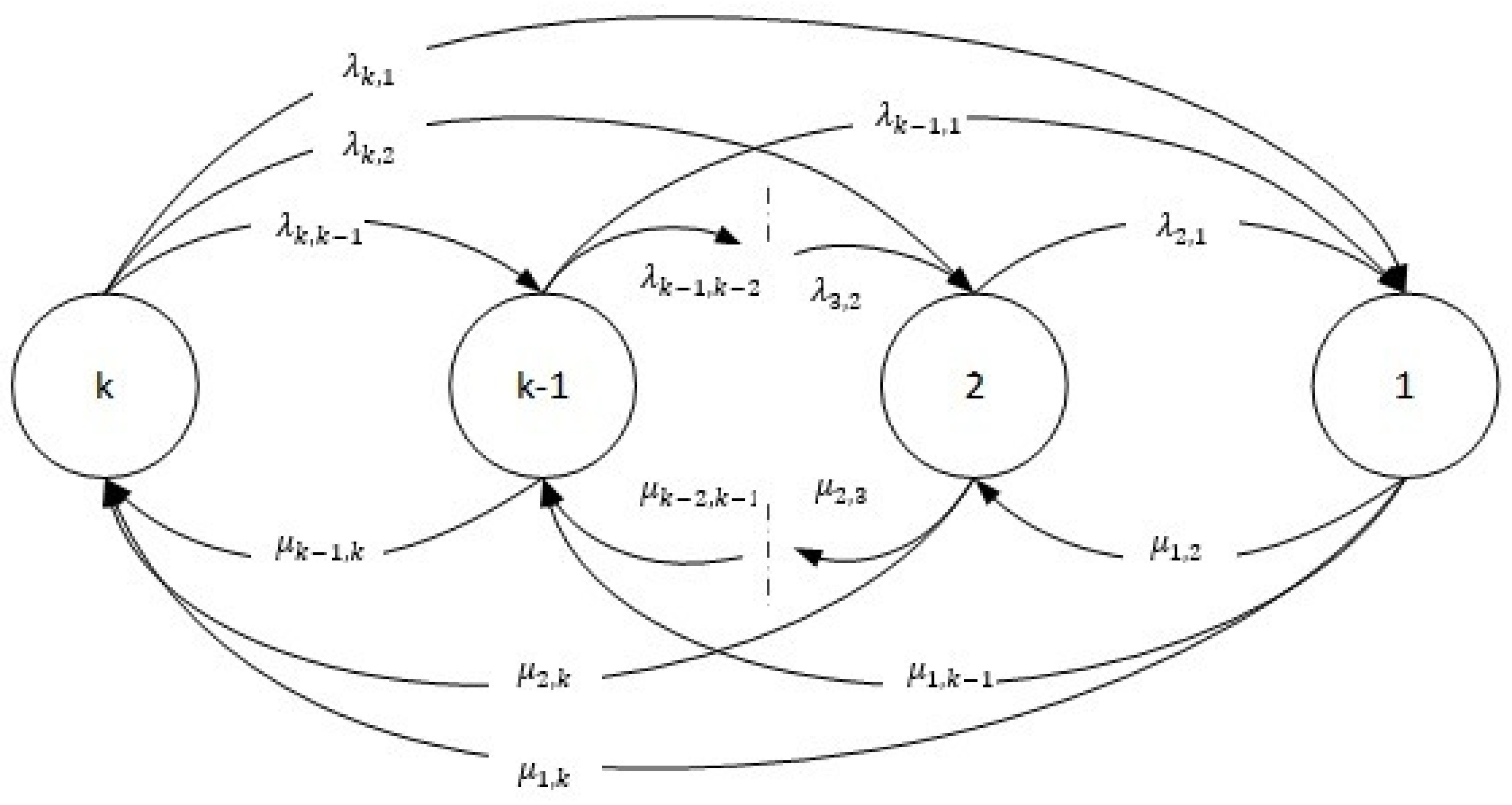
2.2. A Stochastic Approach for Gas Turbine Systems’ Reliability
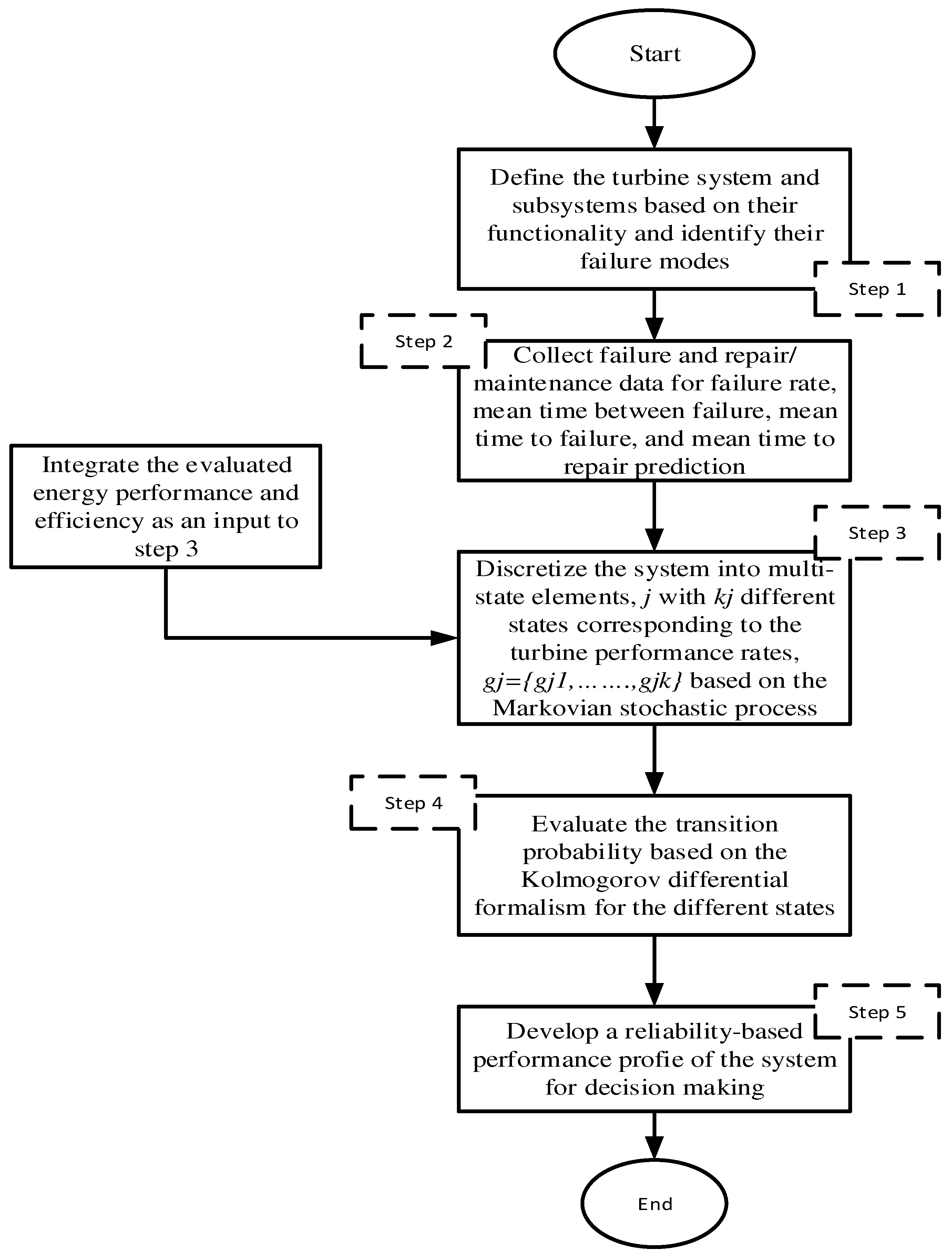
3. Methodology
4. Methodology Implementation
5. Results and Discussion
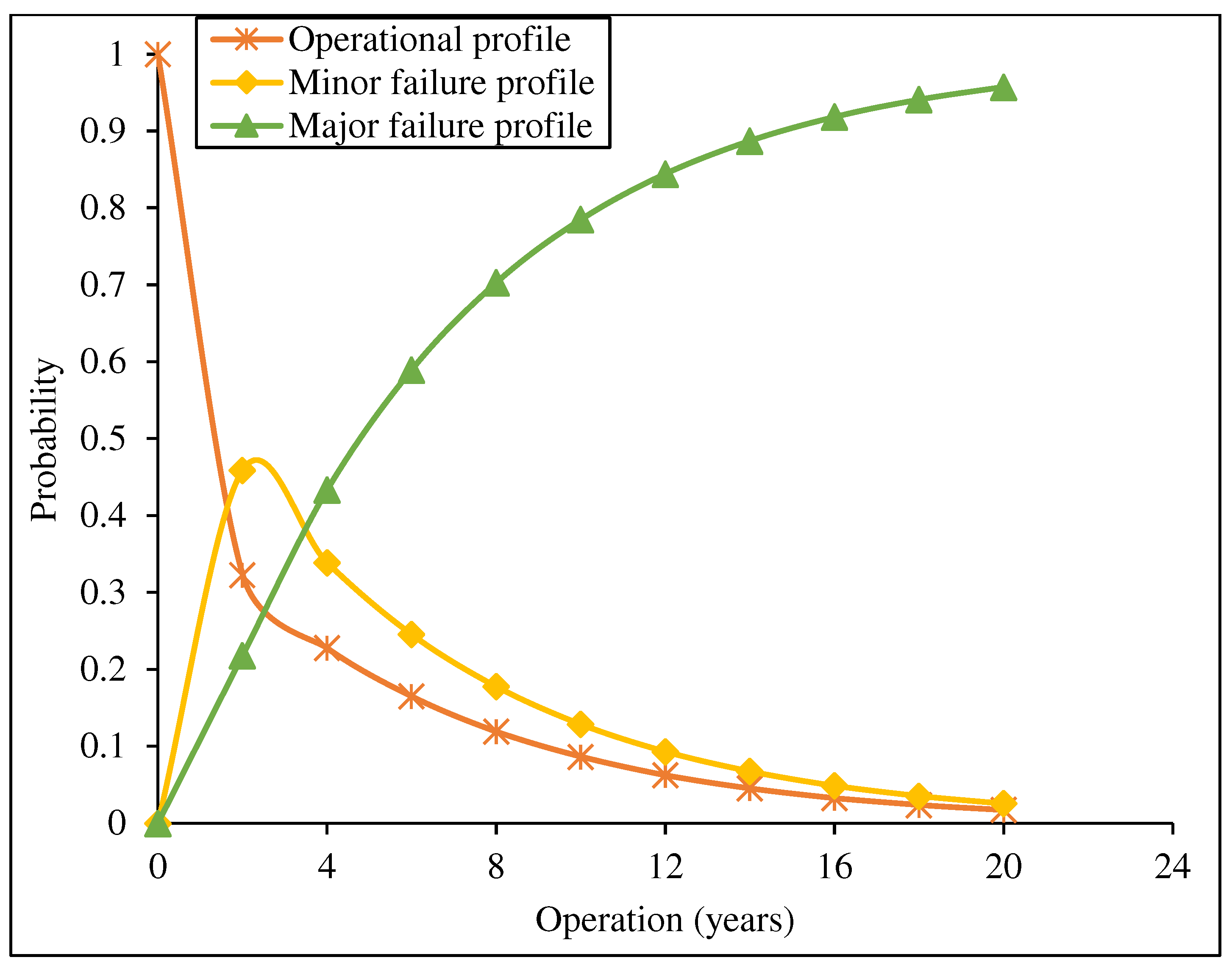
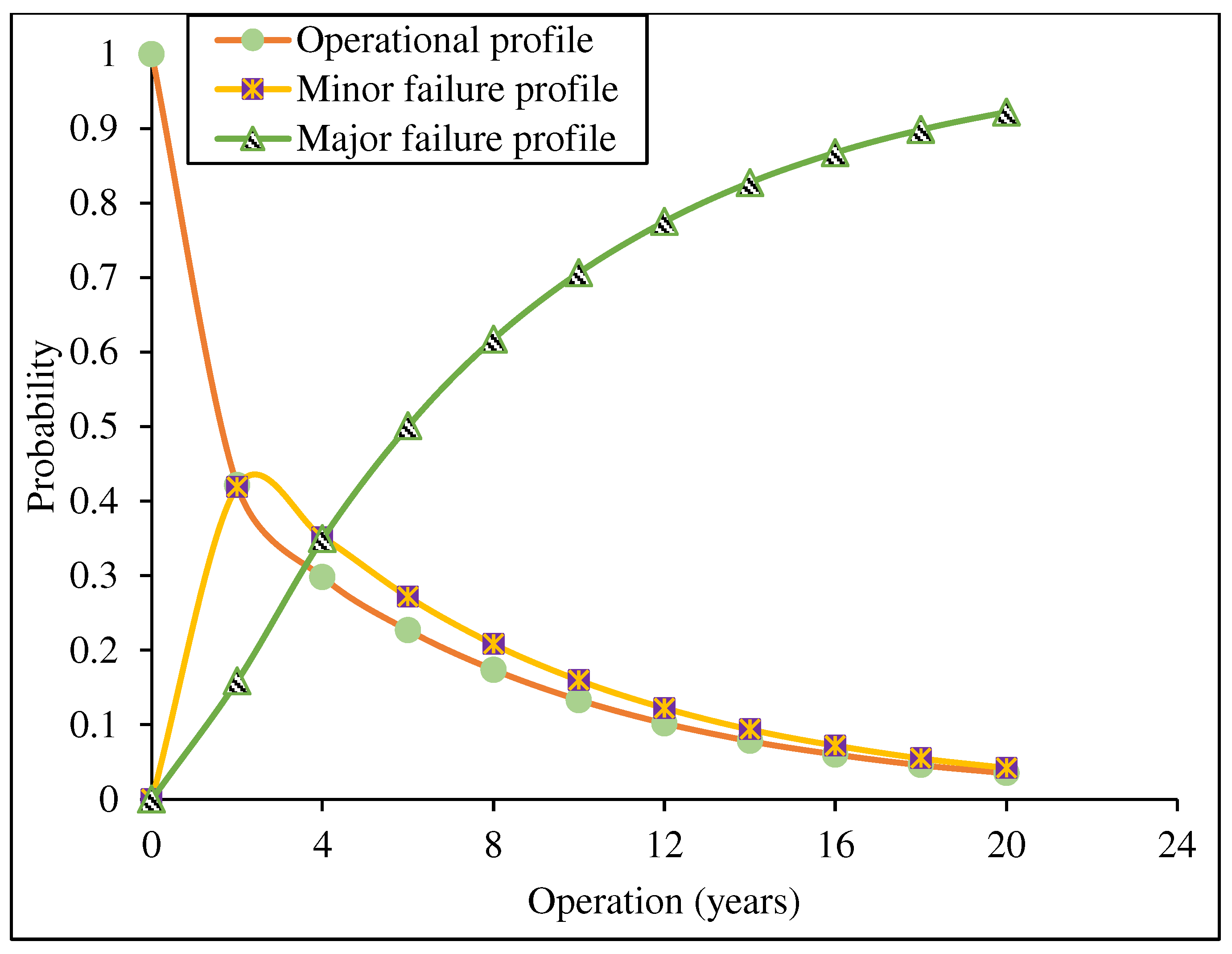
5.1. Failure Modes Analysis of Plants’ Performances
5.2. State Probabilities Prediction Under Different Plants’ Performance
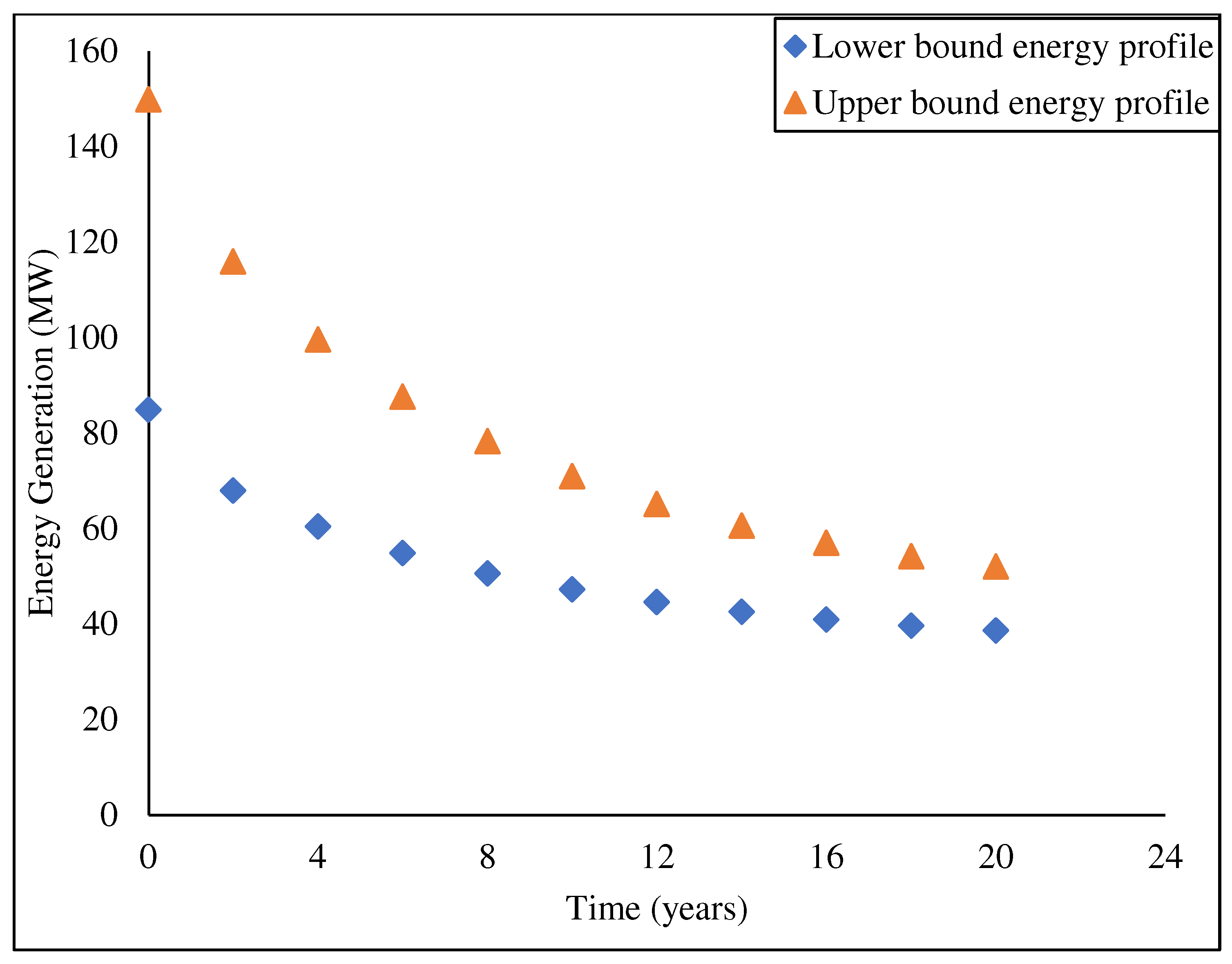
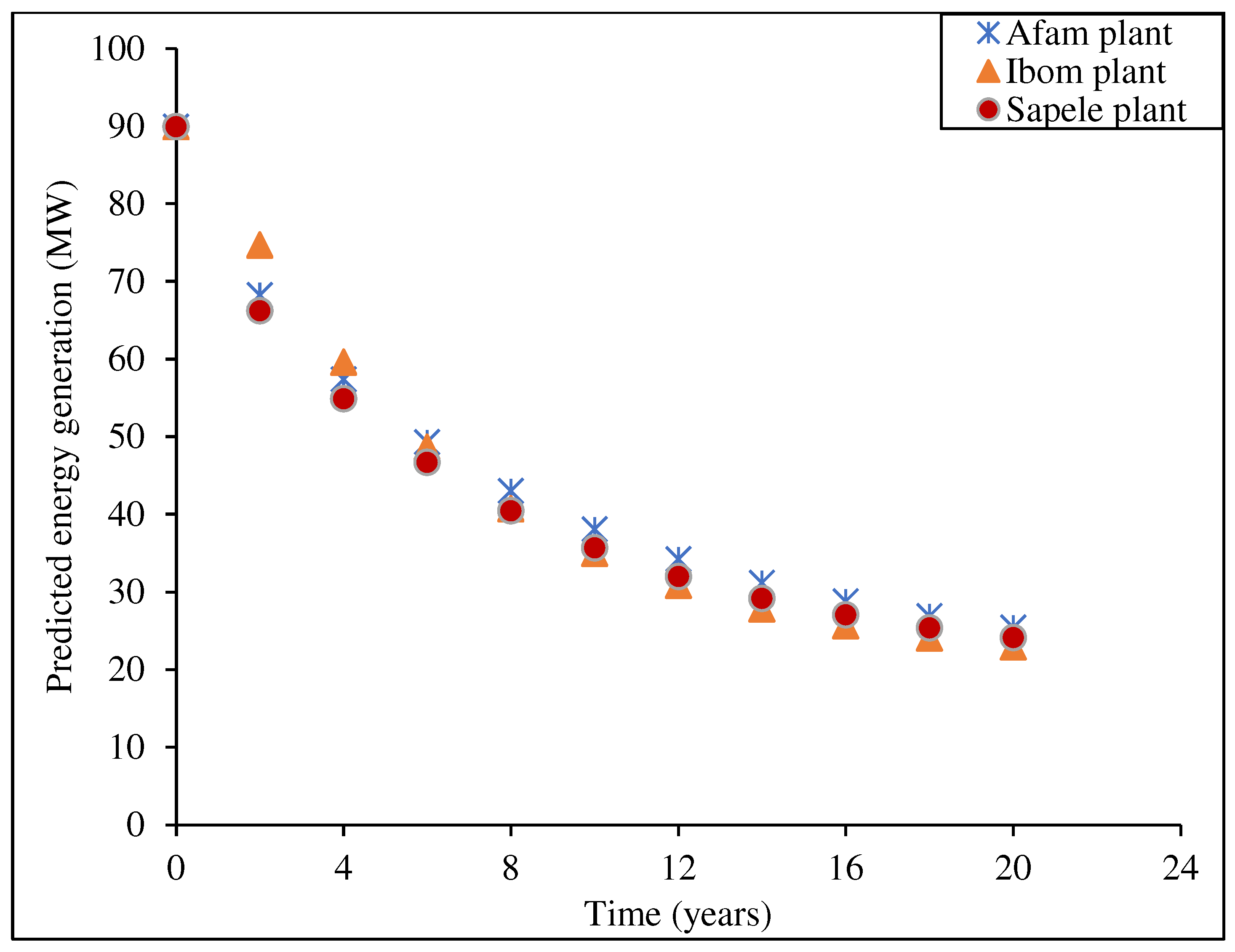
5.3. Instantaneous Energy Performance Under System Degradation
6. Conclusions
- The proposed approach provides a holistic assessment of the failure mode of the gas turbine plant, considering the prevailing operating environment.
- The failure and repair rates, which defined the reliability and maintainability function, were reliably predicted from the failure and repair data. This was used to characterize the state transition of the failure causal elements for the three gas turbine plants, as shown.
- The analysis shows a 10.1%, 4.5%, and 7.8% decline in the system performance reliability for the Afam, Ibom, and Sapele gas turbine plants, respectively.
- The subsystem degradation impacted the mean instantaneous power output by different percentage drops with respect to the design performance rating.
- Under the prevailing deterioration of the subsystems and poor maintenance strategy, the plant’s percentage performance relative to the rated capacity is 37.9%, 35.1%, and 46.3% for the Afam, Ibom, and Sapele gas turbine plants in the 14th year of operation. This shows a different level of performance decline and its implication on the economic viability of the investment.
- The approach provides a performance monitoring tool for gas turbine engine health assessment and energy performance prediction for any given operating state of the asset. A proactive integrity management strategy could be inferred from the analysis of the results to support decision-making in the management options of the gas turbine power plants.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nkoi, B.; Pilidis, P.; Nikolaidis, T. Techno-Economic Assessment of Large-Scale Aero-Derivative Industrial Gas Turbines Combined-Heat-And-Power. Int. J. Eng. Technol. 2015, 5, 225–240. [Google Scholar]
- Meher-Homji, C.B.; Chaker, M.A.; Motiwala, H.M. Gas turbine performance deterioration. In Proceedings of the 30th Turbomachinery Symposium, Houston, TX, USA, 17–20 September 2001; pp. 139–176. [Google Scholar]
- Kolagar, A.M.; Tabrizi, N.; Cheraghzadeh, M.; Shahriari, M.A. Failure analysis of gas turbine first stage blade made of nickelbased superalloy. Case Stud. Eng. Fail. Anal. 2017, 8, 61–68. [Google Scholar] [CrossRef]
- Jagtap, H.; Bewoor, A.; Kumar, R.; Ahmadi, M.H.; Lorenzini, G. Markov-based performance evaluation and availability optimization of the boiler–furnace system in coal-fired thermal power plant using PSO. Energy Rep. 2020, 6, 1124–1134. [Google Scholar] [CrossRef]
- Ghasemian, H.; Zeeshan, Q. Failure Mode and Effect Analysis (FMEA) of Aeronautical Gas Turbine using the Fuzzy Risk Priority Ranking (FRPR) Approach. Int. J. Soft Comput. Eng. 2017, 7, 81–92. [Google Scholar]
- Yuhua, D.; Datao, Y. Estimation of failure probability of oil and gas transmission pipelines by fuzzy fault tree analysis. J. Loss Prev. Process Ind. 2005, 18, 83–88. [Google Scholar] [CrossRef]
- Hunter, I.; Daleo, J.; Wilson, J.; Ellison, K. Analysis of Hot Section Failures on Gas Turbines in Process Plant Service. In 28th Turbomachinery Symposium; Turbomachinery Laboratories, Texas A&M University: College Station, Mexico, TX, USA, 1999. [Google Scholar]
- Ebikeme, D.S. A Feasibility Assessment of a Gas-to-Power Plant Scheme at the Gulf of Guinea, Nigeria. Oil and Gas Engineering, University of Aberdeen: Scotland, UK, 2018. [Google Scholar]
- Bhangu, N.S.; Pahuja, G.L.; Singh, R. Application of Fault Tree Analysis for Evaluating Reliability and Risk Assessment of a Thermal Power Plant. Energy Sources, Part A: Recover. Util. Environ. Eff. 2015, 37, 2004–2012. [Google Scholar]
- Leimeister, M.; Kolios, A. A review of reliability-based methods for risk analysis and their application in the offshore wind industry. Renew. Sustain. Energy Rev. 2018, 91, 1065–1076. [Google Scholar] [CrossRef]
- Abaei, M.M.; Abbassi, R.; Garaniya, V.; Chai, S.; Khan, F. Reliability assessment of marine floating structures using Bayesian network. Appl. Ocean Res. 2018, 76, 51–60. [Google Scholar] [CrossRef]
- Li, Z.; Xu, T.; Gu, J.; Dong, Q.; Fu, L. Reliability modelling and analysis of a multi-state element based on a dynamic Bayesian network. R. Soc. Open Sci. 2018, 5, 171438. [Google Scholar] [CrossRef] [PubMed]
- Lau, B.C.P.; Ma, E.W.M.; Pecht, M. Review of offshore wind turbine failures and fault prognostic methods. In Proceedings of the IEEE 2012 Prognostics and System Health Management Conference PHM-2012, Beijing, China, 23–25 May 2012; pp. 1–5. [Google Scholar]
- Yazdi, M.; Ding, Y.; Adumene, S.; Shafie, P. Progressive system safety and reliability analysis: A sustainable game theory approach. Qual. Reliab. Eng. Int. 2022, 39, 1559–1572. [Google Scholar] [CrossRef]
- Katsavounis, S.; Patsianis, N.; Konstantinidis, E.I.; Botsaris, P.N. Reliability Analysis on Crucial Subsystems of a Wind Turbine through FTA Approach. In Proceedings of the Maintenance Performance Measurement And Management Conference, Coimbra, Portugal, 4–5 September 2014; pp. 221–228. [Google Scholar] [CrossRef][Green Version]
- Scheu, M.N.; Kolios, A.; Fischer, T.; Brennan, F. Influence of statistical uncertainty of component reliability estimations on offshore wind farm availability. Reliab. Eng. Syst. Saf. 2017, 168, 28–39. [Google Scholar] [CrossRef]
- Lazakis, I.; Kougioumtzoglou, M.A. Assessing offshore wind turbine reliability and availability. Sage J. 2018, 233, 1–24. [Google Scholar] [CrossRef]
- Sharma, V.; Kumari, M.; Kumar, S. Reliability improvement of modern aircraft engine through failure modes and effects analysis of rotor support system. Int. J. Qual. Reliab. Manag. 2011, 28, 675–687. [Google Scholar]
- Wojcik, J.D.; Wang, J. Feasibility study of Combined Cycle Gas Turbine (CCGT) power plant integration with Adiabatic Compressed Air Energy Storage (ACAES). Appl. Energy 2018, 221, 477–489. [Google Scholar] [CrossRef]
- Feng, Q.; Xia, J.; Wen, L.; Yazdi, M. Failure analysis of floating offshore wind turbines based on a fuzzy failure mode and effect analysis model. Qual. Reliab. Eng. Int. 2024, 40, 2159–2177. [Google Scholar] [CrossRef]
- Salpingidou, C.; Tsakmakidou, D.; Vlahostergios, Z.; Isirlis, D.M.; Flouros, M.; Yakinthos, K. The effect of turbine blade cooling on the performance of recuperative cycles for gas turbines applications. Chem. Eng. Trans. 2017, 61, 1027–1032. [Google Scholar]
- Lampreia, S.; Vairinhos, V.; Lobo, V.; Requeijo, J. A Statistical State Analysis of a Marine Gas Turbine. Actuators 2019, 8, 54. [Google Scholar] [CrossRef]
- Kappas, J. Review of Risk and Reliability Methods for Aircraft GasTurbine Engine. Van. Nostrand’s Sci. Encycl. 2005, 1–55. [Google Scholar]
- Li, H.; Yazdi, M. Developing failure modes and effect analysis on offshore wind turbines using two-stage optimization probabilistic linguistic preference relations. In Advanced Decision-Making Methods and Applications in System Safety and Reliability Problems: Approaches, Case Studies, Multi-criteria Decision-Making, Multi-objective Decision-Making, Fuzzy Risk-Based Models; Springer International Publishing: Cham, Switzerland, 2022; pp. 47–68. [Google Scholar]
- Bai, Z. Reliability Analysis of Gas Turbine Based on Analytic Hierarchy Process and FTA. In Proceedings of the International Conference on Mathematics, Modeling, Simulation and Statistics Application (MMSSA 2018), Shanghai, China, 22–23 December 2018; pp. 183–186. [Google Scholar]
- Jiang, J.; Wei, X.; Gao, W.; Kuroki, S.; Liu, Z. Reliability and Maintenance Prioritization Analysis of Combined Cooling, Heating and Power Systems. Energies 2018, 11, 1519. [Google Scholar] [CrossRef]
- Nitonye, S.; Adumene, S.; Sigalo, B.M.; Orji, C.U.; Le-ol, A.K. Dynamic failure analysis of renewable energy systems in the remote offshore environments. Qual. Reliab. Eng. Int. 2020, 37, 1436–1450. [Google Scholar] [CrossRef]
- Adumene, S.; Okoro, A. A Markovian reliability approach for offshore wind energy system analysis in harsh environments. Eng. Rep. 2020, 2, e12128. [Google Scholar] [CrossRef]
- Lisnianski, A.; Frenkel, I.; Ding, Y. Multi-State System Reliability Analysis and Optimization for Engineers and Industrial Managers; Springer: London, UK, 2010. [Google Scholar]



| O | FMinor | FMajor | |
| O | |||
| FMinor | |||
| FMajor | 0 | 0 | 1 |
| Main Events | Codes | Intermediate Events | Codes | Basic Events | Codes |
|---|---|---|---|---|---|
| Electric generator system failure | T1 | Generator trip fault | A2 | Damage to generator casing | A11 |
| Starting/governing system failure | K | Generator damage | A1 | Generator Rotor bowing | A12 |
| Failure of compressor system | E | Generator electrical fault | A3 | Damage to generator guide way | A13 |
| Failure of air-inlet system | C | Operational fault due to human error | A4 | Loss of field to the main exciter | T31 |
| Failure of turbine system | I | Failure of relay system | A5 | Short circuit fault | T32 |
| Failure of combustion system | G | Failure due to damaged fuse | A6 | Loss of a.c supply to excitation | T33 |
| Failure to generate output voltage | T2 | Coupling shaft stress | T61 | ||
| Generator excitation system failure | T3 | Loose connectivity | T62 | ||
| Turbine failure to reach desired speed | T4 | Pump motor insulation failure | C71 | ||
| Turbine blade failure due to Improper pressure | T5 | Motor failure due to high current | C72 | ||
| Loose coupling of shaft | T6 | No power supply at the motor terminal | C73 | ||
| Improper burning of fuel | T7 | Motor overload | C91 | ||
| Low/high pressure of combustor air inlet | T8 | Motor overheats due to cooling failure | C92 | ||
| Turning gear failure | K1 | Motor failure due to wrong connection | C93 | ||
| Start-up system failure | K2 | Failure of cooling system of the lube system | E51 | ||
| Gearbox system failure | K3 | Faulty pressure gauge | E61 | ||
| Torque converter system | K4 | Failure of heating system | E62 | ||
| Lubrication system failure | E5 | Failure of temperature sensor | E63 | ||
| Loss of water supply from reservoir | E6 | Ballooning of torque converter | K41 | ||
| Vane system turbine failure | I1 | Clutch of the torque converter | K42 | ||
| Turbine radial bearing failure | I2 | Earth fault-induced failure | A31 | ||
| Turbine cylinder failure | I3 | Copper dusting occur in the generator | A32 | ||
| Turbine exhaust system failure | I4 | Generator fault due to reverse voltage | A33 | ||
| Turbine cylinder exhaust system failure | I5 | Generator failure due to inter turn fault | A34 | ||
| Exhaust connection system failure | I6 | Generator failure due to short circuit fault | A35 | ||
| Combustion system wear and tear | G1 | Too early operation from human operator | A41 | ||
| Igniter system failure | G2 | Too late operation from human operator | A42 | ||
| Combustion cooling system failure | G3 | Out sequence operation by human operator | A43 | ||
| Damaged basket of shell | G4 | Delay in open the relay contact | A51 | ||
| Failure of evaporator cooler | C1 | Relay contacts freeze | A52 | ||
| Failure of water supply system | C3 | Relay contacts bounce | A53 | ||
| Pipe section rupture | C4 | Relay coils burn out | A54 | ||
| Faulty pump system | C5 | Fuse open on low current | A61 | ||
| Valves failed to open on demand | C6 | Fuse fails to open on high current | A62 | ||
| Damaged pump motor | C7 | Fuse partially opened | A63 | ||
| Rupture seal house | C8 | Vane’s damage | I11 | ||
| Motor Overheating | C9 | Pins of vane system damage | I12 | ||
| Compressor blade failure | E1 | Broken blade rings of turbine cylinder system | I31 | ||
| Journal bearing failure | E2 | Broken blade of the turbine system | I33 | ||
| Compressor thrust bearing failure | E3 | Failure of the exhaust collector of the exhaust system | I41 | ||
| Journal bearing casing failure | E4 | Failure of the pads of the radial bearing | I21 | ||
| Failure of thermocouples in the radial bearing system | I22, I52 | ||||
| Damage of the shell of the radial bearing system | I23 | ||||
| Damage of the static seal of the exhaust system | I61 | ||||
| Damage of the exhaust pipes | I62 | ||||
| Damage casing of the exhaust cylinder | I51 | ||||
| Flame tube failure | G11 | ||||
| Shell cylinder failure | G12 | ||||
| Igniter system spring failure | G21 | ||||
| Igniter system piston failure | G22 | ||||
| Failure of the igniter in the igniter system | G23 | ||||
| Blockage of the cooling system vessels | G31 | ||||
| Failed to open of the bypass valve of the cooling system | G32 | ||||
| Cooling system controller failure | G33 | ||||
| Damaged transition piece in the basket | G41 | ||||
| Damaged burner in the basket | G42 | ||||
| Humid badges burst | D1 | ||||
| Water pipes damage | D2 | ||||
| Pipes failure due to corrosion | D3 | ||||
| Valve failure due to mechanical fault | D4 | ||||
| Valve failure due to controller fault | D5 | ||||
| Rupture of seal house due to high temperature | D9 | ||||
| Seal house rupture due to dryness | D10 | ||||
| Motor overload | D11 | ||||
| Filter system clogged | D14 | ||||
| Broken rings in the blade system | F1 | ||||
| Broken inlet guide vane in the blade system | F2 | ||||
| Vibration of shaft | F3 | ||||
| Broken stationary blades in the casing system | F4 | ||||
| Damaged casing in the cooling system | F5 | ||||
| Rupture of the pad in the casing system | F6 | ||||
| Broken housing of the thrust bearing | F7 | ||||
| Broken shoes of the thrust bearing | F8 | ||||
| Broken filler of thrust bearing | F9 | ||||
| Pressure gauge failure | F11 | ||||
| Failure of heating system | F12 | ||||
| Vibration of gearbox bearing | K31 | ||||
| Failure of gearbox self shifting clutch | K32 | ||||
| Excessive hogging of the gearbox bearing | K33 |
| Likely Failure State | Cumulative Mean Time to Failure (hours) | Rate of Failure | Cumulative Mean Time to Repair (h) | Rate of Repair |
|---|---|---|---|---|
| (a) System performance and energy generation loss due to plant health state (Afam Gas Turbine Plant) | ||||
| Axial shaft bearing leakage | 622.98 | 1.61 × 10−3 | 200.9 | 4.98 × 10−3 |
| System disturbance/low system voltage/grid failure | 4499.7 | 2.22 × 10−4 | 398.9 | 2.51 × 10−3 |
| Fan problem | 483.45 | 2.07 × 10−3 | 287.8 | 3.47 × 10−3 |
| Bus bar differential protection failure | 3980.9 | 2.51 × 10−4 | 729.5 | 1.37 × 10−3 |
| Medium pressure turbine differential expansion failure | 90.8 | 1.10 × 10−2 | 25.3 | 3.95 × 10−2 |
| Transformer leakage/GT oil leakage | 105.98 | 9.44 × 10−3 | 65.6 | 1.52 × 10−2 |
| Generator breaker failure | 6789.9 | 1.47 × 10−4 | 698.8 | 1.43 × 10−3 |
| Generator pole slippage | 567.8 | 1.76 × 10−3 | 209.3 | 4.78 × 10−3 |
| Relay system failure | 386 | 2.59 × 10−3 | 117.1 | 8.54 × 10−3 |
| Pump motor system failure | 433 | 2.31 × 10−3 | 89.9 | 1.11 × 10−2 |
| Blade system failure | 98.9 | 1.01 × 10−2 | 76.7 | 1.30 × 10−2 |
| Vane system failure | 105.99 | 9.43 × 10−3 | 55.8 | 1.79 × 10−2 |
| Thrust bearing failure | 144.87 | 6.90 × 10−3 | 98.6 | 1.01 × 10−2 |
| Radial bearing failure | 981.3 | 1.02 × 10−3 | 288.7 | 3.46 × 10−3 |
| Combustion system failure | 166.9 | 5.99 × 10−3 | 67.3 | 1.49 × 10−2 |
| Governing system failure | 188 | 5.32 × 10−3 | 88.2 | 1.13 × 10−2 |
| Turning gear failure | 78.9 | 1.27 × 10−2 | 47.4 | 2.11 × 10−2 |
| Seal house ruptured | 487.2 | 2.05 × 10−3 | 209.7 | 4.77 × 10−3 |
| Rotor bowing failure | 312.8 | 3.20 × 10−3 | 112.5 | 8.89 × 10−3 |
| Mechanical fault failure | 478.6 | 2.09 × 10−3 | 101.4 | 9.86 × 10−3 |
| Vibration induced failure | 201.8 | 4.96 × 10−3 | 89.7 | 1.11 × 10−2 |
| Gearbox system failure | 812.8 | 1.23 × 10−3 | 398.1 | 2.51 × 10−3 |
| Control system failure | 109.87 | 9.10 × 10−3 | 67.8 | 1.47 × 10−2 |
| Turbine system failure | 81.98 | 1.22 × 10−2 | 109.6 | 9.12 × 10−3 |
| Torque system failure | 321.8 | 3.11 × 10−3 | 99.8 | 1.00 × 10−2 |
| Igniter system failure | 657.78 | 1.52 × 10−3 | 110.9 | 9.02 × 10−3 |
| (b) System performance and energy generation loss due plant health state (Ibom Gas Turbine Plant) | ||||
| Axial shaft bearing leakage | 589.7 | 1.70 × 10−3 | 109.8 | 9.11 × 10−3 |
| System disturbance/low system voltage/grid failure | 2199.9 | 4.55 × 10−4 | 483.2 | 2.07 × 10−3 |
| Fan problem | 398.8 | 2.51 × 10−3 | 190.4 | 5.25 × 10−3 |
| Bus bar differential protection failure | 1778.1 | 5.62 × 10−4 | 478.9 | 2.09 × 10−3 |
| Medium pressure turbine differential expansion failure | 100.4 | 9.96 × 10−3 | 144.8 | 6.91 × 10−3 |
| Transformer leakage/GT oil leakage | 39.6 | 2.53 × 10−2 | 12.6 | 7.94 × 10−2 |
| Generator breaker failure | 4987.1 | 2.01 × 10−4 | 289.7 | 3.45 × 10−3 |
| Generator pole slippage | 345.3 | 2.90 × 10−3 | 118.7 | 8.42 × 10−3 |
| Relay system failure | 502.2 | 1.99 × 10−3 | 386.2 | 2.59 × 10−3 |
| Pump motor system failure | 298.9 | 3.35 × 10−3 | 113.1 | 8.84 × 10−3 |
| Blade system failure | 64.2 | 1.56 × 10−2 | 12.5 | 8.00 × 10−2 |
| Vane system failure | 211.8 | 4.72 × 10−3 | 56.7 | 1.76 × 10−2 |
| Thrust bearing failure | 238.9 | 4.19 × 10−3 | 102.4 | 9.77 × 10−3 |
| Radial bearing failure | 1011.9 | 9.88 × 10−4 | 597.8 | 1.67 × 10−3 |
| Combustion system failure | 189.6 | 5.27 × 10−3 | 45.6 | 2.19 × 10−2 |
| Governing system failure | 119.8 | 8.35 × 10−3 | 87.7 | 1.14 × 10−2 |
| Turning gear failure | 88.9 | 1.12 × 10−2 | 31.5 | 3.17 × 10−2 |
| Seal house ruptured | 507.1 | 1.97 × 10−3 | 105.6 | 9.47 × 10−3 |
| Rotor bowing failure | 402 | 2.49 × 10−3 | 209.2 | 4.78 × 10−3 |
| Mechanical fault failure | 339.9 | 2.94 × 10−3 | 89.6 | 1.12 × 10−2 |
| Vibration induced failure | 288 | 3.47 × 10−3 | 66.8 | 1.50 × 10−2 |
| Gearbox system failure | 908 | 1.10 × 10−3 | 206.2 | 4.85 × 10−3 |
| Control system failure | 118.9 | 8.41 × 10−3 | 47.5 | 2.11 × 10−2 |
| Turbine system failure | 67.9 | 1.47 × 10−2 | 109.7 | 9.12 × 10−3 |
| Torque system failure | 409.8 | 2.44 × 10−3 | 211.1 | 4.74 × 10−3 |
| Igniter system failure | 779.7 | 1.28 × 10−3 | 219.4 | 4.56 × 10−3 |
| (c) System performance and energy generation loss due to plant health state (Sapele Gas Turbine Plant) | ||||
| Axial shaft bearing leakage | 543.8 | 1.84 × 10−3 | 112.1 | 8.92 × 10−3 |
| System disturbance/low system voltage/grid failure | 3887.3 | 2.57 × 10−4 | 897.5 | 1.11 × 10−3 |
| Fan problem | 354 | 2.82 × 10−3 | 89.7 | 1.11 × 10−2 |
| Bus bar differential protection failure | 4002.9 | 2.50 × 10−4 | 172.2 | 5.81 × 10−3 |
| Medium pressure turbine differential expansion failure | 97.9 | 1.02 × 10−2 | 56.3 | 1.78 × 10−2 |
| Transformer leakage/GT oil leakage | 105.98 | 9.44 × 10−3 | 57.1 | 1.75 × 10−2 |
| Generator breaker failure | 5986.7 | 1.67 × 10−4 | 456.8 | 2.19 × 10−3 |
| Generator pole slippage | 433.5 | 2.31 × 10−3 | 109.8 | 9.11 × 10−3 |
| Relay system failure | 408.4 | 2.45 × 10−3 | 99.8 | 1.00 × 10−2 |
| Pump motor system failure | 309.7 | 3.23 × 10−3 | 202.6 | 4.94 × 10−3 |
| Blade system failure | 79.9 | 1.25 × 10−2 | 89.9 | 1.11 × 10−2 |
| Vane system failure | 110.7 | 9.03 × 10−3 | 68.7 | 1.46 × 10−2 |
| Thrust bearing failure | 209.5 | 4.77 × 10−3 | 101.2 | 9.88 × 10−3 |
| Radial bearing failure | 1011.4 | 9.89 × 10−4 | 209.7 | 4.77 × 10−3 |
| Combustion system failure | 204.8 | 4.88 × 10−3 | 67.8 | 1.47 × 10−2 |
| Governing system failure | 108 | 9.26 × 10−3 | 77.8 | 1.29 × 10−2 |
| Turning gear failure | 104.8 | 9.54 × 10−3 | 56.2 | 1.78 × 10−2 |
| Seal house ruptured | 508.7 | 1.97 × 10−3 | 201.2 | 4.97 × 10−3 |
| Rotor bowing failure | 411.4 | 2.43 × 10−3 | 78.9 | 1.27 × 10−2 |
| Mechanical fault failure | 399.8 | 2.50 × 10−3 | 103.4 | 9.67 × 10−3 |
| Vibration induced failure | 199.2 | 5.02 × 10−3 | 56.7 | 1.76 × 10−2 |
| Gearbox system failure | 598.2 | 1.67 × 10−3 | 287.5 | 3.48 × 10−3 |
| Control system failure | 249.1 | 4.01 × 10−3 | 97.5 | 1.03 × 10−2 |
| Turbine system failure | 69.9 | 1.43 × 10−2 | 87.9 | 1.14 × 10−2 |
| Torque system failure | 246.5 | 4.06 × 10−3 | 109.8 | 9.11 × 10−3 |
| Igniter system failure | 789.8 | 1.27 × 10−3 | 243.9 | 4.10 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le-ol, A.K.; Adumene, S.; Aziaka, D.S.; Yazdi, M.; Mohammadpour, J. Integrated Stochastic Approach for Instantaneous Energy Performance Analysis of Thermal Energy Systems. Energies 2025, 18, 160. https://doi.org/10.3390/en18010160
Le-ol AK, Adumene S, Aziaka DS, Yazdi M, Mohammadpour J. Integrated Stochastic Approach for Instantaneous Energy Performance Analysis of Thermal Energy Systems. Energies. 2025; 18(1):160. https://doi.org/10.3390/en18010160
Chicago/Turabian StyleLe-ol, Anthony Kpegele, Sidum Adumene, Duabari Silas Aziaka, Mohammad Yazdi, and Javad Mohammadpour. 2025. "Integrated Stochastic Approach for Instantaneous Energy Performance Analysis of Thermal Energy Systems" Energies 18, no. 1: 160. https://doi.org/10.3390/en18010160
APA StyleLe-ol, A. K., Adumene, S., Aziaka, D. S., Yazdi, M., & Mohammadpour, J. (2025). Integrated Stochastic Approach for Instantaneous Energy Performance Analysis of Thermal Energy Systems. Energies, 18(1), 160. https://doi.org/10.3390/en18010160







