Review of Studies on the Hot Spot Temperature of Oil-Immersed Transformers
Abstract
:1. Introduction
2. Transformer Heat Production
2.1. Transformer Core Loss Research Status
2.2. Transformer Winding Loss Research Status
2.3. Research Status of Transformer Stray Loss
3. Transformer Heat Dissipation
3.1. Forms of Heat Transfer
- (1)
- Thermal conduction
- (2)
- Thermal convection
- (3)
- Thermal radiation
3.2. Cooling Method
4. Transformer Hot Spot Temperature Research Methods
4.1. Direct Measurement Method
4.2. Indirect Calculation Method
- (1)
- Empirical formula method
- (2)
- Thermal circuit modeling method
- (3)
- Numerical simulation method
- (4)
- Artificial intelligence algorithm
4.3. Comparison of Transformer Hot Spot Temperature Research Methods
5. Factors
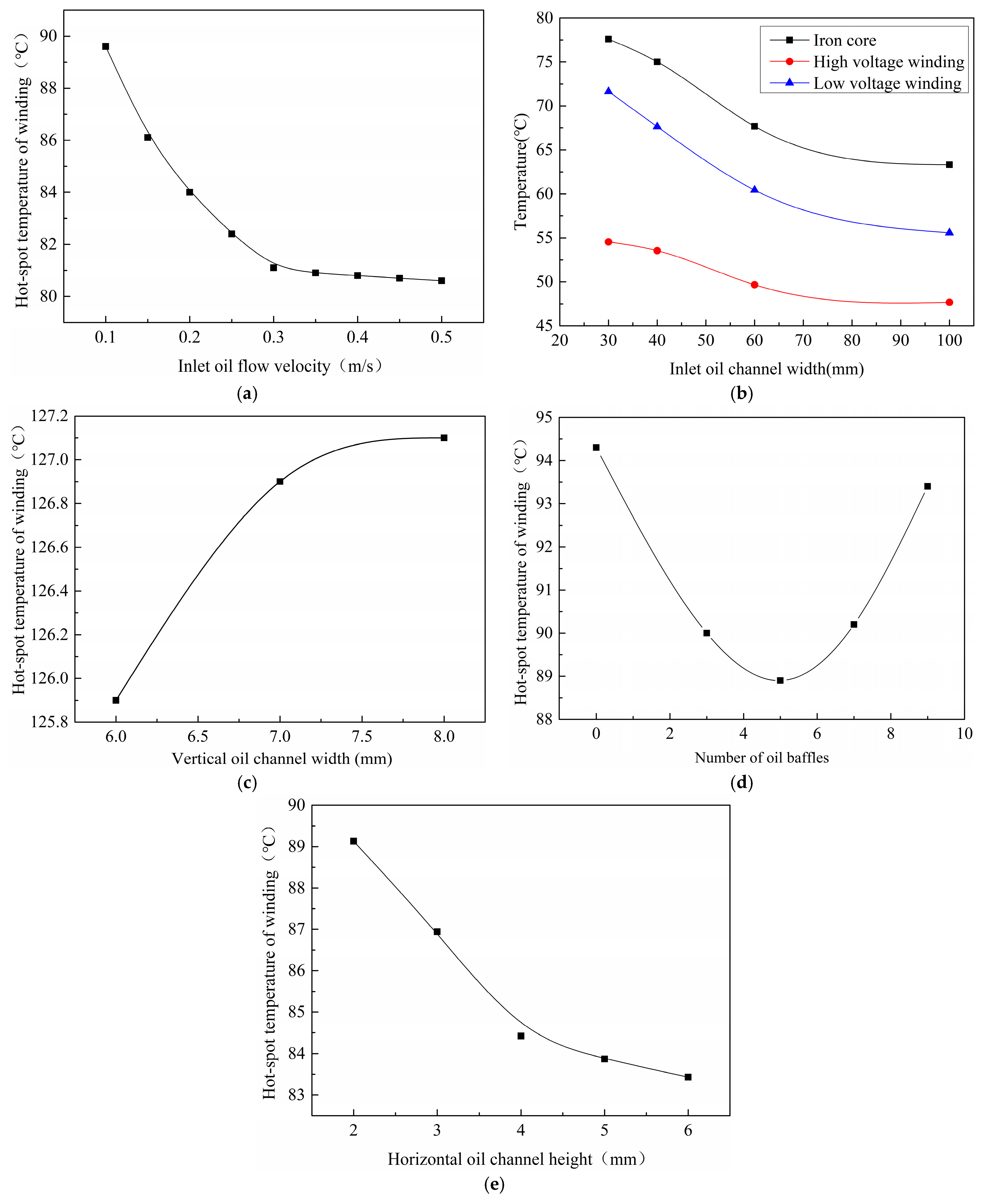
5.1. Factors Influencing Heat Production
5.2. Heat Dissipation Factors
6. Conclusions
- (1)
- Large transformers use the forced oil circulation cooling method to increase heat dissipation; when the oil flow velocity is too high, oil flow electrification will occur, damaging transformer insulation. Therefore, it is necessary to explore the mechanism of oil flow electrification and propose measures to restrain oil flow electrification, which is an urgent problem for improving the heat dissipation capacity of large-capacity transformers.
- (2)
- With the development of intelligent algorithms, some achievements have been made in transformer temperature prediction and load prediction, but the hysteresis problem in model prediction and the improvement of the accuracy of model prediction still need further research.
- (3)
- The temperature increase of the transformer can be reduced by reducing the transformer heat production or improving the transformer heat dissipation ability. Adjusting the size of the transformer structure and increasing the magnetic shield can effectively reduce the eddy current loss and reduce the heat production of the transformer. The heat dissipation capacity of the transformer can be achieved by increasing the insulation oil flow, optimizing the oil channel structure, adjusting the arrangement of the cooler, etc., to improve the hot spot temperature distribution of the transformer.
Author Contributions
Funding
Conflicts of Interest
References
- Liu, Z.; Zhang, Q. Study on the development mode of national power grid of China. Proc. CSEE 2013, 33, 1–10. [Google Scholar]
- Luo, C. Study on Spatial Thermal Circuit Model and Temperature Characteristics of Oil-Immersed Transformer. Doctoral Dissertation, Kunming University of Science and Technology, Kunming, China, 2023. [Google Scholar]
- Lu, C. Power Transformer Theory and Calculation, 4th ed.; Liaoning Science and Technology Publishing House: Shenyang, China, 2007. [Google Scholar]
- Li, S. On Line Prediction Technology for Inner Winding Temperature Rise of EHV Power Transformer. Master’s Thesis, Changchun University of Technology, Changchun, China, 2018. [Google Scholar]
- GB/T 1094.7-2008; Power Transformers—Part 7: Loading Guide for Mineral-Oil-Immersed Power Transformers. China National Standards: Beijing, China, 2008.
- Wu, J. Effect of Partial Overheating on Discharge Characteristics of Oil. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2019. [Google Scholar]
- Bernard, Y.; Mendes, E.; Bouillault, F. Dynamic hysteresis modeling based on Preisach model. IEEE Trans. Magn. 2002, 38, 885–888. [Google Scholar] [CrossRef]
- Jiles, D.; Atherton, D. Ferromagnetic hysteresis. IEEE Trans. Magn. 1983, 19, 2183–2185. [Google Scholar] [CrossRef]
- Steinmetz, C.P. On the law of hysteresis. Proc. IEEE 1984, 72, 197–221. [Google Scholar] [CrossRef]
- Muhlethaler, J.; Biela, J.; Kolar, J.W.; Ecklebe, A. Improved core-loss calculation for magnetic components employed in power electronic systems. IEEE Trans. Power Electron. 2011, 27, 964–973. [Google Scholar] [CrossRef]
- Reinert, J.; Brockmeyer, A.; De Doncker, R.W. Calculation of losses in ferro-and ferrimagnetic materials based on the modified Steinmetz equation. IEEE Trans. Ind. Appl. 2001, 37, 1055–1061. [Google Scholar] [CrossRef]
- Bertotti, G. General properties of power losses in soft ferromagnetic materials. IEEE Trans. Magn. 1988, 24, 621–630. [Google Scholar] [CrossRef]
- Amar, M.; Kaczmarek, R. A general formula for prediction of iron losses under nonsinusoidal voltage waveform. IEEE Trans. Magn. 1995, 31, 2504–2509. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Lazzari, M.; Pastorelli, M. Predicting iron losses in soft magnetic materials with arbitrary voltage supply: An engineering approach. IEEE Trans. Magn. 2003, 39, 981–989. [Google Scholar] [CrossRef]
- Barbisio, E.; Fiorillo, F.; Ragusa, C. Predicting loss in magnetic steels under arbitrary induction waveform and with minor hysteresis loops. IEEE Trans. Magn. 2004, 40, 1810–1819. [Google Scholar] [CrossRef]
- Lavers, J.; Biringer, P.P.; Hollitscher, H. A simple method of estimating the minor loop hysteresis loss in thin laminations. IEEE Trans. Magn. 1978, 14, 386–388. [Google Scholar] [CrossRef]
- Dowell, P.L. Effects of eddy currents in transformer windings. Proc. Inst. Electr. Eng. 1966, 133, 1387–1394. [Google Scholar] [CrossRef]
- Keradec, J.P.; Cogitore, B.; Blache, F. Power transfer in a two-winding transformer: From 1-D propagation to an equivalent circuit. IEEE Trans. Magn. 1996, 32, 274–280. [Google Scholar] [CrossRef]
- Schellmanns, A.; Fouassier, P.; Keradec, J.P.; Schanen, J.L. Equivalent circuits for transformers based on one-dimensional propagation: Accounting for multilayer structure of windings and ferrite losses. IEEE Trans. Magn. 2000, 36, 3778–3784. [Google Scholar] [CrossRef]
- Tria, L.A.R.; Zhang, D.; Fletcher, J.E. Planar PCB transformer model for circuit simulation. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Pang, X. The Study of the Eddy Losses and Temperature Field of Winding in Power Transformer. Master’s Thesis, Hebei University of Technology, Tianjin, China, 2006. [Google Scholar]
- Wang, Y.; Wang, J.; Liu, J.; Zhao, Y.; Li, H.; Li, Z. Research on Winding Eddy Loss and Temperature Rise Distribution for Oil immersed Transformer. Electr. Power Sci. Eng. 2011, 27, 28. [Google Scholar]
- Li, X. The Study of the Eddy Losses and Temperature Field of Winding in Power Transformer. Master’s Thesis, Hebei University of Technology, Tianjin, China, 2005. [Google Scholar]
- Pan, Y.; Wu, M.; Li, Z. Analysis of Transformer Winding Loss for High-Frequency Switching Power Supply Based on FEM. Chin. J. Electron Devices 2012, 35, 558–561. [Google Scholar]
- Васютинский, С.В. Transformer Theory and Calculation, 1st ed.; China Machine Press: Beijing, China, 1983. [Google Scholar]
- Jiang, Y.; Lin, Y. Calculation of Eddy Current Losses in Power Transformer Core Clamps. Electr. Eng. 2017, 8, 25–26. [Google Scholar]
- Guerin, C.; Meunier, G.; Tanneau, G. Surface impedance for 3D nonlinear eddy current problems-application to loss computation in transformers. IEEE Trans. Magn. 1996, 32, 808–811. [Google Scholar] [CrossRef]
- Yan, B. Analysis of 3D Leakage Magnetic Field Coupled with Thermal Field in Large Scale Power Transformer. Doctoral Dissertation, Shenyang University of Technology, Shenyang, China, 2012. [Google Scholar]
- Zhao, Z.; Wen, T.; Wei, L.; Ji, J.; Li, X. Calculation method of transformer stray loss based on surface impedance boundary. Chin. J. Sci. Instrum. 2019, 40, 82–89. [Google Scholar]
- Liu, J.; Tian, D.; Jing, C.; Wang, J.; Wang, X. Simulation Study on Stray Losses and Temperature Rise in Adjacent Parts of Transformer Ascending Flange. Tansformer 2017, 54, 14–18. [Google Scholar]
- Guo, Z. Research on Eddy Loss and Hot Spot Temperature in Large Transformer Windings. Master’s Thesis, Hebei University of Technology, Tianjin, China, 2015. [Google Scholar]
- Yin, J. Research on extraction method of winding temperature field distribution characteristics of large oil immersed transformer. Mach. Electron. 2022, 40, 21–24. [Google Scholar]
- Su, X.; Chen, W.; Hu, Q.; Chen, Y.; Pan, C.; Xu, Q. Calculation for transformer winding temperature distribution by numerical analytical technology. High Volt. Eng. 2014, 40, 3164–3170. [Google Scholar]
- Guo, R. Finite Element Analysis and Influence Factors of Heat Dissipation for Discrete Transformer Temperature Field. Master’s Thesis, Shandong University, Jinan, China, 2019. [Google Scholar]
- Pan, W.; Chen, X.; Zhao, K. Simulation analysis method of hot spot temperature of oil-immersed transformer based on hot spot temperature calculation. Electr. Meas. Instrum. 2023, 44, 6656–6666. [Google Scholar]
- Jiang, H.; Wei, B.; Wen, J.; Dai, M.; Fu, Z.; Liu, Y. Numerical simulation of 3D temperature and flow fields in separated oil-immersed cooling transformer. High Volt. Appar. 2021, 57, 63–69. [Google Scholar]
- Tang, Z.; Qiu, Z.; Liao, C.; Zhou, Y.; Cai, M.; Hao, Y. Influence of External Cooling Modules on Hot-spot Temperature Rise of Distribution Transformer. High Volt. Appar. 2022, 60, 0135–0143. [Google Scholar]
- Schwarzkopf, J.; Cader, T.; Okamoto, K.; Li, B.Q.; Ramaprian, B. Effect of spray angle in spray cooling thermal management of electronics. Heat Transf. Summer Conf. 2004, 46938, 423–431. [Google Scholar]
- Silk, E.A.; Kim, J.; Kiger, K. Spray cooling of enhanced surfaces: Impact of structured surface geometry and spray axis inclination. Int. J. Heat Mass Transf. 2006, 49, 4910–4920. [Google Scholar] [CrossRef]
- Torriano, F.; Chaaban, M.; Picher, P. Numerical study of parameters affecting the temperature distribution in a disc-type transformer winding. Appl. Therm. Eng. 2010, 30, 2034–2044. [Google Scholar] [CrossRef]
- Chereches, N.C.; Chereches, M.; Miron, L.; Hudisteanu, S. Numerical study of cooling solutions inside a power transformer. Energy Procedia 2017, 112, 314–321. [Google Scholar] [CrossRef]
- Alegi, G.L.; Black, W.Z. Real-time thermal model for an oil-immersed, forced-air cooled transformer. IEEE Trans. Power Deliv. 1990, 5, 991–999. [Google Scholar] [CrossRef]
- Mechkov, E.; Tzeneva, R.; Mateev, V.; Yatchev, I. Thermal analysis using 3D FEM model of oil-immersed distribution transformer. In Proceedings of the 2016 19th International Symposium on Electrical Apparatus and Technologies (SIELA), Bourgas, Bulgaria, 29 May–1 June 2016. [Google Scholar] [CrossRef]
- Kim, Y.J.; Jeong, M.; Park, Y.G.; Ha, M.Y. A numerical study of the effect of a hybrid cooling system on the cooling performance of a large power transformer. Appl. Therm. Eng. 2018, 136, 275–286. [Google Scholar] [CrossRef]
- Khandan, S.; Tenbohlen, S.; Breuer, C.; Lebreton, R. CFD study of fluid flow and temperature distributions in a power transformer winding. In Proceedings of the 2017 IEEE 19th International Conference on Dielectric Liquids (ICDL), Manchester, UK, 25–29 June 2017. [Google Scholar] [CrossRef]
- Mufuta, J.M.; van den Bulck, E. Modelling of the mixed convection in the windings of a disc-type power transformer. Appl. Therm. Eng. 2000, 20, 417–437. [Google Scholar] [CrossRef]
- Skillen, A.; Revell, A.; Iacovides, H.; Wu, W. Numerical prediction of local hot-spot phenomena in transformer windings. Appl. Therm. Eng. 2012, 36, 96–105. [Google Scholar] [CrossRef]
- Lin, L.; Chen, Q.; Chi, M.; Wei, X.; Zhu, X.; Gao, Z. Flow electrification characteristics of typical plane oil-pressboard insulation under AC/DC voltage. In Proceedings of the 2015 IEEE 11th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Sydney, Australia, 19–22 July 2015. [Google Scholar] [CrossRef]
- Chen, Q.; Lin, L.; Gao, Y.; Li, J. Flow electrification characteristics of oil-pressboard insulation under ac superimposed on DC electric field. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 2915–2922. [Google Scholar] [CrossRef]
- Liu, D.; Liu, N.; Ye, J. Factors Influencing Electrification of Oil Flow in Transformer and Its Suppression Method. Tansformer 2024, 61, 1–12. [Google Scholar]
- Tang, W.H.; Wu, Q.H. Condition Monitoring and Assessment of Power Transformers Using Computational Intelligence; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Santisteban, A.; Piquero, A.; Ortiz, F.; Delgado, F.; Ortiz, A. Thermal modelling of a power transformer disc type winding immersed in mineral and ester-based oils using network models and CFD. IEEE Access 2019, 7, 174651–174661. [Google Scholar] [CrossRef]
- Wen, B.; Liu, S.; Feng, J.; Chen, Y. Two dimensional simulation analysis of winding temperature field of oil-immersed power transformer. Transformer 2009, 46, 35–38. [Google Scholar]
- García, A.; Espinosa-Paredes, G.; Hernández, I. A thermal study of an encapsulated electrical transformer. Comput. Electr. Eng. 2002, 28, 417–445. [Google Scholar] [CrossRef]
- Betta, G.; Pietrosanto, A.; Scaglione, A. An enhanced fiber-optic temperature sensor system for power transformer monitoring. IEEE Trans. Instrum. Meas. 2001, 50, 1138–1143. [Google Scholar] [CrossRef]
- Kweon, D.J.; Koo, K.S.; Woo, J.W.; Kwak, J.S. A study on the hot spot temperature in 154kV power transformers. J. Electr. Eng. Technol. 2012, 7, 312–319. [Google Scholar] [CrossRef]
- Takasu, N.; Oshi, T.; Miyawaki, F.; Saito, S.; Fujiwara, Y. An experimental analysis of DC excitation of transformers by geomagnetically induced currents. IEEE Trans. Power Deliv. 1994, 9, 1173–1182. [Google Scholar] [CrossRef]
- Sultan, M.F.; O’Rourke, M.J. Temperature sensing by band gap optical absorption in semiconductors. Fiber Opt. Laser Sens. XIV 1996, 2839, 191–202. [Google Scholar] [CrossRef]
- Grattan, K.T.; Sun, T. Fiber optic sensor technology: An overview. Sens. Actuators A Phys. 2000, 82, 40–61. [Google Scholar] [CrossRef]
- Picanco, A.F.; Martinez, M.L.; Rosa, P.C. Bragg system for temperature monitoring in distribution transformers. Electr. Power Syst. Res. 2010, 80, 77–83. [Google Scholar] [CrossRef]
- Kim, M.; Lee, J.H.; Koo, J.Y.; Song, M. A study on internal temperature monitoring system for power transformer using pptical Fiber Bragg Grating sensors. In Proceedings of the 2008 International Symposium on Electrical Insulating Materials (ISEIM 2008), Yokkaichi, Japan, 7–11 September 2008; pp. 163–166. [Google Scholar] [CrossRef]
- McNutt, W.J.; McIver, J.C.; Leibinger, G.E.; Fallon, D.J.; Wickersheim, K.A. Direct measurement of transformer winding hot spot temperature. IEEE Trans. Power Appar. Syst. 1984, PAS-103, 1155–1162. [Google Scholar] [CrossRef]
- Xin, S.J.; Chai, W. Study on encapsulating method of FBG temperature sensor. J. Transducer Technol. 2004, 23, 10–12. [Google Scholar]
- Ribeiro, A.L.; Eira, N.F.; Sousa, J.M.; Guerreiro, P.T.; Salcedo, J.R. Multipoint fiber-optic hot-spot sensing network integrated into high power transformer for continuous monitoring. IEEE Sens. J. 2008, 8, 1264–1267. [Google Scholar] [CrossRef]
- Qi, Y.; Wu, G.; Wang, Y. Optimum design of fiber Bragg grating real-time online temperature detecting sensor for power cable. J. Cent. South Univ. (Sci. Technol.) 2011, 42, 3415–3420. [Google Scholar]
- Wang, E.; Zhao, Z.; Cao, M.; Tang, B.; Li, C. Multi point temperature monitoring of oil immersed transformer based on fiber Bragg grating. High Volt. Eng. 2017, 43, 1543–1549. [Google Scholar]
- Yilmaz, G.; Karlik, S.E. A distributed optical fiber sensor for temperature detection in power cables. Sens. Actuators A Phys. 2006, 125, 148–155. [Google Scholar] [CrossRef]
- Mandal, J.; Pal, S.; Sun, T.; Grattan, K.T.; Augousti, A.T.; Wade, S.A. Bragg grating-based fiber-optic laser probe for temperature sensing. IEEE Photonics Technol. Lett. 2004, 16, 218–220. [Google Scholar] [CrossRef]
- Lee, Y.W.; Yoon, I.; Lee, B. A simple fiber-optic current sensor using a long-period fiber grating inscribed on a polarization-maintaining fiber as a sensor demodulator. Sens. Actuators A Phys. 2004, 112, 308–312. [Google Scholar] [CrossRef]
- Cusano, A.; Cutolo, A.; Nasser, J.; Giordano, M.; Calabro, A. Dynamic strain measurements by fibre Bragg grating sensor. Sens. Actuators A Phys. 2004, 110, 276–281. [Google Scholar] [CrossRef]
- Berkoff, T.A.; Kersey, A.D. Experimental demonstration of a fiber Bragg grating accelerometer. IEEE Photonics Technol. Lett. 1996, 8, 1677–1679. [Google Scholar] [CrossRef]
- Jones, S.; Bucea, G.; McAlpine, A.; Nakanishi, M.; Mashio, S.; Komeda, H.; Jinno, A. Condition monitoring system for TransGrid 330 kV power cable. In Proceedings of the 2004 International Conference on Power System Technology, 2004. PowerCon 2004, Singapore, 21–24 November 2004. [Google Scholar] [CrossRef]
- Jiang, Q.; Sui, Q. Technological study on distributed fiber sensor monitoring of high voltage power cable in seafloor. In Proceedings of the 2009 IEEE International Conference on Automation and Logistics, Shenyang, China, 5–7 August 2009. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, S.G.; Park, H.J.; Song, M. Investigation of Fiber Bragg Grating temperature sensor for applications in electric power systems. In Proceedings of the 2006 IEEE 8th International Conference on Properties & applications of Dielectric Materials, Bali, Indonesia, 26–30 June 2006. [Google Scholar] [CrossRef]
- Cooney, W.H. Predetermination of self-cooled oil-immersed: Transformer temperatures before conditions are constant. J. AIEE 1925, 44, 1324–1331. [Google Scholar] [CrossRef]
- IEEE Std C57.91-2011 (Revision of IEEE Std C57.91-1995); IEEE Guide for Loading Mineral-Oil-Immersed Transformers and Step-Voltage Regulators. Institute of Electrical and Electronics Engineers: New York, NY, USA, 2012.
- IEC 60076-7-2005; Power Transformers—Part 7: Loading Guide for Oil-Immersed Power Transformers. International Electrotechnical Commission: Geneva, Switzerland, 2005.
- Swift, G.; Molinski, T.S.; Lehn, W. A fundamental approach to transformer thermal modeling. I. Theory and equivalent circuit. IEEE Trans. Power Deliv. 2001, 16, 171–175. [Google Scholar] [CrossRef]
- Swift, G.; Molinski, T.S.; Bray, R.; Menzies, R. A fundamental approach to transformer thermal modeling. II. Field verification. IEEE Trans. Power Deliv. 2001, 16, 176–180. [Google Scholar] [CrossRef]
- Galdi, V.; Ippolito, L.; Piccolo, A.; Vaccaro, A. Parameter identification of power transformers thermal model via genetic algorithms. Electr. Power Syst. Res. 2001, 60, 107–113. [Google Scholar] [CrossRef]
- Pierce, L.W. Predicting liquid filled transformer loading capability. In Proceedings of the 1992 Record of Conference Papers Industry Applications Society 39th Annual Petroleum and Chemical Industry Conference, San Antonio, TX, USA, 28–30 September 1992. [Google Scholar] [CrossRef]
- Jiang, T.; Li, J.; Chen, W.; Sun, C.; Zhao, T. Thermal model for hot spot temperature calculation in oil-immersed transformers. High Volt. Eng. 2009, 35, 1635–1640. [Google Scholar]
- Gastelurrutia, J.; Ramos, J.C.; Larraona, G.S.; Rivas, A.; Izagirre, J.; Del Río, L. Numerical modelling of natural convection of oil inside distribution transformers. Appl. Therm. Eng. 2011, 31, 493–505. [Google Scholar] [CrossRef]
- Jiang, B.N. The Least-Squares Finite Element Method: Theory and Applications in Computational Fluid Dynamics and Electromagnetics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Yu, S.T.; Jiang, B.N.; Liu, N.S.; Wu, J. The least-squares finite element method for low-mach-number compressible viscous flows. Int. J. Numer. Methods Eng. 1995, 38, 3591–3610. [Google Scholar] [CrossRef]
- Taghikhani, M.A.; Gholami, A. Prediction of hottest spot temperature in power transformer windings with non-directed and directed oil-forced cooling. Int. J. Electr. Power Energy Syst. 2009, 31, 356–364. [Google Scholar] [CrossRef]
- Chen, W.; Su, X.; Sun, C.; Pan, C.; Tang, J. Temperature distribution calculation based on FVM for oil-immersed power transformer windings. Electr. Power Autom. Equip. 2011, 31, 23–27. [Google Scholar]
- Tsili, M.A.; Amoiralis, E.I.; Kladas, A.G.; Souflaris, A.T. Power transformer thermal analysis by using an advanced coupled 3D heat transfer and fluid flow FEM model. Int. J. Therm. Sci. 2012, 53, 188–201. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, L.; Lv, F.; Bi, J.; Wang, L. Calculation of 3D temperature field of oil immersed transformer by the combination of the finite element and finite volume method. High Volt. Eng. 2014, 40, 3179–3185. [Google Scholar]
- Li, J.; Gu, S.; Wang, Y.; Ye, X.; Wu, H.; Liu, H. Study on influencing factors of converter transformer hot spot temperature based on finite element method. Electron. Test 2022, 19, 76–92. [Google Scholar]
- Yuan, F.; Shi, W.; Wang, Y.; Chen, W.; Tang, B.; Jiang, L. Temperature characteristic analysis and radiator optimization of oil-immersed transformer based on multi-physical field simulation. High Volt. Eng. 2024, 50, 221–231. [Google Scholar]
- Alvarez, D.L.; Rivera, S.R.; Mombello, E.E. Transformer thermal capacity estimation and prediction using dynamic rating monitoring. IEEE Trans. Power Deliv. 2019, 34, 1695–1705. [Google Scholar] [CrossRef]
- Wang, J. The Method Research on Hot-Spot Temperature Prediction Andlocation for Oil-Immersed Transformer. Doctoral Dissertation, Southwest Jiaotong University, Chengdu, China, 2020. [Google Scholar]
- Yang, C. Research on Temperature Characteristics and Hot Spot Temperature Prediction of Oil-Immersed Transformer. Doctoral Dissertation, Nanjing University of Posts and Telecommunications, Nanjing, China, 2023. [Google Scholar]
- Yuan, F.; Shi, W.; Wang, Y. Real-time Prediction Method of Hot Spot Temperature of Oil-Immersed Transformer Based on Flow-thermal Coupling Simulation and EEMD-LSTM Network. High Volt. Eng. 2024, 1–14. [Google Scholar]
- Kumbhar, G.B.; Kulkarni, S.V. Analysis of short-circuit performance of split-winding transformer using coupled field-circuit approach. IEEE Trans. Power Deliv. 2007, 22, 936–943. [Google Scholar] [CrossRef]
- Li, X.; Chen, Q.; Hu, G.; Sun, J.; Long, G. Numerical analysis on magnetic field of HTS transformer with different geometry. IEEE Trans. Magn. 2006, 42, 1343–1346. [Google Scholar] [CrossRef]
- Jing, Y. Study of Oil Flow Distribution and Winding Temperature Field in Large Power Transformers. Doctoral Dissertation, Shenyang University of Technology, Shenyang, China, 2014. [Google Scholar]
- Li, L.; Cui, X.; Zhang, Y.; Cheng, Z. Calculation of the 3d nonlinear magnetic field and eddy current loss of the plate in transformer. Proc. CSEE 1999, 19, 33–36. [Google Scholar]
- Gong, L. Analysis on Magnetic Leakage and Eddy Current Loss of Metal Structure of Power Transformer. Master’s Thesis, Harbin University of Science and Technology, Harbin, China, 2013. [Google Scholar]
- Li, Y.; Eerhemubayaer; Zhang, X.; Jing, Y.; Li, X. Magnetic-thermal coupling calculation and shielding measure of local overheating for transformer. J. Shenyang Univ. Technol. 2012, 34, 366–371. [Google Scholar]
- Hu, Y. Research on the Leakage Magnetic Fields and Local Overheating Due to the Magnetic Shunt and Heavy Current Leads in Large Power Transformers. Doctoral Dissertation, Shenyang University of Technology, Shenyang, China, 2001. [Google Scholar]
- Ho, S.L.; Li, Y.; Tang, R.Y.; Cheng, K.W.E.; Yang, S.Y. Calculation of eddy current field in the ascending flange for the bushings and tank wall of a large power transformer. IEEE Trans. Magn. 2008, 44, 1522–1525. [Google Scholar] [CrossRef]
- Jing, Y.; Li, Y. Eddy current losses calculation and shields of high voltage auto-transformer. High Volt. Eng. 2012, 38, 1988–1994. [Google Scholar]
- Xiao, R. Temperature Field Simulation Modeling and Rapid Prediction Method of Real-time Temperature of Converter Transformer. Doctoral Dissertation, Chongqing University, Chongqing, China, 2022. [Google Scholar]
- Choi, C.; Yoo, H.S.; Oh, J.M. Preparation and heat transfer properties of nanoparticle in transformer oil dispersions as advanced energy-efficient coolants. Curr. Appl. Phys. 2008, 8, 710–712. [Google Scholar] [CrossRef]
- Nazari, M.; Jafarmadar, S.; Gohery, S. Convective heat transfer behavior and AC dielectric breakdown voltage of electric power transformer oil with magnetic colloidal nano-fluid: An experimental study. Case Stud. Therm. Eng. 2023, 45, 103017. [Google Scholar] [CrossRef]
- Wang, B. Study on Multiphysical Properties of Traction Transformer Insulation Modification Based on Molecular Simulation. Master’s Thesis, Shenyang University of Technology, Shenyang, China, 2023. [Google Scholar]
- Khudhair, A.A.; Jabal, M.H.; Ismail, S.J. Corn oil performance’s a bio cooling fluid in electric distribution transformer. Eng. Technol. J. 2022, 40, 20–30. [Google Scholar] [CrossRef]
- Shen, W. Research on Heat Transfer Performance of Large Oil Immersed Natural Ester Oil Transformer. Master’s Thesis, Hebei University of Science and Technology, Hebei, China, 2023. [Google Scholar]
- Ma, B.; Chen, X.; Zheng, Y.; Liu, K.; Tao, Z.; Peng, R.; Wang, B.; Yuan, J. Research Progress and Trends of Eco-Friendly Insulating Oil for Power Transformers. South. Power Syst. Technol. 2024, 18, 12–21. [Google Scholar]
- Zhu, X.; Liu, Z.; Li, S. Simulation analysis of temperature rise characteristics of oil-immersed transformer based on fluid-hot spot temperature coupling. Electr. Eng. 2022, 15, 46–50. [Google Scholar] [CrossRef]
- Wang, F. Research Leakage Magnetic Field and Analyze Winding Temperature Field for Power Transformer. Master’s Thesis, Harbin University of Science and Technology, Harbin, China, 2014. [Google Scholar]
- Hosseini, R.; Nourolahi, M.; Gharehpetian, G.B. Determination of OD cooling system parameters based on thermal modeling of power transformer winding. Simul. Model. Pract. Theory 2008, 16, 585–596. [Google Scholar] [CrossRef]
- Rahimpour, E.; Barati, M.; Schäfer, M. An investigation of parameters affecting the temperature rise in windings with zigzag cooling flow path. Appl. Therm. Eng. 2007, 27, 1923–1930. [Google Scholar] [CrossRef]
- Jiang, Q.; Zhu, Z.; Zhang, Q. Optimal design of the first stage of the plate-fin heat exchanger for the EAST cryogenic system. Plasma Sci. Technol. 2018, 20, 035601. [Google Scholar] [CrossRef]
- Liu, J.C.; Zhang, S.Y.; Zhao, X.Y.; Yi, G.D.; Zhou, Z.Y. Influence of fin arrangement on fluid flow and heat transfer in the inlet of a plate-fin heat exchanger. J. Zhejiang Univ.-Sci. A 2015, 16, 279–294. [Google Scholar] [CrossRef]
- Wen, J.; Li, K.; Liu, Y.; Wu, M.; Wang, S.; Li, Y. Multi-Objective Optimization of Serrated Fin in Plate-Fin Heat Exchanger by Fluid Structure Interaction. J. Xi’an Jiaotong Univ. 2018, 52, 130–135. [Google Scholar]
- Peng, X.; Liu, Z.; Qiu, C.; Tan, J. Effect of inlet flow maldistribution on the passage arrangement design of multi-stream plate-fin heat exchanger. Appl. Therm. Eng. 2016, 103, 67–76. [Google Scholar] [CrossRef]
- Wang, Y. Numerical Analysis of Winding Temperature Field for Large Oil-Immersed Transformer Based on COMSOL. Master’s Thesis, Hebei University of Technology, Hebei, China, 2021. [Google Scholar]

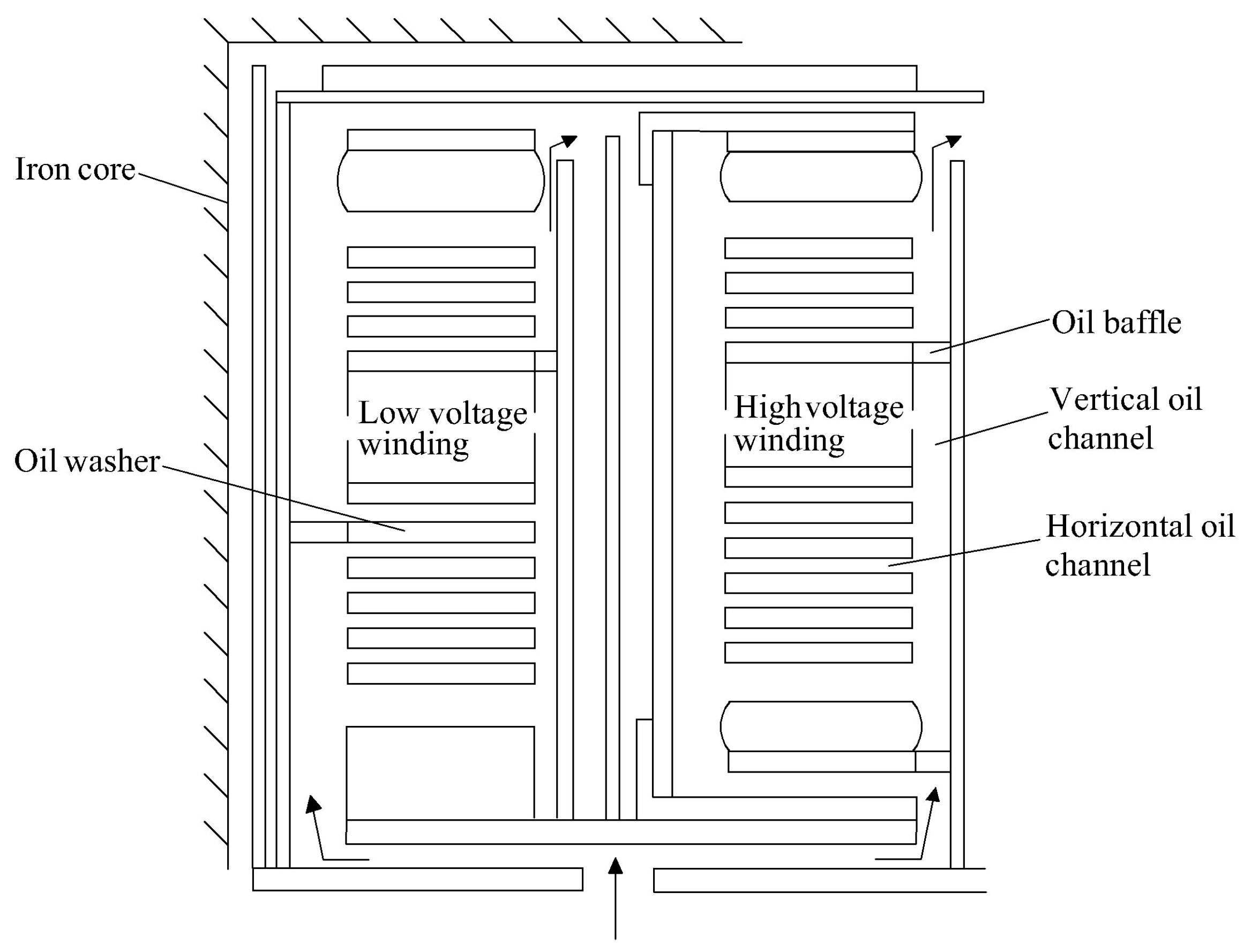
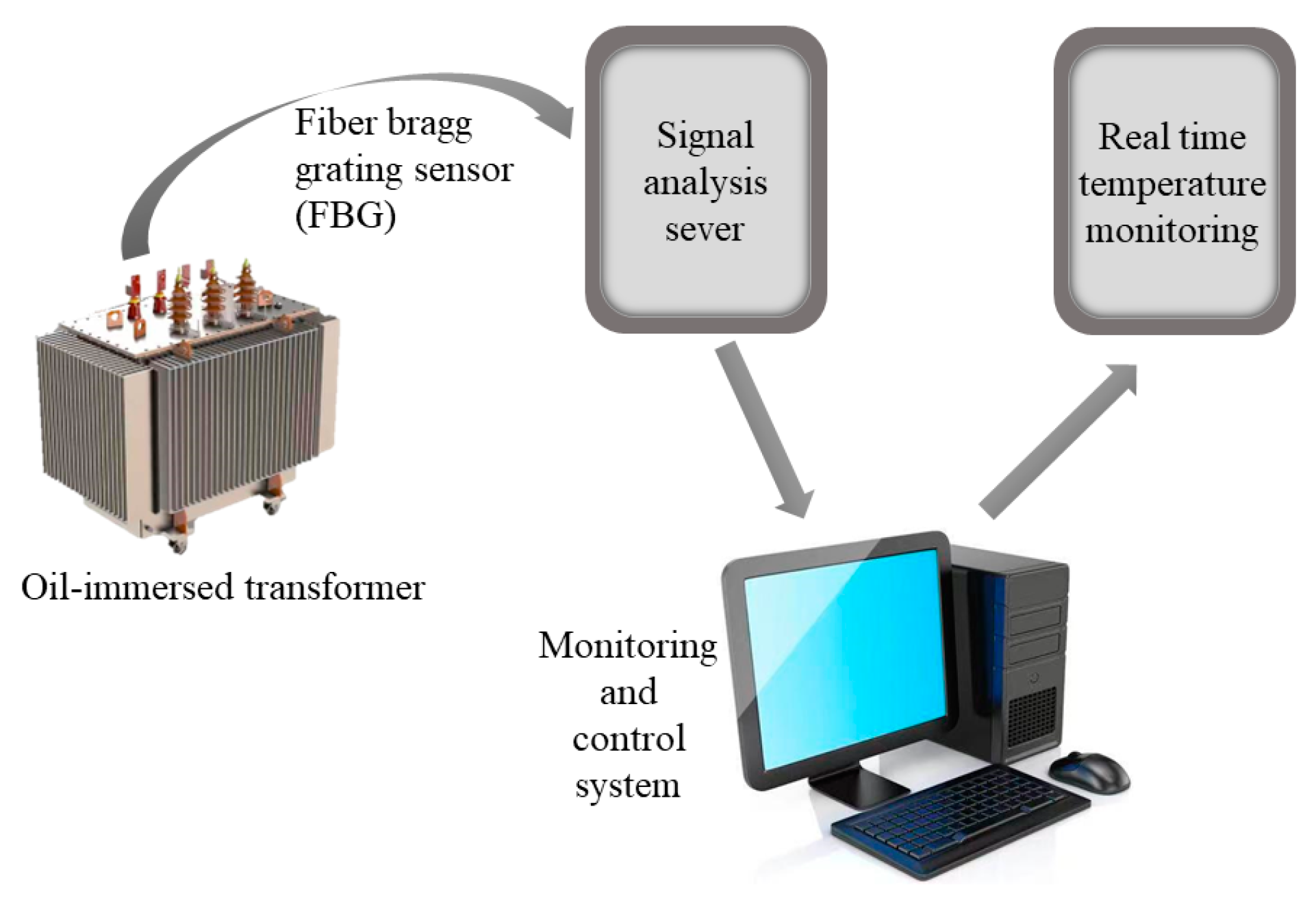
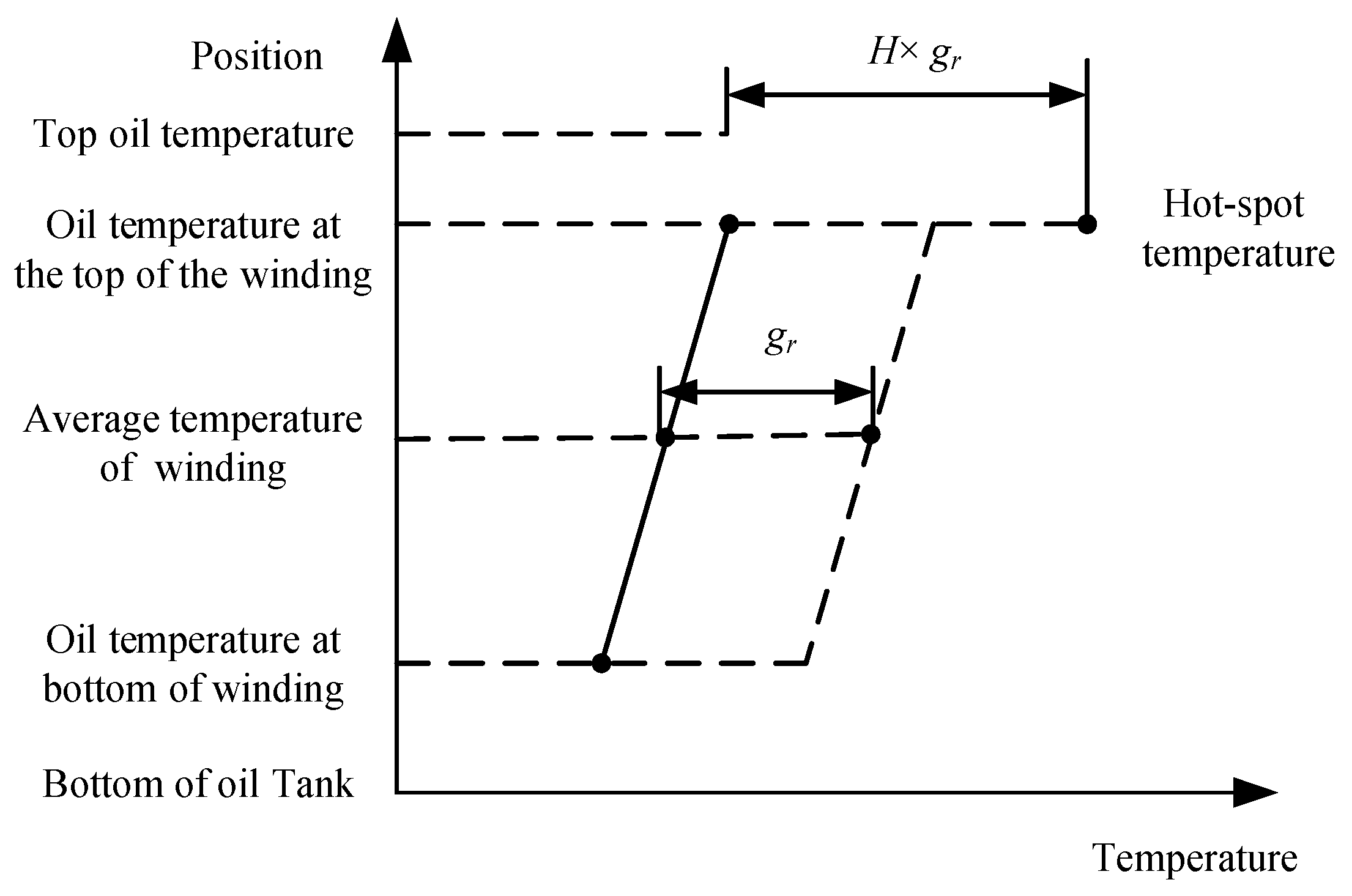
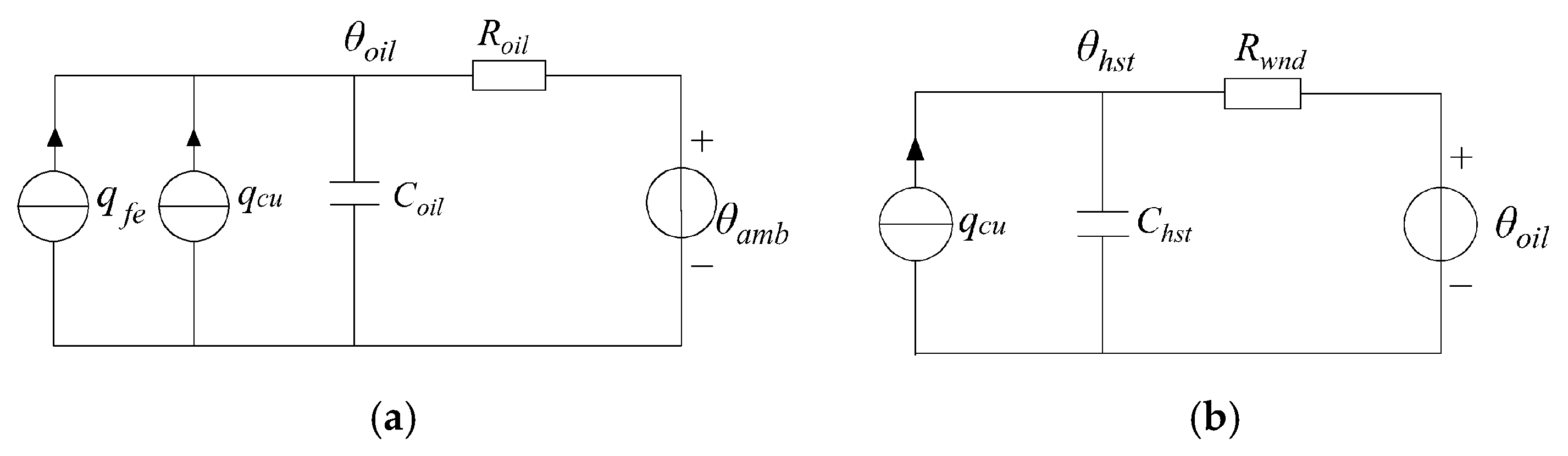
| Calculation Method | Author | Main Research Results | Disadvantages |
|---|---|---|---|
| Hysteresis loss modeling method | Preisach [7] | Proposed Preisach model, the magnetization of the dipole is obtained based on the time–space characteristics of the magnetic dipole, and the macromagnetization of the magnetic core is characterized by the sum of the magnetizations of the dipole. | When the hysteresis model is coupled with the magnetic field solution, the parameters need to change, and the model is very complicated under multi-factor. |
| Jiles and Atherton [8] | Proposed Jiles–Atherton model, the principle of the balance between the movement of the magnetic domain wall and the macroscopic energy to calculate the magnetic core loss. | Based on many experimental results, and the difficulty in achieving the optimal design of the core under nonsinusoidal excitation. | |
| Empirical formula equivalence method | Steinmetz [9,10,11] | Proposed an equivalent model of the empirical formula for the loss calculation of ferromagnetic materials, the model solves the problems of cumbersome application steps and complicated calculations. | The applicable frequency and submagnetic induction intensity range are small, and the calculation accuracy is low. |
| Separation calculation method | Bertotti [12] | Proposed a core loss separation calculation method applicable to sinusoidal and nonsinusoidal excitation. | |
| Amar [13] and Boglietti [14] | Obtained the loss under the nonsinusoidal method by accumulating the loss results of each order of sinusoidal excitation. | ||
| Barbiso [15] | Realized parameter extraction on the basis of the linear relationship between the variables at different frequencies, and then realized the calculation of iron core loss. | ||
| Lavers [16] | Proposed a correction model of iron loss separation. Two correction factors, hysteresis loss correction and eddy current loss, were added to the model to obtain a more widely used model of iron core loss separation. |
| Cooling Method | Principle | Advantages/Disadvantages | Applicable Transformer Capacity and Voltage Class |
|---|---|---|---|
| ONAN [40] | Uses the density difference between transformer oil or air when it is heated or cooled to form natural convection and achieve a cooling effect [41]. | Low noise level; there is no oil-flow electrification, but there is low efficiency. | ≤5000 kVA, 110 kV; ≤31,500 kVA, ≤35 kV |
| ONAF [42] | Fans are added outside the radiator to force air convection, making the radiator achieve a more efficient cooling effect [43]. | Higher cooling efficiency than ONAN; noise and oil-flow electrification problems are not as serious as those in forced-oil cooling. | 12,500–63,000 kVA, 35–110 kV; ≤75,000 kVA, 110 kV; ≤40,000 kVA, 220 kV |
| OFAF [44,45] | A cooling method in which the oil is forced to circulate by a transformer oil pump to dissipate heat through a cooler [46]. | High cooling efficiency; high noise, problem of oil-flow electrification, and limitation on oil flow speed (maximum of 0.5 m/s). | 50,000–90,000 kVA, 220 kV; ≥60,000 kVA, ≥220 kV |
| ODAF/ODWF | On the basis of forced oil circulation, oil guide plates and other guiding structures are added to the winding oil channel to increase the oil flow rate and the cooling effect [47]. | High cooling efficiency; noisy, obvious vibration, problem of oil-flow electrification. | ≥75,000 kVA, 110 kV; ≥120,000 kVA, 220 kV; 330 kV; 550 kV |
| Measurement Method | Classification | Advantages | Suitable for Application | Disadvantages |
|---|---|---|---|---|
| Direct measurement method | Temperature sensors | Highest precision | Little change in the transformer load. | Difficult to implement; Affected transformer internal insulation performance; It is difficult to locate the hot spot of the transformer. |
| Fiber optic temperature sensors | ||||
| Indirect calculation method | Empirical formula method | Data is easily obtained; Easy to implement. | Low precision requirement. | Large error. |
| Thermal circuit modeling method | Low calculation cost; Simple and very straightforward to use. | Power transformers with common structures; Study on nonlinear thermal characteristics of transformers. | Getting parameters requires a lot of offline testing. | |
| Numerical simulation method | Whole temperature distribution of the transformer can be calculated; Result is very close to the real operating condition. | Characteristics of transformer internal temperature distribution were analyzed. | Time-consuming long; Complex modeling and low generality; Require computer with massive processing power. The Accuracy affected by model establishment and boundary condition setting. | |
| Artificial intelligence algorithm | High speed, high efficiency and high precision | Shows very strong practicability and superiority in hot spot temperature prediction. | Prediction accuracy is affected by the topological structure of the model, the selection of input parameters and the reliability of the training samples. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, L.; Qiang, C.; Zhang, H.; Chen, Q.; An, Z.; Xu, W. Review of Studies on the Hot Spot Temperature of Oil-Immersed Transformers. Energies 2025, 18, 74. https://doi.org/10.3390/en18010074
Lin L, Qiang C, Zhang H, Chen Q, An Z, Xu W. Review of Studies on the Hot Spot Temperature of Oil-Immersed Transformers. Energies. 2025; 18(1):74. https://doi.org/10.3390/en18010074
Chicago/Turabian StyleLin, Lin, Chengdan Qiang, Hui Zhang, Qingguo Chen, Zhen An, and Weijie Xu. 2025. "Review of Studies on the Hot Spot Temperature of Oil-Immersed Transformers" Energies 18, no. 1: 74. https://doi.org/10.3390/en18010074
APA StyleLin, L., Qiang, C., Zhang, H., Chen, Q., An, Z., & Xu, W. (2025). Review of Studies on the Hot Spot Temperature of Oil-Immersed Transformers. Energies, 18(1), 74. https://doi.org/10.3390/en18010074






