Research on Torque Compensation Strategy of Wind Maneuver Model Experimental System by Increasing the Analog Multiple of Moment of Inertia
Abstract
1. Introduction
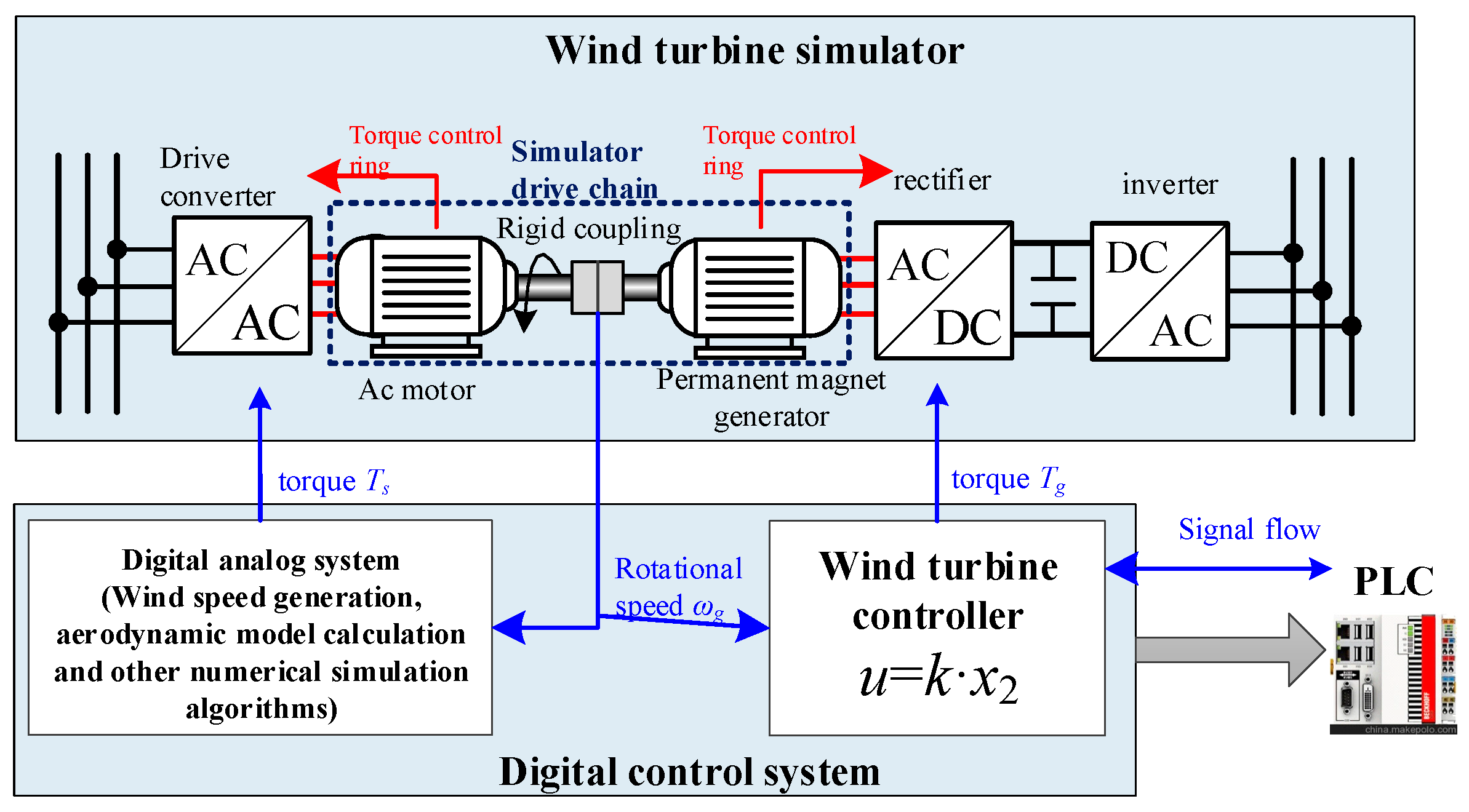
2. Wind Turbine Simulator Modeling
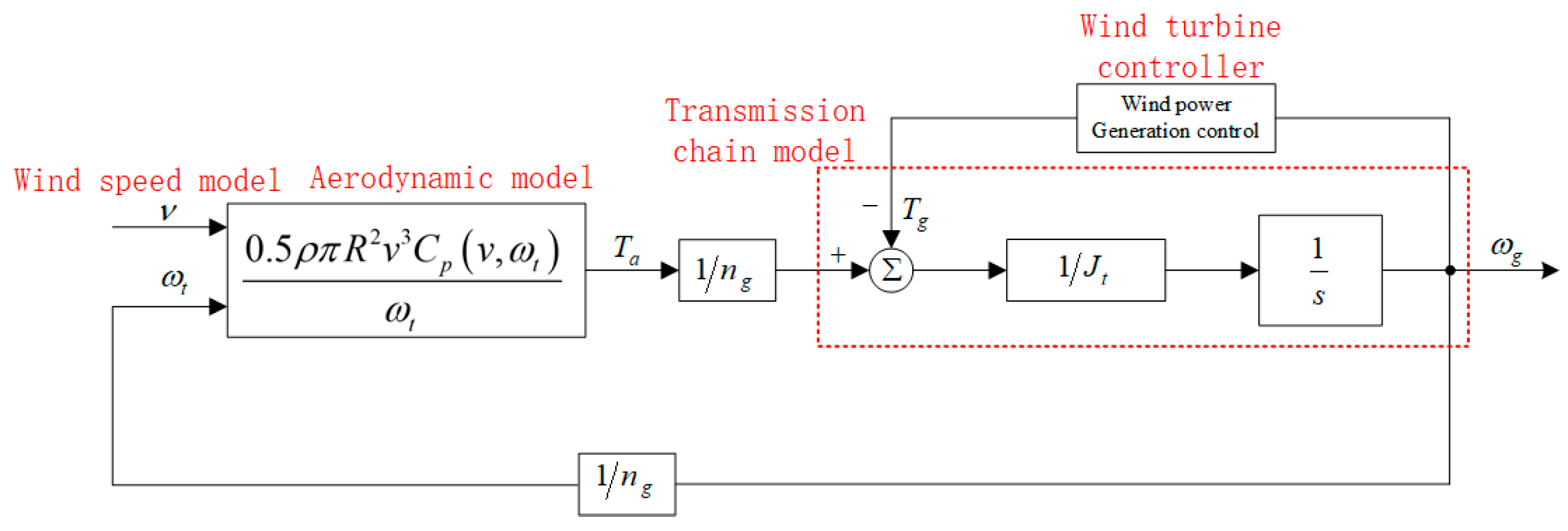
Wind Turbine System Modeling
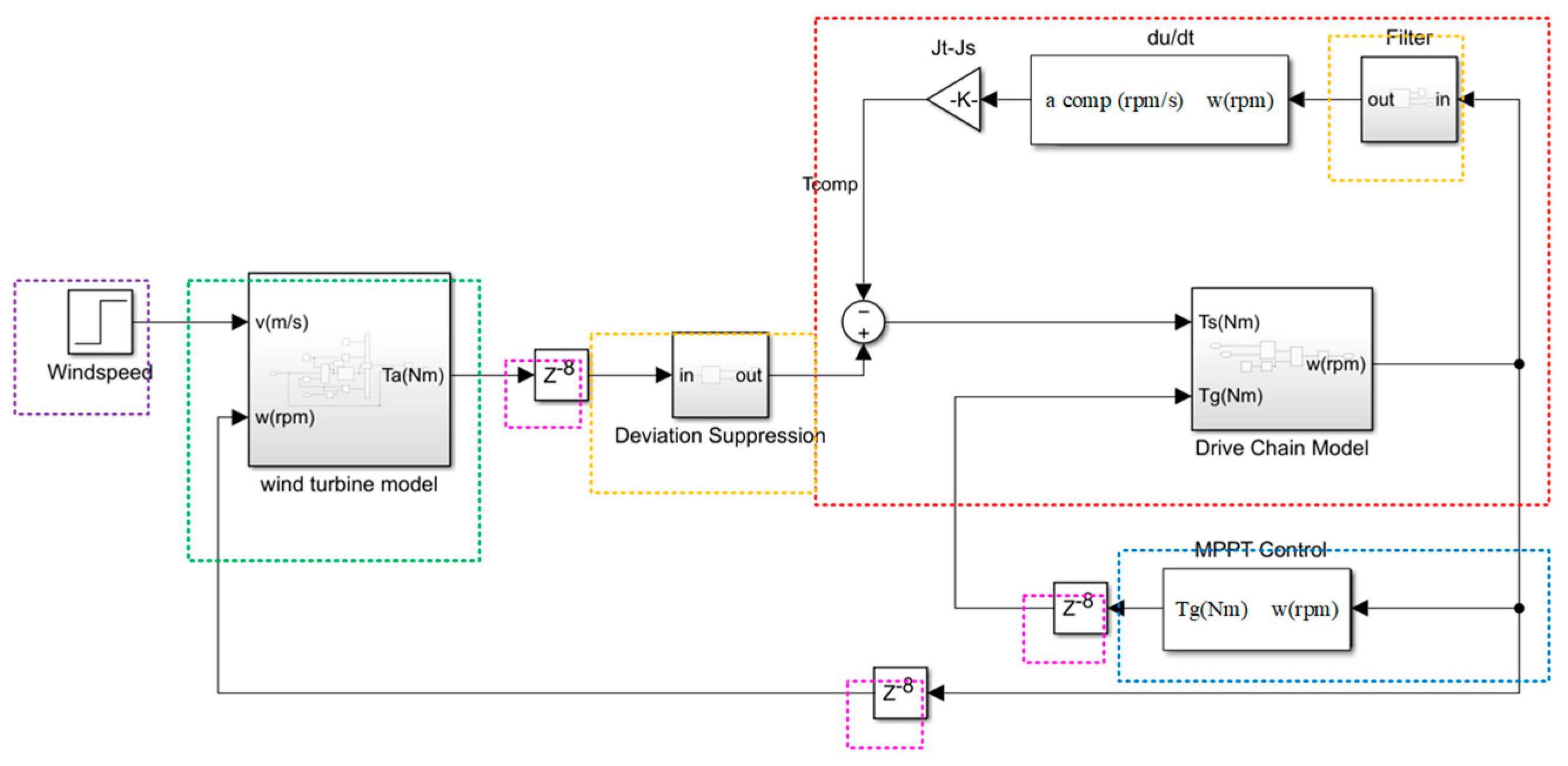
3. Simulation of the Moment of Inertia Compensation Strategy and Comparison of Results
4. Waveform and Result of Simulation Experiment
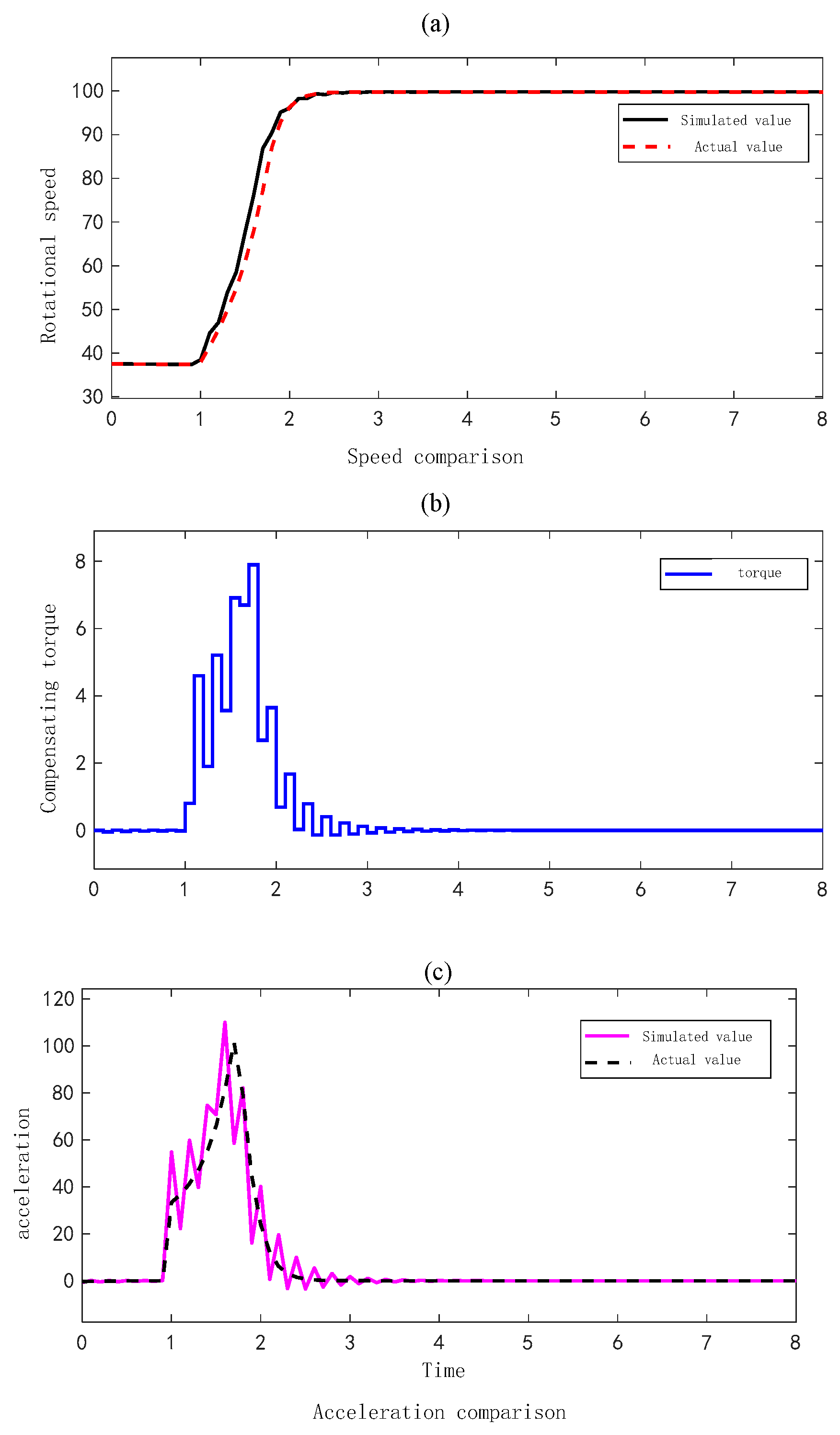
4.1. Traditional Inertia Compensation Strategy
4.2. Moment of Inertia Compensation Strategy Based on First-Order Filter
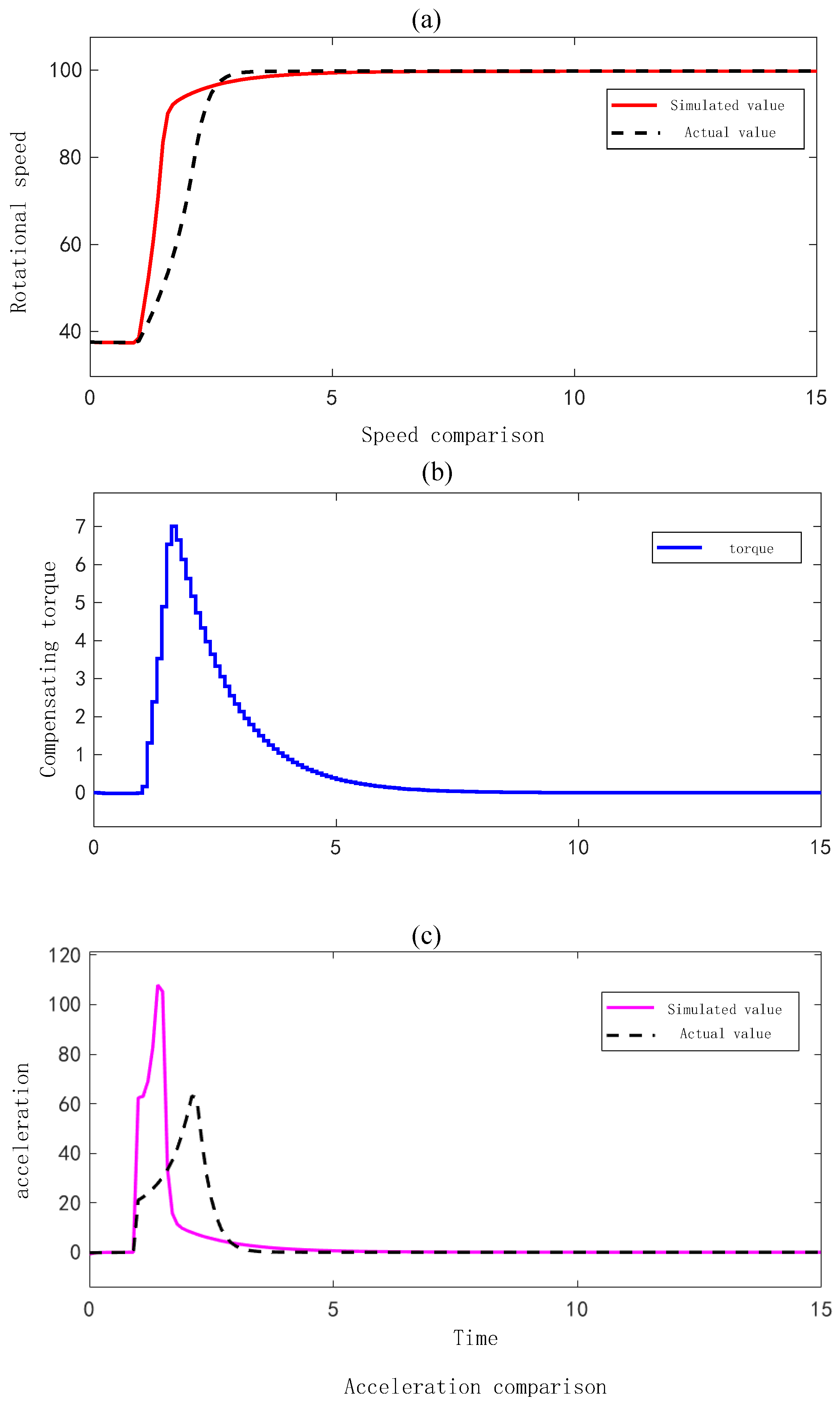
4.3. Rotational Inertia Compensation Strategy Based on High-Order Filter
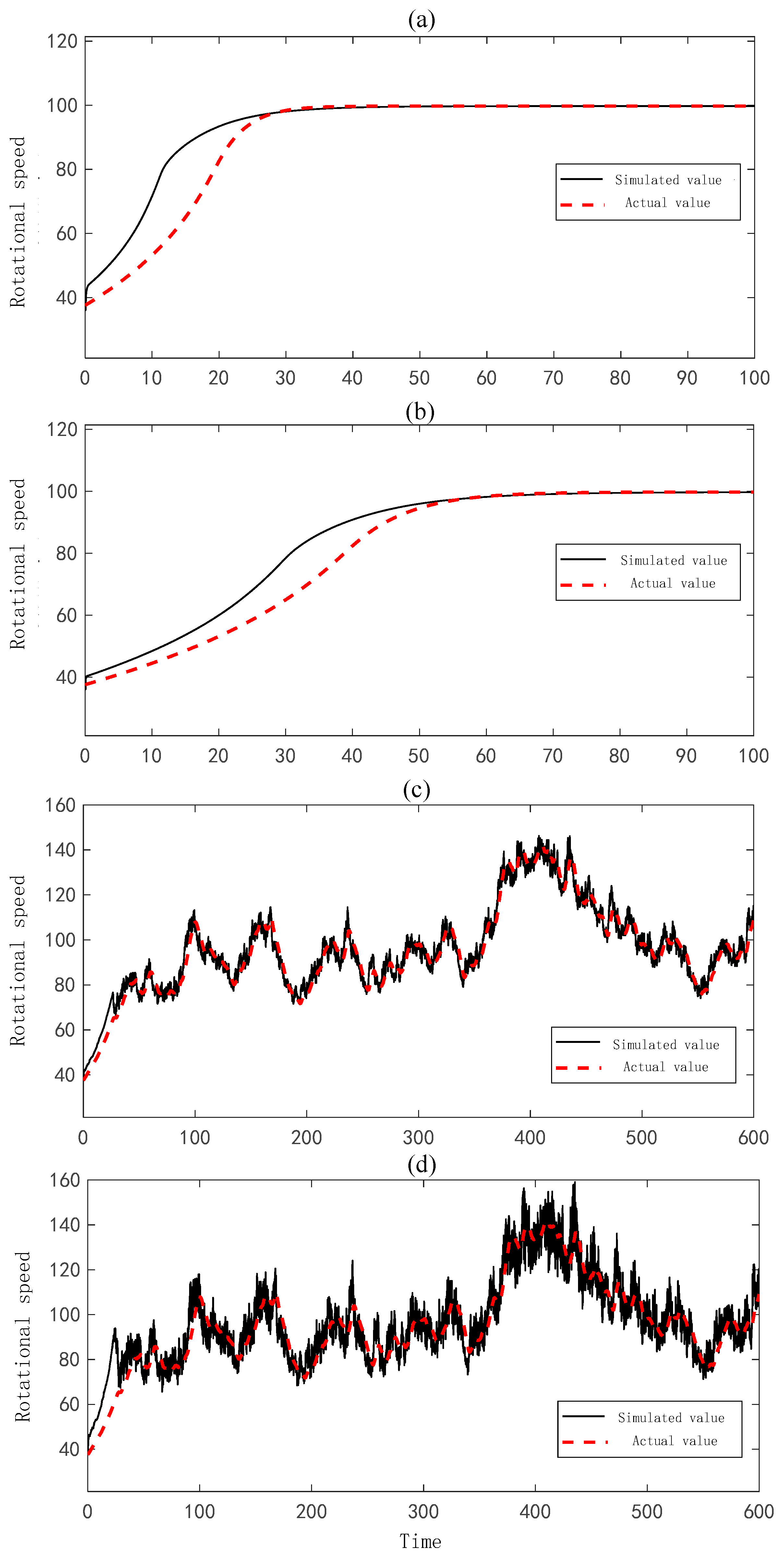
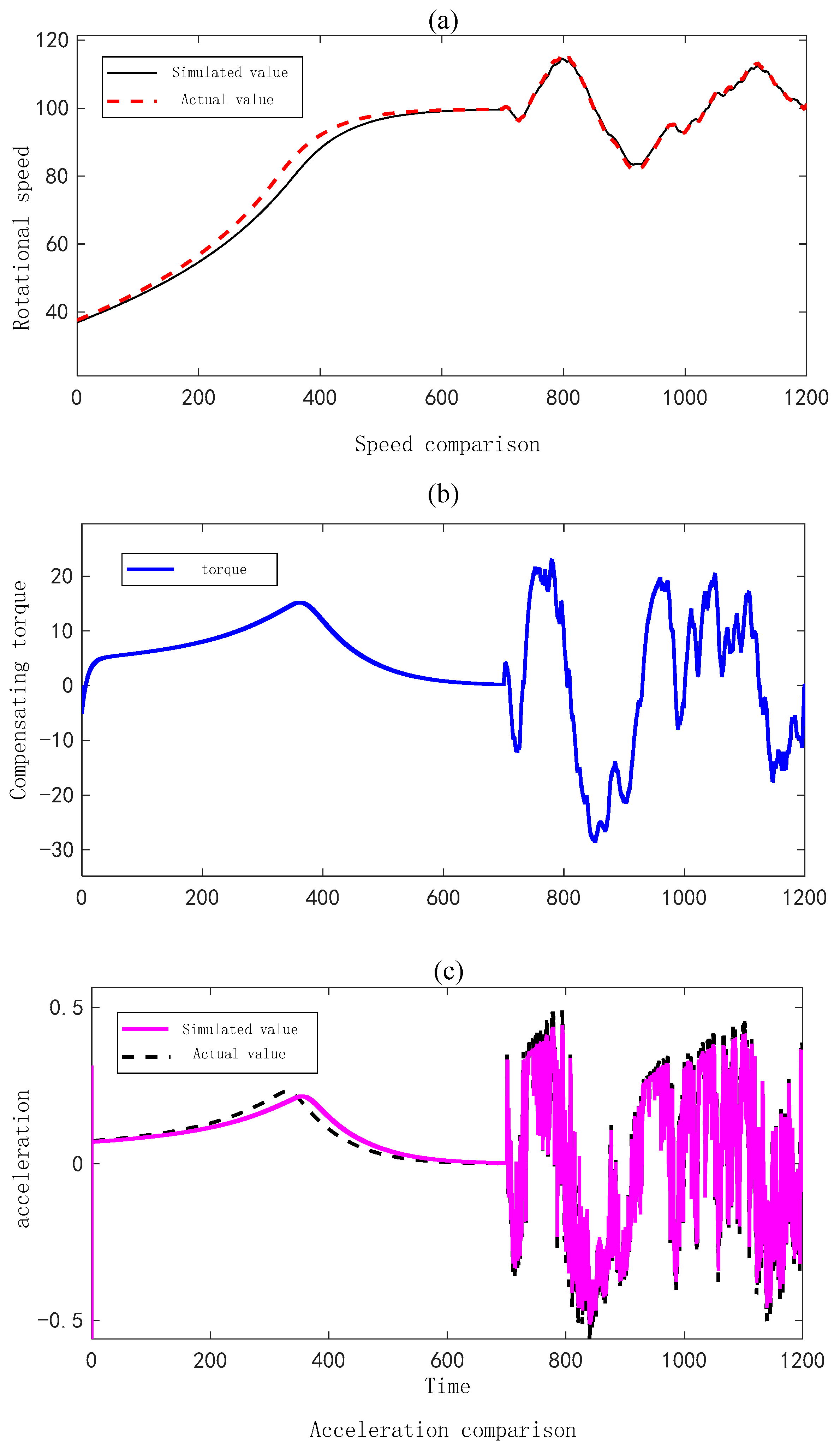
4.4. Moment of Inertia Compensation Strategy Based on Feedforward Torque Deviation Suppression
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jain, H.; Mather, B.; Jain, A.K.; Baldwin, S.F. Grid-Supportive Loads—A New Approach to Increasing Renewable Energy in Power Systems. IEEE Trans. Smart Grid 2022, 13, 2959–2972. [Google Scholar] [CrossRef]
- Echevarria, A.; Rivera-Matos, Y.; Irshad, N.; Gregory, C.; Castro-Sitiriche, M.J.; King, R.R.; Miller, C.A. Sociotechnical Imaginaries to Advance Just and Sustainable Energy Transitions: The Case of Solar Energy in Puerto Rico. IEEE Trans. Technol. Soc. 2023, 4, 255–268. [Google Scholar] [CrossRef]
- Wang, R.; Jiang, S.; Ma, D.; Sun, Q.; Zhang, H.; Wang, P. The Energy Management of Multiport Energy Router in Smart Home. IEEE Trans. Consum. Electron. 2022, 68, 344–353. [Google Scholar] [CrossRef]
- Ren, G.; Liu, J.; Wan, J.; Wang, W.; Fang, F.; Hong, F. Investigating the Complementarity Characteristics of Wind and Solar Power for Load Matching Based on the Typical Load Demand in China. IEEE Trans. Sustain. Energy 2022, 13, 778–790. [Google Scholar] [CrossRef]
- Yang, D.; Wang, X.; Chen, W.; Yan, G.-G.; Jin, Z.; Jin, E. Adaptive Frequency Droop Feedback Control-Based Power Tracking Operation of a DFIG for Temporary Frequency Regulation. IEEE Trans. Power Syst. 2024, 39, 2682–2692. [Google Scholar] [CrossRef]
- Tian, X.; Chi, Y.; Liu, C.; Cheng, P.; Li, Y. Power-balancing Coordinated Control of Wind Power and Demand-side Response Under Post-fault Condition. J. Mod. Power Syst. Clean Energy 2022, 10, 1207–1215. [Google Scholar] [CrossRef]
- Catalán, P.; Wang, Y.; Arza, J.; Chen, Z. A Comprehensive Overview of Power Converter Applied in High-Power Wind Turbine: Key Challenges and Potential Solutions. IEEE Trans. Power Electron. 2023, 38, 6169–6195. [Google Scholar] [CrossRef]
- Pan, C.; Shao, C.; Hu, B.; Xie, K.; Li, C.; Ding, J. Modeling the Reserve Capacity of Wind Power and the Inherent Decision-Dependent Uncertainty in the Power System Economic Dispatch. IEEE Trans. Power Syst. 2023, 38, 4404–4417. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.; Qin, B.; Guo, L. Coordinated Power Smoothing Control Strategy of Multi-Wind Turbines and Energy Storage Systems in Wind Farm Based on MADRL. IEEE Trans. Sustain. Energy 2024, 15, 368–380. [Google Scholar] [CrossRef]
- Li, D.; Yan, W.; Li, W.; Ren, Z. A Two-Tier Wind Power Time Series Model Considering Day-to-Day Weather Transition and Intraday Wind Power Fluctuations. IEEE Trans. Power Syst. 2016, 31, 4330–4339. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, P.; He, Y.; Wang, X.; Zhang, X. Scenario-oriented hybrid particle swarm optimization algorithm for robust economic dispatch of power system with wind power. J. Syst. Eng. Electron. 2022, 33, 1143–1150. [Google Scholar] [CrossRef]
- Villanueva, D.; Feijóo, A. Normal-Based Model for True Power Curves of Wind Turbines. IEEE Trans. Sustain. Energy 2016, 7, 1005–1011. [Google Scholar] [CrossRef]
- Feijóo, A.; Villanueva, D. Wind Farm Power Distribution Function Considering Wake Effects. IEEE Trans. Power Syst. 2017, 32, 3313–3314. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Vu, T.; Ortmeyer, T.; Stefopoulos, G.; Pedrick, G.; MacDowell, J. Real-Time Transient Simulation and Studies of Offshore Wind Turbines. IEEE Trans. Sustain. Energy 2023, 14, 1474–1487. [Google Scholar] [CrossRef]
- Huang, C.; Zhuang, J. Error-Based Active Disturbance Rejection Control for Pitch Control of Wind Turbine by Improved Coyote Optimization Algorithm. IEEE Trans. Energy Convers. 2022, 37, 1394–1405. [Google Scholar] [CrossRef]
- Huang, Y.; Lin, S.; Zhao, X. Multi-Agent Reinforcement Learning Control of a Hydrostatic Wind Turbine-Based Farm. IEEE Trans. Sustain. Energy 2023, 14, 2406–2416. [Google Scholar] [CrossRef]
- Balachandran, T.; Yoon, A.; Lee, D.; Xiao, J.; Haran, K.S. Ultrahigh-Field, High-Efficiency Superconducting Machines for Offshore Wind Turbines. IEEE Trans. Magn. 2022, 58, 8700805. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, G.; Wang, Q.; Ding, D.; Bi, G.; Li, B.; Wang, G.; Xu, D. Torque Disturbance Compensation Method Based on Adaptive Fourier-Transform for Permanent Magnet Compressor Drives. IEEE Trans. Power Electron. 2023, 38, 3612–3623. [Google Scholar] [CrossRef]
- Bao, Y.; Xu, J.; Liao, S.; Sun, Y.; Li, X.; Jiang, Y.; Ke, D.; Yang, J.; Peng, X. Field Verification of Frequency Control by Energy-Intensive Loads for Isolated Power Systems with High Penetration of Wind Power. IEEE Trans. Power Syst. 2018, 33, 6098–6108. [Google Scholar] [CrossRef]
- Jin, X.; Xu, Z.; Qiao, W. Condition Monitoring of Wind Turbine Generators Using SCADA Data Analysis. IEEE Trans. Sustain. Energy 2021, 12, 202–210. [Google Scholar] [CrossRef]
- Peng, Y.; Qiao, W.; Qu, L. Compressive Sensing-Based Missing-Data-Tolerant Fault Detection for Remote Condition Monitoring of Wind Turbines. IEEE Trans. Ind. Electron. 2022, 69, 1937–1947. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, M.; Wu, Z.; Liu, S.; Guo, Z.; Li, G. A Frequency Security Constrained Scheduling Approach Considering Wind Farm Providing Frequency Support and Reserve. IEEE Trans. Sustain. Energy 2022, 13, 1086–1100. [Google Scholar] [CrossRef]
- Sattar, A.; Al-Durra, A.; Caruana, C.; Debouza, M.; Muyeen, S.M. Testing the Performance of Battery Energy Storage in a Wind Energy Conversion System. IEEE Trans. Ind. Appl. 2020, 56, 3196–3206. [Google Scholar] [CrossRef]
- Enalou, H.B.; Lang, X.; Rashed, M.; Bozhko, S. Time-Scaled Emulation of Electric Power Transfer in the More Electric Engine. IEEE Trans. Transp. Electrif. 2020, 6, 1679–1694. [Google Scholar] [CrossRef]
- Ammar, M.; Joós, G. A Short-Term Energy Storage System for Voltage Quality Improvement in Distributed Wind Power. IEEE Trans. Energy Convers. 2014, 29, 997–1007. [Google Scholar] [CrossRef]
- Tang, X.; Yin, M.; Shen, C.; Xu, Y.; Dong, Z.Y.; Zou, Y. Active Power Control of Wind Turbine Generators via Coordinated Rotor Speed and Pitch Angle Regulation. IEEE Trans. Sustain. Energy 2019, 10, 822–832. [Google Scholar] [CrossRef]
- Castaignet, D.; Couchman, I.; Poulsen, N.K.; Buhl, T.; Wedel-Heinen, J.J. Frequency-Weighted Model Predictive Control of Trailing Edge Flaps on a Wind Turbine Blade. IEEE Trans. Control Syst. Technol. 2013, 21, 1105–1116. [Google Scholar] [CrossRef]
- Yang, Y.; Ren, X.; Qin, W.; Wu, Y.; Zhi, X. Analysis on the nonlinear response of cracked rotor in hover flight. Nonlinear Dyn. 2010, 61, 183–192. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Yang, C.; Wu, X.; Xu, T. A Learning-Based Stable Servo Control Strategy Using Broad Learning System Applied for Microrobotic Control. IEEE Trans. Cybern. 2022, 52, 13727–13737. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, Y.; Sun, J.; Wang, H. Adaptive Visual Servoing Shape Control of a Soft Robot Manipulator Using Bézier Curve Features. IEEE/ASME Trans. Mechatron. 2023, 28, 945–955. [Google Scholar] [CrossRef]
- Zhu, W.; Yang, Y.; Tian, B.; Zong, Q. Global Finite-Time Adaptive Attitude Control for Coupled Spacecraft With Model Uncertainty and Actuator Faults. IEEE Trans. Control Syst. Technol. 2024, 32, 2428–2435. [Google Scholar] [CrossRef]
- Mahdavi, M.; Jurado, F.; Schmitt, K.; Chamana, M. Electricity Generation From Cow Manure Compared to Wind and Photovoltaic Electric Power Considering Load Uncertainty and Renewable Generation Variability. IEEE Trans. Ind. Appl. 2024, 60, 3543–3553. [Google Scholar] [CrossRef]
- Yang, Z.; Peng, X.; Song, J.; Duan, R.; Jiang, Y.; Liu, S. Short-Term Wind Power Prediction Based on Multi-Parameters Similarity Wind Process Matching and Weighed-Voting-Based Deep Learning Model Selection. IEEE Trans. Power Syst. 2024, 39, 2129–2142. [Google Scholar] [CrossRef]



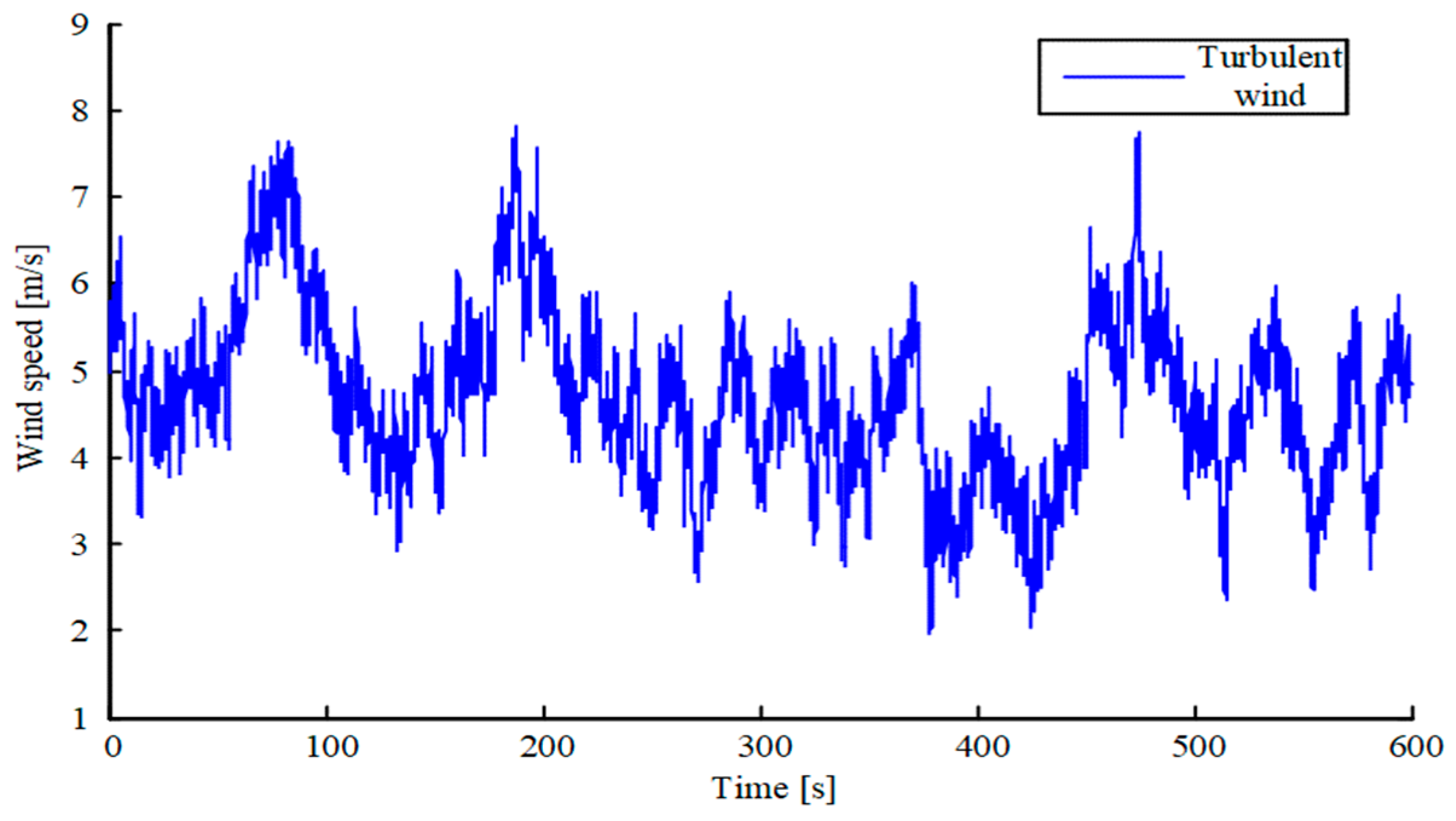


| Average Wind Speed | Turbulence Intensity | Integral Scale |
|---|---|---|
| 9 m/s | Class C | 250 |
| Parameter | Value |
|---|---|
| R: Wind wheel radius (m) | 20 |
| ρ: Air density (kg/m3) | 1.225 |
| ν: Cutting wind speed (m/s) | 8 |
| : Optimal torque gain (Nm/rpm2) | 0.002 |
| : Rated generator speed (rpm) | 1780 |
| : Rated speed of wind turbine (rad/s) | 3.64 |
| : Gearbox change ratio | 43.165 |
| λ: Optimum tip ratio | 5.8 |
| : Maximum wind energy utilization factor | 0.467 |
| : Rotor moment of inertia (kg·m2) | 5.492 × 105 |
| : Generator moment of inertia (kg·m2) | 34.4 |
| : Rated power (kW) | 600 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Q.; Qiu, Y.; Zhang, C. Research on Torque Compensation Strategy of Wind Maneuver Model Experimental System by Increasing the Analog Multiple of Moment of Inertia. Energies 2025, 18, 87. https://doi.org/10.3390/en18010087
Sun Q, Qiu Y, Zhang C. Research on Torque Compensation Strategy of Wind Maneuver Model Experimental System by Increasing the Analog Multiple of Moment of Inertia. Energies. 2025; 18(1):87. https://doi.org/10.3390/en18010087
Chicago/Turabian StyleSun, Qiming, Yaqin Qiu, and Chao Zhang. 2025. "Research on Torque Compensation Strategy of Wind Maneuver Model Experimental System by Increasing the Analog Multiple of Moment of Inertia" Energies 18, no. 1: 87. https://doi.org/10.3390/en18010087
APA StyleSun, Q., Qiu, Y., & Zhang, C. (2025). Research on Torque Compensation Strategy of Wind Maneuver Model Experimental System by Increasing the Analog Multiple of Moment of Inertia. Energies, 18(1), 87. https://doi.org/10.3390/en18010087






