Prediction of Remaining Service Life of Miniature Circuit Breakers Based on Wiener Process
Abstract
1. Introduction
2. Failure Causes of MCBs and Kinetic Analysis
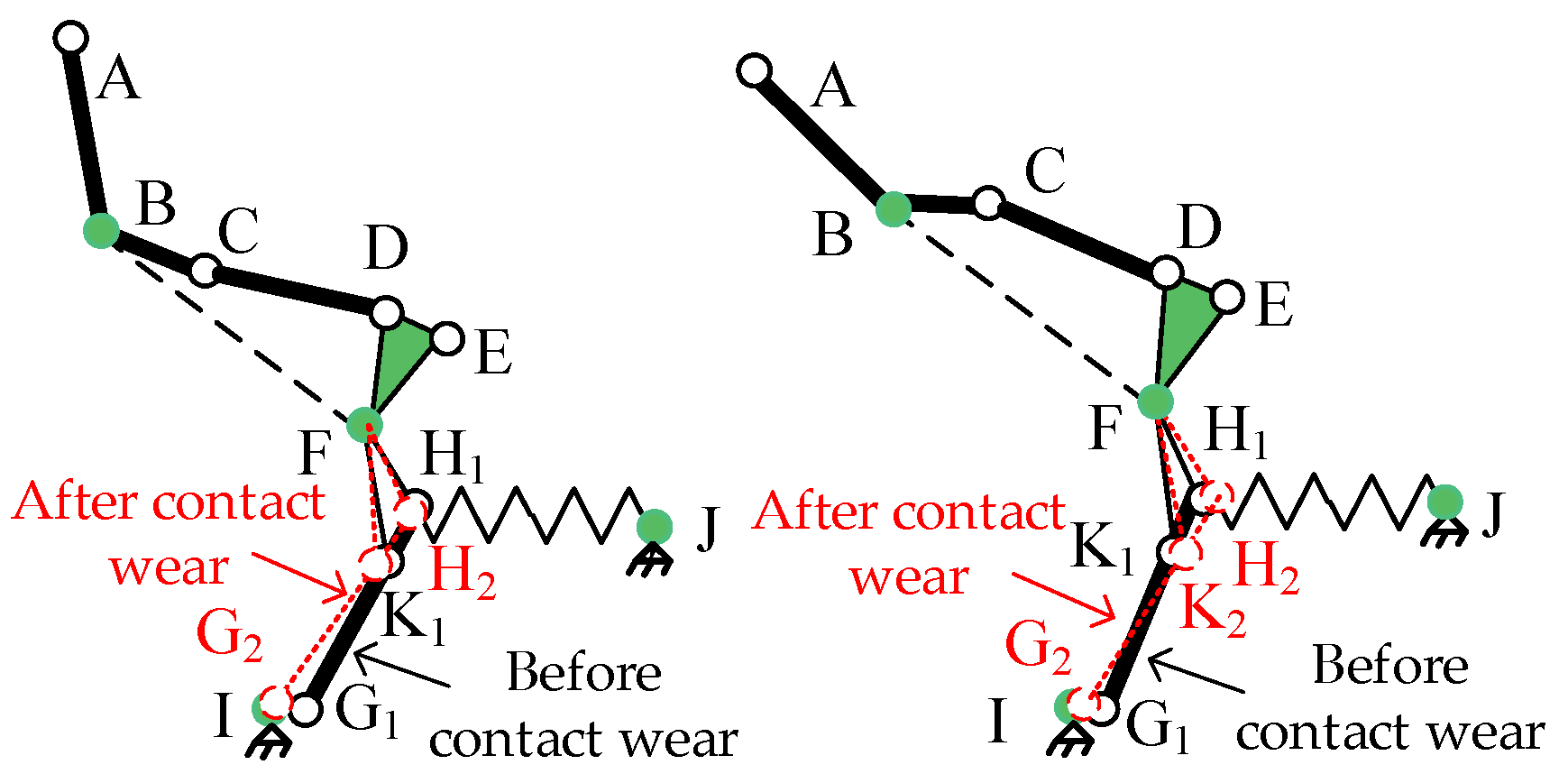
2.1. Failure Causes of MCBs
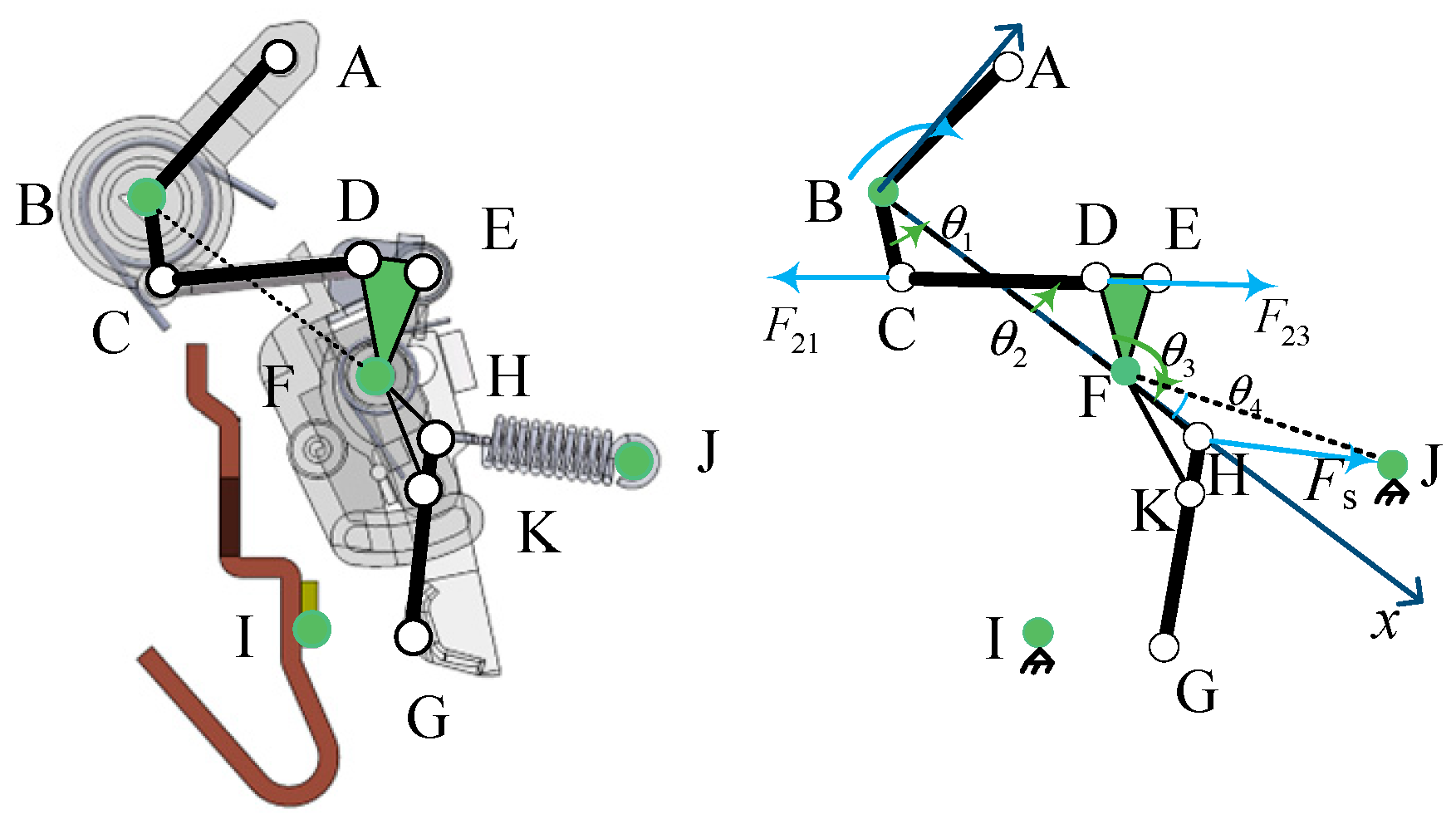
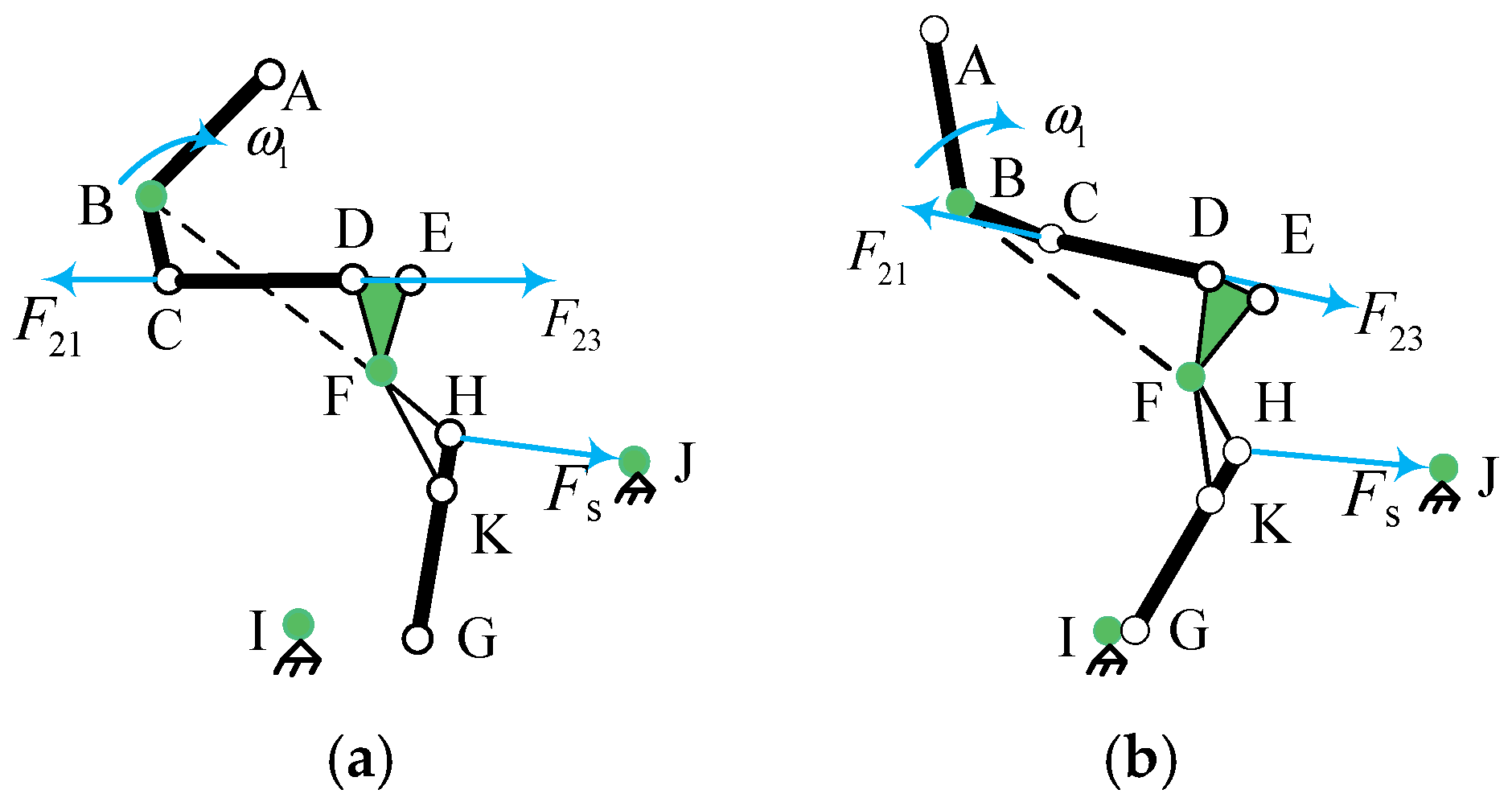
2.2. Closing Process Analysis
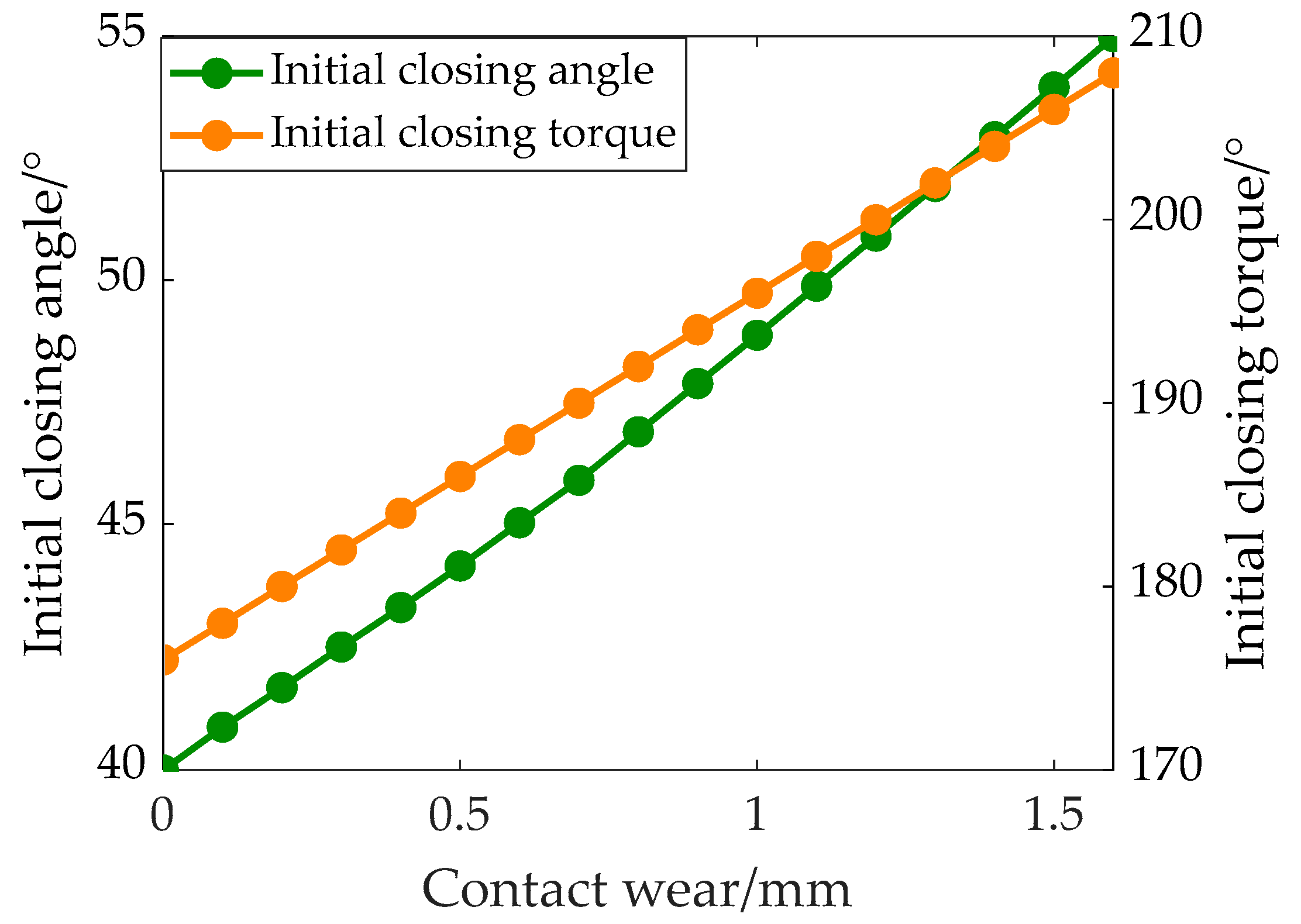
2.3. Dynamic Simulation Analysis
3. Electrical Life Prediction Method for MCBs
3.1. Electrical Performance Degradation Model
3.2. Residual Electric Life Prediction Model
4. Simulation Results Analysis
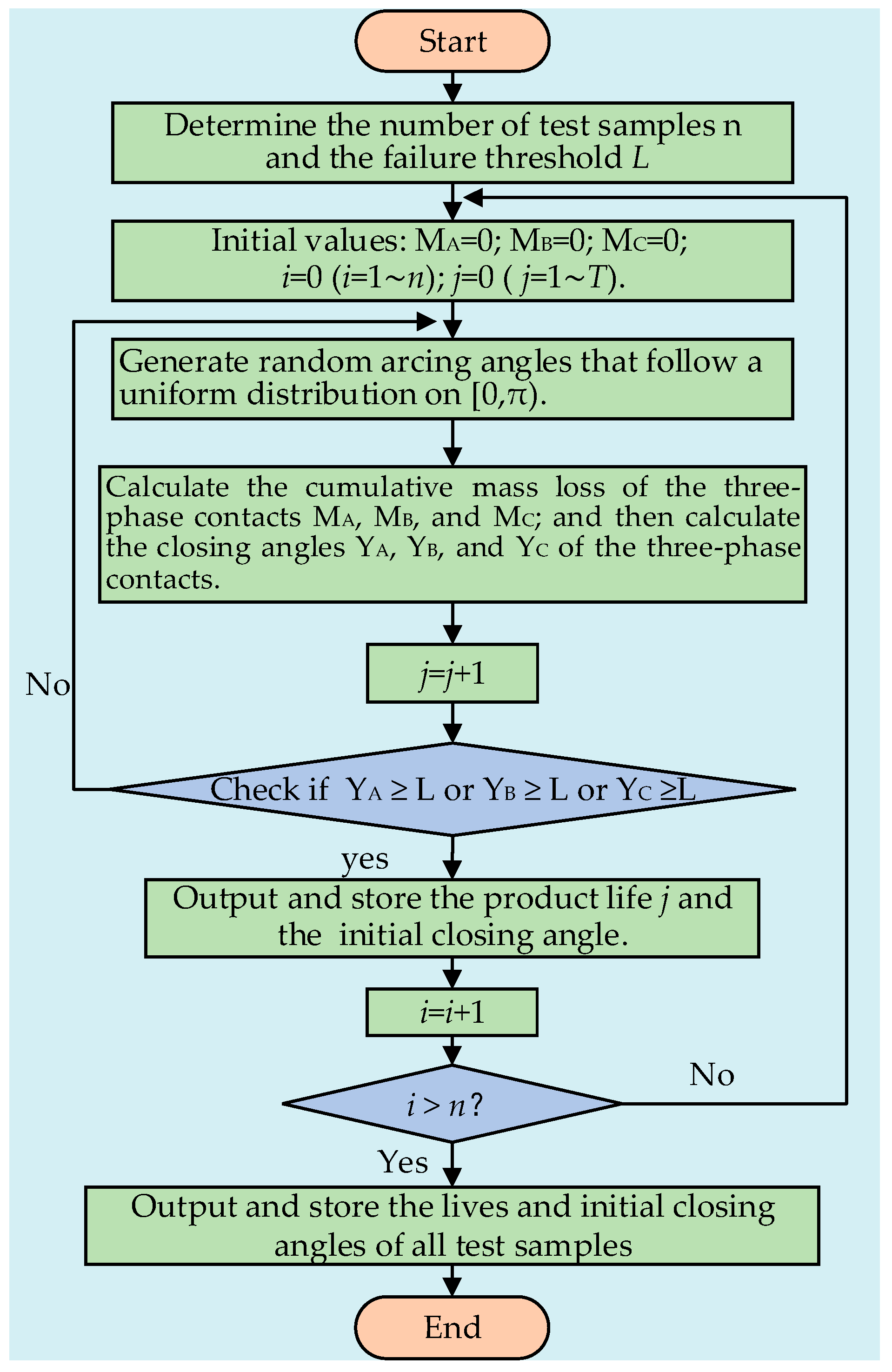
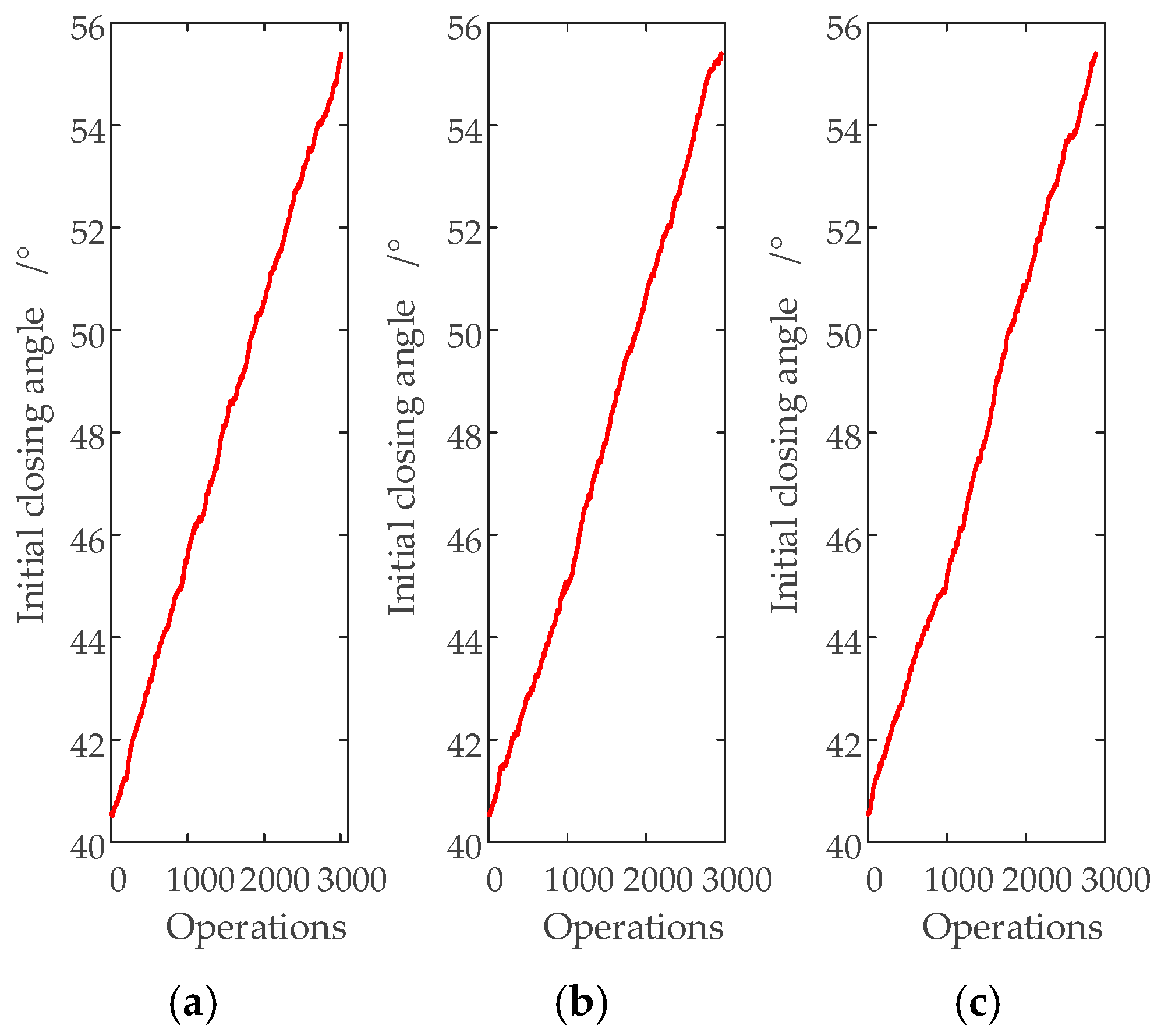
4.1. Monte Carlo Based Electrical Life Simulation
4.2. Normal Distribution Test
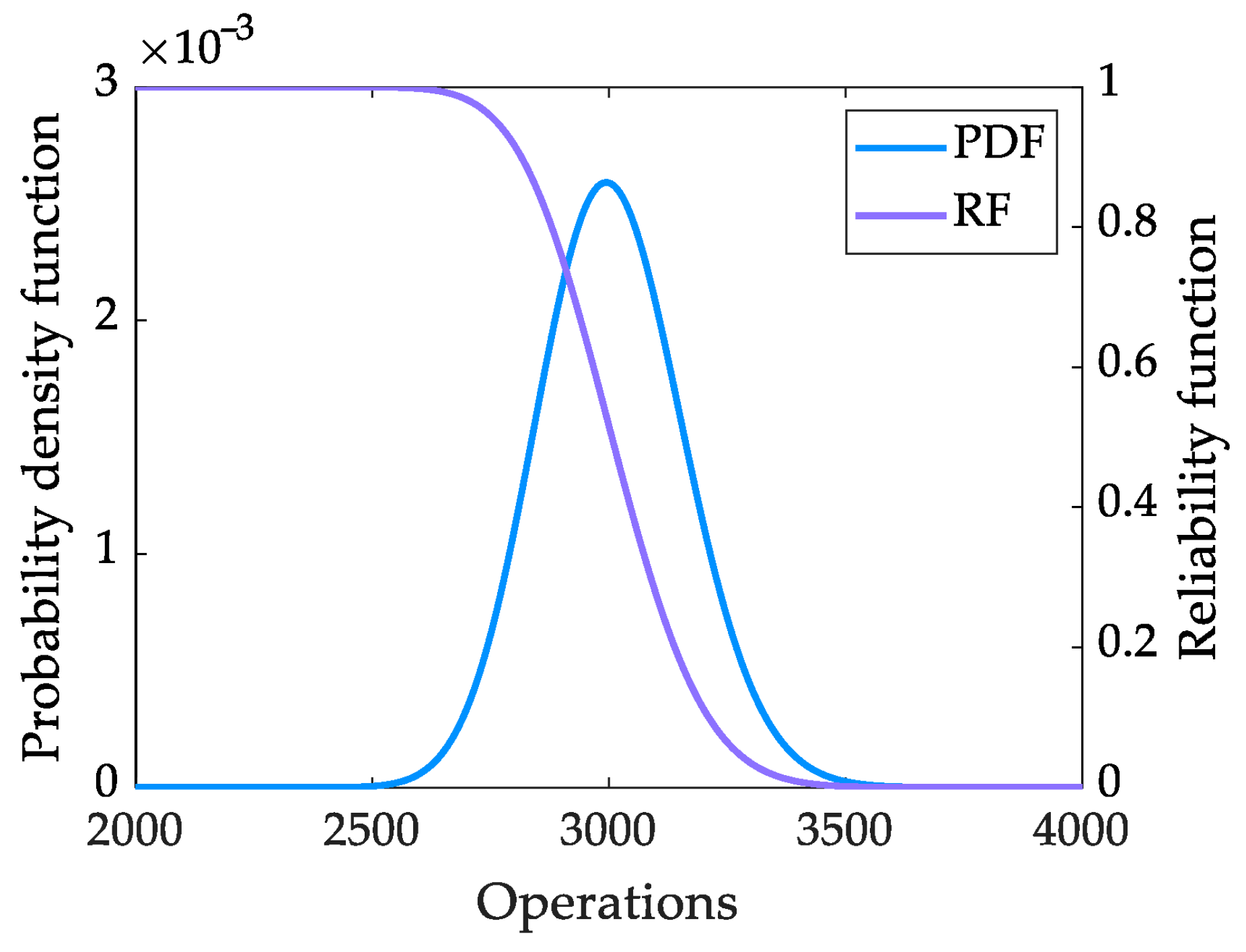
4.3. Residual Electrical Life Prediction Based on Simulation Data
5. Experimental Result Analysis
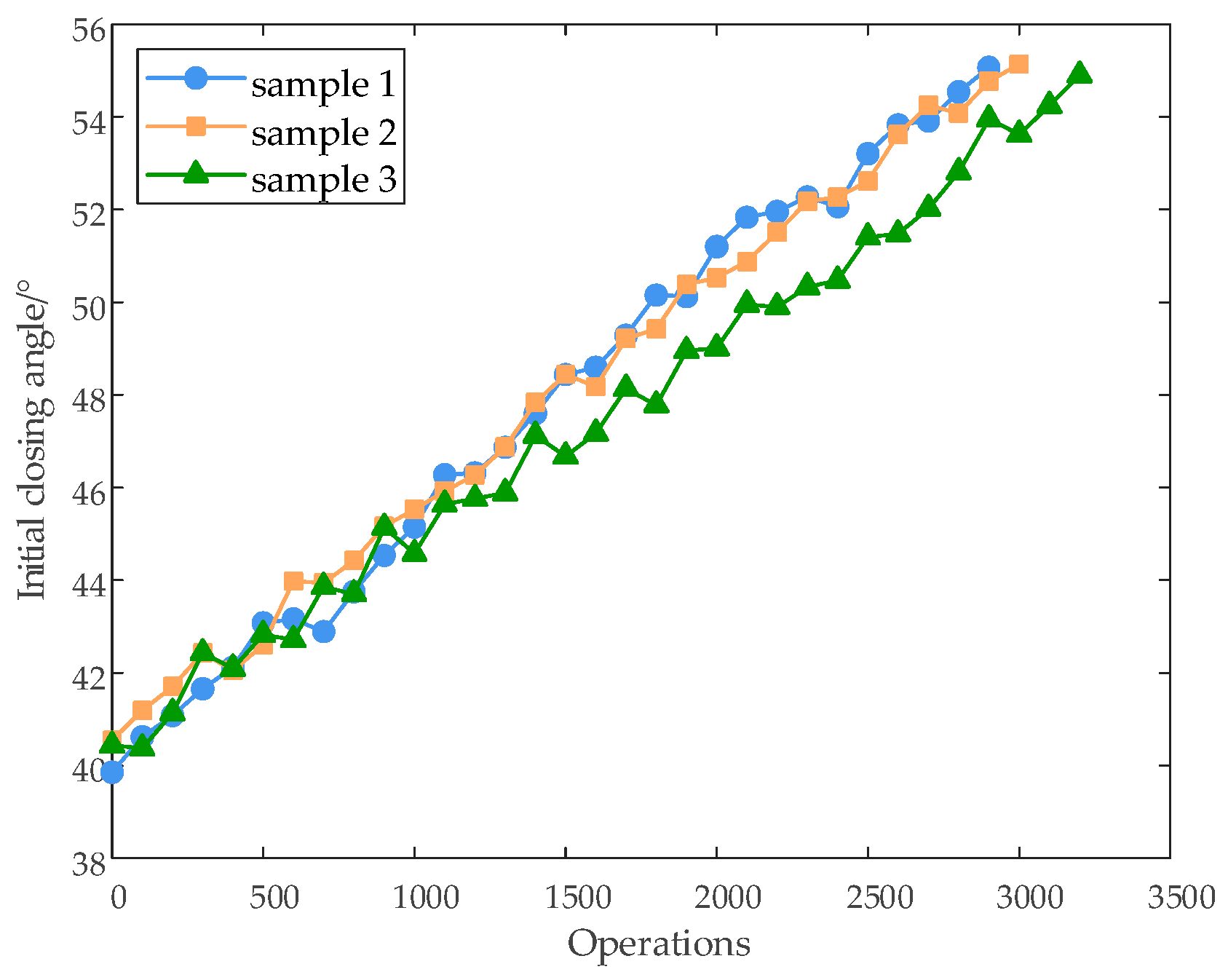
5.1. Experimental Data Analysis
5.2. Normal Distribution Test
5.3. Experimental Data Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheng, S.; Liu, J.; Wu, X.; Yu, T.; Xiang, C.; Yuan, D. Residual life prediction of metallized film capacitors based on feature extraction and error compensation. Chin. J. Electr. Eng. 2022, 42, 2672–2681. [Google Scholar]
- You, Y.; Wang, J.; Shu, L.; Ni, K.; Zhou, X. An electrical life prediction method for AC contactors based on audio features. J. Electrotechnol. 2021, 36, 1986–1998. [Google Scholar]
- Sun, S.; Wang, Z.; Wang, J.; Yang, F.; Ji, W. Remaining useful life prediction for circuit breaker based on SM-CFE and SA-BiLSTM. IEEE Trans. Instrum. Meas. 2023, 72, 1–14. [Google Scholar]
- Su, X.; Wang, L.; Zhang, Z.; Wang, D. Residual Life Prediction of Low-Voltage Circuit Breaker Thermal Trip Based on the Wiener Process. Energies 2024, 17, 1189. [Google Scholar] [CrossRef]
- Kong, W.; Shi, J.; Du, G.; Yuan, C.; Zhang, X. Research on Life Prediction Method of Earth Leakage Circuit Breaker Based on Statistical Test. J. Electr. Eng. 2024, 19, 382–390. [Google Scholar]
- Liu, G.; Miao, J.; Zhao, X.; Wang, Z.; Li, X. Life prediction of residual current circuit breaker with overcurrent protection based on BP neural network optimized by genetic algorithm. J. Electr. Eng. Technol. 2022, 17, 2003–2014. [Google Scholar]
- Razi-Kazemi, A.A.; Niayesh, K.; Nilchi, R. A probabilistic model-aided failure prediction approach for spring-type operating mechanism of high-voltage circuit breakers. IEEE Trans. Power Deliv. 2018, 34, 1280–1290. [Google Scholar]
- Li, K.; Ma, D.; Zhao, C.; Hu, B.; Wang, H. Prediction of the remaining electrical life of AC contactors based on Bayesian inference. J. Instrum. Meas. 2024, 45, 34–45. [Google Scholar]
- Chen, K.; Wang, F.; Li, H.; Gao, H.; Xia, Y.; Liu, Y. Remaining Life Prediction of High-Voltage Circuit Breakers Based on Optimized Particle Swarm-Bidirectional Long Short-Term Memory Neural Network. In Proceedings of the 2024 7th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Xiamen, China, 10–13 November 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 697–701. [Google Scholar]
- Huang, K.; Zhao, S. Evaluation of residual service life of high voltage circuit breaker. In Proceedings of the 2012 China International Conference on Electricity Distribution, Shanghai, China, 10–14 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–4. [Google Scholar]
- Lu, C.; Wang, C.; Xie, J. Online estimation of residual electrical lifetime for PV low voltage circuit breaker based grey algorithm. In Proceedings of the 2023 IEEE 3rd International Conference on Power, Electronics and Computer Applications (ICPECA), Shenyang, China, 29–31 January 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1216–1220. [Google Scholar]
- Yang, J.; Chi, C. The Prediction of Residual Electrical Life in Alternating Current Circuit Breakers Based on Savitzky-Golay-Long Short-Term. Sensors 2023, 23, 6860. [Google Scholar]
- Wu, T.; Yao, Y.; Li, Z.; Chen, B.; Wu, Y.; Sun, W. Remaining useful life prediction of circuit breaker operating mechanisms based on wavelet-enhanced dual-tree residual networks. J. Power Electron. 2024, 24, 78–91. [Google Scholar]
- Ma, H.; Zhou, S.; Gao, C.; Zhou, F.; Yang, Y.; Yang, H. Research on the Reliability Test and Life Assessment Methods of Relays Used in Circuit Breaker Operating Mechanism. Energies 2023, 16, 4843. [Google Scholar] [CrossRef]
- Cao, P.; Li, J.; Han, Y.; Shi, S.; Wang, Q.; Peng, Z.; Zhou, G. Mechanical remaining Life Prediction of Circuit Breaker based on long-term and short-term memory Neural Network. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 2734–2738. [Google Scholar]
- Zhao, X.; Wu, G.; Yang, D.; Xu, G.; Xing, Y.; Yao, C.; Abu-Siada, A. Enhanced detection of power transformer winding faults through 3D FRA signatures and image processing techniques. Electr. Power Syst. Res. 2025, 242, 111433. [Google Scholar] [CrossRef]
- Su, X.; Zhang, Z.; Wei, J. Remaining Useful Life Prediction of Electromagnetic Release Based on Whale Optimization Algorithm—Particle Filtering. Energies 2024, 17, 670. [Google Scholar] [CrossRef]
- Aizpurua, J.I.; Catterson, V.M.; Abdulhadi, I.F.; del Carmen Segovia García, M. A model-based hybrid approach for circuit breaker prognostics encompassing dynamic reliability and uncertainty. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 1637–1648. [Google Scholar]
- Liu, G.; Wang, L.; Yang, Y.; Liu, D.; Miao, J. Life prediction of residual current circuit breaker with overcurrent protection based on Tweedie exponential dispersion process with random effects. Electr. Eng. 2024, 107, 7027–7039. [Google Scholar]
- Zhao, S.; Yan, X.; Wang, B.; Wang, E.; Ma, L. Research on reliability evaluation method of DC circuit breaker based on Markov model. Electr. Power Syst. Res. 2019, 173, 1–5. [Google Scholar]
- Li, K.; Zhao, C.; Niu, F.; Zheng, S.; Duan, Y.; Huang, S.; Wu, Y. Electrical performance degradation model and residual electrical life prediction for AC contactor. IEEE Trans. Compon. Packag. Manuf. Technol. 2020, 10, 400–417. [Google Scholar]
- Khoddam, M.; Sadeh, J.; Pourmohamadiyan, P. Performance evaluation of circuit breaker electrical contact based on dynamic resistance signature and using health index. IEEE Trans. Compon. Packag. Manuf. Technol. 2016, 6, 1505–1512. [Google Scholar]








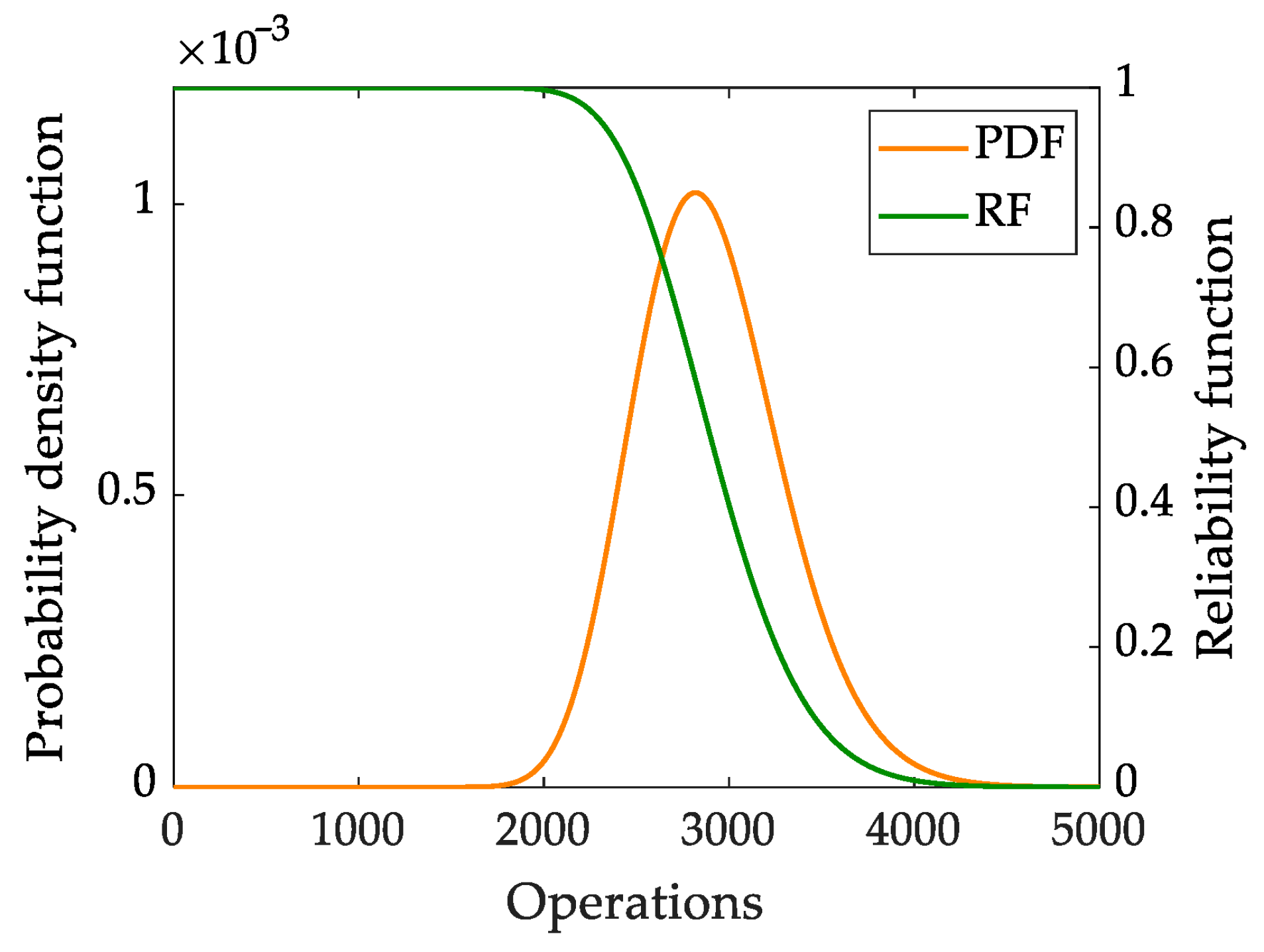
| Case | MCB 1 | MCB 2 | MCB 3 |
|---|---|---|---|
| Test statistic | 0.0614 | 0.0757 | 0.0645 |
| Threshold value | 0.27 | 0.24 | 0.23 |
| Obedience test | obey | Obey | obey |
| Parameters | µ1 Estimated Value | σ1 Estimated Value |
|---|---|---|
| MCB 1 | 0.005 | 0.0138 |
| MCB 2 | 0.0049 | 0.0138 |
| MCB 3 | 0.0048 | 0.0138 |
| Average value | 0.0049 | 0.0138 |
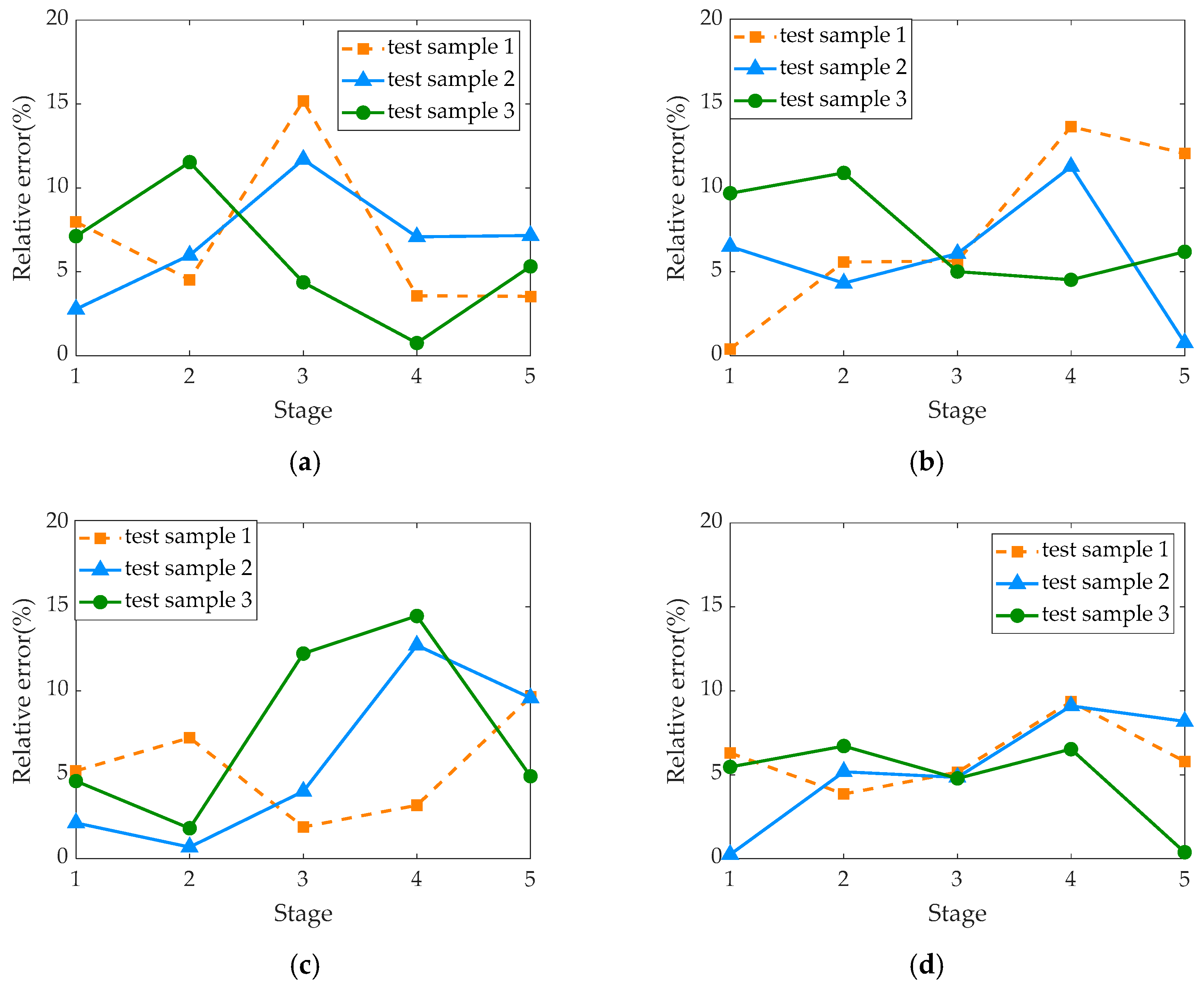
| Stage | Actual Residual Electric Life | Prediction of Remaining Electrical Life | Relative Error |
|---|---|---|---|
| 1–500 | 2509 | 2465 | 3.80% |
| 501–1000 | 2009 | 1965 | 1.29% |
| 1001–1500 | 1509 | 1429 | 3.68% |
| 1501–2000 | 1009 | 957 | 1.76% |
| 2001–2500 | 509 | 497 | 2.36% |
| Experimental Parameters | Numerical Value |
|---|---|
| Rated current Ie/A | 63 |
| Rated voltage Ue/V | 380 |
| Operating frequency/(times/h) | 120 |
| Coil voltage/V | 380 |
| Test current I/A | 63 |
| Test voltage U/V | 380 |
| Power supply frequency/Hz | 50 |
| Power factor | 0.65 |
| Movable contact material | AgNi(10) |
| Movable contact size/(mm3) | 3.8 × 2 × 1.1(R) |
| Static contact material | AgCdO(15) |
| Static contact size/(mm3) | 4 × 4 × 1 |
| Case | Test Statistic | Threshold Value | Obedience Test |
|---|---|---|---|
| MCB 1 | 0.1245 | 0.24 | obey |
| MCB 2 | 0.1279 | 0.24 | obey |
| MCB 3 | 0.1165 | 0.24 | obey |
| Parameters | µ1 Estimated Value | σ1 Estimated Value |
|---|---|---|
| MCB 1 | 0.0052 | 0.0389 |
| MCB 2 | 0.0049 | 0.0398 |
| MCB 3 | 0.0045 | 0.0437 |
| Average value | 0.0049 | 0.0408 |
| Stage | Actual Residual Electric Life | Prediction of Remaining Electrical Life | Relative Error |
|---|---|---|---|
| 1–500 | 2397 | 2206 | 7.97% |
| 501–1000 | 1897 | 1811 | 4.53% |
| 1001–1500 | 1397 | 1344 | 3.79% |
| 1501–2000 | 897 | 865 | 3.57% |
| 2001–2500 | 397 | 383 | 3.53% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Hou, L.; He, P.; Wang, C.; Xie, Z.; Wang, Y. Prediction of Remaining Service Life of Miniature Circuit Breakers Based on Wiener Process. Energies 2025, 18, 3639. https://doi.org/10.3390/en18143639
Ma L, Hou L, He P, Wang C, Xie Z, Wang Y. Prediction of Remaining Service Life of Miniature Circuit Breakers Based on Wiener Process. Energies. 2025; 18(14):3639. https://doi.org/10.3390/en18143639
Chicago/Turabian StyleMa, Lin, Linming Hou, Puquan He, Changxian Wang, Zhenhua Xie, and Yao Wang. 2025. "Prediction of Remaining Service Life of Miniature Circuit Breakers Based on Wiener Process" Energies 18, no. 14: 3639. https://doi.org/10.3390/en18143639
APA StyleMa, L., Hou, L., He, P., Wang, C., Xie, Z., & Wang, Y. (2025). Prediction of Remaining Service Life of Miniature Circuit Breakers Based on Wiener Process. Energies, 18(14), 3639. https://doi.org/10.3390/en18143639







