An Analytical Method to the Economics of Pumped Storage Power Plants Based on the Real Options Method
Abstract
1. Introduction
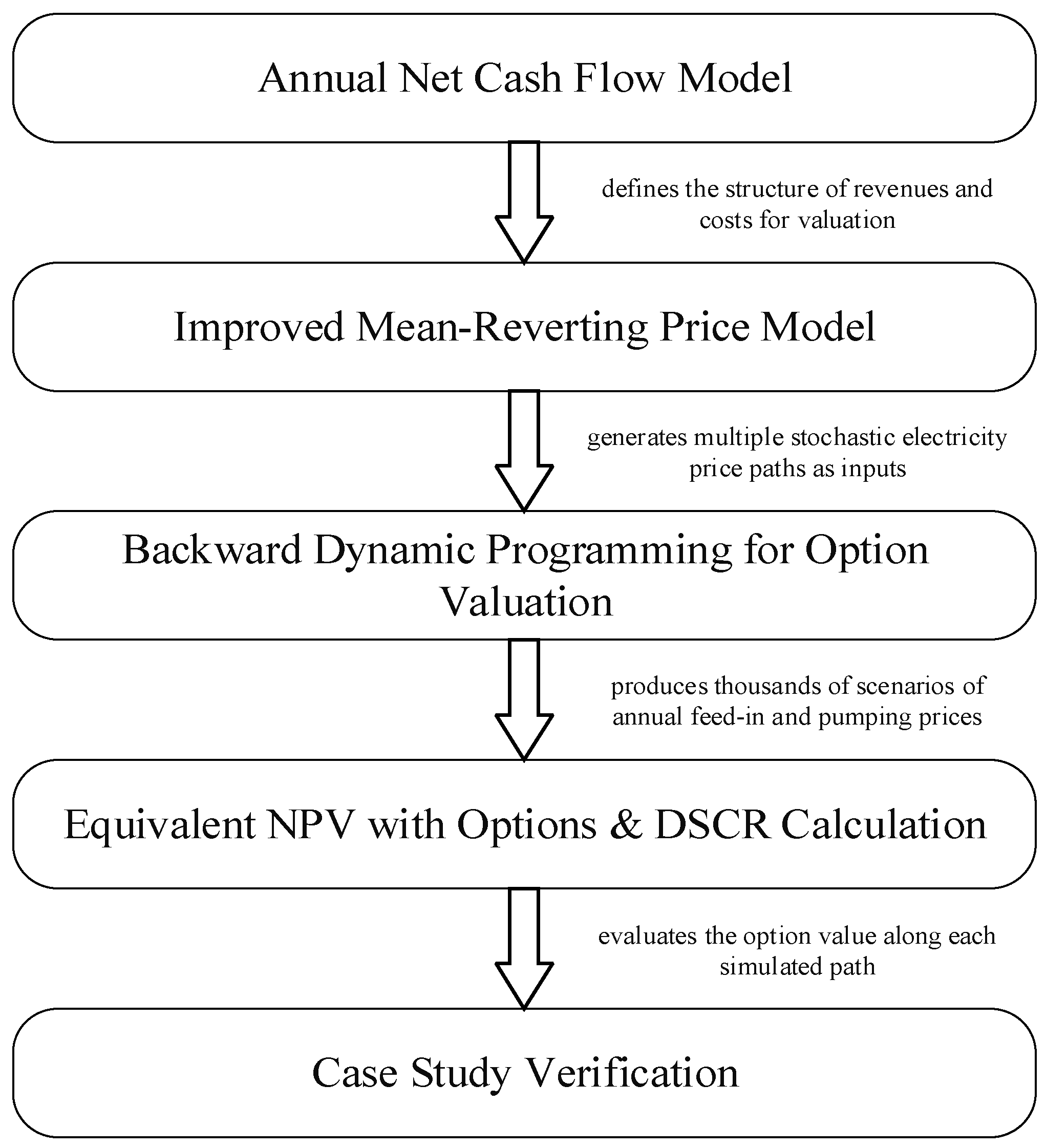
2. Economy Modeling Based on Real Options
2.1. Improved Mean-Reverting Electricity Price Model
2.2. Annual Net Cash Flow Model
2.2.1. Annual Pumping and Generation
2.2.2. Annual Revenues and Expenditures
2.3. Real Options Pricing Model
2.4. NPV and IRR Calculation
3. Case Analysis
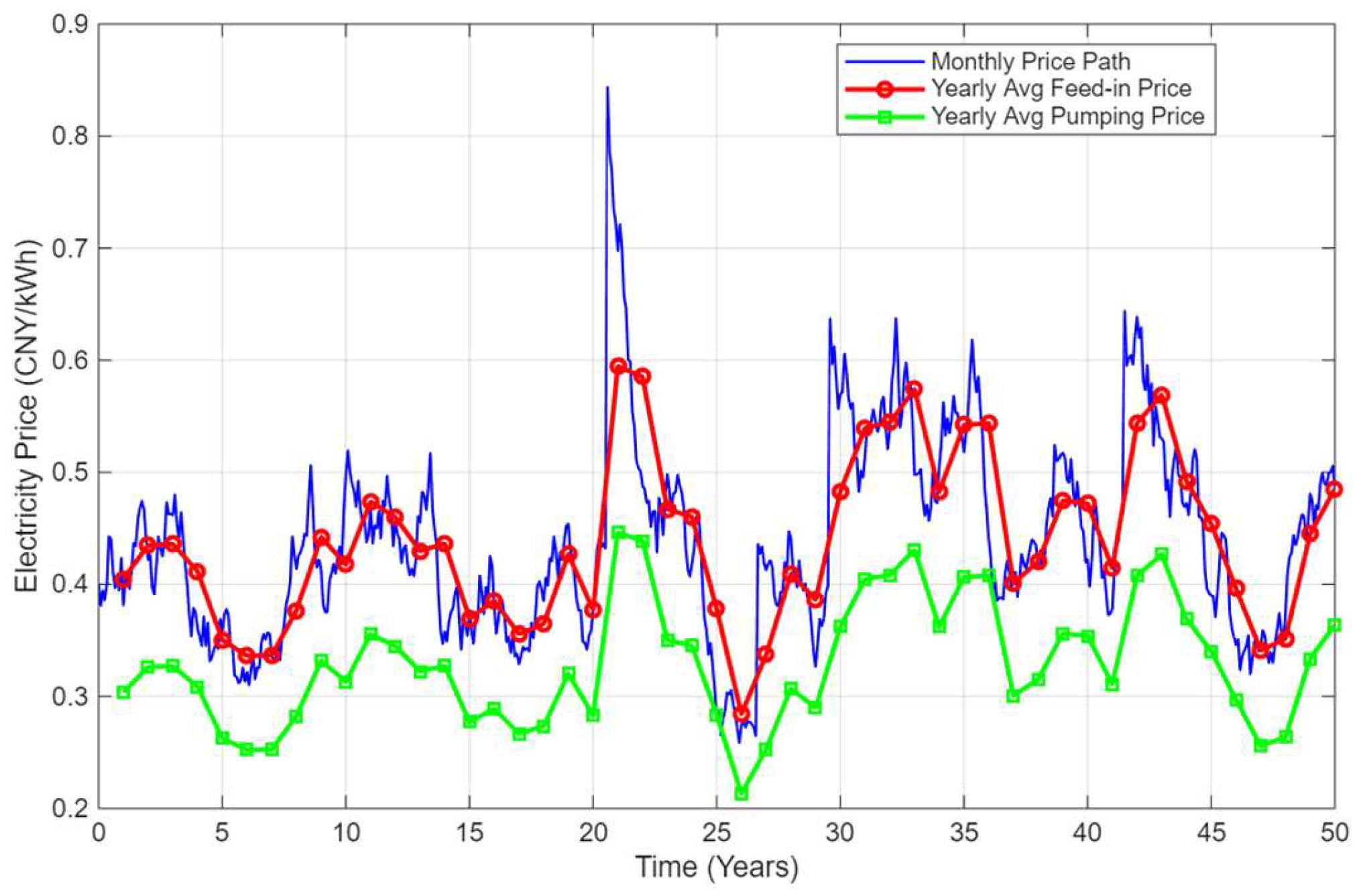
3.1. Typical Electricity Price Simulation Path
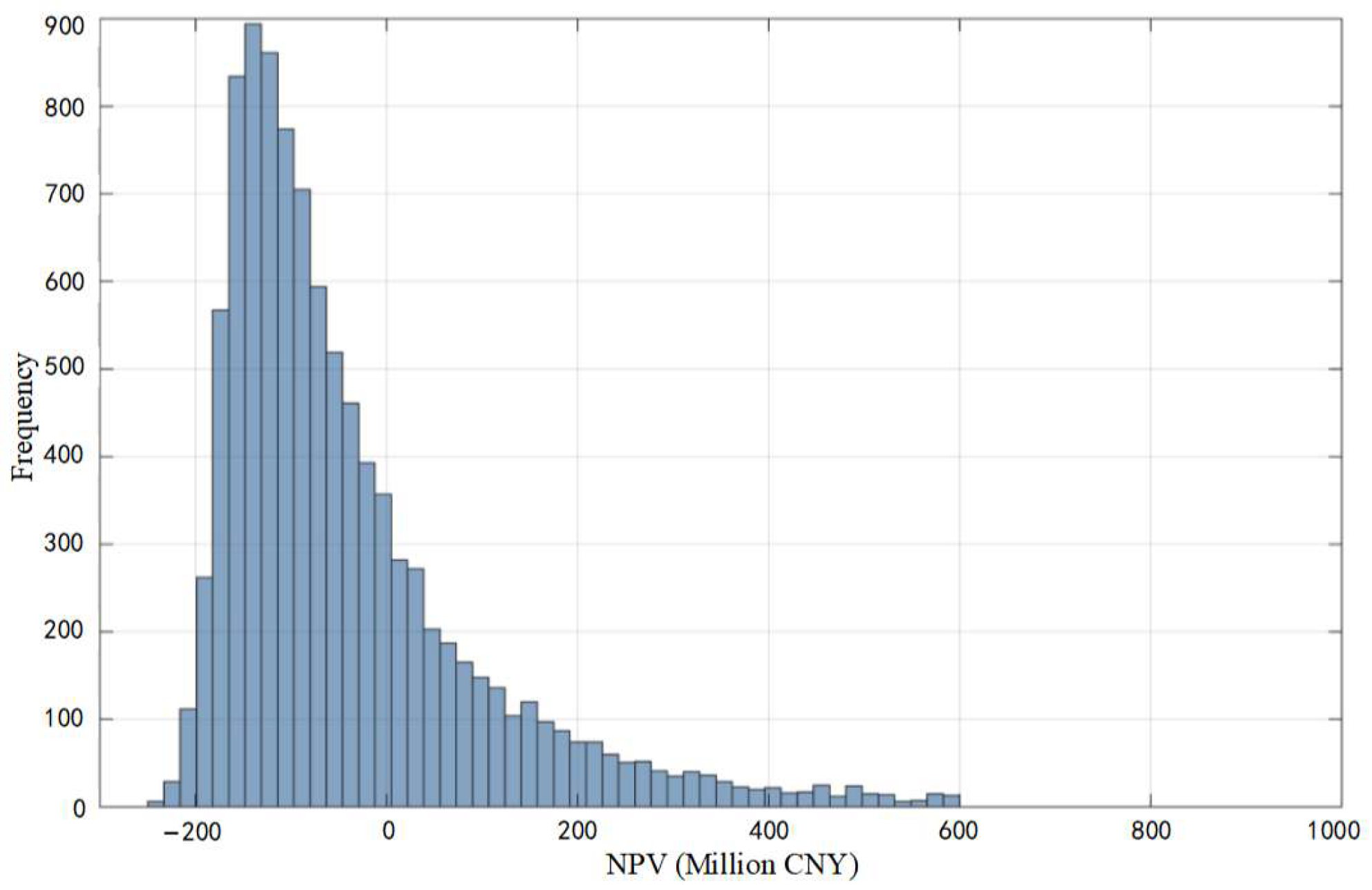
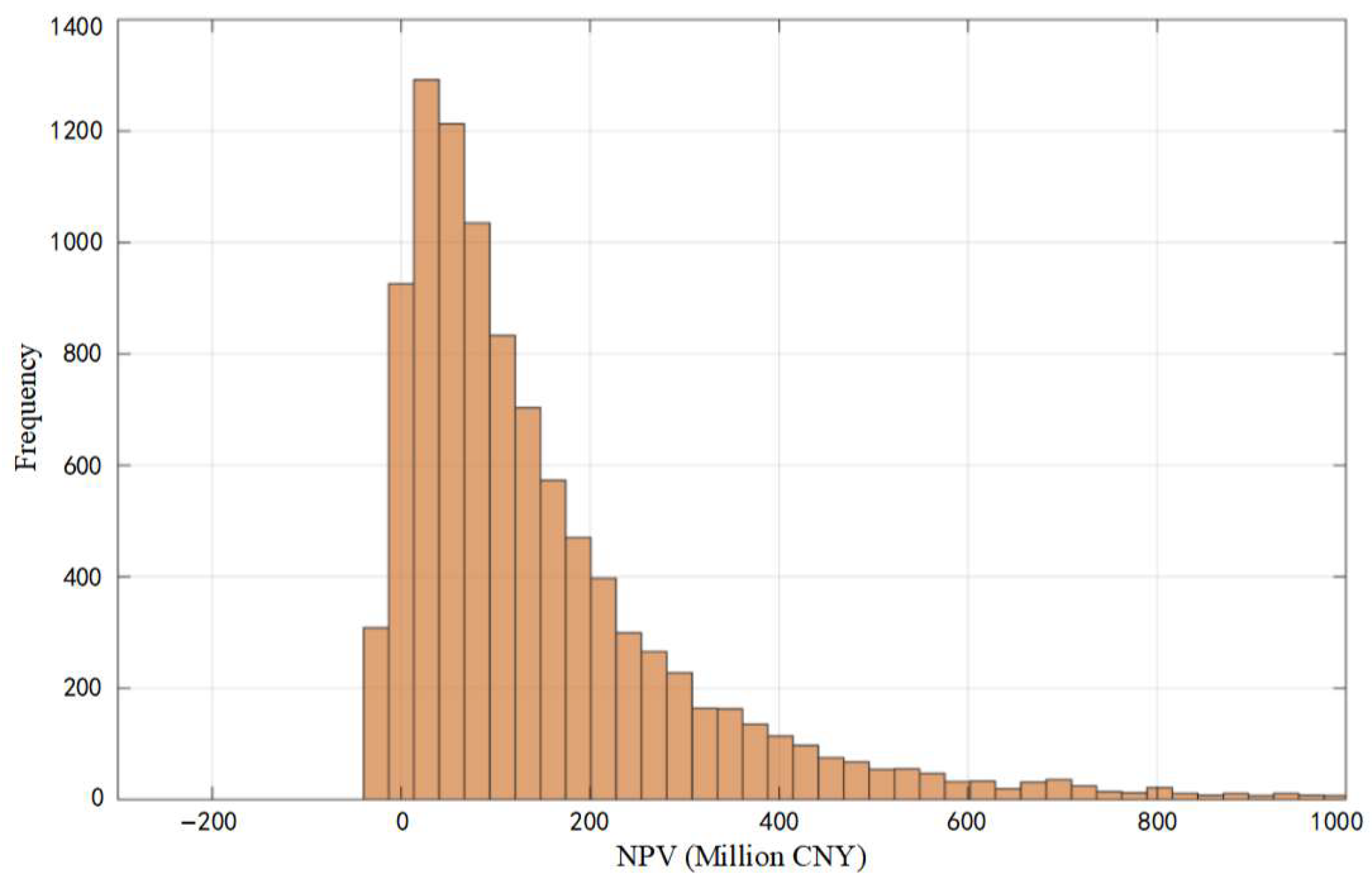
3.2. Analysis of Model Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Castagneto Gissey, G.; Subkhankulova, D.; Dodds, P.E.; Barrett, M. Value of energy storage aggregation to the electricity system. Energy Policy 2019, 128, 685–696. [Google Scholar] [CrossRef]
- Masoumzadeh, A.; Nekouei, E.; Alpcan, T.; Chattopadhyay, D. Impact of Optimal Storage Allocation on Price Volatility in Energy-Only Electricity Markets. IEEE Trans. Power Syst. 2018, 33, 1903–1914. [Google Scholar] [CrossRef]
- IHA Water Batteries for the Renewable Energy Sector. Available online: https://www.hydropower.org/factsheets/pumped-storage (accessed on 3 September 2025).
- Li, Y.; Yang, W.; Zhao, Z.; Huang, Y.; Liao, Y.; Yang, J. Ancillary service quantitative evaluation for primary frequency regulation of pumped storage units considering refined hydraulic characteristics. J. Energy Storage 2022, 45, 103414. [Google Scholar] [CrossRef]
- Tian, B.; He, Y.; Zhou, J.; Wang, B.; Wang, Y.; Shi, W. Cost-sharing mechanisms for pumped storage plants at different market stages in China. Renew. Energy 2023, 217, 119183. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, T.; Sun, L.; Zhao, X.; Tong, L.; Wang, L.; Ding, J.; Ding, Y. Energy storage for black start services: A review. Int. J. Miner. Metall. Mater. 2022, 29, 691–704. [Google Scholar] [CrossRef]
- Kong, Y.; Kong, Z.; Liu, Z.; Wei, C.; Zhang, J.; An, G. Pumped storage power stations in China: The past, the present, and the future. Renew. Sustain. Energy Rev. 2017, 71, 720–731. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, Y.; Lu, Q.; Liu, D.; Xie, P.; Wang, M.; Yu, Z.; Liu, Y. Comprehensive Evaluation of a Pumped Storage Operation Effect Considering Multidimensional Benefits of a New Power System. Energies 2024, 17, 4449. [Google Scholar] [CrossRef]
- Tang, H.; Li, R.; Song, T.; Ju, S. Short-term optimal scheduling and comprehensive assessment of hydro-photovoltaic-wind systems augmented with hybrid pumped storage hydropower plants and diversified energy storage configurations. Appl. Energy 2025, 389, 125787. [Google Scholar] [CrossRef]
- Xie, Z.; Wang, Y.; Chang, J.; Guo, A.; Niu, C.; Zheng, Y.; Tian, Z. Optimal scheduling and benefit sharing of hybrid pumped storage hydropower plants with multiple operators. Energy 2025, 333, 137242. [Google Scholar] [CrossRef]
- Ruppert, L.; Schürhuber, R.; List, B.; Lechner, A.; Bauer, C. An analysis of different pumped storage schemes from a technological and economic perspective. Energy 2017, 141, 368–379. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, L.; Wang, Q.; Zhou, D. Valuing investment decisions of renewable energy projects considering changing volatility. Energy Econ. 2020, 92, 104954. [Google Scholar] [CrossRef]
- Shimbar, A.; Ebrahimi, S.B. Political risk and valuation of renewable energy investments in developing countries. Renew. Energy 2020, 145, 1325–1333. [Google Scholar] [CrossRef]
- Liu, Y.; He, Y.; Li, M.; Zhang, Y. Design of Price Market Linkage Mechanism and Economic Benefit Evaluation of Pumped Storage Power Station Under the Power Market Environment. Mod. Electr. Power 2023, 40, 42–49. [Google Scholar] [CrossRef]
- Li, H.; Li, X. Research on High Quality Development of Pumped Storage Stations under New Power System. J. N. China Electr. Power Univ. (Soc. Sci.) 2024, 5, 51–59. [Google Scholar]
- Wei, Z. Research on Market-based Transaction Model of Pumped Storage Power Stations in Shandong Province. Sino Glob. Energy 2025, 30, 7. [Google Scholar]
- Isaza Cuervo, F.; Arredondo-Orozco, C.A.; Marenco-Maldonado, G.C. Photovoltaic power purchase agreement valuation under real options approach. Renew. Energy Focus 2021, 36, 96–107. [Google Scholar] [CrossRef]
- Delapedra-Silva, V.; Ferreira, P.; Cunha, J.; Kimura, H. Methods for Financial Assessment of Renewable Energy Projects: A Review. Processes 2022, 10, 184. [Google Scholar] [CrossRef]
- Bangjun, W.; Feng, Z.; Feng, J.; Yu, P.; Cui, L. Decision making on investments in photovoltaic power generation projects based on renewable portfolio standard: Perspective of real option. Renew. Energy 2022, 189, 1033–1045. [Google Scholar] [CrossRef]
- Yang, X.; Yang, F. Investment Decision of Energy Storage in Wind Power Generation Based on Real Options. Mod. Electr. Power 2021, 38, 442–448. [Google Scholar] [CrossRef]
- Shi, X.; Wang, L.; Mo, Y. Research on Investment Decision of Hydropower Project Based on Fuzzy Real Option. Yellow River 2023, 45, 141–145. [Google Scholar]
- Hu, J.; Chen, H. Flexible Investment Decision of Waste-to-energy Projects under Carbon Trading Mechanism. Chin. J. Manag. Sci. 2025, 33, 320–331. [Google Scholar]
- Opinions on Further Improving the Pricing Mechanism for Pumped Storage Energy. Available online: https://www.gov.cn/zhengce/zhengceku/2021-05/08/content_5605367.htm (accessed on 1 September 2025).
| Parameters | Symbol | Data |
|---|---|---|
| Total Installed Capacity | C | 1000 MW |
| Annual operating hours for power generation | 1365 h | |
| Annual pumping operation hours | 1665 h | |
| Generator set operational efficiency | 70% | |
| Pump unit operational efficiency | 68% | |
| Initial year average grid-connected electricity price | 0.3949 CNY/kWh | |
| Initial year average pumping electricity purchase price | 0.2962 CNY/kWh | |
| Capacity charge | 347.99 CNY/kW·Year | |
| Annual fixed operation and maintenance fee | 36 million CNY | |
| Annual unit generation operation and maintenance fee | 0.04 CNY/kWh | |
| Initial investment amount | 4326 million CNY | |
| Residual value | 433 million CNY | |
| Power plant lifespan | T | 50 Years |
| Tax rate | 10% | |
| Mean reversion speed | 0.6 | |
| Annual electricity price volatility | σ | 0.15 |
| Mean jump magnitude | μJ | 0.2 |
| Jump magnitude volatility | σJ | 0.3 |
| Discount rate | r | 6.5% |
| Indicator | Data |
|---|---|
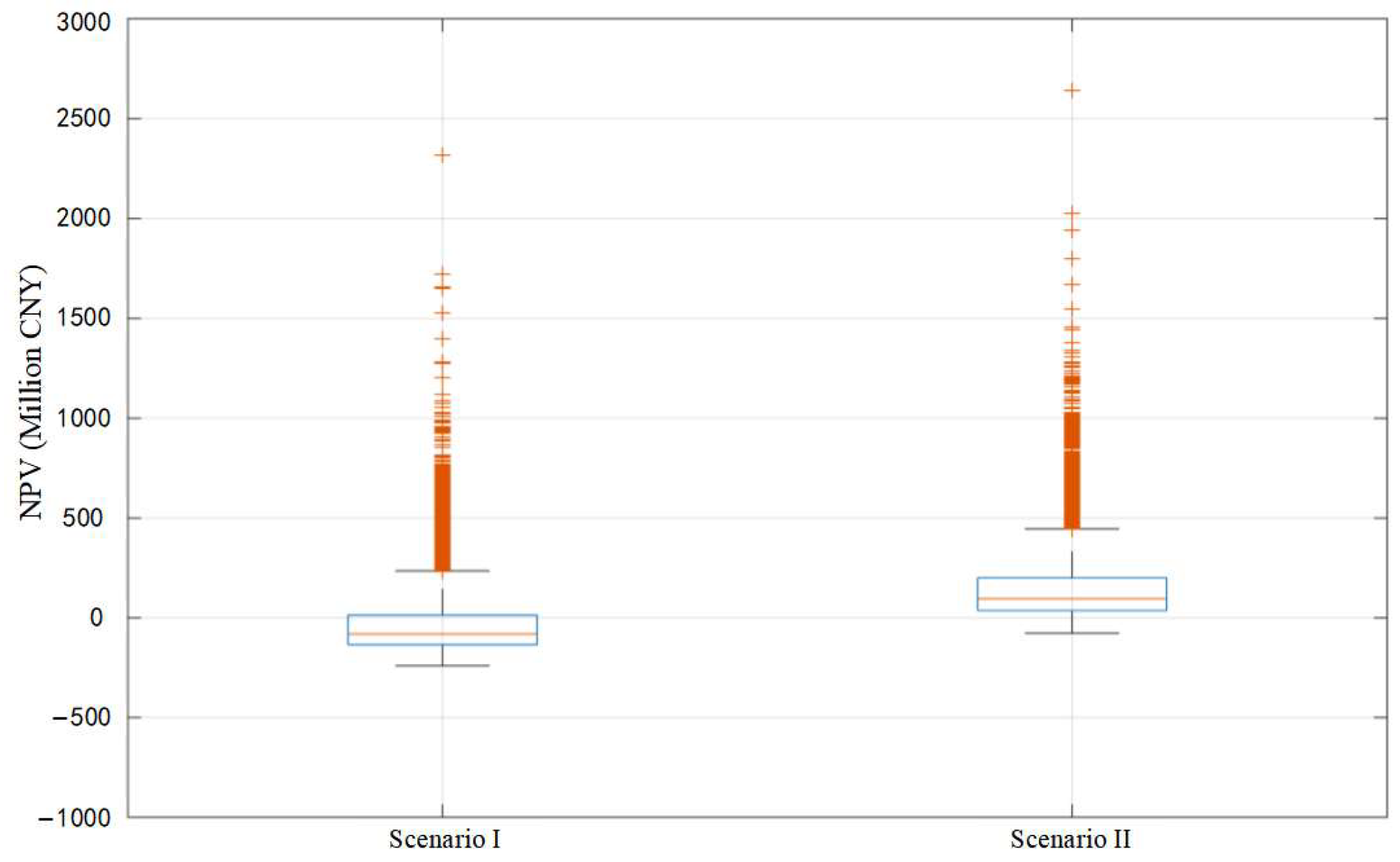
| Average NPV of scenario I | −38.35 Millon CNY |
| Average NPV of scenario II | 143.15 Millon CNY |
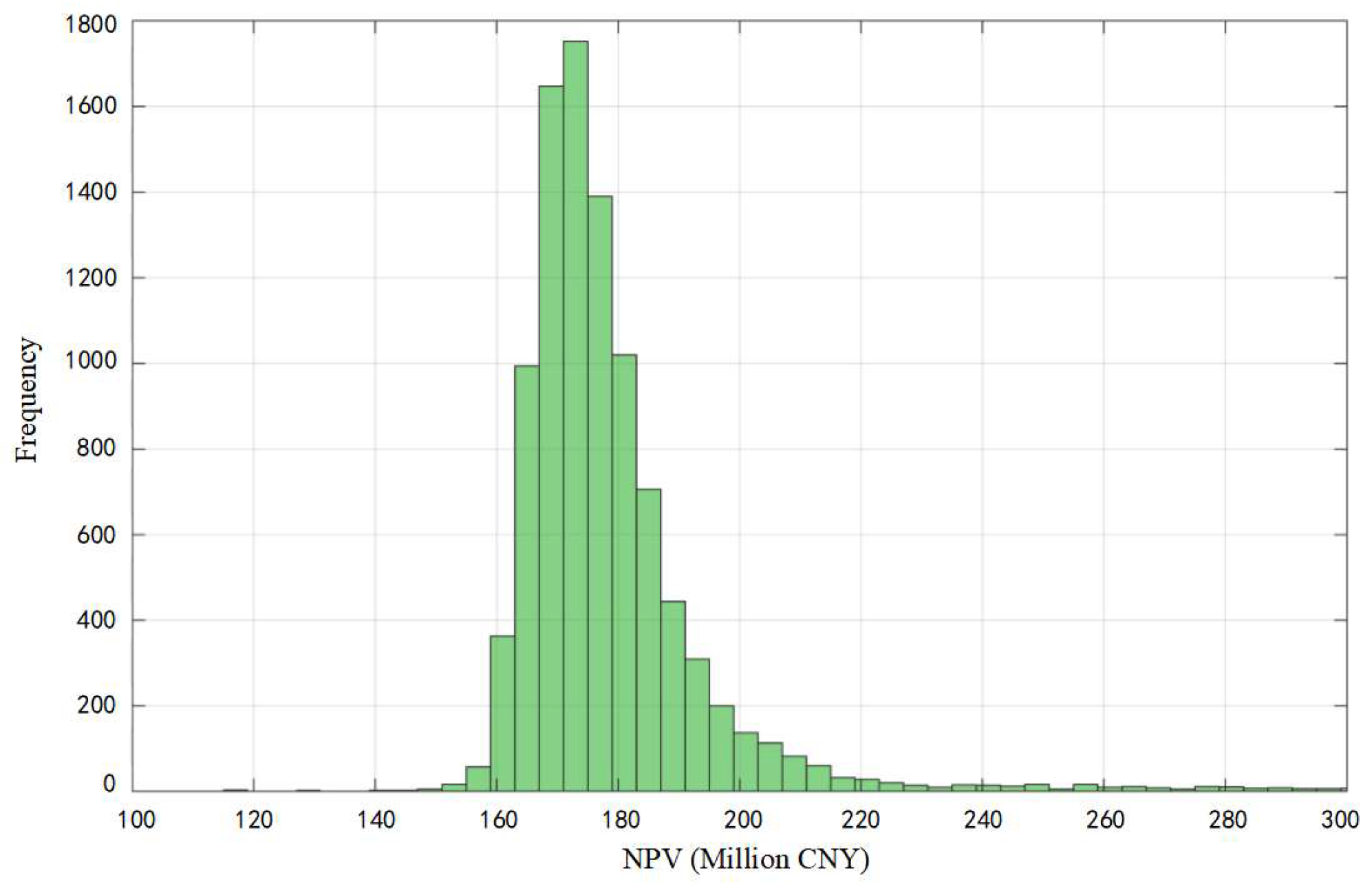
| Average real option value | 181.50 Millon CNY |
| Average IRR of scenario I | 6.10% |
| Average IRR of scenario II | 6.44% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Fan, J.; Le, J.; Zhang, G.; Chen, L.; Deng, L. An Analytical Method to the Economics of Pumped Storage Power Plants Based on the Real Options Method. Energies 2025, 18, 5291. https://doi.org/10.3390/en18195291
Wang W, Fan J, Le J, Zhang G, Chen L, Deng L. An Analytical Method to the Economics of Pumped Storage Power Plants Based on the Real Options Method. Energies. 2025; 18(19):5291. https://doi.org/10.3390/en18195291
Chicago/Turabian StyleWang, Weihao, Jianbin Fan, Jian Le, Gong Zhang, Longxiang Chen, and Lei Deng. 2025. "An Analytical Method to the Economics of Pumped Storage Power Plants Based on the Real Options Method" Energies 18, no. 19: 5291. https://doi.org/10.3390/en18195291
APA StyleWang, W., Fan, J., Le, J., Zhang, G., Chen, L., & Deng, L. (2025). An Analytical Method to the Economics of Pumped Storage Power Plants Based on the Real Options Method. Energies, 18(19), 5291. https://doi.org/10.3390/en18195291






