Flexible Reconfiguration for Optimal Operation of Distribution Network Under Renewable Generation and Load Uncertainty
Abstract
1. Introduction
- (1)
- Considering the effect of DR on the optimal operation of the distribution network.
- (2)
- Considering the hourly variations and stochastic characteristics of renewable generation (wind and solar) and load.
- (3)
- Improving the operating cost function of the distribution network by utilizing voltage deviation, renewable generation, and switching costs.
- (4)
- Using the coati optimization algorithm (COA) to solve the DR problem for optimal operation of the distribution network.
2. Proposed Approach
2.1. Scenario-Based Uncertainty Representation
2.1.1. Probabilistic Wind Power Modeling
2.1.2. Probabilistic Solar Power Modeling
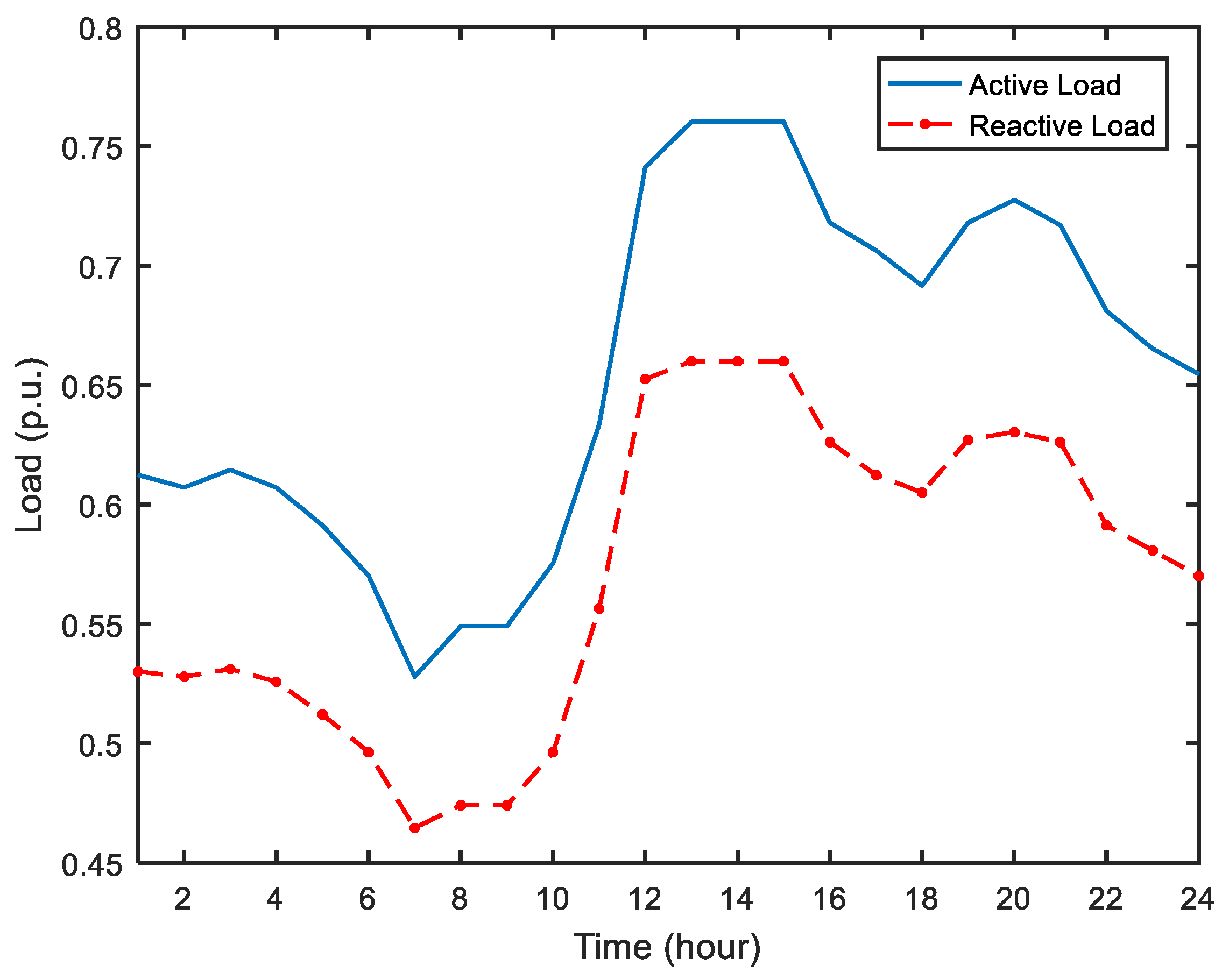
2.1.3. Probabilistic Load Modeling
2.2. Objective Function
2.3. Constraints
2.3.1. Power Balances
2.3.2. Bus Voltage
2.3.3. Distribution Feeder VA Constraint
2.3.4. Output Power of DGs
2.3.5. Radial Structure of the Distribution Network
2.3.6. Number of Switching
3. Solution Methodology
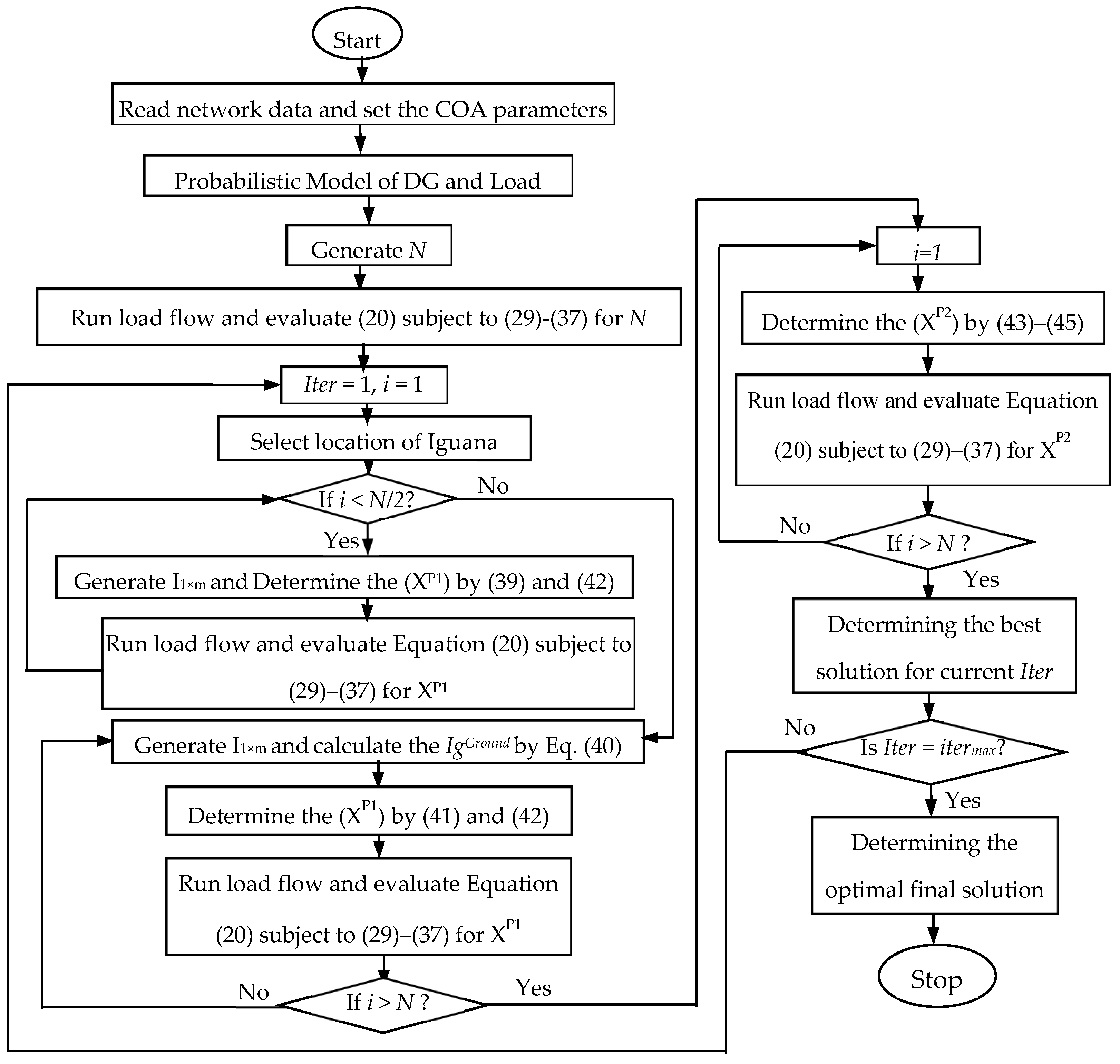
3.1. Coati Optimization Algorithm (COA)
3.1.1. Initialization
3.1.2. Hunting Strategy for Iguanas (Position Updating Phase 1)
3.1.3. Escape Strategy from Predators (Position Updating Phase 2)
3.1.4. Repetition Process of COA
3.2. Implementation of the COA for DR
4. Case Study and Discussion
4.1. Case Study Network Overview (IEEE 33-Bus)
4.2. Discussion (IEEE 33-Bus)
4.2.1. Comparison Test of COA with PSO
4.2.2. Reliability Analysis
4.3. Case Study Network Overview (TPC 83-Bus)
4.4. Discussion (TPC 83-Bus)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| COA | Coati Optimization algorithm |
| DN | Distribution Network |
| DG | Distributed Generation |
| RCSs | Remote-Controlled Switches |
| DR | Dynamic Reconfiguration |
| SR | Static Reconfiguration |
| MFSMA | Multi-group Flight Slime Mold Algorithm |
| FCMC | Fuzzy C-Means Clustering |
| PSO | Particle Swarm Optimization |
| MILP | Mixed-Integer Linear Programming |
| GWO | Grey Wolf Optimizer |
| MISOCP | Mixed-Integer Second-Order Cone Programming |
| IMODBO | Improved Multi-Objective Dung Beetle Optimizer |
References
- Ehsan, A.; Yang, Q. State-of-the-art techniques for modelling of uncertainties in active distribution network planning: A review. Appl. Energy 2019, 239, 1509–1523. [Google Scholar] [CrossRef]
- Golshannavaz, S.; Afsharnia, S.; Aminifar, F. Smart distribution grid: Optimal day-ahead scheduling with reconfigurable topology. IEEE Trans. Smart Grid 2014, 5, 2402–2411. [Google Scholar] [CrossRef]
- Amini, H.; Mehrizi-Sani, A.; Noroozian, R. Passive Islanding Detection of Inverter-Based Resources in a Noisy Environment. Energies 2024, 17, 4405. [Google Scholar] [CrossRef]
- Alqahtani, M.; Marimuthu, P.; Moorthy, V.; Pangedaiah, B.; Reddy, C.R.; Kumar, M.K.; Khalid, M. Investigation and Minimization of Power Loss in Radial Distribution Network Using Gray Wolf Optimization. Energies 2023, 16, 4571. [Google Scholar] [CrossRef]
- Amini, H.; Mehrizi-Sani, A.; Liu, C.C. Substation Cyberattack Detection and Mitigation in a High-Noise Environment. In Proceedings of the IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 19–22 February 2024. [Google Scholar]
- Pan, J.-S.; Wang, H.-J.; Nguyen, T.-T.; Zou, F.-M.; Chu, S.-C. Dynamic reconfiguration of distribution network based on dynamic optimal period division and multi-group flight slime mould algorithm. Electr. Power Syst. Res. 2022, 208, 107925. [Google Scholar] [CrossRef]
- Cao, H.; Gao, C.; Chen, P.; He, X.; Dong, Z.; Lin, L. Distribution Network Dynamic Reconfiguration Based on Improved Fuzzy C-Means Clustering with Time Series Analysis. IEEJ Trans. Electr. Electron. Eng. 2022, 17, 174–182. [Google Scholar] [CrossRef]
- Zhan, J.; Liu, W.; Chung, C.; Yang, J. Switch opening and exchange method for stochastic distribution network reconfiguration. IEEE Trans. Smart Grid 2020, 11, 2995–3007. [Google Scholar] [CrossRef]
- Azizivahed, A.; Narimani, H.; Fathi, M.; Naderi, E.; Safarpour, H.R.; Narimani, M.R. Multi-objective dynamic distribution feeder reconfiguration in automated distribution systems. Energy 2018, 147, 896–914. [Google Scholar] [CrossRef]
- Dorostkar-Ghamsari, M.R.; Fotuhi-Firuzabad, M.; Lehtonen, M.; Safdarian, A. Value of distribution network reconfiguration in presence of renewable energy resources. IEEE Trans. Power Syst. 2015, 31, 1879–1888. [Google Scholar] [CrossRef]
- Jafari, A.; Ganjehlou, H.G.; Darbandi, F.B.; Mohammadi-Ivatloo, B.; Abapour, M. Dynamic and multi-objective reconfiguration of distribution network using a novel hybrid algorithm with parallel processing capability. Appl. Soft Comput. 2020, 90, 106146. [Google Scholar] [CrossRef]
- Ji, X.; Yin, Z.; Zhang, Y.; Xu, B. Real-time autonomous dynamic reconfiguration based on deep learning algorithm for distribution network. Electr. Power Syst. Res. 2021, 195, 107132. [Google Scholar] [CrossRef]
- Kovački, N.V.; Vidović, P.M.; Sarić, A.T. Scalable algorithm for the dynamic reconfiguration of the distribution network using the Lagrange relaxation approach. Int. J. Electr. Power Energy Syst. 2018, 94, 188–202. [Google Scholar] [CrossRef]
- Li, L.-L.; Xiong, J.-L.; Tseng, M.-L.; Yan, Z.; Lim, M.K. Using multi-objective sparrow search algorithm to establish active distribution network dynamic reconfiguration integrated optimization. Expert Syst. Appl. 2022, 193, 116445. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Das, D. Multi-objective dynamic and static reconfiguration with optimized allocation of PV-DG and battery energy storage system. Renew. Sustain. Energy Rev. 2020, 124, 109777. [Google Scholar] [CrossRef]
- Peng, C.; Xu, L.; Gong, X.; Sun, H.; Pan, L. Molecular evolution based dynamic reconfiguration of distribution networks with DGs considering three-phase balance and switching times. IEEE Trans. Ind. Inform. 2018, 15, 1866–1876. [Google Scholar] [CrossRef]
- Popović, Ž.N.; Kovački, N.V. Multi-period reconfiguration planning considering distribution network automation. Int. J. Electr. Power Energy Syst. 2022, 139, 107967. [Google Scholar] [CrossRef]
- Popovic, Z.N.; Knezevic, S.D. Dynamic reconfiguration of distribution networks considering hosting capacity: A risk-based approach. IEEE Trans. Power Syst. 2022, 38, 3440–3450. [Google Scholar] [CrossRef]
- Santos, S.F.; Gough, M.; Fitiwi, D.Z.; Pogeira, J.; Shafie-khah, M.; Catalão, J.P. Dynamic distribution system reconfiguration considering distributed renewable energy sources and energy storage systems. IEEE Syst. J. 2022, 16, 3723–3733. [Google Scholar] [CrossRef]
- Qiao, J.; Mi, Y.; Shen, J.; Xia, D.; Li, D.; Wang, P. Active and reactive power coordination optimization for active distribution network considering mobile energy storage system and dynamic network reconfiguration. Electr. Power Syst. Res. 2025, 238, 111080. [Google Scholar] [CrossRef]
- Home-Ortiz, J.M.; Macedo, L.H.; Vargas, R.; Romero, R.; Mantovani, J.R.S.; Catalao, J.P.S. Increasing RES hosting capacity in distribution networks through closed-loop reconfiguration and Volt/VAr control. IEEE Trans. Ind. Appl. 2022, 58, 4424–4435. [Google Scholar] [CrossRef]
- Zhan, H.; Jiang, C.; Lin, Z. A Novel Graph Reinforcement Learning-Based Approach for Dynamic Reconfiguration of Active Distribution Networks with Integrated Renewable Energy. Energies 2024, 17, 6311. [Google Scholar] [CrossRef]
- Lotfi, H.; Shojaei, A.A. A dynamic model for multi-objective feeder reconfiguration in distribution network considering demand response program. Energy Syst. 2023, 14, 1051–1080. [Google Scholar] [CrossRef]
- Tu, N.; Fan, Z. IMODBO for optimal dynamic reconfiguration in active distribution networks. Processes 2023, 11, 1827. [Google Scholar] [CrossRef]
- Kayal, P.; Chanda, C. Optimal mix of solar and wind distributed generations considering performance improvement of electrical distribution network. Renew. Energy 2015, 75, 173–186. [Google Scholar] [CrossRef]
- Khatod, D.K.; Pant, V.; Sharma, J. Evolutionary programming based optimal placement of renewable distributed generators. IEEE Trans. Power Syst. 2012, 28, 683–695. [Google Scholar] [CrossRef]
- Nikkhah, S.; Rabiee, A. Multi-objective stochastic model for joint optimal allocation of DG units and network reconfiguration from DG owner’s and DisCo’s perspectives. Renew. Energy 2019, 132, 471–485. [Google Scholar]
- Wang, W.; Huang, Y.; Yang, M.; Chen, C.; Zhang, Y.; Xu, X. Renewable energy sources planning considering approximate dynamic network reconfiguration and nonlinear correlations of uncertainties in distribution network. Int. J. Electr. Power Energy Syst. 2022, 139, 107791. [Google Scholar] [CrossRef]
- Conejo, A.J.; Carrión, M.; Morales, J.M. Decision Making Under Uncertainty in Electricity Markets; Springer: Berlin/Heidelberg, Germany, 2010; Volume 1. [Google Scholar]
- Arefifar, S.A.; Mohamed, Y.A.-R.I.; El-Fouly, T.H. Supply-adequacy-based optimal construction of microgrids in smart distribution systems. IEEE Trans. Smart Grid 2012, 3, 1491–1502. [Google Scholar] [CrossRef]
- Xia, S.; Luo, X.; Chan, K.W.; Zhou, M.; Li, G. Probabilistic transient stability constrained optimal power flow for power systems with multiple correlated uncertain wind generations. IEEE Trans. Sustain. Energy 2016, 7, 1133–1144. [Google Scholar] [CrossRef]
- Atwa, Y.; El-Saadany, E.; Salama, M.; Seethapathy, R. Optimal renewable resources mix for distribution system energy loss minimization. IEEE Trans. Power Syst. 2009, 25, 360–370. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovský, P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Chandramohan, S.; Atturulu, N.; Devi, R.K.; Venkatesh, B. Operating cost minimization of a radial distribution system in a deregulated electricity market through reconfiguration using NSGA method. Int. J. Electr. Power Energy Syst. 2010, 32, 126–132. [Google Scholar] [CrossRef]
- Esmailnezhad, B.; Shayeghi, H. Simultaneous distribution network reconfiguration and DG allocation for loss reduction by invasive weed optimization algorithm. In Proceedings of the 2013 Smart Grid Conference (SGC), Tehran, Iran, 17–18 December 2013; IEEE: Tehran, Iran, 2013; pp. 166–172. [Google Scholar]
- Amini, H. Islanding Detection and Cybersecurity in Inverter-Based Microgrids Under a High-Noise Environment. Ph.D. Dissertation, Virginia Tech, Blacksburg, VA, USA, 2024. Available online: https://hdl.handle.net/10919/120981 (accessed on 4 January 2025).
- Li, C.; Dai, Y.; Wang, P.; Xia, S. Active and reactive power coordinated optimization of active distribution networks considering dynamic reconfiguration and SOP. IET Renew. Power Gener. 2023, 17, 1–12. [Google Scholar] [CrossRef]
- Taylor, J.A.; Hover, F.S. Convex models of distribution system reconfiguration. IEEE Trans. Power Syst. 2012, 27, 1407–1413. [Google Scholar] [CrossRef]
- Abdelaziz, A.; Mohamed, F.; Mekhamer, S.; Badr, M. Distribution system reconfiguration using a modified Tabu Search algorithm. Electr. Power Syst. Res. 2010, 80, 943–953. [Google Scholar] [CrossRef]
- Ben Hamida, I.; Salah, S.B.; Msahli, F.; Mimouni, M.F. Optimal integration of distributed generations with network reconfiguration using a Pareto algorithm. Int. J. Renew. Energy Res. 2018, 8, 345–356. [Google Scholar]
- Bahmanifirouzi, B.; Farjah, E.; Niknam, T.; Farsani, E.A. A new hybrid HBMO-SFLA algorithm for multi-objective distribution feeder reconfiguration problem considering distributed generator units. Iran. J. Sci. Technol. Trans. Electr. Eng. 2012, 36, 51. [Google Scholar]
- Lotfi, H. Multi-objective network reconfiguration and allocation of capacitor units in radial distribution system using an enhanced artificial bee colony optimization. Electr. Power Compon. Syst. 2022, 49, 1130–1142. [Google Scholar] [CrossRef]
- Su, C.-T.; Chang, C.-F.; Chiou, J.-P. Distribution network reconfiguration for loss reduction by ant colony search algorithm. Electr. Power Syst. Res. 2005, 75, 190–199. [Google Scholar] [CrossRef]
- Niknam, T.; Farsani, E.A.; Nayeripour, M.; Firouzi, B.B. A new tribe modified shuffled frog leaping algorithm for multi-objective distribution feeder reconfiguration considering distributed generator units. Eur. Trans. Electr. Power 2012, 22, 308–333. [Google Scholar] [CrossRef]







| Ref. | DR Type * | Minimize Objective Function | Solution Method | DG | Uncertainty | Test Systems | |
|---|---|---|---|---|---|---|---|
| D | C | ||||||
| [6] | ✓ | 🗴 | Power loss, voltage stability, and load balance | MFSMA | Yes | No | 33- and 118-bus |
| [7] | ✓ | 🗴 | Total energy losses | FCMC and PSO | Yes | Yes | 70-bus |
| [8] | ✓ | 🗴 | Power loss | SOE | Yes | Yes | 33-, 119-,84-, 136-, and 417-bus |
| [9] | 🗴 | ✓ | ENS, power loss, and operation cost | Integrated GWO and PSO | Yes | No | 95-bus |
| [10] | 🗴 | ✓ | Total daily losses | MOSEK | Yes | Yes | 33-bus |
| [11] | 🗴 | ✓ | Power loss, SAIFI, SAIDI, and AENS | Hybrid EMA and WGA | No | No | 15-, 33-, 69- and, 85-bus |
| [12] | 🗴 | ✓ | Switching and power loss | Deep Learning Algorithm | Yes | No | 33- and 84-bus |
| [13] | 🗴 | ✓ | Reliability, switching, and power loss | Lagrange Relaxation | Yes | No | 15- and 1021-bus |
| [14] | 🗴 | ✓ | Losses, VDI, and economic cost | MOSSA | Yes | No | 33-bus |
| [15] | 🗴 | ✓ | Losses, VDI, and load ability | Circular mechanism | Yes | No | 69-bus |
| [16] | 🗴 | ✓ | Unbalance factor and switching factor | MOMDE | Yes | No | 34-bus |
| [17] | 🗴 | ✓ | Cost of losses, wwitching, and ENS | MO Switching and ENS Programming | Yes | Yes | 83-bus |
| [18] | 🗴 | ✓ | Hosting capacity, cost of losses, switching, and interruptions | MO MILP | Yes | Yes | 33-bus |
| [19] | 🗴 | ✓ | Cost of emissions and switching | Stochastic MILP | Yes | Yes | 119-bus |
| [20] | 🗴 | ✓ | Operation cost | MISOCP | Yes | No | 33 bus |
| [21] | ✓ | 🗴 | Hosting capacity and CO2 emissions | MISOCP | Yes | No | 33- and 84-bus |
| [22] | 🗴 | ✓ | Power loss and voltage deviations | graph reinforcement learning | Yes | No | 33 bus |
| [23] | 🗴 | ✓ | Cost of losses, operation, and ENS | IPSO | Yes | Yes | 95 bus |
| [24] | ✓ | 🗴 | Power loss and voltage deviations | IMODBO | Yes | Yes | 33- and 69-bus |
| This work | 🗴 | ✓ | Cost (Cupn + Closs + CVD + CSW + CPV + CWind) | COA | Yes | Yes | 33- and 84-bus |
| DG Type | Location (No. Bus) | Size (kW) | Location (No. Bus) | Size (kW) |
|---|---|---|---|---|
| PV | 7 | 350 | 14 | 450 |
| Wind | 10 | 400 | 33 | 500 |
| References | Optimization Method | Results | |
|---|---|---|---|
| Open Switches | Loss (kW) | ||
| [6] | MFSMA | S7, S9, S14, S32, S37 | 144.43 |
| [8] | SOE | S7, S9, S14, S32, S37 | 139.55 |
| [10] | GAMS Solver | S7, S9, S14, S32, S37 | 139.55 |
| [11] | Hybrid EMA and WGA | S7, S9, S14, S32, S37 | 139.55 |
| [38] | Convex Models | S7, S9, S14, S32, S37 | 139.55 |
| [39] | Tabu Search algorithm | S7, S9, S14, S32, S37 | 139.55 |
| [40] | Pareto algorithm | S7, S9, S14, S32, S37 | 139.55 |
| This work | COA | S7, S9, S14, S32, S37 | 139.55 |
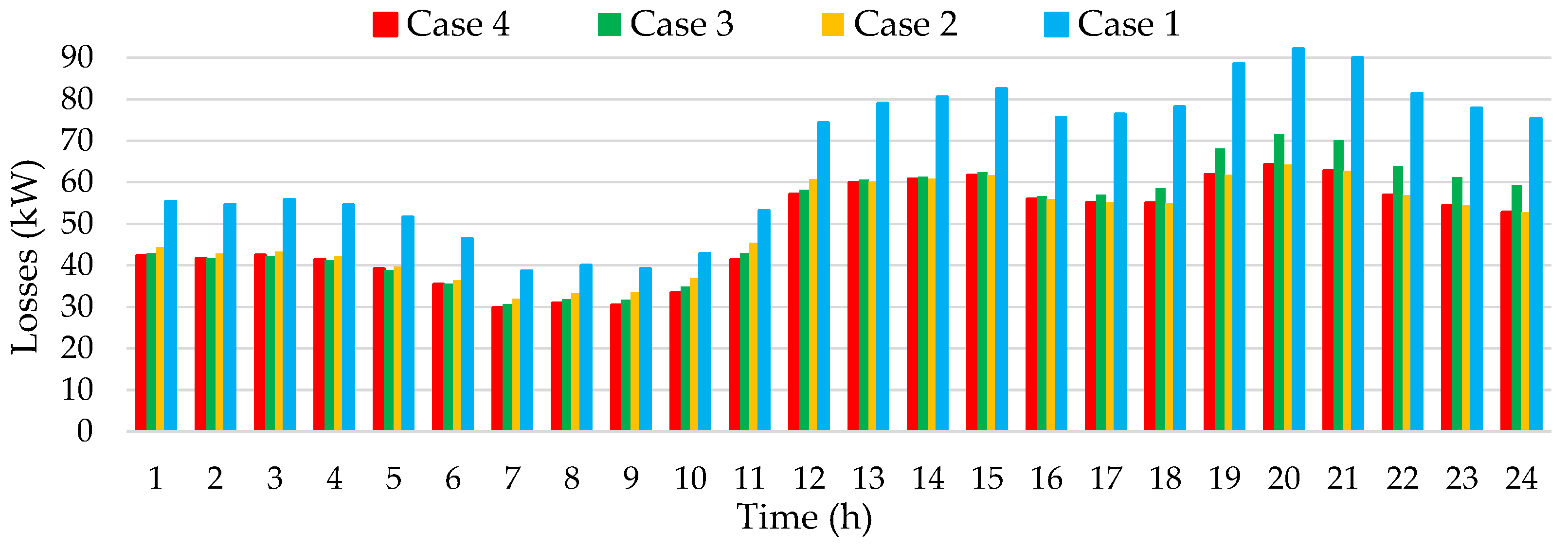
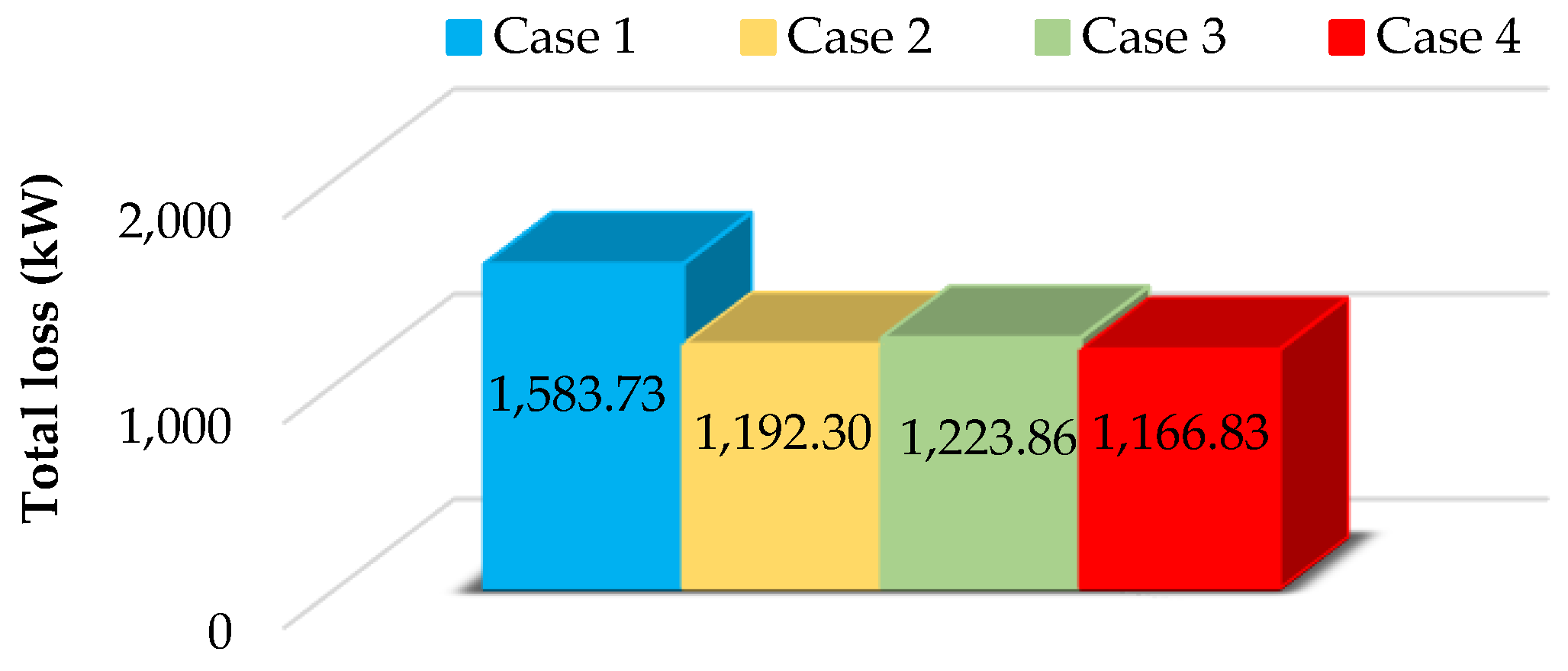
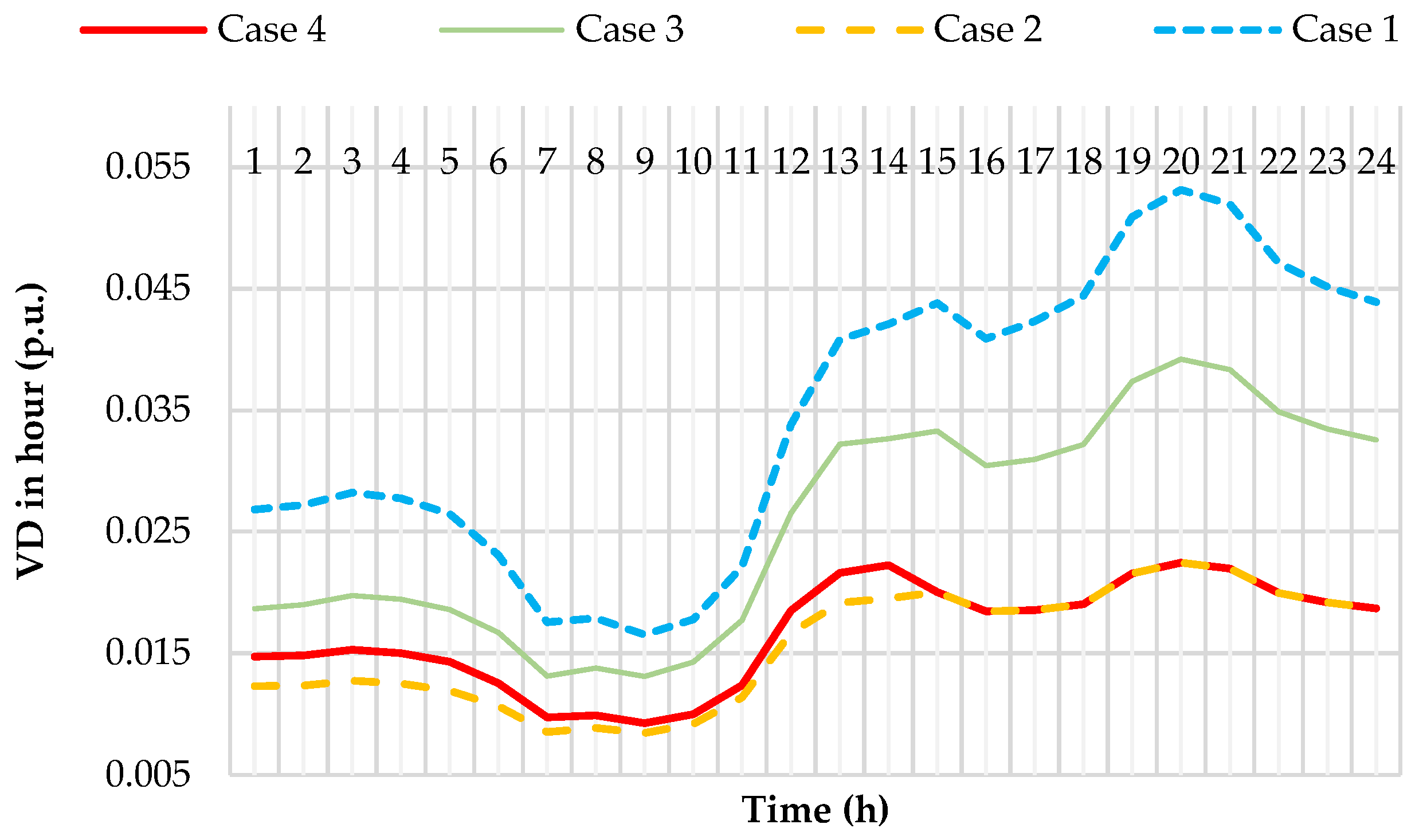
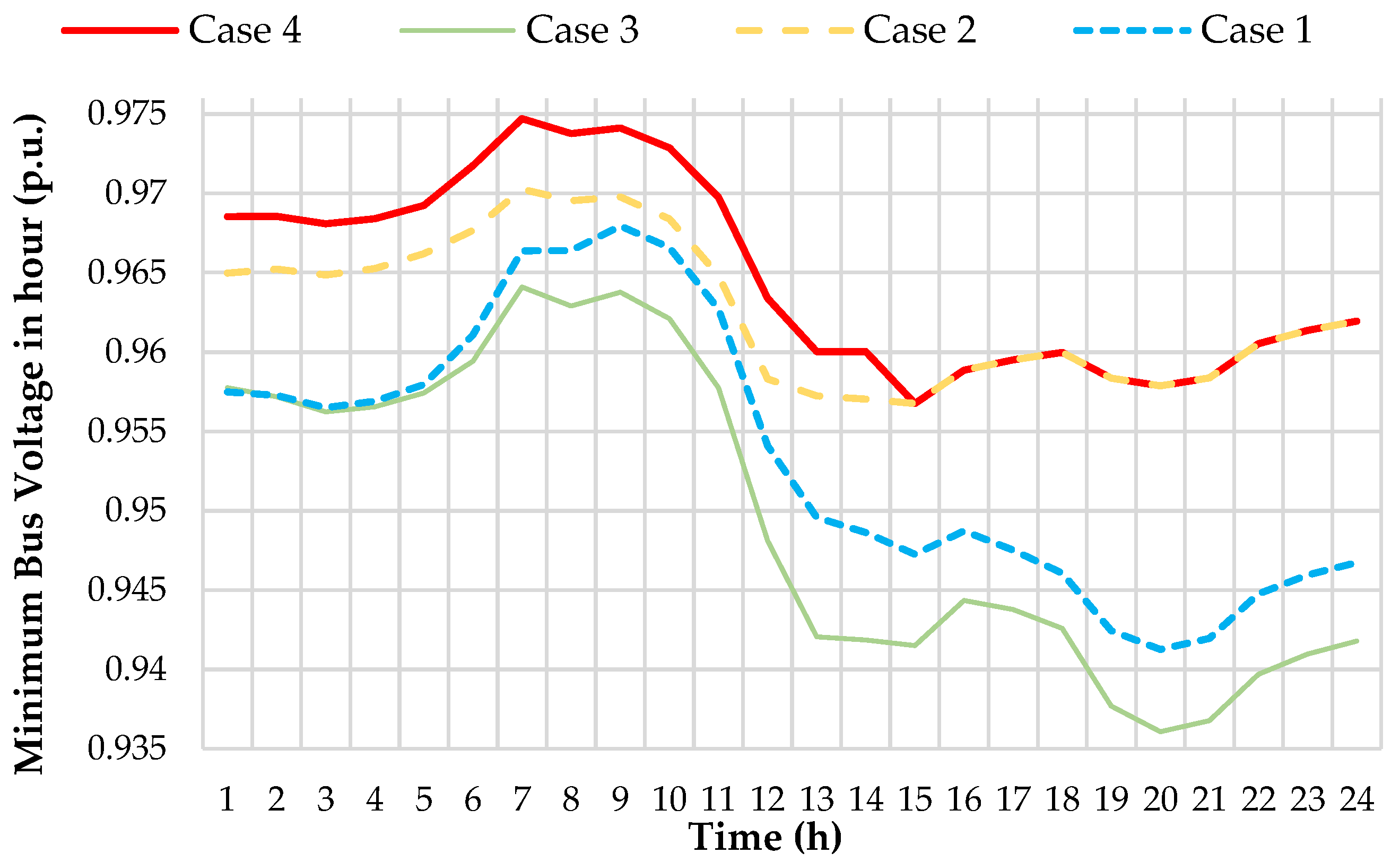
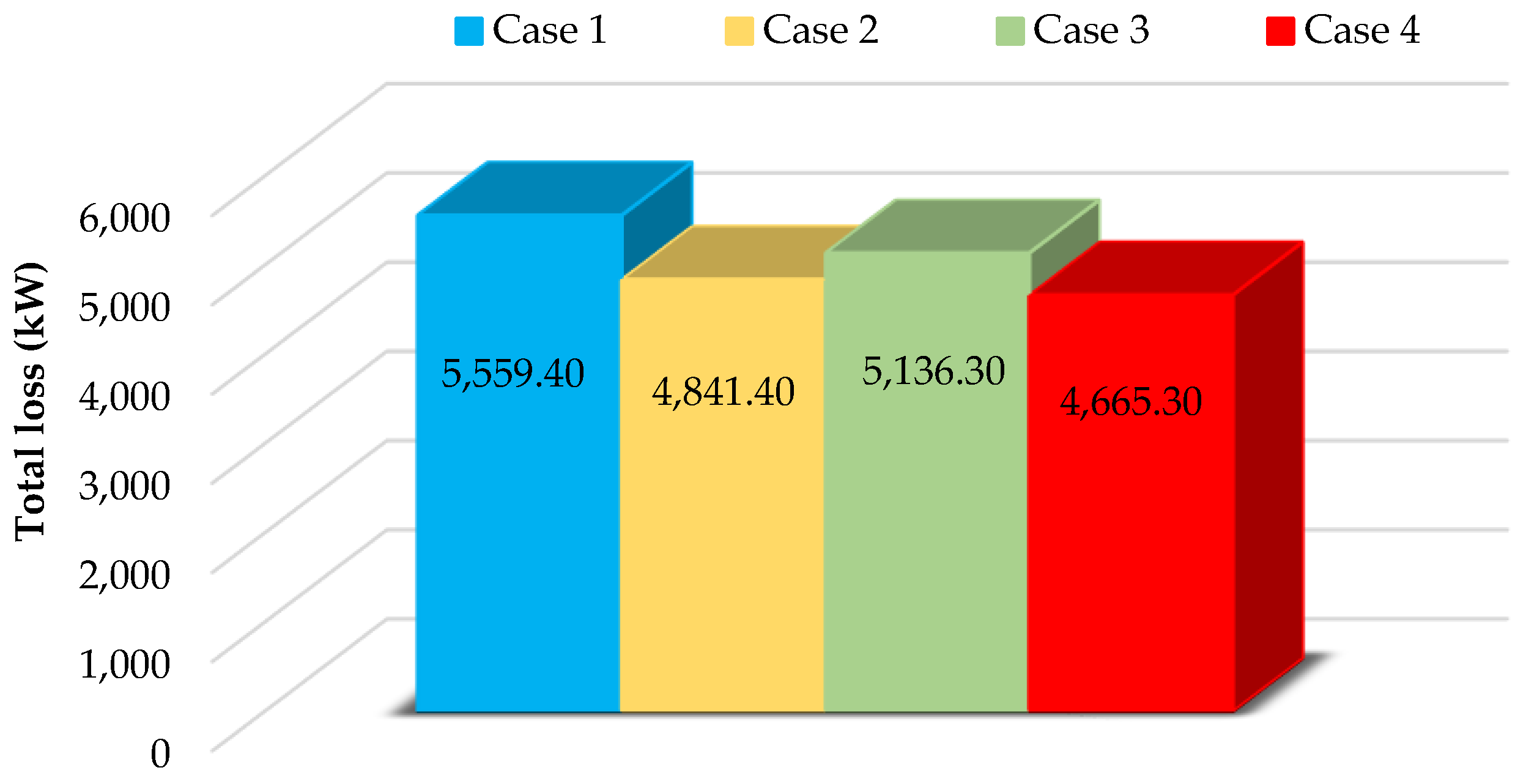
| Case | Time Period | Open Switches | Cost (USD) | Closs (USD) | CVD (USD) | CSW (USD) | Cupn (USD) | CPV (USD) | Cwind (USD) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 24 h | S33, S34, S35, S36, S37 | 2799.20 | 633.49 | 0.581 | 0 | 1873.28 | 60.518 | 231.32 |
| 2 | 24 h | S7, S9, S14, S32, S37 | 2635.45 | 476.92 | 0.260 | 8 | 1858.42 | 60.518 | 231.32 |
| 3 | 24 h | S7, S10, S14, S30, S37 | 2649.57 | 489.54 | 0.431 | 8 | 1859.75 | 60.518 | 231.32 |
| 4 | 1–14 h | S6, S9, S34, S36, S37 | 2626.39 | 466.73 | 0.279 | 10 | 1857.53 | 60.518 | 231.32 |
| 15–24 h | S7, S9, S14, S32, S37 |
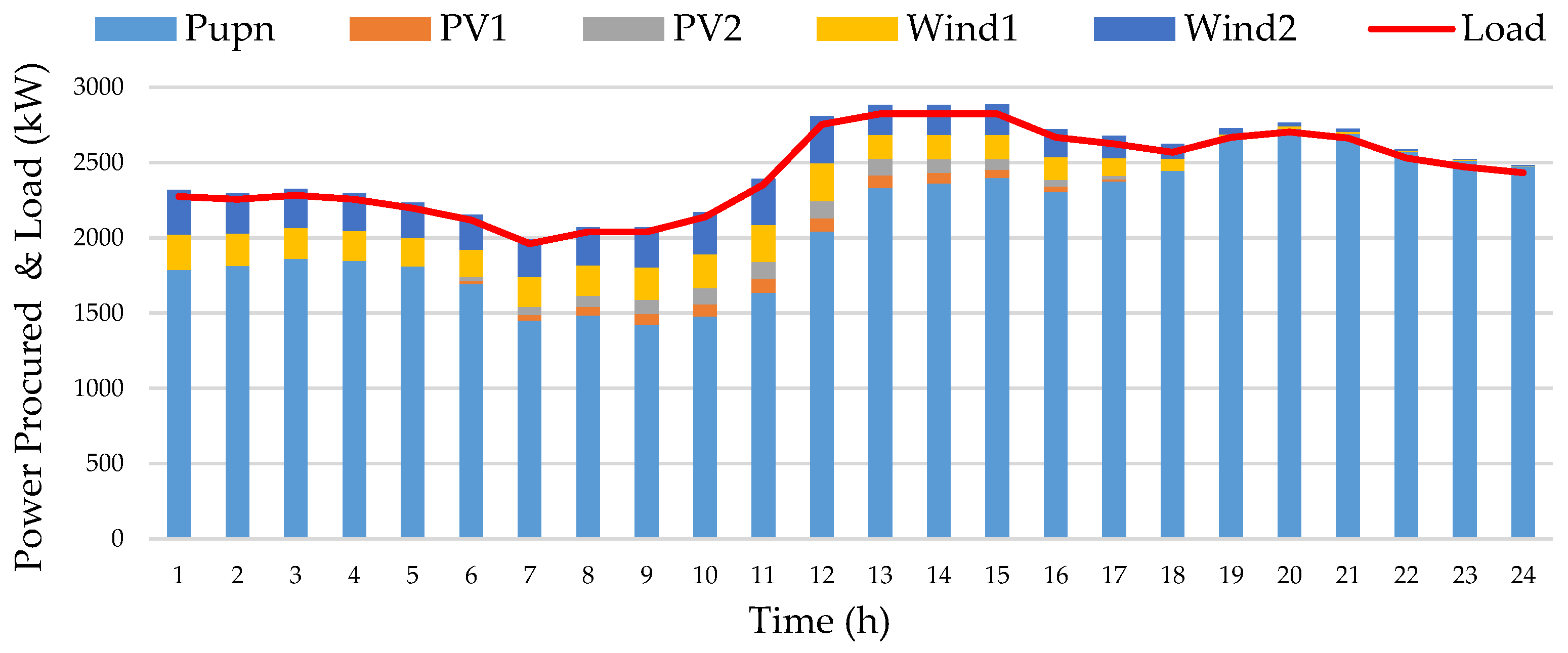
| Time (h) | Pupst (kW) | PPVt,i (kW) | PWindt,i (kW) | |||||
|---|---|---|---|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | Case 4 | Bus 7 | Bus 14 | Bus 10 | Bus 33 | |
| 1 | 1799.61 | 1788.58 | 1787.19 | 1786.61 | 0 | 0 | 235.99 | 294.99 |
| 2 | 1827.26 | 1815.46 | 1814.32 | 1814.28 | 0 | 0 | 214.67 | 268.33 |
| 3 | 1873.89 | 1861.41 | 1860.39 | 1860.54 | 0 | 0 | 206.67 | 258.33 |
| 4 | 1860.19 | 1847.81 | 1846.88 | 1847.11 | 0 | 0 | 199.99 | 249.99 |
| 5 | 1823.11 | 1811.18 | 1810.40 | 1810.71 | 1.01 | 1.29 | 187.99 | 234.99 |
| 6 | 1704.40 | 1694.38 | 1693.49 | 1693.37 | 20.28 | 26.09 | 184.00 | 230.00 |
| 7 | 1459.67 | 1452.96 | 1451.68 | 1450.79 | 39.50 | 50.81 | 199.99 | 249.98 |
| 8 | 1494.89 | 1488.26 | 1486.76 | 1485.79 | 57.71 | 74.22 | 201.32 | 251.65 |
| 9 | 1432.54 | 1426.89 | 1425.05 | 1423.82 | 72.82 | 93.66 | 213.32 | 266.65 |
| 10 | 1488.07 | 1482.11 | 1480.07 | 1478.57 | 82.54 | 106.16 | 223.99 | 279.98 |
| 11 | 1647.52 | 1639.75 | 1637.31 | 1635.64 | 90.65 | 116.60 | 245.31 | 306.64 |
| 12 | 2059.78 | 2046.15 | 2043.67 | 2042.55 | 89.34 | 114.91 | 250.64 | 313.31 |
| 13 | 2352.92 | 2334.06 | 2334.53 | 2333.79 | 84.58 | 108.79 | 158.65 | 198.32 |
| 14 | 2381.40 | 2361.74 | 2362.26 | 2361.71 | 71.45 | 91.90 | 159.98 | 199.98 |
| 15 | 2420.55 | 2399.77 | 2400.43 | 2399.77 | 55.17 | 70.96 | 159.98 | 199.97 |
| 16 | 2326.42 | 2306.76 | 2307.52 | 2306.77 | 35.14 | 45.19 | 149.30 | 186.63 |
| 17 | 2396.16 | 2374.89 | 2376.79 | 2374.89 | 16.45 | 21.16 | 118.67 | 148.33 |
| 18 | 2470.62 | 2447.57 | 2451.04 | 2447.57 | 0 | 0 | 78.67 | 98.34 |
| 19 | 2680.77 | 2654.08 | 2660.39 | 2654.08 | 0 | 0 | 33.46 | 41.83 |
| 20 | 2753.97 | 2726.12 | 2733.57 | 2726.12 | 0 | 0 | 18.18 | 22.73 |
| 21 | 2718.13 | 2690.95 | 2698.29 | 2690.95 | 0 | 0 | 15.71 | 19.64 |
| 22 | 2596.53 | 2572.06 | 2579.08 | 2572.06 | 0 | 0 | 6.56 | 8.20 |
| 23 | 2538.06 | 2514.69 | 2521.44 | 2514.69 | 0 | 0 | 4.79 | 5.99 |
| 24 | 2501.18 | 2478.58 | 2485.21 | 2478.58 | 0 | 0 | 2.57 | 3.21 |
| Time (h) | Cupnt (USD) | CPVt (USD) | Cwindt (USD) | |||||
|---|---|---|---|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | Case 4 | Bus 7 | Bus 14 | Bus 10 | Bus 33 | |
| 1 | 50.38 | 50.08 | 50.04 | 50.02 | 0 | 0 | 4.72 | 5.89 |
| 2 | 43.85 | 43.57 | 43.54 | 43.54 | 0 | 0 | 4.29 | 5.36 |
| 3 | 41.22 | 40.95 | 40.92 | 40.93 | 0 | 0 | 4.13 | 5.16 |
| 4 | 42.78 | 42.49 | 42.47 | 42.48 | 0 | 0 | 3.99 | 4.99 |
| 5 | 43.75 | 43.46 | 43.44 | 43.45 | 0.025 | 0.032 | 3.76 | 4.69 |
| 6 | 42.61 | 42.35 | 42.33 | 42.33 | 0.51 | 0.65 | 3.68 | 4.60 |
| 7 | 39.41 | 39.23 | 39.19 | 39.17 | 1.38 | 1.78 | 3.99 | 4.99 |
| 8 | 47.83 | 47.62 | 47.57 | 47.54 | 2.02 | 2.59 | 4.02 | 5.03 |
| 9 | 53.00 | 52.79 | 52.72 | 52.68 | 2.55 | 3.27 | 7.46 | 9.33 |
| 10 | 65.47 | 65.21 | 65.12 | 65.05 | 2.89 | 3.71 | 7.83 | 9.79 |
| 11 | 69.19 | 68.86 | 68.76 | 68.69 | 3.17 | 4.08 | 8.58 | 10.73 |
| 12 | 82.39 | 81.84 | 81.74 | 81.70 | 3.12 | 4.02 | 8.77 | 10.96 |
| 13 | 98.82 | 98.03 | 98.05 | 98.02 | 2.96 | 3.80 | 5.55 | 6.94 |
| 14 | 102.40 | 101.55 | 101.57 | 101.55 | 2.50 | 3.21 | 5.59 | 6.99 |
| 15 | 111.34 | 110.38 | 110.42 | 110.38 | 2.76 | 3.54 | 7.19 | 8.99 |
| 16 | 109.34 | 108.41 | 108.45 | 108.41 | 1.75 | 2.26 | 6.71 | 8.39 |
| 17 | 116.21 | 115.18 | 115.27 | 115.18 | 0.82 | 1.05 | 5.34 | 6.67 |
| 18 | 119.82 | 118.71 | 118.87 | 118.71 | 0 | 0 | 3.54 | 4.42 |
| 19 | 134.04 | 132.70 | 133.02 | 132.70 | 0 | 0 | 1.50 | 1.88 |
| 20 | 123.92 | 122.67 | 123.01 | 122.67 | 0 | 0 | 0.81 | 1.02 |
| 21 | 103.28 | 102.25 | 102.53 | 102.25 | 0 | 0 | 0.70 | 0.88 |
| 22 | 93.47 | 92.59 | 92.84 | 92.59 | 0 | 0 | 0.29 | 0.36 |
| 23 | 76.14 | 75.44 | 75.64 | 75.44 | 0 | 0 | 0.17 | 0.21 |
| 24 | 62.53 | 61.96 | 62.13 | 61.96 | 0 | 0 | 0.09 | 0.11 |
| ∑ | 1873.28 | 1858.42 | 1859.75 | 1857.53 | 26.47 | 34.04 | 102.81 | 128.51 |
| Time (h) | Closst (USD) | |||
|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | Case 4 | |
| 1 | 22.14 | 17.73 | 17.17 | 16.94 |
| 2 | 21.84 | 17.12 | 16.66 | 16.64 |
| 3 | 22.31 | 17.31 | 16.91 | 16.97 |
| 4 | 21.81 | 16.86 | 16.49 | 16.58 |
| 5 | 20.64 | 15.87 | 15.55 | 15.68 |
| 6 | 18.57 | 14.57 | 14.21 | 14.16 |
| 7 | 15.47 | 12.78 | 12.27 | 11.91 |
| 8 | 16.00 | 13.35 | 12.75 | 12.36 |
| 9 | 15.67 | 13.41 | 12.67 | 12.18 |
| 10 | 17.15 | 14.76 | 13.95 | 13.35 |
| 11 | 21.26 | 18.15 | 17.17 | 16.51 |
| 12 | 29.73 | 24.28 | 23.29 | 22.84 |
| 13 | 31.60 | 24.06 | 24.25 | 23.95 |
| 14 | 32.20 | 24.33 | 24.54 | 24.32 |
| 15 | 32.99 | 24.68 | 24.95 | 24.68 |
| 16 | 30.24 | 22.38 | 22.68 | 22.38 |
| 17 | 30.54 | 22.03 | 22.79 | 22.03 |
| 18 | 31.25 | 22.03 | 23.42 | 22.03 |
| 19 | 35.40 | 24.72 | 27.24 | 24.72 |
| 20 | 36.84 | 25.69 | 28.67 | 25.69 |
| 21 | 35.98 | 25.11 | 28.05 | 25.11 |
| 22 | 32.53 | 22.74 | 25.55 | 22.74 |
| 23 | 31.12 | 21.77 | 24.47 | 21.77 |
| 24 | 30.14 | 21.10 | 23.75 | 21.10 |
| ∑ | 633.39 | 476.92 | 489.54 | 466.73 |
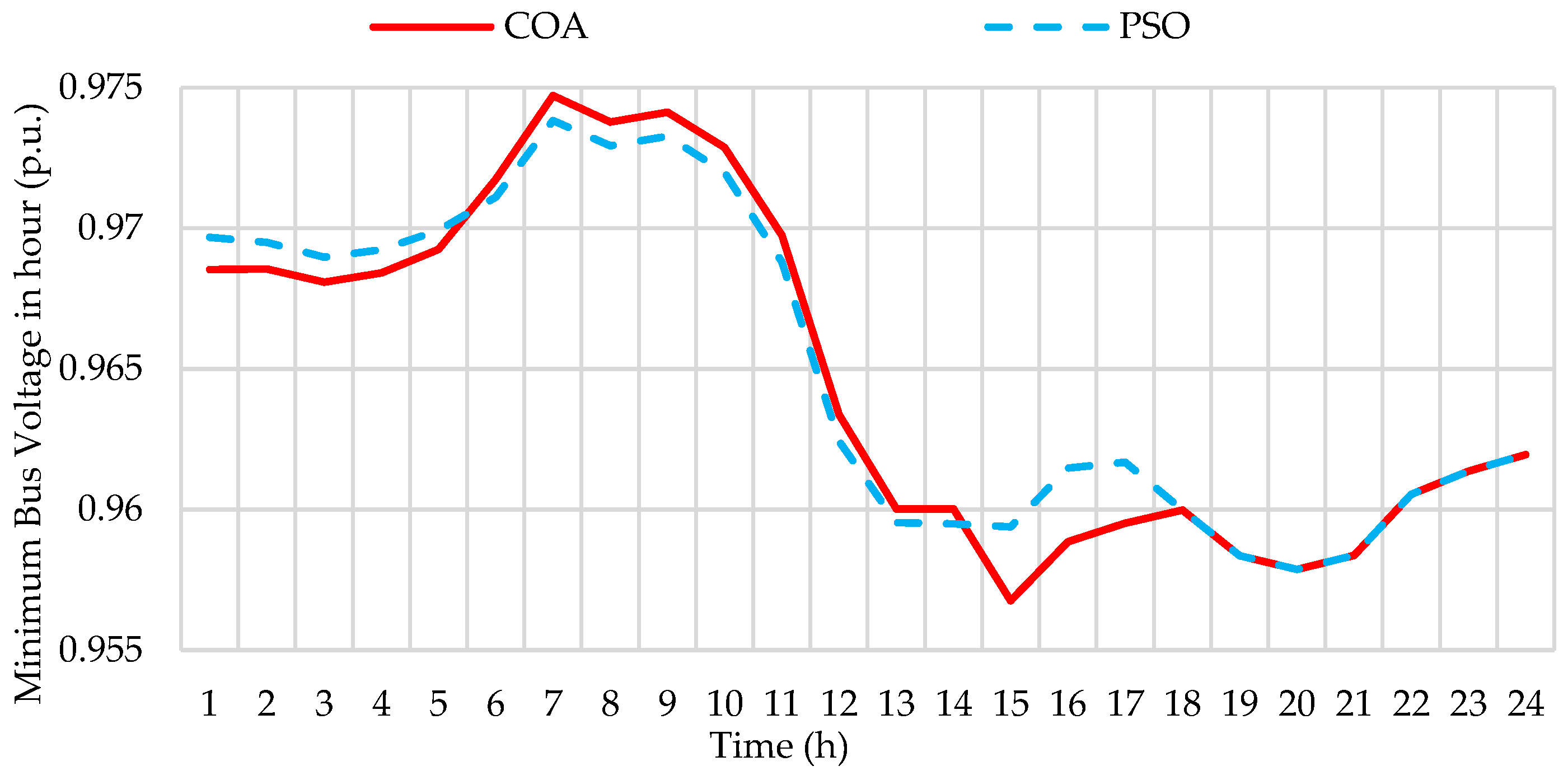
| Method | Time Period | Open Switches | Cost (USD) | Closs (USD) | CVD (USD) | CSW (USD) | Cupn (USD) | CPV (USD) | Cwind (USD) |
|---|---|---|---|---|---|---|---|---|---|
| PSO | 1–4 h | S7, S11, S28, S34, S36 | 2634.58 | 466.85 | 0.261 | 18 | 1857.63 | 60.518 | 231.32 |
| 5–11 h | S7, S9, S28, S34, S36 | ||||||||
| 13–17 h | S7, S11, S28, S34, S36 | ||||||||
| 18–24 h | S7, S9, S14, S32, S37 | ||||||||
| COA | 1–14 h | S6, S9, S34, S36, S37 | 2626.39 | 466.73 | 0.279 | 10 | 1857.53 | 60.518 | 231.32 |
| 15–24 h | S7, S9, S14, S32, S37 |
| EENS | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| Average (MWh/year) | 0.6192 | 0.5106 | 0.6245 | 0.5037 |
| Total (MWh/year) | 14.8602 | 12.2543 | 14.9887 | 12.0879 |
| DG Type | Location (No. Bus) | Size (kW) | Location (No. Bus) | Size (kW) | Location (No. Bus) | Size (kW) | Location (No. Bus) | Size (kW) |
|---|---|---|---|---|---|---|---|---|
| PV | 6 | 500 | 13 | 500 | 53 | 500 | 60 | 500 |
| Wind | 18 | 500 | 36 | 500 | 71 | 500 | 83 | 500 |
| References | Optimization Method | Results | |
|---|---|---|---|
| Open Switches | Loss (kW) | ||
| [41] | MHBMO-SFLA | S7, S14, S34, S39, S42, S55, S62, S72, S83, S86, S88, S90, S92 | 463.28 |
| [42] | PSO-EABCO | S7, S14, S34, S39, S42, S55, S62, S72, S83, S86, S88, S90, S92 | 463.28 |
| [43] | ACO | S7, S34, S39, S41, S55, S62, S72, S83, S86, S88, S89, S90, S92 | 469.88 |
| [44] | T-MSFLA | S7, S34, S39, S41, S55, S62, S72, S83, S86, S88, S89, S90, S92 | 469.88 |
| This work | COA | S7, S14, S34, S39, S42, S55, S62, S72, S83, S86, S88, S90, S92 | 463.28 |
| Case | Time Period | Open Switches | Cost (USD) | Closs (USD) | CVD (USD) | CSW (USD) | Cupn (USD) | CPV (USD) | Cwind (USD) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 24 h | S84, S85, S86, S87, S88, S89, S90, S91, S92, S93, S94, S95, S96 | 18,751.93 | 2223.8 | 0.813 | 0 | 15,861.9 | 151.32 | 514.05 |
| 2 | 24 h | S7, S14, S34, S39, S42, S55, S62, S72, S83, S86, S88, S90, S92 | 18,455.35 | 1936.6 | 0.364 | 18 | 15,835.1 | 151.32 | 514.05 |
| 3 | 24 h | S1, S6, S29, S86, S66, S88, S89, S90, S91, S92, S94, S95, S96 | 18,574.61 | 2054.5 | 0.603 | 8 | 15,846.1 | 151.32 | 514.05 |
| 4 | 1–19 h | S7, S34, S39, S41, S55, S62, S72, S83, S86, S88, S89, S90, S92 | 18,378.23 | 1866.1 | 0.368 | 18 | 15,825.3 | 151.32 | 514.05 |
| 20–24 h | S7, S14, S34, S39, S42, S55, S62, S72, S83, S86, S88, S90, S92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esmaeilnezhad, B.; Amini, H.; Noroozian, R.; Jalilzadeh, S. Flexible Reconfiguration for Optimal Operation of Distribution Network Under Renewable Generation and Load Uncertainty. Energies 2025, 18, 266. https://doi.org/10.3390/en18020266
Esmaeilnezhad B, Amini H, Noroozian R, Jalilzadeh S. Flexible Reconfiguration for Optimal Operation of Distribution Network Under Renewable Generation and Load Uncertainty. Energies. 2025; 18(2):266. https://doi.org/10.3390/en18020266
Chicago/Turabian StyleEsmaeilnezhad, Behzad, Hossein Amini, Reza Noroozian, and Saeid Jalilzadeh. 2025. "Flexible Reconfiguration for Optimal Operation of Distribution Network Under Renewable Generation and Load Uncertainty" Energies 18, no. 2: 266. https://doi.org/10.3390/en18020266
APA StyleEsmaeilnezhad, B., Amini, H., Noroozian, R., & Jalilzadeh, S. (2025). Flexible Reconfiguration for Optimal Operation of Distribution Network Under Renewable Generation and Load Uncertainty. Energies, 18(2), 266. https://doi.org/10.3390/en18020266






