Enhancing Thermal-Hydraulic Modelling in Dual Fluid Reactor Demonstrator: The Impact of Variable Turbulent Prandtl Number
Abstract
:1. Introduction
2. Numerical Details
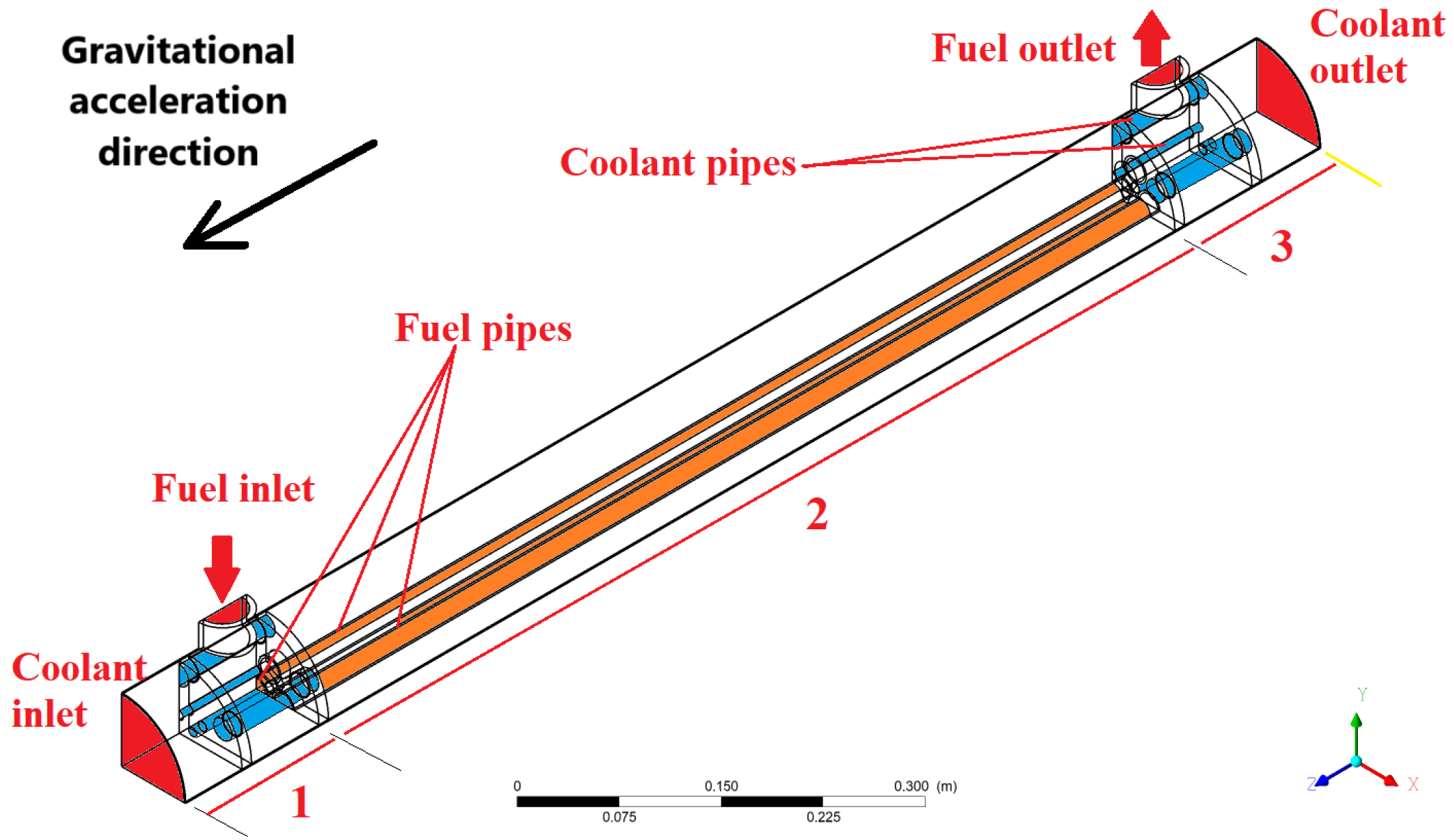
2.1. Description of Test Case
2.2. Governing Equations and Heat Transfer Model
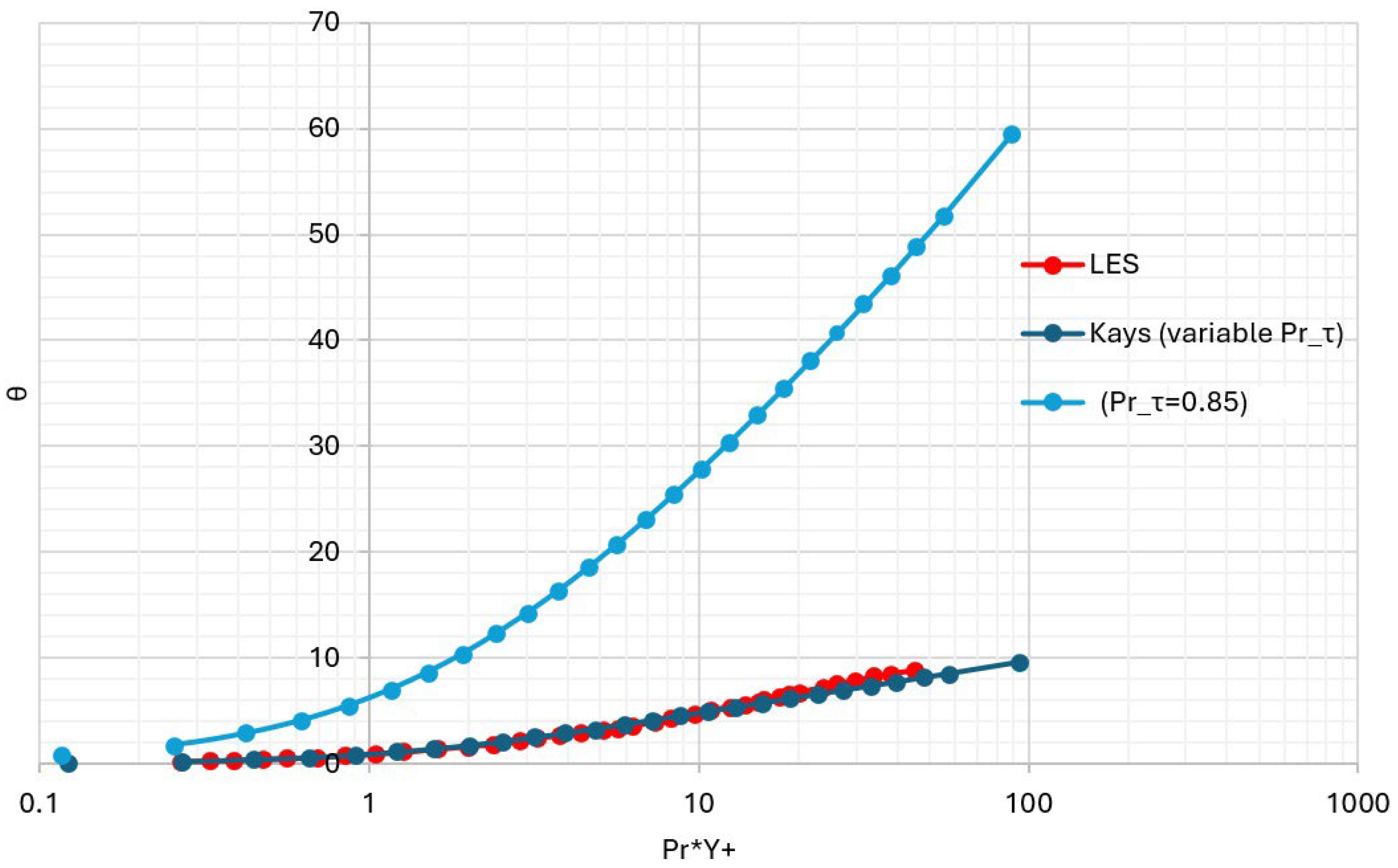
2.3. Validation of Heat Transfer Model
2.4. Computational Details and Boundary Conditions
3. Results and Discussion
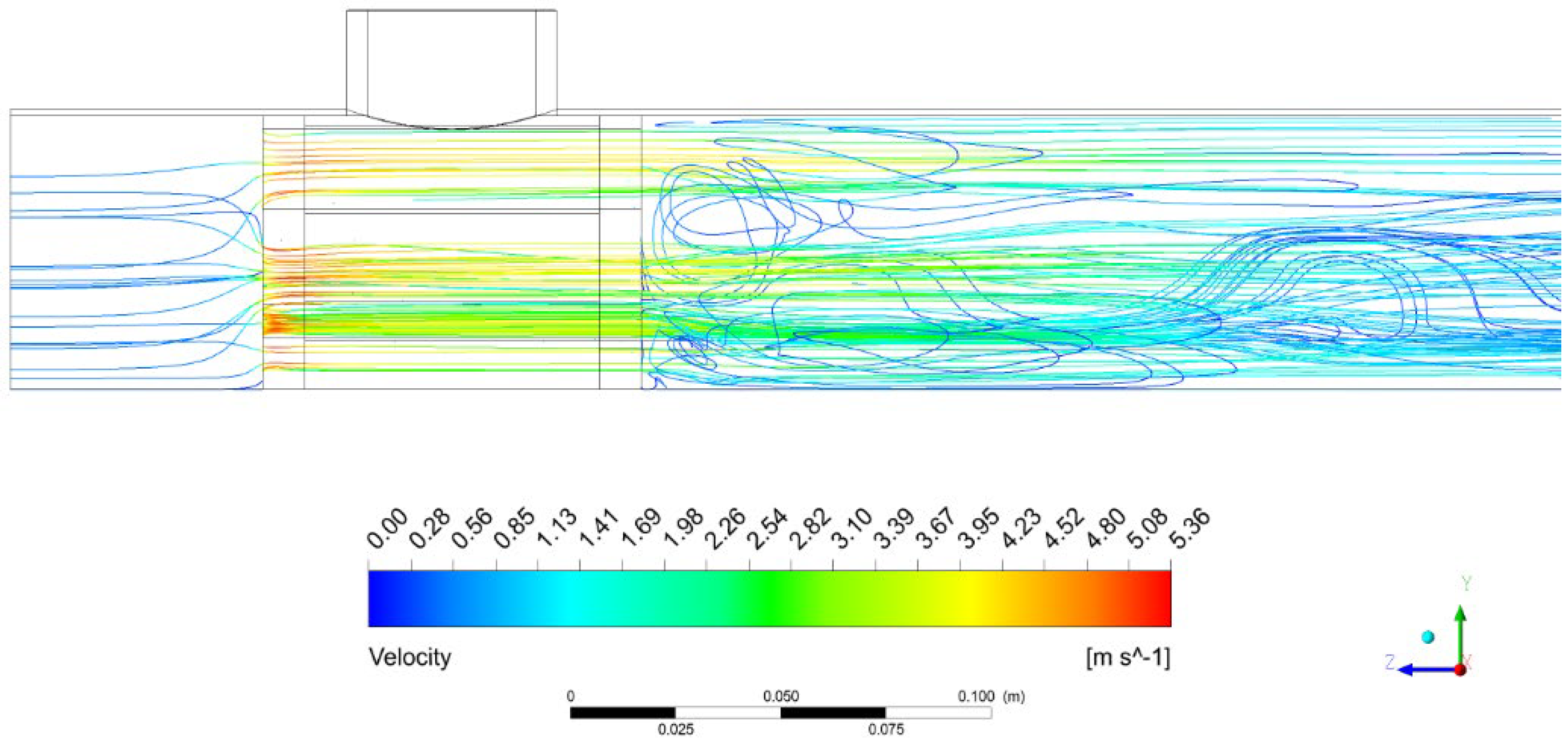
3.1. Velocity Field in the Fuel Region
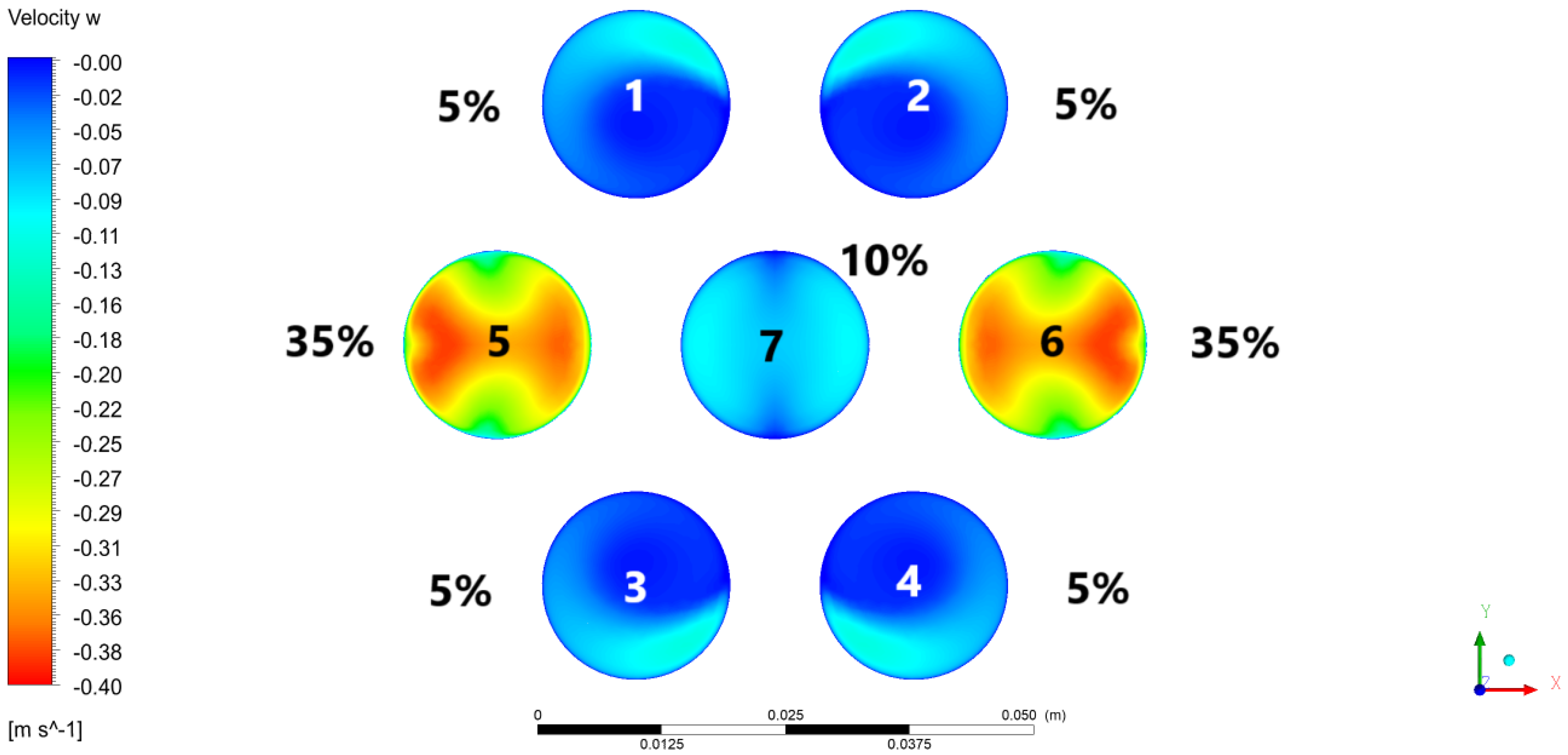
3.2. The Velocity Field in the Coolant Region
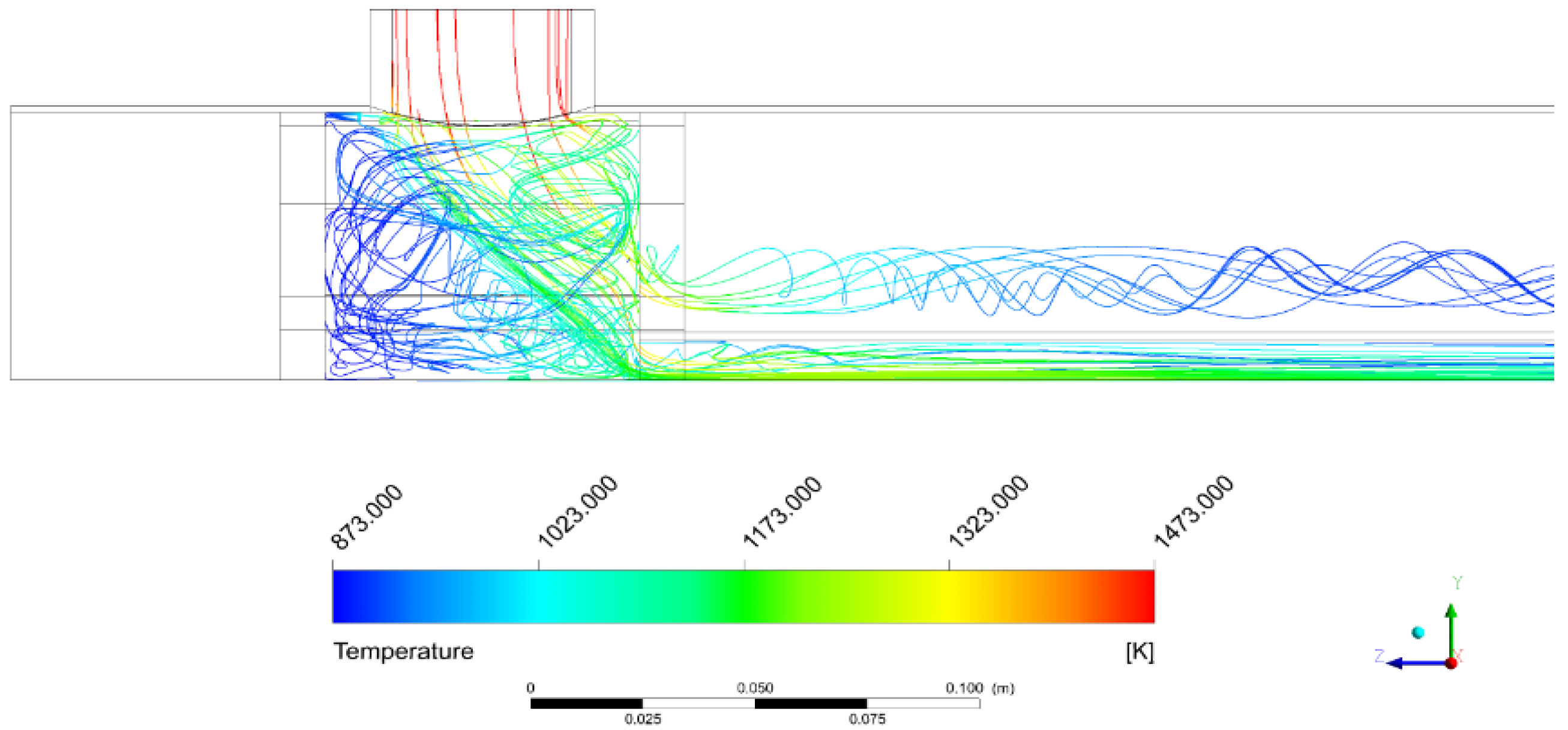
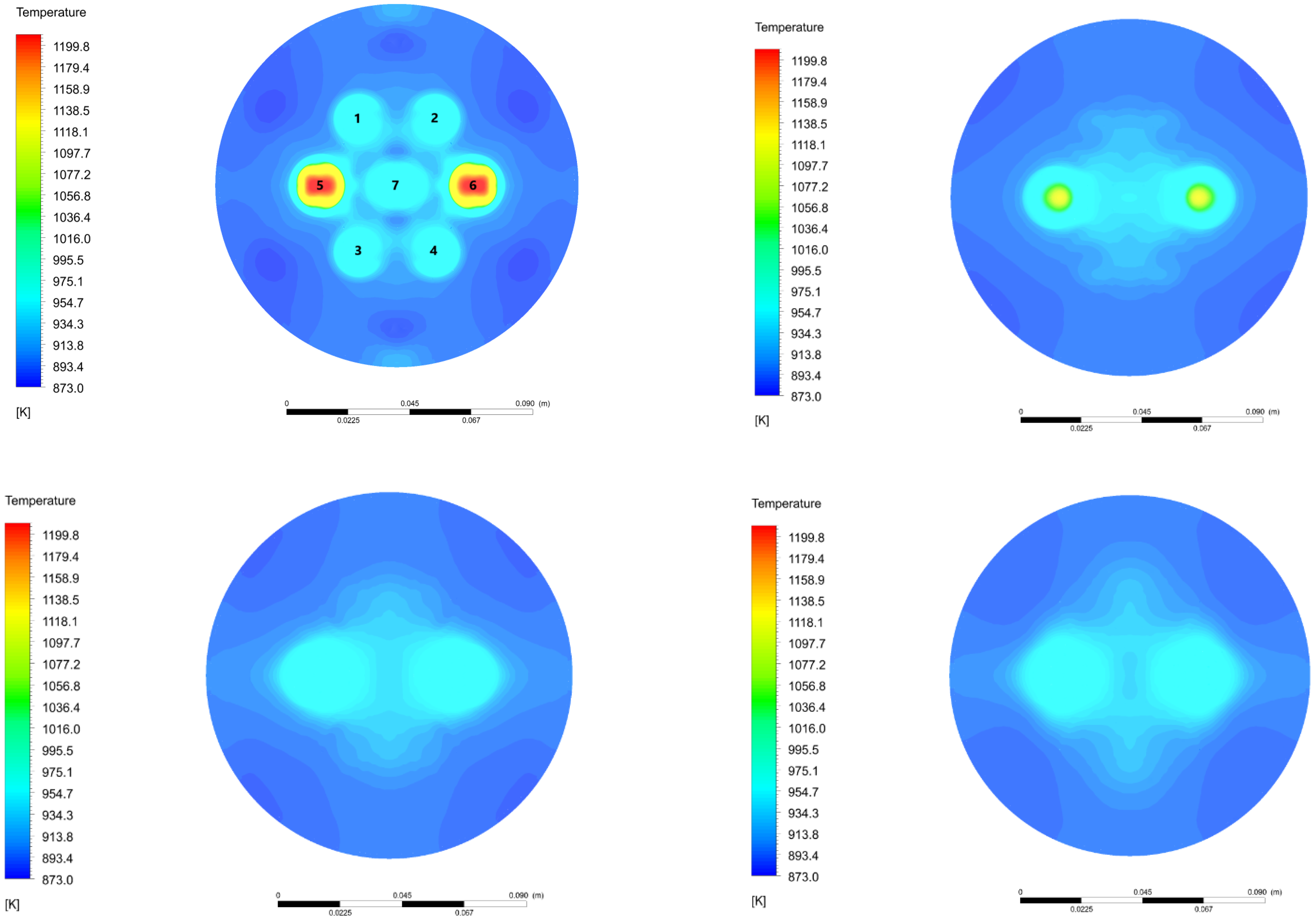
3.3. Heat Transfer in the Fuel Region
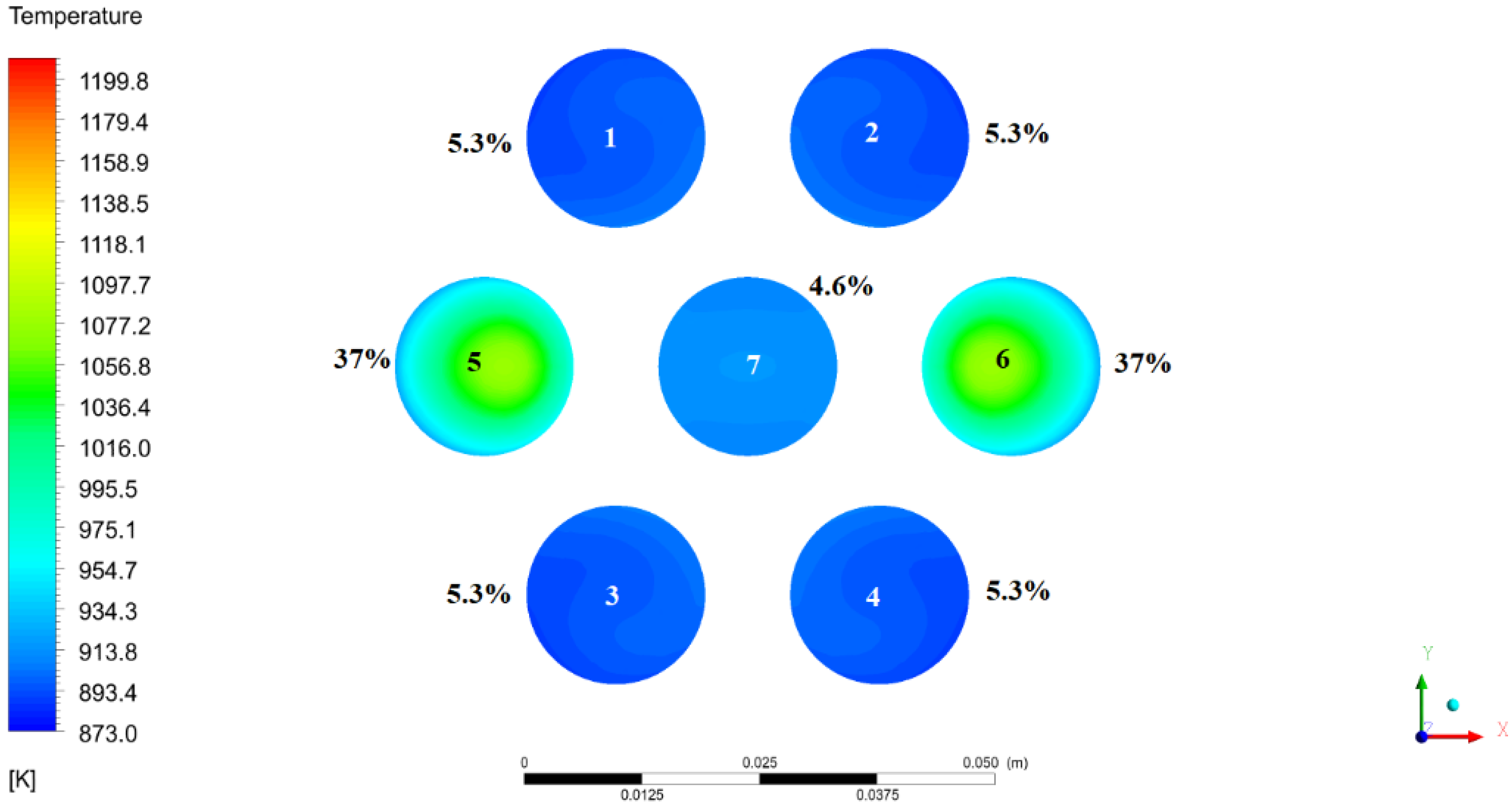
3.4. Heat Transfer in the Coolant Region
3.5. Global Heat Transfer Characteristics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Greek Symbols | |
| θ⁺ | Non-dimensional temperature |
| κ | Thermal conductivity |
| μ | Dynamic molecular viscosity |
| ρ | Density |
| ω | Specific dissipation rate |
| Latin Symbols | |
| cp | Specific heat at constant pressure |
| k | Turbulent kinetic energy |
| Nu | Nusselt number |
| Pet | Turbulent Peclet number |
| Pr | Prandtl number |
| Prt | Turbulent Prandtl number |
| qw | Mean heat flux |
| Re | Reynolds number |
| Reτ | Friction Reynolds number |
| T | Temperature |
| Tw | Mean wall temperature |
| u | Velocity |
| uτ | Friction velocity |
| y⁺ | Non-dimensional wall distance |
| Abbreviations | |
| CFD | Computational Fluid Dynamics |
| DFR | Dual Fluid Reactor |
| DNS | Direct Numerical Simulation |
| LES | Large Eddy Simulation |
| MD | Mini Demonstrator/Middle Core Distribution |
| MHD | Magneto-Hydraulic Pumps |
| SGDH | Standard Gradient Diffusion Hypothesis |
| SST | Shear Stress Transport |
References
- Muellner, N.; Arnold, N.; Gufler, K.; Kromp, W.; Renneberg, W.; Liebert, W. Nuclear Energy—The Solution to Climate Change? Energy Policy 2021, 155, 112363. [Google Scholar] [CrossRef]
- Nuclear Energy Agency (NEA). Technology Roadmap Update for Generation IV Nuclear Energy Systems; Technical Report; U.S. DOE Nuclear Energy Research Advisory Committee and the Generation IV International Forum: Washington, DC, USA, 2014. [Google Scholar]
- Wang, X.; Macian-Juan, R. Comparative Study of Basic Reactor Physics of the DFR Concept Using U-Pu and TRU Fuel Salts. In Proceedings of the International Conference on Nuclear Engineering, Shanghai, China, 2 July 2017; ASME International: New York, NY, USA, 2017. [Google Scholar]
- Huke, A.; Ruprecht, G.; Weißbach, D.; Czerski, K.; Gottlieb, S.; Hussein, A.; Herrmann, F. Dual-Fluid Reactor. In Molten Salt Reactors and Thorium Energy; Elsevier: Amsterdam, The Netherlands, 2017; pp. 619–633. ISBN 9780081012437. [Google Scholar]
- Wang, X.M. Analysis and Evaluation of the Dual Fluid Reactor Concept. Ph.D. Thesis, Technischen Universität München, Munich, Germany, 2017. [Google Scholar]
- Singh, O.P. Nuclear Reactors of the Future. In Physics of Nuclear Reactors, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Roelofs, F. Liquid Metal Thermal Hydraulics: State-of-the-Art and Future Perspectives. Nucl. Eng. Des. 2020, 362, 110590. [Google Scholar] [CrossRef]
- Grötzbach, G. Challenges in Low-Prandtl Number Heat Transfer Simulation and Modelling. Nucl. Eng. Des. 2013, 264, 41–55. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Macian-Juan, R.; Wang, X.; Liu, C.; Macian-Juan, R. Preliminary Hydraulic Analysis of the Distribution Zone in the Dual Fluid Reactor Concept. In Proceedings of the International Topical Meeting on Nuclear Reactor Thermal Hydraulics, Xi’an, China, 3–8 September 2017. [Google Scholar]
- Toki, T.; Teramoto, S.; Okamoto, K. Velocity and Temperature Profiles in Turbulent Channel Flow at Supercritical Pressure. J. Propuls. Power 2020, 36, 3–13. [Google Scholar] [CrossRef]
- Elgendy, H.; Czerski, K. Numerical Study of Flow and Heat Transfer Characteristics in a Simplified Dual Fluid Reactor. Energies 2023, 16, 4989. [Google Scholar] [CrossRef]
- Shams, A.; De Santis, D.; Padee, A.; Wasiuk, P.; Jarosiewicz, T.; Kwiatkowski, T.; Potempski, S. High-Performance Computing for Nuclear Reactor Design and Safety Applications. Nucl. Technol. 2020, 206, 283–295. [Google Scholar] [CrossRef]
- Kays, W.-M. Turbulent Prandtl Number. Where Are We? ASME J. Heat Transf. 1994, 116, 284–295. [Google Scholar] [CrossRef]
- Weigand, B.; Ferguson, J.R.; Crawford, M.E. An Extended Kays and Crawford Turbulent Prandtl Number Model. Int. J. Heat Mass Transf. 1997, 40, 4191–4196. [Google Scholar] [CrossRef]
- Huang, J.; Nicholson, G.L.; Duan, L.; Choudhari, M.M.; Bowersox, R.D. Simulation and Modeling of Cold-Wall Hypersonic Turbulent Boundary Layers on Flat Plate. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2020. [Google Scholar]
- Shams, A.; De Santis, A. Towards the Accurate Prediction of the Turbulent Flow and Heat Transfer in Low-Prandtl Fluids. Int. J. Heat Mass Transf. 2019, 130, 290–303. [Google Scholar] [CrossRef]
- De Santis, D.; De Santis, A.; Shams, A.; Kwiatkowski, T. The Influence of Low Prandtl Numbers on the Turbulent Mixed Convection in an Horizontal Channel Flow: DNS and Assessment of RANS Turbulence Models. Int. J. Heat Mass Transf. 2018, 127, 345–358. [Google Scholar] [CrossRef]
- Liu, C.; Li, X.; Luo, R.; Macian-Juan, R. Thermal Hydraulics Analysis of the Distribution Zone in Small Modular Dual Fluid Reactor. Metals 2020, 10, 1065. [Google Scholar] [CrossRef]
- Huke, A.; Ruprecht, G.; Weißbach, D.; Gottlieb, S.; Hussein, A.; Czerski, K. The Dual Fluid Reactor—A Novel Concept for a Fast Nuclear Reactor of High Efficiency. Ann. Nucl. Energy 2015, 80, 225–235. [Google Scholar] [CrossRef]
- Al-Habahbeh, O.M.; Al-Saqqa, M.; Safi, M.; Abo Khater, T. Review of Magnetohydrodynamic Pump Applications. Alex. Eng. J. 2016, 55, 1347–1358. [Google Scholar] [CrossRef]
- Nowak, M.; Spirzewski, M.; Czerski, K. Optimization of the DC Magnetohydrodynamic Pump for the Dual Fluid Reactor. Ann. Nucl. Energy 2022, 174, 109142. [Google Scholar] [CrossRef]
- Smith, C.F.; Halsey, W.G.; Brown, N.W.; Sienicki, J.J.; Moisseytsev, A.; Wade, D.C. SSTAR: The US Lead-Cooled Fast Reactor. J. Nucl. Mater. 2008, 376, 255–259. [Google Scholar] [CrossRef]
- Smith, C.F.; Cinotti, L. Lead-Cooled Fast Reactors. In Handbook of Generation IV Nuclear Reactors, 2nd ed.; Pioro, I.L., Ed.; Woodhead Publishing: Cambridge, UK, 2022. [Google Scholar]
- Smith, C. Lead-Cooled Fast Reactor (LFR) Design: Safety, Neutronics, Thermal Hydraulics, Structural Mechanics, Fuel, Core, and Plant Design; U.S. Department of Energy, Office of Scientific and Technical Information: Oak Ridge, TN, USA, 2010.
- Kawamura, H.; Ohsaka, K.; Abe, H.; Yamamoto, K. DNS of Turbulent Heat Transfer in Channel Flow with Low to Medium-High Prandtl Number Fluid. Int. J. Heat Fluid Flow 1998, 19, 482–491. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Hanjalić, K.; Launder, B. Modelling Turbulence in Engineering and the Environment; Cambridge University Press: Cambridge, UK, 2022; ISBN 9781108875400. [Google Scholar]
- Duponcheel, M.; Bricteux, L.; Manconi, M.; Winckelmans, G.; Bartosiewicz, Y. Assessment of RANS and Improved Near-Wall Modeling for Forced Convection at Low Prandtl Numbers Based on LES up to ReT = 2000. Int. J. Heat Mass Transf. 2014, 75, 470–482. [Google Scholar] [CrossRef]
- Nilsson, O.; Mehling, H.; Horn, R.; Fricke, J.; Hofmann, R.; Müller, S.; Eckstein, R.; Hofmann, D. Determination of the Thermal Diffusivity and Conductivity of Monocrystalline Silicon Carbide (300–2300 K). High Temp. High Press. 1997, 29, 73–79. [Google Scholar] [CrossRef]
- Nuclear Energy Agency. Handbook on Lead-Bismuth Eutectic Alloy and Lead Properties, Materials Compatibility, Thermal-Hydraulics and Technologies; Organisation for Economic Co-Operation and Development: Paris, France, 2015. [Google Scholar]
- ANSYS, Inc. ANSYS Fluent Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
- Ferziger, J.H. High-Order Methods for Computational Physics, 3rd ed.; Springer: Berlin, Germany, 2002. [Google Scholar]
- Incropera, F.P.; Dewitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Todreas, N.E.; Kazimi, M.S. Nuclear Systems: Thermal Hydraulic Fundamentals, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2011; Volume 1. [Google Scholar]

















| Property | Interpolation/Value |
|---|---|
| Thermal Conductivity (W/(m K)) | (611/(T − 115)) × 100 |
| Density (kg/m3) | 3210 |
| Temperature | Specific Heat (J/(kg K)) |
|---|---|
| 880 | 500 |
| 1060 | 625 |
| 1100 | 750 |
| 1220 | 1000 |
| 1280 | 1250 |
| Property | Interpolation Function |
|---|---|
| Density (kg/m3) | 11,463 − (1.32 × T) |
| Heat Capacity (J/(kg K)) | 175.1 − (4.961 × 10−2 × T) + (1.985 × 10−5 × T2) − (2.099 × 10−9 × T3) − (1.524 × 106 × T2) |
| Viscosity (Pa s) | EXP [(1032.2/T) − 7.6354] |
| Name | Variable | Value | Unit |
|---|---|---|---|
| Fuel Inlet | Velocity magnitude | 0.1 | m/s |
| Total temperature | 1473 | K | |
| Turbulent intensity | 4 | % | |
| The ratio of turbulent to molecular viscosity | 100 | - | |
| Coolant Inlet | Velocity magnitude | 0.5 | m/s |
| Total temperature | 873 | K | |
| Turbulent intensity | 4 | % | |
| The ratio of turbulent to molecular viscosity | 100 | - |
| Zone | Total Heat Transfer Rate Per Zone [kW] | Percentage of Heat Transfer [%] |
|---|---|---|
| Distribution zone | 19 | 41.6 |
| Middle Core zone | 24.76 | 54.3 |
| Collection zone | 1.84 | 4.0 |
| Total | 45.6 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elgendy, H.; Kubacki, S.; Czerski, K. Enhancing Thermal-Hydraulic Modelling in Dual Fluid Reactor Demonstrator: The Impact of Variable Turbulent Prandtl Number. Energies 2025, 18, 396. https://doi.org/10.3390/en18020396
Elgendy H, Kubacki S, Czerski K. Enhancing Thermal-Hydraulic Modelling in Dual Fluid Reactor Demonstrator: The Impact of Variable Turbulent Prandtl Number. Energies. 2025; 18(2):396. https://doi.org/10.3390/en18020396
Chicago/Turabian StyleElgendy, Hisham, Sławomir Kubacki, and Konrad Czerski. 2025. "Enhancing Thermal-Hydraulic Modelling in Dual Fluid Reactor Demonstrator: The Impact of Variable Turbulent Prandtl Number" Energies 18, no. 2: 396. https://doi.org/10.3390/en18020396
APA StyleElgendy, H., Kubacki, S., & Czerski, K. (2025). Enhancing Thermal-Hydraulic Modelling in Dual Fluid Reactor Demonstrator: The Impact of Variable Turbulent Prandtl Number. Energies, 18(2), 396. https://doi.org/10.3390/en18020396








