Study on Surface Charge Inversion and Accumulation Characteristics of DC Pillar Insulators Based on B-Spline Basis Functions
Abstract
1. Introduction
2. Experimental Platform and Method
2.1. Surface Potential Measurement System
2.2. Experimental Method
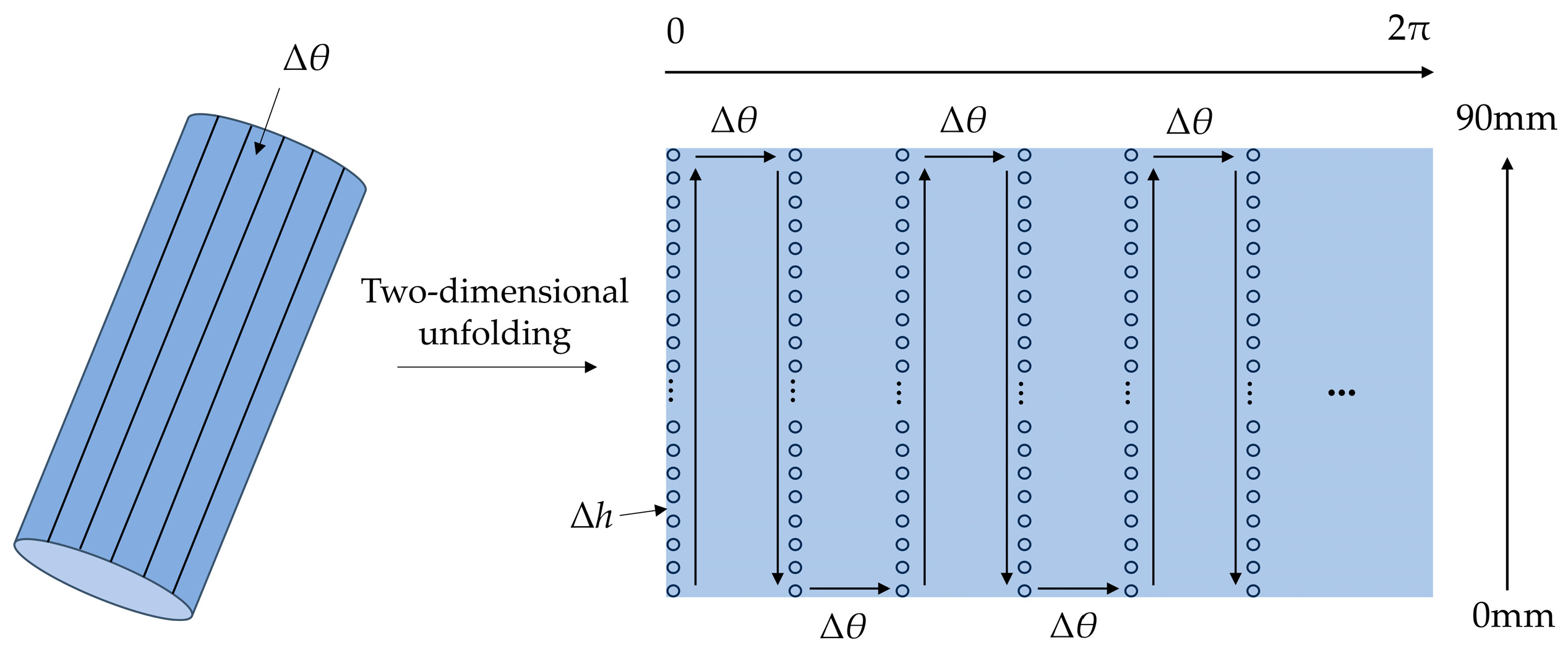
3. Charge Inversion Method Based on B-Spline Basis Function
3.1. Principle of Surface Charge Inversion
3.2. The Calculation Process of Surface Charge Inversion
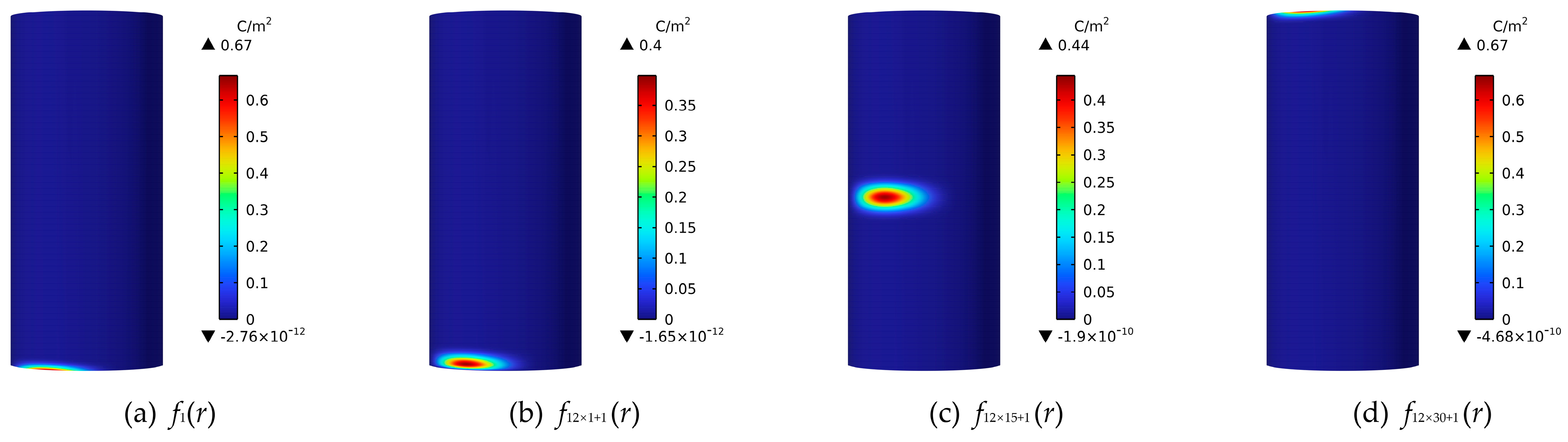
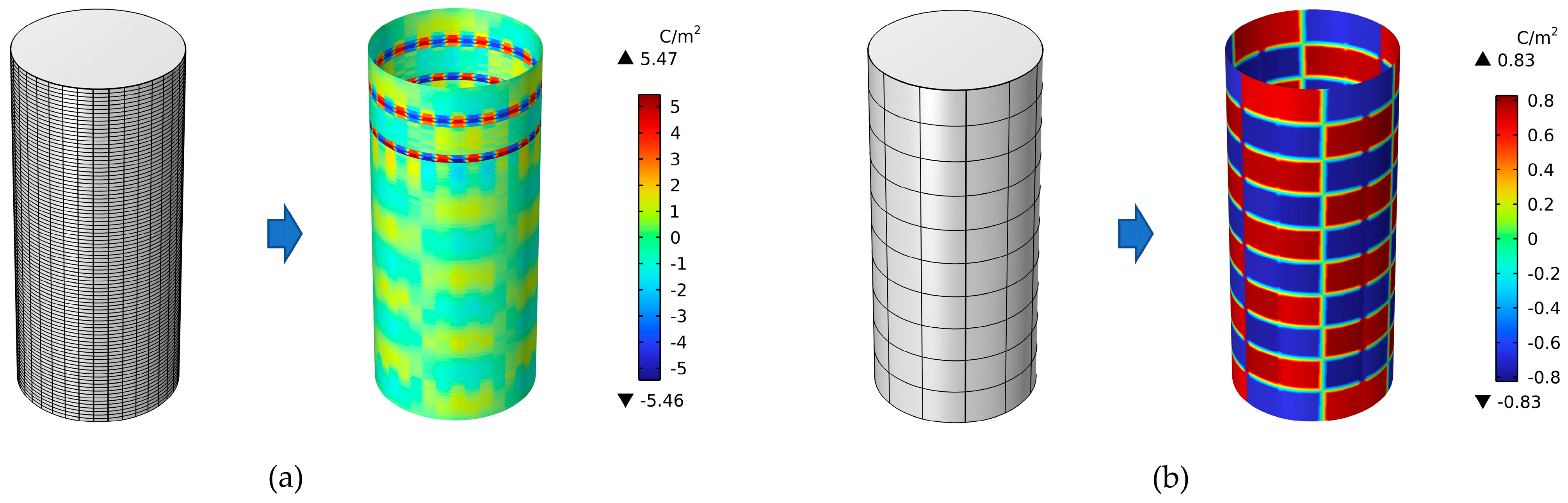
3.3. Verification of Inversion Calculation Method
4. DC Field Calculation Method Based on Charge Accumulation
4.1. Solid Side Conductance Equation
4.2. Gas-Side Conductance Equation
4.3. Gas–Solid Interface Charge Density Equation
4.4. Boundary Condition Setting
5. Surface Charge Accumulation Characteristics and Mechanism Analysis
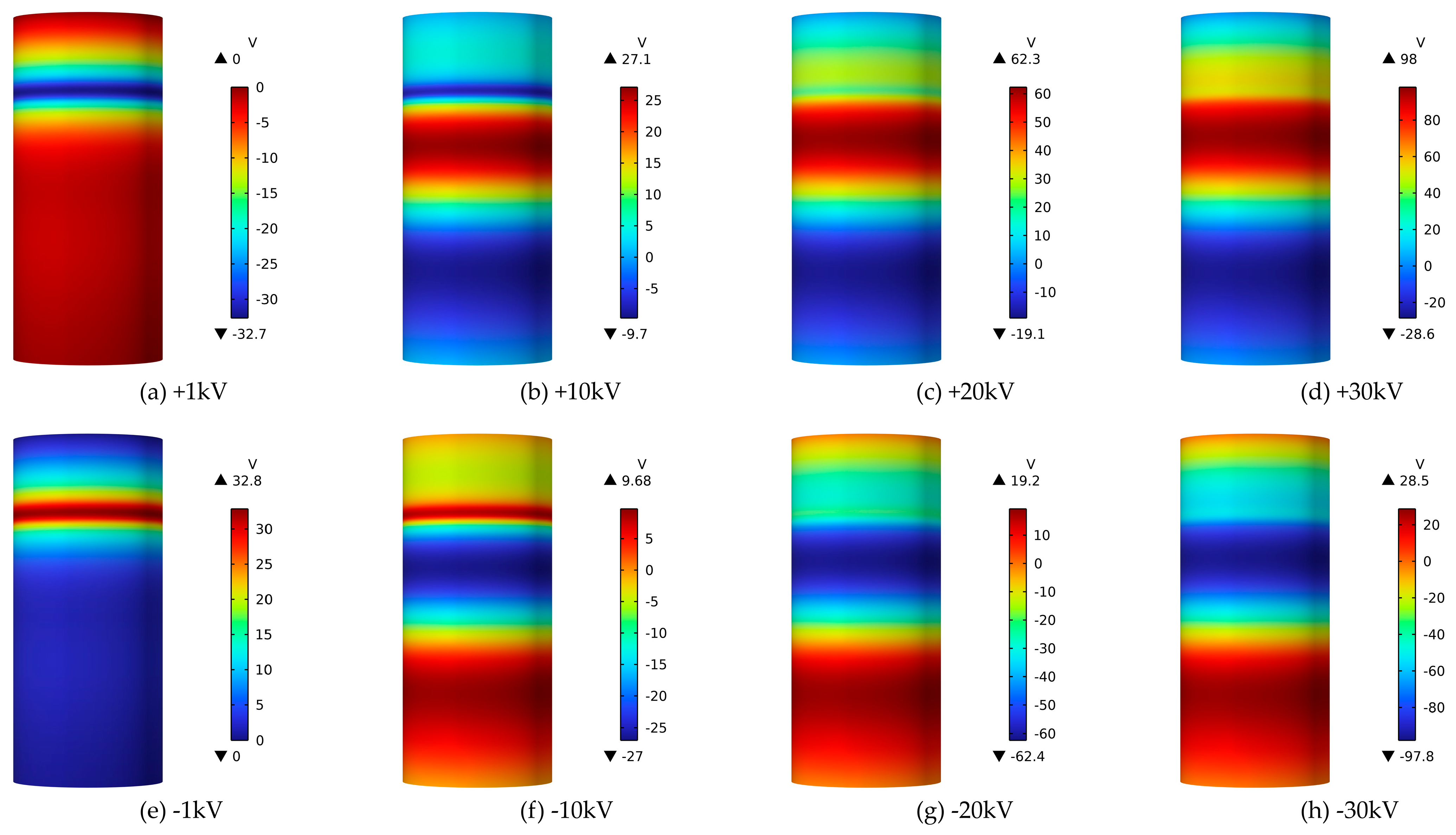
5.1. Surface Charge Distribution Characteristics
5.2. Analysis of Surface Charge Accumulation Mechanism
6. Conclusions
- (1)
- A surface charge inversion method of pillar insulators based on the B-spline basis function is proposed. The inversion shows smooth continuity in the circumferential and axial directions. The density peak error is only 2%, and the mean square error peak is 1.05%. Compared with the traditional inversion algorithm, it has obvious advantages in computational efficiency and accuracy. The charge distribution obtained by the proposed multi-physics coupling simulation model is consistent with the inverted charge distribution from the change trend, the position of the charge peak, and the size of the charge peak.
- (2)
- The surface potential distribution is basically the same in the ring direction, but it shows an oscillating distribution in the axial direction. It changes dynamically with the increase in voltage, and the overall trend is increasing. The potential distribution under positive and negative voltages is approximately mirror symmetry. The surface charge density almost does not change in the ring direction, but shows significant non-uniformity in the axial direction. The lower part of the sample always accumulates the same charge as the lower electrode symbol. The upper part of the sample accumulates a small amount of charge opposite to the upper electrode symbol when the voltage is 1 kV. With the increase in voltage, the same charge as the upper electrode symbol begins to accumulate. In the amplitude range of 1~30 kV, the charge peak opposite to the upper electrode symbol always exists in the upper part of the sample, and gradually decreases with the increase in voltage.
- (3)
- The modulation mechanism of the amplitude of the applied voltage on the dynamic balance of the gas–solid interface current and the surface charge accumulation is revealed: the current density on the upper part of the gas side is larger, and the current density on the lower part is smaller. Under low-voltage conditions, the current density on the upper solid side is less than that on the gas side, and the charge on the upper part of the insulator accumulates with the opposite sign of the upper electrode. With the increase in the applied voltage, the current density on the solid side increases, and the charge on the surface of the insulator accumulates with the same sign of the electrode to weaken the field strength and balance the normal electric field components on both sides.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, H.; Wu, G.; Chen, M.; Deng, J.; Li, X. Analysis and Disposal of Typical Breakdown Failure for Resin Impregnated Paper Bushing in the Valve Side of HVDC Converter Transformer. Energies 2019, 12, 4303. [Google Scholar] [CrossRef]
- Muzzammel, R. Traveling Waves-Based Method for Fault Estimation in HVDC Transmission System. Energies 2019, 12, 3614. [Google Scholar] [CrossRef]
- Zhu, C.; Duan, X.; Li, S.; Zhang, Z.; Guan, J.; Xin, Y.; Gao, Y. Effect of Gas Content on Surface Charge Accumulation of Epoxy Insulator in C4F7N/CO2/O2 Mixture Under AC Voltage. Energies 2025, 18, 4390. [Google Scholar] [CrossRef]
- Moukengué Imano, A. Accumulation of surface charges on the particle contaminated spacer surface in compressed gas under impulse voltage stress. J. Electrostat. 2004, 61, 1–19. [Google Scholar]
- Feng, W.; Yuchang, Q.; Pfeiffer, W.; Kuffel, E. Insulator surface charge accumulation under impulse voltage. IEEE Trans. Dielectr. Electr. Insul. 2004, 11, 847–854. [Google Scholar] [CrossRef]
- Zhu, F.; Fouracre, R.A.; Fairish, O. Investigations of surface charging of DC insulator spacers. In Proceedings of the 1995 Conference on Electrical Insulation and Dielectric Phenomena, Virginia Beach, VA, USA, 22–25 October 1995; pp. 428–431. [Google Scholar]
- Ma, J.; Zhang, Q.; You, H.; Wu, Z.; Wen, T.; Guo, C.; Wang, G.; Gao, C. Study on insulation characteristics of GIS under combined voltage of DC and lightning impulse. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 893–900. [Google Scholar] [CrossRef]
- Du, B.; Huang, P.; Xing, Y. Surface charge and flashover characteristics of fluorinated PP under pulse voltage. IET Sci. Meas. Technol. 2017, 11, 18–24. [Google Scholar] [CrossRef]
- Gao, Y.; Zhao, H.; Yuan, X.; Wang, H. Numerical simulation of surface charge inhibition performance on epoxy insulator under DC voltage by flexible coating strategy. High Volt. 2022, 7, 553–563. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, L.; Yin, F.; Farzaneh, M.; Mei, H.; Wen, L. The Effect of a Vertical Electric Field on the Surface Flashover Characteristics of a Bushing Model. Energies 2018, 11, 1607. [Google Scholar] [CrossRef]
- Xing, Y.; Wang, Z.; Liu, L.; Xu, Y.; Yang, Y.; Liu, S.; Zhou, F.; He, S.; Li, C. Defects and failure types of solid insulation in gas-insulated switchgear: In situ study and case analysis. High Volt. 2022, 7, 158–164. [Google Scholar] [CrossRef]
- Ma, J.; Tao, F.; Ma, Y.; Zhao, K.; Li, H.; Wen, T.; Zhang, Q. Quantitative Analysis on the Influence of Surface Charges on Flashover of Insulators in SF6. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 274–281. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, G.; Wang, X. Characteristics and mechanisms of surface charge accumulation on a cone-type insulator under dc voltage. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 150–155. [Google Scholar] [CrossRef]
- Qi, B.; Gao, C.; Liu, S.; Zhao, L.; Li, C. Surface charge distribution on GIS insulator under DC/AC voltage. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3173–3181. [Google Scholar] [CrossRef]
- Ootera, H.; Nakanishi, K. Analytical method for evaluating surface charge distribution on a dielectric from capacitive probe measurement-application to a cone-type spacer in +or-500 kV DC-GIS. IEEE Trans. Power Deliv. 1988, 3, 165–172. [Google Scholar] [CrossRef]
- Kumada, A.; Okabe, S. Charge distribution measurement on a truncated cone spacer under DC voltage. IEEE Trans. Dielectr. Electr. Insul. 2004, 11, 929–938. [Google Scholar] [CrossRef]
- Wang, H.; Xue, J.Y.; Wang, Y.B.; Su, G.Q.; Deng, J.B.; Mu, H.B.; Zhang, G.J. Improved algorithm of surface charge density distribution and electric field distribution on insulating materials. In Proceedings of the 2017 1st International Conference on Electrical Materials and Power Equipment, Xi’an, China, 14–17 May 2017; pp. 332–335. [Google Scholar]
- Okabe, S.; Kumada, A. Measurement Methods of Accumulated Electric Charges on Spacer in Gas Insulated Switchgear. IEEE Trans. Power Deliv. 2007, 22, 1547–1556. [Google Scholar] [CrossRef]
- Lutz, B.; Kindersberger, J. Surface charge accumulation on cylindrical polymeric model insulators in air: Simulation and measurement. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 2040–2048. [Google Scholar] [CrossRef]
- Schueller, M.; Straumann, U.; Franck, C.M. Role of ion sources for spacer charging in SF6 gas insulated HVDC systems. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 352–359. [Google Scholar] [CrossRef]
- Guillermin, C.; Rain, P.; Rowe, S.W. Transient and steady-state currents in epoxy resin. J. Phys. D Appl. Phys. 2006, 39, 515. [Google Scholar] [CrossRef]
- Kindersberger, J.; Lederle, C. Surface charge decay on insulators in air and sulfurhexafluorid—Part I: Simulation. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 941–948. [Google Scholar] [CrossRef]
- Volpov, E. HVDC gas insulated apparatus: Electric field specificity and insulation design concept. IEEE Electr. Insul. Mag. 2002, 18, 7–36. [Google Scholar] [CrossRef]
- Straumann, U.; Schuller, M.; Franck, C.M. Theoretical investigation of HVDC disc spacer charging in SF6 gas insulated systems. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 2196–2205. [Google Scholar] [CrossRef]
- Chen, M.; Liu, X.; Liang, C.; Zhao, Y.; Tang, H. Study on Surface Charge Accumulation Characteristics of Resin Impregnated Paper Wall Bushing Core Under Positive DC Voltage. Energies 2019, 12, 4420. [Google Scholar] [CrossRef]









| Name | Physical Quantity | Numerical Value | Reference |
|---|---|---|---|
| Formation Rate of Gas Ion Pair | S/(IP·cm−3·s−1) | 50 | [20] |
| Positive and Negative Ion Mobility | μp, μn/(cm2·V−1·s−1) | 4.8 | [20] |
| Ion Recombination Coefficient | α/(cm3·s−1) | 2.3 × 10−7 | [24] |
| Boltzmann’s Constant | kB/(J·K−1) | 1.38 × 10−23 | [25] |
| Relative Dielectric Constant of SF6 | ε2 | 1.002 | [25] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Xu, H.; Wang, J.; Zhang, J.; Li, S.; Fang, X. Study on Surface Charge Inversion and Accumulation Characteristics of DC Pillar Insulators Based on B-Spline Basis Functions. Energies 2025, 18, 5531. https://doi.org/10.3390/en18205531
Yang X, Xu H, Wang J, Zhang J, Li S, Fang X. Study on Surface Charge Inversion and Accumulation Characteristics of DC Pillar Insulators Based on B-Spline Basis Functions. Energies. 2025; 18(20):5531. https://doi.org/10.3390/en18205531
Chicago/Turabian StyleYang, Xi, Houde Xu, Jie Wang, Jian Zhang, Shun Li, and Xinran Fang. 2025. "Study on Surface Charge Inversion and Accumulation Characteristics of DC Pillar Insulators Based on B-Spline Basis Functions" Energies 18, no. 20: 5531. https://doi.org/10.3390/en18205531
APA StyleYang, X., Xu, H., Wang, J., Zhang, J., Li, S., & Fang, X. (2025). Study on Surface Charge Inversion and Accumulation Characteristics of DC Pillar Insulators Based on B-Spline Basis Functions. Energies, 18(20), 5531. https://doi.org/10.3390/en18205531





