A Review of Diagnostic Methods for Yaw Errors in Horizontal Axis Wind Turbines
Abstract
:1. Introduction
2. Yaw Control System and Yaw Error
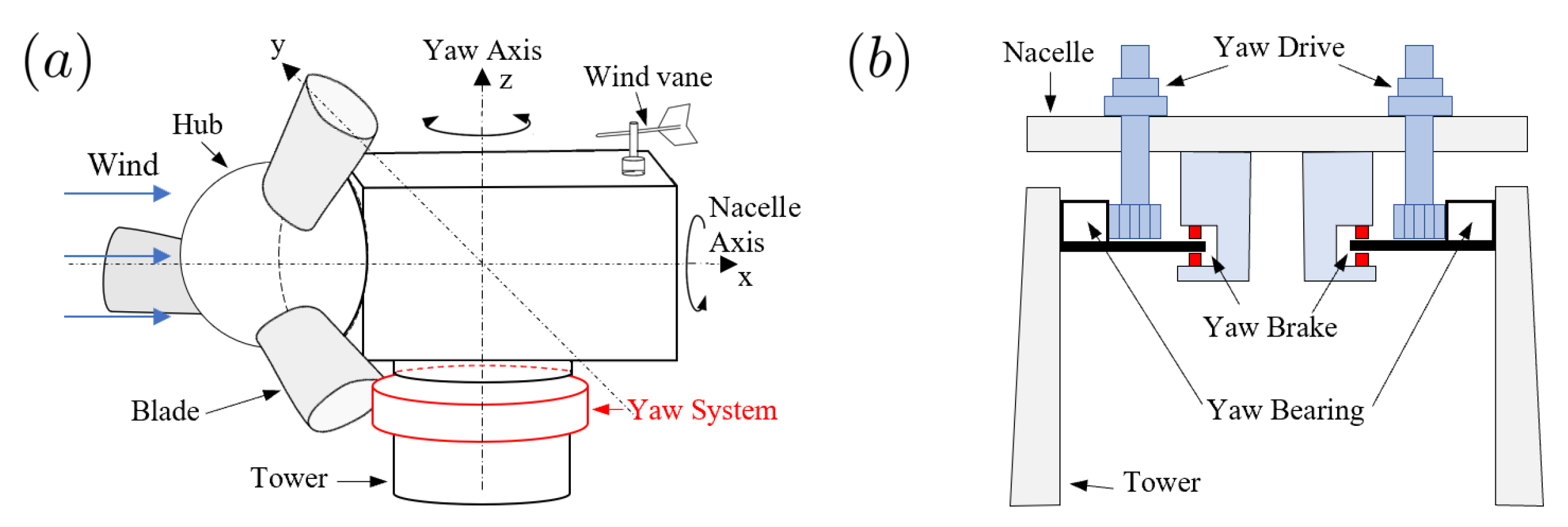
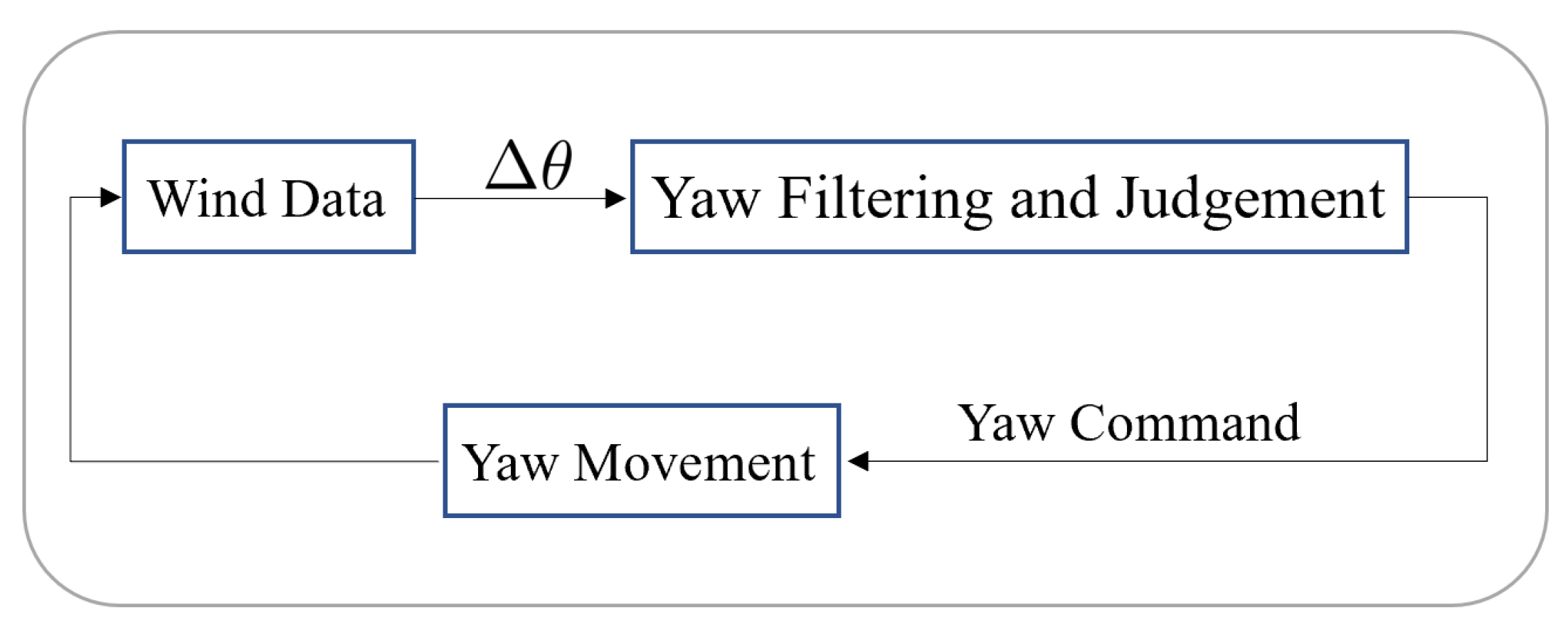
2.1. Yaw Control System
- Temporally filter the input yaw angle for different periods.
- Decide the need for the rotor rotation by comparing the result of the first step with the predefined threshold. If yes, compute the information about yaw braking.
- Rotate the rotor against the wind based on yaw braking information to reduce the yaw angle.
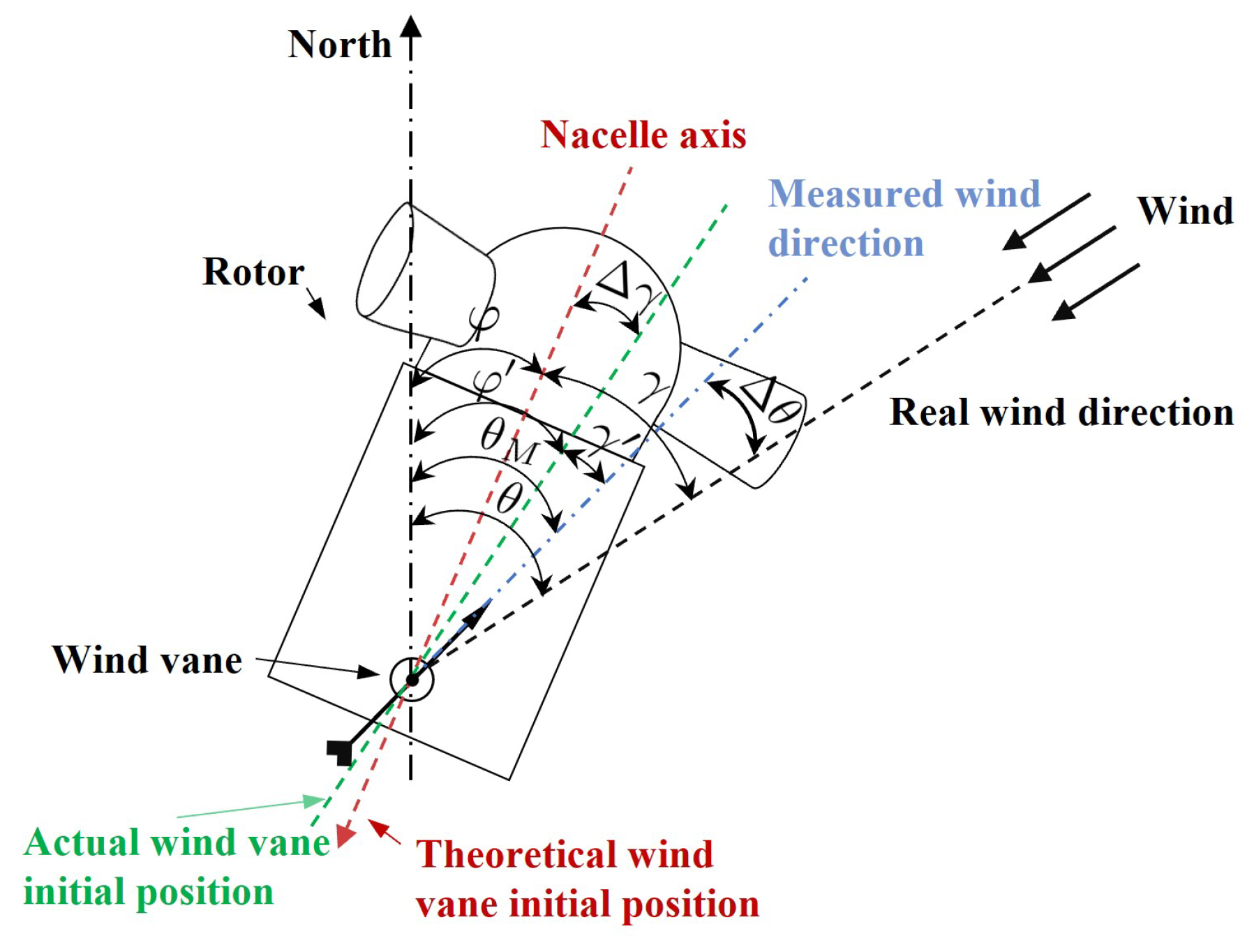
2.2. Definition and Classification of Yaw Error
3. Diagnostic Methods for Yaw Error
3.1. Diagnostic Methods Based on LiDAR Data
3.2. Diagnostic Methods Based on SCADA Data
3.3. Diagnostic Methods Based on the LiDAR and SCADA Data
4. Summary of the Review
Funding
Data Availability Statement
Conflicts of Interest
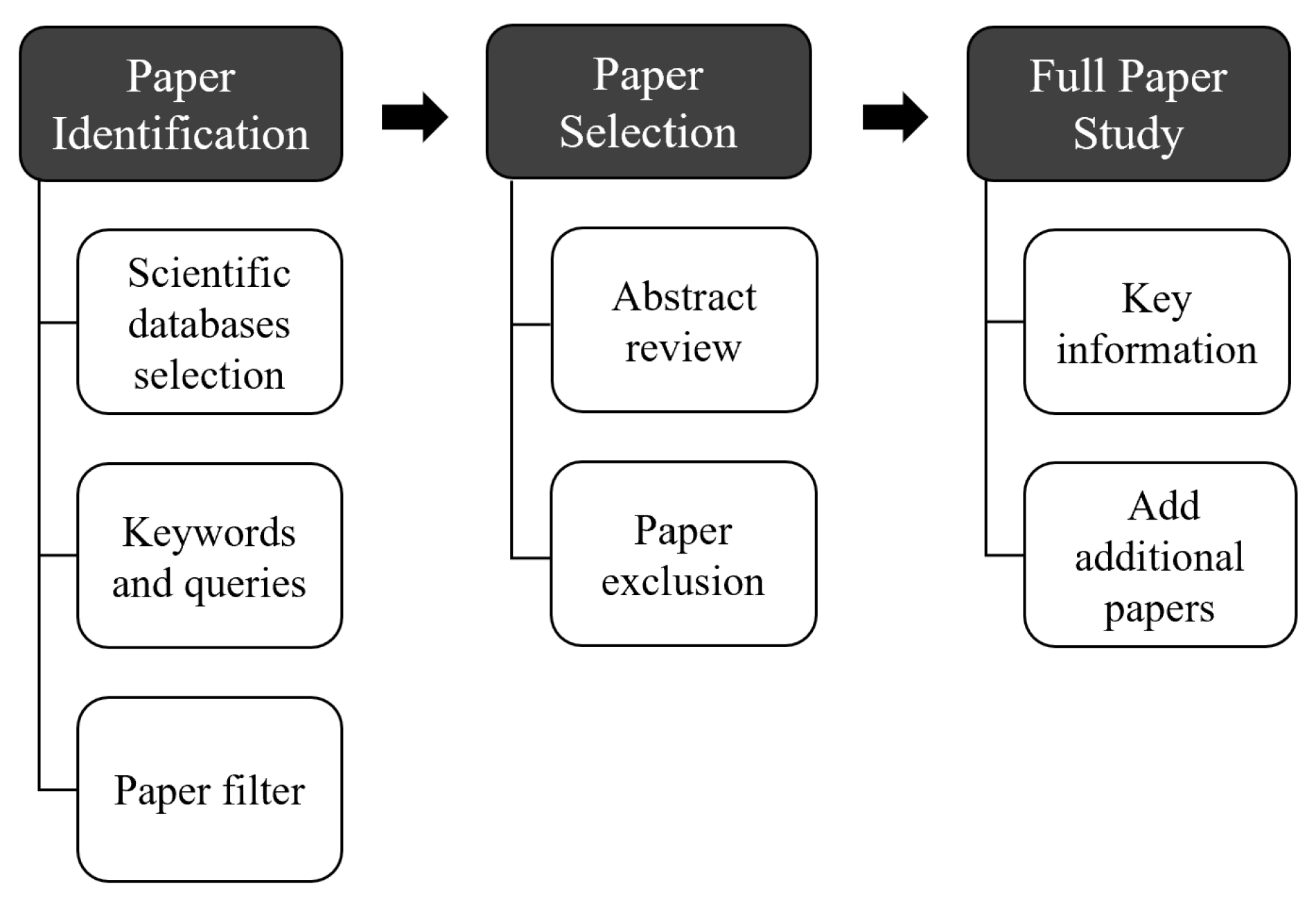
Appendix A. Procedure of the Literature Review
| Keywords | Web of Science | Scopus |
|---|---|---|
| wind turbine, wind turbines, yaw error, yaw misalignment, detection, detecting, diagnosis, diagnostic | TS = (wind turbine OR wind turbines) AND TS = (yaw error OR yaw misalignment AND TS = (detection OR detecting OR diagnosis OR diagnostic) | (TITLE-ABS-KEY(“wind turbine”) OR TITLE-ABS-KEY(“wind turbines”) AND TITLE-ABS-KEY(“yaw error”) OR TITLE-ABS-KEY(“yaw misalignment”) AND TITLE-ABS-KEY(“detection”) OR TITLE-ABS-KEY(“detecting”) OR TITLE-ABS-KEY(“diagnosis”) OR TITLE-ABS-KEY(“diagnostic”) |
- The source of the data (e.g., SCADA, LiDAR, etc.) used for diagnosis.
- The methods employed for diagnosis.
- The types of errors that can be identified.
- The merits and demerits of the employed diagnostic methods.

References
- Sadorsky, P. Wind energy for sustainable development: Driving factors and future outlook. J. Clean. Prod. 2021, 289, 125779. [Google Scholar] [CrossRef]
- Chang, L.; Saydaliev, H.B.; Meo, M.S.; Mohsin, M. How renewable energy matter for environmental sustainability: Evidence from top-10 wind energy consumer countries of European Union. Sustain. Energy Grids Netw. 2022, 31, 100716. [Google Scholar] [CrossRef]
- GWEC. Global Wind Report 2024; Technical Report; Global Wind Energy Council: Lisbon, Portugal, 2024. [Google Scholar]
- IRENA. World Energy Transitions Outlook 2023: 1.5 °C Pathway; Technical Report; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2023. [Google Scholar]
- Gebraad, P.M.O.; Teeuwisse, F.W.; van Wingerden, J.W.; Fleming, P.A.; Ruben, S.D.; Marden, J.R.; Pao, L.Y. Wind plant power optimization through yaw control using a parametric model for wake effects-a CFD simulation study. Wind Energy 2016, 19, 95–114. [Google Scholar] [CrossRef]
- Bowen, A.; Zakay, N.; Ives, R. The field performance of a remote 10 kW wind turbine. Renew. Energy 2003, 28, 13–33. [Google Scholar] [CrossRef]
- Rauh, A.; Seelert, W. The Betz Optimum Efficiency for Windmills. Appl. Energy 1984, 17, 15–23. [Google Scholar] [CrossRef]
- Wan, S.; Cheng, L.; Sheng, X. Effects of Yaw Error on Wind Turbine Running Characteristics Based on the Equivalent Wind Speed Model. Energies 2015, 8, 6286–6301. [Google Scholar] [CrossRef]
- Astolfi, D.; Pandit, R.; Lombardi, A.; Terzi, L. Diagnosis of wind turbine systematic yaw error through nacelle anemometer measurement analysis. Sustain. Energy Grids Netw. 2023, 34, 101071. [Google Scholar] [CrossRef]
- Boorsma, K. Power and Loads for Wind Turbines in Yawed Conditions. Analysis of Field Measurements and Aerodynamic Predictions. 2012. Available online: https://publications.tno.nl/publication/34629178/y56dz3/e12047.pdf (accessed on 15 August 2024).
- Jeong, M.S.; Kim, S.W.; Lee, I.; Yoo, S.J.; Park, K.C. The impact of yaw error on aeroelastic characteristics of a horizontal axis wind turbine blade. Renew. Energy 2013, 60, 256–268. [Google Scholar] [CrossRef]
- Dai, L.; Zhou, Q.; Zhang, Y.; Yao, S.; Kang, S.; Wang, X. Analysis of wind turbine blades aeroelastic performance under yaw conditions. J. Wind. Eng. Ind. Aerodyn. 2017, 171, 273–287. [Google Scholar] [CrossRef]
- Bernardoni, F.; Rotea, M.A.; Leonardi, S. Impact of yaw misalignment on turbine loads in the presence of wind farm blockage. Wind Energy 2024, 27, 535–548. [Google Scholar] [CrossRef]
- Howland, M.F.; Bas Quesada, J.; Pena Martinez, J.J.; Palou Larranaga, F.; Yadav, N.; Chawla, J.S.; Sivaram, V.; Dabiri, J.O. Collective wind farm operation based on a predictive model increases utility-scale energy production. Nat. Energy 2022, 7, 818–827. [Google Scholar] [CrossRef]
- Lopez, D.; Kuo, J.; Li, N. A novel wake model for yawed wind turbines. Energy 2019, 178, 158–167. [Google Scholar] [CrossRef]
- Medici, D. Experimental Studies of Wind Turbine Wakes: Power Optimisation and Meandering. Doctoral Dissertation, KTH, Stockholm, Sweden, 2005. [Google Scholar]
- Cherdantseva, Y.; Burnap, P.; Blyth, A.; Eden, P.; Jones, K.; Soulsby, H.; Stoddart, K. A review of cyber security risk assessment methods for SCADA systems. Comput. Secur. 2016, 56, 1–27. [Google Scholar] [CrossRef]
- Kim, M.G.; Dalhoff, P.H. Yaw Systems for wind turbines—Overview of concepts, current challenges and design methods. J. Phys. Conf. Ser. 2014, 524, 012086. [Google Scholar] [CrossRef]
- Fleming, P.A.; Scholbrock, A.K.; Jehu, A.; Davoust, S.; Osler, E.; Wright, A.D.; Clifton, A. Field-test results using a nacelle-mounted lidar for improving wind turbine power capture by reducing yaw misalignment. J. Phys. Conf. Ser. 2014, 524, 012002. [Google Scholar] [CrossRef]
- Song, D.; Yang, J.; Fan, X.; Liu, Y.; Liu, A.; Chen, G.; Joo, Y.H. Maximum power extraction for wind turbines through a novel yaw control solution using predicted wind directions. Energy Convers. Manag. 2018, 157, 587–599. [Google Scholar] [CrossRef]
- Kragh, K.; Fleming, P. Rotor Speed Dependent Yaw Control of Wind Turbines Based on Empirical Data. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, Tennessee, 9–12 January 2012. [Google Scholar] [CrossRef]
- Choi, D.; Shin, W.; Ko, K.; Rhee, W. Static and Dynamic Yaw Misalignments of Wind Turbines and Machine Learning Based Correction Methods Using LiDAR Data. IEEE Trans. Sustain. Energy 2019, 10, 971–982. [Google Scholar] [CrossRef]
- Bao, Y.; Yang, Q. A Data-Mining Compensation Approach for Yaw Misalignment on Wind Turbine. IEEE Trans. Ind. Informatics 2021, 17, 8154–8164. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Q. A Method for Yaw Error Alignment of Wind Turbine Based on LiDAR. IEEE Access 2020, 8, 25052–25059. [Google Scholar] [CrossRef]
- Jing, B.; Qian, Z.; Pei, Y.; Zhang, L.; Yang, T. Improving wind turbine efficiency through detection and calibration of yaw misalignment. Renew. Energy 2020, 160, 1217–1227. [Google Scholar] [CrossRef]
- Pei, Y.; Qian, Z.; Jing, B.; Kang, D.; Zhang, L. Data-Driven Method for Wind Turbine Yaw Angle Sensor Zero-Point Shifting Fault Detection. Energies 2018, 11, 553. [Google Scholar] [CrossRef]
- Yang, J.; Wang, L.; Song, D.; Huang, C.; Huang, L.; Wang, J. Incorporating environmental impacts into zero-point shifting diagnosis of wind turbines yaw angle. Energy 2022, 238, 121762. [Google Scholar] [CrossRef]
- Astolfi, D.; Castellani, F.; Terzi, L. An Operation Data-Based Method for the Diagnosis of Zero-Point Shift of Wind Turbines Yaw Angle. J. Sol. Energy Eng. 2019, 142, 024501. [Google Scholar] [CrossRef]
- Kragh, K.; Hansen, M.; Mikkelsen, T. Improving Yaw Alignment Using Spinner Based LIDAR. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. [Google Scholar] [CrossRef]
- Kragh, K.A.; Hansen, M.H.; Mikkelsen, T. Precision and shortcomings of yaw error estimation using spinner-based light detection and ranging. Wind Energy 2013, 16, 353–366. [Google Scholar] [CrossRef]
- Scholbrock, A.K.; Fleming, P.A.; Wright, A.; Slinger, C.; Medley, J.; Harris, M. Field Test Results from Lidar Measured Yaw Control for Improved Power Capture with the NREL Controls Advanced Research Turbine. In Proceedings of the 33rd Wind Energy Symposium, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Bakhshi, R.; Sandborn, P. Analysis of Wind Turbine Capacity Factor Improvement by Correcting Yaw Error Using LIDAR. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2017; Volume 6, p. V006T08A092. [Google Scholar] [CrossRef]
- Bakhshi, R.; Sandborn, P. Using LIDAR on Wind Turbines for Yaw Error Correction: A Financial Prospective. In ASME Power Conference; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 2, p. V002T12A007. [Google Scholar] [CrossRef]
- Bao, Y.; Yang, Q.; Li, S.; Miao, K.; Sun, Y. A data-driven approach for identification and compensation of wind turbine inherent yaw misalignment. In Proceedings of the 2018 33rd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Nanjing, China, 18–20 May 2018; pp. 961–966. [Google Scholar] [CrossRef]
- Qu, C.; Lin, Z.; Chen, P.; Liu, J.; Chen, Z.; Xie, Z. An improved data-driven methodology and field-test verification of yaw misalignment calibration on wind turbines. Energy Convers. Manag. 2022, 266, 115786. [Google Scholar] [CrossRef]
- Gao, L.; Hong, J. Data-driven yaw misalignment correction for utility-scale wind turbines. J. Renew. Sustain. Energy 2021, 13, 063302. [Google Scholar] [CrossRef]
- Astolfi, D.; Castellani, F.; Scappaticci, L.; Terzi, L. Diagnosis of wind turbine misalignment through SCADA Data. Diagnostyka 2017, 18, 17–24. [Google Scholar]
- Astolfi, D.; Castellani, F.; Becchetti, M.; Lombardi, A.; Terzi, L. Wind Turbine Systematic Yaw Error: Operation Data Analysis Techniques for Detecting It and Assessing Its Performance Impact. Energies 2020, 13, 2351. [Google Scholar] [CrossRef]
- Sheibat-Othman, N.; Othman, S.; Tayari, R.; Sakly, A.; Odgaard, P.F.; Larsen, L.F. Estimation of the wind turbine yaw error by support vector machines. IFAC-PapersOnLine 2015, 48, 339–344. [Google Scholar] [CrossRef]
- Tsioumas, E.; Karakasis, N.; Jabbour, N.; Mademlis, C. Indirect estimation of the Yaw-Angle misalignment in a horizontal axis wind turbine. In Proceedings of the 2017 IEEE 11th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Tinos, Greece, 29 August–1 September 2017; pp. 45–51. [Google Scholar] [CrossRef]
- Ouyang, T.; Kusiak, A.; He, Y. Predictive model of yaw error in a wind turbine. Energy 2017, 123, 119–130. [Google Scholar] [CrossRef]
- Pandit, R.; Astolfi, D.; Tang, A.M.; Infield, D. Sequential Data-Driven Long-Term Weather Forecasting Models’ Performance Comparison for Improving Offshore Operation and Maintenance Operations. Energies 2022, 15, 7233. [Google Scholar] [CrossRef]
- Solomin, E.V.; Terekhin, A.A.; Martyanov, A.S.; Shishkov, A.N.; Kovalyov, A.A.; Ismagilov, D.R.; Ryavkin, G.N. Horizontal axis wind turbine yaw differential error reduction approach. Energy Convers. Manag. 2022, 254, 115255. [Google Scholar] [CrossRef]
- Chen, P.; Lin, Z.; Xie, Z.; Qu, C. Real-time yaw-misalignment calibration and field-test verification of wind turbine via machine learning methods. Mech. Syst. Signal Process. 2024, 208, 110972. [Google Scholar] [CrossRef]
- Held, D.P.; Mann, J. Lidar estimation of rotor-effective wind speed—An experimental comparison. Wind. Energy Sci. 2019, 4, 421–438. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, H.; Shi, P.; Chen, X.; Fang, C. Overview of fault diagnosis and life prediction for wind turbine Yaw system. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2022, 42, 4871–4883. [Google Scholar] [CrossRef]
- Yang, X.; Howard, K.B.; Guala, M.; Sotiropoulos, F. Effects of a three-dimensional hill on the wake characteristics of a model wind turbine. Phys. Fluids 2015, 27, 025103. [Google Scholar] [CrossRef]
- Porte-Agel, F.; Bastankhah, M.; Shamsoddin, S. Wind-Turbine and Wind-Farm Flows: A Review. Bound.-Layer Meteorol. 2020, 174, 1–59. [Google Scholar] [CrossRef]
- Astolfi, D.; Pandit, R.; Gao, L.; Hong, J. Individuation of Wind Turbine Systematic Yaw Error through SCADA Data. Energies 2022, 15, 8165. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Zhang, L.; Cao, F.; Wang, L. Optimization of the Yaw Control Error of Wind Turbine. Front. Energy Res. 2021, 9, 626681. [Google Scholar] [CrossRef]
- Little, M.; Pope, K. Performance modelling for wind turbines operating in harsh conditions. Int. J. Energy Res. 2017, 41, 417–428. [Google Scholar] [CrossRef]
- Skvorc, P.; Kozmar, H. Wind energy harnessing on tall buildings in urban environments. Renew. Sustain. Energy Rev. 2021, 152, 111662. [Google Scholar] [CrossRef]
- Mittelmeier, N.; Kühn, M. Determination of optimal wind turbine alignment into the wind and detection of alignment changes with SCADA data. Wind Energy Sci. 2018, 3, 395–408. [Google Scholar] [CrossRef]
- Yang, J.; Wang, L.; Song, D. Diagnostic Method of Zero-point Shifting of Wind Turbine Yaw Angle Based on Isolated Forest and Sparse Gaussian Process Regression. Proc. CSEE 2021, 41, 6198–6211. [Google Scholar] [CrossRef]
- Kou, P.; Wang, C.; Liang, D.; Cheng, S.; Gao, L. Deep learning approach for wind speed forecasts at turbine locations in a wind farm. IET Renew. Power Gener. 2020, 14, 2416–2428. [Google Scholar] [CrossRef]
- Pargoo, N.S.; Amini, E.; Zadeh, M.M.; Hajj, M. A Swarm Intelligence Approach for Statistical Modeling of Wind Speed and Direction: A Case Study of New York Bight. In Computing in Civil Engineering 2023; ASCE: Reston, VA, USA, 2023; pp. 176–185. [Google Scholar] [CrossRef]
- Dinh, M.C.; Ngo, M.T.; Kim, C.; Lee, S.J.; Yu, I.K.; Park, M. Implementation of Digital Twin-Assisted Condition Monitoring and Fault Diagnosis for Wind Turbines. In Proceedings of the 2023 12th International Conference on Renewable Energy Research and Applications, ICRERA, Oshawa, ON, Canada, 29 August–1 September 2023; pp. 146–150. [Google Scholar] [CrossRef]
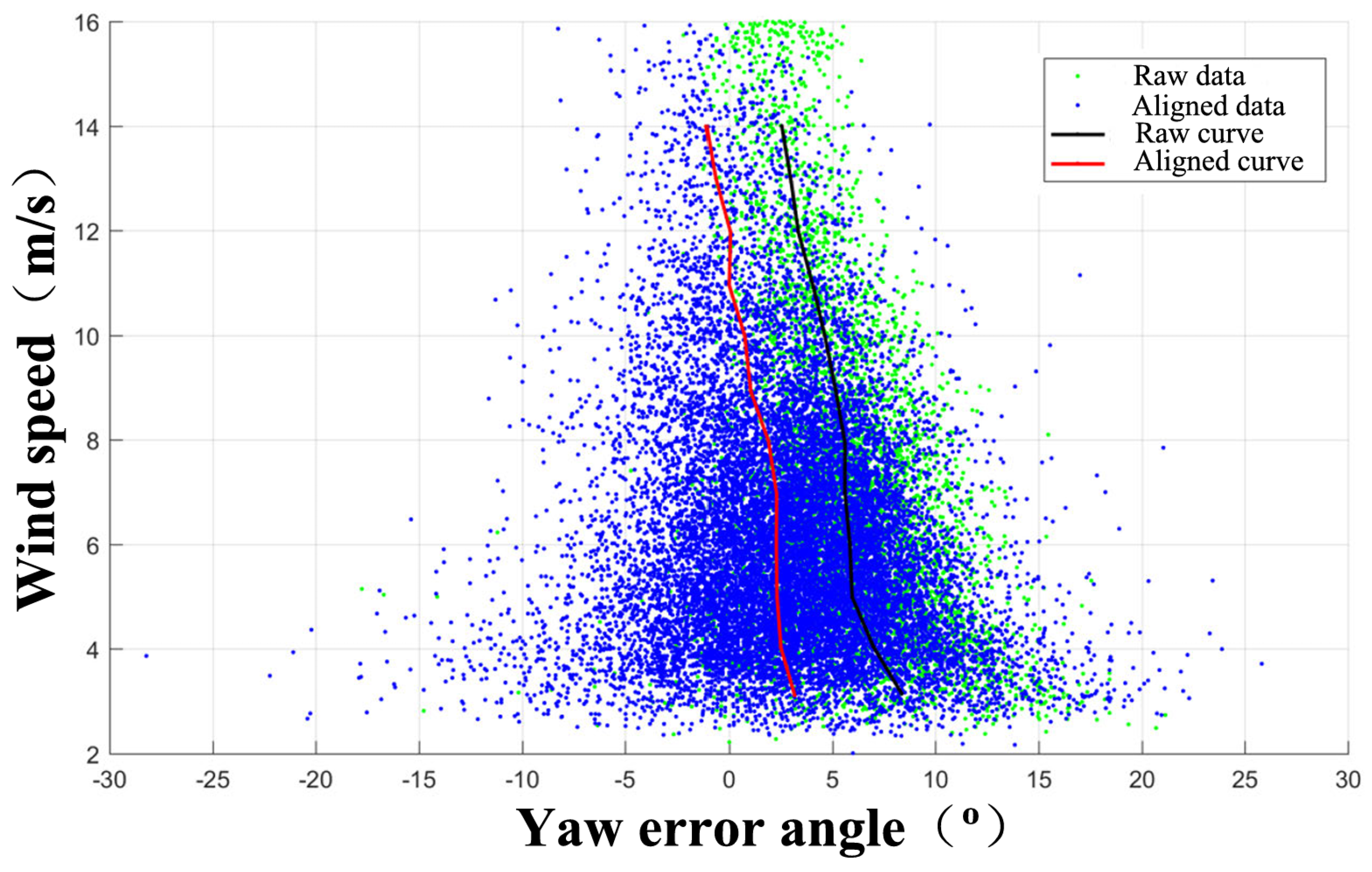
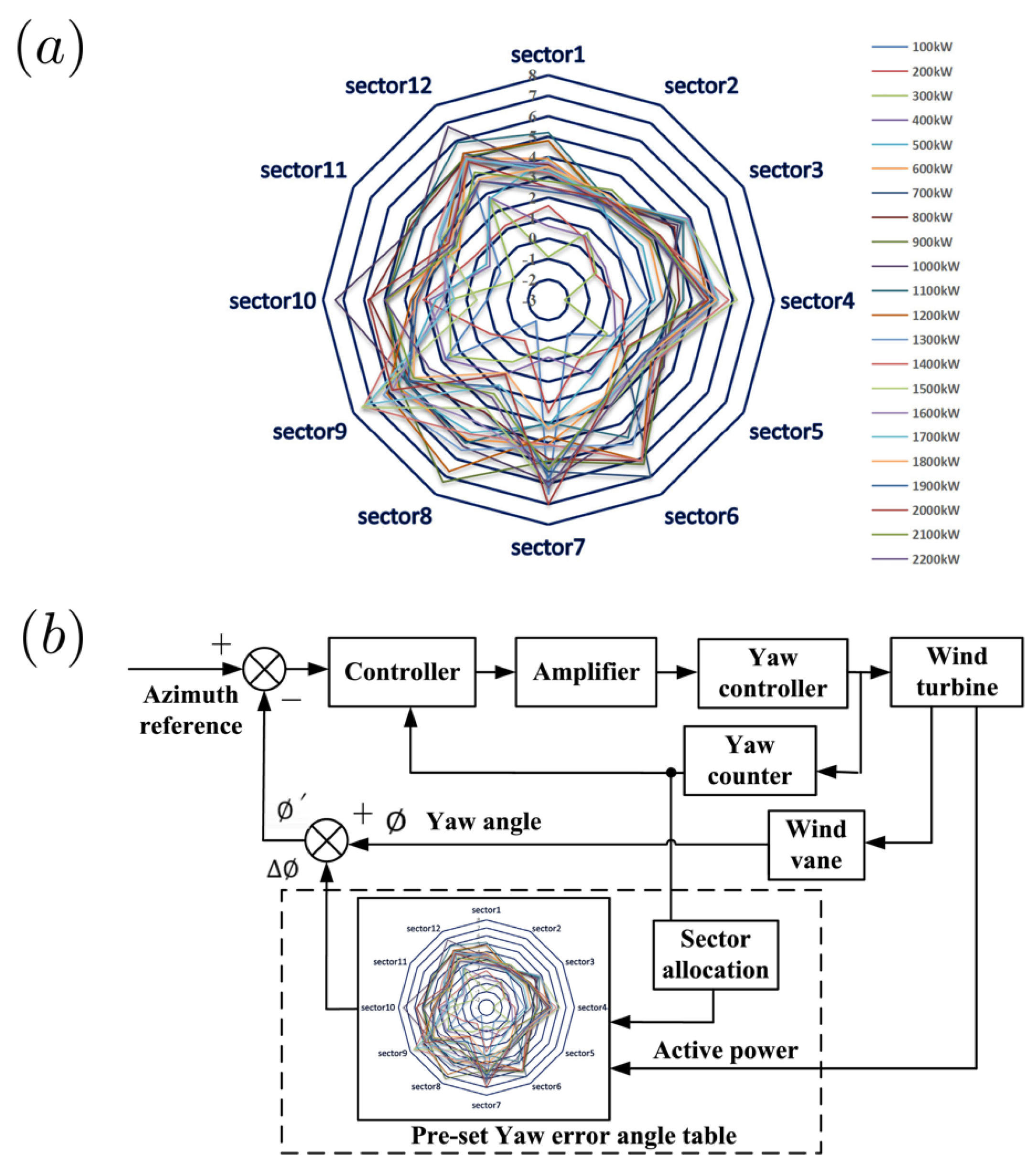

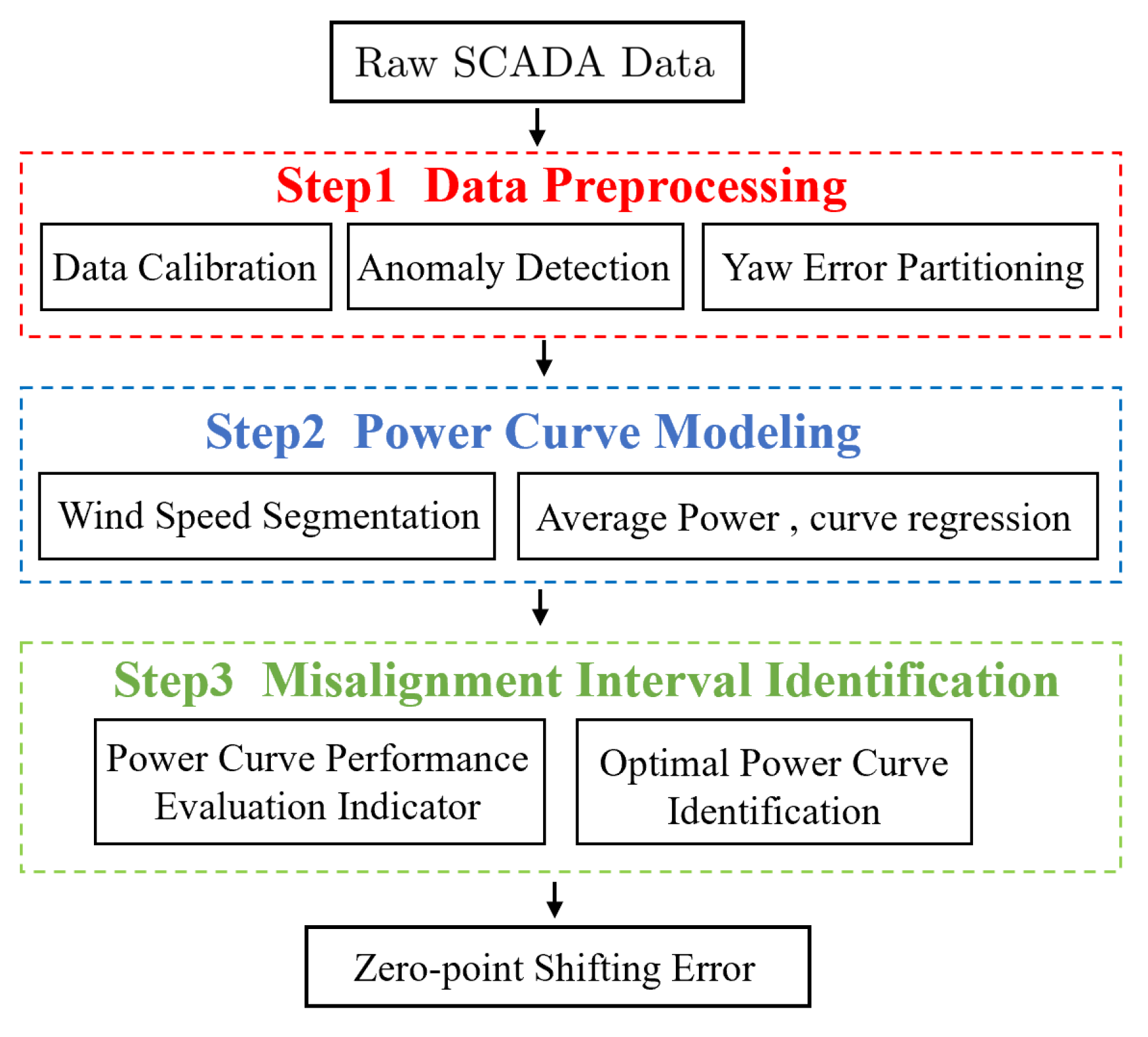
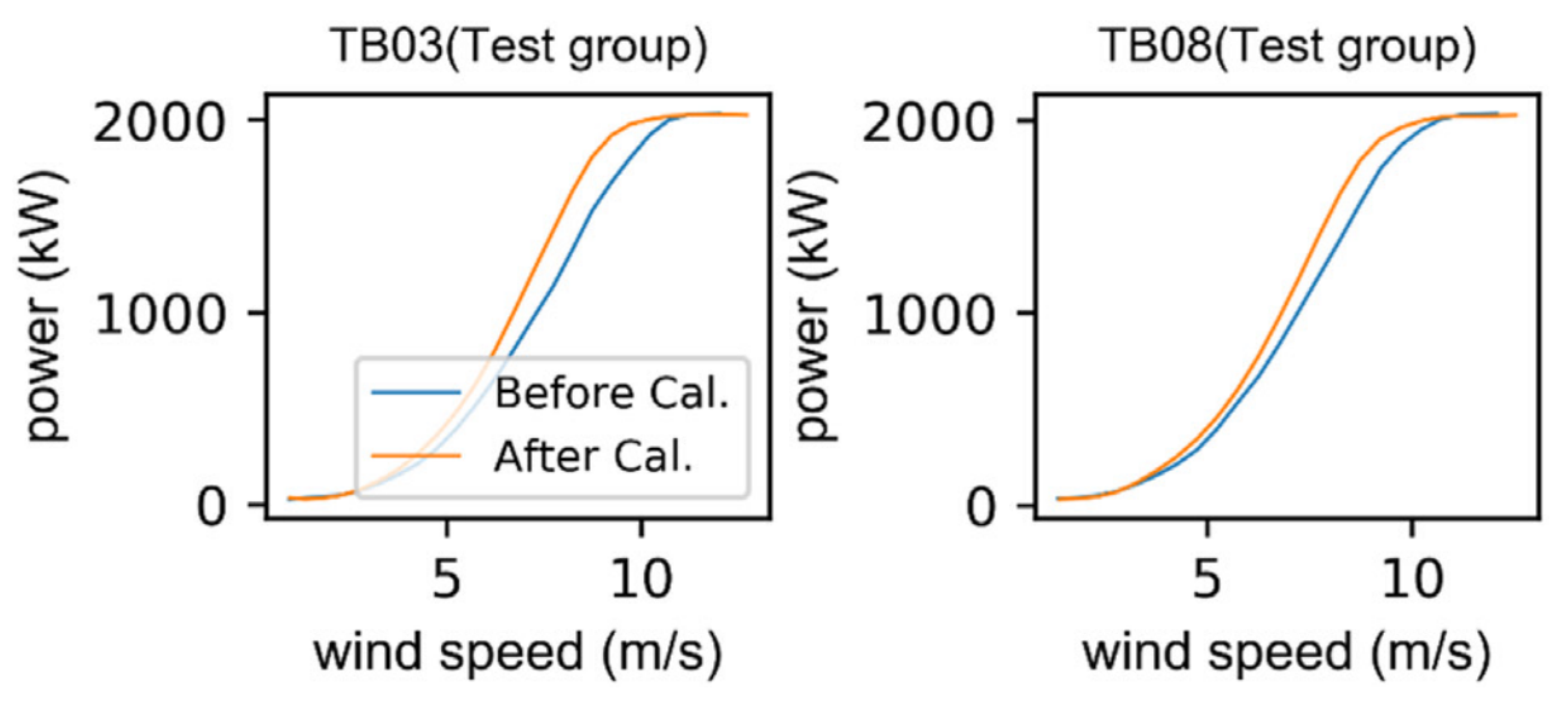
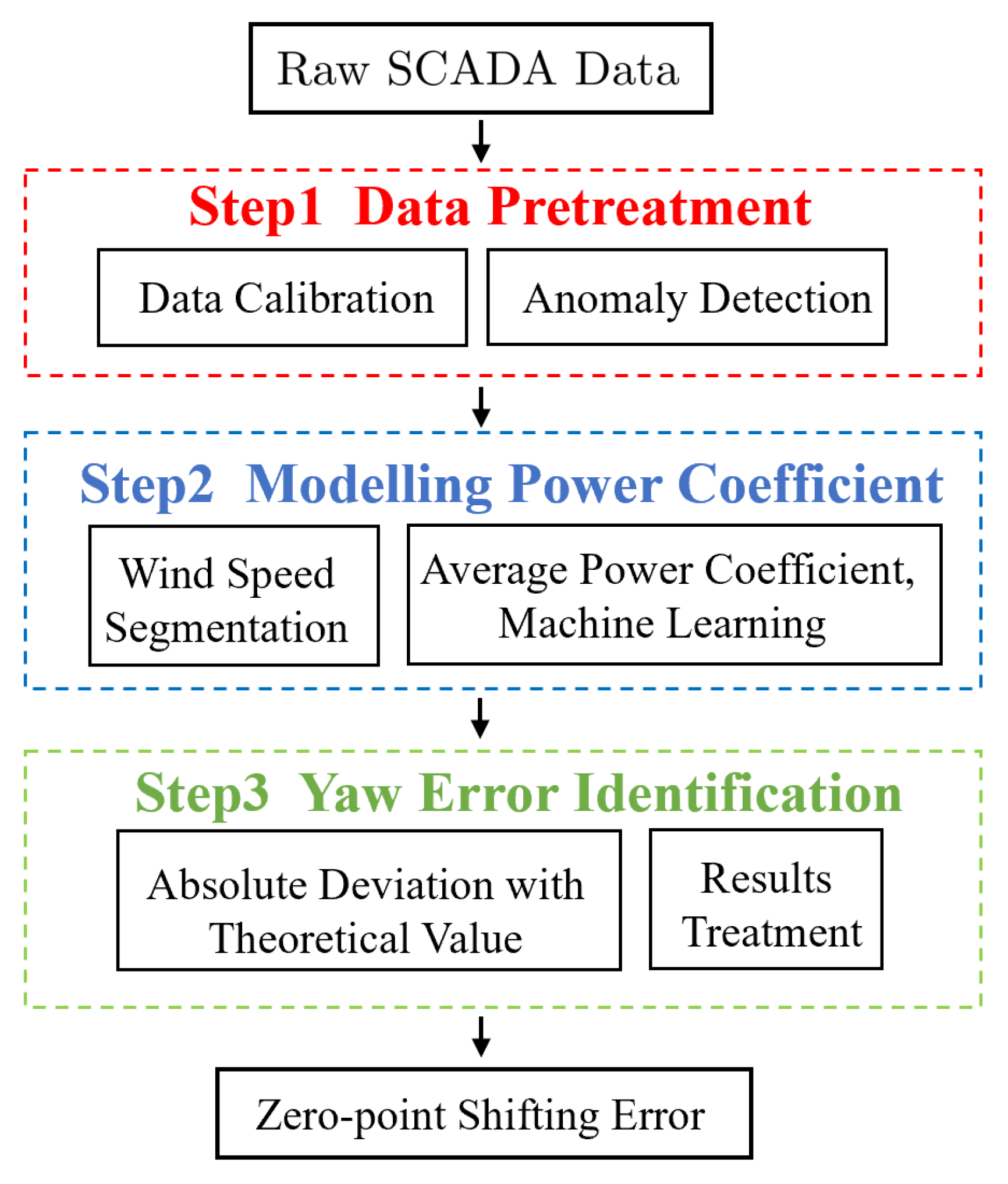
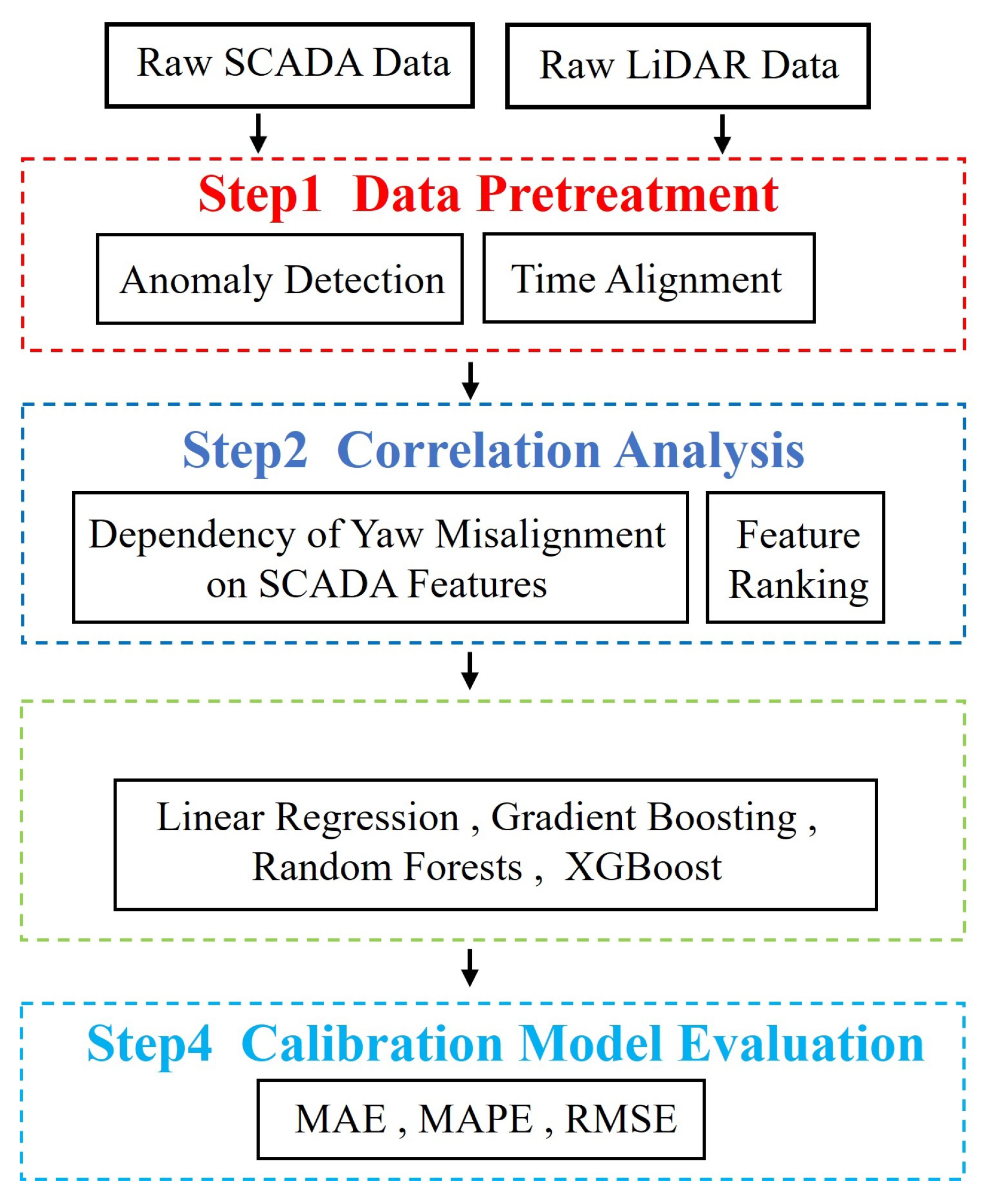
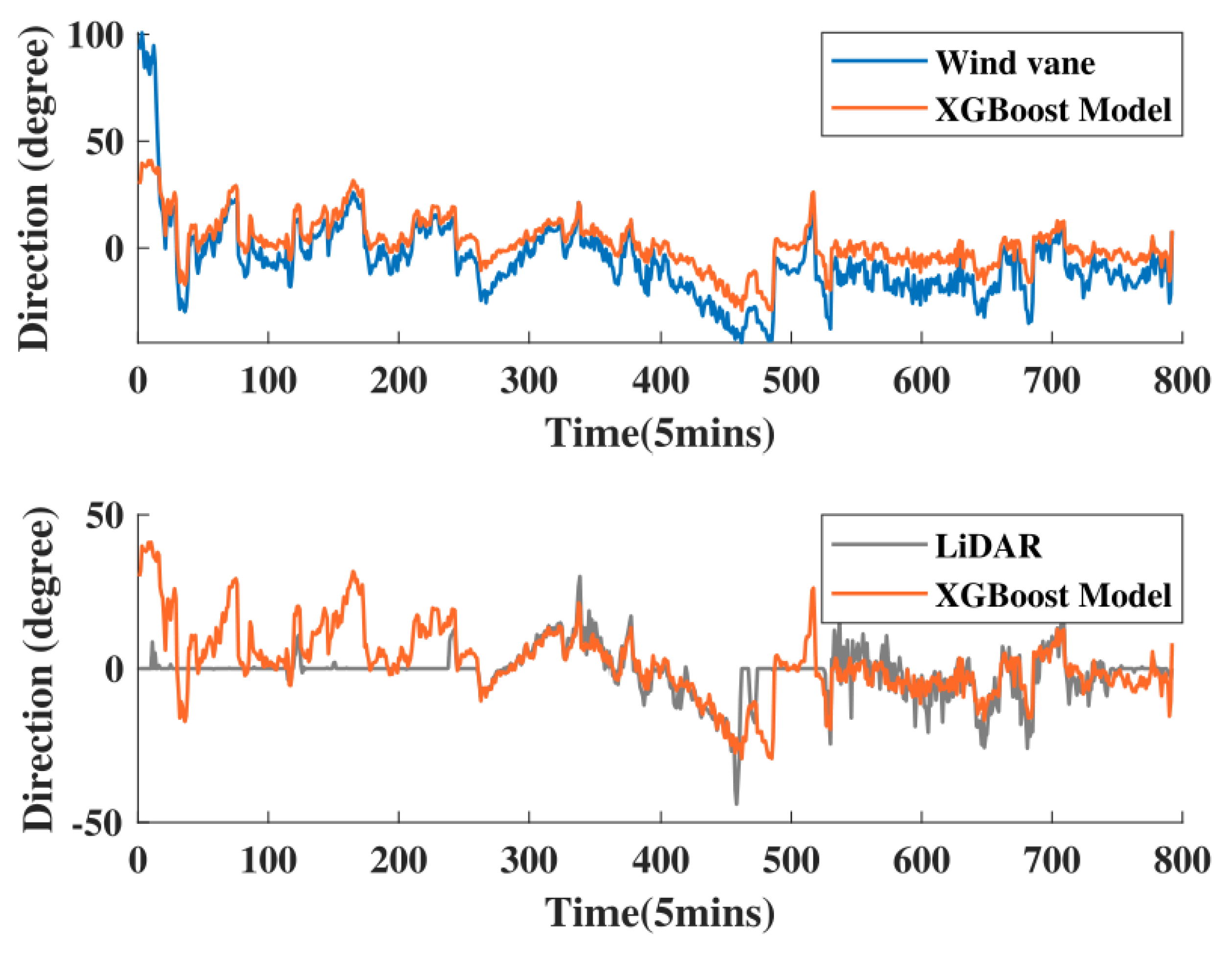
| Diagnostic Methods | Method Description | Type of Error | Advantages and Disadvantages |
|---|---|---|---|
| Based on LiDAR data | Time-averaged yaw error [19,29,30,31,32,33] | Static yaw error | Designed for static yaw error. |
| Yaw error table [24] | Yaw error | Accurate for static yaw error; insufficient for dynamic yaw error. | |
| Based on SCADA data | Analysis of power curves [23,25,26,34,35,36,37] | Zero-point shifting error | Widely applicable with straightforward principles and accuracy depending on the quality and quantity of monitoring data. |
| Analysis of power coefficients [27,28,38] | Zero-point shifting error | Low data requirements, while susceptible to environmental factors. | |
| Prediction of yaw angle utilizing wind speed and direction [9,20,36,39,40,41,42] | Dynamic yaw error | Accurate diagnosis of dynamic yaw error, with high data requirements. | |
| Dynamic response model [43] | Yaw error | Accurate diagnosis of static and dynamic yaw error but troublesome modelling. | |
| Based on both LiDAR and SCADA data | Yaw error model based on machine learning [44] | Yaw error | Accurate diagnosis of yaw error, requires analysis of historical data. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Chen, D.; Lin, H.; Yang, X. A Review of Diagnostic Methods for Yaw Errors in Horizontal Axis Wind Turbines. Energies 2025, 18, 588. https://doi.org/10.3390/en18030588
Li Q, Chen D, Lin H, Yang X. A Review of Diagnostic Methods for Yaw Errors in Horizontal Axis Wind Turbines. Energies. 2025; 18(3):588. https://doi.org/10.3390/en18030588
Chicago/Turabian StyleLi, Qian, Danyang Chen, Hangbing Lin, and Xiaolei Yang. 2025. "A Review of Diagnostic Methods for Yaw Errors in Horizontal Axis Wind Turbines" Energies 18, no. 3: 588. https://doi.org/10.3390/en18030588
APA StyleLi, Q., Chen, D., Lin, H., & Yang, X. (2025). A Review of Diagnostic Methods for Yaw Errors in Horizontal Axis Wind Turbines. Energies, 18(3), 588. https://doi.org/10.3390/en18030588








