The Influence of Electrode Shape on the Electric and Temperature Fields in an Immersed High-Voltage Electrode Boiler
Abstract
1. Introduction
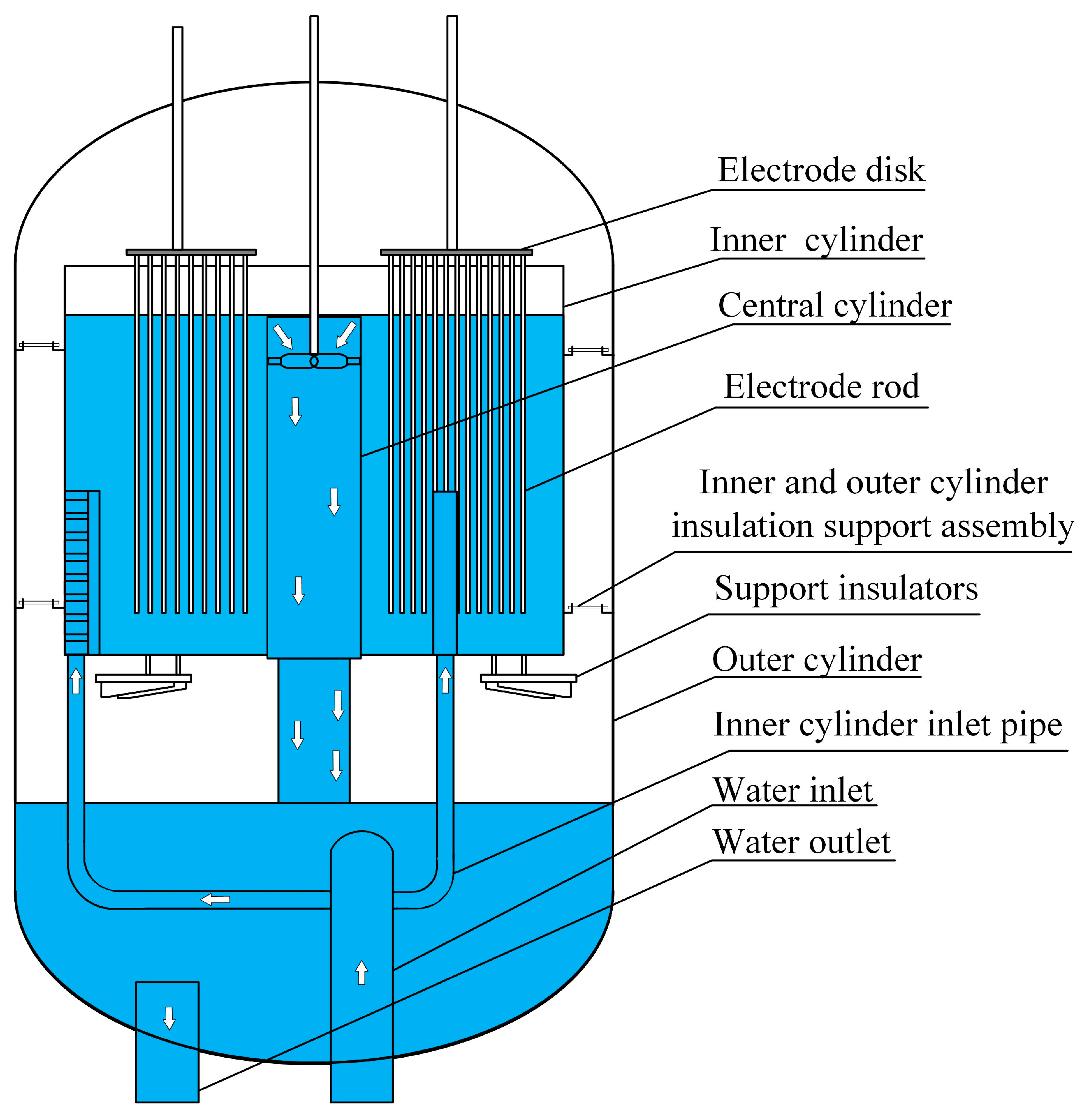
2. Principle of Immersed HVEB
2.1. Boundary Condition Setting
2.2. Simulation Equations for Electric and Temperature Fields
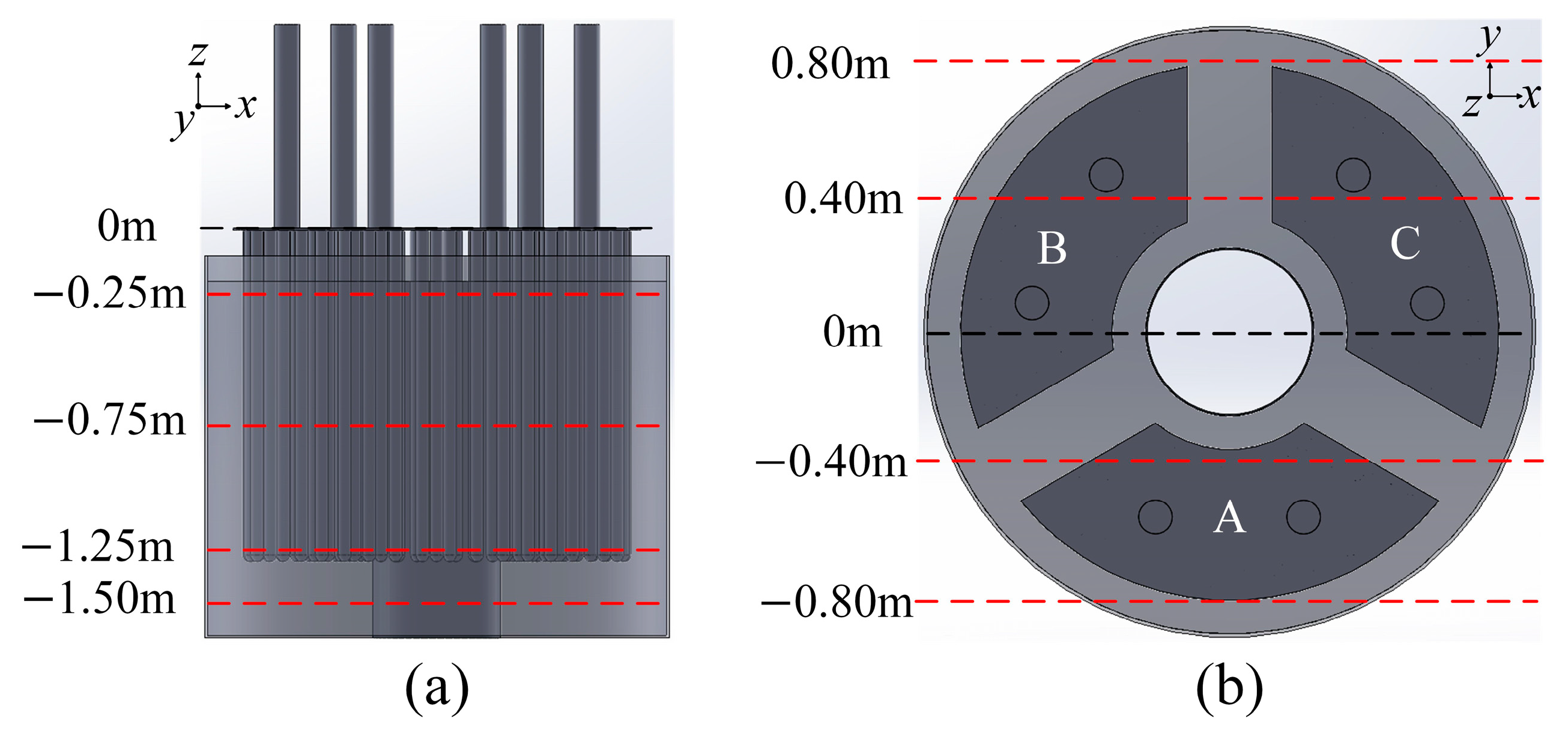
2.3. Division of the Grid
3. Analysis and Discussion of Electric Field Simulation Results
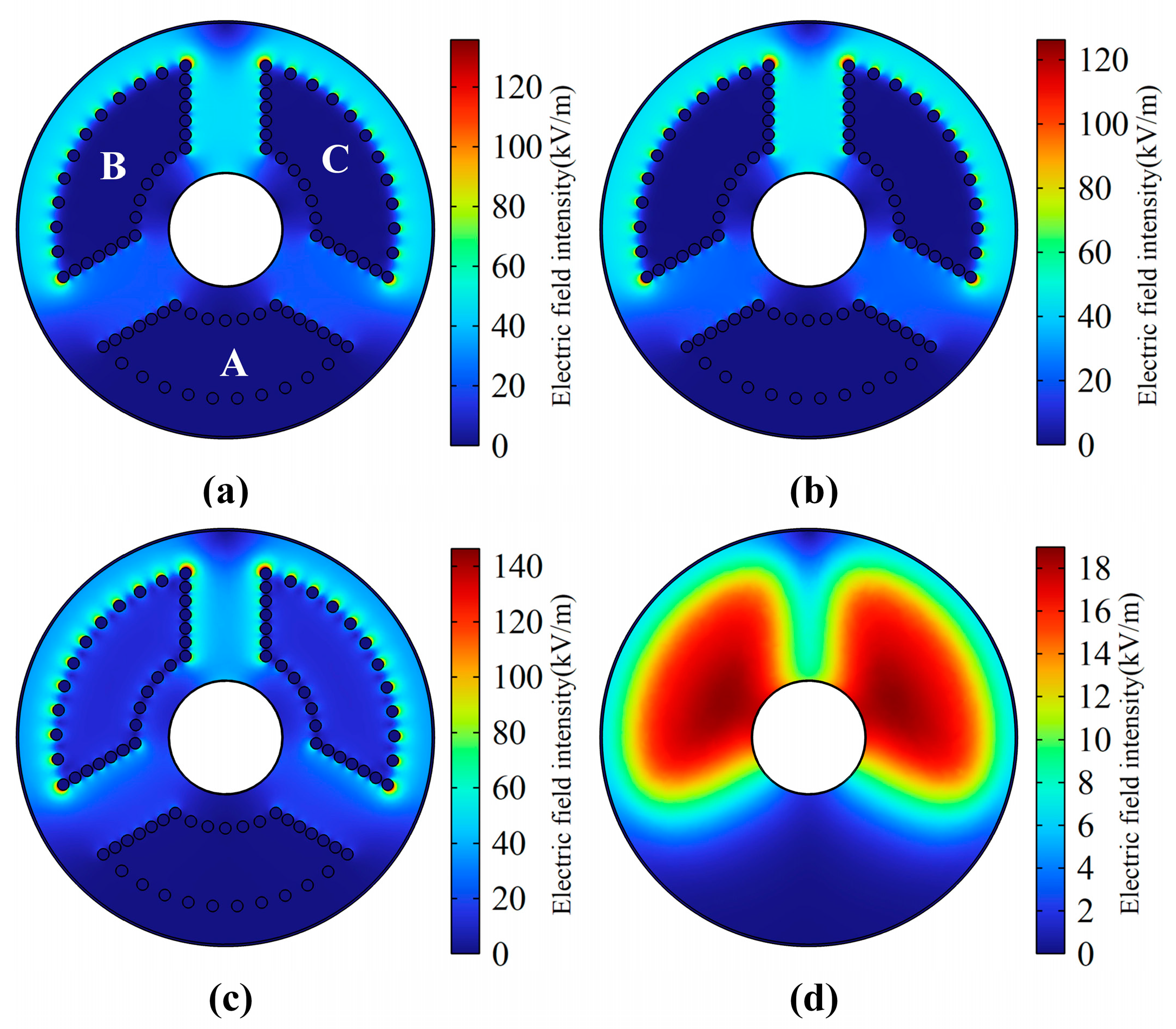
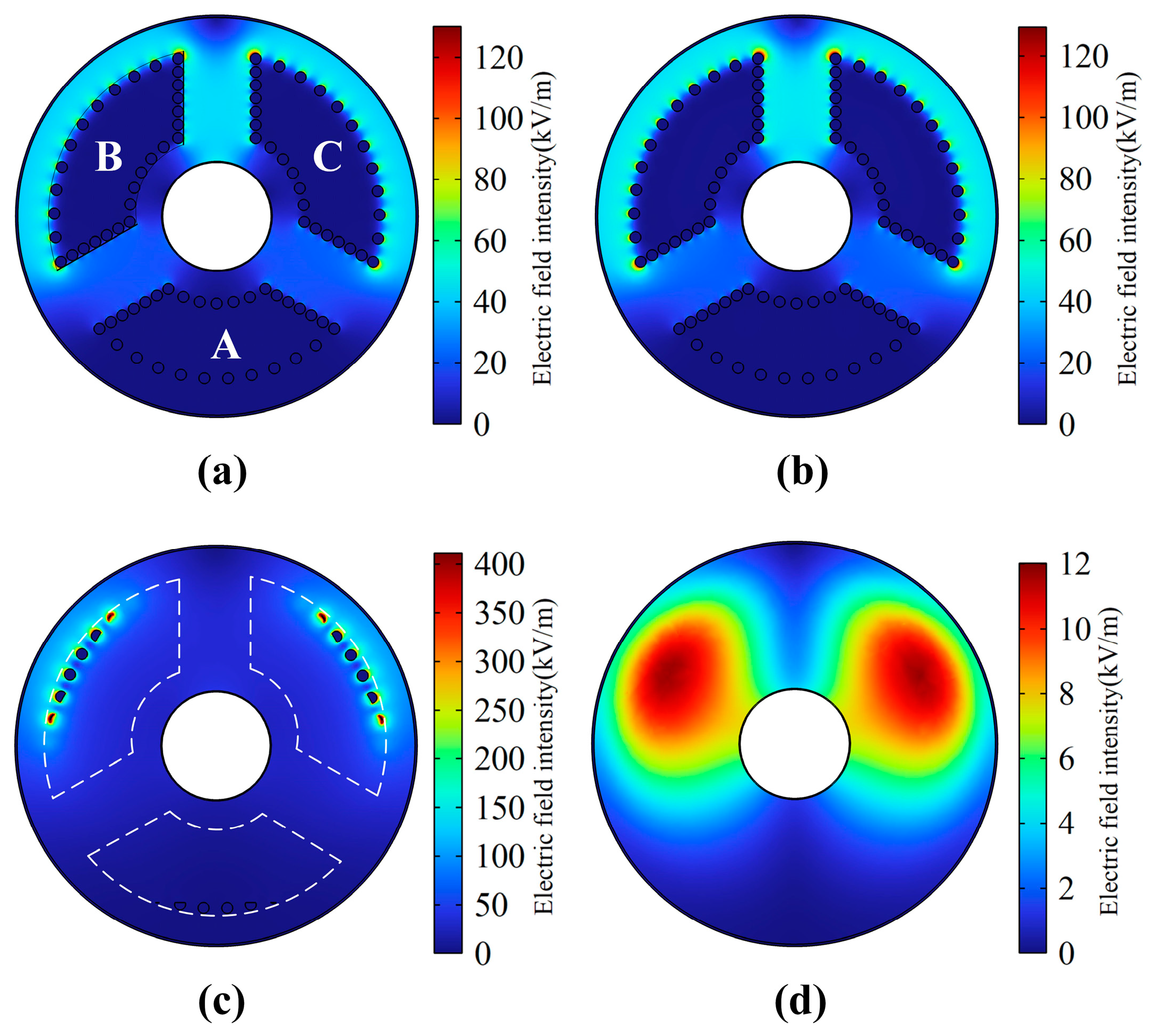
3.1. Electric Field Distribution for Different Electrode Structures
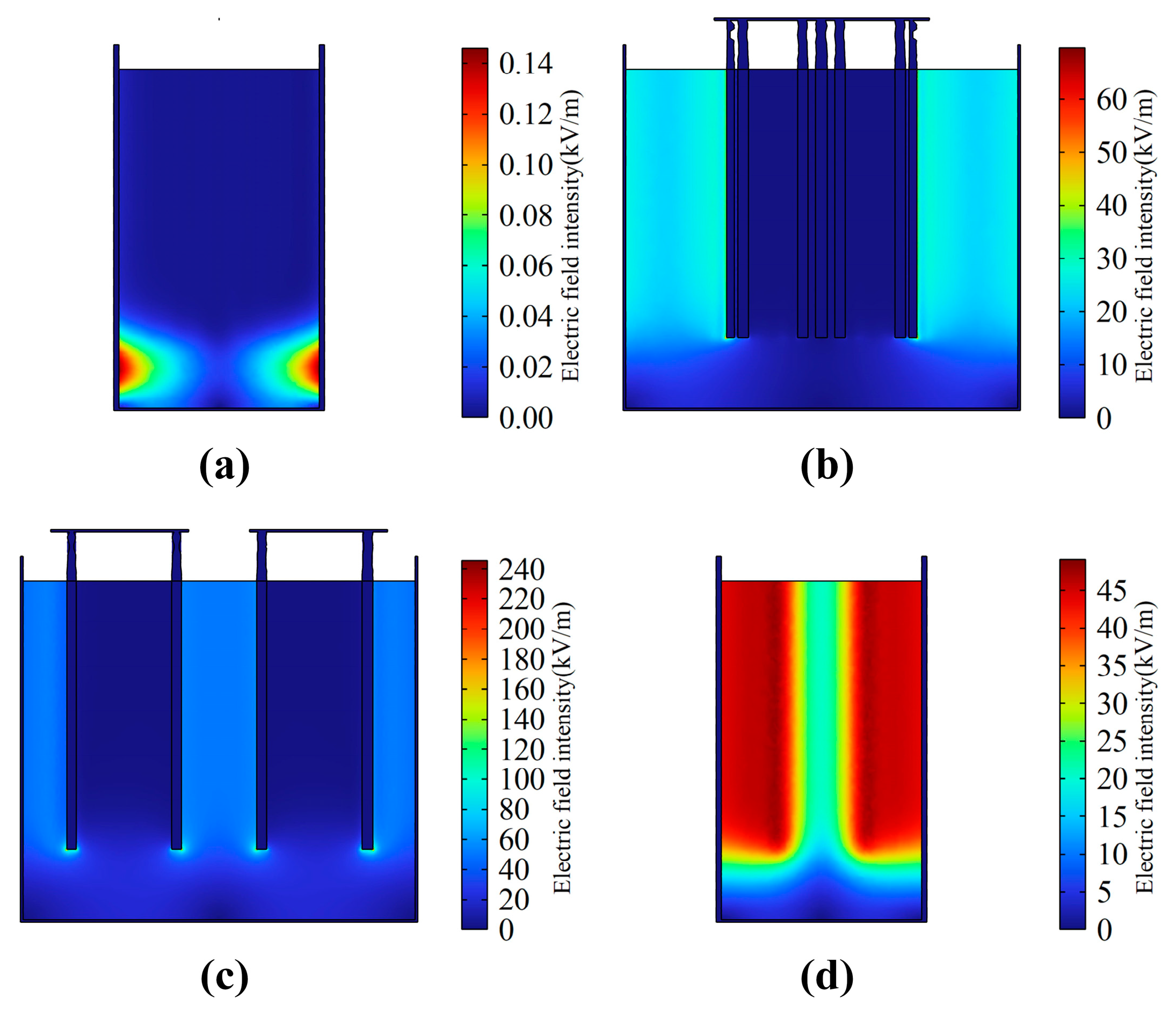
3.1.1. Cross-Sectional Electric Field Distribution
3.1.2. Longitudinal Cross-Section Electric Field Distribution
3.2. Electric Field Inhomogeneity Coefficient
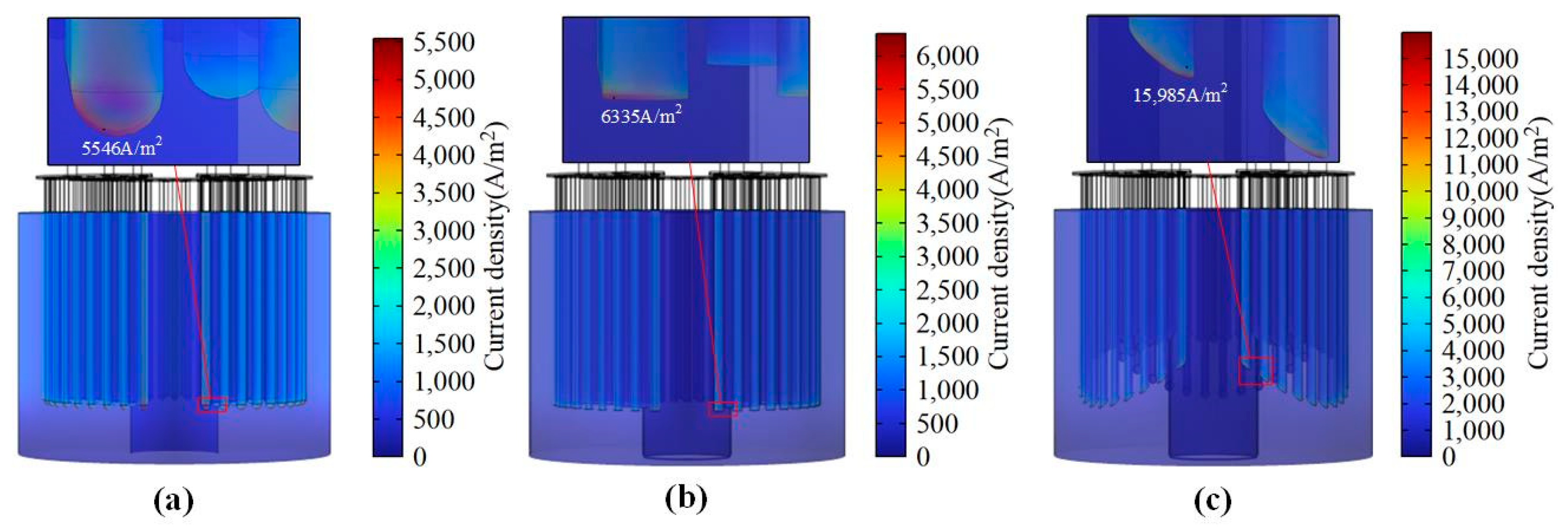
3.3. Current Density
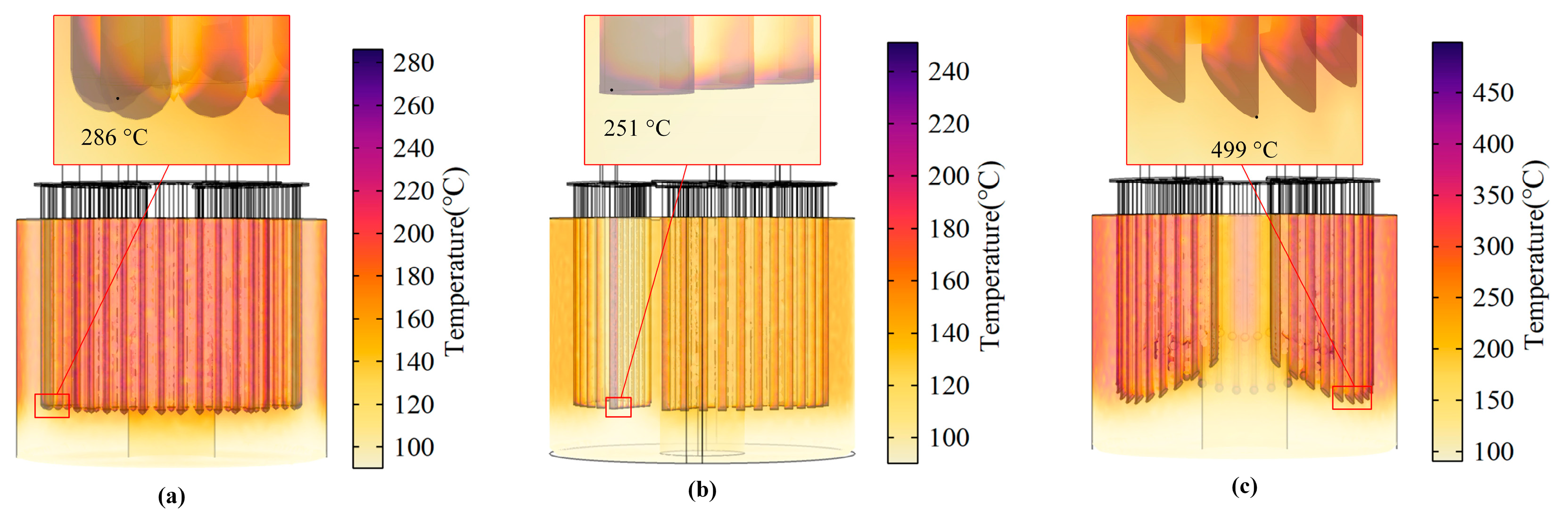
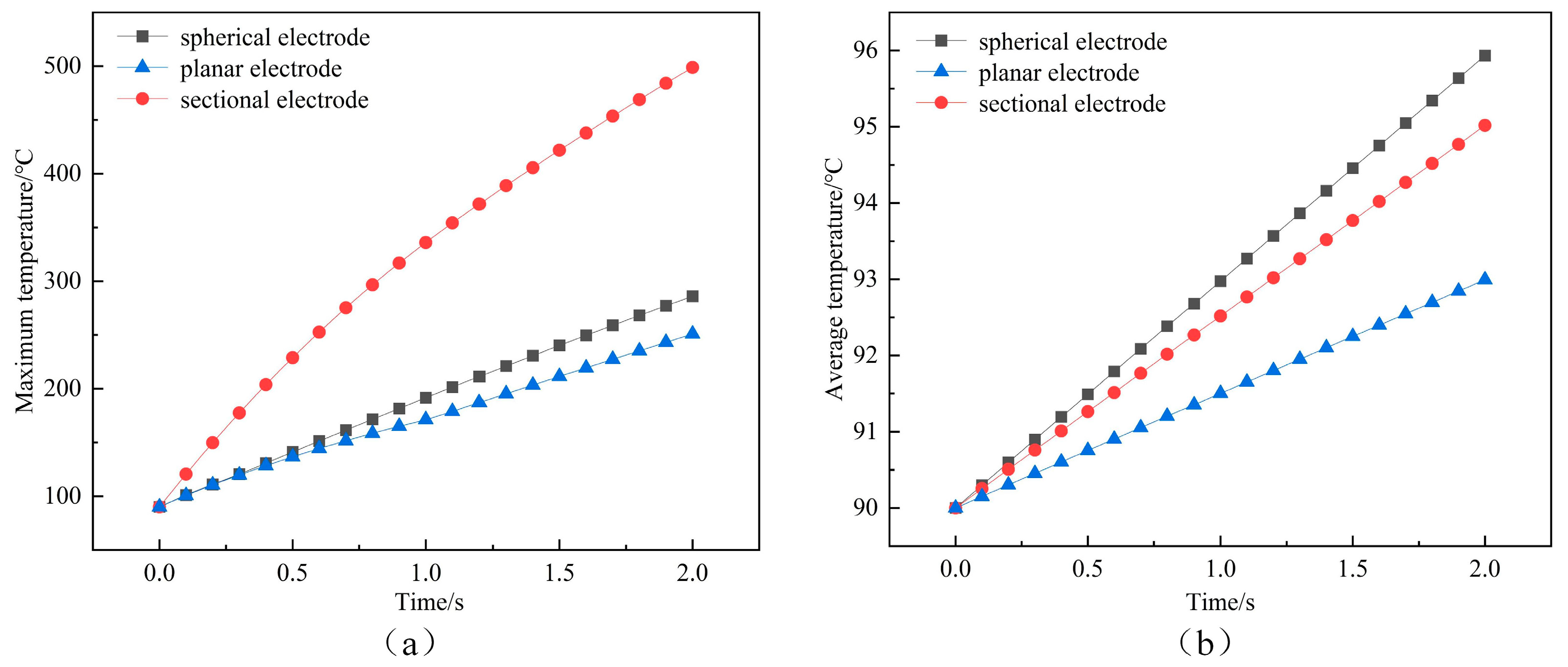
4. Temperature Field Simulation Results Analysis and Discussion
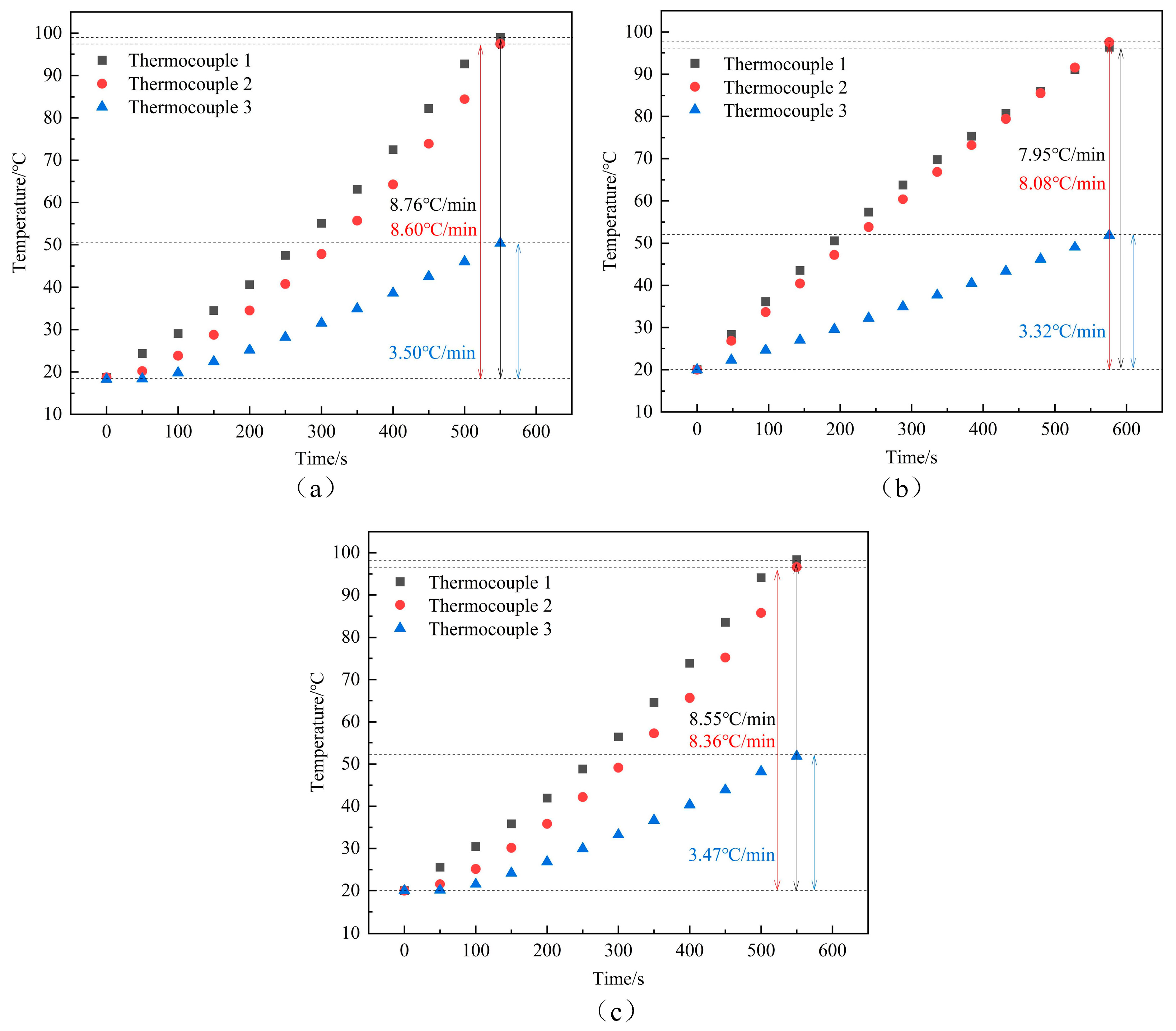
5. Experimental Verification
6. Conclusions
- Under the spherical electrode, the electric field distribution in the furnace water is more uniform; the maximum field strength change value, the uneven coefficient, and the fluctuation value of the body electric field are all the smallest; and the electric field distortion degree is the lowest, which is more conducive to the uniform heating of the furnace water.
- The maximum value of the current density of the furnace water under the spherical electrode is lower than that of the planar electrode and the sectional electrode. The maximum value of the current density of the furnace water under the three electrodes is located at the bottom end of the electrode, i.e., the sharper the bottom end of the electrode, the greater the curvature, the higher the current density of the furnace water, and the probability of over-temperature phenomenon of the furnace water at the bottom end of the electrode will be sharply increased, which can easily lead to the electrolysis of the furnace water.
- Temperature field simulations show that the spherical electrode structure has the largest heating area, the highest average temperature rise of the furnace water, and the highest heating efficiency.
- Through the temperature rise test of the small model spherical electrode, the simulation data of the small model spherical electrode and the temperature rise test were compared and analyzed in terms of the average temperature rise rate at special points, and the results showed that the maximum error percentage was within 10%; and after correcting the conductivity of the simulation model, the maximum error ratio was reduced to 3%, which proved the accuracy of the simulation method.
- The spherical electrode structure has the best overall performance among the three electrode structures, which can effectively improve the safety of the high-voltage electrode boiler in actual operation. In the following research, the electrode materials should be researched to obtain low-cost, conductive, and corrosion-resistant materials to improve the life and safety of the high-voltage electrode boilers.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| HVEB | High-Voltage Electrode Boiler |
| N2 | Nitrogen |
| Symbols and their units | |
| Symbol | Unit |
| φ | kV |
| E | kV/m |
| f | Hz |
| r | m |
| l | m |
| h | m |
| σ | S/m |
| ρ | C/m3 |
| J | A/m2 |
| T | ℃ |
| Time | s |
| Tag | ℃/min |
| q | W/m2 |
References
- Dong, Y.; Yu, S.; He, C.; Yu, Q.; Fang, F. Optimal Multi-Mode Flexibility Operation of CHP Units with Electrode Type Electric Boilers: A Case Study. Energies 2022, 15, 9337. [Google Scholar] [CrossRef]
- Manni, M.; Nicolini, A.; Cotana, F. Performance assessment of an electrode boiler for power-to-heat conversion in sustainable energy districts. Energy Build. 2022, 277, 112569. [Google Scholar] [CrossRef]
- Yuan, R.; Yan, H.; Chen, W.; Liu, M. Design and performance evaluation of a shared energy storage system integrated within combined heat and power plants in an energy network. J. Energy Storage 2024, 103, 114324. [Google Scholar] [CrossRef]
- Shi, T.; Chen, Z.; Guo, S.; Li, D. Fast-Frequency-Response Control Method for Electrode Boilers Supporting New Energy Accommodation. Processes 2023, 11, 3098. [Google Scholar] [CrossRef]
- Ding, T.; Mou, C.; He, Y.; Sun, Y.; Liu, R.; He, F.; Ren, C. Analyzing current development and typical cases of clean heating supply in Northwest China (II): Typical cases and techno-economic analysis. Proc. CSEE 2020, 40, 5126–5136. [Google Scholar]
- National Energy Administration. Transcript of the National Energy Board’s Online Press Conference for the Third Quarter of 2022[EB/OL]. (2022-08-02). Available online: http://www.nea.gov.cn/2022-08/02/c_1310648934.htm (accessed on 1 July 2024).
- Wang, Z.; Yang, L.; Tian, C.; Li, G. Energy Optimization for the combined system of wind-electric energy storage-regenerative electric boiler considering wind consumption. Proc. CSEE 2017, 37, 137–143. [Google Scholar]
- Wang, K.; Xie, L.; Qiao, Y.; Wang, C.; Fan, X.; Liang, W. Optimization and economic analysis of multi-boiler coupled coordination heating considering abandoned wind power. Acta Energ. Sol. Sin. 2021, 42, 104–109. [Google Scholar]
- Yang, Q.; Zhi, C.; Yuan, D.; Yang, H. Wind power accommodation low-carbon economic dispatch based on coordination between automatic start-stop electric boiler and heat accumulator. Acta Energiae Solaris Sin. 2020, 41, 21–28. [Google Scholar]
- Dai, B.; Xie, L.; Gao, Y.; Li, J.; Qiao, C.; Zhang, Y. Research on multi-boiler heating scheme considering wind abandonment and difference of users response behaviors. Acta Energiae Solaris Sin. 2023, 44, 437–443. [Google Scholar]
- Wang, H.; Dong, H.; Du, Q.; Wei, G. Current situation and prospect of electrode boiler in China. Therm. Energy Power Eng. 2023, 38, 1–12. [Google Scholar]
- Gicevskis, K.; Linkevics, O. The Role of Decentralized Electrode Boiler in Ancillary Services and District Heating: A Feasibility Assessment. Latv. J. Phys. Tech. Sci. 2023, 60, 32–42. [Google Scholar] [CrossRef]
- Nielsen, R.J.; Pedersen, T.E. Electrode boiler model for ancillary service simulation. In Proceedings of the 15th International Modelica Conference 2023, Aachen, Germany, 9–11 October 2023; pp. 589–598. [Google Scholar]
- Guo, F.; Xia, Q.; Liu, Y. Application of immersion electrode boilers in nuclear power plants. Therm. Power Gener. 2012, 41, 88. [Google Scholar]
- Jiang, S.; Zhou, Y. Research on electric field Distribution Characteristics of Immersed electrode Boiler. Comput. Simul. 2022, 39, 248–252. [Google Scholar]
- Wu, B.; Wu, H. Reverse power control method of steam water parameters for nuclear power electrode Immersion Boiler. Electr. Power China 2017, 50, 107–112+123. [Google Scholar]
- Zheng, Z.; Zhou, Y.; Li, Y. AC corrosion behavior of several metallic materials as a candidate for boiler electrode. J. Chin. Soc. Corros. Prot. 2023, 43, 202–208. [Google Scholar]
- Zheng, Z. Study on Corrosion Characteristics of Boiler High Pressure Electrode. Master’s Thesis, Xinjiang University, Urumqi, China, 2021. [Google Scholar]
- He, X.; Ruan, Y.; Wang, W. Three-Dimensional Transient Electric Field Characteristics of High Pressure Electrode Boilers. Electronics 2024, 13, 1615. [Google Scholar] [CrossRef]
- Ruan, Y. Study on New Electrode System and Electric Field Characteristics of High Voltage Electrode Boiler. Master’s Thesis, North China University of Water Resources and Electric Power, Zhengzhou, China, 2021. [Google Scholar]
- Liu, H.; Song, H.; Pan, H.; Ying, Q.; Ge, W.; Jiang, J.; Liu, Y. Numerical simulation of power variation characteristics of an immersion electrode boiler. Ind. Boil. 2023, 2, 1–6. [Google Scholar]
- Ma, J.; Qiang, S.; Yuan, X. Research on Mathematical Modeling of Electrode Boiler Based on Dynamic Neural Network. Comput. Simul. 2019, 36, 126–130. [Google Scholar]
- Yuan, X. Study on Mechanism Modeling and Dynamic Characteristics of the Submerged Electrode Boiler System. Master’s Thesis, North China Electric Power University, Baoding, China, 2019. [Google Scholar]






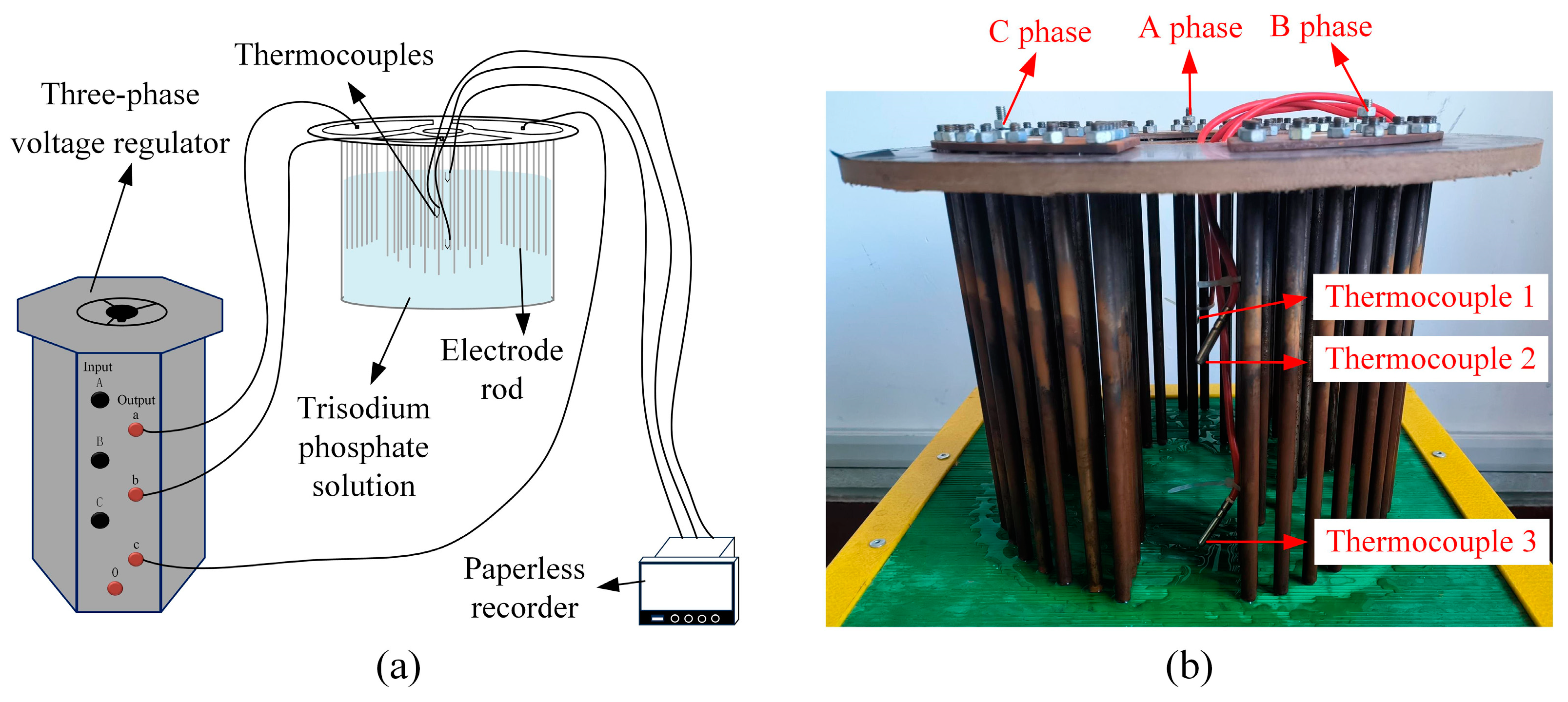
| Model | Material | Relative Permittivity | Electrical Conductivity/S∙m−1 |
|---|---|---|---|
| High-voltage electrode | 20#steel | 1 | 1.12 × 107 |
| Electrode disk | 20#steel | 1 | 1.12 × 107 |
| Electrode rod | 20#steel | 1 | 1.12 × 107 |
| Inner cylinder | 20#steel | 1 | 1.12 × 107 |
| Furnace water | Trisodium phosphate solution | 2.9 | 200 × 10−4 |
| Center cylinder | Polytetrafluoroethylene | 2.1 | 10 × 10−14 |
| Phase Sequence | Expression |
|---|---|
| A phase | |
| B phase | |
| C phase |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Wang, J.; Zhang, Y.; Li, L.; Zhou, W.; Lei, Z. The Influence of Electrode Shape on the Electric and Temperature Fields in an Immersed High-Voltage Electrode Boiler. Energies 2025, 18, 825. https://doi.org/10.3390/en18040825
Wang M, Wang J, Zhang Y, Li L, Zhou W, Lei Z. The Influence of Electrode Shape on the Electric and Temperature Fields in an Immersed High-Voltage Electrode Boiler. Energies. 2025; 18(4):825. https://doi.org/10.3390/en18040825
Chicago/Turabian StyleWang, Mingyong, Jianfei Wang, Yiling Zhang, Lu Li, Wenkai Zhou, and Zhipeng Lei. 2025. "The Influence of Electrode Shape on the Electric and Temperature Fields in an Immersed High-Voltage Electrode Boiler" Energies 18, no. 4: 825. https://doi.org/10.3390/en18040825
APA StyleWang, M., Wang, J., Zhang, Y., Li, L., Zhou, W., & Lei, Z. (2025). The Influence of Electrode Shape on the Electric and Temperature Fields in an Immersed High-Voltage Electrode Boiler. Energies, 18(4), 825. https://doi.org/10.3390/en18040825






