Analysis and Suppression of Thrust Ripple in a Permanent Magnet Linear Synchronous Motor—A Review
Abstract
1. Introduction
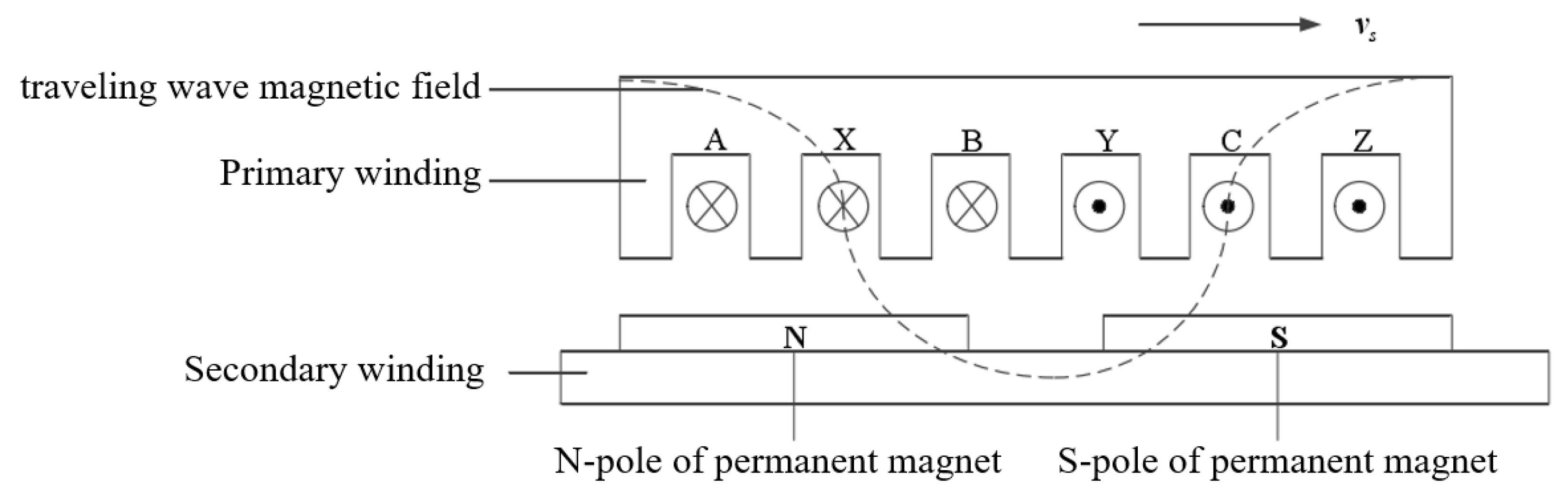
2. Structural Characteristics and Operating Principles of PMLSMs
2.1. Structural Characteristics of PMLSM
2.2. Operating Principles of PMLSM
2.2.1. Ripple Force
2.2.2. Cogging Force
- (1)
- When the cogging of the mover moves over the primary winding, there are moments when the cogging is precisely above the single-pole magnetic steel of the primary winding, as shown in Figure 3a. At this point, the magnetic field of the permanent magnet exerts equal forces on both sides of the cogging, so the movement of the motor is not affected by external forces.
- (2)
- At other moments, the cogging of mover moves over the gaps between the magnetic steel of the primary winding, as shown in Figure 3b. At this point, the forces exerted by PMs on the cogging are unequal on both sides, meaning that the motor experiences cogging force, which affects the operational accuracy of the motor.
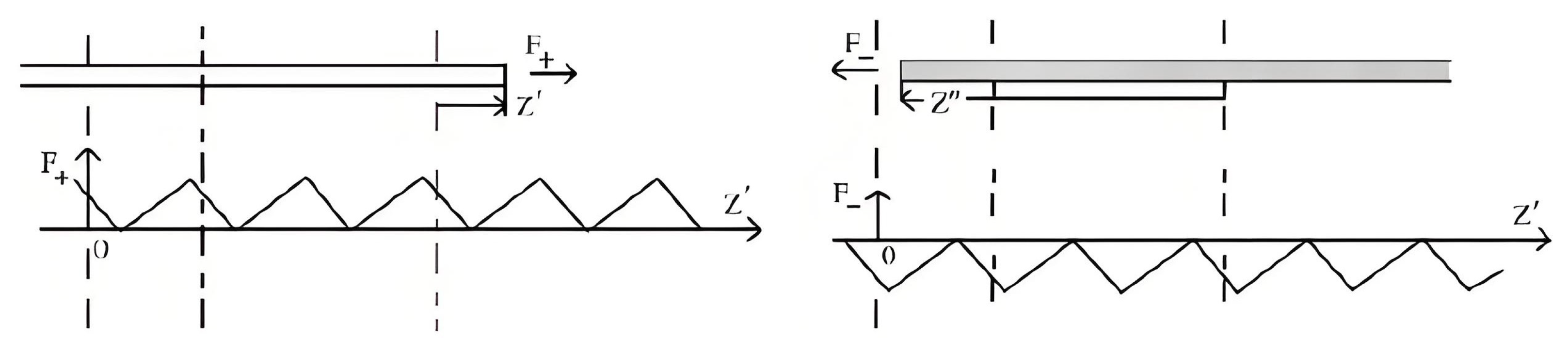
2.2.3. Analysis of the End Force
3. Structural Optimization Methods for PMLSM
3.1. Adjusting the Shape and Length of the Mover or Stator
3.2. Adding Auxiliary Structures
3.3. Additional Compensation Windings
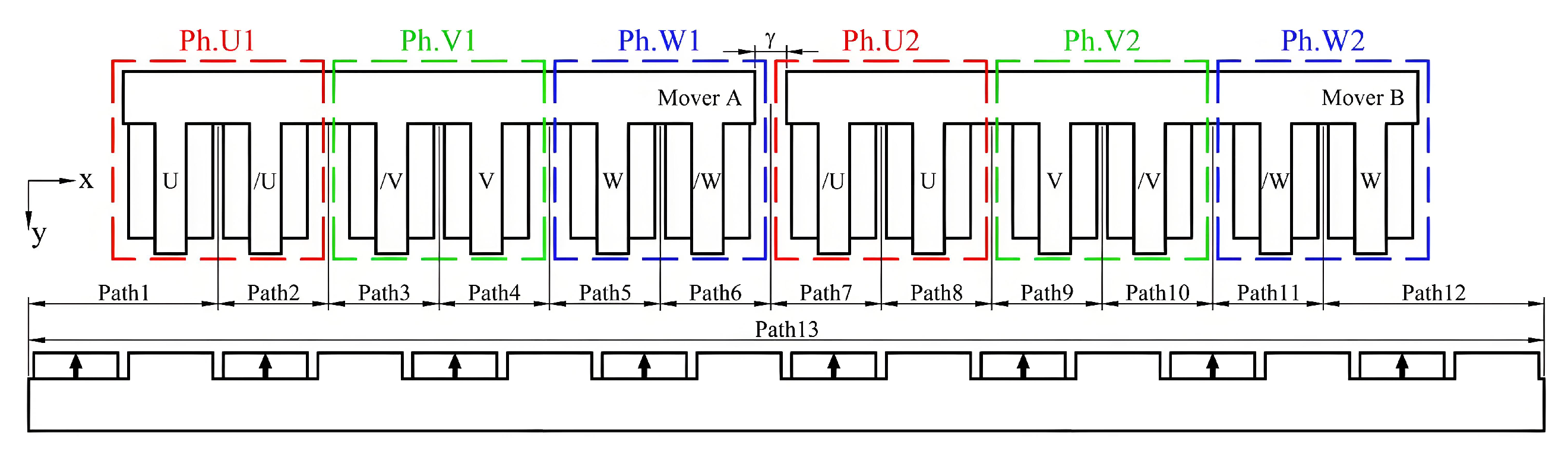
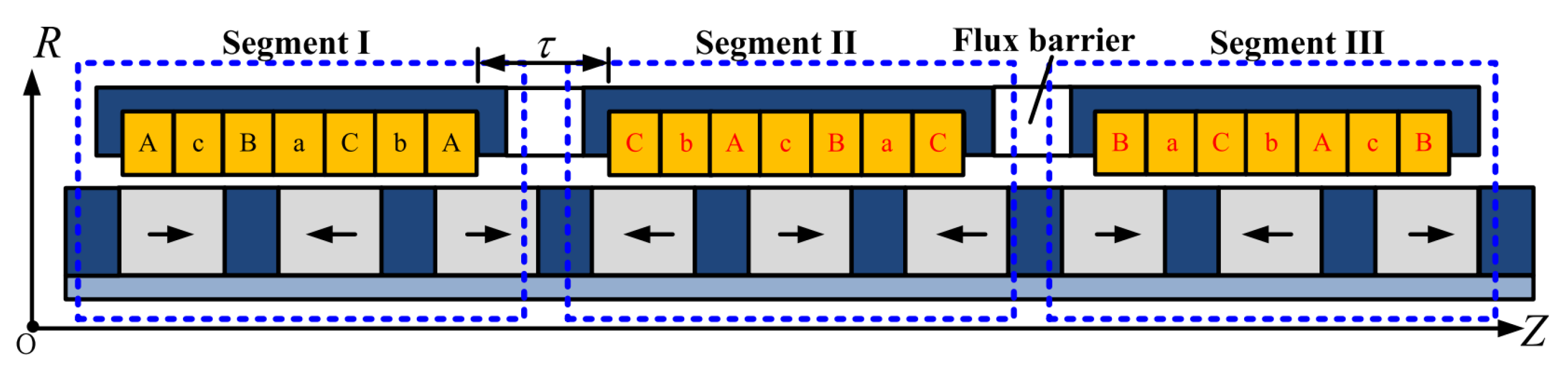
3.4. Modular Design
4. Control Strategy for PMLSM
4.1. Sliding-Mode Control
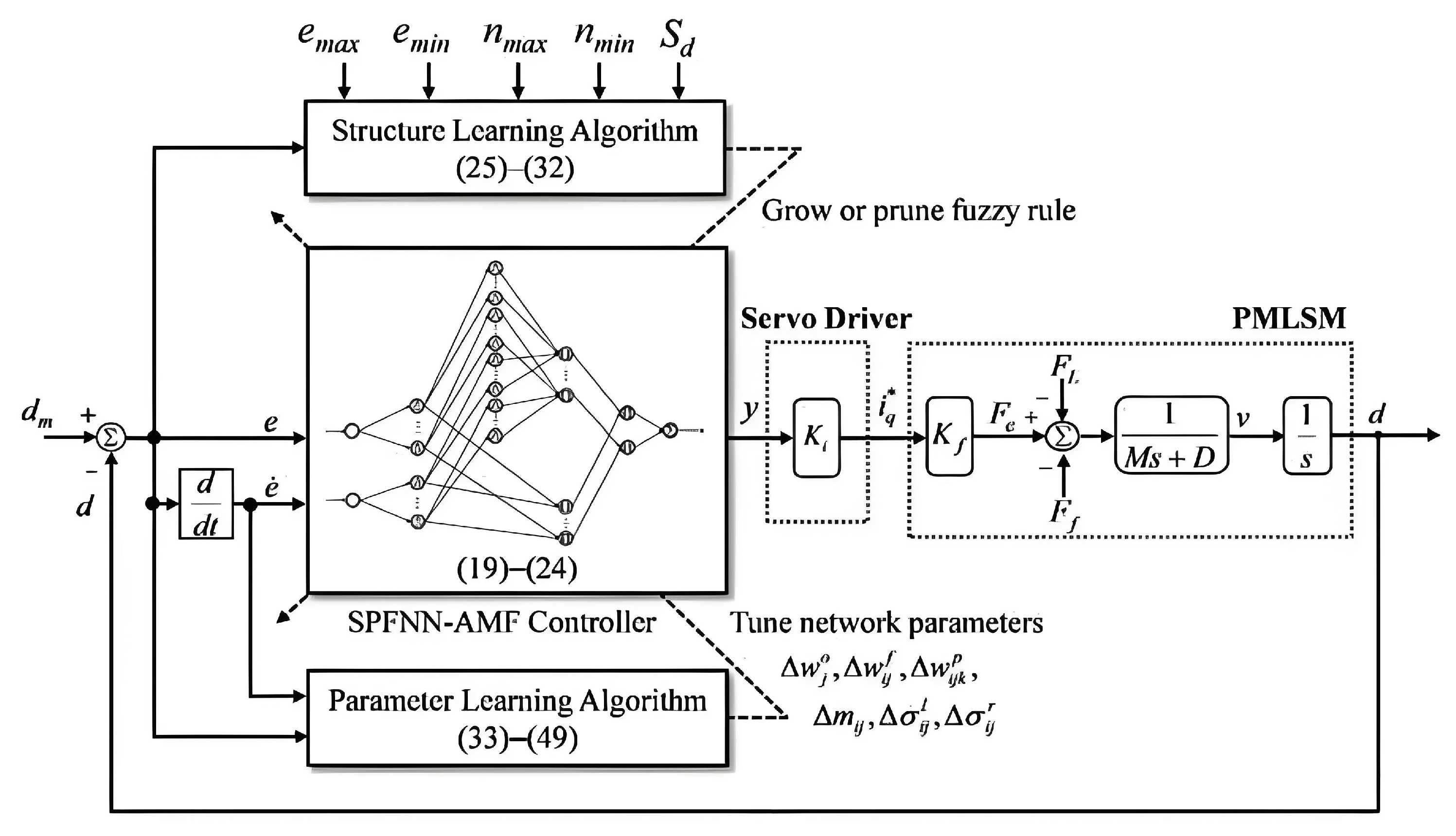
4.2. Fuzzy Neural Network Control
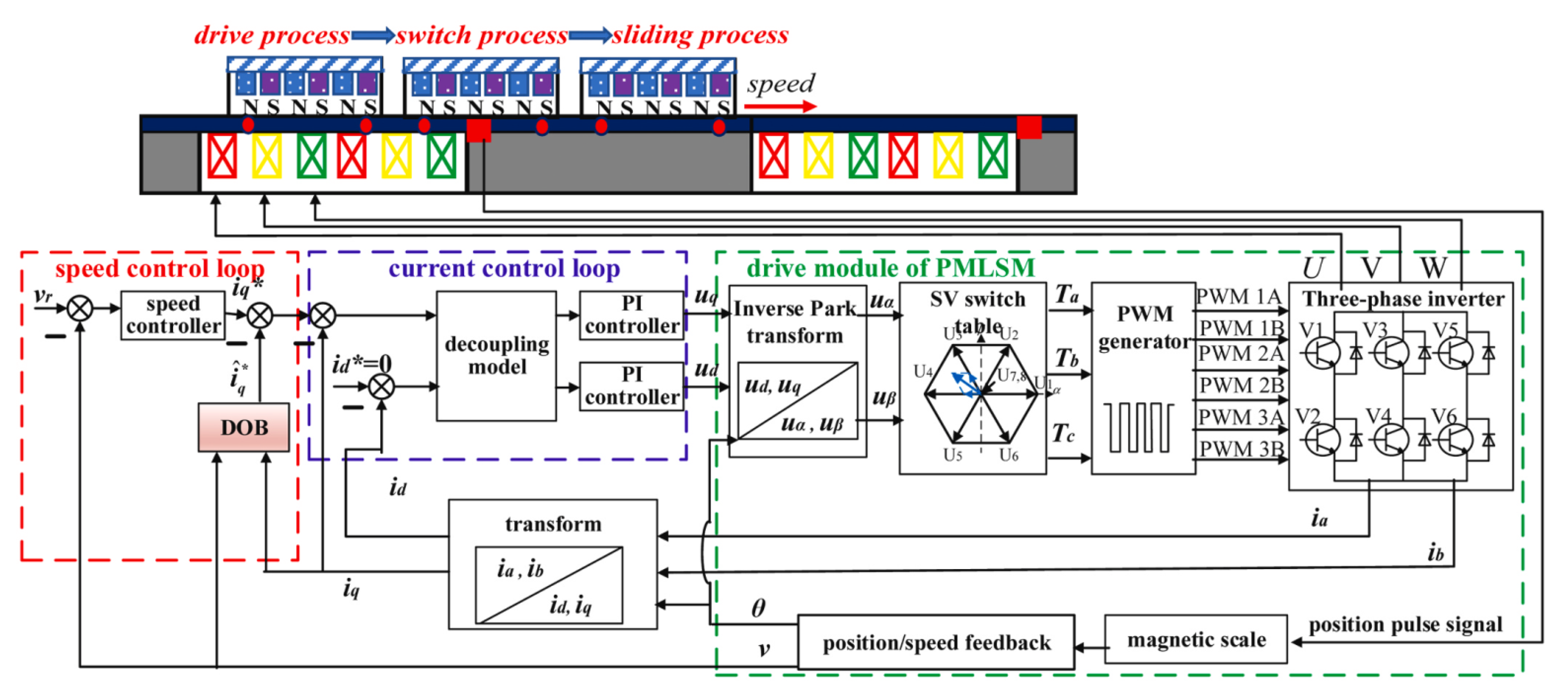
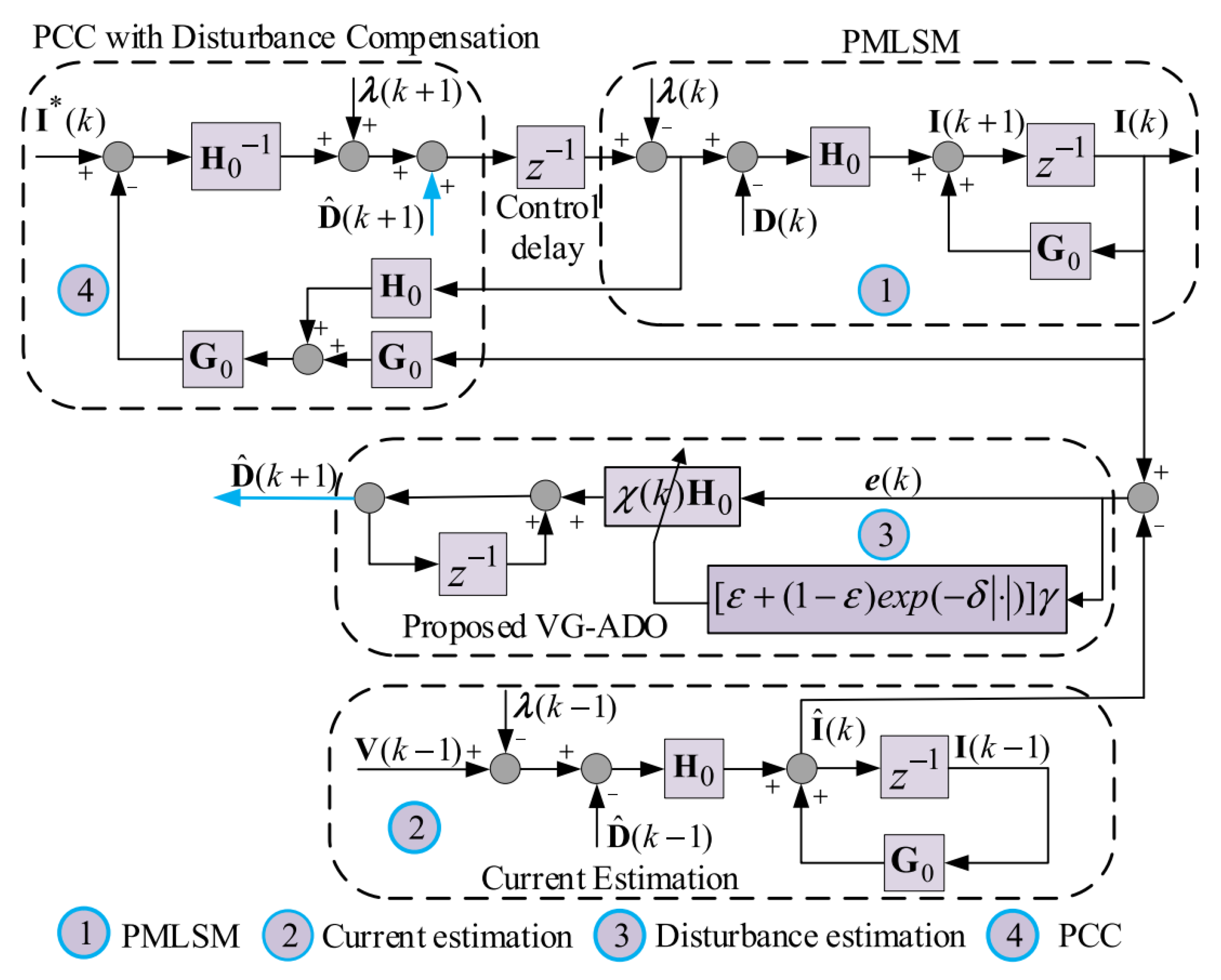
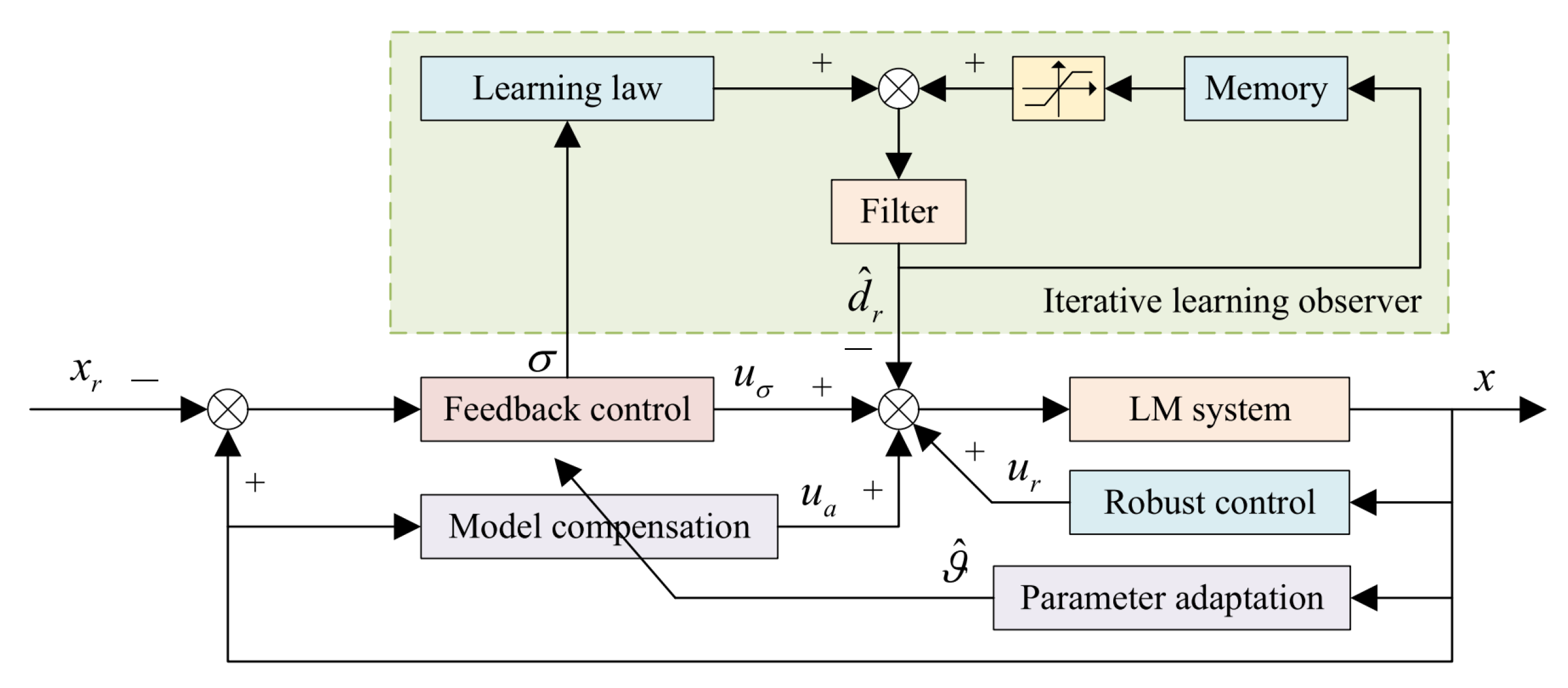
4.3. Observer-Based Control
4.4. Others
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bramerdorfer, G.; Tapia, J.A.; Pyrhonen, J.J.; Cavagnino, A. Modern electrical machine design optimization: Techniques, trends, and best practices. IEEE Trans. Ind. Electron. 2018, 65, 7672–7684. [Google Scholar] [CrossRef]
- Eguren, I.; Almandoz, G.; Egea, A.; Ugalde, G.; Escalada, A.J. Linear Machines for Long Stroke Applications-A Review. IEEE Access 2020, 9, 3960–3979. [Google Scholar] [CrossRef]
- Wang, X.Z.; Chen, F.X.; Zhu, R.F.; Huang, X.L.; Sang, N.; Yang, G.L.; Zhang, C. A Review on Disturbance Analysis and Suppression for Permanent Magnet Linear Synchronous Motor. Actuators 2021, 10, 77. [Google Scholar] [CrossRef]
- Lin, F.J.; Shen, P.H. Robust Fuzzy Neural Network Sliding-Mode Control for Two-Axis Motion Control System. IEEE Trans. Ind. Electron. 2006, 53, 1209–1225. [Google Scholar] [CrossRef]
- Kang, K.; Wang, M.Y.; Sun, J.X.; Zhang, C.M.; Li, L.Y. Nonlinear Friction Compensation for PMLSM Using an Enhanced Adaptive Friction Observer. IEEE Trans. Ind. Electron. 2024, 71, 16234–16244. [Google Scholar] [CrossRef]
- Danielsson, O.; Leijon, M. Flux distribution in linear permanent-magnet synchronous machines including longitudinal end effects. IEEE Trans. Magn. 2007, 43, 3197–3201. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, L.; Huang, X.; Yang, J.; Shen, L. Research on the method of suppressing the end detent force of permanent magnet linear synchronous motor based on stepped double auxiliary pole. IEEE Access 2018, 8, 112539–112552. [Google Scholar] [CrossRef]
- Lu, Q.F.; Wu, B.C.; Yao, Y.H.; Shen, Y.M.; Jiang, Q. Analytical model of permanent magnet linear synchronous machines considering end effect and slotting effect. IEEE Trans. Energy Convers. 2020, 35, 139–148. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, W.; Song, B. Thrust Force Calculation and Analysis for the Permanent Magnet Linear Motor Motion System Considering the Encoder Errors. IEEE Trans. Ind. Electron. 2022, 69, 6069–6079. [Google Scholar] [CrossRef]
- Tootoonchian, F.; Nasiri-Gheidari, Z. Cogging force mitigation techniques in a modular linear permanent magnet motor. IET Electr. Power Appl. 2016, 10, 667–674. [Google Scholar] [CrossRef]
- Boff, B.H.B.; Eckert, P.R.; Amara, Y. A Comprehensive Review on the End Effects of Linear Permanent Magnet Machines. IEEE Trans. Ind. Appl. 2023, 59, 1728–1741. [Google Scholar] [CrossRef]
- Wang, M.; Li, L.; Pan, D. Detent Force Compensation for PMLSM Systems Based on Structural Design and Control Method Combination. IEEE Trans. Ind. Electron. 2015, 62, 6845–6854. [Google Scholar] [CrossRef]
- Li, B.; Zhao, J.; Liu, X.; Guo, Y.; Hu, H.; Li, J. Detent Force Reduction of an Arc-Linear Permanent-Magnet Synchronous Motor by Using Compensation Windings. IEEE Trans. Ind. Electron. 2017, 64, 3001–3011. [Google Scholar] [CrossRef]
- Chung, S.U.; Lee, H.J.; Woo, B.C.; Kim, J.W.; Lee, J.Y.; Moon, S.R.; Hwang, S.M. A Feasibility Study on a New Doubly Salient Permanent Magnet Linear Synchronous Machine. IEEE Trans. Ind. Electron. 2010, 46, 1572–1575. [Google Scholar] [CrossRef]
- Ge, J.; Xu, W.; Liu, Y.; Xiong, F.; Li, D. Investigation on Winding Theory for Short Primary Linear Machines. IEEE Trans. Veh. Technol. 2021, 70, 7400–7412. [Google Scholar] [CrossRef]
- Tan, Q.; Huang, X.; Li, L.; Wang, M. Analysis of Flux Linkage and Detent Force for a Modular Tubular Permanent Magnet Synchronous Linear Motor with Large Slots. IEEE Trans. Energy Convers. 2019, 34, 1532–1541. [Google Scholar] [CrossRef]
- Cao, R.; Cheng, M.; Mi, C.C.; Hua, W. Influence of Leading Design Parameters on the Force Performance of a Complementary and Modular Linear Flux-Switching Permanent-Magnet Motor. IEEE Trans. Ind. Electron. 2014, 61, 2165–2175. [Google Scholar] [CrossRef]
- Cao, R.; Cheng, M.; Hua, W. Investigation and General Design Principle of a New Series of Complementary and Modular Linear FSPM Motors. IEEE Trans. Ind. Electron. 2013, 60, 5436–5446. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Huang, X.; Zhou, B. End Force Modeling and Modular-Secondary Optimization of Long-Secondary Permanent Magnet Linear Synchronous Motor. IEEE Trans. Ind. Appl. 2023, 59, 6625–6633. [Google Scholar] [CrossRef]
- Huang, X.; Qian, Z.; Tan, Q.; Li, J.; Zhou, B. Suppressing the Thrust Ripple of the Permanent Magnet Linear Synchronous Motors with Different Pole Structures by Setting the Modular Primary Structures Differently. IEEE Trans. Energy Convers. 2018, 33, 1815–1824. [Google Scholar] [CrossRef]
- Min, S.G.; Sarlioglu, B. 3-D Performance Analysis and Multiobjective Optimization of Coreless-Type PM Linear Synchronous Motors. IEEE Trans. Ind. Electron. 2018, 65, 1855–1864. [Google Scholar] [CrossRef]
- Chen, Z.; Kong, W.B.; Zhang, X.H.; Shi, C.J.; Qu, R.H.; Long, J.; Li, Z.Y. Novel Virtual Winding Current Controller for Suppression of Linear Permanent Magnet Machine Electromagnetic Thrust Ripple. IEEE Trans. Ind. Electron. 2023, 70, 9835–9846. [Google Scholar] [CrossRef]
- Du, H.; Chen, X.; Wen, G.; Yu, X.; Lu, J. Discrete-Time Fast Terminal Sliding Mode Control for Permanent Magnet Linear Motor. IEEE Trans. Ind. Electron. 2018, 65, 9916–9927. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, J.; Yu, Z.; Pan, Z.; Zheng, Z. High-Precision Position Control of PMLSM Using Fast Recursive Terminal Sliding Mode with Disturbance Rejection Ability. IEEE Trans. Ind. Inform. 2024, 20, 2577–2588. [Google Scholar] [CrossRef]
- Huang, Y.S.; Sung, C.C. Function-Based Controller for Linear Motor Control Systems. IEEE Trans. Ind. Electron. 2010, 57, 1096–1105. [Google Scholar] [CrossRef]
- Liu, W.; Shu, F.; Xu, Y.; Ding, R.; Yang, X.; Li, Z.; Liu, Y. Iterative learning based neural network sliding mode control for repetitive tasks: With application to a PMLSM with uncertainties and external disturbances. Mech. Syst. Signal Process. 2022, 172, 108950. [Google Scholar] [CrossRef]
- Lin, F.J.; Shen, P.H.; Fung, R.F. RFNN Control for PMLSM Drive via Backstepping Technique. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 620–644. [Google Scholar]
- Lin, F.J.; Chen, S.Y.; Teng, L.T.; Chu, H. Recurrent Functional-Link-Based Fuzzy Neural Network Controller with Improved Particle Swarm Optimization for a Linear Synchronous Motor Drive. IEEE Trans. Ind. Electron. 2009, 45, 3151–3165. [Google Scholar]
- Wang, M.Y.; Yang, R.; Tan, Q.; Cao, J.W.; Zhang, C.M.; Li, L.Y. A High-Bandwidth and Strong Robust Current Control Strategy for PMLSM Drives. IEEE Access 2018, 6, 40929–40939. [Google Scholar] [CrossRef]
- El-Sousy, F.F.M.; Abuhasel, K.A. Nonlinear Robust Optimal Control via Adaptive Dynamic Programming of Permanent-Magnet Linear Synchronous Motor Drive for Uncertain Two-Axis Motion Control System. IEEE Trans. Ind. Appl. 2020, 56, 1940–1952. [Google Scholar] [CrossRef]
- Dong, F.; Zhao, J.; Zhao, J.; Song, J.; Chen, J.; Zheng, Z. Robust Optimization of PMLSM Based on a New Filled Function Algorithm with a Sigma Level Stability Convergence Criterion. IEEE Trans. Ind. Inform. 2021, 17, 4743–4754. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhao, H.; Sun, H.; Shao, K. Diffeomorphism-Based Robust Bounded Control for Permanent Magnet Linear Synchronous Motor with Bounded Input and Position Constraints. IEEE Trans. Ind. Inform. 2023, 19, 5387–5399. [Google Scholar] [CrossRef]
- Wang, G.; Valla, M.; Solsona, J. Position Sensorless Permanent Magnet Synchronous Machine Drives—A Review. IEEE Trans. Ind. Electron. 2020, 67, 5830–5842. [Google Scholar] [CrossRef]
- Yuan, H.; Zhao, X.M.; Fu, D.X. A novel high-precision motion control for permanent magnet linear synchronous motor servo system. Int. J. Appl. Electromagn. Mech. 2021, 66, 181–201. [Google Scholar] [CrossRef]
- Inoue, M.; Sato, K. An Approach to a Suitable Stator Length for Minimizing the Detent Force of Permanent Magnet Linear Synchronous Motors. IEEE Trans. Ind. Electron. 2000, 36, 1890–1893. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, X.; Watanabe, K. Minimizing detent force of permanent magnet linear synchronous machines by designing mover using mesh-level stochastic shaping. Energy Rep. 2023, 9, 859–869. [Google Scholar] [CrossRef]
- Chung, M.K.; Kim, J.W.; Woo, B.C.; Hong, D.K.; Lee, J.Y.; Koo, D.H. Force Ripple and Magnetic Unbalance Reduction Design for Doubly Salient Permanent Magnet Linear Synchronous Motor. IEEE Trans. Ind. Electron. 2011, 47, 4207–4210. [Google Scholar] [CrossRef]
- Chung, M.K.; Kim, J.W.; Woo, B.C.; Hong, D.K.; Lee, J.Y.; Chun, Y.D.; Koo, D.H. Design and experimental validation of doubly salient permanent magnet linear synchronous motor for precision position control. Mechatronics 2013, 23, 172–181. [Google Scholar] [CrossRef]
- Chung, S.K.; Kim, J.M. Double-Sided Iron-Core PMLSM Mover Teeth Arrangement Design for Reduction of Detent Force and Speed Ripple. IEEE Trans. Ind. Electron. 2016, 63, 3000–3008. [Google Scholar] [CrossRef]
- Kwon, Y.S.; Kim, W.J. Detent-Force Minimization of Double-Sided Interior Permanent-Magnet Flat Linear Brushless Motor. IEEE Trans. Ind. Electron. 2016, 52, 8201609. [Google Scholar] [CrossRef]
- Deng, C.; Ye, C.; Yang, J.; Sun, S.; Yu, D. A Novel Permanent Magnet Linear Motor for the Application of Electromagnetic Launch System. IEEE Trans. Appl. Supercond. 2020, 30, 4902005. [Google Scholar] [CrossRef]
- Zhu, Y.W.; Lee, S.G.; Chung, K.S.; Cho, Y.H. Investigation of Auxiliary Poles Design Criteria on Reduction of End Effect of Detent Force for PMLSM. IEEE Trans. Ind. Electron. 2009, 45, 2863–2866. [Google Scholar]
- Huang, X.; Tan, Q.; Wang, Q.; Li, J. Optimization for the Pole Structure of Slot-Less Tubular Permanent Magnet Synchronous Linear Motor and Segmented Detent Force Compensation. IEEE Trans. Appl. Supercond. 2016, 26, 0611405. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, K.; Chen, P.; Huang, J. Reduction of Detent Force in Permanent Magnet Linear Synchronous Motor with Double Secondary Side. In Proceedings of the 17th IEEE International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014. [Google Scholar]
- Huang, X.Z.; Yu, H.C.; Zhou, B.; Li, L.Y.; Gerada, D.; Gerada, C.; Qian, Z.Y. Detent-Force Minimization of Double-Sided Permanent Magnet Linear Synchronous Motor by Shifting One of the Primary Components. IEEE Trans. Ind. Electron. 2020, 67, 180–191. [Google Scholar] [CrossRef]
- Huang, X.Z.; Li, J.; Zhang, C.; Qian, Z.Y.; Li, L.Y.; Gerada, D. Electromagnetic and Thrust Characteristics of Double-sided Permanent Magnet Linear Synchronous Motor Adopting Staggering Primaries Structure. IEEE Trans. Ind. Electron. 2019, 66, 4826–4836. [Google Scholar] [CrossRef]
- Lan, Z.; Chen, L.; Xiao, X.; Luo, Y.; Deng, M.; Zhu, S. Detent force suppression of permanent magnet linear synchronous motor based on a V-shaped tooth-slot structure. IET Electr. Power Appl. 2023, 17, 535–546. [Google Scholar] [CrossRef]
- Yong, J.Y.; Lang, J.H.; Trumper, D.L. Double-Sided Linear Iron-Core Fine-Tooth Motor for Low Acoustic Noise and High Acceleration. IEEE/ASME Trans. Mechatron. 2019, 24, 2161–2170. [Google Scholar]
- Xu, X.; Sun, Z.; Du, B.; Ai, L. Pole Optimization and Thrust Ripple Suppression of New Halbach Consequent-Pole PMLSM for Ropeless Elevator Propulsion. IEEE Access 2020, 8, 62042–62052. [Google Scholar] [CrossRef]
- Lee, S.G.; Kim, S.A.; Saha, S.; Zhu, Y.W.; Cho, Y.H. Optimal Structure Design for Minimizing Detent Force of PMLSM for a Ropeless Elevator. IEEE Trans. Ind. Electron. 2014, 50, 4001104. [Google Scholar] [CrossRef]
- Park, E.J.; Kim, Y.J.; Jung, S.Y. Optimal design of semi-arch auxiliary teeth of stationary discontinuous armature PMLSM with concentrated winding using design of experiment. In Proceedings of the 9th IET International Conference on Computation in Electromagnetics (CEM 2014), London, UK, 31 March–1 April 2014. [Google Scholar]
- Kim, S.J.; Park, E.J.; Jung, S.Y.; Kim, Y.J. Optimal design of reformed auxiliary teeth for reducing end detent force of stationary discontinuous armature PMLSM. IEEE Trans. Appl. Supercond. 2016, 26, 5203305. [Google Scholar] [CrossRef]
- Zhao, J.; Mou, Q.; Guo, K.; Liu, X.; Li, J.; Guo, Y. Reduction of the Detent Force in a Flux-Switching Permanent Magnet Linear Motor. IEEE Trans. Energy Convers. 2019, 34, 1695–1705. [Google Scholar] [CrossRef]
- Zhao, J.; Mou, Q.; Zhu, C.; Chen, C.; Li, J. Study on a Double-Sided Permanent-Magnet Linear Synchronous Motor with Reversed Slots. IEEE/ASME Trans. Mechatron. 2021, 26, 3–12. [Google Scholar] [CrossRef]
- Wu, Q.; Yang, G.; Tang, E.; Wang, L.; Wang, Z. A Slotted Double-Primaries Permanent Magnet Synchronous Linear Motor with a Low Thrust Ripple. IEEE/ASME Trans. Mechatron. 2024, 29, 3786–3798. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, L.; Wang, R. Hierarchical Multi-Objective Optimization of a Multi-Sided Permanent Magnet Linear Synchronous Motor with Ring Structure Winding for Conveyor Systems. IEEE Access 2024, 12, 128833–128842. [Google Scholar] [CrossRef]
- Mao, Y.; Sun, Z.; Huang, C.; Jia, G.; Ding, A. Electromagnetic Characteristics Analysis of a Novel Ironless Double-Sided Halbach Permanent Magnet Synchronous Linear Motor for Electromagnetic Launch Considering Longitudinal End Effect. IEEE Trans. Transp. Electrif. 2024, 10, 7467–7477. [Google Scholar] [CrossRef]
- Bai, Y.; Yang, T.; Kou, B. Reducing Detent Force and Three-phase Magnetic Paths Unbalance of PM Linear Synchronous Motor Using Modular Primary Iron-Core Structure. In Proceedings of the 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014. [Google Scholar]
- Tan, Q.; Huang, X.; Li, L.; Wang, M. Research on Inductance Unbalance and Thrust Ripple Suppression of Slot-Less Tubular Permanent Magnet Synchronous Linear Motor. IEEE Access 2018, 6, 51011–51020. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, W.; Ji, J.; Liu, G.; Du, Y.; Fang, Z.; Mo, L. Design and Analysis of a New Linear Hybrid Excited Flux Reversal Motor with Inset Permanent Magnets. IEEE Trans. Ind. Electron. 2014, 50, 8202204. [Google Scholar] [CrossRef]
- Huang, X.; Liang, J.; Zhou, B.; Zhang, C.; Li, L.; Gerada, D. Suppressing the Thrust Ripple of the Consequent-Pole Permanent Magnet Linear Synchronous Motor by Two-Step Design. IEEE Access 2018, 6, 32935–32944. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Zhou, B.; Liu, Y.S.; Huang, Q. Design Criterion for Dual-Modular Permanent Magnet Linear Synchronous Motor with Long Stroke and High Flexibility. IEEE Trans. Ind. Electron. 2022, 69, 10428–10436. [Google Scholar] [CrossRef]
- Wu, L.; Li, Y.; Lu, Q. Detent Force Fast Optimization Method of Modular Permanent-Magnet Linear Synchronous Motors. IEEE Trans. Ind. Electron. 2024, 71, 16191–16199. [Google Scholar] [CrossRef]
- Tan, Q.; Huang, X.; Li, L.; Wang, M. Magnetic Field Analysis and Flux Barrier Design for Modular Permanent Magnet Linear Synchronous Motor. IEEE Trans. Ind. Electron. 2020, 67, 3891–3900. [Google Scholar] [CrossRef]
- Lin, F.J.; Hwang, J.C.; Chou, P.H.; Hung, Y.C. FPGA-Based Intelligent-Complementary Sliding-Mode Control for PMLSM Servo-Drive System. IEEE Trans. Power Electron. 2010, 25, 2573–2587. [Google Scholar] [CrossRef]
- Chen, S.Y.; Chiang, H.H.; Liu, T.S.; Chang, C.H. Precision Motion Control of Permanent Magnet Linear Synchronous Motors Using Adaptive Fuzzy Fractional-Order Sliding-Mode Control. IEEE/ASME Trans. Mechatron. 2019, 24, 741–752. [Google Scholar] [CrossRef]
- Fu, D.; Zhao, X.; Zhu, J. A Novel Robust Super-Twisting Nonsingular Terminal Sliding Mode Controller for Permanent Magnet Linear Synchronous Motors. IEEE Trans. Power Electron. 2022, 37, 2936–2945. [Google Scholar] [CrossRef]
- Fu, D.; Zhao, X. A Novel Robust Adaptive Nonsingular Fast Integral Terminal Sliding Mode Controller for Permanent Magnet Linear Synchronous Motors. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 1672–1683. [Google Scholar] [CrossRef]
- Chen, M.Y.; Lu, J.S. High-Precision Motion Control for a Linear Permanent Magnet Iron Core Synchronous Motor Drive in Position Platform. IEEE Trans. Ind. Inform. 2014, 10, 99–108. [Google Scholar] [CrossRef]
- Wang, M.; Yang, R.; Zhang, C.; Cao, J.; Li, L. Inner Loop Design for PMLSM Drives with Thrust Ripple Compensation and High-Performance Current Control. IEEE Trans. Ind. Electron. 2018, 65, 9905–9915. [Google Scholar] [CrossRef]
- Yu, L.; Huang, J.; Luo, W.; Chang, S.; Sun, H.; Tian, H. Sliding-Mode Control for PMLSM Position Control—A Review. Actuators 2023, 12, 31. [Google Scholar] [CrossRef]
- Lin, F.J.; Lin, C.H. On-Line Gain-Tuning IP Controller Using RFNN. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 655–670. [Google Scholar]
- Lin, F.J.; Yang, S.L.; Shen, P.H. Self-constructing recurrent fuzzy neural network for DSP-based permanent-magnet linear-synchronousmotor servodrive. IEEE Trans. Aerosp. Electron. Syst. 2006, 153, 236–246. [Google Scholar]
- Chen, S.Y.; Liu, T.S. Intelligent tracking control of a PMLSM using self-evolving probabilistic fuzzy neural network. IET Electr. Power Appl. 2017, 11, 1043–1054. [Google Scholar] [CrossRef]
- Lin, F.J.; Shen, P.H. Adaptive Fuzzy-Neural-Network Control for a DSP-Based Permanent Magnet Linear Synchronous Motor Servo Drive. IEEE Trans. Fuzzy Syst. 2006, 14, 481–495. [Google Scholar]
- Chen, C.S.; Lin, W.C. Self-adaptive interval type-2 neural fuzzy network control for PMLSM drives. Expert Syst. Appl. 2011, 38, 14679–14689. [Google Scholar] [CrossRef]
- Lin, F.J.; Shen, P.H.; Yang, S.L.; Chou, P.H. Recurrent Radial Basis Function Network-Based Fuzzy Neural Network Control for Permanent-Magnet Linear Synchronous Motor Servo Drive. IEEE Trans. Ind. Electron. 2006, 42, 3694–3705. [Google Scholar] [CrossRef]
- Lin, F.J.; Wai, R.J.; Hong, C.M. Hybrid Supervisory Control Using Recurrent Fuzzy Neural Network for Tracking Periodic Inputs. IEEE Trans. Neural Netw. 2001, 12, 68–90. [Google Scholar] [PubMed]
- Cho, K.; Kim, J.; Choi, S.B.; Oh, S. A High-Precision Motion Control Based on a Periodic Adaptive Disturbance Observer in a PMLSM. IEEE/ASME Trans. Mechatron. 2015, 20, 2158–2171. [Google Scholar] [CrossRef]
- Xiang, B.; Wen, T.; Wen, T. The speed control of PMLSM with discontinuous driving coils based on multi-loop DOB model. ISA Trans. 2024, 146, 366–379. [Google Scholar] [CrossRef]
- Yang, R.; Wang, M.Y.; Li, L.Y.; Zhang, C.M.; Jiang, J.L. Robust Predictive Current Control with Variable-Gain Adaptive Disturbance Observer for PMLSM. IEEE Access 2018, 6, 13158–13169. [Google Scholar] [CrossRef]
- Yang, R.; Li, L.Y.; Wang, M.Y.; Zhang, C.M. Force Ripple Compensation and Robust Predictive Current Control of PMLSM Using Augmented Generalized Proportional—Integral Observer. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 302–315. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, X.; Lin, W.; Rodriguez-Andina, J.J. Iterative Learning Observer-Based High-Precision Motion Control for Repetitive Motion Tasks of Linear Motor-Driven Systems. IEEE Open J. Ind. Electron. Soc. 2024, 5, 54–66. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, H.; Li, B.; Wang, Q.; Ding, D.; Wang, G.; Xu, D. Auxiliary Model Compensated RESO-Based Proportional Resonant Thrust Ripple Suppression for PMLSM Drives. IEEE Trans. Transp. Electrif. 2023, 9, 2141–2152. [Google Scholar] [CrossRef]
- Song, F.; Liu, Y.; Xu, J.X.; Yang, X.; He, P.; Yang, Z. Iterative Learning Identification and Compensation of Space-Periodic Disturbance in PMLSM Systems with Time Delay. IEEE Trans. Ind. Electron. 2018, 65, 7579–7589. [Google Scholar] [CrossRef]
- Wang, M.Y.; Kang, K.; Zhang, C.M.; Li, L.Y. Precise Position Control in Air-Bearing PMLSM System Using an Improved Anticipatory Fractional-Order Iterative Learning Control. IEEE Trans. Ind. Electron. 2024, 71, 6073–6083. [Google Scholar] [CrossRef]
- Hu, X.; Zhao, J.; Pan, Z.; Yu, Z.; Yang, X. Optimal Design of PMSLM Based on Extremum Robust Domain Characteristic. IEEE Trans. Ind. Electron. 2024, 71, 6063–6072. [Google Scholar] [CrossRef]
- Xu, J.; Wei, Z.; Wang, S. Active Disturbance Rejection Repetitive Control for Current Harmonic Suppression of PMSM. IEEE Trans. Power Electron. 2023, 38, 14423–14437. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, J.; Wang, L.; Li, M.; Hu, Y. Combined Vector Resonant and Active Disturbance Rejection Control for PMSLM Current Harmonic Suppression. IEEE Trans. Ind. Inform. 2020, 16, 5691–5702. [Google Scholar] [CrossRef]
- Xu, W.; Zou, J.; Liu, Y.; Zhu, J. Weighting Factorless Model Predictive Thrust Control for Linear Induction Machine. IEEE Trans. Power Electron. 2019, 34, 9916–9928. [Google Scholar] [CrossRef]
- Jie, H.; See, K.; Chang, Y.; Gao, R.; Fan, F.; Zhao, Z. Enhancing motor impedance measurements: Broadening the spectrum from low to high frequencies. Meas. Sci. Technol. 2024, 35, 086008. [Google Scholar] [CrossRef]



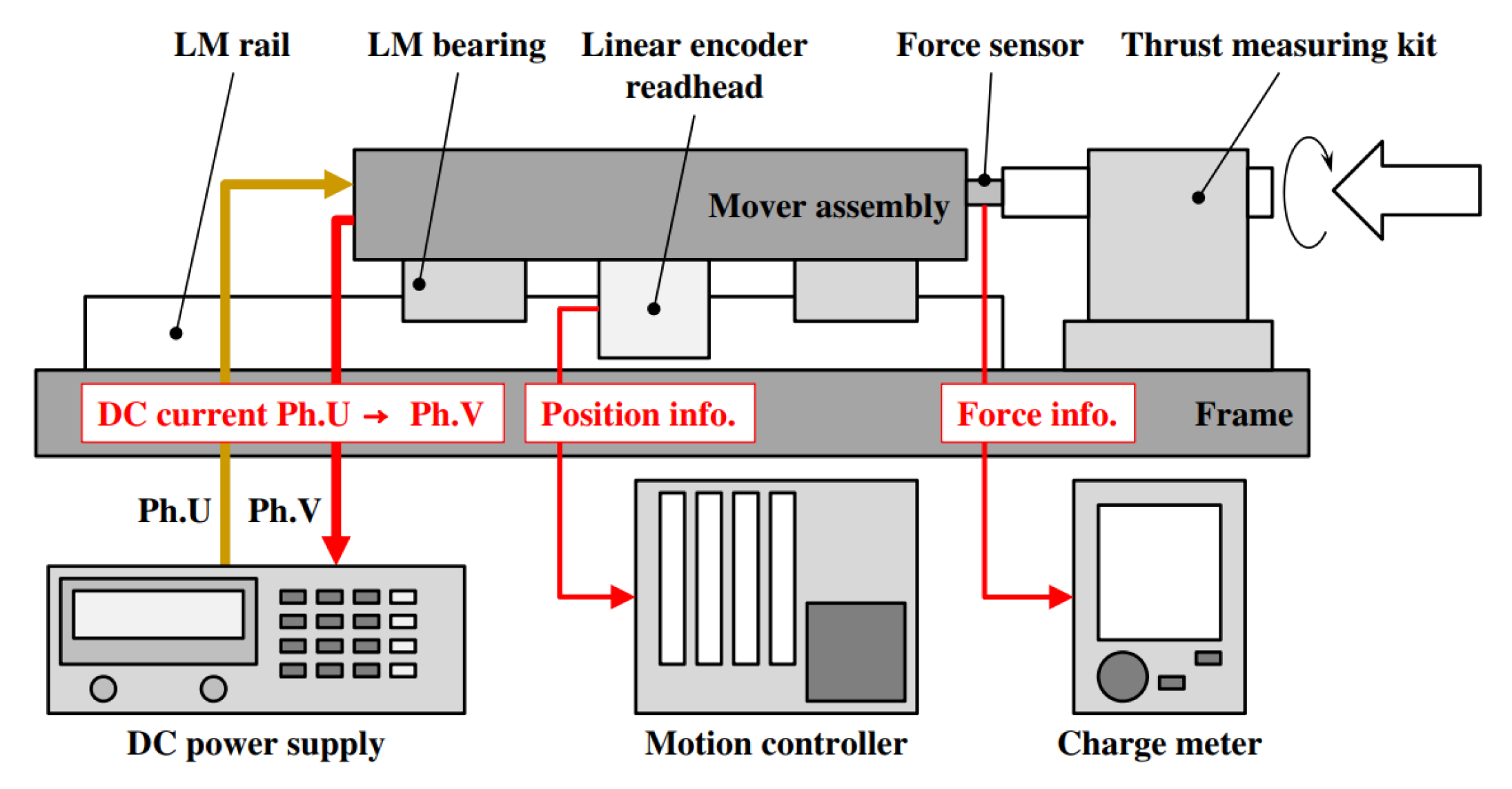
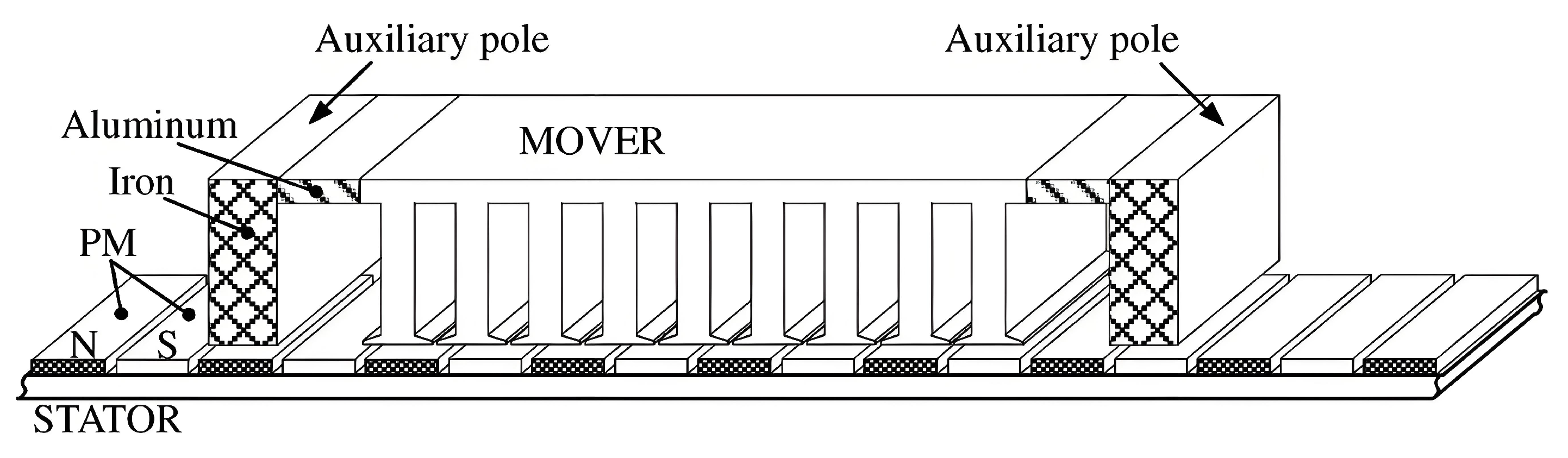


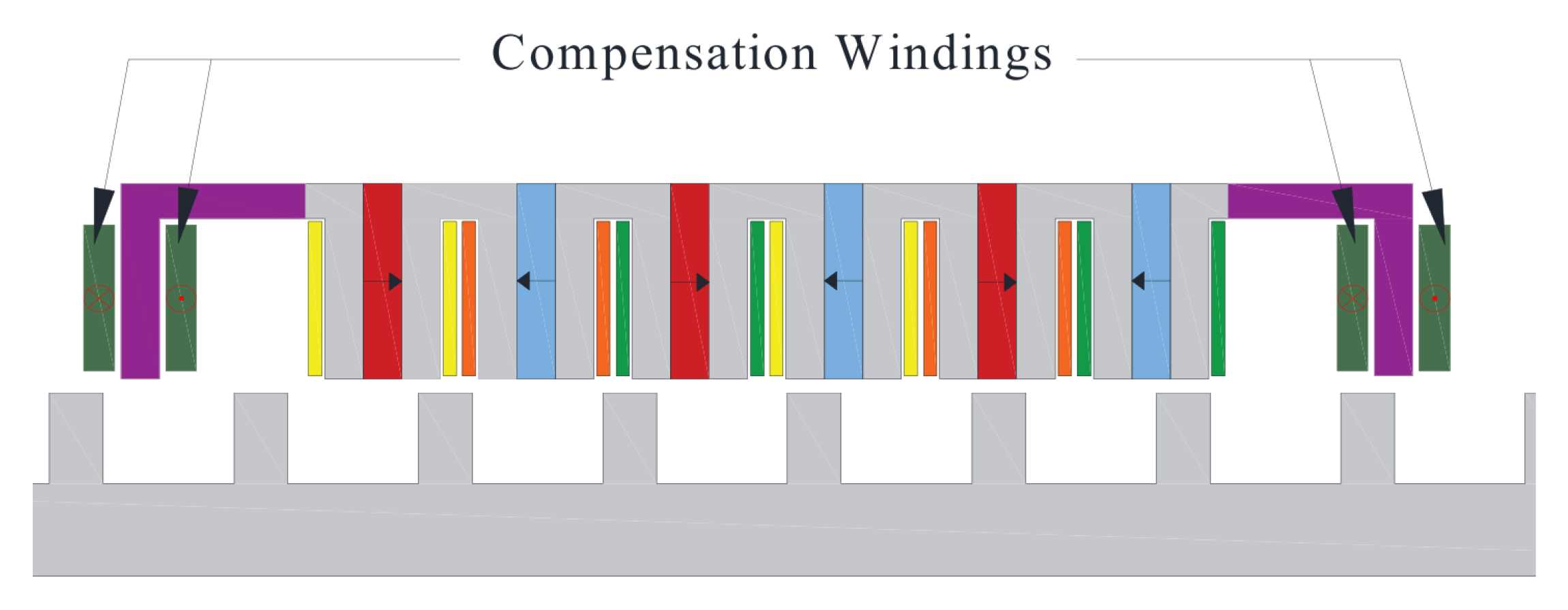
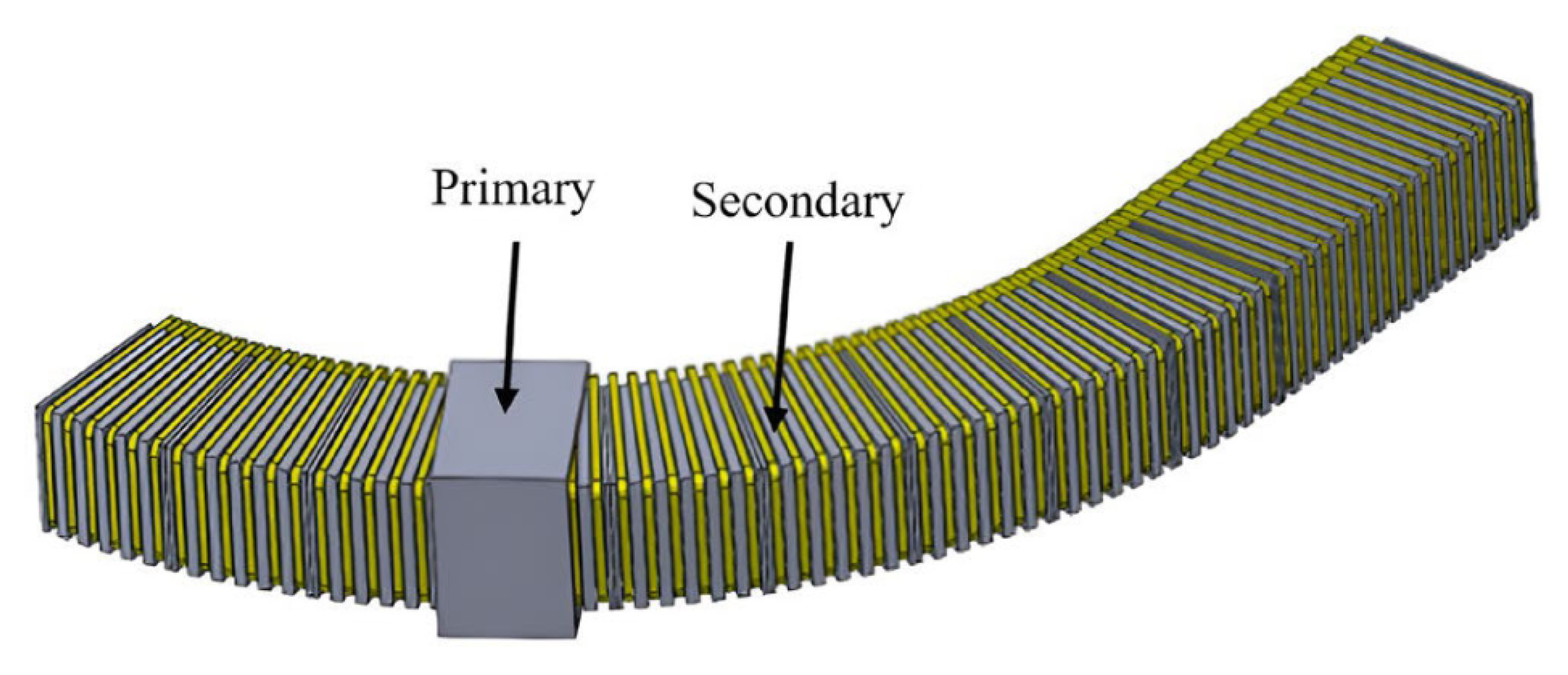




| Methods | Advantages | Disadvantage |
|---|---|---|
| Intuitive design | Complex structure | |
| Adjusting the shape and length of the mover or stator | Significant effect | High manufacturing costs |
| Plentiful achievements | ||
| Active compensation method | Difficult to process | |
| Adding auxiliary structures | Significant effect | Length and weight increase |
| Plentiful achievements | ||
| Plentiful achievements | Relatively few achievements | |
| Additional compensation windings | Magnetic circuit decoupling | Magnetic leakage problem |
| Significant effect | Manufacturing costs increase | |
| Flexible dimensions design | Unit module coupling | |
| Modular design | Most widely applied | |
| Can combine with other methods |
| Methods | Advantages | Disadvantage |
|---|---|---|
| Good robustness | Hard to apply | |
| Sliding-mode control | Suitable for nonlinear systems | Chattering problem |
| Plentiful achievements | ||
| Intelligent control method | High requirements for training | |
| Fuzzy neural network control | Suitable for nonlinear systems | Complex model structure |
| Parameter rapid update | ||
| Plentiful achievements | High dependence on system models | |
| Observer-based control | Enhanced stability and robustness | Complex design and tuning |
| Significant effect | Sensitivity to measurement noise | |
| Weak dependence on system models | Complex parameter tuning | |
| Active disturbance rejection control | Good dynamic performance | High computational cost |
| Wide range of applications | ||
| High control precision | High computational complexity | |
| Model predictive thrust control | Good adaptability to system changes | High dependence on model accuracy |
| Difficulty in parameter tuning |
| Methods | Economic Consumption | Time Consumption | Application Difficulty | Stability |
|---|---|---|---|---|
| Structural optimization | High | No need for further consideration after design completion | Design complexity | Structural parameter drift over time |
| Control strategies | Low | Requirement for extensive time in debugging | Parameter tuning challenges | Ability to dynamically identify parameters |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Liu, Y.; Zhang, Q.; Tan, J. Analysis and Suppression of Thrust Ripple in a Permanent Magnet Linear Synchronous Motor—A Review. Energies 2025, 18, 863. https://doi.org/10.3390/en18040863
Chen S, Liu Y, Zhang Q, Tan J. Analysis and Suppression of Thrust Ripple in a Permanent Magnet Linear Synchronous Motor—A Review. Energies. 2025; 18(4):863. https://doi.org/10.3390/en18040863
Chicago/Turabian StyleChen, Siwen, Yang Liu, Qian Zhang, and Jiubin Tan. 2025. "Analysis and Suppression of Thrust Ripple in a Permanent Magnet Linear Synchronous Motor—A Review" Energies 18, no. 4: 863. https://doi.org/10.3390/en18040863
APA StyleChen, S., Liu, Y., Zhang, Q., & Tan, J. (2025). Analysis and Suppression of Thrust Ripple in a Permanent Magnet Linear Synchronous Motor—A Review. Energies, 18(4), 863. https://doi.org/10.3390/en18040863






