A Comprehensive Review on the Natural Convection Heat Transfer in Horizontal and Inclined Closed Rectangular Enclosures with Internal Objects at Various Heating Conditions
Abstract
1. Introduction
2. Relevant Previous Reviews
3. Statistics of the Previous Studies Reviewed
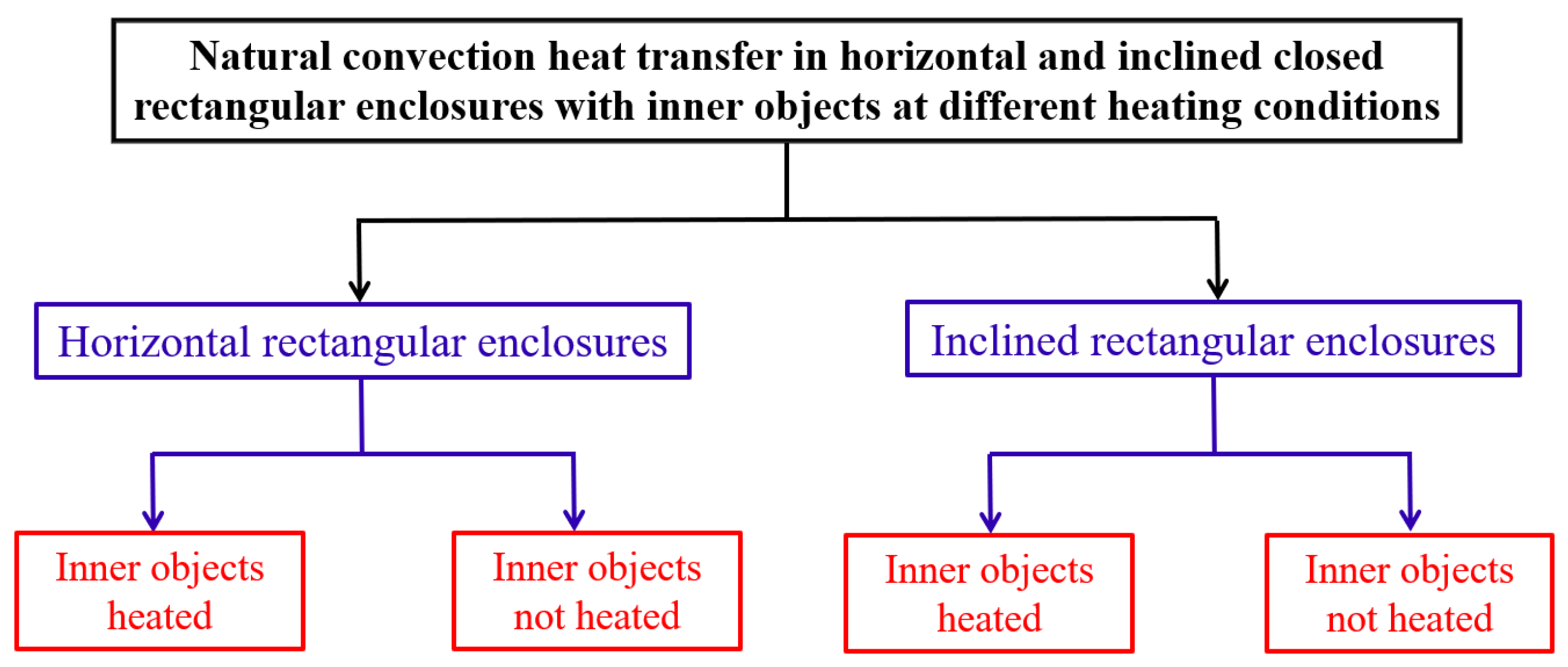
4. Horizontal Closed Rectangular Enclosures
4.1. Inner Objects Heated
4.1.1. Circular Objects
One Circular Cylinder
Two Circular Cylinders
More than Two Circular Cylinders
4.1.2. Square Objects
One Square Cylinder
Multiple Square Cylinders
4.1.3. Objects in Other Shapes
Elliptic Cylinder
Rectangular Cylinder
Triangular Cylinder
Thin Plates
Objects with Other Miscellaneous Shapes
4.2. Inner Objects Not Heated
4.2.1. Circular Objects
4.2.2. Square Objects
4.2.3. Objects in Other Shapes
5. Inclined Closed Rectangular Enclosures
5.1. Inner Objects Heated
5.2. Inner Objects Not Heated
6. Concluding Remarks and Recommendations
- The majority of the previous studies deal with inner objects which are heated/cooled.
- The majority focus on horizontal closed rectangular enclosures and only a small portion of the studies focus on inclined ones.
- The majority were carried out under relatively low values, with the most studied. Some studies extended the maximum to , while only several studies extended the maximum to . Due to these, without any exception, all previous studies assumed laminar flow and heat transfer, which significantly restrict the usefulness of the results for practical applications.
- The FVM (finite volume method), IBM (Immersed boundary method)/FVM, FEM (finite element method), FDM (finite difference method), and LBM (Lattice Boltzmann method) are the main numerical methods used, and only several studies used other methods.
- Only one study is experimental [163], and the remaining 145 studies are numerical.
- The assumption of 2D flow and heat transfer is predominant and only a small number of studies assumed 3D flow and heat transfer. The majority of the studies assumed unsteady flow and heat transfer.
- When the number of the inner objects are more than one, identical objects were considered.
- Only several studies considered time-changing heating conditions on the enclosure walls or the IOs (mainly in the sinusoidal form).
- As in practical applications the maximum values of are generally very high (much large than ), the natural convection flow and heat transfer are usually turbulent and always unsteady; thus, numerical simulations should be carried out by taking into account of turbulence with the assumption of 3D and unsteady flow and heat transfer. Numerical simulations should be carried out using advanced turbulence modeling techniques, such as Direct Numerical Simulation (DNS), Large-Eddy Simulation (LES), various Reynolds-Averaged Navier–Stokes (RANS) turbulence models (such as model and its variants, model, and Reynolds stress model), and Detached Eddy Simulation (DES) which is a hybrid RANS-LES model.
- The studies involving multiple IOs, particularly more than two IOs, should be carried out as they are also very common in practical applications.
- The studies involving multiple IOs which are not identical with different heating conditions and not uniformly distributed in the enclosure should be significantly increased, also due to their practical application importance.
- Inclined enclosures with IOs at different heating conditions are also common in practical applications and are of fundamental significance; thus, the research on such cases should be strengthened significantly.
- Experimental studies on the topic should be substantially increased to provide more insightful results for practical applications.
- In practical applications, it is common that the heat transfer in the enclosure due to the heat generation of the IOs should be reduced and some mechanisms which are time-dependent (such as heat sinking using heat transfer fluid to take away heat from the heat-generating objects) should be used. Research on such cases should be carried out to produce insightful information for practical applications.
- More quantitative results, particular empirical correlations for the heat transfer rate and other pertinent parameters characterizing the natural convection flow and heat transfer, should be obtained, in addition to qualitative results.
- Nanofluids as the medium in enclosures have been found to enhance the natural convection heat transfer in the enclosure; therefore, more research work with other nanofluids in addition to Al2O3, Cu, TiO2, Ag, etc., should be significantly strengthened.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | two-dimensional |
| 3D | three-dimensional |
| CC | circular cylinder |
| EC | elliptic cylinder |
| FDM | finite difference method |
| FEM | finite element method |
| FVM | finite volume method |
| IBM | immersed boundary method |
| IO | inner object |
| LBM | Lattice Boltzmann method |
| NCHF | natural convection heat transfer |
| SC | square cylinder |
| TC | triangular cylinder |
| TP | thin plate |
References
- Cosley, M.R.; Garcia, M.P.; Grzesik, L.K.; Webster, J.; Marongiu, M.J. Thermal development of modular outdoor cabinets. In Proceedings of the 17th International Telecommunications Energy Conference (INTELEC95), The Hague, The Netherlands, 29 October–1 November 1995; pp. 384–391. [Google Scholar]
- Marongru, M.J.; Clarksean, R.L.; Knsha, B.; Watwe, A. Passive thermal management of outdoor enclosures using PCM and enhanced natural convection. In Proceedings of the Power and Energy Systems in Converging Markets, Melbourne, VIC, Australia, 23–23 October 1997; pp. 504–511. [Google Scholar]
- Marongiu, M.J. Some issues in experimental testing and methodologies in the thermal management of telecommunication components, systems and enclosures. In Proceedings of the 17th International Telecommunications Energy Conference (INTELEC95), The Hague, Netherlands, 29 October–1 November 1995; pp. 834–838. [Google Scholar]
- Marongiu, M.J. Thermal management design of battery compartments of outdoor telecommunication cabinets. In Proceedings of the International Telecommunications Energy Conference (INTELEC96), Boston, MA, USA, 6–10 October 1996; pp. 711–717. [Google Scholar]
- Porebski, W.; Ulfvengren, R. Passive cooling of small telecommunication enclosures. Case study and practical approach. In Proceedings of the 20th International Telecommunications Energy Conference (INTELEC98), San Francisco, CA, USA, 4–8 October 1998; pp. 562–567. [Google Scholar]
- Jobby, A.; Khatamifar, M.; Lin, W. Alternative Internal Configurations for Enhancing Heat Transfer in Telecommunication Cabinets. Energies 2023, 16, 3505. [Google Scholar] [CrossRef]
- Baïri, A.; Zarco-Pernia, E.; de María, J.G. A review on natural convection in enclosures for engineering applications. The particular case of the parallelogrammic diode cavity. Appl. Therm. Eng. 2014, 63, 304–322. [Google Scholar] [CrossRef]
- Das, D.; Roy, M.; Basak, T. Studies on natural convection within enclosures of various (non-square) shapes–A review. Int. J. Heat Mass Transf. 2017, 106, 356–406. [Google Scholar] [CrossRef]
- Miroshnichenko, I.V.; Sheremet, M.A. Turbulent natural convection heat transfer in rectangular enclosures using experimental and numerical approaches: A review. Renew. Sustain. Energy Rev. 2018, 82, 40–59. [Google Scholar] [CrossRef]
- Pandey, S.; Park, Y.G.; Ha, M.Y. An exhaustive review of studies on natural convection in enclosures with and without internal bodies of various shapes. Int. J. Heat Mass Transf. 2019, 138, 762–795. [Google Scholar] [CrossRef]
- Rostami, S.; Aghakhani, S.; Hajatzadeh, P.A.; Afrand, M.; Cheraghian, G.; Oztop, H.F.; Shadloo, M.S. A review on the control parameters of natural convection in different shaped cavities with and without nanofluid. Processes 2020, 8, 1011. [Google Scholar] [CrossRef]
- Hussien, A.A.; Al-Kouz, W.; Hassan, M.E.; Janvekar, A.A.; Chamkha, A.J. A review of flow and heat transfer in cavities and their applications. Eur. Phys. J. Plus 2021, 136, 353. [Google Scholar] [CrossRef]
- Abdulkadhim, A.; Abed, I.M.; Said, N.M. Review of natural convection within various shapes of enclosures. Arab. J. Sci. Eng. 2021, 46, 11543–11586. [Google Scholar] [CrossRef]
- Abdulkadhim, A.; Isam, M.A.; Said, N.M. An exhaustive review on natural convection within complex enclosures: Influence of various parameters. Chin. J. Phys. 2021, 74, 365–388. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Abosinnee, A.S.; Al-Hadraawy, S.K.; Ismael, M.A.; Fteiti, M.A.; Hashim, I.; Sheremet, M.; Ghalambaz, M.; Chamkha, A.J. Convection heat transfer in enclosures with inner bodies: A review on single and two-phase nanofluid models. Renew. Sustain. Energy Rev. 2023, 183, 113424. [Google Scholar] [CrossRef]
- Saha, G.; Al-Waaly, A.A.Y.; Paul, M.C.; Saha, S.C. Heat transfer in cavities: Configurative systematic review. Energies 2023, 16, 2338. [Google Scholar] [CrossRef]
- Shu, C.; Xue, H.; Zhu, Y.D. Numerical study of natural convection in an eccentric annulus between a square outer cylinder and a circular inner cylinder using DQ method. Int. J. Heat Mass Transf. 2001, 44, 3321–3333. [Google Scholar] [CrossRef]
- Shu, C.; Zhu, Y.D. Efficient computation of natural convection in a concentric annulus between an outer square cylinder and an inner circular cylinder. Int. J. Numer. Methods Fluids 2002, 38, 429–445. [Google Scholar] [CrossRef]
- Ding, H.; Shu, C.; Yeo, K.S.; Lu, Z.L. Simulation of natural convection in eccentric annuli between a square outer cylinder and a circular inner cylinder using local MQ-DQ method. Numer. Heat Transf. Part Appl. 2005, 47, 291–313. [Google Scholar] [CrossRef]
- Dutta, S.; Kumar, P.; Kalita, J.C. Streamfunction-velocity computation of natural convection around heated bodies placed in a square enclosure. Int. J. Heat Mass Transf. 2020, 152, 119550. [Google Scholar] [CrossRef]
- Hussain, S.H.; Hussein, A.K. Numerical investigation of natural convection phenomena in a uniformly heated circular cylinder immersed in square enclosure filled with air at different vertical locations. Int. Commun. Heat Mass Transf. 2010, 37, 1115–1126. [Google Scholar] [CrossRef]
- Tasnim, S.H.; Mahmud, S.; Das, P.K. Effect of aspect ratio and eccentricity on heat transfer from a cylinder in a cavity. Int. J. Numer. Methods Heat Fluid Flow 2002, 12, 855–869. [Google Scholar] [CrossRef]
- Choi, C.; Cho, H.W.; Ha, M.Y.; Yoon, H.S. Effect of circular cylinder location on three-dimensional natural convection in a cubical enclosure. J. Mech. Sci. Technol. 2015, 29, 1307–1318. [Google Scholar] [CrossRef]
- Seo, Y.M.; Doo, J.H.; Ha, M.Y. Three-dimensional flow instability of natural convection induced by variation in radius of inner circular cylinder inside cubic enclosure. Int. J. Heat Mass Transf. 2016, 95, 566–578. [Google Scholar] [CrossRef]
- Seo, Y.M.; Ha, M.Y.; Park, Y.G. A numerical study on the three-dimensional natural convection with a cylinder in a long rectangular enclosure. Part I: Size effect of a circular cylinder or an elliptical cylinder. Int. J. Heat Mass Transf. 2019, 134, 420–436. [Google Scholar] [CrossRef]
- Seo, Y.M.; Luo, K.; Ha, M.Y.; Park, Y.G. Direct numerical simulation and artificial neural network modeling of heat transfer characteristics on natural convection with a sinusoidal cylinder in a long rectangular enclosure. Int. J. Heat Mass Transf. 2020, 152, 119564. [Google Scholar] [CrossRef]
- Angeli, D.; Levoni, P.; Barozzi, G.S. Numerical predictions for stable buoyant regimes within a square cavity containing a heated horizontal cylinder. Int. J. Heat Mass Transf. 2008, 51, 553–565. [Google Scholar] [CrossRef]
- Doo, J.H.; Mun, G.S.; Ha, M.Y.; Seong, S.Y. Thermo-dynamic irreversibility induced by natural convection in square enclosure with inner cylinder. Part-II: Effect of vertical position of inner cylinder. Int. J. Heat Mass Transf. 2016, 97, 1120–1139. [Google Scholar] [CrossRef]
- Kang, D.H.; Ha, M.Y.; Yoon, H.S.; Choi, C. Bifurcation to unsteady natural convection in square enclosure with a circular cylinder at Rayleigh number of 107. Int. J. Heat Mass Transf. 2013, 64, 926–944. [Google Scholar] [CrossRef]
- Lee, J.M.; Ha, M.Y.; Yoon, H.S. Natural convection in a square enclosure with a circular cylinder at different horizontal and diagonal locations. Int. J. Heat Mass Transf. 2010, 53, 5905–5919. [Google Scholar] [CrossRef]
- Kim, B.S.; Lee, D.S.; Ha, M.Y.; Yoon, H.S. A numerical study of natural convection in a square enclosure with a circular cylinder at different vertical locations. Int. J. Heat Mass Transf. 2008, 51, 1888–1906. [Google Scholar] [CrossRef]
- Liao, C.; Lin, C. Transitions of natural convection flows in a square enclosure with a heated circular cylinder. Appl. Therm. Eng. 2014, 72, 41–47. [Google Scholar] [CrossRef]
- Liao, C.; Lin, C. Influence of Prandtl number on the instability of natural convection flows within a square enclosure containing an embedded heated cylinder at moderate Rayleigh number. Phys. Fluids 2015, 27, 013603. [Google Scholar] [CrossRef]
- Roslan, R.; Saleh, H.; Hashim, I.; Bataineh, A.S. Natural convection in an enclosure containing a sinusoidally heated cylindrical source. Int. J. Heat Mass Transf. 2014, 70, 119–127. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, Y.; Yang, X.; Shi, B.; Chai, Z. A lattice Boltzmann analysis of the conjugate natural convection in a square enclosure with a circular cylinder. Appl. Math. Model. 2019, 71, 31–44. [Google Scholar] [CrossRef]
- Wang, L.; Huang, C.; Hu, J.; Shi, B.; Chai, Z. Effects of temperature-dependent viscosity on natural convection in a porous cavity with a circular cylinder under local thermal non-equilibrium condition. Int. J. Therm. Sci. 2021, 159, 106570. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, T.; Xi, G.; Huang, Z. Periodic unsteady natural convection in square enclosure induced by inner circular cylinder with different vertical locations. Int. Commun. Heat Mass Transf. 2021, 124, 105250. [Google Scholar] [CrossRef]
- Yoon, H.S.; Ha, M.Y.; Kim, B.S.; Yu, D.H. Effect of the position of a circular cylinder in a square enclosure on natural convection at Rayleigh number of 107. Phys. Fluids 2009, 21, 047101. [Google Scholar] [CrossRef]
- Jami, M.; Mezrhab, A.; Bouzidi, M.; Lallemand, P. Lattice Boltzmann method applied to the laminar natural convection in an enclosure with a heat-generating cylinder conducting body. Int. J. Therm. Sci. 2007, 46, 38–47. [Google Scholar] [CrossRef]
- Alhashash, A. Natural convection of nanoliquid from a cylinder in square porous enclosure using Buongiorno’s two-phase model. Sci. Rep. 2020, 10, 140. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.J.; Doo, J.H.; Ha, M.Y.; Yoon, H.S. Effects of thermal boundary conditions on natural convection in a square enclosure with an inner circular cylinder locally heated from the bottom wall. Int. J. Heat Mass Transf. 2013, 65, 435–450. [Google Scholar] [CrossRef]
- Sasaguchi, K.; Kusano, K.; Kitagawa, H.; Kuwabara, K. Effect of density inversion on cooling of water around a cylinder in a rectangular cavity. Numer. Heat Transf. Part A Appl. 1997, 32, 131–148. [Google Scholar] [CrossRef]
- Sasaguchi, K.; Kuwabara, K.; Kusano, K.; Kitagawa, H. Transient cooling of water around a cylinder in a rectangular cavity—a numerical analysis of the effect of the position of the cylinder. Int. J. Heat Mass Transf. 1998, 41, 3149–3156. [Google Scholar] [CrossRef]
- Cesini, G.; Paroncini, M.; Cortella, G.; Manzan, M. Natural convection from a horizontal cylinder in a rectangular cavity. Int. J. Heat Mass Transf. 1999, 42, 1801–1811. [Google Scholar] [CrossRef]
- Boukendil, M.; Moutaouakil, L.E.; Zrikem, Z.; Abdelbaki, A. Coupled thermal radiation and natural convection heat transfer in a cavity with a discretely heated inner body. Mater. Today Proc. 2020, 27, 3065–3070. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Gedik, E.; Chamkha, A.J.; Hashim, I. Impacts of heated rotating inner cylinder and two-phase nanofluid model on entropy generation and mixed convection in a square cavity. Heat Mass Transf. 2020, 56, 321–338. [Google Scholar] [CrossRef]
- Mehryan, S.A.M.; Izadpanahi, E.; Ghalambaz, M.; Chamkha, A.J. Mixed convection flow caused by an oscillating cylinder in a square cavity filled with Cu-Al2O3/water hybrid nanofluid. J. Therm. Anal. Calorim. 2019, 137, 965–982. [Google Scholar] [CrossRef]
- Shyam, R.; Sairamu, M.; Nirmalkar, N.; Chhabra, R.P. Free convection from a heated circular cylinder in confined power-law fluids. Int. J. Therm. Sci. 2013, 74, 156–173. [Google Scholar] [CrossRef]
- Choi, C.; Ha, M.Y.; Park, Y.G. Characteristics of thermal convection in a rectangular channel with an inner cold circular cylinder. Int. J. Heat Mass Transf. 2015, 84, 955–973. [Google Scholar] [CrossRef]
- Lee, S.H.; Seo, Y.M.; Yoon, H.S.; Ha, M.Y. Three-dimensional natural convection around an inner circular cylinder located in a cubic enclosure with sinusoidal thermal boundary condition. Int. J. Heat Mass Transf. 2016, 101, 807–823. [Google Scholar] [CrossRef]
- Kefayati, G.H.R.; Tang, H. Double-diffusive natural convection and entropy generation of Carreau fluid in a heated enclosure with an inner circular cold cylinder (Part I: Heat and mass transfer). Int. J. Heat Mass Transf. 2018, 120, 731–750. [Google Scholar] [CrossRef]
- Kefayati, G.H.R.; Tang, H. Double-diffusive laminar natural convection and entropy generation of Carreau fluid in a heated enclosure with an inner circular cold cylinder (Part II: Entropy generation). Int. J. Heat Mass Transf. 2018, 120, 683–713. [Google Scholar] [CrossRef]
- Xu, H.T.; Wang, T.T.; Qu, Z.G.; Chen, J.; Li, B.B. Lattice Boltzmann simulation of the double diffusive natural convection and oscillation characteristics in an enclosure filled with porous medium. Int. Commun. Heat Mass Transf. 2017, 81, 104–115. [Google Scholar] [CrossRef]
- Vijaybabu, T.R. Influence of porous circular cylinder on MHD double-diffusive natural convection and entropy generation. Int. J. Mech. Sci. 2021, 206, 106625. [Google Scholar] [CrossRef]
- Ekundayo, C.O.; Probert, S.D.; Newborough, M. Heat transfers from a horizontal cylinder in a rectangular enclosure. Appl. Energy 1998, 61, 57–78. [Google Scholar] [CrossRef]
- Butler, C.; Newport, D.; Geron, M. Natural convection experiments on a heated horizontal cylinder in a differentially heated square cavity. Exp. Therm. Fluid Sci. 2013, 44, 199–208. [Google Scholar] [CrossRef]
- Atayılmaz, Ş.Ö.; Teke, İ. Experimental and numerical study of the natural convection from a heated horizontal cylinder. Int. Commun. Heat Mass Transf. 2009, 36, 731–738. [Google Scholar] [CrossRef]
- Atmane, M.A.; Chan, V.S.S.; Murray, D.B. Natural convection around a horizontal heated cylinder: The effects of vertical confinement. Int. J. Heat Mass Transf. 2003, 46, 3661–3672. [Google Scholar] [CrossRef]
- Grafsrønningen, S.; Jensen, A.; Reif, A.A.P. PIV investigation of buoyant plume from natural convection heat transfer above a horizontal heated cylinder. Int. J. Heat Mass Transf. 2011, 54, 4975–4987. [Google Scholar] [CrossRef]
- Grafsrønningen, S.; Jensen, A. Simultaneous PIV/LIF measurements of a transitional buoyant plume above a horizontal cylinder. Int. J. Heat Mass Transf. 2012, 55, 4195–4206. [Google Scholar] [CrossRef]
- Grafsrønningen, S.; Jensen, A. Large eddy simulations of a buoyant plume above a heated horizontal cylinder at intermediate Rayleigh numbers. Int. J. Therm. Sci. 2017, 112, 104–117. [Google Scholar] [CrossRef]
- Kitamura, K.; Kami-Iwa, F.; Misumi, T. Heat transfer and fluid flow of natural convection around large horizontal cylinders. Int. J. Heat Mass Transf. 1999, 42, 4093–4106. [Google Scholar] [CrossRef]
- Kuehner, J.P.; Pflug, J.R.; Tessier, F.A., Jr.; Hamed, A.M.; Marin, F.J.M. Velocity measurements in the free convection flow above a heated horizontal cylinder. Int. J. Heat Mass Transf. 2012, 55, 4711–4723. [Google Scholar] [CrossRef]
- Kuehner, J.P.; Hamed, A.M.; Mitchell, J.D. Experimental investigation of the free convection velocity boundary layer and plume formation region for a heated horizontal cylinder. Int. J. Heat Mass Transf. 2015, 82, 78–97. [Google Scholar] [CrossRef]
- Lin, K.C.; Bhosale, Y.; Huang, C.Z. 3D-CFD investigation into free convection flow above a heated horizontal cylinder: Comparisons with experimental data. Appl. Therm. Eng. 2017, 120, 277–288. [Google Scholar] [CrossRef]
- Ma, H.; He, L. Large eddy simulation of natural convection heat transfer and fluid flow around a horizontal cylinder. Int. J. Therm. Sci. 2021, 162, 106789. [Google Scholar] [CrossRef]
- Sebastian, G.; Shine, S.R. Natural convection from horizontal heated cylinder with and without horizontal confinement. Int. J. Heat Mass Transf. 2015, 82, 325–334. [Google Scholar] [CrossRef]
- Mishra, L.; Chhabra, R.P. Natural Convection in Power-Law Fluids in a Square Enclosure from Two Differentially Heated Horizontal Cylinders. Heat Transf. Eng. 2018, 39, 819–842. [Google Scholar] [CrossRef]
- Baranwal, A.K.; Chhabra, R. Effect of Prandtl number on free convection from two cylinders in a square enclosure. Heat Transf. Eng. 2016, 37, 545–556. [Google Scholar] [CrossRef]
- Baranwal, A.K.; Chhabra, R.P. Free Convection in Confined Power-law Fluids From Two Side-by-Side Cylinders in a Square Enclosure. Heat Transf. Eng. 2016, 37, 1521–1537. [Google Scholar] [CrossRef]
- Baranwal, A.K.; Chhabra, R.P. Effect of Fluid Yield Stress on Natural Convection From Horizontal Cylinders in a Square Enclosure. Heat Transf. Eng. 2017, 38, 557–577. [Google Scholar] [CrossRef]
- Park, Y.G.; Yoon, H.S.; Ha, M.Y. Natural convection in square enclosure with hot and cold cylinders at different vertical locations. Int. J. Heat Mass Transf. 2012, 55, 7911–7925. [Google Scholar] [CrossRef]
- Yoon, H.S.; Park, Y.G.; Jung, J.H. Natural convection in a square enclosure with differentially heated two horizontal cylinders. Numer. Heat Transf. Part A Appl. 2014, 65, 302–326. [Google Scholar] [CrossRef]
- Park, Y.G.; Ha, M.Y.; Yoon, H.S. Study on natural convection in a cold square enclosure with a pair of hot horizontal cylinders positioned at different vertical locations. Int. J. Heat Mass Transf. 2013, 65, 696–712. [Google Scholar] [CrossRef]
- Park, Y.P.; Ha, M.Y.; Choi, C.; Park, J. Natural convection in a square enclosure with two inner circular cylinders positioned at different vertical locations. Int. J. Heat Mass Transf. 2014, 77, 501–518. [Google Scholar] [CrossRef]
- Yoon, H.S.; Jung, J.H.; Park, Y.G. Natural convection in a square enclosure with two horizontal cylinders. Numer. Heat Transf. Part A Appl. 2012, 62, 701–721. [Google Scholar] [CrossRef]
- Lacroix, M.; Joyeux, A. Coupling of wall conduction with natural convection from heated cylinders in a rectangular enclosure. Int. Commun. Heat Mass Transf. 1996, 23, 143–151. [Google Scholar] [CrossRef]
- Spizzichino, A.; Zemach, E.; Feldman, Y. Oscillatory instability of a 3D natural convection flow around a tandem of cold and hot vertically aligned cylinders placed inside a cold cubic enclosure. Int. J. Heat Mass Transf. 2019, 141, 327–345. [Google Scholar] [CrossRef]
- Zemach, E.; Spizzichino, A.; Feldman, Y. Instability characteristics of a highly separated natural convection flow: Configuration of a tandem of cold and hot horizontally oriented cylinders placed within a cold cubic enclosure. Int. J. Therm. Sci. 2021, 159, 106606. [Google Scholar] [CrossRef]
- Kefayati, G.H.R.; Tang, H. MHD thermosolutal natural convection and entropy generation of Carreau fluid in a heated enclosure with two inner circular cold cylinders, using LBM. Int. J. Heat Mass Transf. 2018, 126, 508–530. [Google Scholar] [CrossRef]
- Heo, J.; Chae, M.; Chung, B. Influences of vertical and horizontal pitches on the natural convection of two staggered cylinders. Int. J. Heat Mass Transf. 2013, 57, 1–8. [Google Scholar] [CrossRef]
- Grafsrønningen, S.; Jensen, A. Natural convection heat transfer from two horizontal cylinders at high Rayleigh numbers. Int. J. Heat Mass Transf. 2012, 55, 5552–5564. [Google Scholar] [CrossRef]
- Pelletier, Q.; Murray, D.B.; Persoons, T. Unsteady natural convection heat transfer from a pair of vertically aligned horizontal cylinders. Int. J. Heat Mass Transf. 2016, 95, 693–708. [Google Scholar] [CrossRef]
- Persoons, T.; O’Gorman, I.M.; Donoghue, D.B.; Byrne, G.; Murray, D.B. Natural convection heat transfer and fluid dynamics for a pair of vertically aligned isothermal horizontal cylinders. Int. J. Heat Mass Transf. 2011, 54, 5163–5172. [Google Scholar] [CrossRef]
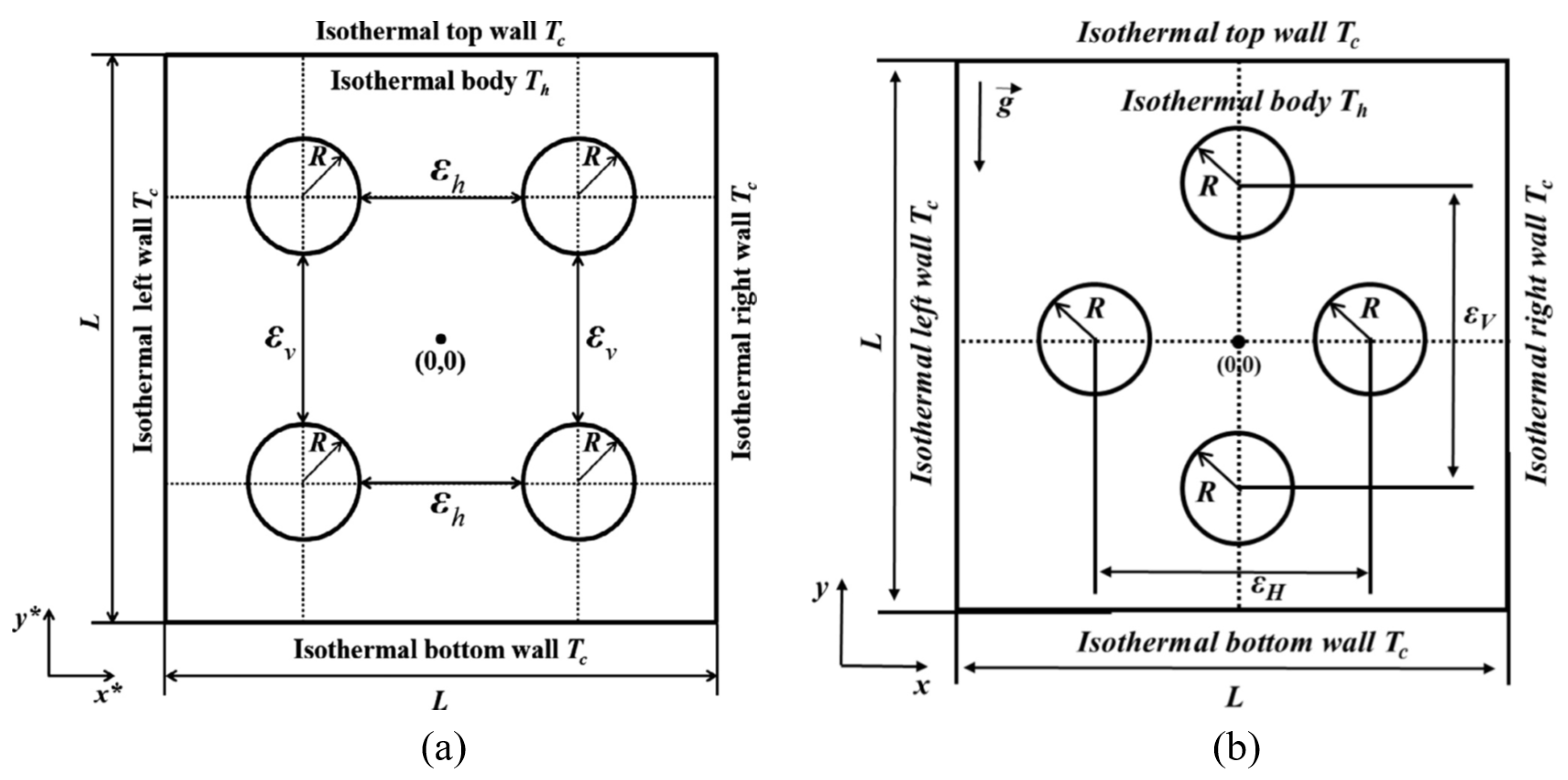
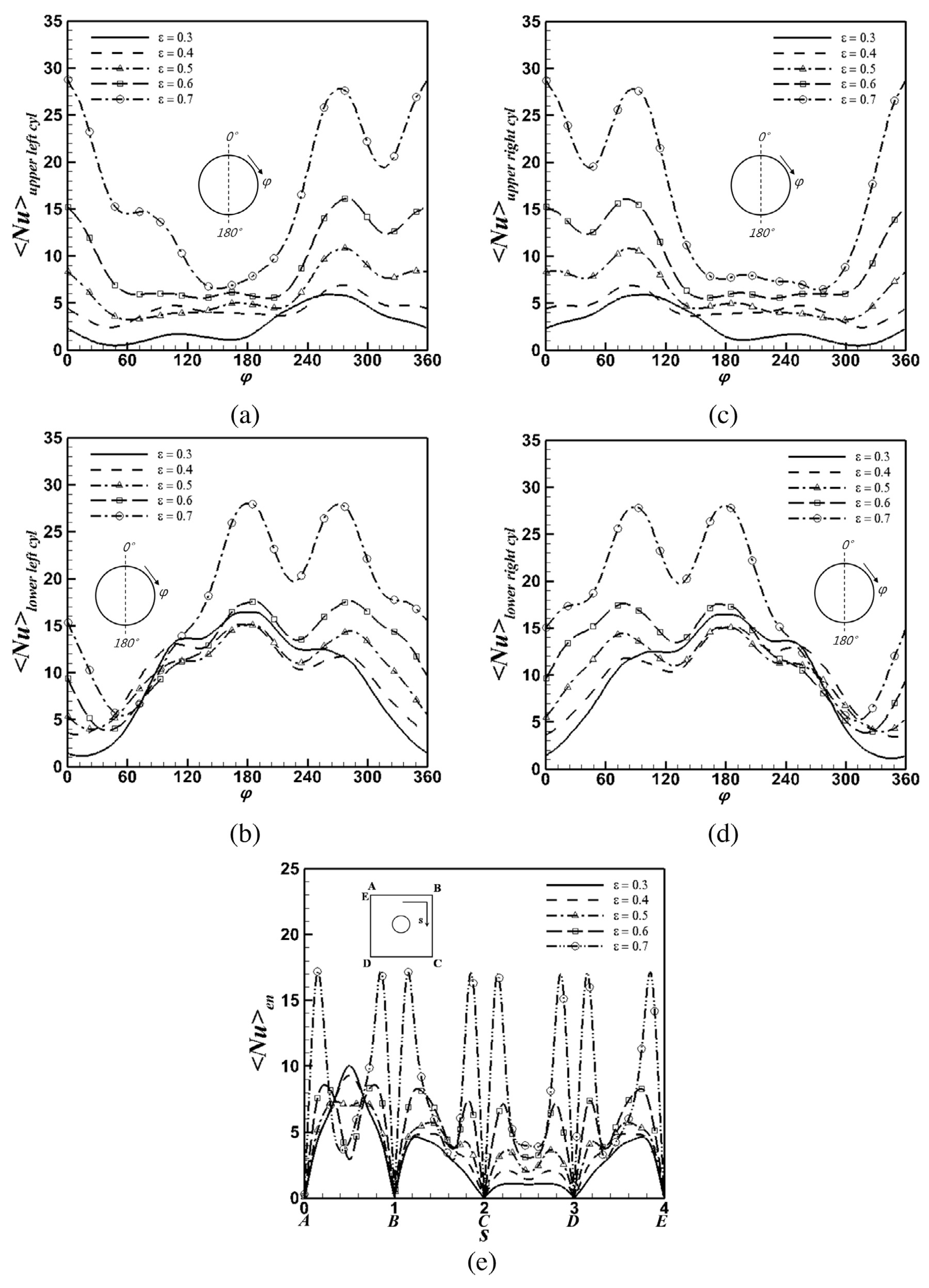
- Seo, Y.M.; Park, Y.G.; Kim, M.; Yoon, H.S.; Ha, M.Y. Two-dimensional flow instability induced by natural convection in a square enclosure with four inner cylinders. Part I: Effect of horizontal position of inner cylinders. Int. J. Heat Mass Transf. 2017, 113, 1306–1318. [Google Scholar] [CrossRef]
- Seo, Y.M.; Mun, G.S.; Gap, Y.G.P.; Ha, M.Y. Two-dimensional flow instability induced by natural convection in a square enclosure with four inner cylinders. Part II: Effect of various positions of inner cylinders. Int. J. Heat Mass Transf. 2017, 113, 1319–1331. [Google Scholar] [CrossRef]
- Park, Y.G.; Ha, M.Y.; Park, J. Natural convection in a square enclosure with four circular cylinders positioned at different rectangular locations. Int. J. Heat Mass Transf. 2015, 81, 490–511. [Google Scholar] [CrossRef]
- Mun, G.S.; Seo, Y.M.; Park, Y.G.; Ha, M.Y. Natural convection in a cold enclosure with four hot inner cylinders in a diamond array (Part-II: Effect of unequal horizontal and vertical distances of inner cylinders). Int. J. Heat Mass Transf. 2018, 120, 1365–1373. [Google Scholar] [CrossRef]
- Corcione, M. Correlating equations for free convection heat transfer from horizontal isothermal cylinders set in a vertical array. Int. J. Heat Mass Transf. 2005, 48, 3660–3673. [Google Scholar] [CrossRef]
- Kitamura, K.; Mitsuishi, A.; Suzuki, T.; Kimura, F. Fluid flow and heat transfer of natural convection induced around a vertical row of heated horizontal cylinders. Int. J. Heat Mass Transf. 2016, 92, 414–429. [Google Scholar] [CrossRef]
- Narayan, S.; Singh, A.K.; Srivastava, A. Interferometric study of natural convection heat transfer phenomena around array of heated cylinders. Int. J. Heat Mass Transf. 2017, 109, 278–292. [Google Scholar] [CrossRef]
- Dash, S.M.; Lee, T.S.; Huang, H. Natural convection from an eccentric square cylinder using a novel flexible forcing IB-LBM method. Numer. Heat Transf. Part Appl. 2014, 65, 531–555. [Google Scholar] [CrossRef]
- Dash, S.M.; Lee, T.S. Natural convection in a square enclosure with a square heat source at different horizontal and diagonal eccentricities. Numer. Heat Transf. Part A Appl. 2015, 68, 686–710. [Google Scholar] [CrossRef]
- Bouafia, M.; Daube, O. Natural convection for large temperature gradients around a square solid body within a rectangular cavity. Int. J. Heat Mass Transf. 2007, 50, 3599–3615. [Google Scholar] [CrossRef]
- Boulahia, Z.; Sehaqui, R. Numerical simulation of natural convection of nanofluid in a square cavity including a square heater. Int. J. Sci. Res. 2015, 4, 1718–1722. [Google Scholar]
- Sairamu, M.; Chhabra, R.P. Natural convection in power-law fluids from a tilted square in an enclosure. Int. J. Heat Mass Transf. 2013, 56, 319–339. [Google Scholar] [CrossRef]
- Ha, M.Y.; Jung, M.J.; Kim, Y.S. Numerical study on transient heat transfer and fluid flow of natural convection in an enclosure with a heat-generating conducting body. Numer. Heat Transf. Part A Appl. 1999, 35, 415–433. [Google Scholar]
- Ha, M.Y.; Jung, M.J. A numerical study on three-dimensional conjugate heat transfer of natural convection and conduction in a differentially heated cubic enclosure with a heat-generating cubic conducting body. Int. J. Heat Mass Transf. 2000, 43, 4229–4248. [Google Scholar] [CrossRef]
- Oh, J.Y.; Ha, M.Y.; Kim, K.C. Numerical study of heat transfer and flow of natural convection in an enclosure with a heat-generating conducting body. Numer. Heat Transf. Part A Appl. 1997, 31, 289–303. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Oztop, H.F.; Pop, I.; Abu-Hamdeh, N. Analysis of entropy generation in natural convection of nanofluid inside a square cavity having hot solid block: Tiwari and Das’ model. Entropy 2016, 18, 9. [Google Scholar] [CrossRef]
- Umadevi, P.; Nithyadevi, N. Convection in a sinusoidally heated square enclosure utilizing Ag-water nanofluid with heat generating solid body. Int. J. Mech. Sci. 2017, 131, 712–721. [Google Scholar] [CrossRef]
- Ali, O.M.; Kahwaji, G.Y. Numerical Investigation of Natural Convection Heat Transferfrom Square Cylinder in an Enclosed Enclosure Filled with Nanofluids. Int. J. Recent Adv. Mech. Eng. 2015, 4, 1–17. [Google Scholar] [CrossRef]
- De, A.K.; Dalal, A. A numerical study of natural convection around a square, horizontal, heated cylinder placed in an enclosure. Int. J. Heat Mass Transf. 2006, 49, 4608–4623. [Google Scholar]
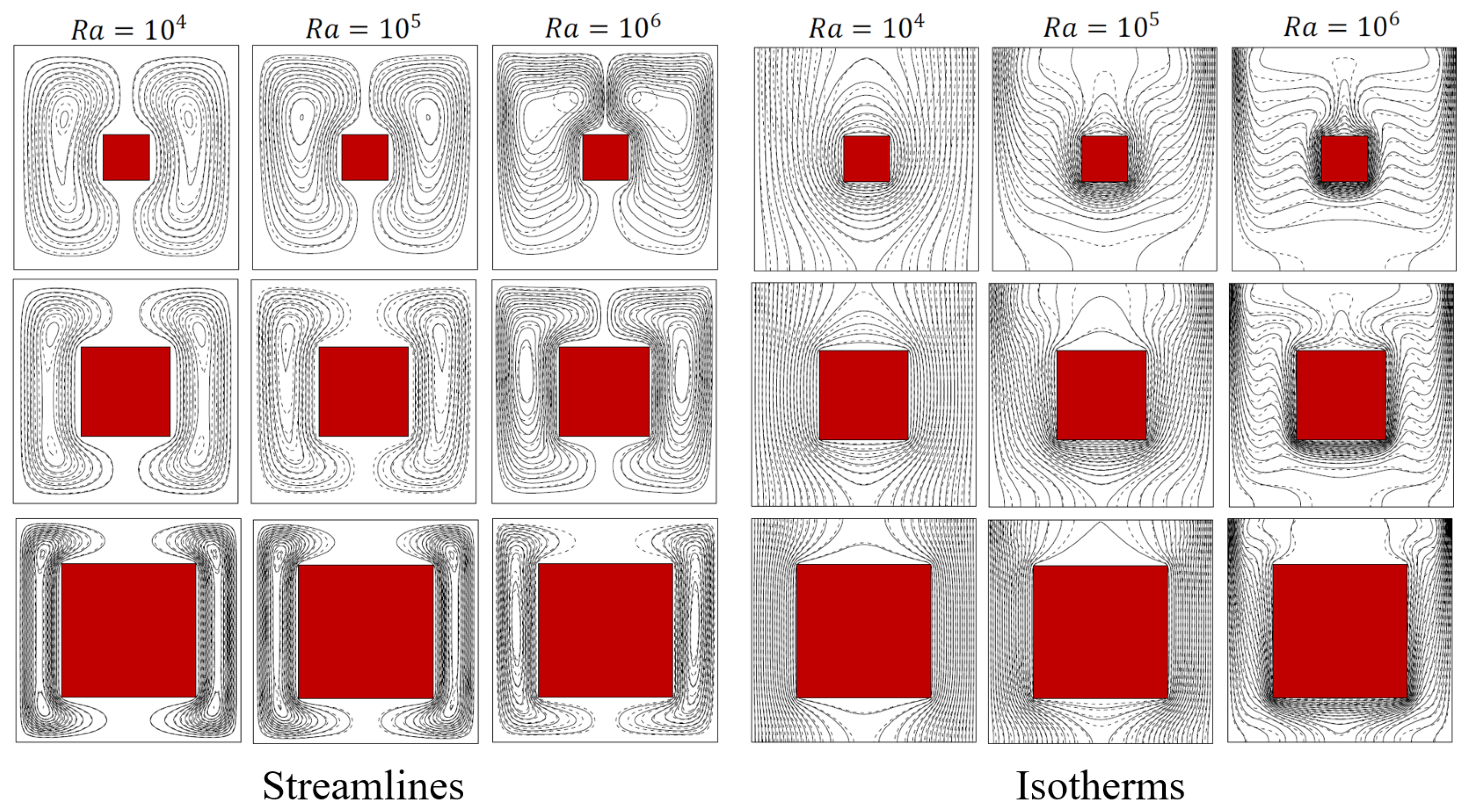
- Ha, M.Y.; Kim, I.; Yoon, H.S.; Yoon, K.S.; Lee, J.R.; Balachandar, S.; Chun, H.H. Two-dimensional and unsteady natural convection in a horizontal enclosure with a square body. Numer. Heat Transf. Part A Appl. 2002, 41, 183–210. [Google Scholar] [CrossRef]
- Lee, J.R.; Ha, M.Y. Numerical simulation of natural convection in a horizontal enclosure with a heat-generating conducting body. Int. J. Heat Mass Transf. 2006, 49, 2684–2702. [Google Scholar] [CrossRef]
- Hidki, R.; Moutaouakil, L.E.; Charqui, Z.; Boukendil, M.; Zrikem, Z. Natural convection in a square cavity containing two heat-generating cylinders with different geometries. Mater. Today Proc. 2021, 45, 7415–7423. [Google Scholar] [CrossRef]
- Hidki, R.; Moutaouakil, L.E.; Charqui, Z.; Boukendil, M.; Zrikem, Z. Effect of the size and position of two heat-generating blocks on natural convection inside a closed cavity. In Proceedings of the 2nd International Conference on Big Data, Modelling and Machine Learning (BML 2021), Kenitra, Morocco, 5–6 June 2022; pp. 376–380. [Google Scholar]
- Hidki, R.; Moutaouakiln, L.E.; Boukendil, M.; Charqui, Z.; Zrikem, Z.; Abdelbaki, A. Natural convection coupled to surface radiation in an air-filled square cavity containing two heat-generating bodies. Heat Transf. 2023, 52, 2143–2164. [Google Scholar] [CrossRef]
- Pordanjani, A.H.; Jahanbakhshi, A.; Nadooshan, A.A.; Afrand, M. Effect of two isothermal obstacles on the natural convection of nanofluid in the presence of magnetic field inside an enclosure with sinusoidal wall temperature distribution. Int. J. Heat Mass Transf. 2018, 121, 565–578. [Google Scholar] [CrossRef]
- Rahimi, A.; Kasaeipoor, A.; Malekshah, E.H. Lattice Boltzmann simulation of natural convection and entropy generation in cavities filled with nanofluid in existence of internal rigid bodies-Experimental thermo-physical properties. J. Mol. Liq. 2017, 242, 580–593. [Google Scholar] [CrossRef]
- Usman, M.; Khan, Z.H.; Liu, M.B. MHD natural convection and thermal control inside a cavity with obstacles under the radiation effects. Phys. A Stat. Mech. Its Appl. 2019, 535, 122443. [Google Scholar] [CrossRef]
- Aly, A.M.; Raizah, Z.A.S. Incompressible smoothed particle hydrodynamics (ISPH) method for natural convection in a nanofluid-filled cavity including rotating solid structures. Int. J. Mech. Sci. 2018, 146, 125–140. [Google Scholar] [CrossRef]
- Hu, J.; Ren, X.; Liu, D.; Zhao, F.; Wang, H. Conjugate natural convection inside a vertical enclosure with solid obstacles of unique volume and multiple morphologies. Int. J. Heat Mass Transf. 2016, 95, 1096–1114. [Google Scholar] [CrossRef]
- Garoosi, F.; Jahanshaloo, L.; Rashidi, M.M.; Badakhsh, A.; Ali, M.E. Numerical simulation of natural convection of the nanofluid in heat exchangers using a Buongiorno model. Appl. Math. Comput. 2015, 254, 183–203. [Google Scholar] [CrossRef]
- Bararnia, H.; Soleimani, S.; Ganji, D.D. Lattice Boltzmann simulation of natural convection around a horizontal elliptic cylinder inside a square enclosure. Int. Commun. Heat Mass Transf. 2011, 38, 1436–1442. [Google Scholar] [CrossRef]
- Hashemi, H.; Namazian, Z.; Zadeh, S.M.H.; Mehryan, S.A.M. MHD natural convection of a micropolar nanofluid flowing inside a radiative porous medium under LTNE condition with an elliptical heat source. J. Mol. Liq. 2018, 271, 914–925. [Google Scholar] [CrossRef]
- Jelita, M.; Mudia, H.; Afriani, S. Analysis of fluid dynamics and heat transfer inside an elliptical cylinder in a square enclosure. Adv. Theor. Appl. Mech. 2017, 10, 11–20. [Google Scholar] [CrossRef]
- Liao, C.; Lin, C. Influences of a confined elliptic cylinder at different aspect ratios and inclinations on the laminar natural and mixed convection flows. Int. J. Heat Mass Transf. 2012, 55, 6638–6650. [Google Scholar] [CrossRef]
- Raman, S.K.; Prakash, K.A.; Vengadesan, S. Natural Convection from a Heated Elliptic Cylinder with a Different Axis Ratio in a Square Enclosure. Numer. Heat Transf. Part A Appl. 2012, 62, 639–658. [Google Scholar] [CrossRef]
- Roy, N.C. Natural convection of nanofluids in a square enclosure with different shapes of inner geometry. Phys. Fluids 2018, 30, 113605. [Google Scholar] [CrossRef]
- Seo, Y.M.; Ha, M.Y.; Park, Y.G. A numerical study on the three-dimensional natural convection with a cylinder in a long rectangular enclosure. Part II: Inclination angle effect of the elliptical cylinder. Int. J. Heat Mass Transf. 2019, 131, 795–806. [Google Scholar] [CrossRef]
- Cho, H.W.; Park, Y.G.; Ha, M.Y. The natural convection in a square enclosure with two hot inner cylinders, Part I: The effect of one elliptical cylinder with various aspect ratios in a vertical array. Int. J. Heat Mass Transf. 2018, 125, 815–827. [Google Scholar] [CrossRef]
- Cho, H.W.; Ha, M.Y.; Park, Y.G. Natural convection in a square enclosure with two hot inner cylinders, Part II: The effect of two elliptical cylinders with various aspect ratios in a vertical array. Int. J. Heat Mass Transf. 2019, 135, 962–973. [Google Scholar] [CrossRef]
- Park, S.H.; Seo, Y.M.; Ha, M.Y.; Park, Y.G. Natural convection in a square enclosure with different positions and inclination angles of an elliptical cylinder. Part I: A vertical array of one elliptical cylinder and one circular cylinder. Int. J. Heat Mass Transf. 2018, 126, 173–183. [Google Scholar] [CrossRef]
- Seo, Y.M.; Ha, M.Y.; Park, Y.G. The effect of four elliptical cylinders with different aspect ratios on the natural convection inside a square enclosure. Int. J. Heat Mass Transf. 2018, 122, 491–503. [Google Scholar] [CrossRef]
- Lu, J.; Shi, B.; Guo, Z.; Chai, Z. Numerical study on natural convection in a square enclosure containing a rectangular heated cylinder. Front. Energy Power Eng. China 2009, 3, 373–380. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Entropy generation of nanofluid in presence of magnetic field using Lattice Boltzmann Method. Phys. A Stat. Mech. Its Appl. 2015, 417, 273–286. [Google Scholar] [CrossRef]
- Olayemi, O.A.; Khaled, A.; Temitope, O.J.; Victor, O.O.; Odetunde, C.B.; Adegun, I.K. Parametric study of natural convection heat transfer from an inclined rectangular cylinder embedded in a square enclosure. Aust. J. Mech. Eng. 2023, 21, 668–681. [Google Scholar] [CrossRef]
- Rahimi, A.; Kasaeipoor, A.; Malekshah, E.H.; Palizian, M.; Kolsi, L. Lattice Boltzmann numerical method for natural convection and entropy generation in cavity with refrigerant rigid body filled with DWCNTs-water nanofluid-experimental thermo-physical properties. Therm. Sci. Eng. Prog. 2018, 5, 372–387. [Google Scholar] [CrossRef]
- Vijaybabu, T.R.; Dhinakaran, S. MHD natural convection around a permeable triangular cylinder inside a square enclosure filled with Al2O3-H2O nanofluid: An LBM study. Int. J. Mech. Sci. 2019, 153, 500–516. [Google Scholar] [CrossRef]
- El Abdallaoui, M.; Amahmid, A. Lattice-Boltzmann Modeling of Natural Convection Between a Square Outer Cylinder and an Inner Isosceles Triangular Heating Body. Numer. Heat Transf. Part A Appl. 2014, 66, 1076–1096. [Google Scholar] [CrossRef]
- Abdallaoui, M.E.; Hasnaoui, M.; Amahmid, A. Numerical simulation of natural convection between a decentered triangular heating cylinder and a square outer cylinder filled with a pure fluid or a nanofluid using the Lattice Boltzmann method. Powder Technol. 2015, 277, 193–205. [Google Scholar] [CrossRef]
- Oztop, H.F.; Dagtekin, I.; Bahloul, A. Comparison of position of a heated thin plate located in a cavity for natural convection. Int. Commun. Heat Mass Ttransfer 2004, 31, 121–132. [Google Scholar] [CrossRef]
- Saravanan, S.; Sivaraj, C. Coupled thermal radiation and natural convection heat transfer in a cavity with a heated plate inside. Int. J. Heat Fluid Flow 2013, 40, 54–64. [Google Scholar] [CrossRef]
- Zadeh, S.M.H.; Mehryan, S.A.M.; Izadpanahi, E.; Ghalambaz, M. Impacts of the flexibility of a thin heater plate on the natural convection heat transfer. Int. J. Therm. Sci. 2019, 145, 106001. [Google Scholar] [CrossRef]
- Mehryan, S.A.M.; Alsabery, A.; Modir, A.; Izadpanahi, E.; Ghalambaz, M. Fluid-structure interaction of a hot flexible thin plate inside an enclosure. Int. J. Therm. Sci. 2020, 153, 106340. [Google Scholar] [CrossRef]
- Hakeem, A.K.A.; Saravanan, S.; Kandaswamy, P. Natural convection in a square cavity due to thermally active plates for different boundary conditions. Comput. Math. Appl. 2011, 62, 491–496. [Google Scholar] [CrossRef]
- Kandaswamy, P.; Lee, J.; Hakeem, A.K.A.; Saravanan, S. Effect of baffle–cavity ratios on buoyancy convection in a cavity with mutually orthogonal heated baffles. Int. J. Heat Mass Transf. 2008, 51, 1830–1837. [Google Scholar] [CrossRef]
- Hakeem, A.K.A.; Saravanan, S.; Kandaswamy, P. Buoyancy convection in a square cavity with mutually orthogonal heat generating baffles. Int. J. Heat Fluid Flow 2008, 29, 1164–1173. [Google Scholar] [CrossRef]
- Choudhary, P.; Pankaj, S.K.; Tomar, M.; Thakur, H.C. Unsteady analysis of heated inclined fin-plate placed inside square enclosure. In Proceedings of the 2nd International Conference for Convergence in Technology (I2CT), Mumbai, India, 7–9 April 2017; pp. 701–708. [Google Scholar]
- Xiong, J.; Mao, G.; Zhang, Y. Numerical computation on cavity natural convection for built-in plate arrays application: Heat transfer analysis and optimization. Numer. Heat Transf. Part A Appl. 2023, 1–20. [Google Scholar] [CrossRef]
- Alomar, O.R.; Basher, N.M.; Yousif, A.A. Analysis of effects of thermal non-equilibrium and non-Darcy flow on natural convection in a square porous enclosure provided with a heated L shape plate. Int. J. Mech. Sci. 2020, 181, 105704. [Google Scholar] [CrossRef]
- Alomar, O.R.; Basher, N.M.; Yousif, A.A. Natural convection heat transfer from a bank of orthogonal heated plates embedded in a porous medium using LTNE model: A comparison between in-line and staggered arrangements. Int. J. Therm. Sci. 2021, 160, 106692. [Google Scholar] [CrossRef]
- Kwak, D.; Noh, J.; Yook, S. Natural convection flow around heated disk in cubical enclosure. J. Mech. Sci. Technol. 2018, 32, 2377–2384. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Tayebi, T.; Chamkha, A.J.; Ganji, D.D. Natural convection analysis in a square enclosure with a wavy circular heater under magnetic field and nanoparticles. J. Therm. Anal. Calorim. 2020, 139, 661–671. [Google Scholar] [CrossRef]
- Lee, D.; Jang, H.; Lee, B.J.; Choi, W.; Byon, C. Internal natural convection around a sphere in a rectangular chamber. Int. J. Heat Mass Transf. 2019, 136, 501–509. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shehzad, S.A.; Li, Z. Water based nanofluid free convection heat transfer in a three dimensional porous cavity with hot sphere obstacle in existence of Lorenz forces. Int. J. Heat Mass Transf. 2018, 125, 375–386. [Google Scholar] [CrossRef]
- Yoon, H.S.; Yu, D.H.; Ha, M.Y.; Park, Y.G. Three-dimensional natural convection in an enclosure with a sphere at different vertical locations. Int. J. Heat Mass Transf. 2010, 53, 3143–3155. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Natural convection and entropy generation of nanofluid filled cavity having different shaped obstacles under the influence of magnetic field and internal heat generation. J. Taiwan Inst. Chem. Eng. 2015, 56, 42–56. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Gedik, E.; Chamkha, A.J.; Hashim, I. Effects of two-phase nanofluid model and localized heat source/sink on natural convection in a square cavity with a solid circular cylinder. Comput. Methods Appl. Mech. Eng. 2019, 346, 952–981. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Ishak, M.S.; Chamkha, A.J.; Hashim, I. Entropy generation analysis and natural convection in a nanofluid-filled square cavity with a concentric solid insert and different temperature distributions. Entropy 2018, 20, 336. [Google Scholar] [CrossRef] [PubMed]
- Alsabery, A.I.; Sheremet, M.A.; Chamkha, A.J.; Hashim, I. Conjugate natural convection of Al2O3-water nanofluid in a square cavity with a concentric solid insert using Buongiorno’s two-phase model. Int. J. Mech. Sci. 2018, 136, 200–219. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Tayebi, T.; Chamkha, A.J.; Hashim, I. Effects of non-homogeneous nanofluid model on natural convection in a square cavity in the presence of conducting solid block and corner heater. Energies 2018, 11, 2507. [Google Scholar] [CrossRef]
- Lee, J.R.; Ha, M.Y. A numerical study of natural convection in a horizontal enclosure with a conducting body. Int. J. Heat Mass Transf. 2005, 48, 3308–3318. [Google Scholar] [CrossRef]
- Hussein, A.K.; Ashorynejad, H.R.; Sivasankaran, S.; Kolsi, L.; Shikholeslami, M.; Adegun, I.K. Modeling of MHD natural convection in a square enclosure having an adiabatic square shaped body using Lattice Boltzmann Method. Alex. Eng. J. 2016, 55, 203–214. [Google Scholar] [CrossRef]
- Mahmoodi, M.; Sebdani, S.M. Natural convection in a square cavity containing a nanofluid and an adiabatic square block at the center. Superlattices Microstruct. 2012, 52, 261–275. [Google Scholar] [CrossRef]
- Liu, D.; Zhao, F.; Tang, G. Conjugate heat transfer in an enclosure with a centered conducting body imposed sinusoidal temperature profiles on one side. Numer. Heat Transf. Part A Appl. 2007, 53, 204–223. [Google Scholar] [CrossRef]
- Lage, J.L.; Junqueira, S.L.M.; Lai, F.C.D.; Franco, A.T. Aspect ratio effect on the prediction of boundary layer interference in steady natural convection inside heterogeneous enclosures. Int. J. Heat Mass Transf. 2016, 92, 940–947. [Google Scholar] [CrossRef]
- Merrikh, A.A.; Lage, J.L. Natural convection in an enclosure with disconnected and conducting solid blocks. Int. J. Heat Mass Transf. 2005, 48, 1361–1372. [Google Scholar] [CrossRef]
- Raji, A.; Hasnaoui, M.; Naïmi, M.; Slimani, K.; Ouazzani, M.T. Effect of the subdivision of an obstacle on the natural convection heat transfer in a square cavity. Comput. Fluids 2012, 68, 1–15. [Google Scholar] [CrossRef]
- Aberuee, M.J.; Ziaei-Rad, M.; Ahmadikia, H. The effects of an internal isolated plate on natural convective heat transfer inside an industrial oven. Appl. Therm. Eng. 2018, 144, 769–778. [Google Scholar] [CrossRef]
- Raisi, A.; Arvin, I. A numerical study of the effect of fluid-structure interaction on transient natural convection in an air-filled square cavity. Int. J. Therm. Sci. 2018, 128, 1–14. [Google Scholar] [CrossRef]
- Wang, Q.W.; Tao, W.Q.; Lin, Z.; Chow, T.T. An experimental investigation of natural convection in a cubic inclined enclosure with multiple isolated plates. J. Heat Transf. 2000, 122, 176–179. [Google Scholar] [CrossRef]
- Park, H.K.; Ha, M.Y.; Yoon, H.S.; Park, Y.G.; Son, C. A numerical study on natural convection in an inclined square enclosure with a circular cylinder. Int. J. Heat Mass Transf. 2013, 66, 295–314. [Google Scholar] [CrossRef]
- Choi, C.; Jeong, S.; Ha, M.Y.; Yoon, H.S. Effect of a circular cylinder’s location on natural convection in a rhombus enclosure. Int. J. Heat Mass Transf. 2014, 77, 60–73. [Google Scholar] [CrossRef]
- Mun, G.S.; Doo, J.H.; Ha, M.Y. Thermo-dynamic irreversibility induced by natural convection in square enclosure with inner cylinder. Part-I: Effect of tilted angle of enclosure. Int. J. Heat Mass Transf. 2016, 97, 1102–1119. [Google Scholar] [CrossRef]
- Souayeh, B.; Ben-Cheikh, N.; Ben-Beya, B. Numerical simulation of three-dimensional natural convection in a cubic enclosure induced by an isothermally-heated circular cylinder at different inclinations. Int. J. Therm. Sci. 2016, 110, 325–339. [Google Scholar] [CrossRef]
- Alshomrani, A.S.; Sivasankaran, S.; Abdulfattah, A.A. Numerical study on convective flow and heat transfer in 3D inclined enclosure with hot solid body and discrete cooling. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 4649–4659. [Google Scholar] [CrossRef]
- Ravnik, J.; Škerget, L. A numerical study of nanofluid natural convection in a cubic enclosure with a circular and an ellipsoidal cylinder. Int. J. Heat Mass Transf. 2015, 89, 596–605. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, X.; Deng, J.; Song, L. A numerical study of natural convection in an inclined square enclosure with an elliptic cylinder using variational multiscale element free Galerkin method. Int. J. Heat Mass Transf. 2016, 99, 721–737. [Google Scholar] [CrossRef]
- Kefayati, G.H.R.; Tang, H. Lattice Boltzmann simulation of viscoplastic fluids on natural convection in an inclined enclosure with inner cold circular/elliptical cylinders (Part I: One cylinder). Int. J. Heat Mass Transf. 2018, 123, 1138–1162. [Google Scholar] [CrossRef]
- Altac, Z.; Kurtul, O. Natural convection in tilted rectangular enclosures with a vertically situated hot plate inside. Appl. Therm. Eng. 2007, 27, 1832–1840. [Google Scholar] [CrossRef]
- Riahi, A.; Ben-Cheikh, N.; Campo, A. Water-based nanofluids for natural convection cooling of a pair of symmetrical heated blocks placed inside a rectangular enclosure of aspect ratio two. Int. J. Therm. Environ. Eng. 2018, 16, 1–10. [Google Scholar]
- Kefayati, G.H.R.; Tang, H. Lattice Boltzmann simulation of viscoplastic fluids on natural convection in inclined enclosure with inner cold circular/elliptical cylinders (Part II: Two cylinders). Int. J. Heat Mass Transf. 2018, 123, 1163–1181. [Google Scholar] [CrossRef]
- Kefayati, G.H.R.; Tang, H. Lattice Boltzmann simulation of viscoplastic fluids on natural convection in inclined enclosure with inner cold circular/elliptical cylinders (Part III: Four cylinders). Int. J. Heat Mass Transf. 2018, 123, 1182–1203. [Google Scholar] [CrossRef]
- Zhang, T.; Che, D. Double MRT thermal lattice Boltzmann simulation for MHD natural convection of nanofluids in an inclined cavity with four square heat sources. Int. J. Heat Mass Transf. 2016, 94, 87–100. [Google Scholar] [CrossRef]
- Das, M.K.; Reddy, K.S.K. Conjugate natural convection heat transfer in an inclined square cavity containing a conducting block. Int. J. Heat Mass Transf. 2006, 49, 4987–5000. [Google Scholar]
- da Silva, G.M.F.; Zdanski, P.S.B.; Vaz, M., Jr. Effects of adiabatic and heat-conducting inserts in natural convection in inclined enclosures. Numer. Heat Transf. Part A Appl. 2022, 82, 812–825. [Google Scholar] [CrossRef]
- Al-Rashed, A.A.A.A.; Kolsi, L.; Kalidasan, K.; Malekshah, E.H.; Borjini, M.N.; Kanna, P.R. Second law analysis of natural convection in a CNT-water nanofluid filled inclined 3D cavity with incorporated Ahmed body. Int. J. Mech. Sci. 2017, 130, 399–415. [Google Scholar] [CrossRef]
- Al-Rashed, A.A.A.A.; Kalidasan, K.; Kolsi, L.; Borjini, M.N.; Kanna, P.R. Three-dimensional natural convection of CNT-water nanofluid confined in an inclined enclosure with Ahmed body. J. Therm. Sci. Technol. 2017, 12, 1–13. [Google Scholar] [CrossRef][Green Version]

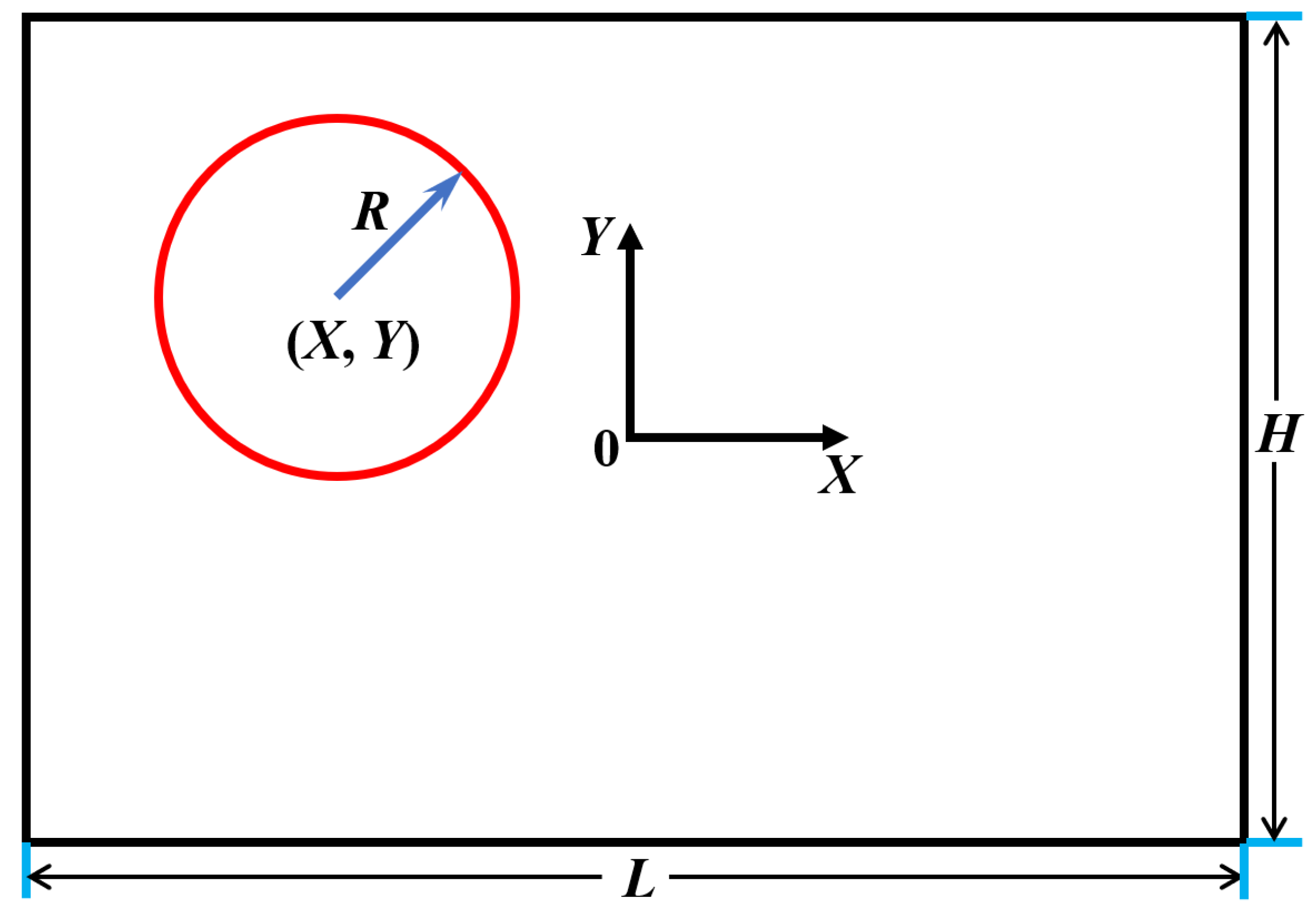
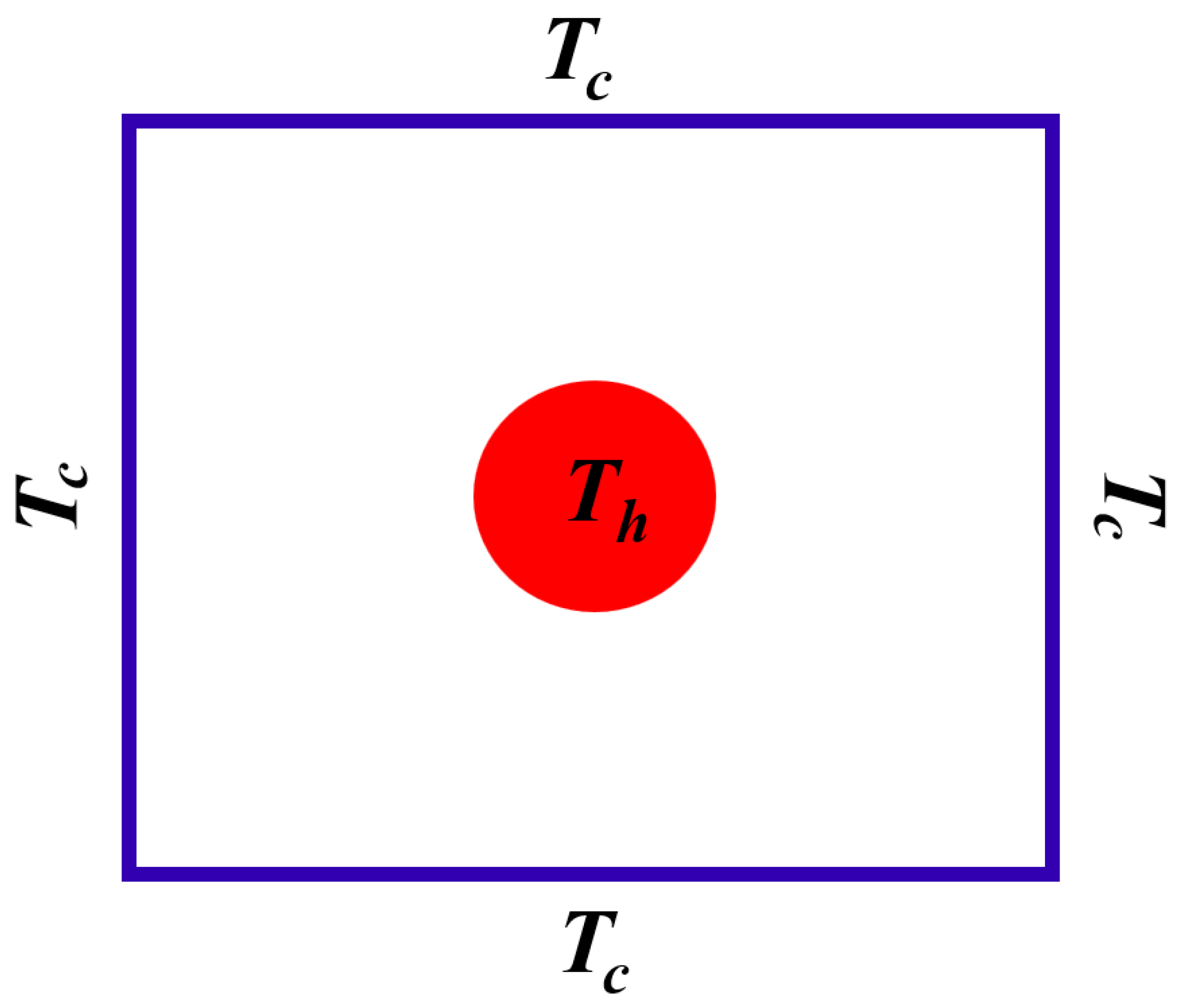
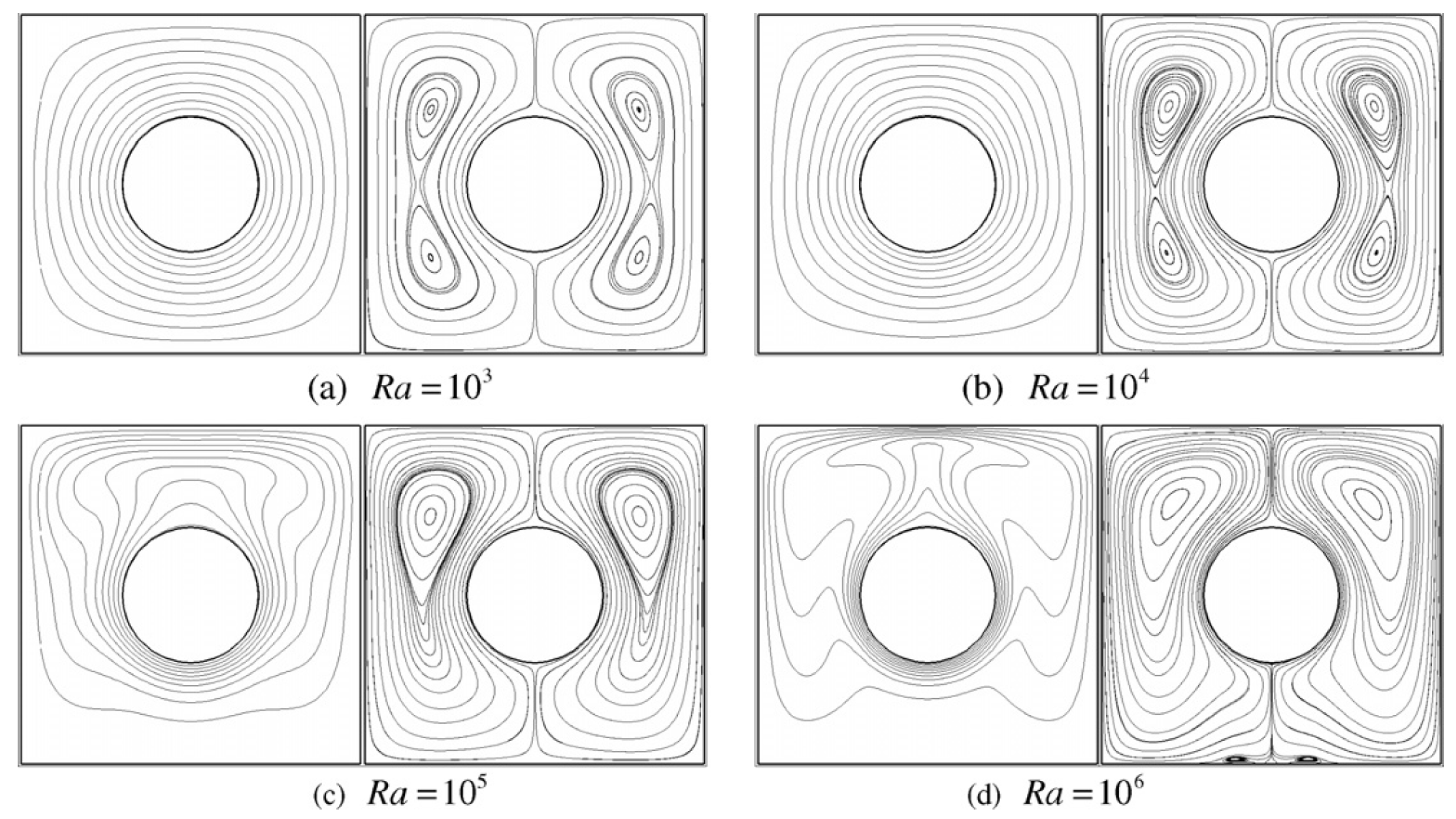




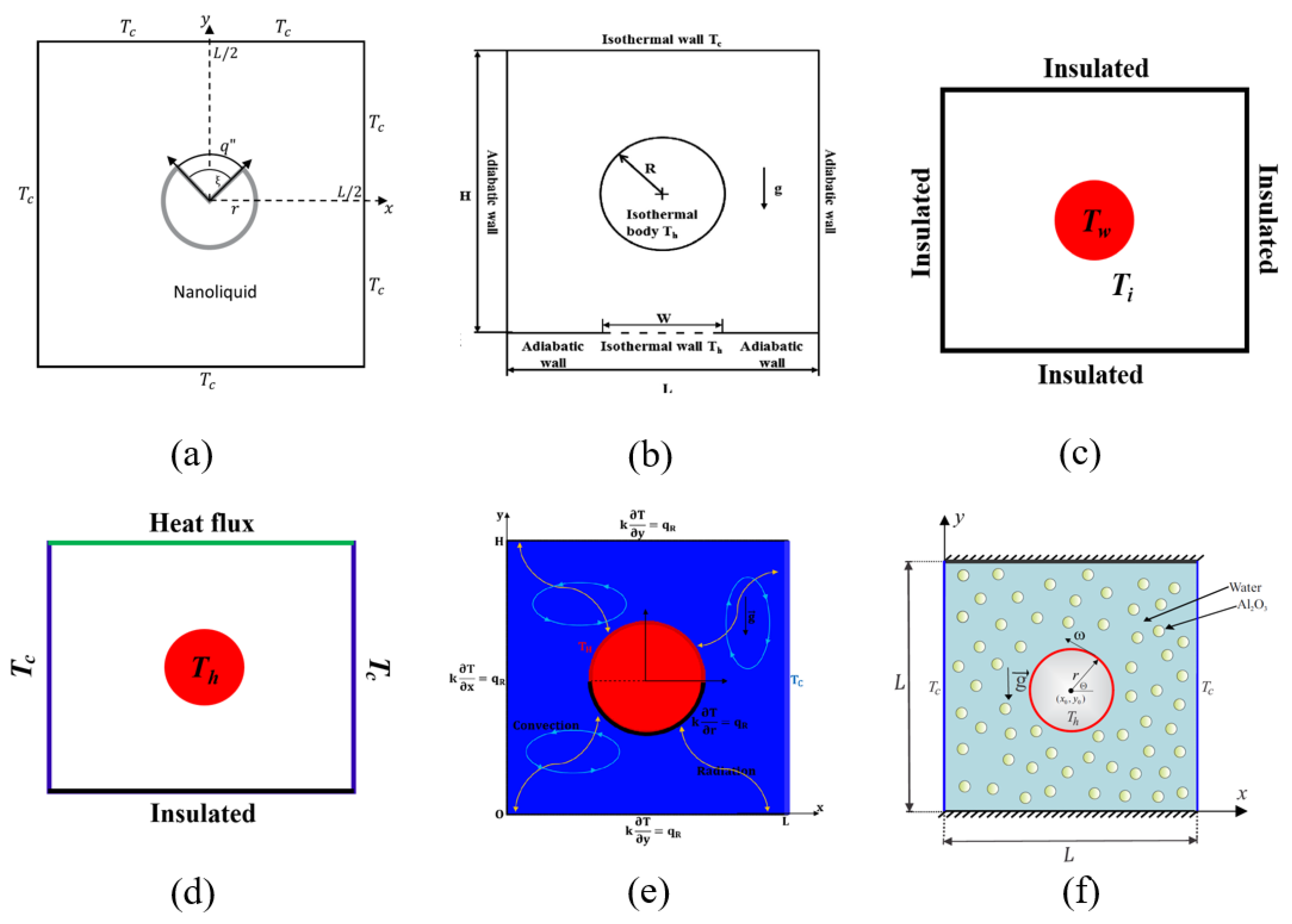

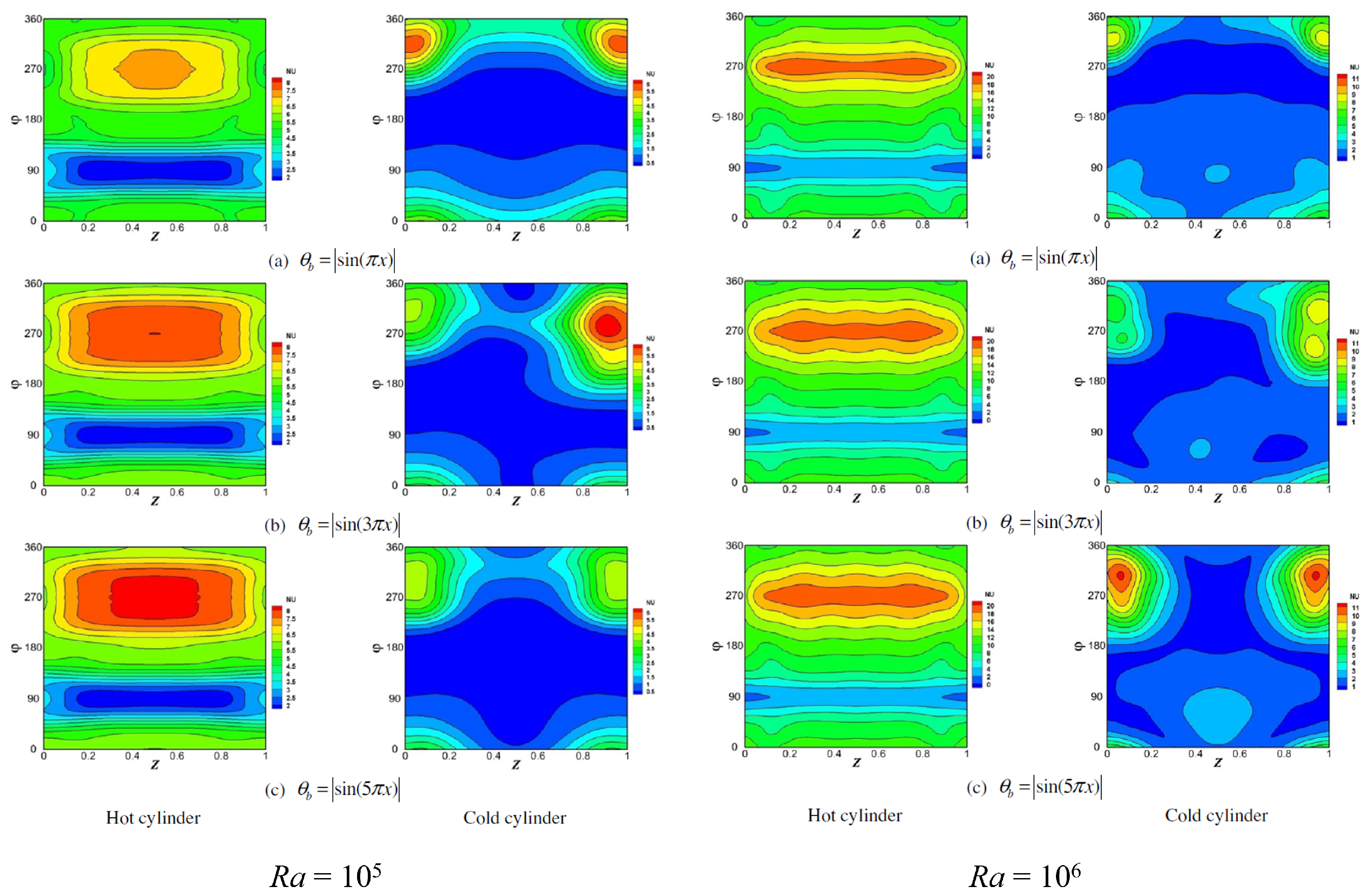
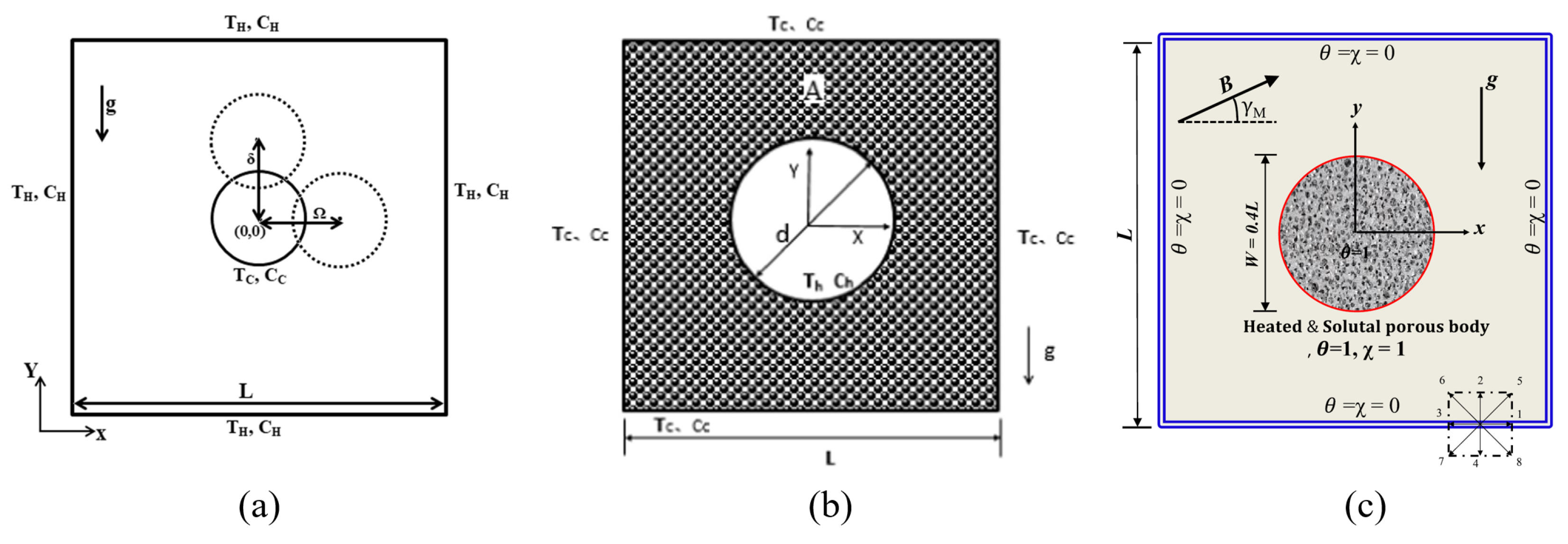
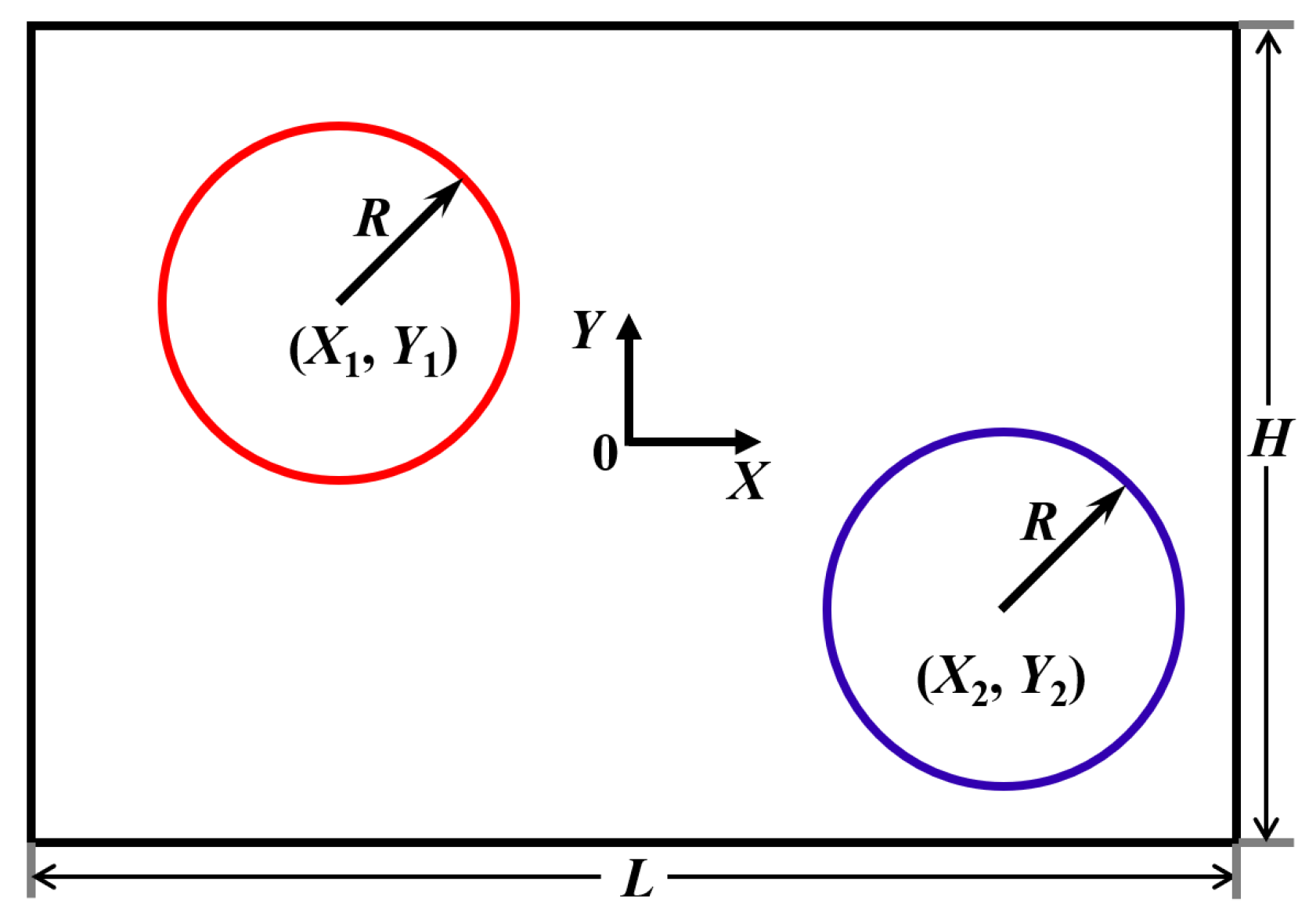
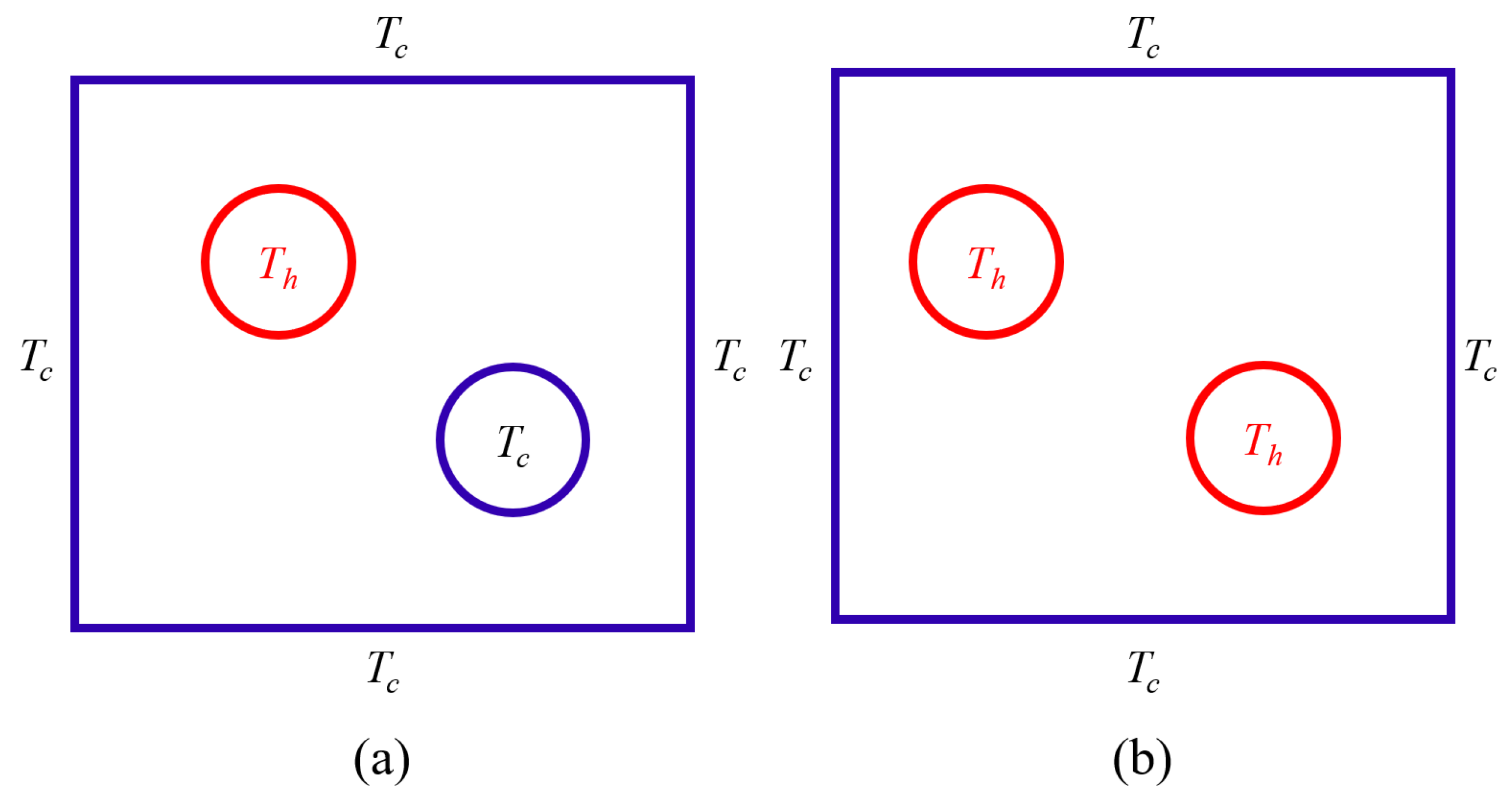




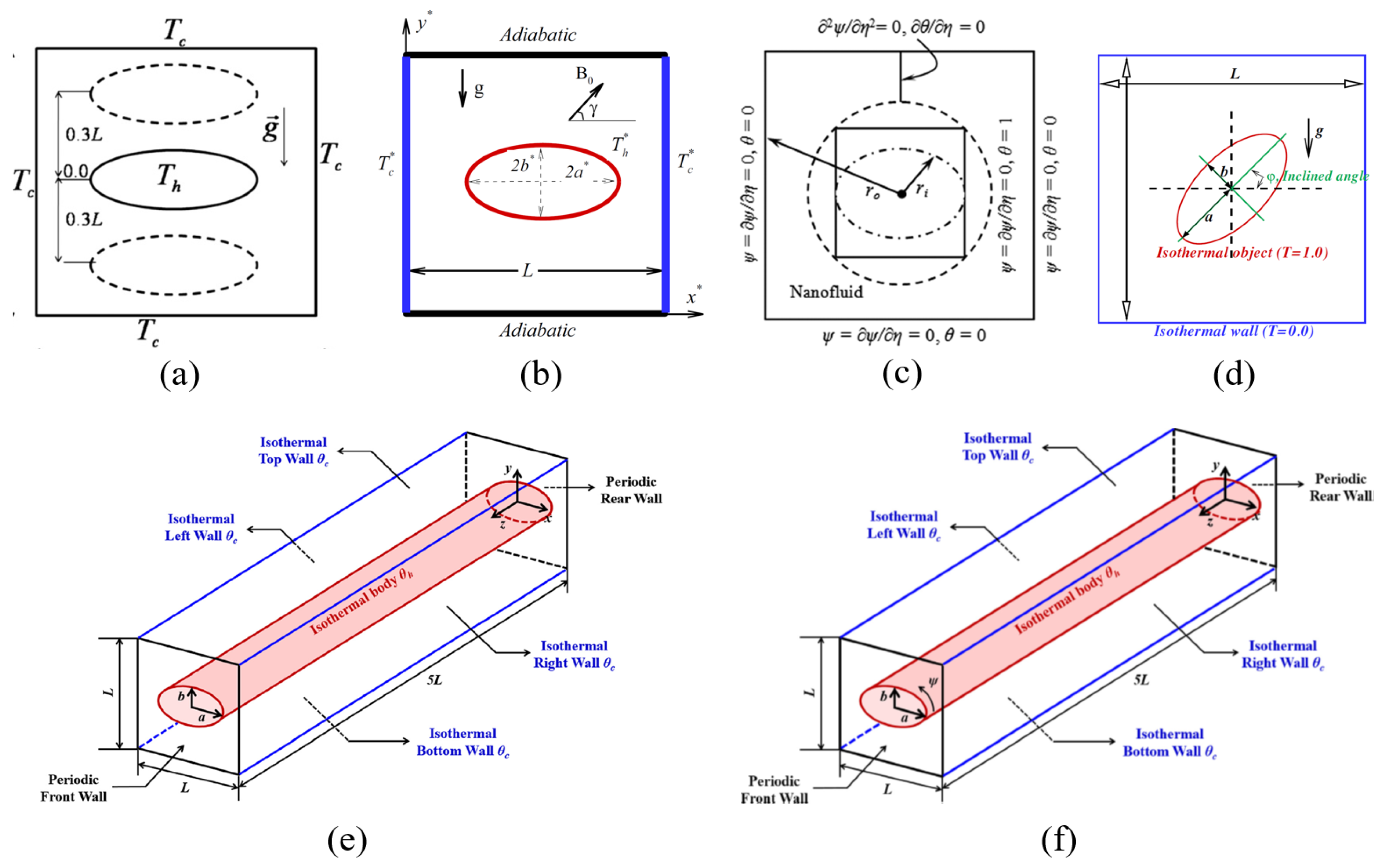
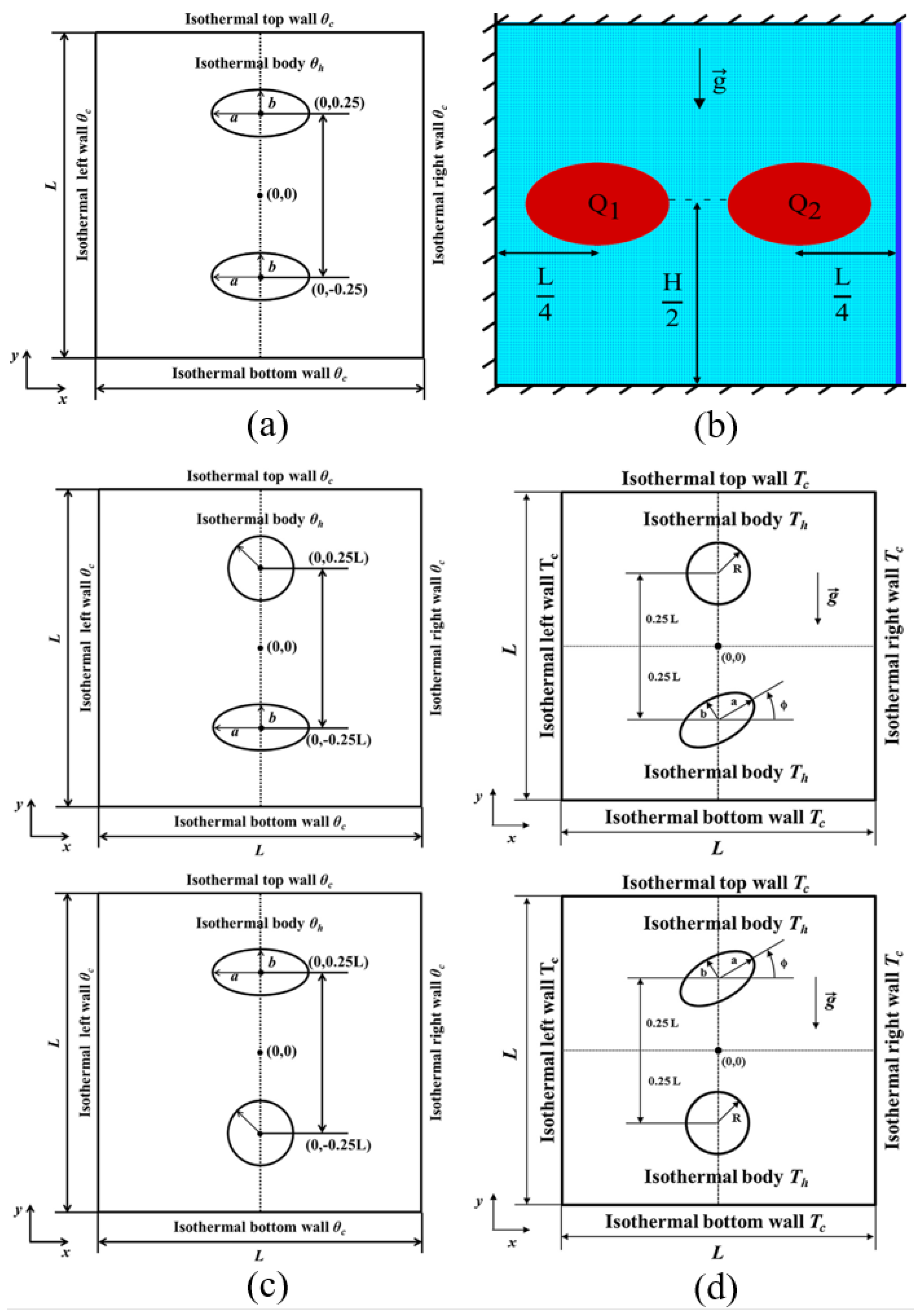
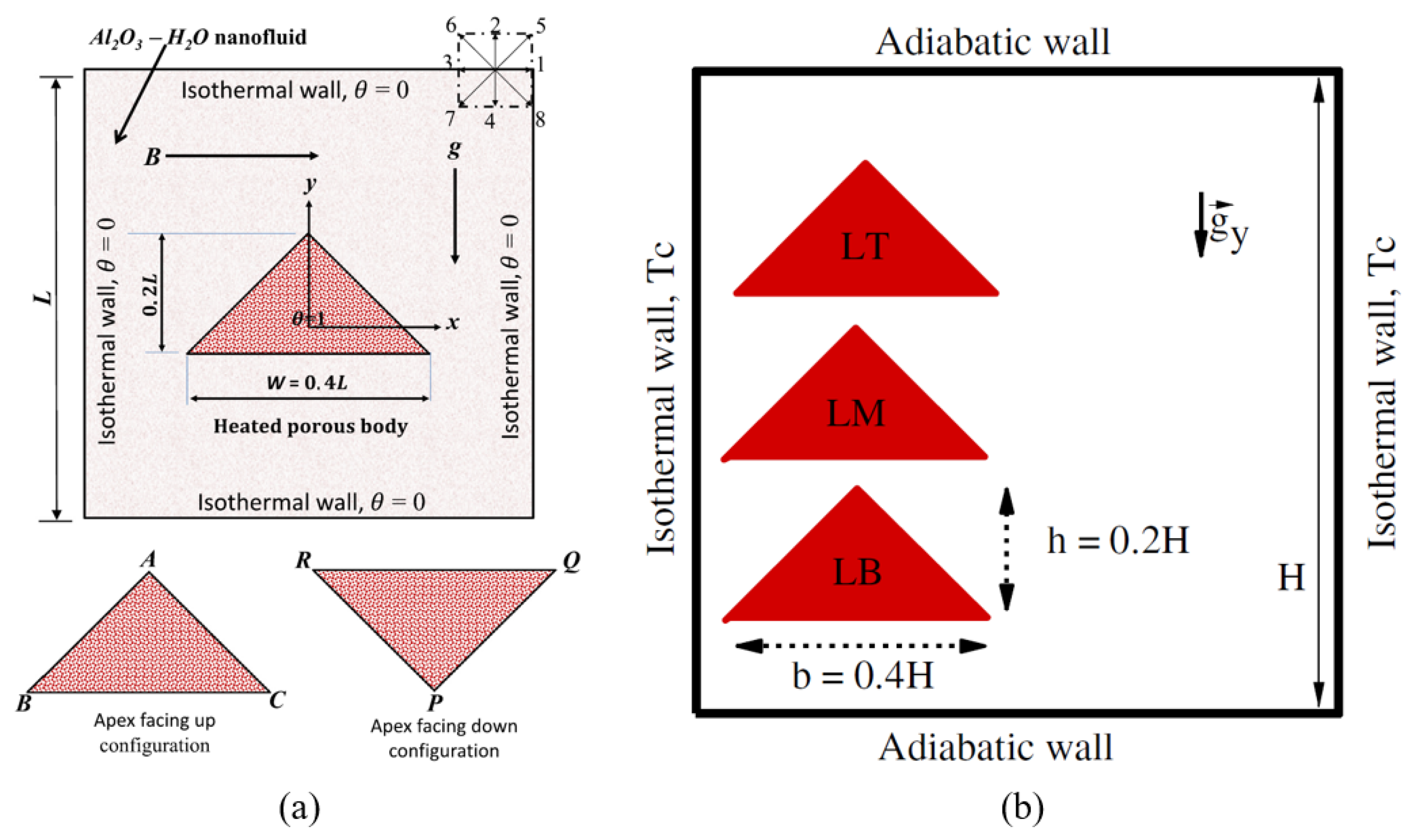
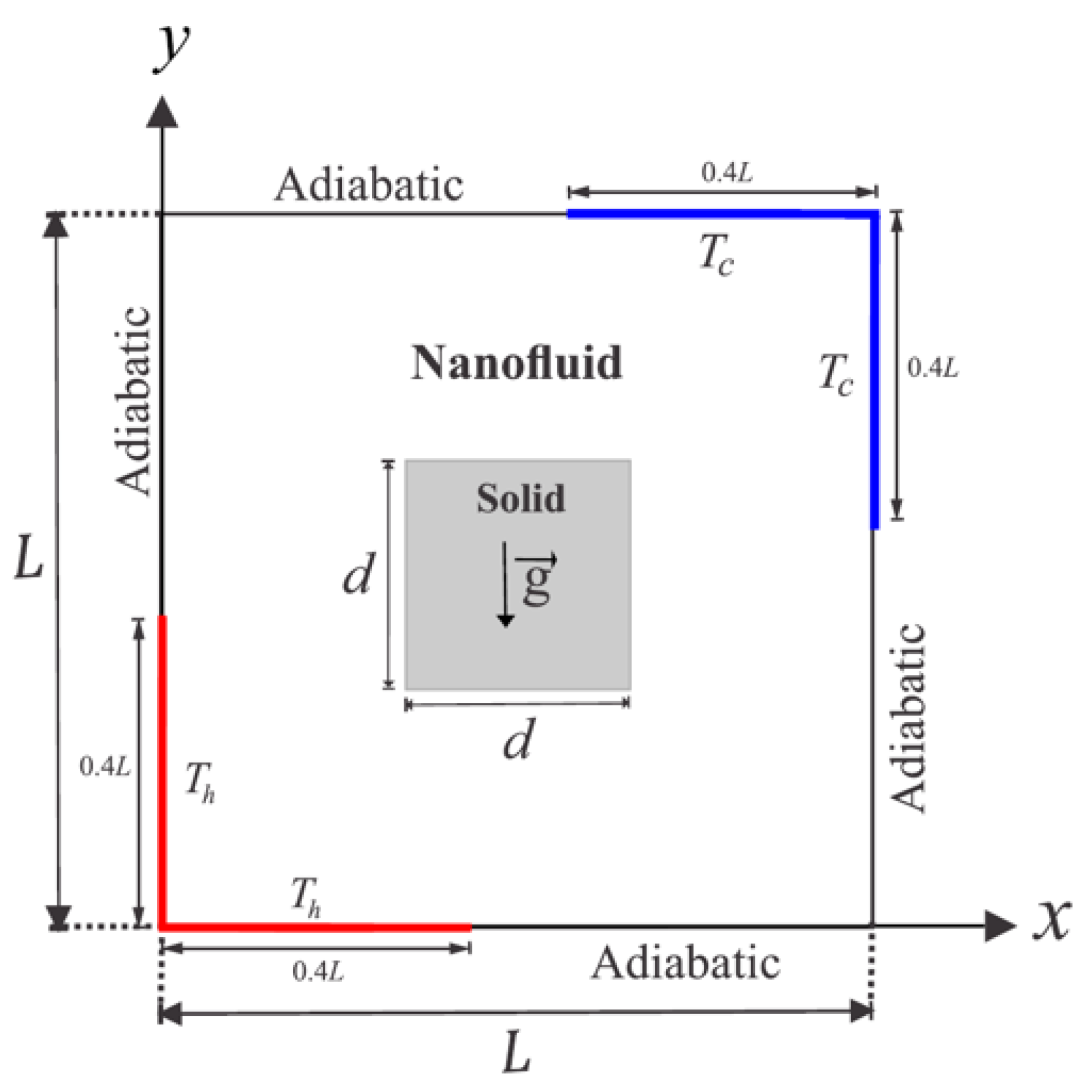
| Ref. | Focus Area | Scope | Main Differences from the Present Review |
|---|---|---|---|
| [7] | Natural convection in cavities | Cavity geometries, thermal boundary conditions, heat source distributions | Limited focus on inclined cavities and IOs |
| [8] | Natural convection in non-square enclosures | Triangular, trapezoidal, parallelogrammic enclosures with pure fluids, porous media, nanofluids | Focuses on non-square enclosures, not rectangular enclosures |
| [9] | Turbulent natural convection in rectangular cavities | Rectangular cavities | Focuses on turbulent convection, while present review deals with laminar convection |
| [10] | Natural convection in enclosures with/without IOs | Various shapes of enclosures | Present review focuses specifically on horizontal and inclined rectangular enclosures |
| [11] | Effects of governing parameters in cavities | Various shapes with and without nanofluids | Less exhaustive and detailed review of studies on IOs and inclined enclosures |
| [13] | Natural convection in complex geometries like trapezoidal, elliptical, and wavy cavities, emphasizing inner-object effects. | Complex geometries | Focuses on nanofluids, volume fraction, and porous layer thickness; not comprehensive for rectangular enclosures |
| [14] | Trapezoidal and other geometries with inner bodies of various shapes, detailing their influence on flow and heat transfer. | Trapezoidal, rhombic, wavy geometries | Focuses on inner-body geometry, Rayleigh numbers; not detailed on rectangular enclosures |
| [12] | Heat transfer and entropy generation in cavities | Various thermal properties, cavity configurations | Limited focus on studies related to the scope of the present review |
| [15] | IOs in cavities with fluids and nanofluids | Regular and nanofluids for natural and mixed convection modes | Limited review of studies on IOs with different shapes |
| [16] | Heat transfer in cavities with fins, obstacles, baffles | Various cavity shapes with pure fluids and nanofluids | Focused on general heat transfer, not systematic or detailed in the specific topic |
| Ref. | Num Method | Cylinder Size (r) | Cylinder Location (x, y) | Major Findings and Remarks | ||
|---|---|---|---|---|---|---|
| [27] | FVM | 0.2, 0.4, 0.6, 0.8 | x: 0, y: 0 | – | 0.7 | • Various flow regime transitions occur at different for different geometries, and larger d induces delayed transitions. • The geometry affects transition and the character of the supercritical flow regimes, and their stability ranges. |
| [23] | IBM/FVM | 0.2 | x: 0, y: −0.25–0.25 | – | 0.7 | • When the cylinder is located in the lower half, the effect of three-dimensionality is great. • As increases, the effect of the cylinder location on the distribution of and increases. |
| [17] | DQ method | 0.19 | x: −0.76–0.76, y: −0.76–0.76 | 0.71 | The differential quadrature (MQ-DQ) method is efficient in computing the weak global circulation and can accurately simulate the natural convection in eccentric annuli between a square outer cylinder and a circular inner cylinder. | |
| [18] | DQ method | 0.1–0.3 | x: 0, y: 0 | – | 0.71 | The Polynomial-Based Diffrential Quadrature (PDQ) and Fourier Expansion-Based Differential Quadrature (FDQ) methods are efficient in accurately simulating the natural convection in eccentric annuli between a square outer cylinder and a heated circular inner cylinder. |
| [19] | Local MQ-DQ method | 0.1–0.3 | x: −0.76–0.76, y: −0.76–0.76 | – | 0.71 | The local multiquadrics-based differential quadrature (MQ-DQ) method is able to accurately simulate the natural convection problem at large with various eccentricities and angular positions. |
| [28] | FVM | 0.2 | x: 0, y: −0.2–0.2 | – | 0.01–100 | • The flow instability is substantially intensified when is relatively high and is relatively small. • The state of the flow is affected by the geometry and position of the inner body as well as the geometry of the enclosure. • When is relatively low, the irreversibility is essentially unchanged despite the variation in the cylinder location. However, when is high, it changes when the cylinder is at different locations, especially with a relatively low , although the magnitudes are still similar to each other at the same . |
| [20] | FDM | 0.2 | x: 0, y: −0.25–0.25 | – | 0.71 | • A compact finite difference scheme for the biharmonic form of the Navier–Stokes equations was combined with a high-order compact scheme for the energy equation to compute the flow around heated circular and diamond cylinders inside a square enclosure. • Substantial computational simplicity was achieved by using a body fitted Cartesian grid which does not require grid transformation, but also uses an immersed interface strategy. • An excellent match was obtained in comparison to available numerical results for results on non-uniform grids without transformation. |
| [21] | FVM | 0.2 | x: 0, y: −0.25–0.25 | – | 0.7 | • For various upper and lower positions of the inner cylinder, the average and local increases with increasing . • The average of the cold enclosure is less than that of the hot inner cylinder because the isotherms have a slight effect and are almost symmetrical. |
| [29] | FVM/IBM | 0.2 | x: −0.25–0.25, y: −0.25–0.25 | 0.7 | • The flow and thermal fields bifurcate from the steady or unsteady to the unsteady or steady states at critical positions, which occurs at both the horizontal and the diagonal lines. • The major origin of the unsteady state depends on the position of the cylinder; thus, the unsteadiness near the upper corners, the center of the enclosure, and the lower corners is governed by a series of Benard cells, the strong sway of the rising upwelling plume from the inner cylinder, and the inner vortices periodically merging and separating within the enlarged lower primary eddy, respectively. • The changes in the local are dominated by the gaps between the cylinder and the enclosure, the upwelling and downwelling thermal plumes, and the upward returning flow. | |
| [30] | IBM/FVM | 0.2 | x: −0.25–0.25, y: −0.25–0.25 | – | 0.7 | • The local peaks occur at the locations where the distance between the cylinder surface and the enclosure wall is the shortest for . • The origin and the inclined direction of the thermal plume strongly influences the location of the local minimum on the cylinder surface as well as the local peaks on the enclosure wall for larger . • The is strongly influenced by and the location of the cylinder. |
| [31] | FVM/IBM | 0.2 | x: 0, y: −0.25–0.25 | – | 0.7 | • and position of the cylinder strongly influences the number, size, and formation of cells. • The distribution of the local and is largely influenced by the presence of the secondary and tertiary vortices close to the upper surface of the cylinder in relation to the variation in the position and . The location of the peak and the valley of the local along the surfaces of the cylinder and enclosure depend on the location of the center of the vortices. • The of the cylinder when the cylinder is at different locations is similar to the variation of the total of the enclosure for different . • on the cylinder was higher than that on the enclosure due to the formation of denser isotherms on the cylinder surface in contrast to the surface of the enclosure. |
| [32] | IBM/FVM | 0.4 | x: 0, y: 0 | – | 0.07–0.71 | • Influence of on the flow structure is studied via the flow structure map in the - plane. • When is reduced, the flow transitions from steady single thermal-plume state, steady double thermal-plume state, and then to an unsteady state for . However beyond , the transition is directly from steady single-plume state to unsteady state without going through double-plume regime. • There are variations in the threshold during transition from single-plume to double-plume or to unsteady regime at different . |
| [33] | IBM/FVM | 0.4 | x: 0, y: 0 | – | 0.07–7 | • In general, deceases because the boundary layer thickness increases when the is reduced. • Different scaling laws for exist due to the change in vortex structures in the steady and unsteady regions. |
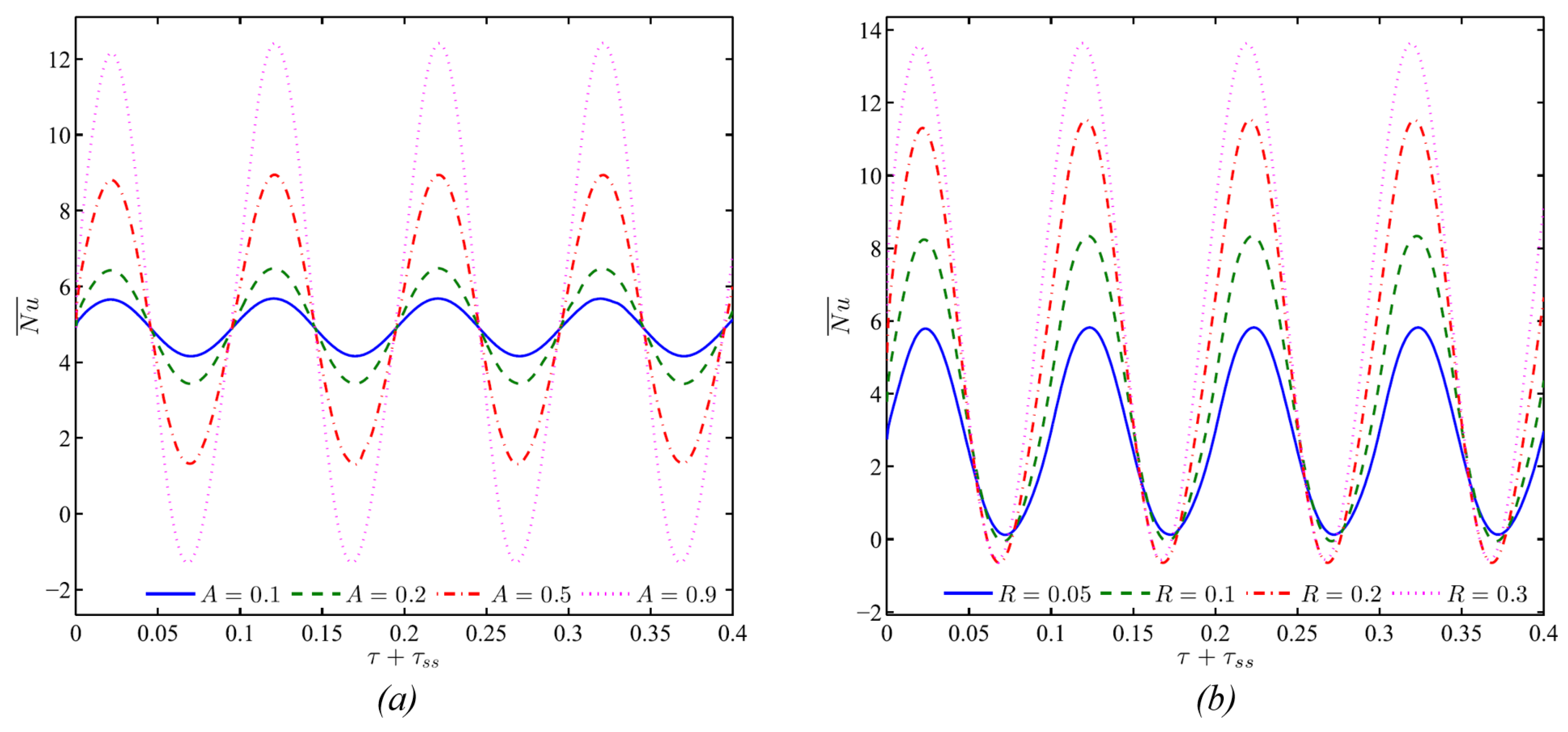
| [34] | FEM | 0.05–0.3 | x: 0, y: 0 | – | 0.7 | • The cylinder temperature was assumed to vary sinusoidally with time and was always larger than the enclosure wall temperature. • Oscillating the source temperature increased the . • The largest heat transfer augmentation for high heating amplitude and moderate source radius occurred at frequency of 25–30. |
| [24] | IBM/FVM | 0.1–0.4 | x: 0, y: 0 | – | 0.7 | • 3D numerical simulations were conducted to examine the three-dimensionality effect. • For various cylinder radius, the flow and thermal structures are almost 2D when . • The flow and thermal structures have an almost 2D structure as increases to , when . When r increases to , the flow transitions from steady to unsteady state. When , the flow and thermal structures exhibit unsteady characteristics. |
| [25] | IBM/FVM | 0.1–0.4 | x: 0, y: 0 | – | 0.7 | • The size effects of circular and elliptical cylinders were examined using 3D numerical simulations. • The major conclusions drawn in [24] were re-confirmed. |
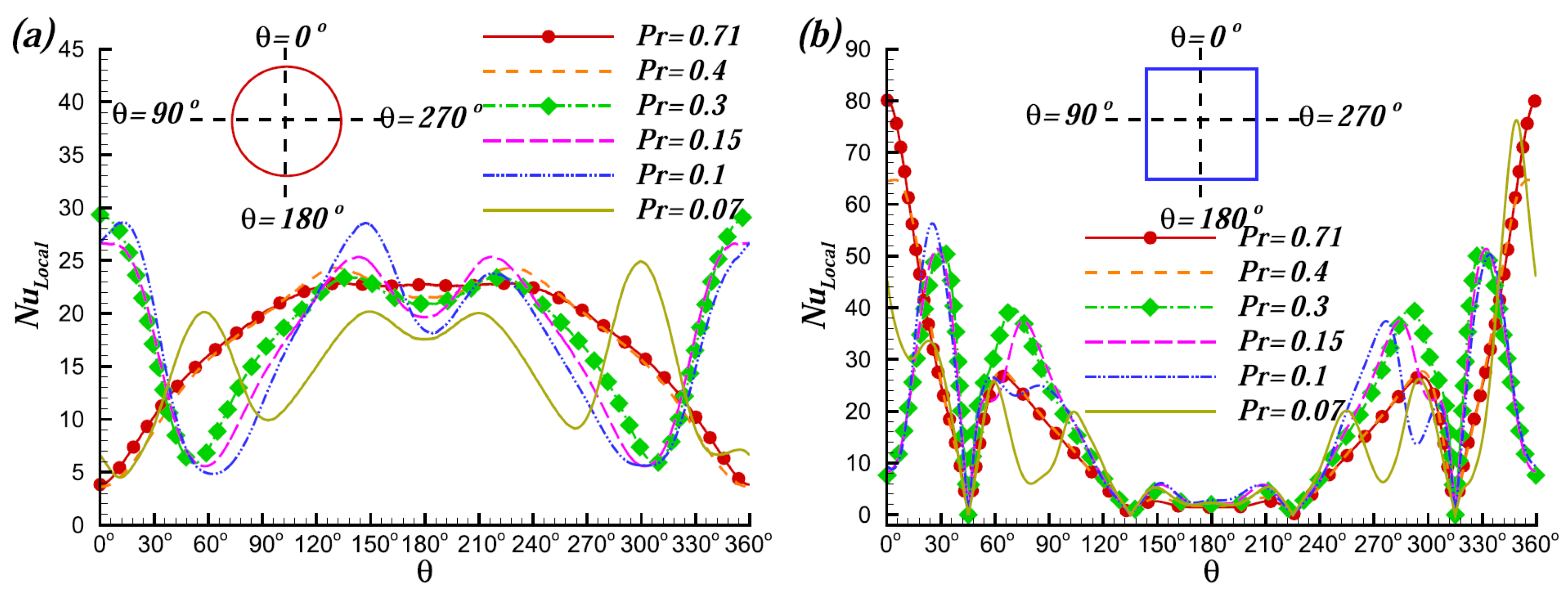
| [26] | IBM/FVM | 0.1–0.4 | x: 0, y: 0 | – | 0.7 | • The ability of a sinusoidal cylinder to improve heat transfer in comparison to a CC in a long rectangular enclosure was examined using 3D numerical simulations. • The shape of the cylinder notably affected at , with up to 27% performance improvement. • The total heat transfer performance at the cylinder surface and the enclosure walls were greatly influenced by and the mean cylinder radius. |
| [22] | FVM | 0.2–0.5 | x: 0, y: −0.5–0.5 | 10– | 1 | • Eccentricity substantially affects the flow and thermal fields as well as the heat transfer distribution, with eccentric positions producing higher than the concentric position. • At all eccentricities considered, a circulatory zone with one core is observed near the upper part of the cylinder. • When the cylinder is at the center, a critical range of is identified below which is higher for a larger cylinder and above which is lower for a smaller cylinder. |
| [35] | LBM | 0.1–0.3 | x: 0, y: 0 | – | 0.71 | • The conductive walls affected the structure of the flow and temperature fields. • for various wall thicknesses was usually lower in comparison to zero wall thickness. For larger wall-to-fluid thermal conductivity ratio, the difference was not apparent. • tended to decrease when the outer wall thickness increased. |
| [36] | LBM | 0.2 | x: 0, y: 0 | – | 6 | • The effects of exponentially temperature-dependent viscosity on natural convection inside a porous cavity containing a hot CC under local thermal non-equilibrium (LTNE) condition was examined using LBM. • When the LTNE parameters are increased, the solid heat transfer rate increased substantially, with only few changes for the fluid heat transfer rate. • Generally, the heat transfer rate of the solid and fluid decreases when the viscosity variation index is increased. However, when the values of the inter-phase heat transfer coefficient and the ratio of fluid-to-solid thermal conductivity are relatively low, the heat transfer of the solid phase has a small dependence on the viscosity variation index. |
| [37] | RBF/MQ | 0.2 | x: 0, y: −0.25–0.25 | 0.71 | • Periodic unsteady natural convection flow and heat transfer inside a square enclosure with a heated CC was simulated. The temperature of the cylinder was oscillating in a time sinusoidal manner. • The vertical position of the cylinder highly influenced . • The time-periodic unsteady natural convection was enhanced in comparison to the steady state case, and increased with temperature pulsating amplitude. | |
| [38] | IBM/FVM | 0.2 | x: 0, y: −0.25–0.25 | 0.7 | • Based on the location of the internal CC (y), the natural convection bifurcates from unsteady to steady state at . • Two critical positions were identified, with as a lower bound and as an upper bound. The thermal and flow fields are steady state within the bounds. • Based on the location of the CC, the natural convection shows single frequency and multiple frequency periodic patterns alternately in the unsteady region. • When , upwelling and downwelling plumes alternately formed as a result of natural convection (characterized as pure Rayleigh–Benard convection) in the region between the upper surface of the internal cylinder and the top surface of the enclosure. • The distribution of the local and is highly influenced by the secondary and tertiary vortices on the upper surface of the cylinder as a result of the change in y. | |
| [39] | LBM/FDM | 1/6 | x: 0, y: 0 | – | 0.71 | • The internal body is a conducting cylinder that generates heat, with the temperature-difference ratio , in the range of . • When is constant, the average varies linearly with at the hot and cold walls ( and ) of the enclosure. • At a constant , when increases, the average decreases, whereas the average increases. • Regardless of the value, the maximal temperature inside the enclosure decreases when is increased. |
| Ref. | Object Size (r) | Object Location (, ), (, ) | Major Findings and Remarks | ||
|---|---|---|---|---|---|
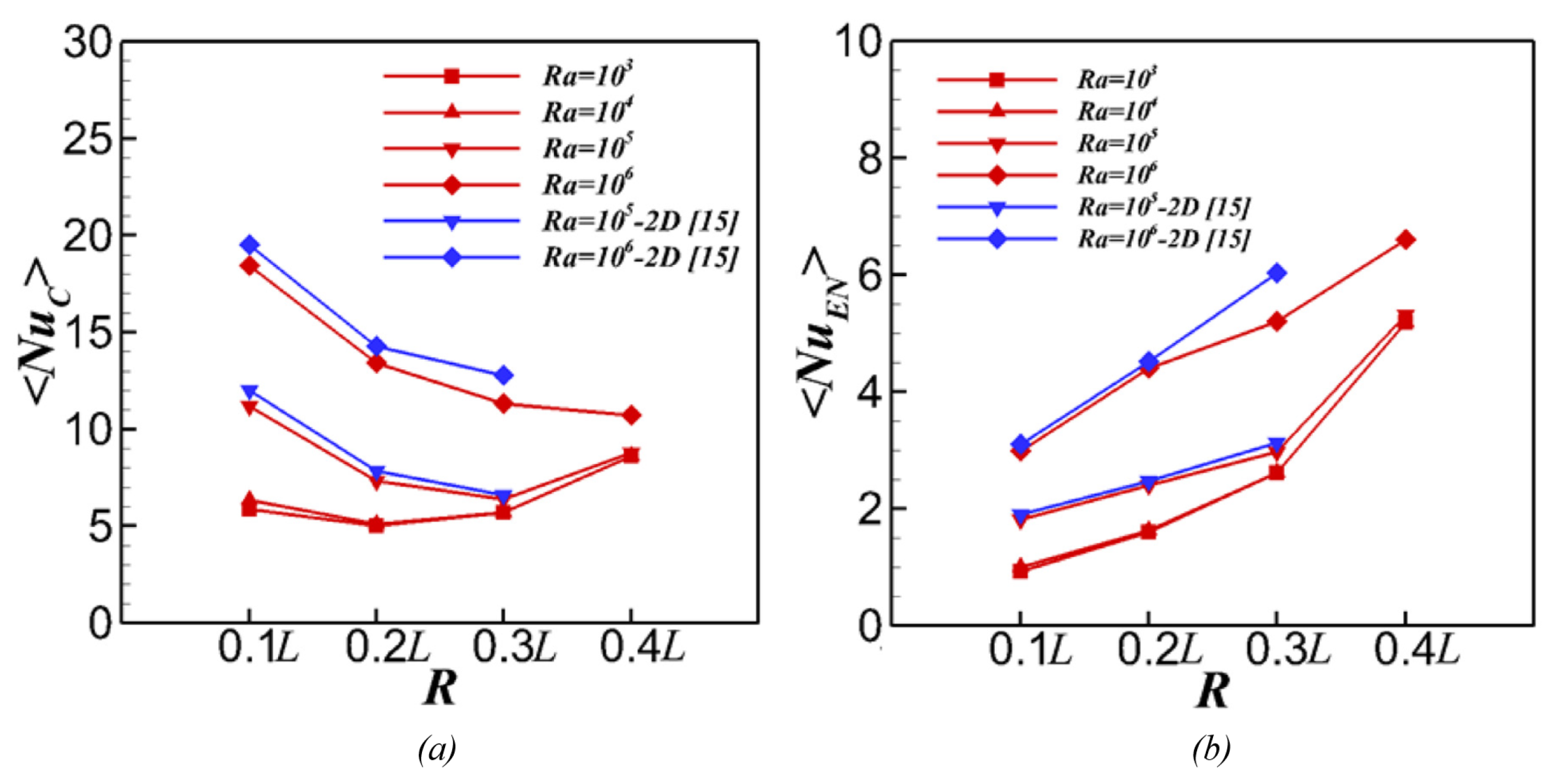
| [72] | 0.2 | : −0.25, : −0.25–0.25; : 0.25, : −0.25–0.25 | – | 0.7 | • Local peaks along the surfaces of the cylinder and enclosure were influenced by the distance between the cylinders and the enclosure and the thermal plume, respectively. • Detailed analysis of the distribution of the streamlines, isotherms, and were presented. |
| [69] | 0.2 | : −0.25, : −0.25–0.25; : 0.25, : −0.25–0.25 | 7– | 0.7–100 | • The effect of is examined, which is only evident when is high so there is a reasonable degree of buoyancy-induced flow. • gradually increases when the magnitudes of decreases as more fluid participates in heat transfer. • An empirical relation was established for the average in terms of , , and . |
| [70] | 0.2 | : −0.25, : −0.25–0.25; : 0.25, : −0.25–0.25 | 7– | 0.7–100 | • Non-Newtonian power-law fluids were used having power-law index (n) from 0.3 to 1.8. • The effects from , , n, and were investigated. • Overall, the average positively depends on irrespective of n and . • With all else being equal, heat transfer is enhanced by shear-thinning fluid behavior in comparison to Newtonian fluids. • At , is augmented with reference to that at , but conversely, is reduced at . |
| [71] | 0.2 | : −0.25, : −0.25–0.25; : 0.25, : −0.25–0.25 | – | 10–100 | • The fluids are non-Newtonian Bingham plastic fluids with the Bingham number () from 0.01 to 100. • The effects of , , , and are examined. • The average increases with the increasing and decreases with the increasing and . • The increase in the magnitude of the negative increasingly enhances heat transfer. • An empirical relation was established for the average in terms of , , and . |
| [68] | 0.2 | : −0.25–, : −0.25–; : −0.25–0, : –0.25 | 70– | 0.7–100 | • The fluids are non-Newtonian power-law fluids with power-law index (n) from 0.2 to 2.
• The relative locations of the cylinders play a pivotal role in determining . • Broadly, asymmetric positioning of the two cylinders leads to some larger , as does the shear-thinning fluid behavior otherwise under identical conditions. • An empirical relation was established for the average in terms of , , and n. |
| [73] | 0.05–0.2 | : 0, : −0.25; : 0, : 0.25 | – | 0.7 | • At higher , the trajectories of the primary eddy and the secondary vortices are significantly influenced by r. • The influence of r and on was analyzed in detail. |
| [74] | 0.2 | : −0.25, : −0.25–0.25; : 0.25, : −0.25–0.25 | – | 0.7 | • The influence of and cylinder heights (), when the two hot cylinders are located at fixed and , were examined. • Based on and , the distribution of isotherms and streamlines reach steady state or change from steady to unsteady state. • For various , the profile of the local on the enclosure walls exhibited an almost symmetric distribution along the center of the enclosure, for . However, the symmetry was broken down when , as a result of the increasing effect of convection as increases. |
| [75] | 0.1 | : 0, : 0.15–0.35; : 0, : −0.35–0.15 | – | 0.7 | • The influence of and the cylinder heights, when the two hot cylinders are located at fixed , were examined. • The surface averaged of the lower cylinder is greater in comparison to the surface averaged of the upper cylinder. • increase with increasing . • along the walls of the enclosure is greater in the case of two cylinders in comparison to one cylinder regardless of and cylinder location. However, and cylinder location influences the difference in of the single cylinder and and of the two cylinders. |
| [76] | 0.05–0.2 | : 0, : 0.25; : 0, : −0.25 | – | 0.7 | • The effects of and r with two hot cylinders are examined. • Increasing caused the horizontal symmetry to be broken and, from the smaller radius, asymmetry was evident. • considerably influences the convection when r decreases. • The influence of r and on was analyzed in detail. |
| Ref. | Case | Cylinder Size () | Cylinder Location (x, y) | Major Findings and Remarks | ||
|---|---|---|---|---|---|---|
| [93] | 1 | 0.4 | x: −0.25–0.25, y: −0.25–0.25 | – | 0.71 | • Effects of and the horizontal and diagonal eccentricity were examined. • Local and distributions strongly depend on and eccentricity. |
| [92] | 1 | 0.4 | x: 0, y: −0.25–0.25 | – | 0.71 | • Effects of and the vertical eccentricity () were examined. • When increases, the increases for all values considered. • For all the considered , as increases from −0.25 to 0.25, of the top wall increases, on the bottom wall decreases, and on the side wall has minor variation, which leads to the almost symmetric profiles of plotted against . |
| [102] | 1 | 0.4 | x: 0, y: 0 | – | 6.2 | • Effects of and nanoparticle concentration (Cu-water, over ) were examined. • When increases, the average increases for all values considered. • An empirical correlation for was developed in terms of . |
| [95] | 2 | 0.2, 0.4, 0.6 | x: 0, y: 0 | – | 6.2 | • Effects of , volume fraction of nanoparticles (Cu-water, 0–0.05), and cylinder size were examined. • By increasing or , increases. • At , is its maximum for due to conduction dominance. • At , is its maximum at about in most cases due to convection dominance. |
| [94] | 2 | 0.125 | x: 0, y: | – | 0.71 | • Effects of and enclosure aspect ratio (A) were examined, focusing on the transition from stability to instability. • For very low , the steady flow is symmetric for all A values considered. • For sufficiently large , the flow becomes unsteady in a periodic manner. • The instabilities which occur through the different Hopf bifurcations are not all of the same type, depending on A. |
| [99] | 3 | 0.5 | x: 0, y: 0 | – | 0.71 | • Inner square was heated with flux quantified by the temperature–difference ratio . • Effects of and were examined. • The average at both the hot and cold walls change with linearly for a specific . |
| [97] | 3 | 0.5 | x: 0, y: 0 | , | 0.0112, 0.707, 5.83 | • Inner square was heated with flux quantified by the temperature–difference ratio . • Effects of , , and (1.71, 240, 5630) were examined. • strongly affects . • When increases, at both the hot and cold walls decrease for the same . |
| [98] | 3 | 0.5 | x: 0, y: 0 | , | 0.0112 | • 3D steady laminar NCHT. • Inner square was heated with flux quantified by the temperature–difference ratio (2.5, 25) and . • When and increase, the local increases. • The local variation at the hot and cold walls of the enclosure in the longitudinal direction is larger when a cubic conducting body is present (in comparison to an enclosure without a cubic conducting body), indicating substantial three-dimensionalities of natural convection. |
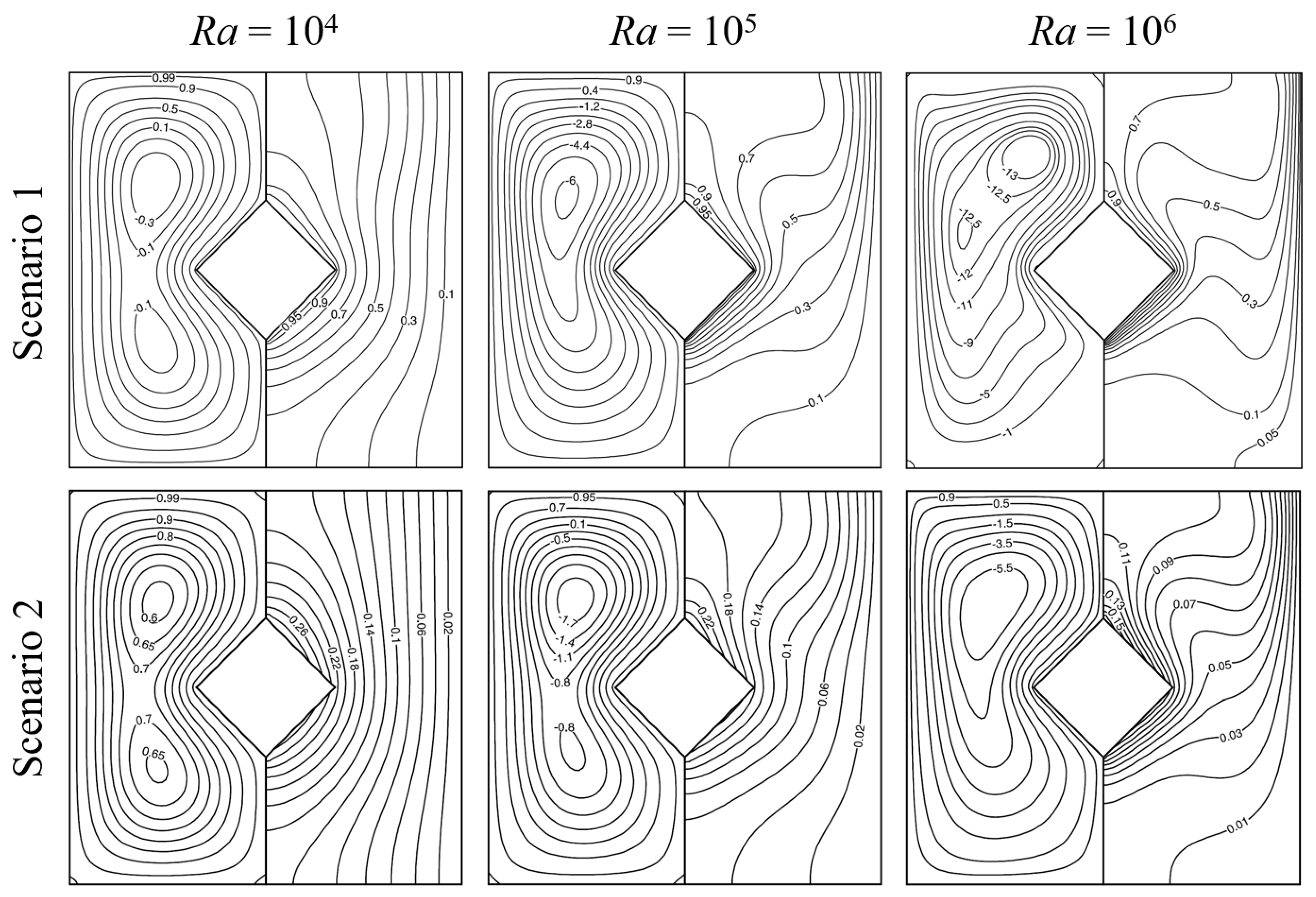
| [103] | 4 | 0.25 | x: 0, y: −0.25, 0, 0.25 | – | 0.71 | • Effects of , enclosure aspect ratio (A) and y were examined for two heating scenarios on the cylinder. • The overall in Scenario 1 where the cylinder is heated with a higher temperature is larger than that in Scenario 2 where the cylinder is heated with a uniform flux. • The effect of y on both local and average is small in Scenario 1. • For larger A, the effect of y becomes important leading to different trends in the local distribution. • The change in A leads to variation in the overall when is lower, but the effect of A diminishes as is increased for Scenario 1. |
| [20] | 4 | x: 0, y: −0.25, 0, 0.25 | – | 0.71 | • Effects of and y were examined. • When increases, the average the cylinder increases, but on the side walls decreases. • and are almost the same for and 0, but they are significantly different for , and the variations increase when increases. • There is substantial difference in the heat transfer patterns for the SC and CC cases. | |
| [96] | 4 | 0.25 | x: 0, y: −0.25, 0, 0.25 | 71– | 0.71–100 | • For the two heating scenarios on the cylinder, the effects of , y, and power-law index () were investigated. • , , and y highly modulate the effect of the power-law fluid behavior. • Empirical correlations were developed for the average in terms of , , n, and y for both scenarios. • For larger A, the effect of h becomes important leading to different trends in the local distribution. |
| Ref. | Case | a | (x, y) | Major Findings and Remarks | ||||
|---|---|---|---|---|---|---|---|---|
| [115] | (a) | 0.312 | 0.3 | 0° | x: 0, y: −0.3–0.3 | – | 0.7 | • The influence of and the vertical position of an EC (y) were investigated. • The streamlines, temperature contours, and vortex formation in the enclosure is significantly influenced by the and y. • When increases, the average also increases and the location of the minimum value of the average becomes further away from the top of the internal cylinder. |
| [119] | (a) | 0.2–1.0 | NA | 0° | x: 0, y: 0 | – | 0.71 | • The influence of axis ratio on fluid flow and heat transfer were investigated for a variety of and cavity aspect ratio. • When the axis ratio and is increased, the also increases. • When the cavity aspect ratio decreases, the increases. |
| [116] | (b) | NA | NA | 0° | x: 0, y: 0 | 10–1000 | 6.2 | • The flow and heat transfer of a micropolar nanofluid was investigated inside a radiative porous enclosure under the influence of MHD with an internal elliptical heater. • When the radiation parameter () is increased, there is a slight increase in the strength of the particles’ microrotations. • The increment of porosity () strengthens flow strength and weakens the micro-rotations of the particles. • When the vortex viscosity parameter, Hartman number, and is increased the is enhanced, but a reverse trend was found for , , interface heat transfer coefficient and thermal conductivity ratio. |
| [120] | (c) | 0.5 | 0.5 | 0° | x: 0, y: 0 | 6.2 | • The influence of , volume fraction of nanoparticles () and the shape of the inner cylinder was investigated. • As and is increased, the intensity of streamlines strengthens. • When was increased, the at the inner cylinder and the enclosure increased approximately linearly; however, when was increased, an exponential increase was observed. • The intensity of the streamlines increases but diminishes with rectangular, circular, and elliptical inner shapes. | |
| [118] | (d) | 0.25–1.0 | varied | 0°–90° | x: 0, y: 0 | – | 0.71 | • Effects of , , and were examined. • A circular-like cylinder has more uniform local along the hot surface in comparison to an elongated cylinder. • The average is weakly dependent on . • When is increased, the mean on the cylinder and enclosure walls also increases. • is significant only when . • A slender EC generates higher . |
| [117] | (d) | 0.125–2.0 | 0.1–0.4 | 0–180° | x: 0, y: 0 | – | 0.7 | • Effects of , and were examined. • The profile exhibits the symmetric distribution to the right angle of the major axis when is increased. • The is lower at in comparison to . • a has a stronger effect on than b does. |
| [25] | (e) | varied | varied | 0° | x: 0, y: 0 | – | 0.7 | • 3D numerical simulations were carried out. • The influence of the sizes of the internal heated circular and ECs were investigated. • Changing the radius of the circular and elliptical cylinders altered the flow and thermal structures. • Generally, the maximum local of the top wall occurs at the center of the top wall, and the minimum occurs at both sides of the top wall. • Based on the cylinder radius, when , the location and peak values of the local of the top wall vary as a result of the flow instabilities increasing. |
| [121] | (f) | varied | varied | 0–90° | x: 0, y: 0 | – | 0.7 | • 3D numerical simulations were carried out. • Effects of and size of 3D ECs were examined. • When was high, the significantly influenced the three-dimensionality and the flow instability. • The influence of on increased when the mean radius was increased. • Altering at a specific mean radius of the cylinder can enhance the global heat transfer characteristics of the enclosure. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jobby, A.; Khatamifar, M.; Lin, W. A Comprehensive Review on the Natural Convection Heat Transfer in Horizontal and Inclined Closed Rectangular Enclosures with Internal Objects at Various Heating Conditions. Energies 2025, 18, 950. https://doi.org/10.3390/en18040950
Jobby A, Khatamifar M, Lin W. A Comprehensive Review on the Natural Convection Heat Transfer in Horizontal and Inclined Closed Rectangular Enclosures with Internal Objects at Various Heating Conditions. Energies. 2025; 18(4):950. https://doi.org/10.3390/en18040950
Chicago/Turabian StyleJobby, Antony, Mehdi Khatamifar, and Wenxian Lin. 2025. "A Comprehensive Review on the Natural Convection Heat Transfer in Horizontal and Inclined Closed Rectangular Enclosures with Internal Objects at Various Heating Conditions" Energies 18, no. 4: 950. https://doi.org/10.3390/en18040950
APA StyleJobby, A., Khatamifar, M., & Lin, W. (2025). A Comprehensive Review on the Natural Convection Heat Transfer in Horizontal and Inclined Closed Rectangular Enclosures with Internal Objects at Various Heating Conditions. Energies, 18(4), 950. https://doi.org/10.3390/en18040950






