Flexible On-Grid and Off-Grid Control for Electric–Hydrogen Coupling Microgrids
Abstract
:1. Introduction
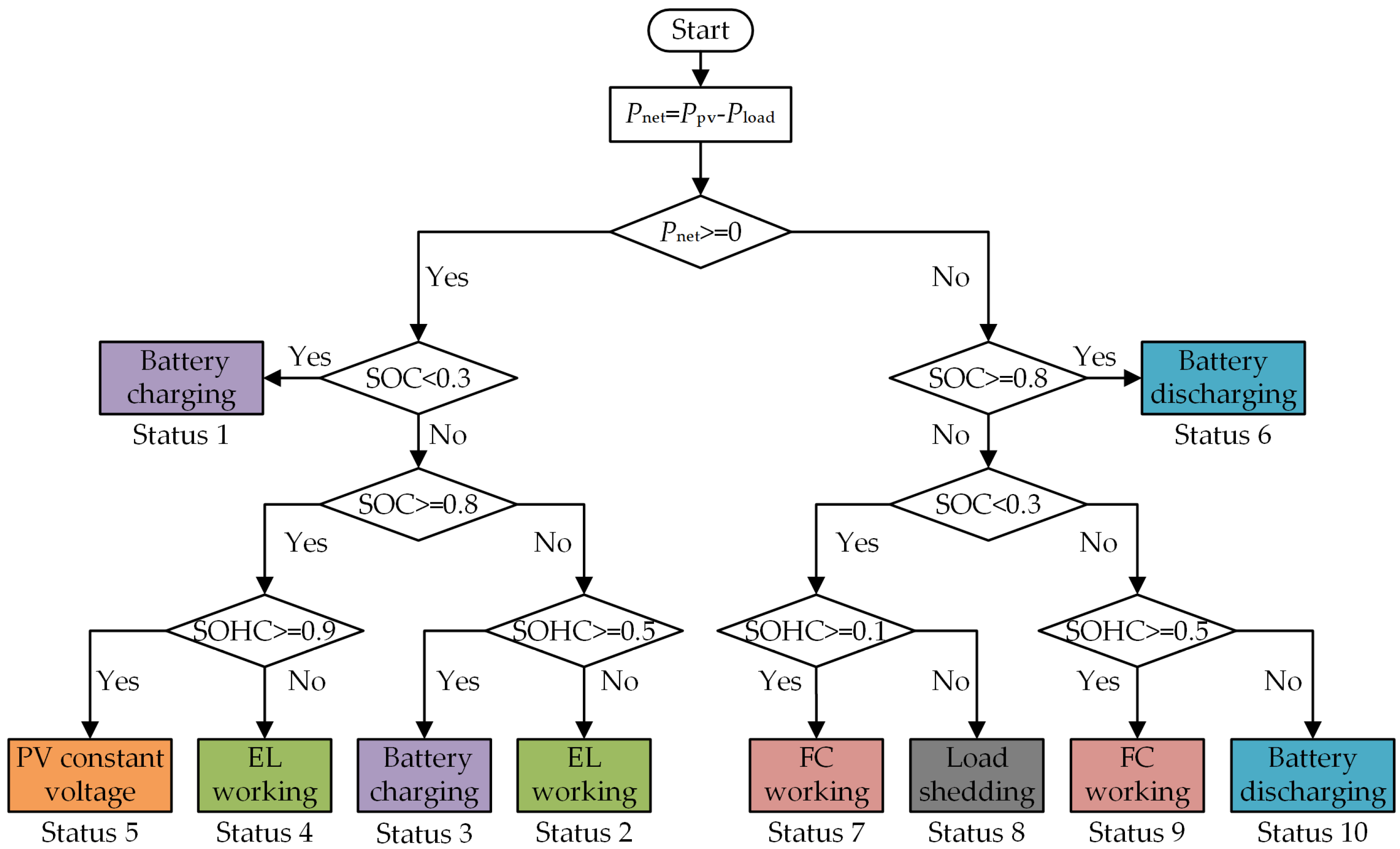
- An upper-level power management strategy (PMS) is developed to sustain source–load balance while managing the SOC of BESS and the state of hydrogen charge (SOHC) of a hydrogen storage tank (HST). The proposed PMS classifies microgrid operation into 10 distinct statuses according to source–load imbalances along with deviations of SOC and SOHC from their respective boundaries, and dispatches multiple components to balance source and load and prevent the HESS from excessive charge or discharge;
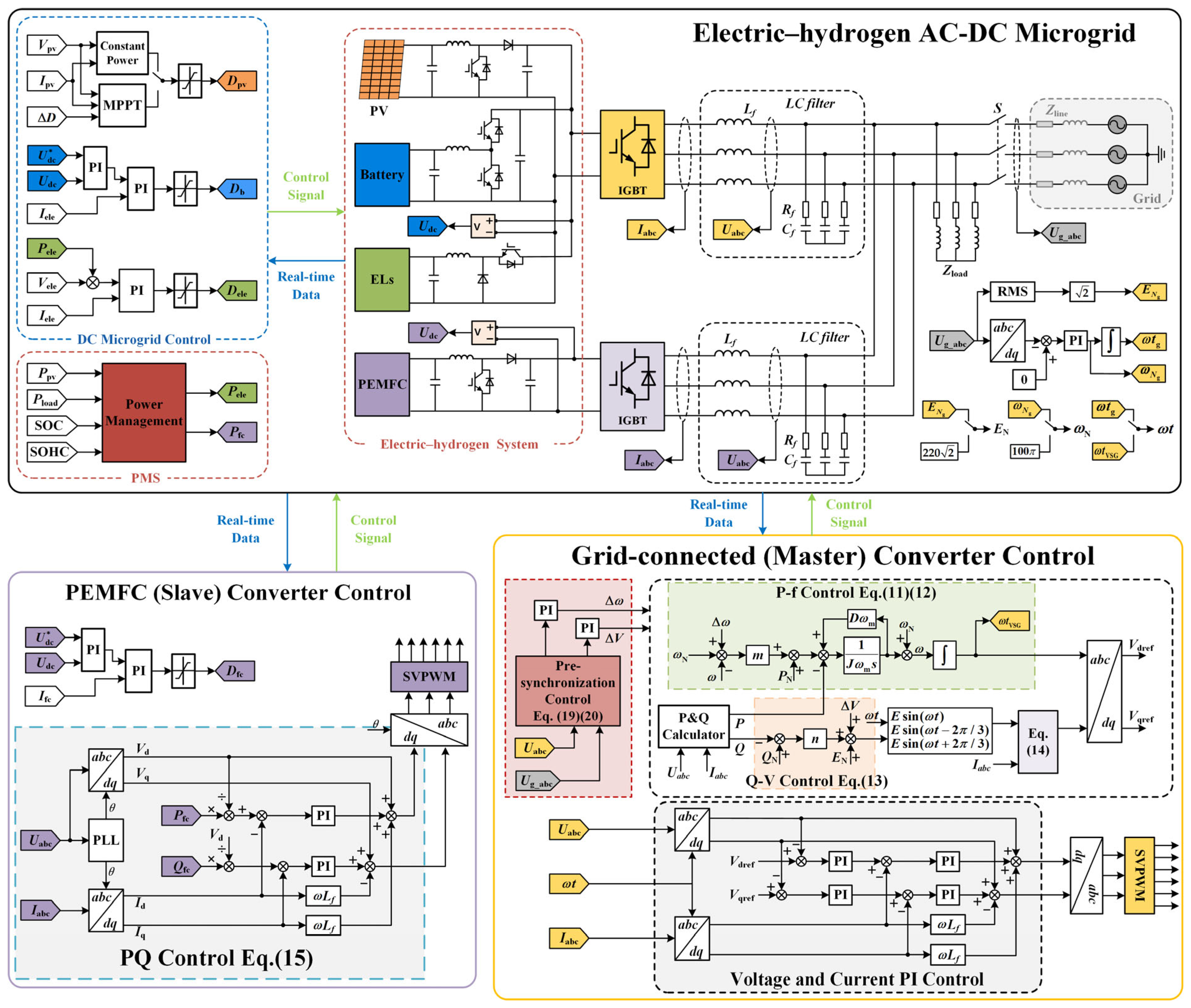
- A lower-level master–slave control method is developed for the AC-DC hybrid microgrid. The master converter is regulated by virtual synchronous generator (VSG) control, which regulates the dynamic characteristics of the microgrid by modelling the behaviour of a synchronous generator. It is used to stabilise voltage and frequency in the off-grid mode and operate synchronously with the upstream grid in the on-grid mode. The slave converter is regulated by active and reactive power (PQ) control, continuously following the voltage and frequency of the master converter;
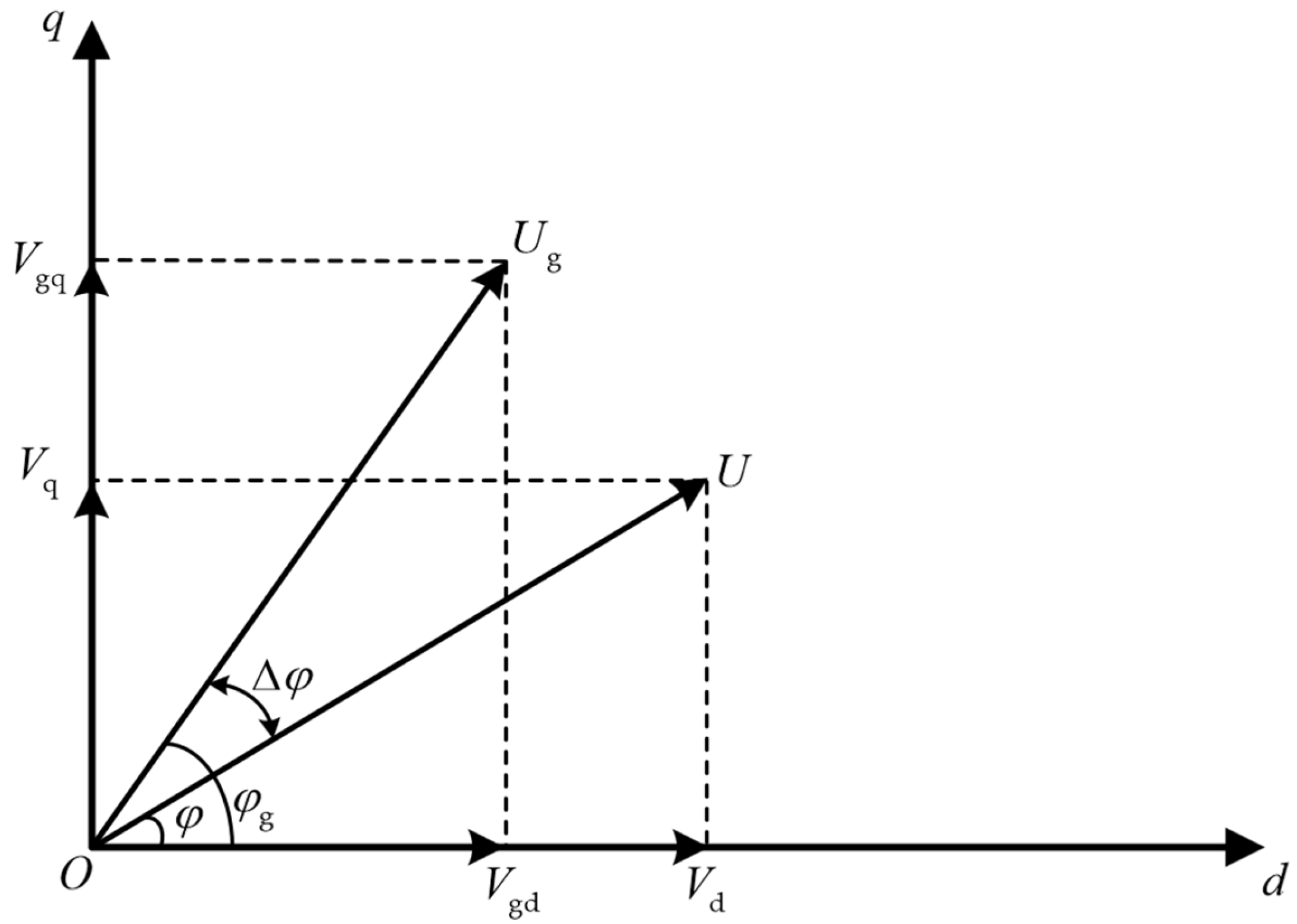
- A pre-synchronisation control strategy is proposed for a smooth transition from the off-grid to on-grid mode by tracking voltage signals on the two sides of the point of common coupling (PCC). Pre-synchronisation control is generally employed to match voltage amplitude, frequency, and phase of generators with those of the grid in order to avoid voltage fluctuations, current shocks, and other disturbances during connection. The pre-synchronisation strategy proposed here eliminates the need of a PLL module, avoiding accuracy issues associated with the traditional PLL-based synchronisation.
2. Electric–Hydrogen Coupling AC-DC Microgrid
2.1. Electric–Hydrogen Coupling AC-DC Microgrid Scheme
2.2. Electric–Hydrogen Coupling Microgrid Modelling
2.2.1. PV Generator Model
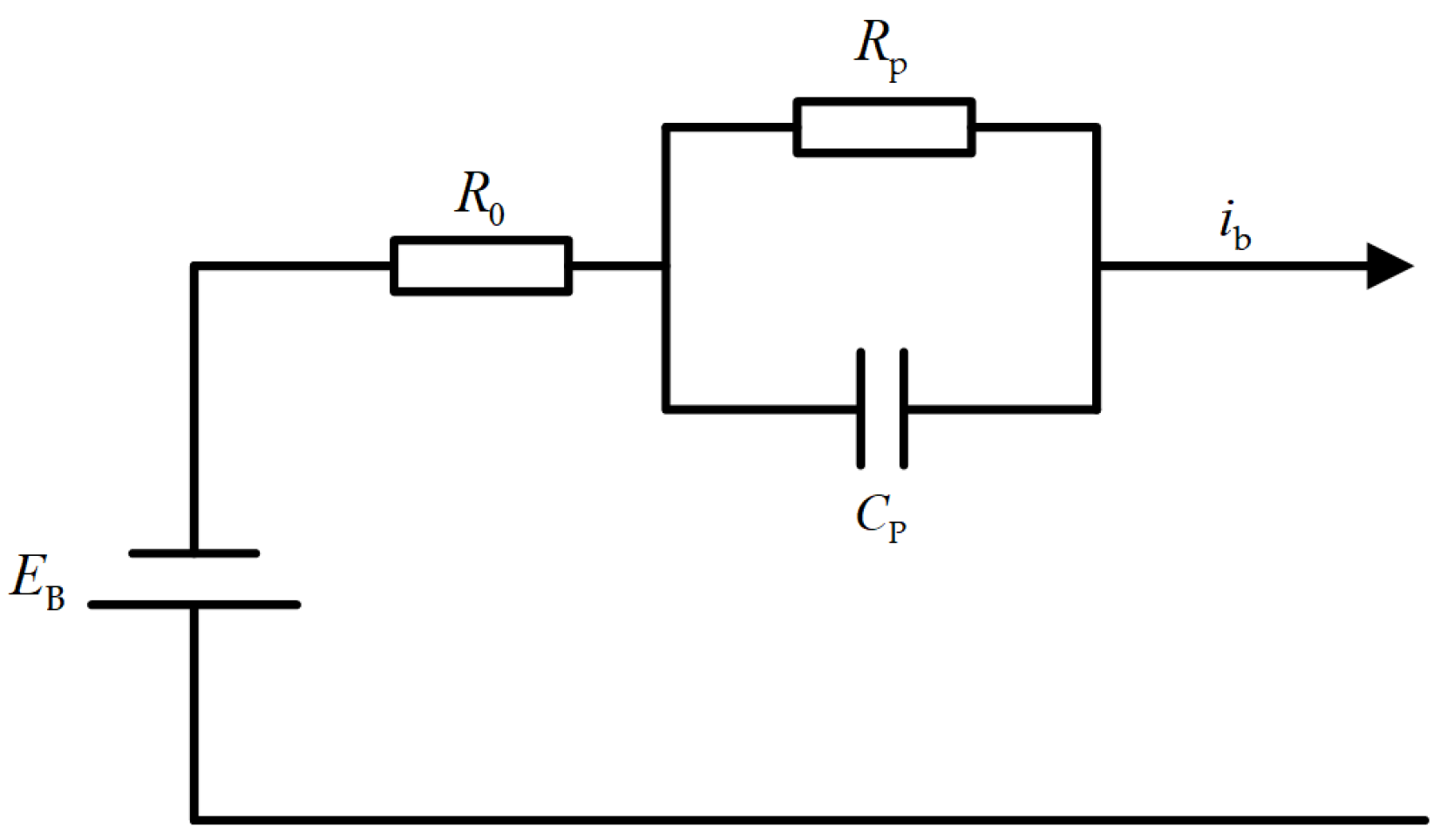
2.2.2. BESS Model
2.2.3. Hydrogen Energy System Model
- PEM FC model
- 2.
- PEM and ALK EL models
- 3.
- HST Model
3. Control of Electric–Hydrogen Coupling AC-DC Microgrid
3.1. DC Microgrid Converter Control
3.2. Power Management Strategy
3.3. DC/AC Converter Control
3.3.1. Master DC/AC Converter Control
- Active power–frequency control [34]
- 2.
- Reactive power–voltage control [34]
- 3.
- Virtual impedance control [35]
3.3.2. Slave DC/AC Converter Control
3.3.3. On-Grid/Off-Grid Switching Strategy
- Analysis of switching from off-grid to on-grid
- 2.
- Pre-synchronisation control for grid connection
- 3.
- Switching from on-grid to off-grid
4. Results and Discussions
4.1. Off-Grid Operation
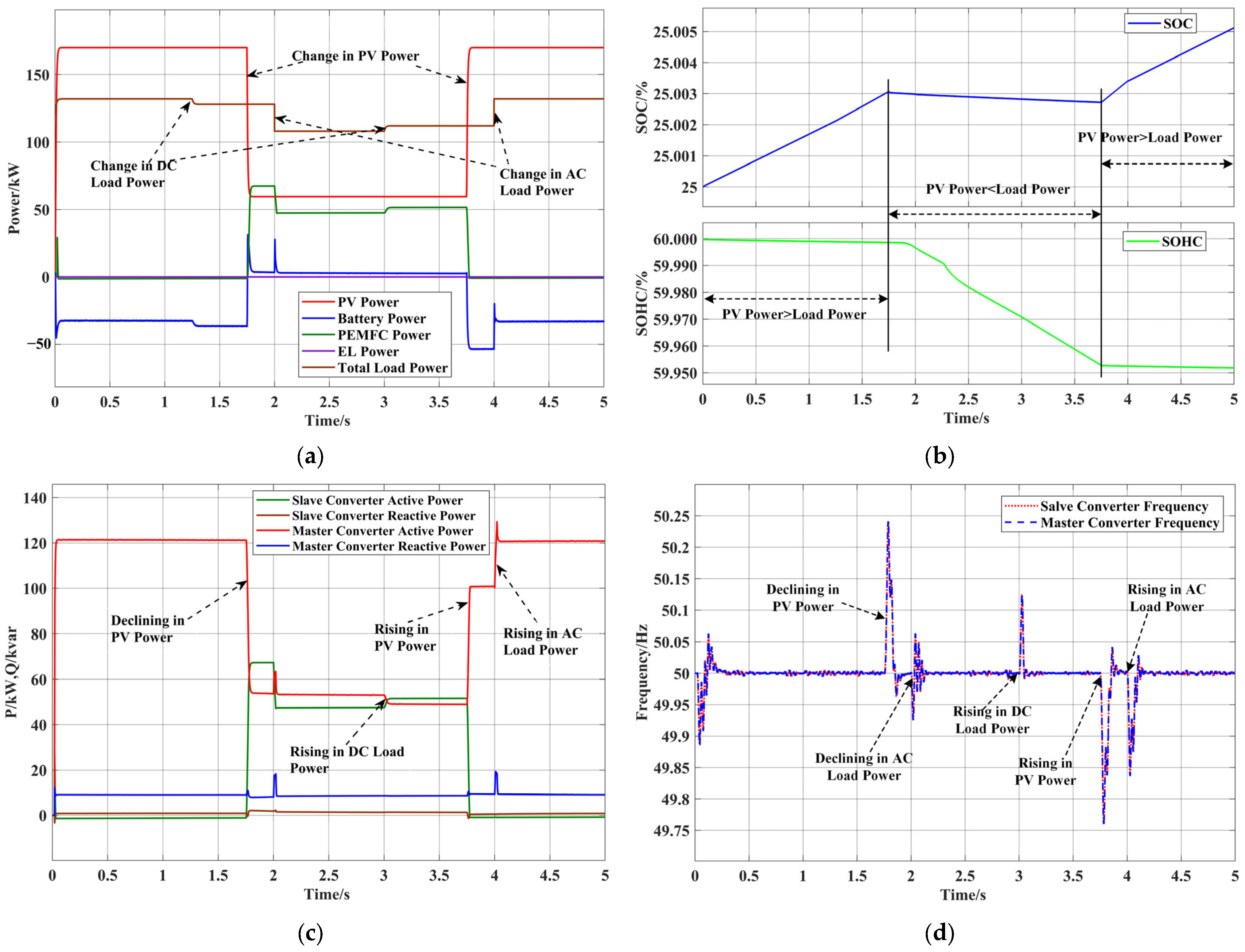
4.1.1. Scenario I
4.1.2. Scenario II
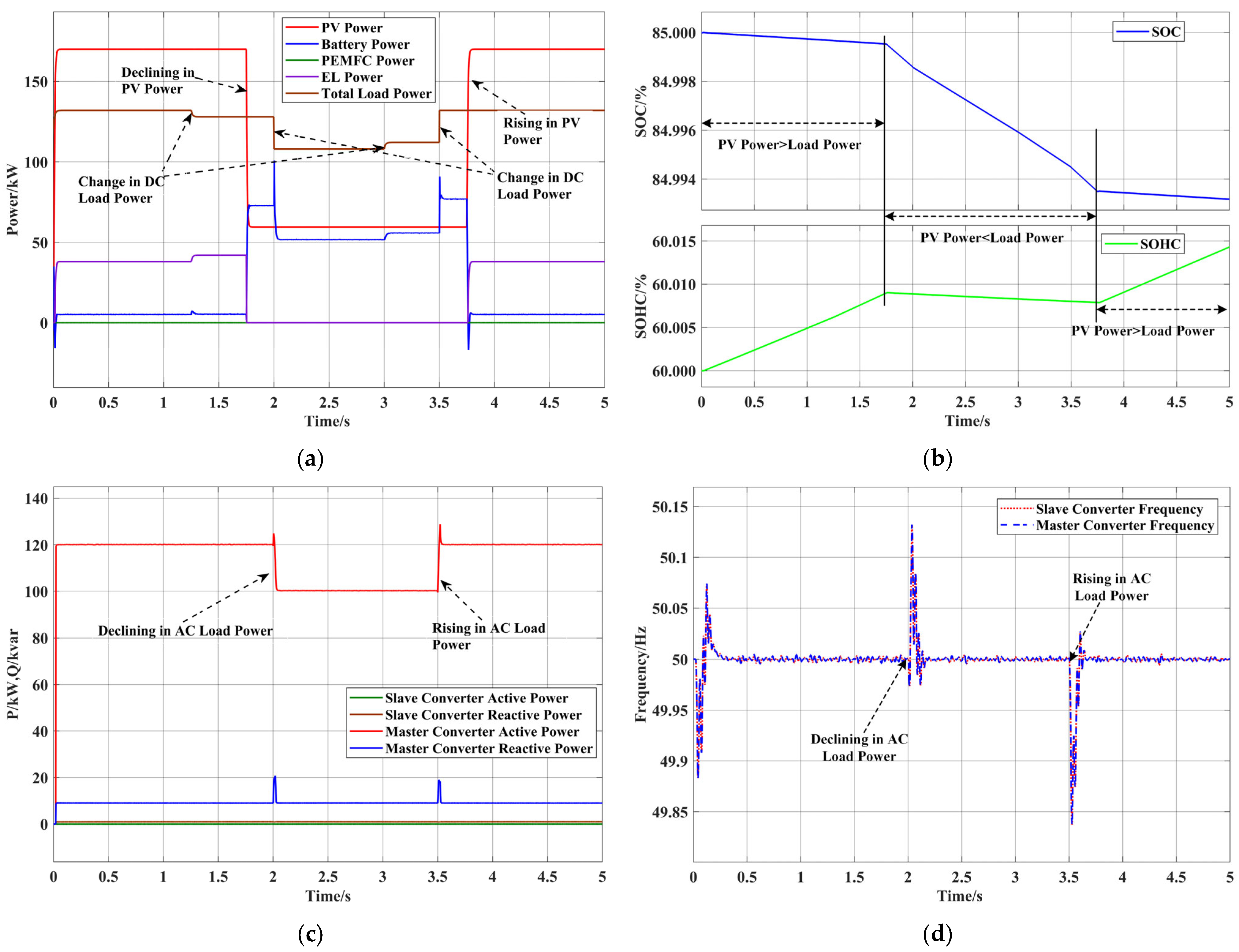
4.2. On-Grid Operation
4.2.1. Scenario III
4.2.2. Scenario IV
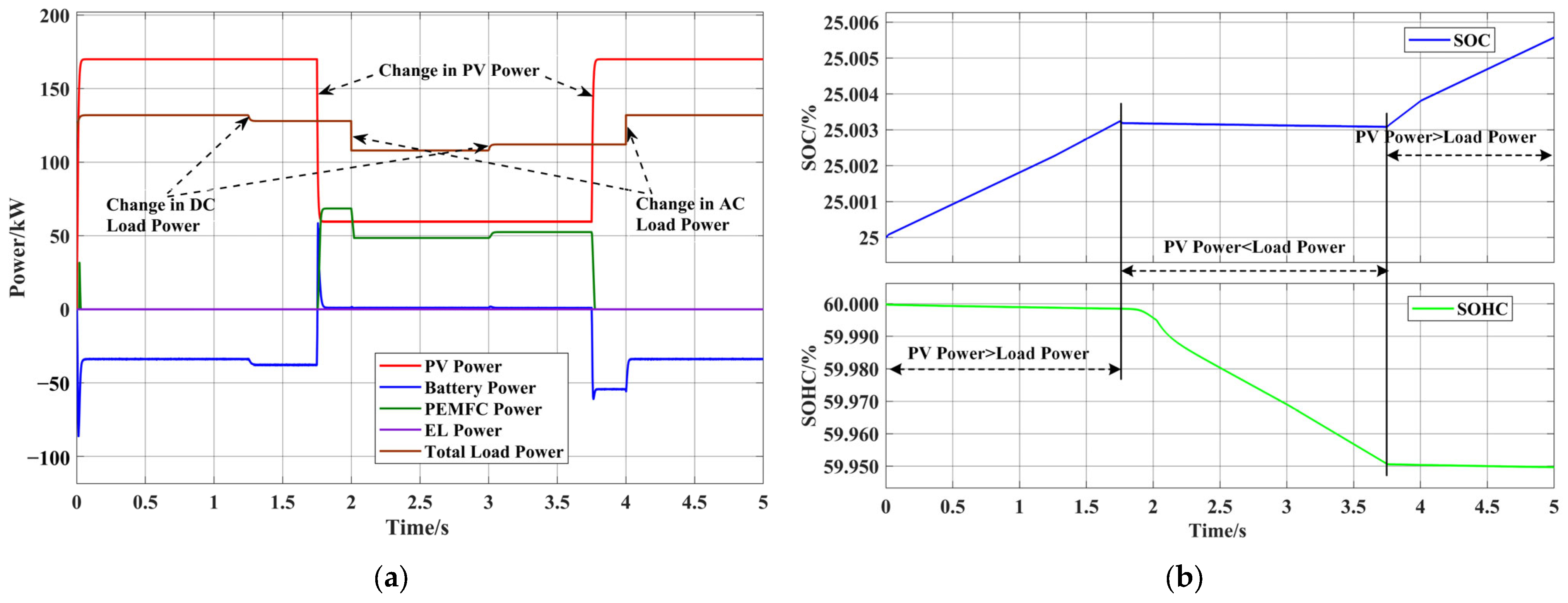
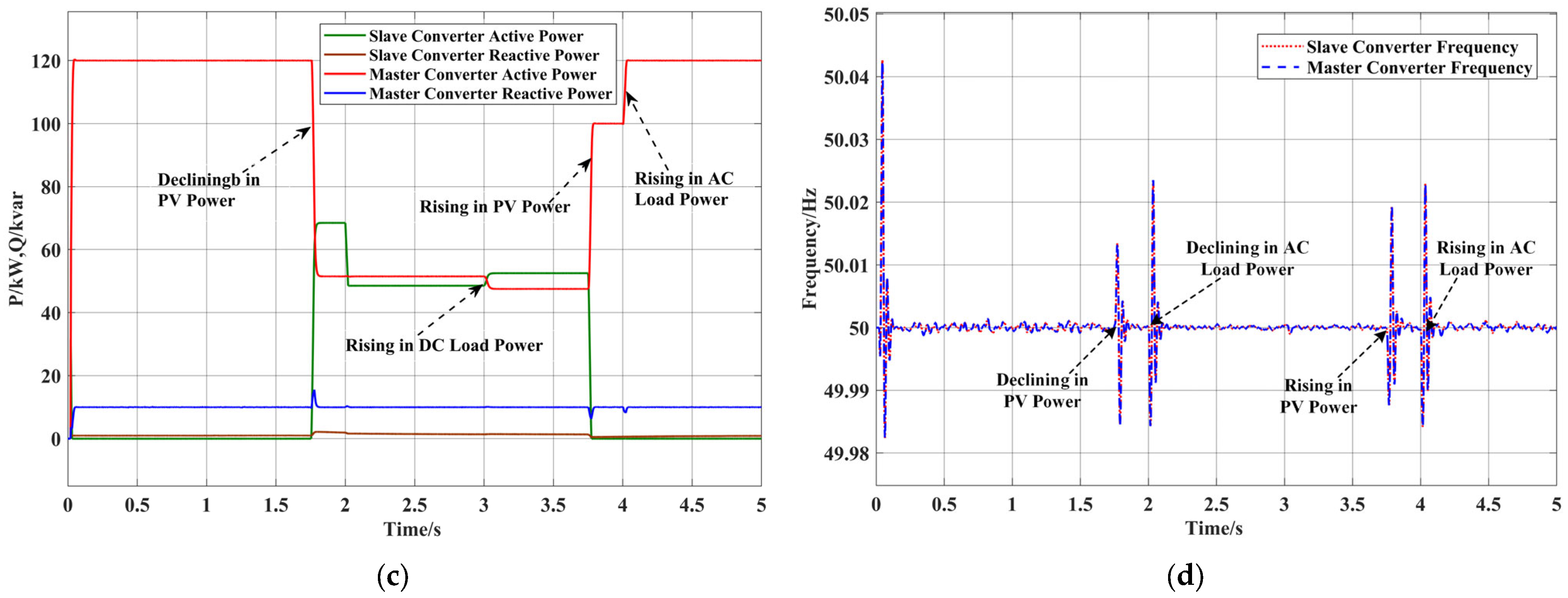
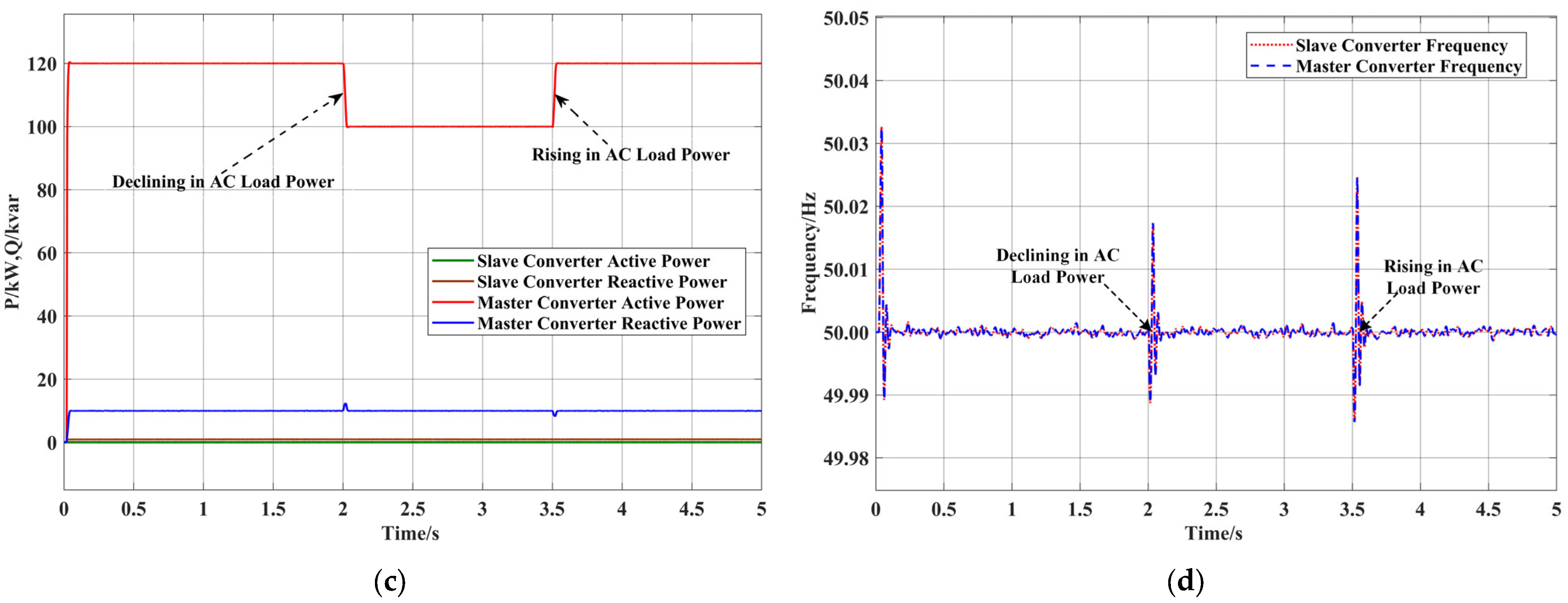
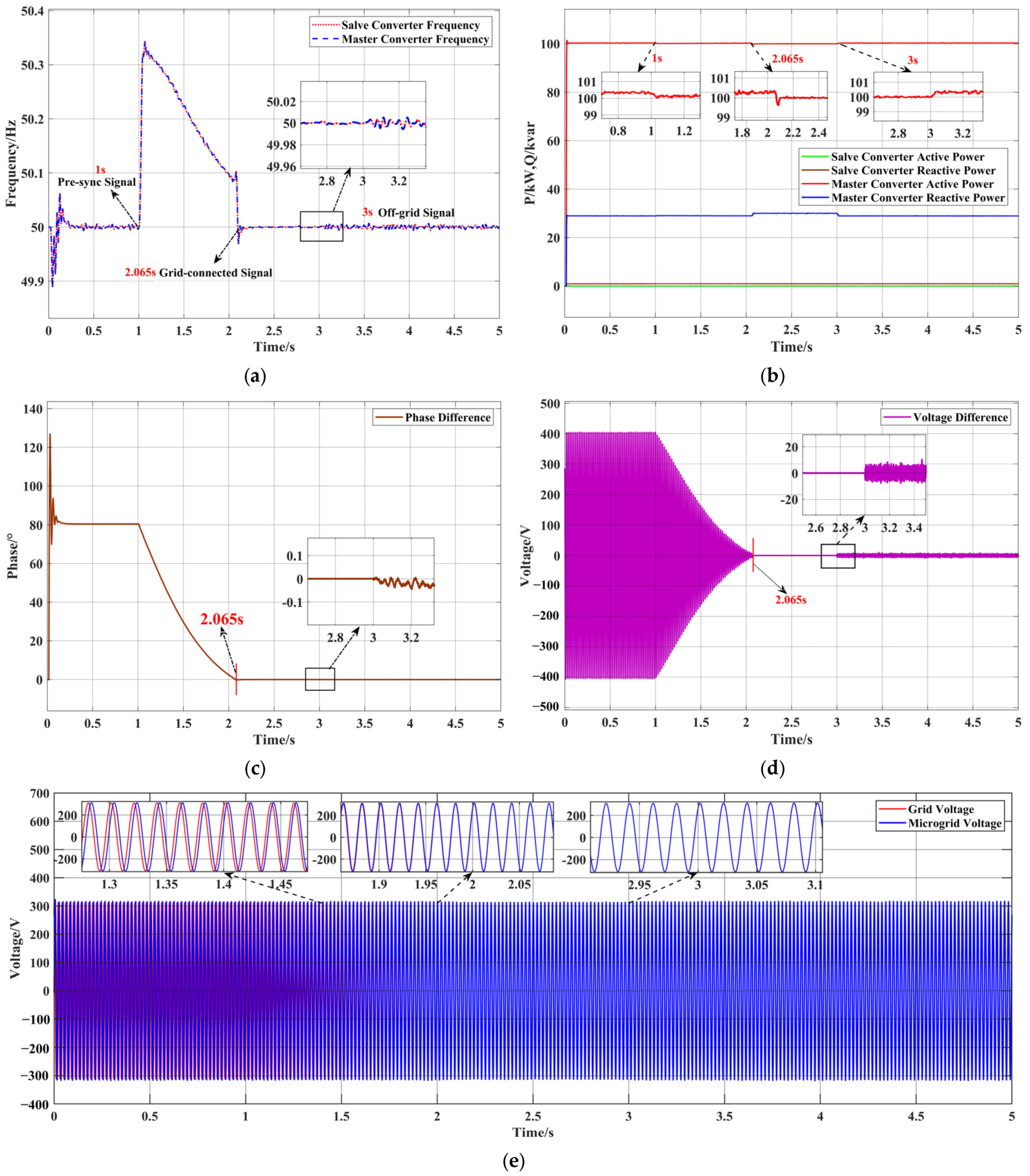
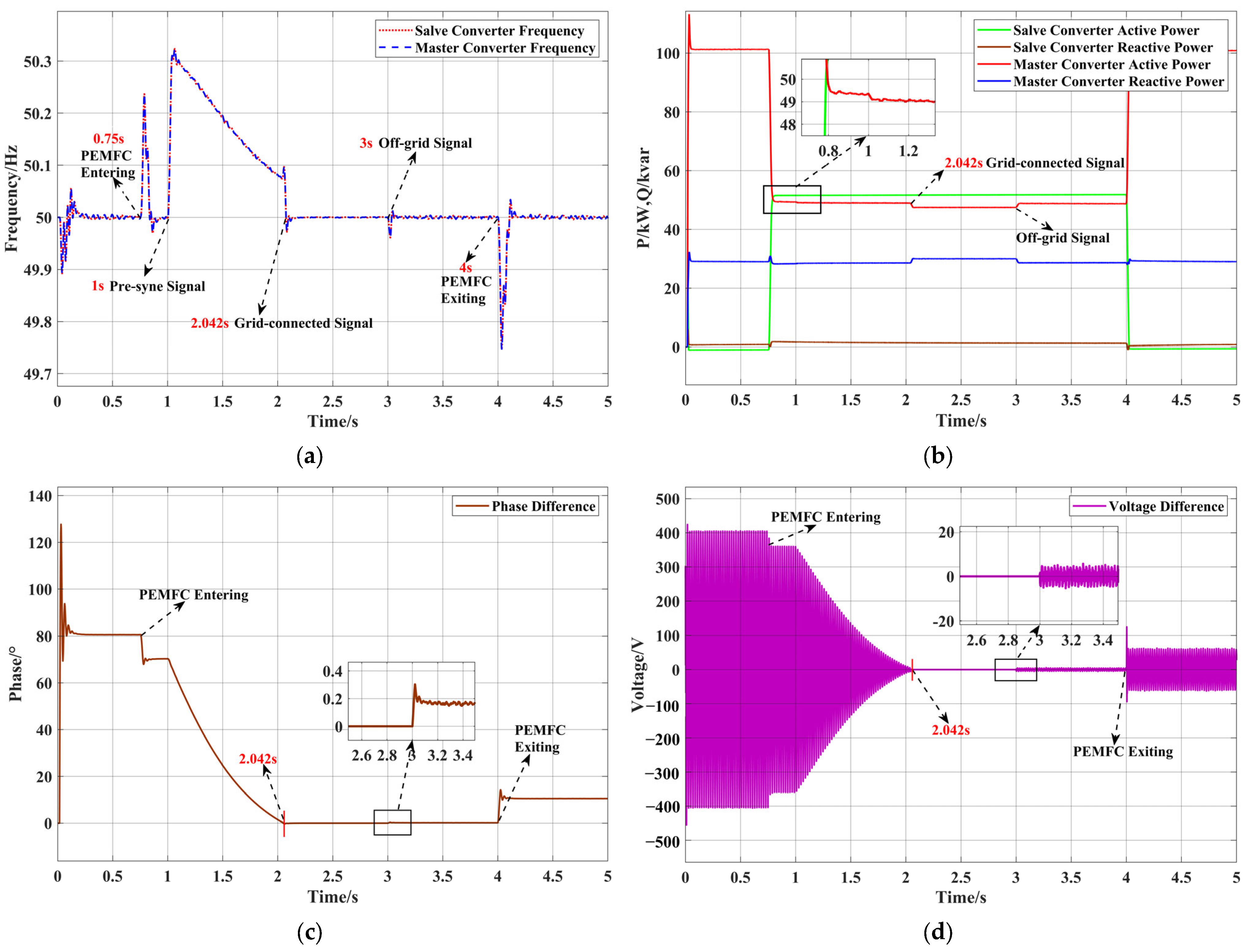
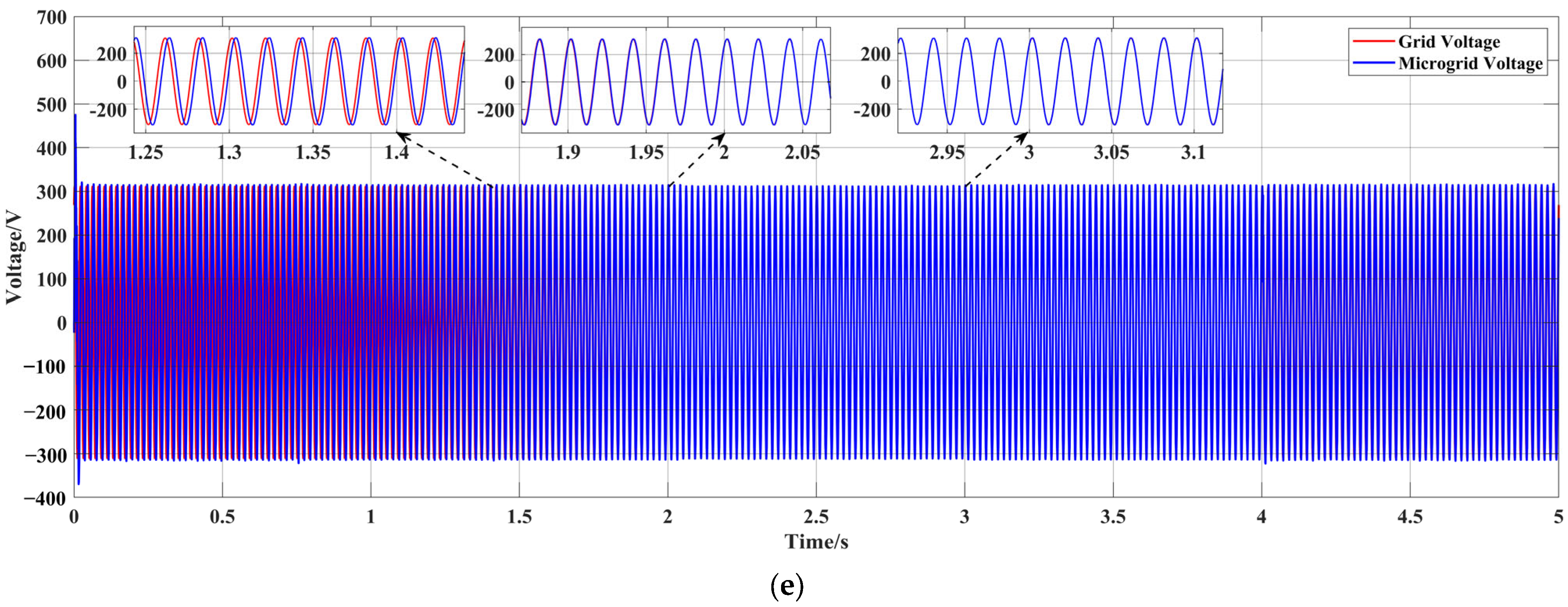
4.3. Off-Grid/On-Grid Switching
4.3.1. Scenario V
4.3.2. Scenario VI
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Østergaard, P.A.; Duic, N.; Kalogirou, S. Sustainable development using integrated energy systems and solar, biomass, wind, and wave technology. Renew. Energy 2024, 235, 121359. [Google Scholar] [CrossRef]
- Peng, B.; Li, Y.; Liu, H.; Kang, P.; Bai, Y.; Zhao, J.; Nian, H. Design of Energy Management Strategy for Integrated Energy System Including Multi-Component Electric–Thermal–Hydrogen Energy Storage. Energies 2024, 17, 6184. [Google Scholar] [CrossRef]
- Elalfy, D.A.; Gouda, E.; Kotb, M.F.; Bureš, V.; Sedhom, B.E. Comprehensive review of energy storage systems technologies, objectives, challenges, and future trends. Energy Strategy Rev. 2024, 54, 101482. [Google Scholar] [CrossRef]
- Ranjan, A.; Bodkhe, S.; Goyal, G.; Belge, A.; Tibude, S. Experimental Study on Heuristics Energy Management Strategy for Hybrid Energy Storage System. Energies 2024, 17, 5850. [Google Scholar] [CrossRef]
- Naseri, F.; Karimi, S.; Farjah, E.; Schaltz, E. Supercapacitor management system: A comprehensive review of modeling, estimation, balancing, and protection techniques. Renew. Sustain. Energy Rev. 2022, 155, 111913. [Google Scholar] [CrossRef]
- Tian, T.; Ma, Z.; Pan, T.; Wu, C.; Shu, J.; Feng, R.; Ding, J. Storage dimensioning and energy management for a grid-connected wind/PV/hydrogen/battery system using MISOCP approach. Int. J. Hydrog. Energy 2025, 100, 779–791. [Google Scholar] [CrossRef]
- Hajiaghasi, S.; Salemnia, A.; Hamzeh, M. Hybrid energy storage system for microgrids applications: A review. J. Energy Storage 2019, 21, 543–570. [Google Scholar] [CrossRef]
- Bade, S.O.; Tomomewo, O.S. Optimizing a hybrid wind-solar-biomass system with battery and hydrogen storage using generic algorithm-particle swarm optimization for performance assessment. Clean. Energy Syst. 2024, 9, 100157. [Google Scholar] [CrossRef]
- Rezk, H.; Fathy, A. Hydrogen reduction-based energy management strategy of hybrid fuel cell/PV/battery/supercapacitor renewable energy system. J. Energy Storage 2024, 86, 111316. [Google Scholar] [CrossRef]
- Van, L.P.; Chi, K.D.; Duc, T.N. Review of hydrogen technologies based microgrid: Energy management systems, challenges and future recommendations. Int. J. Hydrog. Energ. 2023, 48, 14127–14148. [Google Scholar] [CrossRef]
- Tang, Y.; Xun, Q.; Liserre, M.; Yang, H. Energy management of electric-hydrogen hybrid energy storage systems in photovoltaic microgrids. Int. J. Hydrog. Energ. 2024, 80, 1–10. [Google Scholar] [CrossRef]
- Pu, Y.; Li, Q.; Chen, W.; Liu, H. Hierarchical energy management control for islanding DC microgrid with electric-hydrogen hybrid storage system. Int. J. Hydrog. Energ. 2019, 44, 5153–5161. [Google Scholar] [CrossRef]
- Zehra, S.S.; Ur Rahman, A.; Ahmad, I. Fuzzy-barrier sliding mode control of electric-hydrogen hybrid energy storage system in DC microgrid: Modelling, management and experimental investigation. Energy 2022, 239, 122260. [Google Scholar] [CrossRef]
- Abdelhalim, T.; Kouider, L.; Rezk, H.; Abdelkader, R.; Mohamed Amine, H. Optimal energy management based equivalent hydrogen consumption minimization strategy of DC microgrid. Int. J. Hydrog. Energ. 2024, 83, 355–366. [Google Scholar] [CrossRef]
- Basantes, J.A.; Paredes, D.E.; Llanos, J.R.; Ortiz, D.E.; Burgos, C.D. Energy Management System (EMS) Based on Model Predictive Control (MPC) for an Isolated DC Microgrid. Energies 2023, 16, 2912. [Google Scholar] [CrossRef]
- Li, J.; Zhao, J.; Chen, Y.; Mao, L.; Qu, K.; Li, F. Optimal sizing for a wind-photovoltaic-hydrogen hybrid system considering levelized cost of storage and source-load interaction. Int. J. Hydrog. Energ. 2023, 48, 4129–4142. [Google Scholar] [CrossRef]
- Singh, S.; Chauhan, P.; Singh, N. Capacity optimization of grid connected solar/fuel cell energy system using hybrid ABC-PSO algorithm. Int. J. Hydrog. Energ. 2020, 45, 10070–10088. [Google Scholar] [CrossRef]
- Manandhar, U.; Ukil, A.; Gooi, H.B.; Tummuru, N.R.; Kollimalla, S.K.; Wang, B.; Chaudhari, K. Energy Management and Control for Grid Connected Hybrid Energy Storage System Under Different Operating Modes. IEEE Trans. Smart Grid 2019, 10, 1626–1636. [Google Scholar] [CrossRef]
- Peng, W.; Chen, Q.; Manandhar, U.; Wang, B.; Rodriguez, J. Event-Triggered Model Predictive Control for the Inverter of a Grid-Connected Microgrid With a Battery-Supercapacitor HESS. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 5540–5552. [Google Scholar] [CrossRef]
- Ghias, R.; Hasan, A.; Ahmad, I. Artificial neural network based conditional controllers with saturated action for multi-renewable hybrid alternating or direct current microgrids in islanded and grid-connected modes. J. Energy Storage 2024, 94, 112139. [Google Scholar] [CrossRef]
- Kim, T.-G.; Lee, H.; An, C.-G.; Yi, J.; Won, C.-Y.J.E. Hybrid AC/DC Microgrid Energy Management Strategy Based on Two-Step ANN. Energies 2023, 16, 1787. [Google Scholar] [CrossRef]
- Pang, C.; Wu, H.; Jia, B. A multi-mode coordinated operation control strategy for optical storage DC microgrid. Energy Rep. 2023, 9, 230–235. [Google Scholar] [CrossRef]
- Mirshekali, H.; Dashti, R.; Ghaffari, V.; Shaker, H.R.; Mardani, M.M.; Mijatovic, N.; Dragičević, T. A novel RMPC strategy for three-phase inverters operating in grid-connected and standalone modes. Electr. Power Syst. Res. 2024, 234, 110763. [Google Scholar] [CrossRef]
- Mansour, A.M.; Arafa, O.M.; Marei, M.I.; Abdelsalam, I.; Aziz, G.A.A.; Sattar, A.A. Hardware-in-the-Loop Testing of Seamless Interactions of Multi-Purpose Grid-Tied PV Inverter Based on SFT-PLL Control Strategy. IEEE Access 2021, 9, 123465–123483. [Google Scholar] [CrossRef]
- Rahim, N.A.; Ping, H.W.; Selvaraj, J. Photovoltaic Module Modeling using Simulink/Matlab. Procedia Environ. Sci. 2013, 17, 537–546. [Google Scholar]
- Wang, C.; Jiao, S.; Zhang, Y.; Wang, X.; Li, Y. Adaptive Variable Universe Fuzzy Droop Control Based on a Novel Multi-Strategy Harris Hawk Optimization Algorithm for a Direct Current Microgrid with Hybrid Energy Storage. Energies 2024, 17, 5296. [Google Scholar] [CrossRef]
- Mokrani, Z.; Rekioua, D.; Mebarki, N.; Rekioua, T.; Bacha, S. Proposed energy management strategy in electric vehicle for recovering power excess produced by fuel cells. Int. J. Hydrog. Energ. 2017, 42, 19556–19575. [Google Scholar] [CrossRef]
- Alam, M.; Kumar, K.; Verma, S.; Dutta, V. Renewable sources based DC microgrid using hydrogen energy storage: Modelling and experimental analysis. Sustain. Energy Technol. Assess. 2020, 42, 100840. [Google Scholar] [CrossRef]
- Gambou, F.; Guilbert, D.; Zasadzinski, M.; Rafaralahy, H. A Comprehensive Survey of Alkaline Electrolyzer Modeling: Electrical Domain and Specific Electrolyte Conductivity. Energies 2022, 15, 3452. [Google Scholar] [CrossRef]
- Görgün, H. Dynamic modelling of a proton exchange membrane (PEM) electrolyzer. Int. J. Hydrog. Energ. 2006, 31, 29–38. [Google Scholar] [CrossRef]
- Dash, V.; Bajpai, P. Power management control strategy for a stand-alone solar photovoltaic-fuel cell–battery hybrid system. Sustain. Energy Technol. Assess. 2015, 9, 68–80. [Google Scholar] [CrossRef]
- Manna, S.; Singh, D.K.; Akella, A.K.; Kotb, H.; AboRas, K.M.; Zawbaa, H.M.; Kamel, S. Design and implementation of a new adaptive MPPT controller for solar PV systems. Energy Rep. 2023, 9, 1818–1829. [Google Scholar] [CrossRef]
- Manandhar, U.; Tummuru, N.R.; Kollimalla, S.K.; Ukil, A.; Beng, G.H.; Chaudhari, K. Validation of Faster Joint Control Strategy for Battery- and Supercapacitor-Based Energy Storage System. IEEE Trans. Ind. Electron. 2018, 65, 3286–3295. [Google Scholar] [CrossRef]
- Chen, S.; Sun, Y.; Han, H.; Fu, S.; Luo, S.; Shi, G. A Modified VSG Control Scheme With Virtual Resistance to Enhance Both Small-Signal Stability and Transient Synchronization Stability. IEEE Trans. Power Electron. 2023, 38, 6005–6014. [Google Scholar] [CrossRef]
- He, P.; Li, Z.; Jin, H.; Zhao, C.; Fan, J.; Wu, X. An adaptive VSG control strategy of battery energy storage system for power system frequency stability enhancement. Int. J. Electr. Power Energy Syst. 2023, 149, 109039. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| DC bus voltage | 750 V |
| AC rated voltage | 380 V |
| Rated frequency | 50 Hz |
| Filter inductors | 2 mH |
| Filter capacitors | 0.01 mF |
| Line resistor | 5 mΩ |
| Line inductor | 0.036 mH |
| Equipment | Parameter | Value |
|---|---|---|
| PV generator | Maximum power | 170 kW |
| Voltage at MPP | 495.84 V | |
| Current at MPP | 342.94 A | |
| Fuel cells | Rated power | 4 × 50 kW |
| Rated voltage | 625 V | |
| Electrolysers | Rated power (ALK) | 39 kW |
| Rated power (PEM) | 10 kW | |
| Hydrogen storage tank | Maximum pressure | 70 MPa |
| Volume | 50 L | |
| Battery | Capacity | 400 Ah |
| Nominal voltage | 500 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Fan, F.; Zhang, H.; Song, K.; Jiang, J.; Sun, C.; Xue, R.; Zhang, J.; Chen, Z. Flexible On-Grid and Off-Grid Control for Electric–Hydrogen Coupling Microgrids. Energies 2025, 18, 985. https://doi.org/10.3390/en18040985
Wang Z, Fan F, Zhang H, Song K, Jiang J, Sun C, Xue R, Zhang J, Chen Z. Flexible On-Grid and Off-Grid Control for Electric–Hydrogen Coupling Microgrids. Energies. 2025; 18(4):985. https://doi.org/10.3390/en18040985
Chicago/Turabian StyleWang, Zhengyao, Fulin Fan, Hang Zhang, Kai Song, Jinhai Jiang, Chuanyu Sun, Rui Xue, Jingran Zhang, and Zhengjian Chen. 2025. "Flexible On-Grid and Off-Grid Control for Electric–Hydrogen Coupling Microgrids" Energies 18, no. 4: 985. https://doi.org/10.3390/en18040985
APA StyleWang, Z., Fan, F., Zhang, H., Song, K., Jiang, J., Sun, C., Xue, R., Zhang, J., & Chen, Z. (2025). Flexible On-Grid and Off-Grid Control for Electric–Hydrogen Coupling Microgrids. Energies, 18(4), 985. https://doi.org/10.3390/en18040985









