Insulation Aging Evaluation Method of High Voltage Cable Based on Dielectric Loss Characteristics
Abstract
:1. Introduction
2. Sample Preparation
2.1. Cable Sample Preparation
2.2. Cable Slice Sample Preparation
3. Experiment Platform
3.1. High-Voltage Dielectric Property Test
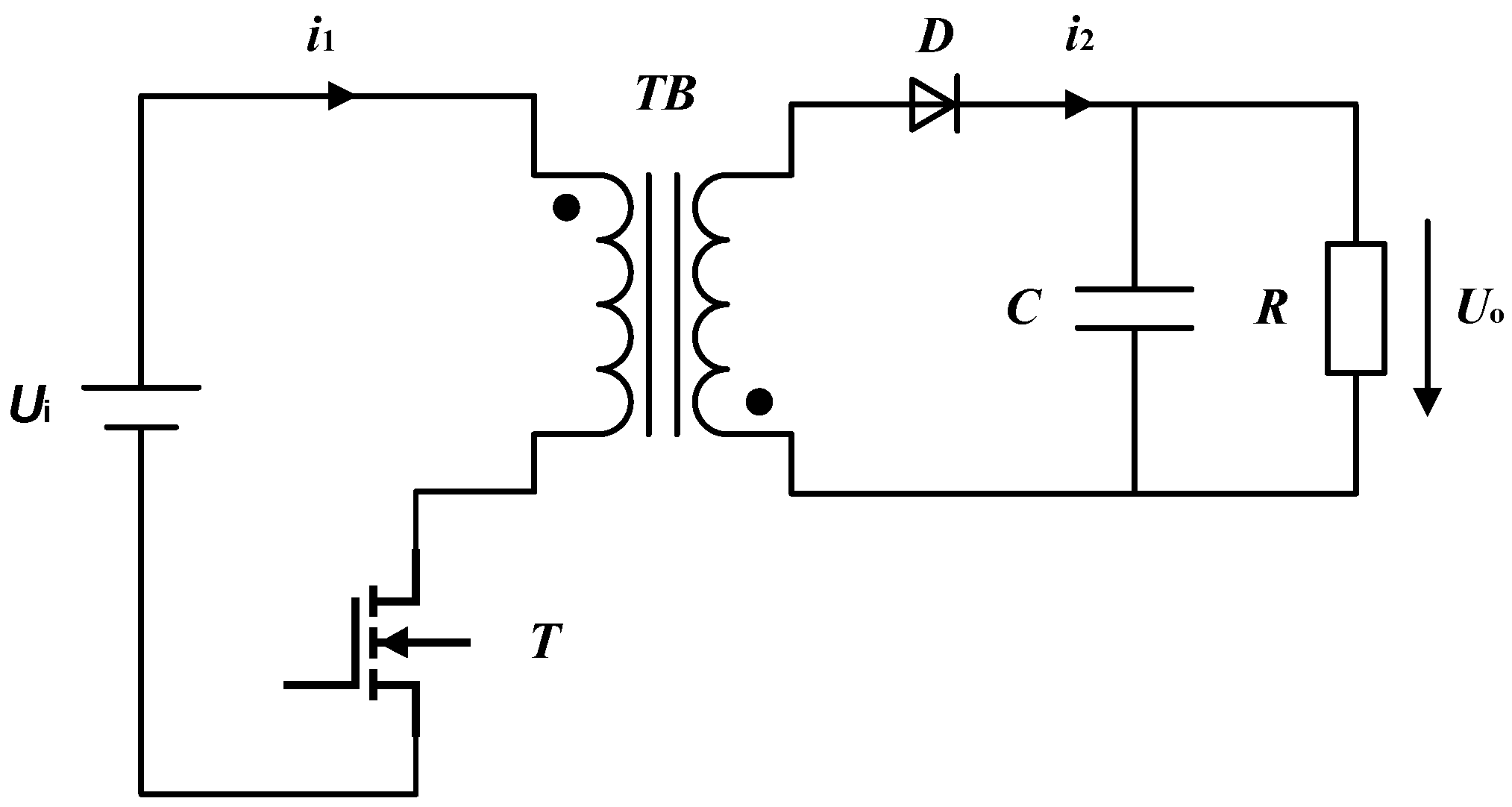
3.1.1. Power Supply Circuit
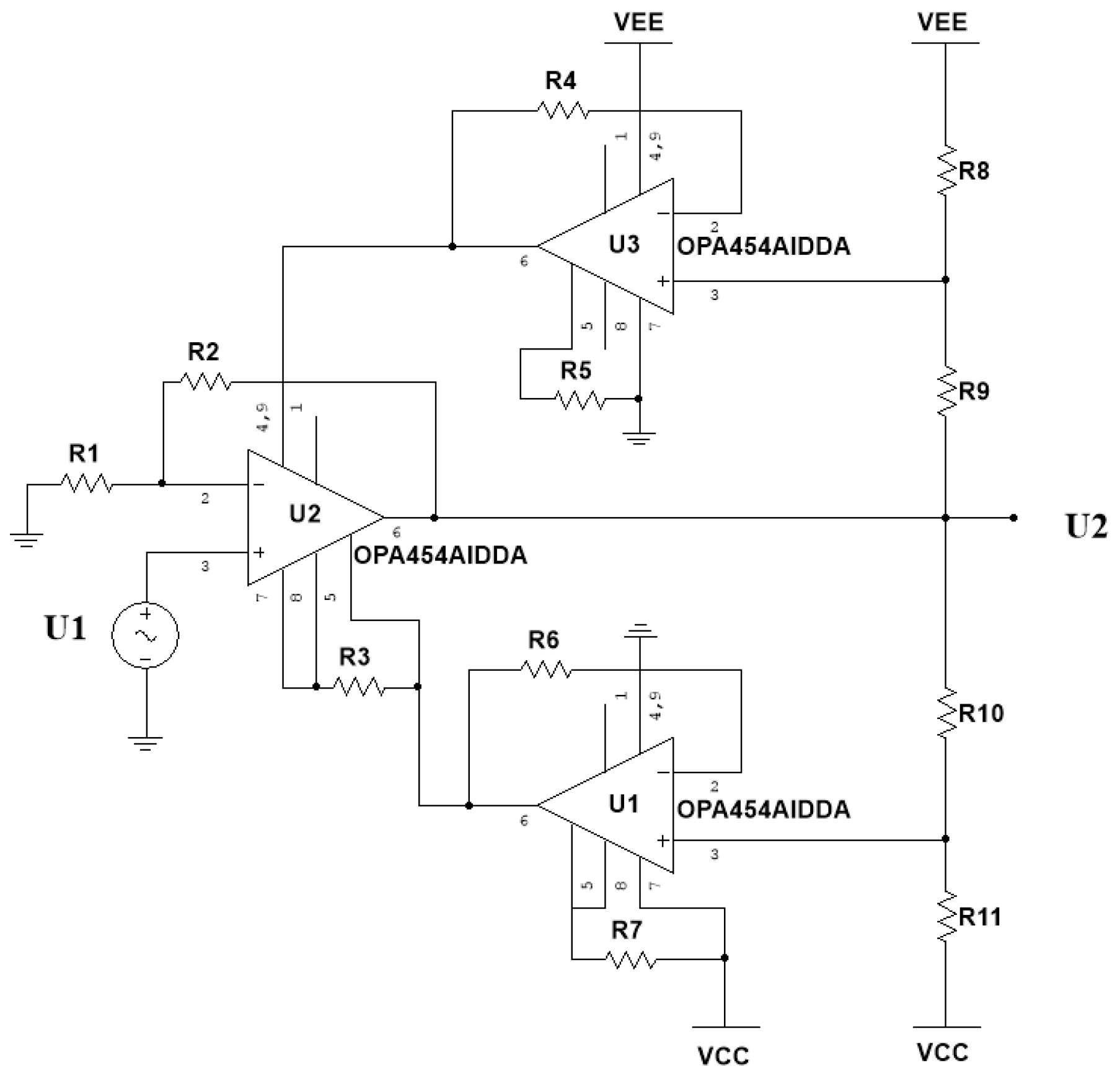
3.1.2. High-Voltage Linear Amplifier Circuit
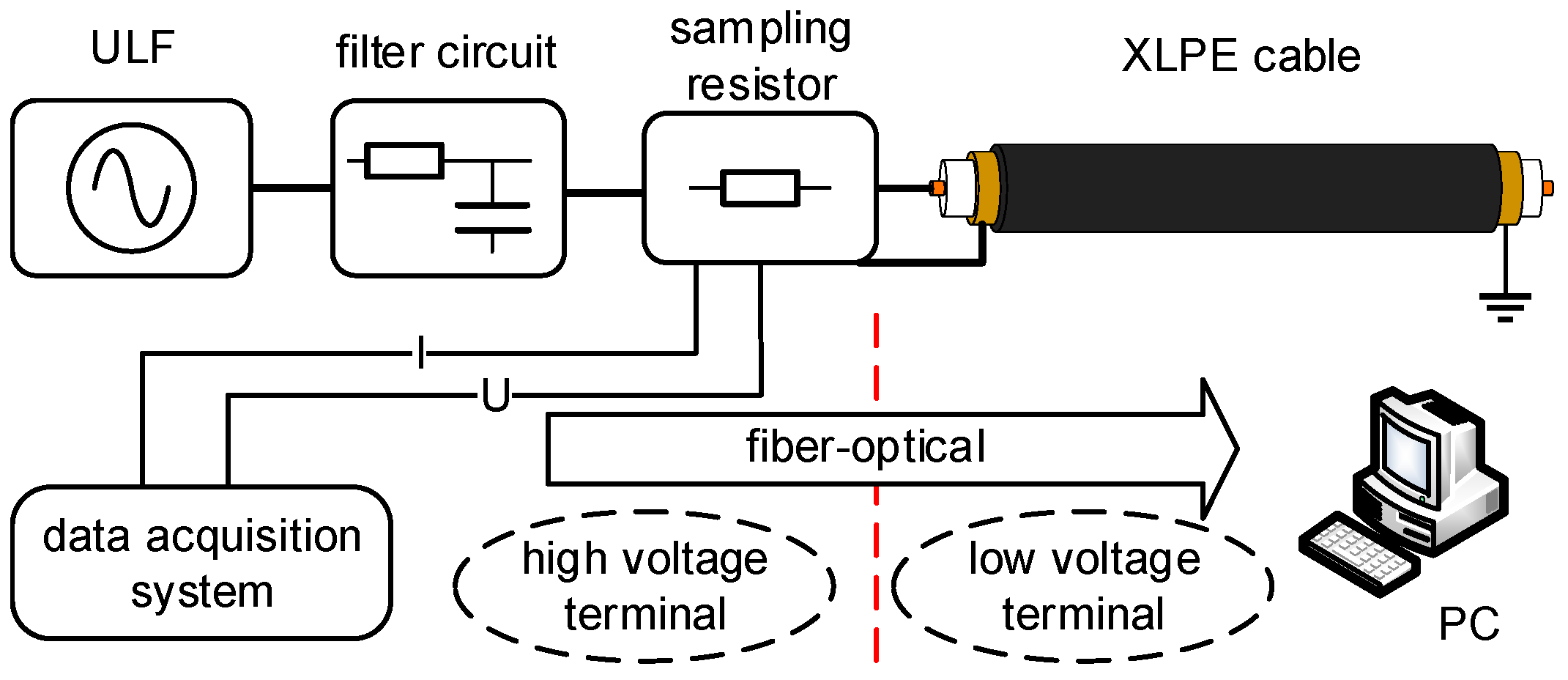
3.1.3. System Structure
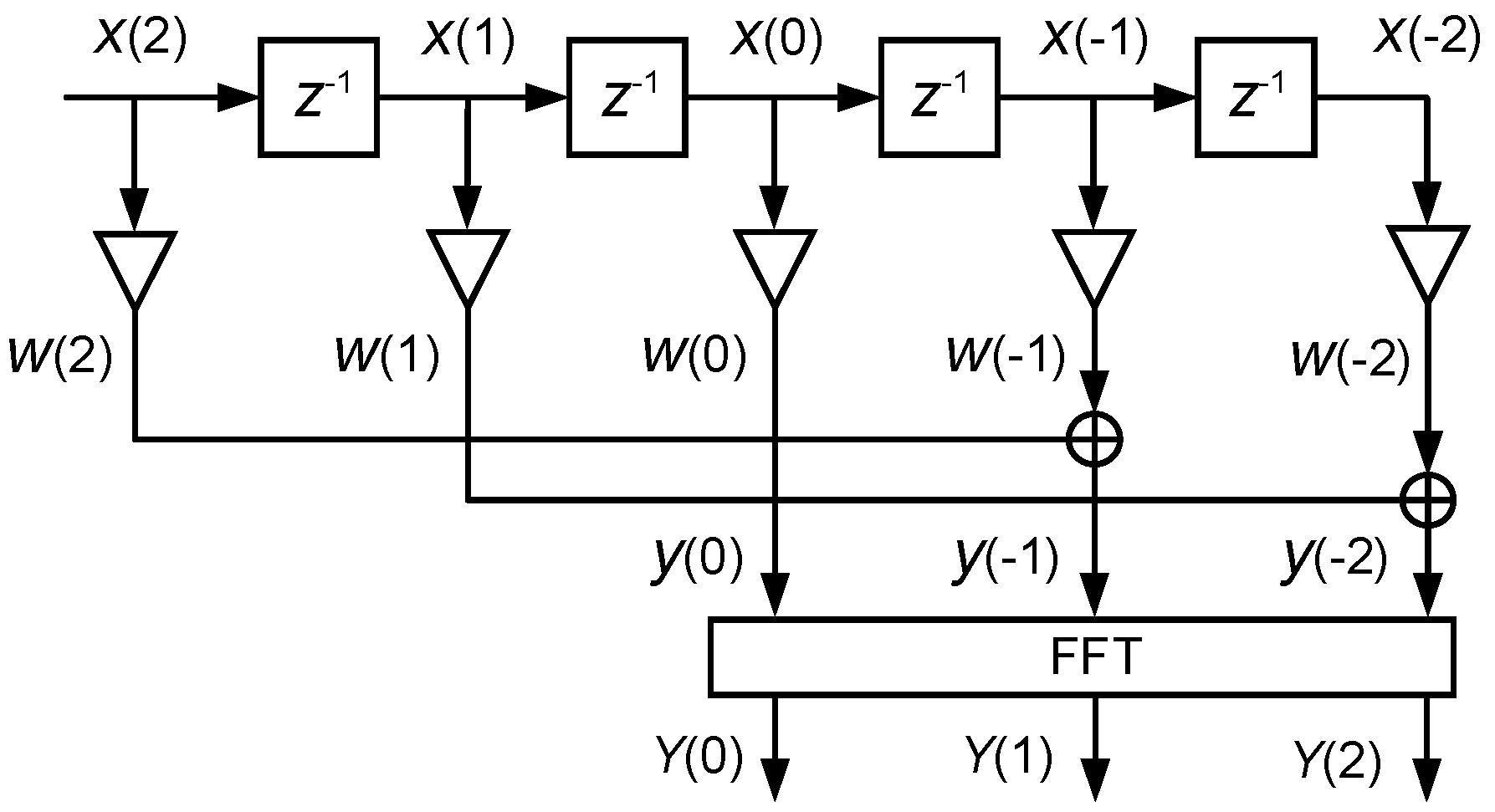
3.1.4. Dielectric Loss Calculation Method
3.2. Fourier Transform Infrared Spectroscopy Test
3.3. Differential Scanning Calorimetry Test
3.4. Mechanical Test
3.5. AC Breakdown Field Strength Test
4. Results and Discussions
4.1. Experimental Test Results
4.1.1. Dielectric Property Analysis
4.1.2. Fourier Transform Infrared Spectroscopy Analysis
4.1.3. Differential Scanning Calorimetry Analysis
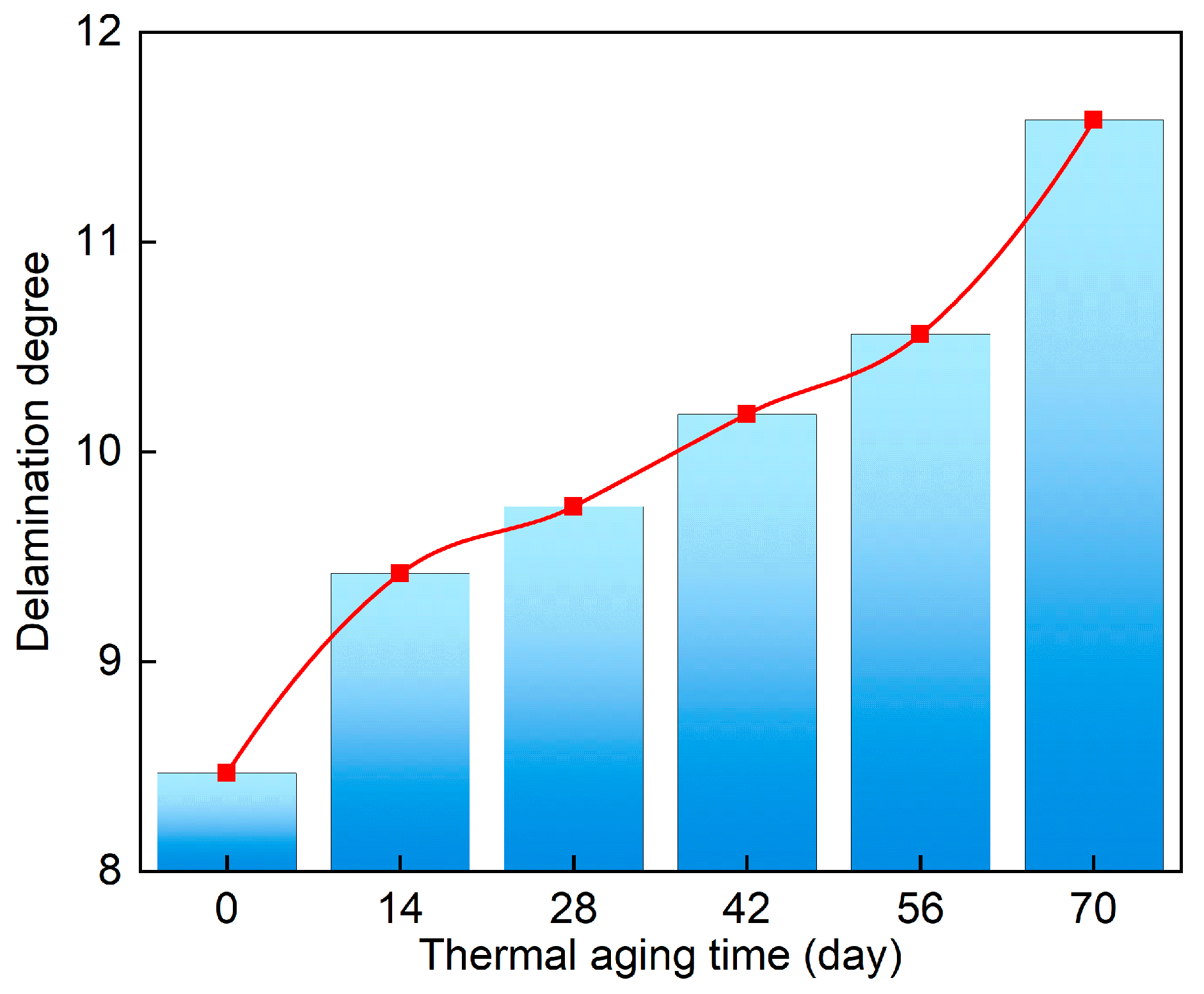
4.1.4. Mechanical Performance Analysis
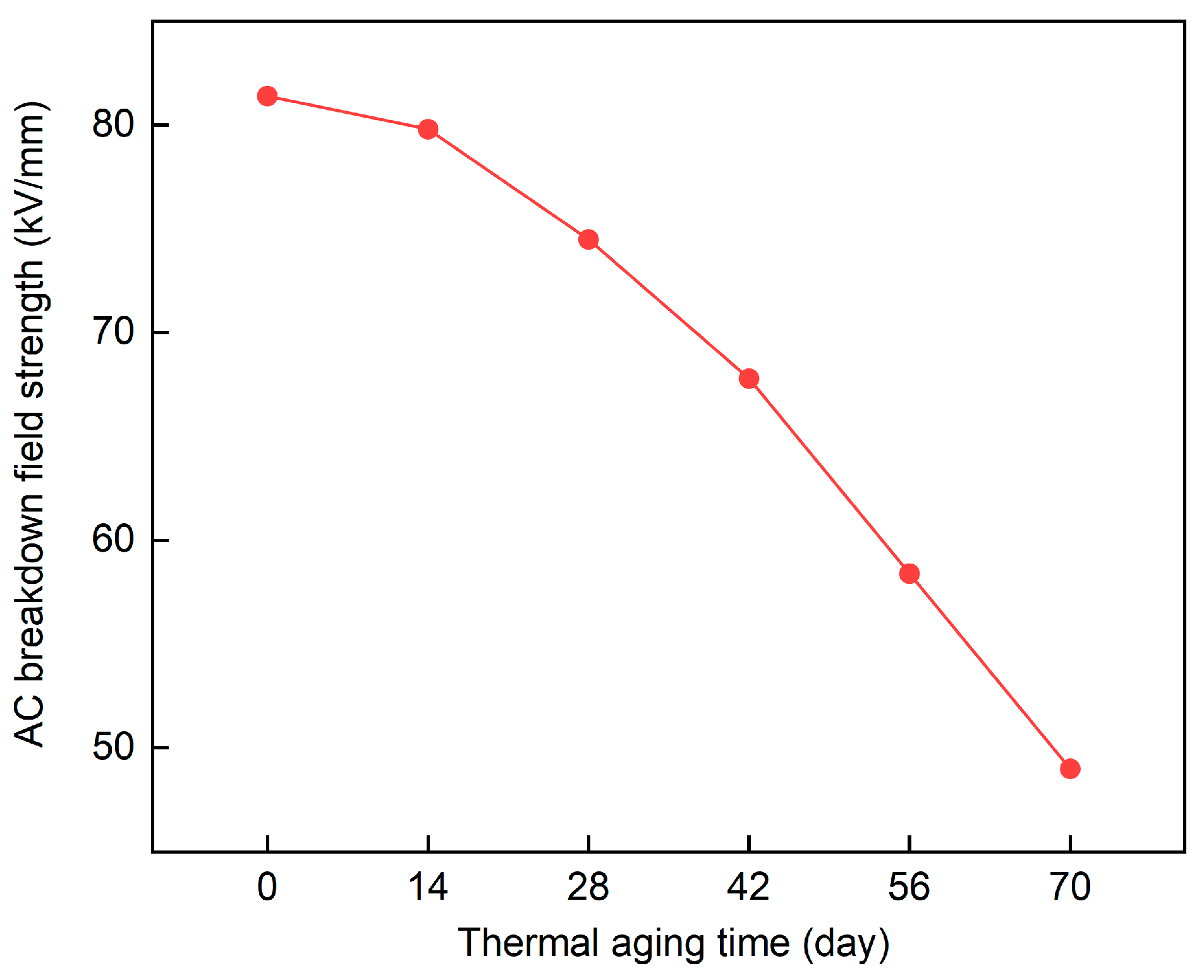
4.1.5. AC Breakdown Field Strength Analysis
4.2. Analysis of Dielectric Characteristic Parameters in Frequency Domain
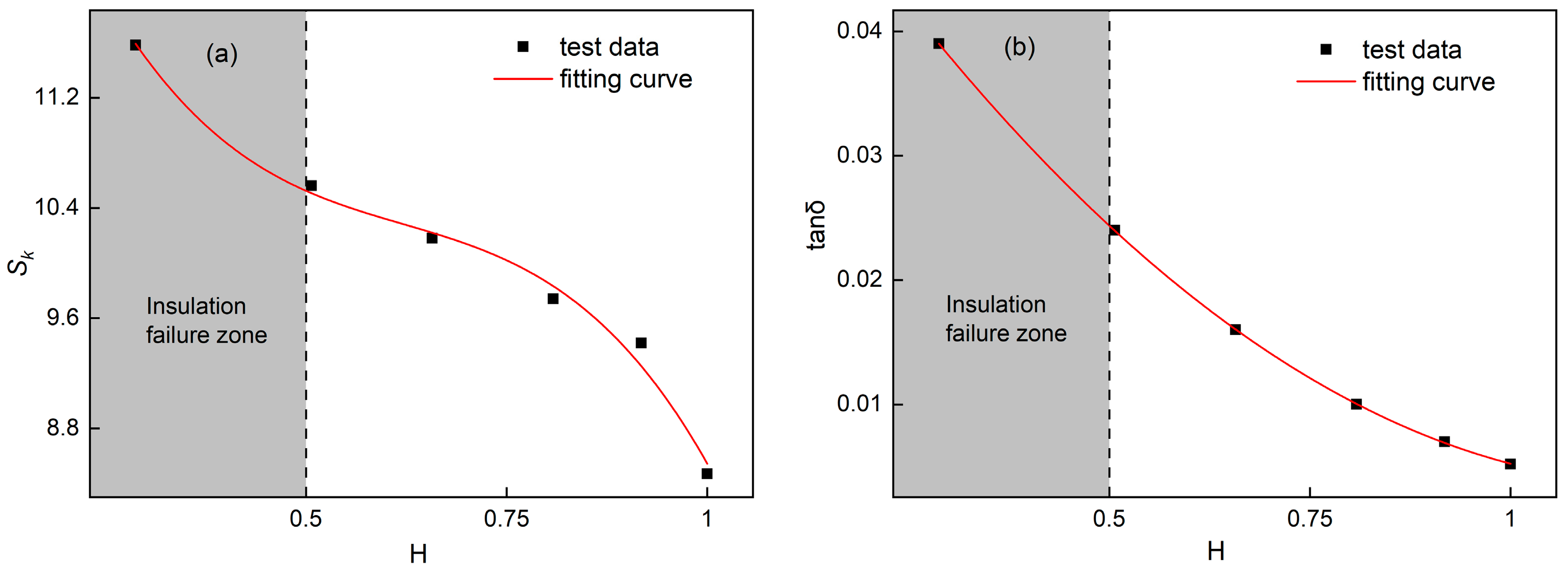
4.3. Determination of Aging Evaluation Criteria
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, K.; Yuan, H.; Li, Y.; Li, M.; Li, Z.; Lin, S. Assessing Aging Status and Type of XLPE Cable Insulation with a Graphic Approach Based on PDC Measurement. IEEE Trans. Power Deliv. 2022, 37, 5114–5123. [Google Scholar] [CrossRef]
- Sebbane, Y.; Boubakeur, A.; Mekhaledi, A. Influence of Thermal Aging and Water Adsorption on XLPE Cables Insulation Mechanical and Physico-chemical Properties. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 1694–1702. [Google Scholar] [CrossRef]
- Zhu, W.; Zhao, Y.; Han, Z.; Wang, X.; Wang, Y.; Liu, G.; Xie, Y.; Zhu, N. Thermal Effect of Different Laying Modes on Cross-Linked Polyethylene (XLPE) Insulation and a New Estimation on Cable Ampacity. Energies 2019, 12, 2994. [Google Scholar] [CrossRef]
- Li, C.; Tan, X.; Liu, L.; Zhang, W.; Yang, Q.; Cao, J.; Zhou, E.; Li, M.; Song, Z. Investigation of Near-Infrared Spectroscopy for Assessing the Macroscopic Mechanical Properties of Cross-Linked Polyethylene During Thermal Aging. Materials 2025, 18, 504. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Cheng, C.; Wang, X.; Wu, K. Space Charge Characteristics for XLPE Coaxial Cable Insulation under Electrothermal Accelerated Aging. IEEE Trans. Dielectr. Electr. Insul. 2022, 29, 727–736. [Google Scholar]
- Wang, Y.; Zhao, A.; Zhang, X.; Shen, Y.; Yang, F.; Deng, J.; Zhang, G. Study of Dielectric Response Characteristics for Thermal Aging of XLPE Cable Insulation. In Proceedings of the 2016 International Conference on Condition Monitoring and Diagnosis (CMD), Xi’an, China, 25–28 September 2016; pp. 602–605. [Google Scholar]
- Jahromi, A.N.; Pattabi, P.; Densley, J.; Lamarre, L. Medium Voltage XLPE Cable Condition Assessment Using Frequency Domain Spectroscopy. IEEE Electr. Insul. Mag. 2020, 32, 9–18. [Google Scholar] [CrossRef]
- Zhu, X.; Yin, Y.; Wu, J.; Wang, X. Study on Aging Characteristics of XLPE Cable Insulation Based on Quantum Chemical Calculation. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 1942–1950. [Google Scholar] [CrossRef]
- Pan, L.; Luo, Y.; Wang, X.; Lei, D.; Wang, J.; Zhang, H.; Yang, Z.; Wei, W. Simulation Research on the Effects of Air Gaps and Ambient Temperature on a 27.5 kV Power Cable. Appl. Sci. 2025, 15, 1028. [Google Scholar] [CrossRef]
- Yang, J.; Li, R.; Hu, L.; Wang, W. Influence of Thermal Aging on Space Charge Characteristics and Electrical Conduction Behavior of Cross-Linked Polyethylene Cable Insulation. Polymers 2024, 16, 1600. [Google Scholar] [CrossRef] [PubMed]
- Boukezzi, L.; Rondot, S.; Jbara, O.; Ghoneim, S.S.M.; Boubakeur, A.; Abdelwahab, S.A.M. Effect of Isothermal Conditions on the Charge Trapping/Detrapping Parameters in e-Beam Irradiated Thermally Aged XLPE Insulation in SEM. Materials 2022, 15, 1918. [Google Scholar] [CrossRef]
- Quercio, M.; Del Pino Lopez, J.C.; Grasso, S.; Canova, A. Numerical and experimental analysis of thermal behaviour of high voltage power cable in unfilled ducts. Sci. Rep. 2024, 14, 20599. [Google Scholar] [CrossRef]
- Sahoo, R.; Karmakar, S. Impact of Accelerated Thermal Aging on Electrical Tree Structure and Physicochemical Characteristics of XLPE Insulation. IEEE Trans. Dielectr. Electr. Insul. 2024, 31, 429–438. [Google Scholar] [CrossRef]
- Wang, X.; Liu, E.; Zhang, B. Reflectometry Based Cable Insulation Aging Diagnosis and Prognosis. IEEE Trans. Ind. Electron. 2021, 69, 4148–4157. [Google Scholar] [CrossRef]
- Wang, H.; Tan, G.; Tan, Y.; Zhou, L.; Lu, Y. Analysis of Thermal Aging Life and Physicochemical Properties of Crosslinked Polyethylene Seabed Cable Insulation. Polym. Mater. Sci. Eng. 2015, 31, 71–75. [Google Scholar]
- Kemari, Y.; Mekhaldi, A.; Teyssèdre, G.; Teguar, M. Correlations Between Structural Changes and Dielectric Behavior of Thermally Aged XLPE. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 1859–1866. [Google Scholar] [CrossRef]
- Boukezzi, L.; Boubakeur, A. Effect of Thermal Aging on the Electrical Characteristics of XLPE for HV Cables. Trans. Electr. Electron. Mater. 2018, 19, 344–351. [Google Scholar] [CrossRef]
- Boukezzi, L.; Boubakeur, A.; Laurent, C.; Lallouani, M. DSC Study of Artificial Thermal Aging of XLPE Insulation Cables. 2007 IEEE Int. Conf. Solid Dielectr. 2007, 1, 146–149. [Google Scholar]
- Sandelin, M.; Gedde, U. Long-term Performance of Cables Based on Chlorosulphonated Polyethylene. Polym. Degrad. Stab. 2004, 86, 331–338. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, X. Insulation Performance Evaluation of HV AC/DC XLPE Cables by 0.1 Hz tan δ Test on Circumferentially Peeled Samples. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3941–3950. [Google Scholar] [CrossRef]
- Afia, R.S.A.; Mustafa, E.; Tamus, Z.Á. Comparison of Mechanical and Low-Frequency Dielectric Properties of Thermally and Thermo-Mechanically Aged Low Voltage CSPE/XLPE Nuclear Power Plant Cables. Electronics 2021, 10, 2728. [Google Scholar] [CrossRef]



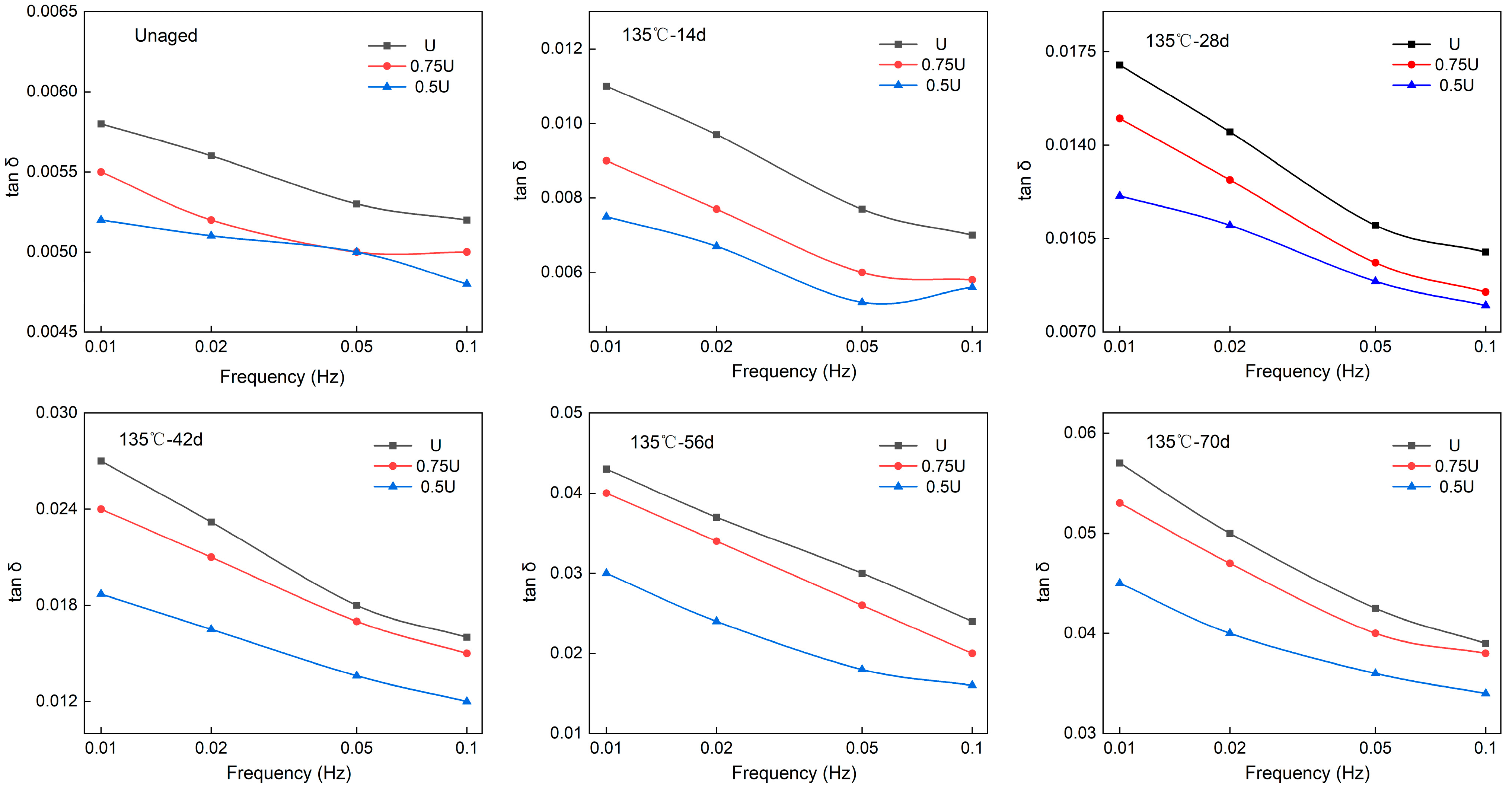

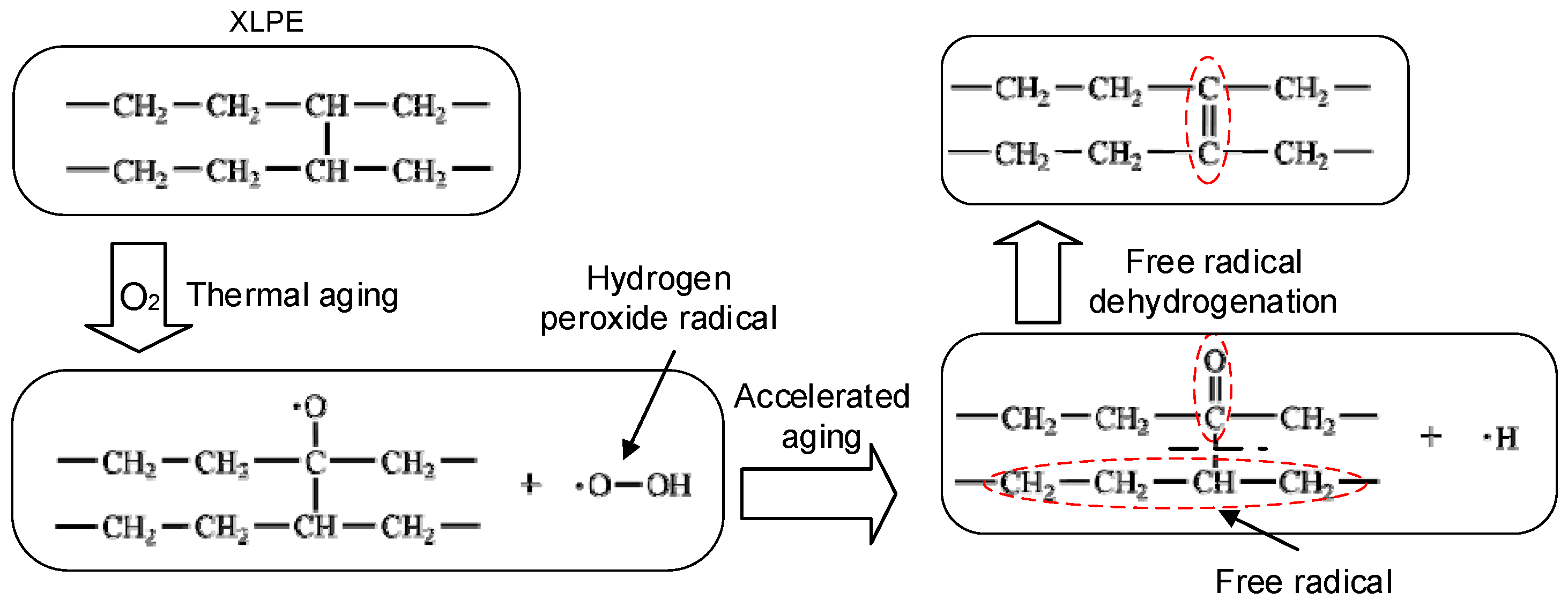
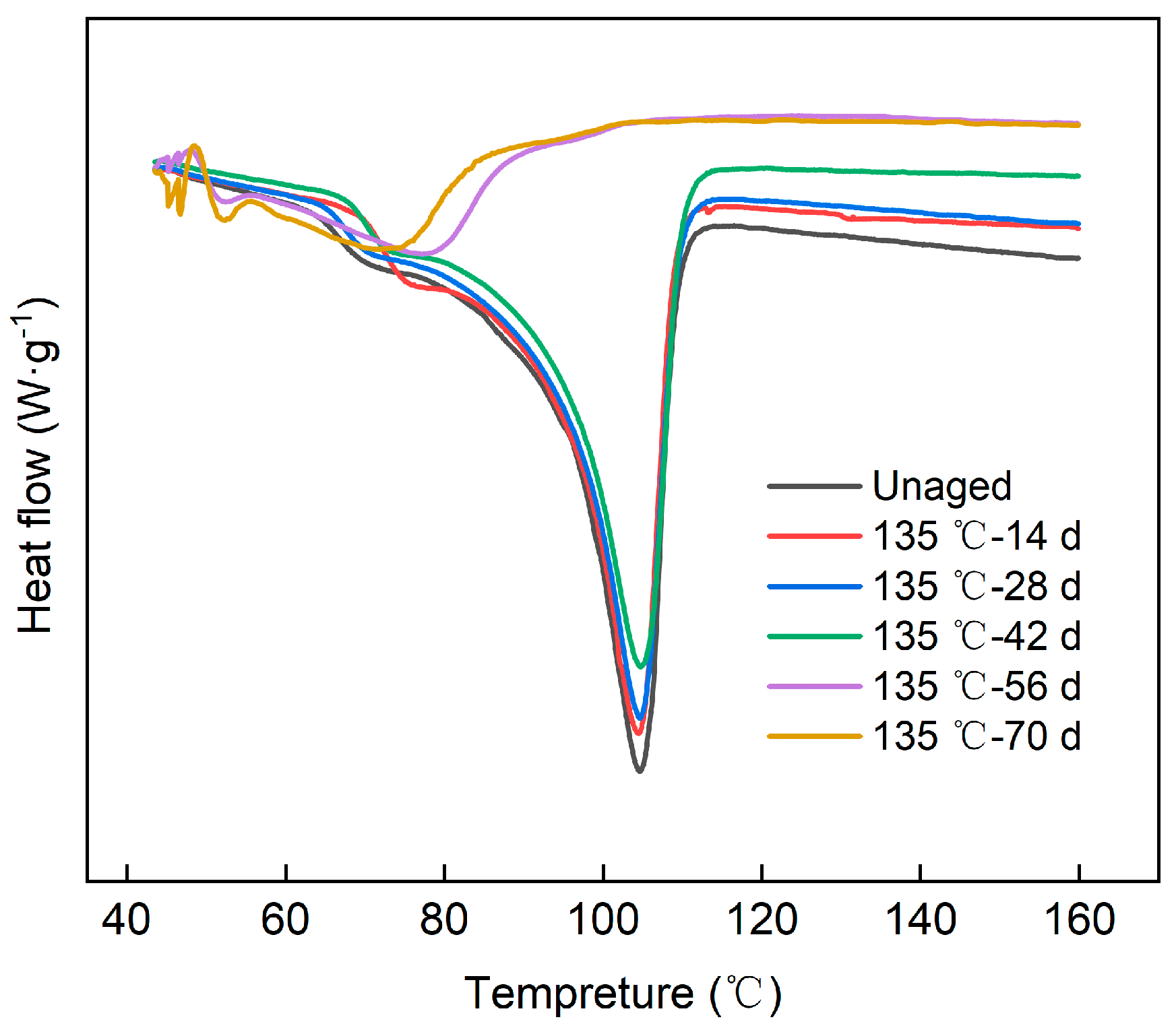
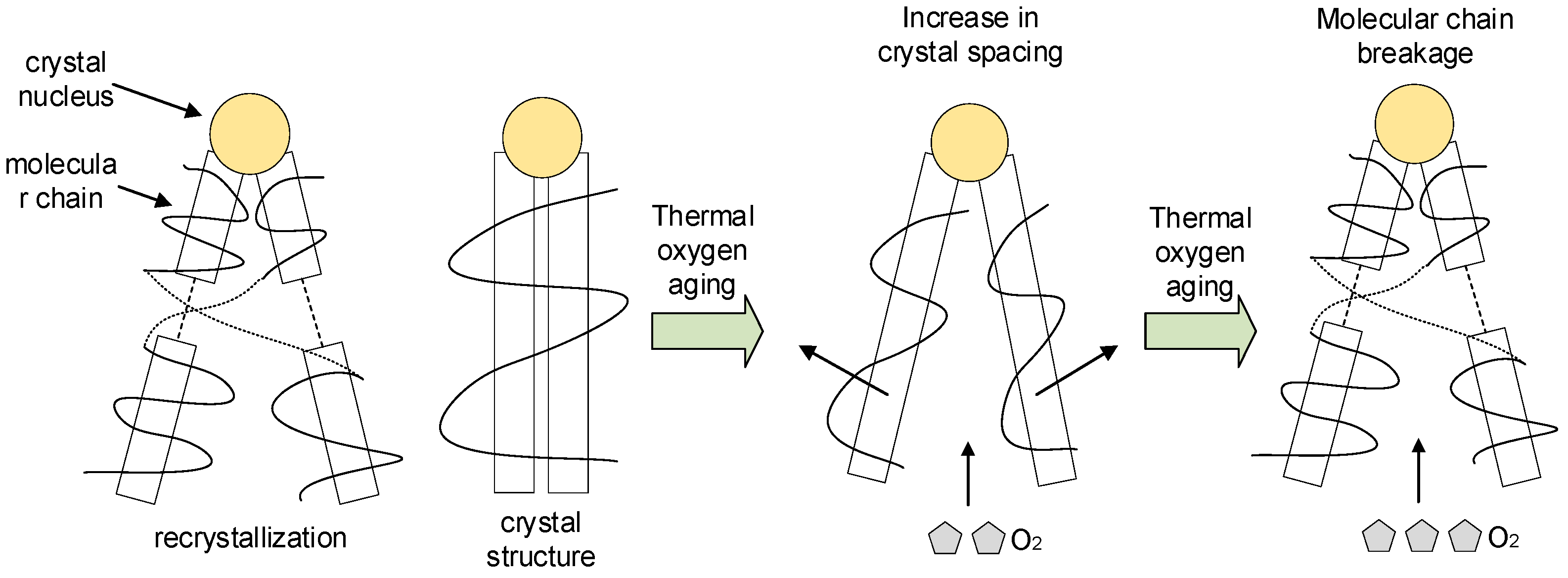


| Thermal aging time (day) | 0 | 14 | 28 | 42 | 56 | 70 |
| Carbonyl index | 1.3 | 1.45 | 1.63 | 2.07 | 2.65 | 3.62 |
| Thermal aging time (day) | 0 | 14 | 28 | 42 | 56 | 70 |
| Crystallinity (%) | 32.4 | 25.5 | 23.4 | 15.1 | 7.1 | 5.3 |
| Thermal aging time (day) | 0 | 14 | 28 | 42 | 56 | 70 |
| tanδ | 0.0052 | 0.007 | 0.01 | 0.016 | 0.024 | 0.039 |
| Characteristic Parameter | Value 1 | Value 2 | Value 3 |
|---|---|---|---|
| H | 1 | 0.75 | 0.5 |
| Sk | 8.47 | 10.01 | 10.56 |
| tanδ | 0.0052 | 0.012 | 0.024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, T.; Li, W.; Zheng, Z.; Li, Y.; Chu, J.; Hao, C. Insulation Aging Evaluation Method of High Voltage Cable Based on Dielectric Loss Characteristics. Energies 2025, 18, 1267. https://doi.org/10.3390/en18051267
Han T, Li W, Zheng Z, Li Y, Chu J, Hao C. Insulation Aging Evaluation Method of High Voltage Cable Based on Dielectric Loss Characteristics. Energies. 2025; 18(5):1267. https://doi.org/10.3390/en18051267
Chicago/Turabian StyleHan, Tao, Wenhao Li, Zeping Zheng, Yanqing Li, Jia Chu, and Chunlin Hao. 2025. "Insulation Aging Evaluation Method of High Voltage Cable Based on Dielectric Loss Characteristics" Energies 18, no. 5: 1267. https://doi.org/10.3390/en18051267
APA StyleHan, T., Li, W., Zheng, Z., Li, Y., Chu, J., & Hao, C. (2025). Insulation Aging Evaluation Method of High Voltage Cable Based on Dielectric Loss Characteristics. Energies, 18(5), 1267. https://doi.org/10.3390/en18051267






