Influence of Impeller–Diffuser Side-Gap Flow with a Simplified Leakage Model on the Performance and Internal Flow of a Centrifugal Pump
Abstract
:1. Introduction
2. Centrifugal Pump and Leakage Flow Model
3. Numerical Methods
4. Performance Parameters
5. Results and Discussion
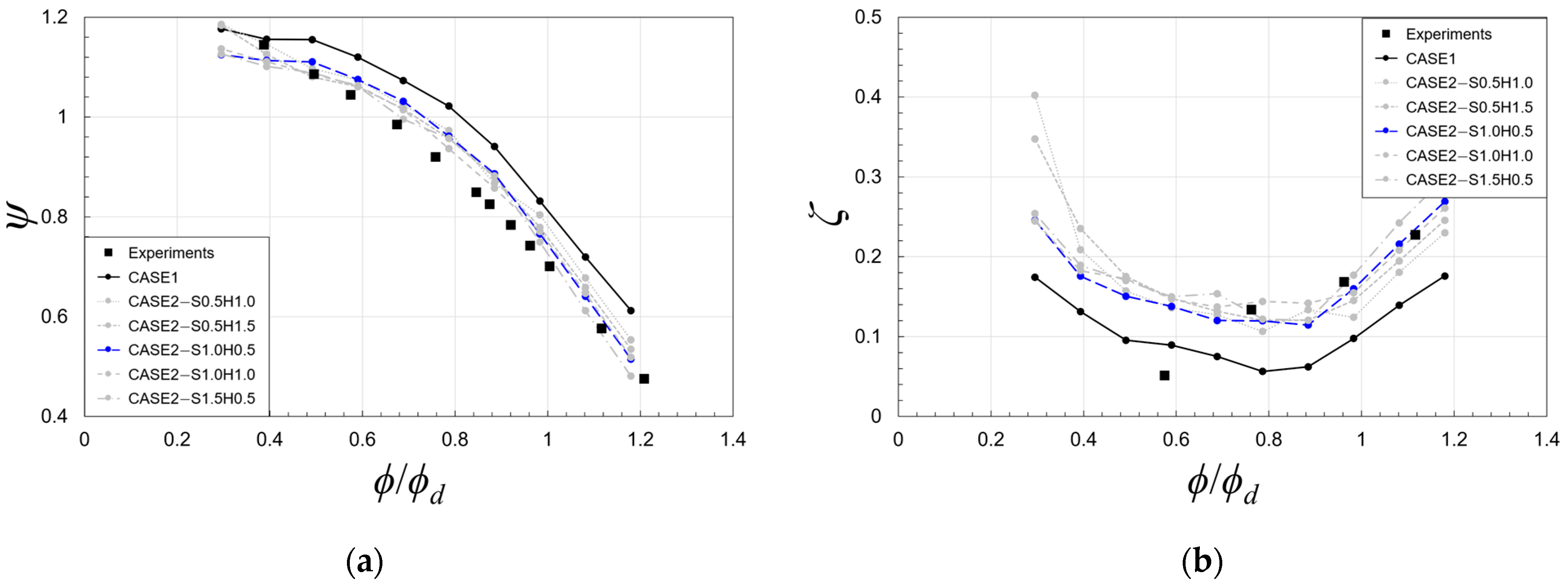
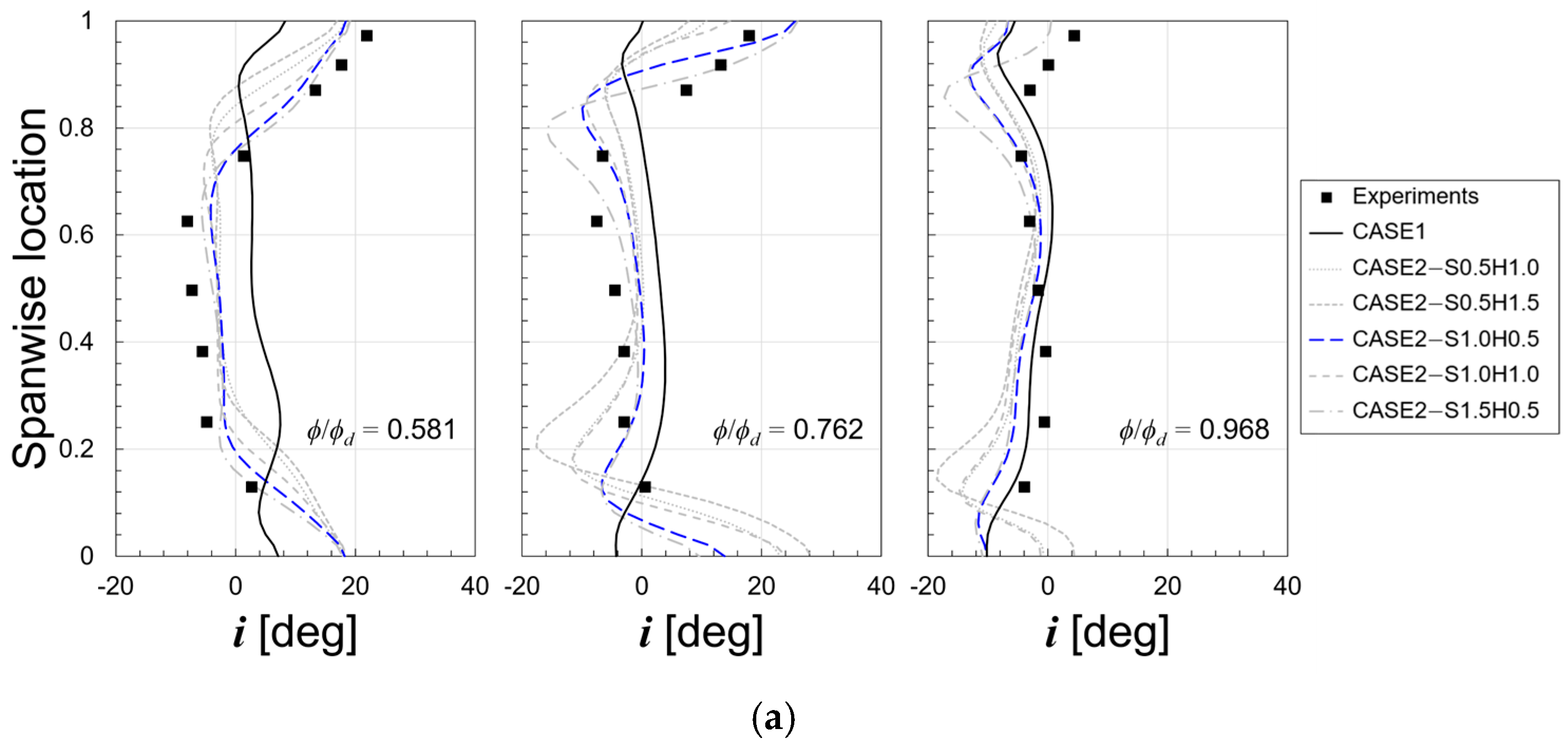
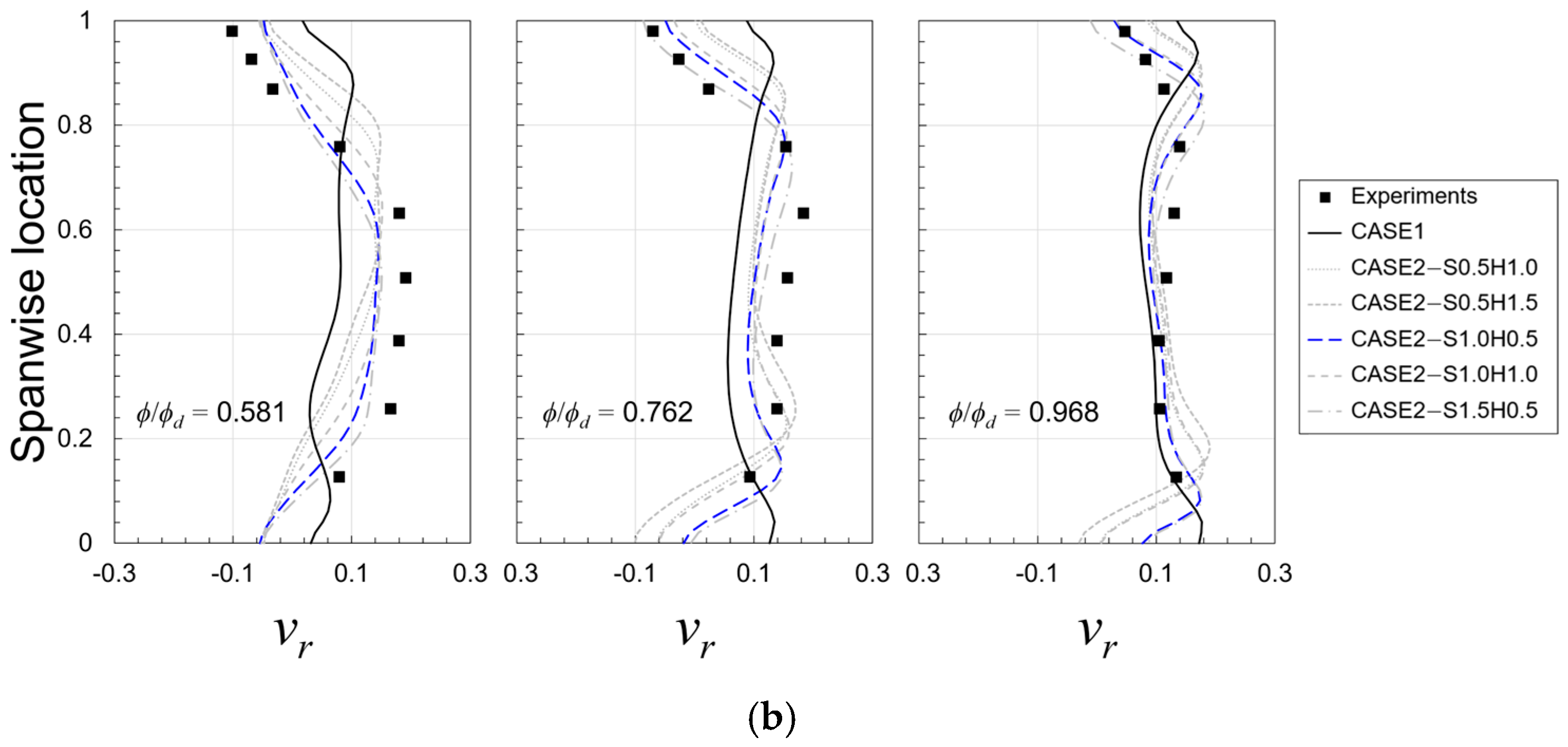
5.1. Validation
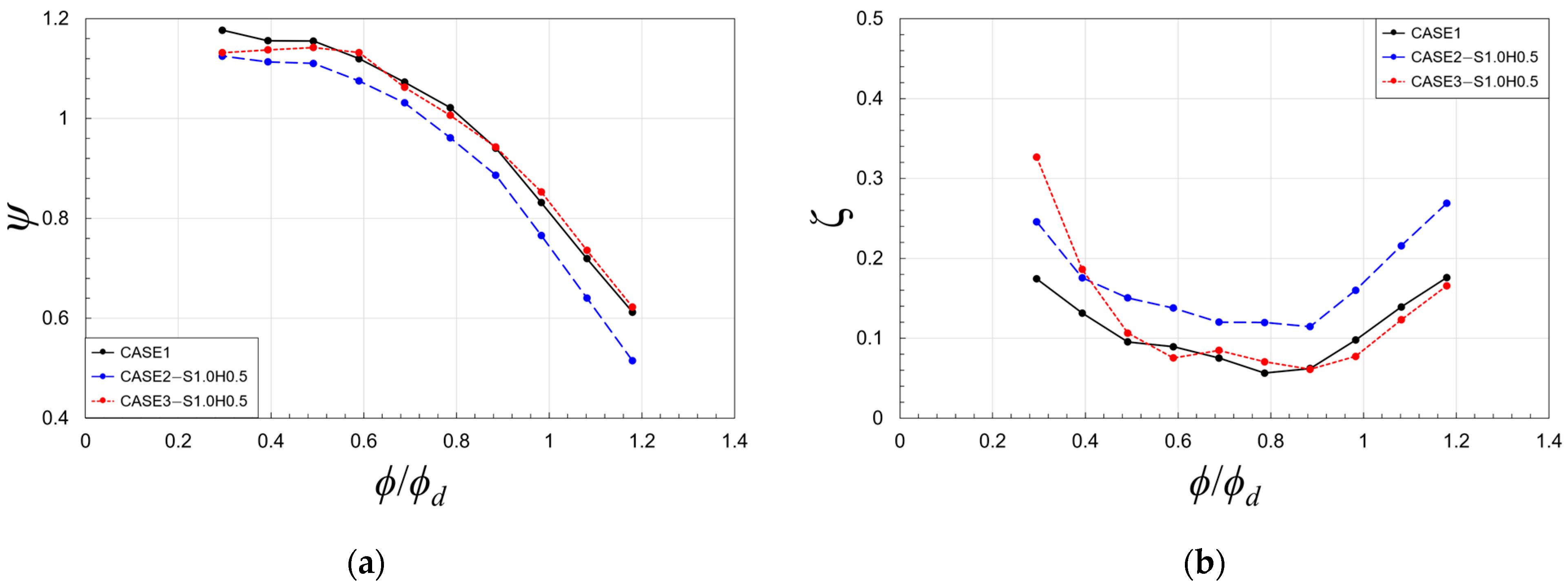
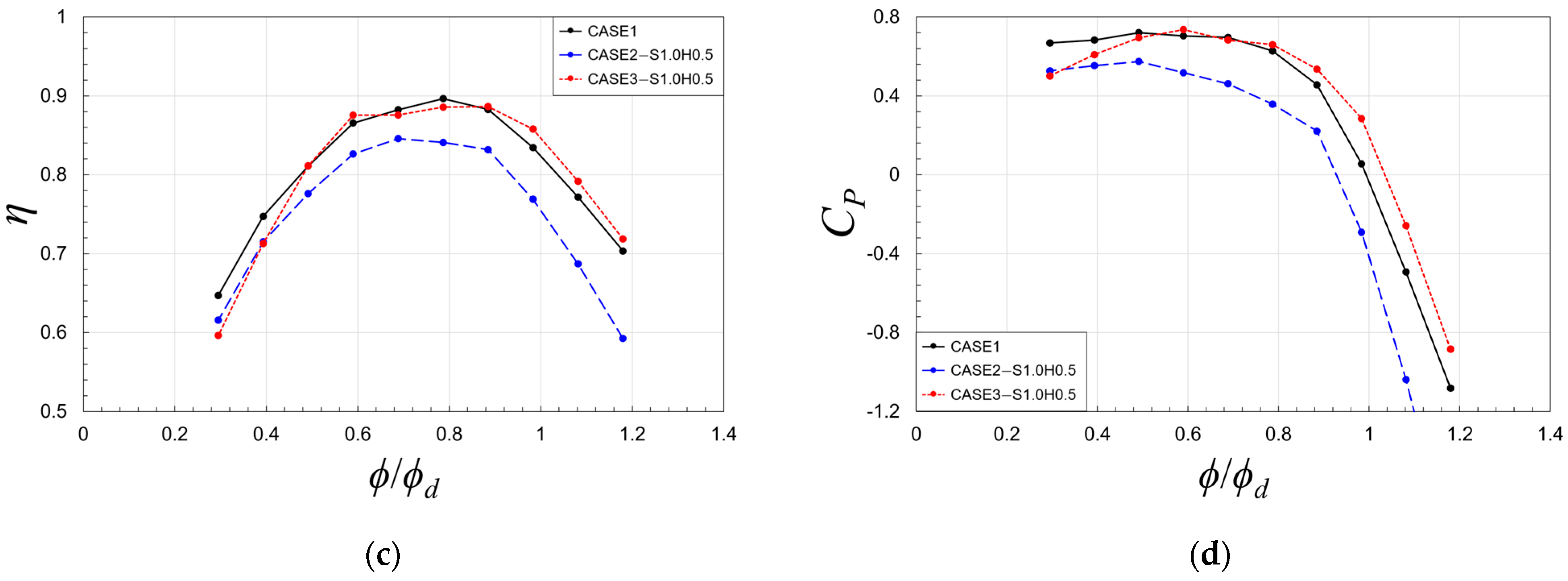
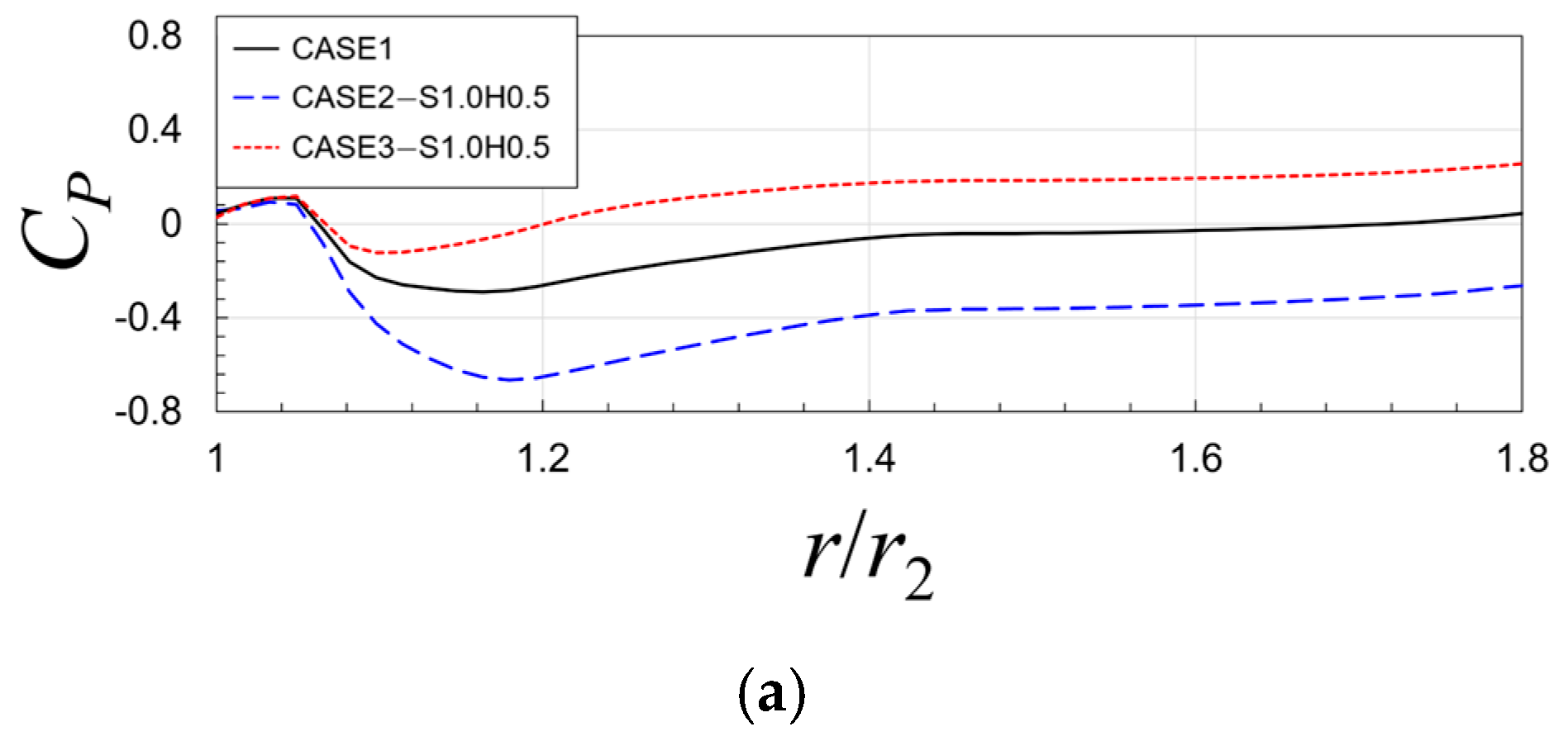
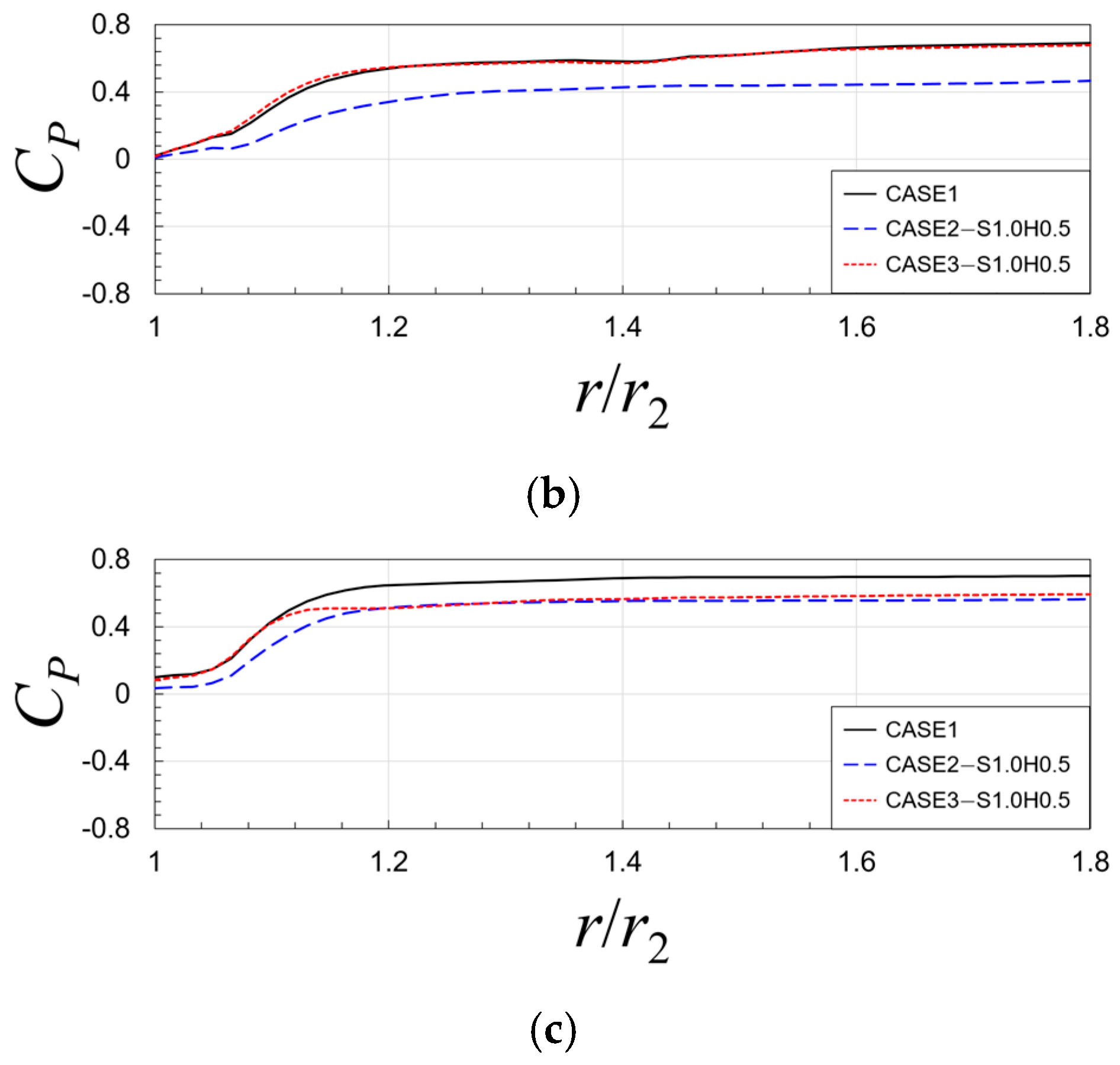
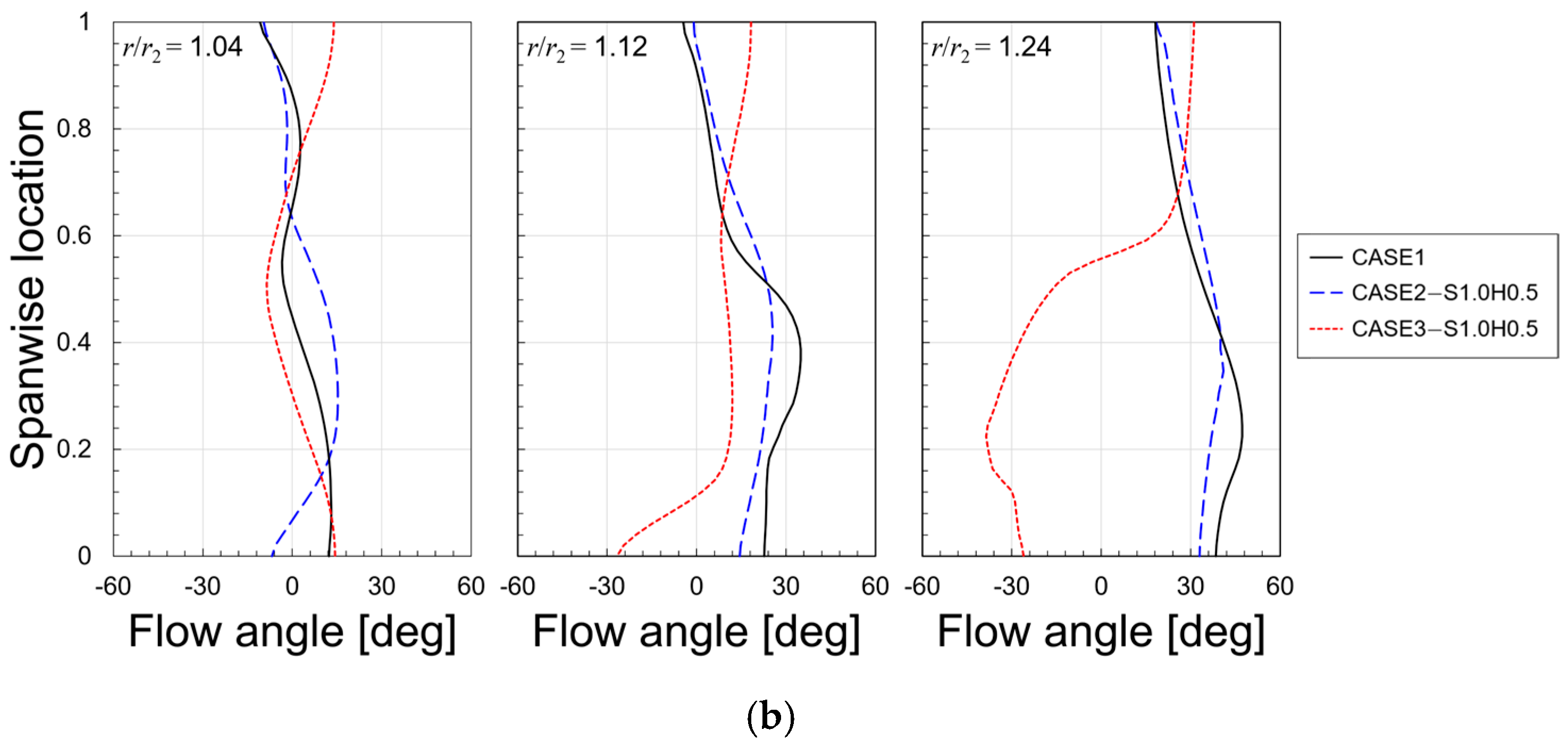
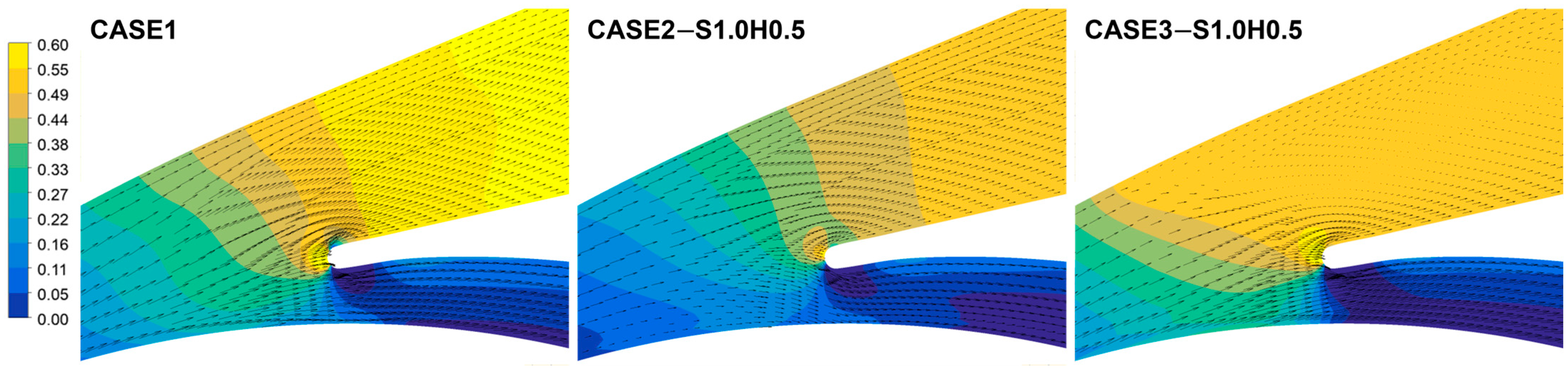
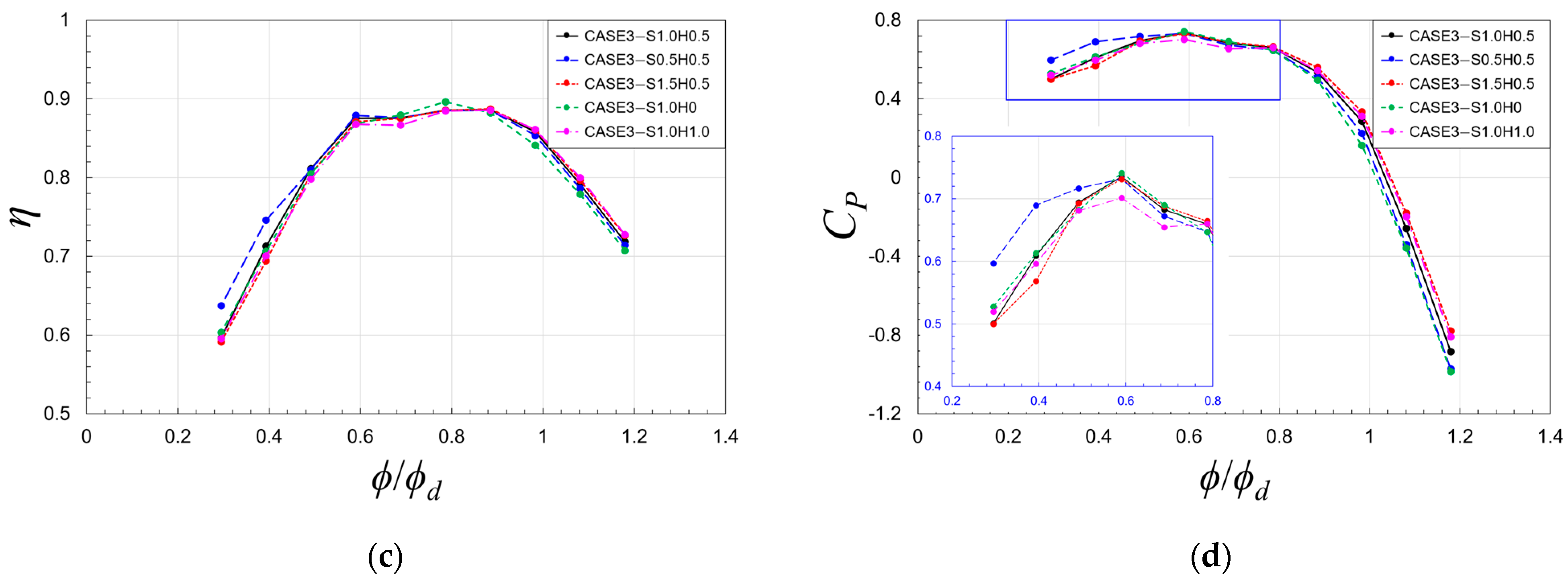
5.2. Effects of Flow Through Impeller–Diffuser Side Gap
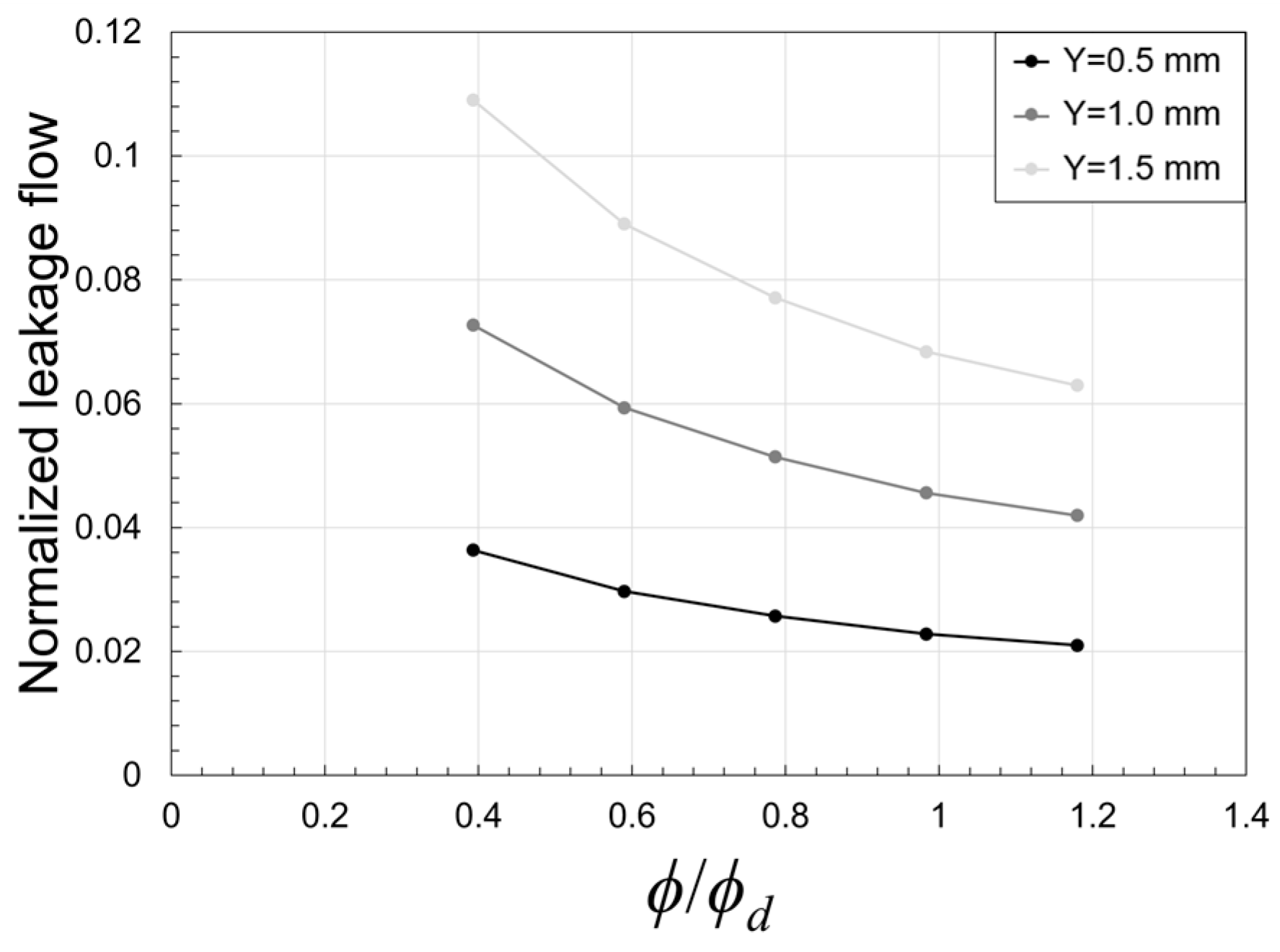
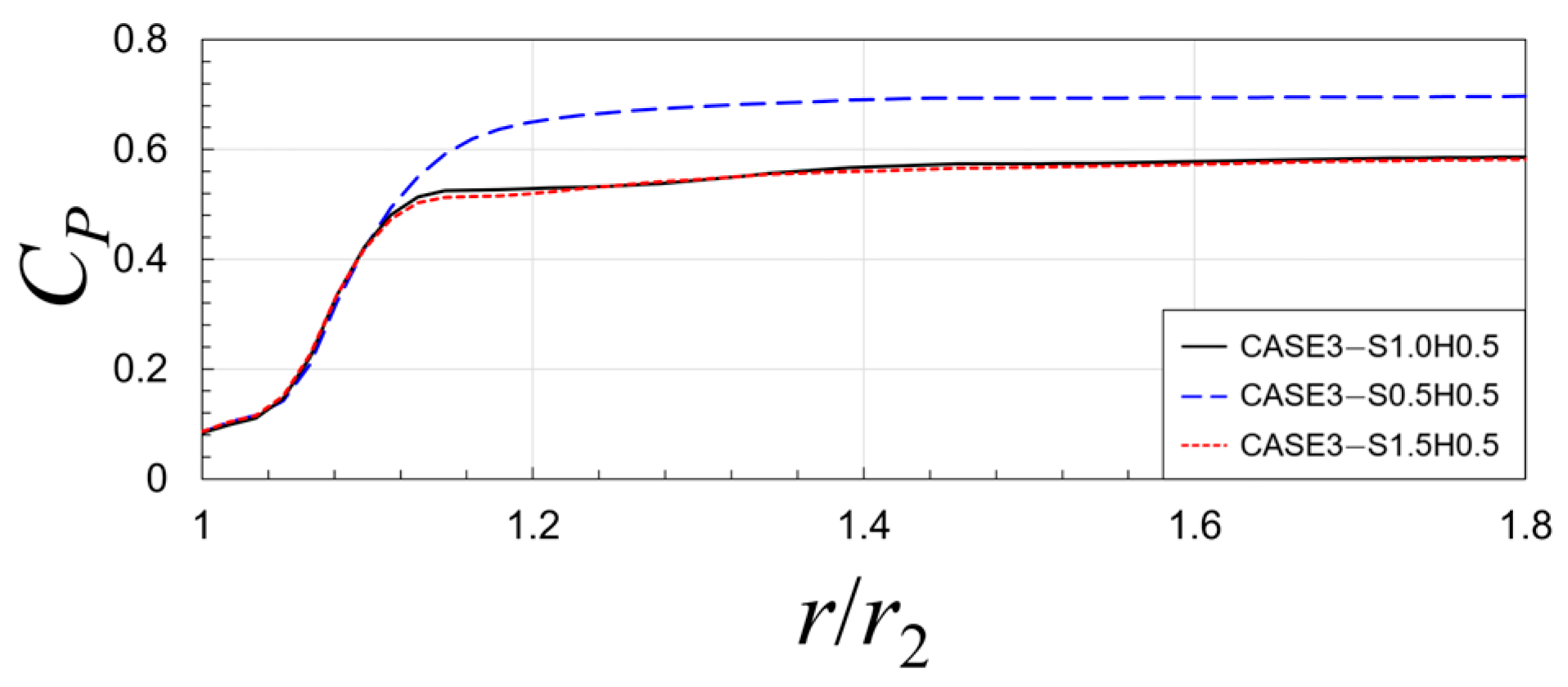
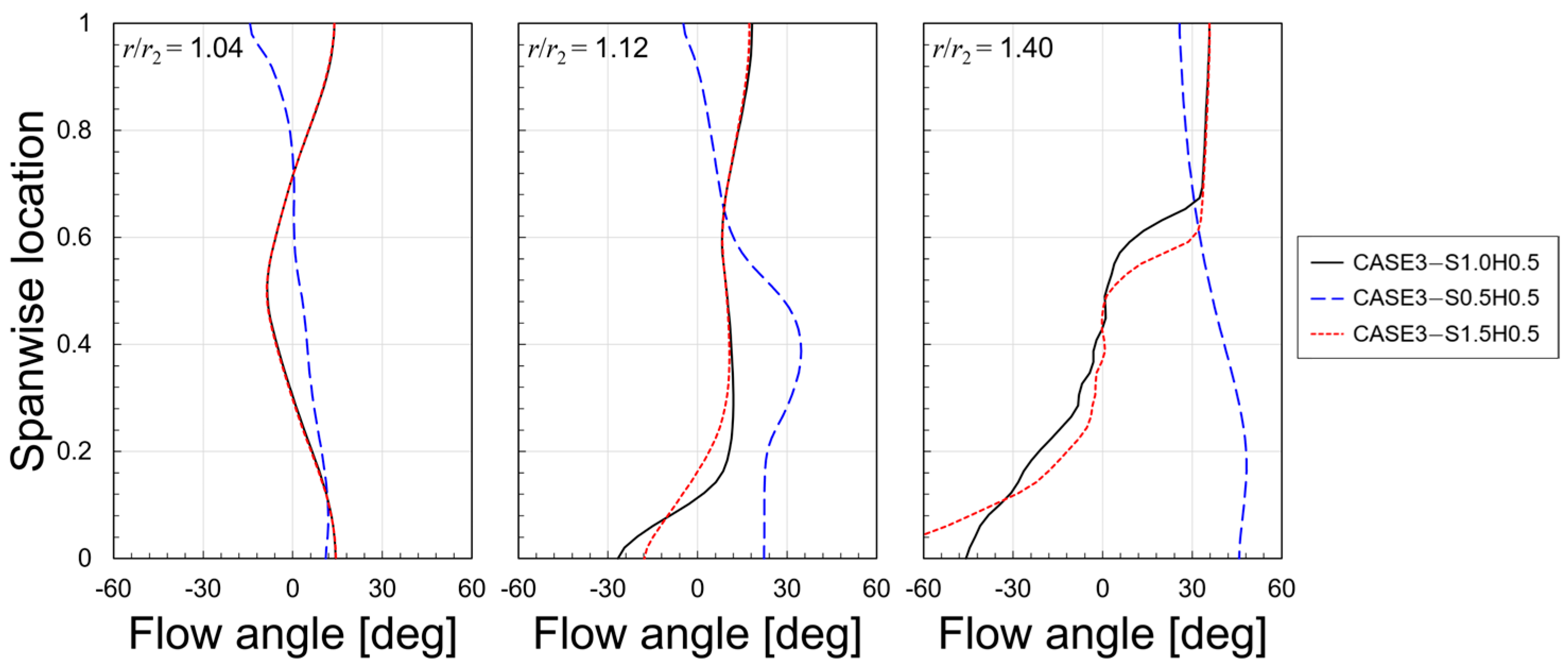
5.3. Effect of Leakage Flow with Variations of Clearances
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | computational fluid dynamics |
| RANS | Reynolds-averaged Navier–Stokes analysis |
| SHF | Société Hydrotechnique de France |
| SST | shear stress transport |
References
- Cooper, P. A Vision and Mission for Pump R & D Over the Next 25 Years. In Proceedings of the 25th International Pump Users Symposium, Turbomachinery Laboratories, Texas A&M Engineering Experiment Station, Houston, TX, USA, 23–26 February 2009; pp. 1–12. [Google Scholar]
- Igor, J.P.M.; Karassik, J.; Cooper, P.; Heald, C.C. Pump Handbook, 4th ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Japikse, D.; Marscher, W.D.; Furst, R.B. Centrifugal Pump Design and Performance; Concepts ETI: Norwich, VT, USA, 1997. [Google Scholar]
- Inoue, M.; Cumpsty, N.A. Experimental Study of Centrifugal Impeller Discharge Flow in Vaneless and Vaned Diffusers. ASME J. Eng. Gas Turbines Power 1984, 106, 455–467. [Google Scholar] [CrossRef]
- Tamaki, H.; Nakao, H.; Saito, M. The Experimental Study of Matching Between Centrifugal Compressor Impellers and Diffuser. ASME J. Turbomach. 1999, 121, 113–118. [Google Scholar] [CrossRef]
- Gao, R.; Spakovszky, Z.; Rusch, D.; Hunziker, R. Area Schedule Based Design of High-Pressure Recovery Radial Diffusion Systems. ASME J. Turbomach. 2016, 139, 011012. [Google Scholar] [CrossRef]
- Shim, H.-S.; Kim, S.-H.; Kim, K.-Y. Analysis and optimization of staggered partial diffuser vanes in a centrifugal pump. ASME J. Fluids Eng. 2020, 142, 051207. [Google Scholar] [CrossRef]
- Arndt, N.; Acosta, A.J.; Brennen, C.E.; Caughey, T.K. Rotor–Stator Interaction in a Diffuser Pump. ASME J. Turbomach. 1989, 111, 213–221. [Google Scholar] [CrossRef]
- Shum, Y.K.P.; Tan, C.S.; Cumpsty, N.A. Impeller–diffuser interaction in a centrifugal compressor. J. Turbomach. 2000, 122, 777–786. [Google Scholar] [CrossRef]
- Zemp, A.; Abhari, R.S. Vaned diffuser induced impeller blade vibrations in a high-speed centrifugal compressor. J. Turbomach. 2012, 135, 021015. [Google Scholar] [CrossRef]
- Storer, J.A.; Cumpsty, N.A. Tip Leakage Flow in Axial Compressors. ASME J. Turbomach. 1991, 113, 252–259. [Google Scholar] [CrossRef]
- Jang, C.-M.; Sato, D.; Fukano, T. Experimental Analysis on Tip Leakage and Wake Flow in an Axial Flow Fan According to Flow Rates. ASME J. Fluids Eng. 2004, 127, 322–329. [Google Scholar] [CrossRef]
- Wu, H.; Miorini, R.L.; Katz, J. Measurements of the tip leakage vortex structures and turbulence in the meridional plane of an axial water-jet pump. Exp. Fluids 2010, 50, 989–1003. [Google Scholar] [CrossRef]
- Launder, B.; Poncet, S.; Serre, E. Laminar, transitional, and turbulent flows in rotor-stator cavities. Annu. Rev. Fluid Mech. 2010, 42, 229–248. [Google Scholar] [CrossRef]
- Lin, A.; Liu, G.; Yu, X.; Chang, R.; Feng, Q. Comprehensive investigations on fluid flow and heat transfer characteristics of a high-speed rotating turbine disk cavity system of aero-engine. Int. Commun. Heat Mass Transf. 2022, 136, 106170. [Google Scholar] [CrossRef]
- Roy, R.P.; Devasenathipathy, S.; Xu, G.; Zhao, Y. A Study of the Flow Field in a Model Rotor-Stator Disk Cavity. In Proceedings of the ASME 1999 International Gas Turbine and Aeroengine Congress and Exhibition. Volume 3: Heat Transfer; Electric Power; Industrial and Cogeneration, Indianapolis, IN, USA, 7–10 June 1999. V003T01A064. ASME. [Google Scholar]
- Kurokawa, J.; Sakura, M. Flow in a narrow gap along an enclosed rotating disk with through-flow. JSME Int. Journal. Ser. Fluids Eng. Heat Transf. Power Combust. Thermophys. Prop. 1988, 31, 243–251. [Google Scholar] [CrossRef]
- Zhang, S.; Li, H.; Xi, D. Investigation of the integrated model of side chamber, wear-rings clearance, and balancing holes for centrifugal pumps. J. Fluids Eng. 2019, 141, 101101. [Google Scholar] [CrossRef]
- Kye, B.; Park, K.; Choi, H.; Lee, M.; Kim, J.-H. Flow characteristics in a volute-type centrifugal pump using large eddy simulation. Int. J. Heat Fluid Flow 2018, 72, 52–60. [Google Scholar] [CrossRef]
- Zhai, L.; Lu, C.; Guo, J.; Zhu, Z.; Cui, B. Flow Characteristics and Energy Loss of a Multistage Centrifugal Pump with Blade-Type Guide Vanes. J. Mar. Sci. Eng. 2022, 10, 180. [Google Scholar] [CrossRef]
- Babayigit, O.; Ozgoren, M.; Aksoy, M.H.; Kocaaslan, O. Experimental and CFD investigation of a multistage centrifugal pump including leakages and balance holes. Desalination Water Treat. 2017, 67, 28–40. [Google Scholar] [CrossRef]
- Guinzburg, A.; Brennen, C.E.; Acosta, A.J.; Caughey, T.K. Experimental Results for the Rotordynamic Characteristics of Leakage Flows in Centrifugal Pumps. ASME J. Fluids Eng. 1994, 116, 110–115. [Google Scholar] [CrossRef]
- Zhou, W.; Ma, J.; Ma, Z.; Yu, W.; Su, H.; Gao, B. Fluid–structure interaction on the rotor-dynamic characteristics of a low-specific-speed centrifugal pump considering multi-scale fluid excitation effects. Phys. Fluids 2024, 36, 117157. [Google Scholar] [CrossRef]
- Gülich, J.F. Disk friction losses of closed turbomachine impellers. Forsch. Im Ingenieurwesen 2003, 68, 87–95. [Google Scholar] [CrossRef]
- Si, Q.; Dupont, P.; Bayeul-Lainé, A.-C.; Dazin, A.; Roussette, O.; Yuan, S. An Experimental Study of the Flow Field Inside the Diffuser Passage of a Laboratory Centrifugal Pump. ASME J. Fluids Eng. 2015, 137, 061105. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Cao, S. Theoretical model of energy performance prediction and BEP determination for centrifugal pump as turbine. Energy 2019, 172, 712–732. [Google Scholar] [CrossRef]
- ANSYS. ANSYS CFX-Solver Theory Guide-Release 15.0; ANSYS: Canonsburg, PA, USA, 2014. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Barth, T.; Jesperson, D. The design and application of upwind schemes on unstructured meshes. In Proceedings of the 27th Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1989. AIAA Paper. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transfer. 2003, 4, 625–632. [Google Scholar]
- Celik, I.; Karatekin, O. Numerical Experiments on Application of Richardson Extrapolation with Nonuniform Grids. ASME J. Fluids Eng. 1997, 119, 584–590. [Google Scholar] [CrossRef]
- Marsan, A.; Trebinjac, I.; Coste, S.; Leroy, G. Influence of Unstead iness on the Control of a Hub-Corner Separation Within a Radial Vaned Diffuser. ASME J. Turbomach. 2015, 137, 021008. [Google Scholar] [CrossRef]
- Deniz, S.; Greitzer, E.M.; Cumpsty, N.A. Effects of Inlet Flow Field Conditions on the Performance of Centrifugal Compressor Diffusers: Part 2—Straight-Channel Diffuser. ASME J. Turbomach. 1998, 122, 11–21. [Google Scholar] [CrossRef]
- Sano, T.; Yoshida, Y.; Tsujimoto, Y.; Nakamura, Y.; Matsushima, T. Numerical study of rotating stall in a pump vaned diffuser. J. Fluids Eng. 2002, 124, 363–370. [Google Scholar] [CrossRef]
- Shim, H.-S.; Kim, K.-Y. Relationship between flow instability and performance of a centrifugal pump with a volute. ASME J. Fluids Eng. 2020, 142, 111208. [Google Scholar] [CrossRef]
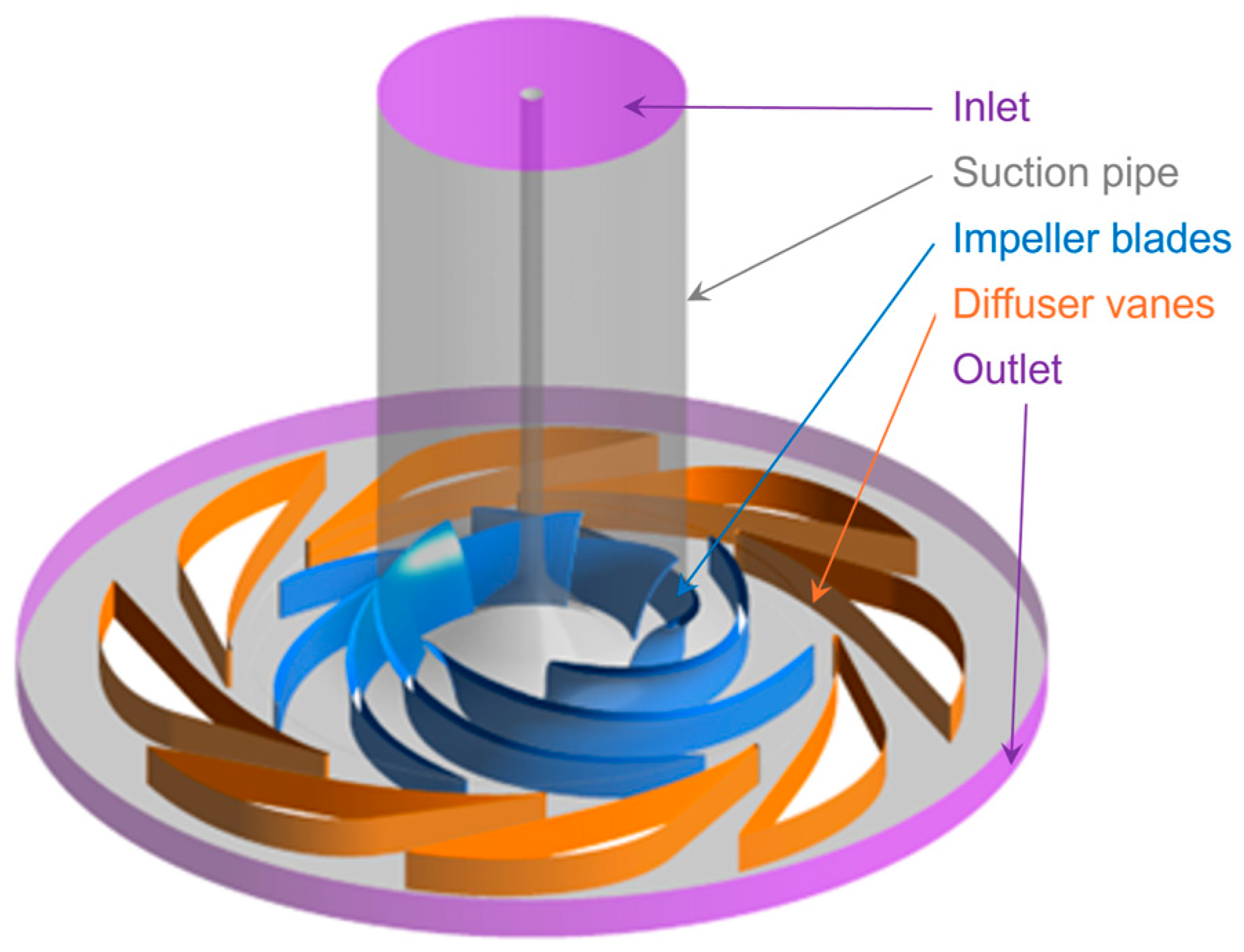

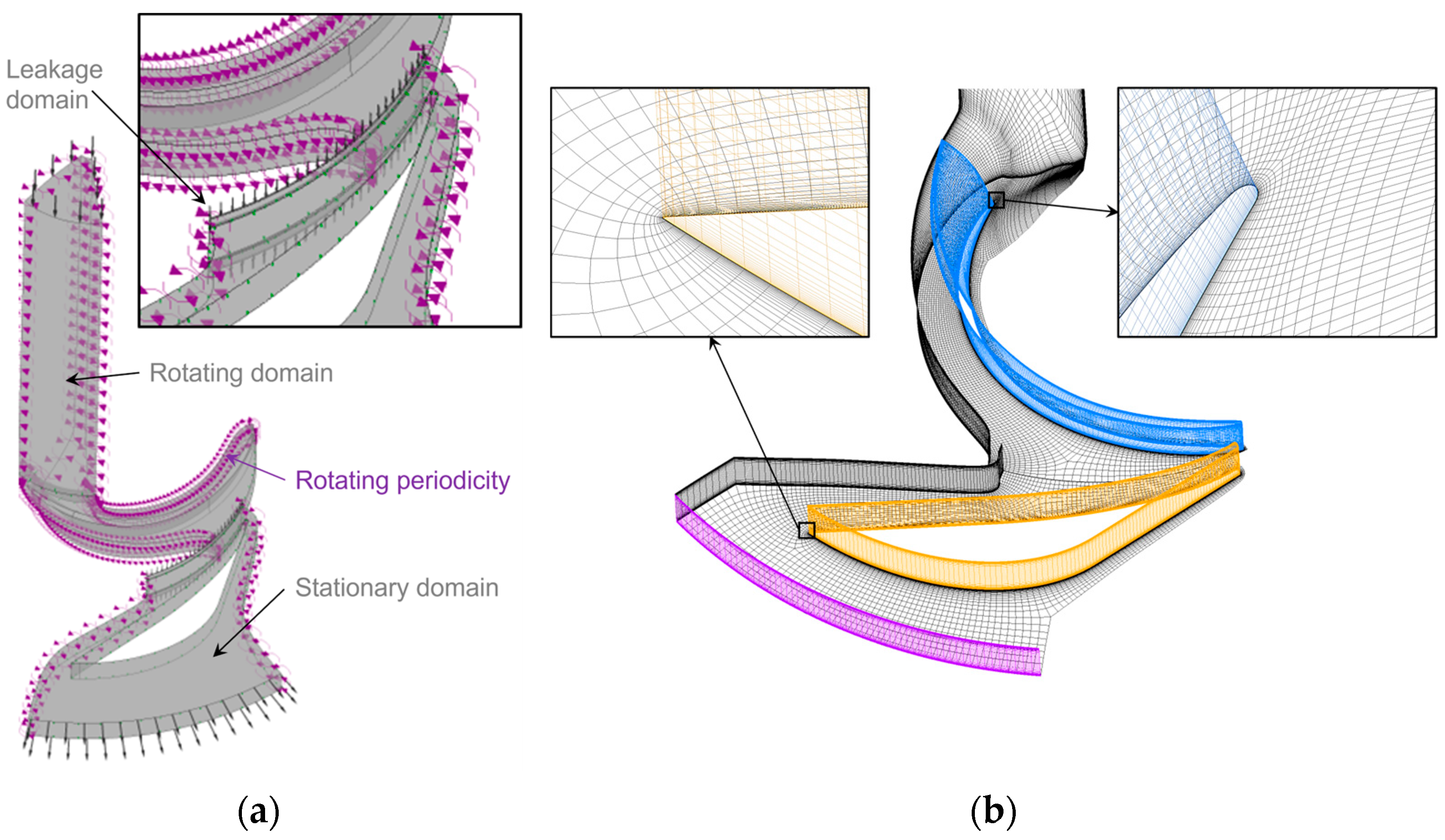




| Impeller | Diffuser | ||
|---|---|---|---|
| Design flow rate (Qd) | 0.337 m3/s | Design flow rate | 0.8 Qd |
| Inlet radius (r1) | 0.1412 m | Inlet radius (r3) | 0.2736 m |
| Outlet radius (r2) | 0.2586 m | Outlet radius (r4) | 0.3978 m |
| Outlet blade angle | 22.3 deg | Inlet vane angle | 10.2 deg |
| Number of blades | 7 | Number of vanes | 8 |
| Rotation speed | 1710 rpm | Width (b3) | 0.04 m |
| Parameter | Head Coefficient | Diffuser Loss Coefficient | |
|---|---|---|---|
| Number of cells | N1/N2/N3 | 2.05 × 106/1.03 × 106/0.518 × 105 | |
| Grid refinement factor | r21/r32 | 1.3/1.3 | |
| Computed values corresponding to N1, N2, and N3 | φ1 | 0.832 | 0.0977 |
| φ2 | 0.840 | 0.0953 | |
| φ3 | 0.881 | 0.0822 | |
| Apparent order | p | 5.81 | 6.47 |
| Extrapolated values | 0.829 | 0.0982 | |
| Approximate relative error | 1.06% | 2.46% | |
| Extrapolated relative error | 0.296% | 0.548% | |
| Grid convergence index | 0.368% | 0.689% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shim, H.-S. Influence of Impeller–Diffuser Side-Gap Flow with a Simplified Leakage Model on the Performance and Internal Flow of a Centrifugal Pump. Energies 2025, 18, 1278. https://doi.org/10.3390/en18051278
Shim H-S. Influence of Impeller–Diffuser Side-Gap Flow with a Simplified Leakage Model on the Performance and Internal Flow of a Centrifugal Pump. Energies. 2025; 18(5):1278. https://doi.org/10.3390/en18051278
Chicago/Turabian StyleShim, Hyeon-Seok. 2025. "Influence of Impeller–Diffuser Side-Gap Flow with a Simplified Leakage Model on the Performance and Internal Flow of a Centrifugal Pump" Energies 18, no. 5: 1278. https://doi.org/10.3390/en18051278
APA StyleShim, H.-S. (2025). Influence of Impeller–Diffuser Side-Gap Flow with a Simplified Leakage Model on the Performance and Internal Flow of a Centrifugal Pump. Energies, 18(5), 1278. https://doi.org/10.3390/en18051278





