Recent Advances in Translational Electromagnetic Energy Harvesting: A Review
Abstract
1. Introduction
- The coil or magnet is attached to a vibrating element;
- A magnet is suspended, and the frame with the coil is mounted on a vibrating element.
2. Translational Electromagnetic Energy Harvesting
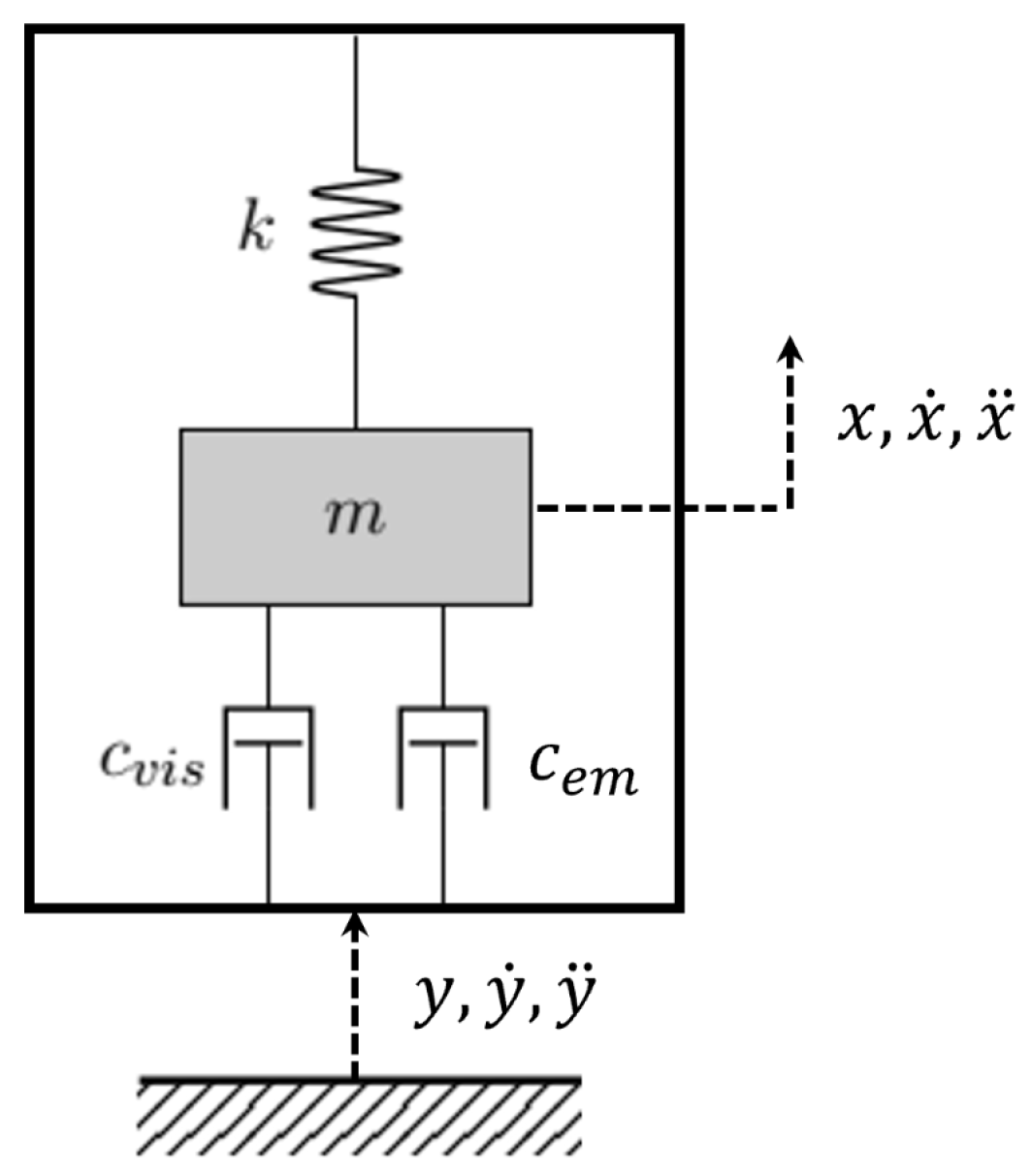
2.1. Electromechanical Harvester Modeling
2.2. Frequency Tuning
2.3. Bandwidth Expansion
- Non-linear suspensions;
- Geometrical non-linearities;
- Non-linear Energy Sinks (NESs);
- Multi-stabilities;
- Multi-DOF systems.
2.4. Suspension Classification
- Mechanical spring;
- MEMS spring;
- Magnetic spring.
3. 1DOF TEMEHs
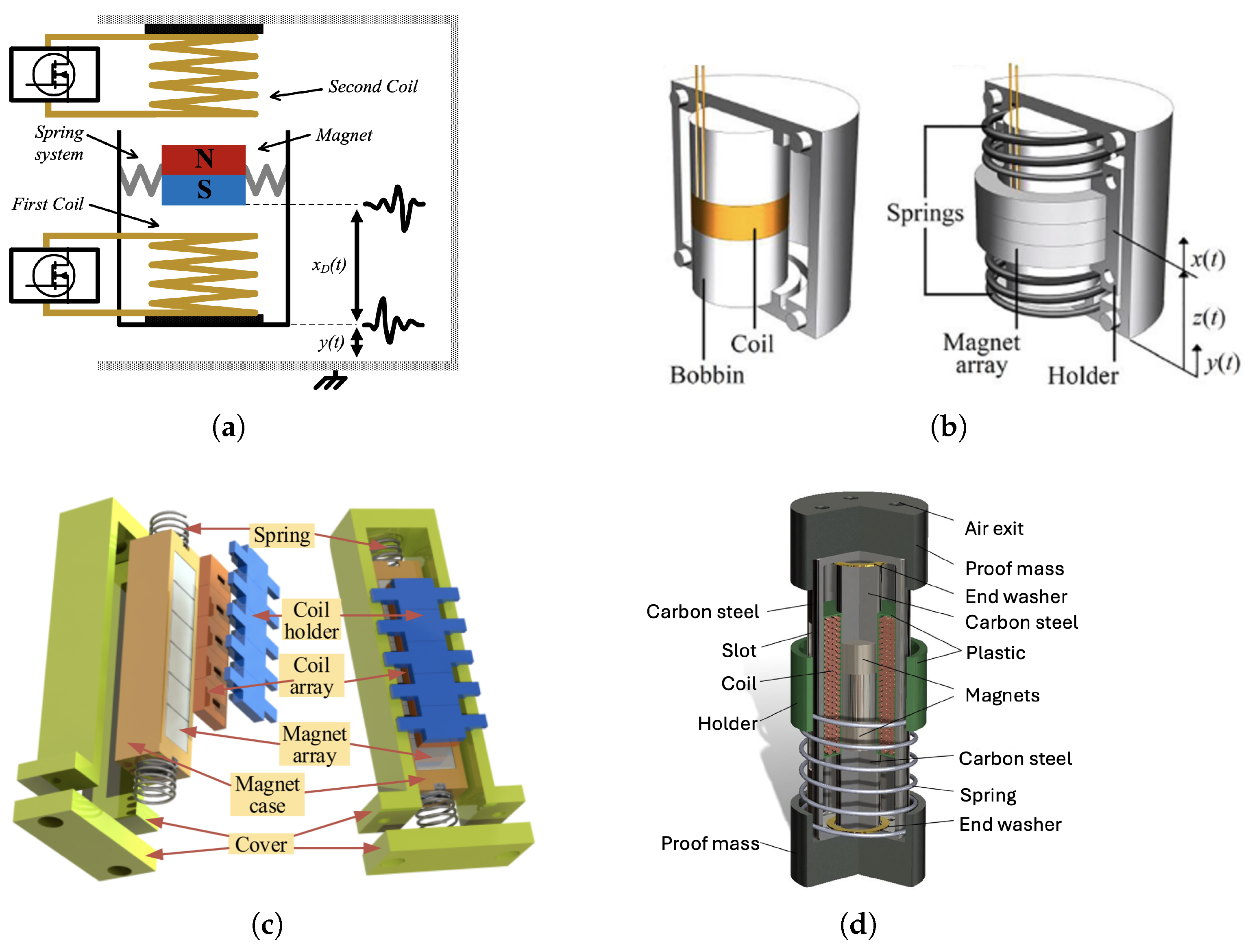
3.1. Mechanical Spring
3.2. MEMS Spring
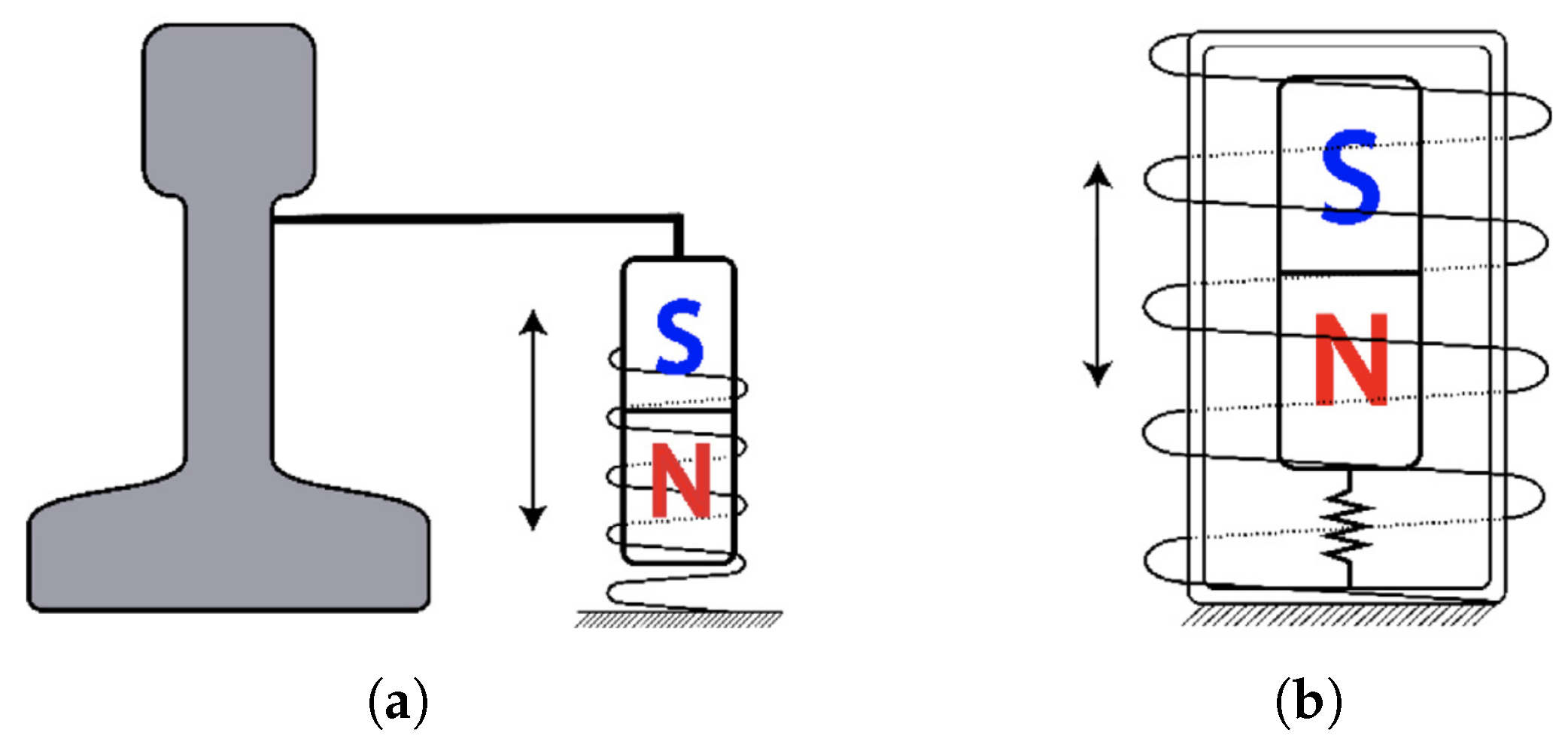
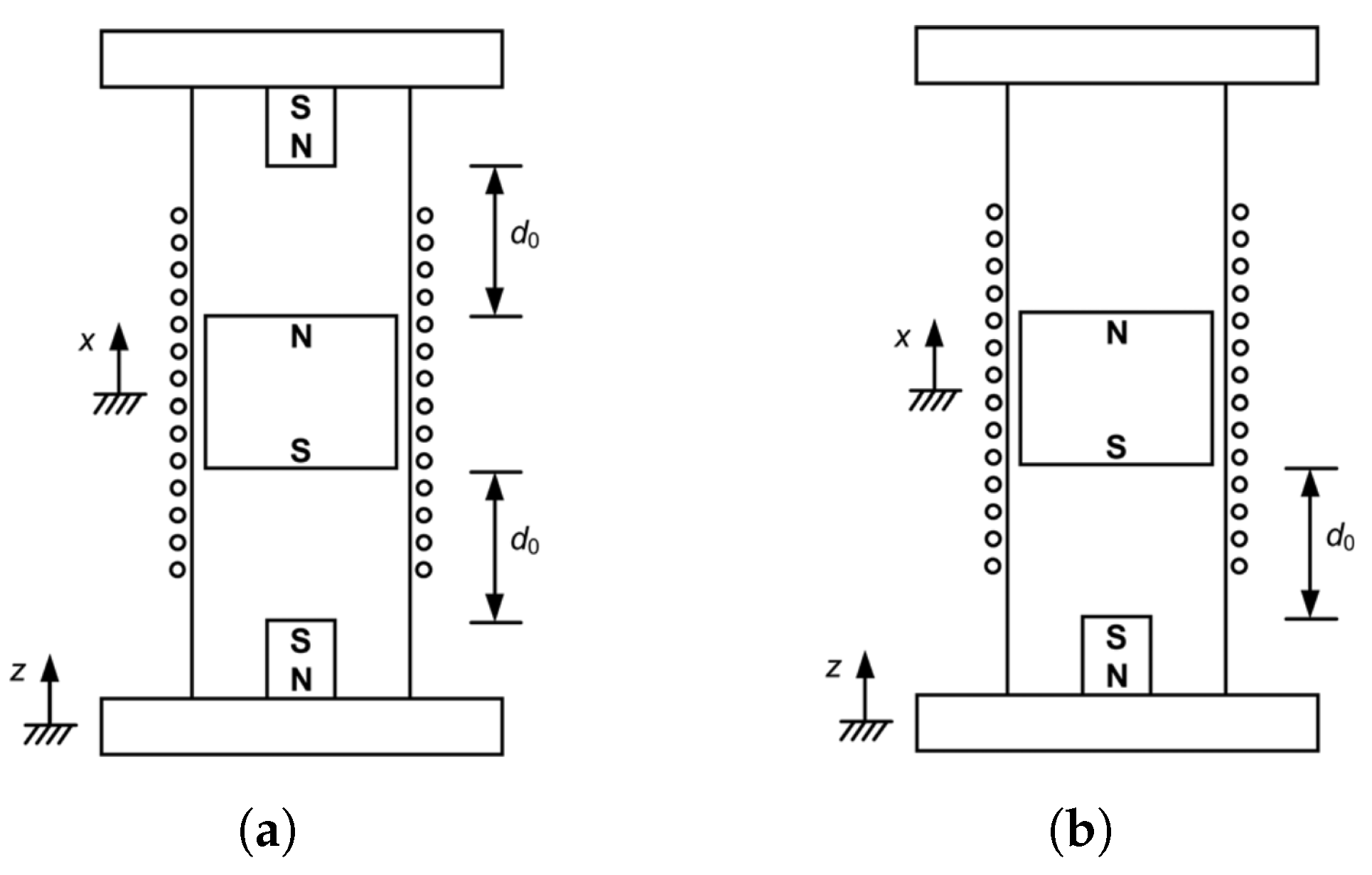
3.3. Magnetic Spring
3.4. Hybrid Suspensions
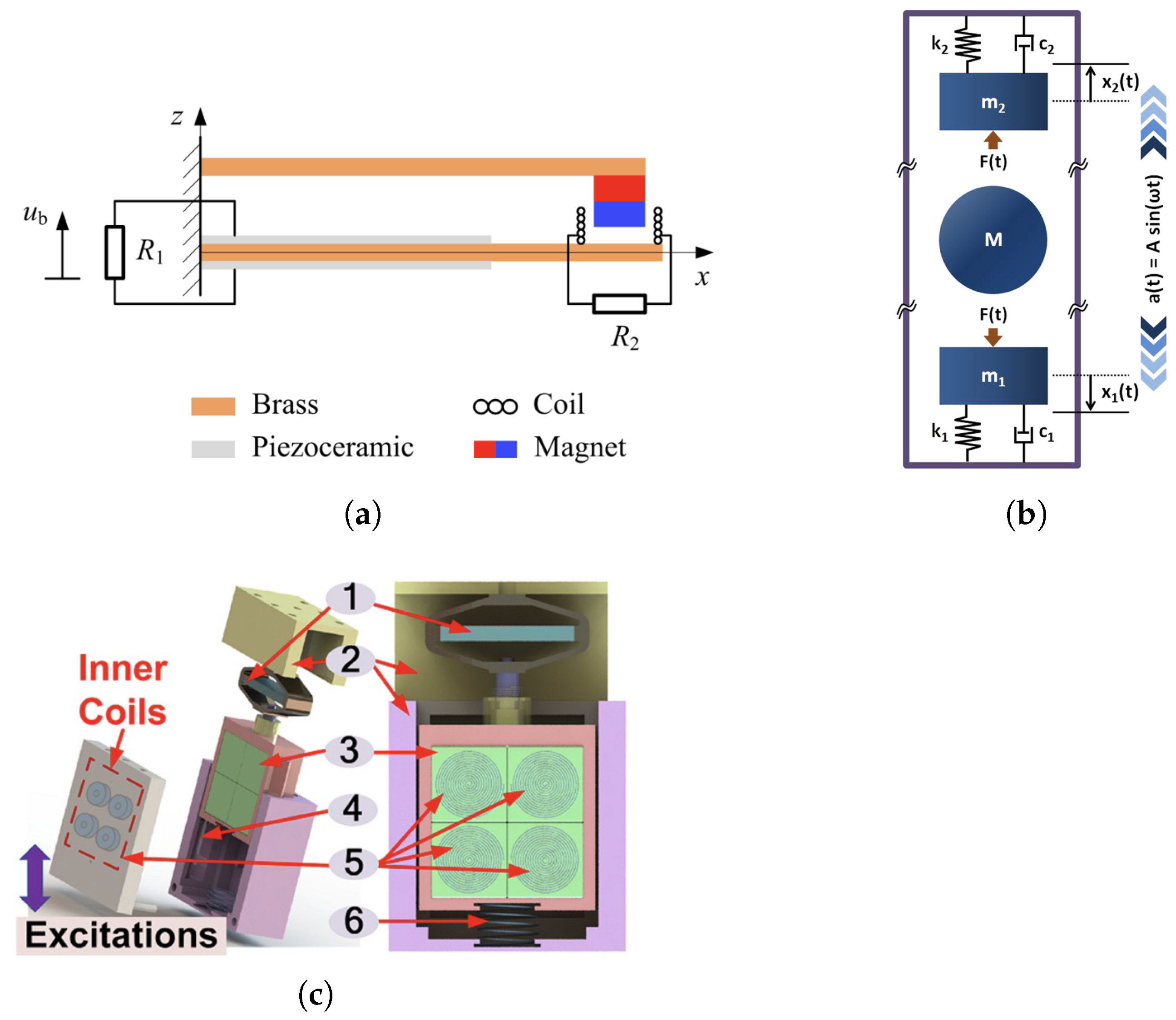
4. 2DOF TEMEHs
4.1. Mechanical Spring
4.2. MEMS Spring
4.3. Magnetic Spring
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| IoT | Internet of Things |
| WSN | Wireless Sensor Node |
| EH | Energy Harvester |
| EMEH | Electromagnetic Energy Harvester |
| TEMEH | Translational Electromagnetic Energy Harvester |
| DOF | Degree of freedom |
| NPD | Normalized Power Density |
| FoMv | Volumetric Figure of Merit |
| FEM | Finite Elements Method |
| PMIC | Power Management Integrated Circuit |
References
- Sohraby, K.; Minoli, D.; Znati, T. Wireless Sensor Networks: Technology, Protocols, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007; pp. 1–307. [Google Scholar]
- Hodge, V.J.; O’Keefe, S.; Weeks, M.; Moulds, A. Wireless sensor networks for condition monitoring in the railway industry: A survey. IEEE Trans. Intell. Transp. Syst. 2014, 16, 1088–1106. [Google Scholar] [CrossRef]
- Taylor, P. Global Number of Connected Devices 2015–2029, by Device. 2024. Available online: https://www.statista.com/statistics/512650/worldwide-connected-devices-amount/ (accessed on 2 February 2025).
- Muscat, A.; Bhattacharya, S.; Zhu, Y. Electromagnetic vibrational energy harvesters: A review. Sensors 2022, 22, 5555. [Google Scholar] [CrossRef]
- Beeby, S.P.; Cao, Z.; Almussallam, A. 11—Kinetic, Thermoelectric and Solar Energy Harvesting Technologies for Smart Textiles; Woodhead Publishing: Hamilton, UK, 2013; pp. 306–328. [Google Scholar]
- Kathiriya, H.; Pandya, A.; Dubay, V.; Bavarva, A. State of art: Energy efficient protocols for self-powered wireless sensor network in IIoT to support industry 4.0. In Proceedings of the 2020 8th International Conference on Reliability, Infocom Technologies and Optimization (Trends and Future Directions) (ICRITO), Noida, India, 4–5 June 2020; pp. 1311–1314. [Google Scholar]
- Harb, A. Energy harvesting: State-of-the-art. Renew. Energy 2011, 36, 2641–2654. [Google Scholar] [CrossRef]
- Choudhary, P.; Bhargava, L.; Singh, V.; Choudhary, M.; Kumar Suhag, A. A survey—Energy harvesting sources and techniques for internet of things devices. Mater. Today Proc. 2020, 30, 52–56. [Google Scholar]
- Singh, J.; Kaur, R.; Singh, D. Energy harvesting in wireless sensor networks: A taxonomic survey. Int. J. Energy Res. 2021, 45, 118–140. [Google Scholar]
- Sherazi, H.H.R.; Zorbas, D.; O’Flynn, B. A comprehensive survey on RF energy harvesting: Applications and performance determinants. Sensors 2022, 22, 2990. [Google Scholar] [CrossRef]
- Aljadiri, R.T.; Taha, L.Y.; Ivey, P. Electrostatic energy harvesting systems: A better understanding of their sustainability. J. Clean Energy Technol. 2017, 5, 409–416. [Google Scholar]
- Hosseinkhani, A.; Younesian, D.; Eghbali, P.; Moayedizadeh, A.; Fassih, A. Sound and vibration energy harvesting for railway applications: A review on linear and nonlinear techniques. Energy Rep. 2021, 7, 852–874. [Google Scholar]
- Castagnetti, D. Wideband fractal-inspired piezoelectric energy harvesters. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 2614–2626. [Google Scholar] [CrossRef]
- De Pasquale, G.; Somà, A.; Fraccarollo, F. Piezoelectric energy harvesting for autonomous sensors network on safety-improved railway vehicles. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 1107–1117. [Google Scholar]
- De Pasquale, G.; Somà, A.; Fraccarollo, F. Comparison between piezoelectric and magnetic strategies for wearable energy harvesting. J. Phys. Conf. Ser. 2013, 476, 012097. [Google Scholar] [CrossRef]
- Munaz, A.; Lee, B.C.; Chung, G.S. A study of an electromagnetic energy harvester using multi-pole magnet. Sens. Actuators A Phys. 2013, 201, 134–140. [Google Scholar] [CrossRef]
- de Araujo, M.V.V.; Nicoletti, R. Electromagnetic harvester for lateral vibration in rotating machines. Mech. Syst. Signal Process. 2015, 52, 685–699. [Google Scholar]
- Fu, H.; Mei, X.; Yurchenko, D.; Zhou, S.; Theodossiades, S.; Nakano, K.; Yeatman, E.M. Rotational energy harvesting for self-powered sensing. Joule 2021, 5, 1074–1118. [Google Scholar] [CrossRef]
- Castagnetti, D. A simply tunable electromagnetic pendulum energy harvester. Meccanica 2019, 54, 749–760. [Google Scholar]
- Chen, J.; Bao, B.; Liu, J.; Wu, Y.; Wang, Q. Pendulum energy harvesters: A review. Energies 2022, 15, 8674. [Google Scholar] [CrossRef]
- Gao, M.; Cong, J.; Xiao, J.; He, Q.; Li, S.; Wang, Y.; Yao, Y.; Chen, R.; Wang, P. Dynamic modeling and experimental investigation of self-powered sensor nodes for freight rail transport. Appl. Energy 2020, 257, 113969. [Google Scholar]
- Carneiro, P.; dos Santos, M.P.S.; Rodrigues, A.; Ferreira, J.A.; Simões, J.A.; Marques, A.T.; Kholkin, A.L. Electromagnetic energy harvesting using magnetic levitation architectures: A review. Appl. Energy 2020, 260, 114191. [Google Scholar]
- Roundy, S.; Wright, P.K.; Rabaey, J.M. Energy scavenging for wireless sensor networks. In Norwell; Springer: Berlin/Heidelberg, Germany, 2003; pp. 45–47. [Google Scholar]
- O’Donnell, T.; Saha, C.; Beeby, S.; Tudor, J. Scaling effects for electromagnetic vibrational power generators. Microsyst. Technol. 2007, 13, 1637–1645. [Google Scholar]
- Melnik, R.; Koziak, S. Rail vehicle suspension condition monitoring-approach and implementation. J. Vibroeng. 2017, 19, 487–501. [Google Scholar]
- Ahmad, M.M.; Khan, F.U. Review of vibration-based electromagnetic–piezoelectric hybrid energy harvesters. Int. J. Energy Res. 2021, 45, 5058–5097. [Google Scholar]
- Xu, Z.; Wang, W.; Xie, J.; Xu, Z.; Zhou, M.; Yang, H. An impact-based frequency up-converting hybrid vibration energy harvester for low frequency application. Energies 2017, 10, 1761. [Google Scholar] [CrossRef]
- Halim, M.A.; Cho, H.; Park, J.Y. Design and experiment of a human-limb driven, frequency up-converted electromagnetic energy harvester. Energy Convers. Manag. 2015, 106, 393–404. [Google Scholar]
- Li, Z.; Li, T.; Yang, Z.; Naguib, H.E. Toward a 0.33 W piezoelectric and electromagnetic hybrid energy harvester: Design, experimental studies and self-powered applications. Appl. Energy 2019, 255, 113805. [Google Scholar]
- Li, Z.; Liu, Y.; Yin, P.; Peng, Y.; Luo, J.; Xie, S.; Pu, H. Constituting abrupt magnetic flux density change for power density improvement in electromagnetic energy harvesting. Int. J. Mech. Sci. 2021, 198, 106363. [Google Scholar]
- Li, Z.; Luo, J.; Xie, S.; Xin, L.; Guo, H.; Pu, H.; Yin, P.; Xu, Z.; Zhang, D.; Peng, Y.; et al. Instantaneous peak 2.1 W-level hybrid energy harvesting from human motions for self-charging battery-powered electronics. Nano Energy 2021, 81, 105629. [Google Scholar]
- Yildirim, T.; Ghayesh, M.H.; Li, W.; Alici, G. A review on performance enhancement techniques for ambient vibration energy harvesters. Renew. Sustain. Energy Rev. 2017, 71, 435–449. [Google Scholar]
- Gao, M.; Wang, Y.; Wang, Y.; Wang, P. Experimental investigation of non-linear multi-stable electromagnetic-induction energy harvesting mechanism by magnetic levitation oscillation. Appl. Energy 2018, 220, 856–875. [Google Scholar]
- Feng, Z.; Peng, H.; Chen, Y. A dual resonance electromagnetic vibration energy harvester for wide harvested frequency range with enhanced output power. Energies 2021, 14, 7675. [Google Scholar] [CrossRef]
- Quinn, D.D.; Gendelman, O.; Kerschen, G.; Sapsis, T.P.; Bergman, L.A.; Vakakis, A.F. Efficiency of targeted energy transfers in coupled nonlinear oscillators associated with 1: 1 resonance captures: Part I. J. Sound Vib. 2008, 311, 1228–1248. [Google Scholar]
- Sapsis, T.; Vakakis, A.F.; Gendelman, O.V.; Bergman, L.A.; Kerschen, G.; Quinn, D. Efficiency of targeted energy transfers in coupled nonlinear oscillators associated with 1: 1 resonance captures: Part II, analytical study. J. Sound Vib. 2009, 325, 297–320. [Google Scholar]
- Kremer, D.; Liu, K. A nonlinear energy sink with an energy harvester: Transient responses. J. Sound Vib. 2014, 333, 4859–4880. [Google Scholar]
- Kremer, D.; Liu, K. A nonlinear energy sink with an energy harvester: Harmonically forced responses. J. Sound Vib. 2017, 410, 287–302. [Google Scholar]
- Pennisi, G.; Mann, B.; Naclerio, N.; Stephan, C.; Michon, G. Design and experimental study of a nonlinear energy sink coupled to an electromagnetic energy harvester. J. Sound Vib. 2018, 437, 340–357. [Google Scholar]
- Andò, B.; Baglio, S.; Marletta, V.; Bulsara, A.R. A comparison of linear and non-linear strategies for energy harvesting from mechanical vibrations. Front. Phys. 2023, 10, 1032978. [Google Scholar]
- Tan, Y.; Dong, Y.; Wang, X. Review of MEMS electromagnetic vibration energy harvester. J. Microelectromech. Syst. 2016, 26, 1–16. [Google Scholar]
- Novak, M.; Cernohorsky, J.; Kosek, M. Simple electro-mechanical model of magnetic spring realized from FeNdB permanent magnets. Procedia Eng. 2012, 48, 469–478. [Google Scholar]
- Ahamed, R.; Howard, I.; McKee, K. Dynamic analysis of magnetic spring-based nonlinear oscillator system. Nonlinear Dyn. 2023, 111, 15705–15736. [Google Scholar]
- De Pasquale, G.; Somà, A.; Zampieri, N. Design, simulation, and testing of energy harvesters with magnetic suspensions for the generation of electricity from freight train vibrations. J. Comput. Nonlinear Dyn. 2012, 7, 41011. [Google Scholar]
- Kloda, L.; Lenci, S.; Warminski, J. Hardening vs. softening dichotomy of a hinged-simply supported beam with one end axial linear spring: Experimental and numerical studies. Int. J. Mech. Sci. 2020, 178, 105588. [Google Scholar]
- Lo Monaco, M.; Russo, C.; Somà, A. Numerical and experimental performance study of two-degrees-of-freedom electromagnetic energy harvesters. Energy Convers. Manag. X 2023, 18, 100348. [Google Scholar]
- Costanzo, L.; Lo Schiavo, A.; Vitelli, M. Improving the electromagnetic vibration energy harvester performance by using a double coil structure. Appl. Sci. 2022, 12, 1166. [Google Scholar] [CrossRef]
- Ordoñez, V.; Arcos, R.; Romeu, J. A high-performance electromagnetic vibration energy harvester based on ring magnets with Halbach configuration. Energy Convers. Manag. X 2022, 16, 100280. [Google Scholar]
- Asadi, M.; Ahmadi, R.; Abazari, A.M. Halbach magnet arrays in electromagnetic kinetic energy harvesters: A review. Energy Convers. Manag. X 2024, 22, 100544. [Google Scholar]
- Ordoñez, V.; Arcos, R.; Romeu, J.; Reina, S. Analysis of different cylindrical magnet and coil configurations for electromagnetic vibration energy harvesters. Period. Eng. Nat. Sci. 2021, 9, 1055–1063. [Google Scholar]
- Phan, T.N.; Aranda, J.J.; Oelmann, B.; Bader, S. Design optimization and comparison of cylindrical electromagnetic vibration energy harvesters. Sensors 2021, 21, 7985. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Liu, Z.; Hu, H.; Hu, J.; Wang, J.; He, Z. Theoretical and experimental investigation of magnet and coil arrays optimization for power density improvement in electromagnetic vibration energy harvesters. Energy Convers. Manag. 2023, 293, 117411. [Google Scholar]
- Shen, Y.; Lu, K.; Xia, Y. Micro electromagnetic vibration energy harvester with mechanical spring and iron frame for low frequency operation. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 2842–2847. [Google Scholar]
- Lei, Y.; Wen, Z.; Chen, L. Simulation and testing of a micro electromagnetic energy harvester for self-powered system. AIP Adv. 2014, 4, 031303. [Google Scholar]
- Roy, S.; Podder, P.; Mallick, D. Nonlinear energy harvesting using electromagnetic transduction for wide bandwidth. IEEE Magn. Lett. 2015, 7, 5701004. [Google Scholar]
- Wang, K.; Dai, X.; Ren, C.; Ding, G. Fully integrated microsolenoid with closed magnetic circuit for high power density MEMS electromagnetic vibration energy harvesters. IEEE Magn. Lett. 2021, 12, 8102905. [Google Scholar]
- Nicolini, L.; Castagnetti, D. A wideband low frequency 3D printed electromagnetic energy harvester based on orthoplanar springs. Energy Convers. Manag. 2024, 300, 117903. [Google Scholar]
- Russo, C.; Lo Monaco, M.; Fraccarollo, F.; Somà, A. Experimental and numerical characterization of a gravitational electromagnetic energy harvester. Energies 2021, 14, 4622. [Google Scholar] [CrossRef]
- Lo Monaco, M.; Russo, C.; Somà, A. Identification procedure for design optimization of gravitational electromagnetic energy harvesters. Appl. Sci. 2023, 13, 2736. [Google Scholar] [CrossRef]
- Somà, A.; De Pasquale, G. Device for Diagnosing Railway Bogies by Applying an Energy-Autonomous Measuring and Transmitting Bolt, and Corresponding Control Method. WIPO Patent WO2011117718, 29 September 2011. [Google Scholar]
- Somà, A.; Fraccarollo, F.; De Pasquale, G. Magneto-Inductive Energy Harvester Device, Having an Internal Guide Magnetic Suspension. WIPO Patent WO2013190585, 12 June 2013. [Google Scholar]
- Lo Monaco, M. Internet of Things for Vehicle Health Monitoring Powered by Electromagnetic Energy Harvesters. Ph.D. Thesis, Politecnico di Torino, Turin, Italy, 2025. [Google Scholar]
- Nico, V.; Boco, E.; Frizzell, R.; Punch, J. A high figure of merit vibrational energy harvester for low frequency applications. Appl. Phys. Lett. 2016, 108, 013902. [Google Scholar]
- Royo-Silvestre, I.; Beato-López, J.; Gómez-Polo, C. Optimization procedure of low frequency vibration energy harvester based on magnetic levitation. Appl. Energy 2024, 360, 122778. [Google Scholar]
- Salauddin, M.; Halim, M.; Park, J. A magnetic-spring-based, low-frequency-vibration energy harvester comprising a dual Halbach array. Smart Mater. Struct. 2016, 25, 095017. [Google Scholar]
- Su, Y.; Zhang, K.; Gong, Q. Theoretical and experimental study of an electromagnetic vibration energy harvester. Ferroelectrics 2019, 551, 60–73. [Google Scholar]
- Constantinou, P.; Roy, S. A 3D printed electromagnetic nonlinear vibration energy harvester. Smart Mater. Struct. 2016, 25, 095053. [Google Scholar]
- Aldawood, G.; Nguyen, H.T.; Bardaweel, H. High power density spring-assisted nonlinear electromagnetic vibration energy harvester for low base-accelerations. Appl. Energy 2019, 253, 113546. [Google Scholar]
- Fan, K.; Cai, M.; Liu, H.; Zhang, Y. Capturing energy from ultra-low-frequency vibrations and human motion through a monostable electromagnetic energy harvester. Energy 2019, 169, 356–368. [Google Scholar]
- Ung, C.; Moss, S.D.; Chiu, W.K. Electromagnetic energy harvester using coupled oscillating system with 2-degree of freedom. In Proceedings of the Active and Passive Smart Structures and Integrated Systems 2015, San Diego, CA, USA, 8–12 March 2015; Volume 9431, pp. 644–651. [Google Scholar]
- Masood Ahmad, M.; Ullah Khan, F. Two degree of freedom vibration based electromagnetic energy harvester for bridge health monitoring system. J. Intell. Mater. Syst. Struct. 2021, 32, 516–536. [Google Scholar] [CrossRef]
- Tao, K.; Wu, J.; Tang, L.; Xia, X.; Lye, S.W.; Miao, J.; Hu, X. A novel two-degree-of-freedom MEMS electromagnetic vibration energy harvester. J. Micromech. Microeng. 2016, 26, 035020. [Google Scholar] [CrossRef]
- Monaco, M.L.; Russo, C. Design methodology of a two-degrees-of-freedom gravitational energy harvester. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1275, 012042. [Google Scholar] [CrossRef]
- Fan, K.; Zhang, Y.; Liu, H.; Cai, M.; Tan, Q. A nonlinear two-degree-of-freedom electromagnetic energy harvester for ultra-low-frequency vibrations and human body motions. Renew. Energy 2019, 138, 292–302. [Google Scholar] [CrossRef]
- Beeby, S.P.; Torah, R.N.; Tudor, M.J.; Glynne-Jones, P.; O’Donnell, T.; Saha, C.R.; Roy, S. A micro electromagnetic generator for vibration energy harvesting. J. Micromech. Microeng. 2007, 17, 1257. [Google Scholar] [CrossRef]
- Mitcheson, P.D.; Yeatman, E.M.; Rao, G.K.; Holmes, A.S.; Green, T.C. Energy harvesting from human and machine motion for wireless electronic devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef]








| Methodology | Power Density | Advantages | Disadvantages |
|---|---|---|---|
| Electromagnetic | 200–800 Wcm−3 | Wide bandwidth | Magnetic leakage |
| High current | Low voltage | ||
| High power | Large size | ||
| Piezoelectric | 20–330 Wcm−3 | High voltage | Low current |
| Simple structure | Easy aging | ||
| Small size | Low power | ||
| Electrostatic | 180 Wcm−3 | Low frequencies | Start-up power |
| High integrability | Low currents |
| Reference | Spring | Volume (cm3) | Frequency (Hz) | Acceleration (g) | Power (mW) | NPD (mWcm−3g−2) | FoMv (%) |
|---|---|---|---|---|---|---|---|
| [28] | Mechanical | 6.47 | 5.17 | 2.06 | 2.15 | 0.078 | 2.25 |
| [47] | Mechanical | - | 78.8 | 2.00 | 7.22 | - | - |
| [48] | Mechanical | 137.9 | 61.7 | 0.03 | 3.61 | 29.1 | 0.37 |
| [51] | Mechanical | 30 | 55 | 0.2 | 28.3 | 23.6 | 3.71 |
| [52] | Mechanical | 34.8 | 41.2 | 1 | 3.71 | 0.107 | 0.11 |
| [53] | Mechanical | 1.6 | 10.1 | 0.52 | 0.72 | 1.66 | 9.84 |
| [54] | MEMS | 1.8 | 124 | 0.5 | 0.21 | 0.47 | 0.21 |
| [55] | MEMS | 5.9 1 | 63.7 | 1 | 1.18 | 0.20 | 0.23 |
| [56] | MEMS | 0.045 | 138 | 1 | 0.265 | 5.89 | 16.12 |
| [57] | MEMS | 173 | 15.1 | 0.37 | 5.0 | 0.21 | 0.12 |
| [59] | Magnetic | 61.5 | 4 | 0.5 | 39.0 | 2.54 | 10.8 |
| [63] | Magnetic | 8.12 | 11.5 | 0.4 | 2.06 | 1.59 | 3.70 |
| [64] | Magnetic | 938 1 | 1.7 | 0.5 | 4.38 | 0.019 | 0.075 |
| [65] | Magnetic | 32.76 | 11 | 0.5 | 1.1 | 0.13 | 0.26 |
| [66] | Magnetic | - | 5 | 0.08 | 7.6 × 10 −5 | - | - |
| [67] | Hybrid 2 | 6 | 147 | 1 | 2.9 | 0.48 | 0.24 |
| [68] | Hybrid 3 | 222 | 11 | 0.4 | 70.0 | 1.97 | 1.59 |
| [69] | Hybrid 3 | 12 | 9 | 0.8 | 1.15 | 0.15 | 0.78 |
| Reference | Spring | Volume (cm3) | Frequency (Hz) | Acceleration (g) | Power (mW) | NPD (mWcm−3g−2) | FoMv (%) |
|---|---|---|---|---|---|---|---|
| [70] | Mechanical | 600 3 | 6.0, 14.6 | 0.5 | 350 1 | 2.33 | 3.10 |
| [34] | Mechanical | 53.9 | 58, 74.5 | 0.27 | 10.9 1 | 2.77 | 0.46 |
| [71] | Mechanical | 333 | 4.4, 5.5 | 0.09 | 10.7 2 | 3.97 | 1.26 |
| [72] | MEMS | 0.29 | 326, 391 | 0.12 | 0.96 × 10−6 2 | 2.2 × 10−4 | 1.4 × 10−5 |
| [46] | Magnetic | 226 | 3.4, 6.7 | 0.4 | 8.25 1 | 0.23 | 0.59 |
| [74] | Magnetic | 26.3 | 7.5, 18.5 | 0.5 | 2.58 1 | 0.39 | 1.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perrozzi, M.V.; Lo Monaco, M.; Somà, A. Recent Advances in Translational Electromagnetic Energy Harvesting: A Review. Energies 2025, 18, 1588. https://doi.org/10.3390/en18071588
Perrozzi MV, Lo Monaco M, Somà A. Recent Advances in Translational Electromagnetic Energy Harvesting: A Review. Energies. 2025; 18(7):1588. https://doi.org/10.3390/en18071588
Chicago/Turabian StylePerrozzi, Marco Valerio, Mirco Lo Monaco, and Aurelio Somà. 2025. "Recent Advances in Translational Electromagnetic Energy Harvesting: A Review" Energies 18, no. 7: 1588. https://doi.org/10.3390/en18071588
APA StylePerrozzi, M. V., Lo Monaco, M., & Somà, A. (2025). Recent Advances in Translational Electromagnetic Energy Harvesting: A Review. Energies, 18(7), 1588. https://doi.org/10.3390/en18071588