Experimental Study on Heat Transfer Coefficients in an Office Room with a Radiant Ceiling During Low Heating Loads
Abstract
1. Introduction
2. Materials and Methods
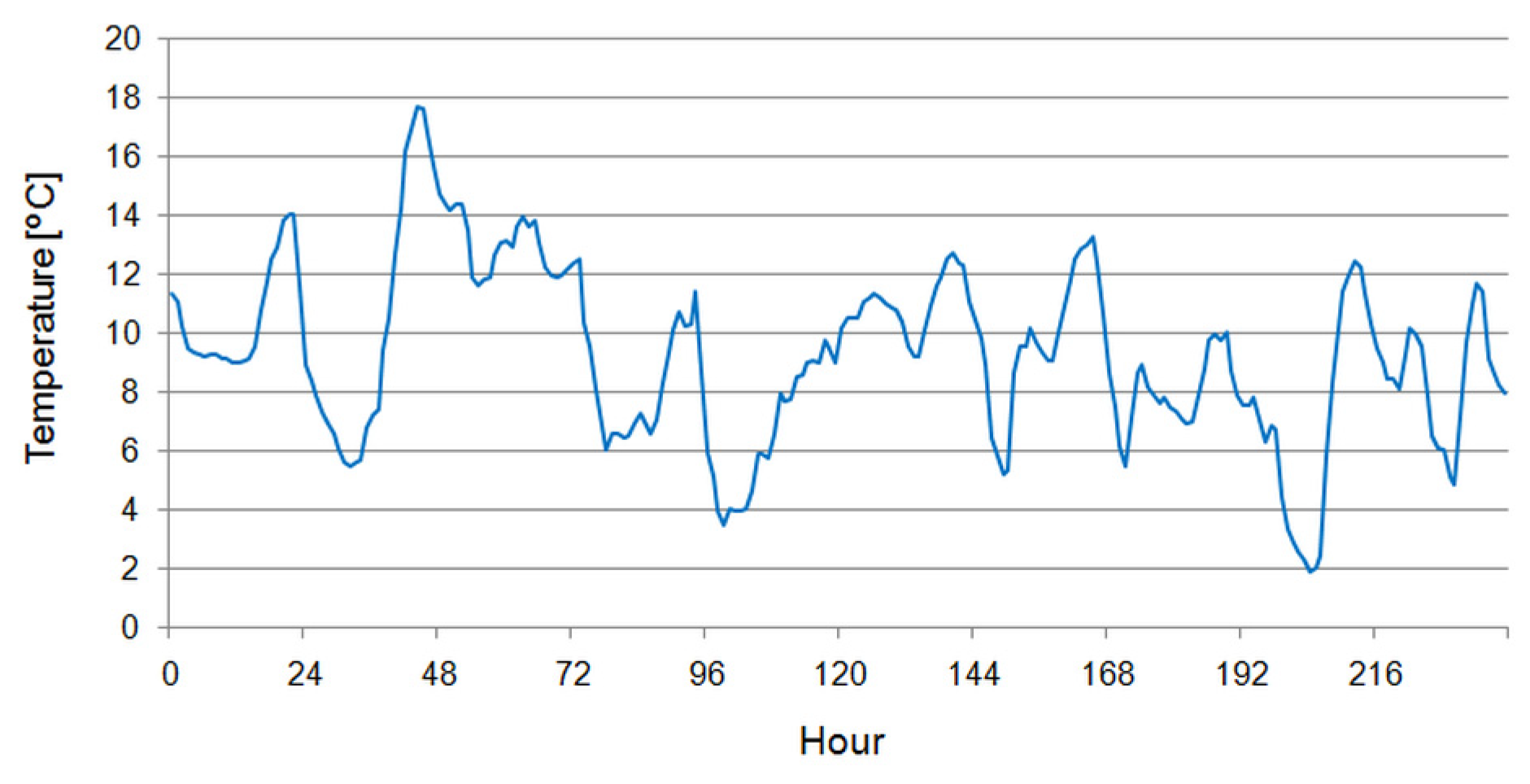
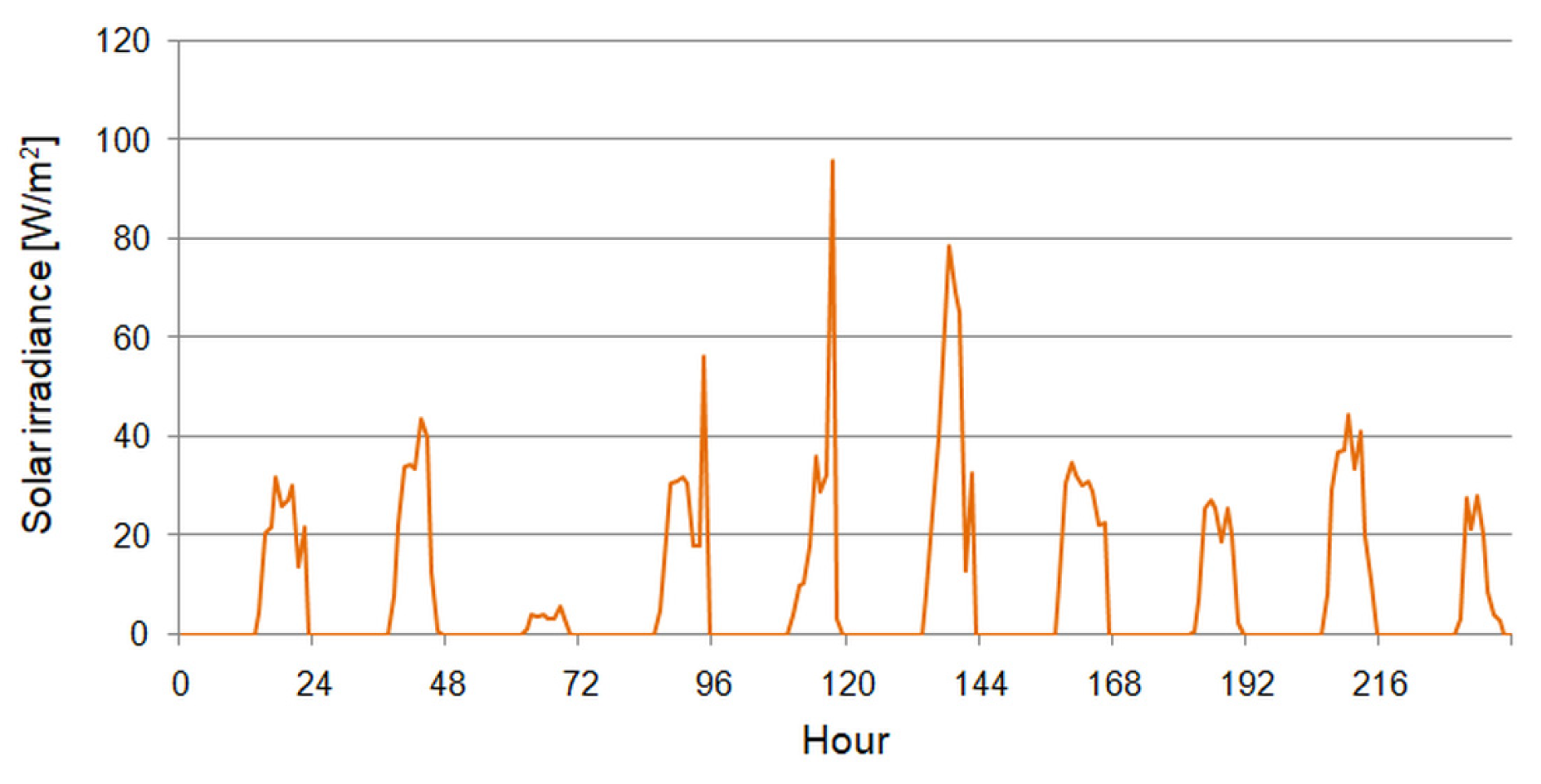
2.1. Building Description
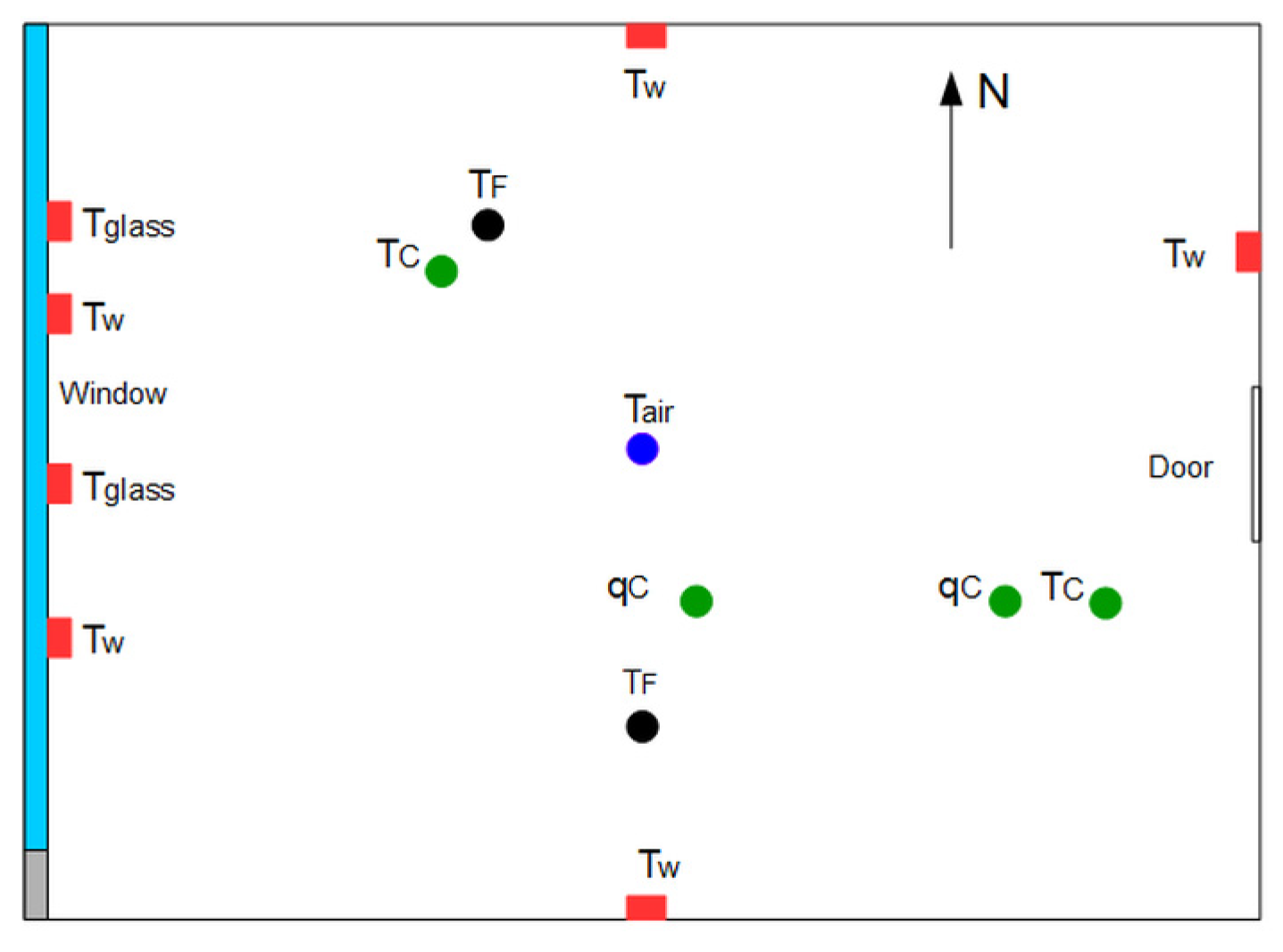
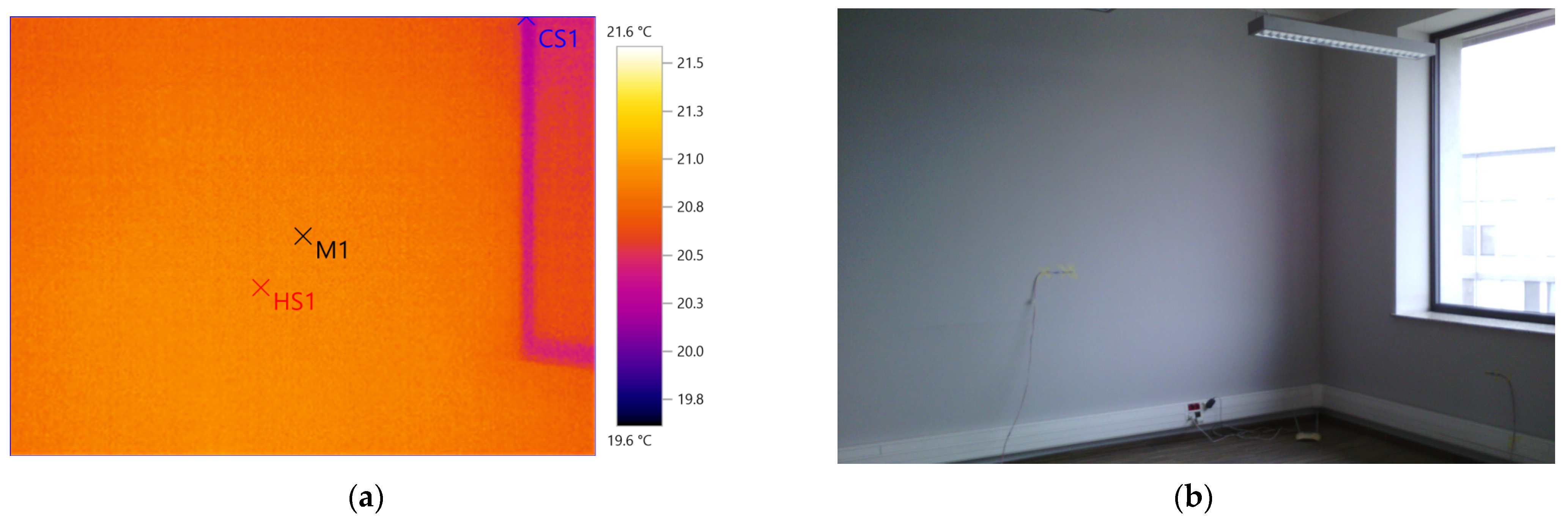
2.2. Experimental Setup
2.3. Calculation Procedure
2.4. Selected Correlations for CHTC Calculations
3. Results and Discussion
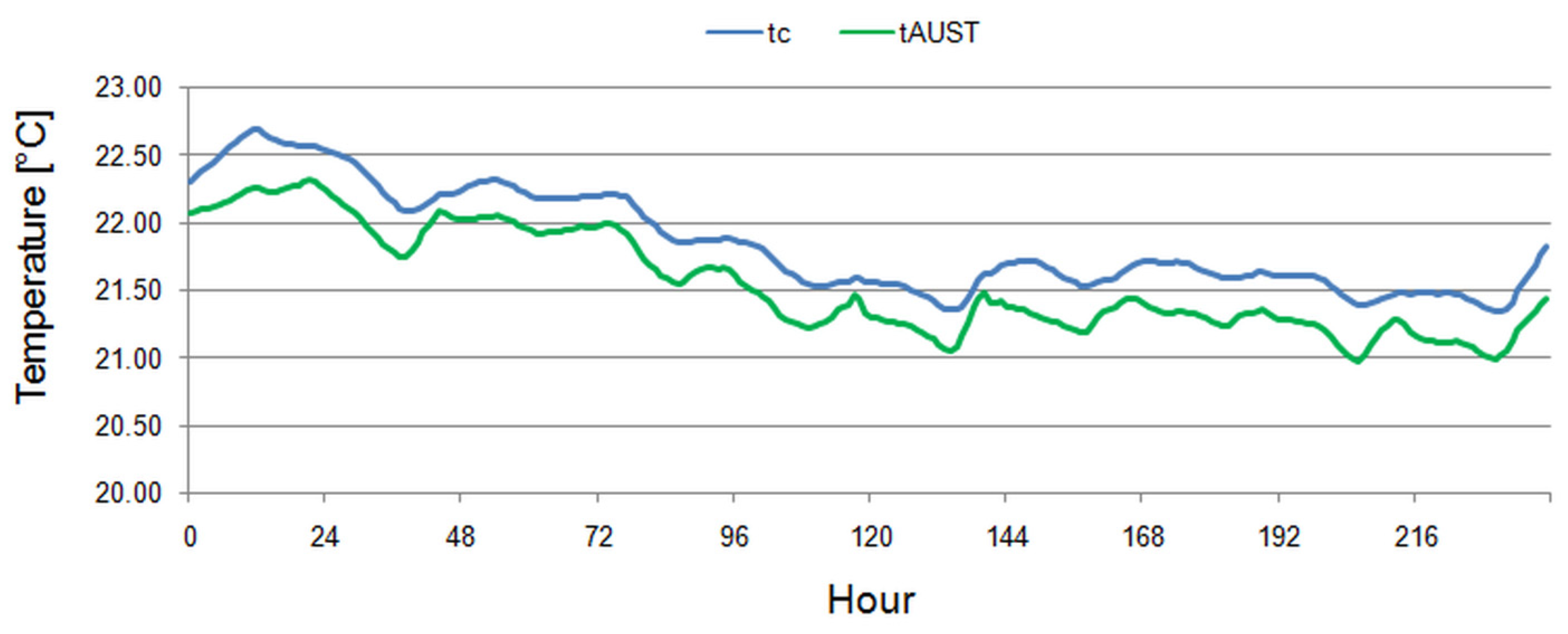
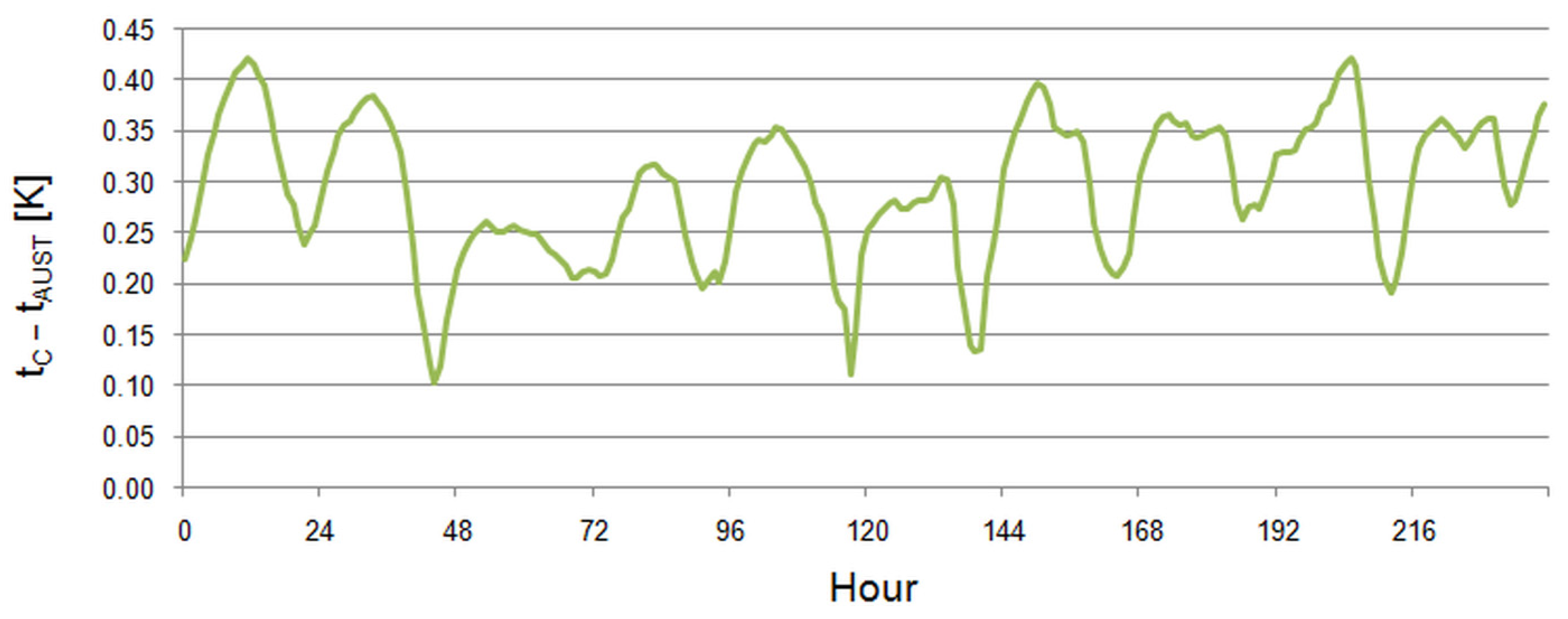
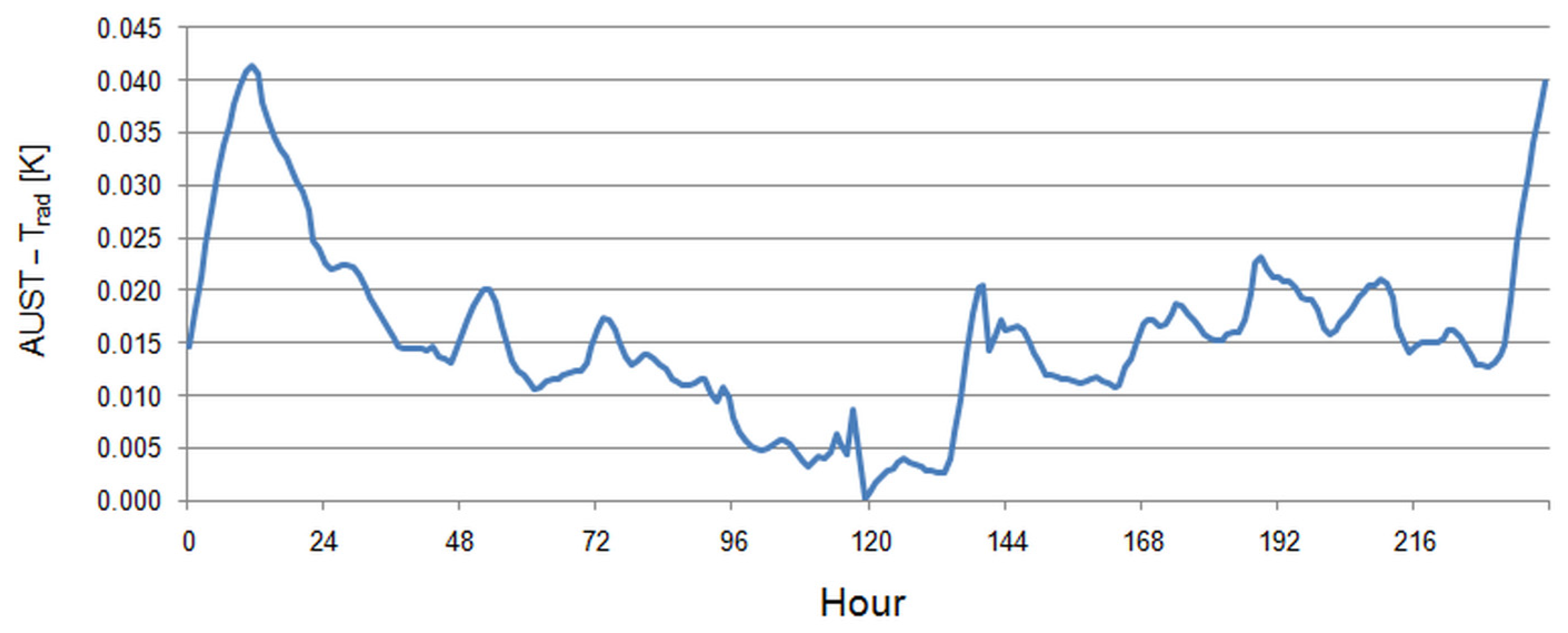
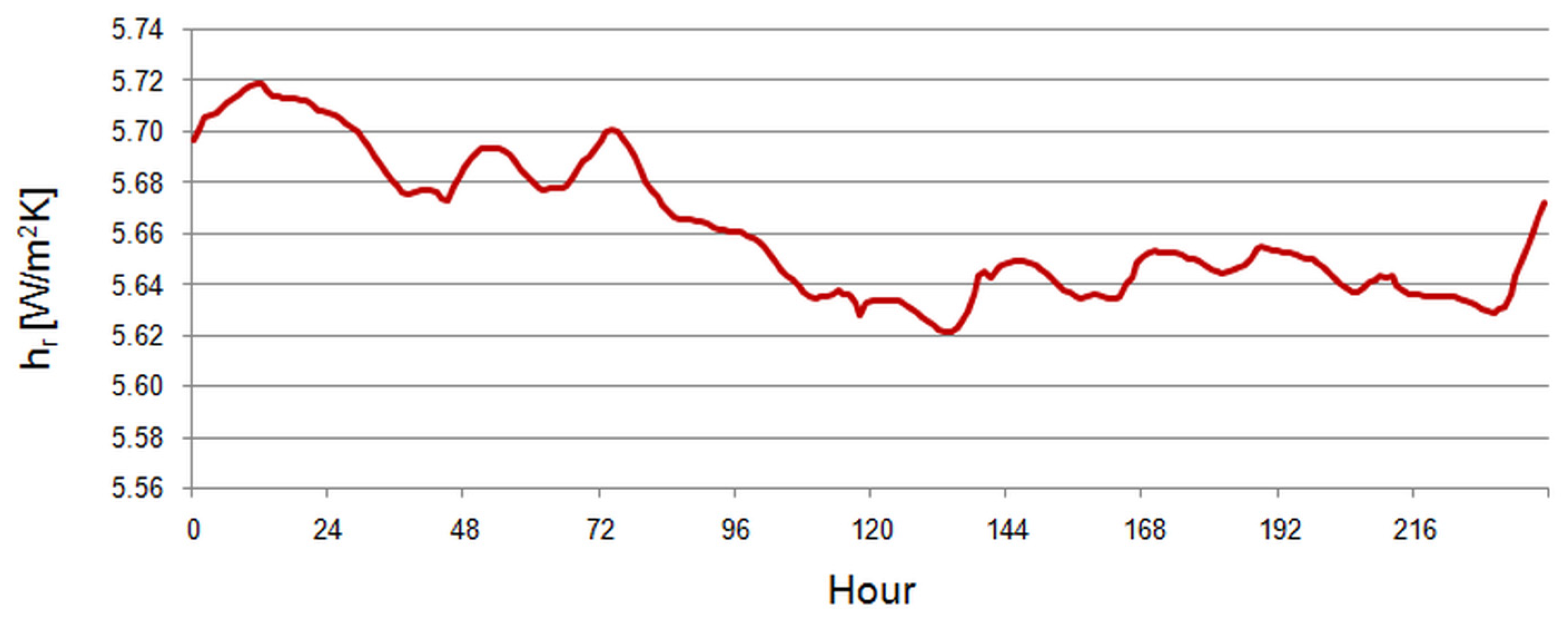
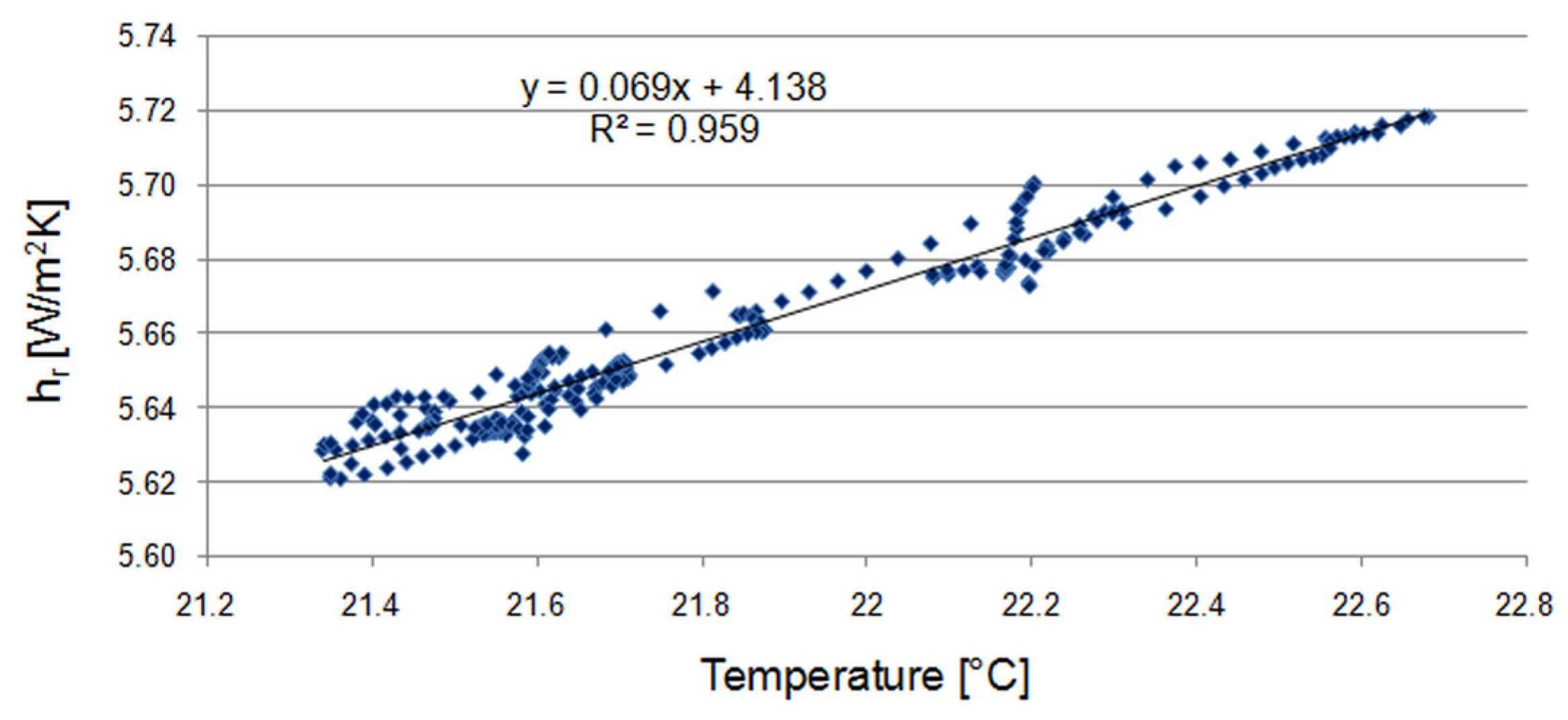
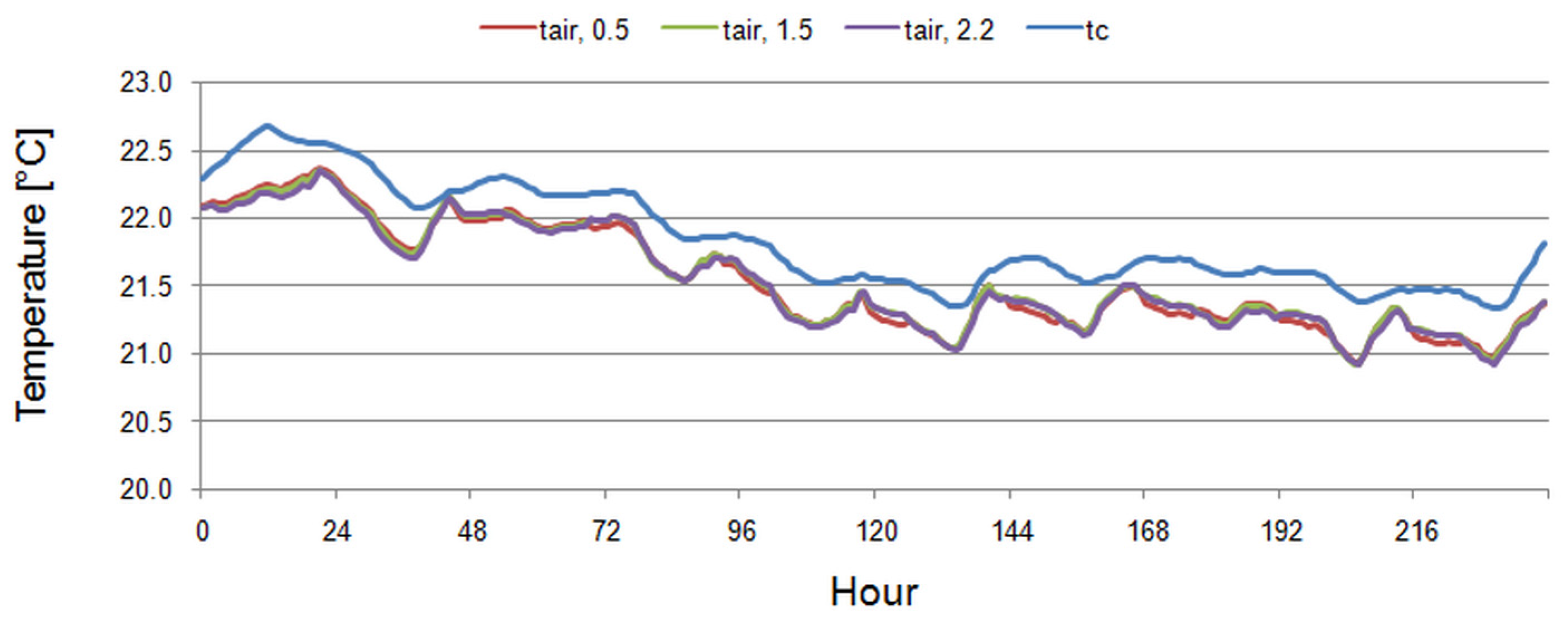
3.1. Radiant Heat Transfer Coefficient
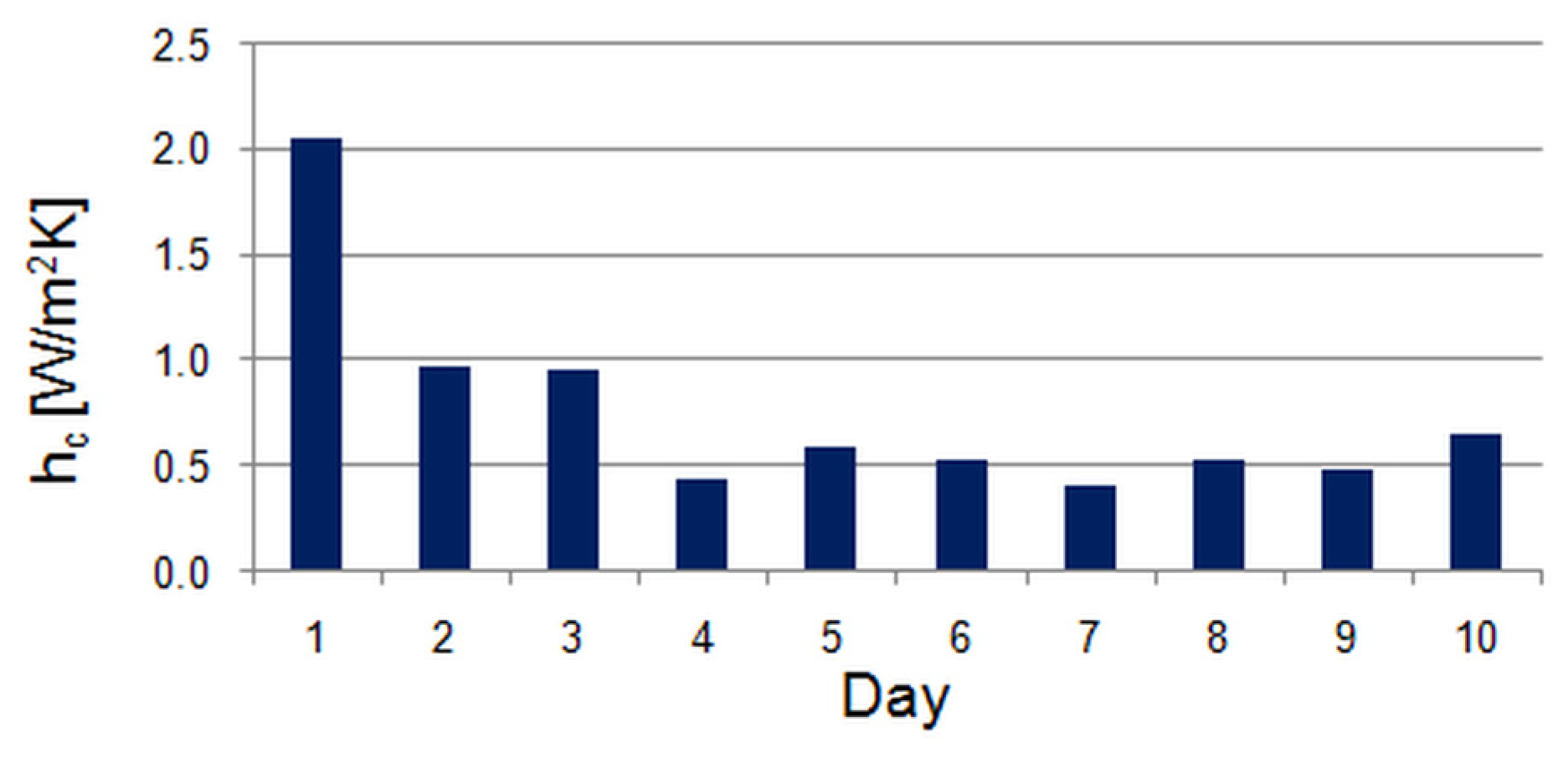
3.2. Convective Heat Transfer Coefficient
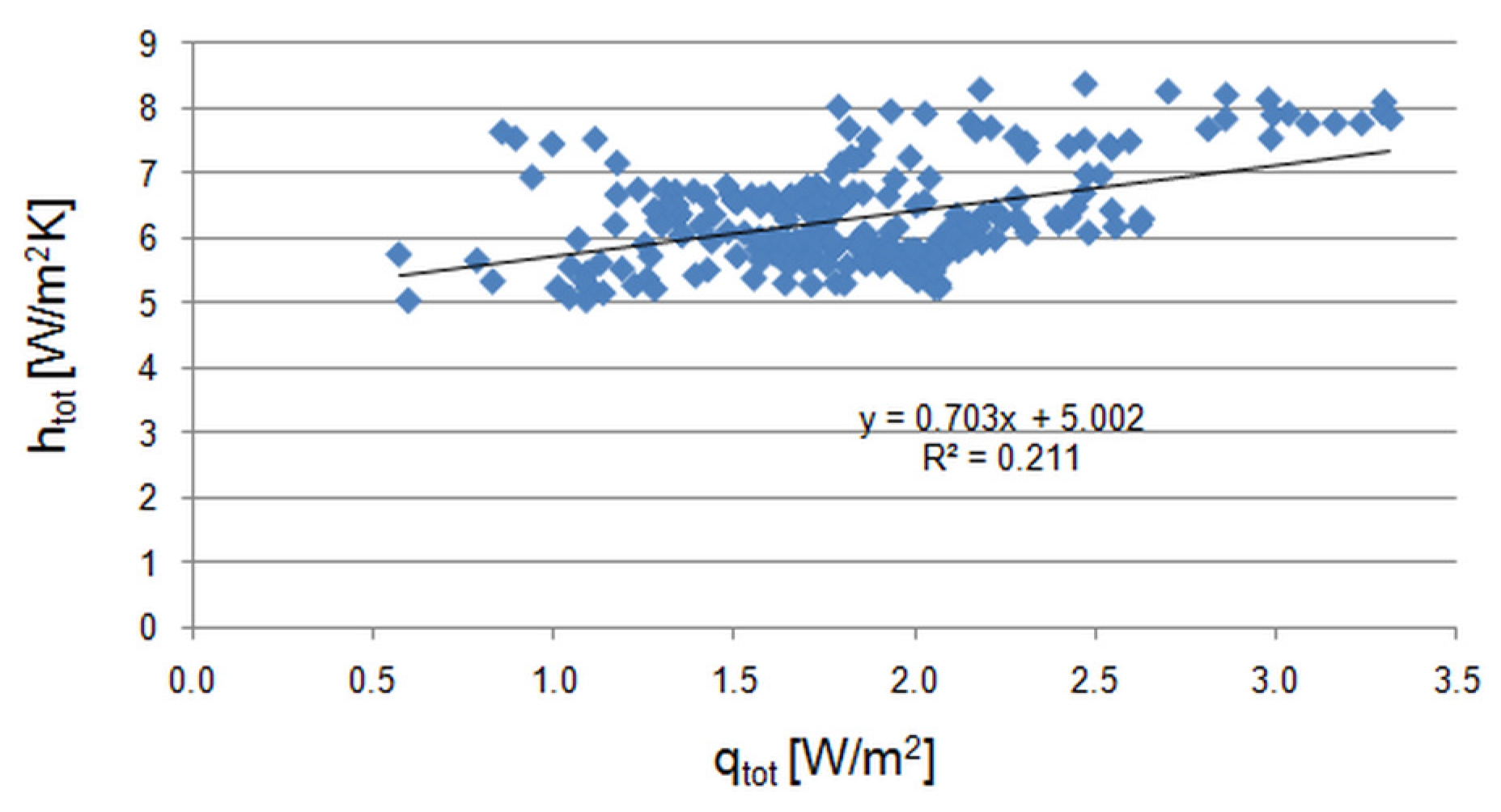
3.3. Total Heat Transfer Coefficient
3.4. Comparison of Results
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Symbols
| AUST | average unheated surface temperature, K |
| hc | convective heat transfer coefficient, W/m2K |
| hr | radiant heat transfer coefficient, W/m2K |
| htot | total heat transfer coefficient, W/m2K |
| k | coverage factor, |
| qc | convective heat flux, W/m2 |
| qr | radiant heat flux, W/m2 |
| qtot | total heat flux, W/m2 |
| t | temperature (general), °C |
| uc | combined uncertainty, |
| R2 | coefficient of determination, |
| Tair | internal air temperature, K |
| Trad | area-weighted radiant temperature, K |
| Tc | ceiling surface temperature, K |
| Top | operative temperature, K |
| U | expanded uncertainty, |
| ε | surface emissivity, |
| σ | Stefan–Boltzmann constant, σ = 5.6697 10−8 W/m2K4 |
Appendix A
| Uncertainty | Value | Unit |
|---|---|---|
| u(qr) | 0.017 | W/m2 |
| u(Tc) | 0.050 | K |
| u(AUST) | 0.648 | K |
| −1.966 × 10–7 | W/m2K | |
| 1.113 × 10–6 | W/m2K2 | |
| 1.113 × 10–6 | W/m2K2 |
| Uncertainty | Value | Unit |
|---|---|---|
| u(qc) | 0.012 | W/m2 |
| u(Ti) | 0.05 | K |
| u(TC) | 0.05 | K |
| 3.268 | W/m2K | |
| −2.617 | W/m2K2 | |
| 2.617 | W/m2K2 |
References
- Junasová, B.; Krajčík, M.; Šikula, O.; Arıcı, M.; Šimko, M. Adapting the construction of radiant heating and cooling systems for building retrofit. Energy Build. 2022, 268, 112228. [Google Scholar] [CrossRef]
- Krajčík, M.; Šimko, M.; Šikula, O.; Szabó, D.; Petráš, D. Thermal performance of a radiant wall heating and cooling system with pipes attached to thermally insulating bricks. Energy Build. 2021, 246, 111122. [Google Scholar] [CrossRef]
- ISO 11855–1:2021.; Building Environment Design. Embedded Radiant Heating and Cooling Systems. Part 2: Determination of the Design Heating and Cooling Capacity. International Organization for Standardization: Geneva, Switzerland, 2021.
- Sinacka, J.; Szczechowiak, E. An Experimental Study of a Thermally Activated Ceiling Containing Phase Change Material for Different Cooling Load Profiles. Energies 2021, 14, 7363. [Google Scholar] [CrossRef]
- Aryal, A.; Chaiwiwatworakul, P.; Chirarattananon, S. An experimental study of thermal performance of the radiant ceiling cooling in office building in Thailand. Energy Build. 2023, 283, 112849. [Google Scholar] [CrossRef]
- Shi, S.; Merabtine, A.; Bennacer, R. Radiant systems and solar-driven overheating: A comprehensive literature analysis over a decade. Build. Environ. 2024, 259, 111659. [Google Scholar] [CrossRef]
- Karakoyun, Y.; Acikgoz, O.; Çebi, A.; Koca, A.; Çetin, G.; Dalkilic, A.S.; Wongwises, S. A comprehensive approach to analyze the discrepancies in heat transfer characteristics pertaining to radiant ceiling heating system. Appl. Therm. Eng. 2021, 187, 116517. [Google Scholar] [CrossRef]
- Hu, R.; Sun, S.; Liang, J.; Zhou, Z.; Yin, Y. A Review of Studies on Heat Transfer in Buildings with Radiant Cooling Systems. Buildings 2023, 13, 1994. [Google Scholar] [CrossRef]
- Liao, W.; Wen, C.; Luo, Y.; Peng, J.; Li, N. Influence of different building transparent envelopes on energy consumption and thermal environment of radiant ceiling heating and cooling systems. Energy Build. 2022, 255, 111702. [Google Scholar] [CrossRef]
- Dogan, A.; Kayaci, N.; Kanbur, B.B.; Demir, H. Experimental Investigation of Mean Radiant Temperature Trends for a Ground Source Heat Pump-Integrated Radiant Wall and Ceiling Heating System. Buildings 2023, 13, 2420. [Google Scholar] [CrossRef]
- Bouacida, T.; Bentoumi, L.; Bessaïh, R. Experimental study of a low-cost ceiling cooling system in the north Algerian climate. Energy Build. 2023, 293, 113196. [Google Scholar] [CrossRef]
- Causone, F.; Corgnati, S.P.; Filippi, M.; Olesen, B.W. Experimental evaluation of heat transfer coefficients between radiant ceiling and room. Energy Build. 2009, 41, 622–628. [Google Scholar] [CrossRef]
- Rahimi, M.; Sabernaeemi, A. Experimental study of radiation and free convection in an enclosure with a radiant ceiling heating system. Energy Build. 2010, 42, 2077–2082. [Google Scholar] [CrossRef]
- Cholewa, T.; Rosiński, M.; Spik, Z.; Dudzińska, M.R.; Siuta-Olchaa, A. On the heat transfer coefficients between heated/cooled radiant floor and room. Energy Build. 2013, 66, 599–606. [Google Scholar] [CrossRef]
- Yu, T.; Heiselberg, P.; Lei, B.; Pomianowski, M.; Zhang, C.; Jensen, R. Experimental investigation of cooling performance of a novel HVAC system combining natural ventilation with diffuse ceiling inlet and TABS. Energy Build. 2015, 105, 165–177. [Google Scholar] [CrossRef]
- Koca, A.; Gürsel, C. Experimental investigation on the heat transfer coefficients of radiant heating systems: Wall, ceiling and wall-ceiling integration. Energy Build. 2017, 148, 311–326. [Google Scholar] [CrossRef]
- Koca, A.; Acikgoz, O.; Çebi, A.; Çetin, G.; Dalkilic, A.S.; Wongwises, S. An experimental investigation devoted to determine heat transfer characteristics in a radiant ceiling heating system. Heat Mass. Transf. 2017, 54, 363–375. [Google Scholar] [CrossRef]
- Cholewa, T.; Anasiewicz, R.; Siuta-Olcha, A.; Skwarczynski, M.A. On the heat transfer coefficients between heated/cooled radiant ceiling and room. Appl. Therm. Eng. 2017, 117, 76–84. [Google Scholar] [CrossRef]
- Szpytma, M.; Rybka, A. Ecological ideas in Polish architecture—environmental impact. J. Civ. Eng. Environ. Arch. 2016, XXXIII, 321–328. [Google Scholar] [CrossRef]
- Michalak, P. Selected Aspects of Indoor Climate in a Passive Office Building with a Thermally Activated Building System: A Case Study from Poland. Energies 2021, 14, 860. [Google Scholar] [CrossRef]
- IEC 60751:2022; Industrial Platinum Resistance Thermometers and Platinum Temperature Sensors. International Electrotechnical Commission: Geneva, Switzerland, 2022.
- ISO 9060:2018; Solar Energy—Specification and Classification of Instruments for Measuring Hemispherical Solar and Direct Solar Radiation. International Organization for Standardization: Geneva, Switzerland, 2018.
- IEC 61724-1:2021; Photovoltaic system performance—Part 1: Monitoring. International Organization for Standardization: Geneva, Switzerland, 2022.
- Diaz, F.N.; Lebrun, J.; André, P. Experimental study and modelling of cooling ceiling systems using steady-state analysis. Int. J. Refrig. 2010, 33, 793–805. [Google Scholar] [CrossRef]
- Atef, A.; Noureddine, Z.; Soufiane, F. SPUCAL_mrt as a New Model for Estimating the Mean Radiant Temperature in Arid Lands. Energy Procedia 2015, 74, 273–280. [Google Scholar] [CrossRef][Green Version]
- Evren, M.F.; Özsunar, A.; Kılkış, B. Experimental investigation of energy-optimum radiant-convective heat transfer split for hybrid heating systems. Energy Build. 2016, 127, 66–74. [Google Scholar] [CrossRef]
- Lauster, M.; Teichmann, J.; Fuchs, M.; Streblow, R.; Mueller, D. Low order thermal network models for dynamic simulations of buildings on city district scale. Build. Environ. 2014, 73, 223–231. [Google Scholar] [CrossRef]
- Cui, Y.; Xie, J.; Liu, J.; Xue, P. Experimental and Theoretical Study on the Heat Transfer Coefficients of Building External Surfaces in the Tropical Island Region. Appl. Sci. 2019, 9, 1063. [Google Scholar] [CrossRef]
- EN ISO 6946:2017; Building Components and Building Elements. Thermal Resistance and Thermal Transmittance. Calculation Methods. International Organization for Standardization: Geneva, Switzerland, 2017.
- Shinoda, J.; Kazanci, O.B.; Tanabe, S.; Olesen, B.W. A Review of the Surface Heat Transfer Coefficients of Radiant Heating and Cooling Systems. Build. Environ. 2019, 159, 106156. [Google Scholar] [CrossRef]
- Awbi, H.B.; Hatton, A. Natural convection from heated room surfaces. Energy Build. 1999, 30, 233–244. [Google Scholar] [CrossRef]
- ASHRAE. Handbook HVAC Fundamentals; ASHRAE: Peachtree Corners, GA, USA, 2009. [Google Scholar]
- ASHRAE. 2012 ASHRAE Handbook—Heating, Ventilating, and Air Conditioning: Systems and Equipment; ASHRAE: Peachtree Corners, GA, USA, 2012. [Google Scholar]
- Min, T.C.; Schutrum, L.F.; Parmelee, G.V. Natural convection and radiation in a panel heated room. ASHRAE Trans. 1956, 62, 337–358. [Google Scholar]
- Wallentén, P. Convective heat transfer coefficients in a full-scale room with and without furniture. Build. Environ. 2001, 36, 743–751. [Google Scholar] [CrossRef]
- Miriel, J.; Serres, L.; Trombe, A. Radiant ceiling panel heating-cooling systems: Experimental and simulated study of the performances, thermal comfort and energy consumptions. Appl. Therm. Eng. 2002, 22, 1861–1873. [Google Scholar] [CrossRef]
- Helm, I.; Jalukse, L.; Leito, I. Measurement Uncertainty Estimation in Amperometric Sensors: A Tutorial Review. Sensors 2010, 10, 4430–4455. [Google Scholar] [CrossRef]
- Alamdari, F.; Hammond, G.P. Improved data correlations for buoyancy-driven convection in rooms. Build. Serv. Eng. Res. Technol. 1983, 4, 106–112. [Google Scholar] [CrossRef]
- Lewandowski, W.M. Natural convection heat transfer from plates of finite dimensions. Int. J. Heat Mass Transf. 1991, 34, 875–885. [Google Scholar] [CrossRef]
- Le Dreau, J.; Heiselberg, P.; Jensen, R.L. Experimental Data From a Full-Scale Facility Investigating Radiant and Convective Terminals: Uncertainty and Sensitivity Analysis, Description of the Experimental Data; DCE Technical reports No. 168; Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2014; Available online: https://vbn.aau.dk/en/publications/experimental-data-from-a-full-scale-facility-investigating-radian (accessed on 10 January 2025).



| Device | Manufacturer | Measured Variable | Measurement Range | Accuracy |
|---|---|---|---|---|
| Pt100 resistance sensor | Limatherm Sensor, Poland | Room air temperature | −50 °C ÷ +150 °C | Class AA 1 |
| Pt100 resistance sensor | Ampero Thermo-Est, Poland | Surface temperature | −50 °C ÷ +150 °C | Class AA 1 |
| Pt1000 resistance sensor | Apator, Poland | Ambient air temperature | −50 °C ÷ +150 °C | Class A 1 |
| LP PYRA03 | Delta Ohm, Italy | Solar irradiance | 0 ÷ 2000 W/m2 | Spectrally Flat Class C 2 |
| HFP01 | Hukseflux, Netherlands | Heat flux | −2000 ÷ 2000 W/m2 | ±3% |
| HFP03 | Hukseflux, Netherlands | Heat flux | −2000 ÷ 2000 W/m2 | ±6% |
| Fluke 2638A data logger | Fluke, U.S.A. | Voltage | 0÷100 mV | 0.0025% MV + 0.0035% FS + 2 μV 3 |
| Fluke 2638A data logger | Fluke, U.S.A. | Temperature | −50 °C ÷ +150 °C | 0.038 °C at 0 °C, 0.073 °C at 300 °C |
| Surface Number | Surface Name | Fc-j [–] |
|---|---|---|
| 1 | East wall | 0.116039641 |
| 2 | North wall | 0.163240031 |
| 3 | External (west) wall | 0.033180406 |
| 4 | External window | 0.082859227 |
| 5 | South wall | 0.163240030 |
| 6 | Floor | 0.441440661 |
| Reference | hc [W/m2K] | Comments |
|---|---|---|
| This study | 0.80 | Whole period |
| [31] | 0.19 | Equation (14) |
| [32] | 0.26 | Equation (15) |
| [33] | 0.09 | Equation (16) |
| [33] | 0.10 | Equation (17) |
| [16] | 0.59 | Equation (18) |
| [29] | 0.70 | Horizontal wall with downward heat flow |
| [16] | 0.82 | Tc—Tair = 10.8 K |
| [12] | 0.0 … 0.60 | Tc—Tair = 6.3 … 11.1 K, Tair at 1.1 m |
| [18] | 0.0 … 0.13 | Tc—Tair = 1.32 … 8.29 K, Tair at 1.1 m |
| [36] | 1.25 | Validated TRNSYS model |
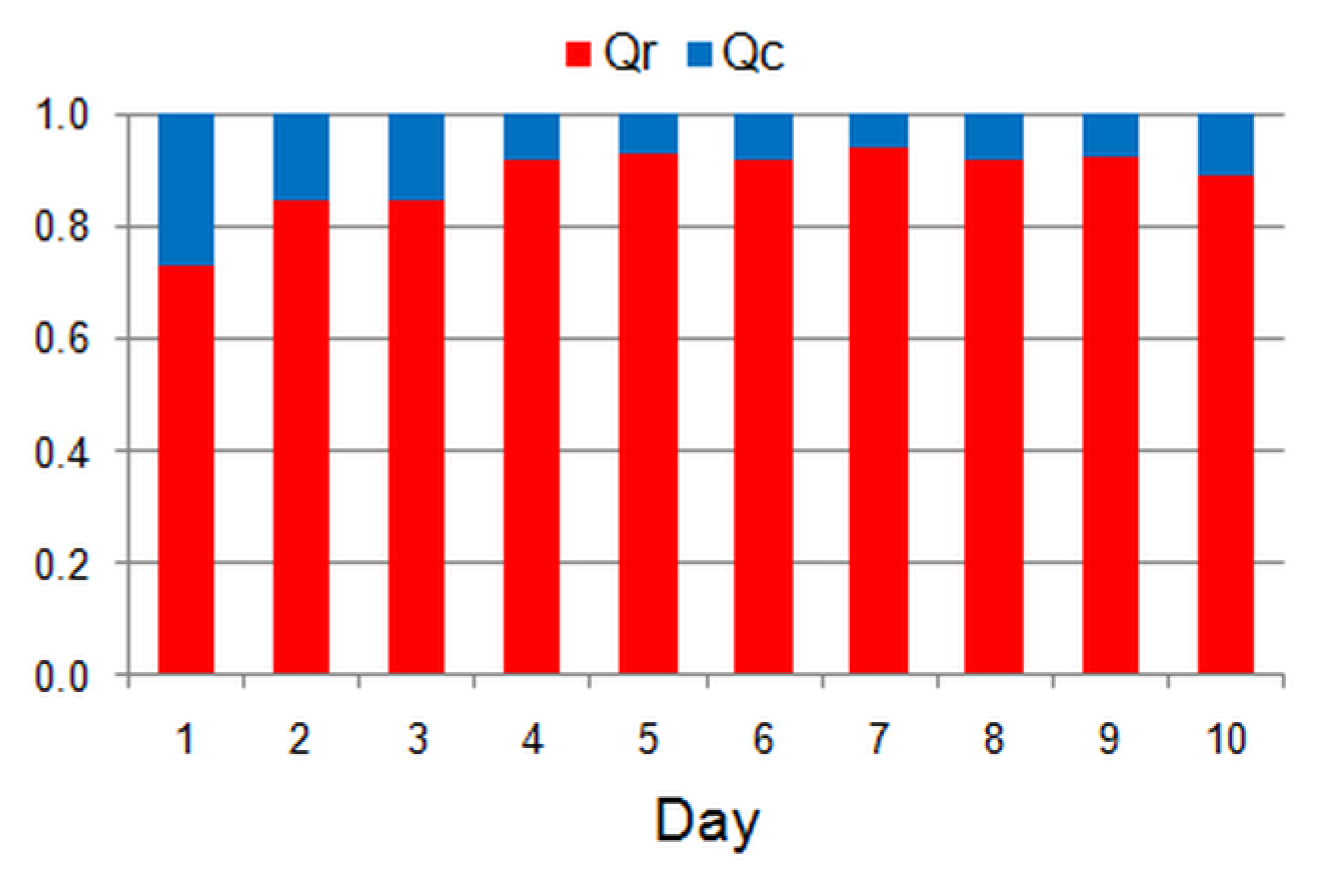
| Variable | Unit | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tc | °C | 22.54 | 22.26 | 22.22 | 21.99 | 21.65 | 21.50 | 21.63 | 21.65 | 21.50 | 21.48 |
| Tair | °C | 22.20 | 21.98 | 21.97 | 21.74 | 21.36 | 21.25 | 21.33 | 21.32 | 21.18 | 21.13 |
| AUST | °C | 22.21 | 21.98 | 21.99 | 21.73 | 21.37 | 21.25 | 21.32 | 21.32 | 21.18 | 21.14 |
| Top | °C | 22.21 | 21.98 | 21.98 | 21.76 | 21.34 | 21.26 | 21.31 | 21.32 | 21.16 | 21.14 |
| qr | W/m2 | 1.88 | 1.62 | 1.35 | 1.44 | 1.58 | 1.40 | 1.76 | 1.85 | 1.83 | 1.91 |
| hr | W/m2K | 5.71 | 5.69 | 5.69 | 5.68 | 5.64 | 5.63 | 5.64 | 5.65 | 5.64 | 5.64 |
| qc | W/m2 | 0.70 | 0.29 | 0.24 | 0.13 | 0.12 | 0.12 | 0.11 | 0.17 | 0.15 | 0.24 |
| hc | W/m2K | 2.05 | 0.97 | 0.96 | 0.45 | 0.59 | 0.54 | 0.40 | 0.53 | 0.50 | 0.65 |
| qtot | W/m2 | 2.58 | 1.84 | 1.59 | 1.51 | 1.62 | 1.52 | 1.76 | 2.02 | 1.94 | 2.14 |
| htot | W/m2K | 7.77 | 6.66 | 6.64 | 6.13 | 6.23 | 6.17 | 6.05 | 6.18 | 6.14 | 6.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michalak, P. Experimental Study on Heat Transfer Coefficients in an Office Room with a Radiant Ceiling During Low Heating Loads. Energies 2025, 18, 1591. https://doi.org/10.3390/en18071591
Michalak P. Experimental Study on Heat Transfer Coefficients in an Office Room with a Radiant Ceiling During Low Heating Loads. Energies. 2025; 18(7):1591. https://doi.org/10.3390/en18071591
Chicago/Turabian StyleMichalak, Piotr. 2025. "Experimental Study on Heat Transfer Coefficients in an Office Room with a Radiant Ceiling During Low Heating Loads" Energies 18, no. 7: 1591. https://doi.org/10.3390/en18071591
APA StyleMichalak, P. (2025). Experimental Study on Heat Transfer Coefficients in an Office Room with a Radiant Ceiling During Low Heating Loads. Energies, 18(7), 1591. https://doi.org/10.3390/en18071591








