Numerical Investigations on the Effects of Inertia on the Startup Dynamics of a Multibladed Savonius Wind Turbine
Abstract
:1. Introduction
2. Materials and Methods
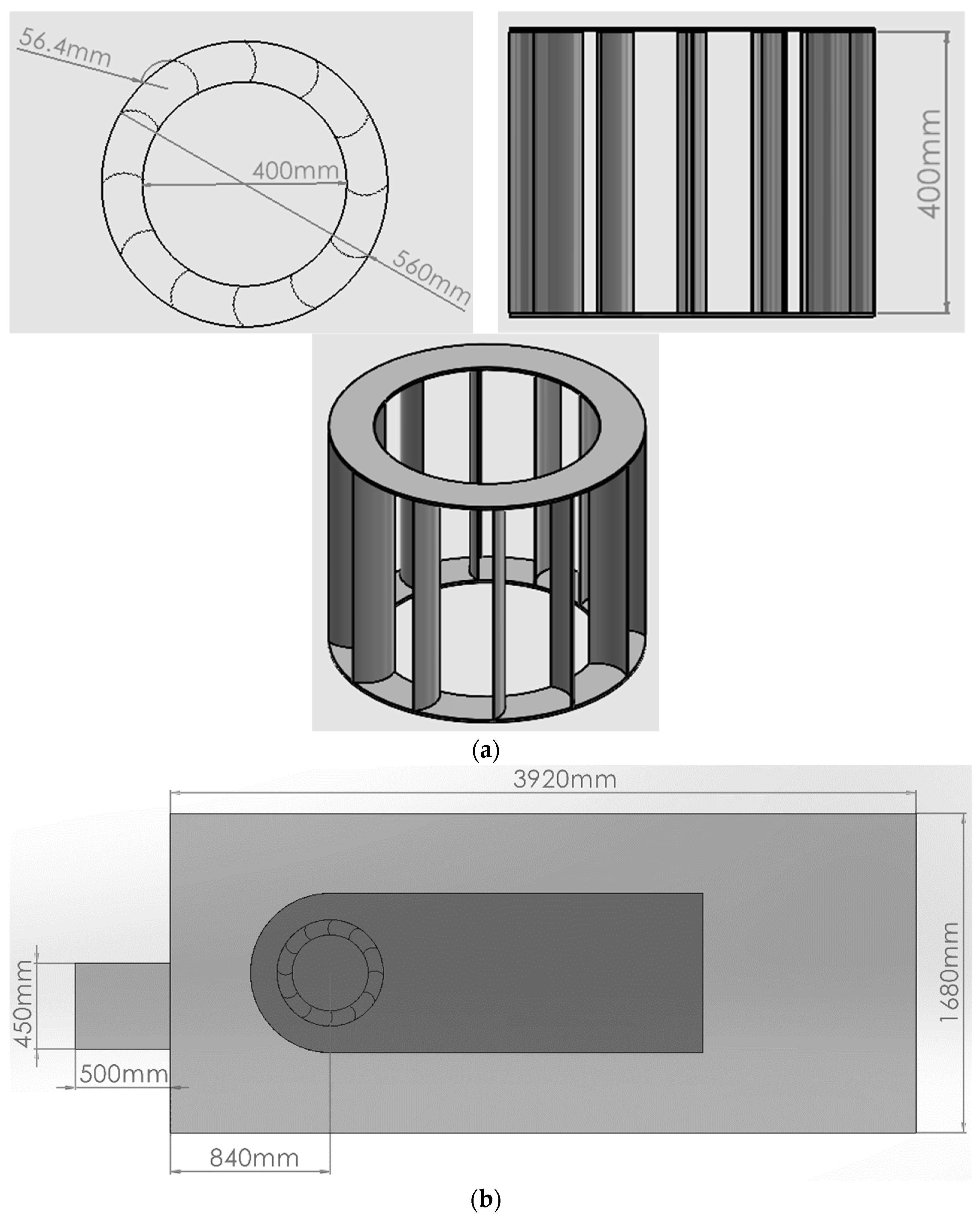
2.1. Geometry of the Multibladed Savonius Wind Turbine
2.2. Meshing of the Flow Domain
2.3. Boundary Conditions and Turbulence Modeling
2.4. Modeling the Rotation of the Turbine
3. Results and Discussion
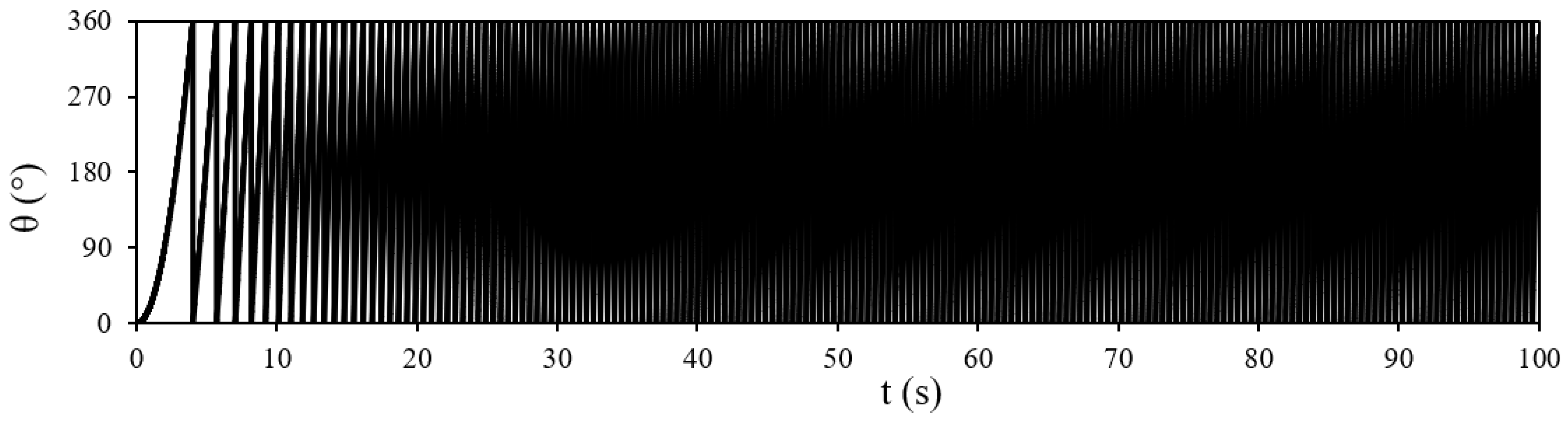
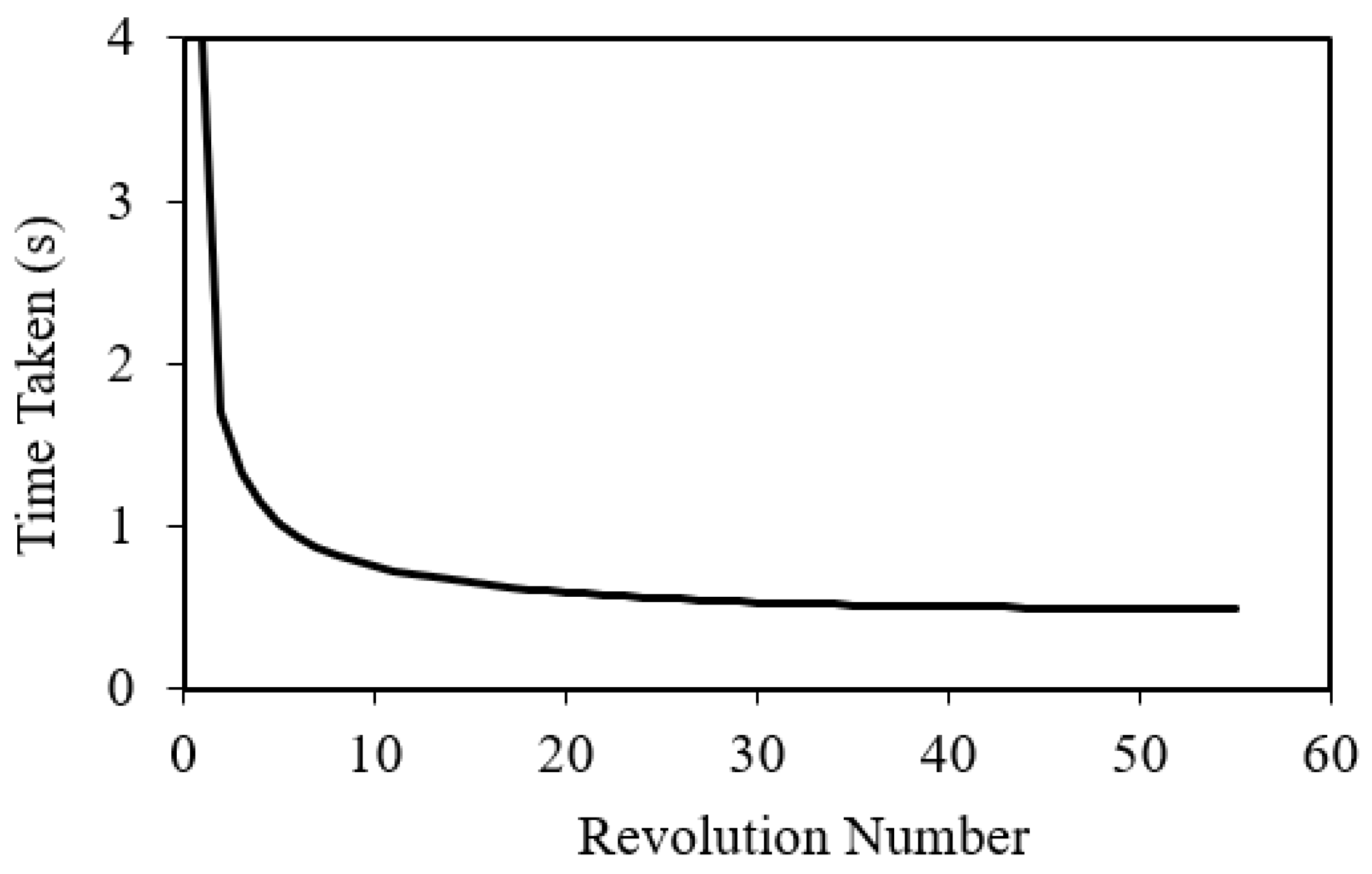
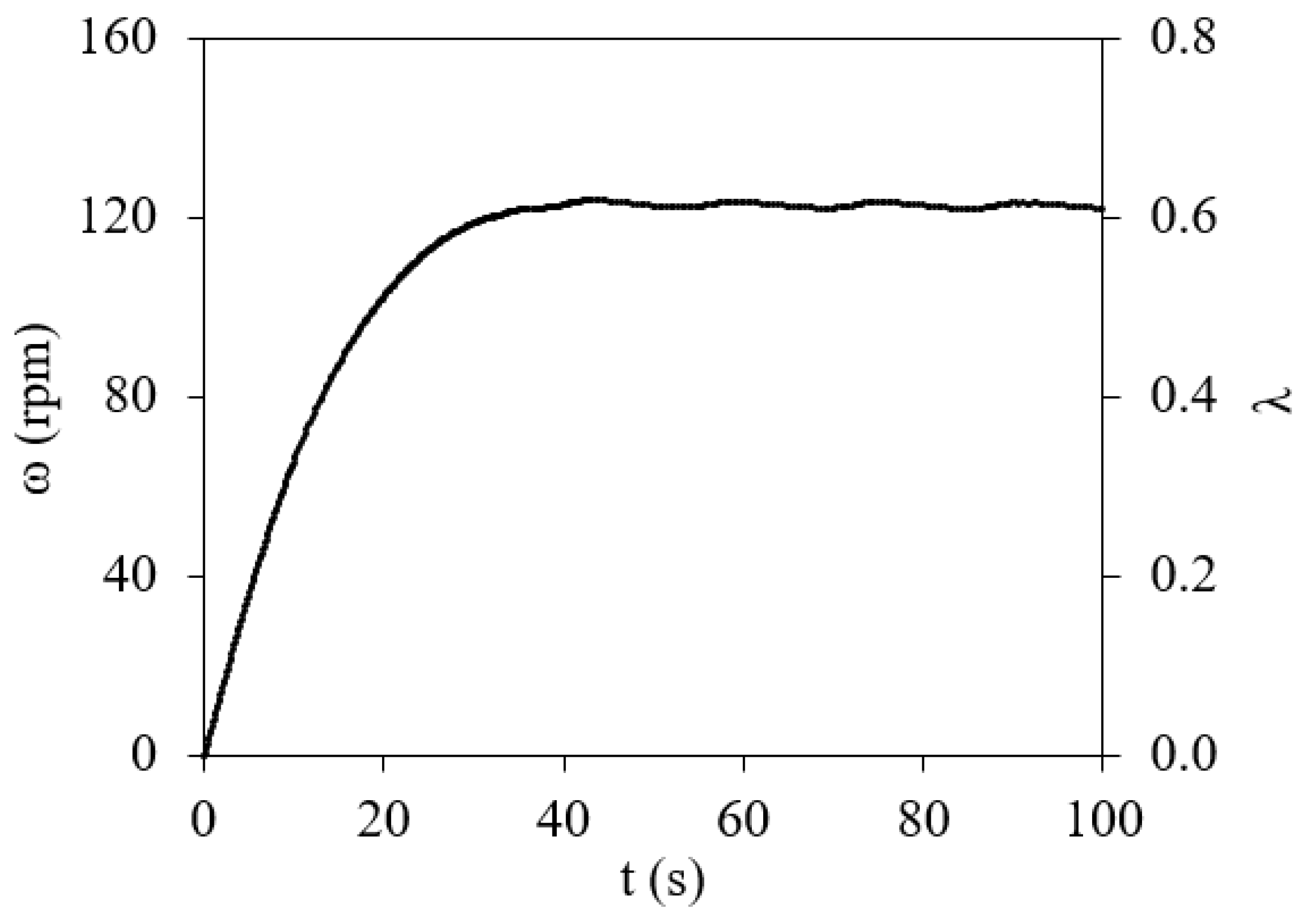
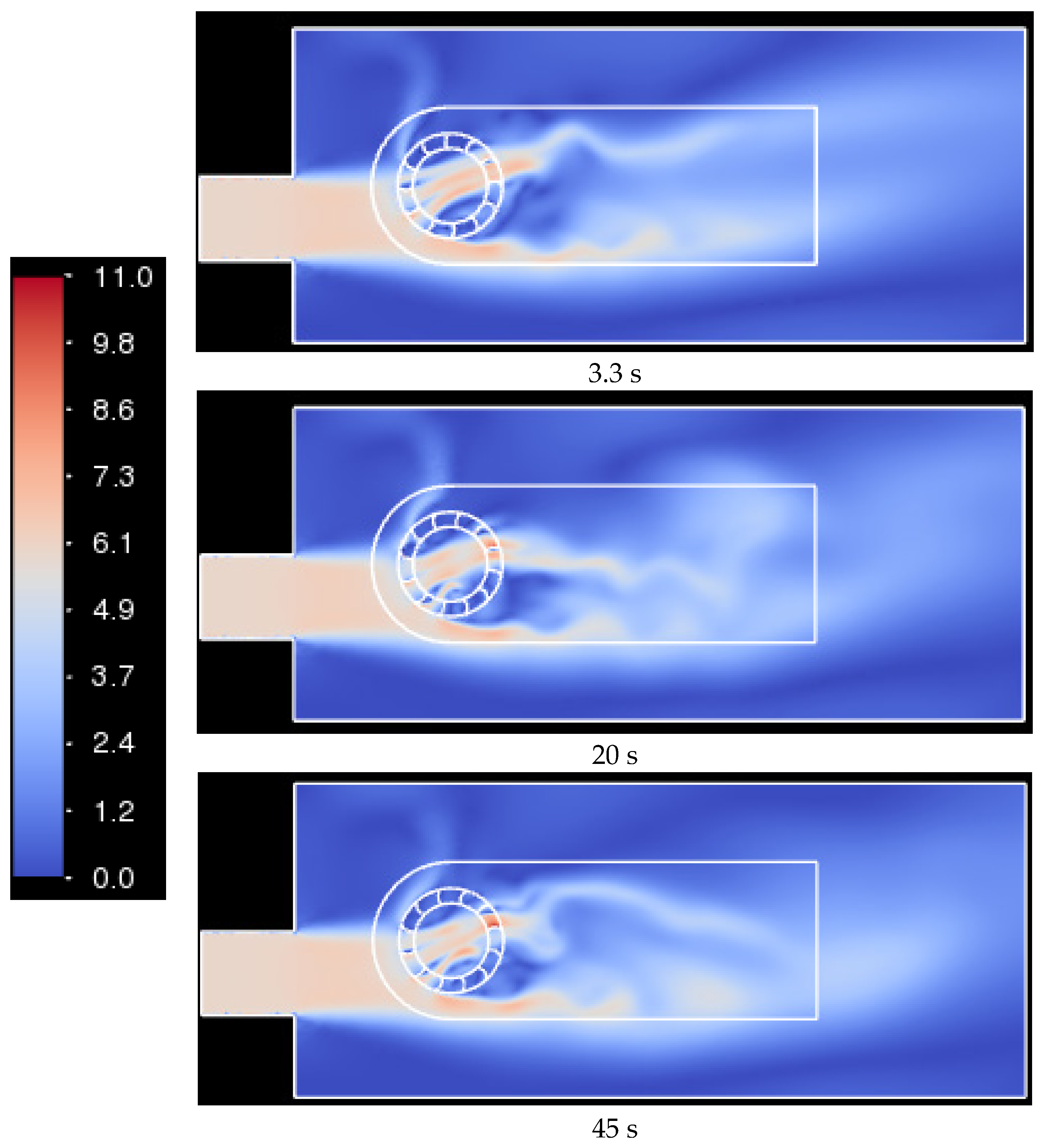
3.1. Startup Dynamics of Savonius Rotor with No Fricitional Losses (100% Inertia Case)
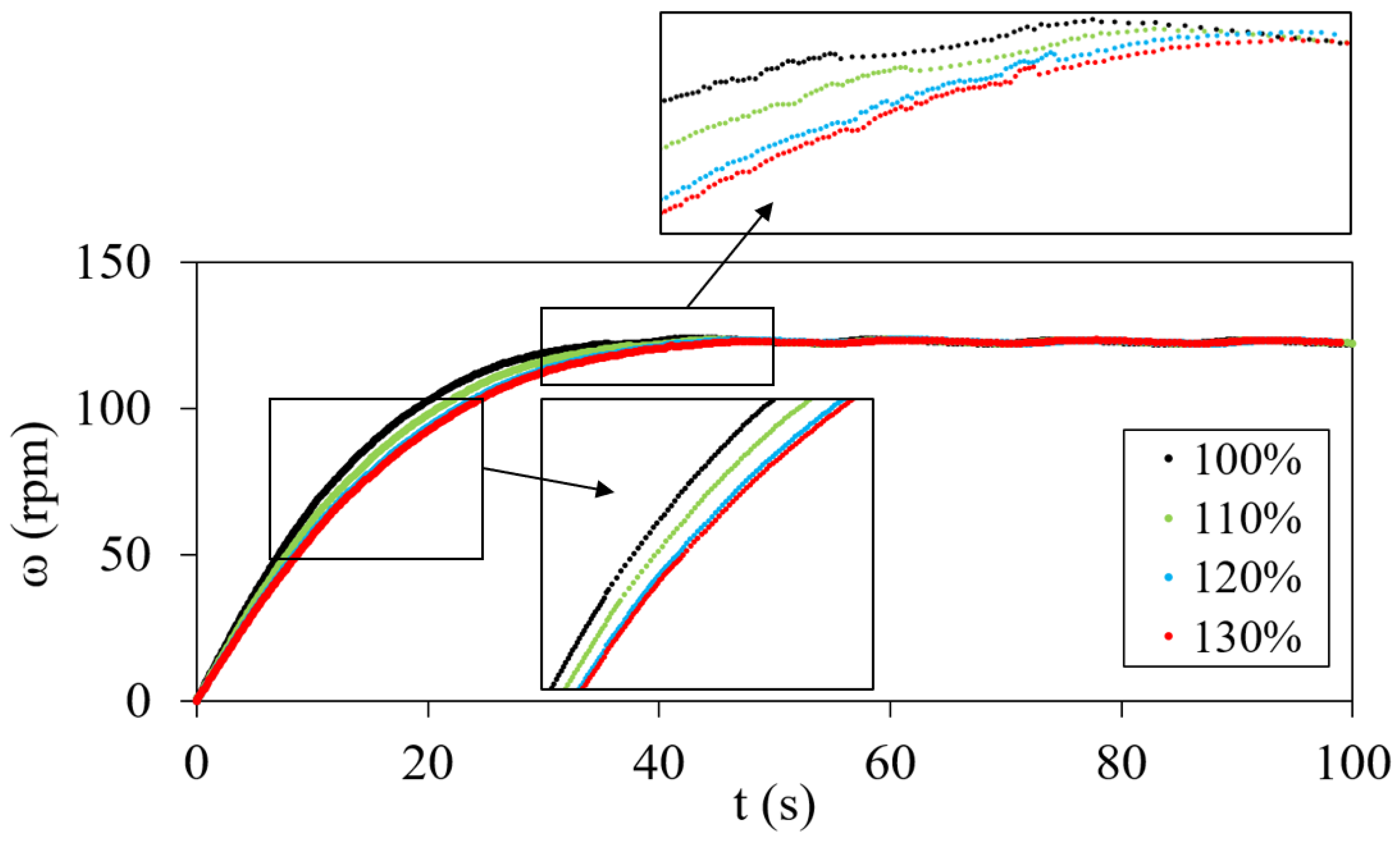
3.2. Effects of Inertia on the Startup Dynamics of a Savonius VAWT
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gerrie, C.; Islam, S.Z.; Gerrie, S.; Turner, N.; Asim, T. 3D CFD modelling of performance of a vertical axis turbine. Energies 2023, 16, 1144. [Google Scholar] [CrossRef]
- Darrieus, G.J.M. Turbine Having Its Rotating Shaft Transverse to the Flow of the Current. U.S. Patent 1,835,018, 8 December 1931. [Google Scholar]
- Savonius, S.J. The S-rotor and its applications. Mech. Eng. Am. Soc. Mech. Eng. 1931, 53, 333. [Google Scholar]
- Asr, M.T.; Nezhad, E.Z.; Mustapha, F.; Wiriadidjaja, S. Study on start-up characteristics of H-Darrieus vertical axis wind turbines comprising NACA 4-digit series blade airfoils. Energy 2016, 112, 528–537. [Google Scholar] [CrossRef]
- Hill, N.; Dominy, R.; Ingram, G.; Dominy, J. Darrieus turbines: The physics of self-starting. Proc. Inst. Mech. Eng. Part A J. Power Energy 2008, 223, 21–29. [Google Scholar] [CrossRef]
- Celik, Y.; Ma, L.; Ingham, D.; Pourkashanian, M. Aerodynamic investigation of the start-up process of H-type vertical axis wind turbines using CFD. J. Wind. Eng. Ind. Aerodyn. 2020, 204, 104252. [Google Scholar] [CrossRef]
- Kirke, B.; Lazauskas, L. Variable Pitch Darrieus Water Turbines. J. Fluid Sci. Technol. 2008, 3, 430–438. [Google Scholar]
- Mitchell, S.; Ogbonna, I.; Volkov, K. Improvement of Self-Starting Capabilities of Vertical Axis Wind Turbines with New Design of Turbine Blades. Sustainability 2021, 13, 3854. [Google Scholar] [CrossRef]
- Zhu, J.; Huang, H.; Shen, H. Self-starting aerodynamics analysis of vertical axis wind turbine. Adv. Mech. Eng. 2015, 7, 1687814015620968. [Google Scholar]
- Dominy, R.; Lunt, P.; Bickerdyke, A.; Dominy, J. Self-starting capability of a Darrieus turbine. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 111–120. [Google Scholar]
- Zhu, J.; Tian, C. Effect of Rotation Friction Ratio on the Power Extraction Performance of a Passive Rotation VAWT. Int. J. Rotating Mach. 2019, 2019, 6580345. [Google Scholar]
- Chegini, S.; Asadbeigi, M.; Ghafoorian, F.; Mehrpooya, M. An investigation into the self-starting of darrieus-savonius hybrid wind turbine and performance enhancement through innovative deflectors: A CFD approach. Ocean Eng. 2023, 287, 115910. [Google Scholar]
- Lough, J.; Asim, T.; Coull, S.; Marshall, A.; Islam, S.Z.; Amber, I. Start-up dynamics of vertical axis wind turbines: A Review. J. Phys. Conf. Ser. 2023, 2626, 012006. [Google Scholar] [CrossRef]
- Mu, Z.; Tong, G.; Xiao, Z.; Deng, Q.; Feng, F.; Li, Y.; Arne, G.A. Study on aerodynamic characteristics of a Savonius wind turbine with a modified blade. Energies 2022, 15, 6661. [Google Scholar] [CrossRef]
- Kang, C.; Zhao, H.; Li, B.; Gong, W.; Zhu, Y. Improvement of startup performance of the drag-type hydrokinetic rotor through two-stage configuration. Ocean Eng. 2021, 238, 109677. [Google Scholar] [CrossRef]
- Tigabu, M.T.; Khalid, M.S.U.; Wood, D.; Admasu, B.T. Some effects of turbine inertia on the starting performance of vertical-axis hydrokinetic turbine. Ocean Eng. 2022, 252, 111143. [Google Scholar]
- Zhao, H.; Kang, C.; Ding, K.; Zhang, Y.; Li, B. Transient startup characteristics of a drag-type hydrokinetic turbine rotor. Energy Convers. Manag. 2020, 223, 113287. [Google Scholar] [CrossRef]
- Mosbahi, M.; Ayadi, A.; Chouaibi, Y.; Driss, Z.; Tucciarelli, T. Performance study of a Helical Savonius hydrokinetic turbine with a new deflector system design. Energy Convers. Manag. 2019, 194, 55–74. [Google Scholar]
- Ushiyama, I.; Nagai, H.; Shinoda, J. Experimentally Determining the Optimum Design Configuration for Savonius Rotors. JSME Int. J. Ser. B-Fluids Therm. Eng. 1986, 29, 4130–4138. [Google Scholar]
- Asim, T.; Singh, D.; Siddiqui, M.S.; McGlinchey, D. Effect of Stator Blades on the Startup Dynamics of a Vertical Axis Wind Turbine. Energies 2022, 15, 8135. [Google Scholar] [CrossRef]
- Asim, T.; Osame, P. Startup Dynamics of Drag-Based Multibladed Vertical Axis Wind Turbine. Eng. Proc. 2024, 71, 5. [Google Scholar] [CrossRef]
- Asim, T.; Mishra, R.; Kaysthagir, S.N.; Aboufares, G. Performance comparison of a vertical axis wind turbine using commercial and open source computational fluid dynamics based codes. In Proceedings of the 5th International Conference on Jets, Wakes and Separated Flows; Springer Proceedings in Physics; Springer: Aachen, Germany, 2016; Volume 185, pp. 589–594. [Google Scholar]
- Asim, T.; Islam, S.Z. Effects of damaged rotor on wake dynamics of vertical axis wind turbines. Energies 2021, 14, 7060. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson: London, UK, 2007. [Google Scholar]
- ANSYS, Inc. ANSYS Fluent User’s Guide; Release 2021 R2; ANSYS, Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
- Sun, X.; Zhu, J.; Li, Z.; Sun, G. Rotation improvement of vertical axis wind turbine by offsetting pitching angles and changing blade numbers. Energy 2021, 215, 119177. [Google Scholar] [CrossRef]
- Zhu, J.; Jiang, L.; Zhao, H. Effect of wind fluctuating on self-starting aerodynamics characteristics of VAWT. J. Cent. South Univ. 2016, 23, 2075–2082. [Google Scholar]
- Li, L.; Xu, P.; Li, Q.; Yin, Z.; Zheng, R.; Wu, J.; Bao, J.; Bai, W.; Qi, H.; Tan, D. Multi-field coupling particle flow dynamic behaviors of the microreactor and ultrasonic control method. Powder Technol. 2025, 454, 120731. [Google Scholar]
- Tan, Y.; Ni, Y.; Xu, W.; Xie, Y.; Li, L.; Tan, D. Key technologies and development trends of the soft abrasive flow finishing method. J. Zhejiang Univ. Sci. A 2023, 24, 1043–1064. [Google Scholar]



| Boundary | Type | Value |
|---|---|---|
| Inlet | Velocity | 6 m/s |
| Outlet | Pressure | 0 Pa |
| Sides of the outer domain | Symmetry | - |
| Blades | Walls | No-slip |
| Revolution | Cumulative Time (s) | Time Taken (s) |
|---|---|---|
| 1st | 4.0197 | 4.0197 |
| 2nd | 5.7168 | 1.6971 |
| 3rd | 7.0473 | 1.3305 |
| 4th | 8.1860 | 1.1387 |
| 5th | 9.2043 | 1.0183 |
| 30th | 25.4273 | |
| 40th | 30.5805 |
| Revolution | Cumulative Time (s) | Time Taken (s) |
|---|---|---|
| 47th | 34.0768 | |
| 48th | 34.5711 | 0.4943 |
| 49th | 35.0660 | 0.4949 |
| 50th | 35.5588 | 0.4928 |
| 51st | 36.0514 | 0.4926 |
| 52nd | 36.5430 | 0.4916 |
| Turbine Inertia | No. of Revs to Peak ω of 122 rpm (s) | Time Taken to Peak ω of 122 rpm (s) |
|---|---|---|
| 100% | 50 | 35.5588 |
| 110% | 54 | 40.3150 |
| 120% | 57 | 41.4951 |
| 130% | 61 | 43.8009 |
| Inertia | Time Taken for 1st Revolution (s) | Time Taken for 2nd Revolution (s) | Time Taken for 3rd Revolution (s) |
|---|---|---|---|
| 100% | 4.0197 | 1.6971 | 1.3305 |
| 110% | 4.2065 | 1.7711 | 1.3886 |
| 120% | 4.3788 | 1.8429 | 1.4436 |
| 130% | 4.4256 | 1.8611 | 1.4586 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asim, T.; Amber, I.; Singh, D.; Siddiqui, M.S. Numerical Investigations on the Effects of Inertia on the Startup Dynamics of a Multibladed Savonius Wind Turbine. Energies 2025, 18, 1638. https://doi.org/10.3390/en18071638
Asim T, Amber I, Singh D, Siddiqui MS. Numerical Investigations on the Effects of Inertia on the Startup Dynamics of a Multibladed Savonius Wind Turbine. Energies. 2025; 18(7):1638. https://doi.org/10.3390/en18071638
Chicago/Turabian StyleAsim, Taimoor, Ityona Amber, Dharminder Singh, and Muhammad Salman Siddiqui. 2025. "Numerical Investigations on the Effects of Inertia on the Startup Dynamics of a Multibladed Savonius Wind Turbine" Energies 18, no. 7: 1638. https://doi.org/10.3390/en18071638
APA StyleAsim, T., Amber, I., Singh, D., & Siddiqui, M. S. (2025). Numerical Investigations on the Effects of Inertia on the Startup Dynamics of a Multibladed Savonius Wind Turbine. Energies, 18(7), 1638. https://doi.org/10.3390/en18071638








