Two-Level Optimal Scheduling of Electric–Aluminum–Carbon Energy System Considering Operational Safety of Electrolytic Aluminum Plants
Abstract
1. Introduction
- (1)
- This paper for the first time evaluates the safety operational boundaries of electrolytic aluminum loads by performing thermal dynamic simulations of aluminum electrolyzers. Based on that, a safety-constrained electrolytic aluminum plant model is presented. The model is formulated as MILP and can be easily adopted in energy system optimization problems.
- (2)
- This paper proposes a two-level economic dispatch framework for the electrolytic aluminum energy system. The framework transmits information between upper and lower levels and achieves mutual benefits for multiple stakeholders.
- (3)
- Carbon mechanisms are further considered within the optimal scheduling of the electrolytic aluminum load. The proposed framework introduces green certificate and tiered carbon trading mechanisms, while coordinating the optimization of electricity, aluminum, and carbon is achieved.
- (4)
- Case studies show that the proposed framework can significantly reduce the system emission by 21.9%, improve the overall economic efficiency by 16.5%, and increase the renewable integration rate by 4.5%, with an additional 8.6% of carbon reduction that be achieved by adopting EU carbon price policies.
2. Two-Level Optimization Framework
3. Mathematical Model
3.1. Upper-Level Optimization Model
3.1.1. Renewable Generation Scenario Reduction
3.1.2. Green Certificate Trading Mechanism
3.1.3. Upper-Level Constraints
3.2. Lower-Level Optimization Model
3.2.1. Electrical Model of Aluminum Electrolyzers
3.2.2. Thermal Dynamics of Aluminum Electrolyzers
3.2.3. Exploring Operational Safety Boundaries
3.2.4. Electrolytic Aluminum Plant Model Reformulation
3.2.5. Additional Lower-Level Constraints
3.2.6. Tiered Carbon Trading Mechanism
4. Case Studies
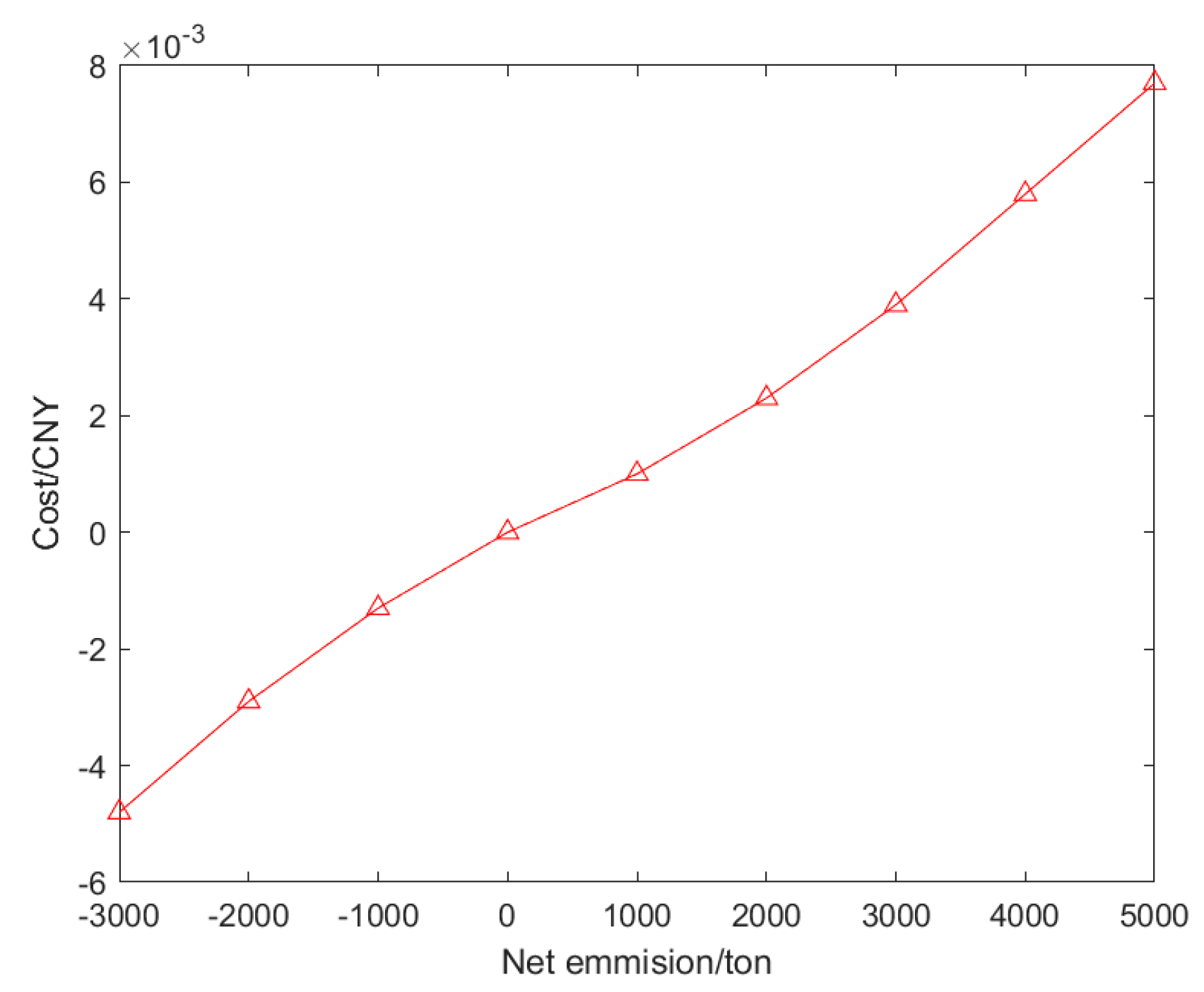
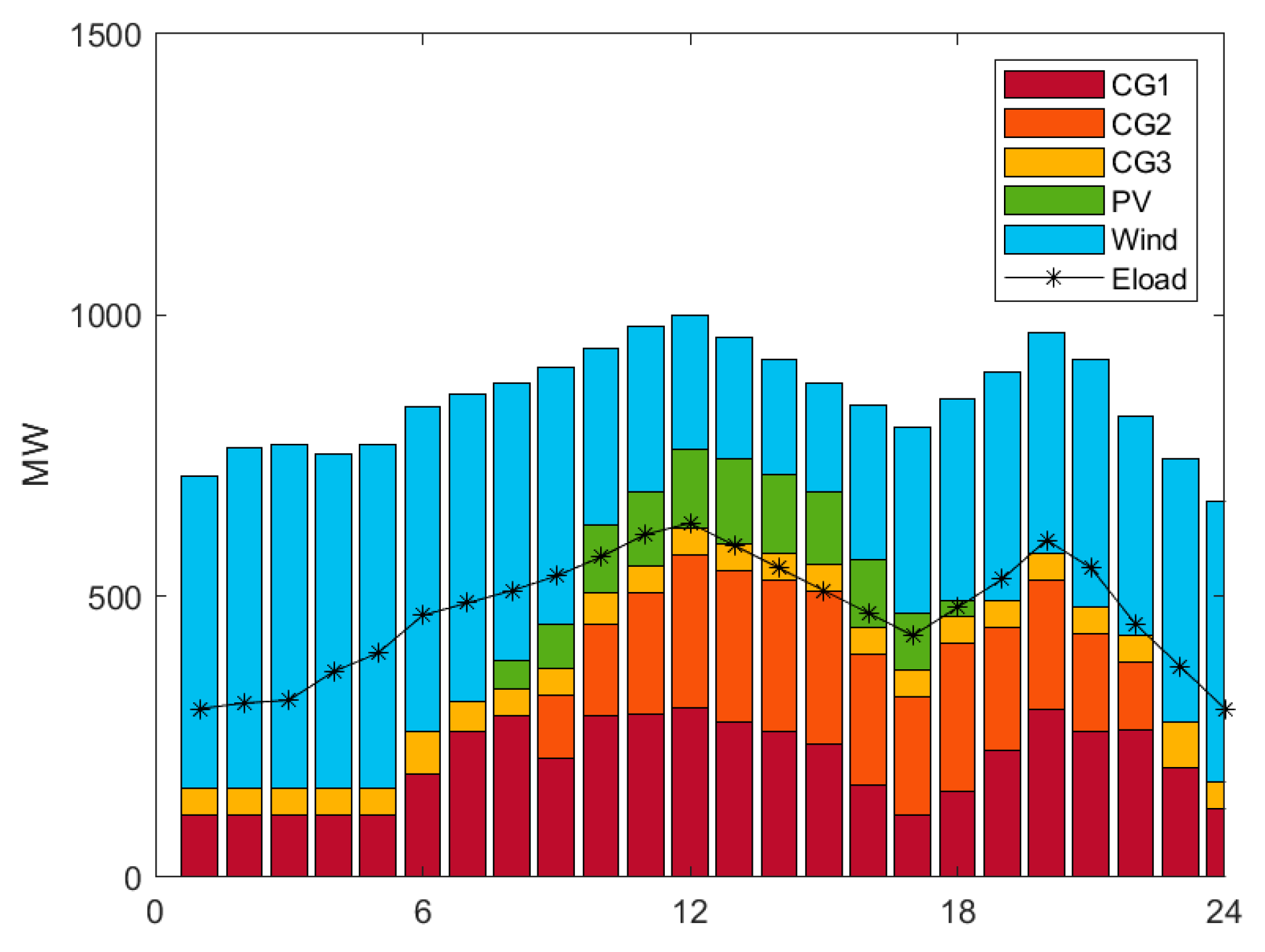
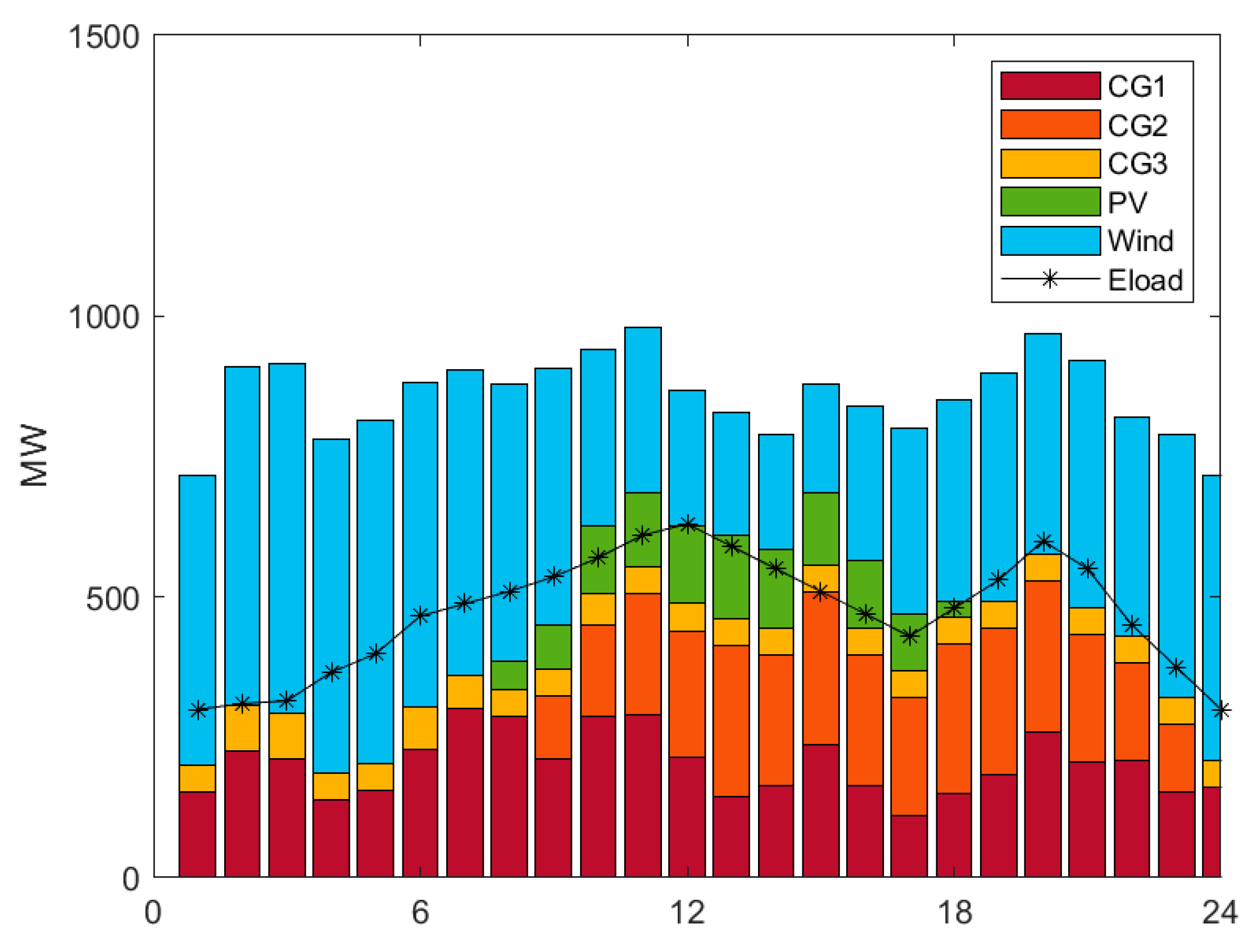
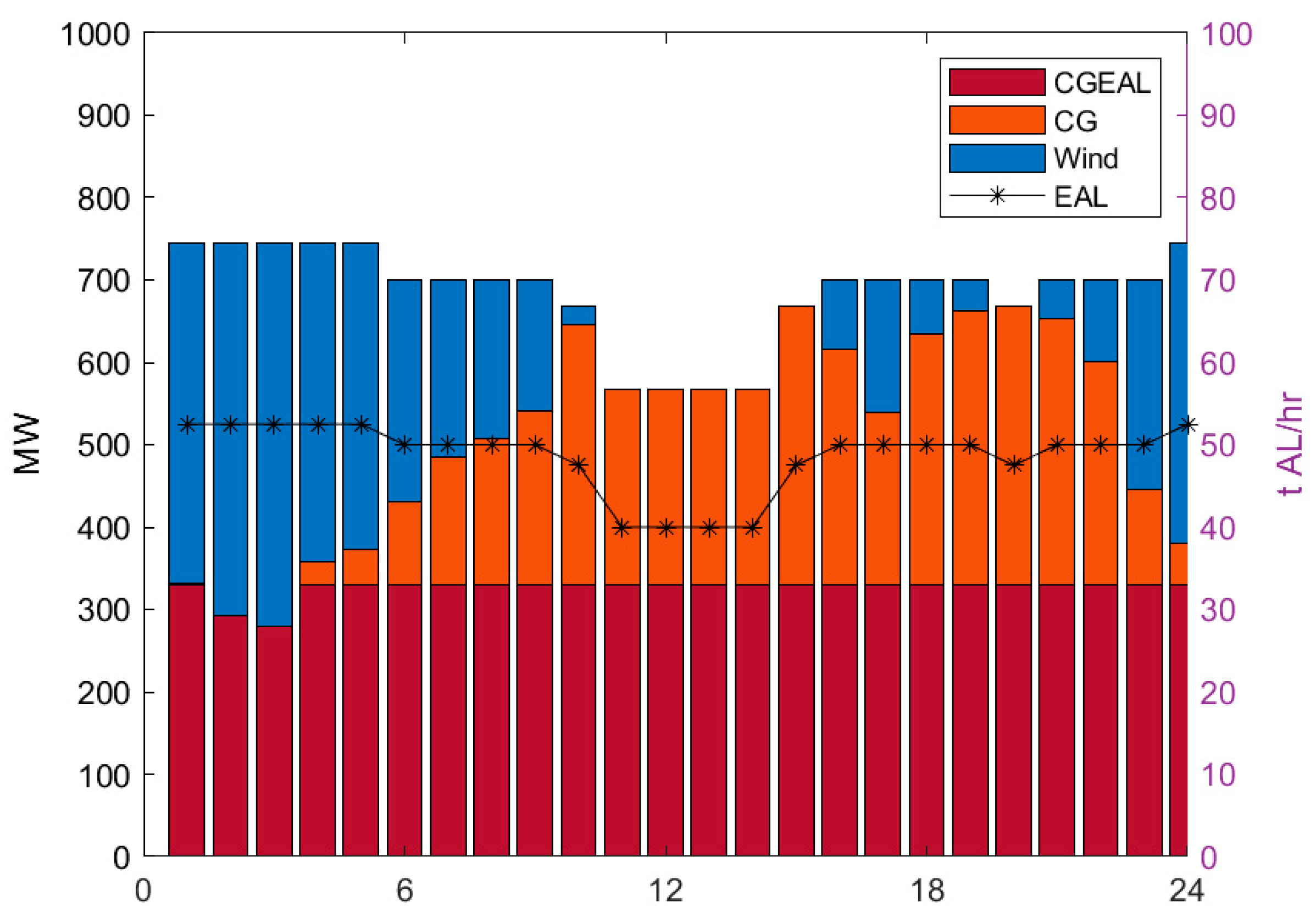
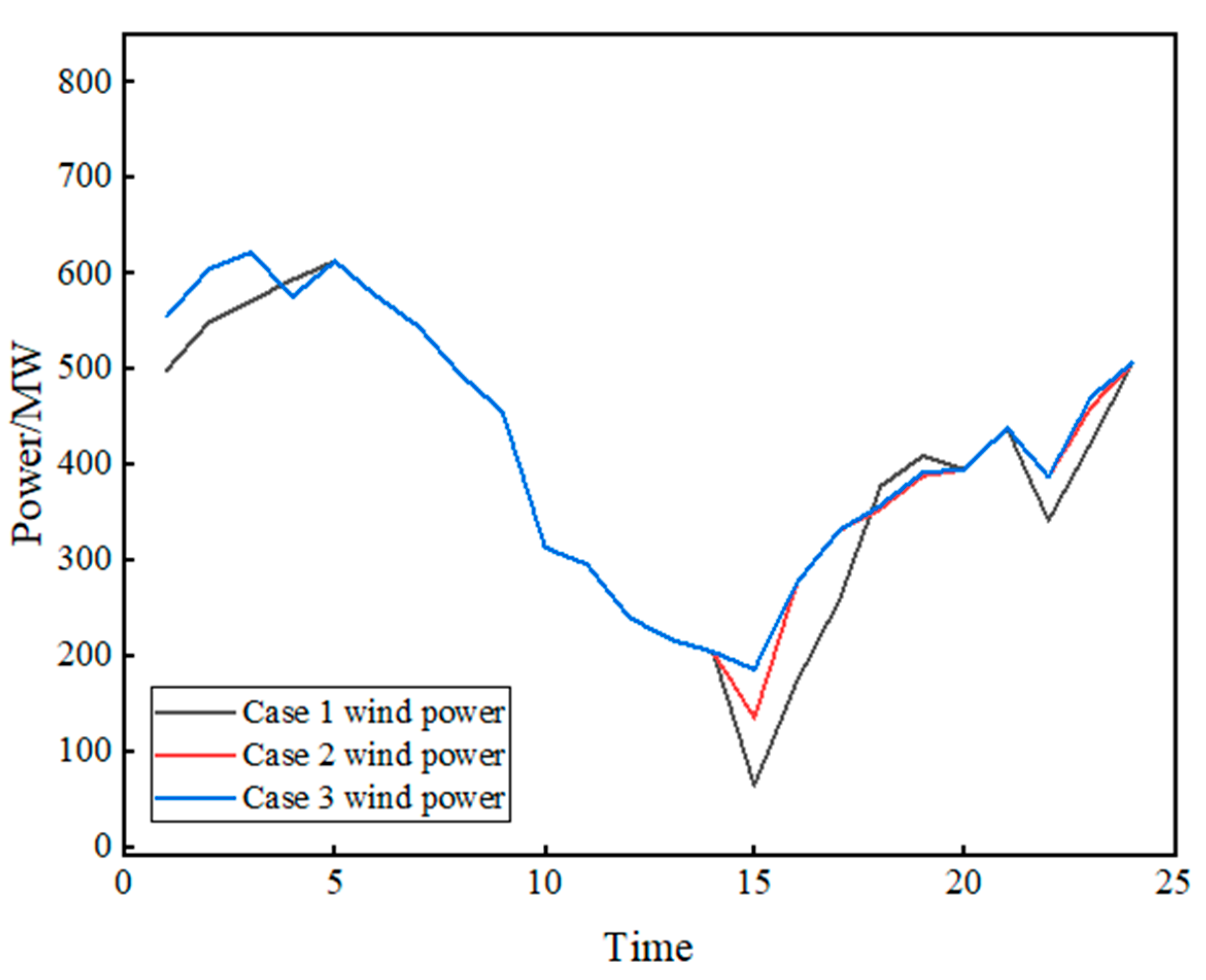
4.1. Dispatching Results
4.2. Cost–Benefit Analysis
4.3. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| CCET:AL | Carbon trading cost of the electrolytic aluminum plant |
| Ce,AL, Cq,AL, | Carbon emissions/quota of the electrolytic aluminum plant |
| CGCT | Green certificate trading cost |
| E″ | Carbon emission rights of the electrolytic aluminum plant |
| EG,buy, Epv, Ew | Thermal plant/PV/wind generation purchased by electrolytic aluminum plant |
| Hs,t | Consecutive period of the operational state of the electrolytic aluminum plant |
| PAL | Input power of the electrolytic aluminum plant |
| Pg,max, Pg,max | Upper/lower generation limits of the thermal power generation |
| Pg,t | Power generation of the thermal power plants |
| Pgreen, Pq | Green electricity integration amount/quota |
| Pload,t | Upper-level electricity load |
| Ppv,max, Pw,max | PV/wind farm generation forecast |
| Ppv,t, Pw,t | PV/wind farm power integration |
| RDg, RUg | Ramp-down/ramp-up rates of the thermal generation plant |
| SUg, SUg | Ramp up, ramp down, start up, and shut down power |
| ug,t, yg,t, zg,t | Operation, turn-on action, and shut-down action of generators |
| us,t, ys,t, zs,t | Operation, switch-in, and switch-out action of aluminum production state s |
| UTg, DTg | Minimum-on and -off period of generators |
| UTs, DTs | Maximum-on and minimum-off periods of the electrolytic aluminum plant |
| Yas,t | Aluminum production rate |
| γAL,γq,AL | Carbon emission coefficient/quota of the electrolytic aluminum plant |
| ηdc0 | Rated electrolysis efficiency of the electrolytic aluminum load |
| λ, β, c | Tiered carbon trading base price/price growth rate/emission range |
| λbuy, λsale | Green certificate purchasing/selling prices |
| λG,λG,buy | Prices of self-owned/purchased thermal power |
| λpv,λw | Prices of PV/wind power generation |
| ρAl | Selling price of the produced aluminum |
| ρpv, ρw | Upper-level operating cost coefficient for the PV/wind power generation |
| ρr,s | Non-electricity production cost of aluminum |
| φq | Upper-level renewable integration quota |
References
- National Development and Reform Commission of China. Guiding Opinions on Vigorously Implementing the Renewable Energy Substitution Action; National Development and Reform Commission of China: Beijing, China, 2024.
- Guiding Opinions on Energy Work in 2024. 2024. Available online: https://www.nea.gov.cn (accessed on 28 February 2025).
- Sharma, R.; Sinha, A.; Kautish, P.; Paul, S.; Dey, T.; Saha, P.; Dey, S.; Sen, R. Review on the development scenario of renewable energy in different country. In Proceedings of the 2021 Innovations in Energy Management and Renewable Resources, Kolkata, India, 30 March 2021. [Google Scholar]
- Zhang, J.; Li, L.; Yan, T.; Yu, J.; He, C.; Liao, S. A collaborative control method for high-proportion renewable energy and flexible loads. In Proceedings of the 2024 4th International Conference on Energy, Power and Electrical Engineering (EPEE), Wuhan, China, 17 February 2025. [Google Scholar]
- Yang, Z.; Ren, Z.; Li, H.; Sun, Z.; Feng, J.; Xia, W. A multi-stage stochastic dispatching method for electricity-hydrogen integrated energy systems driven by model and data. Appl. Energy 2024, 371, 123668. [Google Scholar] [CrossRef]
- Yang, N.; Xu, G.; Fei, Z.; Li, Z.; Du, L.; Guerrero, J.M.; Huang, Y.; Yan, J.; Xing, C.; Li, Z. Two-Stage Coordinated Robust Planning of Multi-Energy Ship Microgrids Considering Thermal Inertia and Ship Navigation. IEEE Trans. Smart Grid 2025, 16, 1100–1111. [Google Scholar] [CrossRef]
- Liu, J.; Wang, K.; Su, Z.; Feng, Y.; Wang, C.; Ai, X. Source-load Coordinated Optimal Scheduling in Stochastic Unit Commitment Considered Electrolytic Aluminum Load and Wind Power Uncertainty. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 11 August 2022. [Google Scholar]
- Li, L.; Chen, Y.; Zhang, J.; Pi, S.; He, C.; Liao, S. High-capacity Multi-level Emergency Load Shedding Technology for Electrolytic Aluminum Load. In Proceedings of the 2023 8th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 22–25 September 2023. [Google Scholar]
- Li, L.; Chen, Y.; Sun, P.; He, C.; Pi, S.; Liao, S. Real-Time Regulation Boundary Solution Method for Electrolytic Aluminum Industrial Park. In Proceedings of the 2024 3rd International Conference on Power Systems and Electrical Technology (PSET), Tokyo, Japan, 30 December 2024. [Google Scholar]
- Adibi, T.; Sojoudi, A.; Saha, S.C. Modeling of thermal performance of a commercial alkaline electrolyzer supplied with various electrical currents. Int. J. Thermofluids 2022, 13, 100126. [Google Scholar] [CrossRef]
- Paulus, M.; Borggrefe, F. The potential of demand-side management in energy-intensive industries for electricity markets in Germany. Appl. Energy 2011, 88, 432–441. [Google Scholar]
- Zeng, K.; Wang, H.; Liu, J.; Dong, C.; Lan, X.; Wang, C.; Le, L.; Ai, X. A bi-level programming guiding electrolytic aluminum load for demand response. In Proceedings of the 2020 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Weihai, China, 13–15 July 2020. [Google Scholar]
- Zhou, B.; Li, J.; Liu, Q.; Li, G.; Gu, P.; Ning, L.; Wang, Z. Optimal operation of energy-intensive load considering electricity carbon market. Heliyon 2024, 10, e34796. [Google Scholar] [PubMed]
- Gong, F.; Ren, K.; Zhang, A.; Chen, S.; Feng, J.; Zhang, K.; Li, D. Review of electrolytic aluminum load participating in demand response to absorb new energy potential and methods. In Proceedings of the 2021 IEEE 2nd International Conference on Big Data, Artificial Intelligence and Internet of Things Engineering (ICBAIE), Nanchang, China, 26–28 March 2021. [Google Scholar]
- Ding, X.; Liao, S.; Xu, J.; Sun, Y. A Source-Load Coordinated Control Strategy in an Industrial Aluminum Production Mircrogrid for Smoothing Wind Power Fluctuations. In Proceedings of the 2023 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Chongqing, China, 7–9 July 2023. [Google Scholar]
- Li, L.F.; Chen, Y.; Zhu, X.; Yu, Q.; Jiang, X.; Liao, S. Electrolytic Aluminum Load Participating in Power Grid Frequency Modulation Method Based on Active Adjustable Capacity Coordination. In Proceedings of the 2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 26–29 March 2021. [Google Scholar]
- Chen, S.; Gong, F.; Sun, T.; Yuan, J.; Yang, S.; Liu, Z. Research on the method of electrolytic aluminum load participating in the frequency control of power grid. In Proceedings of the 2021 IEEE 2nd International Conference on Big Data, Artificial Intelligence and Internet of Things Engineering (ICBAIE), Nanchang, China, 26–28 March 2021. [Google Scholar]
- Liu, J.; Zeng, K.; Wang, C.; Le, L.; Zhang, M.; Ai, X. Unit commitment considering electrolytic aluminum load for ancillary service. In Proceedings of the 2019 4th International Conference on Intelligent Green Building and Smart Grid (IGBSG), Hubei, China, 6–9 September 2019. [Google Scholar]
- Wang, Y.; Fu, B.; Ding, K.; Sun, Y. Day-ahead Economic Dispatch of Power Systems Considering the Demand Response of Electrolytic Aluminum Loads. In Proceedings of the 2024 IEEE 2nd International Conference on Power Science and Technology (ICPST), Dali, China, 9–11 May 2024. [Google Scholar]
- Zheng, W.; Yu, P.; Xu, Z.; Fan, T.; Liu, H.; Yu, M.; Zhang, J.; Li, J. Day-ahead Intra-day Economic Dispatch Methodology Accounting for the Participation of Electrolytic Aluminum Loads and Energy Storage in Power System Peaking. In Proceedings of the 2024 IEEE 2nd International Conference on Power Science and Technology (ICPST), Dali, China, 9–11 May 2024. [Google Scholar]
- Li, X.; Deng, J.; Liu, J. Energy–carbon–green certificates management strategy for integrated energy system using carbon–green certificates double-direction interaction. Renew. Energy 2025, 238, 121937. [Google Scholar]
- Yang, Y.; Li, S.; Zhang, Z.; Zhang, N.; Wang, S.; Wu, X.; Yan, H. The low-carbon economic scheduling method for regional integrated energy systems considering the joint integration of electric vehicles and concentrated solar power plants for wind power consumption. Wind Eng. 2025, 309524, 241302464. [Google Scholar]
- Gao, C.; Lu, H.; Chen, M.; Chang, X.; Zheng, C. A low-carbon optimization of integrated energy system dispatch under multi-system coupling of electricity-heat-gas-hydrogen based on stepwise carbon trading. Int. J. Hydrogen Energy 2025, 97, 362–376. [Google Scholar]
- Sun, H.; Sun, X.; Kou, L.; Zhang, B.; Zhu, X. Optimal scheduling of park-level integrated energy system considering ladder-type carbon trading mechanism and flexible loa. Energy Rep. 2023, 9, 3417–3430. [Google Scholar]
- National Development and Reform Commission of China. Special Action Plan for Energy Conservation and Carbon Emission Reduction in the Electrolytic Aluminum Industry; National Development and Reform Commission of China: Beijing, China, 2024.
- EU Carbon Permits. Available online: https://tradingeconomics.com/commodity/carbon (accessed on 26 February 2025).

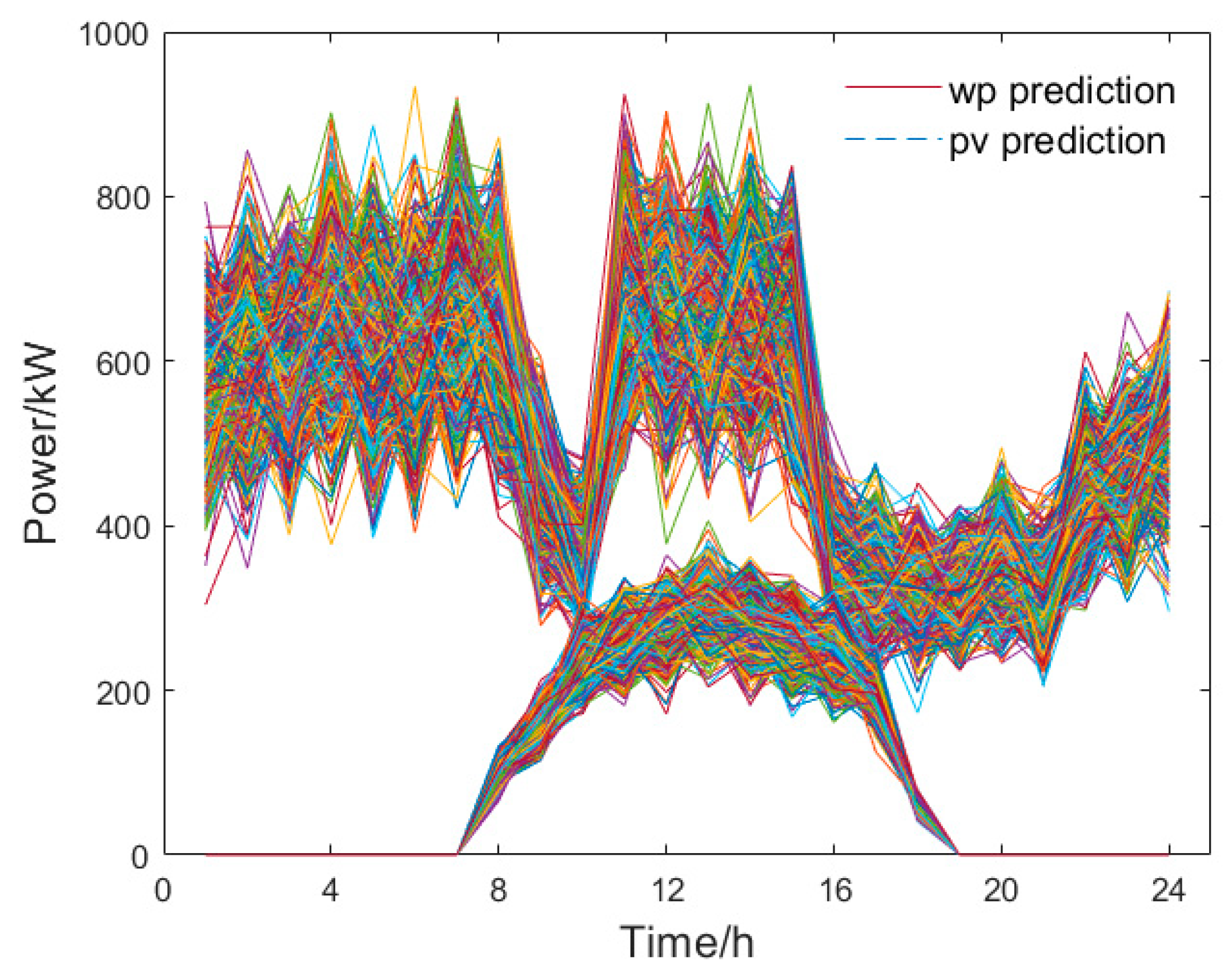

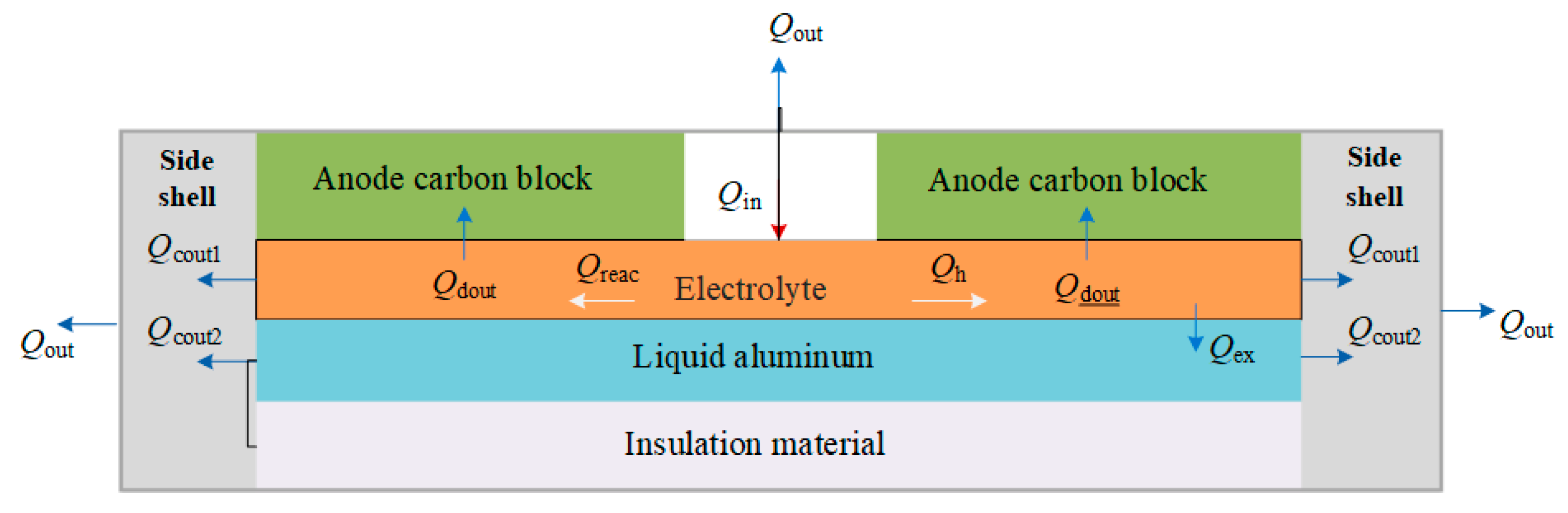
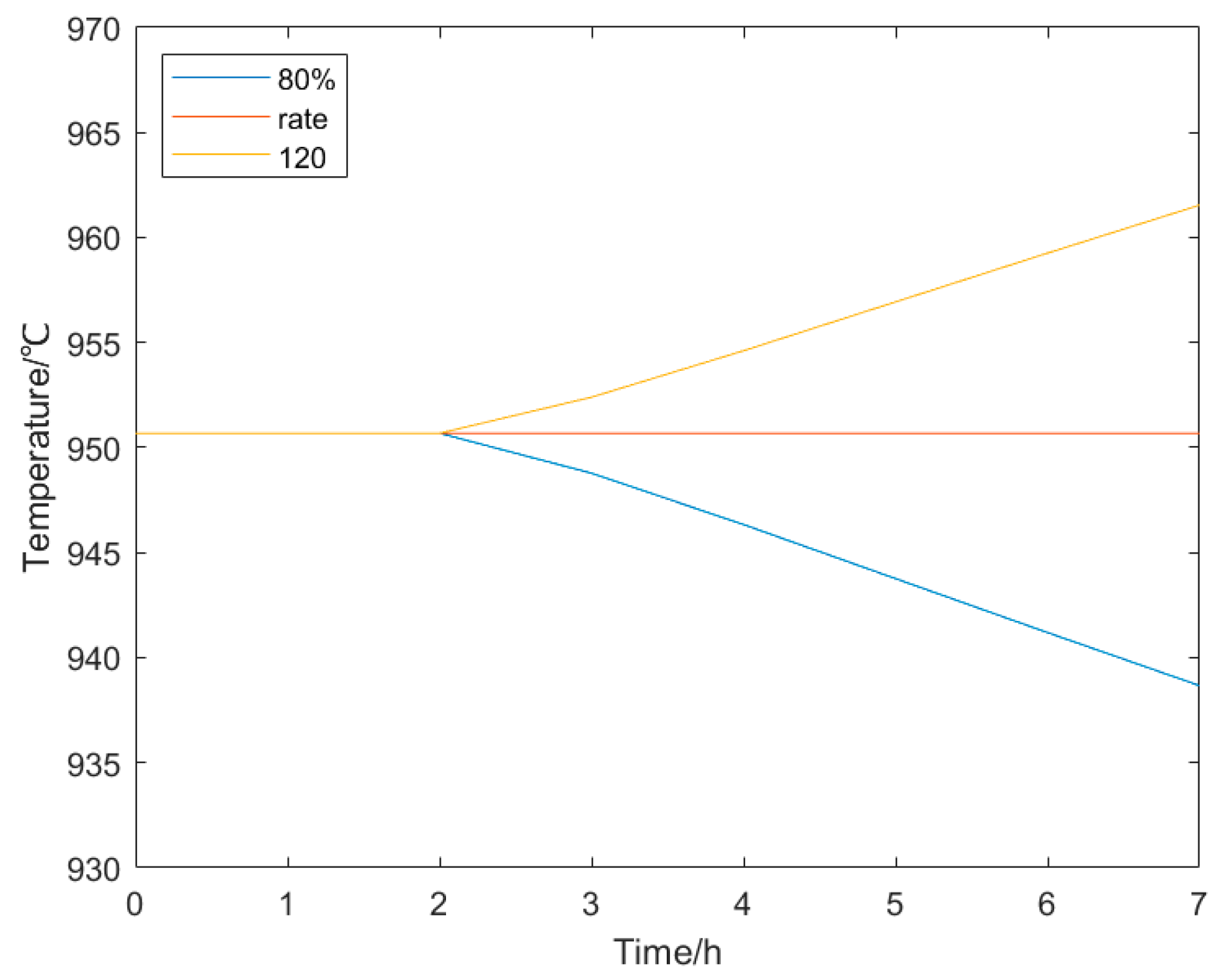


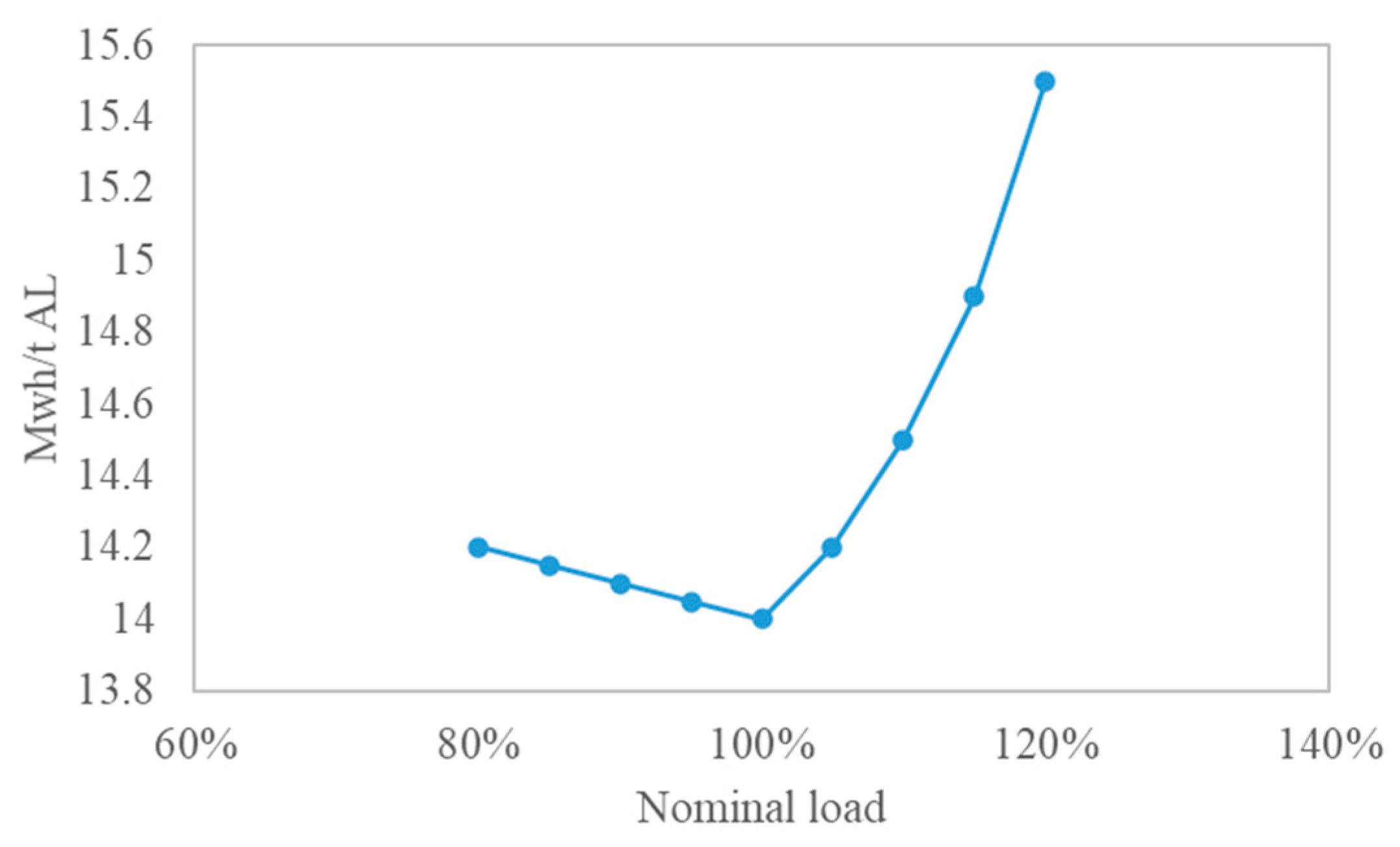



| Reference | Modeling Type | Operational Safety Modeling |
|---|---|---|
| [7] | Continuous model | Aggregate input power constraints |
| [13] | Continuous model | Aggregate input power constraints |
| [14] | Continuous model | No |
| [15] | Continuous model | No |
| [16] | Electric circuit (power dynamic) | No |
| [17] | Electric circuit (power dynamic) | No |
| [18] | Electric circuit (power dynamic) | No |
| [19] | Multi-stage model | State occurrence constraints |
| [20] | Multi-stage model | Regulation occurrence constraints |
| This work | Multi-stage model | Safety constraints verified by thermal dynamics |
| Current | State | Production |
|---|---|---|
| [σ3Idc0, σ4Idc0) | Overload production | [Yas,min, Yas,r1) |
| [σ2Idc0, σ3Idc0) | Rate production | [Yas,r1, Yas,r2) |
| [σ1Idc0, σ2Idc0) | Reduced production | [Yas,r2, Yas,max] |
| State | Maximum-on Period | Minimum-off Period |
|---|---|---|
| Overload production | UThigh | DThigh |
| Rate production | / | / |
| Reduced production | UTlow | DTlow |
| Component | Density/kg/m3 | Volume/m3 | Specific Heat Capacity /J/kg/°C |
|---|---|---|---|
| Electrolyte | 2100 | 4 | 1600 |
| Liquid aluminum | 2700 | 9 | 880 |
| Carbon blocks | 2600 | 9 | 900 |
| Component | Heat Transfer Coefficient/W/m2/°C | Heat Transfer Area/m2 |
|---|---|---|
| Electrolyte–side shell | 300 | 4 |
| Liquid aluminum–side shell | 200 | 4 |
| Electrolyte–carbon blocks | 5 | 3.6 |
| Carbon blocks–air | 5 | 60 |
| Generators | Pmax | Pmin | a | b | c | |
|---|---|---|---|---|---|---|
| Upper Level | CG1 | 370 | 111 | 2.54 × 10−2 | 131.5 | 5904 |
| CG2 | 270 | 81 | 2.09 × 10−2 | 123.1 | 4596 | |
| CG3 | 160 | 48 | 4.89 × 10−2 | 155.5 | 2824 | |
| CG4 | 100 | 30 | 6.20 × 10−2 | 162.3 | 2500 | |
| Lower Level | CGEAL | 330 | 99 | 2.24 × 10−2 | 128.5 | 5310 |
| State | Max-on Period | Min-off Period | Production Range |
|---|---|---|---|
| Overload production | 4 h | 5 h | 105–120% |
| Rate production | / | / | 95–105% |
| Reduced production | 4 h | 5 h | 80–95% |
| Case | Upper-Level Cost (×103 CNY) | Plant Revenue (×103 CNY) | Emission (tons/day) |
|---|---|---|---|
| Case 1 | 1860 | 3855 | 10,198 |
| Case 2 | 1884 | 4142 | 9495 |
| Case 3 | 1554 | 3559 | 7969 |
| Parameters (λ, β) | Production (ton AL) | Plant Revenue (×103 CNY) | Plant Emission (tons/day) |
|---|---|---|---|
| (80, 30%) | 1.173 | 3559 | 7969 |
| (80, 50%) | 1.168 | 3495 | 7906 |
| (200, 50%) | 1.124 | 2884 | 7418 |
| (500, 50%) | 1.095 | 1547 | 7089 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Li, S.; Zhang, N.; Yan, Z.; Liu, W.; Wang, S. Two-Level Optimal Scheduling of Electric–Aluminum–Carbon Energy System Considering Operational Safety of Electrolytic Aluminum Plants. Energies 2025, 18, 1645. https://doi.org/10.3390/en18071645
Yang Y, Li S, Zhang N, Yan Z, Liu W, Wang S. Two-Level Optimal Scheduling of Electric–Aluminum–Carbon Energy System Considering Operational Safety of Electrolytic Aluminum Plants. Energies. 2025; 18(7):1645. https://doi.org/10.3390/en18071645
Chicago/Turabian StyleYang, Yulong, Songyuan Li, Nan Zhang, Zhongwen Yan, Weiyang Liu, and Songnan Wang. 2025. "Two-Level Optimal Scheduling of Electric–Aluminum–Carbon Energy System Considering Operational Safety of Electrolytic Aluminum Plants" Energies 18, no. 7: 1645. https://doi.org/10.3390/en18071645
APA StyleYang, Y., Li, S., Zhang, N., Yan, Z., Liu, W., & Wang, S. (2025). Two-Level Optimal Scheduling of Electric–Aluminum–Carbon Energy System Considering Operational Safety of Electrolytic Aluminum Plants. Energies, 18(7), 1645. https://doi.org/10.3390/en18071645




